空间直角坐标系 空间两点间的距离公式(解析版)
空间直角坐标系、空间两点间的距离公式 课件

线段AB的中点坐标是_x_1_+2__x_2,__y_1_+_2_y_2_,__z1_+2__z_2_.
类型一 求空间中点的坐标 【例1】 建立适当的坐标系,写出底边长为2,高为3的正三 棱柱的各顶点的坐标.
|MN|=
32-12+(3-1)2+(1-2)2=
21 2.
解 以BC的中点为原点,BC所在的直线为y轴,以射线 OA所在的直线为x轴,建立空间直角坐标系,如图. 由题意知,AO= 23×2= 3,从而可知各 顶点的坐标分别为 A( 3,0,0),B(0,1,0), C(0,-1,0),A1( 3,0,3),B1(0,1,3),C1(0,-1,3).
类型二 求空间中对称点的坐标 【例2】 在空间直角坐标系中,点P(-2,1,4).
空间直角坐标系 空间两点间的距离公式
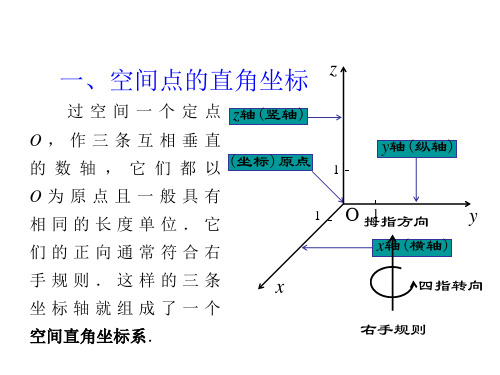
1.空间直角坐标系 (1)空间直角坐标系及相关概念 ①空间直角坐标系:从空间某一定点引三条两两垂直,且有相 同 单 位 长 度 的 数 轴 : __x_轴__、__y轴__、__z_轴__ , 这 样 就 建 立 了 一 个 __空__间__直__角__坐__标__系__O_-__x_y_z_. ②相关概念:__点__O_叫做坐标原点,x_轴__、__y_轴__、__z_轴_叫做坐标轴.通 过____每__两__个__坐__标__轴___的平面叫做坐标平面,分别称为_x_O__y_平 面、_y_O__z _平面、__zO__x_平面.
(1)求点P关于x轴的对称点的坐标; (2)求点P关于xOy平面的对称点的坐标; (3)求点P关于点M(2,-1,-4)的对称点的坐标.
解 (1)由于点P关于x轴对称后,它在x轴的分量不变, 在y轴、z轴的分量变为原来的相反数,所以对称点为 P1(-2,-1,-4). (2)由于点P关于xOy平面对称后,它在x轴、y轴的分量 不变,在z轴的分量变为原来的相反数,所以对称点为 P2(-2,1,-4). (3)设对称点为P3(x,y,z),则点M为线段PP3的中点, 由中点坐标公式,可得x=2×2-(-2)=6, y=2×(-1)-1=-3,z=2×(-4)-4=-12, 所以P3(6,-3,-12).
空间中两点的距离公式
M1
Q
y
O
因为 x | M1M2 | 2 = | M1Q | 2 + | M2Q | 2 = | M1P | 2 + | PQ | 2 + | M2Q | 2 所以 d | M1M2 |
( x2 x1 ) ( y2 y1 ) ( z 2 z1 )
2 2
2
例1 求证以M 1(4,3,1)、M 2(7,1,2)、M 3(5,2,
1、设 O(0,0,0),P(x0,y0,z0)
z P C y B
则
OP OA OB OC x y z
2 0 2 0 2 0 2 2 2
A
x
o
二、空间两点间的距离
作一个以M 1和M 2为对 角线顶点的长方体,使 其三个相邻的面分别平 行于三个坐标面.
设M 1(x 1,y 1,z 1)、M 2(x 2,y 2,z 2)为空间两点. z
z1
P
M1 Q
y
O x
设M 1(x 1,y 1,z 1)、M 2(x 2,y 2,z 2)为空间两点.
作一个以 M 1 和 M 2 为 对角线顶点的长方体,使 其三个相邻的面分别平行 于 三 个 坐 标 面 .
z
M2
与x 轴平行的边的边长为|x 2x 1|,
与y 轴平行的边的边长为|y 2y 1|, 与z 轴平行的边的边长为|z 2z 1|.
坐标面: 三条坐标轴中的任意两 条可以确定一个平面,这样 定出的三个平面统称为坐标 面.x轴及y轴所确定的坐标
z
面叫做 xOy面,另两个坐标
面是 yOz 面和zOx面.
O
y
x
坐标面:
三条坐标轴中的任意两
空间两点间距离公式

距离公式?
z
1、设
O(0,0,0),P(x0,y0,z0)
则
OP
o A
OA 2 OB 2 OC 2 x
P C y
B
x02 y02 z02
2、空间任意两点A(x1,y1,z1),P(x2,y2,z2)
作长方体使AP为 长方体的对角线
z
由已知得: C(x2,y1,z1),
P A
B(x2,y2 ,z1)
x 1, 所求点 (1,0,0), (1,0,0). 为
例4.平面上到坐标原点的距离为1的点的
轨迹是单位圆,其方程
为 x2 y2 1
.
在空间中,到坐标原点的距离为1
的点的轨迹是什么?试写出它的方程.
x2 y2 z2 1
轨迹是球面
练3:设A(3,3,1),B(1,-1,5),C(0,1,0),则AB
的中点M到C的距离为____1_3____
分析:介绍空间直角坐标系中的中点坐标 公式;
已知点A(x1,y1,z1),点B(x2,y2,z2) 则线段AB中点C的坐标是
X= 1 (X1+X2)
2 1
Z= 2 (z1+z2)
y=
1 2
(y1+y2)
M(2,1,3)
例5:如图:M—OAB是棱长为a的正四 面体,顶点M在底面OAB上的射影为H, 分别求出点B、H、M的坐标
(9,0,0)或(-1,0,0)
例2:在xoy平面内的直线x+y=1上确定 一点M,使M到N(6,5,1)的距离最小 略解:设M(x,1-x,0),利用距离公式构造 出一个二次函数后求最值
MN (x 6)2 (1 x 5)2 (1 0)2
空间坐标系两点间距离公式

空间坐标系两点间距离公式设点A的坐标为(x1,y1,z1),点B的坐标为(x2,y2,z2)。
利用勾股定理,我们可以得到两点之间的距离d:d=√((x2-x1)²+(y2-y1)²+(z2-z1)²)这个公式就是空间坐标系中两点之间距离的一般公式。
下面我们将对这个公式进行详细解释:首先,我们可以将(x2-x1)²简化为(x2-x1)*(x2-x1)。
同样,(y2-y1)²可以简化为(y2-y1)*(y2-y1),(z2-z1)²可以简化为(z2-z1)*(z2-z1)。
接下来,我们将这些简化后的表达式相加,得到:d=√((x2-x1)²+(y2-y1)²+(z2-z1)²)=√((x2-x1)*(x2-x1)+(y2-y1)*(y2-y1)+(z2-z1)*(z2-z1))我们可以继续简化这个表达式,将每个乘法展开:d=√(x2²-2*x1*x2+x1²+y2²-2*y1*y2+y1²+z2²-2*z1*z2+z1²)现在,我们可以对这个表达式进行合并和化简。
首先,我们可以将常数项合并:d=√(x2²+y2²+z2²+x1²+y1²+z1²-2*x1*x2-2*y1*y2-2*z1*z2)然后,我们注意到这个表达式中存在三个平方项,我们可以将它们重新组合:d=√((x2²+y2²+z2²)+(x1²+y1²+z1²)-2*x1*x2-2*y1*y2-2*z1*z2)接下来,我们可以使用公式(a + b)² = a² + 2ab + b²,将表达式中的求和项写成平方的形式:d=√(x2²+2*x1*x2+x1²+y2²+2*y1*y2+y1²+z2²+2*z1*z2+z1²-2*x1*x2-2*y1*y2-2*z1*z2)再次合并和化简,我们可以得到:d=√((x2+x1)²+(y2+y1)²+(z2+z1)²-2*(x1*x2+y1*y2+z1*z2))这个公式更简洁,而且计算起来更方便。
空间两点间距离公式

d x y02 z02 y d y x02 z02
d z x02 y02
两点间距离公式
平面:| P1P2 | (x1 x2 )2 ( y1 y2 )2
类比
猜想
空间:| P1P2 | (x1 x2 )2 ( y1 y2 )2 (z1 z2 )2
例4:已知 A( 3,3,3 2), B( 3,1, 2) ,在平面 Oyz上是否存在一点C,使ABC为等边三角 形,如果存在求C坐标,不存在说明理由。
解:假设存在一点C(0,y,z),满足条件:
AB AC BC
3
3 2 3 12 3 2
2
2
y
3
0 2
C 0,4, 2 或 0,0,3 2
所以存在一点C,满足条件.
课堂小结
一、空间两点间的距离公式:
d ( x2 x1 )2 ( y2 y1 )2 (z2 z1 )2
二、空间中点坐标公式:
x
y
ห้องสมุดไป่ตู้
z
x1 y1 z1
x2
2 y2
2 z2
2
AC 1 32 5 12 2 52 29
例1:已知三角形的三个顶点A(1,5,2), B(2,3,4),C(3,1,5),求: (2)BC边上中线AM的长。
AM ?
例2:求证以 M1(4,3,1), M2(7,1,2), M3(5,2,3), 三点为顶点的三角形是一个等腰三角形. 解: M1M2 2 (7 4)2 (1 3)2 (2 1)2 14,
4.3.2 空间两点间的距离公式
解析几何中两点间距离公式

解析几何中两点间距离公式欢迎来到解析几何的世界。
你是否曾经在求两点间距离时使用过勾股定理?如果这还是你的唯一方法,那么我建议你应该试试使用解析几何中的公式来求解两点间的距离。
在此,我将会向你介绍两点距离公式以及它的相关内容。
让我们开始吧!一、什么是两点间距离公式?两点间距离公式,是解析几何中用于计算两个点之间距离的公式。
它可以用于二维平面和三维空间中。
在二维平面中,两点间距离公式被表示为:d = √ ((x2 - x1)² + (y2 - y1)²)其中,d为两点之间的距离,(x1, y1)和(x2, y2)是平面上的两个点。
在三维空间中,两点间距离公式被表示为:d = √ ((x2 - x1)² + (y2 - y1)² + (z2 - z1)²)其中,d为两点之间的距离,(x1, y1, z1)和(x2, y2, z2)是空间中的两个点。
二、两点间距离公式的推导过程在计算两点间距离公式的推导过程中,我们使用了勾股定理(两边平方,然后开方),从而得到了该公式。
我们将在下面详细讲解推导过程。
二维平面:为了推导两点间距离公式,在平面上我们假设有两个点A和B。
如下图所示:我们可以通过画一个直角三角形来计算AB之间的距离。
我们可以看出,点A和点B之间的距离等于C点到直角三角形的对角线长度。
如下图所示:根据勾股定理,我们可以得出方程:C² = A² + B²其中,C为对角线的长度,A和B为直角三角形两条边的长度。
将上述方程稍加变换后,可以得出两点之间的距离公式:d = √ ((x2 - x1)² + (y2 - y1)²)三维空间:在三维空间中,我们同样假设有两个点A和B。
与二维平面的情况类似,我们可以通过画一个直角三角形来计算AB之间的距离。
如下图所示,假设我们要计算点A和点B之间的距离。
我们可以通过勾股定理来计算AB之间的距离。
测量坐标计算公式大全

测量坐标计算公式大全一、两点间距离公式(平面直角坐标系)设两点坐标分别为A(x_1,y_1),B(x_2,y_2),则两点间的距离d为:d = √((x_2 - x_1)^2+(y_2 - y_1)^2)例如,A(1,2),B(4,6),则x_1 = 1,y_1=2,x_2 = 4,y_2 = 6d=√((4 - 1)^2+(6 - 2)^2)=√(3^2 + 4^2)=√(9+16)=√(25) = 5二、中点坐标公式(平面直角坐标系)设两点坐标分别为A(x_1,y_1),B(x_2,y_2),则AB中点M的坐标为(x_m,y_m),其中。
x_m=(x_1 + x_2)/(2)y_m=(y_1 + y_2)/(2)例如,A( - 2,3),B(4,-1),则中点M的坐标为。
x_m=(-2+4)/(2)=1y_m=(3+(-1))/(2)=1即中点M(1,1)三、直线的斜率公式(平面直角坐标系)设直线上两点坐标为A(x_1,y_1),B(x_2,y_2)(x_1≠ x_2),则直线AB的斜率k 为:k=(y_2 - y_1)/(x_2 - x_1)例如,A(1,2),B(3,6),则k=(6 - 2)/(3 - 1)=(4)/(2)=2四、直线的点斜式方程(平面直角坐标系)已知直线过点(x_0,y_0),斜率为k,则直线方程为y - y_0=k(x - x_0)例如,直线过点(1,3),斜率k = 2,则直线方程为y-3 = 2(x - 1),即y=2x+1五、平面直角坐标系中坐标旋转公式。
设点P(x,y)绕原点旋转θ角后得到点P'(x',y')x'=xcosθ - ysinθy'=xsinθ + ycosθ六、极坐标与直角坐标的转换公式。
1. 直角坐标(x,y)转换为极坐标(ρ,θ)ρ=√(x^2 + y^2)θ=arctan(y)/(x)(x≠0)2. 极坐标(ρ,θ)转换为直角坐标(x,y)x = ρcosθy=ρsinθ七、空间直角坐标系中两点间距离公式。
第6章 多元函数微分学

6.4 多元复合函数微分法 6.4.1 多元复合函数微分法 设 z = f (u,v), u = u (x,y), v = v(x,y),则 , ∂z ∂f ∂u ∂f ∂v ∂z ∂f ∂u ∂f ∂v = ⋅ + ⋅ = ⋅ + ⋅ , ∂x ∂u ∂x ∂v ∂x ∂y ∂u ∂y ∂v ∂y 这是本节最重要、最好记忆的公式, 这是本节最重要、最好记忆的公式,也是应 用时最容易出错的公式.只要你不偷懒的话, 用时最容易出错的公式.只要你不偷懒的话,你 是不会出错的. 是不会出错的. 本节假设所有的抽象函数总能 满足所需要的条件. 满足所需要的条件. 的偏微商. 练习 求 z = (x2 + y2)xy 的偏微商. 提示: 提示:令u = x2 + y2, v = xy.
∂z ∂z dz = dx + dy ∂x ∂y
的偏微商与全微分. 例 求z = cos2x + 3siny的偏微商与全微分 的偏微商与全微分 ∂z ∂z 解 = −2sin 2x, = 3cos y. ∂x ∂y
∂z ∂z dz = dx + dy ∂x ∂y
= − 2sin2xdx + 3cosydy
第6章 多元函数微分学
重点: 重点:求偏微商 难点: 难点:多元复合函数微分法 多元函数极值
6.1 空间解析几何
6.1.1 空间直角坐标系
点与坐标
两点间的距离公式 间的距离公式: 间的距离公式:
d = (x1 − x2 ) + ( y1 − y2 )
2
2
间的距离公式: 间的距离公式:
d = (x1 − x2 ) + ( y1 − y2 ) + (z1 − z2 )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
空间直角坐标系空间两点间的距离公式班级:____________ 姓名:__________________
C .(-4,0,-6)
D .(-4,7,0)
解析:点M 关于y 轴对称的点是M ′(-4,7,-6),点M ′在xOz 平面上的射影的坐标为(-4,0,-
6).
答案:C
二、填空题
7.如图,长方体ABCD -A 1B 1C 1D 1中,已知A 1(a,0,c ),C (0,b,0),则点B 1的坐标为________. 解析:由题中图可知,点B 1的横坐标和竖坐标与点A 1的横坐标和竖坐标相
同,点B 1的纵坐标与点C 的纵坐标相同,所以点B 1的坐标为(a ,b ,c ).
答案:(a ,b ,c )
8.在空间直角坐标系中,点(4,-1,2)关于原点的对称点的坐标是________.
解析:空间直角坐标系中关于原点对称的点的坐标互为相反数,故点(4,-1,2)关于原点的对称点的坐标是(-4,1,-2).
答案:(-4,1,-2)
9.点P (-1,2,0)与点Q (2,-1,0)的距离为________.
解析:∵P (-1,2,0),Q (2,-1,0),
∴|PQ |=(-1-2)2+[2-(-1)]2+02=3 2.
答案:3 2
10.已知点P ⎝⎛⎭⎫32,52,z 到线段AB 中点的距离为3,其中A (3,5,-7),B (-2,4,3),则z =________.
解析:由中点坐标公式,得线段AB 中点的坐标为⎝⎛⎭
⎫12,92,-2.又点P 到线段AB 中点的距离为3,所以
⎝⎛⎭⎫32-122+⎝⎛⎭
⎫52-922+[z -(-2)]2=3, 解得z =0或z =-4.
答案:0或-4
三、解答题
11.已知直三棱柱ABC -A 1B 1C 1中,∠BAC =90°,|AB |=|AC |=|AA 1|=4,M 为BC 1的中点,N 为A 1B 1的中点,求|MN |.
解析:如右图,以A 为原点,射线AB ,AC ,AA 1分别为x 轴,y 轴,z 轴的正半轴建立空间直角坐标系,
则B (4,0,0),C 1(0,4,4),A 1(0,0,4),B 1(4,0,4),因为M 为BC 1的中点,N 为A 1B 1的中点,所以由空间
直角坐标系的中点坐标公式得M (4+02,0+42,0+42),N (0+42,0+02,4+42
),即M (2,2,2),N (2,0,4). 所以由两点间的距离公式得
|MN |=(2-2)2+(2-0)2+(2-4)2=2 2.
12.已知点P (2,3,-1),求:
(1)点P 关于各坐标平面对称的点的坐标;
(2)点P 关于各坐标轴对称的点的坐标;
(3)点P 关于坐标原点对称的点的坐标.
解析:(1)设点P 关于xOy 坐标平面的对称点为P ′,则点P ′的横坐标、纵坐标与点P 的横坐标、纵坐标相同,点P ′的竖坐标与点P 的竖坐标互为相反数.
所以点P 关于xOy 坐标平面的对称点P ′的坐标为(2,3,1).同理,点P 关于yOz ,xOz 坐标平面的对称点的坐标分别为(-2,3,-1),(2,-3,-1).
(2)设点P 关于x 轴的对称点为Q ,则点Q 的横坐标与点P 的横坐标相同,点Q 的纵坐标、竖坐标与点P 的纵坐标、竖坐标互为相反数.
所以点P 关于x 轴的对称点Q 的坐标为(2,-3,1).
同理,点P 关于y 轴,z 轴的对称点的坐标分别为(-2,3,1),(-2,-3,-1).
(3)点P (2,3,-1)关于坐标原点对称的点的坐标为(-2,-3,1).
13.如图,已知长方体ABCD -A 1B 1C 1D 1的对称中心在坐标原点,交于同一顶点的三个面分别平行于三个坐标平面,顶点A (-2,-3,-1),求其他七个顶点的坐标.
解析:由题意,得点B 与点A 关于xOz 平面对称,
故点B 的坐标为(-2,3,-1);
点D 与点A 关于yOz 平面对称,故点D 的坐标为(2,-3,-1);
点C 与点A 关于z 轴对称,故点C 的坐标为(2,3,-1);
由于点A 1,B 1,C 1,D 1分别与点A ,B ,C ,D 关于xOy 平面对称,
故点A 1,B 1,C 1,D 1的坐标分别为A 1(-2,-3,1),B 1(-2,3,1),C 1(2,3,1),D 1(2,-3,1).
14.已知点M (3,2,1),N (1,0,5),求:
(1)线段MN 的长度;
(2)到M ,N 两点的距离相等的点P (x ,y ,z )的坐标满足的条件.
解析:(1)根据空间两点间的距离公式得
|MN |=(3-1)2+(2-0)2+(1-5)2=26,
所以线段MN 的长度为2 6.
(2)因为点P (x ,y ,z )到M ,N 两点的距离相等,所以
(x -3)2+(y -2)2+(z -1)2=(x -1)2+(y -0)2+(z -5)2,
化简得x +y -2z +3=0,
因此,到M ,N 两点的距离相等的点P (x ,y ,z )的坐标满足的条件是x +y -2z +3=0.。
