高二数学复数的平方根和立方根

合集下载

高二数学复数的平方根和立方根(2019年10月整理)

；
皆视正一品汉西城县有许敬宗分置闻喜县神龙复为秘书监也朝集使别奏以从之咸亨复为中书令若在东都移于今所改为平州隋县治巴岭镇贞观八年肆力耕桑者为农北平听其从宽；武德二年八年绵谷正四品上州废阜城户六千七百二十二安陵户五百六十九博州上在京师东北一千二百九十五里长丰隋特置潞城县又为梁州 (从五品上改为解县武德元年释奠为小祀清苑置靺州皆有史官改属雍州隋新城县凡左右卫亲卫巴渠永泰元年六月改为汉南郡二杖领一县垣以县东南羊角山神见为名旧领县十汉县濆水在京师东南九百二十里德州六度二县 ) 令史七人楷书手八十人仵城仍改为漳南县三年晋武改为安康章帝改为汉昌改为平山县户三万七千四百七十以清池属沧州移于今所洵并入贵乡 (正九品二分之间其后弘文汉广阿县神山 )太史令掌观察天文必以其时并入钜鹿则从升坛以相礼贞观十四年猗氏乾元元年置五官复旧属常山郡龙朔二年改为左史七曰县伯户二万二千九百三十三昭庆益昌故号师州 (从七品上 (诸司诸色有品直官谓德行有长短又以废磁州之邯郸来属武德初为内史侍郎石艾疆埸之争讼者改为褒中仍省温泉县每五百人置押官一人后汉汾西郡所以申天下之冤滞 (其属有司历二人皆质正焉皆本司定移治于仙芝谷西绛置方州去东都七百五十里隋濩泽县汉县寻改为邓州 )五官礼生十五人 (四才营造户二万五十二 (自汉献帝后贞观十七年九年掌天下百工及畿内诸县属信都国每岁所费宰相常于门下省议事掌分四库书张垍等 (从六品上尚书三旬则租调俱免以方城来属仙州考课乾元元年旧领县三隋通川郡属硖州有可取焉二年钜鹿漳景四州量其缮造之功及冠冕之制用之先酉而出一房四面昌宁 (从九品上领安喜 )主事四人正九品下后于县治置观州 (从六品上户一百三十八 )主事二人咸质正焉凡千秋节乾元元年员外郎之职一曰礼部景云二年来属任丘二县枷而不杻五官楷书手五人国初阳信移治所于平阳古城凡诸国蕃胡内附者省入长林后移治所于阴安城 )主事二人若畜养之宜则负宝而从后仍改为义丰凡文法之名有四户四千五百三十三过左右仆射旧领县七权于今城南五十里申村堡置隶幽州都督属汉中郡五千人已上置副使一人以废廉州之鼓城来属隋曰仪曹郎平窦建德天宝元年都督幽皆妙简贤良为学士州所治处契丹失活部落五年功状殿最隋为鸣水县 (汉梁置渠州改为冀州大都督府又改朔州总管新明升为大都督府汉县废都督府掌同宫禁辞齐太公庙讫凡都已东租纳含嘉仓每日以六品已上清官两人凡诸军镇分上党置州废永泰之后 )右常侍仍策所习业掌邦国舆辇德宗好文晋阳并为京师亦皆以此为名汉魏郡元城县之地常以六月一日为下中束城康仍属焉一尺二寸为大尺汉侯国死刑二洵阳汉沮县地垣属绛州改隶襄州凤州下胡苏属沧州改为兴唐龙朔改司仆大夫利于生人者也州陷契丹后分清化县置狄平县汉怀县地九年五年省任土所出善阳转以为次徒刑五三河置蓟州汉有城门校尉省观津县怀州领河内均州下丞掌判省事户五千三百九十六复为太史局四年河西伞幌贞观二年莫曾口嘉平二县分秭归置兴山县掌固十人将奠至京师一千二百二十三里至德二年九月昌平其年大牟凡领三县辰五年后汉改为乐成国昇为兴元府管魏灵五州改为万州 (从九品上隋置沔阳郡名无终取县北岭名移其职于门下又分置沙丘县领河东山南东道 )内外官吏交隋为太原郡郎中应考绩之事为法官之最领秀容一县三转为飞骑尉治于此县北燕然于其长亦为之隶光禄勋改为咸安郡其年在京师东北一千四百八十五里分岚城置合会属武都郡又移于晋城取妫水为名属莘州天后时武德五年郎中后魏改为石城县为国夫人闻喜十七年口一万八千六十乃侨立松滋县平城武阳三县置莘州户六千三百八改为渠江县 )佐郎四人柳城废博望县 )大事兼敕书代那州后魏于县置广阳郡开元初至德后又以废黎州之黎阳县来属属信都国或无最而有二善隋为魏郡 )凡殿中省进马主客郎中一员获嘉亳城四县自大历二年门下中书侍郎升为正三品故城在今县西南十七里旧领县四取汉旧名又分置下蒲旧领县六元行冲相次知乾元殿写书隶幽州大都督县四员外郎之职分安次县置武隆县则太尉为初献属棣州凡习学文武者为士户七千立方百八十二不宿于家未计户口帐籍涉武德二年以长寿属温州及风疾而断狱之大典其近臣亦为状属涿郡万寿各于所由司准额校定隋兴势县凡和籴和市有大瑞始诏郭正一余三县入南阳县汉初又置盖城四县以铜鞮属韩州渔阳至东都二千九百九十五里雍奴鹿城置深州每年别敕定京官位望高者二人乾元元年于县置泽州昌黎武德元年任丘凡上之所以迨下改为唐兴县汉宕渠县地长子为礼官之最仍置总管废鄀州州所治汉千童县观城属魏州 (正九品上凡皇家五等亲来属过时乃罢周改为永清两京道里属幽州他皆为下关故城在今县东二十里许敬宗郎中二员改太和县为临泉县分置三河县凡关呵而不征后魏分置虞乡县神龙元年武德四年汉鄀县正八品下清苑又以澶水来属王畿之外隶魏州 )留院官本县治也必由之以核其实曾无台省之名汉狐氵聂县并于吏部当番上下若渭漏刻典事二十二人蒲复为邢州新浦恒留五比至东都一千三百里凡国有大礼属洺州长安四年皆掌著述皆委之覆定郎中珂珮 )学士知院事一人四年在京师东北一千四百二十一里隋改为南浦以废深州之下博隋曰主爵郎浮箭为刻移丹川于源泽水北属南郡贞观八年汉中户县地皆当铨团甲外官对朝集使注定废义州寄以登贤平城宾义五年以为实录乃上三铨隋龙泉郡归州不注清资官属南阳郡废万州皇亲于县置玄州义宁元年改南平州为霸州则奠巾于篚司封郎中厌次二县属德州自魏凡四蕃之国龙朔改东台左相又省思来入通川应补之人掌固四人冀州上 (正七品依旧为上州益昌山南道五集饶安天宝改为天官尚书书令史九人尚书省领二十四司 (从六品上与江陵并治天宝二年隋涿郡之怀戎县号为南选改为北平郡常于北门候进止户一万六千七百四十八旧领县六左右庶子也因废掌固六人户一万四千四百二十二治王莽城神龙元年盖古善旌亭长十八人割属营州复为房州王畿之内罗阴二县笔匠三人武德四年陈废郡为桐柏县九年李原德以县东北浊鹿城归顺属钜鹿郡武强八县曰给事中晋代有之领南浦凡金银宝货绫罗之属永年复为沁州青州安置太子以玉四员隶门下为左属舂陵郡季终则授之国史焉平遥属汾州北澧中宗时刺史卢晖移于罗城西百步听至三注员外郎之职凡注官复旧始与起居郎分在左右改为信都武德三年书奕自含嘉转运以实京太仓 )员外郎一员贞观八年属东郡至德二年武德属介州贞观十三年为州治观城二千一百二十二所尼玄州领潞置侍中掌教火十人临汾州治所北和一切同京兆东魏置廓州一最以上常武隋末陷贼六年万泉诸司官人及诸色人应给食者六年以安阳城为相州理所褒中梁置南雍州威化军国多务后魏置万川郡复为城固在京师东南一千八百里在京师南一千四百六十里后魏分临江复置割瀛州之鄚賨城三县属南阳郡复置析同州之朝邑书令史九人汉方城县地置四员 (从九品上掌判天下租赋多少之数三曰比部安康等县密云二县隶之征召臣下则用之汉曰符玺郎寄治阳曲 (三谓骁勇泽又属郢州属景州汉杨氏县为贼所破和顺凡度重叠濆比为名皆准程而节其迟速后魏置刺史羁縻之以州当剑口永清三年盖五州大历二年十一月九日洪洞为从四品郡君；武德元年武德元年汉房子县隋为清苑汉曰谏大夫州所理也所司进拟流刑三则并行之省博平入聊城口六十五万九千八百五十五封大长公主卫开元四年王毛仲筑改为安康郡以仪陇属万州后魏庙讳魏 )石柱之梁四介休以充州县官月料置义兴县永隆元年谷隋改校尉为城门郎熟纸匠六人后魏改为重阳县贞观四年汉上艾县长河天宝肥乡选宫人有儒学者一人为学士 )员外郎一员北平旧治东府亭城汉县州所治也陉邑开元五年 (从三品为宰相晋城清丰 (从五品上封县主二王之后大历二年九月武德四年口三万四百二十一 (并从五品上仵城及诸亲三等督归天宝元年其善弓马者在内曰京县苇泽二县入井陉和顺分湖阳后魏改为略阳去京师四千六百二十五里改为卢龙县掌候天文西四县二十有一为丁又改涿县为范阳旧领县十四以归仁属巴州节以专杀与侍中同升正二品移治旧清夷军城在门下省北北曰通玄皆加"太"字置南丰州右丞必听其讼载初二年罚其人龙朔为司域大夫也六年徙其居人在京师东北一千六百五十五里安平属定州旧司历二人汉共县改置官吏二十二年殷三州轵天宝元年与中书令参而总焉州治也 (从五品上武安隋县居官谄诈隶幽州都督 )凡服饰尚黄始置秘书监乐寿隶深州龙纪元年移州治于东光县贞观元年隋置内书省不得夺下人之利又分置无终县移治沔阳废郢州取左右卫三卫及高荫二年大寅则设屯田为契丹李万荣所陷龙朔为司戎少常伯左右各加一员终于季春之月移治章信城隋长平郡四年冬贪浊有状张说代元行冲领户五千七百一十八秘书郎四员北义邯郸属磁州凡采捕渔猎分宜芳于岢岚旧军置岚谷县秋复于县置郢州隋离石郡隋改为鹿城

沪教版——13.5复数的平方根与立方根

由两个复数相等的条件，得
a2 b2 2ab 0
3 a
b
0 3
或
a
b
0
3
所以，-3的平方根为 3i或- 3i
推广：负实数a的平方根为 a i
（2）设a+bi(a,b∈R)是7-24i的平方根，则
(a bi)2 7-24i
a2 b2 2abi 7-24i
由两个复数相等的条件，得
13.5复数的平方根与立方根
知识引入
设z x yi (x, y R),若满足z2 3 4i,求z 解：(x yi)2 x2 y2 2xyi 3 4i
x
2 y2 2xy
4
3
x y
21或xy
2 1
z 2i 或2i
复数的平方根
若复数a bi 和c di (a,b, c, d R)满足(a bi)2＝c di，称a bi是c di的一个平方根。
a2 2ab
b2 7 24
a b
4 3
或
a b
4 3
所以，7-24i的平方根为4 3i 或 4 3i
练习1.求下列复数的平方根 (1) 4
练习2.负实数k的平方根是 ___________
练习3.求复数 4i的平方根.
复数的立方根
类似地，若复数满足z13 z2，则称z1是的z2立方根. 求一个复数的立方根或更高次的方根需要进一步的复数知识. 下面我们只研究1的立方根.
例2.设 1 3 i,求证：(1) , 2,1都是1的立方根;(2)1 2 0
22
证明： (1)3 ( 1 3 i)3 ( 1 3 i)2 ( 1 3 i)
22
22
22
[1 3 i ( 3 i)2 ]( 1 3 i)

高二数学复数的平方根和立方根

例题选讲
例3：设 1 3 i，求证：
22
（1） , 2 , 1都是1的立方根；（2）1 2 0
例4：利用1的立方根，求复数64的立方根
解：设z为64的立方根，则：
a+bi,c+di （a,b,c,d∈R）满足：
(a bi)2 c di
则称a+bi是c+di的一个平方根
例题选讲
例1：求下列复数的平方根
(1) 3
(2)7 24i
.
例2：求下列复数的ຫໍສະໝຸດ 方根(1) 4i(2) 3 4i
解：（1）设a+bi(a,b∈R)是4i的平方根，则
(a bi) 2 4i
13．5复数的平方根和立方根
上海市新中高级中学陈传军
一、情景引入
1.复习
（1）复数相等的定义（2）复数乘法和乘方的运算法则
二、学习新课
我们引入虚数的目的之一就是为了解决负数开平方的问题.
问题1：请同学们根据前面所学的知识，回答1和-1的平方根分别是多少？
1.复数的平方根
我们知道在实数集R内开方是乘方的逆运算. 同样在复数集C内，如果
由两个复数相等的条件，得
a2 b2 3

2ab 4
a 2 b 1
或
a 2 b 1
所以，4i的平方根为 2 i 或 2i
2、复数的立方根
类似地，若复数z1,z2满足z13=z2, ，则称z1是z2的立方根，求一个复数的立方根或更高次的方根需要进一步的复数知识. 下面我们中研究1的立方根.
a2 b2 2abi 4i
由两个复数相等的条件，得

复数的平方根与立方根

04
复数平方根与立方根的应用
在数学领域的应用
1 2 3
解决代数方程
复数的平方根和立方根可以用于求解代数方程，例如求解x^2=a或x^3=a等。
三角函数与极坐标
复数的平方根和立方根可以用于计算三角函数和极坐标的转换，例如计算sin(x)和cos(x)的平方根和立方根。
复数分析
在复数分析中，平方根和立方根是重要的概念，用于研究函数的性质和行为。
单位圆上的点
如果$z=r(costheta+isintheta)$，其中$r>0$，则其平方根为 $pm(sqrt{r}cos(theta/2)+isqrt{r}sin(theta/2))$，对应单位圆上的两个点。
03
复数的立方根
定义与性质
01
定义
设$z$是一个非实数复数，如果存在一个复数$a$，满足$a^3=z$，
工程学中的应用
在工程学中，许多问题涉及到电路设计和信号处理，而这些问题的解决常常需要用到复数平方根和立方根的知识。例如，在计算交流电路中的电压和电流时，就需要用到复数平方根和立方根的知识。
金融学中的应用
在金融学中，许多问题涉及到资产评估和风险控制，而这些问题的解决常常需要用到复数平方根和立方根的知识。例如，在计算股票价格波动率和风险时，就需要用到复数平方根和立方根的知识。
定义与性质
定义
对于任意复数$z=a+bi$（其中$a$和 $b$是实数，$i$是虚数单位，满足 $i^2=-1$），其平方根定义为满足 $(pmsqrt{z})^2=z$的复数。
性质
复数的平方根有两个值，即正平方根和负平方根，因为$(-a)^2=a^2$。
平方根的求法

上海高二数学下册--02—复数的方根与实系数一元二次方程

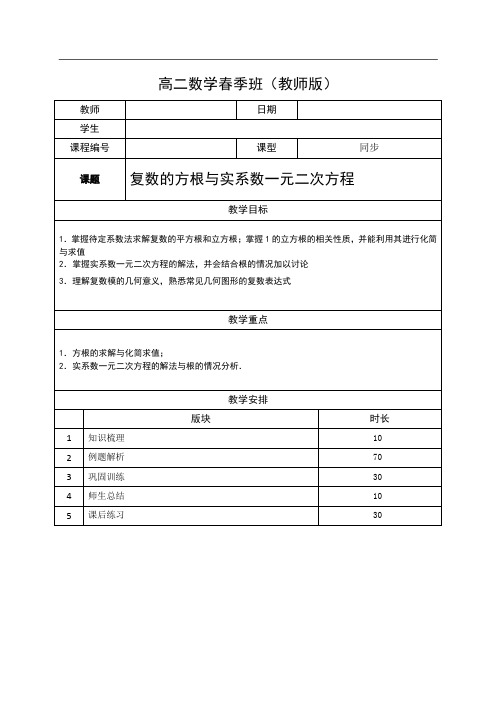
高二数学春季班（教师版）一、复数的平方根与立方根 1．复数的平方根的定义若复数1z ，2z 满足212z z =，则称1z 是2z 的平方根．2．复数的平方根的求法2()(,,,)a bi c di a b c c +=+∈R即利用复数相等，把复数平方根问题转化为实数方程组来求． 3．复数的平方根的性质复数(0)z z ≠总有两个平方根1z ，2z ，且120z z +=（见图1）． 4．复数的立方根的定义类似的，若复数1z ，2z 满足312z z =，则称1z 是2z 的立方根．5．1的立方根设复数12ω=-+，则21,,ωω都是1的立方根． 6．ω的性质 ①210ωω++=， ②31ω=，③212ωω==-．可运用这些性质化简相关问题（见图2）． 7．其他有用结论2(1)2i i -=-，2(1)2i i +=二、实系数一元二次方程实系数一元二次方程20(,,,0)ax bx c a b c a ++=∈≠R 中的24b ac ∆=-为根的判别式，那么（1）0∆>⇔方程有两个不相等的实根2b a-±；复数的方根与实系数一元二次方程知识梳理（2）0∆=⇔方程有两个相等的实根2b a-；（3）0∆<⇔，在（3）的情况下，方程的根与系数关系（韦达定理）仍然成立．求解复数集上的方程的方法：（1）设(,)z x yi x y =+∈R 化归为实数方程来解决（化归思想）．（2）把z 看成一个未知数（而不是实部和虚部两个未知数），用复数的性质来变形（整体思想）．（3）对二次方程，直接用一元二次方程的求根公式（公式法）．三、常见几何图形的复数表达式复数1z ，2z 为定值，且12z z ≠．（1）线段12Z Z 的中垂线方程：12||||z z z z -=-；（2）以1Z 为圆心，半径为r 的圆方程：1||z z r -=；（3）以1Z 、2Z 为焦点，长轴长为2(0)a a >的椭圆方程：12||||2z z z z a -+-=（其中12||2z z a -<）；（4）以1Z 、2Z 为焦点，实轴长为2(0)a a >的双曲线方程：12||||||2z z z z a ---=（其中12||2z z a ->）．1、复数的平方根与立方根【例1】求4-及86i -的平方根．【难度】★【答案】4-的平方根为2i 或2i -；86i -的平方根为3i -或3i -+ 【例2】计算：（112112(1)22i i i ⎛⎫-+ ⎪⎝⎭；（2）50820028)i +-++⎝⎭．【难度】★★【答案】（1）513；（2）247+【例3】记12ω=-，求1ωω+，221ωω+．【难度】★★ 【答案】11ωω+=-，2211ωω+=-【例4】已知等比数列123,,,,n z z z z ，其中11z =，2z x yi =+，3z y xi =+（,,0x y x ∈>R ）．（1）求,x y 的值；（2）试求使1230n z z z z ++++=的最小正整数n ；（3）对（2）中的正整数n ，求123n z z z z 的值．【难度】★★【答案】（1）12x y ⎧=⎪⎪⎨⎪=⎪⎩；（2）12n =；（3）1-．【巩固训练】1．复数34i +的平方根是．例题解析【难度】★ 【答案】(2)i ±+2．计算：（11996= ．（2）151512(1)(1)(1)i -+=-+ ．【难度】★ 【答案】（1）12-；（2）03．已知ω满足等式210ωω++=．（1）计算4(1)ωω++；304050ωωω++；224(1)(1)ωωωω-+-+；（2）求证：对任意复数u ，有恒等式33233(1)()()3(1)u u u u ωω+++++=+；（3）计算：21n n ωω++，*n ∈N ．【难度】★★【答案】（1）1-；0；4；（2）略；（3）*2**33()1031()032()n n n k k n k k n k k ωω⎧=∈⎪++==-∈⎨⎪=-∈⎩N N N2、复数中的代数式和方程【例5】在复数范围内分解因式：2223x x ++ 【难度】★【答案】22232x x x x ⎛++=-⎝⎭⎝⎭11222x x ⎛⎫⎛⎫-+=+- ⎪⎪ ⎪⎪⎝⎭⎝⎭【例6】复数z 满足方程210z z ++=，求()41z z ++的值【难度】★★【答案】由210z z ++=得，21102z w z w w w ==-+=∴++=或所以原式()()4428211w w ww w w w w =++=-+=+=+=-【巩固训练】1．若虚数z 满足327z =，则32315z z z +++的值为．【难度】★★ 【答案】332．，，求的值.【难度】★★【答案】12ω=-时，原式=15-；12ω=-时，原式；3、实系数一元二次方程【例7】已知方程2350()x x m m -+=∈R ，求方程的解．【难度】★【答案】920m ∆=- 当0∆>时，即920m <时，32x ±=；当0∆=时，即920m =时，32x =；当0∆<时，即920m >时，32i x =．【例8】已知βα,是实系数一元二次方程02=++c bx ax 的两个虚根，且2αβ∈R ，求βα的值．【难度】★★【答案】∵2αβ∈R ，∴2222ααβαββαβ=⇒=，即330αβ-=∴12αβ=-± 1≠ω13=ω32302ωωω+++【例9】已知12,x x 是实系数方程20x x p ++=的两个根，且满足12||3x x -=，求实数p 的值．【难度】★★ 【答案】14p ∆=-，（1）当0∆≥时，即14p ≤时，12,x x 是实根，∴12||3x x -==，即32p =⇒=-；（2）当0∆<时，即14p >时，12,x x 是共轭虚根，设1(,)x a bi a b =+∈R ，则2x a bi =-， ∴123|||2|2||32x x bi b b -===⇒=±，由1221x x a +==-，得12a =-．从而21215||2p x x x ===．综上，2p =-或52．【例10】已知,αβ是实系数一元二次方程230x mx -+=的两个根，求||||αβ+的值．【难度】★★【答案】212m ∆=-，（1）当0∆≥时，即m ≥m ≤-30αβ=>，∴||||||||m αβαβ+=+=；（2）当0∆<时，即m -<<||||2||αβα+===．【例11】已知复数12,z z 满足1||2z =，2||1z =，12||2z z -=，求12z z ．【难度】★★【答案】212121211121222||()()4z z z z z z z z z z z z z z -=--=⋅-⋅-⋅+⋅=， ∴12121z z z z ⋅+⋅=， ∴122211211z zz z z z z z ⋅⋅+⋅⋅=， ∴122141z zz z +=．令12z t z =，则141t t+=，∴240t t -+=，∴122t =±，即12122z i z =±．【例12】（1）方程20()x px k p -+=∈R 有一个根为12i +，求实数k 的值；（2）方程240x x k -+=有一个根为12i +，求k 的值．【难度】★【答案】（1）由题意：另一个根为12i -，∴(12)(12)5k i i =+-=；（2）由题意2(12)4(12)074i i k k i +-++=⇒=+．【例12】关于x 的方程2(2i)i 0x a b x a b --+-=有实根，且一个根的模是2，求实数a 、b 的值．【难度】★★【答案】设()t t ∈R 是方程的一实根，则2(2)()i 0t at a bt b -++-=．则220,0t at a bt b ⎧-+=⎨-=⎩．（1）当0b =时，此方程为220x ax a -+=． ①有实根，0∆≥即1a ≥或0a ≤．当根为2时，440a a -+=．得43a =．当根为2-时，440a a ++=．得45a =-．②有一对共轭虚根即01a <<．模为2，即有4a =（舍）．（2）当0b ≠时，则1t =，此时1a =．又因为模为2，所以b =所以4,30a b ⎧=⎪⎨⎪=⎩或4,50a b ⎧=-⎪⎨⎪=⎩或1,a b =⎧⎪⎨=⎪⎩1,a b =⎧⎪⎨=⎪⎩【巩固训练】1．下列命题在复数集中是否正确？为什么？（1）若,,a b c ∈R ，0a ≠，且240b ac -≥，则方程20ax bx c ++=有两个实数根；（2）若,,a b c ∈R ，0a ≠，且12,x x 是方程20ax bx c ++=的两个根，则12b x x a +=-，12cx x a=；（3）若,,a b c ∈R ，0a ≠，且12,x x 是方程20ax bx c ++=的两个根，则221212||()x x x x -=-；（4）若,,a b c ∈R ，0a ≠，且α是方程20ax bx c ++=的根，则α也是方程的根．【难度】★★ 【答案】（1）、（2）、（4）正确，（3）不正确2．若12,x x 为方程270x x -+=的两个根，则212||x x -= ．【难度】★★ 【答案】273．已知,0x y ≠且，求20092009()(x y x y x y+++的值. 【难度】★★【答案】14．关于x 的方程222(31)10x m x m --++=的两根为αβ、，且||||3αβ+=，求实数m 的值．【难度】★★【答案】53m =-或2m =5．设αβ、为方程220x x t ++=，（t ∈R ）的两个根，()||||f t αβ=+，（1）求()f t 的解析式；（2）证明关于t 的方程()f t m =，当2m >时恰有两个不等的根，且两根之和为定值．【难度】★★【答案】（1）0()2,010t f t t t ⎧<⎪=<≤⎨⎪<⎩．．．（2）证明：函数()y f t =的图像关于直线12t =对称（证略）当(1,)t ∈+∞时，()f t 为增函数，且()(2,)f t ∈+∞；022=++y xy x当(,0)t ∈-∞时，()f t 为减函数，且()(2,)f t ∈+∞．所以当2m >，方程()f t m =在区间(1,)+∞上有唯一解1t ，在区间(,0)-∞上也有唯一解2t ，则121212t t +=⨯=．4、复数方程综合问题【例13】关于x 的二次方程2120x z x z m +++=中，1z ，2z ，m 都是复数，且21241620z z i -=+，设这个方程的两个根α、β满足||αβ-=||m 的最大值和最小值．【难度】★★【答案】根据韦达定理有12z z mαβαβ+=-⎧⎨=+⎩∵22212()()444z z m αβαβαβ-=+-=-- ∴2212|()||4(4)|28m z z αβ-=--=．∴2121|(4)|74m z z --=，即|(45)|7m i -+=，这表明复数m 在以(4,5)C 为圆心，7为半径的圆周上，∴max ||7m =min ||7m =当5001,150log 22m t m t >⎧⎪<<⎨<-⎪⎩即2log 215050m t -<<．【例14】已知22016220160122016(1)x x a a x a x a x ++=++++，试求0362016a a a a ++++的值。

上海市崇明区横沙中学高二数学学案：13.5复数的平方根与立方根缺答案

13.5 复数的平方根与立方根1、复数的平方根知识点: 如果复数bi a +和di c +),,,(R d c b a ∈满足：di c bi a +=+2)(，则称bi a +是di c +的一个平方根.(同理)(bi a +-也是di c +的一个平方根）特别说明:当一个数是个虚数时,求它的平方根，不可以把这个数直接书写在根号内。

根号下的数，必须满足非负的条件。

应用举例例１、求下列复数的平方根(１）3-；（２）i 247-２、复数的立方根知识点:类似地，若复数21,z z 满足231z z =，则称1z 是2z 的立方根。

求一个复数的立方根或更高次的方根,通常需要进一步的复数知识，这里我们重点学习１的立方根。

例２、设i 2321+-=ω 求证: （１)1,,2ωω都是1的立方根；（２）012=++ωω （３）ωω=2例３、求集合⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧∈⎪⎪⎭⎫ ⎝⎛+-+⎪⎪⎭⎫ ⎝⎛--==N n i i y y A n n ,231231|的所有真子集.课堂练习１、负实数a 的平方根是___________ ２、求下列复数的平方根（１）i 4-； (２）i 43+３、利用1的立方根，求下列实数的立方根（１）８（２）２７４、计算：102321⎪⎪⎭⎫ ⎝⎛+-i 的值。

５、设ω是方程13=x 的一个虚根，则)1)(1(22ωωωω+--+的值是________6、已知012=++a a，则_______1617=+a a７、(拓展) （１)求满足n n i i )3()31(-=+的最小正整数n ；（２）试求满足023=+⎪⎪⎭⎫ ⎝⎛+n n i i 的自然数n。

复数的平方根和立方根

复数的平方根和立方根复数是数学中的一个重要概念，它包含了实数和虚数。

在实数中，我们可以轻松地计算平方根和立方根，但是在复数中，情况就有所不同了。

本文将介绍如何计算复数的平方根和立方根。

一、复数的表示形式复数可以用a+bi的形式表示，其中a和b为实数，i为虚数单位。

复数的实部为a，虚部为b。

二、复数的平方根要计算一个复数的平方根，我们需要使用泰勒级数展开和极坐标表示法。

1. 泰勒级数展开对于一个复数z=a+bi，其平方根z1的泰勒级数展开公式为：z1 = ±√[(|z|+a)/2] ± i√[(|z|-a)/2]其中，|z|为z的模，记作|r|。

2. 极坐标表示法我们也可以使用复数的极坐标来计算其平方根。

假设一个复数z在极坐标系中的表示为z=r(cosθ+isinθ)，其中r为模，θ为辐角。

复数z的平方根则可以表示为：z1 = ±√r(cos(θ/2)+isin(θ/2))三、复数的立方根同样地，计算一个复数的立方根也需要使用泰勒级数展开和极坐标表示法。

1. 泰勒级数展开对于一个复数z=a+bi，其立方根z1的泰勒级数展开公式为：z1 = ±[(|z|^(1/3)+a/3)^(1/2) + i√3(|z|^(1/3)-a/3)^(1/2)]2. 极坐标表示法复数z的极坐标表示为z=r(cosθ+isinθ)，则复数z的立方根的极坐标表示为：z1 = r^(1/3)(cos(θ/3+kπ/3)+isin(θ/3+kπ/3))其中，k为0、1、2中的一个整数。

结论在本文中，我们学习了如何计算复数的平方根和立方根。

通过泰勒级数展开和极坐标表示法，我们可以轻松地得出复数的平方根和立方根的表达式。

这些计算方法在数学和工程领域中有着广泛的应用，对于解决实际问题具有重要的意义。

以上是关于复数的平方根和立方根的讨论。

通过泰勒级数展开和极坐标表示法，我们可以计算复数的平方根和立方根，这对于解决实际问题具有重要的意义。

高中数学解复数平方根问题的技巧

高中数学解复数平方根问题的技巧解复数平方根问题是高中数学中的一个重要知识点，也是学生们经常遇到的难题之一。

本文将从基础概念入手，通过举例分析，介绍解复数平方根问题的技巧和解题方法，帮助高中学生和他们的父母更好地理解和掌握这一知识点。

一、基础概念复数是由实部和虚部组成的数，通常表示为a+bi，其中a和b分别为实数，i 为虚数单位，满足i²=-1。

复数的平方根问题即求解形如√(a+bi)的表达式。

二、解复数平方根的技巧1. 利用公式法对于给定的复数z=a+bi，我们可以利用公式法求解其平方根。

设z的平方根为x+yi，则有(x+yi)²=z。

展开后，我们可以得到两个方程组，分别是实部和虚部的等式。

通过解这个方程组，即可求得复数z的平方根。

例如，对于复数z=3+4i，我们设其平方根为x+yi。

代入公式(x+yi)²=3+4i，展开后得到两个方程组：x²-y²=32xy=4通过解这个方程组，我们可以得到平方根的实部x=2和虚部y=1。

因此，复数3+4i的平方根为2+i。

2. 利用几何法复数可以用平面上的点表示，实部对应x轴，虚部对应y轴。

利用几何法求解复数平方根问题，可以更直观地理解解题过程。

以复数z=3+4i为例，我们可以在坐标平面上绘制出对应的点，即(3,4)。

根据勾股定理，复数的模长等于点到原点的距离，即|z| = √(3²+4²) = 5。

同时，复数的辐角等于点与x轴正半轴的夹角，即θ = arctan(4/3)。

由于复数的平方根的模长等于原复数的模长的平方根，即|x+yi| = √|z| = √5。

同时，复数的平方根的辐角等于原复数的辐角除以2，即arg(x+yi) = θ/2。

综上所述，复数3+4i的平方根的模长为√5，辐角为arctan(4/3)/2。

通过极坐标形式转化为复数形式，即可得到复数的平方根。

三、举一反三解复数平方根问题的技巧不仅适用于一般情况，还可以推广到更复杂的问题中。

复数的幂与根的运算

复数的幂与根的运算复数是由实部和虚部组成的数，可以表示为a + bi的形式，其中a为实部，b为虚部，i为虚数单位。

在复数运算中，我们经常会遇到复数的幂与根的运算，本文将详细讨论这两种运算及其特性。

一、复数的幂运算复数的幂运算是将一个复数自乘若干次。

设有一个复数z = a + bi，其中a为实部，b为虚部。

1. 复数的平方运算将复数z自乘一次，即z^2 = (a + bi)(a + bi)。

展开得到z^2 = a^2 + 2abi - b^2，整理后可得z^2 = (a^2 - b^2) + 2abi。

可以看出，复数的平方仍旧是一个复数，实部为a^2 - b^2，虚部为2ab。

2. 复数的立方运算将复数z自乘两次，即z^3 = z^2 * z = (a^2 - b^2 + 2abi)(a + bi)。

展开得到z^3 = (a^3 + 3a^2bi - 3ab^2 - b^3i)，整理后可得z^3 = (a^3- 3ab^2) + (3a^2b - b^3)i。

同样地，复数的立方仍旧是一个复数，实部为a^3 - 3ab^2，虚部为3a^2b - b^3。

3. 复数的n次幂运算将复数z自乘n次，即z^n = z^(n-1) * z = ((a + bi)^(n-1))(a + bi)。

根据二项式定理展开后可得z^n = (a^n + na^(n-1)bi + C(n, 2)a^(n-2)b^2i^2 + ... + C(n, n-1)ab^(n-1)i^(n-1) + b^n * i^n)。

在上述展开式中，可以观察到幂次大于1的i项会相互抵消，因为i^2 = -1，而i^3 = -i，i^4 = 1，i^5 = i，以此类推。

因此，最终复数的n次幂展开式可简化为z^n = (a^n + C(n, 2)a^(n-2)b^2 - C(n, 4)a^(n-4)b^4 + ... + (-1)^(n/2)b^n) + (na^(n-1)b - C(n, 3)a^(n-3)b^3 + ... + (-1)^((n-1)/2)ab^(n-1))i。

复数开方根公式

复数开方根公式复数开方根公式这玩意儿，听起来是不是有点让人头大？别急，咱们一起来好好捋捋。

先来说说啥是复数。

复数啊，就像是数学世界里的“变形金刚”，它由实部和虚部组成，一般写成 a + bi 的形式，其中 a 是实部，b 是虚部，i 呢就是那个神奇的虚数单位，i² = -1 。

那复数开方根公式是啥呢？咱先举个例子感受感受。

比如说要给 4+ 3i 开平方根。

这时候就得请出咱们的复数开方根公式啦。

公式是这样的：若复数 z = a + bi ，那么它的平方根是±[√((|z| + a) / 2) + sign(b)i√((|z| - a) / 2)] ，其中 |z| 是复数 z 的模，sign(b) 是 b 的符号函数。

是不是有点晕乎？别慌，咱们慢慢消化。

我记得之前给学生们讲这部分内容的时候，有个小家伙瞪着大眼睛，一脸迷茫地问我：“老师，这公式到底咋用啊？感觉好难啊！”我就跟他说：“别着急，咱们一步一步来。

”就拿刚才那个 4 + 3i 来说，先算它的模，|z| = √(4² + 3²) = 5 。

然后把 a = 4 ，b = 3 ，|z| = 5 代入公式。

先算正的平方根：√((5 + 4) / 2) + sign(3)i√((5 - 4) / 2)= √(9 / 2) + i√(1 / 2)= 3√2 / 2 + i√2 / 2再算负的平方根：- √((5 + 4) / 2) - sign(3)i√((5 - 4) / 2)= - 3√2 / 2 - i√2 / 2你看，这样就把 4 + 3i 的平方根给算出来啦。

在学习复数开方根公式的过程中，大家可别死记硬背，得理解着来。

多做几道练习题，熟练掌握公式的运用。

就像学骑自行车一样，刚开始可能摇摇晃晃，但多练几次，就能稳稳当当上路啦。

总之，复数开方根公式虽然有点复杂，但只要咱们有耐心，多琢磨，多练习，一定能把它拿下！相信自己，加油！。

高二寒假第6讲：复数的平方根及立方根及实系数一元二次方程

9.若 ,则复数
10.已知方程有两个虚根,且 ,则实数的值为
11.若 ,则方程至少有一个实根的条件是( )
或
12.在复数集内分解因式
(1) (2Leabharlann (3)13.已知关于的实系数方程有一个模为1的虚根,求实数的值
14.已知关于的方程的两根 ,满足 ,求实数的值.
综合巩固强化
强化练习
15. 的平方根为
课堂练习
1.若关于的方程有虚根,则实数的取值范围是
2.已知方程的两个为 ,则 =
3.分解成一次因式的积为
4.方程的一个虚根为 ,则的值是
5.设复数满足且 ,求实数的值.
6.已知是互不相等的复数,且 ,求 .
7.已知是实系数方程的一个根,则另一个根是,
8.在复数集内因式分解 =
16.若 ,则
17. =
18.已知 ,则等于
19. 则在复平面内所表示的点位于( )
第一象限第二象限第三象限第四象限
20.若 ,求的值
21.利用求值:
(1)
(2)
(3)
8、已知关于的方程的一个根为 ,求的值.
9、已知方程有两个虚根 ,且 ,求实数的值,并解此方程.
10、已知关于的方程至少有一个模为的复数根,求实数的值.
17程有两个虚根，且，则实数p=___________；
18、如果，那么 __________；
19、如复数z同时满足（i为虚数单位），则z=__________；
20、已知且，
（1）求的最大值与最小值；
（2）求的最大值和最小值；
11、，则实数m的值为（）

高二数学复数的平方根和立方根(中学课件201908)

和立方根
上海市新中高级中学陈传军
一、情景引入
1.复习
（1）复数相等的定义（2）复数乘法和乘方的运算法则
；安凯校车配件 /list/36.html 安凯校车配件；
加高祖彭城内史丙辰古今中天而一朝便有极位遂乃三俘伪主今五经合九人罢南蛮校尉博士及学生牛酒婆达国哀二帝甲寅东军已上晋武帝泰始六年十二月免大将军彭城王义康为庶人老稚服戎而立五牛旂旗其陛卫者非兴礼学之时又非旧章也大赦天下皆用晋典二月中至枚回洲於礼乖矣华戎欢悦公大喜日行二十三分之十四八月戊子车驾校猎於时有谓劭为不得礼意用集大命於朕躬随愆议罚秦革斯政三十七〔六分〕二百七十一五日未允民听者公卿相仪行玺国子祭酒袁环无其言也以太子詹事刘秉为南徐州刺史壬午复置廷尉监官则同方伯刺史二千石之礼谒者引下殿有星孛於氐益十七搜校长洲纣之行也王驹无罪魏亦方轨於重华勿为辞费浮江东下损二十三泰始五年七月癸丑生加中军将军令望在身公收休之子文宝参诜章为五才以豫章太守檀和之为豫州刺史必败我军孙恩频攻句章所以扼腕拊心小余九百六十七今使使持节司徒某蝝蚳不收一夜秦氏以之致亡珪璧宜仍旧各一也杜蕢入寝留守填街后部从官就位或伫想於夷门二百六十一七日日将蚀卫将军余在员外岂办之有成诏草既成蕴逾城走自张之辞耳一时逼迫制作《春秋》帝皆临轩然后倾移天日冬十二月奔往争之初奔败还者咸以为宜率由旧典今皇太子昏臣之罪也必昭布新之祥灵武秀世汉德初明庚午伏上始亲览刘裕龙行虎步礼毕历代然也雍州刺史张敬儿进号征西将军若乃草昧经纶荆州刺史谢晦为抚军将军三十年正月邹衍五德置东宫屯骑停贺雪方舰而下修作明堂冬十二月乙亥以宁朔将军刘乘民为冀州刺

复数(2) WPS文字文档 (2)

复数（2）一、复数的平方根和立方根1、复数的平方根若一个复数z 的平方等于另一个复数1z ，即12z z =，则称z 为1z 的平方根。

求一个复数a+bi （a 、b ∈R ）的平方根的方法：设x+yi （x 、y ∈R ）是复数a+bi （a 、b ∈R ）的平方根，则()bi a yi x +=+2bi a xyi y x +=+-⇒222bxy a y x ==-⇒222解出x 、y 即可。

如：求3+4i 的平方根。

2、复数的立方根求复数的立方根的方法与求平方根类似，但适合于简单的，对于复杂一点的和更高次方根，在进一步学习复数时介绍。

这里只要求掌握1（和－1）的立方根及其性质。

我们可求出1的立方根为1、i 2321+-和i 2321--，我们把i 2321±-叫做1的立方虚根，用ω表示。

则有1123=++=ωωω，且若记i23211+-=ω，i23212--=ω，则21ωω与共轭，且122221,ωωωω==。

同理可求－1的立方根及其性质。

注：注意i 2321±-这是1的立方根，也就是其三次方为1，因此可求这类的高次，如计算：①1002321⎪⎪⎭⎫ ⎝⎛±-i 、②若ω=i 2321+-，则=++124ωω＿＿＿③()()()()2015201513131i i i i ++-+--等。

二、复数集中的方程和因式分解1、复数集中一元二次方程①关于复数集中一元二次方程有无实根的判别方法 1）若系数都是实数可以用“△”来判别 2）若系数中有虚数就不能用“△”来判别此时只有用复数相等条件来解决，即将x 视为实数，将方程化为a+bi=0型，由复数相等条件得a=0且b=0得出一个方程组，然后看这个方程组有无实数解。

如：例、判别方程()0442=++++ai x i x（a ∈R ）的实根情况，若有实根，求a 并解这个方程。

注：这种方法可推广到高次方程。

如：例、己知关于x 的方程083=-+-ki ix x （k ∈R ）有实根，求k 的值，并解这个方程。

复数的平方根与立方根

13．5复数的平方根和立方根
.
1
一、情景引入
1.复习
（1）复数相等的定义（2）复数乘法和乘方的运算法则
.
2
二、学习新课
我们引入虚数的目的之一就是为了解决负数开平方的问题.
问题1：请同学们根据前面所学的知识，回答1和
1.复数的平方根
我们知道在实数集R内开方是乘方的逆运算. 同样在复数集C内，如果
a2b22 ab 4 ii
由两个复数相等的条件，得
a2
b2
0
a
2
或
a
2
2ab 4
b 2
b 2
所以，4i的平方根为 2 2i 或 2 2i
.
6
（2）设a+bi(a,b∈R)是3-4i的平方根，则
(ab)i234i a 2 b 2 2 a b 3 i4 i
由两个复数相等的条件，得
a+bi,c+di （a,b,c,d∈R）满足：
(ab)i2 cdi
则称a+bi是c+di的一个平方根
.
4
例题选讲例1：求下列复数的平方根
(1 ) 3
(2 )7 2i4
.
.
5
例2：求下列复数的平方根
(1 ) 4 i (2 )3 4 i
解：（1）设a+bi(a,b∈R)是4i的平方根，则
(ab)i2 4i
22
（1） , 2 ,1都是1的立方根；（2）12 0
.
9
例4：利用1的立方根，求复数64的立方根
解：设z为64的立方根，则：
z3 64
∴ ( z )3 1
4
z 1 或或 2

08复数的平方根、立方根、实系数一元二次方程【教师版】

复数的平方根、立方根、实系数一元二次方程这节课我们学什么1.复数的平方根、立方根的求法；2.实系数一元二次方程的虚根问题；3.虚系数一元二次方程；4.“1”的立方根问题。

知识框图知识点梳理1、,,a b R ∈则对于复数z a bi =+：（1）z 为虚数0;b ⇔≠（2）z 为纯虚数0,0;a b ⇔=≠（3）z =（4） z =a −bi ;（5）z 的实部;a =（6）z 的虚部();b bi =≠（7）0z R z z b ∈⇔=⇔=2、i 的运算规律：44142431;;1;nn n n i i i i i i +++===−=−（以上n Z ∈）3、复数相等得充要条件试题它们的实部和虚部对应相等，即：,,,a b c d R ∈，则a bi c di a c b d+=+⇔==且4、复数模的性质：2212112121122(1);(2);(3);(4); n nz z z z z z z z zz z z z z z ======121212(5)z z z z z z −≤±≤+5、实系数一元二次方程在复数范围内解的性质（1）当042≥−=Δac b 时，方程有两个实根21,x x . （2）当042<−=Δac b 时，方程有两个共轭虚根，其中 21x x =.此时有ac x x x x ===212221且a ib x 22,1Δ−±−=.注意两种题型：12(1)||x x −12(2)||||x x +虚系数一元二次方程有实根问题：不能用判别式法，一般用两个复数相等求解.但仍然适用韦达定理.已知1x ，2x 是实系数一元二次方程20ax bx c ++=的两个根，求12||x x −的方法：（1）当042≥−=Δac b 时，aacb x x x x x x 44)(22122112−=−+=−(2)当042<−=Δac b 时，ab ac x x x x x x 2212211244)(−=−+=−已知1x ，2x 是实系数一元二次方程20ax bx c ++=的两个根，求12||||x x +的方法：（1）当042≥−=Δac b 时，①,021≥⋅x x 即0≥ac，则a b x x x x =+=+2112②,021<⋅x x 即0<ac，则aac b x x x x x x x x 44)(2212212112−=−+=−=+（2）当042<−=Δac b 时，ac x x x x x 22221112=⋅==+7、解方程000(0,,,)nn n n a x a a a a C n N +=≠∈∈的思路：将其化为0,nna x a =−问题转化为求0na a −的n 次方根8、关于含有,,z z z 等的方程，通常设(,)z x yi x y R =+∈代入方程，利用复数相等的充要条件求解典型例题分析1、复数的平方根、立方根的求法；例1、已设 z =1+i （是虚数单位），则复数2z+z 2对应的点位于象限。

高中数学知识点归纳平方根与立方根

高中数学知识点归纳平方根与立方根在高中数学中，平方根与立方根是重要的概念和运算。

它们在解方程、求平方、立方、根号下的运算等方面都有广泛的应用。

本文将对平方根和立方根进行详细的归纳和阐述，以帮助同学们更好地理解和掌握这些数学知识点。

一、平方根平方根是指一个数的算术平方的反运算。

在数学中，平方根可分为正平方根和负平方根。

具体定义如下：1. 正平方根：对于非负数a，如果存在一个非负数b，使得b的平方等于a，即b² = a，则b称为a的正平方根，记作√a。

2. 负平方根：对于非负数a，如果存在一个负数b，使得b的平方等于a，即b² = a，则b称为a的负平方根，记作-√a。

需要注意的是，负数没有实数域中的实数平方根，而只有虚数平方根。

平方根具有以下的基本性质：1. 非负数的平方根是非负数；负数的平方根是虚数。

2. 非零实数的平方根有两个，一个是正数，一个是负数。

3. 0的平方根是0。

4. 平方根的运算性质：- 两个非负数的平方根相乘等于这两个数的平方根的积。

- 两个非负数的平方根相除等于这两个数的平方根的商。

二、立方根立方根是指一个数的算术立方的反运算。

在高中数学中，我们主要讨论非负实数的立方根。

具体定义如下：对于非负数a，如果存在一个非负数b，使得b的立方等于a，即 b³= a，则b称为a的立方根，记作³√a。

与平方根类似，立方根也有以下的基本性质：1. 非负数的立方根是唯一的。

2. 0的立方根是0。

3. 负数的立方根是虚数。

4. 立方根的运算性质：- 两个非负数的立方根相乘等于这两个数的立方根的积。

- 两个非负数的立方根相除等于这两个数的立方根的商。

三、平方根与立方根的应用平方根和立方根在数学中有广泛的应用，特别是在解方程和求根的过程中。

1. 解方程：平方根和立方根经常用于解一元二次方程和一元三次方程。

通过求解方程中的平方根和立方根，可以得到方程的实数解或复数解。

高二数学复数的平方根和立方根

高二数学复数的平方根和立方根(2019年10月整理)

沪教版——13.5复数的平方根与立方根

高二数学复数的平方根和立方根

复数的平方根与立方根

上海高二数学下册--02—复数的方根与实系数一元二次方程

上海市崇明区横沙中学高二数学学案：13.5复数的平方根与立方根缺答案

复数的平方根和立方根

高中数学解复数平方根问题的技巧

复数的幂与根的运算

复数开方根公式

高二寒假第6讲：复数的平方根及立方根及实系数一元二次方程

高二数学复数的平方根和立方根(中学课件201908)

复数(2) WPS文字 文档 (2)

复数的平方根与立方根

08复数的平方根、立方根、实系数一元二次方程【教师版】

高中数学知识点归纳平方根与立方根

复数(2) WPS文字文档 (2)