高中数学函数的解析式
高中数学-求函数解析式的六种常用方法

求函数解析式的六种常用方法一、换元法已知复合函数f [g (x )]的解析式,求原函数f (x )的解析式.令g (x )= t ,求f (t )的解析式,再把t 换为x 即可.例1 已知f (xx 1+)= x x x 1122++,求f (x )的解析式. 解: 设x x 1+= t ,则 x= 11-t (t ≠1), ∴f (t )= 111)11(1)11(22-+-+-t t t = 1+2)1(-t +(t -1)= t 2-t+1 故 f (x )=x 2-x+1 (x ≠1).评注: 实施换元后,应注意新变量的取值范围,即为函数的定义域.二、配凑法例2 已知f (x +1)= x+2x ,求f (x )的解析式.解: f (x +1)= 2)(x +2x +1-1=2)1(+x -1,∴ f (x +1)= 2)1(+x -1 (x +1≥1),将x +1视为自变量x ,则有f (x )= x 2-1 (x ≥1).评注: 使用配凑法时,一定要注意函数的定义域的变化,否则容易出错.三、待定系数法例3 已知二次函数f (x )满足f (0)=0,f (x+1)= f (x )+2x+8,求f (x )的解析式.解:设二次函数f (x )= ax 2+bx+c ,则 f (0)= c= 0 ①f (x+1)= a 2)1(+x +b (x+1)= ax 2+(2a+b )x+a+b ② 由f (x+1)= f (x )+2x+8 与①、② 得⎩⎨⎧=++=+822b a b b a 解得 ⎩⎨⎧==.7,1b a 故f (x )= x 2+7x. 评注: 已知函数类型,常用待定系数法求函数解析式.x ≥0, x <0. 四、消去法例4 设函数f (x )满足f (x )+2 f (x1)= x (x ≠0),求f (x )函数解析式. 分析:欲求f (x ),必须消去已知中的f (x 1),若用x1去代替已知中x ,便可得到另一个方程,联立方程组求解即可. 解:∵ f (x )+2 f (x1)= x (x ≠0) ① 由x 1代入得 2f (x )+f (x 1)=x1(x ≠0) ② 解 ①② 构成的方程组,得 f (x )=x 32-3x (x ≠0). 五、特殊值法例5 设是定义在R 上的函数,且满足f (0)=1,并且对任意的实数x ,y , 有f (x -y )= f (x )- y (2x -y+1),求f (x )函数解析式.分析:要f (0)=1,x ,y 是任意的实数及f (x -y )= f (x )- y (2x -y+1),得到f (x )函数解析式,只有令x = y.解: 令x = y ,由f (x -y )= f (x )- y (2x -y+1) 得f (0)= f (x )- x (2x -x+1),整理得 f (x )= x 2+x+1.六、对称性法即根据所给函数图象的对称性及函数在某一区间上的解析式,求另一区间上的解析式.例6 已知是定义在R 上的奇函数,当x ≥0时,f (x )=2x -x 2,求f (x )函数解析式.解:∵y=f (x )是定义在R 上的奇函数, ∴y=f (x )的图象关于原点对称. 当x ≥0时,f (x )=2x -x 2的顶点(1,1),它关于原点对称点(-1,—1),因此当x<0时,y=2)1(+x -1= x 2 +2x.故 f (x )=⎩⎨⎧+-xx x x 2222 评注: 对于一些函数图象对称性问题,如果能结合图形来解,就会使问题简单化.。
函数的解析式

2-x 1-x
③,
解由 ①, ②, ③ 组成的方程组,
得:
f(x)=
x3-x2-1 2x(x-1)
.
评注:
把
f(x),
f(
x-1 x
),
f(
1 1-x
)
都看作“未x). 又如: 已知 af(x)+b1xf( )=cx, 其
中, |a|≠|b|, 求 f(x).
恨恨地说,怎么着?这评书我是每天都听的,莫非今天拉了你,就得坏了我的规矩,让我不知道肖飞是怎么从鬼子眼皮底下逃出去的?你这个女人脑子有毛病! 我虽从感情上向着艨,但司机的话也不无道理. 别说肖飞还是有趣的故事,赶上毛头司机让你听汗毛都炸起的摇滚,不也 得忍了吗?我忙打圆场说,师傅,我这位朋友爱静,就请您把喇叭声拧小点,大家将就一下吧. 没想到首先反对我的是艨. 她说,这不是可以将就的事. 师傅愿意听《肖飞买药》,可以. 您把车停了,自个儿坐在树荫下,爱怎么听就怎么听,那是你的自由 .既然您是在从事服务性的 工作,就得以顾客为上帝. 司机故意让车颠簸起来,冷笑着说,怎么着?我就是听,你能把我如何?说完把声音扩到震耳欲聋. 艨毫不示弱地说,那你把车停下. 我们下车! 司机说,我就不停,你有什么办法?莫非你还敢跳车?! 艨坚定地说,我为什么要跳车?我坐 车,就是为了寻求便利. 我付了钱,就该得到相应的待遇,你无法提供合乎质量的服务,我就不付你报酬. 天经地义的事情,走遍天下我也有理. 我以为司机一定会大怒,把我们抛在公路上. 没想到在艨的逻辑面前,他真的把收音机关了,虽然脸色黑得好似被微波炉烘烤过度的虾饼. 司机终于把我们平安拉到了目的地. 下车后,我心有余悸. 艨却说,这个司机肯定会记住这件事的,以后也许会懂得尊重乘客. 吃饭时落座艨挑选的小馆,她很熟练地点了招牌菜. 艨说此次回国,除了见老朋友,最重要的是让自己的胃享享福,它被洋餐折磨得太久太痛苦了. 菜上得 很快,好像是自己的厨艺,艨一个劲地劝我品尝. 我一吃,果然不错,轮到艨笑眯眯地动了筷子,入了口,脸上却变了颜色,招来小姐. 你们掌勺的大厨,是不是得了重感冒?不舒服,休息就是,不宜再给客人做饭的. 艨很严肃地说. 小姐一路小跑去了操作间,很快回来报告说, 掌勺的人很健康,没有病的. 她一边说着,一边脸上露出嫌艨多此一举的神色. 我也有些怪艨,你也不是防疫站的官员,管得真宽. 忙说,快吃快吃,要不菜就凉了. 艨又夹了一筷子菜,仔细尝尝,然后说,既然大厨没生病,那就一定是换了厨师. 这菜的味道和往日不一样,盐 搁得尤其多. 我原以为是厨师生了感冒,舌苔黄厚,辨不出咸淡,现在可确定是换了人. 对吗?她征询地望着小姐. 小姐一下子萎靡起来,又有几分佩服地说,你的舌头真是神. 大厨今天有急事没来,菜果真是二厨代炒的. 真对不起. 小姐的态度亲切可人,我觉得大可到此为止. 不想艨根本不吃这一套,缓缓地说,在饭店里,是不应该说“对不起”这几个字的. 艨说,如果我享受了你的服务,出门的时候,不付钱,只说一声“对不起”,行吗? 小姐不语,答案显然是否定的. 艨循循善诱地说,在你这里,我所要的一切都是付费的. 用“对不起” 这种话安慰客人,不做实质的解决,往轻点说是搪塞,重说就是巧取豪夺. 这时一个胖胖的男人走过来,和气地说,我是这里的老板,你们的谈话我都听到了,有什么要求,就同我说吧. 是菜不够热,还是原料不新鲜?您要是觉得口感太咸的话,我这就叫厨房再烧一盘,您以为如何? 我想,艨总该借坡下驴了吧. 没想到艨说,我想要少付你钱. 老板压着怒火说,菜的价钱是在菜谱上明码标了的,你点了这道菜,就是认可了它的价钱,怎么能吃了之后杀价呢?看来您是常客,若还看得起小店,这道菜我可以无偿奉送,少收钱却是不能开例的. 艨不慌不忙地说, 菜谱上是有价钱不假,可你那是根据大厨的手艺定的单,现在换了二厨,他的手艺的确不如大厨,你就不能按照原来的定价收费. 因为你付给大厨的工钱和付给二厨的工钱是不一样的. 既然你按他们的手艺论价,为什么到了我这里,就行不通了呢? 话被艨这样掰开揉碎一说,理就 是很分明的事了. 于是艨达到了目的. 和艨进街上的公共厕所,艨感叹地说,真豪华啊,厕所像宫殿,这好像是中国改变最大的地方. 女厕所里每一扇洗手间的门都禁闭着,女人们站在白瓷砖地上,看守着那些门,等待轮到自己的时刻. 我和艨各选了一列队伍,耐心等待. 我的那扇门还好,不断地开启关闭,不一会就轮到了我. 艨可惨了,像阿里巴巴不曾说出“芝麻开门”的口诀,那门总是庄严地紧闭着. 我受不了气味,对艨说了声,我到外面去等你啊,便撤了出去. 等了许久,许多比艨晚进去的女人,都出来了,艨还在等待……等艨终于解决问题了以 后,我对艨说,可惜你站错了队啊. 艨嘻嘻笑着说,烦你陪我去找一下公共厕所的负责人. 我说,就是门口发手纸的老大妈. 艨说,你别欺我出国多年,这点规矩还是记得的. 她管不了事. 我要找一位负责公共设施的官员. 我表示爱莫能助,不知道这类官司是找环保局还是 园林局(因为那厕所在一处公园内). 艨思索了片刻. 找来报纸,毫不犹豫地拨打了上面刊登的市长电话. 我吓得用手压住电话叉簧,说艨你疯了,太不注意国情! 艨说,我正是相信政府是为人民办事的啊. 我说,一个厕所,哪里值得如此兴师动众? 艨说,不单单是 厕所. 还有邮局、银行、售票处等等,中国凡是有窗口和门口的地方,只要排队,都存在这个问题. 每个工作人员速度不同,需要服务的人耗时也不同,后面等待的人不能预先获知准确信息. 如果听天由命,随便等候,就会造成不合理、不平等、不公正……关于这种机遇的分配问题,作 为个人调查起来很困难,甚至无能为力. 比如我刚才不能一个个地问排在前面的女人,你是解大手还是解小手,以确定我该排在哪一队后…… 我说,艨你把一个简单的问题说得很复杂,简明扼要地告诉我,你打算在厕所里搞一场什么样的革命? 艨说,要求市长在厕所里设条一 米线,等候的人都在线外,这样就避免了排错队的问题,提高效率,大家心情愉快. 北美就是这样的. 我说,艨,你在国内还会上几次厕所?还会给谁寄钱或取邮件?我们浸泡其中都置若惘闻,你又何必这样不依不饶?你已是一个北美人,马上就要回北美去,还是到那里安稳享受你 的厕所一米线吧. 艨说,这些年,我在国外,没有什么本事,就是买买东西上上街. 我不像别的留学生回国,有很多报效国家的能力. 我只是一个家庭妇女,觉得那里有些比咱高明的地方,就想让这边学了来. 这几天我让你们陪我,是想让你们明白我的心. 我不是英雄,没法振臂一 呼,宣传我的主张;也不是作家,不会写了文章,让更多的人知道我的想法. 我只有让你们从我看似乖张的举动里,感觉到这世上有一个更合理的标准存在着,可以学习借鉴. 我为艨的苦心感动,但还是说,就算你说的有理,这些事也太小了. 要知道中国有些地方连温饱都没有解决 啊. 艨说,我对中国充满信心. 温饱解决之后,马上就会遭遇这些问题. 对于普通人来说,我们流泪,有多少是为了远方的难民?基本上都是因为眼睛里进了沙子. 身边的琐事标志着文明的水准. 现代化不是一个空壳,它是一种更公正更美好的社会. 我把压在电话叉簧之上的手 指松开了,让艨去完成找市长的计划. 那个电话打了很长,艨讲了许多她以为中国可以改进的地方,十分动情. 分手的时候,艨说,有些中国人入了外国籍以后,标榜自己是个“香蕉人”,意思是自己除了外皮是黄色的,内心已变得雪白. 而我是一个“芒果人”. 我说“芒果 人”,好新鲜. 怎么讲? 艨说,芒果皮是黄的,瓤也是黄的. 我永远爱我的祖国。 名家散文汇编:毕淑敏 风的青睐 ? 400年前的法国人蒙田,说过这样一句话——风不会对漫无目的者有所青睐…… 青睐是指一个人用黑眼珠子看着你。这是一句反话。意思是假如你有了坚定的 目的,整个大自然将帮助你。 风是什么呢?风是一股看不见摸不着的力量。风吹的时候,影响着我们,逆风或是顺风,对我们的速度和方向都强有力地制约着。就连飞机的钢铁巨翅,也不敢对风等闲置之。 人生的目的很重要。这个目的,是谁给我们预定的呢?没有人。你的父 母你的师长你的朋友,都可能参与你的目的的制定,但他们不是决定的力量。最后的赞成或是否决票,在你手里。如果你对自己说,我才不要什么人生的目的这种奇怪的东西,那么,你也是有一个目的了,那就是“虚无”。 一个没有方向感的人,如何行走呢?看看醉汉就明白了。 踉踉跄跄,东倒西歪,昏乱地嘟囔着,没有人知道他要到哪里去,更不知道他的归宿在何方……这种精神的吉普赛人,终生流浪在灵魂的荒原。 还有一些人,把某种流行的腐朽说法或是沉沦的误区,当成了自己的目的。这种镜花水月的伪目的,只能引诱感官的沉没和本能的麻痹。 目的的特征:通常是阔大的,依稀的,但它确实存在着,一如晨曦。你从未摸到晨曦,但你每天都可以看到它。即使乌云蔽日的时候,你也坚韧不拔地确信,在高远之处,晨曦依然发出红色温暖的光芒。 一个有目的的人,走路的姿势是向前的。他们通常不会在跌到之后,太长地抚 摸伤痛,短暂的昏厥之后迅速地清醒,用身边的树枝或是草叶,捆扎好伤口,蹒跚着上路了。他们走得慢,但很坚定,不会因为风险而避开既定的方向,也不会为路边一些小的花果而长期间地流连忘返。当然也有痴迷和混沌的时候,但他们能够重新恢复思考的冷静,从容向前…… 风的 青睐,是无价的礼物。只要你坚定地确立了自己的目标,努力下去,就会发现天地万物都来帮你了。 每天都冒一点险 一 ? ?"衰老很重要的标志,就是求稳怕变。所以,你想保持年轻吗?你希望自己有活力吗?你期待着清晨能在新生活的憧憬中醒来吗?有一个好办法——每天都冒一点 险。" ? ?以上这段话,见于一本国外的心理学小册子。像给某种青春大力丸做广告。本待一笑了之,但结尾的那句话吸引了我——每天都冒一点险。 ? ? "险"有灾难狠毒之意。如果把它比成一种处境一种状态,你说是现代人碰到它的时候多呢,还是古代甚至原始时代碰到的多呢?粗粗 一想,好像是古代多吧。茹毛饮血刀耕火种时,危机四伏。细一想,不一定。那时的险多属自然灾害,虽然凶残,但比较单纯。现代了,天然险这种东西,也跟热
高中数学教案:函数的图像与解析式

高中数学教案:函数的图像与解析式一、引言函数是数学中的重要概念之一,研究函数的图像与解析式可以帮助我们更好地理解和应用函数。
本教案旨在通过深入剖析函数的图像与解析式,帮助高中学生掌握这一知识点。
二、函数的图像1. 线性函数线性函数是最基本也是最简单的一类函数,其图像为直线。
线性函数的形式可以表示为y = kx + b,其中k为斜率,b为截距。
根据斜率和截距的正负关系可以判断直线在坐标平面上的走向和位置。
2. 平方函数平方函数或二次函数具有y = ax^2 + bx + c的形式,其中a、b和c为常数,a 不等于零。
平方函数的图像通常为开口向上或开口向下的抛物线。
通过观察a、b 和c确定抛物线开口方向及位置。
3. 指数函数指数函数具有y = a^x 的形式,其中a为底数。
指数函数以不同速度递增或递减,并且对称于y轴(当底数小于1时)。
观察底数大小和曲线行为对理解指数函数图像非常重要。
4. 对数函数对数函数与指数函数互为反函数。
对数函数的一般形式为y = log_a(x),其中a 为底数。
不同底数的对数函数图像在x轴和y轴上的截距不同,因此观察底数变化有助于理解对数函数图像。
三、函数的解析式1. 通过图像获取解析式根据已知的函数图像,可以推导出其解析式。
以线性函数为例,通过观察直线斜率和截距的信息,可以得到相应的解析式。
通过实际运用不同类型的图像来找出特定模式,并将其转化为解析式是掌握这一技能的关键。
2. 利用已知条件确定参数值一些特殊类型的函数图像可以利用已知条件确定参数值。
例如,在平方函数中,实根、定点和对称轴等信息可以帮助我们找到a、b和c的值。
3. 求数学问题中未知量时使用解析式在应用题中,往往需要求出某个未知量。
通过建立方程并利用相关的解析式,将问题转化为代数求解。
例如,在经济学领域中,利润和成本之间通常存在着特定关系,可通过建立方程求得最优点。
四、教学示范与练习1. 示范:教师通过投影仪展示各种函数的图像,并要求学生分析其特点,给出解析式。
高中数学必修一《求函数解析式》优秀教学设计

求函数解析式教学设计一、教学内容教学重点:如何求函数解析式教学难点:换元法、待定系数法与方程法及适用条件二、教学目标1、理解掌握求函数解析式的方法2、培养学生分析归纳、类比推理判断能力三、教学过程1.引入函数解析式是函数与自变量之间建立联系的桥梁,许多和函数有关的问题都离不开函数解析式,因此准确理解函数解析式,掌握函数解析式所蕴含的式子特征及变形技巧尤其重要,下面对函数解析式的常用方法进行归类解析.一、换元法例3(1)().,lg 12x f x xf 求已知=⎪⎭⎫ ⎝⎛+ ()()()()112lg 112lg 12,10,12>-=∴>-=∴-=>∴>=+x x x f t t t f t x t x t x 且【解析】令 【点评】在换元时,需注意所换元的取值范围,并在最后注明所求函数的定义域.二、待定系数法例3(2)()()()()().,11,20x f x x f x f f x f 求是二次函数,且已知-=-+=()()()()()()()().223212321112,12,1111.2,20,02222+-=∴⎪⎩⎪⎨⎧-==⎩⎨⎧-=+=∴-=++-=--+++=-+==≠++=x x x f b a b a a x b a ax x bx ax x b x a x f x f c f a c bx ax x f 即即又得由【解析】设【点评】在已知函数具体类型时,大多采用待定系数法,其具体做法通常是根据条件列出以参数为未知数的方程或方程组求解.三、方程法例3(3)()()().,012x f x x x f x f 求已知≠=⎪⎭⎫ ⎝⎛+ ()()()()()().033212112.12112≠-=⎪⎪⎩⎪⎪⎨⎧=+⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛+=+⎪⎭⎫ ⎝⎛∴=⎪⎭⎫ ⎝⎛+x x x x f x x f x f x x f x f x x f x f x x f x f 得解方程组【解析】 例3(4)()()()().,2R 2x f x x x f x f x f 求,且的定义域为已知函数-=-+()()()()().31,2,2222x x x f x x x f x f x x x f x f +=+=+--=-+解方程组得得【解析】由【点评】本题是利用方程的思想,将()()()x f x f x f x f -⎪⎭⎫ ⎝⎛与或与1看作两个未知数,通过解方程组求得.2总结【解题心得】函数解析式的求法:(1)换元法,已知复合函数()()x g f 的解析式,可用换元法,此时要注意新元的取值范围.(2)待定系数法,若已知函数的类型(如一次函数、二次函数),可用待定系数法.(3)方程法,已知关于()()x f x f x f -⎪⎭⎫ ⎝⎛或与1的表达式,可根据已知条件再构造出另外一个等式组成方程组,通过解方程组求出()x f .【提醒】因为函数的解析式相同,定义域不同,则为不相同的函数,因此求函数解析式时,如果定义域不是R ,一定要注明函数的定义域.3练习【对点训练3】()()()11.D 11.C 11.B 1.A .10,111---≠≠-=⎪⎭⎫ ⎝⎛x x x x x f x x x x x f 等于时,,且则当若()()()()().,17212132=+=--+x f x x f x f x f 则是一次函数,且满足已知()()()().,3123==⎪⎭⎫ ⎝⎛+x f x x f x f x f 则满足已知 4教学反思方程法的掌握有一定困难,学生应加强练习;换元法的掌握为重中之重,应反复练习.。
函数的解析式

高中数学求函数解析式解题方法大全与配套练习
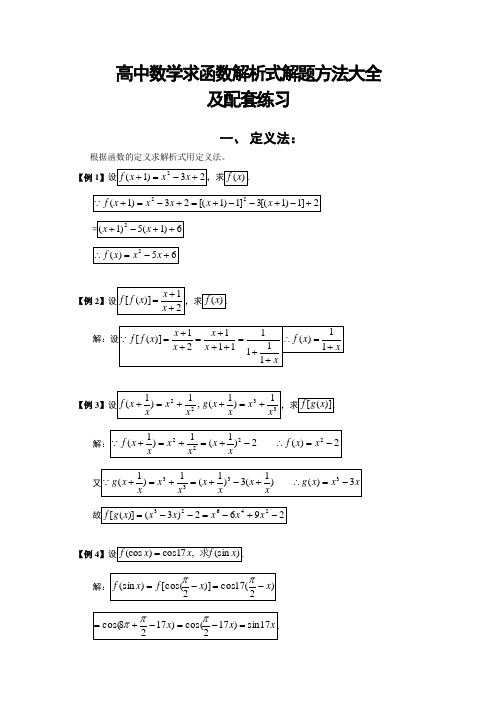
高中数学求函数解析式解题方法大全及配套练习一、定义法:根据函数的定义求解析式用定义法。
【例1】【例2】【例3】【例4】二、待定系数法:(主要用于二次函数)已知函数解析式的类型,可设其解析式的形式,根据已知条件建立关于待定系数的方程,从而求出函数解析式。
它适用于已知所求函数类型(如一次函数,二次函数,正、反例函数等)及函数的某些特征求其解析式的题目。
其方法:已知所求函数类型,可预先设出所求函数的解析式,再根据题意列出方程组求出系数。
【例1】【解析】【例2】已知二次函数f(x)满足f(0)=0,f(x+1)= f(x)+2x+8,求f(x)的解析式.解:设二次函数f(x)= ax2+bx+c,则f(0)= c= 0 ①f(x+1)(x+1)= ax2+(2a+b)x+a+b②由f(x+1)= f(x)+2x+8 与①、②得解得故f(x)= x2+7x.【例3】三、换元(或代换)法:道所求函数的类型,且函数的变量易于用另一个变量表示的问题。
使用换元法时要注意新元定义域的变化,最后结果要注明所求函数的定义域。
如:已知复合函数f [g(x)]的解析式,求原函数f(x)的解析式,把g(x)看成一个整体t,进行换元,从而求出f(x)的方法。
实施换元后,应注意新变量的取值围,即为函数的定义域.【例1】【解析】【例2】【例3】【例4】(1)在(1(2)1(3)【例5】(1(2)由【例6】四、代入法:求已知函数关于某点或者某条直线的对称函数时,一般用代入法.【例1】解则解得,上,(五)配凑法【例1】:2x当然,上例也可直接使用换元法即由此可知,求函数解析式时,可以用配凑法来解决的,有些也可直接用换元法来求解。
【例2】:分析:此题直接用换元法比较繁锁,而且不易求出来,但用配凑法比较方便。
实质上,配凑法也缊含换元的思想,只是不是首先换元,而是先把函数表达式配凑成用此复合函数的函数来表示出来,在通过整体换元。
和换元法一样,最后结果要注明定义域。
高中数学例题:函数解析式的求法

高中数学例题:函数解析式的求法例. 求函数的解析式(1)已知()f x 是二次函数,且(0)2,(1)()1f f x f x x =+-=-,求()f x ;(2)若f(2x-1)=x 2,求f(x);(3)已知3()2()3f x f x x +-=+,求()f x .【答案】(1)213()222f x x x =-+;(2)21()()2x f x +=;(3)3()5f x x =+. 【解析】求函数的表达式可由两种途径.(1)设2()(0)f x ax bx c a =++≠,由(0)2,f =得2c =由(1)()1f x f x x +-=-,得恒等式2ax+a+b=x-1,得13,22a b ==-,故所求函数的解析式为213()222f x x x =-+. (2) ∵f(2x-1)=x 2,∴令t=2x-1,则12t x += 2211()(),()()22t x f t f x ++∴=∴= (3)因为3()2()3f x f x x +-=+,①x 用x -代替得3()2()3f x f x x -+=-+,②由①②消去()f x -,得3()5f x x =+. 【总结升华】(1)解析式类型已知的,如本例(1),一般用待定系数法,对于二次函数问题要注意对一般式2y ax bx c =++,顶点式2()y a x h k =-+和两点式12()()y a x x x x =--的选择.(2)已知[()]f g x 求()f x 的问题,方法一是用配凑法;方法二是用换元法,如本例(2).(3)函数方程问题,需建立关于()f x 的方程组,如本例(3),若函数方程中同时出现()f x 、1()f x ,则一般x 用1x代之,构造另一个方程.举一反三:【变式1】 已知f(x+1)=x 2+4x+2,求f(x).【答案】f(x)=x 2+2x-1.【解析】(1)(法1)f(x+1)=x 2+4x+2=(x+1)2+2(x+1)-1 ∴f(x)=x 2+2x-1;(法2)令x+1=t ,∴x=t-1,∴f(t)=(t-1)2+4(t-1)+2=t 2+2t-1 ∴f(x)=x 2+2x-1;(法3)设f(x)=ax 2+bx+c 则f(x+1)=a(x+1)2+b(x+1)+c∴a(x+1)2+b(x+1)+c=x 2+4x+21x 2x )x (f 1c 2b 1a 2c b a 4b a 21a 2-+=∴⎪⎩⎪⎨⎧-===⇒⎪⎩⎪⎨⎧=++=+=∴;【总结升华】求函数解析式常用方法:(1)换元法;(2)配凑法;(3)定义法;(4)待定系数法等.注意:用换元法解求对应法则问题时,要关注新变元的范围.。
高中数学:函数解析式的十一种方法

高中数学:函数解析式的十一种方法一、定义法 二、待定系数法 三、换元(或代换)法 四、配凑法 五、函数方程组法七、利用给定的特性求解析式.六、特殊值法 八、累加法 九、归纳法 十、递推法 十一、微积分法一、定义法:【例1】设23)1(2+-=+x x x f ,求)(x f .2]1)1[(3]1)1[(23)1(22+-+--+=+-=+x x x x x f =6)1(5)1(2++-+x x65)(2+-=∴x x x f【例2】设21)]([++=x x x f f ,求)(x f . 【解析】设xx x x x x f f ++=+++=++=111111121)]([xx f +=∴11)(【例3】设33221)1(,1)1(x x x x g x x x x f +=++=+,求)]([x g f .【解析】2)(2)1(1)1(2222-=∴-+=+=+x x f x x x x x x f又x x x g x x x x xx x x g 3)()1(3)1(1)1(3333-=∴+-+=+=+ 故2962)3()]([24623-+-=--=x x x x x x g f【例4】设)(sin ,17cos )(cos x f x x f 求=.【解析】)2(17cos )]2[cos()(sin x x f x f -=-=ππx x x 17sin )172cos()1728cos(=-=-+=πππ.二、待定系数法:在已知函数解析式的构造时,可用待定系数法。
【例1】 设)(x f 是一次函数,且34)]([+=x x f f ,求)(x f 【解析】设b ax x f +=)( )0(≠a ,则bab x a b b ax a b x af x f f ++=++=+=2)()()]([∴⎩⎨⎧=+=342b ab a ∴⎩⎨⎧⎩⎨⎧=-===3212b a b a 或 32)(12)(+-=+=∴x x f x x f 或 【例2】已知1392)2(2+-=-x x x f ,求)(x f .【解析】显然,)(x f 是一个一元二次函数。
人教版高中数学高一《函数的解析式》教学设计附反思

函数的单调性与导数教学内容:人教版《普通高中课程标准实验教科书数学》选修1- 1 P 97—101教学目标:(1)知识目标:能探索并应用函数的单调性与导数的关系求单调区间,能由导数信息绘制函数大致图象。
⑵能力目标:培养学生的观察能力、归纳能力,增强数形结合的思维意识。
(3)情感目标:通过在教学过程中让学生多动手、多观察、勤思考、善总结,引导学生养成自主学习的学习习惯。
b5E2RGbCAP教学重点:探索并应用函数单调性与导数的关系求单调区间。
教学难点:利用导数信息绘制函数的大致图象。
教学方法:发现式、启发式教学手段:多媒体课件等辅助手段教具、学具准备:CAI课件一套、学生每人一份实验表格及一支牙签教学过程预设:、观察与表达(探索函数的单调性和导数的关系)问:函数的单调性和导数有何关系呢?教师仍以y=x2为例,借助几何画板动态演示, 让学生记录结果在课前发的表格第二行中: 1 •这一部分是后面利用导数求函数单调区间的理论依据,重要性不言而喻,而学生又只学习了导数的意义和一些基本运算,要想得到严格的证明是不现实的,因此,只要求学生能借助几何直观得出结论,这与新课标中的要求是相吻合的。
2 •教师对具体例子进行动态演示,学生对一般情况进行实验验证。
由观察、猜想到归纳、总结,让学生体验知识的发现、发生过程,变灌注知识为学生主动获取知识,从而使之成为课堂教学活动的主体。
问:有何发现?(学生回答)问:这个结果是否具有一般性呢?我们来考察两个一般性的例子:(教师指导学生动手实验:把准备的牙签放在表中曲线y=f(x)的图象上,作为曲线的切线,移动切线并记录结果在上表第三、四行中。
)问:能否得出什么规律?让学生归纳总结,教师简单板书:在某个区间(a,b)内,若f ' (x)>0,则f(x)在(a,b)上是增函数;若f ' (x)<0,则在f(x)(a,b)上是减函数。
教师说明:要正确理解某个区间”的含义,它必需是定义域内的某个区间。
求函数解析式的几种方法及题型

求函数解析式的几种方法及题型【最新版3篇】篇1 目录一、引言二、求函数解析式的常用方法1.待定系数法2.交点式3.顶点式4.换元法5.归纳法三、求函数解析式的题型及应用1.已知三个点求解析式2.已知顶点求解析式3.已知交点求解析式4.抽象复杂函数问题四、结论篇1正文一、引言求函数解析式是高中数学中的常见问题,也是高考的常规题型之一。
解决这类问题需要掌握一定的方法和技巧。
本文将介绍几种常用的求函数解析式的方法及题型,帮助同学们更好地理解和应用这些方法。
二、求函数解析式的常用方法1.待定系数法待定系数法是一种求未知数的方法。
将一个多项式表示成另一种含有待定系数的新的形式,这样就得到一个恒等式。
然后根据恒等式的性质得出系数应满足的方程或方程组,其后通过解方程或方程组便可求出待定的系数,或找出某些系数所满足的关系式。
2.交点式交点式适用于已知抛物线与 x 轴的两个交点的情况。
通过已知的交点,我们可以得到两个方程,解这两个方程可以求得抛物线的解析式。
3.顶点式顶点式适用于已知抛物线的顶点的情况。
通过已知的顶点,我们可以得到一个方程,这个方程包含了抛物线的顶点坐标和抛物线的解析式中的待定系数。
解这个方程可以求得抛物线的解析式。
4.换元法换元法是一种通用的求函数解析式的方法,适用于各种复杂的函数问题。
通过换元,我们可以将复杂的函数问题转化为简单的函数问题,从而求得函数的解析式。
5.归纳法归纳法适用于具有一定规律的函数问题。
通过观察函数的规律,我们可以猜测函数的解析式,然后通过数学归纳法证明我们的猜测是正确的。
三、求函数解析式的题型及应用1.已知三个点求解析式已知函数上的三个点,我们可以通过待定系数法求解函数的解析式。
设定函数的形式为 y=ax^2+bx+c,然后将三个点的坐标代入方程,得到三个方程组成的线性方程组,解这个方程组可以求得函数的解析式。
2.已知顶点求解析式已知抛物线的顶点,我们可以通过顶点式求解抛物线的解析式。
高中数学:求函数解析式的10种常见方法

高中数学:求函数解析式的10种常见方法一、配凑法:给定$f(x+1)=x-3x+2$,求$f(x)$。
练1:设函数$f(x)=2x+3$,$g(x+2)=f(x)$,求$g(x)$。
练2:设$f(f(x))=x^2+2$,求$f(x)$。
练3:设$f(x+2)+f(x)=x^3+x$,求$f(x)$。
二、待定系数法:例1:如果反比例函数的图像经过点$(1,-2)$,那么这个反比例函数的解析式为$\frac{-2}{x-1}$,求$f(x)$。
练1:在反比例函数$y=\frac{k}{x}$的图像上有一点P,它的横坐标$m$与纵坐标$n$是方程$t^2-4t-2=0$的两个根,求$k$。
练2:已知二次函数$f(x)$满足$f(x+1)=f(x)+2x+8$,求$f(x)$的解析式。
练3:已知$f(x-2)=2x-9x+13$,求$f(x)$。
三、换元(或代换)法:例1:已知函数$f(\frac{1-x}{1+x})=\frac{1+x}{1-x}$,求:(1)$f(2)$的值;(2)$f(x)$的表达式。
练1:已知$f(x+1)=x+2x$,求$f(x)$及$f(x^2)$;练2:已知$f(x)=\frac{1}{2}x+\frac{1}{x}$,求$f(x+1)$.四、消去法:例1:设函数$f(x)$满足$f(x)+2f(\frac{1}{x})=x$,求$f(x)$.练1:已知$f(x)-2f(-x)=3x+2$,求$f(x)$.练2:已知定义在R上的函数$f(x)$满足$f(-x)+2f(x)=x+1$,求$f(x)$.练3:已知$f(x)+3f(-x)=2x+1$,求$f(x)$.练4:设函数$f(x)$满足$af(x)+bf(\frac{1}{x})=cx$(其中$a,b,c$均不为$0$,且$a\neq\pm b$),求$f(x)$.五、反函数法:例1:已知$f(a^2-x^2)=x$,求$f(x)$。
高中数学-求函数解析式的六种常用方法

高中数学-求函数解析式的六种常用方法求函数解析式是高中数学中的重要内容之一,常用的方法有六种。
下面分别介绍这六种方法。
一、换元法如果已知复合函数$f[g(x)]$的解析式,要求原函数$f(x)$的解析式,可以令$g(x)=t$,求$f(t)$的解析式,再把$t$换为$x$即可。
例如,已知$f(x)=\frac{x^2+11x+1}{x(x+1)}$,要求$f(x)$的解析式。
设$g(x)=\frac{1}{x}$,则$x=\frac{1}{g(x)}$,代入$f(x)$得$f(g(x))=\frac{g(x)^2+11g(x)+1}{g(x)+1}$,再令$t=g(x)$,则$f(t)=\frac{t^2+11t+1}{t+1}$,最后把$t$换为$x$,得到$f(x)=\frac{x^2+11x+1}{x(x+1)}$。
二、配凑法如果已知$f(x+1)=x+2x^2$,要求$f(x)$的解析式,可以使用配凑法。
首先,把$x+1$视为自变量$x$,则有$f(x)=x^2-1$,但要注意函数的定义域的变化,即$x+1\geq 1$,即$x\geq 0$。
三、待定系数法如果已知函数类型,可以使用待定系数法求函数的解析式。
例如,已知二次函数$f(x)$满足$f(0)=0$,$f(x+1)=f(x)+2x+8$,要求$f(x)$的解析式。
设$f(x)=ax^2+bx+c$,代入已知条件得到$c=0$,$a+b=8$,$2a+b=0$,解得$a=1$,$b=7$,$c=0$,所以$f(x)=x^2+7x$。
四、消去法如果已知$f(x)+2f(\frac{1}{x})=\frac{x}{x-1}$,要求$f(x)$的解析式,可以使用消去法。
把已知中的$f(\frac{1}{x})$用$f(x)$表示出来,得到$2f(x)+f(\frac{1}{x})=\frac{x}{x-1}$,再把$x$换成$\frac{1}{x}$,得到$2f(\frac{1}{x})+f(x)=\frac{1}{x-1}$,解得$f(x)=-\frac{x}{3(x-1)}$。
高中数学:函数解析式的十一种方法

高中数学:函数解析式的十一种方法一、定义法六、特殊值法二、待定系数法八、累加法三、换元(或代换)法九、归纳法四、配凑法十、递推法五、函数方程组法十一、微积分法七、利用给定的特性求解析式.一、定义法:2 x【例1】设f (x 1) x 3 2,求f ( x) .2 x x 2 x 2 xf ( x 1) x 3 2 [( 1)1] 3[( 1) 1] 2 = (x 1) 5( 1) 6f (x) 2 xx 56【例2】设x 1f [ f ( x)] ,求f (x) .x 2【解析】设 f [ f ( x)] xx12x 11f(x)1x 1 1 111x1x【例3】设1 2 1 1 13f (x ) x , g(x ) x ,求f [ g( x)] .2 3x x x x1 1 12 f x x2 2【解析】) 2 ( ) 2f (x) x (x2x x x1 1 1 13 3 3又g x x xg( x) x (x ) 3(x ) ( ) 33x x x x3 x x x x2 6 4 2故f [ g( x)] (x 3 ) 2 6 9 2【例4】设f (cos x) cos17 x, 求f (sin x) .【解析】)f (sin x) f [cos( x)] cos17 ( x2 2cos(8 17 x) cos( 17 x) sin17x.2 2二、待定系数法:在已知函数解析式的构造时,可用待定系数法。
【例1】设f (x) 是一次函数,且 f [ f ( x)] 4x3,求 f (x)【解析】设f (x) ax b (a 0),则f [ f ( x)] af (x) b a( ax b) b a 2 x ab ba ab 2 4b 3ab2 a或1 b23f (x) 2x 1或 f (x) 2x 32 x【例2】已知f (x 2) 2x 9 13,求f (x) .2 bx c a 【解析】显然, f (x) 是一个一元二次函数。
高中数学求解函数解析式方法(附例题)

求解函数解析式基本方法(附例题)一、求解函数解析式 1、换元法汇总,切记定义域综上所述:新元代换旧元可化作:则取值范围换元,立刻确定新元的则令变形由解:由题意可知:的解析式求已知11,1)(f t 1f(t)①1t 1,cos t 1sin cos ①cos 1)(cos )(f ,sin )(cos f 222222≤≤--=-=≤≤-==+-==x x x x x x x x f x x x 练习一:)的解析式(答案见文末求已知)(,2)1(2x f x x x f -=+2、凑配法汇总,切记定义域求解定义域又运用完全平方公式解:的解析式求已知2,2)(21,02)1()1()(,0,1)1(2222≥-=∴≥+∴>-+=+>+=+x x x f xx x xx x x f x f x x x x x f练习二:解析式求已知)(,45)2(2x f x x x f ++=+换元法和凑配法在实际运用过程中,以计算简单、准确为原则,根据题目恰当选择。
3、待定系数法5)1(5)(505)10()0(0,05)1()(5,15,1)()()(5,1)(2222+--=-==+-=∴+-===+-=x x f a a f x a x f h k hk x a x f x f x f 综上所述,解得:)点,代入计算图像过(图像过原点又故值根据物理意义,直接赋)可得,由顶点为(数顶点式根据题意,选择二次函解:由题意可设:的解析式),且经过原点,求(是二次函数,其顶点为已知练习三:的解析式(求且是二次函数,已知),3)0(,12)()1()(x f f x x f x f x f =+=-+4、构造方程组法:),(联立方程组,求解:)式联立方程组,解得)、(将(合适替换元得:替换用注意定义域,选取),(,且解:的解析式(求满足)上的函数,定义在(∞+∈--==-∴∞+∈=-=-∞+0,323)(21)2(1)(2)1(,10)1()1(2)(),)1(2)()(0x xx x f x x f x f x xx x xf x f x f x xf x f x f 练习四:的解析式求满足)上的函数定义在()(,1)1(2)()(,0x f x xf x f x f -⋅=+∞求解函数解析式,一般出填空题,或者大题的第一小问。
高中数学:求函数解析式的10种常见方法

求函数解析式的几种常用方法一、配凑法:例1:设23)1(2+-=+x x x f ,求)(x f .练1:设函数()23,(2)()f x x g x f x =++=,求()g x 。
练2:设21)]([++=x x x f f ,求)(x f .练3:设33221)1(,1)1(xx x x g x x x x f +=++=+,求)]([x g f .二、待定系数法:例1:如果反比例函数的图象经过点(1,2)-,那么这个反比例函数的解析式为 。
练1:在反比例函数k y x=的图象上有一点P ,它的横坐标m 与纵坐标n 是方程2420t t --=的两个根,求反比例解析式。
练2:已知二次函数()x f 满足()00=f ,()()821++=+x x f x f ,求()x f 的解析式。
练3:已知1392)2(2+-=-x x x f ,求)(x f .三、换元(或代换)法: 例1:已知函数1()1x f x x-=+. 求:(1)(2)f 的值; (2)()f x 的表达式练1:已知1)f x =+()f x 及2()f x ;练2:已知22111(),x x f x x x++=+求()f x .四、消去法:例1:设函数()f x 满足()x x f x f =⎪⎭⎫ ⎝⎛+12,()0≠x ,求()f x .练1:已知1()2()32f x f x x-=+,求()f x .练2:已知定义在R 上的函数()f x 满足()()12+=+-x x f x f ,()0≠x ,求()f x .练3:已知()3()21f x f x x +-=+,求()f x .练4:设函数()f x 满足1()()af x bf cx x+=(其中,,a b c 均不为0,且a b ≠±),求()f x .五、反函数法:例1:已知2)(21+=-x af x ,求)(x f .练1:已知函数1ln +=x y ,()0>x ,求它的反函数六:函数性质法例1:已知()f x 是定义在R 上的奇函数,当0x >时,2()31f x x x =+-,求()f x 的解析式.练1:已知()f x 是定义在R 上的奇函数,当0<x 时,()13-=x x f ,求()f x 的解析式.例1:设)(x f 是定义在N 上的函数,满足1)1(=f ,对于任意正整数y x ,,均xy y x f y f x f -+=+)()()(,求)(x f .练1:设定义在R 上的函数)(x f ,且满足()10=f ,并且对于任意实数y x ,均有()()()12+--=-y x y x f y x f ,求)(x f .练2:设定义在R 上的函数)(x f ,对于任意实数y x ,均有()()()()1232++-+=-y x x y f x f y x f ,求)(x f .练3:已知偶函数()f x 的定义域是R ,当0x ≤时2()31f x x x =--,求()f x 的解析式.例1:已知a f N x x f x f =*∈+=+)1()(),(212)1(且,求)(x f .综合运用 例1:(1)已知3311()f x x x x+=+,求()f x ; (2)已知2(1)lg f x x+=,求()f x ; (3)已知()f x 是一次函数,且满足3(1)2(1)217f x f x x +--=+,求()f x ;(4)已知()f x 满足12()()3f x f x x+=,求()f x 。
函数的解析式

当 0<a<1 时, xx2--bb≤>(0x,2 -b)2, 解得: x≥2b+2+2 b+1 .
综上所述: 当 a>1 时, 2b<x≤2b+2+2 b+1 ;
当 0<a<1 时, x≥2b+2+ 2 b+1.
2-x 1-x
③,
解由 ①, ②, ③ 组成的方程组,
得:
f(x)=
x3-x2-1 2x(x-1)
.
评注:
把
f(x),
f(
x-1 x
),
f(
1 1-x
)
都看作“未知数”,
把已知条
件化为方程组的形式解得 f(x). 又如: 已知 af(x)+b1xf( )=cx, 其
中, |a|≠|b|, 求 f(x).
f(x) 是一次函数,
f(4x+1)=
4x+6 16x2+1
,
f( x +1)=x+2 x ,
且 求 求
fff[((fxx())x.)的]f=(解x4)x=析-x12式,-f1求.((xx)≥f=(-1xf2))(xx的)+=1解或x析2x-2+2式x5x-+. 213
4.已知 2f(x)+f(-x)=10x ,
四、递推求和法
f(x)=
c a2-b2
(ax-
b x
).
例4 已知 f(n)-f(n-1)=an, n 为不小于 2 的自然数, a≠0 且 f(2)=8, 求 f(n) 的解析式.
解: 由已知, f(3)-f(2)=a3, f(4)-f(3)=a4, …, f(n)-f(n-1)=an,
高中数学解析式的求法

解析式的求法1、代人法:已知()x f 的解析式,求()()x u f 的解析式常用此法。
如已知()12-=x x f ,求()2x x f +时,有()()1222-+=+x x x x f . 2、配凑法:已知()()x g f 的解析式,要求()x f 的解析式时,可从()()x g f 的解析式中配凑出()x g ,即用()x g 来表示,将解析式两边的()x g 用x 代替即可。
如已知()x x x f 21+=+,可以将右边凑成()112-+x 的形式再求解。
3、换元法:已知()()x g f 的解析式,要求()x f 的解析式时,可令()x g t =,再求出()t f 的解析式,然后用x 代替t 即可。
如已知()x x x f 21+=+,我们可以设t x =+1,解出x 代入求解。
4、待定系数法:如果已知函数类型,可设出函数解析式,再代人条件解方程(组),求出参数,即可确定函数解析式。
5、方程组法:已知()x f 与()()x g f 满足的关系式,要求()x f 时,可用()x g 代替两边所有的x ,得到关于()x f 与()()x g f 的方程组,消去()()x g f 解出()x f 即可。
常见的有:已知()x f 与()x f -,()x f 与⎪⎭⎫ ⎝⎛x f 1满足的关系式时,可将原式中的x 用x -或x1代替,从而得到另一个同时含()x f 与()x f -,()x f 与⎪⎭⎫ ⎝⎛x f 1的关系式,将这两个关系式联立,列方程组解出()x f 。
当所给函数关系式含有两个变量时,可对这两个变量交替用特殊值代人,或使这两个变量相等再代人,然后利用已知条件,可求出未知的函数。
至于取什么特殊值,应根据题目特征而定。
练习题:求出下列函数的值域。
(1)已知一次函数()x f 满足()()64+=x x f f ,则()x f 的解析式为?(2)已知二次函数()x f 满足()10=f ,()21=f ,()52=f ,,则该二次函数的解析式为?(3)已知函数()x x x f 212-=+,则()x f 的解析式为?(4)已知函数()x f 满足()x x f x f =⎪⎭⎫ ⎝⎛+12,则()x f 的解析式为? (5)已知111+=⎪⎭⎫ ⎝⎛x x f ,则()x f 的解析式为?。
高中数学求函数解析式的方法大全及配套练习

求函数解析式专项练习一.配凑法:1.设23)1(2+-=+x x x f ,求)(x f .2]1)1[(3]1)1[(23)1(22+-+--+=+-=+x x x x x f=6)1(5)1(2++-+x x65)(2+-=∴x x x f2.设21)]([++=x x x f f ,求)(x f . 解:设xx x x x x f f ++=+++=++=111111121)]([ x x f +=∴11)(3.设33221)1(,1)1(xx x x g x x x x f +=++=+,求)]([x g f . 解:2)(2)1(1)1(2222-=∴-+=+=+x x f x x xx x x f又x x x g x x x x xx x x g 3)()1(3)1(1)1(3333-=∴+-+=+=+故2962)3()]([24623-+-=--=x x x x x x g f4.已知1)f x =+求()f x 的解析式。
解:由21))1f x =+=-令t =01x t ≥∴≥则2()1f t t =-,即2()1(1)f x x x =-≥当然,上例也可直接使用换元法令t =则1t =得222(1)()(1)2(1)1x t f t t t t =-∴=-+-=-即 2()1(1)f x x x =-≥由此可知,求函数解析式时,可以用配凑法来解决的,有些也可直接用换元法来求解。
二.待定系数法:1.设)(x f 是一次函数,且34)]([+=x x f f ,求)(x f 【解析】设b ax x f +=)( )0(≠a ,则bab x a b b ax a b x af x f f ++=++=+=2)()()]([∴⎩⎨⎧=+=342b ab a ∴⎩⎨⎧⎩⎨⎧=-===3212b a b a 或 32)(12)(+-=+=∴x x f x x f 或 2.已知二次函数f (x )满足f (0)=0,f (x+1)= f (x )+2x+8,求f (x )的解析式.解:设二次函数f (x )= ax 2+bx+c ,则 f (0)= c= 0 ①f (x+1)= a 2)1(+x +b (x+1)= ax 2+(2a+b )x+a+b ② 由f (x+1)= f (x )+2x+8 与①、② 得⎩⎨⎧=++=+822b a b b a 解得 ⎩⎨⎧==.7,1b a 故f (x )= x 2+7x.3.已知1392)2(2+-=-x x x f ,求)(x f .解:显然,)(x f 是一个一元二次函数。
数学高中数学专练:函数的解析式

同步练习 函数的解析式1、下列各函数解析式中,满足)(21)1(x f x f =+的是 (A )2x (B )21+x (C ) (D )x 21log 2、已知32)121(+=-x x f ,且 6)(=m f ,则等于(A ) 41- (B )41 (C ) 23 (D )23-3、若2)(,2)(xx x x e e x g e e x f --+=-=,则)2(x f 等于 (A ) )(2x f (B ) )]()([2x g x f + (C ) )(2x g (D ))()(2x g x f ⋅ 4.(04年江苏卷.8)若函数)1,0)((log ≠>+=a a b x y a 的图象过两点(-1,0)和(0,1),则(A)a=2,b=2 (B)a= 2 ,b=2 (C)a=2,b=1 (D)a= 2 ,b= 25练习.(04年湖北卷.理3)已知221111xxx x f +-=⎪⎭⎫ ⎝⎛+-,则的解析式可取为 (A )21x x + (B )212x x +-(C )212x x + (D )-21x x+ 6.(04年湖北卷.理7)函数()log (1)x a f x a x =++在[0,1]上的最大值与最小值之和为a,则a 的值为(A )41 (B )21(C )2 (D )47.(04年湖南卷.理6)设函数⎩⎨⎧≤++〉=,0,.0,2)(2x c bx x x x f 若f(--4)=f(0),f(--2)=--2,则关于x 的方程x x f =)(的解的个数为(A )1 (B )2 (C )3 (D )48.(浙江)设f (x )=|x -1|-|x |,则f [f (21)]=( )(A) -21 (B)0 (C)21(D) 19、若函数满足关系式x xf x f 3)1(2)(=+,则的表达式为__________.10、设函数11)(+=x x f 的图象为,若函数的图象与关于轴对称,则的解析式为________________.班级 姓名 座号 题号 1 2 3 4 5 6 7 8 答案9..10. . 11、已知,sin )cos 1(2x x f =-求()2x f 的解析式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课题:___函数的解析式___
教学任务
教 学 目 标 知识与技能目标
会求简单函数的解析式
过程与方法目标
学生通过“回顾-反思-巩固-小结”的过程中 总结简单函数的解析式三种类型及解法。
理解掌握
换元法、待定系数法,体会建立数学模型。
培养学 生分类讨论的数学思想。
情感,态度与价值观目标 使学生认识到数学与生活紧密相连,数学活动充满着探索与创造,让他们在学习活动中培养独立的分析和建模的能力。
重点 理解掌握应用换元法、待定系数法求简单函数的解析式
难点 能初步掌握用数学模型解决实际问题,并能注意实际问题中的定义域
教学过程设计
问题与情境
设计意图 活动1课前热身(资源如下)
1、设⎪⎩
⎪
⎨⎧<=>+=)0(0)0()0(1)(x x x x x f π,则
f{f[f(-1)]}=_______ ___
2、若一次函数f(x),使f[f(x)]=9x+1,则()f x =
3、已知:)(x f =x 2-x+3 ,则 f(x+1) = ,
f(
x
1
)= 4、若x
x
x f -=1)1( 求f(x) =
5、客车从甲地以60km/h 的速度匀速行驶1小时到达乙地,在乙地停留了半小时,然后以80km/h 的速度匀速行驶1小时到达丙地,下列描述客车从甲地出发.经过乙地,最后到达丙地所经过的路程s 与时间t 之间关系的图象中,正确的是( ).
A. B. C. D. .
从正反两种情况出发,让学生回忆体会函数解析式用法和求法。
活动2类型解法
函数的解析式的几种类型及解法:
1、已知所要求的函数类型(一次、二次、反比例、指对数等),利用待定系数法来求;
2、已知复合函数一般用变量代换(换元)法;
3、涉及实际问题求解析式,需建立数学模型即:把实际问题转化为数学问题。
培
养学生用自己的语言来总结类型与解
法
活动3提高探究
资源1、求满足下列条件的函数()f x 的解析式:
① 已知一次函数()f x ,满足3(1)2(1)217f x f x x +--=+.
② 若二次函数满足(0)0f =,且(1)()1f x f x x +=++
③ 设二次函数f (x )满足f (x -2)=f (-x -2),且图象在y 轴上的截距为1,在x 轴上截得的线段长为22.
掌握利用待定系数法求解析式。
函数的解析式
一、选择:
1、若)0(1)]([,21)(2
2≠-=
-=x x x x g f x x g ,则f )2
1
(的值是
( )
A .1
B .3
C .15
D .30 2、f(x)满足f(a)+f(b)=f(ab),且f(2)=p ,f(3)=q ,则f(72)= ( ) A .p+q B .2p+2q C .2p+3q D .3p+2q 3、已知)(,11)11(2
2x f x x x x f 则+-=+-的解析式可取为
( )
A .
2
1x
x
+ B .2
12x
x
+-
C .
2
12x
x
+ D .2
1x
x
+-
二、填空: 4、已知f(x)=
11+-x x ,则f(x)+f()1
x
=____________ 5、已知)3(4
1)(,2)(2
+=
+=x x g a x x f ,若g[f(x)]=x 2+x+1,则a=_____________ 6、已知函数)(x f =⎪⎩
⎪
⎨
⎧<-≥+)
0(2)0(12x x x x 并且)(x f =10,那么x =
7、已知x x x f 2)1(+=+,则f(x)=____ ______
8、1992年底世界人口达到54.8亿,若人口的年平均增长率为x%,到2000年底,世界人口数为y
亿,那么y 与x 的函数关系为________________
三、解答:
9、已知y=f(x)表示过(0,-2)点的一直线,y=g(x)表示过(0,0)点的另一直线,又f[g(x)]=g[f(x)]=3x-2,求这两条直线的交点坐标.
10、在如图所示的直角坐标系中,一个运动物体经过点A(0,9),其轨迹方
程为y=ax2+c (a<0),D=(6,7)为x轴上的给定开区间.
⑴为使物体落在D内,求a的取值范围;
⑵如果物体运动时又经过点P(2,8.1),问它能否落在D内,为什么?
11、某单位用木料制作如图所示的框架, 框架的下部是边长分别为x、y(单位:m)的矩形.上部是等
腰直角三角形. 要求框架围成的总面积8m2. 问:y与x的函数关系式。
