07第七章 理想流体动力学
第7章_理想流体动力学基本方程

④列动量方程求解。
Fx p1A1 p2 A2 cos Rx Qv2x v1x
Fy p2 A2 sin Ry Q v2y v1y
Fx p1A1 p2 A2 cos Rx Qv2 cos v1
Fy p2 A2 sin Ry Qv2 sin 0
Rx p1A1 p2 A2 cos Qv2 cos v1
动量方程:反映了流体的动量变 化与外力之间的关系
粘性流体:实际流体都具有粘性。既有粘性切应力,又有法向压应力。
0
理想流体:理想流体可忽略粘性。即无粘性切应力,只有法向压应力。
0
粘性流体:
理想流体:
一、动量方程——流体的运动方程
1、积分形式的动量方程——流体的运动方程
质点系的动量定理:
系统的动量对时间的变化率等于作
第7章 理想流体动力学动量方程
粘性流体:实际流体都具有粘性,致使所研究的问题比较复杂。 理想流体:指粘性为零的流体,实际上并不存在,但在有些问题
中,粘性的影响很小,可以忽略不计,致使所研究的 问题简单化。 理想流体动力学规律可以应用于粘性的影响很小的实 际流体中,所以本章的研究具有实际意义。
主要内容
过流断面是均匀流或渐(缓)变流断面不可压缩流体
Fx Q(2v2x 1v1x ) Fy Q(2v2 y 1v1y ) Fz Q(2v2z 1v1z )
④当沿程有分流和汇流时:
Fx (3Q3v3x 2Q2v2x 1Q1v1x ) Fy (3Q3v3y 2Q2v2 y 1Q1v1y ) Fz (3Q3v3z 2Q2v2z 1Q1v1z )
对1-1,2-2断面列伯努利方程
p1 v12 p2 v22
g 2g g 2g
v1 1.42m / s v2 3.18m / s
不可压缩粘性流体动力学基础_OK
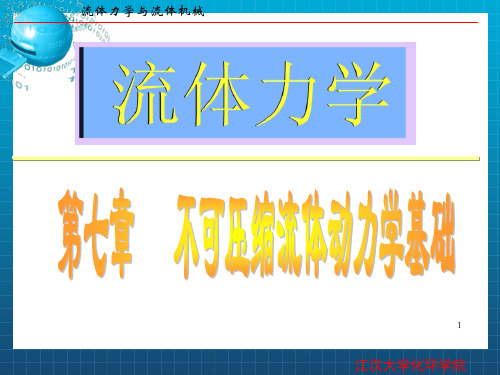
uz y
u y z
zx
xz
1 ux 2 z
uz x
(7—3)
14
江汉大学化环学院
流体力学与流体机械
综上所述,可写出表示流体微团运动的基本形式如下:
表示平移的平移速度:u x、u、y u。z
表示线变形的线变形速度(又称线变率):
x
u x x
y
u y y
z
u z y
表示角变形的角变形速度(又称角变率):
一、流体微团(Material Elements of Fluid) 流体微团是由大量的流体质点所组成的一个微小质团,它
具有微小的体积,是研究流体运动的一个基本单元。
4
江汉大学化环学院
流体力学与流体机械
流体微团的尺度在微观上足够大,大到能包含大量的 分子,使得在统计平均后能得到其物理量的确定值,质 点的尺度在宏观上又足够小,远小于所研究问题的特征 尺度,使得其平均物理量可看成是均匀的;而且可以把 流体微团看成是几何上的一个点。
dx dy dz
x y z
21
江汉大学化环学院
流体力学与流体机械
在给定瞬时,在漩涡场中任取一个不是涡线的封闭曲线, 通过这条曲线上每一点作一根涡线,这些涡线就构成一个管 状曲面,称为涡管(Vortex Tube);涡管中充满着作旋涡运 动的流体,称为涡束,或称为元涡(Vortex Filament)。 涡通量(Vortex Flux)或旋涡强度(Intensity of Vorticity),以 J表示。元涡的涡通量为微元涡的断面积和速度涡量(简称涡 量)的乘积,即
y
ux d yd t y
D
C
C
uy
u y y
dy
《工程流体力学》第七章 粘性流体动力学
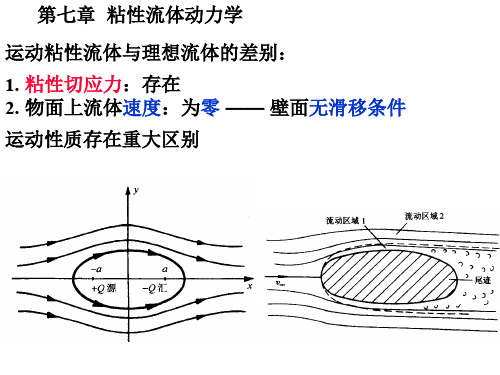
x方向 : 1)表面力:作用在左右两面上力的合力:
作用在上下两面上力的合力:
作用在前后两面上力的合力:
作用在整个六面体上表面力沿x轴方向的合力:
2) x方向质量力 : 单位质量流体受到的质量力分量:X;
六面体受到的质量力: Xrdxdydz
牛顿第二定律:
—— 以应力形式表示的粘性流体运动微分方程 再把表面应力和变形率之间关系代入上3式:
应力:各向同性
运动粘性流体:存在法向、切向表面力 应力:各向异性
流体中:任一点c :绕c任意方位
c点应力定义: 要计算两个向量的比值
用作用在dAx, dAy, dAz上的dFx, dFy, dFz:定义c上的应力
需要2个下标表示:9个应力分量
第1个下标i:应力作用方向 第2个下标j:作用面方向
第七章 粘性流体动力学
运动粘性流体与理想流体的差别: 1. 粘性切应力:存在 2. 物面上流体速度:为零 —— 壁面无滑移条件 运动性质存在重大区别
第一节 粘性流体中作用力
一、粘性应力: 1.质量力:与流体质量有关
与流体粘性无关 粘性流体中质量力考虑方法:和理想流体相同
2. 表面力: 静止和运动理想流体:仅存在指向作用面法向表面力
由于外部无粘流:受到分离流的排挤 明显改变:其中压强分布 实际计算:用实测物面压力分布计算分离点前附面层流动 附面层分离:使流体一部分机械能损失在涡流中
绕流物体阻力增加 流体机械效率降低 甚至产生不稳定流动 导致机器损坏 防止或推迟附面层分离现象发生:是工程上一个重要问 题
边界层分离后:形成尾涡区 尾涡区压强:基本上等于分离点压强 压强:上下对称 若将压强在圆柱面上积分:则得压差阻力
流体在y+l层时均速度:
流体力学第七章不可压缩流体动力学基础
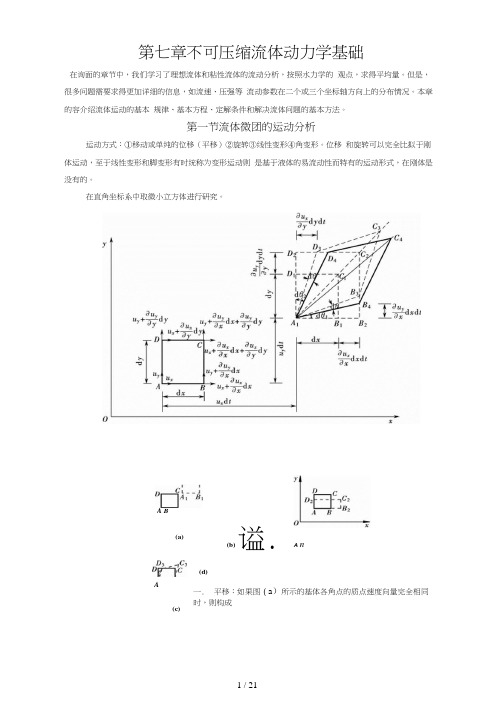
第七章不可压缩流体动力学基础在询面的章节中,我们学习了理想流体和粘性流体的流动分析,按照水力学的 观点,求得平均量。
但是,很多问题需要求得更加详细的信息,如流速、压强等 流动参数在二个或三个坐标轴方向上的分布情况。
本章的容介绍流体运动的基本 规律、基本方程、定解条件和解决流体问题的基本方法。
第一节流体微团的运动分析运动方式:①移动或单纯的位移(平移)②旋转③线性变形④角变形。
位移 和旋转可以完全比拟于刚体运动,至于线性变形和脚变形有时统称为变形运动则 是基于液体的易流动性而特有的运动形式,在刚体是没有的。
在直角坐标系中取微小立方体进行研究。
(b)谥.A n(d)一. 平移:如果图(a )所示的基体各角点的质点速度向量完全相同时,则构成(c)A B(a)A了液体基体的单纯位移,其移动速度为心、®、“,。
基体在运动中可能沿直线也 可能沿曲线运动,但其方位与形状都和原来一样(立方基体各边的长度保持不 变)。
二、 线变形:从图(b )中可以看出,由于沿y 轴的速度分量,B 点和C 点都比 A 点和D 点大了竺如 而比就代表〃y = l 时液体基体运动时,在单位时间沿勿dyy 轴方向的伸长率。
du x °"、. du : dxdydz三、 角变形(角变形速度)—BIA ■ dp -------------------------------- Jda-0 = dp + 00 =J"些+些k dz. dx四、旋转(旋转角速度)1O = —0 =—21勿du vdx—dx角变形:血 A那么,代入欧拉加速度表达式,得:du r du Tdu r八 八5=说=古叫 云+"卑+"0+-叭巴加、6仇 du Ya v = ----- = — + u v ---------- + U.0, +ii t a ). -iLCoydt dt dy “'2 …加.du diL q 。
理想流体

为流体在该点的“静流体压强”,简称压
n
· d S A
二、静止流体内任意两点的压强关系
(P dP)S PS gsdy 0
dP gdy
PB PA
yB gdy
yA
g( yB
yA)
gh
PB PA gh
同种液体内压强随高度而变化,离 液面深处,压强大
§11.1 理想流体
一.理想流体
在流体运动的问题中,可压缩性和粘性都处
于极为次要的地位,就可以把它当作理想流体。 力
理想流体是不可压缩又无粘性的流体。
学
新乡学院物理系
§11.2 静止流体内的压强
一、静止流体内某点的压强
在静止流体内任意一点,设想作的任意方
向面上受的应力总垂直作用在该 面上 ,而
且应力数值与面的方向无关,这种应力称
3. 流线 4. 流管
····
··· ·
二、理想流体的连续性方程 (the equation of continuity )
流体力学的质量守恒定律:单位时间内穿过流体中任一 封闭曲面流入(或流出)的流体质量必等于这封闭曲面 内流体质量的增加(或减少)。
单位时间内通过流管横截面的流体质量称为质量流 量,设截面积为S,截面上各点流速相等且为v,则质 量流量
粘性阻力的大小与流体的粘度系数 有关,与物体的
运体动中速以度速度v和v运物动体,线受度到有粘关性。阻半力径f 为Rl的球在粘性流
f 6Rv
设一半径为r的小球,质量为m,在粘度系数 为的流体中静
止下落。小球受重力;粘性阻力由零增大,球不断加速,
直至重力、浮力、粘性阻力平衡,小球下落速度不再增加, 为常数,此速度称为终极速度
理想流体动力学理论

第四章 流体的积分关系式及其应用众所周知,一个固体质点在保守力场中运动时,质点的动能和势能之和保持不变,这就是经典物理中的机械能守恒定律。
从数学的观点看,机械能守恒是动量方程的一次积分,称为能量积分。
有了能量积分方程,我们在处理保守场中的动力学问题时,就可通过该方程将始、末两态直接联系起来,而不必考虑中间过程的细节。
在流体力学中也有类似的积分。
前面一章建立了控制流体流动的微分方程组,原则上利用该方程组可以求解满足Stokes 假设的Newton 流体的任意流动问题。
对于理想流体流动问题,可以直接积分微分方程,得到积分方程。
利用积分方程求解流动问题显然更为简便,因而这些积分方程得到广泛应用。
什么样的流体是理想流体呢?当流体发生剪切变形时总会伴有粘性应力。
粘性应力不仅与流体的粘性性质(以粘性系数表征)有关,还依赖于速度梯度,对于低粘(μ小)流体的流动,如果速度的空间变化不太急剧,粘性应力就比较小。
如果粘性应力对所研究的流动问题影响较小,可以忽略流体的粘性,认为流体是无粘的,即理想流体。
一般常见的流体,如空气和水,粘性系数很小,在自然界和工程中遇到的这些流体的大多数流动,粘性的影响都可以忽略,都可以近似看作理想流体流动。
在流体力学发展的历史上,无粘流理论是流体力学中历史悠久,发展完善,成果辉煌,应用广泛的一个分支领域。
§4.1理想流体运动方程的进一步化简理想流体满足Euler 方程:dV pF dt ρ∇=-, (4-1)或者改写成兰姆—葛罗米柯形式2rot 2VV p V V F t ρ⎛⎫∂∇+∇+⨯=-⎪∂⎝⎭。
(4-2)若体力有势F π=-∇,(4-3)其中π代表体力势,即单位质量流体的势能。
如果体力仅为重力,取z 轴沿g -方向,并取0z =为零势能面,则gz π=。
若流体密度是常量或仅为压强的函数,则称流体是正压流体。
若流体正压,)(p ρρ=,此时可定义压力函数()dpP p ρ=⎰(4-4-1)或()dpdP p ρ=。
清华大学流体力学课件-4-理想流体动力学

D p 1 p 2 1 e 2 V f V q qR Dt t
理想 流体
Di 1 Dp q qR Dt Dt
1. 理想流体运动的基本方程 —— Euler 方程
V V t
V 1 V V f T t
Tij p ij
Cv 0 m
ek
p ij ei e j p ei p xi xk
De D1 p q qR Dt Dt
D p 0 Dt
2017年春-本科生-流体力学
Ds 理想、常比热、完全气体 0 绝热连续流动 Dt
理想流体动力学 16
基本内容
1. 理想流体运动的基本方程和初边值条件
2. 理想流体在势力场中运动的主要性质
理想流体动力学
4
§4.1 理想流体运动基本方程和初边值条件
V V t
V j Vj t x j x j
V 1 V V p f t
Vi Vi 1 p Vj fi t x j xi
Hale Waihona Puke 不封闭!
2017年春-本科生-流体力学 理想流体动力学 5
§4.1 理想流体运动基本方程和初边值条件
2. 理想流体能量方程的讨论
1 2 2 1 1 (e 2 V ) V (e 2 V ) f V pV q qR t
D 2 e 1 V 2 Dt
D p 1 p 2 1 e V f V q q R 2 Dt t
第七章 粘性流体动力学基础

第七章 粘性流体动力学基础实际流体都具有粘性,而在研究粘性较小的流体的某些流动现象时,可将有粘性的实际流体近似地按无粘性的理想流体处理。
例如,粘性小的流体在大雷诺数情况下,其流速和压强分布等均与理想流体理论十分接近。
但在研究粘性小的流体的另一些问题时,与实际情况不符,如按照理想流体理论得到绕流物体的阻力为零。
产生矛盾的主要原因是未考虑实际流体所具有的粘性对流动的影响。
本章,首先建立具有粘性的实际流体运动微分方程,并介绍该方程的在特定条件下的求解。
由于固体边界对流体与固体的相互作用有重要的影响,本章后面主要介绍边界层的一些基本概念、基本原理和基本的分析方法。
§7.1 纳维—斯托克斯方程7.1.1 粘性流体的应力实际流体具有粘性,运动时会产生切应力,它的力学性质不同于理想流体,在作用面上的表面应力既有压应力,也有切应力。
在流场中任取一点M ,过该点作一垂直于z 轴的水平面,如图7-1 所示。
过M 点作用于水平面上的表面应力p n 在x 、y 、z 轴上的分量为一个垂直于水平面的压应力p zz 和两个与水平面相切的切应力τzx 、τzy 。
压应力和切应力的下标中第一个字母表示作用面的法线方向,第二个字母表示应力的作用方向。
显然,通过M 点在三个相互垂直的作用面上的表面应力共有九个分量,其中三个是压应力p xx 、p yy 、p zz ,六个是切应力τxy 、τxz 、τyx 、τyz 、τzx 、τzy ,将应力分量写成矩阵形式:图7-1 作用于水平面的表面应力⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧ττττττzz zyzxyz yy yxxz xy xx p p p (7-1) 九个应力分量中,由于τxy =τyx 、τyz =τzy 、τzx =τxz ,粘性流体中任意一点的应力分量只有6个独立分量,即τxy 、τyz 、τzx 、p xx 、p yy 、p zz 。
7.1.2 应力形式的运动方程在粘性流体的流场中,取一以点M 为中心的微元直角六面体,其边长分别为dx 、dy 、 dz 。
理想流体动力学

2 r0 ln r 1 2 r 2
当 r = r0时 , =
2
ln r0 常 数 , 可见,圆柱表面为一流线。
2
2、速度分布 流场中任一点 p r ,
的速度分量为:
2 r0 v v 1 2 sin r r 2 r
J
A
d J 2 n d A
A
18
2、速度环量 流体质点的旋转角速度矢量无法直接测量,所以旋涡强 度不能直接计算。但是,旋涡强度与它周围的速度密切相关, 旋涡强度愈大,对周围流体速度的影响也就愈大。因此,这 里引入与旋涡周围速度场有关的速度环量的概念。 给定瞬时,在流场的任意封闭曲线上,流体速度矢量沿 封闭曲线的线积分,定义为速度环量,用符号 表示,即
2 r0 vr v 1 2 co s r r
当 r 时 , v r v cos , v v ห้องสมุดไป่ตู้ sin
表明流体在远离圆柱体处保持原来的均匀流,即满足无穷远 处的边界条件。
3
柱面上 r r0 速度分布:
2 r0 v v 1 2 sin r r 2 r
L
2 0
2 1 2 p v 2 v sin r0 sin d v 2 2 r0
12
L v
上式就是著名的库塔-儒可夫斯基(Kutta-Zhoukowski)升力 公式。上面的计算结果表明,理想流体对圆柱体作有环量绕 流时,流体作用在圆柱体上的阻力等于零,而作用在单位长 度圆柱体上的升力等于流体密度、来流速度和速度环量三者 的乘积。 升力的方向由前方来流速 度矢量 v 沿反环流的方 向旋转 9 0 0 来确定,如图 所示。
理想流体动力学

特性1
证明:在流场中任取一流线
s
, y
则流线上任一点的速度与流
线相切。微元线段 矢量 d s 与
对应的速度矢量 v 之间的关系
式为
dx dy vx vy
流线微分方程
o
v s
ds dy
vy
dx
vx
x
v ydx vxdy 0 d 0
流函数值相等的点 可连成一条流线
证明了沿一条流线各点的流函数值相等。
q 2 1
特性3
证明:对于平面势流,有
z
1 ( v y 2 x
v x y
)
0
代入
x
v y
,
y
vx
得到 即
( ) ( ) 0
x x y y
2 2
x2 y2 0
例 3. 一平面恒定流动的流函数为 (x, y) 3x y
试求速度分布,写出通过 A(1,0)和 B(2, 3 ) 两点的流线方程,和两点之间连线的通过流量。
(
z
)
z
(
y
)]
0
类似可推出 y z 0
因此,存在速度势函数的流动必定无旋。
流动无旋的充分必要条件是流场有速度势函数存在。
特性3
等势面:速度势函数取相同值的点构成空间曲面, 即 Φ(x, y, z)=C
证明:在等势面上取一点O,并在该面上过O任
取一微元线段矢量 d L dxi dy j dz,k该点
特性2
设ψ1、ψ2是两条相邻流线,作其间一曲线AB,要 求证明通过AB两点间单位厚度的流量q=ψ2-ψ1。
证明: 取微元线段 d s ,过微元线段的速度为 v , 则单位厚度的微元流量dq的表达式为
流体动力学方程

流体动力学方程
《流体动力学方程》
一、定义
流体动力学方程又称为气体动力学方程。
它描述了理想流体在特定条件下的流动规律。
它是一组称为Navier-Stokes方程的微分方程,用来描述流体的压力、速度、温度和其他物理量之间的关系。
二、表达式
Navier-Stokes方程又称为流体动力学方程,包括控制方程和物理方程两部分。
控制方程:
u/t + (u)u = -P + μ2u
其中,u为物质的速度,t为时间,P为压强,μ为粘性系数。
物理方程:
u/t + (u)u = -P + c(T) + 2u
其中,t为时间,P为压强,T为温度,C为热扩散系数。
三、应用
1、气体动力学:流体动力学研究的最重要应用之一就是对于气
体动力学的研究,包括非定常气流、边界层气流、喷气发动机气流等。
2、水力机械:流体动力学方程在水力机械方面也有重要应用,
它可以用来研究水力机械系统中的液体流动特性。
3、流体动力:流体动力学方程可用于研究流体中的动力学特性,从而求解流体在某种特定条件下的动力学参数。
粘性流体动力学基础
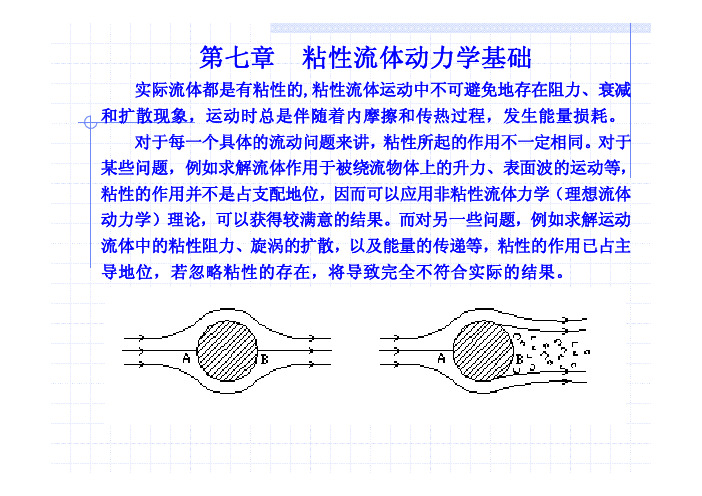
= τ xz
=
μ ( ∂vz
∂x
+
∂vx ) ∂z
=
2με zx
五、法向应力与变形速度的关系
在理想流体中,同一点各个方向的法向应力(压强)与作用的方位无
关而且相等,即: pxx = pyy = pzz = p 但在粘性流体中,流体微团除了发生角变形(角变形引起切应力),同时
发生直线变形,使微团产生拉伸或压缩。
方程。 N-S 方程表示了质量力、表面力、粘性力、惯性力的平衡关系(∑ Fv = m av )。
一、实际流体中的应力 在讨论理想流体(平衡流体)时,作用在流体微团表面上的力只有一
个与表面垂直的压应力,这个压应力称为理想流体的动压强(= 平衡流体 的静压强)。其特性为:1)方向沿作用面的内法线方向,2)大小与作用 面的方位无关。
对于实际流体,由于具有粘性,不仅在表面应力中存在切向应力,而 且在法线方向上也不再具有理想流体中的与方位无关的性质。
在实际流体中,一点处的三个方向的应力由于切应力的存在,不再 垂直于作用面,而与作用面斜交,即具有某一方向,应写成,
pvx , pv y , pvz 对任一面积,设作用在其上任一点的表面应力为 pv ,如图所示, pv 分解 为:
第七章 粘性流体动力学基础
实际流体都是有粘性的,粘性流体运动中不可避免地存在阻力、衰减 和扩散现象,运动时总是伴随着内摩擦和传热过程,发生能量损耗。
对于每一个具体的流动问题来讲,粘性所起的作用不一定相同。对于 某些问题,例如求解流体作用于被绕流物体上的升力、表面波的运动等, 粘性的作用并不是占支配地位,因而可以应用非粘性流体力学(理想流体 动力学)理论,可以获得较满意的结果。而对另一些问题,例如求解运动 流体中的粘性阻力、旋涡的扩散,以及能量的传递等,粘性的作用已占主 导地位,若忽略粘性的存在,将导致完全不符合实际的结果。
流体力学 第7章 不可压缩流体动力学基础

i ×u = x ux
i y uy
k z uz
u z u y x = y z u x u z y = z x u y u x z = x y
u y u x u x u z u z u y =( )i + ( )j+( )k y z z x x y
与
= 2ω = x i + y j + z k
ρ u x dx ( ρ )(u x )dydzdt x x 2
dt时段从前面流出的流体质量为 时段从前面流出的流体质量为
u x dx ρ ( ρ + )(u x + )dydzdt x x 2
规定流入为正,流出为负, 时段从前后面流入 规定流入为正,流出为负, dt时段从前后面流入 流出的质量差为
( ρu x ) ( ρu y ) ( ρu z ) ρ dxdydzdt = + + dxdydzdt t y z x
可压缩流体非恒定流的连续性微分方程
ρ ( ρu x ) ( ρu y ) ( ρu z ) + + + =0 t x y z
对于不可压缩流体: 对于不可压缩流体:
= 2ω = x i + y j + z k
涡量是空间坐标和时间的矢性 函数,有涡流则构成一个矢量场, 函数,有涡流则构成一个矢量场, 也称为涡量场. 也称为涡量场.
u z u y x = y z u x u z y = z x u y u x z = x y
哈米尔顿算子 是一个矢性微分算子
速度环量符号: 速度环量符号:
Γ
Γ = lim ∑ u cos α ds = ∫ u cos αds = ∫ u cos(u , ds ) ds
7第七章粘性流体动力学基础

2、应力与变形速率的关系在流体中各向同性。
3、在静止流体中,切应力为零,正应力的数值为静压力p。
在建立应力—变形速率关系之前,我们还要澄清一个概念,前 P 面已将应力张量分解为: D pm ,其中pm为平均正应力,尚不是热 力学平衡意义上的压力p,严格说来,这两者之间不一定相等。我们 定义pm - p为平均压力偏量,其目的是为了将来能应用假设3。 在建立应力—变形速率关系时,我们分两步走:第一步,建立偏 应力张量D与变形速率张量E之间的关系;第二步,建立平均压力偏 量pm - p与变形速率E之间的关系,这里可以设想,pm和p不会直接与 E发生关系。
其中:
φ表示的是粘性力所做的功,它的物理意义是单位质量流体在单位时 间内,由于粘性摩擦而耗散的机械能,这部分能量完全转变成了热能 的形式,故φ又称耗散函数,可以证明φ永远大于零。 由焓的定义: ,经整理后能量方程还可以写成:
四、粘性流体动力学方程组的封闭性
一、圆柱绕流
利用流场叠加法,均直流+偶极子,求得理想流体作圆柱绕流的 流场,流谱左右和上下对称。当Re很小时,这时惯性力相对粘性力 很小,可忽略惯性力。可得到粘性流场的精确解,如图。从流谱图 上看,两者非常接近。两个极限情况图画是很相似的,但在细节上 还是有不同的。1,速度分布如图。2,压力分布的左右不对称。
三、管内流动
1、充分发展段的速度分布 2、进口段的附面层发展。 层流 L≈120D 湍流 L≈50D 3、弯管段的二次流动 4、缓变流和急变流,流动损失。 已知真实流体流动过程的伯努利方程为:
其中, pl12 、 hl12 分别代表流体从1点流到2点时,损失的总压力和总 水头。在缓变流中是沿程损失,急变流中是局部损失。
流体力学--理想流体的流动

2p1 p2
S12 S22
p1 p2 gH
流速:2 S1
2gH S12 S22
,
1
S2
2gH S12 S22
体积流量:QV S22 S1S2
2gH S12 S22
只要读出两个 竖管的高度差, 就可以测量流 速和流量
•二. 流速的测定:
应用实例3. 皮托管:常用的流速测定装置;
补充例题, 水管里的水在压强为p=4×105 Pa的作用下流入房间, 水管的内直径为2.0 cm,管内水的流速为4 m/s。引入 到5 m高处二楼浴室的水管,内直径为1.0 cm,
试求浴室水管内水的流速和压强? (已知水的密度为=103 kg/m3)。
2 16m / s
p2 2.25105 (Pa)
伯努利方程:理想流体在重力场中作稳定流动时,能量守
衡定律在流动液体中的表现形式。
一. 伯努利方程的推导:
稳定流动的理想流体中,忽略流体的粘滞性,任意细流管中的 液体满足能量守恒和功能原理!
设:流体密度,细流管中分析一段流体a1 a2 : a1处:S1,1,h1, p1 a2处:S2,2,h2, p2 经过微小时间t后,流体a1 a2 移到了b1 b2, 从 整体效果看,相当于将流体 a1 b1 移到了a2 b2, 设a1 b1段流体的质量为m,则:
粘滞力:
粘滞流体在流动中各层的流速不同,相邻两流层之间有相 对运动,互施摩擦力,快的一层给慢的一层以向前的拉力; 慢的一层则给快的一层以向后的阻力,这种摩擦力称为内 摩擦,又称粘滞力;
粘滞力和哪些因素有关?
流体内相邻两层内摩擦力的大小:
与两流层的接触面积大小有关; 还与两流层间速度变化的快慢有关;
七章不可压缩流体动力学基础-

二 涡通量和速度环量
1. பைடு நூலகம்通量
定义: 在微元涡管中,二倍角速度与涡管断面面积dA的
乘积称为微元涡管的涡通量(旋涡强度)dJ
dJ2dA
(2)
对任一微元面积dA而言,有
dJ2dA2ndA
对有限面积,则通过这一面积的涡通量应为
J 2AndA
(3)
2.速度环量
定义: 某一瞬时在流场中取任意闭曲线 l,在线上取一微 元线段 d l ,速度v 在d l 切线上的分量沿闭曲线 l 的线积分, 即为沿该闭合曲线的速度环量。
得到
dx dy dz
(1)
x y z
这就是涡线的微分方程。
2. 涡管 定义: 某一瞬时,在漩涡场中任取 一封闭曲线c(不是涡线),通过曲线 上每一点作涡线,这些涡线形成封 闭的管形曲面。 如果曲线c构成的是微小截面,那 么该涡管称为微元涡管。 横断涡管并与其中所有涡线垂直的 断面称为涡管断面,在微小断面 上,各点的旋转角速度相同。 3.涡束 涡管内充满着作旋转运动的流体称为涡束,微元涡管中 的涡束称为微元涡束。
dy,设顶点A坐标为(x,y),流速分量为u ,v。
利用泰勒级数展开且仅保留一阶小量,可得微团各顶点 的速度分量,
正四边形微团在经历了时间后将变成斜平 行四边形
1.正四边形微团ABCD在经历了 dt时间后将变成斜平行
四边形 A’B’C’D’(略,请参考书中证明过程)。 2.微团运动过程分解
1) 平移:正四边形流体微团作为一个整体平移到新的
u x u x 0 x z d y y d z x d x x x d y y x d z z
u y u y 0 x x d z z d x y d y y y d z z y d x x
理想流体动力学

,
vy y
,
vz z
2 2 2 0 x y z
即 0 ,满足Laplace方程。而满足Laplace方程的函数 就叫做调和函数
2
§8.2 平面无旋流动
平面流动是指对任一时刻,流场中各点的 速度都平行于某一固定平面的流动,并且流场 中物理量(如温度、速度、压力、密度等)在 流动平面的垂直方向上没有变化。即所有决定 运动的函数仅与两个坐标及时间有关。 在实际流动中,并不存在严格意义上的平 面流动,而只是一种近似。如果流动的物理量 在某一个方向的变化相对其他方向上的变化可 以忽略,而且在此方向上的速度很小时,就可 简化为平面流动问题处理。(图1)
§8.1 无旋流动
无旋流动就是其流场中每个流体微团不发生旋转, 角速度 ,即 0 1 vz v y x ( )0 2 y z
y (
1 vx vz )0 2 z x
1 v y vx z ( )0 2 x y
一 速度势函数
得到 1 ( v z v y ) 0 y 1 ( vx vz ) 0 1 ( v y vx ) 0 x z 2 z x
特性2
设对某一流动,存在势函数Φ(x,y,z,t),流动的角 速度分量 v
x (
1 v z 1 y ) [ ( ) ( )] 0 2 y z 2 y z z y
类似的推出
y z 0
可见,流场存在速度势函数则流动无旋,因此流动无旋 的充分必要条件势流场有速度势函数存在。
特性3
等势面:在任意瞬时t0,速度势函数取同一值的点构 成流动空间一个连续曲面,Φ(x,y,z,t0)=常数。 在等势面上取一点A,并在该面上过A任取一微元矢 量 d L dxi dy j dzk 0 ,求 d L 与点A处速度 v 的标量积。
理想流体的流动

(2)对实际流体,只要其黏滞性很小,就可应用伯努利方程。 如空气、水和酒精。
(3)伯努利方程广泛应用于水利、造船、化工、航天等领域。
三、伯努利方程的应用
(1)等高流线中流速与压强的关系
P 1 v2 C
2
Sv qV 常量 C
当S较小时,v 较大,P较小。
由 S1v1 =S2v2
得 v2 = 4v1 = 4 m•s-1
又由
p1
1 2
v12
p2
1 2
v22
得
p1
p2
1 2
v22
v12
1 1.0103 42 12 7.5103 Pa 2
粗管内的压强高于细管
例 水从图示的水平管道1中流入,并通过支管2和3流入管4。
如管1中的流量为900cm3•s-1. 管1、2、3的截面积均为15cm2,
管4的截面积为10cm2,假设水在管内作稳恒流动,
求 (1)管2、3、4的流量; (2)管2、3、4的流速;
(3)管1、4中的压强差.
2
v2
1
v1
4
v4
3
v3
解 (1)由连续性原理知 Q4= Q1 = 900cm3•s-1 ∵ S2 = S3 Q2 + Q3 = Q1 ∴ Q2 = Q3 = 450cm3•s-1
v2
所以流线不会相交。
流速大
流线密处,表示流速大。
四、流管(flow tube) 流管:由一组流线围成的管状区域称为流管。
流管内、外的流体都不会穿越管壁。
通常所取的“流管”都是“细流管”。 细流管的截面积S 0 ,就称为流线。 作定常流动的液体可以视为由无数稳定的细流管组成,所以, 任一流管中的流动可以代表整个流体的流动。
流体力学第七章_理想流体平面运动

速度环量Г:速度V沿封闭曲线L的线积分。
L
ds α V
Γ LV ds LV cosds L (udx vdy wdz) L d
按照惯例,曲线积分的方向规定为逆时针方向为 正,顺时针方向为负。
12
二、旋涡(涡旋)强度
旋涡中某点涡量的大小是流体微 团绕该点旋转的平均角速度的2倍, 方向与微团的瞬时转动轴线重合。
园盘绕流 尾流场中 的旋涡
3
机翼绕流(LES)
流体的无旋流动虽然在工程上出现得较少,但无旋流动 比有旋流动在数学处理上简单得多,因此,对二维平面势流 在理论研究方面较成熟。
对工程中的某些问题,在特定条件下对粘性较小的流体 运动进行无旋处理,用势流理论去研究其运动规律,特别是 绕流物体的流动规律,对工程实践具有指导意义和应用价值。
流线方程: dx dy 或 vdx udy 0
uv
连续性方程: u v 0或 u =- v (充分必要条件)
x y
x y
均可构造标量函数 x, y,
使
u , v
y
x
则 vdx udy dx dy d 0
17
斯托克斯定理说明:速度环量是否为零可以判断流动是 否有旋。如果任意一条封闭曲线上的速度环量都为零,则此 区域的旋涡强度为零,即旋转角速度为零,是无旋流动。但 是,如果有一条封闭曲线上的速度环量不为零,则此区域的 旋涡强度不为零,是有旋流动。
讨论:包围某区域的速度环量为零,则此区域是否一定是 无旋流动?
Г= 0 不一定是无旋运动,如图。
对强制线涡,包含涡的 2 crd 2c 0
任意封闭曲线 L 有:
0r
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
v x v 1 cos2
v y v sin 2
合速即为周向速度如下,径向速度为0
2 2 v vx vy 2v sin
压强系数:
v2 C p 1 2 1 4 sin 2 v
驻点A(θ=π)处的Cp是+1。
从驻点往后流,在θ=150°处流速加快到和来流的流 速一样大了。以后继续加速,在θ=π/2处达最大速度,其 值二倍于来流的速度,Cp是(–3.0)。 过了最大速度点以后,气流减速,在θ=0°处降为零 ,这一点称为后驻点。 这个流动不仅上下是对称的,而且左右也是对称的, 物面上的压强分布也是对称的,结果哪个方向的合力也没 有。 不过实际流动左右是不对称的,由于实际流体是有粘 性的缘故,气流过了最大速度点以后,不可能始终贴着物 体流下去,不可能进行完全的减速,结果水平方向是有一 个阻力的 。
第七章 理想流体动力学
平面不可压位流的基本方程 几种简单的二维位流 一些简单流动的迭加
平面不可压位流的基本方程
前一章介绍了流体运动所必须遵守的规律:质量方程及 欧拉方程。 这一章应该讨论怎样求解这些方程。 但是,要求得这些偏微分方程的解,是要满足一定边界 条件的,否则求出来的解没有实际意义。不过,飞行器的外 形都比较复杂,要在满足如此复杂的边界条件之下来求得这 些方程的解,实际上是办不到的。
sin 2 sin Cp
2
驻点的Cp一定等于+1。 从驻点往后,Cp迅速下降,在距A不很远的地方,Cp 降到零,该点流速已达远前方的来流速度。此后气流继沿 物面加速,走了一段之后,流速达最大值,Cp达最小值。 这一点称最大速度点,或最低压强点 ,过了最大速度点之 后,气流开始减速,到无限远的右方,流速减到和远前方 来流一样大。这是大多钝头物体低速流动的特点:头部 附近形成一个低速高压区,随后速度迅速上升,压强急剧 下降。
v 0
定出来
用动量定理来计算 , 以原点为中心,画一个半 径为r1很大的控制面S,整
个的控制面还包括圆的表
面S1以及连接S和S1的两条 割线 。
不过这两条割线上的压力和动量进出都对消了,不必
管它。 S上的压力积分是物体所受的合力。受力情况左右对
称,不会有X合力。我们计算Y方向合力就行了,彻体力略
Q y Q v y arctg A 2 x 2
通常将压强表为无量纲的压强系数 C p ,其定义是当地 静压减去来流静压再除以来流的动压头:
Cp
p p 1 2 v 2
2
不可压无粘流时:
v Cp 1 v
沿这个半无限体的外表面,压强系数是:
M
4、点涡
点涡是位于原点的一个点涡的流动,流线是一些同心 圆。流速只有 v ,而没有 vr 。
v (2 r )
1 v 2 r
式中的 是个常数,称为点涡的强度,反时针方向为 正。分速 v 和离中心点的距离r成反比,指向是反时针方 向的。 其位函数和流函数是:
M (2 xy) sin 2 vy 2 M 2 2 y (x y ) r2
合速度:
v v v M r
2 x 2 y
2
它是有轴线方向的,原来的源和汇放在哪条直线上,那条直线就是
它的轴线。前面表示的偶极子是以x轴为轴线的其正向为轴线上的流线 方向,前面的偶极子是指向负x方向的。如果偶极子轴线和x轴成θ角,
r
x2 y2
如果源的位置不在坐标原点,而在A(ξ,η)处
Q y arctg 2 x
Q ln ( x ) 2 ( y ) 2 2
Q (x ) vx x 2 ( x ) 2 ( y ) 2 Q ( y ) vy y 2 ( x ) 2 ( y ) 2
正向指向第三象限
M x cos y sin 2 2 x y
如果偶极子位于(ξ,η),轴线和x轴成θ角,正向
指向第三象限,则
M
( x ) cos ( y )sin ( x )2 ( y )2
( y ) cos ( x )sin ( x )2 ( y )2
若不考虑粘性的作用,流动原来是无旋的,后来必然 还是无旋的 。这一条假设在实际流场的大部分区域都是成 立的。用这条假设可以求流场的初步解。 二维流动 一切流动参数都只是x和y的函数,而与z无关,即一切流 动参数在z向都没有变化,且
vz 0 的一种三维流。计算
作用力时,物体在z向要取一定的尺寸,这通常取为1。 绕圆柱体的有环量绕流的解析解
去不计;流动是定常的,第一项就没有,因此:
L
S
p cos n, y dS vnv y dS
3、偶极子
等强度的一个源和一个汇,放在x轴线上,源放在(-h,0)处,汇放在 (0,0)处。从源出来的流量都进入汇。
应用叠加原理,位函数和流函数如下
Q [ln ( x h) 2 y 2 ln x 2 y 2 ] 2 Q 1 2 2
其中
y 1 arctg xh
2、直匀流加偶极子
只有当正源和负源的总强度等于零时,物形才是封闭的。设 直匀流 v 平行于x轴,由左向右流。再把一个轴线指向负x 的偶极子放在坐标原点处。这时,流动的位函数是:
x ( x, y ) v x M 2 r
流动是直匀流流过一个圆。圆的半径可以从驻点A的 坐标定出来。令:
偶极子。等位线是一些圆心在x轴上的圆,且都过原点。
流函数的式子取h→0而 Qh M 保持不变的极限结果,是:
2
y M 2 x y2
流线也是一些圆,圆心都在y轴上,且都过源点O。两个 分速度的表达式是:
M ( y 2 x 2 ) cos2 vx M 2 2 2 x (x y ) r2
1 , 2 ,..., n a11 a2 2 an n
不可压平面流必有流函数
vx y
无旋条件
vy x
v y
v x x y
也满足拉普拉斯方程
2 2 2 0 2 x y
几种简单的二维位流
1、直匀流
直匀流是一种速度不变的最简单的平行流动。其流速为
a2 1 v v 1 2 sin r 2r r
r a vr 0
仍是一条流线。在这个圆上
v 2v sin
驻点的位置可从
2 a
sin A 4 av
在第三和第四象限内,前后驻点对y轴是对称的。 这个角度离开π和0°的多少决定于环量对之比值; A 越大, 驻点越往下移。
价值的合乎逻辑的抽象,它能使我们把影响流动的各种因 素分开来看清楚。
譬如,早期由经验得出来的良好翼型,最大的升力对
阻力的比不过是几十比一,后来在位流理论指导下,设计 出来的翼型的最大升阻比竟达三百比一。这就是无粘抽象
的指导意义 。
3、直匀流加偶极子加点涡
在直匀流加偶极子的流动之上再在圆心处加一个强度 为(– )的点涡(顺时针转为负)。
末这流动便只有υr,而没有v 。 设半径为r处的流速是υr,那末这个源的总流量是:
Q 2rv r
流量是常数,故流速υr与半径成反比:
Q 1 vr 2 r
流函数的表达式是:
Q 或 2
Q y arctg 2 x
位函数从 vr 的式子积分得到:
Q ln r 2
;
位函数为
vx a vy b
ax by
常用的是这样的直匀流,它与x轴平行,从左面远方流
来,流速为v 的。 此时
v x
v y
2、点源
源可以有正负。正源是从流场上某一点有一定的流量 向四面八方流开去的一种流动。负源(又名汇)是一种与
正源流向相反的向心流动。如果把源放在坐标原点上,那
2
2
ln r
如果点涡的位置不在原点,而在(ξ,η),则点涡
的位函数和流函数的式子是:
y arctg 2 x
ln 2
x y
2
2
沿任意形状的围线计算环量,值都是 ,只要这个围 线把点涡包围在内 ,但不包含点涡在内的围线,其环量却 是等于零的。
a2 ( x, y ) v r r sin
,
时 0 0或 ,这就是x轴线;另外还有r 半径为a 的圆 。
a,这是一个
两个分速的式子是:
用在 r
a 的圆上时,得:
a2 vx v 1 2 cos 2 x r 2 a vy v 2 的迭加
1 、直匀流加点源
在一个平行于x轴由左向右流去的直匀流里,加一个强 度为Q的源,把坐标原点放在源所在的地方,迭加得到的 位函数是:
( x, y ) v x
两个分速是:
Q Q ln r v x ln x 2 y 2 2 4
Q x vx v x 2 x 2 y 2
这时位函数和流函数分别是
在极坐标下,两个分速是:
a2 ( x, y) v 1 x r 2 a2 ( x, y ) v 1 y ln r r 2
a2 vr v 1 2 cos r r
有无旋条件,就有位函数存在。
x vx
平面流动的连续方程是
y vy
结合两式,得平面不可压位流必须满足的方程:
v x v y 0 x y
2 2
