天津理工大学物理同步训练狭义相对论答案
狭义相对论基础习题解答

狭义相对论基础习题解答一 选择题1.判断下面几种说法是否正确 ( ) (1) 所有惯性系对物理定律都是等价的。
(2) 在真空中,光速与光的频率和光源的运动无关。
(3) 在任何惯性系中,光在真空中沿任何方向传播的速度都相同。
A. 只有 (1) (2) 正确B. 只有 (1) (3) 正确C. 只有 (2) (3) 正确D. 三种说法都正确解:答案选D 。
2. (1)对某观察者来说,发生在某惯性系中同一地点、同一时刻的两个事件,对于相对该惯性系作匀速直线运动的其它惯性系中的观察者来说,它们是否同时发生?(2)在某惯性系中发生于同一时刻、不同地点的两个事件,它们在其它惯性系中是否同时发生?关于上述两个问题的正确答案是:( )A. (1) 同时, (2) 不同时B. (1) 不同时, (2) 同时C. (1) 同时, (2) 同时D. (1)不同时, (2) 不同时 解:答案选A 。
3.在狭义相对论中,下列说法中哪些是正确的?( )(1) 一切运动物体相对于观察者的速度都不能大于真空中的光速.(2) 质量、长度、时间的测量结果都随物体与观察者的相对运动状态而改变 (3) 在一惯性系中发生于同一时刻,不同地点的两个事件在其他一切惯性系中也是同时发生的.(4) 惯性系中的观察者观察一个与他作匀速相对运动的时钟时,会看到这时钟比与他相对静止的相同的时钟走得慢些。
A. (1),(3),(4)B.(1),(2),(4)C.(1),(2),(3)D.(2),(3),(4) 解:同时是相对的。
答案选B 。
4. 一宇宙飞船相对地球以0.8c 的速度飞行,一光脉冲从船尾传到船头。
飞船上的观察者测得飞船长为90m ,地球上的观察者测得光脉冲从船尾发出和到达船头两个事件的空间间隔为 ( )A. 90mB. 54mC. 270mD. 150m 解:x ′=90m, u =0.8c ,8790/(310)310s t -'∆=⨯=⨯2()/1(/)270m x x u t u c ''∆=∆+∆-=。
练习册-第3章《狭义相对论》答案

练习册-第3章《狭义相对论》答案第3章 狭义相对论 一、选择题1(B),2(C),3(C),4(B),5(B),6(D),7(C),10(D),11(D),12(C) 二、填空题 (1). c(2). 4.33×10-8s (3). ∆x /v , 2)/(1)/(c x v v -∆(4). c(5). 0.99c (6). 0.99c (7). 8.89×10-8s(8). c 321 (9). 5.8×10-13, 8.04×10-2(10). lS m , lS m925 三、计算题1.在惯性系K 中,有两个事件同时发生在 x 轴上相距1000 m 的两点,而在另一惯性系K ′(沿x 轴方向相对于K系运动)中测得这两个事件发生的地点相距2000 m .求在K '系中测得这两个事件的时间间隔.解:根据洛仑兹变换公式: 2)(1/c t x x v v --=' ,22)(1//c c x t t v v --='可得2222)(1/c t x x v v --=' ,2111)(1/c t x x v v --='在K 系,两事件同时发生,t 1 = t 2,则 21212)(1/c x x x x v --='-' ,∴21)/()()/(112122='-'-=-x x x x c v解得 2/3c =v . 在K ′系上述两事件不同时发生,设分别发生于1t '和 2t '时刻,则 22111)(1//c c x t t v v --=',22222)(1//c c x t t v v --='由此得 221221)(1/)(/c c x x t t v v --='-'=5.77×10-6s2.在K 惯性系中,相距∆x = 5×106 m 的两个地方发生两事件,时间间隔∆t = 10-2s ;而在相对于K 系沿正x 方向匀速运动的K '系中观测到这两事件却是同时发生的.试计算在K '系中发生这两事件的地点间的距离∆x '是多少?解:设两系的相对速度为v .根据洛仑兹变换, 对于两事件,有2)/(1c t x x v v -'+'=∆∆∆22)/(1(c x )/c t tv v -'+'=∆∆∆由题意:='∆t且第二事件比第一事件晚发生∆t =2s ;而在另一惯性系S '中,观测第二事件比第一事件晚发生∆t '=3s .那么在S '系中发生两事件的地点之间的距离是多少?解:令S '系与S 系的相对速度为v ,有2)/(1c t t v -='∆∆, 22)/(1)/(c t t v -='∆∆则 2/12))/(1(t t c '-⋅=∆∆v ( = 2.24×108 m ·s -1 )那么,在S '系中测得两事件之间距离为: 2/122)(t t c t x ∆∆∆∆-'='⋅='v = 6.72×108 m5. 一飞船和慧星相对于地面分别以0.6c 和0.8c速度相向运动,在地面上观察,5s 后两者将相撞,问在飞船上观察,二者将经历多长时间间隔后相撞?解:两者相撞的时间间隔Δt = 5s 是运动着的对象—飞船和慧星—发生碰撞的时间间隔,因此是运动时.在飞船上观察的碰撞时间间隔Δt`是以速度v = 0.6c 运动的系统的本征时,根据时间膨胀公式21(/)t v c ∆=-,可得时间间隔为2`1(/)t v c ∆=∆-4(s).6.设有一个静止质量为m 0的质点,以接近光速的速率v 与一质量为M 0的静止质点发生碰撞结合成一个复合质点.求复合质点的速率v f . 解:设结合后复合质点的质量为M ′,根据动量守恒和能量守恒定律可得f M c m v v v '=-220/1/ 222202/1c c m c M c M v /-+='由上面二个方程解得 )/1/(22000c M m m f v v v -+=四 研讨题1. 相对论的时间和空间概念与牛顿力学的有何不同?有何联系?参考解答:牛顿力学时空观的基本观点是,长度和时间的测量与运动(或说与参考系)无关;而相对论时空观的基本观点是,长度和时间的测量不仅与运动有关,还与物质分布有关。
狭义相对论习题、答案与解法(2010.11.22)

狭义相对论习题、答案与解答一. 选择题 1. 有下列几种说法:(1) 真空中,光速与光的频率、光源的运动、观察者的运动无关; (2) 在所有惯性系中光在真空中沿任何方向的传播速率都相同; (3) 所有惯性系对物理基本规律都是等价的。
请在以下选择中选出正确的答案(C )A 、 只有(1)、(2)正确;B 、 只有(1)、(3)正确;C 、 只有(2)、(3)正确;D 、 3种说法都不正确。
2.(1)对某观察者来说,发生在某惯性系同一地点、同一时刻两个事件,对于相对该惯性系做匀速直线运动的其他惯性系中的观察者来说,它们是否同时发生?(2)在某惯性系不同地点、同一时刻的两个事件,它们在其他惯性系中是否同时发生?(A )A 、(1)同时,(2)不同时;B 、(1)不同时,(2)同时;C 、(1)同时,(2)同时;D 、(1)不同时,(2)不同时。
参考答案:(1) ⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎨⎧=∆=∆-∆-∆='∆001222x t c v x c v t t 0='∆t(2) ⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎨⎧≠'∆='∆-''∆+'∆=∆001222x t c v x cv t t 2221c v x c v t -'∆=∆3.K 系中沿x 轴方向相距3m 远的两处同时发生两事件,在K '系中上述两事件相距5m 远,则两惯性系间的相对速度为(A ) A 、c )54( ; B 、c )53(; C 、c )52(; D 、c )51(。
参考答案:221cv vt x x --=' 221cv t v x x -∆-∆='∆ c c x x c v 54531122=⎪⎭⎫⎝⎛-=⎪⎭⎫ ⎝⎛'∆∆-=4.两个惯性系K 和K ',沿x x '轴方向作相对运动,相对速度为v ,设在K '系中某点先后发生两个事件,用固定于该系的钟测出两事件的时间间隔为0t ∆,而用固定在K 系的钟测出这两个事件的时间间隔为t ∆。
大学物理 狭义相对论 习题及答案

第5章 狭义相对论 习题及答案1. 牛顿力学的时空观与相对论的时空观的根本区别是什么?二者有何联系?答:牛顿力学的时空观认为自然界存在着与物质运动无关的绝对空间和时间,这种空间和时间是彼此孤立的;狭义相对论的时空观认为自然界时间和空间的量度具有相对性,时间和空间的概念具有不可分割性,而且它们都与物质运动密切相关。
在远小于光速的低速情况下,狭义相对论的时空观与牛顿力学的时空观趋于一致。
2. 狭义相对论的两个基本原理是什么? 答:狭义相对论的两个基本原理是:(1)相对性原理 在所有惯性系中,物理定律都具有相同形式;(2)光速不变原理 在所有惯性系中,光在真空中的传播速度均为c ,与光源运动与否无关。
3.你是否认为在相对论中,一切都是相对的?有没有绝对性的方面?有那些方面?举例说明。
解 在相对论中,不是一切都是相对的,也有绝对性存在的方面。
如,光相对于所有惯性系其速率是不变的,即是绝对的;又如,力学规律,如动量守恒定律、能量守恒定律等在所有惯性系中都是成立的,即相对于不同的惯性系力学规律不会有所不同,此也是绝对的;还有,对同时同地的两事件同时具有绝对性等。
4.设'S 系相对S 系以速度u 沿着x 正方向运动,今有两事件对S 系来说是同时发生的,问在以下两种情况中,它们对'S 系是否同时发生?(1)两事件发生于S 系的同一地点; (2)两事件发生于S 系的不同地点。
解 由洛伦兹变化2()vt t x cγ'∆=∆-∆知,第一种情况,0x ∆=,0t ∆=,故'S 系中0t '∆=,即两事件同时发生;第二种情况,0x ∆≠,0t ∆=,故'S 系中0t '∆≠,两事件不同时发生。
5-5 飞船A 中的观察者测得飞船B 正以0.4c 的速率尾随而来,一地面站测得飞船A 的速率为0.5c ,求:(1)地面站测得飞船B 的速率; (2)飞船B 测得飞船A 的速率。
章狭义相对论基础习题解答

狭义相对论基础习题解答一选择题1. 判断下面几种说法是否正确( )(1)所有惯性系对物理定律都是等价的。
(2)在真空中,光速与光的频率和光源的运动无关。
(3)在任何惯性系中,光在真空中沿任何方向传播的速度都相同。
A. 只有(1) (2) 正确B. 只有(1) (3) 正确C. 只有(2) (3) 正确D. 三种说法都正确解:答案选D 。
2. (1) 对某观察者来说,发生在某惯性系中同一地点、同一时刻的两个事件,对于相对该惯性系作匀速直线运动的其它惯性系中的观察者来说,它们是否同时发生?(2) 在某惯性系中发生于同一时刻、不同地点的两个事件,它们在其它惯性系中是否同时发生?关于上述两个问题的正确答案是:( )A.(1) 同时,(2) 不同时B. (1) 不同时,(2) 同时C.(1) 同时,(2) 同时D. (1) 不同时,(2) 不同时解:答案选A 。
3.在狭义相对论中,下列说法中哪些是正确的?()1)一切运动物体相对于观察者的速度都不能大于真空中的光速.2)质量、长度、时间的测量结果都随物体与观察者的相对运动状态而改变3)在一惯性系中发生于同一时刻,不同地点的两个事件在其他一切惯性系中也是同时发生的.(4)惯性系中的观察者观察一个与他作匀速相对运动的时钟时,会看到这时钟比与他相对静止的相同的时钟走得慢些。
A. (1),⑶,⑷B. (1) ,⑵,⑷C. (1),⑵,⑶D.⑵,⑶,⑷解:同时是相对的。
答案选B。
4.一宇宙飞船相对地球以0.8 c的速度飞行,一光脉冲从船尾传到船头。
飞船上的观察者测得飞船长为90m地球上的观察者测得光脉冲从船尾发出和到达船头两个事件的空间间隔为()A. 90mB. 54mC. 270mD. 150m解:?x‘ =90m, u=0.8 c, f = 90/(3 108)=3 10^s_x = (=x u=t)/ .. 1 - (u/c)2二270m。
答案选C。
5.在某地发生两事件,与该处相对静止的甲测得时间间隔为4s , 若相对甲作匀速直线运动的乙测得时间间隔为5s,贝卩乙相对于甲的运动速度是:()A. 4 c /5B. 3 c /5C. c /5D. 2 c/5解:固有时'0=4, =5, = 0/ ..1-(u/c)2, u=(3/5) c。
第四章 狭义相对论习题以及答案

第4章狭义相对论习题及答案一 选择题1.下列几中说法:(1) 所有惯性系对物理基本规律都是等价的。
(2) 在真空中,光的速度与光的频率、光源的运动状态无关。
(3) 在任何惯性系中,光在真空中沿任何方向的传播速度都相同。
其中哪些说法是正确的?(A) 只有(1)、(2)是正确的。
(B) 只有(1)、(3)是正确的。
(C) 只有(2)、(3)是正确的。
(D) 三种说法都是正确的。
2.边长为a 的正方形薄板静止于惯性系K 的XOY 平面内,且两边分别与X ,Y 轴平行。
今有惯系K ′以0.8c(c 为真空中的光速)的速度相对于K 系沿X 轴作匀速直线运动,则从K ′系测得薄板的面积为(A)a ². (B)0.6a ² (C)0.8a ² (D)a ²/0.63.在某地发生两件事,静止位于该地的甲测得时间间隔为4s ,若相对于甲作匀速直线运动的乙测得时间间隔为5s ,测乙相对于甲的运动速度是(C 表示真空中光速)(A )(4/5)C (B )(3/5)C (C )(1/5)C (D )(2/5)C4.α粒子在加速器中被加速,其质量为静止质量的3倍时,动能为静止能量的(A)2倍 (B)3倍 (C)4倍 (D)5倍5.把一个静止质量为m 0的粒子,由静止加速到v=0.6c(c 为真空中光速)需作的功等于(A)0.18m 0c2 (B)0.25m 0c 2 (C)0.36m 0c 2 (D)1.25m 0c 2二 填空题1.狭义相对论的两条基本原理中,相对性原理说的是 __;光速不变原理说的是__________________________________.2.已知惯性系S ′相对于惯性系S 系以0.5c 的匀速度沿X轴的负方向运动,若从S ′系的坐标原点O′沿X轴正方向发出一光波,则S 系中测得此光波的波速为_____ ____.3.π+介子是不稳定的粒子,在它自己的参照系中测得平均寿命是2.6×10-8s ,如果它相对实验以0.8c (c 为真空中光速)的速度运动,那么实验坐标系中测得π+介子的寿命是____s.4.一门宽为 a.今有一固有长度为l 0(l 0>a)的水平细杆,在门外贴近门的平面内沿其长度方向匀速运动。
狭义相对论课后题目解答

狭义相对论课后题目解答思考题1 在狭义相对论中,下列说法中哪些是正确的?(A) 一切运动物体相对于观察者的速度都不能大于真空中的光速.(B) 质量、长度、时间的测量结果都是随物体与观察者的相对运动状态而改变的. (C) 在一惯性系中发生于同一时刻,不同地点的两个事件在其他一切惯性系中也是同时发生的.(D) 惯性系中的观察者观察一个与他作匀速相对运动的时钟时,会看到这时钟比与他相对静止的相同的时钟走得慢些.[A ,B ,D]解答:真空中的光速为自然界的极限速率,任何物体的速度都不大于光速;质量、长度、时间与运动是紧密联系的,这些物理量的测量结果与参考系的选择有关,也就是与观察者的相对运动状态有关;同时同地具有绝对性,同时异地则具有相对性;相对论时间膨胀效应即运动的时钟变慢。
答案:(A 、B 、D )2 两个惯性系K 与K '坐标轴相互平行,K '系相对于K 系沿x 轴作匀速运动,在K '系的x '轴上,相距为L '的A '、B '两点处各放一只已经彼此对准了的钟,试问在K 系中的观测者看这两只钟是否也是对准了?[ 没对准 ]解答:在K ’系中,A ’、B ’点的时空坐标分别为:()(),,,A A B B A x t B x t ''''''由题意:0A B t t t '''∆=-=,A B x x x L ''''∆=-=在K 系中,这两点的时空坐标分别为:()(),,,A A B B A x t B x t根据洛仑兹变换,220A B u ut x L t t t '''∆+∆∆=-==≠ 故,在K 系中的观测者看到这两只钟没有对准。
3 静止的μ子的平均寿命约为τ0 =2×10-6 s .今在8 km 的高空,由于π介子的衰变产生一个速度为v = 0.998 c (c 为真空中光速)的μ子,此μ子有无可能到达地面?[有可能]解答:μ子的固有寿命为:60210s τ-=⨯,根据相对论时间膨胀效应,对于地面参考系运动μ子的寿命为:653.1610s τ--==≈⨯μ子在τ时间内运动的距离为:50.998 3.16109461s u c m τ-==⨯⨯≈而μ在8km 的高空,小于它运动的距离,所以μ子可以到达地面。
大学物理-狭义相对论习题和解答

⎪ ⎪⎪ v第十七章 狭义相对论17—1 设有一宇宙飞船,相对于地球作匀速直线运动,若在地球上测得飞船的长度为其静止长度的一半,问飞船相对地球的速度是多少?[解] 飞船静止长度l 0 为其固有长度,地球上测得其长度为运动长度,由长度收缩公式,有:l = l 0= l 0 2解得: = c 2即: v =c = 0.866c 217—2 宇宙射线与大气相互作用时能产生 介子衰变,此衰变在大气上层放出 粒子,已知 粒子的速率为 v = 0.998c ,在实验室测得静止 粒子的平均寿命为2.2 ⨯10-6 s ,试问在 8000m 高空产生的 粒子能否飞到地面?[解] 地面上观测到的 子平均寿命与固有寿命之间的关系t = t 0子运行距离l = vt = v t 0子能飞到地面。
= 0.998c ⨯ 2.2⨯10- = 1042m17—3 在 S 系中观测到两个事件同时发生在 x 轴上,其间距离为 1m ,在 S ,系中观测这两个事件之间的距离是 2m 。
求在 S ,中测得的这两个事件发生的时间间隔。
[解] 在 S 系中两事件时间间隔∆t = 0, 由 Lorentz 变换x ' = x - ut t ' = t - u x c 2 ⎧ ∆x ' ⎪ 得: =⎨ ⎪∆t ' = ⎩∆t - ∆x ∆x c 2 = - c 2 将∆x ' = 2m , ∆x = 1m 代入上两式,得u = 3 c , 2∆t ' = -5.77 ⨯10-9 s 17—4 远方一颗星体以 0.80c 的速率离开我们,我们接收到它辐射来的闪光按 5 昼夜的周期变化,求固定在这星 1 - ( v )2 c 3 3 1 - ⎪ ⎛ v ⎫2 ⎝ c ⎭1 - ⎪ ⎛ v ⎫2 ⎝ c ⎭ 1 - (u / c )2 1 - (u / c )21 - (u / c )2 1 - (u / c )21 - 0.8021 - 0.99652 1 - (u / c )2 1 - (u / c )2 0 体上的参考系中测得的闪光周期。
狭义相对论习题和答案

狭义相对论习题和答案(总5页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--作业6 狭义相对论基础研究:惯性系中的物理规律;惯性系间物理规律的变换。
揭示:时间、空间和运动的关系.知识点一:爱因斯坦相对性原理和光速不变1.相对性原理:物理规律对所有惯性系都是一样的,不存在任何一个特殊 (如“绝对静止”)惯性系。
2.光速不变原理:任何惯性系中,光在真空中的速率都相等。
( A )1(基础训练1)、宇宙飞船相对于地面以速度v 作匀速直线飞行,某一时刻飞船头部的宇航员向飞船尾部发出一个光讯号,经过t (飞船上的钟)时间后,被尾部的接收器收到,则由此可知飞船的固有长度为(c 表示真空中光速)(A) c ·t (B) v ·t (C) 2/1(v /)c t c ∆⋅-(D) 2)/(1c t c v -⋅⋅∆【解答】飞船的固有长度为飞船上的宇航员测得的长度,即为c ·t 。
知识点二:洛伦兹变换由牛顿的绝对时空观伽利略变换,由爱因斯坦相对论时空观洛仑兹变换。
(1)在相对论中,时、空密切联系在一起(在x 的式子中含有t ,t 式中含x)。
(2)当u << c 时,洛仑兹变换 伽利略变换。
(3)若u c, x 式等将无意义xxx v cv vv v 21'--= 1(自测与提高5)、地面上的观察者测得两艘宇宙飞船相对于地面以速度 v = 逆向飞行.其中一艘飞船测得另一艘飞船速度的大小v ′=_0.994c _. 【解答】2222()220.9'0.994()1/10.91v v v c v c v v c v c --⨯====-++-知识点三:时间膨胀(1)固有时间0t ∆:相对事件发生地静止的参照系中所观测的时间。
(2)运动时间t ∆:相对事件发生地运动的参照系中所观测的时间。
201⎪⎭⎫ ⎝⎛-∆=∆c v t t (B )1(基础训练2)、在某地发生两件事,静止位于该地的甲测得时间间隔为4 s ,若相对于甲作匀速直线运动的乙测得时间间隔为5 s ,则乙相对于甲的运动速度是(c 表示真空中光速)(A) (4/5) c . (B) (3/5) c . (C) (2/5) c . (D) (1/5) c . 【解答】()2220024311551/t v t v c c c t v c ∆⎛⎫⎛⎫⎛⎫∆⇒=-⇒=-= ⎪ ⎪ ⎪∆⎝⎭⎝⎭⎝⎭-2(自测与提高12)、飞船A 以的速度相对地球向正东飞行,飞船B 以的速度相对地球向正西方向飞行.当两飞船即将相遇时A 飞船在自己的天窗处相隔2s 发射两颗信号弹.在B 飞船的观测者测得两颗信号弹相隔的时间间隔为多少 【解答】以地面为K 系,飞船A 为K ˊ系,以正东为x 轴正向;则飞船B 相对于飞船A 的相对速度220.60.8 1.4'0.9460.810.80.61(0.6)1B A B A B v v c c v c c v cc v c c----====-+⨯---' 6.17()t s ∆===知识点四:长度收缩(1)固有长度0l :相对物体静止的参照系测得物体的长度。
狭义相对论练习(答案版)

狭义相对论练习4-1 一飞船以0.99c 的速率平行于地面飞行,宇航员测得此飞船的长度为400 m 。
(1)地面上的观察者测得飞船长度是多少?(2)为了测得飞船的长度,地面上需要有两位观察者携带着两只同步钟同时站在飞船首尾两端处。
那么这两位观察者相距多远?(3)宇航员测得两位观察者相距多远?【解】(1))(4.5699.01400/12220m c u l l =-=-=(2)这两位观察者需同时测量飞船首尾的坐标,相减得到飞船长度,所以两位观察者相距是56.4 m 。
(3)上的两位观察者相距56.4 m ,这一距离在地面参考系中是原长,宇航员看地面是运动的,他测得地面上两位观察者相距为)(96.799.014.56/12220m c u l l =-=-=所以宇航员测得两位观察者相距7.96 m 。
4-2 一艘飞船原长为l 0,以速度v 相对于地面作匀速直线飞行。
飞船内一小球从尾部运动到头部,宇航员测得小球运动速度为u ,求地面观察者测得小球运动的时间。
【解】宇航员测得小球离开尾部的时空坐标为)','11t x (,小球到达头部的时空坐标为)','22t x (。
地面上测得小球运动的时间为:)''(/11)''(/11)''(/11222211222222212c x v t c v c vx t cv c vx t c v t t t ∆+∆-=+--+-=-=∆012''l x x =- ,u l t t /''012=-2220222/1)/1()''(/11cv u c uv l c x u t c u t -+=∆+∆-=∆∴4-3 在实验室中测得两个粒子均以0.75c 的速度沿同一方向飞行,它们先后击中同一静止靶子的时间间隔为5×10-8 s 。
求击中靶子前两个粒子相互间的距离。
章狭义相对论基础习题解答

20章狭义相对论基础习题解答(总8页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--狭义相对论基础习题解答一选择题1. 判断下面几种说法是否正确 ( )(1) 所有惯性系对物理定律都是等价的。
(2) 在真空中,光速与光的频率和光源的运动无关。
(3) 在任何惯性系中,光在真空中沿任何方向传播的速度都相同。
A. 只有 (1) (2) 正确B. 只有 (1) (3) 正确C. 只有 (2) (3) 正确D. 三种说法都正确解:答案选D 。
2. (1)对某观察者来说,发生在某惯性系中同一地点、同一时刻的两个事件,对于相对该惯性系作匀速直线运动的其它惯性系中的观察者来说,它们是否同时发生(2)在某惯性系中发生于同一时刻、不同地点的两个事件,它们在其它惯性系中是否同时发生关于上述两个问题的正确答案是:( )A. (1) 同时, (2) 不同时B. (1) 不同时, (2) 同时C. (1) 同时, (2) 同时D. (1) 不同时, (2) 不同时解:答案选A 。
3.在狭义相对论中,下列说法中哪些是正确的( )(1)一切运动物体相对于观察者的速度都不能大于真空中的光速.(2)质量、长度、时间的测量结果都随物体与观察者的相对运动状态而改变(3)在一惯性系中发生于同一时刻,不同地点的两个事件在其他一切惯性系中也是同时发生的.(4)惯性系中的观察者观察一个与他作匀速相对运动的时钟时,会看到这时钟比与他相对静止的相同的时钟走得慢些。
A. (1),(3),(4)B. (1),(2),(4)C. (1),(2),(3)D. (2),(3),(4)解:同时是相对的。
答案选B 。
4. 一宇宙飞船相对地球以的速度飞行,一光脉冲从船尾传到船头。
飞船上的观察者测得飞船长为90m,地球上的观察者测得光脉冲从船尾发出和到达船头两个事件的空间间隔为 ( )1A. 90mB. 54mC. 270mD. 150m 解:x ′=90m, u = c , 8790/(310)310s t -'∆=⨯=⨯ 2()/1(/)270m x x u t u c ''∆=∆+∆-=。
狭义相对论初步-答案(1)

4、答:黑洞是一种特殊星体,一切有质量的物质都将在其引力作用下吸引到星体内部。自 由光子能量为 E h ,由质能公式 E mc 得,光子质量为 m
2
h ,光子在引力作用下 c2
有引力势能, 在引力场中光子的总能量包括动能和势能。 由于在引力场中时空量度发生变化, 光子在引力场中的不同地点有不同频率。根据能量守恒可以找到光子频率随地点变化的规 律。存在光子的条件为 0 ,据此可得星体成为黑洞的临界半径。 自由光子无质量,因此无静止能量,其全部能量为动能,频率为 的光子的动能为
代入得
3、解:(1)观测站测得飞船船身长度为 L L 0 1 v / c =60m
2
则 t1 L / v 2.5 10 s (2)宇航员测得飞船船身的长度为 t2 L0 / v 4.17 10 s 4、解: (1) E mc me c / 1 (v / c)
-
5、 3c / 2 m/s(或 2.6×108 m/s ) ; 6、(1) v
3c / 2 ; (2) v 3c / 2 ;
16
7、(1) 9×10 J; (2) 8、 (n-1)m0c2。 9、 10 / 3 s 10、0.005m0c2;
1.5×10 J;
17
4.795 m0c2
三、计算题
5、解: 质量亏损为 m0 m1 m2 m3 m4 =0.0344×10 27 Kg 相应释放能量 E m0 c =2.799×10 12J
2
-
因此核燃料所释放的能量为:
E 14 =3.35×10 J/Kg m1 m2
四、讨论题
1、解: (1)一定同时;(2)一定不同时;(3)不一定同时。 2、解:以地球为参照系,子的寿命
狭义相对论练习册答案

狭义相对论练习册答案狭义相对论是爱因斯坦于1905年提出的理论,它主要研究在不同惯性参考系中物理定律的不变性。
以下是一些狭义相对论的练习题及其答案。
练习一:时间膨胀假设一个宇航员以接近光速的速度(例如0.9c)旅行了10光年。
根据狭义相对论,宇航员经历的时间与地面观察者测量的时间有何不同?答案:根据狭义相对论的时间膨胀公式:\[ \Delta t' = \frac{\Delta t}{\gamma} \]其中,\( \Delta t \) 是地面观察者测量的时间,\( \Delta t' \) 是宇航员经历的时间,\( \gamma = \frac{1}{\sqrt{1-v^2/c^2}} \) 是洛伦兹因子。
对于0.9c的速度,\( \gamma \) 大约为2.294。
因此,宇航员经历的时间是:\[ \Delta t' = \frac{10}{2.294} \approx 4.36 \text{ 光年} \]练习二:长度收缩一个物体在静止参考系中的长度是10米。
当它以0.9c的速度相对于观察者运动时,观察者会测量到的长度是多少?答案:长度收缩公式为:\[ L = L_0 \sqrt{1-v^2/c^2} \]其中,\( L \) 是运动参考系中的长度,\( L_0 \) 是静止参考系中的长度。
代入数值:\[ L = 10 \times \sqrt{1-(0.9)^2} \approx 4.5 \text{ 米} \]练习三:质能等价一个质量为1千克的物体,当它以接近光速的速度运动时,它的相对论质量是多少?答案:相对论质量公式为:\[ m = m_0 / \sqrt{1-v^2/c^2} \]其中,\( m \) 是相对论质量,\( m_0 \) 是静止质量。
对于0.9c的速度,\( \gamma \) 大约为2.294。
因此,相对论质量是:\[ m = 1 / \sqrt{1-(0.9)^2} \approx 2.294 \text{ 千克} \]练习四:速度相加两个物体A和B,A相对于地面以0.6c的速度运动,B相对于A以0.8c的速度运动。
16.狭义相对论 大学物理习题答案

m
m0 1 v / c
2 2
, v 1 ( m0 / m) c 1 (3.16 / 8.85) 3 10 2.8 10 m/s
2
2
8
8
p mv 8.85 10 27 2.8 10 8 2.48 10 18 kg m/s
16-12 解: ( 1)
16-2 解:设较快的飞船为 K 系,较慢的飞船为 K 系,则 u 0.98c
x
16-3
x ut 1 u2 / c2
20 0.98c 1 0.98 2
20 c 199 m
解:设地球为 K 系,飞船为 K 系
(1) t 16-4
L 。 v
u L u x 2 L 2 1 u L c v c (2) t ( 2) v c 1 u2 / c2 1 u2 / c2 1 u2 / c2 t
解: (1)设航天器为 K 系,飞船为 K 系,则 u 1.2 10 m/s , v x 1.0 10 m/s
8
8
v x
vx u 1.0 10 8 1.2 10 8 1.94 10 8 m/s (2)根据光束不变原理,激光束相对于宇宙飞船的速度仍为 c 。 16-5 解:设某参考系为 K 系,尺子甲为 K 系,且向右( x 正向)运动。尺子乙相对于甲的速度为 v
解: E k mc m0 c
2
2
E k mc 2 m0 c 2 ( m0 c 2 ( 1 (
1
2 1 v2 / c2
1 1 v12 / c 2 1 1 (
) ) 0.046m0 c 2
近代物理 4,16,17章习题参考答案

l
2
dx
1
0
l 0
2
dx
l
C
2
x
2
l
0
x2 dx
1
由此解得 C 2 30 , C 30 / l / l 2 l5
设在 0 ~ 1 l 区间内发现该粒子的几率为 P 3
则 P=
l
2
3 dx
0
l3 30x 2 l x2 dx 17
0
l5
81
2. 粒子在宽度为 a 的一维无限深势阱中运动,其波函数为:
6. 1 条 2 条
7.
8. 巴尔末系 赖曼系 红外线
-5-
二、选择题(每题 1 分,共 6 分)
1. A 2. C 3. B
4. A、D 5. C 6.B
三、计算题。
1. (1) n=4 (2) 6 条
(3) 2 条
2. (1) E 12.78eV
(2)E4,3 0.66eV , E4,2 2.56eV , E4,1 12.78eV , E3,2 1,89eV , E3,1 12.1eV , E2,1 10.2eV (3) 4.08m s 1
P mv h
德布罗意波(或物质波)
2.
xPx
2
(
h 2
)
Et 2
微观粒子
3. 1nm
4. 1.33 10 23
5. 几率波 6. 德布罗意波(或物质波)
概率密度
(r ,
t)
(r ,
t
)
|
(t,
x,
y,
z)
|2
7. 1
2
dV 1
V
8. 单值性 有限性 连续性
大学物理练习题狭义相对论的基本原理及其时空观

⼤学物理练习题狭义相对论的基本原理及其时空观练习⼗九狭义相对论的基本原理及其时空观⼀、选择题1. 静⽌参照系S中有⼀尺⼦沿x⽅向放置不动,运动参照系S′沿x轴运动,S、S′的坐标轴平⾏。
在不同参照系测量尺⼦的长度时必须注意(A) S′与S中的观察者可以不同时地去测量尺⼦两端的坐标。
(B)S′中的观察者可以不同时,但S中的观察者必须同时去测量尺⼦两端的坐标。
(C)S′中的观察者必须同时,但S中的观察者可以不同时去测量尺⼦两端的坐标。
(D) S′与S中的观察者都必须同时去测量尺⼦两端的坐标。
2. 下列⼏种说法:(1)所有惯性系对⼀切物理规律都是等价的。
(2)真空中,光的速度与光的频率、光源的运动状态⽆关。
(3)在任何惯性系中,光在真空中沿任何⽅向的传播速度都相同。
其中哪些正确的?(A)只有(1)、(2)是正确的。
(B)只有(1)、(3)是正确的。
(B)只有(2)、(3)是正确的。
(D)三种说法都是正确的。
3. 边长为a的正⽅形薄板静⽌于惯性系S的xOy平⾯内,且两边分别与x轴、y轴平⾏,今有惯性系S′以0.8c(c为真空中光速)的速度相对于K系沿x轴作匀速直线运动,则从S′系测得薄板的⾯积为(A)a2。
(B) 0.6a2。
(C) 0.8 a2。
(D)a2/0.6。
4. 在某地发⽣两件事,静⽌位于该地的甲测得时间间隔为6s,若相对甲以4c/5(c表⽰真空中光速)的速率作匀速直线运动的⼄测得时间间隔为(A) 10s。
(B) 8s。
(C) 6s。
(D) 3.6s。
(E) 4.8s。
5. (1)对某观察者来说,发⽣在某惯性系中同⼀地点,同⼀时刻的两个事件,对于相对该惯性系作匀速直线运动的其它惯性系的观察者来说,它们是否同时发⽣?(2)在某惯性系中发⽣于同⼀时刻,不同地点的两个事件,它们在其它惯性系中是否同时发⽣?关于上述两问题的正确答案是:(A)(1)⼀定同时,(2)⼀定不同时。
(B)(1)⼀定不同时,(2)⼀定同时。
天津理工大学 大学物理同步训练下 答案.
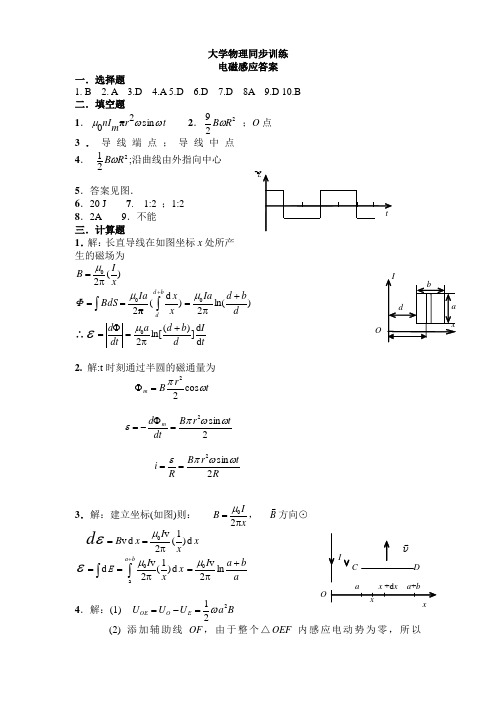
大学物理同步训练 电磁感应答案一.选择题1. B2. A3.D4.A5.D6.D7.D 8A 9.D 10.B 二.填空题1.t r m nI ωωμsin 20π 2.229R B ω ;O 点3.导线端点;导线中点 4. 221R B ω;沿曲线由外指向中心5.答案见图. 6.20 J 7. 1:2 ;1:28.2A 9.不能三.计算题1.解:长直导线在如图坐标x 处所产生的磁场为)(20x IB π=μ )d (20⎰⎰+==bd d x x Ia BdS πμΦ)ln(20d bd Ia +π=μ ∴εtI d b d a dt d d d ])(ln[20+π=Φ=μ2. 解:t 时刻通过半圆的磁通量为t r B m ωπcos 22=Φ2sin 2t r B dt d m ωωπε=Φ-=Rt r B R i 2sin 2ωωπε==3.解:建立坐标(如图)则: xIB π=20μ, B 方向⊙εd x x I x B d )1(2v d v 0π==μ ε⎰⎰+π==x x I ba d )1(2v d a0μE a b a I +π=ln 2v 0μ4.解:(1) B a U U U E O OE 221ω=-=(2) 添加辅助线OF ,由于整个△OEF 内感应电动势为零,所以LtxIOd a ba x +d x a +bI C D vxOxOFEF OE E E E =+即可直接由辅助线上的电动势 OF 来代替OE 、EF 两段内的电动势.a a OF 245cos 2=︒= B a a B U U U F O OF 22)2(21ωω==-=(3) O 点电势最高 .《机械振动》答案一、 选择题CDBBB CACAA DC二、 填空题1、n T /2、T 4,2/2S3、0sin A ωϕ,-02cos ϕωA4、2rad/s ,0,t x 2cos 2=(SI ),212N ,负方向5、10cm ,π32,4.8s ,)32125cos(1.0ππ+=t x (SI )6、如图所示7、k m π221+,02x m k8、m k π1,mkπ19、238kA10、π 三、 计算题1、解:处于平衡位置时,弹簧的伸长量L ∆满足如下关系Mg L k =∆(1) 对滑块m ,M 进行受力分析,设绳子的张力为T ,则当滑块M 位移为x 时,有Ma T Mg =-a m T L x k '=+∆+-)(由于绳子不可伸长,故有a a =',则上述两式联立消去T 并考虑(1)式可得a m M kx )(+=-由上式可知滑块M 做简谐振动,其振动原频率为mM k+=ω 已知0=t 时滑块M 处于负的最大位移处,即M 滑块的振幅及初相为kMgL A =∆=,πϕ= 则可得M 滑块的运动方程⎪⎪⎭⎫ ⎝⎛++=πt m M kk Mg x cos (SI ) 2、解:设该质点的简谐运动方程为)cos(ϕω+=t A x (SI )则可以知道该质点的速度满足)2cos(πϕωωυ++=t A (SI )由图可以看出速度振幅为10=A ω,利用旋转矢量法可得速度方程的初相与圆频率为ππϕ322=+→ 6πϕ= 14433t ωππ∆Φ===∆ → 1030/3A ππ==因此可以得到该质点的振动方程30cos 36x t πππ⎛⎫=+ ⎪⎝⎭(SI ) 3、解:如图所示,画出旋转矢量图,可以知道质点从2/A 处(速度为正)运动到2/A 处(速度为正)时旋转矢量转过的角度为π1219=∆Φ已知旋转矢量的旋转角速度(即质点振动圆频率)为4/πω=,故需要的时间为319=∆Φ=∆ωt (s )4、解:将振动方程2x 写为t x πcos 32=(SI )画出三个旋转矢量,如右图所示。
NO.8狭义相对论基础答案

《大学物理》作业(狭义相对论基础) NO.8答案班级: 学号: 姓名: 日期: 成绩:一 选择题1.下列几种说法:(1)所有惯性系对物理基本规律都是等价的;(2)在真空中,光的速度与光的频率、光源的运动状态无关;(3)在任何惯性系中,光在真空中沿任何方向的传播速度都相同。
(A )只有(1)、(2)对; (B )只有(1)、(3)对; (C )只有(2)、(3)对; (D )(1)(2)(3)都对。
[ D ]解:爱因斯坦狭义相对论的两个基本假设2.k 系与k ′系是坐标相互平行的两个惯性系,k ′系相对于k 系沿OX 轴正方向匀速运动,一根刚性尺静止在k ′系中,与O ′X ′ 轴成30°角,而在k 系中观察到该尺与OX 轴成45°角,则k ′系相对于k 系的速度是:(A )32c ; (B )31c ; (C )21)(32c ; (D )21)(31c 。
解:'1'200''230453y yy tg u c x x ⎫∆=∆∆⎪⎛⎫⇒=⇒=⇒= ⎪∆=∆⎝⎭ [ C ]※3.一宇宙飞船相对地球以0.8c 的速度飞行,一光脉冲从船尾传到船头,飞船上的观察者测得飞船长为90m ,则地球上的观察者测得光脉冲从船尾发出和到达船头两个事件的空间间隔为:(A )90m ; (B )54m ; (C )270m ; (D )150m.4.如图,地面上的观察者认为A 、B 两事件同时发生,则在火箭上的观察者看来:(A )A 早于B ; (B )B 早于A ;(C )A 、B 同时; (D )条件不够,不能判断。
解: '''21'220,00x t v t t t x v t t x cc γγ∆>∆=⎫⎪⇒∆=-=-∆<⎬⎛⎫∆=∆-∆ ⎪⎪⎝⎭⎭[ B ]5.若粒子的动能等于它本身的静止能量,这时粒子的速度为: (A )23c ; (B )41c ; (C )21c ; (D )0.8c 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
狭义相对论答案
一.选择题
1.D 注释: 狭义相对论基本原理: 在所有惯性系中,真空中的光速具有相同的量值c ;在所有惯性系中,物理定律的表达式都相同。
2.A 注释:同时的相对性
3.A
注释:长度收缩0l
l =4.D 注释:时间延缓,长度收缩
5.B 注释: 运动方向上长度收缩,从'
k 系看,薄板沿x
方向收缩为a '=
y 方向不变。
6.C 注释: 长度收缩公式应用前提: 两个物理事件在其中一个惯性系要同时发生. 时间延缓公式应用前提: 两个物理事件在其中一个惯性系要同一地点发生.) 地球上的观察者看光信号从头部传到尾部,两个物理事件发生既不同时,也不在同一地点,所以长度收缩和时间延缓公式均不可用,需要利用洛仑兹变换求解. 注: 洛仑兹变换解题思路: 1.确定惯性系S 和S ’系, 确定物理事件 2. 将S 和S ’系的已知条件分别列出.
3.根据已知条件利用洛仑兹变换(或逆变换)求解. 设飞船为S ’系, 物理事件1: 光信号头部发出 物理事件2: 光信号到达尾部 S ’ :100 100t x c
''∆=
∆=
S:
x
∆待求
根据洛伦兹坐标逆变换 可知
x ''∆=
=200m
7.A 注释:2
E
m c
=
8.C 注释 静能2
0o
E m c
=
,相对论动能22
22
k
o o E m c m c m c
=-=
-
9.C 注释:静能2
0o
E m c
=
,相对论动能22
22
k
o o E m c m c m c
=-=
-
二.填空题
1.所有惯性系对于物理学定律都是等价的 所有惯性系中,真空中的光速都是相等的 2.c 注释:光速不变原理 3. t c ∆ 注释:略 4. c 6.0 注释:长度收缩
l l =
5. 2
0)
/(1l l c - 注释: 根据运动杆长度收缩公式 2
0)
/(1c v l l -=
则
2
0)
/(1c v l l -≥,
2
0)
/(1l l c v -≥
6. c
8.0 注释
长度收缩l
l =
7. 同时;不同地 注释:同时的相对性 8.
2
2
)
/(1c v m m -=
;22
0K
E m c m c
=- 注释略
9.225.0c m e
注释:相对论动能2
2
22
k
o o E m c m c m c =-=
- 动能定理
k
W E =∆
三.计算题
1解:(1) 观测站测得飞船船身的长度为
=
-=2
0)
/(1c L L v 60m 则
t
∆= L /v =2.5×10-7 s
(2) 宇航员测得飞船船身的长度为L 0,则 t '∆= L 0/v =4.17×10-7 s 2.解:根据已知条件观察者O 测得距离为固有长度, 对O ′观察者来看,初始距离是运动的,发生收缩
0L L =8
028.8910
L
t s v
-∆=
=⨯
或对O ′观察者来讲,从开始到相遇的时间间隔为固有时,因此
8
0200.88.8910
0.6t t c
-∆=
=⨯
=⨯s
3.解:已知条件 30
=τ
天60
602430⨯⨯⨯=
s
由0
γτ
τ
= τ
τ2
20
1c
v -
= 07
.0)11(2
20=--
=-=∆τττc
v t s
如果=v
c
8.0
12
)11(220=-
-
=-=∆τττc
v t 天=6
10
04
.1⨯s
4.解: (1) 2
2
2
)
/(1/
c c m mc
E e v -== =1.37×10-13 J
(2) 2
0v
2
1e K m E =
= 0.26×10-13 J
2
2
c
m mc E e K -=2
2]1))/(1/
1[(c
m c e --=v =0.55×10-13 J
=
K K E E /00.47
若=v
c
99.0
则
2
0v
2
1e K m E =
= 4.01×10-14 J
2
2
c
m mc E e K -=2
2]1))/(1/
1[(c
m c e --=v = 4.99×10-13 J
=
K K E E /00.08。
