2021年因式分解法解一元二次方程练习题
因式分解解一元二次方程136题

分解因式法解一元二次方程专项练习136题(有答案)1.3(x﹣2)2﹣x(x﹣2)=0,2.3x(x+2)=5(x+2)3.2x2﹣8x=04.x2﹣3x﹣4=0.5.x2﹣2x﹣3=0.6.x(x﹣3)﹣4(3﹣x)=0,7. 3(x﹣2)2=x(x﹣2);8. 2x2﹣5x﹣3=09. (3x﹣1)2=(x+1)210. x(x﹣6)=2(x﹣8)11.4+4(1+x)+4(1+x)2=19 12.x2﹣4x﹣5=013. 3(5﹣x)2=2(5﹣x)14.(x﹣3)2=2(3﹣x).15.2x2+x﹣6=0.16.2x2﹣x﹣1=0;17. 3x(x﹣1)=2(x﹣1)2.18.x(x﹣5)+4x=019. x2﹣2x=020.(x﹣3)2+2x(x﹣3)=0;21.x2﹣3x=0;22.(x﹣2)2=(2x+3)223.3x2﹣11x﹣4=0.24.2x(x﹣1)﹣x+1=0 25. 2x2+x﹣3=026.x2﹣2x﹣15=0;27. 2x(x﹣3)+x=3.28. x(x﹣3)=15﹣5x;29.(x﹣1)2﹣2(x﹣1)=0 30.x(x﹣2)﹣x+2=0;31. 2x2﹣3x﹣5=0.32..4x2﹣x﹣1=3x﹣2,33.34.(x﹣3)2﹣2(x﹣1)=x﹣7.35. 3x(x﹣2)﹣2(x﹣2)=036. 3x2﹣x﹣2=0;37. (x﹣6)2﹣(3﹣2x)2=0.38.(x﹣3)2=5(3﹣x)(x﹣3)2=5(3﹣x)39.(2x+1)2=2(2x+1)40.(3x﹣1)(x﹣1)=(4x+1)(x﹣1).41.x2﹣x﹣6=0,42.x2﹣8(x+6)=043.2x2﹣6x=0.44.(x﹣3)(x+1)=545.2x2﹣8x=0;46.x2+2x﹣15=047. 2x2﹣5x﹣7=048. 2y(y﹣3)=4(y﹣3)49. x2﹣7x﹣18=050. 3x2+8x﹣3=051. 2x(x﹣3)=9﹣3x 52.x2﹣4x=553. ﹣8x2+10x=054.3x2+4x﹣7=0,55. 3x2﹣5x+2=056. 2(x﹣3)2=x2﹣3x 57.x2=3x;58. (3x﹣2)2=(2x﹣3)259. (y﹣2)2+2y(y﹣2)=060.2y(y+2)=y+2.61. 5x2+3x=062. (3x﹣2)2=(2x﹣3)263. x(x﹣3)=5(x﹣3);64. (2x+3)2﹣5(2x+3)+4=0.65. (2x﹣7)2﹣5(2x﹣7)+4=066. (3x﹣1)2=x2+6x+967.(2x+2)2=3(2x+2)(x﹣1)68.(x+7)(x﹣3)+4x(x+1)=069.2x(x+3)﹣3(x+3)=070. x﹣2=x(x﹣2)71. x2+8x﹣9=072.x(2x﹣5)=4x﹣10.73.(2x﹣5)2﹣(x+4)2=074.2(x﹣1)2=x2﹣175.76. 4x(2x﹣1)=3(2x﹣1);77. 2x2+x﹣1=0.78. (3x﹣2)(x+4)=(3x﹣2)(5x ﹣1);79. (x+1)(x+3)=15.80.x2﹣5x﹣6=081. x2﹣2x=9982. (x﹣3)2﹣4x+12=083. 4(x+1)2=9(x﹣2)284. x2=2x85. (x+4)2=5(x+4)87. 16(x﹣1)2=22588. 4x2﹣4x+1=x2﹣6x+989. 9(x+1)2=4(x﹣1)2(4)x2﹣4x+4=(3﹣2x)290. (x﹣2)2=(3﹣2x)2.91. (x+2)2﹣10(x+2)+25=0 92.x2﹣2(p﹣q)x﹣4pq=0.93.x2+10x+21=0,94.2(x﹣2)2=3(x﹣2)95. 3(x﹣5)2=2(5﹣x),96. ,97. 5x2﹣4x﹣12=0,98. (x ﹣)=5x (﹣x),99.9(x﹣2)2﹣4(x+1)2=0.100..101.(2)x2﹣8x+15=0;103. 6x2﹣x﹣12=0.104. 2x2﹣x﹣6=0105. ﹣x2+6x﹣5=0106. (x﹣5)2=(2x﹣1)(5﹣x)107. (x+1)(x+2)=3x+6.108. x2﹣9=0,109. x2+3x﹣4=0,110. x2﹣3x+2=0,111. 4(3x﹣1)2 =25(2x+1)2.112. (3x+5)2﹣4(3x+5)+3=0113. (3x+2)(x+3)=x+14114. 3(x+1)2=(x+1)115.(x ﹣2)2﹣4=0116.(x ﹣3)2+2x (x ﹣3)=0117.(3x ﹣1)2=(x+1)2118.(x+5)2﹣2(x+5)﹣8=0.119. x 2﹣8x=9120. (x ﹣2)2=(2x+3)2. 121. x 2﹣3=3(x+1); 122. (y ﹣3)2+3(y ﹣3)+2=0 123. 7x (5x+2)=6(5x+2) 124.(3)6(x+4)2﹣(x+4)﹣2=0125. x 2﹣(3m ﹣1)x+2m 2﹣m=0,126.x 2﹣2x ﹣224=0. 127..128.5x (x ﹣3)﹣(x ﹣3)(x+1)=0.129.x 2﹣11x+28=0130. 4y 2﹣25=0;131.(2x+3)2﹣36=0;132. x 2﹣3x+2=0;133. 2t 2﹣7t ﹣4=0;134. 5y (y ﹣1)=2(y ﹣1)135. x 2+(1+2)x+3+=0;136.(x﹣3)2+(x+4)2﹣(x﹣5)2=17x+24.137.x2﹣3|x|﹣4=0 参考答案:1.3(x﹣2)2﹣x(x﹣2)=0,(x﹣2)(3x﹣6﹣x)=0,x﹣2=0或2x﹣6=0,解得:x1=2,x2=3;2.3x(x+2)=5(x+2)原方程可化为3x(x+2)﹣5(x+2)=0,(3x﹣5)(x+2)=0,解得x1=﹣2,3.2x2﹣8x=0因式分解,得2x(x﹣4)=0,于是得,2x=0或x﹣4=0,即x1=0,x2=4.4. x2﹣3x﹣4=0.因式分解,得(x﹣4)(x+1)=0,于是得,x﹣4=0或x+1=0,解得:x1=4,x2=﹣15.x2﹣2x﹣3=0.原方程可以变形为(x﹣3)(x+1)=0x﹣3=0,x+1=0∴x1=3,x2=﹣1.6.x(x﹣3)﹣4(3﹣x)=0,(x﹣3)(x+4)=0,x﹣3=0或x+4=0,解得:x1=3,x2=﹣4;7. 3(x﹣2)2=x(x﹣2);整理得3(x﹣2)2﹣x(x﹣2)=0 即(x﹣2)(x﹣3)=0x1=2,x2=38. 2x2﹣5x﹣3=0(2x+1)(x﹣3)=0 x1=﹣0.5,x2=39. (3x﹣1)2=(x+1)2原方程可化为:(3x﹣1)2﹣(x+1)2=0,(3x﹣1+x+1)(3x﹣1﹣x﹣1)=0,∴4x=0或2x﹣2=0,解得:x1=0,x2=1;10. x(x﹣6)=2(x﹣8)x2﹣6x=2x﹣16x2﹣8x+16=0(x﹣4)2=0x1=x2=411.4+4(1+x)+4(1+x)2=19原式可变为4(1+x)2+4(1+x)﹣15=0 [2(1+x)﹣3][2(1+x)+5]=0x1=,x2=﹣12.x2﹣4x﹣5=0(x﹣5)(x+1)=0x﹣5=0或x+1=0x1=5,x2=﹣113. 3(5﹣x)2=2(5﹣x)原方程可变形为:3(5﹣x)2﹣2(5﹣x)=0(5﹣x)[3(5﹣x)﹣2]=0(5﹣x)(13﹣3x)=0则x1=5,x2=14.(x﹣3)2=2(3﹣x).原式可变为(x﹣3)2﹣2(3﹣x)=0(x﹣3)(x﹣1)=0x1=3,x2=115.2x2+x﹣6=0.2x2+x﹣6=0(x+2)(2x﹣3)=0x+2=0或2x﹣3=0∴x1=﹣2,x2=.16.2x2﹣x﹣1=0;原方程可化为:(x﹣1)(2x+1)=0,x﹣1=0或2x+1=0,解得:x1=1,x2=﹣.17. 3x(x﹣1)=2(x﹣1)2.原方程可化为:3x(x﹣1)﹣2(x﹣1)2=0,(x﹣1)(3x﹣2x+2)=0,x﹣1=0或x+2=0,解得:x1=1,x2=﹣218.x(x﹣5)+4x=0即x(x﹣5+4)=0x(x﹣1)=0∴x1=0,x2=119. x2﹣2x=0x(x﹣2)=0∴x=0或x﹣2=0∴x1=0,x2=2.20.(x﹣3)2+2x(x﹣3)=0;原方程可化为:(x﹣3)(x﹣3+2x)=0(x﹣3)(x﹣1)=0x1=3,x2=1.21.x2﹣3x=0;x(x﹣3)=0∴x1=0,x2=322.(x﹣2)2=(2x+3)2(x﹣2)2=(2x+3)2即(x﹣2)2﹣(2x+3)2=0(3x+1)(x+5)=0x1=﹣5,x2=23.3x2﹣11x﹣4=0.把方程3x2﹣11x﹣4=0即(x﹣4)(3x+1)=0,解得x1=4,x2=.24.2x(x﹣1)﹣x+1=0原方程变形为:2x(x﹣1)﹣(x﹣1)=0∴(x﹣1)(2x﹣1)=0∴x﹣1=0或2x﹣1=0解得x1=1,x2=;25. 2x2+x﹣3=0原方程变形为:(x﹣1)(2x+3)=0∴x1=1,x2=26.x2﹣2x﹣15=0;原式可化为:(x﹣5)(x+3)=0得x1=5,x2=﹣327. 2x(x﹣3)+x=3.原式可化为:(x﹣3)(2x+1)=0得,x2=328. x(x﹣3)=15﹣5x;x(x﹣3)=﹣5(x﹣3)(x﹣3)(x+5)=0x1=3,x2=﹣529.(x﹣1)2﹣2(x﹣1)=0(x﹣1)2﹣2(x﹣1)=0,(x﹣1)(x﹣1﹣2)=0,∴x﹣1=0或x﹣3=0,∴x1=1,x2=330.x(x﹣2)﹣x+2=0;原方程可化为:x(x﹣2)﹣(x﹣2)=0,(x﹣2)(x﹣1)=0,解得:x1=2,x2=1;31. 2x2﹣3x﹣5=0.原方程可化为:(2x﹣5)(x+1)=0,2x﹣5=0或x+1=0,解得:x1=,x2=﹣132..∵4x2﹣x﹣1=3x﹣2,∴4x2﹣4x+1=0即(2x﹣1)2=0,解得33.解:∴∴34.(x﹣3)2﹣2(x﹣1)=x﹣7.移项,合并同类项得,(x﹣3)2﹣3x+9=0,即,(x﹣3)2﹣3(x﹣3)=0,因式分解得,(x﹣3﹣3)(x﹣3)=0则x﹣3=0或(x﹣6)=0,解得,x1=3,x2=6.35. 3x(x﹣2)﹣2(x﹣2)=0(x﹣2)(3x﹣2)=0x1=2,x2=;36. 3x2﹣x﹣2=0;原方程变形得,(3x+2)(x﹣1)=0∴,x2=1;37. (x﹣6)2﹣(3﹣2x)2=0.原方程变形得,(x﹣6+3﹣2x)(x﹣6﹣3+2x)=0(x+3)(3x﹣9)=0∴x1=3,x2=﹣338.(x﹣3)2=5(3﹣x)(x﹣3)2=5(3﹣x)(x﹣3)2+5(x﹣3)=0(x﹣3)(x+2)=0∴x1=3,x2=﹣2.39.(2x+1)2=2(2x+1)原方程可化为:(2x+1)2﹣2(2x+1)=0,(2x+1)(2x+1﹣2)=0,(2x+1)(2x﹣1)=0,解得:x1=﹣,x2=.40.(3x﹣1)(x﹣1)=(4x+1)(x﹣1).(3x﹣1)(x﹣1)﹣(4x+1)(x﹣1)=0,(x﹣1)[(3x﹣1)﹣(4x+1)]=0,(x﹣1)(x+2)=0,∴x1=1,x2=﹣2.41.∵x2﹣x﹣6=0,∴(x+2)(x﹣3)=0,∴x+2=0或x﹣3=0,解得x1=3,x2=﹣2.42.x2﹣8(x+6)=0原方程化为x2﹣8x﹣48=0(x+4)(x﹣12)=0解得x1=﹣4,x2=12.43.2x2﹣6x=0.原方程变形为2x(x﹣3)=0∴2x=0或x﹣3=0∴x1=0,x2=344.(x﹣3)(x+1)=5x2﹣2x﹣8=0,(x﹣4)(x+2)=0∴x1=4,x2=﹣2.45.2x2﹣8x=0;因式分解,得2x(x﹣4)=0,2x=0或x﹣4=0,解得,x=0或x=4;46.x2+2x﹣15=0(x+5)(x﹣3)=0x+5=0或x﹣3=0∴x1=﹣5,x2=3;47. 2x2﹣5x﹣7=0因式分解得(x+1)(2x﹣7)=0解得:,x2=﹣1;48. 2y(y﹣3)=4(y﹣3)2y(y﹣3)﹣4(y﹣3)=0(y﹣3)(2y﹣4)=0(2分)∴y1=3,y2=249. x2﹣7x﹣18=0解:(x﹣9)(x+2)=0x﹣9=0或x+2=0∴x1=9,x2=﹣250. 3x2+8x﹣3=0解:方程可以化为(x+3)(3x﹣1)=0 ∴x+3=0或3x﹣1=0即x1=﹣3,x2=.51. 2x(x﹣3)=9﹣3x2x(x﹣3)﹣(9﹣3x)=02x(x﹣3)+3(x﹣3)=0(x﹣3)(2x+3)=0x1=3,x2=﹣52.x2﹣4x=5x2﹣4x﹣5=0(x﹣5)(x+1)=0∴x﹣5=0,x+1=0∴原方程的解为:x1=5,x2=﹣1.53. ﹣8x2+10x=0x(10﹣8x)=0∴x1=0,x2=54.3x2+4x﹣7=0,(x﹣1)(3x+7)=0,x﹣1=0或3x+7=0,解得:55. 3x2﹣5x+2=0原式变形为:(3x﹣2)(x﹣1)=0∴x1=1,x2=56. 2(x﹣3)2=x2﹣3x原方程变形为:2(x﹣3)2=x(x﹣3)(x﹣3)[2(x﹣3)﹣x]=0(x﹣3)(x﹣6)=0∴x1=3,x2=657.(1)x2=3x;移项得,x2﹣3x=0,因式分解得,x(x﹣3)=0,解得,x1=0,x2=3;58. (3x﹣2)2=(2x﹣3)2解:3x﹣2=±(2x﹣3)3x﹣2=2x﹣3或3x﹣2=﹣(2x﹣3)解得:x1=﹣1,x2=1;59. (y﹣2)2+2y(y﹣2)=0解:(y﹣2)(y﹣2+2y)=0解得:y1=2,y2=60..2y(y+2)=y+2.原方程变形为:2y(y+2)﹣(y+2)=0,即(y+2)(2y﹣1)=0,解得y1=﹣2,y2=.61. 5x2+3x=0x(5x+3)=0,即:x=0或5x+3=0,∴x1=0,x2=﹣.62. (3x﹣2)2=(2x﹣3)2(3x﹣2)2﹣(2x﹣3)2=0,(3x﹣2+2x﹣3)(3x﹣2﹣2x+3)=0,5(x﹣1)(x+1)=0,即:x﹣1=0或x+1=0∴x1=1,x2=﹣163. x(x﹣3)=5(x﹣3);x(x﹣3)﹣5(x﹣3)=0,(x﹣3)(x﹣5)=0,∴x1=3,x2=5;64. (2x+3)2﹣5(2x+3)+4=0.(2x+3)2﹣5(2x+3)+4=0(2x+3﹣4)(2x+3﹣1)=0(2x﹣1)(x+1)=0,∴x1=,x2=﹣165. (2x﹣7)2﹣5(2x﹣7)+4=0 (2x﹣7﹣4)(2x﹣7﹣1)=0;x2=466. (3x﹣1)2=x2+6x+9(3x﹣1)2﹣(x﹣3)2=0即(2x+1)(x﹣2)=0x1=2,x2=﹣0.567.(2x+2)2=3(2x+2)(x﹣1)(2x+2)2﹣3(2x+2)(x﹣1)=0即(2x+2)【2x+2﹣3(x﹣1)】=0∴(x﹣5)(x+1)=0x1=﹣1,x2=568.(x+7)(x﹣3)+4x(x+1)=0化简:(x+7)(x﹣3)+4x(x+1)=0整理得,5x2+8x﹣21=0,因式分解得,(5x﹣7)(x+3)=0,即5x﹣7=0或x+3=0,所以x1=,x2=﹣3.69..2x(x+3)﹣3(x+3)=0根据题意,原方程可化为:(x+3)(2x﹣3)=0,∴方程的解为:x1=,x2=﹣370. x﹣2=x(x﹣2)即x﹣2﹣x(x﹣2)=0(x﹣2)(1﹣x)=0x1=2,x2=1;71. x2+8x﹣9=0(x+9)(x﹣1)=0x1=﹣9,x2=172.x(2x﹣5)=4x﹣10.原方程可变形为:x(2x﹣5)﹣2(2x﹣5)=0,(2x﹣5)(x﹣2)=0,2x﹣5=0或x﹣2=0;解得x1=,x2=2.74.(2x﹣5)2﹣(x+4)2=0因式分解,得[(2x﹣5)+(x+4)][(2x﹣5)﹣(x+4)]=0,整理得,(3x﹣1)(x﹣9)=0解得,x1=,x2=9.74.2(x﹣1)2=x2﹣1原方程即为2(x﹣1)2﹣(x2﹣1)=0,2(x﹣1)2﹣(x+1)(x﹣1)=0,(x﹣1)[2(x﹣1)﹣(x+1)]=0,(x﹣1)(x﹣3)=0,x1=1,x2=3;75.(x﹣1)(x ﹣+3)=0,∴x1=1,x2=-376. 4x(2x﹣1)=3(2x﹣1);原方程可化为:4x(2x﹣1)﹣3(2x﹣1)=0,(2x﹣1)(4x﹣3)=0,2x﹣1=0或4x﹣3=0,解得:,;77. 2x2+x﹣1=0.原方程可化为:(2x﹣1)(x+1)=0,2x﹣1=0或x+1=0,解得:,x2=﹣1.78. (3x﹣2)(x+4)=(3x﹣2)(5x﹣1);解:(3x﹣2)(x+4)﹣(3x﹣2)(5x﹣1)=0 (3x﹣2)[(x+4)﹣(5x﹣1)]=0(3x﹣2)(﹣4x+5)=03x﹣2=0或﹣4x+5=0;79. (x+1)(x+3)=15.方程整理得:x2+4x﹣12=0( x+6)(x﹣2)=0x1=﹣6,x2=2.80. x2﹣5x﹣6=0解:(x﹣6)(x+1)=0,x﹣6=0或x+1=0,∴原方程的解是x1=6,x2=﹣1.81. x2﹣2x=99解:(x﹣11)(x+9)=0,x﹣11=0或x+9=0,∴原方程的解是x1=11,x2=﹣9.82. (x﹣3)2﹣4x+12=0解:(x﹣3)2﹣4(x﹣3)=0,(x﹣7)(x﹣3)=0,x﹣3=0或x﹣7=0,∴原方程的解是x1=3,x2=7.83. 4(x+1)2=9(x﹣2)2解:(2x+2)2=(3x﹣6)2,(2x+2+3x﹣6)(2x+2﹣3x+6)=0,即:(5x﹣4)(8﹣x)=0,x=8或x=,∴原方程的解是84. x2=2x移项,得x2﹣2x=0,因式分解,得x(x﹣2)=0,所以x=0或x=2.85. (x+4)2=5(x+4)移项,得,(x+4)2﹣5(x+4)=0,因式分解得,(x+4)[(x+4)﹣5]=0,x+4=0或x﹣1=0,解得,x1=﹣4,x2=187. 16(x﹣1)2=22516(x﹣1)2﹣152=0,所以[4(x﹣1)+15][4(x﹣1)﹣15]=0,即4x+11=0,4x﹣19=0,得x1=﹣,x2=.88. 4x2﹣4x+1=x2﹣6x+9方程变为(2x﹣1)2﹣(x﹣3)2=0,所以[(2x﹣1)+(x﹣3)][(2x﹣1)﹣(x﹣3)]=0,即3x﹣4=0,x+2=0,得x1=,x2=﹣2.89. 9(x+1)2=4(x﹣1)2(4)x2﹣4x+4=(3﹣2x)2原方程变为[3(x+1)]2﹣[2(x﹣1)]2=0,所以[3(x+1)+2(x﹣1)][3(x+1)﹣2(x﹣1)]=0,即(5x+1)(x+5)=0,得x1=﹣,x2=﹣5.90. (x﹣2)2=(3﹣2x)2.(x﹣2)2﹣(3﹣2x)2=0,(x﹣2+3﹣2x)(x﹣2﹣3+2x)=0,(1﹣x)(3x﹣5)=0,所以x1=1,x2=91. (x+2)2﹣10(x+2)+25=0因式分解得,[(x+2)﹣5]2=0,解得,x1=x2=392.x2﹣2(p﹣q)x﹣4pq=0.∵x2﹣2(p﹣q)x﹣4pq=0∴(x﹣2p)(x+2q)=0,∴x1=2p,x2=﹣2q.93.x2+10x+21=0,把左边分解因式得:(x+3)(x+7)=0,则:x+3=0,x+7=0,解得:x1=﹣3,x2=﹣7.94.2(x﹣2)2=3(x﹣2)∵2(x﹣2)2=3(x﹣2),∴(x﹣2)(2x﹣4﹣3)=0,即x﹣2=0或2x﹣7=0,解得:x1=2,x2=;95. 3(x﹣5)2=2(5﹣x),变形得:3(5﹣x)2=2(5﹣x),移项得:3(5﹣x)2﹣2(5﹣x)=0,分解因式得:(5﹣x)(13﹣3x)=0,则:5﹣x=0,13﹣3x=0,解得:x1=5,x2=;96. ,分解因式得:(x ﹣)(x ﹣)=0,则x ﹣=0,x ﹣=0,解得:x1=,x2=.97. 5x2﹣4x﹣12=0,(5x+6)(x﹣2)=0,5x+6=0,x﹣2=0,x1=﹣,x2=2.98. (x ﹣)=5x (﹣x),(x ﹣)+5x(x ﹣)=0,(x ﹣)(1+5x)=0,x ﹣=0,1+5x=0,x1=,x2=﹣.99.9(x﹣2)2﹣4(x+1)2=0.9(x﹣2)2﹣4(x+1)2=0(3x﹣6+2x+2)(3x﹣6﹣2x﹣2)=0,整理得:(5x﹣4)(x﹣8)=0,解方程得:x1=,x2=8100..x(x﹣2)=2(x+6),x2﹣2x=2x+12,x2﹣4x﹣12=0,(x﹣6)(x+2)=0,x1=6,x2=﹣2.∴原方程的根为x1=6,x2=﹣2101.(2)x2﹣8x+15=0;把左边分解因式得:(x﹣3)(x﹣5)=0,则x﹣3=0,x﹣5=0,解得:x1=5,x2=3;102. ;移项得:y2﹣2y+2=0,(y ﹣)2=0,两边开方得:y ﹣=0,则y1=y2=;103. 6x2﹣x﹣12=0.由原方程,得(2x﹣3)(3x+4)=0,解得,x=,或x=﹣104. 2x2﹣x﹣6=0原方程化为(2x+3)(x﹣2)=0,解得x1=﹣,x2=2;105. ﹣x2+6x﹣5=0原方程化为x2﹣6x+5=0分解因式,得(x﹣1)(x﹣5)=0,解得x1=1,x2=5;106. (x﹣5)2=(2x﹣1)(5﹣x)移项,得(x﹣5)2+(2x﹣1)(x﹣5)=0,提公因式,得(x﹣5)(x﹣5+2x﹣1)=0,解得x1=5,x2=2107. (x+1)(x+2)=3x+6.∵(x+1)(x+2)=3x+6,∴(x+1)(x+2)=3(x+2),∴(x+1)(x+2)﹣3(x+2)=0,∴(x+2)(x+1﹣3)=0,∴x+2=0或x+1﹣3=0∴x1=﹣2,x2=2108. x2﹣9=0,x2=9,解得:x1=3,x2=﹣3,109. x2+3x﹣4=0,(x﹣1)(x+4)=0,解得:x1=1,x2=﹣4,110. x2﹣3x+2=0,(x﹣1)(x﹣2)=0,解得:x1=1,x2=2111. 4(3x﹣1)2 =25(2x+1)2.∵4(3x﹣1)2﹣25(2x+1)2=0,∴[2(3x﹣1)﹣5(2x+1)][2(3x﹣1)+5(2x+1)]=0,∴2(3x﹣1)﹣5(2x+1)=0或2(3x﹣1)+5(2x+1)=0,∴x1=﹣,x2=﹣.112. (3x+5)2﹣4(3x+5)+3=0 设3x+5=y,则原方程变为y2﹣4y+3=0,∴(y﹣1)(y﹣3)=0,解得,y=1或y=3;①当y=1时,3x+5=1,解得x=﹣;②当y=3时,3x+5=3,解得,x=﹣;∴原方程的解是x=﹣,或x=﹣;113. (3x+2)(x+3)=x+14 由原方程,得(x+4)(3x﹣2)=0,解得x=﹣4,或x=;114. 3(x+1)2=(x+1)移项得,3(x+1)2﹣(x+1)=0,提公因式得,(x+1)(3x+3﹣1)=0,即x+1=0或3x+3﹣1=0,解得x1=﹣1,x2=﹣115.(x﹣2)2﹣4=0∵(x﹣2﹣2)(x﹣2+2)=0,∴x﹣2﹣2=0或x﹣2+2=0,∴x1=4,x2=0;116.(x﹣3)2+2x(x﹣3)=0∵(x﹣3)(x﹣3+2x)=0,∴x﹣3=0或x﹣3+2x=0,∴x1=3,x2=1;117.(3x﹣1)2=(x+1)2∵3x﹣1=±(x+1),即3x﹣1=x+1或3x﹣1=﹣(x+1),∴x1=1,x2=0;118.(x+5)2﹣2(x+5)﹣8=0.∵[(x+5)﹣4][(x+5)+2]=0,∴(x+5)﹣4=0或(x+5)+2=0,∴x1=﹣1,x2=﹣7.119. x2﹣8x=9变形为:x2﹣8x﹣9=0,(x﹣9)(x+1)=0,则:x﹣9=0或x+1=0,解得:x1=9,x2=﹣1;120. (x﹣2)2=(2x+3)2.变形为:(x﹣2)2﹣(2x+3)2=0,(x﹣2+2x+3)(x﹣2﹣2x﹣3)=0,(3x+1)(﹣x﹣5)=0,则:3x+1=0,﹣x﹣5=0,解得:x1=﹣,x2=﹣5.121. x2﹣3=3(x+1);整理得x2﹣3x﹣4=0,∴(x+1)(x﹣4)=0,∴x+1=0或x﹣4=0,∴x1=﹣1,x2=4;122. (y﹣3)2+3(y﹣3)+2=0 ∵(y﹣3+2)(y﹣3+1)=0,∴y﹣3+2=0或y﹣3+1=0,∴y1=1,y2=2;123. 7x(5x+2)=6(5x+2)∵7x(5x+2)﹣6(5x+2)=0,∴(5x+2)(7x﹣6)=0,∴5x+2=0或7x﹣6=0,∴x1=﹣,x2=124.(3)6(x+4)2﹣(x+4)﹣2=06(x+4)2﹣(x+4)﹣2=0,[3(x+4)﹣2][2(x+4)+1]=0,(3x+4)(2x+7)=0,3x+4=0,2x+7=0,解得:x1=﹣,x2=﹣;125. x2﹣(3m﹣1)x+2m2﹣m=0,(x﹣m)[x﹣(2m﹣1)]=0,x﹣m=0,x﹣(2m﹣1)=0,解得:x1=m,x2=2m﹣1126.x2﹣2x﹣224=0.x2﹣2x﹣224=0(x﹣16)(x+14)=0,解得:x1=16;x2=﹣14.127..方程两边同时乘以2,得(x+3)2=4(x+2)2,移项,得(x+3)2﹣4(x+2)2,=0,(x+3+4x+8)(x+3﹣4x﹣8)=0,即5x+11=0或﹣3x﹣5=0,解得x1=﹣,x2=﹣;128.5x(x﹣3)﹣(x﹣3)(x+1)=0.∵(x﹣3)(5x﹣x﹣1)=0,∴x﹣3=0或5x﹣x﹣1=0,∴x1=3,x2=129.x2﹣11x+28=0x2﹣11x+28=0,(x﹣4)(x﹣7)=0,x﹣4=0,x﹣7=0,x1=4,x2=7130. 4y2﹣25=0;(2y+5)(2y﹣5)=0,所以y1=﹣,y2=;131.(2x+3)2﹣36=0;(2x+3)2﹣36=0;(2x+3+6)(2x+3﹣6)=0,所以x1=﹣,x2=;132. x2﹣3x+2=0;(x﹣1)(x﹣2)=0,所以x1=1,x2=2;133. 2t2﹣7t﹣4=0;(t﹣4)(2t+1)=0,所以t1=4,t2=﹣;134. 5y(y﹣1)=2(y﹣1)方程变形得:5y(y﹣1)﹣2(y﹣1)=0,因式分解得:(y﹣1)(5y﹣2)=0,可得y﹣1=0或5x﹣2=0,解得:y1=1,y2=.135. x2+(1+2)x+3+=0;(x+)(x+1+)=0x+=0或x+1+=0∴x1=﹣,x2=﹣1﹣.136.(x﹣3)2+(x+4)2﹣(x﹣5)2=17x+24.原方程整理得:x2﹣5x﹣24=0(x﹣8)(x+3)=0∴x1=8,x2=﹣3.137.x2﹣3|x|﹣4=0|x|2﹣3|x|﹣4=0 (|x|﹣4)(|x|+1)=0 |x|﹣4=0|x|+1≠0∴|x|=4∴x1=4,x2=﹣4.。
17.2因式分解法解一元二次方程(第2课时)(4种题型基础练+提升练)(原卷版)

17.2因式分解法解一元二次方程(第2课时)(4种题型基础练+提升练)考查题型一 提公因式法解一元二次方程1.方程:2331()()()0442x x x -+--=的较小的根是()A .34B .34-C .12D .582.(2021·上海市培佳双语学校八年级期中)方程x 2=2x 的解是_______.3.方程x (x ﹣3)=3﹣x 的根是 ___.4.(2022·上海松江·八年级期末)一元二次方程()()()1121x x x +-=+的根是__________.5.解关于x 的方程(因式分解方法):(1)230x -=; (2)7(3)39x x x -=-.考查题型二 平方差公式法解一元二次方程6.(2021·上海虹口·八年级期末)方程x 2﹣9=0的解是_____.7.用因式分解法解下列方程:(2x+3)2-25=0.8.解关于x 的一元二次方程:22(2016)(2015)1x x -+-=.考查题型三 完全平分公式法解一元二次方程9.(2021·上海市第四中学八年级阶段练习)方程x 2+4x +4=0的根是_____.10.解下列一元二次方程:(2x+1)2+4(2x+1)+4=0;考查题型四 十字相乘法解一元二次方程11.解下列关于x 的方程:(1)2(1(30x x +-+=; (2)2(35)5(35)40x x +-++=;12.解关于x 的方程(1)236350x x +-=; (2)2(41)10(14)240x x -+--=.一、单选题13.(2021·上海市罗星中学八年级期中)如果关于x 的一元二次方程ax 2+bx +c =0(a ≠0)有两个实数根,且其中一个根是另一根的一半,则称这样的方程为“半根方程”.以下关于半根方程的说法,正确的是( )A .若方程(x ﹣2)(mx +n )=0是半根方程,则4m 2+5mn +n 2=0B .方程x 2﹣x ﹣2=0是半根方程C .方程x 2﹣4=0是半根方程D .若点A (m ,n )在函数y =2x 的图象上,则关于x 的方程mx 2﹣n =0是半根方程二、填空题14.若方程(x 2+y 2)2﹣(x 2+y 2)﹣2=0,则x 2+y 2=___.15.(2022·上海·八年级期末)方程(3)3(3)x x x -=-的解是___________.16.(2022·上海·八年级期末)现定义运算“☆”,对于任意实数a 、b ,都有a ☆25b a a b =-+,如3☆6=23536-´+,若x ☆12=6,则实数x 的值是____________17.(2021·上海·八年级期中)已知:(x 2+y 2)(x 2+y 2-4)-12=0,则x 2+y 2的值为_____________.18.(2021·上海市南洋模范中学八年级阶段练习)已知三角形两边长分别是2和9,第三边的长为一元二次方程214480x x -+=的一个根,则这个三角形的周长为19.(2021·上海·八年级期中)对于实数,a b ,定义运算“*”:)()0a b a b a b £<*=³.例如92*,因为92³,所以92*==.若12,x x 是一元二次方程212270x x -+=的两个根,则12x x *=_________.20.(2021·上海·八年级期中)方程23280x x --=的根为_______.21.(2021·上海·八年级期中)已知等腰三角形的边长是方程213360x x -+=的两个根,则这个等腰三角形的周长是______.22.(2021·上海市徐汇中学八年级期中)已知x =1是一元二次方程(m -2)x 2+4x -m 2=0的一个根,则m 的值是_____.23.(2021·上海市莘光学校八年级期中)一个三角形的两边长分别为3和5,其第三边是方程2x ﹣13x +40=0的根,则此三角形的周长为 ___.三、解答题24.(2021·上海市洋泾菊园实验学校八年级期末)解方程:(x 2﹣9)+x (x ﹣3)=0.25.(2021·上海市莘光学校八年级期中)解方程:(y ﹣2)(1+3y )=6.26.(2021·上海市泗塘中学八年级阶段练习)解方程:(x +8)(x +1)=﹣1227.(2020·上海市西南位育中学八年级期中)用适当的方法解方程:2x(x﹣2)=x2+5 28.(2021·上海民办行知二中实验学校八年级期中)解方程(2x+1)2=x(2x+1).29.(2021·上海市培佳双语学校八年级期中)解方程:4x(x﹣6)+3(6﹣x)=0.30.(2021·上海长宁·八年级期末)解方程:3(x﹣2)2=x(2﹣x).31.(2020·上海市浦东模范中学八年级期末)解方程:x2﹣4x﹣9996=0.32.(2021·上海·八年级期中)解方程:2(1)5(1)140x x -+--=33.(2021·上海市罗南中学八年级阶段练习)解关于x 的一元二次方程()282--=x x mx ,其中m 是满足不等式组430530m m +>ìí->î的整数.。
一元二次方程的解法综合练习题及答案

一元二次方程的解法专题训练1、因式分解法 ①移项:使方程右边为0②因式分解:将方程左边因式分解;方法:一提,二套,三十字,四分组③由A ∙B=0,那么A=0或B=0,解两个一元一次方程2、开平方法 )0(2≥=a a x3、配方法 ①移项:左边只留二次项与一次项,右边为常数项 〔移项要变号.....〕 ②同除:方程两边同除二次项系〔每项都要除.....〕 ③配方:方程两边加上一次项系数一半的平方.......④开平方:注意别忘根号与正负⑤解方程:解两个一元一次方程4、公式法① 将方程化为一般式② 写出a 、b 、c③ 求出ac b 42-,④ 假设b 2-4ac <0,那么原方程无实数解⑤ 假设b 2-4ac >0,那么原方程有两个不相等的实数根,代入公式x= ⑥ 假设b 2-4ac =0,那么原方程有两个相等的实数根,代a x a x -==21入公式2b x a=-求解。
例1、利用因式分解法解以下方程(x -2) 2=(2x-3)2 042=-x x 3(1)33x x x +=+ x 2()()0165852=+---x x例2、利用开平方法解以下方程51)12(212=-y 4〔x-3〕2=25 24)23(2=+x例3、利用配方法解以下方程7x=4x 2+2 01072=+-x x 例4、利用公式法解以下方程-3x 2+22x -24=0 2x 〔x -3〕=x -3. 3x 2+5(2x+1)=0课后练习1、方程2x 2-3x+1=0化为(x+a)2=b 的形式,正确的选项是 ( )A 、 23162x ⎛⎫-= ⎪⎝⎭B 、2312416x ⎛⎫-= ⎪⎝⎭C 、 231416x ⎛⎫-= ⎪⎝⎭ D 、以上都不对2、用__________________法解方程(x-2)2=4比拟简便。
3、一元二次方程x 2-ax+6=0, 配方后为(x-3)2=3, 那么a=______________.4、解方程〔x+a 〕2=b 得〔 〕A 、x=-a B 、x=±039922=--x xC 、当b ≥0时,x=-aD 、当a ≥0时,x=a5、关于x 的方程〔a 2-1〕x 2+〔1-a 〕x+a-2=0,以下结论正确的选项是〔 〕A 、当a ≠±1时,原方程是一元二次方程。
因式分解法解一元二次方程典型例题

例 用因式分解法解下列方程: (1)y 2+7y +6=0; (2)t (2t -1)=3(2t -1); (3)(2x -1)(x -1)=1. 解:(1)方程可变形为(y +1)(y +6)=0 y +1=0或y +6=0 ∴y 1=-1,y 2=-6(2)方程可变形为t (2t -1)-3(2t -1)=0 (2t -1)(t -3)=0,2t -1=0或t -3=0 ∴t 1=21,t 2=3.(3)方程可变形为2x 2-3x =0 x (2x -3)=0,x =0或2x -3=0 ∴x 1=0,x 2=23说明:(1)在用因式分解法解一元二次方程时,一般地要把方程整理为一般式,如果左边的代数式能够分解为两个一次因式的乘积,而右边为零时,则可令每一个一次因式为零,得到两个一元一次方程,解出这两个一元一次方程的解就是原方程的两个解了.(2)应用因式分解法解形如(x -a )(x -b )=c 的方程,其左边是两个一次因式之积,但右边不是零,所以应转化为形如(x -e )(x -f )=0的形式,这时才有x 1=e ,x 2=f ,否则会产生错误,如(3)可能产生如下的错解:原方程变形为:2x -1=1或x -1=1.∴x 1=1,x 2=2.(3)在方程(2)中,为什么方程两边不能同除以(2t -1),请同学们思考典型例题二例 用因式分解法解下列方程6223362+=+x x x解:把方程左边因式分解为:0)23)(32(=-+x x∴032=+x 或023=-x ∴ 32,2321=-=x x 说明: 对于无理数系数的一元二次方程,若左边可分解为一次因式积的形式,均可用因式分解法求出方程的解。
例 用因式分解法解下列方程。
1522+=y y解: 移项得:01522=--y y 把方程左边因式分解 得:0)3)(52(=-+y y ∴052=+y 或03=-y∴.3,2521=-=y y说明: 在用因式分解法解一元二次方程时,一定要注意,把方程整理为一般式,如果左边的代数式能够分解为两个一次因式的乘积,而右边为零时,则可令每一个一次因式都为零,得到两个一元一次方程,解出这两个一元一次方程的解就是原方程的两个解了。
2021一元二次方程练习题(含答案)
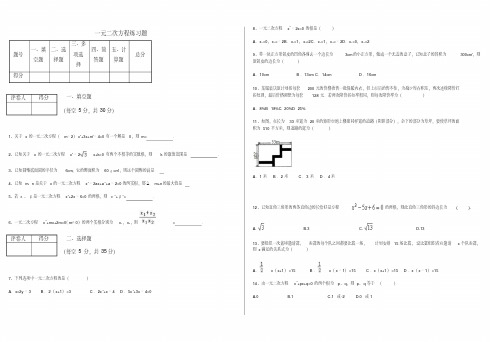
一元二次方程练习题题号一、填空题二、选择题三、多项选择四、简答题五、计算题总分得分一、填空题(每空5分,共30分)1、关于x的一元二次方程(m﹣2)x2+3x+m2﹣4=0有一个解是0,则m= .2、已知关于x的一元二次方程x2﹣2x+k=0有两个不相等的实数根,则k的取值范围是.3、已知圆锥底面圆的半径为6cm,它的侧面积为60πcm2,则这个圆锥的高是4、已知m、n是关于x的一元二次方程x2﹣2ax+a2+a﹣2=0的两实根,那么m+n的最大值是5、若α、β是一元二次方程x2+2x﹣6=0的两根,则α2+β2= .6、一元二次方程x2+mx+2m=0(m≠0)的两个实根分别为x1,x2,则= .二、选择题(每空5 分,共35分)7、下列选项中一元二次方程的是()A.x=2y﹣3 B.2(x+1)=3 C.2x2+x﹣4 D.5x2+3x﹣4=0 8、一元二次方程x2﹣2x=0的根是()A.x1=0,x2=﹣2B.x1=1,x2=2C.x1=1,x2=﹣2D.x1=0,x2=29、将一块正方形铁皮的四角各剪去一个边长为3cm的小正方形,做成一个无盖的盒子,已知盒子的容积为300cm3,则原铁皮的边长为()A.10cm B.13cm C.14cm D.16cm10、某服装店原计划按每套200元的价格销售一批保暖内衣,但上市后销售不佳,为减少库存积压,两次连续降价打折处理,最后价格调整为每套128元.若两次降价折扣率相同,则每次降价率为()A.8%B.18%C.20%D.25%11、如图,在长为33米宽为20米的矩形空地上修建同样宽的道路(阴影部分),余下的部分为草坪,要使草坪的面积为510平方米,则道路的宽为()A.1米 B.2米 C.3米 D.4米12、已知直角三角形的两条直角边的长恰好是方程的两根,则此直角三角形的斜边长为( ).A. B.3 C. D.1313、要组织一次篮球邀请赛,参赛的每个队之间都要比赛一场,计划安排15场比赛,设比赛组织者应邀请x个队参赛,则x满足的关系式为()A.x(x+1)=15 B.x(x﹣1)=15 C.x(x+1)=15 D.x(x﹣1)=1514、由一元二次方程x2+px+q=0的两个根为p、q,则p、q等于()A.0B.1C.1或-2D.0或1评卷人得分评卷人得分三、多项选择(每空5 分,共5分)15、方程的两根分别为,,且,则的取值范围是.四、简答题(每题10 分,共110 分)16、试求实数(≠1),使得方程的两根都是正整数.17、已知关于的一元二次方程有两个实数根和.(1)求实数的取值范围;(2)当时,求的值.18、如图,在矩形ABCD中,AB=4cm,BC=cm,点P从点A出发以1cm/s的速度移动到点B;点P出发几秒后,点P、A的距离是点P、C距离的倍?19、某汽车销售公司6月份销售某厂家的汽车,在一定范围内,每部汽车的进价与销售量有如下关系:若当月仅售出1部汽车,则该部汽车的进价为27万元,每多售出1部,所有售出的汽车的进价均降低0.1万元/部,月底厂家根据销售量一次性返利给销售公司,销售量在10部以内(含10部),每部返利0.5万元;销售量在10部以上,每部返利1万元.(1)若该公司当月售出3部汽车,则每部汽车的进价为万元;(2)如果汽车的售价为28万元/部,该公司计划当月盈利12万元,那么需要售出多少部汽车?(盈利=销售利润+返利)20、某花圃用花盆培育某种花苗,经试验发现每盆花的盈利与每盆花中花苗的株数有如下关系:每盆植入花苗4株时,平均单株盈利5元;以同样的栽培条件,若每盆每增加1株花苗,平均单株盈利就会减少0.5元.要使每盆花的盈利为24元,且尽可能地减少成本,则每盆花应种植花苗多少株?21、一个足球被从地面向上踢出,它距地面高度可以用二次函数刻画,其中表示足球被踢出后经过的时间.(1)解方程,并说明其根的实际意义;(2)求经过多长时间,足球到达它的最高点?最高点的高度是多少?22、随着人民生活水平的不断提高,我市家庭轿车的拥有量逐年增加.据统计,某小区2014年底拥有家庭轿车64辆,2016年底家庭轿车的拥有量达到100辆.(1)若该小区2014年底到2016年底家庭轿车拥有量的年平均增长率都相同,求该小区到2017年底家庭轿车将达到多少辆?(2)为了缓解停车矛盾,该小区决定投资15万元再建造若干个停车位.据测算,建造费用分别为室内车位5000元/个,露天车位1000元/个,考虑到实际因素,计划露天车位的数量不少于室内车位的2倍,求该小区最多可建室内车位多少个?23、某商店销售一种销售成本为40元/千克的水产品,若按50元/千克销售,一个月可售出500千克,销售价每涨价1元,月销售量就减少10千克.评卷人得分评卷人得分(1) 写出月销售利润y(单位:元) 与售价x(单位:元/千克)之间的函数解析式.(2)当售价定为多少时会获得最大利润?求出最大利润.(3) 商店想在月销售成本不超过10000元的情况下,使月销售利润达到8000元,销售单价应定为多少?24、.要制作一个如图所示(图中阴影部分为底与盖,且SⅠ=SⅡ)的钢盒子,在钢片的四个角上分别截去两个相同的正方形与两个相同的小长方形,然后折合起来既可,求有盖盒子的高x.25、如图,中间用相同的白色正方形瓷砖,四周用相同的黑色长方形瓷砖铺设矩形地面,请观察图形并解答下列问题.(1)问:在第6个图中,黑色瓷砖有__________块,白色瓷砖有__________块;(2)某商铺要装修,准备使用边长为1米的正方形白色瓷砖和长为1米、宽为0.5米的长方形黑色瓷砖来铺地面.且该商铺按照此图案方式进行装修,瓷砖无须切割,恰好能完成铺设.已知白色瓷砖每块100元,黑色瓷砖每块50元,贴瓷砖的费用每平方米15元.经测算总费用为15180元.请问两种瓷砖各需要买多少块?26、已知:平行四边形ABCD的两边AB、BC的长是关于的方程的两个实数根.(1)试说明:无论取何值方程总有两个实数根(2)当为何值时,四边形ABCD是菱形?求出这时菱形的边长;(3)若AB的长为2,那么平行四边形ABCD的周长是多少?五、计算题(每题5分,共35 分)27、用恰当的方法解下列方程:28、解方程:29、x2﹣7x﹣18=0.30、2x2+12x﹣6=031、解方程:.评卷人得分参考答案一、填空题1、﹣2 .【考点】一元二次方程的解.【分析】一元二次方程的解就是能够使方程左右两边相等的未知数的值.即用这个数代替未知数所得式子仍然成立.将x=0代入方程式即得.【解答】解:把x=0代入一元二次方程(m﹣2)x2+3x+m2﹣4=0,得m2﹣4=0,即m=±2.又m﹣2≠0,m≠2,取m=﹣2.故答案为:m=﹣2.【点评】此题要注意一元二次方程的二次项系数不得为零.2、k<3 .【考点】根的判别式.【分析】根据一元二次方程的根的判别式,建立关于k的不等式,求出k的取值范围.【解答】解:∴a=1,b=﹣2,c=k,方程有两个不相等的实数根,∴△=b2﹣4ac=12﹣4k>0,∴k<3.故填:k<3.3、8 cm.【考点】圆锥的计算.【专题】计算题.【分析】设圆锥的母线长为l,由于圆锥的侧面展开图为扇形,扇形的弧长等于圆锥底面圆的周长,扇形的半径等于圆锥的母线长,则l?2π?6=60π,然后利用勾股定理计算圆锥的高.【解答】解:设圆锥的母线长为l,根据题意得l?2π?6=60π,解得l=10,所以圆锥的高==8(cm).故答案为8.【点评】本题考查了圆锥的计算:圆锥的侧面展开图为扇形,扇形的弧长等于圆锥底面圆的周长,扇形的半径等于圆锥的母线长.也考查了勾股定理.4、4 .【考点】根与系数的关系;根的判别式.【专题】计算题.【分析】先根据判别式的意义确定a≤2,再根据根与系数的关系得到m+n=2a,然后利用a的取值范围确定m+n的最大值.【解答】解:根据题意得△=4a2﹣4(a2+a﹣2)≥0,解得a≤2,因为m+n=2a,所以m+n≤4,所以m+n的最大值为4.故答案为4.【点评】本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=﹣,x1x2=.也考查了一元二次方程根的判别式.5、16 .【考点】根与系数的关系.【分析】利用根与系数的关系可得出α+β和αβ,且α2+β2=(α+β)2﹣2αβ,代入计算即可.【解答】解:∵α、β是一元二次方程x2+2x﹣6=0的两根,∴α+β=﹣2,αβ=﹣6,∴α2+β2=(α+β)2﹣2αβ=(﹣2)2﹣2×(﹣6)=4+12=16,故答案为:16.【点评】本题主要考查一元二次方程根与系数的关系,把α2+β2化成(α+β)2﹣2αβ是解题的关键.6、﹣.【考点】根与系数的关系.【分析】由根与系数的关系可得x1+x2=﹣m,x1?x2=2m,继而求得答案.【解答】解:∵一元二次方程x2+mx+2m=0(m≠0)的两个实根分别为x1,x2,∴x1+x2=﹣m,x1?x2=2m,∴==﹣.二、选择题7、D【考点】一元二次方程的定义.【分析】本题根据一元二次方程的定义解答.一元二次方程必须满足四个条件:(1)未知数的最高次数是2;(2)二次项系数不为0;(3)是整式方程;(4)含有一个未知数.由这四个条件对四个选项进行验证,满足这四个条件者为正确答案.【解答】解:A、是二元一次方程,故此选项错误;B、是一元一次方程,故此选项错误;C、不是方程,故此选项错误;D、符合一元二次方程的定义,故此选项正确;故选:D.【点评】本题考查了一元二次方程的概念,判断一个方程是否是一元二次方程,首先要看是否是整式方程,然后看化简后是否是只含有一个未知数且未知数的最高次数是2.8、D【考点】解一元二次方程-因式分解法.【分析】先分解因式,即可得出两个一元一次方程,求出方程的解即可.【解答】解:x2﹣2x=0,x(x﹣2)=0,x=0,x﹣2=0,x1=0,x2=2,故选D.9、D【考点】一元二次方程的应用.【分析】设正方形铁皮的边长应是x厘米,则做成没有盖的长方体盒子的长、宽为(x﹣3×2)厘米,高为3厘米,根据长方体的体积计算公式列方程解答即可.【解答】解:正方形铁皮的边长应是x厘米,则没有盖的长方体盒子的长、宽为(x﹣3×2)厘米,高为3厘米,根据题意列方程得,(x﹣3×2)(x﹣3×2)×3=300,解得x1=16,x2=﹣4(不合题意,舍去);答:正方形铁皮的边长应是16厘米.故选:D.10、C【分析】设每次降价的百分率为x,则第一次降价后的售价为200(1﹣x)元,第二次降价后的售价为200(1﹣x)(1﹣x)元,根据第二降价后的售价为128元建立方程求出其解即可.【解答】解:设每次降价的百分率为x,由题意,得200(1﹣x)2=128,解得:x1=0.2,x2=1.8(不符合题意,舍去).答:每次降价的百分率为20%.故选C.【点评】本题考查了列一元二次方程解降低率的问题的运用,一元二次方程的解法的运用,解答时根据降低率的数量关系建立方程是关键,检验根是否符合题意是容易忘记的过程.11、C【考点】一元二次方程的应用.【专题】几何图形问题.【分析】设道路的宽为x,利用“道路的面积”作为相等关系可列方程20x+33x﹣x2=20×33﹣510,解方程即可求解.解题过程中要根据实际意义进行x的值的取舍.【解答】解:设道路的宽为x,根据题意得20x+33x﹣x2=20×33﹣510整理得x2﹣53x+150=0解得x=50(舍去)或x=3所以道路宽为3米.故选C.【点评】本题考查的是一元二次方程的实际运用.找到关键描述语,找到等量关系准确的列出方程是解决问题的关键.12、C13、B【考点】由实际问题抽象出一元二次方程.【分析】关系式为:球队总数×每支球队需赛的场数÷2=15,把相关数值代入即可.【解答】解:每支球队都需要与其他球队赛(x﹣1)场,但2队之间只有1场比赛,所以可列方程为:x(x﹣1)=15.故选B.【点评】本题考查了由实际问题抽象出一元二次方程,解决本题的关键是得到比赛总场数的等量关系,注意2队之间的比赛只有1场,最后的总场数应除以2.14、C三、多项选择15、.四、简答题16、解:因式分解得:,………….5分所以或. ………….7分因为,所以,,………….9分因为两根都是正整数,所以,. ………….12分17、解:(1)一元二次方程x2+(2m-1)x+m2=0有两个实数根,∴△=(2m-1)2-4×1×m2=-4m+1≥0,∴m≤;(2)当x12-x22=0时,即(x1+x2)(x1-x2)=0,∴x1-x2=0或x1-x2=0当x1+x2=0,依据一元二次方程根与系数的关系可得x1+x2=-(2m-1)∴-(2m-1)=0,∴m=又∵由(1)一元二次方程x2+(2m-1)x+m2=0有两个实数根时的取值范围是m≤,∴m=不成立,故m无解;当时x1-x2=0,x1=x2,方程有两个相等的实数根,∴△=(2m-1)2-4×1×m2=-4m+1=0,∴m=综上所述,当x1-x2=0时,m=。
21.2.3降次--解一元二次方程(因式分解法)

A.直接开平方法 B.配方法 C.公式法 D.因式分解法 5.方程x( x 1) x的解是_______. 6.方程x 2 10 x 25 0的解是_______. 7.课本P17第6大题(1).(2).(3).(4)
解:( x 4) (5 2x) 0
2 2
( x 1)(3x 9) 0
(4) x 6 x 9 0
2
(5)4x 4x 1 0
2
解:(x 3) =0
2
解:(2x 1) =0
2
x-3=0
2x-1=0
1 x1 x2 2
x1 x2 3.
课后作业: 1.方程(x 3)( x 4) 0的根是(
)
A.x 3 B.x1 3, x2 4 C.x 4 D.x 1 3, x2 4 2.方程x( x 2) 0的根是(
2
) )
A.x 2 B.x 0 C.x 1 0, x2 2 D.x 1 0, x2 4 3.解方程(x 2) 2( x 2)最适当的方法是( 4.方程x x 0的解是_______.
x 2 0, 或1 x 0. x1 2; x2 1.
解: ( x 1)( x 7) 0 x 1 0或x 7 0
4 x1 0; x2 . 5 (3)利用十字相乘法: x2+(a+b)x+ab=(x+a)(x+b).
1 1
1 7
x1 1, x2 7
(2x 1)2x 1 0.
4 x 1 0,
2
2x 1 0, 或2x 1 0. x1 2, x2 1. 1 1 x1 ; x2 . 2 2 分解因式法解一元二次方程的步骤是:
因式分解法解一元二次方程专题训练

y 一 2 = 0 ,则 与 Y之 积 等 于
一 m 一 .
●
1 5 . 关 于 的一 元 二 次 方 程 ( m+ 2 ) 5 m一 6 = 0有一 根为 0 , 则 m:
2 1 . 已知 等腰 三 角形 两边 长分 别是 x  ̄8 x + 1 5 =
0 的两根, 求此等腰三角形的周长 。
, - … _ — … … _ - … ^ … … 。 … , . . … ^ — … 。 - - 。 … — … …
、
;
+
…
…
. 。 一
‘ …
‘ - - , ,
( 口 一 b ) ( a - c ) = 0 , 贝 U AA BC是 ( A. 直 角三角 形 B . 钝 角三 角形
‘
) .
( 2 ) ( 2 x 一 1 ) 2 + ( 1 一 ) 一 6 = 0 ;
C . 等边三 角形 D . 等腰 三 角形或 等边 三角形
所有 实数 根之 积为 (
A. 一 2 B . 一 6
( 3 ) 9 ( x 一 2 ) 2 = 4 ( x + 1 ) ;
。
( 4 ) 2 ( 5 x — I ) 2 = 3 ( 1 - 5 x ) .
’ D. 一 3
7 . 一 元 二次 方程 x 2 - 3 x 一 2 = 0与 2 X 2 - 3 x + 3 = O的 ) .
”
,
l
1 6 . 方程 ( 一 : 1 ) ( 一 2 ) - - - o的 两 根 为 l , 2 , 且 x l >
x 2则 x l - 2 x 2 的值 是 .
.
r
— —一 . 1 8 . 已知一 个矩形 的长 比宽 多 2 c m, 其 面积 为
因式分解法解一元二次方程(含答案)

因式分解法解一元二次方程一.解答题(共11小题)1.用适当的方法解下列一元二次方程:(1)x2﹣2x﹣15=0;(2)(x+4)2﹣5(x+4)=0.2.解方程:(1)(x﹣3)2﹣16=0;(2)x2+2x﹣3=0.3.解下列方程:(1)x2﹣4x=0;(2)x(x﹣2)=x﹣2.4.解方程:(1)(x﹣1)2﹣4=0;(2)(x﹣2)2=3x﹣6.5.解一元二次方程:(1)(x﹣2)2=9;(2)x2+2x﹣3=0.6.解下列方程:(1)x2﹣3x=0(2)x2+4x﹣5=07.请用适当的方法解下列方程:(1)4x﹣2=2x2;(2)(x+1)2+2=3(x+1).8.用适当的方法解下列方程:(1)2x2+5x=7.(2)x2+8x+15=0.9.解方程:(1)x2﹣2x﹣15=0;(2)(x+4)2﹣5(x+4)=0.10.用适当的方法解方程:(1)x2=7x;(2)x2+4x﹣5=0.11.阅读下面例题的解题过程,体会、理解其方法,并借鉴该例题的解法解方程.例:解方程:x2﹣|x|﹣2=0解:当x≥0时,原方程化为x2﹣x﹣2=0.解得:x1=2,x2=﹣1∵x≥0,故x=﹣1舍去,∴x=2是原方程的解;当x<0时,原方程化为x2+x﹣2=0.解得:x1=﹣2,x2=1∵x<0,故x=1舍去,∴x=﹣2是原方程的解;综上所述,原方程的解为x1=2,x2=﹣2.解方程x2+2|x+2|﹣4=0.参考答案与试题解析一.解答题(共11小题)1.用适当的方法解下列一元二次方程:(1)x2﹣2x﹣15=0;(2)(x+4)2﹣5(x+4)=0.【分析】(1)利用十字相乘法把方程的左边变形,进而解出方程;(2)利用提公因式法把方程的左边变形,进而解出方程.【解答】(1)∵x2﹣2x﹣15=0,∴(x﹣5)(x+3)=0,∴x﹣5=0或x+3=0,∴x1=5,x2=﹣3;(2)∵(x+4)2﹣5(x+4)=0,∴(x+4)(x+4﹣5)=0,∴x+4=0或x﹣1=0,∴x1=﹣4,x2=1.【点评】本题考查了解一元二次方程,掌握因式分解法解一元二次方程的一般步骤是解题的关键.2.解方程:(1)(x﹣3)2﹣16=0;(2)x2+2x﹣3=0.【分析】(1)先移项得到(x﹣3)2=16,然后利用直接开平方法解方程;(2)利用因式分解法解方程.【解答】解:(1)(x﹣3)2=16,x﹣3=±4,所以x1=7,x2=﹣1;(2)x2+2x﹣3=0,(x+3)(x﹣1)=0,x+3=0或x﹣1=0,所以x1=﹣3,x2=1.【点评】本题考查了解一元二次方程﹣因式分解法:因式分解法就是利用因式分解求出方程的解的方法,这种方法简便易用,是解一元二次方程最常用的方法.也考查了直接开平方法.3.解下列方程:(1)x2﹣4x=0;(2)x(x﹣2)=x﹣2.【分析】(1)将等号左边提公因式,用因式分解法即可求出方程的解;(2)移项将等号右边化为0,左边因式分解,再用因式分解法求出方程的解.【解答】解:(1)∵x2﹣4x=0,∴(x﹣4)=0,∴x=0或x﹣4=0,∴x1=0,x2=4;(2)∵x(x﹣2)=x﹣2,∴(x﹣2)(x﹣1)=0,∴x﹣2=0或x﹣1=0,∴x1=2,x2=1.【点评】本题考查用因式分解法解一元二次方程,解题的关键是掌握因式分解法解一元二次方程的一般步骤.4.解方程:(1)(x﹣1)2﹣4=0;(2)(x﹣2)2=3x﹣6.【分析】(1)将方程变形后用直接开平方法可求出方程的解;(2)将方程变形,右边化为0,左边分解因式,即可把原方程化为两个一元一次方程,从而求出原方程的解.【解答】解:(1)(x﹣1)2=4,∴x﹣1=2或x﹣1=﹣2,∴x1=3,x2=﹣1;(2)(x﹣2)2﹣3(x﹣2)=0,∴(x﹣2)(x﹣2﹣3)=0,∴x﹣2=0或x﹣5=0,∴x1=2,x2=5.【点评】本题考查解一元二次方程,解题的关键是掌握直接开平方法和因式分解法解一元二次方程.5.解一元二次方程:(1)(x﹣2)2=9;(2)x2+2x﹣3=0.【分析】(1)利用直接开平方法求解即可;(2)利用因式分解法求解即可.【解答】(1)解:(x﹣2)2=9,x﹣2=±3,x﹣2=3或x﹣2=﹣3,∴x1=5,x2=﹣1.(2)解:x2+2x﹣3=0,∴(x﹣1)(x+3)=0,则x﹣1=0或x+3=0,∴x1=1,x2=﹣3.【点评】本题主要考查解一元二次方程的能力,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法是解题的关键.6.解下列方程:(1)x2﹣3x=0(2)x2+4x﹣5=0【分析】(1)利用因式分解法把原方程化为x=0或x﹣3=0,然后解两个一次方程即可;(2)利用因式分解法把原方程化为x+5=0或x﹣1=0,然后解两个一次方程即可.【解答】解:(1)x(x﹣3)=0,x=0或x﹣3=0,所以x1=0,x2=3;(2)(x+5)(x﹣1)=0,x+5=0或x﹣1=0,所以x1=﹣5,x2=1..【点评】本题考查了解一元二次方程﹣因式分解法:因式分解法就是利用因式分解求出方程的解的方法,这种方法简便易用,是解一元二次方程最常用的方法.7.请用适当的方法解下列方程:(1)4x﹣2=2x2;(2)(x+1)2+2=3(x+1).【分析】(1)先化成一般式,再因式分解即可;(2)把x+1看成一个整体,利用因式分解法解即可.【解答】解:(1)原方程化为x2﹣2x+1=0;∴(x﹣1)2=0,∴x﹣1=0或x﹣1=0,∴x1=x2=1;(2)移项得(x+1)2﹣3(x+1)+2=0,因式分解得(x+1﹣1)(x+1﹣2)=0,∴x+1﹣1=0或x+1﹣2=0,∴x1=0,x2=1.【点评】本题考查了解一元二次方程﹣因式分解法:先把方程右边变形为0,然后把方程左边进行因式分解,这样把一元二次方程转化为两个一元一次方程,再解一次方程可得到一元二次方程的解.也考查了直接开平方法解一元二次方程.8.用适当的方法解下列方程:(1)2x2+5x=7.(2)x2+8x+15=0.【分析】(1)利用十字相乘法因式分解,解出x的值即可;(2)利用十字相乘法因式分解,解出x的值即可.【解答】解:(1)2x2+5x=7,因式分解得,(2x+7)(x﹣1)=0,所以x1=﹣,x2=1;(2)x2+8x+15=0,因式分解得(x+3)(x+5)=0,所以x1=﹣3,x2=﹣5.【点评】本题考查了解一元二次方程﹣因式分解法:因式分解法就是先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).9.解方程:(1)x2﹣2x﹣15=0;(2)(x+4)2﹣5(x+4)=0.【分析】(1)利用解一元二次方程﹣因式分解法,进行计算即可解答;(2)利用解一元二次方程﹣因式分解法,进行计算即可解答.【解答】解:(1)x2﹣2x﹣15=0,(x﹣5)(x+3)=0,x﹣5=0或x+3=0,x1=5,x2=﹣3;(2)(x+4)2﹣5(x+4)=0,(x+4)(x+4﹣5)=0,(x+4)(x﹣1)=0,x+4=0或x﹣1=0,x1=﹣4,x2=1.【点评】本题考查了解一元二次方程﹣因式分解法,熟练掌握解一元二次方程的方法是解题的关键.10.用适当的方法解方程:(1)x2=7x;(2)x2+4x﹣5=0.【分析】(1)先移项,再利用提公因式法将方程的左边因式分解,继而得出两个关于x 的一元一次方程,再进一步求解即可;(2)利用十字相乘法将方程的左边因式分解,继而得出两个关于x的一元一次方程,再进一步求解即可.【解答】解:(1)∵x2=7x,∴x2﹣7x=0,∴x(x﹣7)=0,则x=0或x﹣7=0,解得x1=0,x2=7;(2)∵x2+4x﹣5=0,∴(x+5)(x﹣1)=0,则x+5=0或x﹣1=0,解得x1=﹣5,x2=1.【点评】本题主要考查解一元二次方程,解一元二次方程常用的方法有:直接开平方法、因式分解法、公式法及配方法,解题的关键是根据方程的特点选择简便的方法.11.阅读下面例题的解题过程,体会、理解其方法,并借鉴该例题的解法解方程.例:解方程:x2﹣|x|﹣2=0解:当x≥0时,原方程化为x2﹣x﹣2=0.解得:x1=2,x2=﹣1∵x≥0,故x=﹣1舍去,∴x=2是原方程的解;当x<0时,原方程化为x2+x﹣2=0.解得:x1=﹣2,x2=1∵x<0,故x=1舍去,∴x=﹣2是原方程的解;综上所述,原方程的解为x1=2,x2=﹣2.解方程x2+2|x+2|﹣4=0.【分析】分x+2大于等于0与小于0两种情况,利用绝对值的代数意义化简所求方程,求出解即可.【解答】解:当x+2≥0,即x≥﹣2时,方程变形得:x2+2x=0,即x(x+2)=0,解得:x1=0,x2=﹣2;当x+2<0,即x<﹣2时,方程变形得:x2﹣2x﹣8=0,即(x﹣4)(x+2)=0,解得:x1=4(不合题意,舍去),x2=﹣2(不合题意,舍去),综上,原方程的解为x=0或x=﹣2.【点评】此题考查了解一元二次方程﹣因式分解法,熟练掌握因式分解的方法是解本题的关键.。
因式分解解一元二次方程136题(有答案)ok

分解因式法解一元二次方程专项练习136题(有答案)题(有答案)1.3(x ﹣2)2﹣x (x ﹣2)=0=0,,2.3x 3x((x+2x+2))=5=5((x+2x+2))3.2x 2﹣8x=04.4. x 2﹣3x 3x﹣﹣4=04=0..5.x 2﹣2x 2x﹣﹣3=03=0..6.x (x ﹣3)﹣)﹣44(3﹣x )=0=0,,7. 3(x ﹣2)2=x =x((x ﹣2);8. 2x 2﹣5x 5x﹣﹣3=09. (3x 3x﹣﹣1)2=(x+1x+1))210. x (x ﹣6)=2=2((x ﹣8)1111..4+44+4((1+x 1+x))+4+4((1+x 1+x))2=191212..x 2﹣4x 4x﹣﹣5=013. 13. 33(5﹣x )2=2=2((5﹣x )14.14.((x ﹣3)2=2=2((3﹣x ).1515..2x 2+x +x﹣﹣6=06=0..1616..2x 2﹣x ﹣1=01=0;;17. 3x (x ﹣1)=2=2((x ﹣1)2.1818..x (x ﹣5)+4x=01919.. x 2﹣2x=02020..(x ﹣3)2+2x +2x((x ﹣3)=0=0;;2121..x 2﹣3x=03x=0;;2222..(x ﹣2)2=(2x+32x+3))22323..3x 2﹣11x 11x﹣﹣4=04=0..2424..2x 2x((x ﹣1)﹣)﹣x+1=0 x+1=025. 2x 2+x +x﹣﹣3=02626..x 2﹣2x 2x﹣﹣15=015=0;;27. 2x (x ﹣3)+x=3+x=3..28. x (x ﹣3)=15=15﹣﹣5x 5x;;2929..(x ﹣1)2﹣2(x ﹣1)=03030..x (x ﹣2)﹣)﹣x+2=0x+2=0x+2=0;;31. 2x 2﹣3x 3x﹣﹣5=05=0..32.32...4x 2﹣x ﹣1=3x 1=3x﹣﹣2, 33.34.34.((x ﹣3)2﹣2(x ﹣1)=x =x﹣﹣7. 35. 3x (x ﹣2)﹣)﹣22(x ﹣2)=036. 3x 2﹣x ﹣2=02=0;;37. (x ﹣6)2﹣(﹣(33﹣2x 2x))2=0=0..3838..(x ﹣3)2=5=5((3﹣x )(x ﹣3)2=5=5((3﹣x )3939..(2x+12x+1))2=2=2((2x+12x+1))4040..(3x 3x﹣﹣1)(x ﹣1)=(4x+14x+1))(x ﹣1).4141..x 2﹣x ﹣6=06=0,,4242..x 2﹣8(x+6x+6))=04343..2x 2﹣6x=06x=0..4444..(x ﹣3)(x+1x+1))=54545..2x 2﹣8x=08x=0;;4646..x 2+2x +2x﹣﹣15=047. 2x 2﹣5x 5x﹣﹣7=048. 2y (y ﹣3)=4=4((y ﹣3)49. x 2﹣7x 7x﹣﹣18=050. 3x 2+8x +8x﹣﹣3=05151.. 2x (x ﹣3)=9=9﹣﹣3x5252..x 2﹣4x=553. ﹣8x 2+10x=05454..3x 2+4x +4x﹣﹣7=07=0,,55. 3x 2﹣5x+2=056. 2(x ﹣3)2=x 2﹣3x5757..x 2=3x =3x;; 58. (3x 3x﹣﹣2)2=(2x 2x﹣﹣3)259. (y ﹣2)2+2y +2y((y ﹣2)=060.2y 60.2y((y+2y+2))=y+2=y+2..61. 5x 2+3x=062. (3x 3x﹣﹣2)2=(2x 2x﹣﹣3)263. x (x ﹣3)=5=5((x ﹣3);64. (2x+32x+3))2﹣5(2x+32x+3))+4=0+4=0..65. (2x 2x﹣﹣7)2﹣5(2x 2x﹣﹣7)+4=066. (3x 3x﹣﹣1)2=x 2+6x+967.67.((2x+22x+2))2=3=3((2x+22x+2))(x ﹣1)68.68.((x+7x+7))(x ﹣3)+4x +4x((x+1x+1))=069.2x 69.2x((x+3x+3)﹣)﹣)﹣33(x+3x+3))=070. x ﹣2=x 2=x((x ﹣2)71. x 2+8x +8x﹣﹣9=07272..x (2x 2x﹣﹣5)=4x =4x﹣﹣1010..7373.(.(.(2x 2x 2x﹣﹣5)2﹣(﹣(x+4x+4x+4))2=07474..2(x ﹣1)2=x 2﹣1 75.76. 4x (2x 2x﹣﹣1)=3=3((2x 2x﹣﹣1);77. 2x 2+x +x﹣﹣1=01=0..78. (3x 3x﹣﹣2)(x+4x+4))=(3x 3x﹣﹣2)(5x 5x﹣﹣1); 79. (x+1x+1))(x+3x+3))=15=15..80.x 2﹣5x 5x﹣﹣6=081. x 2﹣2x=9982. (x ﹣3)2﹣4x+12=083. 4(x+1x+1))2=9=9((x ﹣2)284. x 2=2x85. (x+4x+4))2=5=5((x+4x+4))87. 16(x ﹣1)2=22588. 4x 2﹣4x+1=x 2﹣6x+989. 9(x+1x+1))2=4=4((x ﹣1)2(4)x 2﹣4x+4=4x+4=((3﹣2x 2x))290. (x ﹣2)2=(3﹣2x 2x))2.91. (x+2x+2))2﹣1010((x+2x+2))+25=09292..x 2﹣2(p ﹣q )x ﹣4pq=04pq=0..9393..x 2+10x+21=0+10x+21=0,,9494..2(x ﹣2)2=3=3((x ﹣2)95. 3(x ﹣5)2=2=2((5﹣x ), 96. ,97. 5x 2﹣4x 4x﹣﹣12=012=0,, 98. (x ﹣)=5x =5x((﹣x ),9999..9(x ﹣2)2﹣4(x+1x+1))2=0=0.. 100100...101101..(2)x 2﹣8x+15=08x+15=0;; 103. 6x 2﹣x ﹣12=012=0..104. 2x 2﹣x ﹣6=0105. ﹣x 2+6x +6x﹣﹣5=0106. (x ﹣5)2=(2x 2x﹣﹣1)(5﹣x )107. (x+1x+1))(x+2x+2))=3x+6=3x+6..108. x 2﹣9=09=0,,109. x 2+3x +3x﹣﹣4=04=0,,110. x 2﹣3x+2=03x+2=0,,111. 4(3x 3x﹣﹣1)2 =25=25((2x+12x+1))2.112. (3x+53x+5))2﹣4(3x+53x+5))+3=0113. (3x+23x+2))(x+3x+3))=x+14114. 3(x+1x+1))2=(x+1x+1))115.115.((x ﹣2)2﹣4=0116.116.((x ﹣3)2+2x +2x((x ﹣3)=0117.117.((3x 3x﹣﹣1)2=(x+1x+1))2118.118.((x+5x+5))2﹣2(x+5x+5)﹣)﹣)﹣8=08=08=0..119. x 2﹣8x=9120. (x ﹣2)2=(2x+32x+3))2.121. x 2﹣3=33=3((x+1x+1));122. (y ﹣3)2+3+3((y ﹣3)+2=0123. 7x (5x+25x+2))=6=6((5x+25x+2))124124..(3)6(x+4x+4))2﹣(﹣(x+4x+4x+4)﹣)﹣)﹣2=0 2=0 125. x 2﹣(﹣(3m 3m 3m﹣﹣1)x+2m 2﹣m=0m=0,,126126..x 2﹣2x 2x﹣﹣224=0224=0..127.127...128128..5x 5x((x ﹣3)﹣()﹣(x x ﹣3)(x+1x+1))=0=0..129129..x 2﹣11x+28=0130. 4y 2﹣25=025=0;;131.131.((2x+32x+3))2﹣36=036=0;;132. x 2﹣3x+2=03x+2=0;;133. 2t 2﹣7t 7t﹣﹣4=04=0;;134. 5y (y ﹣1)=2=2((y ﹣1)135. x 2+(1+2)x+3+=0=0;;136.136.((x ﹣3)2+(x+4x+4))2﹣(﹣(x x ﹣5)2=17x+24=17x+24..137.x 2﹣3|x|3|x|﹣﹣4=0参考答案:1.3(x ﹣2)2﹣x (x ﹣2)=0=0,, (x ﹣2)(3x 3x﹣﹣6﹣x )=0=0,, x ﹣2=0或2x 2x﹣﹣6=06=0,, 解得:解得:x x 1=2=2,,x 2=3=3;; 2.3x 3x((x+2x+2))=5=5((x+2x+2))原方程可化为3x 3x((x+2x+2)﹣)﹣)﹣55(x+2x+2))=0=0,, (3x 3x﹣﹣5)(x+2x+2))=0=0,, 解得x 1=﹣2,3.2x 2﹣8x=0因式分解,得因式分解,得2x 2x((x ﹣4)=0=0,, 于是得,于是得,于是得,2x=02x=0或x ﹣4=04=0,, 即x 1=0=0,,x 2=4=4..4. x 2﹣3x 3x﹣﹣4=04=0..因式分解,得(因式分解,得(x x ﹣4)(x+1x+1))=0=0,, 于是得,于是得,x x ﹣4=0或x+1=0x+1=0,, 解得:解得:x x 1=4=4,,x 2=﹣15.x 2﹣2x 2x﹣﹣3=03=0..原方程可以变形为(原方程可以变形为(x x ﹣3)(x+1x+1))=0 x ﹣3=03=0,,x+1=0 ∴x 1=3=3,,x 2=﹣1.6.x (x ﹣3)﹣)﹣44(3﹣x )=0=0,, (x ﹣3)(x+4x+4))=0=0,, x ﹣3=0或x+4=0x+4=0,, 解得:解得:x x 1=3=3,,x 2=﹣4;7. 3(x ﹣2)2=x =x((x ﹣2); 整理得3(x ﹣2)2﹣x (x ﹣2)=0 即(即(x x ﹣2)(x ﹣3)=0 x 1=2=2,,x 2=3 8. 2x 2﹣5x 5x﹣﹣3=0 9. (3x 3x﹣﹣1)2=(x+1x+1))2原方程可化为:(3x 3x﹣﹣1)2﹣(﹣(x+1x+1x+1))2=0=0,, (3x 3x﹣﹣1+x+11+x+1))(3x 3x﹣﹣1﹣x ﹣1)=0=0,, ∴4x=0或2x 2x﹣﹣2=02=0,, 解得:解得:x x 1=0=0,,x 2=1=1;;10. x (x ﹣6)=2=2((x ﹣8)x 2﹣6x=2x 6x=2x﹣﹣16x 2﹣8x+16=0(x ﹣4)2=0 x 1=x 2=4 =41111..4+44+4((1+x 1+x))+4+4((1+x 1+x))2=19原式可变为4(1+x 1+x))2+4+4((1+x 1+x)﹣)﹣)﹣15=0 15=0 [2[2((1+x 1+x)﹣)﹣)﹣3][23][23][2((1+x 1+x))+5]=0 x 1=,x 2=﹣1212..x 2﹣4x 4x﹣﹣5=0 (x ﹣5)(x+1x+1))=0 x ﹣5=0或x+1=0 x 1=5=5,,x 2=﹣1 13. 13. 33(5﹣x )2=2=2((5﹣x ) 原方程可变形为:原方程可变形为:3(5﹣x )2﹣2(5﹣x )=0 (5﹣x )[3[3((5﹣x )﹣)﹣2]=0 2]=0 (5﹣x )(1313﹣﹣3x 3x))=0 则x 1=5=5,,x 2=14.14.((x ﹣3)2=2=2((3﹣x ). 原式可变为原式可变为原式可变为 (x ﹣3)2﹣2(3﹣x )=0 (x ﹣3)(x ﹣1)=0 x 1=3=3,,x 2=1(x+2x+2))(2x 2x﹣﹣3)=0 x+2=0或2x 2x﹣﹣3=0 ∴x 1=﹣2,x 2=.1616..2x 2﹣x ﹣1=01=0;;原方程可化为:原方程可化为:(x ﹣1)(2x+12x+1))=0=0,, x ﹣1=0或2x+1=02x+1=0,, 解得:解得:解得:x x 1=1=1,,x 2=﹣. 17. 3x (x ﹣1)=2=2((x ﹣1)2.原方程可化为:原方程可化为:3x 3x 3x((x ﹣1)﹣)﹣22(x ﹣1)2=0=0,, (x ﹣1)(3x 3x﹣﹣2x+22x+2))=0=0,, x ﹣1=0或x+2=0x+2=0,, 解得:解得:x x 1=1=1,,x 2=﹣21818..x (x ﹣5)+4x=0 即x (x ﹣5+45+4))=0 x (x ﹣1)=0 ∴x 1=0=0,,x 2=11919.. x 2﹣2x=0 x (x ﹣2)=0 ∴x=0或x ﹣2=0 ∴x 1=0=0,,x 2=2=2..2020..(x ﹣3)2+2x +2x((x ﹣3)=0=0;;原方程可化为:(x ﹣3)(x ﹣3+2x 3+2x))=0 (x ﹣3)(x ﹣1)=0 x 1=3=3,,x 2=1=1.. 2121..x 2﹣3x=03x=0;; x (x ﹣3)=0 ∴x 1=0=0,,x 2=3 =32222..(x ﹣2)2=(2x+32x+3))2(x ﹣2)2=(2x+32x+3))2 即(即(x x ﹣2)2﹣(﹣(2x+32x+32x+3))2=0(3x+13x+1))(x+5x+5))=0 x 1=﹣5,x 2=2323..3x 2﹣11x 11x﹣﹣4=04=0.. 把方程3x 2﹣11x 11x﹣﹣4=0 即(即(x x ﹣4)(3x+13x+1))=0=0,, 解得x 1=4=4,,x 2=.∴(∴(x x ﹣1)(2x 2x﹣﹣1)=0 ∴x ﹣1=0或2x 2x﹣﹣1=0 解得x 1=1=1,,x 2=; 25. 2x 2+x +x﹣﹣3=0原方程变形为:原方程变形为:(x ﹣1)(2x+32x+3))=0 ∴x 1=1=1,,x 2=2626..x 2﹣2x 2x﹣﹣15=015=0;;原式可化为:原式可化为:原式可化为: (x ﹣5)(x+3x+3))=0 得x 1=5=5,,x 2=﹣327. 2x (x ﹣3)+x=3+x=3..原式可化为:(x ﹣3)(2x+12x+1))=0 得,x 2=328. x (x ﹣3)=15=15﹣﹣5x 5x;;x (x ﹣3)=﹣5(x ﹣3)(x ﹣3)(x+5x+5))=0 x 1=3=3,,x 2=﹣52929..(x ﹣1)2﹣2(x ﹣1)=0 (x ﹣1)2﹣2(x ﹣1)=0=0,, (x ﹣1)(x ﹣1﹣2)=0=0,, ∴x ﹣1=0或x ﹣3=03=0,, ∴x 1=1=1,,x 2=33030..x (x ﹣2)﹣)﹣x+2=0x+2=0x+2=0;;原方程可化为:原方程可化为:x x (x ﹣2)﹣()﹣(x x ﹣2)=0=0,, (x ﹣2)(x ﹣1)=0=0,, 解得:解得:x x 1=2=2,,x 2=1=1;;31. 2x 2﹣3x 3x﹣﹣5=05=0..原方程可化为:(2x 2x﹣﹣5)(x+1x+1))=0=0,, 2x 2x﹣﹣5=0或x+1=0x+1=0,, 解得:解得:x x 1=,x 2=﹣1 32.32..∵.∵.∵4x 4x 2﹣x ﹣1=3x 1=3x﹣﹣2,∴4x 2﹣4x+1=0 即(即(2x 2x 2x﹣﹣1)2=0=0,, 解得33.33.解:解:34.34.((x ﹣3)2﹣2(x ﹣1)=x =x﹣﹣7.移项,合并同类项得,移项,合并同类项得,(x ﹣3)2﹣3x+9=03x+9=0,, 即,(x ﹣3)2﹣3(x ﹣3)=0=0,, 因式分解得,(x ﹣3﹣3)(x ﹣3)=0 则x ﹣3=0或(或(x x ﹣6)=0=0,, 解得,解得,x x 1=3=3,,x 2=6=6.. 35. 3x (x ﹣2)﹣)﹣22(x ﹣2)=0 (x ﹣2)(3x 3x﹣﹣2)=0 x 1=2=2,,x 2=; 36. 3x 2﹣x ﹣2=02=0;; 原方程变形得,原方程变形得, (3x+23x+2))(x ﹣1)=0 ∴,x 2=1=1;;37. (x ﹣6)2﹣(﹣(33﹣2x 2x))2=0=0.. 原方程变形得,原方程变形得,(x ﹣6+36+3﹣﹣2x 2x))(x ﹣6﹣3+2x 3+2x))=0 (x+3x+3))(3x 3x﹣﹣9)=0∴x 1=3=3,,x 2=﹣33838..(x ﹣3)2=5=5((3﹣x )(x ﹣3)2=5=5((3﹣x ) (x ﹣3)2+5+5((x ﹣3)=0 (x ﹣3)(x+2x+2))=0 ∴x 1=3=3,,x 2=﹣2.3939..(2x+12x+1))2=2=2((2x+12x+1))原方程可化为:(2x+12x+1))2﹣2(2x+12x+1))=0=0,, (2x+12x+1))(2x+12x+1﹣﹣2)=0=0,, (2x+12x+1))(2x 2x﹣﹣1)=0=0,, 解得:解得:x x 1=﹣,x2=.4040..(3x 3x﹣﹣1)(x ﹣1)=(4x+14x+1))(x ﹣1). (3x 3x﹣﹣1)(x ﹣1)﹣()﹣(4x+14x+14x+1))(x ﹣1)=0=0,, (x ﹣1)[(3x 3x﹣﹣1)﹣()﹣(4x+14x+14x+1))]=0]=0,, (x ﹣1)(x+2x+2))=0=0,, ∴x 1=1=1,,x 2=﹣2.4141.∵.∵.∵x x 2﹣x ﹣6=06=0,, ∴(∴(x+2x+2x+2))(x ﹣3)=0=0,, ∴x+2=0或x ﹣3=03=0,, 解得x 1=3=3,,x 2=﹣2.4242..x 2﹣8(x+6x+6))=04343..2x 2﹣6x=06x=0..原方程变形为2x 2x((x ﹣3)=0 ∴2x=0或x ﹣3=0 ∴x 1=0=0,,x 2=34444..(x ﹣3)(x+1x+1))=5 x 2﹣2x 2x﹣﹣8=08=0,, (x ﹣4)(x+2x+2))=0∴x 1=4=4,,x 2=﹣2.4545..2x 2﹣8x=08x=0;;因式分解,得2x 2x((x ﹣4)=0=0,, 2x=0或x ﹣4=04=0,, 解得,解得,x=0x=0或x=4x=4;;4646..x 2+2x +2x﹣﹣15=0 (x+5x+5))(x ﹣3)=0 x+5=0或x ﹣3=0 ∴x 1=﹣5,x 2=3=3;;47. 2x 2﹣5x 5x﹣﹣7=0因式分解得(因式分解得(x+1x+1x+1))(2x 2x﹣﹣7)=0 解得:,x 2=﹣1;48. 2y (y ﹣3)=4=4((y ﹣3) 2y 2y((y ﹣3)﹣)﹣44(y ﹣3)=0 (y ﹣3)(2y 2y﹣﹣4)=0=0((2分)分) ∴y 1=3=3,,y 2=249. x 2﹣7x 7x﹣﹣18=0 解:(x ﹣9)(x+2x+2))=0 x ﹣9=0或x+2=0 ∴x 1=9=9,,x 2=﹣250. 3x 2+8x +8x﹣﹣3=0解:方程可以化为(解:方程可以化为(x+3x+3x+3))(3x 3x﹣﹣1)=0 ∴x+3=0或3x 3x﹣﹣1=0 即x 1=﹣3,x 2=.5151.. 2x (x ﹣3)=9=9﹣﹣3x 2x 2x((x ﹣3)﹣()﹣(99﹣3x 3x))=0 2x 2x((x ﹣3)+3+3((x ﹣3)=0 (x ﹣3)(2x+32x+3))=0 x 1=3=3,,x 2=﹣x 2﹣4x 4x﹣﹣5=0 (x ﹣5)(x+1x+1))=0 ∴x ﹣5=05=0,,x+1=0∴原方程的解为:∴原方程的解为:x x 1=5=5,,x 2=﹣1.53. ﹣8x 2+10x=0 x (1010﹣﹣8x 8x))=0 ∴x 1=0=0,,x 2= 5454..3x 2+4x +4x﹣﹣7=07=0,, (x ﹣1)(3x+73x+7))=0=0,, x ﹣1=0或3x+7=03x+7=0,, 解得:55. 3x 2﹣5x+2=0原式变形为:(3x 3x﹣﹣2)(x ﹣1)=0 ∴x 1=1=1,,x 2=56. 2(x ﹣3)2=x 2﹣3x 原方程变形为:原方程变形为:原方程变形为: 2(x ﹣3)2=x =x((x ﹣3) (x ﹣3)[2[2((x ﹣3)﹣)﹣x]=0 x]=0 (x ﹣3)(x ﹣6)=0 ∴x 1=3=3,,x 2=6 5757..(1)x 2=3x =3x;; 移项得,移项得,x x 2﹣3x=03x=0,, 因式分解得,因式分解得,x x (x ﹣3)=0=0,, 解得,解得,x x 1=0=0,,x 2=3=3;;58. (3x 3x﹣﹣2)2=(2x 2x﹣﹣3)2解:解:3x 3x 3x﹣﹣2=2=±(±(±(2x 2x 2x﹣﹣3)3x ﹣2=2x 2=2x﹣﹣3或3x 3x﹣﹣2=2=﹣(﹣(﹣(2x 2x 2x﹣﹣3) 解得:解得:x x 1=﹣1,x 2=1=1;;59. (y ﹣2)2+2y +2y((y ﹣2)=0解:(y ﹣2)(y ﹣2+2y 2+2y))=0 解得:解得:y y 1=2=2,,y2=60.60...2y 2y((y+2y+2))=y+2=y+2..原方程变形为:原方程变形为:2y 2y 2y((y+2y+2)﹣()﹣()﹣(y+2y+2y+2))=0=0,, 即(即(y+2y+2y+2))(2y 2y﹣﹣1)=0=0,, 解得y 1=﹣2,y2=.∴x 1=0=0,,x 2=﹣.62. (3x 3x﹣﹣2)2=(2x 2x﹣﹣3)2(3x 3x﹣﹣2)2﹣(﹣(2x 2x 2x﹣﹣3)2=0=0,, (3x 3x﹣﹣2+2x 2+2x﹣﹣3)(3x 3x﹣﹣2﹣2x+32x+3))=0=0,, 5(x ﹣1)(x+1x+1))=0=0,, 即:即:x x ﹣1=0或x+1=0 ∴x 1=1=1,,x 2=﹣163. x (x ﹣3)=5=5((x ﹣3); x (x ﹣3)﹣)﹣55(x ﹣3)=0=0,,(x ﹣3)(x ﹣5)=0=0,, ∴x 1=3=3,,x 2=5=5;;64. (2x+32x+3))2﹣5(2x+32x+3))+4=0+4=0.. (2x+32x+3))2﹣5(2x+32x+3))+4=0 (2x+32x+3﹣﹣4)(2x+32x+3﹣﹣1)=0 (2x 2x﹣﹣1)(x+1x+1))=0=0,, ∴x 1=,x 2=﹣165. (2x 2x﹣﹣7)2﹣5(2x 2x﹣﹣7)+4=0 (2x 2x﹣﹣7﹣4)(2x 2x﹣﹣7﹣1)=0;x 2=466. (3x 3x﹣﹣1)2=x 2+6x+9 (3x 3x﹣﹣1)2﹣(﹣(x x ﹣3)2=0 即(即(2x+12x+12x+1))(x ﹣2)=0 x 1=2=2,,x 2=﹣0.567.67.((2x+22x+2))2=3=3((2x+22x+2))(x ﹣1) (2x+22x+2))2﹣3(2x+22x+2))(x ﹣1)=0 即(即(2x+22x+22x+2))【2x+22x+2﹣﹣3(x ﹣1)】=0 ∴(∴(x x ﹣5)(x+1x+1))=0 x 1=﹣1,x 2=568.68.((x+7x+7))(x ﹣3)+4x +4x((x+1x+1))=0 化简:(x+7x+7))(x ﹣3)+4x +4x((x+1x+1))=0 整理得,整理得,5x 5x 2+8x +8x﹣﹣21=021=0,, 因式分解得,因式分解得,(5x 5x﹣﹣7)(x+3x+3))=0=0,, 即5x 5x﹣﹣7=0或x+3=0x+3=0,, 所以x 1=,x 2=﹣3.69.69...2x 2x((x+3x+3)﹣)﹣)﹣33(x+3x+3))=070. x ﹣2=x 2=x((x ﹣2) 即x ﹣2﹣x (x ﹣2)=0 (x ﹣2)(1﹣x )=0 x 1=2=2,,x 2=1=1;;71. x 2+8x +8x﹣﹣9=0 (x+9x+9))(x ﹣1)=0 x 1=﹣9,x 2=17272..x (2x 2x﹣﹣5)=4x =4x﹣﹣1010.. 原方程可变形为:原方程可变形为: x (2x 2x﹣﹣5)﹣)﹣22(2x 2x﹣﹣5)=0=0,, (2x 2x﹣﹣5)(x ﹣2)=0=0,, 2x 2x﹣﹣5=0或x ﹣2=02=0;; 解得x1=,x 2=2=2..7474.(.(.(2x 2x 2x﹣﹣5)2﹣(﹣(x+4x+4x+4))2=0因式分解,得因式分解,得[(2x 2x﹣﹣5)+(x+4x+4))][][((2x 2x﹣﹣5)﹣()﹣(x+4x+4x+4))]=0]=0,, 整理得,(3x 3x﹣﹣1)(x ﹣9)=0 解得,解得,x x 1=,x 2=9=9..7474..2(x ﹣1)2=x 2﹣1 原方程即为2(x ﹣1)2﹣(﹣(x x 2﹣1)=0=0,, 2(x ﹣1)2﹣(﹣(x+1x+1x+1))(x ﹣1)=0=0,, (x ﹣1)[2[2((x ﹣1)﹣()﹣(x+1x+1x+1))]=0]=0,, (x ﹣1)(x ﹣3)=0=0,, x 1=1=1,,x 2=3=3;; 75.(x ﹣1)(x ﹣+3+3))=0=0,, ∴x 1=1=1,,x 2=-376. 4x (2x 2x﹣﹣1)=3=3((2x 2x﹣﹣1); 原方程可化为:原方程可化为:原方程可化为:4x 4x 4x((2x 2x﹣﹣1)﹣)﹣33(2x 2x﹣﹣1)=0=0,, (2x 2x﹣﹣1)(4x 4x﹣﹣3)=0=0,, 2x ﹣1=0或4x 4x﹣﹣3=03=0,, 解得:,;77. 2x 2+x +x﹣﹣1=01=0..原方程可化为:(2x 2x﹣﹣1)(x+1x+1))=0=0,, 2x ﹣1=0或x+1=0x+1=0,, 解得:,x 2=﹣1.78. (3x 3x﹣﹣2)(x+4x+4))=(3x 3x﹣﹣2)(5x 5x﹣﹣1); 解:(3x 3x﹣﹣2)(x+4x+4)﹣()﹣()﹣(3x 3x 3x﹣﹣2)(5x 5x﹣﹣1)=0 (3x 3x﹣﹣2)[(x+4x+4)﹣()﹣()﹣(5x 5x 5x﹣﹣1)]=0(3x 3x﹣﹣2)(﹣(﹣4x+54x+54x+5))=0 3x 3x﹣﹣2=0或﹣或﹣4x+5=0 4x+5=0;79. (x+1x+1))(x+3x+3))=15=15.. 方程整理得:方程整理得:方程整理得:x x 2+4x +4x﹣﹣12=0 ( x+6)(x ﹣2)=0 x 1=﹣6,x 2=2=2..80. x 2﹣5x 5x﹣﹣6=0 解:(x ﹣6)(x+1x+1))=0=0,, x ﹣6=0或x+1=0x+1=0,,∴原方程的解是x 1=6=6,,x 2=﹣1. 81. x 2﹣2x=99解:解:(x ﹣1111))(x+9x+9))=0=0,, x ﹣11=0或x+9=0x+9=0,, ∴原方程的解是x 1=11=11,,x 2=﹣9. 82. (x ﹣3)2﹣4x+12=0解:解:(x ﹣3)2﹣4(x ﹣3)=0=0,, (x ﹣7)(x ﹣3)=0=0,,x ﹣3=0或x ﹣7=07=0,, ∴原方程的解是x 1=3=3,,x 2=7=7.. 83. 4(x+1x+1))2=9=9((x ﹣2)2解:(2x+22x+2))2=(3x 3x﹣﹣6)2, (2x+2+3x 2x+2+3x﹣﹣6)(2x+22x+2﹣﹣3x+63x+6))=0=0,, 即:(5x 5x﹣﹣4)(8﹣x )=0=0,, x=8或x=,∴原方程的解是84. x 2=2x移项,得x 2﹣2x=02x=0,, 因式分解,得x (x ﹣2)=0=0,, 所以x=0或x=2x=2..85. (x+4x+4))2=5=5((x+4x+4))移项,得,移项,得,(x+4x+4))2﹣5(x+4x+4))=0=0,, 因式分解得,(x+4x+4))[(x+4x+4)﹣)﹣)﹣5]=05]=05]=0,, x+4=0或x ﹣1=01=0,, 解得,解得,解得,x x 1=﹣4,x 2=187. 16(x ﹣1)2=225 16(x ﹣1)2﹣152=0=0,,所以所以[4[4[4((x ﹣1)+15][4+15][4((x ﹣1)﹣)﹣15]=015]=015]=0,, 即4x+11=04x+11=0,,4x 4x﹣﹣19=019=0,, 得x 1=﹣,x 2=.88. 4x 2﹣4x+1=x 2﹣6x+9方程变为(方程变为(2x 2x 2x﹣﹣1)2﹣(﹣(x x ﹣3)2=0=0,,所以所以[[(2x 2x﹣﹣1)+(x ﹣3)][][((2x 2x﹣﹣1)﹣()﹣(x x ﹣3)]=0]=0,, 即3x 3x﹣﹣4=04=0,,x+2=0x+2=0,, 得x 1=,x 2=﹣2.89. 9(x+1x+1))2=4=4((x ﹣1)2(4)x 2﹣4x+4=4x+4=((3﹣2x 2x))2原方程变为原方程变为[3[3[3((x+1x+1))]2﹣[2[2((x ﹣1)]2=0=0,,所以所以[3[3[3((x+1x+1))+2+2((x ﹣1)][3][3((x+1x+1)﹣)﹣)﹣22(x ﹣1)]=0]=0,, 即(即(5x+15x+15x+1))(x+5x+5))=0=0,, 得x 1=﹣,x 2=﹣5.90. (x ﹣2)2=(3﹣2x 2x))2. (x ﹣2)2﹣(﹣(33﹣2x 2x))2=0=0,, (x ﹣2+32+3﹣﹣2x 2x))(x ﹣2﹣3+2x 3+2x))=0=0,, (1﹣x )(3x 3x﹣﹣5)=0=0,, 所以x 1=1=1,,x 2=91. (x+2x+2))2﹣1010((x+2x+2))+25=0 因式分解得,因式分解得,因式分解得,[[(x+2x+2)﹣)﹣)﹣5]5]2=0=0,, 解得,解得,x x 1=x 2=39292..x 2﹣2(p ﹣q )x ﹣4pq=04pq=0.. ∵x 2﹣2(p ﹣q )x ﹣4pq=0 ∴(∴(x x ﹣2p 2p))(x+2q x+2q))=0=0,, ∴x 1=2p =2p,,x 2=﹣2q 2q..9393..x 2+10x+21=0+10x+21=0,,把左边分解因式得:(x+3x+3))(x+7x+7))=0=0,, 则:则:x+3=0x+3=0x+3=0,,x+7=0x+7=0,, 解得:解得:x x 1=﹣3,x 2=﹣7.94.294.2((x ﹣2)2=3=3((x ﹣2)∵2(x ﹣2)2=3=3((x ﹣2), ∴(∴(x x ﹣2)(2x 2x﹣﹣4﹣3)=0=0,, 即x ﹣2=0或2x 2x﹣﹣7=07=0,, 解得:解得:x x 1=2=2,,x2=;95. 3(x ﹣5)2=2=2((5﹣x ), 变形得:变形得:33(5﹣x )2=2=2((5﹣x ), 移项得:移项得:33(5﹣x )2﹣2(5﹣x )=0=0,, 分解因式得:(5﹣x )(1313﹣﹣3x 3x))=0=0,, 则:则:55﹣x=0x=0,,1313﹣﹣3x=03x=0,, 解得:解得:x x 1=5=5,,x 2=;96.,分解因式得:(x ﹣)(x ﹣)=0=0,,则x ﹣=0=0,,x ﹣=0=0,, 解得:解得:x x 1=,x 2=.97. 5x 2﹣4x 4x﹣﹣12=012=0,, (5x+65x+6))(x ﹣2)=0=0,, 5x+6=0,x ﹣2=02=0,, x 1=﹣,x 2=2=2.. 98. (x ﹣)=5x =5x((﹣x ), (x ﹣)+5x +5x((x ﹣)=0=0,,(x ﹣)(1+5x 1+5x))=0=0,,x ﹣=0=0,,1+5x=01+5x=0,, x 1=,x 2=﹣.9999..9(x ﹣2)2﹣4(x+1x+1))2=0=0..9(x ﹣2)2﹣4(x+1x+1))2=0(3x 3x﹣﹣6+2x+26+2x+2))(3x 3x﹣﹣6﹣2x 2x﹣﹣2)=0=0,, 整理得:(5x 5x﹣﹣4)(x ﹣8)=0=0,, 解方程得:解方程得:x x 1=,x 2=8 100100...x (x ﹣2)=2=2((x+6x+6)), x 2﹣2x=2x+122x=2x+12,, x 2﹣4x 4x﹣﹣12=012=0,, (x ﹣6)(x+2x+2))=0=0,, x 1=6=6,,x 2=﹣2. ∴原方程的根为x 1=6=6,,x 2=﹣2101101..(2)x 2﹣8x+15=08x+15=0;;把左边分解因式得:(x ﹣3)(x ﹣5)=0=0,, 则x ﹣3=03=0,,x ﹣5=05=0,,解得:解得:x x 1=5=5,,x 2=3=3;; 102. ; 移项得:移项得:y y 2﹣2y+2=0y+2=0,, (y ﹣)2=0=0,,两边开方得:两边开方得:两边开方得:y y ﹣=0=0,,则y 1=y 2=; 103. 6x 2﹣x ﹣12=012=0.. 由原方程,得由原方程,得由原方程,得 (2x 2x﹣﹣3)(3x+43x+4))=0=0,, 解得,解得,x=x=,或x=x=﹣﹣104. 2x 2﹣x ﹣6=0原方程化为(原方程化为(2x+32x+32x+3))(x ﹣2)=0=0,, 解得x 1=﹣,x 2=2=2;; 105. ﹣x 2+6x +6x﹣﹣5=0 原方程化为原方程化为x 2﹣6x+5=0分解因式,得(分解因式,得(分解因式,得(x x ﹣1)(x ﹣5)=0=0,, 解得x 1=1=1,,x 2=5=5;;106. (x ﹣5)2=(2x 2x﹣﹣1)(5﹣x ) 移项,得(移项,得(x x ﹣5)2+(2x 2x﹣﹣1)(x ﹣5)=0=0,, 提公因式,得(提公因式,得(x x ﹣5)(x ﹣5+2x 5+2x﹣﹣1)=0=0,, 解得x 1=5=5,,x 2=2107. (x+1x+1))(x+2x+2))=3x+6=3x+6.. ∵(∵(x+1x+1x+1))(x+2x+2))=3x+6=3x+6,, ∴(∴(∴(x+1x+1x+1))(x+2x+2))=3=3((x+2x+2)), ∴(∴(∴(x+1x+1x+1))(x+2x+2)﹣)﹣)﹣33(x+2x+2))=0=0,, ∴(∴(∴(x+2x+2x+2))(x+1x+1﹣﹣3)=0=0,, ∴x+2=0或x+1x+1﹣﹣3=0 ∴x 1=﹣2,x 2=2108. x 2﹣9=09=0,, x 2=9=9,, 解得:解得:解得:x x 1=3=3,,x 2=﹣3,109. x 2+3x +3x﹣﹣4=04=0,, (x ﹣1)(x+4x+4))=0=0,, 解得:解得:x x 1=1=1,,x 2=﹣4,110. x 2﹣3x+2=03x+2=0,, (x ﹣1)(x ﹣2)=0=0,, 解得:解得:x x 1=1=1,,x 2=2111. 4(3x 3x﹣﹣1)2=25=25((2x+12x+1))2.∵4(3x 3x﹣﹣1)2﹣2525((2x+12x+1))2=0=0,,∴[2[2((3x 3x﹣﹣1)﹣)﹣55(2x+12x+1))][2][2((3x 3x﹣﹣1)+5+5((2x+12x+1))]=0]=0,, ∴2(3x 3x﹣﹣1)﹣)﹣55(2x+12x+1))=0或2(3x 3x﹣﹣1)+5+5((2x+12x+1))=0=0,, ∴x 1=﹣,x 2=﹣.112. (3x+53x+5))2﹣4(3x+53x+5))+3=0 设3x+5=y 3x+5=y,则原方程变为,则原方程变为,则原方程变为 y 2﹣4y+3=04y+3=0,,∴(∴(y y ﹣1)(y ﹣3)=0=0,, 解得,解得,y=1y=1或y=3y=3;;①当y=1时,时,3x+5=13x+5=13x+5=1,解得,解得x=x=﹣﹣;②当y=3时,时,3x+5=33x+5=33x+5=3,解得,,解得,,解得,x=x=x=﹣﹣;∴原方程的解是x=x=﹣﹣,或x=x=﹣﹣; 113. (3x+23x+2))(x+3x+3))=x+14 由原方程,得由原方程,得 (x+4x+4))(3x 3x﹣﹣2)=0=0,, 解得x=x=﹣﹣4,或x=;114. 3(x+1x+1))2=(x+1x+1)) 移项得,移项得,33(x+1x+1))2﹣(﹣(x+1x+1x+1))=0=0,, 提公因式得,(x+1x+1))(3x+33x+3﹣﹣1)=0=0,, 即x+1=0或3x+33x+3﹣﹣1=01=0,, 解得x 1=﹣1,x 2=﹣115.115.((x ﹣2)2﹣4=0∵(∵(x x ﹣2﹣2)(x ﹣2+22+2))=0=0,, ∴x ﹣2﹣2=0或x ﹣2+2=02+2=0,,∴x 1=4=4,,x 2=0=0;; 116.116.((x ﹣3)2+2x +2x((x ﹣3)=0 ∵(∵(x x ﹣3)(x ﹣3+2x 3+2x))=0=0,, ∴x ﹣3=0或x ﹣3+2x=03+2x=0,, ∴x 1=3=3,,x 2=1=1;;117.117.((3x 3x﹣﹣1)2=(x+1x+1))2∵3x 3x﹣﹣1=1=±(±(±(x+1x+1x+1)), 即3x 3x﹣﹣1=x+1或3x 3x﹣﹣1=1=﹣(﹣(﹣(x+1x+1x+1)), ∴x 1=1=1,,x 2=0=0;;118.118.((x+5x+5))2﹣2(x+5x+5)﹣)﹣)﹣8=08=08=0..∵[(x+5x+5)﹣)﹣)﹣4][4][4][((x+5x+5))+2]=0+2]=0,, ∴(∴(x+5x+5x+5)﹣)﹣)﹣4=04=0或(或(x+5x+5x+5))+2=0+2=0,, ∴x 1=﹣1,x 2=﹣7.119. x 2﹣8x=9 变形为:变形为:x x 2﹣8x 8x﹣﹣9=09=0,, (x ﹣9)(x+1x+1))=0=0,, 则:则:x x ﹣9=0或x+1=0x+1=0,, 解得:解得:x x 1=9=9,,x 2=﹣1;120. (x ﹣2)2=(2x+32x+3))2. 变形为:(x ﹣2)2﹣(﹣(2x+32x+32x+3))2=0=0,, (x ﹣2+2x+32+2x+3))(x ﹣2﹣2x 2x﹣﹣3)=0=0,, (3x+13x+1))(﹣(﹣x x ﹣5)=0=0,, 则:则:3x+1=03x+1=03x+1=0,﹣,﹣,﹣x x ﹣5=05=0,, 解得:解得:x x 1=﹣,x 2=﹣5.121. x 2﹣3=33=3((x+1x+1)); 整理得整理得x 2﹣3x 3x﹣﹣4=04=0,, ∴(∴(∴(x+1x+1x+1))(x ﹣4)=0=0,, ∴x+1=0或x ﹣4=04=0,, ∴x 1=﹣1,x 2=4=4;;122. (y ﹣3)2+3+3((y ﹣3)+2=0 ∵(∵(y y ﹣3+23+2))(y ﹣3+13+1))=0=0,, ∴y ﹣3+2=0或y ﹣3+1=03+1=0,, ∴y 1=1=1,,y 2=2=2;;123. 7x (5x+25x+2))=6=6((5x+25x+2)) ∵7x 7x((5x+25x+2)﹣)﹣)﹣66(5x+25x+2))=0=0,, ∴(∴(5x+25x+25x+2))(7x 7x﹣﹣6)=0=0,, ∴5x+2=0或7x 7x﹣﹣6=06=0,, ∴x 1=﹣,x 2=124124..(3)6(x+4x+4))2﹣(﹣(x+4x+4x+4)﹣)﹣)﹣2=0 2=06(x+4x+4))2﹣(﹣(x+4x+4x+4)﹣)﹣)﹣2=02=02=0,, [3[3((x+4x+4)﹣)﹣)﹣2][22][22][2((x+4x+4))+1]=0+1]=0,, (3x+43x+4))(2x+72x+7))=0=0,, 3x+4=03x+4=0,,2x+7=02x+7=0,, 解得:解得:x x 1=﹣,x 2=﹣;125. x 2﹣(﹣(3m 3m 3m﹣﹣1)x+2m 2﹣m=0m=0,, (x ﹣m )[x [x﹣(﹣(﹣(2m 2m 2m﹣﹣1)]=0]=0,, x ﹣m=0m=0,,x ﹣(﹣(2m 2m 2m﹣﹣1)=0=0,, 解得:解得:x x 1=m =m,,x 2=2m =2m﹣﹣1126126..x 2﹣2x 2x﹣﹣224=0224=0.. x 2﹣2x 2x﹣﹣224=0 (x ﹣1616))(x+14x+14))=0=0,, 解得:解得:x x 1=16=16;;x 2=﹣1414.. 127.127...方程两边同时乘以2,得(,得(x+3x+3x+3))2=4=4((x+2x+2))2, 移项,得(移项,得(x+3x+3x+3))2﹣4(x+2x+2))2,=0=0,, (x+3+4x+8x+3+4x+8))(x+3x+3﹣﹣4x 4x﹣﹣8)=0=0,, 即5x+11=0或﹣或﹣3x 3x 3x﹣﹣5=05=0,, 解得x 1=﹣,x 2=﹣;128128..5x 5x((x ﹣3)﹣()﹣(x x ﹣3)(x+1x+1))=0=0..∵(∵(x x ﹣3)(5x 5x﹣﹣x ﹣1)=0=0,, ∴x ﹣3=0或5x 5x﹣﹣x ﹣1=01=0,,∴x 1=3=3,,x 2=129129..x 2﹣11x+28=0 x 2﹣11x+28=011x+28=0,, (x ﹣4)(x ﹣7)=0=0,, x ﹣4=04=0,,x ﹣7=07=0,,x 1=4=4,,x 2=7130. 4y 2﹣25=025=0;; (2y+52y+5))(2y 2y﹣﹣5)=0=0,, 所以y 1=﹣,y 2=;131.131.((2x+32x+3))2﹣36=036=0;; (2x+32x+3))2﹣36=036=0;; (2x+3+62x+3+6))(2x+32x+3﹣﹣6)=0=0,, 所以x 1=﹣,x 2=;132. x 2﹣3x+2=03x+2=0;; (x ﹣1)(x ﹣2)=0=0,, 所以x 1=1=1,,x 2=2=2;;133. 2t 2﹣7t 7t﹣﹣4=04=0;; (t ﹣4)(2t+12t+1))=0=0,, 所以t 1=4=4,,t 2=﹣;134. 5y (y ﹣1)=2=2((y ﹣1)方程变形得:方程变形得:5y 5y 5y((y ﹣1)﹣)﹣22(y ﹣1)=0=0,, 因式分解得:(y ﹣1)(5y 5y﹣﹣2)=0=0,, 可得y ﹣1=0或5x 5x﹣﹣2=02=0,, 解得:解得:y y 1=1=1,,y 2=.135. x 2+(1+2)x+3+=0=0;;(x+)(x+1+)=0x+=0或x+1+=0∴x 1=﹣,x 2=﹣1﹣.136.136.((x ﹣3)2+(x+4x+4))2﹣(﹣(x x ﹣5)2=17x+24=17x+24.. 原方程整理得:原方程整理得:x x 2﹣5x 5x﹣﹣24=0 (x ﹣8)(x+3x+3))=0 ∴x 1=8=8,,x 2=﹣3.137.x 2﹣3|x|3|x|﹣﹣4=0|x|2﹣3|x|3|x|﹣﹣4=0 (|x||x|﹣﹣4)(|x|+1|x|+1))=0|x||x|﹣﹣4=0|x|+14=0|x|+1≠≠0 ∴|x|=4∴x 1=4=4,,x 2=﹣4.。
因式分解法解一元二次方程练习题及答案

因式分解法解一元二次方程练习题1.选择题(1)方程(x -16)(x +8)=0的根是( )A .x 1=-16,x 2=8B .x 1=16,x 2=-8C .x 1=16,x 2=8D .x 1=-16,x 2=-8(2)下列方程4x 2-3x -1=0,5x 2-7x +2=0,13x 2-15x +2=0中,有一个公共解是( )A .x =21B .x =2C .x =1D .x =-1 (3)方程5x (x +3)=3(x +3)解为( )A .x 1=53,x 2=3 B .x =53 C .x 1=-53,x 2=-3 D .x 1=53,x 2=-3(4)方程(y -5)(y +2)=1的根为( )A .y 1=5,y 2=-2B .y =5C .y =-2D .以上答案都不对(5)方程(x -1)2-4(x +2)2=0的根为( )A .x 1=1,x 2=-5B .x 1=-1,x 2=-5C .x 1=1,x 2=5D .x 1=-1,x 2=5(6)一元二次方程x 2+5x =0的较大的一个根设为m ,x 2-3x +2=0较小的根设为n ,则m +n 的值为( )A .1B .2C .-4D .4(7)已知三角形两边长为4和7,第三边的长是方程x 2-16x +55=0的一个根,则第三边长是( )A .5B .5或11C .6D .112.填空题(1)方程t (t +3)=28的解为_______.(2)方程(2x +1)2+3(2x +1)=0的解为__________.(3)方程(2y +1)2+3(2y +1)+2=0的解为__________.(4)关于x 的方程x 2+(m +n )x +mn =0的解为__________.(5)方程x (x -5)=5 -x 的解为__________.3.用因式分解法解下列方程:(1)x 2+12x =0; (2)4x 2-1=0; (3) x 2=7x ;(4)x 2-4x -21=0; (5)(x -1)(x +3)=12; (6)3x 2+2x -1=0;(7)10x 2-x -3=0; (8)(x -1)2-4(x -1)-21=0.4.用适当方法解下列方程:(1)x2-4x+3=0;(2)(x-2)2=256;(3)x2-3x+1=0;(4)x2-2x-3=0;(5)(2t+3)2=3(2t+3);(6)(3-y)2+y2=9;(7)2x2-8x=7;(8)(x+5)2-2(x+5)-8=0.5.解关于x的方程:(1)x2-4ax+3a2=1-2a;(2)x2+5x+k2=2kx+5k+6;(3)x2-2mx-8m2=0;(4)x2+(2m+1)x+m2+m=0.6.已知(x2+y2)(x2-1+y2)-12=0.求x2+y2的值.7.解方程:x(x+12)=864.8.已知x2+3x+5的值为9,试求3x2+9x-2的值.。
用因式分解法解一元二次方程(知识点+经典例题+综合练习)---详细答案

用因式分解法解一元二次方程【主体知识归纳】1.因式分解法 若一元二次方程的一边是0,而另一边易于分解成两个一次因式时,例如,x 2-9=0,这个方程可变形为(x +3)(x -3)=0,要(x +3)(x -3)等于0,必须并且只需(x +3)等于0或(x -3)等于0,因此,解方程(x +3)(x -3)=0就相当于解方程x +3=0或x -3=0了,通过解这两个一次方程就可得到原方程的解.这种解一元二次方程的方法叫做因式分解法.2.因式分解法其解法的关键是将一元二次方程分解降次为一元一次方程.其理论根据是:若A ·B =0A =0或B =0.【基础知识讲解】1.只有当方程的一边能够分解成两个一次因式,而另一边是0的时候,才能应用因式分解法解一元二次方程.分解因式时,要根据情况灵活运用学过的因式分解的几种方法.2.在一元二次方程的四种解法中,公式法是主要的,公式法可以说是通法,即能解任何一个一元二次方程.但对某些特殊形式的一元二次方程,有的用直接开平方法简便,有的用因式分解法简便.因此,在遇到一道题时,应选择适当的方法去解.配方法解一元二次方程是比较麻烦的,在实际解一元二次方程时,一般不用配方法.而在以后的学习中,会常常用到因式分解法,所以要掌握这个重要的数学方法.【例题精讲】例1:用因式分解法解下列方程:(1)y 2+7y +6=0; (2)t (2t -1)=3(2t -1); (3)(2x -1)(x -1)=1.解:(1)方程可变形为(y +1)(y +6)=0,y +1=0或y +6=0,∴y 1=-1,y 2=-6.(2)方程可变形为t (2t -1)-3(2t -1)=0,(2t -1)(t -3)=0,2t -1=0或t -3=0,∴t 1=21,t 2=3. (3)方程可变形为2x 2-3x =0.x (2x -3)=0,x =0或2x -3=0.∴x 1=0,x 2=23. 说明:(1)在用因式分解法解一元二次方程时,一般地要把方程整理为一般式,如果左边的代数式能够分解为两个一次因式的乘积,而右边为零时,则可令每一个一次因式为零,得到两个一元一次方程,解出这两个一元一次方程的解就是原方程的两个解了.(2)应用因式分解法解形如(x -a )(x -b )=c 的方程,其左边是两个一次因式之积,但右边不是零,所以应转化为形如(x -e )(x -f )=0的形式,这时才有x 1=e ,x 2=f ,否则会产生错误,如(3)可能产生如下的错解: 原方程变形为:2x -1=1或x -1=1.∴x 1=1,x 2=2.(3)在方程(2)中,为什么方程两边不能同除以(2t -1),请同学们思考例2:用适当方法解下列方程: (1)3(1-x )2=27;(2)x 2-6x -19=0;(3)3x 2=4x +1;(4)y 2-15=2y ;(5)5x (x -3)-(x -3)(x +1)=0;(6)4(3x +1)2=25(x -2)2.剖析:方程(1)用直接开平方法,方程(2)用配方法,方程(3)用公式法,方程(4)化成一般式后用因式分解法,而方程(5)、(6)不用化成一般式,而直接用因式分解法就可以了.解:(1)(1-x )2=9,(x -1)2=3,x -1=±3,∴x 1=1+3,x 2=1-3.(2)移项,得x 2-6x =19,配方,得x 2-6x +(-3)2=19+(-3)2,(x -3)2=28,x -3=±27, ∴x 1=3+27,x 2=3-27.(3)移项,得3x 2-4x -1=0,∵a =3,b =-4,c =-1,∴x =37232)1(34)4()4(2±=⨯-⨯⨯--±--, ∴x 1=372+,x 2=372-. (4)移项,得y 2-2y -15=0,把方程左边因式分解,得(y -5)(y +3)=0;∴y -5=0或y +3=0,∴y 1=5,y 2=-3.(5)将方程左边因式分解,得(x -3)[5x -(x +1)]=0,(x -3)(4x -1)=0,∴x -3=0或4x -1=0,∴x 1=3,x 2=41. (6)移项,得4(3x +1)2-25(x -2)2=0,[2(3x +1)]2-[5(x -2)]2=0,[2(3x +1)+5(x -2)]·[2(3x +1)-5(x -2)]=0,(11x -8)(x +12)=0,∴11x -8=0或x +12=0,∴x 1=118,x 2=-12. 说明:(1)对于无理系数的一元二次方程解法同有理数一样,只不过要注意二次根式的化简.(2)直接因式分解就能转化成两个一次因式乘积等于零的形式,对于这种形式的方程就不必要整理成一般式了.例3:解关于x 的方程:(a 2-b 2)x 2-4abx =a 2-b 2.解:(1)当a 2-b 2=0,即|a |=|b |时,方程为-4abx =0.当a =b =0时,x 为任意实数.当|a |=|b |≠0时,x =0.(2)当a 2-b 2≠0,即a +b ≠0且a -b ≠0时,方程为一元二次方程.分解因式,得[(a +b )x +(a -b )][(a -b )x -(a +b )]=0,∵a +b ≠0且a -b ≠0,∴x 1=b a a b +-,x 2=ba b a -+. 说明:解字母系数的方程,要注意二次项系数等于零和不等于零的不同情况分别求解.本题实际上是分三种情况,即①a =b =0;②|a |=|b |≠0;③|a |≠|b |.例4:已知x 2-xy -2y 2=0,且x ≠0,y ≠0,求代数式22225252y xy x y xy x ++--的值. 剖析:要求代数式的值,只要求出x 、y 的值即可,但从已知条件中显然不能求出,要求代数式的分子、分母是关于x 、y 的二次齐次式,所以知道x 与y 的比值也可.由已知x 2-xy -2y 2=0因式分解即可得x 与y 的比值.解:由x 2-xy -2y 2=0,得(x -2y )(x +y )=0,∴x -2y =0或x +y =0,∴x =2y 或x =-y .当x =2y 时,135y 13y 5y 5y y 22)y 2(y 5y y 22)y 2(y 5xy 2x y 5xy 2x 2222222222-=-=+⋅⋅+-⋅⋅-=++--. 当x =-y 时,21y4y 2y 5y )y (2)y (y 5y )y (2)y (y 5xy 2x y 5xy 2x 222222222-=-=+⋅-⋅+--⋅-⋅--=++--2. 说明:因式分解法体现了“降次”“化归”的数学思想方法,它不仅可用来解一元二次方程,而且在解一元高次方程、二元二次方程组及有关代数式的计算、证明中也有着广泛的 应用.【同步达纲练习】1.选择题(1)方程(x -16)(x +8)=0的根是( )A .x 1=-16,x 2=8B .x 1=16,x 2=-8C .x 1=16,x 2=8D .x 1=-16,x 2=-8(2)下列方程4x 2-3x -1=0,5x 2-7x +2=0,13x 2-15x +2=0中,有一个公共解是( )A ..x =21 B .x =2 C .x =1 D .x =-1(3)方程5x (x +3)=3(x +3)解为( )A .x 1=53,x 2=3 B .x =53C .x 1=-53,x 2=-3D .x 1=53,x 2=-3 (4)方程(y -5)(y +2)=1的根为( )A .y 1=5,y 2=-2B .y =5C .y =-2D .以上答案都不对(5)方程(x -1)2-4(x +2)2=0的根为( )A .x 1=1,x 2=-5B .x 1=-1,x 2=-5C .x 1=1,x 2=5D .x 1=-1,x 2=5(6)一元二次方程x 2+5x =0的较大的一个根设为m ,x 2-3x +2=0较小的根设为n ,则m +n 的值为( )A .1B .2C .-4D .4(7)已知三角形两边长为4和7,第三边的长是方程x 2-16x +55=0的一个根,则第三边长是( )A .5B .5或11C .6D .11(8)方程x 2-3|x -1|=1的不同解的个数是( )A .0B .1C .2D .32.填空题(1)方程t (t +3)=28的解为_______.(2)方程(2x +1)2+3(2x +1)=0的解为__________.(3)方程(2y +1)2+3(2y +1)+2=0的解为__________.(4)关于x 的方程x 2+(m +n )x +mn =0的解为__________.(5)方程x (x -5)=5 -x 的解为__________.3.用因式分解法解下列方程:(1)x 2+12x =0;(2)4x 2-1=0; (3)x 2=7x ;(4)x 2-4x -21=0;(5)(x -1)(x +3)=12; (6)3x 2+2x -1=0;(7)10x 2-x -3=0;(8)(x -1)2-4(x -1)-21=0.4.用适当方法解下列方程:(1)x 2-4x +3=0;(2)(x -2)2=256; (3)x 2-3x +1=0;(4)x 2-2x -3=0;(5)(2t +3)2=3(2t +3);(6)(3-y )2+y 2=9;(7)(1+2)x 2-(1-2)x =0;(8)5x 2-(52+1)x +10=0;(9)2x 2-8x =7(精确到0.01);(10)(x +5)2-2(x +5)-8=0.5.解关于x 的方程:(1)x 2-4ax +3a 2=1-2a ;(2)x 2+5x +k 2=2kx +5k +6;(3)x 2-2mx -8m 2=0; (4)x 2+(2m +1)x +m 2+m =0.6.已知x 2+3xy -4y 2=0(y ≠0),试求yx y x +-的值.7.已知(x 2+y 2)(x 2-1+y 2)-12=0.求x 2+y 2的值.8.请你用三种方法解方程:x(x+12)=864.9.已知x2+3x+5的值为9,试求3x2+9x-2的值.10.一跳水运动员从10米高台上跳水,他跳下的高度h(单位:米)与所用的时间t(单位:秒)的关系式h=-5(t-2)(t+1).求运动员起跳到入水所用的时间.11.为解方程(x2-1)2-5(x2-1)+4=0,我们可以将x2-1视为一个整体,然后设x2-1=y,则y2=(x2-1)2,原方程化为y2-5y+4=0,解此方程,得y1=1,y2=4.当y=1时,x2-1=1,x2=2,∴x=±2.当y=4时,x2-1=4,x2=5,∴x=±5.∴原方程的解为x1=-2,x2=2,x3=-5,x4=5.以上方法就叫换元法,达到了降次的目的,体现了转化的思想.(1)运用上述方法解方程:x4-3x2-4=0.(2)既然可以将x2-1看作一个整体,你能直接运用因式分解法解这个方程吗参考答案【同步达纲练习】1.(1)B (2)C (3)D (4)D (5)B (6)A (7)A (8)D2.(1)t 1=-7,t 2=4(2)x 1=-21,x 2=-2(3)y 1=-1,y 2=-23(4)x 1=-m ,x 2=-n (5)x 1=5,x 2=-1 3.(1)x 1=0,x 2=-12;(2)x 1=-21,x 2=21;(3)x 1=0,x 2=7;(4)x 1=7,x 2=-3;(5)x 1=-5,x 2=3;(6)x 1=-1,x 2=31; (7)x 1=53,x 2=-21;(8)x 1=8,x 2=-2. 4.(1)x 1=1,x 2=3;(2)x 1=18,x 2=-14;(3)x 1=253+,x 2=253-;(4)x 1=3,x 2=-1; (5)t 1=0,t 2=-23;(6)y 1=0,y 2=3;(7)x 1=0,x 2=22-3; (8)x 1=55,x 2=10;(9)x 1≈,x 2=-;(10)x 1=-1,x 2=-7. 5.(1)x 2-4ax +4a 2=a 2-2a +1,(x -2a )2=(a -1)2,∴x -2a =±(a -1),∴x 1=3a -1,x 2=a +1.(2)x 2+(5-2k )x +k 2-5k -6=0,x 2+(5-2k )x +(k +1)(k -6)=0,[x -(k +1)][x -(k -6)]=0,∴x 1=k +1,x 2=(k -6).(3)x 2-2mx +m 2=9m 2,(x -m )2=(3m )2∴x 1=4m ,x 2=-2m(4)x 2+(2m +1)x +m (m +1)=0,(x +m )[x +(m +1)]=0,∴x 1=-m ,x 2=-m -16.(x +4y )(x -y )=0,x =-4y 或x =y当x =-4y 时,y x y x +-=3544=+---y y y y ; 当x =y 时,y x y x +-=yy y y +-=0. 7.(x 2+y 2)(x 2+y 2-1)-12=0,(x 2+y 2)2-(x 2+y 2)-12=0,(x 2+y 2-4)(x 2+y 2+3)=0,∴x 2+y 2=4或x 2+y 2=-3(舍去)8.x 1=-36,x 2=24 9.∵x 2+3x +5=9,∴x 2+3x =4,∴3x2+9x-2=3(x2+3x)-2=3×4-2=10 10.10=-5(t-2)(t+1),∴t=1(t=0舍去) 11.(1)x1=-2,x2=2(2)(x2-2)(x2-5)=0,(x+2)(x-2)(x+5)(x-5)=0。
九年级数学: 因式分解法解一元二次方程练习题及答案

因式分解法解一元二次方程练习题1.选择题(1)方程(x -16)(x +8)=0的根是( )A .x 1=-16,x 2=8B .x 1=16,x 2=-8C .x 1=16,x 2=8D .x 1=-16,x 2=-8(2)下列方程4x 2-3x -1=0,5x 2-7x +2=0,13x 2-15x +2=0中,有一个公共解是( )A .x =21 B .x =2 C .x =1 D .x =-1 (3)方程5x (x +3)=3(x +3)解为( )A .x 1=53,x 2=3B .x =53C .x 1=-53,x 2=-3D .x 1=53,x 2=-3 (4)方程(y -5)(y +2)=1的根为( )A .y 1=5,y 2=-2B .y =5C .y =-2D .以上答案都不对(5)方程(x -1)2-4(x +2)2=0的根为( )A .x 1=1,x 2=-5B .x 1=-1,x 2=-5C .x 1=1,x 2=5D .x 1=-1,x 2=5(6)一元二次方程x 2+5x =0的较大的一个根设为m ,x 2-3x +2=0较小的根设为n ,则m +n 的值为( ) A .1 B .2 C .-4 D .4(7)已知三角形两边长为4和7,第三边的长是方程x 2-16x +55=0的一个根,则第三边长是( )A .5B .5或11C .6D .112.填空题(1)方程t (t +3)=28的解为_______.(2)方程(2x +1)2+3(2x +1)=0的解为__________.(3)方程(2y +1)2+3(2y +1)+2=0的解为__________.(4)关于x 的方程x 2+(m +n )x +mn =0的解为__________.(5)方程x (x -5)=5 -x 的解为__________.3.用因式分解法解下列方程:(1)x 2+12x =0; (2)4x 2-1=0; (3) x 2=7x ;(4)x 2-4x -21=0; (5)(x -1)(x +3)=12; (6)3x 2+2x -1=0;(7)10x 2-x -3=0; (8)(x -1)2-4(x -1)-21=0.4.用适当方法解下列方程:(1)x 2-4x +3=0; (2)(x -2)2=256; (3)x 2-3x +1=0;(4)x 2-2x -3=0; (5)(2t +3)2=3(2t +3); (6)(3-y )2+y 2=9;(7)2x2-8x=7; (8)(x+5)2-2(x+5)-8=0.5.解关于x的方程:(1)x2-4ax+3a2=1-2a; (2)x2+5x+k2=2kx+5k+6;(3)x2-2mx-8m2=0; (4)x2+(2m+1)x+m2+m=0.6.已知(x2+y2)(x2-1+y2)-12=0.求x2+y2的值.7.解方程:x(x+12)=864.8.已知x2+3x+5的值为9,试求3x2+9x-2的值.9.一跳水运动员从10米高台上跳水,他跳下的高度h(单位:米)与所用的时间t(单位:秒)的关系式h =-5(t-2)(t+1).求运动员起跳到入水所用的时间.10.解方程(x2-1)2-5(x2-1)+4=0 x4-3x2-4=0.。
因式分解法解一元二次方程

2x 32x Βιβλιοθήκη 0猜一猜方程的根2x 32x 3 0
4x2 9
用因式分解法解下列方程:
x2 3x
x2 2 2x 2
3x 42 4x 32
x 53x 2 10
1、由4x 32 3xx 3 0,得:x 3__x____1__2___ 0 2、由x2 9 6x,得:__x____3__2 0 3、由7x 12 4x2,得:__9_x____1____5__x____1___ 0 4、由x 12 x 1 0,得:x 1___x____2____ 0
1、关于x的一元二次方程 x2 5x p2 2 p 5 0
的一个根为x=1,则实数p的值是( ) A. 4 B. 0或2 C. 1 D. —1
2、若代数式 2x x 1 与 3(x 1) 的值
互为相反数,则x的值为( )
A. 1或- 3 B. 1或- 2 C. —1或 2 D. 1或 3
D. 由 x 32 x 3 0,得 x 3 x 4 0
用因式分解法解下列方程:
x2 3x
x2 2 2x 2
3x 42 4x 32
x 53x 2 10
若代数式 2x x 1 与 3(x 1) 的值互为
相反数,则x的值为( )
A. 1或- 3 2
若代数式 值应为(
B. 1或- 2 C. —1或 2 D. 1或 3
3
3
2
x 2 x 1
x 1
的值为零,则x的取
)
A. x=2或x=1 C. x=2
B. x=2 且 x=1 D. x=1
2
3
3
2
已知一元二次方程(x-a)(2x-3)=6的一个根是 x=0,求a的值及方程的另一个根。
因式分解法解一元二次方程练习题及答案

因式分解法解一元二次方程练习题及答案一、选择题1.以下方程,适合用因式分解法解的是( )A.x2−4√2x+1=0B.2x²=x-3C.(x-2)²=3x-6D. x²-10x-9=02.方程3(x-3)²=2(x-3)的根是( )A. x=3B.x=113C.x1=3,x2=113D.x1=3,x2=233.以下一元二次方程最适合用因式分解法来解的是( )A.(x-2)(x+5)=2B.(x-2)²=x²-4C. x²+5x-2=0D.12(2-x)²=34.解方程7(8x+3)=6(8x+3)²的最正确方法应选择( )A.因式分解法B.直接开平方法C.配方法D.公式法5.如果(x-1)(x+2)=0,那么以下结论正确的选项是( )A. x=1或x=-2B.必须x=1C. x=2或x=-1D.必须 x=1且x=-2二、填空题1.方程x(x-2)=0的解为 .2.方程 (x-2)²=3(x-2) 的解是 .3.假设方程x²- x=0 的两根为 x₁, x₂(x₁<x₂), 则:X₂-x₁=4.假设x²-mx-15=(x+3)(x+n), 则1nᵐ的值为 .5. y=x²+x-6,当x= 时, y的值为0; 当x= 时, y的值等于24.参考答案:一、选择题1.答案为: C2.答案为: C3.答案为: B.4.答案为: A.5.答案为: A.二、填空题1.答案为: 0或2.2.答案为:x₁=2, x₂=5.3.答案为: 1.4.答案为: 25.5.答案为: -3或2, -6或5。
因式分解法解一元二次方程练习题

因式分解法解一元二次方程练习题编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(因式分解法解一元二次方程练习题)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为因式分解法解一元二次方程练习题的全部内容。
因式分解法解一元二次方程练习题 姓名:1.选择题(1)方程(x -16)(x +8)=0的根是( )A .x 1=-16,x 2=8B .x 1=16,x 2=-8C .x 1=16,x 2=8D .x 1=-16,x 2=-8(2)下列方程4x 2-3x -1=0,5x 2-7x +2=0,13x 2-15x +2=0中,有一个公共解是( )A .x =B .x =2C .x =1D .x =-1 (3)方程5x (x +3)=3(x +3)解为( )A .x 1=,x 2=3B .x =C .x 1=-,x 2=-3D .x 1=,x 2=-3(4)方程(y -5)(y +2)=1的根为( )A .y 1=5,y 2=-2B .y =5C .y =-2D .以上答案都不对(5)方程(x -1)2-4(x +2)2=0的根为( )A .x 1=1,x 2=-5B .x 1=-1,x 2=-5C .x 1=1,x 2=5D .x 1=-1,x 2=5(6)一元二次方程x 2+5x =0的较大的一个根设为m ,x 2-3x +2=0较小的根设为n ,则m +n的值为( )A .1B .2C .-4D .4(7)已知三角形两边长为4和7,第三边的长是方程x 2-16x +55=0的一个根,则第三边长是( )A .5B .5或11C .6D .11(8)方程x 2-3|x -1|=1的不同解的个数是( )A .0B .1C .2D .32.填空题(1)方程t (t +3)=28的解为_______.(2)方程(2x +1)2+3(2x +1)=0的解为__________.(3)方程(2y +1)2+3(2y +1)+2=0的解为__________.(4)关于x 的方程x 2+(m +n )x +mn =0的解为__________.(5)方程x (x -)= -x 的解为__________.3.用因式分解法解下列方程:(1)x 2+12x =0; (2)4x 2-1=0; (3) x 2=7x ; (4)x 2-4x -21=0;(5)(x -1)(x +3)=12;(6)3x 2+2x -1=0;(7)10x 2-x -3=0; (8)(x-1)2-4(x -1)-21=0.4.用适当方法解下列方程:(1)x 2-4x +3=0; (2)(x -2)2=256;(3)x 2-3x +1=0; (4)x 2-2x -3=0;215353535355(5)(2t +3)2=3(2t +3); (6)(3-y )2+y 2=9;(7)(1+)x 2-(1-)x =0; (8)x 2-(5+1)x +=0;(9)2x 2-8x =7; (10)(x +5)2-2(x +5)-8=0.5.解关于x 的方程:(1)x 2-4ax +3a 2=1-2a ; (2)x 2+5x +k 2=2kx +5k +6;(3)x 2-2mx -8m 2=0; (4)x 2+(2m +1)x +m 2+m =0.6.已知x 2+3xy -4y 2=0(y ≠0),试求的值.7.已知(x 2+y 2)(x 2-1+y 2)-12=0.求x 2+y 2的值.8.请你用三种方法解方程:x (x +12)=864.9.已知x 2+3x +5的值为9,试求3x 2+9x -2的值.10.一跳水运动员从10米高台上跳水,他跳下的高度h (单位:米)与所用的时间t (单位:秒)的关系式h =-5(t -2)(t +1).求运动员起跳到入水所用的时间.11.为解方程(x 2-1)2-5(x 2-1)+4=0,我们可以将x 2-1视为一个整体,然后设x 2-1=y ,则y 2=(x 2-1)2,原方程化为y 2-5y +4=0,解此方程,得y 1=1,y 2=4.当y =1时,x 2-1=1,x 2=2,∴x =±.当y =4时,x 2-1=4,x 2=5,∴x =±.∴原方程的解为x 1=-,x 2=,x 3=-,x 4=.以上方法就叫换元法,达到了降次的目的,体现了转化的思想.(1)运用上述方法解方程:x 4-3x 2-4=0.225210y x yx +-252255(2)既然可以将x2-1看作一个整体,你能直接运用因式分解法解这个方程吗?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
因式分解法解一元二次方程练习题姓
名:
欧阳光明(2021.03.07)
1.选择题
(1)方程(x -16)(x +8)=0的根是( )
A .x1=-16,x2=8
B .x1=16,x2=-8
C .x1=16,x2=8
D .x1=-16,x2=-8
(2)下列方程4x2-3x -1=0,5x2-7x +2=0,13x2-15x +2=0中,有一个公共解是( )
A .x =21
B .x =2
C .x =1
D .x =-1
(3)方程5x(x +3)=3(x +3)解为( )
A .x1=5
3,x2=3 B .x =53 C .x1=-53,x2=-3
D .x1=53,x2=-3 (4)方程(y -5)(y +2)=1的根为( )
A .y1=5,y2=-2
B .y =5
C .y =-2
D .以上答案都不对
(5)方程(x -1)2-4(x +2)2=0的根为( )
A .x1=1,x2=-5
B .x1=-1,x2=-5
C .x1=1,x2=5
D .x1=-1,x2=5
(6)一元二次方程x2+5x =0的较大的一个根设为m ,x2-3x +2=0较小的根设为n ,则m +n 的值为( )
A.1 B.2 C.-4 D.4
(7)已知三角形两边长为4和7,第三边的长是方程x2-16x+55=0的一个根,则第三边长是( )
A.5 B.5或11 C.6 D.11 (8)方程x2-3|x-1|=1的不同解的个数是( )
A.0 B.1 C.2 D.3
2.填空题
(1)方程t(t+3)=28的解为_______.
(2)方程(2x+1)2+3(2x+1)=0的解为__________.
(3)方程(2y+1)2+3(2y+1)+2=0的解为__________.
(4)关于x的方程x2+(m+n)x+mn=0的解为__________.
(5)方程x(x-5)=5-x的解为__________.
3.用因式分解法解下列方程:
(1)x2+12x=0;(2)4x2-1=0;(3)x2=7x;
(4)x2-4x-21=0;
(5)(x-1)(x+3)=12;(6)3x2+2x-1=0;(7)10x2-x-3=0;
(8)(x-1)2-4(x-1)-21=0.
4.用适当方法解下列方程:
(1)x2-4x+3=0;(2)(x-2)2=256;(3)x2-3x+1=0;
(4)x2-2x-3=0;
(5)(2t+3)2=3(2t+3);(6)(3-y)2+y2=9;
(7)(1+2)x2-(1-2)x=0;(8)5x2-(52+1)x+10=0;
(9)2x2-8x=7;(10)(x+5)2-2(x+5)-8=0.
5.解关于x 的方程:
(1)x2-4ax +3a2=1-2a ; (2)x2+5x +k2=2kx +5k +6;
(3)x2-2mx -8m2=0; (4)x2+(2m +1)x +m2+m =0.
6.已知x2+3xy -4y2=0(y≠0),试求y
x y x +-的值. 7.已知(x2+y2)(x2-1+y2)-12=0.求x2+y2的值.
8.请你用三种方法解方程:x(x +12)=864.
9.已知x2+3x +5的值为9,试求3x2+9x -2的值.
10.一跳水运动员从10米高台上跳水,他跳下的高度h(单位:米)与所用的时间t(单位:秒)的关系式h =-5(t -2)(t +1).求运动员起跳到入水所用的时间.
11.为解方程(x2-1)2-5(x2-1)+4=0,我们可以将x2-1视为一个整体,然后设x2-1=y ,则y2=(x2-1)2,原方程化为y2-5y +4=0,解此方程,得y1=1,y2=4.
当y =1时,x2-1=1,x2=2,∴x =±2.
当y =4时,x2-1=4,x2=5,∴x =±5.
∴原方程的解为x1=-2,x2=2,x3=-5,x4=5. 以上方法就叫换元法,达到了降次的目的,体现了转化的思想.
(1)运用上述方法解方程:x4-3x2-4=0.
(2)既然可以将x2-1看作一个整体,你能直接运用因式分解法解这个方程吗?。
