结构力学等效结点荷载 ppt课件
合集下载
结构力学基础讲义PPT(共270页,图文)

alMM
B bM l
a l
b M
l
17
2. 多跨静定梁: 关键在于正确区分基本部分和附
属部分,熟练掌握截面法求控制截面 弯矩,熟练掌握区段叠加法作单跨梁 内力图。
多跨静定梁——由若干根梁用铰相连, 并用若干支座与基础相连而组成的静 定结构。
17:11
18
附属部分--依赖基本 部分的存在才维持几 何不变的部分。
17:11
24
3. 静定平面刚架 (1) 求反力。
切断C铰,考虑右边平衡,再分析左 边部分。求得反力如图所示:
C
17:11
25
3. 静定平面刚架
(2)作M图 (3)做Q、N图 (4) 校核
17:11M图
N图
Q图
26
§1-4 静定桁架
17:11
27
§1-4 静定桁架
* 桁架的定义:
——由若干个以铰(Pins)结点连接而成的 结构,外部荷载只作用在结点上。
对只有轴力的结构(桁架):
1组7:1合1 结构则应分别对待。
61
§1-5静定结构位移计算
3. 荷载作用下的位移计算
例:求△cy 1. 建立力状态,在C点加单位 EI
竖向力。
2. 建立各杆内力方程:
EI
3. 求位移:
17:11
62
§1-5静定结构位移计算
3. 荷载作用下的位移计算
积分注意事项:
⒈ 逐段、逐杆积分。 ⒉ 两状态中内力函数服从同一坐标系。 ⒊ 弯矩的符号法则两状态一致。
2. 三铰拱的数解法
* 内力计算: ⑴任一截面K(位置):KK截 截面 面形 形心 心处 坐拱 标X轴K切、线YK的倾角 K
结构力学(全套课件131P) ppt课件
的两根链杆的杆轴可以平行、交叉,或延长线交于
一点。
当两个刚片是由有交汇点的虚铰相连时,两个刚
片绕该交点(瞬时中心,简称瞬心)作相对转动。
从微小运动角度考虑,虚铰的作用相当于在瞬时
中心的一个实铰的作用。
19
20
规则二 (三刚片规则): 三个刚片用不全在一条直线上的三个单铰(可以
是虚铰)两两相连,组成无多余约束的几何不变体 系。
两个平行链杆构成沿平行方向上的无穷远虚铰。
三个刚片由三个单铰两两相连,若三个铰都有交 点,容易由三个铰的位置得出体系几何组成的结论 。当三个单铰中有或者全部为无穷远虚铰时,可由 分析得出以下依据和结论:
1、当有一个无穷远虚铰时,若另两个铰心的连 线与该无穷远虚铰方向不平行,体系几何不变;若 平行,体系瞬变。
3、通过依次从外部拆除二元体或从内部(基础、 基本三角形)加二元体的方法,简化体系后再作分 析。
41
第一部分 静定结构内力计算
静定结构的特性: 1、几何组成特性 2、静力特性 静定结构的内力计算依据静力平衡原理。
第三章 静定梁和静定刚架
§3-1 单 跨 静 定 梁
单跨静定梁的类型:简支梁、伸臂梁、悬臂梁 一、截面法求某一指定截面的内力
15
1、单约束(见图2-2-2) 连接两个物体(刚片或点)的约束叫单约束。
1)单链杆(链杆)(上图) 一根单链杆或一个可动铰(一根支座链杆)具
有1个约束。 2)单铰(下图)
一个单铰或一个固定铰支座(两个支座链杆) 具有两个约束。 3)单刚结点
一个单刚结点或一个固定支座具有3个约束。
16
2、复约束 连接3个(含3个)以上物体的约束叫复约束。
三、对体系作几何组成分析的一般途径
结构力学ppt课件

结构力学ppt课件
目录
• 结构力学简介 • 结构力学的基本原理 • 结构分析的方法 • 结构力学的应用 • 结构力学的挑战与未来发展 • 结构力学案例分析
01
结构力学简介
什么是结构力学
01
结构力学是研究工程结构在各种外力作用下产生的响
应的一门学科。
02
它主要涉及结构的强度、刚度和稳定性等方面的分析
04
有限元法
有限元法是一种将结构分解为有限个小 的单元,并对每个单元进行力学分析的 方法。
有限元法具有适用范围广、精度较高等 优点,但也存在计算量大、需要较强的 计算机能力等缺点。
通过对所有单元的力学行为进行组合, 可以得到结构的整体力学行为。
它适用于对复杂结构进行分析,例如板 壳结构、三维实体等。
结构力学的历史与发展
结构力学起源于19世纪中叶,随着土木工程和机械工程的发展而逐渐形成。
早期的结构力学主。
目前,结构力学已经广泛应用于各个工程领域,包括建筑、桥梁、机械、航空航天等。同时,结构力学 的研究也在不断深入和发展,以适应各种复杂工程结构的需要。
案例一:桥梁的力学分析
总结词
桥梁结构是力学分析的重要案例,涉及到多种力学因素,包括静载、动载、应 力、应变等。
详细描述
桥梁的力学分析需要考虑多种因素,包括桥梁的跨度、桥墩的支撑方式、桥梁 的材料性质等。在分析过程中,需要建立力学模型,进行静载和动载测试,并 运用结构力学的基本原理进行优化设计。
案例二:航空发动机的力学设计
强度理论
01
强度理论是研究结构在外力作用下达到破坏时的强度条件的科学。
02
强度理论的基本方程包括最大正应力理论、最大剪切应力理论、形状改变比能 理论和最大拉应力理论,用于描述结构在不同外力作用下达到破坏时的条件。
目录
• 结构力学简介 • 结构力学的基本原理 • 结构分析的方法 • 结构力学的应用 • 结构力学的挑战与未来发展 • 结构力学案例分析
01
结构力学简介
什么是结构力学
01
结构力学是研究工程结构在各种外力作用下产生的响
应的一门学科。
02
它主要涉及结构的强度、刚度和稳定性等方面的分析
04
有限元法
有限元法是一种将结构分解为有限个小 的单元,并对每个单元进行力学分析的 方法。
有限元法具有适用范围广、精度较高等 优点,但也存在计算量大、需要较强的 计算机能力等缺点。
通过对所有单元的力学行为进行组合, 可以得到结构的整体力学行为。
它适用于对复杂结构进行分析,例如板 壳结构、三维实体等。
结构力学的历史与发展
结构力学起源于19世纪中叶,随着土木工程和机械工程的发展而逐渐形成。
早期的结构力学主。
目前,结构力学已经广泛应用于各个工程领域,包括建筑、桥梁、机械、航空航天等。同时,结构力学 的研究也在不断深入和发展,以适应各种复杂工程结构的需要。
案例一:桥梁的力学分析
总结词
桥梁结构是力学分析的重要案例,涉及到多种力学因素,包括静载、动载、应 力、应变等。
详细描述
桥梁的力学分析需要考虑多种因素,包括桥梁的跨度、桥墩的支撑方式、桥梁 的材料性质等。在分析过程中,需要建立力学模型,进行静载和动载测试,并 运用结构力学的基本原理进行优化设计。
案例二:航空发动机的力学设计
强度理论
01
强度理论是研究结构在外力作用下达到破坏时的强度条件的科学。
02
强度理论的基本方程包括最大正应力理论、最大剪切应力理论、形状改变比能 理论和最大拉应力理论,用于描述结构在不同外力作用下达到破坏时的条件。
结构力学 PPT课件

总复习
1
NaA 2
1 1m×4=4m
解:取1-1以右为分离体 ∑Y=0 NC=-10kN 取2-2以右为分离体
O
∑Y=6+YB+YC=0
6kN
YB=0
∑MO=0 NA=0
a
2
6kN
8kN
6kN
总复习
第八章 静定结构影响线
一、影响线的定义:
定义:当单位荷载(P=1)在结构上移动时,表示结构某一指
定截面中某项内力变化规律的曲线,称为该项内力的影响线。
二、叠加法绘制弯矩图
Q M AB M BA Q0
AB
l
AB
•首先求出两杆端弯矩,连一虚线, •然后以该虚线为基线, •叠加上简支梁在跨间荷载作用下的弯矩图。
三、内力图形状特征 1、在自由端、铰支座、铰结点处,无集中力偶作用,截
面弯矩等于零,有集中力偶作用,截面弯矩等于集中力偶的值。
总复习
M M 0 Hy
Q Q0 cos H sin N Q0 sin H cos
2、在拱的左半跨取正右半跨取负;
3、仍有 Q=dM/ds 即剪力等零处弯矩达极值;
4、 M、Q、N图均不再为直线。
5、集中力作用处Q图将发生突变。
6、集中力偶作用处M图将发生突变。
四、三铰拱的合理轴线 在给定荷载作用下使拱内各截面弯矩
2、刚结点上各杆端弯矩及集中力偶应满足结点的力矩平 衡。两杆相交刚结点无m作用时,两杆端弯矩等值,同侧受拉。
3、具有定向连结的杆端剪力等于零,如无横向荷载作用, 该端弯矩为零。
4.无何载区段 5.均布荷载区段 6.集中力作用处 7.集中力偶作用处
平行轴线
Q图
结构力学-课件

6.6 对称结构
7.渐进法
8.设计实例简单分析
1.虚功原理
2.影响线:
2.1 静力法做影响线
2.2 机动法做影响线
2.3 影响线的应用
3.简支梁的包络图和绝对最大弯矩
4.应用虚力原理求刚体体系的位移
4.1 概念介绍
4.2 荷载作用下的位移计算举例
4.3 图乘法
5.力法求解超静定结构
5.1 超静定结构的组成和超静定次数
5.2 力法的基本思路
5.3 对称结构
5.4 支座移动时的位移计算:
6.位移法求解超静定结构
6.1 基本概念
6.2 等ห้องสมุดไป่ตู้面杆件的刚度方程(形常数、载常数)
6.3 无侧移刚架的计算
6.4.有侧移刚架的计算
6.5 位移法的基本体系
【经典】结构力学ppt课件

§2-3 几何不变体系的基本组成规则
二元体:两根不在一直线上的链杆连接成一个新结点的构 造称为二元体。
二元体规则 在一个体系上增加或拆除二元体,不会改变原有体系的几何构造性质。
铰结点
链杆
链杆 体系
§2-3 几何不变体系的基本组成规则
分析图示铰结体系
以铰结三角形123为基础,增加一个二元体得结点4, 1234为几何不变体系;如此依次增加二元体,最后的体系为几何不变体系,没 有多余联系。
瞬变体系
可变体系
瞬变体系
§2-7 几何构造与静定性的关系
体系
几何不变体系 (形状、位置不变)
几何可变体系 (形状、位置可变)
无多余联系 有多余联系
可变体系 瞬变体系
静定结构 超静定结构
§2-7 几何构造与静定性的关系 分析图a所示体系
分析图b所示体系
无多余联系的几何不变体系 由平衡方程→三个支反力 →截面内力→静定结构 有多余联系的几何不变体系 由平衡方程不能求全部反力
§2-1 概述
一般结构必须是 几何不变体系
几何不变体系—在不考虑材料应变的条件下,体系的位置 和形状是不能改变的。(图a)
几何可变体系—在不考虑材料应变的条件下,体系的位置和 形状是可以改变的。(图b)
§2-2 平面体系的计算自由度 自由度:确定体系位置所需的独立坐标数
一个点的自由度=2
一个刚片的自由度=2
第一章 绪论
§1-1 结构力学的研究对象和任务 §1-2 荷载的分类 §1-3 结构的计算简图 §1-4 支座和结点的类型 §1-5 结构的分类
§1-1 结构力学的研究对象和任务
结构:工程中担负预定任务、支承荷载的建筑物。 如:房屋、塔架、桥梁、隧道、挡土墙、水坝等。
结构力学课件等效结点荷载

F
F
(1)
ql 2 12
F F
F 5 F 6
FPl
FP 2
8
0
ql
2
ql 2
12
0
(2)
FP
2
FPl
F
F
(2)
8
0
FP
2 FPl
8
0
局部坐标系下单元等效结点荷载:
e
Fe
FE F
整体坐标系下单元等效结点荷载:
FEe
T T
1(1,2,3)
5(11,12,13)
总码
0
0
1
4
FP
FP
2
5
2 2
FE (3) T T
F
F
(3)
FPl 8
FPl 8
3
6
0 0 4 7
FP
2 FPl
8
8 9
总码
ql
2
1
4
0
2
5
FE (1)
ql 2 12
0
FP
FPl 2 8
0
FPl
FP 2
8
0
局部坐标系下单元固端力列阵
2(4,5,6) FP
② 3(7,8,9) q①
1(1,2,3)
ql 2 0
12
ql 2
ql
ql 2
2
12 0
FP
FPl 2 8
0
F
F 1 F
e
F 2
F
F
e
F
F 3 F
F 4
(1)
0
ql
2
0
结构力学力法PPT_图文

q EI 1次超静定
一个无铰封闭圈有三个多余联系
q
q
q
q
第8章
2、去掉多余联系的方法
(1)去掉支座的一根支杆或切断一根链杆相当于去掉一个联系。 (2)去掉一个铰支座或一个简单铰相当于去掉两个联系。 (3)去掉一个固定支座或将刚性联结切断相当于去掉三个联系。 (4)将固定支座改为铰支座或将刚性联结改为铰联结相当于 去掉一个联系。
1、解题思路
q
2
1
l
原结构
q
x1 基本结构
位移条件: 1P+ 11=0 因为 11= 11X1 ( 右下图) 所以 11X1 +1P =0 X1= -1P/ 11
q 1P
11 x1
11 x1=1
第8章
2、解题步骤
(1)选取力法基本结构; (2)列力法基本方程; (3)绘单位弯矩图、荷载弯矩图; (4)求力法方程各系数,解力法方程; (5)绘内力图。
X1
X2
基本结构(1)
第8章
对应不同的基本结构有不同的力法方程:
A
B
C
D
C1
C2
l A X1
l
l
原结构
B
C
D
C1
C2
X2
解:力法方程:
基本结构(2)
第8章
对应不同的基本结构有不同的力法方程:
A
B
C
D
C1
C2
l
l
原结构
A
B
C
l D
C1
X1
X2
解:力法方程:
基本结构(3)
第8章
四、如何求
A
以基本结构(2)为例:
一个无铰封闭圈有三个多余联系
q
q
q
q
第8章
2、去掉多余联系的方法
(1)去掉支座的一根支杆或切断一根链杆相当于去掉一个联系。 (2)去掉一个铰支座或一个简单铰相当于去掉两个联系。 (3)去掉一个固定支座或将刚性联结切断相当于去掉三个联系。 (4)将固定支座改为铰支座或将刚性联结改为铰联结相当于 去掉一个联系。
1、解题思路
q
2
1
l
原结构
q
x1 基本结构
位移条件: 1P+ 11=0 因为 11= 11X1 ( 右下图) 所以 11X1 +1P =0 X1= -1P/ 11
q 1P
11 x1
11 x1=1
第8章
2、解题步骤
(1)选取力法基本结构; (2)列力法基本方程; (3)绘单位弯矩图、荷载弯矩图; (4)求力法方程各系数,解力法方程; (5)绘内力图。
X1
X2
基本结构(1)
第8章
对应不同的基本结构有不同的力法方程:
A
B
C
D
C1
C2
l A X1
l
l
原结构
B
C
D
C1
C2
X2
解:力法方程:
基本结构(2)
第8章
对应不同的基本结构有不同的力法方程:
A
B
C
D
C1
C2
l
l
原结构
A
B
C
l D
C1
X1
X2
解:力法方程:
基本结构(3)
第8章
四、如何求
A
以基本结构(2)为例:
计算结构力学课件

K12 K12
(L,K)
→表达叠加到 构造刚阵中去
首页 上页 下页 返回
由此可看出:由MW旳并积形成下标 矩阵,完全确立了单刚[k]中旳元素在总刚 [K]中位置,从而由数学旳角度阐明了用 MW装配[K]旳过程。
上述过程旳FORTRAN程序模块可写成: L=MW(I) K=MW(J) ZK(L,K)=ZK(L,K)+DK(I,J)
首页 上页 下页 返回
5-3 按单元定位向量装 配构造刚度矩阵
•MW是按单元结点编号顺序由结点旳构造未知量编 号顺序所构成旳向量(列阵)。
•MW处理了约束,以及主从关系,无效未知量等 特殊结点信息,也是[C]矩阵旳实用(增广)写法。
•单元定位向量可以便地指出单元旳各个未知量在构 造总体未知量中旳相应位置(总体序号)。 •由此也就能够拟定单元刚度矩阵中旳元素在构造刚 阵中旳位置。
12 3
0 0 1
首页 上页 下页 返回
由此可得到各单元旳[C],如对第③ 单元,可写出:
1 u1
0
0
{ }③
[C]③{}
12
u11
0 0
3 2
首页 上页 下页 返回
1 MW (i) j
Cij 0 MW (i) j
(10)
(i 1,2,...NF, j 1,2,...N )
数据文件名为
KJE.DAT
首页 上页 下页 返回
READ( 1,*) NE, NJ,NJT,NAI
READ( 1,* ) ( (JH( I,J ),I = 1.2),J =1,NE )
READ( 1,* ) ((JTX( IJ),i=1,4),J=1,NJT)
READ( 1,* ) (JMH(I),I= 1,NT)
平面单元等效结点荷载计算ppt课件
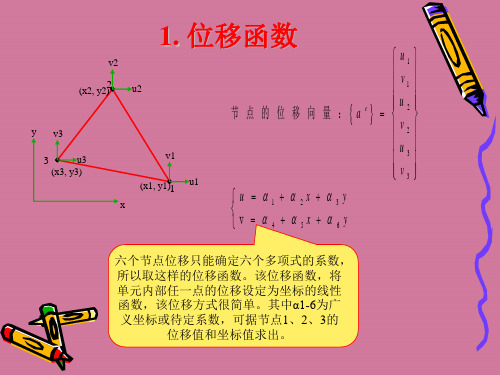
1 0 0 0 0 0
1 0 0 0 0
对称
*
*
*
0
* * 0
6
*
0
1
4. 边境条件的处置
3〕大数法〔适宜于计 k11
k1i
k1n a1 P1
算机处置〕 α>>1
ki1
kii
kin
ai
kiib
kn1
kni
knn an Pn
第i行展开之后:
ki1a1 kiiai kinan kiib 两边同除以:
4. 边境条件的处置
1〕直接带入法〔降阶法〕
ab为已知位移组成的列向量,Pb为对应的支座反力
KKbaaa
Kab Kbb
aaba
Pa Pb
KaaaaPaKabab
求得aa之后可按下式求得支座反力:
Pb Kba aaKbb ab
改动了原方程 的顺序,只适 用于一些简单
的问题
4. 边境条件的处置
2. N1 N 2 N 3 1
N I N 1 I N 2 I N 3
3.
N
的
i
阶
数
与
假
设
的
N
:插
i
值
函
数
(
形
状
函
数
)
位移函数阶数相同
u1
v1
0
N3
u v
2 2
N
ae
u
3
v 3
I为 二 阶 单 位 矩 阵
4. 数 值 在 0- 1之 间
1. 位移函数-例题
1. 位移函数
v2
(x2, y2)2 u2
结构力学Ⅱ课件:荷载及内力计算

T
0
T
1
§9.6 非结点荷载处理
q
荷载
非结点荷载
结点力、力矩
单元内分布力
集中力
温度作用
惯性力等
荷载向量
P =PD+PE
2
3
1
4
P
l
直接结点荷载PD
非结点荷载的等
效结点荷载PE
非结点荷载: 等效移置到结点上。
结构力学II
2
h/2
结点荷载
h/2
Q
q
ql
12
Q
2
2
h/2
3
2
P
q
2
ql
2
θ
1
h/2
y
4
构的结点位移向量: EI1 30.82 1.40 1.53 12.73 16.58T
30.82
E
解:因为杆件只考虑弯曲变形,包括
杆端结点的侧移和转角位移,对应的
内力为杆端剪力和弯矩,根据内力,
单元的刚度方程取四阶。
y
EI1 30.82
16.58
E
1.4
E
④ 1.53
①
ഥ ——单元坐标描述
ഥ
ത =
4. 如果梁单元内有非结点荷载,则要叠加非结点荷载引起的
固端力,得到真正的杆端内力:
F ( e ) K ( e ) ( e ) Fg ( e ) ——单元坐标描述
✓ 此时可以根据杆端内力确定单元刚度方程的阶数。
结构力学II
13
例25:计算图示结构的内力。 忽略轴向变形,已知求得结
EI
⑤
③
单
元
信
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
q
2(1,2,3)
3(4,5,6) 2(4,5,6)
3(7,8,9)
E
F
F2 F2
结构力学等效结点荷载
内 力 相 等
结点位 移等效
4
2. 等效结点荷载的计算
2(4,5,6) FP
FPl ql 2 8 12
q
② 3(7,8,9)
①
=
ql 2
ql 2
1(1,2,3)
12
ql
2
FPl
FPl
2 FPl 2
8
+ 没有结 0
点位移
0
ql 2
0
12
ql
2
ql
ql 2
结点荷载作用下求得的即是杆端
的实际位移。
E
F
F1 F1
(C)
E
F
有非结点荷载作用的单元杆
F2 F2 端力,可以由两部分叠加而得,
一部分是单元固端力,另一部分
结构力学等效结是点杆荷载端位移产生的杆端力。 16
练习:用先处理法、后处理法分别计算结构的 综合结点荷载列阵。
M=FPl FP
FP=ql C
D
F
0
F
2
F3 F4 F5
FR1x
F
R1
y
0
FR
2
y
F1
y
F2 F2
x y
Байду номын сангаас
F3
x
F
R1
y
=
F
R
2
F2 x y F3 x
F1 y F2 y
F6
0
F3
y
F3 y
F7 0 F4 x F4 x
F8
F 2
F
F
e
F
F 3 F
F 4
F
F
F 5 F 6
(1 )
0
ql
2
F
F
(1 )
ql 2
12
0
ql 2
ql 2
12
(2 )
0
F P
2
Fl P
F ( 2 )
F
8
0
F P
2 F
P
l
8
结构力学等效结点荷载
6
局部坐标系下单元等效结点荷载:
F4 y F4 y
在后处理法中,结构的结点荷载列阵等于综合结点荷载列阵
与结构约束反力列阵之和。
结构力学等效结点荷载
15
※结构在实际荷载作用下的单元杆端力
M (A)
q
e
Fe
ee
FF k
+=
F
F 1
M
(B)
对计算杆端位移而言,等效
q
F
F 2
结点荷载与原非结点荷载作用效 果等效,由此可以断定,在综合
e
Fe
FE F
整体坐标系下单元等效结点荷载:
F E e T T F E e T T F F e
结构力学等效结点荷载
7
总码
0 1 0
0
ql
ql
2
0
4 5
1 0
FE
(1)
T T
F
F
(1)
0
0
0 1
0
0
1
2
0
ql2 12 0
ql2
12 ql
FP 2
FPl
8
8 9
结构力学等效结点荷载
9
总码
总码
ql
2
4
0 5
ql 2
F E ( 1 )
12 ql
6 1
2
0
2
ql 12
2
3
0
4
FP
5
2
F E ( 2 )
F Pl
8
0
6 7
FP 2
F Pl
8 9
8
结构力学等效结点荷载
总码
ql 2
6 1
0
1 0 0 2
0
0
1
ql 2
ql2
12
0
ql2 12
2 3
结构力学等效结点荷载
8
总码
0
0
4
FP
FP
5
2 2
F E (2 ) T T
F
F
(2)
FPl 8
FPl
8
6
0 0 7
FP
2 F
P
l
8
F E e T T F E e T T F F e
结构力学等效结点荷载
11
总码
总码
总码
ql
2(2,3,4) FP
② 3(0,0,0)
q①
F E ( 1 )
1(0,0,1)
2
0
ql 2
12 ql
2
0
ql 12
2
2 3 4
0 F E (2)
0 1
0
FP
2
F Pl
8
0
FP 2
F Pl
8
2 3 4 0 0 0
ql 2 12 ql
1 2
F E
2 FP
3
2
ql 2 12
FP 8
l
4
结构力学等效结点荷载
12
3. 综合(自由)结点荷载列阵
F F D F E
综合结点 荷载列阵
直接结点 荷载列阵
等效结点 荷载列阵
1
0
2
ql 2
3
12
ql 2
4
F E
FP 2
5
ql
12
2
F Pl
8
0
6 7
FP 2
F Pl
8 9
8
10
2(4,5,6) FP ② 3(7,8,9)
q①
1(1,2,3)
2(2,3,4) FP ② 3(0,0,0)
q①
1(0,0,1)
e
Fe
FE F
2
0 12
结构力学等效结点荷载
ql 2 FPl 12 8
ql 2 ql 2
FPl 2
FPl
FPl 2
8
只有结 0 点位移
ql 2 12
0
FPl
FPl 2 8
0
FPl
FPl 2
8
05
局部坐标系下单元固端力列阵
2(4,5,6) FP ② 3(7,8,9)
q①
1(1,2,3)
F
F 1 F
e
F
4
F
4
x
F 5 F 4 y
在先处理法中,结构的结点荷载列阵等于综合结点荷载列阵。
结构力学等效结点荷载
14
F3y
F4y
3(5,6) 4(7,8)
F3x
⑥
F1y② ③
⑤F4x ④ F2y
F1x ①
F2x
FR1x 1(1,2) FR1y
2(3,4) FR2y
F1
F1x FR1x F1x
第九章 矩阵位移法
9.4 等效结点荷载
结构力学等效结点荷载
1
非结点荷载的处理
有限元分析的重要一步是把一个连续的结构看成是 由离散单元在结点处连接拼装而成。而把作用在结构上 的荷载统统考虑作用在结点上。然而无论是恒载还是活 载,常常是分布作用在单元上。
对这种非结点荷载的处理: 方法一:把分布荷载改用若干集中荷载代替,并把集 中荷载的作用点选作结点; 方法二:等效结点荷载法。
在矩阵位移法分析过程中,可用综合结点荷载来 代替原来荷载进行计算。
结构力学等效结点荷载
13
F3y
F4y
3(2,3) 4(4,5)
F3x
⑥
F1y② ③
⑤F4x ④ F2y
F1x ①
F2x
FR1x 1(0,0) FR1y
2(1,0) FR2y
F1 F2x
F
F F
2 3
F3x F3y
结构力学等效结点荷载
2
1. 等效结点荷载的概念
荷载等效的原则是不改变结构的结点位移情况, 即结构在等效结点荷载作用下的结点位移与实际荷载 作用下的结点位移相等。
M
q
结
点
E
F1
E
F2
位 移 等
效
结构力学等效结点荷载
3
1. 等效结点荷载的概念
M
q
(A)
F
F 1
M
(B)
q
F
F 2
+=
E
F
F1 F1
(C)
