磁学 第二章 原子的磁矩
磁学 第二章 原子的磁矩

s
p
d
f
l=0
1
23
6s 5s
6p 5d
5p
4d
4p
3d
4f
4s
3p
3s
2p
2s
1s
spdfFra bibliotekl=0
1
23
6s 5s
6p 5d
5p
4d
4p
3d
4f
4s
3p
3s
2p
2s
1s
为什么电子先占4s,再占3d ?
如果轨道的电荷分布偏离球对称,玻尔轨道的形状发生变化。 如图3s轨道是椭圆形的,一部分轨道离核近,s电子的原子波函数在核 附近非常大。S电子与核的库仑相互作用(相互吸引,能量低),使电子 先占4s轨道,后占3d轨道。同样5S电子先于4f电子占据轨道。
L l(l 1)h l 1, 2,3,,n 角量子数 Lz mlh ml 0, 1, 2,, l 轨道磁量子数
S s(s 1)h s 1 自旋量子数 2
Sz msh
1 ms 2
自旋磁量子数
“轨道”
用波函数描述 nlm Rnl (r)Ylm ( ,)
Rnl (r)决定电子离开核距离分布
-3
d电子轨道取向量子数,ml 2,1,0, 1, 2
f电子轨道取向量子数,m l
3, 2,1,0, 1, 2, 3
ml =0 -1 -2
1 2
Mn3的d轨道有4个电子 总轨道角动量L=2+1+0+(-1)=2 Co2的d轨道有7个电子 总轨道角动量L=2+1=(3 其余5个的总L=0) Nd 3(4f4 6s2,f轨道有3个电子) 总轨道角动量L 3 2 1 6
d
第二章 第二节 原子磁矩

PJ H mJ
总磁量子数:mJ = J, J-1, …… -J共2J+1个可能值
按原子矢量模型,角动量PL与PS绕PJ 进动。故μL与μS也绕 PJ 进动。
第二节 原子磁矩
二、原子磁矩表达式的推导
μL与μS在垂直于PJ 方向的分量(μL)┴与(μS)┴在一个进动周期中平 均值为零。 ∴原子的有效磁矩等于μL与μS平行于PJ的分量和,即:
J gJ J J 1B
J 6.7B
如果已知原子基态光谱基项
L 2S 1 J
,则可以直接得到S、L、J
三个量子数,从而算出原子基态的磁矩。
第二节 原子磁矩 四、随堂练习 1、试计算自由原子Fe (3d6) 、Co (3d7) 、Ni (3d8) 、Gd (4f75d1) 、 Dy (4f10)等的基态具有的原子磁距μ各为多少?并写出基态光谱 基项。(课后习题1)当堂交作业
S1113
L 210 3
222 2
基态光谱基项的表示方法: 2S 1 LJ
J LS 3 2
轨道量 子数L
0
1
2
3
4
5
6
大写英 文字母
S
P
D
F
G
H
I
所以, Cr3+的基态光谱基项表示为:4 F3 2
第二节 原子磁矩
三、计算原子磁矩实例
2、Dy3+,4f9电子组态 f 电子,l = 3,磁量子数m = +3, +2, +1, 0, -1, -2, -3
2、原子磁矩μJ在磁场中的取向是量子化的 μJ 在H方向的分量为:
J
mJ
J J 1
gJ mJ B
J gJ J J 1B
原子的磁矩

●ms决定电子自旋角动量在磁场方向分量Msz的大 小: h 1
M s z ms 2 ms 2
e h s ge s( s 1) g e s( s 1) e 2me 2
s ge
z
ge=2.00232 称为电子自旋因子;电子自旋磁矩方向 与角动量正好相反,故加负号
2
2. 角量子数l:决定电子的原子轨道角动量的大小。
h 2 ˆ M l (l 1) 2
h h 2 M l (l 1) , M l (l 1) 2 2
2
2
l 0,1,2,, n - 1
原子的磁矩:
e h eh l (l 1) l (l 1) l (l 1) e 2me 2 4me
●
h 1 1 2 ˆ M 2[ (sin ) 2 ] 2 4 sin sin
2 2
h R R ˆ M [ (sin ) 2 ] 2 2 4 sin sin
2 2 2
h ( 1) 2 4
1 3 m j , , , j 2 2
ˆ E H n n n 1. 主量子数n:决定体系能量的高低。
解此方程得出的每一个n正好被体系的Hamilton算符 作用后都等于一个常数En乘以n,即, n代表的状态具 有能量En,这是解R方程对En的限制。 单电子原子的能级公式(选电子离核无穷远处的能量为 零):
2.2 量子数的物理意义
e Z Z En 2 2 2 13.6 2 (eV ) 8 0 h n n
4 2 2
n 1,2,3,
H原子基态能量E1=-13.6eV<0,仍有零点能, 如何理解? ●virial theorem(维里定理):对势能服 从rn规律的体系,其平均势能<V>与平均动能 <T>的关系为: <T>=n<V>/2. ●H原子势能服从r-1规律,所以<T>=-<V>/2 E1=-13.6eV=<T>+<V>=<V>/2, <V>=-27.2eV, <T>=-<V>/2=13.6eV,即为零点能。
原子`离子的磁矩(顺`抗磁)

率温度关系服从居里-外斯定律。
C
4. 在居里温度附近出现比热等性质的反常。
T Tp
5. 磁化强度M和磁场H之间不是单值函数,存在磁滞效应。
构成这类物质的原子也有一定的磁矩,但宏观表现却完 全不同于顺磁性,解释铁磁性的成因已成为对人类智力的最 大挑战,虽然经过近100年的努力已经有了比较成功的理论, 但仍有很多问题有待后人去解决。
在测量材料磁化曲线前可以通过交流退磁;形变退磁; 热退磁等方法,使材料达到退磁状态。
2.磁化曲线 反映材料特性的基本曲线,从中可以得到标
志材料的参量:饱和磁化强度Ms、起始磁化率a 和最大磁化率m
Ms
Ms可以理解为 该温度下的自
发磁化强度M0
顺磁性物质磁化曲线 抗磁性物质磁化曲线
铁磁体的磁化过程
就是亚铁磁性物质上世纪3040年代开始在此基础上人工合成了一些具有亚铁磁性的氧化物但其宏观磁性质和铁磁物质相似很长时间以来人们并未意识到它的特殊性1948neel在反铁磁理论的基础上创建了亚铁磁性理论后人们才认识到这类物质的特殊性在磁结构的本质上它和反铁磁物质相似但宏观表现上却更接近于铁磁物质
1.3 宏观物质的磁性
O2,有机物中的双自由基等
3. 铁磁性(Ferromagnetism)
这是人类最早发现并利用的强磁性,它的主要特征是:
1. >>0,磁化率数值很大, 100 105
2. 磁化率数值是温度和磁场的函数;
3. 存在磁性转变的特征温度——居里温度TC,温度低于居里 温度时呈铁磁性,高于居里温度时表现为顺磁性,其磁化
1.77 39.95 0.85
-28.0
3.09 83.80 1.03
-43
3.78 131.3 1.24
第二章 磁学性能 第一讲

U m B
磁场强度
根据产生磁场的方式,有两种表达式:
电流产生的磁场
一个每米有N匝线圈,通以电流强度为i (A)的无线 长螺线管轴线中央的磁场强度。
H Ni
( A/m)
磁铁在其周围产生的磁场
极强为m1的磁极,在距离 r 处产生的磁场强度是 单位极强 (m2=1wb) 在该处所受到的作用力 m1 F H k 2 ( A/m) m2 r
Ek K 0 K1 ( 2 2 2 2 2 2 ) K 2 2 2 2
(6.24)
K1、K2为晶体各向异性能常数。 铁在20℃时的值约为4.2×104J/m3,钴的值 为4.1×105J/m3,镍的值为-0.34×104J/m3。
磁性基本量总结
1.磁学基本量:
2.磁性参数与介电参数的比较
A/m
磁 感 应 强 度
特斯拉:T
1)H(A/m) ---E (V/m) : 导致极化的外部驱动力的量度; 2)B ( VS/m2) ----P (C/m2):材料对外部作用场的响应的量度; 3) X() ----------- Xe 无量纲,描述材料对外部作用场的响应; 4) μ0---------------ε0 建立材料的相应参数和尺度参比量
TN
T
四、铁磁性 (1)很容易被磁化到饱和(只 需要很小的磁场) (2) f > 0,且为101~106 (3)也存在一个临界温度TC
(4)M-H呈非线性关系
代表性物质:11种金属元素和 众多的化合物和合金
铁磁性
X>>1, 在较低的温度下,铁磁物质中相邻原子磁偶极矩之间的交 换作用,其强度可以克服热起伏的影响,结果没有外部磁场的作用下, 相邻的偶极子也彼此整齐的排列。 例:纯铁--- B0=10-6T时,其磁化强度M=104A/m FeSO4(顺磁性), B0=10-6T时,其磁化强度M=0.001A/m
原子磁矩的计算

原子磁矩的计算子磁矩(AtomicMagneticMoment),是物理学中非常重要的物理量,它反映了原子本身电子轨道中电子环境对原子空间结构的影响。
原子磁矩的大小取决于原子的结构,也是化学性质的重要参量,是探究物质结构、性质的重要物理量之一。
原子磁矩的计算是一个非常重要的物理学研究课题,它包括原子磁矩的理论计算、实验测量和数值模拟计算等,因此,原子磁矩的计算的方法也有很多种。
理论计算原子磁矩是一种比较常见的原子磁矩计算方法,它包括基于程序的理论计算和量子原子磁矩理论(QMOM)。
基于程序的理论计算是用特定的计算程序来去建模原子磁矩,然后使用可用于任何原子计算的计算机程序来计算原子磁矩。
量子原子磁矩理论(QMOM)则是基于量子力学的理论来计算原子磁矩,它需要简化的量子力学模型,以找到给定原子结构的原子磁矩。
实验测量原子磁矩是另一种常见的原子磁矩计算方法,它包括Boltzmann散射测量技术,Kohn-Sham自洽场理论测量,核磁共振(NMR)测量,物理质量测量,电子双重转动差测量等。
Boltzmann散射测量技术是一种直接测量原子磁矩的方法,它基于基态原子的Boltzmann 散射来获取原子磁矩,通过同步辐射照射原子并观察由此引起的散射的强度和其他特性来测量原子磁矩。
Kohn-Sham理论测量是一种利用基于电子云的自洽场理论来计算原子磁矩的方法,结合多态微观理论,能够比较准确地测量原子磁矩。
核磁共振(NMR)测量,是用核磁共振方法来直接测量原子磁矩的方法,它利用电子轨道及其相关能级变化,测量原子磁矩。
物理质量测量是一种比较简单的原子磁矩测量方法,它利用物理质量比(PMB)去测量原子磁矩。
最后,电子双重转动差测量也是一种常用的原子磁矩测量方法,它是利用电子轨道中双重转动差来测量原子磁矩的方法。
最后,数值模拟计算也是一种常用的原子磁矩计算方法,它是利用数值模拟技术来计算原子磁矩的方法。
数值模拟技术是一种利用数值模型来模拟物理和化学系统的技术,可以用来测量原子磁矩。
第二章原子的磁性及物质的顺磁性

06
应用领域及前景展望
Chapter
材料科学中应用
1 2
磁性材料
利用原子的磁性,可以设计和合成具有特定磁性 能的磁性材料,如永磁体、超导磁体等。
磁记录材料
利用物质的顺磁性,可以开发用于信息存储和读 取的磁记录材料,如硬盘、磁带等。
3
磁流体
通过控制磁性颗粒在液体中的分布和排列,可以 制备具有特殊磁学性质的磁流体,用于密封、润 滑、减震等领域。
数据处理与结果分析
数据处理
对于实验得到的数据,需要进行适当的处理 以消除误差并提高数据精度。常用的数据处 理方法包括平滑处理、背景扣除、归一化等 。
结果分析
通过对实验数据的分析,可以得到物质的顺 磁性参数,如磁化率、磁滞回线等。进一步 分析这些参数可以了解物质的磁性特征以及 与温度、压力等外部条件的关系。同时,还 可以将实验结果与理论预测进行比较,以验 证理论模型的正确性。
02
原子半径与未成对 电子数
原子半径越大,其未成对电子数 可能越多,从而使得原子具有更 强的顺磁性。
03
原子半径与磁矩大 小
原子半径的大小还会影响原子磁 矩的大小,进而影响物质的顺磁 性。
原子间相互作用与顺磁性
01
原子间相互作用影响电子自旋状态
原子间的相互作用会改变电子的自旋状态,从而影响原子的磁性。
原子核磁矩与电子磁矩
原子核磁矩远小于电子磁矩,通常可 忽略不计。
电子磁矩包括轨道磁矩和自旋磁矩, 其中自旋磁矩起主导作用。
磁矩间相互作用
偶极相互作用
原子磁矩之间通过磁场相互作用,形成偶极相互作用。
交换相互作用
在某些材料中,原子磁矩之间还存在一种特殊的相互作用——交换相互作用,它是导致铁磁性材料自发磁化的根 本原因。
铁磁学PPT课件-物质磁性分类和原子磁矩

3 孤立原子的磁矩
1) 电子的磁矩:
电子自旋磁矩
S
e m
S
(S为自旋动量矩)
自旋磁矩在外磁场方向上的投影为:
SH
e m ms
1 ms 2
SH
e 2m
Bohr磁子B
e 2m
0.92731023( A m2 )
电子轨道磁矩
L
e 2m
L
(L为轨道动量矩)
gJ mJ
mJ
gJ B
mJ J ,(J 1),,0,......( J 1), J
当L 0, 当S 0,
J S J L
gJ gS 2 gJ gL 1
J J
e
S
me
L
2m
(自旋贡献) (轨道贡献)
3 Hund规则
a) 在泡利原理许可的条件下,总自旋量子数S取最大值。 b) 在满足(a)条件下,总轨道角动量量子数L取最大值。 c)在未满壳层中,电子数小于壳层总电子数一半时,总角动 量量子数J=|L-S|;电子数大于或等于壳层总电子数一半时, J=L+S
H 2 2 ze2 V
2 4 0r
例:立方晶场中的3d电子波函数
3z2 r 2
Y20
1 4
15
1 r2
(3z 2
r2)
x2 y2
1 2
(Y22
Y22
)
1 4
15
1 r2
(x2
y2)
xy
i
1 2
(Y22
Y22 )
1 2
15 1 xy
r2
yz
i
1 2
(Y21
原子核的磁矩

则仅有两相临能级间可以进行跃迁,跃迁的能量△E为:
E gI N H
由此可见,只要想法测出△E,则可求出 gI ,从而就可得到核
的磁矩 I gI N I
在垂直于均匀磁场的方向再加上一个强度较弱的高频磁场,当 其频率ν满足下列条件时,
h E
则样品的原子核将会吸收高频磁场的能量而使得核的取向发生 改变,从而实现由低的子能级向相邻较高子能级的跃迁。此时, 高频磁场的能量将被原子核强烈吸收,称为共振吸收。此时的 频率称为共振频率。则:
10 27 J .T 1
称为核磁子。
因为 mp : me 1836
所以 B : N 1836
说明:1)由于核的磁矩比原子中电子的磁矩小的多,这就是为 什么超精细谱线的间距比精细结构谱线的间距小得多的原因。
2)通常是用核磁矩在给定Z方向投影的最大值来衡量核 磁矩的大小。
3)核磁矩常用核磁子为 N 单位 则质子的磁矩为: p 2.793 中子的磁矩为:n 1.913
gI
h N H
只要测得ν和H,则可求得
g因I 子。
§1.6 、原子核的电四极矩
原子核是接近球形的。实验表明大多数原子核的形状是偏离于球 形不大的轴对称椭球。这一点由原子核具有电四极矩得到证明。
1、电四极矩的引入
原子核有电荷 Ze,这些电荷在核内的不同分布就产生不同的 电势。
如果核的电荷均匀分布于轴对称椭球形的核内,则在原子核
原子核是由质子和中子组成,质子、中子不仅有自旋磁矩, 而且有轨道磁矩。所以核也具有磁矩。
质子、中子的磁矩为:
p
g
p
(
e 2mN
c
)
ps
n
原子的有效磁矩

原子的有效磁矩
原子的有效磁矩是指在外加磁场作用下,原子对外界磁场的响应能力。
原子的有效磁矩可以分为轨道磁矩和自旋磁矩两部分。
1. 轨道磁矩:当电子在原子核周围运动时,其轨道运动形成一个磁场,称为轨道磁场。
轨道磁矩是由轨道运动产生的,大小与电子的轨道角动量以及运动质量有关。
2. 自旋磁矩:电子除了具有轨道运动外,还有自旋运动,自旋是电子的一种内禀属性。
自旋磁矩是由电子的自旋运动产生的,大小与电子的自旋角动量有关。
原子的有效磁矩是轨道磁矩和自旋磁矩之和。
对于原子内部的电子,由于自旋和轨道角动量的量级相近,两者对有效磁矩的贡献相当重要。
由于电子相互作用以及其他因素的影响,原子的有效磁矩大小和方向具有一定的复杂性,需要通过实验和数值计算进行确定。
原子核的磁矩与自旋

原子核的磁矩与自旋原子核是构成原子的基本粒子之一,它具有独特的性质和行为。
其中,磁矩和自旋是原子核的两个重要特征,它们与原子核的结构和性质密切相关。
本文将探讨原子核的磁矩和自旋,并阐述它们对原子核物理和相关研究的重要性。
1. 原子核的磁矩原子核的磁矩是指原子核围绕内禀轴的旋转运动所产生的磁性效应。
磁矩的大小与原子核的质量、电荷和自旋等因素有关。
原子核的磁矩通常用磁核子(nuclear magneton)来表示,记作μ。
磁核子是国际单位制中用于表示原子核的磁矩的单位,其数值约为5.05 × 10^-27 J/T。
2. 磁矩的来源原子核的磁矩主要来源于其组成粒子的自旋和轨道运动。
自旋磁矩是由于核子自身的自旋而产生的,而轨道磁矩则是由于核子围绕原子核内禀轴的轨道运动而产生的。
磁矩的大小与核子的质量、电荷以及自旋的大小有关。
3. 原子核的自旋原子核的自旋指的是原子核内各个核子的自旋矢量之和。
自旋是粒子内禀的属性,类似于粒子的旋转,但并不意味着物体在空间中的真正旋转。
原子核的自旋用核子的自旋量子数I来表示,其中I可以是整数或半整数。
自旋量子数I越大,原子核的自旋越大。
4. 磁矩与自旋的关系原子核的磁矩与自旋之间存在一定的关系。
根据量子力学的理论,原子核的磁矩与自旋之间的关系可以用以下公式来描述:μ = γ × I其中,μ表示原子核的磁矩,γ是一个比例系数,I表示自旋量子数。
这个公式表明,原子核的磁矩与自旋量子数之间存在着线性关系。
磁矩的方向与自旋的方向一致。
5. 实验观测和应用通过实验手段,科学家们可以测定各种原子核的磁矩和自旋。
利用核磁共振(NMR)和电子自旋共振(ESR)等技术,可以研究原子核的结构特性、核自旋磁矩比和核磁共振现象等。
这些实验观测不仅对于理论物理学和核物理学有重要意义,也广泛应用于其他领域,如化学、生物学和医学等。
总结:原子核的磁矩和自旋是原子核的重要特征。
磁矩主要与原子核内禀轨道运动和核子自旋有关,而自旋则代表了原子核内各个核子的自旋矢量之和。
第2章 原子磁矩

Fe 原子:Z = 26, 电子分布是:······3d6
根据洪德法则1,5个电子自旋占据5个 1 的
另一个只能占据
1 2
的
ms
2 状态,所以总自旋:
ms
状态,
S 5 1 1 1 2 22
L ml 2 1 0 (1) (2) 2 2 (根据法则 2)
所以原子序数不太大的原子的基态和低激发态,均可使用第一种耦合 (简称 L-S 耦合),我们以后经常讨论到的3d族和4f 族元素都可以使用L-S 耦合方式。
下面以原子某一壳层包含两个电子为例说明 L-S 的耦合方法:
设两个电子的轨道角动量量子数分布为:l1,l2 则其总轨道角动量量子数的可取值为:
L l1 l2, l1 l2 1, ..., l1 l2
r ij
S j sj 第j个原子的总自旋
Aij
PL L(L 1) , L L(L 1)B
自旋情况相同: S s1 s2, s1 s2 1, ..., s1 s2 PS S(S 1) , S 2 S(S 1)B
两个电子的总角动量量子数: J L S
如果 L>S, J 的取值为:
J L S, L S 1,, L S (共2S+1个值)
§ 2.1.1电子轨道运动产生的轨道磁矩
从经典观点看:一个绕原子核运动的电子,相当于一个环形电流,根 据定义,它的轨道磁矩为:
l
iS
e T
S
S 是环形轨道面积
电子具有质量 m,其轨道运动同时具有角动量 pl,在圆形轨道近似 下计入方向
pl
mr 2 ,
l
[磁性物理学(第二章讲稿)

nP = 2 S (S + 1), µ = nP µ B 外场方向 µ J = 2 Sµ B
说明过渡族元素的离子磁矩主要由电子自旋作贡献,而 轨道角动量不作贡献,这是“轨道角动量猝灭”所致。
过渡元素的原子或离子组成物质时,电子的外 层由于受到晶体场作用,方向是变动的,不能产 生轨道磁矩,即轨道角动量冻结,因而不考虑L 磁性物质中(朗之万定理修正—即外场方向):
根据原子的矢量模型,原子总角动量PJ是总 轨道角动量PL与总自旋角动量PS的矢量和:
v v v PJ = PL + PS = J ( J + 1)h
总角量子数:J=L+S, L+S-1,…… |L-S|。 原子总角动量在外磁场方向的分量为
(PJ )H = m J h
总磁量子数:mJ =J,J-1,……-J
结论:满壳层电子的总动量矩和总磁矩为零,只有未
成对的电子磁矩对原子的总磁矩作贡献,未满壳层——
磁性电子壳层
2.角动量耦合 原子的总动量由电子的轨道角动量和自旋 角动量以矢量叠加方式合成,主要由:L- S,jj和LS+jj 耦合三种 L-S耦合:各电子的轨道运动间有较强的相 互作用∑li → L,∑si →S , J=S+L 发生与原子序数较小的原子中(Z<32)。 j-j耦合:各电子轨道运动与本身的自旋相互 作用较强,∑(li+si) → ji,∑ji →J ,Z>82 LS+jj耦合: 32<Z<82 铁磁体中,原子的总角动量大都属于L-S耦合
Pl = l (l + 1)h
其中l=0,1,2…n-1 ,h
=h
2π
e ∴ µ l = l (l + 1) h 2m
原子核的磁矩
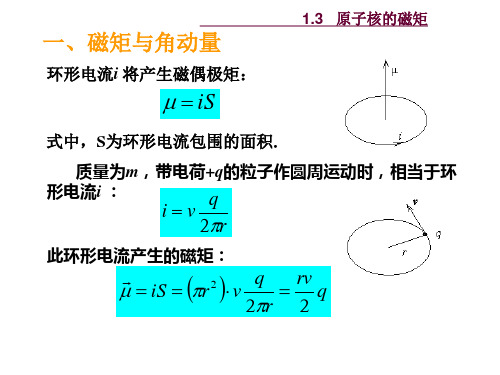
q
L
2m
在量子力学中,若粒子的角动量为 J,则
q
J
2m
1.3 原子核的磁矩
一、原子中电子的磁矩
自旋磁矩:
s
e me
Ps
gs
e 2me
Ps
gs 2
轨道磁矩:
l
e 2me
Pl
gl
e 2me
Pl
gl 1
玻尔磁子
B
e 2me
9.2740
10 24 A m2
总磁矩: s l
gB Pj ,
实验上: 在 B的垂直方向上加一强度较弱的高频磁场,
当其频率满足 h = △EI 时,核会强烈吸收其能
量(此现象即为核磁共振),则
gI = h /NB 只要测得了 和B,即可求出gI。
返回上级菜单
1.3 原子核的磁矩
图1-4 核磁共振实验原理图
1.3 原子核的磁矩
图1-5 核磁共振成像术(简称MRI)
g
1
j j 1 ll 1 ss 1 2 j j 1
二、核的磁矩
1.3 原子核的磁矩
1、核子的磁矩
质子:
P
gP
e 2mP
Ps
gP N Ps
核磁子
中子:
N
n
e 2mP
gnN
5.0508
Ps
10
27
A
m2
按常规: g P 2
gn 0
实际上: gP 5.586 gn 3.826
2、核的磁矩:
1.3 原子核的磁矩
I gI N PI
在给定方向的投影值
PI II 1
Iz g I N mI mI = I,I–1,…,–I+1,–I
2 原子磁矩(1)

Fe 原子:Z = 26, 电子分布是:· · · · · · 3d6
1 根据洪德法则1,5个电子自旋占据5个 的 ms 状态, 2 1 另一个只能占据 的 ms 状态,所以总自旋: 2
1 1 S 5 1 2 2 2 L ml 2 1 0 ( 1) ( 2) 2 2
(2)每个电子的轨道矢量li的排列,电子倾向于同样的方向绕核旋转, 以避免靠近而增加库仑排斥能,使总的轨道角动量L取 最大值。(如3d 电子,ml=2时该轨道磁矩在外场方向上的分量最大,轨道磁矩与外磁 场平行能量最低,最稳定)。 (3)由于L和S间的耦合,电子数n小于半满时 J=L-S,电 子 数n大于半满时 J=L+S。
s
e ps s ps m
s
e m
:自旋旋磁比
s 1 2
s 2 l
s
e ps 2 s( s 1) B 3B m
sz B
LS
耦合
L L( L 1) B S 2 S (S 1) B
PJ
PL L( L 1) ,
常将原子的量子态用光谱学的方法来标记:
2 S 1
FJ
将总自旋量子数、总角量子数的数字填入相应位置即可,
总轨道量子数 L = 0, 1, 2, 3, 4, 5, 6, · · · · · ,分别记为: S, P,D, F, G, H, I, 例如:某元素的基态记作:
5
D4
即指该元素基态的总自旋量子数:S = 2 总轨道量子数:L= 2 总角量子数:J = 4
(根据法则 2)
J LS 4
(根据法则 3,电子数超过一半)
gJ
3 S ( S 1) L( L 1) 1.5 2 2 J ( J 1)
原子磁矩的计算

原子磁矩的计算磁矩既能反映物质的性质,又能反映物质内部结构的特征,它是物质性质和结构描述的重要指标之一。
磁矩是一种强烈而细微的力,是物理世界中一种重要的能量。
磁矩是构成大自然一切现象的基本定律之一。
原子磁矩是物质内部结构中磁性粒子运动而产生的磁场,是磁矩最小的单位,它们可以由其他基本磁性粒子构成,比如原子、电子等。
因此,计算原子磁矩的关键是理解其结构,包括它的原子结构、电子结构和空间结构。
原子结构能够影响原子磁矩。
原子结构通常是指原子的核外电子结构,即原子的化学性质及其原子的构成原子核的质子数和中子数。
原子结构是由原子中电子组成的,因此,原子结构的计算又可以归结为电子结构的计算。
电子结构计算是原子磁矩计算的核心,它是描述原子中电子特性和动力学行为的理论模型。
它使用费米-能量(FEM)理论,分析电子的局域性性质,并计算电子的休止能量和运动能量,从而计算出原子磁矩。
费米-能量理论也可以解释电子共振及空间结构中电子的跨越性。
另外,空间结构也能影响原子磁矩,由三维空间结构确定的局域性磁矩,是确定原子磁矩最重要的因素之一。
通常,这些空间结构由电子共价键组成,而这些共价键由电子结构和外界影响构成。
因此,空间结构的计算,也要考虑电子结构和外界影响的空间磁矩的变化。
为了解决原子磁矩的计算,我们必须利用有限元力学方法,充分利用现代计算机和计算机编程语言,构建精确的原子结构和空间结构。
利用费米-能量理论和有限元力学的方法,可产生精确的质点-极化矩阵,以及空间结构的负载矩阵,可根据电子跃迁能与近似波函数拟合而得到电子能量,最终可以计算得到原子磁矩。
总之,原子磁矩的计算要从原子结构、电子结构和空间结构三个方面着手,借助于费米-能量理论和有限元力学方法,可以得出精确的原子磁矩。
原子磁矩的计算

原子磁矩的计算自德国物理学家Maxwell发现磁矩的存在以来,原子磁矩也就成为了物理学家们研究的重要课题。
原子磁矩是构成物质单元中原子中磁能量的产物,是一个微弱的矢量,它可以帮助我们理解物质的性质及其结构。
物理学家们自始至终都在努力探索原子层面的磁能量的特征,研究原子磁矩的计算也是其中一个重要的方向。
原子磁矩的计算,首先要明确它的基本概念,即原子磁矩就是由原子的内部质量分布的一种磁性体现。
换句话说,它是由原子内部的各种层次上的电子能量转移而产生的一个统计量。
接下来,根据原子磁矩的基本特性,我们可以采用小能量理论、哈密顿量矢分解法等来求解它们。
小能量理论是一种量子力学思想,它可以用于求解原子磁矩的数值。
在这种理论的基础上,原子磁矩的计算可以分为两步:第一步,计算原子电子的能量;第二步,计算原子磁矩。
首先,我们可以使用密度泛函(DFT)方法,求解原子电子的能量。
密度泛函方法专门用于求解原子中的电子态,它可以让我们计算出原子电子的能量。
而这些能量可以用于计算原子磁矩。
接下来,为了计算原子磁矩,我们需要使用哈密顿量矢分解法(HFD)。
在哈密顿量矢分解法中,将系统的哈密顿量分解成一系列的矢量,每个矢量代表系统中的某一部分,而每个矢量的模表示系统中特定的部分的能量。
基于这些矢量,我们可以计算出系统中总体的磁矩。
最后,我们可以使用共振态理论(RPA)来计算原子磁矩。
这种理论可以模拟系统的共振状态,从而计算出系统的总磁矩。
总的来说,原子磁矩的计算是一个具有挑战性的任务,也是物理学家们努力探索的课题之一。
在这一领域中,我们可以应用小能量理论、哈密顿量矢分解法以及共振态理论等多种方法,来计算原子磁矩,使我们有望在深入了解原子磁性特性方面取得令人惊喜的突破。
实际上,原子磁矩的计算和研究可以指导和更好地理解物质结构及其特性,也可以帮助我们开发出更多有效的材料。
因此,原子磁矩的计算仍然是当今物理学家们关注的课题之一,也是当今许多研究者努力努力探索的方向。
原子磁矩的计算

原子磁矩的计算磁矩是物理学中最重要的特征之一,它可以描述物体的磁场分布。
磁矩的计算是物理学家和化学家认识物质和它们之间相互作用的重要研究课题。
另外,磁矩也可以用于对非结构化物质性质的研究。
原子磁矩是指某个原子的磁场中形成的磁矩,它是由原子核产生的核磁矩的特殊形式,主要受原子电子的构型和极化偏差的影响。
原子磁矩的计算技术发展到今天,已经能够进行相当精确的计算,并且对某些物质性质的研究有着重要意义。
其原理主要是利用量子力学和多中心理论,计算和分析某种物质的磁场分布,最后得到原子磁矩的值和方向。
由于原子磁矩的计算需要考虑到复杂的量子力学理论,它的计算相当复杂,算法非常复杂,耗费的计算时间也非常长。
为了解决这一问题,已经出现了一系列的计算方法。
常见的原子磁矩计算方法有基于Hartree-Fock理论的原子磁矩计算、基于激励性多中心理论的原子磁矩计算、基于前向散射理论的原子磁矩计算以及基于差分法和核磁共振法的原子磁矩计算。
Hartree-Fock理论是一种基于电子密度的量子力学理论,它以电子密度为基础,用一种独立的近似的方式来描述一个原子的电子态。
在Hartree-Fock理论的框架下,原子磁矩可以从电子密度计算出来。
激励性多中心理论是一种结合了Hartree-Fock理论和多中心理论的方法,利用多中心理论可以表示出原子及其邻居的磁场,从而可以计算出原子磁矩。
前向散射理论是一种新兴的量子力学理论,它基于电子-核散射概念,通过一系列的计算步骤,可以获得原子磁矩的准确值。
差分法利用多中心理论,结合数值计算的方法,它假设的每个原子核的磁场分布是球型的,以此逐步计算出原子磁矩的值和方向。
核磁共振法是一种新兴的技术,它利用磁共振的原理,速度的测量原子磁矩和空间分布,并且根据电子态能量的变化,从而得出原子磁矩的值和分布。
原子磁矩的计算一直是物理学家和化学家关注的重要研究课题。
它有助于我们认识物质和它们之间相互作用的机制,以及对非结构化物质性质的研究,可以为人们提供更多有关某些物质性质的相关信息,并在多学科之间建立起联系,为人类的先进技术起到重要的作用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Ylm ( ,)决定电子分布的形状
波函数的实数表示
能量简并
1
2
n=7 6 5 4 3
s
p
l=0
1
d
f
g
23
4
二、多电子原子
1。能级结构
不考虑电子间的相互作用
能量
En
13.(6
1 n12
+1 n22
+
1 nN 2
)
能量简并
考虑电子间的相互作用 简并减除 能级交错
2、电子结构
泡里原理: 不可能有两个和两个以上的电子处于 完全相同的状态,或具有完全相同的 量子数。
L
i ev S
一个电子的L和S总是 方向相反
例子
Sm3+
未半满
S
Dy3+
超过半满
S
m
Sm3+的4f轨道有5个电子,不超过半满
L=5,S=5/2,
3
J=L-S=5/2.
2
1L
0
Dy3+的4f轨道有9个电子,超过半满
-1
轨道角动量L是由自旋向下的二个轨道决定
———— -2
L=3+2=5,
第二章 原子的磁矩
第一节 原子的电子结构
一、类氢原子的电子结构
1、玻尔-索莫菲理论
En
mZ 2e4 2h2n2
13.6 n2 eV
n 1, 2,3主量子数
L lh l 1, 2,3,,n 角量子数 Lz mlh ml 0, 1, 2,, l 轨道磁量子数
S sh s 1 自旋量子数 2
J L
(S 0)
mJ J , J 1,... J 1, J
2、洪特定则
(1) 电子自旋的排列,是使总白旋在泡利不相容原理的限 制内取最大值。
其理由是:电子由于库仑排斥而倾向于取不同的轨道,而原子内的自旋与 自旋相互作用倾向于使这些自旋相互平行。
Mn2 的3d轨道有5个电子,根据定则1:总自旋S=5 1 5 22
-3
d电子轨道取向量子数,ml 2,1,0, 1, 2
f电子轨道取向量子数,m l
3, 2,1,0, 1, 2, 3
ml =0 -1 -2
1 2
Mn3的d轨道有4个电子 总轨道角动量L=2+1+0+(-1)=2 Co2的d轨道有7个电子 总轨道角动量L=2+1=(3 其余5个的总L=0) Nd 3(4f4 6s2,f轨道有3个电子) 总轨道角动量L 3 2 1 6
计算机画出4s电子含Z轴原子波函数空间分 布图,在原点4S电子波函数不为零
第二节 矢量模型
1、角动量耦合
轨道 L1 l1(l1 1) h l1 0,1, 2,.....
L2 l2 (l2 1) h l2 0,1, 2,.....
自旋
L L(L 1) h L l1 1l2 ,l1 l2 1,......, l1 l2 . S1 s1(s1 1) h s1 2
●
v °e i
3
(3) 第三条涉及L和S间的耦合: 当某壳层中的电子数n小于最大数目的一半时 (例4f壳层中
的电子数n<7),J=L-S。 当某壳层中的电子数n超过半满(例4f壳层中的电子数>7 ),
J=L+S。
一个电子的L和S总是方向相反,壳层中电子数目少 于最大数目一半时,所有电子的 l 和 s都是相反。同时轨 道磁矩 µl 和µs也是反平行。
Sz msh
ms
1 2
自旋磁量子数
椭圆轨道
a a0 n2 Z
b a0 nl Z a0=0.529 1010米,玻尔原子半径
空间取向量子化
氢原子能级
1
2
n=7 6 5 4 3
s
p
l=0
1
d
f
g
23
4
2、量子力学
力学量
En
mZ 2e4 2h2n2
13.6 n2 eV
n 1, 2,3主量子数
L l(l 1)h l 1, 2,3,,n 角量子数 Lz mlh ml 0, 1, 2,, l 轨道磁量子数
S s(s 1)h s 1 自旋量子数 2
Sz msh
1 ms 2
自旋磁量子数
“轨道”
用波函数描述 nlm Rnl (r)Ylm ( ,)
Rnl (r)决定电子离开核距离分布
S2 s2 (s2 1) h
s2
1 2
S S (S 1) h S s 1s2 , s 1s2 1,...... s 1s2
总角动量
v vv J LS
S 1, 0
J J (J 1) h J L S, L S 1,......, L S .
J z mJ h
J L 1, L, L 1 (S 1)
通常用符号 L 2 S+1
J
来描述原子的状态
L=0,1,2,3,4,5,6,…. 并记号为S,P,D,F,G,H,I,….. 左上角2S+1,右下角为总角动量量子数。
例如:Fe2+ S=2 ,L=2 ,J=4 记为 5D4 ; Pr3+:S=1, L=5 , J=4 记为 3H4
Nd
3的原子态为
4
I 9/
2
4、三价稀土离子的自旋角动量S、轨道角动量L和总角动量J 与4f电子数的关系
3 原子的磁矩
1 电子的轨道磁矩
电子的轨道磁矩 电子的角动量是:
M 0iS
0
e 2
r2
0er 2
2
L mr2
电子的轨道磁矩:
L l(l 1)h
M 0e L
2m
ML
0eh
2m
l(l 1) M B
ML
s
p
d
f
l=0
1
23
6s 5s
6p 5d
5p
4d
4p
3d
4f
4s
3p
3s
2p
2s
1s
s
p
d
f
l=0
1
23
6s 5s
6p 5d
5p
4d
4p
3d
4f
4s
3p
3s
2p
2s
1s
为什么电子先占4s,再占3d ?
如果轨道的电荷分布偏离球对称,玻尔轨道的形状发生变化。 如图3s轨道是椭圆形的,一部分轨道离核近,s电子的原子波函数在核 附近非常大。S电子与核的库仑相互作用(相互吸引,能量低),使电子 先占4s轨道,后占3d轨道。同样5S电子先于4f电子占据轨道。
Mn3 的3d轨道有4个电子,根据定则1:总自旋S=4 1 2 2
Co2的3d轨道有7个电子,其总自旋S=2 1 1 2
(2) 每个电子的轨道矢量的排列,是使总的轨道角动量L 在泡利不相容原理和条件(1)的限制下取最大值。
其理由是:,电子倾向于在同样的方向绕核旋转以避免相互靠近而增 加库仑能。
———— - 3
L- S
L+S
自旋角动量S是由未成对的另外五个自旋向 上电子决定
µl↑L+S=15/2.
Nd 3(4f4 6s2,f轨道有3个电子) 总轨道角动量L 3 2 1 6 自旋角动量S 3
2
总角动量J 6 3 9 22
3、原子态符号
