用数学方程描述的非圆曲线的轮廓数值计算
非圆曲线的等误差直线逼近

曲线 的起点, 为 编程许 用
误差。现以 P 0 为圆心、 为
半径作 一 个误 差圆, 然 后 作
一条与误差圆、非圆曲线 y =
f ( x ) 均相切的直线, 即公切
线 m m , 切 点 分 别 为: PS
图 1 线性非 圆曲 线逼近图
( xS , yS ) 、PT ( xT , yT ) , 由此可得:
The lapping and cutting experiment of the diamond tools
Song Jian Wu Minjing
Abstract In this paper, four types material of diamond( natural singe crystal、DEBEERS MONODITE、PCD、CVD) are applied in the ex periment. Some basic data is gained and emphatically discusses the experimental conclusion. In the lapping experiment, the lapping meth od and efficiency and integrity of diamond tool are comprised, While the super precise cutting is done. Key words: PCD tools CVD tools Natural diamond tools Surface finish
PCD 聚晶金刚石刀具、PCBN( 聚晶立方氮化硼) 切 削工具以及 CVD 薄膜与厚膜金刚石切削工具、类金刚 石膜( DLC) 、金刚石膜和 CBN 膜涂层切削工具有广阔 的应用前景, 尤其是精密和超精密加工技术发展对切 削工具的需求, 促使这些切削工具迅猛发展。
程序编制中的数学处理--非圆曲线节点的计算

程序编制中的数学处理--非圆曲线节点的计算数控系统一般只有直线和圆弧插补功能,对于非圆曲线轮廓,只能用直线或圆弧去逼近它。
节点就是逼近线段与非圆曲线的交点,也是个逼近线段的起点和终点。
一个已知曲线方程的节点数与逼近线段的形状(直线还是圆弧)、曲线方程的特性以及允许的逼近误差有关。
节点计算,就是利用这三者之间的数学关系,求解出各节点的坐标。
一、等间距的直线逼近的节点计算已知非圆曲线方程 y=f(x)从曲线X轴的起点坐标开始,以等间距Δx来划分曲线起点到终点的区间,可得一系列X 轴的坐标点的值,设起点的X坐标值为x0=a,则有:x1=a+Δx,x2=a+2Δx,x3=a+3Δx,…. X i=a+iΔx,..将这些X坐标值代入方程 y=f(x),则求得一系列Y坐标值:y i=f(x i)(i=1,2,3,…..)那么(xi,yi)(i=1,2,3……)就是所求得的节点坐标值。
相邻两点的直线段就是逼近线段。
等间距法的关键是合理确定Δx,既要满足允许误差的要求,又要使节点尽可能少。
通常采用试算和校验的方法确定Δx,方法步骤如下:1.取Δx初值,一般取0.1。
2.计算(xi,yi)(i=1,2,3……)。
3.误差验算:设任一逼近直线MN,其方程为:ax+by+c=0,则与MN平行且距离为δ允的直线MˊNˊ的方程为:求解联立方程:若:只有一个解,则逼近误差等于δ允,Δx正好满足误差要求。
没有解,则逼近误差小于δ允,Δx满足误差要求,可适当增大其取值,返回2。
有两个解,则逼近误差大于δ允,Δx太大,应减小其取值。
返回2。
等间距法计算简单,但由于必须保证曲线曲率最大处的逼近误差小于允许值,所以程序可能过多。
二、等弦长直线逼近的节点计算使所有逼近线段的长度相等。
计算步骤如下:(1)确定允许的弦长。
用等弦长逼近,最大误差δmax一定在曲线的曲率半径最小Rmin处,则为:(2)求Rmin。
曲线任一点的曲率半径为:取dR/dx=0,即根据求得,并由式(2-3)求得x后,将x值代入式(2-2)求、得Rmin。
用数学方程描述的非圆曲线的轮廓数值计算

用数学方程描述的非圆曲线的轮廓数值计算数控加工中把除了直线与圆弧之外用数学方程式表达的平面轮廓曲线称为非圆曲线。
非圆曲线的节点就是逼近线段的交点。
一个已知曲线)(x f y =的节点数目主要取决于所用逼近线段的形状(直线或圆弧)、曲线方程的特性以及允许的拟合误差。
将这三个方面利用数学关系来求解,即可求得相应的节点坐标。
下面简要介绍常用的直线逼近节点的计算方法。
(1)等间距直线逼近的节点计算 1)基本原理等间距法就是将某一坐标轴划分成相等的间距,然后求出曲线上相应的节点。
如图3.1所示,已知曲线方程为)(x f y =,沿X 轴方向取Δx 为等间距长。
根据曲线方程,由i x 求得i y ,ix +1=i x +Δx ,)(1x x f y i i ∆+=+,如此求得的一系列点就是节点。
2) 误差校验方法由图3.1知,当x ∆取得愈大,产生的拟和误差愈大。
设工件的允许拟合误差为δ,一般δ取成零件公差的1/5~1/10,要求曲线)(x f y =与相邻两节点连线间的法向距离小于δ。
实际处理时,并非任意相邻两点间的误差都要验算,对于曲线曲率半径变化较小处,只需验算两节点间距最长处的误差,而对曲线曲率变化较大处,应验算曲率半径较小处的误差,通常由轮廓图形直接观察确定校验的位置。
其校验方法如下:设需校验mn 曲线段。
n m 和的坐标分别为(m m y x ,)和(n n y x ,),则直线mn 的方程为:nm n m nn y y x x y y x x --=--令A=n m y y -,B=m n x x -,C=n m n m y x x y -,则上式可改写为A x +B y =C 。
表示公差带范围的直线n m ''与mn 平行,且法向距离为δ。
n m ''直线方程可表示为:22B AC By Ax +±=+δ式中,当直线n m ''在mn 上边时取“+”号,在mn 下边时“-”号。
略谈数控加工中图形处理方法论文

略谈数控加工中的图形处理方法摘要:无论采用何种编程方法,对零件图进行数学处理、尤其对于非圆曲线的拟合加工,是数控编程的一个主要准备工作。
本文在讨论数控加工中的图形处理方法的基础上,给出正弦曲线手工编程的宏程序应用实例。
关键词:数控编程数学处理宏程序对零件图进行数学处理是编程前的主要准备工作之一,不但对手工编程来说是必不可少的工作步骤,而且即便采用计算机进行自动编程,也经常需要先对工件的轮廓图形进行数控预处理,才能对有关任何元素进行定义。
1 数控加工中的图形处理方法非圆曲线处理包括除圆以外的各种可以用方程描述的圆锥二次曲线(如抛物线、椭圆、双曲线)、阿基米德螺旋线、对数螺旋线各种参数方程、极坐标方程所描述的平面曲线与列表曲线等。
数控机床在加工上述各种曲线平面轮廓时,一般都不能直接进行编程,而必须经过数学处理以后,采用相互连接的直线逼近和圆弧逼近方法,才能通过设置宏变量和演算式,并引入加工程序,同时在加工程序中使用逻辑判断语句进行编程。
这里介绍常用的直线逼近的数值计算方法。
一般来说,由于直线逼近法的插补节点均在曲线轮廓上(图),容易计算,编程也简便一些,所以常用直线逼近法来逼近非圆曲线。
其缺点是插补误差较大,但只要处理得当还是可以满足加工需要的,关键在于插补长度及插补误差控制。
由于各种曲线上各点的曲率不同,如果要使各插补段长度均相等,则各段插补祯的误差大小不同。
反之,如果要使各段插补误差相同,则各插补段长度不等。
1.1 等间距直线逼近法等间距直线逼近法是在一坐标轴方向,将拟合轮廓的总增量(极坐标系中,指转角或径向坐标的总增量)进行等分后,对其设定节点所进行的坐标值计算方法,如图所示。
已知方程y=f (x),根据给定的△x求出xi,将xi代入y=f (x)即可求出一系列的(x0y0),…(xi,yi),即每个线段的终点坐标,并以该坐标值编制直线程序段。
△x取决于曲线的曲率和允许误差δ,一般δ取零件的1/5~1/10,验算的方法如图2所示。
非线性方程数值解法详解课件

例如,对于求解非线性方程$f(x)=0$的 应用实例中需要注意选择合适的初始近
根,可以先选择一个初始近似解$x_0$, 似解和设置合适的精度要求,以确保算
然后按照弦截法的迭代过程逐步逼近方
法能够快速收敛到真实解。
程的真实解。
05 共轭梯度法
共轭梯度法的原理
它利用共轭方向的概念,通过迭代过程中不断更新搜 索方向,使得函数值逐渐减小,最终找到方程的解。
牛顿法的实现步骤
确定初始点x0,计算f(x0)和f'(x0),如果f(x0)不等于0,则按照牛顿法的迭代公式 进行迭代,直到满足精度要求。
1. 选取初始点x0;2. 计算函数值f(x0)和导数值f'(x0);3. 如果f(x0)不等于0,则 按照牛顿法的迭代公式x1=x0-f(x0)/f'(x0)进行迭代;4. 重复步骤2和3,直到满 足精度要求。
以求解非线性方程为例,通过选择合 适的迭代法和初值,可以有效地求解 非线性方程的近似解。
03 牛顿法
牛顿法的原理
01
基于函数f(x)的泰勒级数的前两项, 通过迭代的方式逼近方程f(x)=0 的解。
02
牛顿法的基本思想是通过泰勒级 数的近似,将非线性方程f(x)=0 转化为线性方程,然后利用线性 方程的解来逼近非线性方程的解。
当达到预设的迭代次数或满足一定的收敛 条件时,停止迭代,输出结果。
共轭梯度法的收敛性分析
共轭梯度法具有全局收敛性和局部收敛性,即只要初始点 选择得当,算法能够找到方程的解,且在局部范围内具有 快速收敛的特点。
收敛性分析主要涉及算法的迭代矩阵和函数的性质,如连 续性和可微性等。
共轭梯度法的应用实例
牛顿法的收敛性分析
在一定的条件下,牛顿法是收敛的, 且具有二阶收敛速度。
用MasterCAM编制非圆曲线轮廓加工程序

用MasterCAM编制非圆曲线轮廓加工程序蒋英汉2008.6.15用MasterCAM编制非圆曲线轮廓加工程序关键词:自动编程、非圆曲线、NC程序中国一拖高级技工学校蒋英汉随着数字控制技术与数控机床出现,给机械制造业带来了翻天覆地的变化。
数控技术已成为制造业实现自动化、柔性化、集成化生产的基础技术。
自90年代至今我国的数控机床在机械制造业的占有率不断提高,在航天、军工模具等行业已经成为主要的加工手段。
现在数控技术已经成为体现一个国家综合国力水平的重要标志。
新世纪机械制造业的竞争,其实就是数控技术的竞争。
目前,我国的数控机床已经有了数量,但使用确不高,其原因,不能及时合理的编制出加工程序就是其中只一。
所以提高我国编程人员的编程能力已经是迫在眉睫了。
CAD/CAM技术则是建立在数控技术之上的一种科学,它对数控技术和数控机床的应用提供了一个坚实的平台。
为提高编程人员的编程能力提供了一个途径。
Ma ste rC AM 软件是美国的CNC Software公司开发的基于PC平台的CAD/CAM系统,由于它对硬件要求不高,并且操作灵活、易学易用并具有良好的价格性能比,因而深受广大企业用户和工程技术人员的欢迎,广泛应用于机械加工、模具制造、汽车工业和航天工业等领域,它具有二维几何图形设计、三维曲面设计、刀具路径模拟、加工实体模拟等功能,并提供友好的人机交互,从而实现了从产品的几何设计到加工制造的CAD/CAM一体化。
是目前世界上应用最广泛的CAD/CAM软件之一。
以下介绍MasterCAM在编制非圆曲线轮廓加工程序的应用:虽然非圆曲线轮廓可以在数控机床上用宏程序编制,但它对编程人员的编程能力要求特别高,时间周期较长,精度难以保证,而且不同系统的数控机床也不统用。
所以用CAD/CAM软件编制非圆曲线轮廓加工程序已经成了必然。
MasterCAM编制非圆曲线轮廓加工程序的主要步骤是:(一)设计非圆曲线方程式文件运用MasterCAM的方程式功能设计非圆曲线轮廓。
非球面轮廓测量与分析

a is the indexed Polynomial Coefficient a为多项式系数
C is the reciprocal of the Base Radius C为基圆半径的倒数
K is the Conic Constant of the Surface K为二次常数
Xp是指非球面光轴到轮廓最高点之间的距 离。
非球面参数简介
• Xt:
Xt is the distance of the aspheric axis from the measured data.
Xt是指非球面光轴到测量起始点之间的距 离。
非球面参数简介
• Xv:
Xv is the distance of the lowest valley from the aspheric axis .
6) Residual Error After Form Removal 形状去除之后的残余误差
+Z 轴
Aspherics axis 非球面轴线
+X 轴
-X轴
D=B-C(Residual error after
absolute aspheric form removal)
-Z 轴
去除绝对形状后的残余误差
• 之所以称为“锥面”项,是由于我们可以用 不同方位的面与圆锥相切可以得到以上表面
基本形式:球面(K=0)
相切面平行于圆锥底面
圆的标准方程: x2 y2 R2 (R 0)
基本形式:抛物面(K=-1)
相切面平行于圆锥侧面
抛物线标准方程 : y2 2 px或y2 2 px或 x2 2 py或x2 2 py( p 0)
基于Matlab的非圆行星齿轮机构节曲线求解

基于Matlab 的非圆行星齿轮机构节曲线求解李 磊,杜长龙,杨善国(中国矿业大学机电工程学院,江苏徐州221008)摘要:合理的节曲线设计是可用于低速大扭矩液压马达的变中心距非圆行星齿轮机构正常工作的关键。
非圆太阳轮的节曲线由椭圆演变而来,非圆内齿圈的节曲线通过非圆行星齿轮机构的转化机构求解。
在理论分析的基础上,采用Matlab 为工具,以某型变中心距非圆行星齿轮机构为例对其节曲线进行了求解。
关键词:节曲线;非圆行星齿轮;Matlab 中图分类号:TH1321425 文献标志码:A 文章编号:100320794(2008)0120023203Solving of N on -circular Planetary G ear Pitch Curve B ased on MatlabLI Lei ,DU Ch ang -long ,YANG Sh an -guo(C ollege of Mechanical and E lectronic Engineering of China University of M ining and T echnology ,Xuzhou 221008,China )Abstract :Appropriate pitch curve designing is a key of regularly w orking for non -circular planetary gear mechanism with variable center distance which can be used in low speed high torque hydraulic m otor.The pitch curve of sun gear is ev olved from ellipse and that of internal gear is s olved through the invert mechanism of the non -circular planetary gear mechanism.The pitch curve of a non -circular planetary gear mechanism with variable center distance is s olved with Matlab based on the theory analysis.K ey w ords :pitch curve ;non -circular planetary gear ;Matlab0 前言1977年波兰人B.Sieniawski 开发出了S OK 型非圆行星齿轮低速大扭矩液压马达,相比于传统的低速大扭矩液压马达具有结构简单、体积重量小、效率高及对污染敏感性低等优点。
非球面轮廓测量与分析(课堂PPT)

.
28
Form Talysurf 测量非球面
3) Standard Equation for an Aspheric Surface 非球面的标准方程
• 测定方式: • 1.接触式测定方式
--测量探针从补测物表面滑过,电脑通过精密传感器记 录下探针所走过的轨迹.此轨迹即为被测表面的轮廓形状.
2.非接触式测定方式
--非接触测量是以光电、电磁等技术为基础,在不接触 被测物体表面的情况下,得到物体表面参数信息的测量方 法。典型的非接触测量方法如激光三角法、电涡流法、超 声测量法、机器视觉测量等等。
.
20
刀尖的形状误差
• 刀具刀尖的形状误差将会被复制到工件的 表面上
• 许多用户从未想过用FTS去检查刀具的半径 和形状误差
.
21
形状误差的方向
• 对于非球面,误差平行于非球面轴 • 对于球面,误差沿最佳拟合圆的法向
Asp here
Sp here
.
22
非球面轮廓测量方法简介
.
23
非球面測定
• 目的:求测定过非球面形状与设计非球面形 状之差值
.
10
圆锥曲线
圆锥曲线统一定义:平面内到一个定点F和到一条定直 线L(F不在L上)的距离的比等于常数e的点的轨迹.当 0<e<1时,它表示椭圆;当e>1时,它表示双曲线; 当e=1时,它表示抛物线.(其中e是圆锥曲线的离心 率,定点F是圆锥曲线的焦点,定直线是圆锥曲线的准 线)
• 之所以称为“锥面”项,是由于我们可以用
.
24
非球面測定方式
• 1.接触式测定方式 a)Form Talysurf(T/H) b) UA3P(Panasonic)
非圆曲线数控编程技巧

极坐标是描述曲线的另一种方法,通过极坐标可以表示出曲线上任意一点的极坐标
参数方程和极坐标都可以用于非圆曲线的编程,但参数方程更常用于描述复杂的曲线形状,而极坐标更常用于描述简单的曲线形状
贝塞尔曲线与B样条曲线
贝塞尔曲线与B样条曲线的数学基础:贝塞尔曲线与B样条曲线的数学基础是微积分和线性代数,通过求解微分方程和线性方程组来获得曲线的参数方程和形状。
选择合适的编程算法:根据非圆曲线的特点和加工要求,选择合适的编程算法,如B样条曲线、NURBS曲线等。
优化算法参数:根据加工精度和效率要求,优化算法参数,如控制点分布、曲率变化等。
减少计算量:通过优化算法,减少计算量,提高编程效率。
提高加工精度:通过优化算法,提高加工精度,减少加工误差。
提高加工效率:通过优化算法,提高加工效率,减少加工时间。
软件更新:及时更新软件版本,获取最新的功能和优化方法
非圆曲线编程的学习资源与交流平台
学习资源:在线教程、视频教程、书籍等
添加标题
交流平台:论坛、QQ群、微信群等
添加标题
软件工具:AutoCAD、Solidworks、UG等
添加标题
资源共享:代码库、模型库、插件等
添加标题
THANKS
汇报人:
确定非圆曲线的起点和终点
确定非圆曲线的半径和弧长
确定非圆曲线的旋转角度和旋转方向
确定非圆曲线的切线方向和切线长度
确定非圆曲线的曲率半径和曲率变化率
确定非圆曲线的法线方向和法线长度
Part Three
非圆曲线编程的数学基础
参数方程与极坐标
非圆曲线编程的数学基础主要包括参数方程和极坐标
参数方程是描述曲线的一种方法,通过参数方程可以表示出曲线上任意一点的坐标
数控编程中非圆曲线的数学处理

来源于:注塑财富网数控编程中非圆曲线的数学处理非圆曲线包括除圆以外的各种可以用方程描述的圆锥二次曲线(如:抛物线、椭圆、双曲线)、阿基米德螺线、对数螺旋线及各种参数方程、极坐标方程所描述的平面曲线与列表曲线等等。
数控铣床在加工上述各种曲线平面轮廓时,一般都不能直接进行编程,而必须经过数学处理以后,以直线一圆弧逼近的方法来实现。
但这一工作一般都比较复杂,有时靠手工处理已经不大可能,必须借助计算机作辅助处理,最好是采用计算机自动编程高级语言来编制加工程序。
处理用数学方程描述的平面非圆曲线轮廓图形,常采用相互连接的弦线逼近和圆弧逼近方法,下面将分别进行介绍。
(1)弦线逼近法一般来说,由于弦线法的插补节点均在曲线轮廓上,容易计算,程编也简便一些,所以常用弦线法来逼近非圆曲线,其缺点是插补误差较大,但只要处理得当还是可以满足加工需要的,关键在于插补段长度及插补误差控制。
由于各种曲线上各点的曲率不同,如果要使各插补段长度均相等,则各段插补的误差大小不同。
反之,如要使各段插补误差相同,则各插补段长度不等。
下面是常用的两种处理方法。
1)等插补段法等插补段法是使每个插补段长度相等,因而插补误差补等。
编程时必须使产生的最大插补误差小于允差的1/2~1/3,以满足加工精度要求。
一般都假设最大误差产生在曲线的曲率半径最小处,并沿曲线的法线方向计算,见图所示。
这一假设虽然不够严格,但数控加工实践表明,对大多数情况是适用的。
2)等插补误差法等插补误差法是使各插补断的误差相等,并小于或等于允许的插补误差,这种确定插补段长度的方法称为“等插补误差法”。
显然,按此法确定的各插补段长度是不等的,因此又叫“变步长法”。
这种方法的优点是插补段数目比上述的“等插补段法”少。
这对于一些大型和形状复杂的非圆曲线零件有较大意义。
对于曲率变化较大的曲线,用此法求得的节点数最少,但计算稍繁。
(2)圆弧逼近法曲线的圆弧逼近有曲率圆法、三点圆法和相切圆法等方法。
非圆曲线数学处理的一般方法
非圆曲线非圆曲线数学处理数学处理数学处理的一般的一般的一般方法方法方法数控系统一般只有直线和圆弧插补的功能,对于非圆曲线轮廓,只有用直线或圆弧去逼近它,“节点”就是逼近线段与非圆曲线的交点。
一个已知曲线的节点数主要取决于逼近线段的形状(直线段还是圆弧段),曲线方程的特性以及允许的逼近误差。
将这三者利用数学关系求解,即可求得一系列的节点坐标,并按节点划分程序段。
以下简介常用的直线逼近及圆弧逼近的数学处理方法。
2.1 常用非圆曲线直线逼近方法常用非圆曲线直线逼近方法2.1.1 等间距的直线逼近的节点计算这是一种最简单的算法。
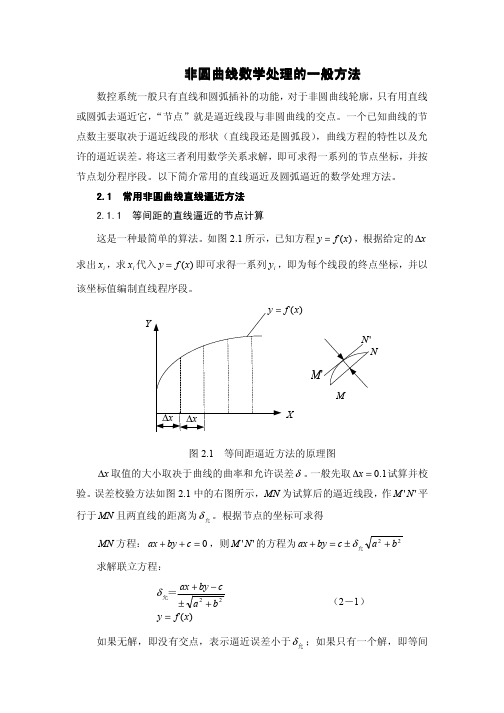
如图2.1所示,已知方程)(x f y =,根据给定的x ∆求出i x ,求i x 代入)(x f y =即可求得一系列i y ,即为每个线段的终点坐标,并以该坐标值编制直线程序段。
XYNMM )(x f图2.1 等间距逼近方法的原理图x ∆取值的大小取决于曲线的曲率和允许误差δ。
一般先取1.0=∆x 试算并校验。
误差校验方法如图2.1中的右图所示,MN 为试算后的逼近线段,作''N M 平行于MN 且两直线的距离为允δ。
根据节点的坐标可求得MN 方程:0=++c by ax ,则''N M 的方程为22b a c by ax +±=+允δ 求解联立方程:)(22x f y b a cby ax =+±−+=允δ (2-1)如果无解,即没有交点,表示逼近误差小于允δ;如果只有一个解,即等间距与轮廓线相切,表示逼近误差等于允δ;如果有两个或两个以上的解,表示逼近误差大于允δ,这时应缩小等间距坐标的增量值,重新计算节点和验算逼近误差,直至最大的逼近误差小于等于允δ。
等间距法计算简单,但由于取定值x ∆应保证曲线曲率最大处的逼近误差允许值,所以程序可能过多。
用此种方法进行数学处理,它的逼近曲线与轮廓线的逼近误差参差不齐,程序明显增多,影响机床的加工效率,不适合大批量的加工,成本也比较高。
轮廓度的计算公式

轮廓度的计算公式轮廓度是描述曲面或曲线形状偏差的一个重要概念,在工程制造、设计等领域有着广泛的应用。
那咱们就来好好聊聊轮廓度的计算公式。
咱们先从一个简单的例子说起。
有一次我去工厂参观,看到工人们正在加工一批零件。
其中有个零件的外形要求非常精确,就涉及到了轮廓度的控制。
这个零件就像是一个小小的雕塑,它的边缘形状必须完美符合设计要求,偏差不能太大,不然整个产品就可能出问题。
轮廓度的计算公式其实有多种形式,这取决于具体的测量方法和应用场景。
常见的有最大内切圆法和最小外接圆法。
最大内切圆法,就是找到能完全内切于被测轮廓的最大圆,然后计算这个圆与实际轮廓之间的偏差。
比如说,我们有一个不规则的封闭曲线,就像是小朋友画的歪歪扭扭的圈圈。
我们要找到一个最大的圆,能刚好在这个圈圈里面,而且和圈圈的每一个点都接触到。
这个圆的半径与理想轮廓半径的差值,就是轮廓度的一种度量。
最小外接圆法呢,则是反过来,要找到能完全外接于被测轮廓的最小圆。
还是拿那个小朋友画的圈圈举例,这次我们要找一个最小的圆,能把这个圈圈完全包在里面,而且圈圈上的每一个点都能碰到这个圆。
同样,这个圆的半径与理想轮廓半径的差值,也是轮廓度的一种表现。
在实际应用中,还会用到两点法、三点法等等。
两点法就是通过测量轮廓上两个特定点之间的距离来评估轮廓度。
想象一下,在那个不规则的圈圈上,选取两个特殊的点,然后测量它们之间的直线距离,再和理想的距离进行比较。
三点法就更复杂一些啦,需要在轮廓上选取三个特定的点,形成一个三角形,通过计算这个三角形的一些参数来评估轮廓度。
这就好像是在圈圈上找三个好朋友,通过他们的位置关系来判断圈圈是不是画得标准。
当然啦,轮廓度的计算可不是那么简单的事儿。
有时候,还需要考虑测量的精度、测量工具的误差,以及环境因素的影响。
就像在那个工厂里,温度的变化、测量仪器的校准,都会对最终的轮廓度测量结果产生影响。
而且,不同的行业对于轮廓度的要求也不一样。
非圆曲线逼近的算法实现

目录一、概述 (1)1.1、摘要 (1)1.2、设计的目的和意义 (1)1.3、逼近算法的发展概况 (1)二、算法的设计思路及实现 (3)3.1、等间距法 (3)3.2、等弦长法 (6)3.3、等误差法 (8)3.4、伸缩步长法 (12)三、算法优化的工作流程图 (14)四、软件开发介绍 (18)4.1主界面介绍 (18)4.2数控加工抛物线界面介绍 (19)4.3数控加工椭圆曲线界面介绍 (26)五、设计总结 (30)六、参考文献 (30)一、概述1.1、摘要数控系统一般都只有直线和圆弧插补的功能,对于非圆曲线的轮廓,只有用到直线或圆弧去逼近它。
这就要求我们对非圆曲线的逼近的数学处理要有一定的了解。
而关键的是我们要知道什么是节点,如何求节点。
非圆曲线的逼近方法可以分为直线逼近和圆弧逼近,每一种又可以有若干种方法求节点坐标。
本设计是有关抛物线和椭圆曲线的逼近,利用VB编程,用各种直线逼近方法得到最优的算法。
,关键词:非圆曲线, 逼近, 等间距法, 等弦长法,等误差法,伸缩步长法1.2、设计的目的和意义数控机床课程设计是机电专业教学活动的一个重要的实践性环节,是对学生所学《数控机床》课程和其它有关课程知识和技能的一次综合性练习,旨在使之巩固、充实、系统化,并得到进一步扩展。
课程设计是培养学生理论联系实际、解决生产实际问题的机会。
通过对非圆曲线逼近编程的具体问题的解决,使学生对数控机床的结构原理、设计方法以及用编程方法处理实际问题的一般步骤和具体技巧得到训练,提高运用所学专业知识分析问题和解决问题的能力。
CAD/CAM(计算机辅助设计/计算机辅助制造)的能力和水平是一个国家自动化程度的标志之一。
而曲线曲面造型技术则是CAD/CAM的基础,曲线曲面表示的精确度和造型灵活性是评定CAD系统功能强弱的重要因素。
1.3、逼近算法的发展概况数控系统一般都只有直线和圆弧插补的功能,对于非圆曲线的轮廓,只有用到直线或圆弧去逼近它。
非圆弧曲线计算公式

非圆弧曲线计算公式在数学和工程领域中,曲线是一种非常重要的概念,它们可以用来描述各种各样的现象和物体。
在实际应用中,我们经常会遇到各种各样的曲线,其中包括非圆弧曲线。
非圆弧曲线是指那些不能用圆弧来描述的曲线,它们可能是由多个不同的曲线段组成的,也可能是由一些特殊的曲线方程所描述的。
在本文中,我们将讨论一些常见的非圆弧曲线,并给出它们的计算公式。
1. 抛物线。
抛物线是一种非常常见的曲线,它的数学描述是一个二次方程。
一般来说,抛物线的标准方程可以写成,y=ax^2+bx+c,其中a、b和c是常数。
根据这个方程,我们可以计算出抛物线上任意一点的坐标,从而可以对抛物线进行各种各样的分析和应用。
2. 椭圆。
椭圆是另一种常见的非圆弧曲线,它的数学描述是一个二次方程。
椭圆的标准方程可以写成,(x-h)^2/a^2+(y-k)^2/b^2=1,其中(a,b)是椭圆的半长轴和半短轴的长度,(h,k)是椭圆的中心点的坐标。
通过这个方程,我们可以计算出椭圆上任意一点的坐标,从而可以对椭圆进行各种各样的分析和应用。
3. 双曲线。
双曲线是一种非常特殊的曲线,它的数学描述是一个二次方程。
双曲线的标准方程可以写成,(x-h)^2/a^2-(y-k)^2/b^2=1,其中(a,b)是双曲线的半长轴和半短轴的长度,(h,k)是双曲线的中心点的坐标。
通过这个方程,我们可以计算出双曲线上任意一点的坐标,从而可以对双曲线进行各种各样的分析和应用。
4. 抛物线。
抛物线是一种非常常见的曲线,它的数学描述是一个二次方程。
一般来说,抛物线的标准方程可以写成,y=ax^2+bx+c,其中a、b和c是常数。
根据这个方程,我们可以计算出抛物线上任意一点的坐标,从而可以对抛物线进行各种各样的分析和应用。
5. 椭圆。
椭圆是另一种常见的非圆弧曲线,它的数学描述是一个二次方程。
椭圆的标准方程可以写成,(x-h)^2/a^2+(y-k)^2/b^2=1,其中(a,b)是椭圆的半长轴和半短轴的长度,(h,k)是椭圆的中心点的坐标。
关于非圆曲线的数学结论

关于非圆曲线的数学结论非圆曲线是指在平面上不满足圆的几何属性的曲线。
它们包括椭圆、双曲线和抛物线等几种不同类型的曲线。
首先我们来讨论一下椭圆曲线。
椭圆曲线是一个非常重要的数学对象,在密码学、编码理论等领域有广泛的应用。
椭圆曲线是一条形状像椭圆一样的曲线,它由满足一个特定方程的点构成。
椭圆曲线的方程为 y^2 = x^3 + ax + b,其中a和b是常数。
椭圆曲线上的点满足这个方程,并且还满足一条称为“群律”的运算法则。
在椭圆曲线上,我们可以定义加法运算,将两个点相加得到另一个点,同时还有一个单位元0。
椭圆曲线上的点的运算形成了一个群结构,这个群结构具有一些特殊的性质,例如封闭性、结合律、交换律和存在单位元等。
接下来我们来讨论一下双曲线。
双曲线是一类形状类似于两个开口的抛物线的曲线。
它的方程一般为x^2/a^2 - y^2/b^2 = 1,其中a和b是常数。
双曲线具有一些特殊的几何性质。
首先,双曲线有两个分支,在无穷远处相交。
其次,双曲线有两条渐近线,这两条线对曲线的形态有重要影响。
双曲线还具有对称性质,它在横轴和纵轴两个方向上都有对称轴。
双曲线是一种非常重要的几何形态,在电磁学、光学等领域中有广泛的应用。
最后我们来讨论一下抛物线。
抛物线是一种非常常见的几何曲线,它的形状类似于开口向上或向下的碗状曲线。
抛物线的方程一般为 y = ax^2 + bx + c,其中a、b和c是常数。
抛物线具有一些特殊的性质。
首先,它有一个顶点,也就是曲线的最高点或最低点。
其次,它具有对称性质,它关于顶点对称。
抛物线还具有一些重要的应用,例如在物理学中,我们可以利用抛物线的性质来描述近似平抛运动或抛体运动。
总结起来,非圆曲线是一类不满足圆的几何属性的曲线,包括椭圆曲线、双曲线和抛物线等几种类型。
这些曲线具有一些特殊的几何性质,在数学、物理等领域有广泛的应用。
研究非圆曲线及其性质,有助于我们深入理解几何学的基本概念和数学的抽象思维方式,并且为解决实际问题提供了重要的工具和方法。
《数控技术与应用》试题库

《数控技术与应用》试题库1数控编程局部:一、填空题1、从工件图*始,到获得数控机床所需控制匝的全过程称为程序编制,程序编制的方法有I手工编程I和I百动编程I。
2、数控机床实现插补运算较为成熟并得到广泛应用的是匝插补和瓯插补。
3、穿孔带是数控机床的一种控制介质,国际上通用标准是函和®两种,我国采用的标准是回。
4、自动编程根据编程信息的输入与计算机对信息的处理方式不同,分为以|自动编程商为根底的自动编程方法和以|计算机绘图|为根底的自动编程方法。
5、数控机床由控制介质、|数控装置|和阀限系细、两函等局部组成。
6、数控机床按控制运动轨迹可分为点位控制、点位直线控制和轮廓控制等几种。
按控制方式又可分为开环控制、闭环控制和半闭环控制等。
7、对刀点既是程序的起点,也是程序的终点。
为了提高零件的加工精度,对刀点应尽量选在零件的设it基准或工艺基准上。
8、在数控加工中,刀具刀位点相对于工件运动的轨迹称为虹路线。
9、在轮廓控制中,为了保证一定的精度和编程方便,通常需要有刀具瓯和留圈补偿功能。
10、编程时的数值计算,主要是计算零件的基点和节点的坐标,或刀具中心轨迹的基点和节点的坐标。
直线段和圆弧段的交点和切点是基点,逼近直线段或圆弧小段轮廓曲线的交点和切点是|节点。
二、判断题1、数控加工程序是由假设干程序段组成,而且一般常采用可变程序进行编程。
2、只需根据零件图样进行编程,而不必考虑是刀具运动还是工件运动。
3、两轴联动坐标数控机床只能加工平面零件轮廓,曲面轮廓零件必须是三轴坐标联动的数控机床。
4、进给路线确实定一是要考虑加工精度,二是要实现最短的进给路线。
5、刀位点是刀具上代表刀具在工件坐标系的一个点,对刀时,应使刀位点与对刀点重合。
6、数控机床的进给路线就是刀具的刀尖或刀具中心相对机床的运动轨迹和方向。
7、数控机床的进给路线不但是作为编程轨迹计算的依据,而且还会影响工件的加工精度和外表粗糙度。
8、机床的原点就是机械零点,编制程序时必须考虑机床的原点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
用数学方程描述的非圆曲线的轮廓数值计算
数控加工中把除了直线与圆弧之外用数学方程式表达的平面轮廓曲线称为非圆曲线。
非圆曲线的节点就是逼近线段的交点。
一个已知曲线)(x f y =的节点数目主要取决于所用逼近线段的形状(直线或圆弧)、曲线方程的特性以及允许的拟合误差。
将这三个方面利用数学关系来求解,即可求得相应的节点坐标。
下面简要介绍常用的直线逼近节点的计算方法。
(1)等间距直线逼近的节点计算 1)基本原理
等间距法就是将某一坐标轴划分成相等的间距,然后求出曲线上相应的节点。
如图3.1所示,已知曲线方程为)(x f y =,沿X 轴方向取Δx 为等间距长。
根据曲线方程,由i x 求得i y ,i
x +1
=i x +Δx ,
)(1x x f y i i ∆+=+,如此求得的一系列点就是节点。
2) 误差校验方法
由图3.1知,当x ∆取得愈大,产生的拟和误差愈大。
设工件的允许拟合误差为δ,一般δ取成零件公差的1/5~1/10,要求曲线)(x f y =与相邻两节点连线间的法向距离小于δ。
实际处理时,并非任意相邻两点间的误差都要验算,对于曲线曲率半径变化较小处,只需验算两节点间距最长处的误差,而对曲线曲率变化较大处,应验算曲率半径较小处的误差,通常由轮廓图形直接观察确定校验的位置。
其校验方法如下:
设需校验mn 曲线段。
n m 和的坐标分别为(m m y x ,)和(n n y x ,),则直线mn 的方程为:
n
m n m n
n y y x x y y x x --=--
令A=n m y y -,B=m n x x -,C=n m n m y x x y -,则上式可改写为A x +B y =C 。
表示公差带范围的直线n m ''与mn 平行,且法向距离为δ。
n m ''直线方程可表示为:
2
2
B A
C By Ax +±=+δ
式中,当直线n m ''在mn 上边时取“+”号,在mn 下边时“-”号。
联立求解方程组:
()⎪⎩⎪⎨⎧+±=+=2
2B
A C By Ax x f y δ
上式若无解,表示直线n m ''不与轮廓曲线)(x f y =相交,拟合误差在允许范围内;若只有一个解,表示直线n m '
'图3.1 等间距直线逼近
图3.2 等步长直线逼近
与)(x f y =相切,拟合误差等于δ;若有两个解,且m x ≤x ≤n x ,则表示超差,此时应减小x ∆重新进行计算,直到满足要求为止。
(2) 等步长直线逼近的节点计算
这种计算方法是使所有逼近线段的长度相等,从而求出节点坐标。
如图3.2所示,计算步骤如下:
1) 求最小曲率半径min R 曲线)(x f y =上任意点的曲率半径为:
y y R '
''+=
2
/32
)
1(
取0/=dx dR ,即:
0)1(32
2
=''''--'''y y y y
根据)(x f y =求得y '、y ''、y ''',并代入上式得x ,再将x 代入前式求得min R 。
2)确定允许的步长l 由于曲线各处的曲率半径不等,等步长后,最大拟合误差max δ必在最小曲率半径min R 处。
因此步长应为:
δδmin 2
min 2
min 8)(2R R R l ≈
--=
3)计算节点坐标 以曲线的起点),(a a y x a 为圆心,步长l 为半径的圆交)(x f y =于b 点,求解圆和曲线的方程组:
⎩⎨
⎧==-+-)
()()(2
22x f y l y y x x a a 求得b 点坐标),(b b y x 。
顺序以b 、c ……为圆心,即可求得c 、d ……各节点的坐标。
由于步长l 决定于最小曲率半径,致使曲率半径较大处的节点过密过多,所以等步长法适用于曲率半径相差不大的曲线。
(3)等误差直线逼近的节点计算
等误差法就是使所有逼近线段的误差δ相等。
如图3.3所示,其计算步骤如下: 1)确定允许误差δ的圆方程 以曲线起点),(
a a y x a 为圆心,δ为半径作圆,此圆方程式为:
2
2
2
)
()(δ
=-+-a a y y x x
2)求圆与曲线公切线PT 的斜率k
P
T P T x x y y k --=
图3.3 等误差直线段逼近
其中T x 、P x 、T y 、P y 由下面的联立方程组求解:
a
P a P P
T P T y y x x x x y y ---
=-- (圆切线方程)
a a P P y x x y +--=
2
2
)(δ
(圆方程)
)(T P
T P T x f x x y y '=-- (曲线切线方程)
)(T T x f y = (曲线方程)
3)求弦长ab 的方程 过a 作直线PT 的平行线,交曲线于b 点,ab 的方程为:
)(a a x x k y y -=-
4)计算节点坐标 联立曲线方程和弦长方程即可求得b 点坐标),(b b y x 。
)
()(x f y x x k y y a a =-=-
按上述步骤顺次求得c 、d 、e ……各节点坐标。
由上可知,等误差法程序段数目最少,但计算较复杂,可用计算机辅助完成。
在采用直线逼近非圆曲线的拟合方法中,是一种较好的方法。
