哈工大一阶倒立摆
直线一级倒立摆控制器设计(哈工大2013)资料

291. 概述自动控制理论(包括古典部分和现代部分)是电气工程系学生的一门必修专业基础课,课程中的一些概念相对比较抽象,如系统的稳定性、可控性、收敛速度和抗干扰能力等。
倒立摆系统是一个典型的非线性、强耦合、多变量和不稳定系统,作为控制系统的被控对象,它是一个理想的教学实验设备,许多抽象的控制概念都可以通过倒立摆直观地表现出来。
本课程设计的目的是让学生以一阶倒立摆为被控对象,了解用古典控制理论设计控制器(如PID 控制器)的设计方法和用现代控制理论设计控制器(极点配置)的设计方法,掌握MATLAB 仿真软件的使用方法及控制系统的调试方法,加深学生对所学课程的理解,培养学生理论联系实际的能力。
本课程设计的被控对象采用固高公司生产的GIP-100-L 型一阶倒立摆系统,课程设计包括三方面的内容:(1)建立直线一级倒立摆的线性化数学模型;(2)倒立摆系统的PID 控制器设计、MATLAB 仿真及实物调试;(3)倒立摆系统的状态空间极点配置控制器设计、MATLAB 仿真及实物调试。
1.1 实验设备简介一级倒立摆系统的结构示意图如图1-1所示。
小车滑轨皮带电机摆杆图1-1 一阶倒立摆结构示意图系统组成框图如图1-2所示。
图1-2 一级倒立摆系统组成框图系统是由计算机、运动控制卡、伺服机构、倒立摆本体和光电码盘几大部分组成的闭环系统。
光电码盘1将小车的位移、速度信号反馈给伺服驱动器和运动控制卡,摆杆的角度、角速度信号由光电码盘2反馈给运动控制卡。
计算机从运动控制卡中读取实时数据,确定控制决策(小车运动方向、移动速度、加速度等),并由运动控制卡来实现29该控制决策,产生相应的控制量,使电机转动,通过皮带,带动小车运动,保持摆杆平衡。
1.2设计内容1.2.1.建立一级倒立摆数学模型在《自动控制理论》课程中,有一章专门讲述控制系统的数学模型的建立方法,并将非线性数学模型在一定条件下化简成线性数学模型,在此以一级倒立摆为例,建立其数学模型,并在摆角0=φ附近将其非线性数学模型线性化,学生通过实际数学模型的推导,熟悉机理建模的一般方式,加深对控制对象的理解。
一阶倒立摆的控制方法

一阶倒立摆的控制方法
一阶倒立摆是一种非常有趣的机械系统,它提供了在控制和稳定化方面的许多挑战。
一阶倒立摆的控制方法取决于许多因素,包括机械结构、系统响应、控制信号和传感器输入等。
在一阶倒立摆中,一个质点在垂直支撑物上平衡,支撑物可以是摆锤也可以是其他机械结构。
在“正常”情况下,质点的位置会小幅度波动,但总体上保持平衡。
在不正常的情况下,例如外力干扰或系统响应问题,质点的位置可能会失去平衡,导致设备失效。
为了解决这些问题,一些常见的控制方法包括PID控制、神经网络控制和模糊控制等。
其中,最常用的PID控制方法是基于比例、积分和微分控制来实现的。
这种方法可以计算出当前状态和目标状态的差异,然后调节偏差的大小和方向,以让设备回归到稳定状态。
另一种常见的控制方法是神经网络控制。
这种方法的理念是通过构建一个基于神经网络结构的模型来控制设备。
神经网络具有学习和记忆功能、非线性映射和复杂的自适应能力等特点,可以较好地应对一阶倒立摆的不稳定性与外部干扰的问题。
最后,模糊控制是一种模糊数学技术,它可以将输入和输出模糊化,以便通过一系列规则来达到控制目标。
模糊控制方法较为简单,但需要有丰富经验和良好的控制规则,否则很容易导致控制结果的不稳定性。
总的来说,在一阶倒立摆的控制中,各种方法都有自己的优缺点。
开发一种切实可行的控制方法需要考虑到各种因素,包括系统响应时间、控制稳定性、控制信号噪声干扰、成本等等。
因此,为了实现一
阶倒立摆的各种应用,需要有较为全面的控制方案和少量控制策略的
实践应用。
哈工大一阶倒立摆

2.1
倒立摆系统其本身是自不稳定系统,实验建模存在一些问题和困难,在忽略掉一些次要的因素后,倒立摆系统是一个典型的运动的刚体系统,可以再惯性坐标系中运用经典力学对它进行分析,来建立系统动力学方程。
在忽略掉了空气阻力和各种摩擦力之后,可以讲一阶倒立摆系统抽象成小车和均匀杆组成的系统,一阶倒立摆系统的结构示意图如下:
四预防和控制轰燃的灭火救援对策一全面侦查火情注意轰燃征兆在处置建筑室内火灾时应全面侦查火情快速掌握起火房间位置火势大小人员被困情况室内可燃物数量与类别建筑结构特点周围毗邻建筑情况等尤其对于通风不好且室内可燃物数量较多时应提高警惕密切监视谨防轰燃突发造成恶性事故
哈尔滨工业大学
控制科学与工程系
控制系统设计课程设计报告
(2-8)
微分方程的建立:
因为 ,假设φ<<1弧度,则可以进行近似处理: 来实现线性化。
用上述近似进行线性化得直线一阶倒立摆的微分方程为:
一阶倒立摆的传递函数模型:
对上式进行拉普拉斯变换,得:
推导传递函数时假设初始条件为0。
由于输出为角度φ,求解方程组的第一个方程,可得:
或
如果令 ,则有:
把上式代入方程组(2-1)的第二个方程,得:
该系统的输出为
其中: num——被控对象传递函数的分子项
den——被控对象传递函数的分母项
numPID——PID控制器传递函数的分子项
denPID——PID控制器传递函数的分母项
通过分析上式就可以得到系统的各项性能。
由(2-13)可以得到摆杆角度和小车加速度的传递函数:
PID控制器的传递函数为:
只需调节PID控制器的参数,就可以得到满意的控制效果。
一级倒立摆分析

一级倒立摆的极点配置及仿真摘要倒立摆系统是一个复杂的、高度非线性的、不稳定的高阶系统,是学习和研究现代控制理论最合适的实验装置。
倒立摆的控制是控制理论应用的一个典型范例,一个稳定的倒立摆系统对于证实状态空间理论的实用性是非常有用的。
本文主要研究的是一级倒立摆,首先应用动力学方程建立一级倒立摆的非线性数学模型,采用小偏差线性化的方法在平衡点附近局部线性化得到线性化的数学模型。
然后通过输入单位阶跃信号分析系统的开环稳定性,由线性化得到的状态方程判断系统的能控性和能观性,结合系统的稳定性条件、调整时间以及超调量找到合适的极点,运用极点的配置方法(Matlab的acker函数)算出状态反馈增益矩阵K,运用状态空间分析方法,采用状态反馈为倒立摆系统建立稳定的控制律,并判断加入反馈矩阵K后的能观性和能控性是否改变。
最后应用Matlab中的Simulink建立相应框图,得到输出变量水平位置和角度随时间的变化曲线,验证加入反馈矩阵K后一级倒立摆系统的稳定性。
关键词:一级倒立摆状态反馈极点配置Matlab Simulink目录1、一级倒立摆系统简介 (3)2、一级倒立摆系统的数学模型 (4)2.1、数学模型的建立 (4)2.2、运动分析 (5)2.2.1、沿水平方向运动(直线运动) (5)2.2.2、绕轴线的转动(旋转运动) (6)3、状态空间极点配置 (8)3.1、系统开环稳定性分析 (8)3.2、开环系统的能控性分析 (10)3.3、开环系统的能观性分析 (11)3.4、系统极点配置 (12)3.5、闭环系统的能控性和能观性分析 (15)4、一级倒立摆系统Matlab仿真 (17)4.1、系统开环Simulink搭建及仿真 (17)4.2、系统极点配置后的Simulink仿真 (19)5、总结 (23)6、参考文献 (24)1、一级倒立摆系统简介倒立摆系统是一种很常见的又和人们的生活密切相关的系统,它深刻揭示了自然界一种基本规律,即自然不稳定的被控对象,通过控制手段可使之具有良好的稳定性。
一级倒立摆控制系统设计说明

基于双闭环PID控制的一阶倒立摆控制系统设计一、设计目的倒立摆是一个非线性、不稳定系统,经常作为研究比较不同控制方法的典型例子。
设计一个倒立摆的控制系统,使倒立摆这样一个不稳定的被控对象通过引入适当的控制策略使之成为一个能够满足各种性能指标的稳定系统。
二、设计要求倒立摆的设计要使摆杆尽快地达到一个平衡位置,并且使之没有大的振荡和过大的角度和速度。
当摆杆到达期望的位置后,系统能克服随机扰动而保持稳定的位置。
实验参数自己选定,但要合理符合实际情况,控制方式为双PID控制,并利用 MATLAB进行仿真,并用simulink对相应的模块进行仿真。
三、设计原理倒立摆控制系统的工作原理是:由轴角编码器测得小车的位置和摆杆相对垂直方向的角度,作为系统的两个输出量被反馈至控制计算机。
计算机根据一定的控制算法,计算出空置量,并转化为相应的电压信号提供给驱动电路,以驱动直流力矩电机的运动,从而通过牵引机构带动小车的移动来控制摆杆和保持平衡。
四、设计步骤首先画出一阶倒立摆控制系统的原理方框图一阶倒立摆控制系统示意图如图所示:分析工作原理,可以得出一阶倒立摆系统原理方框图:一阶倒立摆控制系统动态结构图下面的工作是根据结构框图,分析和解决各个环节的传递函数!1.一阶倒立摆建模在忽略了空气流动阻力,以及各种摩擦之后,可将倒立摆系统抽象成小车和匀质杆组成的系统,如下图所示,其中: M :小车质量 m :为摆杆质量 J :为摆杆惯量 F :加在小车上的力 x :小车位置θ:摆杆与垂直向上方向的夹角l :摆杆转动轴心到杆质心的长度根据牛顿运动定律以及刚体运动规律,可知: (1) 摆杆绕其重心的转动方程为(2) 摆杆重心的运动方程为得sin cos ..........(1)y x J F l F l θθθ=-2222(sin ) (2)(cos ) (3)x y d F m x l d td F mg m l d t θθ=+=-(3)小车水平方向上的运动为22..........(4)x d xF F M d t-=联列上述4个方程,可以得出一阶倒立精确气模型:()()()()()()()2222222222222222sin .sin cos cos cos .sin cos .lg sin cos J ml F ml J ml m l g x J ml M m m l ml F m l M m m m l M m J ml θθθθθθθθθθθθ⎧+++-⎪=++-⎪⎨+-+⎪=⎪-++⎩式中J 为摆杆的转动惯量:32ml J =若只考虑θ在其工作点附近θ0=0附近(︒︒≤≤-1010θ)的细微变化,则可以近似认为:⎪⎩⎪⎨⎧≈≈≈1cos sin 02θθθθ ⎪⎪⎩⎪⎪⎨⎧++-+=++-+=2..2222..)(lg )()()(Mml m M J mlF m m M Mml m M J g l m F ml J x θθθ 若取小车质量M=2kg,摆杆质量m=1kg,摆杆长度2 l =1m,重力加速度取g=2/10s m ,则可以得 一阶倒立摆简化模型:....0.44 3.330.412x F F θθθ⎧=-⎪⎨⎪=-+⎩即 G 1(s)= ; G 2(s)=一阶倒立摆环节问题解决!2.电动机驱动器选用日本松下电工MSMA021型小惯量交流伺服电动机,其有关参数如下:222()0.4()12() 1.110()s F s s x s s s s θθ-⎧=⎪-⎪⎨-+⎪=⎪⎩驱动电压:U=0~100V 额定功率:PN=200W 额定转速:n=3000r/min 转动惯量:J=3×10-6kg.m2 额定转矩:TN=0.64Nm 最大转矩:TM=1.91Nm 电磁时间常数:Tl=0.001s 电机时间常数:TM=0.003s经传动机构变速后输出的拖动力为:F=0~16N ;与其配套的驱动器为:MSDA021A1A ,控制电压:UDA=0~±10V 。
一阶倒立摆系统模型分析状态反馈与观测器设计

一阶倒立摆系统模型分析状态反馈与观测器设计一阶倒立摆系统是控制工程中常见的一个具有非线性特点的系统,它由一个摆杆和一个质点组成,质点在摆杆上下移动,而摆杆会受到重力的作用而产生摆动,需要通过控制来实现倒立的功能。
以下是一阶倒立摆系统的模型分析、状态反馈与观测器设计的详细介绍。
一、系统模型分析:一阶倒立摆系统是一个非线性动力学系统,可以通过线性化的方式来进行模型分析。
在进行线性化之前,首先需要确定系统的状态变量和输入变量。
对于一阶倒立摆系统,可以将摆杆角度和质点位置作为状态变量,将水平推力作为输入变量。
在对系统进行线性化之后,可以得到系统的状态空间表达式:x_dot = A*x + B*uy=C*x+D*u其中,x是状态向量,u是输入向量,y是输出向量。
A、B、C和D是系统的矩阵参数。
二、状态反馈设计:状态反馈是一种常用的控制方法,通过测量系统状态的反馈信号,计算出控制输入信号。
在设计状态反馈控制器之前,首先需要确定系统的可控性。
对于一阶倒立摆系统,可以通过可控性矩阵的秩来判断系统是否是可控的。
如果可控性矩阵的秩等于系统的状态数量,则系统是可控的。
在确定系统可控性之后,可以通过状态反馈控制器来实现控制。
状态反馈控制器的设计可以通过选择适当的反馈增益矩阵K来实现。
具体的设计方法是,根据系统的状态空间表达式,将状态反馈控制器加入到系统模型中。
状态反馈控制器的输入是状态变量,输出是控制输入变量。
然后,通过调节反馈增益矩阵K的值,可以实现对系统的控制。
三、观测器设计:观测器是一种常用的状态估计方法,通过测量系统的输出信号,估计系统的状态。
在设计观测器之前,首先需要确定系统的可观性。
对于一阶倒立摆系统,可以通过可观性矩阵的秩来判断系统是否是可观的。
如果可观性矩阵的秩等于系统的状态数量,则系统是可观的。
在确定系统可观性之后,可以通过观测器来实现状态估计。
观测器的设计可以通过选择适当的观测增益矩阵L来实现。
具体的设计方法是,根据系统的状态空间表达式,将观测器加入到系统模型中。
一阶倒立摆的LQR稳定控制

1 0 0 0
0 0 0 3g 4l
0 0 1 0
00 00 00 00 00 00 00 00 00 00 00 00
0 0 0 0 1 0 觶 0 x + 0 0 u′ 0 准 0 3 0 0 觶 准 4l 0 0 x
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
在此我们采用牛顿 - 欧拉方法建立直线型一级倒立摆系统的数学 模型 , 在忽略了空气阻 力 和 各 种 摩 擦 之 后 , 可 将 直 线 一 级 倒 立 摆 系 统 抽象成小车和匀质杆组成的系统 , 我们不妨做以下假设 ( 小车质量 M 、 摆 杆 质 量 m、 小 车 摩 擦 系 数 b、 摆 杆 转 动 轴 心 到 杆 质 心 的 长 度 l、 加 在 小车上的力 F 、 小车位置 x )[1]。 最后得出的数学模型 :
图5
未加扰动
图6
加入轻微扰动
计算得出 K=31.6228 ,1.4046 ,-22.3514 ,0.1188
图7
加入较大扰动
图3
参数 :Q11=2000 ,Q33=500 的图像
计算得出 K=44.7214 ,17.0411 ,-22.0184 ,0.7188
三组图像比较得出 : 小车基本能稳定在一个位置 , 不会有太大的漂移 。 即使受到外界 干扰 , 小车也很快能够稳定下来 。 摆杆也相对稳定 , 没有太大的抖动 。 3.2 LQR 实时控制有比较好的控制效果 , 既能控制小车的位移 , 又能 控制摆杆的角度 。 基本与 Matlab 仿真的结果相吻合 。 因此 ,LQR 控制 法是值得我们提倡和进一步研究的 。 3.3 图 6 、 图 7 的 尖 角 处 为 受 到 外 界 干 扰 的 时 刻 , 小 车 会 有 轻 微 的 漂 移 , 但小车很快就会稳定下来 。 3.4 实时控制也告诉我们 :Matlab 仿真能达到的控制效 果 , 由 于 现 实 条件的制约 , 实时控制未必能达到 。
一阶倒立摆控制设计与实现

一阶倒立摆控制设计与实现一阶倒立摆是一种常见的控制系统模型,它由一个垂直的支柱和一个质量为m 的物体组成,物体通过支柱与地面相连。
在控制系统中,我们需要设计一个控制器来控制物体的位置和速度,使其保持在垂直位置上。
本文将介绍一阶倒立摆控制设计与实现的相关内容。
一、一阶倒立摆模型一阶倒立摆模型可以用以下方程描述:m*d^2y/dt^2 = -mg*sin(y) + u其中,y是物体的位置,u是控制器的输出,m是物体的质量,g是重力加速度,t是时间。
该方程可以通过拉普拉斯变换转换为传递函数:G(s) = Y(s)/U(s) = 1/(ms^2 + mg)二、控制器设计为了控制一阶倒立摆,我们需要设计一个控制器来产生控制信号u。
常见的控制器包括比例控制器、积分控制器和微分控制器,它们可以组合成PID控制器。
在本文中,我们将使用比例控制器来控制一阶倒立摆。
比例控制器的输出与误差成正比,误差越大,输出越大。
比例控制器的传递函数为:Gc(s) = Kp其中,Kp是比例增益。
三、闭环控制系统将控制器和一阶倒立摆模型组合起来,得到闭环控制系统的传递函数:G(s) = Y(s)/R(s) = Kp/(ms^2 + mg + Kp)其中,R(s)是参考信号,表示我们期望物体保持的位置。
四、控制系统实现在实现控制系统之前,我们需要对一阶倒立摆进行建模和仿真。
我们可以使用MATLAB等工具进行建模和仿真。
在MATLAB中,我们可以使用Simulink模块来建立一阶倒立摆模型和控制器模型。
在建立模型之后,我们可以进行仿真,观察系统的响应和稳定性。
在实现控制系统时,我们需要选择合适的硬件平台和控制器。
常见的硬件平台包括Arduino和Raspberry Pi等,常见的控制器包括PID控制器和模糊控制器等。
在实现控制系统之后,我们需要进行调试和优化,以达到最佳控制效果。
五、总结本文介绍了一阶倒立摆控制设计与实现的相关内容,包括一阶倒立摆模型、控制器设计、闭环控制系统和控制系统实现。
哈工大倒立摆实验报告

研究生自动控制专业实验地点:A区主楼518房间平面二级倒立摆系统实验报告主编:钱玉恒,杨亚非哈工大航天学院控制科学实验室平面二级倒立摆控制系统实验报告一、实验内容1、熟悉平面二级倒立摆控制系统的结构和原理;2、了解平面二级倒立摆物理模型建模与控制器设计;3、掌握LQR控制器仿真与实验;二、实验设备1、平面二级倒立摆控制系统一套平面二级倒立摆控制系统包括平面二级倒立摆控制器、平面二级倒立摆本体实验装置等组成。
在平面二级倒立摆本体上有起动/停止电源开关,螺旋浆起动/停止开关。
2、平面二级倒立摆控制系统计算机部分平面二级倒立摆控制系统计算机部分主要有计算机、SV-400控制卡等;三、实验步骤1、系统实验的线路连接平面二级倒立摆本体与计算机全部采用标准线连接,电源部分有标准电源线,在试验前,实验装置的线路已经连接完毕。
2、启动实验装置通电之前,请详细检察电源等连线是否正确,确认无误后,可接平面二级倒立摆本体电源,随后起动计算机和控制器。
3、系统实验的参数调试根据仿真的数据及控制规则进行参数调试,直到获得较理想参数为止。
四、实验要求1、学生上机前要求学生在实际上机调试之前,必须用自己的计算机,对系统的仿真全部做完,并且经过老师的检查许可后,才能申请上机调试。
2、学生上机要求上机的同学要按照要求进行实验,不得有违反操作规程的现象,严格遵守实验室的有关规定。
五、实验结果与分析 经过实际调试,实验结果如下:当LQR 控制参数为:14.142x K =, 15.722a K =, 74.93b K = ,29.49x K =, ,196.29a K =, ,34.83b K =系统的时间运行曲线如图1、图2所示。
图1 第一组参数X 方向实际运动曲线图2 第二组参数Y 方向实际运动曲线从图1、图2中可以看出,X 方向控制较好,但Y 方向控制的波动幅度比较大,为此,需要进一步调整LQR 控制参数。
经过多次试验,得到如下一组比较好的控制参数:14.142x K =, 15.892a K =, 77.71b K = ,30.018x K =, ,193.73a K =, ,33.355b K =该组参数下,系统的实际运行曲线如下图3、图4所示。
一阶倒立摆控制设计与实现

一阶倒立摆控制设计与实现以一阶倒立摆控制设计与实现为题,本文将介绍倒立摆控制系统的设计原理和实现过程。
倒立摆是一种经典的控制系统问题,它涉及到动力学建模、控制算法设计和实时控制等多个方面。
本文将从这些方面逐步展开,为读者介绍一阶倒立摆控制的基本知识。
1. 动力学建模倒立摆是一个复杂的动力学系统,它由一个可以旋转的杆和一个连接在杆末端的质点组成。
杆的旋转可以由一个电机控制,质点则受到重力和杆的作用力。
为了建立倒立摆的动力学模型,我们需要考虑杆的旋转角度和质点的位置。
2. 控制算法设计一阶倒立摆的控制目标是使杆保持竖直位置,即旋转角度为零,并且使质点保持在某个给定的位置上。
为了实现这个目标,我们可以设计一个控制器来控制杆的旋转角度和质点的位置。
常用的控制算法有PID控制算法、模糊控制算法和神经网络控制算法等。
PID控制算法是一种经典的控制算法,它通过调节比例、积分和微分三个参数来实现控制效果。
模糊控制算法则利用模糊逻辑的思想,将输入和输出之间的关系用模糊集合表示。
神经网络控制算法则利用神经网络的学习能力,通过训练网络来实现控制效果。
3. 实时控制倒立摆的控制需要实时采集传感器数据,并根据这些数据计算控制信号。
在实际应用中,我们可以使用编码器来测量杆的旋转角度,使用加速度计来测量质点的加速度,然后通过控制器来计算电机的控制信号。
为了实现实时控制,我们可以使用嵌入式系统来实现。
嵌入式系统是一种专门设计用于控制和处理实时数据的计算机系统,它通常由微处理器、存储器和输入输出设备组成。
通过将控制算法和传感器接口集成到嵌入式系统中,我们可以实现倒立摆的实时控制。
总结本文介绍了一阶倒立摆控制的基本原理和实现方法。
倒立摆是一个复杂的动力学系统,控制它需要建立动力学模型,并设计合适的控制算法。
通过实时采集传感器数据并计算控制信号,我们可以实现倒立摆的控制。
希望本文对读者理解一阶倒立摆控制有所帮助,同时也希望读者能够进一步探索和研究这个有趣的控制问题。
一级倒立摆系统分析

一级倒立摆系统分析一级倒立摆系统由一个垂直的支撑杆和一个质量为m、长度为l的摆杆组成。
摆杆的一端通过一个旋转关节连接在支撑杆的顶端,另一端可以自由地在重力作用下摆动。
我们将摆杆的摆动角度定义为θ,并假设摆杆的运动是平面运动,不考虑摆杆在垂直方向上的移动。
首先,我们需要建立一级倒立摆系统的动力学方程。
根据牛顿第二定律和角动量守恒定律,可以得到以下方程:1.支撑杆垂直方向受力平衡方程:-mgl sinθ = 0其中g为重力加速度。
2. 摆杆绕旋转关节的转动惯量为I = ml^2/3,根据转动惯量的定义可以得到角加速度α与力矩τ之间的关系:τ=Iα其中τ = ml^2/3α。
3.摆杆绕旋转中心的转动方程:τ = Iα = ml^2/3α = -mgl sinθ可以得到α与θ之间的关系:α = -3g/(2l)sinθ。
以上方程可以描述一级倒立摆系统在垂直方向上的平衡和旋转运动。
其中,第一条方程表示摆杆在垂直方向上的受力平衡,第二条方程表示摆杆的转动惯量及其与角加速度之间的关系,第三条方程表示摆杆绕旋转中心的转动方程。
接下来,我们可以通过线性化分析来研究一级倒立摆系统的稳定性。
线性化是一种将非线性系统近似为线性系统的方法,通过计算系统在一些平衡点附近的一阶导数来实现。
我们首先要找到一级倒立摆系统的平衡点。
根据第一条方程,当θ=0时,系统达到平衡。
在这个平衡点,摆杆不再摆动,所有受力均平衡。
接下来,我们对系统进行线性化。
首先将θ分解为平衡点的偏差值Δθ和小量δθ,即:θ=θ_e+Δθ+δθ其中θ_e为平衡点的角度。
将上述表达式带入到第三条方程中,并只保留一阶项,可以得到线性化的转动方程:α = -3g/(2l)(sinθ_e + cosθ_e Δθ +cosθ_e δθ)。
我们可以进一步线性化该方程,即将sinθ_e和cosθ_e在一阶项展开,并忽略二阶项,得到:α=-3g/(2l)(θ_e+Δθ+δθ)。
一阶倒立摆的数学模型

一阶倒立摆的数学模型好啦,今天咱们来聊聊一阶倒立摆。
听起来挺复杂的,其实就是一个小摆子,站在一根杆子上面,像个小丫头在平衡木上玩儿。
你有没有想过,为什么这个简单的东西能让科学家们绞尽脑汁?这就像你和朋友一起玩平衡游戏,谁摔倒谁就得请客,呵呵。
想象一下,那个小摆子,就像一颗苹果,静静地待在杆子的顶端。
它看起来很稳,但其实它随时可能倾倒。
风一吹,或者你稍微碰一下,它就可能开始摇晃。
这就是一阶倒立摆的魅力所在:看似简单,实则深奥。
其实啊,倒立摆的运动就像生活,有时候一不小心就会摔得四脚朝天,嘿嘿。
在物理学里,这种摆动其实可以用一组方程来描述。
别怕,听起来复杂,但实际上就像做数学题时,那些公式就像调皮的孩子,让你既爱又恨。
摆子的运动可以用牛顿第二定律来解释,就是说,力等于质量乘以加速度。
这里面有个小秘密哦,那就是摆子的质量和重力都影响它的运动。
如果摆子太重了,或者你施加的力不够,嘿嘿,它就没法保持平衡了。
说到平衡,真是个难题。
生活中也一样,工作和休息、家庭和朋友,所有的东西都得拿捏得当。
就像那个倒立摆,要时刻保持平衡,稍不留神就可能倾斜。
想象一下,当你走在悬崖边缘,心里一定咯噔一下吧?其实倒立摆也是一样,重力就像那无形的悬崖,随时准备让它掉下去。
那要怎么才能让这个小摆子不倒呢?聪明的科学家们可不止是站着想。
他们设计了一些控制器,像小小的守护者,时刻监测着摆子的倾斜角度。
只要一发现不对劲,就会迅速调整力的方向,帮助摆子重新找回平衡。
这就好比你在街上遇到突如其来的风,立马稳住自己的身子,别让自己摔倒,哈哈。
说到底,一阶倒立摆不仅仅是物理上的问题,更是一种哲学。
它教会我们,生活中有很多不确定的因素。
我们永远无法预料下一秒会发生什么,但只要我们能及时调整自己的状态,就能保持在“平衡”的位置上,过上更精彩的生活。
这种灵活应对的智慧,就像古人说的“应变随时”,我们在面对挑战时总能找到办法。
当然了,搞定这个倒立摆的过程并不是一帆风顺的。
一阶倒立摆动力学方程推导
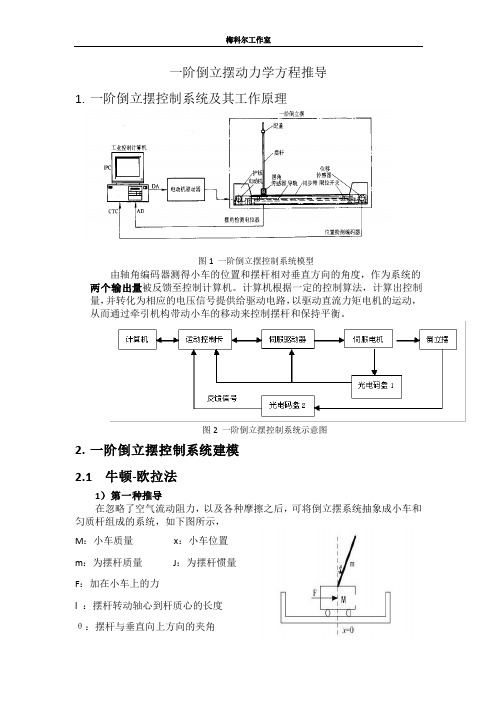
(3) 简单的二阶动力学方程如何化为传递函数
x Ax Bu y Jy ku y Cx Du
x 为 n 维状态向量; y 为 m 维输出向量; u 为 r 维输入向量; A 为
B 为 n r 维输入矩阵; n n 维系统矩阵, C 为m n 由系统参数决定;
梅科尔工作室
根据牛顿运动定律以及刚体运动规律,可知: (1) 摆杆绕其重心的转动方程为(以重心为转动中心)
J Fyl sin Fxl cos ..........(1)
(2) 摆杆重心的运动方程为(直线运动)
d2 ( x l sin )..........(2) d 2t d2 Fy mg m 2 (l cos ).........(3) d t 得 Fx m
梅科尔工作室
(3-8) 设θ=φ+π( φ是摆杆与垂直向上方向之间的夹角) ,假设φ与1(单位是弧 度)相比很小,即φ<<1,则可以进行近似处理:
用u 来代表被控对象的输入力F,线性化后两个运动方程如下:
(3-9) 对式(3-9)进行拉普拉斯变换,得到
(3-10) 注意:推导传递函数时假设初始条件为0。 由于输出为角度φ,求解方程组的第一个方程,可以得到:
由(3-9)的第一个方程为: (只用了第一个方程式为了建立水平加速度与转角之间 的关系)
对于质量均匀分布的摆杆有:
梅科尔工作室
于是可以得到:
化简得到:
设
则有:
另外, 也可以利用MATLAB 中tf2ss 命令对(3-13)式进行转化, 求得上述状态方程。 在固高科技所有提供的控制器设计和程序中,采用的都是以小车的加速度作为 系统的输入,如果用户需要采用力矩控制的方法,可以参考以上把外界作用力作 为输入的各式。 2.2 拉格朗日法 拉格朗日方程的表达式:
一阶倒立摆状态空间表达式

一阶倒立摆状态空间表达式一阶倒立摆是一种具有重力作用下的平衡控制系统,常用于研究控制理论和机器人技术。
在这篇文章中,我将介绍一阶倒立摆的状态空间表达式,以及其在控制系统中的应用。
我们需要了解一阶倒立摆的基本结构。
一阶倒立摆由一个质点和一个固定的支点组成,质点在一个直立的杆上运动。
质点在杆上的位置可以用角度θ来描述,而质点的速度可用角速度ω表示。
此外,我们还需要考虑质点与支点之间的距离L和质点的质量m。
为了建立一阶倒立摆的状态空间表达式,我们可以采用以下方式:1. 定义状态变量:我们可以选择角度θ和角速度ω作为状态变量。
这两个变量可以完整地描述一阶倒立摆的状态。
2. 建立状态方程:根据牛顿第二定律和刚体运动学原理,可以得到一阶倒立摆的状态方程。
通过对质点的受力分析,可以得到以下方程:(mL^2 + I)θ'' + mgLsinθ = 0其中,I为质点的转动惯量,θ''为角加速度,g为重力加速度。
同时,我们还可以得到角速度ω的表达式:ω = θ'其中,θ'为角速度。
3. 转化为状态空间形式:为了方便进行控制系统的设计和分析,我们将状态方程转化为状态空间形式。
首先,我们引入两个新的状态变量x1和x2,分别表示θ和ω。
然后,我们可以得到如下的状态空间表达式:x1' = x2x2' = -(mL^2 + I)^-1 * mgLsin(x1)其中,x1'和x2'分别表示x1和x2的一阶导数。
此外,我们还可以定义输入变量u,来表示对一阶倒立摆的控制输入。
通过引入输入变量u,我们可以进一步改写状态空间表达式: x1' = x2x2' = -(mL^2 + I)^-1 * mgLsin(x1) + u一阶倒立摆的状态空间表达式提供了一个描述系统动力学行为的数学模型。
通过这个模型,我们可以进行系统的分析和控制设计。
例如,我们可以通过状态空间表达式来计算系统的响应特性,如阻尼比、自然频率等。
一阶倒立摆系统建模与仿真研究

一阶倒立摆系统建模与仿真研究一阶倒立摆系统是一种典型的非线性控制系统,具有多种状态和复杂的运动特性。
在实际生活中,倒立摆被广泛应用于许多领域,如机器人平衡控制、航空航天、制造业等。
因此,对一阶倒立摆系统进行建模与仿真研究具有重要的理论价值和实际意义。
ml''(t) + b*l'(t) + k*l(t) = F(t)其中,m为质量,b为阻尼系数,k为弹簧常数,l(t)为摆杆的位移,l'(t)为摆杆的加速度,l''(t)为摆杆的角加速度,F(t)为外界作用力。
在仿真过程中,需要设定摆杆的初始位置和速度。
一般而言,初始位置设为0,初始速度设为0。
边界条件则根据具体实验需求进行设定,如限制摆杆的最大位移、最大速度等。
利用MATLAB/Simulink等仿真软件进行建模和实验,可以方便地通过改变输入信号的参数(如力F)或系统参数(如质量m、阻尼系数b、弹簧常数k)来探究一阶倒立摆系统的性能和反应。
通过仿真实验,我们可以观察到一阶倒立摆系统在受到不同输入信号的作用下,会呈现出不同的运动规律。
在适当的输入信号作用下,摆杆能够达到稳定状态;而在某些特定的输入信号作用下,摆杆可能会出现共振现象。
在仿真过程中,我们可以发现一阶倒立摆系统具有一定的鲁棒性。
在一定范围内,即使输入信号发生变化或系统参数产生偏差,摆杆也能够保持稳定状态。
然而,当输入信号或系统参数超过一定范围时,摆杆可能会出现共振现象,导致系统失稳。
因此,在实际应用中,需要对输入信号和系统参数进行合理控制,以保证系统的稳定性。
为了避免共振现象的发生,可以通过优化系统参数或采用其他控制策略来实现。
例如,适当增加阻尼系数b能够减小系统的振荡幅度,有利于系统尽快达到稳定状态。
可以采用反馈控制策略,根据摆杆的实时运动状态调整输入信号,以抑制系统的共振响应。
本文对一阶倒立摆系统进行了建模与仿真研究,通过观察不同参数设置下的系统性能和反应,对其运动规律、鲁棒性及稳定性进行了分析。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
哈尔滨工业大学控制科学与工程系控制系统设计课程设计报告姓名:院(系):专业:自动化班号:任务起至日期: 2014 年9 月9 日至 2014 年9 月20 日课程设计题目:直线一级倒立摆控制器设计已知技术参数和设计要求:本课程设计的被控对象采用固高公司的直线一级倒立摆系统GIP-100-L。
系统内部各相关参数为:M小车质量0.5kg; m摆杆质量0.2kg; b小车摩擦系数0.1N/m/sec; l摆杆转动轴心到杆质心的长度0.3m; I摆杆惯量0.006kg*m*m; T采样时间0.005秒。
设计要求:1.推导出系统的传递函数和状态空间方程。
用Matlab进行阶跃输入仿真,验证系统的稳定性。
2.设计PID控制器,使得当在小车上施加0.1N的脉冲信号时,闭环系统的响应指标为:(1)稳定时间小于5秒;(2)稳态时摆杆与垂直方向的夹角变化小于0.1弧度。
3.设计状态空间极点配置控制器,使得当在小车上施加0.2m的阶跃信号时,闭环系统的响应指标为:(1)摆杆角度错误!未找到引用源。
和小车位移x的稳定时间小于3秒(2)x的上升时间小于1秒(3)错误!未找到引用源。
的超调量小于20度(0.35弧度)(4)稳态误差小于2%。
工作量:1.建立直线一级倒立摆的线性化数学模型;2.倒立摆系统的PID控制器设计、Matlab仿真及实物调试;3.倒立摆系统的极点配置控制器设计、Matlab仿真及实物调试。
哈尔滨工业大学 (1)控制系统设计课程设计报告 (1)一.实验设备简介 (3)二.直线一阶倒立摆数学模型的推导 (6)2.1概述 (6)2.2数学模型的建立 (7)2.3一阶倒立摆的状态空间模型: (9)2.4实际参数代入: (10)三.定量、定性分析系统的性能 (11)3.1 对系统的稳定性进行分析 (11)3.2 对系统的稳定性进行分析: (12)四. 实际系统的传递函数与状态方程 (13)五. 系统阶跃响应分析 (14)六.一阶倒立摆PID控制器设计 (15)6.1 PID控制分析 (15)6.2 PID控制参数设定及MATLAB仿真 (17)6.3 PID控制实验 (18)七.状态空间极点配置控制器设计 (19)7.1 状态空间分析 (20)7.2 极点配置及MA TLAB仿真 (21)7.3 利用爱克曼公式计算 (21)八.课程设计心得与体会 (22)一.实验设备简介倒立摆控制系统:Inverted Pendulum System (IPS)倒立摆控制系统是一个复杂的、不稳定的、非线性系统,是进行控制理论教学及开展各种控制实验的理想实验平台。
对倒立摆系统的研究能有效的反映控制中的许多典型问题:如非线性问题、鲁棒性问题、镇定问题、随动问题以及跟踪问题等。
通过对倒立摆的控制,用来检验新的控制方法是否有较强的处理非线性和不稳定性问题的能力。
同时,其控制方法在军工、航天、机器人和一般工业过程领域中都有着广泛的用途,如机器人行走过程中的平衡控制、火箭发射中的垂直度控制和卫星飞行中的姿态控制等。
倒立摆是进行控制理论研究的典型实验平台。
倒立摆是机器人技术、控制理论、计算机控制等多个领域、多种技术的有机结合,其被控系统本身又是一个绝对不稳定、高阶次、多变量、强耦合的非线性系统,可以作为一个典型的控制对象对其进行研究。
最初研究开始于二十世纪50 年代,麻省理工学院(MIT)的控制论专家根据火箭发射助推器原理设计出一级倒立摆实验设备。
近年来,新的控制方法不断出现,人们试图通过倒立摆这样一个典型的控制对象,检验新的控制方法是否有较强的处理多变量、非线性和绝对不稳定系统的能力,从而从中找出最优秀的控制方法。
倒立摆系统作为控制理论研究中的一种比较理想的实验手段,为自动控制理论的教学、实验和科研构建一个良好的实验平台,以用来检验某种控制理论或方法的典型方案,促进了控制系统新理论、新思想的发展。
由于控制理论的广泛应用,由此系统研究产生的方法和技术将在半导体及精密仪器加工、机器人控制技术、人工智能、导弹拦截控制系统、航空对接控制技术、火箭发射中的垂直度控制、卫星飞行中的姿态控制和一般工业应用等方面具有广阔的利用开发前景。
平面倒立摆可以比较真实的模拟火箭的飞行控制和步行机器人的稳定控制等方面的研究。
一阶倒立摆系统的结构示意图如下所示: 摆杆滑轨 电机小车图1-1 一阶倒立摆结构示意图系统组成框图如下所示:图1-2 一级倒立摆系统组成框图系统是由计算机、运动控制卡、伺服机构、倒立摆本体和光电码盘几大部分组成的闭环系统。
光电码盘1将小车的位移、速度信号反馈给伺服驱动器和运动控制卡,白干的角度、角速度信号由光电码盘2反馈给运动控制卡。
计算机从运动控制卡中读取实时数据,确定控制决策(小车运动方向、移动速度、加速度等),并由运动控制卡来实现控制决策,产生相应的控制量,使电机转动,通过皮带带动小车运动吗,保持摆杆平衡。
二.直线一阶倒立摆数学模型的推导2.1概述倒立摆系统其本身是自不稳定系统,实验建模存在一些问题和困难,在忽略掉一些次要的因素后,倒立摆系统是一个典型的运动的刚体系统,可以再惯性坐标系中运用经典力学对它进行分析,来建立系统动力学方程。
在忽略掉了空气阻力和各种摩擦力之后,可以讲一阶倒立摆系统抽象成小车和均匀杆组成的系统,一阶倒立摆系统的结构示意图如下:计算机运动控制卡 伺服驱动器伺服电机倒立摆光电码盘1光电码盘2图2 一阶倒立摆系统的结构示意图定义的参数为:M小车质量m摆杆质量b小车摩擦系数I摆杆惯量F加在小车上的力x小车位置φ摆杆与垂直向上方向的夹角l摆杆转动轴心到杆质心的长度θ摆杆与垂直向下方向的夹角(摆杆初始位置为竖直向下)得到小车和摆杆的受力图:图3 小车和摆杆的受力图2.2数学模型的建立运用牛顿定理分析受力得到下列方程:(2-1)由摆杆水平方向的受力进行分析可以得到下面等式:(2-2)求导得到:(2-3)代入第一个方程得到:(2-4)在摆杆垂直方向上的合力进行分析得到方程:(2-5)即:(2-6)力矩平衡方程:(2-7)又因为θ为摆杆与垂直向下方向的夹角(摆杆初始位置为竖直向下),φ为摆杆与垂直向上方向的夹角,由θ和φ关系得合并这两个方程,约去P 和N,得到第二个运动方程:(2-8)微分方程的建立:因为,假设φ<<1弧度,则可以进行近似处理:错误!未找到引用源。
来实现线性化。
用上述近似进行线性化得直线一阶倒立摆的微分方程为:一阶倒立摆的传递函数模型:对上式进行拉普拉斯变换,得:(2-9)推导传递函数时假设初始条件为 0。
由于输出为角度φ,求解方程组的第一个方程,可得:或如果令错误!未找到引用源。
,则有:把上式代入方程组(2-1)的第二个方程,得:()()()222222()()()()I ml I ml g g M m s s b s s ml s s U s ml s ml s ⎡⎤⎡⎤++⎢⎥⎢⎥+-Φ+-Φ-Φ=⎢⎥⎢⎥⎣⎦⎣⎦整理后得到传递函数:()()212432()()()ml s s q G s U s b I ml M m mgl bmgl s s s sqqqΦ==+++--其中。
2.3一阶倒立摆的状态空间模型:设系统状态空间方程为:方程组(2-9)对错误!未找到引用源。
解代数方程,得到解如下:(2-10)(2-14)(2-11)(2-12)(2-13)(2-15)(2-16)整理后得到系统状态空间方程:2.4实际参数代入:GIP-100-L型一阶倒立摆系统,系统内部各相关参数为:M小车质量0.5 Kg ;m摆杆质量0.2 Kg ;b小车摩擦系数0.1 N/m/sec ;l摆杆转动轴心到杆质心的长度0.3 m ;I摆杆惯量0.006 kg*m*m ;T采样时间0.005秒。
将上述参数代入得实际模型:摆杆角度和小车位移的传递函数:摆杆角度和小车所受外界作用力的传递函数:以外界作用力作为输入的系统状态方程:(2-17)(2-18)(2-19)(2-21)(2-20)(2-22)三.定量、定性分析系统的性能3.1 对系统的稳定性进行分析在MATLAB中运行以下程序:A=[ 0 1 0 0; 0 -0.181818 2.672727 0; 0 0 0 1; 0 -0.454545 31.181818 0];B=[ 0 1.818182 0 4.545455]';C=[ 1 0 0 0; 0 0 1 0];D=[ 0 0 ]';[z,p,k]=ss2zp(A,B,C,D)z =-4.9497 0.0000 + 0.0000i4.9497 0.0000 - 0.0000ip =-5.6041-0.14285.5651k =1.81824.5455>> impulse(A,B,C,D)1234x 1027T o : O u t (1)02468101212345x 1028T o : O u t (2)Impulse ResponseTime (sec)A m p l i t u d e图4 系统脉冲响应由图可得,系统在单位脉冲的输入作用下,小车的位移和摆杆的角度都是发散的,同时,由以上程序的零极点得极点有一个大于零,因此系统不稳定。
3.2 对系统的稳定性进行分析:A=[ 0 1 0 0; 0 -0.181818 2.672727 0; 0 0 0 1; 0 -0.454545 31.181818 0]; B=[ 0 1.818182 0 4.545455]'; C=[ 1 0 0 0; 0 0 1 0]; D=[ 0 0 ]';>> Qc=ctrb(A,B); >> Qo=obsv(A,C); >> rank(Qc)ans =4>> rank(Qo)ans =4因此系统为完全能观测和完全能控的。
四. 实际系统的传递函数与状态方程实际系统的模型参数如下:M 小车质量 0.5 Kg m 摆杆质量 0.2 Kgb 小车摩擦系数 0 .1N/m/sec l 摆杆转动轴心到杆质心的长度 0.3mI 摆杆惯量 0.006 kg*m*m代入上述参数可得系统的实际模型。
摆杆角度和小车位移的传递函数:摆杆角度和小车加速度之间的传递函数为:摆杆角度和小车所受外界作用力的传递函数:以外界作用力作为输入的系统状态方程:以小车加速度为输入的系统状态方程:(4-2)(4-3)(4-4)(4-1)(4-5)五. 系统阶跃响应分析上面已经提到系统的状态方程,先对其进行阶跃响应分析,在Matlab中键入以下命令:得到以下计算结果:直线一级倒立摆单位阶跃响应仿真可以看出,在单位阶跃响应作用下,小车位置和摆杆角度都是发散的。
