解二元一次方程组练习题代入消元法
8.2.1代入消元法解二元一次方程组

y=ax+b或x=my+n
1、用含x的代数式表示y: x + y = 22 y = 22-x 2、用含y的代数式表示x: 2x - 7y = 8 2x = 8+7y
8 7y x 2
篮球联赛中每场比赛都要分出胜负,每队胜 一场得2分,负一场得1分.如果某队为了争取较 好名次,想在全部22场比赛中得40分,那么这个 队胜、负场数应分别是多少? 解:设胜x场,负y场. x y 22 ① 2 x y 40 ② 解:设胜x场. 2 x (22 x) 40 ③
解:设这些消毒液应该分装x大瓶、y小瓶. ① 5 x 2 y 由题意得 ② 500 x 250 y 22500000
由①,得
5 y x 2
③
5 500 x 250 x 22500000 2
把③代入②,得 解得 x=20000 把x=20000代入③,得
x 20000 y 50000
x=13 – 4y
③
把③代入① ,得 2(13 – 4y)+ 3y=16 26 –8y +3y =16 13-4y+4y=13 把y=2代入① 或②可以吗? – 5y= – 10 0y=0 y=2 把求出的解 把y=2代入③ ,得 x=5
x 5 ∴原方程组的解是 y 2
代入原方程 组,可以知 道你解得对 不对。
① ②
4 x 5 y 460 2 x 3 y 240
①
②
由②, 得 2x=240-3y
③
把③代入①,得 2(240-3y)+5y=460 480-6y+5y=460 -y=-20 y=20. 把y=20代入③,得 2x+3×20=240 x=90.
用代入消元法解二元一次方程组练习题

用代入消元法解二元一次方程组练习题IMB standardization office【IMB 5AB- IMBK 08- IMB 2C】消元(一)一、填空题 1.已知-=1x y ,用含有x 的代数式表示y 为:=y ; 用含有y 的代数式表示x 为:x = . 2.已知4+5=3x y ,用含有x 的代数式表示y 为:=y ; 用含有y 的代数式表示x 为:x =. 3..若⎩⎨⎧-==1,1y x 和⎩⎨⎧==3,2y x 是关于x ,y 的方程y =kx +b 的两个解,则k =_____,b =______.4.在方程3x +5y =10中,若3x =6,则x =______,y =______.二、选择题5..以方程组⎩⎨⎧-=+-=1,2x y x y 的解为坐标的点(x ,y )在平面直角坐标系中的位置是(). (A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限三、用代入消元法解下列方程7.⎩⎨⎧=+=+.53,1y x y x 8.⎩⎨⎧==-.3:4:,52y x y x . 9.326431m n m n +=⎧⎨-=⎩ ① ②10.用代入消元法解方程组⎩⎨⎧=-=+②①52,243y x y x 使得代入后化简比较容易的变形是(). (A)由①得342y x -=(B)由①得432x y -= (C)由②得25+=y x (D)由②得y =2x -511.把x =1和x =-1分别代入式子x 2+bx +c 中,值分别为2和8,则b 、c 的值是().(A)⎩⎨⎧==4,3c b (B)⎩⎨⎧-==4,3c b (C)⎩⎨⎧-=-=4,3c b (D)⎩⎨⎧=-=4,3c b 12如果关于x ,y 的方程组⎪⎩⎪⎨⎧-=-+=-321,734k y x k y x 的解中,x 与y 互为相反数,求k 的值.13.若|x -y -1|+(2x -3y +4)2=0,则x,y 各是多少?。
用加减消元法解二元一次方程组练习题

是通常的加法和乘法运算,已知 3*5=15,4*7=28,则 a+b=
.
6.将方程 1 x+2y=1 中的 x 项的系数化为 2,则下列结果中正确的是( ) 3
A、2x+6y=1 B、2x+2y=6 C、2x+6y=3 D、2x+12y=6
7.某校课外小组的学生准备分组外出活动,若每组 7 人,则余下 3 人;若每组 8 人,则最后一组只有 3 人,设课外小组的人数为 x,分成的组数为 y.依题意
2x+3y=6 ②
(2)
5x-5y=7 ① 15x+20y=7 ②
10.已知代数式 x2+bx+c,当 x=-3 时,它的值为 9,当 x=2 时,它的值为 14,当 x=-8 时,求代数式的值。
11.若∣m+n-5∣+(2m+3n-5)2=0,求(m+n)2 的值
12.甲、乙两个小马虎,在练习解方程组
可得方程组为( )
A、 7y=x+3 B、 8y+5=x
7x+3=y 8ቤተ መጻሕፍቲ ባይዱ-5=y
C、 7y=x-3 8y=x+5
D、 7y=x+3 8y=x+5
8.用代入法解下列方程组: (1) y=x+6 ①
2x+3y=8 ②
2x+3y=-19 ① x+5y=1 ②(2)
9.用加减法解下列方程组: (1) 2x+5y=12 ①
了方程组中的 a,得到方程组的解为 x=1
程组的解为
y=6
问原方程组的解为多少?
ax+y=10 x+by=7 时,由于粗心,甲看错 ;乙看错了方程组中的 b,得到方
x=-1 y=12
用加减消元法解二元一次方程组练习题
1.用代入法解方程组3xx8yy
3(1) 14(2)
由①可得
.
8.2《消元——解二元一次方程组》同步练习题(2)及答案

。
二. 选择题 10. 若 y=kx+b中,当 x=-1 时,y=1;当 x=2 时,y=-2,则 k 与 b 为( )
k 1 A. b 1
k 1 B. b 0
k 1 C. b 2
k 1 D. b 4
x 1
ax by 0
8.2《消元——解二元一次方程组》同步练习题(2)
知识点:
1、代入法:用代入消元法解二元一次方程组的步骤: (1)从方程组中选取一个系数比较简单的方程,把其中的某一个未知数用 含另一个未知数的式子表示出来. (2)把(1)中所得的方程代入另一个方程,消去一个未知数.
(3)解所得到的一元一次方程,求得一个未知数的值.
13. 对于方程组 4x 5y 17 ,用加减法消去 x,得到的方程是(
)
A. 2y=-2
B. 2y=-36 C. 12y=-2 D. 12y=- 36
14.
将方程-
1 2
x+y=1中
x
的系数变为
5,则以下正确的是(
)
A. 5x+y=7
B. 5x+10y=10 C. 5x-10y=10 D. 5x-10y=-10
∴原方程组解为 x 2 y 2
(4)解:由②得:x=3y-7……③ ③代入① :2(3y-7)+5y=8 11y=22 y=2
把 y=2代入③得 x=-1 ∴原方程组解为
x 1 y 2
16. (1)解:②×4-①×3 得:11y=-33 ∴y=-3 把 y=-3 代入①得:4x-9=3 x=3
7. 二元一次方程组 kx 2 y 5 的解是方程 x-y=1的解,则 k=
。
解二元一次方程50道练习题(带答案)

解二元一次方程50道练习题(带答案)
1. 解方程组:
{2x - y = 3
{3x + 2y = 8
解答:
首先,可以通过消元法来解决这个问题。
将第一个方程乘以2,并将第二个方程乘以3,得到:
{4x - 2y = 6
{9x + 6y = 24
接下来,将第一个方程的两倍加到第二个方程上,得到:
{4x - 2y = 6
{13x + 4y = 30
然后,将第一个方程的2倍加到第二个方程上,得到:
{4x - 2y = 6
{8x - 8y = 12
接下来,将第二个方程的两倍加到第一个方程上,得到:
{36x = 18
{8x - 8y = 12
最后,解方程得到:
{x = 0.5
{y = 2
2. 解方程组:
{3x + 2y = 7
{5x + 3y = 11
解答:
可以使用消元法来解决这个方程组。
将第一个方程乘以3,并将第二个方程乘以2,得到:
{9x + 6y = 21
{10x + 6y = 22
接下来,将第二个方程的两倍减去第一个方程,得到:
{9x + 6y = 21
{2x = 1
最后,解方程得到:
{x = 0.5
{y = 2
3. ...
...
50. ...
...
这是前面五道解二元一次方程的练习题,你可以根据相同的方法解答剩下的题目。
希望这些练习题对你有帮助!。
专题 解二元一次方程组(计算题50题)(原卷版)
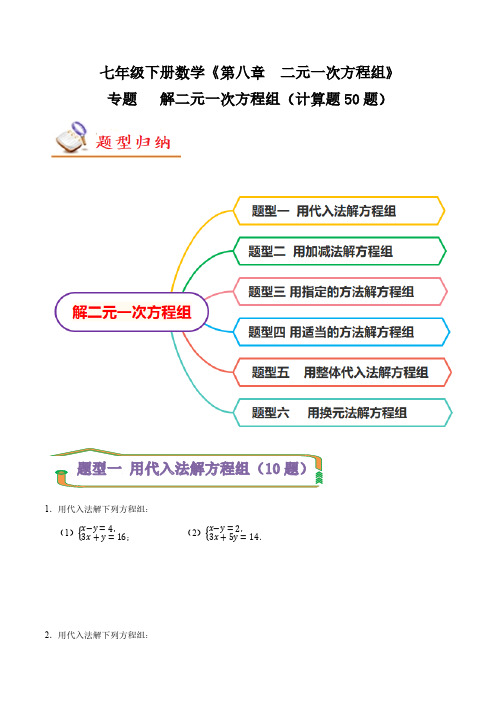
七年级下册数学《第八章二元一次方程组》专题解二元一次方程组(计算题50题)1.用代入法解下列方程组:(1)x−y=4,3x+y=16;(2)x−y=2,3x+5y=14.2.用代入法解下列方程组:(1)2x−y=33x+2y=8;(2)u+v=103u−2v=5.3.用代入法解下列方程组:(1)3x−y=2,9x+8y=17;(2)3x−4y=10x+3y=12.4.用代入法解下列方程组.(1)x+2y=4y=2x−3;(2)x−y=44x+2y=−2.5.用代入法解下列方程组:(1)5x+4y=−1.52x−3y=4(2)4x−3y−10=03x−2y=06.用代入法解下列方程组:(1)x−y=42x+y=5;(2)3x−y=29x+8y=17;(3)3x+2y=−8 6x−3y=−9.7.用代入法解下列方程组:(1)3x+2y=11,①x=y+3,②(2)4x−3y=36,①y+5x=7,②(3)2x−3y=1,①3x+2y=8,②8.用代入法解下列方程组:(1)5x+2y=15①8x+3y=−1②;(2)3(y−2)=x−172(x−1)=5y−8.9.用代入法解下列方程组:(1)x=6−5y3x−6y=4(2)5x+2y=15x+y=6(3)3x+4y=22x−y=5(4)2x+3y=73x−5y=110.用代入法解下列方程组:(1)2x+y=3x+2y=−6;(2)x+5y=43x−6y=5;(3)2x−y=63x+2y=2;(4)5x+2y=113y−x=−9;1.用加减法解下列方程组:(1)4x−y =143x +y =7 (2x−2y =7x−3y =−82.用加减法解下列方程组:(1)2m +7n =53m +n =−2(2)2u−5v =124u +3v =−2(3y 7=12+y 7=133.用加减法解下列方程组:(1)x−y =52x +y =4;(2)x−2y =33x +4y =−1.4.用加减法解下列方程组:(1)4x−3y =11,2x +y =13;(2)x−y =3,2y +3(x−y)=115.用加减法解下列方程组:(1)3μ+2t =76μ−2t =11 (2)2a +b =33a +b =4.6.(2023•市北区校级开学)用加减法解下列方程组:(1)3y−4x =04x +y =8; (2+y =3x−32y =−1.7.(2022秋•陕西期末)用加减法解下列方程组:(1)x−y =33x−8y =14; (2+2y =10=1+y 13.8.用加减法解下列方程组:(1)x +3=y ,2(x +1)−y =6; (2)x +y =2800,96%x +64%y =2800×92%.9.用加减法解下列方程组:(1)x−y =5,①2x +y =4;②(2)x−2y =1,①x +3y =6;②(3)2x−y =5,①x−1=12(2y−1).②10.用加减法解下列方程组:(1)x +3y =62x−3y =3 (2)7x +8y =−57x−y =4(3)y−1=3(x−2)y+4=2(x+1)(4+y4=1−y3=−1.1.(2022春•新田县期中)用指定的方法解下列方程组:(1)2x−5y=14①y=−x②(代入法);(2)2x+3y=9①3x+5y=16②(加减法).2.(2022春•安岳县校级月考)解下列方程组:(1)3x−y=75x+2y=8(用代入法);(2+n3=10−n4=5(用加减法).3.(2022春•大连期中)用指定的方法解下列方程组:(1)x−3y=42x+y=13(代入法);(2)5x+2y=4x+4y=−6(加减法).4.(2022春•宁远县月考)请用指定的方法解下列方程组(1)5a−b=113a+b=7(代入消元法);(2)2x−5y=245x+2y=31(加减消元法).5.(2021秋•蒲城县期末)请用指定的方法解下列方程组:(1)2x+3y=11①x=y+3②(代入消元法);(2)3x−2y=2①4x+y=10②(加减消元法).6.(2022秋•历下区期中)请用指定的方法解下列方程组:(1)m−n2=22m+3n=12(代入法);(2)6s−5t=36s+t=−15(加减法).7.(2022春•泰安期中)用指定的方法解下列方程组(1)3x+4y=19x−y=4(代入消元法);(2)2x+3y=−53x−2y=12(加减消元法);(35(x−9)=6(y−2)−y13=2.8.(2021秋•历下区期中)请用指定的方法解下列方程组:(1)3x+2y=14x=y+3;(代入法)(2)2x+3y=123x+4y=17.(加减法)9.(2021春•沙河口区期末)用指定的方法解下列方程组:(1)y=2x−33x+2y=8(代入法);(2)3x+4y=165x−6y=33(加减法).10.用指定的方法解下列方程组:(1)3x+4y=19x−y=4(代入法);(2)2x+3y=−53x−2y=12(加减法).1.(2022•苏州模拟)用适当的方法解下列方程组.(1)x+2y=9y−3x=1;(2x−34y=1=4.2.(2022秋•锦江区校级期末)用适当的方法解下列方程组.(1)x=2y−14x+3y=7;(2)3x+2y=22x+3y=28,.3.用适当的方法解下列方程组:(1)x+2y=0,3x+4y=6;(2=2y1)−y=11(3)x+0.4y=40,0.5x+0.7y=35;(4+n−m4=−14,5(n1)12=2.4.(2022•天津模拟)用适当的方法解下列方程组:(1)x +y =52x−y =4; (2=y 24−y−33=112.5.(2021•越城区校级开学)用适当的方法解下列方程组:(1)2x−3y =7x−3y =7. (2)0.3p +0.4q =40.2p +2=0.9q .6.(2022春•东城区校级月考)用适当的方法解下列方程组(1)x +y =52x +y =8; (2)2x +3y =73x−2y =4.7.(2021春•哈尔滨期末)用适当的方法解下列方程组(1)x +2y =93x−2y =−1 (2)2x−y =53x +4y =28.(2022春•椒江区校级期中)用适当的方法解下列方程组:(1)2x +3y =16①x +4y =13②; (2)2s t 3=3s−2t 8=3.9.(2022春•诸暨市期中)用适当的方法解下列方程组:(1)y=2x−1x+2y=−7(2+y3=7+y2=810.(2021春•南湖区校级期中)用适当的方法解下列方程组:(1)3x+2y=9x−y=8;(2=x y2=7.1.先阅读材料,然后解方程组:材料:解方程组x+y=4①3(x+y)+y=14②在本题中,先将x+y看作一个整体,将①整体代入②,得3×4+y=14,解得y=2.把y=2代入①得x=2,所以x=2 y=2这种解法称为“整体代入法”,你若留心观察,有很多方程组可采用此法解答,请用这种方法解方程组x−y−1=0①4(x−y)−y=5②.2.(2021秋•乐平市期末)解方程组3x−2y=8⋯⋯⋯①3(3x−2y)+4y=20⋯.②时,可把①代入②得:3×8+4y=20,求得y=﹣1,从而进一步求得x=2y=−1这种解法为“整体代入法“,请用这样的方法解下列方程组2x−3y=123(2x−3y)+5y=26.3.先阅读,然后解方程组.解方程组x−y−1=0①4(x−y)−y=5②时,可由①得x﹣y=1.③,然后再将③代入②得4×1﹣y=5,求得y=﹣1,从而进一步求得x=0y=−1这种方法被称为“整体代入法”,请用这样的方法解下列方程组:=0=2y+1.4.(2022春•太和县期末)先阅读,然后解方程组.解方程组x−y−1=0①4(x−y)−y=5②时,可由①得x﹣y=1,③然后再将③代入②得4×1﹣y=5,求得y=﹣1,从而进一步求得x=0①y=−1②这种方法被称为“整体代入法”,+2y=9.5.先阅读,然后解方程组.解方程组x−y−1=0①4(x−y)−y=5②时,可由①得x﹣y=1③,然后再将③代入②得4×1﹣y=5,求得y=﹣1,从而进一步求得x这种方法被称为“整体代入法”,请用这样的方法解下列方程组:2x−3y−2=03(2x−3y)+y=7.1.用换元法解下列方程组+2y=12−1y=342.用换元法解下列方程组:(1)3(x+y)+2(x−y)=36(x+y)−4(x−y)=−16(2+x5y3=2−(x+5y)=5.3.(2022春•云阳县期中)阅读探索:解方程组(a−1)+2(b+2)=62(a−1)+(b+2)=6解:设a﹣1=x,b+2=y原方程组可以化为x+2y=62x+y=6,解得x=2y=2,即:a−1=2b+2=2∴a=3b=0,此种解方程组的方法叫换元法.(1)拓展提高运用上述方法解下列方程组(a4−1)+2(b5+2)=102(a4−1)+(b5+2)=11;(2)能力运用已知关于x,y的方程组a1x+b1y=c1a2x+b2y=c2的解为x=6y=7,求关于m、n的方程组a1(m−2)+b1(n+3)=c1a2(m−2)+b2(n+3)=c2的解.4+x−y10=3①−x−y10=−1②,你会解这个方程组吗?小明、小刚、小芳争论了一会儿,他们分别写出了一种方法:小明:把原方程组整理得8x+2y=90③2x+8y=−30④④×4﹣③得30y=﹣210,所以y=﹣7把y=﹣7代入③得8x=104,所以x=13,即x=13y=−7小刚:设x y6=m,x−y10=n,则m+n=3③m−n=−1④③+④得m=1,③﹣④得m=2,=1=2,所以x+y=6x−y=20,所以x=13y=−7.小芳:①+②得2(x y)6=2,即x+y=6.③①﹣②得2(x−y)10=4,即x﹣y=20.④③④组成方程组得x=13③﹣④得y =﹣7,即x =13y =−7.老师看过后,非常高兴,特别是小刚的方法独特,像小刚的这种方法叫做换元法,你能用换元法解下列方程组吗?+2x 3y 7=1−2x 3y 7=5.5.(2022春•卧龙区校级月考)阅读探索(1)知识积累解方程组(a−1)+2(b +2)=62(a−1)+(b +2)=6.解:设a ﹣1=x ,b +2=y .原方程组可变为x +2y =62x +y =6,解这个方程组得x =2y =2,即a−1=2b +2=2,所以a =3b =0,这种解方程组的方法叫换元法.(2)拓展提高运用上述方法解下列方程组:(m 3−1)+2(n 5+2)=43(m 3−1)−(n 5+2)=5.(3)能力运用已知关于x ,y 的方程组a 1x +b 1y =c 1a 2x +b 2y =c 2的解为x =3y =4,请直接写出关于m 、n 的方程组a 1(m +2)−b 1n =c 1a 2(m +2)−b 2n =c 2的解是 .。
求解二元一次方程组代入消元法

求解二元一次方程组代入消元法《求解二元一次方程组代入消元法》嗨,同学们!今天咱们来一起探索一下二元一次方程组的代入消元法,这可超有趣呢!我先给大家讲个小故事。
有一天,小明和小红去买文具。
小明买了2支铅笔和3本本子花了10元钱,小红买了3支铅笔和1本本子花了8元钱。
咱们设一支铅笔的价格是x元,一本本子的价格是y元。
那就能得到两个方程啦,2x + 3y = 10和3x + y = 8。
这就像两个小谜团,我们要把x和y找出来呢。
那代入消元法是啥呢?就像是我们在玩一个找宝藏的游戏。
我们要先从一个方程里,把一个未知数用含有另一个未知数的式子表示出来。
就拿3x + y = 8这个方程来说吧。
我们可以把y表示出来,y = 8 - 3x。
这一步就像是我们找到了一把小钥匙,能打开通往宝藏的一道门呢。
然后呢,我们把这个表示y的式子代入到另一个方程2x + 3y = 10里面。
这就变成了2x + 3(8 - 3x)=10。
这一步可关键啦,就好像我们用找到的小钥匙打开了另一扇有宝藏的门。
这时候呢,我们要好好计算这个式子。
2x + 3×8 - 3×3x = 10,2x + 24 - 9x = 10。
这就像在整理一堆小积木,得把它们摆放整齐才能找到我们要的东西。
那就是- 7x = 10 - 24,- 7x = - 14,x = 2。
哇,我们找到了x的值,就像挖到了宝藏的一部分,是不是很兴奋呢?那找到x = 2之后呢?我们再把x = 2代入到之前表示y的式子y = 8 - 3x里面。
y = 8 - 3×2,y = 8 - 6,y = 2。
哈哈,x和y都被我们找到了。
这就像我们把宝藏完全挖出来了,多有成就感呀。
我再给大家举个例子吧。
比如说方程组x + 2y = 5和2x - y = 1。
我们从2x - y = 1这个方程里把y表示出来,y = 2x - 1。
然后把y = 2x - 1代入到x + 2y = 5里面,就得到x + 2(2x - 1)=5。
代入消元法解二元一次方程组

代入消元法解二元一次方程组
代入消元法是一种解决二元一次方程组的方法。
二元一次方程组由两个未知数和两个方程组成,通常形式为:
ax + by = c
dx + ey = f
首先,我们可以利用其中一条方程式将其中一个未知数表示为另一个未知数的函数。
例如,如果我们用第一个方程式表示x,我们可以得到:
x = (c - by)/a
然后我们将这个表达式代入另一个方程式中,得到:
d(c - by)/a + ey = f
接下来,我们可以将方程式中的未知数y解出来。
首先,我们将方程式化简:
dc/a - dby/a + ey = f
然后,我们将所有包含y的项移到等式左边,所有不包含y的项移到等式右边:
dby/a + ey = dc/a - f
接下来,我们可以将y的系数提取出来并因式分解:
y(db/a + e) = dc/a - f
最后,我们将y解出来:
y = (dc/a - f)/(db/a + e)
一旦我们求出了y,我们可以将其代入最初的方程式中,求解出x。
二元一次方程组解法练习题精选(含答案)
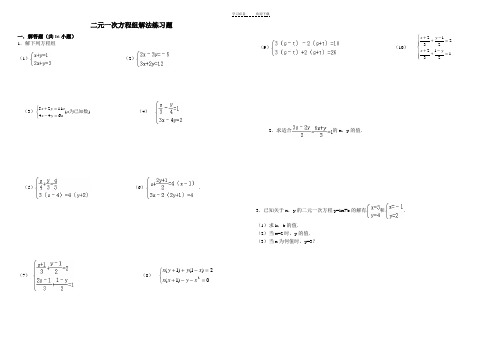
二元一次方程组解法练习题一.解答题(共16小题) 1.解下列方程组 (1)(2)(3))(6441125为已知数a a y x a y x ⎩⎨⎧=-=+ (4)(5)(6).(7)(8)⎩⎨⎧=--+=-++0)1(2)1()1(2x y x x x y y x(9)(10) ⎪⎪⎩⎪⎪⎨⎧=-++=-++1213222132y x y x2.求适合的x ,y 的值.3.已知关于x ,y 的二元一次方程y=kx+b 的解有和.(1)求k ,b 的值.(2)当x=2时,y 的值. (3)当x 为何值时,y=3?1.解下列方程组(1)(2);(3);(4)(5).(6)(7)(8)(9)(10);2.在解方程组时,由于粗心,甲看错了方程组中的a ,而得解为,乙看错了方程组中的b ,而得解为.(1)甲把a看成了什么,乙把b看成了什么?(2)求出原方程组的正确解..求适合得到一组新的方程解:由题意得:﹣,((()故原方程组的解为.故原方程组的解为.)原方程组可化为.所以原方程组的解为)原方程组可化为:x=x=代入×所以原方程组的解为:原方程组可化为,所以方程组的解为4.解方程组:)原方程组化为y=所以原方程组的解为5.解方程组:解:即解得所以方程组的解为.6.已知关于x,y的二元一次方程y=kx+b的解有和.(1)求k,b的值.(2)当x=2时,y的值.(3)当x为何值时,y=3?的二元一次方程组,再运用加减消元)依题意得:,.y=,.x+7.解方程组:(1);(2).)原方程组可化为∴方程组的解为)原方程可化为,,∴方程组的解为解:原方程组可化为则原方程组的解为.9.解方程组:解:原方程变形为:y=解之得10.解下列方程组: (1)(2),,代入=.所以原方程组的解为)原方程组整理为所以原方程组的解为.(2),解得∴原方程组可化为,解得∴∴原方程组的解为.12.解二元一次方程组: (1);.则方程组的解是)此方程组通过化简可得:则方程组的解是13.在解方程组时,由于粗心,甲看错了方程组中的a ,而得解为,乙看错了方程组中的b ,而得解为.(1)甲把a 看成了什么,乙把b 看成了什么? (2)求出原方程组的正确解. 代入方程组,得解得:把,得解得:∴方程组为则原方程组的解是.,x=y=∴原方程组的解为;.,故原方程组的解为.)化简整理为,故原方程组的解为.(∴原方程组的解为;)原方程组可化为∴原方程组的解为.。
七年级数学(下)_二元一次方程练习题(代入消元法和加减消元法)之欧阳德创编

二元一次方程组一、选择:1.方程-x+4y=-15用含y的代数式表示,x是()A.-x=4y-15 B.x=-15+4y C.x=4y+15 D.x=-4y+152.将y=-2x-4代入3x-y=5可得()A.3x-2x+4=5 B.3x+2x+4=5 C.3x+2x-4=5 D.3x-2x-4=53.二元一次方程组941611x yx y+=⎧⎨+=-⎩的解满足2x-ky=10,则k的值等于( )A.4 B.-4 C.8 D.-84.解方程组35123156x yx y+=⎧⎨-=-⎩比较简便的方法为( )A.代入法 B.加减法 C.换元法 D.三种方法都一样5.若二元一次方程2x+y=3,3x-y=2和2x-my=-1有公共解,则m取值为( )A.-2 B.-1 C.3 D.46.甲、乙两人同求方程ax -by=7的整数解,甲正确的求出一个解为11x y =⎧⎨=-⎩,•乙把ax -by=7看成ax -by=1,求得一个解为12x y =⎧⎨=⎩,则a 、b 的值分别为( ) A . 25a b =⎧⎨=⎩ B . 52a b =⎧⎨=⎩ C . 35a b =⎧⎨=⎩ D . 53a b =⎧⎨=⎩7.用代入法解方程组252138x y x y +=-⎧⎨+=⎩较为简便的方法是( ) A .先把①变形 B .先把②变形C .可先把①变形,也可先把②变形D .把①、②同时变形8.把方程7x-2y=15写成用含x 的代数式表示y 的形式,得( )A .x=215152715157 (7722)x x yx x B x C y D y ----=== 二、填空:1.在方程2x+3y-6=0中,用含x 的代数式表示y ,则y=_______,用含y 的代数式表示x ,则x=_______.2.用代入法解方程组59224x y x y -=⎧⎨-=⎩最好是先把方程______•变形为________,•再代入方_______求得_______的值,最后再求______的值,最后写出方程组的解.3.方程4(3x-y )=x-3y ,用含x 的代数式表示,则y=________.4.将y=12x+3代入2x+4y=-1后,化简的结果是________,从而求得x 的值是_____.5.当a=3时,方程组122ax y x y +=⎧⎨+=⎩的解是_________. 6.已知方程2x+3y=2,当x 与y 互为相反数时,x=______,y=_______.7.若方程组431(1)3x y kx k y +=⎧⎨+-=⎩的解x 和y 的值相等,则k=________.8.已知x=-1,y=2是方程组的1311ax by bx ay +=⎧⎨+=-⎩解,则ab=________.9.如果12x y =⎧⎨=⎩是方程2mx-7y=10的解,则m=_______.10.用加减法解下列方程组34152410x y x y +=⎧⎨-=⎩较简便的消元方法是:将两个方程_______,消去未知数_______.11.已知方程组234321x y x y -=⎧⎨+=⎩ ,用加减法消x 的方法是__________;用加减法消y 的方法是________.12.方程组241x y x y +=⎧⎨+=⎩ 的解_________.13.方程2353x y x -+==3的解是_________.14.已知方程342--n m x -5143-+n m y =8是关于x 、y 的二元一次方程,则m=_____,n=_______.15.已知方程组51mx n my m +=⎧⎨-=⎩的解是12x y =⎧⎨=⎩,则m=________,n=________.16.已知(3x+2y -5)2与│5x+3y-8│互为相反数,则x=______,y=________.17.若方程组22ax by ax by +=⎧⎨-=⎩与234456x y x y +=⎧⎨-=-⎩的解相同,则a=________,b=_________.18.若x-3y=2x+y-15=1,则x=______,y=_______.19.在y=kx+b 中,当x=1时,y=2;当x=2时,y=4,那么k=_______,b=_______.①②20.已知1331024x ax y y x by =--=⎧⎧⎨⎨=+=⎩⎩是方程组的解,求a 、b 的值. 21.若│x+y-2│+(x-y )2=0,那么x=________,y=________.22.已知x=5-t ,y-3=2t ,则x 与y 之间的关系式是_______.三、计算1.(1)23328y x x y =-⎧⎨-=⎩3(2)3814x y x y -=⎧⎨-=⎩23(3)253s t t s =⎧⎪+⎨=⎪⎩356(4)415x y x y -=⎧⎨+=-⎩(5)用代入法解方程组1235x y x y -=⎧⎨+=⎩ (6)23123417x y x y +=⎧⎨+=⎩2.把下列方程写成用含x 的代数式表示y 的形式: ①3x+5y=21 ②2x-3y=-11③4x+3y=x-y+1 ④2(x+y )=3(x-y )-13.若方程组23352x y m x y m +=⎧⎨+=+⎩的解满足x+y=12,求m 的值.4.已知方程组25264x y ax by +=-⎧⎨-=-⎩和方程组35368x y bx ay -=⎧⎨+=-⎩的解相同,求(2a+b)2005的值.5.已知方程组82x yx y+∆=⎧⎨∆-=⎩中,x、y的系数部已经模糊不清,但知道其中□表示同一个数, △也表示同一个数,11xy=⎧⎨-⎩是这个方程组的解,你能求出原方程组吗?。
2.3.1 代入消元法 浙教版七年级数学下册同步练习(含解析)

2.3 解二元一次方程组第1课时 代入消元法基础过关全练知识点 代入消元法1.(2022湖南株洲中考)对于二元一次方程组{y =x −1,①x +2y =7,②将①式代入②式,消去y 可以得到( ) A.x+2x-1=7 B.x+2x-2=7C.x+x-1=7D.x+2x+2=72.四名学生利用代入法解二元一次方程组{3x −4y =5,①x −2y =3②时,提出四种不同的解法,其中解法不正确的是( ) A.由①得x=5+4y 3③,将③代入② B.由①得y=3x−54③,将③代入② C.由②得y=-x−32③,将③代入①D.由②得x=3+2y ③,将③代入①3.(2022江苏无锡中考)二元一次方程组{3x +2y =12,2x −y =1的解为 .4.【新独家原创】 已知关于a,b 的二元一次方程组{a +m =3,b −3=m,则-a-b 的值为 .5.(2021浙江丽水中考)解方程组:{x =2y,x −y =6.6.【易错题】下面是老师在铭铭的数学作业本上截取的部分内容:解方程组{2x −y =3,①x +y =−12.②解:方程①变形,得y=2x-3③, 第一步把方程③代入方程①,得2x-(2x-3)=3, 第二步整理,得3=3, 第三步因为x 可以取任意实数,所以原方程组有无数个解.问题:这种解方程组的方法叫 ;铭铭的解法正确吗?如果不正确,错在哪一步?并求出正确的解.能力提升全练7.已知单项式-3x m-1y 3与52x n y m+n 是同类项,那么m,n 的值分别是 ( )A.2,1B.1,2C.0,-1D.-1,28.小明说{x =−1,y =2为方程ax+by=10的解,小惠说{x =2,y =−1为方程ax+by=10的解,两人谁也不能说服对方.若他们的说法都正确,则a,b 的值分别为 ( )A.12,10B.9,10C.10,11D.10,109.(2022浙江杭州西湖期中,9,)在解关于x,y 的方程组{ax −2by =8①,2x =by +2②时,小明将方程①中的“-”看成了“+”,得到的解为{x =2,y =1,则原方程组的解为 ( ) A.{a =2b =2 B.{x =2y =2 C.{x =−2y =−3 D.{x =2y =−110.如果|x-2y+1|+|x+y-5|=0,那么x= .11.(2022浙江杭州期中改编,15,)若 1 314x+17y=2y+x-5=2x-3,则2(x-2y)= .12.(2022浙江杭州萧山期中,14,)对于有理数x,y,定义一种新运算:x ⊕y=ax+by-5,其中a,b 为常数.已知1⊕2=9,(-3)⊕3=-2,则2a+b= .13.(2022浙江杭州余杭月考,15,)已知关于x,y 的二元一次方程(3x-2y+9)+m(2x+y-1)=0,无论m 取何值,方程总有一个固定不变的解,这个解是 .14.【一题多解】当关于x,y 的二元一次方程组{2x −y −4m =0,14x −3y −20=0中y 的值是x 值的3倍时,求x,y 的值.15.已知关于x,y 的二元一次方程组{ax +5y =4,5x +y =3与{x −2y =5,5x +by =1的解相同,求a,b 的值.素养探究全练16.【运算能力】材料:解方程组{x −y −1=0①,4(x −y)−y =5②时,可由①得x-y=1③,然后将③代入②得4×1-y=5,解得y=-1,将y=-1代入③,得x-(-1)=1,解得x=0,∴方程组的解为{x =0,y =−1,这种方法被称为“整体代入法”.请用这样的方法解方程组{2x −y −2=0,6x−3y+45+2y =12.17.【运算能力】三个同学对问题“若关于x,y 的二元一次方程组{a 1x +b 1y =c 1,a 2x +b 2y =c 2的解是{x =3,y =4,求关于x,y 的二元一次方程组{3a 1x +2b 1y =5c 1,3a 2x +2b 2y =5c 2的解”提出各自的想法.甲说:“这个题目条件不够,不能求解.”乙说:“它们的系数有一定的规律,可以试试.”丙说:“能不能把第二个方程组的两个方程的两边都除以5,通过换元的方法来解决?”参考他们的讨论,解决上述问题.答案全解全析基础过关全练1.B 将①式代入②式,得x+2(x-1)=7,∴x+2x-2=7,故选B.2.C C 中,应该由②得y=x−32,故选项C 解法错误,符合题意,故选C.3.答案 {x =2y =3 解析 {3x +2y =12,①2x −y =1②,由②得y=2x-1③,将③代入①得3x+2(2x-1)=12,解得x=2,将x=2代入③得y=3,∴原方程组的解为{x =2,y =3. 4.答案 -6解析 {a +m =3①,b −3=m②,把②代入①,得a+b-3=3, ∴a+b=6,∴-a-b=-6.5.解析 {x =2y①,x −y =6②,把①代入②得,2y-y=6,解得y=6, 把y=6代入①得,x=12, 则原方程组的解为{x =12,y =6. 6.解析 代入消元法.铭铭的解法不正确,错在第二步,正确解法:将方程①变形,得y=2x-3③,把③代入②,得x+2x-3=-12,解得x=-3,把x=-3代入③,得y=-9,所以原方程组的解为{x =−3,y =−9.能力提升全练7.A 根据题意得{m −1=n,m +n =3,解得{m =2,n =1.故选A. 8.D 由{x =−1,y =2为方程ax+by=10的解,{x =2,y =−1为方程ax+by=10的解,得{−a +2b =10,2a −b =10,解得{a =10,b =10.故选D. 9.C 把{x =2,y =1代入{ax +2by =8,2x =by +2,得{2a +2b =8,4=b +2,解得{a =2,b =2, ∴原方程组为{2x −4y =8,2x =2y +2,解得{x =−2,y =−3.故选C. 10.答案 3解析 ∵|x-2y+1|+|x+y-5|=0,∴{x −2y +1=0,①x +y −5=0,②由①得x=2y-1③,把③代入②,得2y-1+y-5=0,解得y=2,把y=2代入③,得x=2×2-1=3,∴原方程组的解为{x =3,y =2.11.答案 -4解析 由2y+x-5=2x-3得2y+x-2x=-3+5,∴2y-x=2,∴x-2y=-2.∴2(x-2y)=2×(-2)=-4.12.答案 13解析 根据题中的新定义得{a +2b −5=9,−3a +3b −5=−2,整理得{a +2b =14,①−a +b =1,②由②得b=1+a ③,把③代入①,得a+2(1+a)=14,解得a=4,把a=4代入③,得b=1+4=5.则原方程组的解为{a =4,b =5,则2a+b=8+5=13.13.答案 {x =−1y =3解析 ∵无论m 取何值,方程总有一个固定不变的解,∴{2x +y −1=0,3x −2y +9=0,解得{x =−1,y =3. 14.解析 解法一:∵y 的值是x 值的3倍,∴y=3x,∴{2x −3x −4m =0,14x −9x −20=0,解得{x =4,m =−1, ∴y=3×4=12.故x 的值为4,y 的值为12.解法二:{2x −y −4m =0,①14x −3y −20=0,② 由①得,y=2x-4m,③把③代入②,得14x-3(2x-4m)-20=0,∴x=−3m+52,∴y=-7m+5,∵y 的值是x 值的3倍,∴y=3x,∴-7m+5=3×−3m+52,解得m=-1.∴x=4,y=12.故x 的值为4,y 的值为12.15.解析 ∵两个方程组的解相同,∴可用方程5x+y=3,x-2y=5组成新方程组,得{5x +y =3,①x −2y =5,②由①得,y=3-5x ③,把③代入②,得x-2(3-5x)=5,解得x=1,把x=1代入③得y=-2,∴此方程组的解为{x =1,y =−2,把{x =1,y =−2代入{ax +5y =4,5x +by =1,得{a −10=4,5−2b =1,解得{a =14,b =2.素养探究全练16.解析 {2x −y −2=0,①6x−3y+45+2y =12,② 由①得2x-y=2③,将③代入②得3×2+45+2y=12,解得y=5,把y=5代入③得2x-5=2,解得x=3.5.所以原方程组的解为{x =3.5,y =5.17.解析 方程组{3a 1x +2b 1y =5c 1,3a 2x +2b 2y =5c 2中的两个方程的两边都除以5,得{a 1(35x)+b 1(25y)=c 1,a 2(35x)+b 2(25y)=c 2, 因为方程组{a 1x +b 1y =c 1,a 2x +b 2y =c 2的解是{x =3,y =4,所以{35x =3,25y =4,解得{x =5,y =10.所以方程组{3a 1x +2b 1y =5c 1,3a 2x +2b 2y =5c 2的解是{x =5,y =10.。
代入法解二元一次方程组(二)专题训练

目录代入法解二元一次方程组(二)专题训练 (2)(一)导入新课 (3)(二)讲解新知 (3)(三)课堂练习 (4)(四)小结作业 (4)解二元一次方程组(专题练习二) (23)代入法解二元一次方程组(二)专题训练真题示例:《代入法解二元一次方程组》【考题回顾】1.题目:代入法解二元一次方程组2.内容:3.基本要求:(1)试讲时间10分钟以内;(2)讲解要目的明确、条理清楚、重点突出;【考题解析】【教案设计】(一)导入新课创设两名同学去文具店买文具的情境,引导学生列出方程组,点明这是前面所学的二元一次方程组,这节课学习如何解二一次方程组。
引入课题。
(或者复习导入:回顾一元一次方程及其求解方法。
)(二)讲解新知请学生同桌两人为一组,尝试解方程组:,教师巡视并提示:学过解什么样的方程?可否将二元一次方程组转化为会求解的方程?请学生上黑板板演计算过程,结合板书教师讲解,由②知x=13-4y③,将③代入①,则:2(13-4y)+3y=16,化简求得:y=2。
将y=2代入③中,求得:x=5。
所以原方程组的解是。
教师肯定学生作答,并请学生尝试用x表示y进行求解,比较求得的结果是否一样。
请学生比较两次求解过程,思考上面解方程组的基本思路是什么,主要步骤又有哪些。
预设学生能够回答出。
上题是将二元一次方程组转化为一元一次方程来进行求解。
师生共同总结步骤:(1)将其中一个方程中的某个未知数用含有另一个未知数的代数式表示出来,(2)把得到的式子代入另一个方程中,从而消去一个未知数,化二元一次方程组为一元一次方程,并求解;(3)把求得的解代入方程,求得另一个未知数的解。
教师总结:这种解方程组的方法称为代入消元法。
简称代入法。
(三)课堂练习练习:用代入法解下列方程组:(1)(2)(四)小结作业小结:重点回顾代入法解二元一次方程组的基本思路及步骤。
作业:思考练习题中的两个方程组是否有其他的求解方法。
【板书设计】【答辩解析】1.二元一次方程组有哪些解法?答:初中所学解二元一次方程组主要有以下两种解法:①代入消元法:将方程组中的一个方程的某个未知数用含有另一个未知数的代数式表示出来,代入到另一个方程中,消去一个未知数,得到一个一元一次方程,最后求得方程的解。
二元一次方程代入消元法

二元一次方程代入消元法要使用代入消元法解决二元一次方程,我们需要以下步骤:第一步:将两个方程用字母表示出来。
设方程一为ax+by=c,方程二为dx+ey=f。
第二步:用其中一个方程表示出一个变量。
在这里我们以x为例,假设方程一为ax+by=c,可以通过移项将x表示为x=(c-by)/a。
现在,我们有了x的表达式。
第三步:将x的表达式代入另一个方程。
将x=(c-by)/a代入到方程二dx+ey=f,即可消去变量x,从而得到一个只含有y的方程。
第四步:解决只含有一个变量的方程。
现在我们得到了一个只含有y 的方程,我们可以通过解这个方程得到y的值。
第五步:将y的值代入到方程一或方程二中,以求得x的值。
将y的值代入到方程一ax+by=c或方程二dx+ey=f中,即可求得x的值。
第六步:检验解是否确切。
将求得的x和y的值代入到原来的两个方程中,检验解是否成立。
下面,我们来通过一个例子来说明代入消元法的具体步骤。
例子:解二元一次方程组{5x+2y=10,2x-y=5}。
首先,将两个方程用字母表示出来,方程一为5x+2y=10,方程二为2x-y=5然后,用方程二来表示变量x,假设方程二为2x-y=5,我们可以通过移项将x表示为x=(5+y)/2接下来,将x的表达式代入方程一,即将x=(5+y)/2代入到方程一5x+2y=10中,得到5((5+y)/2)+2y=10。
化简方程得到25+5y+2y=20,得到7y=-5,所以y=-5/7将y的值代入方程二2x-y=5中,得到2x-(5/7)=5,化简方程得到14x-5=35,所以x=40/14=20/7最后,将求得的x和y的值代入到原来的两个方程中检验解是否成立,代入方程一得到5(20/7)+2(-5/7)=10,化简方程得到50/7-10/7=10,化简后得到10=10.代入方程二2(20/7)-(-5/7)=5,化简得到40/7+5/7=5,化简后得到45/7=5、乘以7,得到45=5*7,即45=35,这个方程不成立,说明解不正确。
代入消元法解二元一次方程组

由① ,得 x=35-y. ③ 把③代入② ,得 2(35-y)+4y=94.
70-2y+4y=94 2y=24 y=12
把y=12代入③ ,得 x=23.
x 23
y
12
3、今有鸡兔同笼,上有三十五头, 下有九十四足,问鸡兔各几何.
解:设鸡有x只,兔有y只.
x+y=35 2x+4y=94
(4)回代:将求得的未知数的值代入到变形后的方程
中求出另一个未知数的值.
(5)写解:用
x a
y
bБайду номын сангаас
的形式写出方程组的解.
例4
二元一次方程组
3x 4x
y 12 ay 12
的解中
y与x互为相反数,求a的值.
解:由题意得 3xxyy012,
x y
6
6
把
x 6
y
6
代入4x+ay=12,
得 a=2.
例5
x 2
用代入法解方程组 3
y4 5
①
2 x 7 y 90 ②
解:由①,得 5(x-2)=3(y+4)
5x-10=3y+12
5x-3y=22
x 223y ③ 5
例5
用代入法解方程组
x 2
3
y4 5
①
2 x 7 y 90 ②
解:令 x2 y4 = k,则x=3k+2,③y=5k-4,④
4x 5y 460 ① 2x 3y 240 ②
由②, 得 2x=240-3y ③
把③代入①,得 2(240-3y)+5y=460 480-6y+5y=460 -y=-20 y=20.
二元一次方程代入消元法

二元一次方程代入消元法是一种求解含有两个未知数的一次方程组的方法。
其基本思想是将其中一个方程中的一个未知数表示成另一个方程中的未知数的函数,然后将其代入另一个方程中消去这个未知数,从而得到只含有一个未知数的方程,进而求解。
具体步骤如下:
1、给定一个二元一次方程组,例如:
a₁x + b₁y = c₁
a₂x + b₂y = c₂
2、选取其中一个方程(通常选择系数较小或较简单的方程),假设为第一个方程a₁x + b₁y = c₁。
3、将第一个方程中的一个未知数(通常选择x)表示成另一个方程中的未知数的函数。
假设将x 表示成y 的函数,即x = f(y)。
4、将代入公式x = f(y) 代入第二个方程a₂x + b₂y = c₂ 中,将x 用f(y) 替换,得到只含有一个未知数y 的方程。
5、解这个只含有一个未知数y 的方程,求得y 的值。
6、将求得的y 的值代入步骤3 中的代入公式x = f(y),求得x 的值。
7、得到方程组的解(x, y)。
通过二元一次方程代入消元法,我们可以较为方便地求解含有两个未知数的方程组,并得到方程组的解。
这种方法在数学问题和实际应用中具有一定的实用性和便利性。
《用代入消元法解二元一次方程组》同步练习1(北京课改七年级下)

用代入消元法解二元一次方程组同步练习【主干知识】认真预习教材,尝试完成下列各题:1.我们把________,从而求出方程组的解的方法,叫做代入消元法,简称代入法.2.用代入法解二元一次方程组的步骤是:(1)把方程组中的一个方程变形,写出_________的形式;(2)把它_________中,得到一个一元一次方程;(3)解这个__________;(4)把求得的值代入到_________,从而得到原方程组的解.3.在方程2x+3y-6=0中,用含x的代数式表示y,则y=_______,用含y的代数式表示x,则x=_______.4.•用代入法解方程组最好是先把方程______•变形为________,•再代入方程_______求得_______的值,最后再求______的值,最后写出方程组的解.5.用代入法解方程组.【点击思维】1.用代入法解二元一次方程组时,•要把一个未知数用含另一个未知数的代数式来表示,你认为应该选择哪一个方程来变形?2.检验方程组的解时,必须将求得的未知数的值代入________方程,看左右两边的值是否相等.3.方程4(3x-y)=x-3y,用含x的代数式表示,则y=________.【典例分析】例1解方程组思路分析:本例这两个方程中①较简单,且x、y的系数均为1,故可把①变形,•把x 用y表示,或把y用x来表示皆可,然后将其代入②,消去一个未知数,化成一元一次方程,进而再求出方程组的解.解:把①变形为y=4-x ③把③代入②得:-=1即-=1,=-1,=∴x=把x=代入③得y=4-=3所以原方程的解是.若想知道解的是否正确,可作如下检验:检验:把x=,y=3代入①得,左边=x+y=+3=4,右边=4.所以左边=右边.再把x=,y=3代入②得左边=-=1,右边=1.所以左边=右边.所以是原方程组的解.【基础能力训练】1.方程-x+4y=-15用含y的代数式表示,x是()A.-x=4y-15 B.x=-15+4y C.x=4y+15 D.x=-4y+152.将y=-2x-4代入3x-y=5可得()A.3x-2x+4=5 B.3x+2x+4=5 C.3x+2x-4=5 D.3x-2x-4=53.判断正误:(1)方程x+2y=2变形得y=1-3x ()(2)方程x-3y=写成含y的代数式表示x的形式是x=3y+ ()4.将y=x+3代入2x+4y=-1后,化简的结果是________,从而求得x的值是_____.5.当a=3时,方程组的解是_________.6.把方程7x-2y=15写成用含x的代数式表示y的形式,得()A.x=7.用代入法解方程组较为简便的方法是()A.先把①变形 B.先把②变形C.可先把①变形,也可先把②变形 D.把①、②同时变形8.已知方程2x+3y=2,当x与y互为相反数时,x=______,y=_______.9.若方程组的解x和y的值相等,则k=________.10.已知x=-1,y=2是方程组的解,则ab=________.11.把下列方程写成用含x的代数式表示y的形式:①3x+5y=21 ②2x-3y=-11; ③4x+3y=x-y+1 ④2(x+y)=3(x-y)-112.如果是方程2mx-7y=10的解,则m=_______.13.下面方程组的解法对不对?为什么?解方程组解:把①代入②得3x+2x=5,5x=5,所以x=1是方程组的解.14.已知方程组(1)求出方程①的5个解,其中x=0,,1,3,4;(2)求出方程②的5个解,其中x=0,,1,3,4;(3)求出这个方程组的解.15.若x-3y=2x+y-15=1,则x=______,y=_______.16.用代入法解下列方程组:(1)【综合创新训练】17.在y=kx+b中,当x=1时,y=2;当x=2时,y=4,那么k=_______,b=_______.18.已知的解,求a、b的值.19.若│x+y-2│+(x-y)2=0,那么x=________,y=________.20.请思考:方程组的解是不是方程8x-10y=6的一个解.21.已知二元一次方程组的解为x=a,y=b,则│a-b│=()A.1 B.11 C.13 D.1622.已知x=5-t,y-3=2t,则x与y之间的关系式是_______.【探究学习】苏步青巧解数学趣题的启示我国著名数学家苏步青在访问德国时,德国一位数学家给他出了这样一道题目:甲、乙二人相对而行,他们相距10千米,甲每小时走3千米,乙每小时走2千米,甲带着一条狗,狗每小时跑5千米,狗跑得快,它同甲一起出发,碰到乙的时候向甲跑去,碰到甲的时候又向乙跑去,问当甲、乙两人相遇时,这条狗一共跑了多少千米?苏步青教授很快就解出了这道题目.同学们,你知道他是怎么解的吗?这道题最让人迷惑不解的是甲身边的那条狗.•如果我们先计算狗从甲的身边跑到乙的身边的路程s,再计算狗从乙的身边跑到甲的身边的路程s,……,•显然把狗跑的路程相加,这样很繁琐,笨拙且不易计算.苏教授从整体着眼,根据甲、乙出发到相遇经历的时间与狗所走的时间相等,即10÷(3+2)=2(小时),•这样就不难求出狗一共跑的路程是:5×2=10(千米).苏步青教授在解题时,把注意力和着眼点放在问题的整体结构上,从而能触及问题的实质:狗从出发到甲、乙两相遇所用的时间,恰好是甲、乙二人相遇所用的时间,从而使问题得到巧妙的解决.苏教授这种解决问题的思想方法实际上就是数学中的整体思想的应用.对于某些数学问题,灵活运用整体思想,常可化难为易,捷足先登.•在解二元一次方程组时,也要注意这种思想方法的应用.比如解方程组解:把②代入①得x+2×1=4,所以x=2把x=2代入②得2+2y=1,解之,得y=所以方程组的解为同学们,你会用同样的方法解下面两个方程吗?试试看!(1)答案:【主干知识】1.通过“代入”消去一个未知数2.(1)用一个未知数表示另一个未知数的代数式.(2)代入到另一个方程中(3)一元一次方程(4)变形的的方程中,求得另一个未知数的值3.或y=2-x 或3-y4.② x=4+2y ① y x 5.【点击思维】1.选一个较简单的方程.最好该方程中有一个未知数的系数为1或-1,比如是3x-y=4,应把y变成用含x的代数式来表示,即y=3x-4,若未知数的系数不是1或-1,•将会出现分数,例如3x-y=4,若把x变出为用含y的代数式来表示,是x=,将会给解题带来很大的麻烦.2.方程组中的每一个解析:只有方程组中每个方程左、右两边的值相等了,•它才是各个方程的解,即它们的公共解,从而是原方程组的解.3.y=11x 解析:去括号,得12x-4y=x-3y,移项得12x-x=4y-3y,•合并同类项,•得11x=y 即y=11x.【基础能力训练】1.C 2.B 3.(1)×(2)×4.4x=-13 - 5.6.C 7.B 8.-2 2 9.11 10.-1511.①y=或y=(x-1)12.1213.不对,方程组的解应是一对未知数的值,不能求出一个就完了,还得求出y•的值,并且把这一对x、y的值用大括号括起来.14.(1)x=0,,1,3,4时,y=-1,-,1,5,7;(2)x=0,,1,3,4时,y=-,-,-,-,-;(3)方程组的解是15.7 216.(1)【综合创新训练】17.2 0 解析:把x=1,y=2及x=2,y=4分别代入到y=kx+b中,•得到一个方程组.18.把代入到方程组中得19.-1 -1 解析:由│x+y+2│+(x-y)2=0得│x+y+2│=0及(x-y)=0 即得方程组所以,x=-1,y=-1.20.是解析:先求出的解为,把代入到方程8x-10y=6中,左边=8×2-10×1=6,•右边=6,所以方程组的解是方程8x-10y=6的解.21.B 解析:先求出方程组,根据题意得a=5,b=16,所以│a-b│=│5-•16│=11.选B.22.y=13-2x 解析:需把t消去,由x=5-t得t=5-x把它代入到y-3=2t中得y-3=•2(5-x),变形得y=13-2x或2x+y=13.【探究学习】(1)。
二元一次方程组解法代入消元法

二元一次方程组解法代入消元法嘿,朋友!咱们来唠唠二元一次方程组的代入消元法。
就好比有两个超级神秘的小怪兽,一个叫x,一个叫y,它们藏在两个方程里。
比如说方程一是3x + 2y = 10,方程二是2x - y = 3。
这y就像个调皮的小跟班,在方程二里看着就比较好欺负。
那咱就从方程二开始下手,把y单独拎出来,就像从一群小伙伴里把那个最弱小的揪出来一样。
从2x - y = 3,咱能得到y = 2x - 3。
这就好像是把小跟班y的身份给彻底曝光了,它现在只能听咱们的话啦。
然后呢,咱们就把这个被驯服的y = 2x - 3代入到方程一里面,就像是把小跟班送进了另一个神秘基地一样。
方程一就变成了3x+2(2x - 3)=10。
这时候就像是把两个原本分开的小怪兽世界给打通了。
接着展开括号,3x + 4x - 6 = 10,这就像把小怪兽们的秘密武器都给亮出来了。
然后7x - 6 = 10,就好像小怪兽们要开始最后的决战啦。
把 - 6移到等号右边,7x = 10 + 6,这就像是小怪兽在给自己补充能量呢。
7x = 16,然后算出x = 16/7,这就像终于找到了小怪兽x的老巢。
再把x = 16/7代入y = 2x - 3里,这就像是拿着找到的宝藏钥匙去开另一个宝箱。
y = 2×(16/7)-3,这就像沿着小怪兽留下的痕迹去寻找另一个小怪兽y。
计算一下,y = 32/7 - 21/7 = 11/7。
就好像把另一个小怪兽也给收服了。
再比如说方程组是x + 3y = 8和4x - y = 6。
这里面的y在4x - y = 6里就像个刺头,不过咱还是能把它变成y = 4x - 6。
然后代入x + 3y = 8,就成了x + 3(4x - 6)=8,就像把刺头送到了一个新的包围圈。
展开括号,x+12x - 18 = 8,就像打开了刺头的秘密防线。
13x - 18 = 8,算出x = 26/13 = 2。
再把x = 2代入y = 4x - 6,得到y = 8 - 6 = 2。
