计量经济学实验二 一元回归模型
计量经济学实验一 一元回归模型
实验二一元回归模型【实验目的】掌握一元线性、非线性回归模型的建模方法【实验内容】建立我国税收预测模型【实验步骤】【例1】建立我国税收预测模型。
表1列出了我国1985-1998年间税收收入Y和国内生产总值(GDP)x的时间序列数据,请利用统计软件Eviews建立一元线性回归模型。
一、建立工作文件⒈菜单方式在录入和分析数据之前,应先创建一个工作文件(Workfile)。
启动Eviews软件之后,在主菜单上依次点击File\New\Workfile(菜单选择方式如图1所示),将弹出一个对话框(如图2所示)。
用户可以选择数据的时间频率(Frequency)、起始期和终止期。
图1 Eviews菜单方式创建工作文件示意图图2 工作文件定义对话框本例中选择时间频率为Annual(年度数据),在起始栏和终止栏分别输入相应的日期85和98。
然后点击OK,在Eviews软件的主显示窗口将显示相应的工作文件窗口(如图3所示)。
图3 Eviews工作文件窗口一个新建的工作文件窗口内只有2个对象(Object),分别为c(系数向量)和resid(残差)。
它们当前的取值分别是0和NA(空值)。
可以通过鼠标左键双击对象名打开该对象查看其数据,也可以用相同的方法查看工作文件窗口中其它对象的数值。
⒉命令方式还可以用输入命令的方式建立工作文件。
在Eviews软件的命令窗口中直接键入CREATE命令,其格式为:CREATE 时间频率类型起始期终止期本例应为:CREATE A 85 98二、输入数据在Eviews软件的命令窗口中键入数据输入/编辑命令:DA TA Y X此时将显示一个数组窗口(如图4所示),即可以输入每个变量的数值图4 Eviews数组窗口三、图形分析借助图形分析可以直观地观察经济变量的变动规律和相关关系,以便合理地确定模型的数学形式。
⒈趋势图分析命令格式:PLOT 变量1 变量2 ……变量K作用:⑴分析经济变量的发展变化趋势⑵观察是否存在异常值本例为:PLOT Y X⒉相关图分析命令格式:SCAT 变量1 变量2作用:⑴观察变量之间的相关程度⑵观察变量之间的相关类型,即为线性相关还是曲线相关,曲线相关时大致是哪种类型的曲线说明:⑴SCAT命令中,第一个变量为横轴变量,一般取为解释变量;第二个变量为纵轴变量,一般取为被解释变量⑵SCAT命令每次只能显示两个变量之间的相关图,若模型中含有多个解释变量,可以逐个进行分析⑶通过改变图形的类型,可以将趋势图转变为相关图本例为:SCA T Y X图5 税收与GDP趋势图图5、图6分别是我国税收与GDP时间序列趋势图和相关图分析结果。
《计量经济学》eviews实验报告一元线性回归模型详解

计量经济学》实验报告一元线性回归模型-、实验内容(一)eviews基本操作(二)1、利用EViews软件进行如下操作:(1)EViews软件的启动(2)数据的输入、编辑(3)图形分析与描述统计分析(4)数据文件的存贮、调用2、查找2000-2014年涉及主要数据建立中国消费函数模型中国国民收入与居民消费水平:表1年份X(GDP)Y(社会消费品总量)200099776.339105.72001110270.443055.42002121002.048135.92003136564.652516.32004160714.459501.02005185895.868352.62006217656.679145.22007268019.493571.62008316751.7114830.12009345629.2132678.42010408903.0156998.42011484123.5183918.62012534123.0210307.02013588018.8242842.82014635910.0271896.1数据来源:二、实验目的1.掌握eviews的基本操作。
2.掌握一元线性回归模型的基本理论,一元线性回归模型的建立、估计、检验及预测的方法,以及相应的EViews软件操作方法。
三、实验步骤(简要写明实验步骤)1、数据的输入、编辑2、图形分析与描述统计分析3、数据文件的存贮、调用4、一元线性回归的过程点击view中的Graph-scatter-中的第三个获得在上方输入Isycx回车得到下图DependsntVariable:Y Method:LeastSquares□ate:03;27/16Time:20:18 Sample:20002014 Includedobservations:15VariableCoefficientStd.Errort-StatisticProb.C-3J73.7023i820.535-2.1917610.0472X0416716 0.0107S838.73S44 a.ooao R-squared0.991410 Meandependentwar119790.2 AdjustedR.-squared 0.990750 S.D.dependentrar 7692177 S.E.ofregression 7J98.292 Akaike infocriterion20.77945 Sumsquaredresid 7;12E^-08 Scliwarz 匚「爬伽20.37386 Loglikelihood -1&3.3459Hannan-Quinncriter. 20.77845 F-statistic 1I3&0-435 Durbin-Watsonstat0.477498Prob(F-statistic)a.oooooo在上图中view 处点击view-中的actual ,Fitted ,Residual 中的第一 个得到回归残差打开Resid 中的view-descriptivestatistics 得到残差直方图/icw Proc Qtjject PrintN^me FreezeEstimateForecastStatsResids凹Group:UNIIILtD Worktile:UN III LtLJ::Unti1DependentVariablesMethod;LeastSquares□ate:03?27/16Time:20:27Sample(adjusted):20002014Includedobservations:15afteradjustmentsVariable Coefficient Std.Errort-Statistic ProtJ.C-3373.7023^20.535-2.191761 0.0472X0.4167160.01075S38.735440.0000R-squared0.991410 Meandependeniwar1-19790.3 AdjustedR-squa.red0990750S.D.dependentvar 76921.77 SE.ofregre.ssion 7J98.292 Akaike infacriterion20.77945 Sumsquaredresid 7.12&-0S Schwarzcriterion 20.S73S6 Laglikelihood -153.84&9Hannan-Quinncrite匚20.77545 F-statistic1I3&0.435Durbin-Watsonstat 0.477498 ProbCF-statistic) a.ooaooo在回归方程中有Forecast,残差立为yfse,点击ok后自动得到下图roreestYFM J訓YForea空巾取且:20002015 AdjustedSErmpfe:2000231i mskJddd obaerratire:15Roof kter squa red Error理l%2Mean/^oLteError畐惯啟iJean Afe.PereersErro r5.451SSQThenhe鼻BI附GKWCE口.他腐4Prop&niwi□ooooooVactaree Propor^tori0.001^24G M『倚■底Props^lori09®475在上方空白处输入lsycs…之后点击proc中的forcase根据公式Y。
计量经济学的2.2 一元线性回归模型的参数估计

基于样本数据,所得到的总体回归函数的一个估 计函数称为样本回归函数。
问题:当我们设定总体回归模型的函数形式后, 如何通过样本数据得到总体回归函数的一个估计 (即样本回归函数)?--参数估计问题
E (Y | X i ) 0 1 X i
ˆ ˆ ˆ Yi f ( X i ) 0 1 X i
Xi确定
作此假设的理由:当我们把PRF表述为 时,我们假定了X和u(后者代表所有被省略的变量的影 响)对Y有各自的(并且可加的)影响。但若X和u是相关 25 的,就不可能评估它们各自对Y的影响。
线性回归模型的基本假设(4)
假设4、服从零均值、同方差、零协方差的正态分布 i~N(0, 2 ) i=1,2, …,n 意为:ui服从正态分布且相互独立。因为对两个正态 分布的变量来说,零协方差或零相关意为这两个变量 独立。 作该假设的理由:i代表回归模型中末明显引进的许多解释
Yi 0 1 X i i
i=1,2,…,n
Y为被解释变量,X为解释变量,0与1为待估 参数, 为随机干扰项
3
回归分析的主要目的是要通过样本回归函 数(模型)SRF尽可能准确地估计总体回归函 数(模型)PRF。
ˆ ˆ ˆ Yi 0 1 X i
ˆ ˆ ˆ Yi 0 1 X i ui
同方差假设表明:对应于不同X值的全部Y值具有同 样的重要性。
22
线性回归模型的基本假设(2-3)
假设2、随机误差项具有零均值、同方差和不自相关 性(不序列相关): (2.3) 不自相关: Cov(i, j|Xi, Xj)=0 i≠j i,j= 1,2, …,n 或记为 Cov(i, j)=0 i≠j i,j= 1,2, …,n 意为:相关系数为0, i, j非线性相关。 几何意义如下
计量经济学【一元线性回归模型——回归分析概述】

四、随机误差项的涵义
随机误差项是在模型设定中省略下来而又集体的
影响着被解释变量 Y 的全部变量的替代物。涵义如
下: 1、在解释变量中被忽略的因素的影响; 2、变量观测值观测误差的影响; 3、模型关系的设定误差的影响; 4、其它随机因素的影响。 设定随机误差项的主要原因: 1、理论的含糊性; 2、数据的欠缺; 3、节省的原则。
➢ 例如:
二、总体回归函数(方程)PRF Population regression function
由于变量间统计相关关系的随机性(非确定性),回归 分析关心的是根据解释变量的已知或给定值,考察被解 释变量的总体均值,即当解释变量取某个确定值时,与 之统计相关的被解释变量所有可能出现的对应值的平均 值。
样本回归函数的随机形式:
其中 为(样本)残差(Residual),可看成是随机误差项 的 的具体估计值。由于引入随机项,称为样本回归 模型。
总体回归线与样本回归线的基本关系
例2.1:一个假想的社区是由60户家庭组成的总体,要
研究该社区每月家庭消费支出Y 与每月家庭可支配收入 X 的关系;即知道了家庭的每月收入,预测该社区家庭
每月消费支出的 (总体) 平均水平。为达到此目的,将该 60户家庭划分为组内收入差不多的10组,以分析每一收 入组的家庭消费支出。
表2.1 某社区家庭每月收入与消费支出调查统计表
回归分析是研究因果相关,也就是有因果关系的相关关 系;既然回归分析是研究变量之间的因果关系,因此回归 分析对变量的处理方法存在不对称性,也就是说,回归分 析将变量区分为被解释变量和解释变量,其中被解释变量 是“结果”,解释变量是“原因”,并且回归分析方法认为作 为“原因”的解释变量属于非随机变量,作为“结果”的被解 释变量为随机变量;也就是说,作为“原因”的解释变量取 确定值时,作为“结果”的被解释变量取值是随机的。
计量经济学: 一元回归模型

• 关于变量的术语
– Explained Variable ~ Explanatory Variable
– – – – 相关系数(correlation coefficient) 正相关(positive correlation) 负相关(negative correlation) 不相关(non-correlation)
• 回归分析仅对存在因果关系而言。
• 注意:
–不存在线性相关并不意味着不相关。
i i i 0 1 i i
i
i
i
0
1
i
i
§2.2 一元线性回归模型的基本假设 (Assumptions of Simple Linear Regression Model)
一、关于模型设定的假设 二、关于解释变量的假设 三、关于随机项的假设
说明
• 为保证参数估计量具有良好的性质,通常对模型 提出若干基本假设。 • 实际上这些假设与所采用的估计方法紧密相关。 • 下面的假设主要是针对采用普通最小二乘法 (Ordinary Least Squares, OLS)估计而提出的。 所以,在有些教科书中称为“The Assumption Underlying the Method of Least Squares”。 • 在不同的教科书上关于基本假设的陈述略有不同, 下面进行了重新归纳。
2无偏性即估计量的均值期望等于总体回归参数真值3有效性最小方差性即在所有线性无偏估计量中最小二乘估计量2证明最小方差性假设为不全为零的常数则容易证明具有最的小方差由于最小二乘估计量拥有一个好的估计量所应具备的小样本特性它自然也拥有大样本特性
计量经济学第2章 一元线性回归模型

15
~ ~ • 因为 2是β2的线性无偏估计,因此根据线性性, 2 ~ 可以写成下列形式: 2 CiYi
• 其中αi是线性组合的系数,为确定性的数值。则有
E ( 2 ) E[ Ci ( 1 2 X i ui )]
E[ 1 Ci 2 Ci X i Ci ui ]
6
ˆ ˆ X )2 ] ˆ , ˆ ) [ (Yi Q( 1 2 i 1 2 ˆ ˆ X 2 Yi 1 2 i ˆ ˆ 1 1 2 ˆ ˆ ˆ ˆ [ ( Y X ) ] 1 2 i Q( 1 , 2 ) i ˆ ˆ X X 2 Yi 1 2 i i ˆ ˆ 2 2
16
~
i
i
• 因此 ~ 2 CiYi 1 Ci 2 Ci X i Ci ui 2 Ci ui
• 再计算方差Var( ) 2 ,得 ~ ~ ~ 2 ~ Var ( 2 ) E[ 2 E ( 2 )] E ( 2 2 ) 2
C E (ui )
2 i 2 i
i
~
i
i
i
i
E ( 2 Ci ui 2 ) 2 E ( Ci ui ) 2
i
2 u
C
i
2 i
i
~ ˆ)的大小,可以对上述表达式做一 • 为了比较Var( ) 和 Var( 2 2
些处理: ~ 2 2 2 2 Var ( 2 ) u C ( C b b ) i u i i i
8
• 2.几个常用的结果
• (1) • (2) • (3) • (4)
计量经济学-2.1 一元回归模型

1122 1298 1496 1716 1969 1155 1331 1562 1749 2013
2244 2585 2299 2640
1188 1364 1573 1771 2035 2310
1210 1408 1606 1804 2101
1430 1650 1870 2112 1485 1716 1947 2200
–“衍生的随机误差”包含上述所有内容,并不一定 服从极限法则,不一定满足基本假设。
–在§9.3中将进一步讨论。
四、样本回归函数 Sample Regression Function, SRF
1、样本回归函数
• 问题:能否从一次抽样中获得总体的近似信息? 如果可以,如பைடு நூலகம்从抽样中获得总体的近似信息?
• 随机误差项主要包括下列因素:
–在解释变量中被忽略的因素的影响;
• 影响不显著的因素 • 未知的影响因素 • 无法获得数据的因素
–变量观测值的观测误差的影响;
–模型关系的设定误差的影响;
–其它随机因素的影响。
• 关于随机项的说明:
–将随机项区分为“源生的随机扰动”和“衍生的随 机误差”。
–“源生的随机扰动”仅包含无数对被解释变量影响 不显著的因素的影响,服从极限法则(大数定律和 中心极限定理),满足基本假设。
• 关于变量的术语
– Explained Variable ~ Explanatory Variable – Dependent Variable ~ Independent Variable – Endogenous Variable ~ Exogenous Variable – Response Variable ~ Control Variable – Predicted Variable ~ Predictor Variable – Regressand ~ Regressor
计量经济学 第二章 一元线性回归模型
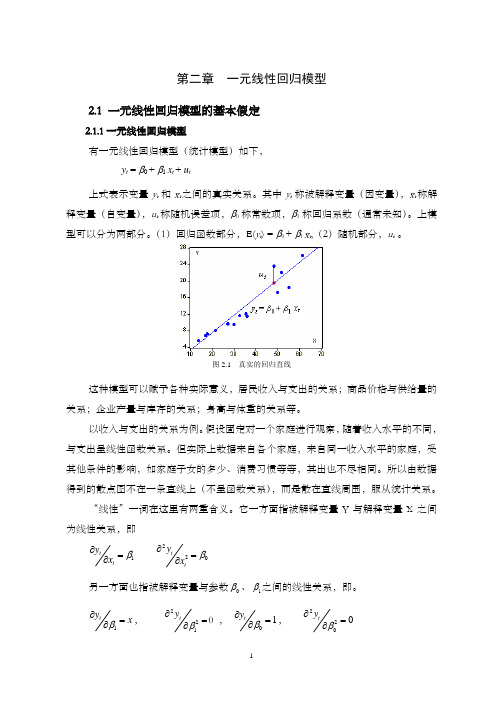
第二章 一元线性回归模型2.1 一元线性回归模型的基本假定2.1.1一元线性回归模型有一元线性回归模型(统计模型)如下, y t = β0 + β1 x t + u t上式表示变量y t 和x t 之间的真实关系。
其中y t 称被解释变量(因变量),x t 称解释变量(自变量),u t 称随机误差项,β0称常数项,β1称回归系数(通常未知)。
上模型可以分为两部分。
(1)回归函数部分,E(y t ) = β0 + β1 x t ,(2)随机部分,u t 。
图2.1 真实的回归直线这种模型可以赋予各种实际意义,居民收入与支出的关系;商品价格与供给量的关系;企业产量与库存的关系;身高与体重的关系等。
以收入与支出的关系为例。
假设固定对一个家庭进行观察,随着收入水平的不同,与支出呈线性函数关系。
但实际上数据来自各个家庭,来自同一收入水平的家庭,受其他条件的影响,如家庭子女的多少、消费习惯等等,其出也不尽相同。
所以由数据得到的散点图不在一条直线上(不呈函数关系),而是散在直线周围,服从统计关系。
“线性”一词在这里有两重含义。
它一方面指被解释变量Y 与解释变量X 之间为线性关系,即1tty x β∂=∂220tt y x β∂=∂另一方面也指被解释变量与参数0β、1β之间的线性关系,即。
1ty x β∂=∂,221ty β∂=∂0 ,1ty β∂=∂,2200ty β∂=∂2.1.2 随机误差项的性质随机误差项u t 中可能包括家庭人口数不同,消费习惯不同,不同地域的消费指数不同,不同家庭的外来收入不同等因素。
所以在经济问题上“控制其他因素不变”是不可能的。
随机误差项u t 正是计量模型与其它模型的区别所在,也是其优势所在,今后咱们的很多内容,都是围绕随机误差项u t 进行了。
回归模型的随机误差项中一般包括如下几项内容: (1)非重要解释变量的省略, (2)数学模型形式欠妥, (3)测量误差等,(4)随机误差(自然灾害、经济危机、人的偶然行为等)。
计量经济学实验二-一元线性回归模型的估计、检验和预测

目录一、加载工作文件 (7)二、选择方程 (7)1.作散点图 (7)2.进行因果关系检验 (9)三、一元线性回归 (10)四、经济检验 (12)五、统计检验 (13)六、回归结果的报告 (15)七、得到解释变量的值 (15)八、预测应变量的值 (17)实验二一元线形回归模型的估计、检验和预测实验目的:掌握一元线性回归模型的估计、检验和预测方法。
实验要求:选择方程进行一元线性回归,进行经济、拟合优度、参数显著性和方程显著性等检验,预测解释变量和应变量。
实验原理:普通最小二乘法,拟合优度的判定系数R2检验和参数显著性t检验等,计量经济学预测原理。
实验步骤:已知广东省宏观经济部分数据如表2-1所示,要根据这些数据研究和分析广东省宏观经济,建立宏观计量经济模型,从而进行经济预测、经济分析和政策评价。
实验二~实验十二主要都是用这些数据来完成一系列工作。
表2-1 广东省宏观经济数据续上表续上表一、加载工作文件广东省宏观经济数据已经制成工作文件存在盘中,命名为GD01.WF1,进入EViews后选择File/Open打开GD01.WF1。
二、选择方程根据广东数据(GD01.WF1)选择收入法国国内生产总值(GDPS)、财政收入(CS)、财政支出(CZ)和社会消费品零售额(SLC),分别把①CS作为应变量,GDPS作为解释变量;②CZ作为应变量,CS作为解释变量;③SLC作为应变量,GDPS作为解释变量进行一元线性回归分析。
1.作散点图从三个散点图(图2-1~图2~3)可以看出,三对变量都呈现线性关系。
图2-1 图2-2图2-3 2.进行因果关系检验从三个因果关系检验可以看出,GDPS是CS的因;CS不是CZ 的因;GDPS不是SLC的因。
但根据理论CS是CZ的因,GDPS是SLC的因,可能是由于指标设置问题。
所以还是把CS作为应变量,GDPS作为解释变量;CZ作为应变量,CS作为解释变量;SLC作为应变量,GDPD作为解释变量进行一元线性回归分析。
计量经济学实验二 一元线性回归模型

实验二一元线性回归模型2.1 实验目的掌握一元线性回归模型的基本理论,一元线性回归模型的建立、估计、检验及预测的方法,以及相应的EViews软件操作方法。
2.2 实验内容建立中国消费函数模型。
以表2.1中国的收入与消费的总量数据为基础,建立中国消费函数的一元线性回归模型。
表2.1数据来源:2004年中国统计年鉴,中国统计出版社2.3 实验步骤2.3.1 散点相关图分析将表1.1的GDP设为变量X,总消费设为Y,建立变量X和Y的相关图,如图2.1所示。
可以看X和Y之间呈现良好的线性关系。
可以建立一元线性回归模型。
2.3.2 估计线性回归模型在数组窗口中点击Proc\Make Equation ,如果不需要重新确定方程中的变量或调整样本区间,可以直接点击OK 进行估计。
也可以在EViews 主窗口中点击Quick\Estimate Equation ,在弹出的方程设定框(见图2.2)内输入模型:Y C X 或 Y = C (1) + C (2) * X图2.2图2.3还可以通过在EViews 命令窗口中键入LS 命令来估计模型,其命令格式为:LS 被解释变量 C 解释变量系统将弹出一个窗口来显示有关估计结果(如图2.3 所示)。
因此,我国消费函数的估计式为:ˆY2329.4010.547*X =+St 1191.923 0.014899t 1.95 36.71R 2=0.99 s.e.=2091s.e .是回归函数的标准误差,即σˆ=)216(ˆ2-∑t u。
R 2是可决系数。
R 2 = 0.99,说明上式的拟合情况好,y t 变差的99%由变量x t 解释。
因为t = 36.71> t 0.05 (15) = 2.13,所以检验结果是拒绝原假设β1 = 0,即总消费和GDP 之间存在线性回归关系。
上述模型的经济解释是,GDP 每增长1 亿元,我国消费将总额将增加0.547亿元。
图2.42.3.3 残差图在估计方程的窗口选择View\ Actual, Fitted,Residual\Actual, Fitted,Residual Table,得到相应的残差图2.4。
计量经济学习题第2章-一元线性回归模型

第2章 一元线性回归模型一、单项选择题1、变量之间的关系可以分为两大类。
A 函数关系与相关关系B 线性相关关系和非线性相关关系C 正相关关系和负相关关系D 简单相关关系和复杂相关关系 2、相关关系是指。
A 变量间的非独立关系B 变量间的因果关系C 变量间的函数关系D 变量间不确定性的依存关系 3、进行相关分析时的两个变量。
A 都是随机变量B 都不是随机变量C 一个是随机变量,一个不是随机变量D 随机的或非随机都可以 4、表示x 和y 之间真实线性关系的是。
A 01ˆˆˆt tY X ββ=+ B 01()t t E Y X ββ=+ C 01t t t Y X u ββ=++ D 01t t Y X ββ=+5、参数β的估计量ˆβ具备有效性是指。
A ˆvar ()=0βB ˆvar ()β为最小C ˆ()0ββ-= D ˆ()ββ-为最小 6、对于01ˆˆi i i Y X e ββ=++,以σˆ表示估计标准误差,Y ˆ表示回归值,则。
A i i ˆˆ0Y Y 0σ∑=时,(-)=B 2iiˆˆ0Y Y σ∑=时,(-)=0 C ii ˆˆ0Y Y σ∑=时,(-)为最小 D 2iiˆˆ0Y Yσ∑=时,(-)为最小 7、设样本回归模型为i 01i i ˆˆY =X +e ββ+,则普通最小二乘法确定的i ˆβ的公式中,错误的是。
A ()()()i i 12iX X Y -Y ˆX X β--∑∑=B()i iii122iin X Y -X Y ˆn X -X β∑∑∑∑∑=C ii122iX Y -nXY ˆX -nXβ∑∑= D i i ii12xn X Y -X Y ˆβσ∑∑∑=8、对于i 01i iˆˆY =X +e ββ+,以ˆσ表示估计标准误差,r 表示相关系数,则有。
A ˆ0r=1σ=时, B ˆ0r=-1σ=时, C ˆ0r=0σ=时, D ˆ0r=1r=-1σ=时,或 9、产量(X ,台)与单位产品成本(Y ,元/台)之间的回归方程为ˆY 356 1.5X -=,这说明。
计量经济学实验指导书

计量经济学实验指导书《计量经济学》实验指导书⼭东经济学院统计与数学学院2006年11⽉6⽇⽬录实验⼀、⼀元线性回归模型 (3)实验⽬的实验内容简介实验步骤实验⼆、多元线性回归模型 (6)实验⽬的实验内容简介实验步骤实验三、异⽅差 (9)实验⽬的实验内容简介实验步骤实验四、⾃相关性 (14)实验⽬的实验内容简介实验步骤实验五、多重共线性 (18)实验⽬的实验内容简介实验步骤实验⼀、⼀元线性回归模型【实验⽬的】掌握⼀元线性回归模型的估计⽅法。
【实验内容】根据表1-1案例,建⽴⼀元回归模型。
表1-1 我国各地区2003年FDI和GDP的数据项⽬2003年FDI(万美元)2003GDP(亿元)项⽬2003年FDI(万美元)2003GDP(亿元)北京2191263663.10河南539037048.59天津1534732447.66湖北1568865401.71河北964057098.56湖南1018354638.73⼭西213612456.59⼴东78229413625.87内蒙88542150.41⼴西418562735.13辽宁2824106002.54海南42125670.93吉林190592522.62重庆260832250.56⿊龙江321804430.00四川412315456.32上海5468496250.81贵州45211356.11江苏105636512460.83云南83842465.29浙江4980559395.00陕西331902398.58安徽367203972.38⽢肃23421304.60福建2599035232.17青海2522390.21江西1612022830.46宁夏1743385.34⼭东60161712435.93新疆15341877.61【实验步骤】⼀、模型设定1.菜单⽅式建⽴⼀个新的⼯作⽂件,表1-1的数据分别命名为GDP和FDI。
建⽴⼀个数组,包含GDP和FDI两个序列。
计量经济学第二章经典单方程计量经济学模型:一元线性回归模型

第二章经典单方程计量经济学模型:一元线性回归模型一、内容提要本章介绍了回归分析的基本思想与基本方法。
首先,本章从总体回归模型与总体回归函数、样本回归模型与样本回归函数这两组概念开始,建立了回归分析的基本思想。
总体回归函数是对总体变量间关系的定量表述,由总体回归模型在若干基本假设下得到,但它只是建立在理论之上,在现实中只能先从总体中抽取一个样本,获得样本回归函数,并用它对总体回归函数做出统计推断。
本章的一个重点是如何获取线性的样本回归函数,主要涉及到普通最小二乘法(OLS)的学习与掌握。
同时,也介绍了极人似然估计法(ML)以及矩估计法(MM)。
本章的另一个重点是对样本回归函数能否代表总体回归函数进行统计推断,即进行所谓的统计检验。
统计检验包括两个方面,一是先检验样本回归函数与样本点的“拟合优度”, 第二是检验样本回归函数与总体回归函数的“接近”程度。
后者又包扌舌两个层次:第一,检验解释变量对被解释变量是否存在着显著的线性影响关系,通过变量的t检验完成:第二,检验回归函数与总体回归函数的“接近”程度,通过参数估计值的“区间检验”完成。
本章还有三方面的内容不容忽视。
其一,若干基本假设。
样本回归函数参数的估计以及对参数估计量的统计性质的分析以及所进行的统计推断都是建立在这些基本假设之上的。
其二,参数估计量统计性质的分析,包括小样本性质与大样本性质,尤其是无偏性、有效性与一致性构成了对样本估计量优劣的最主要的衡量准则oGoss-niarkov定理表明OLS估计量是最佳线性无偏估计量。
其三,运用样本回归函数进行预测,包扌舌被解释变量条件均值与个值的预测,以及预测置信区间的计算及其变化特征。
二、典型例题分析例1、令kids表示一名妇女生育孩子的数目,educ表示该妇女接受过教育的年数。
生育率对教育年数的简单回归模型为kids= 00 + P i educ+ “(1)随机扰动项〃包含什么样的因素?它们可能与教育水平相关吗?(2)上述简单回归分析能够揭示教育对生育率在其他条件不变卞的影响吗?请解释。
第二章 一元线性回归模型

__
__
2
/n
★样本相关系数r是总体相关系数 的一致估计
相关系数有以下特点:
• • • • 相关系数的取值在-1与1之间。 (2)当r=0时,线性无关。 (3)若r>0 ,正相关,若r<0 ,负相关。 (4)当0<|r|<1时,存在一定的线性相关 关系, 越接近于1,相关程度越高。 • (5)当|r|=1时,表明x与y完全线性相关 (线性函数),若r=1,称x与y完全正相关; 若r=-1,称x与y完全负相关。 • 多个变量之间的线性相关程度,可用复相 关系数和偏相关系数去度量。
●假定解释变量X在重复抽样中取固定值。 但与扰动项u是不相关的。(从变量X角度看是外生的)
注意: 解释变量非随机在自然科学的实验研究中相对
Yi 1 2 X i ui
●假定解释变量X是非随机的,或者虽然X是随机的,
容易满足,经济领域中变量的观测是被动不可控的, X非随机的假定并不一定都满足。
E( y xi ) 0 1xi
11
• 可以看出,虽然每个家庭的消费支出存在差 异,但平均来说,家庭消费支出是随家庭可 支配收入的递增而递增的。当x取各种值时, y的条件均值的轨迹接近一条直线,该直线称 为y对x的回归直线。(回归曲线)。 • 把y的条件均值表示为x的某种函数,可写 为:
E( y xi ) 0 1xi
Var ( y xi ) 2
Cov( yi , y j ) 0
y | xi ~ N (0 1xi , )
2
22
第三节 参数估计
• 一、样本回归方程
• 对于
yi 0 1 xi ui
• 在满足古典假定下,两边求条件均值,得到总体 回归函数:
计量经济学 第二章 一元线性回归模型

计量经济学第二章一元线性回归模型第二章一元线性回归模型第一节一元线性回归模型及其古典假定第二节参数估计第三节最小二乘估计量的统计特性第四节统计显著性检验第五节预测与控制第一节回归模型的一般描述(1)确定性关系或函数关系:变量之间有唯一确定性的函数关系。
其一般表现形式为:一、回归模型的一般形式变量间的关系经济变量之间的关系,大体可分为两类:(2.1)(2)统计关系或相关关系:变量之间为非确定性依赖关系。
其一般表现形式为:(2.2)例如:函数关系:圆面积S =统计依赖关系/统计相关关系:若x和y之间确有因果关系,则称(2.2)为总体回归模型,x(一个或几个)为自变量(或解释变量或外生变量),y为因变量(或被解释变量或内生变量),u为随机项,是没有包含在模型中的自变量和其他一些随机因素对y的总影响。
一般说来,随机项来自以下几个方面:1、变量的省略。
由于人们认识的局限不能穷尽所有的影响因素或由于受时间、费用、数据质量等制约而没有引入模型之中的对被解释变量有一定影响的自变量。
2、统计误差。
数据搜集中由于计量、计算、记录等导致的登记误差;或由样本信息推断总体信息时产生的代表性误差。
3、模型的设定误差。
如在模型构造时,非线性关系用线性模型描述了;复杂关系用简单模型描述了;此非线性关系用彼非线性模型描述了等等。
4、随机误差。
被解释变量还受一些不可控制的众多的、细小的偶然因素的影响。
若相互依赖的变量间没有因果关系,则称其有相关关系。
对变量间统计关系的分析主要是通过相关分析、方差分析或回归分析(regression analysis)来完成的。
他们各有特点、职责和分析范围。
相关分析和方差分析本身虽然可以独立的进行某些方面的数量分析,但在大多数情况下,则是和回归分析结合在一起,进行综合分析,作为回归分析方法的补充。
回归分析(regression analysis)是研究一个变量关于另一个(些)变量的具体依赖关系的计算方法和理论。
计量经济学【一元线性回归模型——参数估计】

ˆ0计量ˆ1 和
可以分别表示为被解释变量观测Y值i
的线
性组合(线性函数);
ˆ证1 明
如( X下i : X )(Yi (Xi X )2
Y
)
(Xi X) (Xi X )2
(Yi
Y
)
ki (Yi Y )
其中ki :
(Xi X) (Xi X )2
ki
对ki于引0 进的 ki (X容i 易X证) 明有k如i X下i 的1 特性k:i2
2
,
,
,
,
,
,
,
,
i
1,
2,
n
假设3:随机误差项在不同样本点之间是独立的,不
存
Cov(i , j ) 0,,,,,,,i j,,,,i, j 1, 2, n
在序列相关,即:
一、一元线性回归模型的基本假设
假设 4:随机误差项与解释变量之间不相关, 即:
Cov( Xi , i ) 0,,,,,,,,,,,i 1, 2, n
:待估
E(Y
总样体本回回归归函函数数形形式式::Yˆi
| Xi)
ˆ0
0 ˆ1X i
1X i
其 计
中 估
方
ˆ0 , ˆ1 法ˆ0,, ˆ1求
是ˆ00,,ˆ11 出
的估计值,我们需要找到一种参数 , 并0 ,且1 这 种 参 数 估 计 方 法 保 证 了 估
计值 数
与总体真值
尽可能地接近;这种参
i
根据微 小,
积
分中
ˆ0 , ˆ1
求
极
值
的
原
理
,
要
使 i
ei2
待定系数
实验二 一元线性回归模型的估计、检验、预测和应用-分解

实验场地及仪器、设备和材料 实验室:普通配置的计算机,Eviews 软件及常用办公软件。
实验训练内容(包括实验原理和操作步骤):
【实验原理】
相关分析,格兰杰因果关系检验,普通最小二乘法(OLS),拟合优度的判定系数 检验和参数显著性t检验等,计量经济学预测原理。
552.2429
Median
201.0450
Maximum
2289.070
Minimum
27.04000
Std. Dev.
653.1881
Skewness
1.213628
Kurtosis
3.336095
Jarque-Bera
7.005291
Probability
0.030118
Sum
15462.80
GDPS
SLC
Mean
5442.928
2163.893
Median
2170.420
948.0950
Maximum
22366.54
7882.640
Minimum
185.8500
79.86000
Std. Dev.
6300.570
2340.232
Skewness
1.190005
0.972056
Kurtosis
注:在实验中对应的空白处写出实验的结果。全部完成后,把该文档自己学号
为名进行命名,提交到教师机。
(一)建立工作文件
进入Eviews,建立一工作文件,并命名为GD,新建4个序列,并对应输入广东省 经济数据表中的数据:收入法国内生产总值-GDPS,财政收入-CS,财政支出-CZ,社 会消费品零售额-SLC。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验二一元回归模型
【实验目的】
掌握一元线性、非线性回归模型的建模方法
【实验内容】
建立我国税收预测模型
【实验步骤】
【例1】建立我国税收预测模型。
表1列出了我国1985-1998年间税收收入Y和国内生产总值(GDP)x的时间序列数据,请利用统计软件Eviews建立一元线性回归模型。
一、建立工作文件
⒈菜单方式
在录入和分析数据之前,应先创建一个工作文件(Workfile)。
启动Eviews软件之后,在主菜单上依次点击File\New\Workfile(菜单选择方式如图1所示),将弹出一个对话框(如图2所示)。
用户可以选择数据的时间频率(Frequency)、起始期和终止期。
图1 Eviews菜单方式创建工作文件示意图
图2 工作文件定义对话框
本例中选择时间频率为Annual(年度数据),在起始栏和终止栏分别输入相应的日期85和98。
然后点击OK,在Eviews软件的主显示窗口将显示相应的工作文件窗口(如图3所示)。
图3 Eviews工作文件窗口
一个新建的工作文件窗口内只有2个对象(Object),分别为c(系数向量)和resid(残差)。
它们当前的取值分别是0和NA(空值)。
可以通过鼠标左键双击对象名打开该对象查看其数据,也可以用相同的方法查看工作文件窗口中其它对象的数值。
⒉命令方式
还可以用输入命令的方式建立工作文件。
在Eviews软件的命令窗口中直接键入CREATE命令,其格式为:
CREATE 时间频率类型起始期终止期
本例应为:CREATE A 85 98
二、输入数据
在Eviews软件的命令窗口中键入数据输入/编辑命令:
DA TA Y X
此时将显示一个数组窗口(如图4所示),即可以输入每个变量的数值
图4 Eviews数组窗口
三、图形分析
借助图形分析可以直观地观察经济变量的变动规律和相关关系,以便合理地确定模型的数学形式。
⒈趋势图分析
命令格式:PLOT 变量1 变量2 ……变量K
作用:⑴分析经济变量的发展变化趋势
⑵观察是否存在异常值
本例为:PLOT Y X
⒉相关图分析
命令格式:SCAT 变量1 变量2
作用:⑴观察变量之间的相关程度
⑵观察变量之间的相关类型,即为线性相关还是曲线相关,曲线相关时大致是哪种类型的曲线
说明:⑴SCAT命令中,第一个变量为横轴变量,一般取为解释变量;第二个变量为纵轴变量,一般取为被解释变量
⑵SCAT命令每次只能显示两个变量之间的相关图,若模型中含有多个解释变量,可以逐个进行分析
⑶通过改变图形的类型,可以将趋势图转变为相关图
本例为:SCA T Y X
图5 税收与GDP趋势图
图5、图6分别是我国税收与GDP时间序列趋势图和相关图分析结果。
两变量趋势图
分析结果显示,我国税收收入与GDP 二者存在差距逐渐增大的增长趋势。
相关图分析显示,我国税收收入增长与GDP 密切相关,二者为非线性的曲线相关关系。
图6 税收与GDP 相关图
三、估计线性回归模型
在数组窗口中点击Proc\Make Equation ,如果不需要重新确定方程中的变量或调整样本区间,可以直接点击OK 进行估计。
也可以在Eviews 主窗口中点击Quick\Estimate Equation ,在弹出的方程设定框(图7)内输入模型:
Y C X 或 X C C Y *+=)2()1(
图7 方程设定对话框
还可以通过在Eviews 命令窗口中键入LS 命令来估计模型,其命令格式为:
LS 被解释变量 C 解释变量
系统将弹出一个窗口来显示有关估计结果(如图8所示)。
因此,我国税收模型的估计式为:
x y
0946.054.987ˆ+= 这个估计结果表明,GDP 每增长1亿元,我国税收收入将增加0.09646亿元。
图8 我国税收预测模型的输出结果
五、估计非线性回归模型
由相关图分析可知,变量之间是非线性的曲线相关关系。
因此,可初步将模型设定为指数函数模型、对数模型和二次函数模型并分别进行估计。
在Eviews 命令窗口中分别键入以下命令命令来估计模型:
双对数函数模型:LS log(Y) C log(X) 对数函数模型:LS Y C log(X) 指数函数模型:LS log(Y) C X 二次函数模型:LS Y C X X^2
还可以采取菜单方式,在上述已经估计过的线性方程窗口中点击Estimate 项,然后在弹出的方程定义窗口中依次输入上述模型(方法通线性方程的估计),其估计结果显示如图9、图10、图11图、12所示。
双对数模型:x y
ln 6823.02704.1ˆln += (3.8305) (21.0487)
9736.02=R 9714.02=R 05.443=F
对数模型:
x y ln 92.298532.26163ˆ+-=
(-8.3066) (9.6999)
8869.02=R 8775.02=R 0875.94=F
指数模型:x y
5
1007.25086.7ˆln -*+= (231.7463) (27.2685)
9841.02=R 9828.02=R 57.743=F
二次函数模型:2
71058.50468.07.1645ˆx x y -*++=
(7.4918) (3.3422) (3.4806)
9918.02=R 9903.02=R 78.661=F
图9 双对数模型回归结果
图10 对数模型回归结果
图11 指数模型回归结果
图12 二次函数模型回归结果
六、模型比较
四个模型的经济意义都比较合理,解释变量也都通过了T检验。
但是从模型的拟合优
R值最大,其次为指数函数模型。
因此,对这两个模型再做进一度来看,二次函数模型的2
步比较。
在回归方程(以二次函数模型为例)窗口中点击View\Actual,Fitted,Residual\ Actual,Fitted,Residual Table(如图13),可以得到相应的残差分布表。
图13 回归方程残差分析菜单
上述两个回归模型的残差分别表分别如下(图14、图15)。
比较两表可以发现,虽然二次函数模型总拟合误差较小,但其近期误差却比指数函数模型大。
所以,如果所建立的模型是用于经济预测,则指数函数模型更加适合。
图14 二次函数回归模型残差分别表
图15 指数函数模型残差分布表。
