结构动力学习题解答一二章
结构动力学习题解答一二章

2、 动量距定理法
适用范围:绕定轴转动的单自由度系统的振动。
解题步骤:(1) 对系统进行受力分析与动量距分析;
(2) 利用动量距定理J ,得到系统的运动微分方程;
(3) 求解该方程所对应的特征方程的特征根,得到该系统的固有频率。
3、 拉格朗日方程法:
;
1、7求图1-36所示齿轮系统的固有频率。已知齿轮A的质量为mA,半径为rA,齿轮B的质量为mB,半径为rB,杆AC的扭转刚度为KA,,杆BD的扭转刚度为KB,
解:由齿轮转速之间的关系 得角速度 ;转角 ;
系统的动能为:
CA
;B D
图1-36
系统的势能为:
;
系统的机械能为
;
由 得系统运动微分方程
;
适用范围:所有的单自由度系统的振动。
解题步骤:(1)设系统的广义坐标为 ,写出系统对于坐标 的动能T与势能U的表达式;进一步写求出拉格朗日函数的表达式:L=T-U;
(2)由格朗日方程 =0,得到系统的运动微分方程;
(3) 求解该方程所对应的特征方程的特征根,得到该系统的固有频率。
4、 能量守恒定理法
1、2叙述用衰减法求单自由度系统阻尼比的方法与步骤。
用衰减法求单自由度系统阻尼比的方法有两个:衰减曲线法与共振法。
方法一:衰减曲线法。
求解步骤:(1)利用试验测得单自由度系统的衰减振动曲线,并测得周期与相邻波峰与波谷的幅值 、 。
(2)由对数衰减率定义 , 进一步推导有
,
因为 较小,所以有
。
方法二:共振法求单自由度系统的阻尼比。
;L/2L/2
则固有频率为:
图1-33(b)
结构动力学题解(1)

FN 力所作的虚功:
Y (t ) F δY = N Y δY = kG * Y δY 2l 2l 3 广义质量 m* = m l 4 广义劲度 k * = k 1 广义阻尼 c* = (c1 + c2 ) 4 3 广义载荷 F * (t ) = lq(t ) 4 F 广义几何劲度 kG * = N 2l F * 组合广义劲度 k * = k * − kG = k − N ,欧拉临界力 FNcr = 2lk 2l δWn = FN
代入 y1 ,经整理得:
广义质量 m* =
m 3
广义劲度 k * =
广义阻尼 c* = c
广义载荷 F * (t ) =
5、试列出图(a)与(b)所示系统的运动方程,并计算各系数(不考虑阻尼的影响) (a)
F(t)
m
m
EI 常数
l
[解] 取质体的水平位移为 Y ,水平虚位移为 δY 质体上的惯性力
h
答图
(c) 解:单位力单独作用下的位移
δ1 =
l3 3EI =δ
题图
由质体 m 的竖向位移关系可知:
(1 − Fs0 )δ1 = Fs0
k
由上式解出:
Fs 0 =
kδ1 1 + kδ1
δ=
δ1 l3 = 1 + kδ1 3EI + kl 3
答图
其自振频率:
ω=
1 3EI + kl 3 = mδ ml 3
k1
Fs1
EI = ∞
结构动力学-习题解答
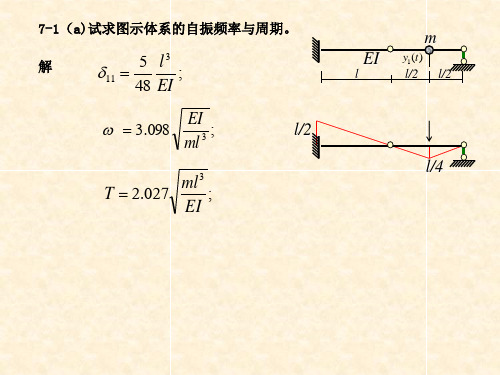
7-1(a)试求图示体系的自振频率与周期。
解
11
5 48
l3 EI
;
3.098
EI ml 3
;
l/2
T 2.027
ml 3 ;
7-6 某结构在自振10个周期后,振幅降为原来初始位移的10% (初位移为零),试求其阻尼比。
解: 1 ln10 0.0366 2 10
8-1试求图示梁的自振频率和振型。 m
y1(t)
解
EI 2m
a
a
y2
(t
)
a
12
21
1 4
a3 EI
a
I 2 m 0
11m1 1/ 2
m212
0
m1 21
22m2 1/ 2
1 1.153
a/2
2 0.181
令
1
11m1
2
1 1/ 2
0
1/ 4 1/3 2 4 / 3 5 / 24 0
x11 / x21 3.277; x12 / x22 0.61
;
9l / 64 (a)
5l / 32
11.817
EI ml 3 ;
l/2
T 0.531
ml3 ;
(b)
EI
7-1(c)试求图示体系的自振频率与周期。
m 刚性杆
解 由右面竖杆的平衡可求出铰处约束力。
EI
由水平杆的平衡:
结构动力学习题答案
3.4
m2 g k
( m1 + m2 ) u (0) = m2 2 gh
即 u (0) =
i
i
m2 2 gh m1 + m2
动力方程: ( m1 + m2 )( u − ust )′′ + K ( u − ust ) = 0
5 .0 1 = u st 2ξ
(1)
当 w wn = 1 时,发生共振有: Rd 1 =
当 w wn = 1 10 时, Rd 1 =
0 .5 = u st
(1 − 0.1 ) + (2ξ × 0.1)
2 2
1
(2)
2
由式(1),(2)可以解得 ξ = 4.95%
3.6 解:
TR =
[1 − (w w ) ] + [2ξ w w ]
ii
ii
ii
ii
ii
δ Wp = −m2 g sin θ i Lδθ
虚 功原理: δ Ws
+ δ WI + δ W D +δ W p = 0 得:
⎡ m1 + m2 ⎢ mL ⎣ 2
2.6 解:
ii ⎫ ⎧i⎫ m2 L ⎤ ⎧ 0 ⎫ ⎪ u ⎪ ⎡C 0 ⎤ ⎪ u ⎪ ⎡ k 0 ⎤ ⎧ u ⎫ ⎧ +⎢ ⎨ i ⎬+ ⎢ ⎨ ⎬=⎨ ⎬ ⎥ ⎥ 2 ⎥ ⎨ ii ⎬ m2 L ⎦ ⎪ ⎪ ⎣ 0 0 ⎦ ⎪ ⎪ ⎣ 0 0 ⎦ ⎩θ ⎭ ⎩−m2 g sin θ i L ⎭ ⎩θ ⎭ ⎩θ ⎭
[美]R.克里夫《结构动力学》补充详解及习题解
![[美]R.克里夫《结构动力学》补充详解及习题解](https://img.taocdn.com/s3/m/198055225627a5e9856a561252d380eb629423b8.png)
前言结构动力学是比较难学的一门课程,但是你一旦学会并且融会贯通,你就会为成为结构院士、大师和总工垫定坚实的基础。
结构动力学学习的难点主要有以下两个方面。
1 概念难理解,主要表现在两个方面,一是表达清楚难,如果你对概念理解的很透彻,那么你写的书对概念的表述也会言简意赅,切中要害(克里夫的书就是这个特点),有的书会对一个概念用了很多文字进行解释,但是还是没有说清楚,也有的书受水平限制,本身表述就不清楚。
二是理解难,有点只可意会不可言传的味道,老师讲的头头是道,自己听得云山雾绕。
2 公式推导过程难,一是力学知识点密集,推导过程需要力学概念清析,并且需要每一步的力学公式熟悉;二是需要一定的数学基础,而且有的是在本科阶段并没有学习的数学知识。
克里夫《结构动力学》被称为经典的结构动力学教材,但是也很难看懂。
之所以被称为经典,主要就是对力学的概念表达的语言准确,概念清楚。
为什么难懂呢?是因为公式的推导过程比较简单,省略过多。
本来公式的推导过程既需要力学概念清楚也需要数学公式熟悉,但是一般人不是力学概念不清楚,就是数学公式不熟悉,更有两者都不熟悉者。
所以在学习过程中感觉很难,本学习详解是在该书概念清楚的基础上,对力学公式推导过程进行详细推导,并且有的加以解释,帮助你在学习过程中加深理解和记忆。
达到融会贯通,为你成为结构院士、大师和总工垫定坚实的基础。
以下黑体字是注释,其它为原书文字。
[美] R∙克里夫《结构动力学》辅导学习详解第1章结构动力学概述… …第Ⅰ篇单自由度体系第2章基本动力体系的组成… …§2-5 无阻尼自由振动分析如上一节所述,有阻尼的弹簧-质量体系的运动方程可表示为mv̈(t)+cv̇(t)+kν(t)=p(t)(2-19)其中ν(t)是相对于静力平衡位置的动力反应;p(t)是作用于体系的等效荷载,它可以是直接作用的或是支撑运动的结构。
为了获得方程(2-19)的解,首先考虑方程右边等于零的齐次方程,即mv̈(t)+cv̇(t)+kν(t)=0(2-20)mv(t)+kν(t)=0(2-20a)此处公式应该为mv(t)+kν(t)=0,因为该节是无阻尼自由振,而且(2-20)的解,式(2-21)也是公式mv(t)+kν(t)=0的解在作用力等于零时产生的运动称为自由振动,现在要研究的即为体系的自由振动反应。
结构动力学1~15

《结构动力学》习题答案1~151. 1简述求多自由度体系时程反应的振型叠加法的主要步骤 答1)建立多自由度体系的运动方程)()()()(t p t kv t v c t vm =++ 2)进行振型和频率分析对无阻尼自由振动,这个矩阵方程能归结为特征问题)(ˆ2t p vm k =-ω 由此确定振型矩阵φ和频率向量ω 3)求广义质量和荷载依次取每一个振型向量n φ,计算每一个振型的广义质量和广义荷载n T n nm Mφφ= )()(t p t p Tn n φ=4)求非耦合运动方程用每个振型的广义质量、广义力、振型频率n ω和给定的振型阻尼比n ξ就能写出每一个振型的运动方程2)(2)(ωωξ++t Y t Y n n n n nn nMt P t Y )()(=5)求对荷载的振型反应根据荷载类型,用适当的方法解这些单自由度方程,每一个振型的一般动力反应表达式用Duhamel 积分给出ττωτωξτωd t t P M t Y Dn n n tn nn n )(sin )](exp[)(1)(0---=⎰写出标准积分形式τττd t h P t Y n tn n )()()(0-=⎰式中)](exp[)(sin 1)(τωξτωωτ---=-t t M t h n n Dn nn n 10<<n ξ6)振型自由振动每一个振型有阻尼自由振动反应的通式为)exp[]sin )0()0(cos )0([)(t t Y Y t Y t Y n n Dn Dnnn n n Dn n n ωξωωωξω-++=7)求在几何坐标中的位移反应通过正规坐标变换求几何坐标表示的位移式)()()()(2211t Y t Y t Y t V n n φφφ+++=显然,它反映了各个振型贡献的叠加。
因此命名为振型叠加法。
8)弹性力反应抵抗结构变形的弹性力)()()(t Y k t kv t f s φ==当频率、振型从柔度形式的特征方程中求出时,可以采用另一种弹性力的表达式。
结构动力学习题解答(一二章)

第一章 单自由度系统1。
1 总结求单自由度系统固有频率的方法和步骤。
单自由度系统固有频率求法有:牛顿第二定律法、动量距定理法、拉格朗日方程法和能量守恒定理法。
1、 牛顿第二定律法适用范围:所有的单自由度系统的振动。
解题步骤:(1) 对系统进行受力分析,得到系统所受的合力;(2) 利用牛顿第二定律∑=F x m,得到系统的运动微分方程;(3) 求解该方程所对应的特征方程的特征根,得到该系统的固有频率.2、 动量距定理法适用范围:绕定轴转动的单自由度系统的振动。
解题步骤:(1) 对系统进行受力分析和动量距分析;(2) 利用动量距定理J ∑=M θ,得到系统的运动微分方程;(3) 求解该方程所对应的特征方程的特征根,得到该系统的固有频率。
3、 拉格朗日方程法:适用范围:所有的单自由度系统的振动.解题步骤:(1)设系统的广义坐标为θ,写出系统对于坐标θ的动能T 和势能U 的表达式;进一步写求出拉格朗日函数的表达式:L=T —U ; (2)由格朗日方程θθ∂∂-∂∂∂LL dt )( =0,得到系统的运动微分方程; (3) 求解该方程所对应的特征方程的特征根,得到该系统的固有频率。
4、 能量守恒定理法适用范围:所有无阻尼的单自由度保守系统的振动。
解题步骤:(1)对系统进行运动分析、选广义坐标、写出在该坐标下系统的动能T 和势能U 的表达式;进一步写出机械能守恒定理的表达式 T+U=Const (2)将能量守恒定理T+U=Const 对时间求导得零,即0)(=+dtU T d ,进一步得到系统的运动微分方程;(3) 求解该方程所对应的特征方程的特征根,得到该系统的固有频率。
1.2 叙述用衰减法求单自由度系统阻尼比的方法和步骤.用衰减法求单自由度系统阻尼比的方法有两个:衰减曲线法和共振法。
方法一:衰减曲线法.求解步骤:(1)利用试验测得单自由度系统的衰减振动曲线,并测得周期和相邻波峰和波谷的幅值i A 、1+i A .(2)由对数衰减率定义 )ln(1+=i iA A δ, 进一步推导有 212ζπζδ-=,因为ζ较小, 所以有πδζ2=。
结构动力学习题答案

结构动力学习题答案结构动力学学习题答案结构动力学是土木工程中的一个重要分支,它研究结构在受到外部荷载作用下的响应和变形规律。
在学习结构动力学的过程中,我们经常会遇到一些复杂的问题和难题。
下面我将为大家提供一些常见结构动力学学习题的答案,希望能够帮助大家更好地理解和掌握这门学科。
1. 什么是结构的固有频率?结构的固有频率是指结构在没有外部激励作用下,自由振动时的频率。
它是结构的固有特性之一,与结构的质量、刚度和几何形状有关。
固有频率越高,结构的振动越快。
2. 如何计算结构的固有频率?计算结构的固有频率需要先求解结构的固有振型和固有频率。
常用的方法有模态分析法和有限元法。
模态分析法是通过求解结构的特征方程得到结构的固有频率和振型;有限元法则是将结构离散化为有限个单元,通过求解单元的振动特征得到整体结构的固有频率和振型。
3. 结构的固有频率对结构有何影响?结构的固有频率与结构的动态特性密切相关。
当外部激励频率接近结构的固有频率时,会引起共振现象,使结构的振幅急剧增大,从而可能导致结构的破坏。
因此,在结构设计和抗震设计中,需要合理选择结构的固有频率,以避免共振现象的发生。
4. 什么是结构的阻尼?结构的阻尼是指结构在振动过程中能量损耗的程度。
阻尼可以分为线性阻尼和非线性阻尼。
线性阻尼是指结构的阻尼与结构的振幅成正比,非线性阻尼则是指结构的阻尼与结构的振幅不成正比。
5. 如何考虑结构的阻尼?在结构动力学分析中,通常会考虑结构的阻尼对结构响应的影响。
常用的阻尼模型有粘滞阻尼模型和柱塞阻尼模型。
粘滞阻尼模型是指结构的阻尼与结构的速度成正比;柱塞阻尼模型是指结构的阻尼与结构的速度平方成正比。
根据结构的实际情况和要求,可以选择适当的阻尼模型进行分析。
6. 结构的地震反应分析中常用的方法有哪些?在结构的地震反应分析中,常用的方法有等效静力法、响应谱法和时程分析法。
等效静力法是一种简化的方法,将地震作用等效为静力作用进行计算;响应谱法是一种基于地震响应谱的方法,通过将地震作用转化为结构的响应谱进行计算;时程分析法是一种基于地震时程的方法,通过模拟地震过程对结构进行动力响应分析。
结构动力学习题+讲解

&&(t ) + (ω2 – n2 )S (t) = 0 --------------------------------------------(5) S
1.当 n >ω时(强阻尼) 方程(5)的解为: S (t) = A1sh n − ω t +A2ch n − ω t
2 2 2 2
从而,方程(4)的解为:
若时间 t 不是从 0 开始,而是从τ开始的,则(9)式写为:
y (t ) =
p∆t sinω(t-τ) mω
---------------------------------------(10)
写作: ,记ω2 =
K m
,2n =
C ,又可写作: m
& &(t ) + 2n y & (t ) +ω2 y (t ) = 0 y
利用常数变易法,令 y (t ) = e
− nt
---------------------------------------------(4)
S (t ) 代入方程(4)中 得:
K/2 VBA
48i/7L
2
A
取横梁为研究对象,Σ X=0,得:K= 4)振动方程
24 EI L3
即,
&(t ) - K y(t ) + Psinθt = 0 y - 2 m& &(t ) + y 2 m&
24 EI y(t ) = Psinθt L3
一、 无阻尼的自由振动
振动方程
&(t ) +K y (t ) = 0 , m& y & &(t ) + y K y (t ) = 0 m
中国大学MOOC结构动力学习题含答案-精品

中国大学MOOC结构动力学习题(含答案)1、忽略杆件的轴向变形和分布质量,图示结构动力自由度的个数()oA、1B、2C、3D、4答案:22、忽略杆件的轴向变形和分布质量,图示结构动力自由度的个数()oA、1B、2C、3D、4答案:23、忽略杆件的轴向变形和分布质量,图示结构动力自由度的个数()oA、0B、1C、2D、3答案:24、在很短时间内,荷载值急剧增大或急剧减小的荷载是()oA、可变荷载B、偶然荷载C、冲击荷载D、爆炸答案:冲击荷载5、动力自由度的个数()集中质量的个数。
图所示刚架结构,不计分布质量,动力自由度个数为()o 此题为多项选择题。
请帮忙给出正确答案和分析,谢谢! •日目•2EI:一.c(A)2个(B)3个(C)4个(D)5个答案:B自由度个数有3个,因此正确答案为(B)。
1、一、单项选择题(每题2分,共6分)答案:ABDAC二.实验探究题(共20分)2、二、填空题(每题2分,共4分)1.相比静力计算,动力计算列平衡方程时,在所考虑的力系中要包括。
2. 爆炸荷载属于。
答案:1、从力系平衡角度建立自由振动微分方程的方法是()oA、刚度法B、柔度法C、静力法D、动力法答案:刚度法2、忽略杆件的轴向变形和均布质量,各图质点的质量、杆长、质点位置相同,杆件EI相同且为常数。
结构自振频率最大的是()oA、coaB、3bC、3cD、3d答案:3a3、与单自由度体系自由振动的频率有关的量是()oA、初速度vOB、初位移yOC、相位角aD、质量m答案:阻尼越大,振幅越大4、按照GB50009-2012《建筑结构荷载规范》,高度为2001Tl的高耸钢筋混凝土结构的基本周期一般为()0A、0.14sB、1.4sC、14sD、140s答案:1.4s5、yst是指()oA.自然伽码与电阻率B.方位与井斜C.工具与井斜D.工具面与方位答案:A1、一、填空题(每题5分,共20分)答案:【计分规贝":Am=K/c2.72X10-268.41X10- 4437.82X10-4;145.94X10-42、二、计算题(每题20分,共80分)答案:【计分规则】:一、回答问题(每题2分、共10分)二、分析(每题10分、共30分)三、计算题(第1题40分, 第2题20分、共60分)1、当。
最新克拉夫《结构动力学》习题答案汇总

第二章自由振动分析2-1(a )由例2 2W Tgk22()W K Tg 因此max()()D t kT 其中k=0、1、2……T D =0.64sec如果很小,T D =T222200()49.9/0.64sec 386/sec kips k kips inin 50/k kips in(b )211ln ln n n v v v v 222121()11.2ln0.3330.86210.05292()10.33320.053025.3%(a ’)21D2T21D TT 249.950/1kkips in(c)2c mW mg2T4cTg21D T T 241WcTg2240.05292000.64sec 386/sec 10.0529kipsc in 0.539sec/ckips inT=T D 0.538sec/ckips in 0.54sec/ckips in2-22k m40 4.472(1/sec )(0)(0)()sin(0)costDDDv v t et v t(0)(0)()sin(0)(0)(0))costDDDv v t et v v v t22(0)(0)()(0)cossinDtDDDv v t ev tt21D()(0)cos(0)(0)sintDDDt ev t v v t2(0)(0)()(0)c o s s i n1tD D v v t ev tt 0.055922(2)(4.47)c c cm(a) c=00D5.6(1)sin 4.470.7cos4.47 1.384.47v t in(1) 5.6cos 4.47 4.47(0.7)sin 4.47 1.69/secv t in (1) 1.4v in ,(1) 1.7/secv in (b) c=2.80.0559(2.8)0.15724.4710.1574.41D(1/sec )(0.157)(4.41)5.60.7(0.157)(4.47)(1)sin 4.410.7cos 4.414.41t e(1)0.764t in(0.157)(4.41)20.157(5.6) 4.41(0.7)(1) 5.6cos 4.41sin 4.4110.157t e (1) 1.10/sect in (1)0.76v in ,(1) 1.1/secv in 第三章谐振荷载反应3-1根据公式有21sin sin 1R t wt wt0.8w w2.778sin 0.8sin1.25R twt wt将t 以80°为增量计算)(t R 并绘制曲线如下:0 80°160°240°320°400°480°560°640°720°800°00.5471.71 -0.481 -3.214 0.357 4.33-0.19 -4.9244.9241.25w wt)(t R3-2解:由题意得:22mkips s in ,20kkips in ,(0)(0)0v v ,w w20 3.162sec2k w rad m8wt(a )0c1sin cos 2R twt wt wt将8wt 代入上式得:()412.566R t (b )0.5ck s in0.50.0395222 3.162cc c c mw1exp1cos exp sin 2R twtwtwt wt将8wt 代入上式得:()7.967R t (c ) 2.0ck s in2.00.158222 3.162cc c c mw1exp1cos exp sin 2R twtwtwt wt将8wt 代入上式得:() 3.105R t 3-3解:(a ):依据共振条件可知:1003860.0810.983sec4000k kg wwrad m W由2LTVw 得:10.9833662.96022wL V ft s(b ):122max2221212tgovv 1w w 0.41.2gov in 代入公式可得:max1.921tv in(c ):2L T Vw45m i n 66Vhf t s226611.51336V wrad secL11.513 1.04810.983w w0.4代入数据得:122max22212=1.85512t govv in3-4解:按照实际情况,当设计一个隔振系统时,将使其在高于临界频率比2下运行,在这种情况下,隔振体系可能有小的阻尼。
结构动力学习题答案

结构动力学习题答案结构动力学学习题答案结构动力学是一门研究结构在外部力作用下的运动和响应的学科。
在学习结构动力学时,学生通常会遇到各种各样的学习题,这些学习题既考验了学生对知识的掌握程度,又帮助他们加深对结构动力学理论的理解。
下面我们就来看一些结构动力学学习题的答案。
1. 什么是结构动力学?结构动力学是研究结构在外部力作用下的振动特性和响应的学科。
它主要研究结构在地震、风载等外部力作用下的动力响应,以及结构的振动特性和控制。
2. 结构的自由振动频率如何计算?结构的自由振动频率可以通过结构的刚度矩阵和质量矩阵来计算。
首先需要求解结构的特征值和特征向量,然后根据特征值来计算结构的自由振动频率。
3. 结构的阻尼比对结构动力学有什么影响?阻尼比是衡量结构在振动过程中能量损失的比例。
阻尼比越大,结构的振动响应越快速衰减;阻尼比越小,结构的振动响应越慢。
因此,阻尼比对结构的振动特性和稳定性有着重要的影响。
4. 结构的地震响应如何进行分析?结构的地震响应可以通过有限元分析、时程分析和频率响应分析等方法进行。
这些方法可以帮助工程师评估结构在地震作用下的受力情况,从而指导结构的设计和加固。
5. 结构的振动控制方法有哪些?结构的振动控制方法包括主动控制、被动控制和半主动控制等。
主动控制是通过外部激励来控制结构的振动;被动控制是通过阻尼器、减震器等被动装置来控制结构的振动;半主动控制则是结合了主动和被动控制的特点,通过智能控制系统来控制结构的振动。
通过以上学习题的答案,我们可以看到结构动力学是一个复杂而又有趣的学科,它涉及到结构的振动特性、动力响应和振动控制等多个方面。
通过对这些学习题的学习和理解,我们可以更好地掌握结构动力学的理论知识,为今后的工程实践打下坚实的基础。
结构动力学参考答案

m u + c u + ku = Pu (t ) 2.13 一根均匀杆,图 P2.13 其单位体积质量密度 ρ ,并具有顶部质量 M,应 用假定法ψ ( x) = x L 来推导该系统轴向自由振动的运动方程。假定 AE = 常数。 解:
.. 1 EA ( ρAL + M ) u + u = P(t ) 3 L
结构动力学习题 参考答案
1
2.3 一根刚梁 AB,用力在弹簧 BC 上去激励它,其 C 点的运动规定为 Z(t),如 图 P2.3. 按 B 点的垂直运动 u 来确定系统的运动方程,假定运动是微小的。 解: 4M u + 3c u + (3k1 + 12k 2 )u = 12k 2 Z (t )
.. .
4
4.17 在振动的结构上一个点,已知其运动为 Ζ = Ζ1 cos(Ω1t ) + Ζ 2 cos(Ω 2 t ) =
0.05 cos ( 60π t ) + 0.02 cos(120π t ) 。
(a)用一加速度计其阻尼因数 ξ = 0.70 和 20 KHz 共振频率来确定振动记录 w p (t ) 。 (b) 加速度计是否会引起有效幅值或相位畸变? 解: (a) w p (t ) = w p1 (t ) + w p 2 (t ) = 6.339 × 10 −11 A1 cos 60π (t − 1.1145 × 10 −5 ) + 6.339 × 10 −11 A2 • cos 120π (t − 1.1146 × 10 −5 ) (b) w p (t ) = C[ A1 cos Ω1 (t − τ ) + A2 cos Ω 2 (t − τ )] A1 , A2 分别表示 Z1 , Z 2 的加速度幅值,所以输出 w p (t ) 与加速度输 入成正比,所以不会发生幅值畸变或相位畸变。 5.2 运送一件仪器设备重 40 1b,是用泡沫包装在一容器内。该容器的有效刚度 k=100 1b/in,有效阻尼因数 ξ = 0.05 ,若整个容器和它的包装以垂直速度 V=150 in/s 碰撞在地面上,求泡沫包装在仪器设备的最大总应力。 (如图 P5.2 所示) 解: f max = 451.739 (1b) 6.5 例 题 4.3 中的 车辆 , 已知 k = 400 × 10 3 , m = 1200kg , ξ = 0.4。 当满 载时以
结构动力学试题及答案

结构动力学试题及答案一、选择题(每题2分,共10分)1. 结构动力学中,动力响应分析通常不包括以下哪一项?A. 自振频率分析B. 模态分析C. 静力分析D. 动力放大系数分析答案:C2. 在结构动力学中,下列哪一项不是确定结构动力特性的基本参数?A. 质量B. 刚度C. 阻尼D. 材料强度答案:D3. 单自由度振动系统的动力平衡方程中,下列哪一项是正确的?A. m\(\ddot{x}\) + c\(\dot{x}\) + kx = F(t)B. m\(\ddot{x}\) + c\(\dot{x}\) + kx = 0C. m\(\ddot{x}\) + c\(\dot{x}\) + kx = FD. m\(\ddot{x}\) + c\(\dot{x}\) + kx = F(t) - F答案:A4. 对于多自由度振动系统,下列哪一项不是求解动力响应的方法?A. 模态叠加法B. 直接积分法C. 能量守恒法D. 振型分解法答案:C5. 在结构动力学中,阻尼比通常用来描述阻尼的相对大小,其定义为:A. 临界阻尼比B. 阻尼比C. 阻尼比的倒数D. 阻尼比的平方答案:B二、填空题(每题2分,共10分)1. 结构动力学中,当外力作用频率与结构的_________相等时,结构会发生共振。
答案:自振频率2. 多自由度振动系统的振型是指系统在自由振动时的_________。
答案:位移分布模式3. 动力响应分析中,_________是指在给定的外力作用下,结构的响应随时间变化的过程。
答案:动力响应4. 在结构动力学中,_________是指结构在动力作用下,其响应与外力作用的关系。
答案:动力特性5. 阻尼比越大,结构的_________越小,振动衰减越快。
答案:振幅三、简答题(每题5分,共20分)1. 简述结构动力学中模态分析的目的和意义。
答案:模态分析的目的是确定结构的自振频率和振型,意义在于了解结构的动力特性,为结构设计提供依据,以及评估结构在动力作用下的安全性和稳定性。
结构动力学习题+讲解

结构动力学*本章讨论结构在动力荷载作用下的反应。
**学习本章注重动力学的特征------惯性力。
*结构动力计算的目的在于确定结构在动力荷载作用下的位移、内力等量值随时间变化的规律,从而找出其最大值作为设计的依据。
*动力学研究的问题:动态作用下结构或构件的强度、刚度及稳定性分析。
一、本章重点1.振动方程的建立2.振动频率和振型的计算3.振型分解法求解多自由度体系4.最大动位移及最大动应力二、基础知识1.高等数学2.线性代数3.结构力学三、动力荷载的特征1.大小和方向是时间t的函数例如:地震作用,波浪对船体的作用,风荷载,机械振动等2.具有加速度,因而产生惯性力四、动力荷载的分类1.周期性动力荷载例如:①机械运转产生的动力荷载,②打桩时的锤击荷载。
P(t) Pt t(机械运转荷载)(打桩荷载)2.冲击荷载例如:①爆炸力产生的动力荷载,②车轮对轨道连接处的冲击。
P(t)P(t)P(t)t t t(爆炸力动力荷载)(吊车起吊钢索的受力)(随机动力荷载)3.突加常量荷载例如:吊车起吊重物时钢索的受力。
4.随机动力荷载前3类荷在是时间t的确定函数,称为确定性动力荷载;而地震作用,波浪对船体的作用,风荷载等其作用大小只能用统计的方法获得。
五、动力荷载的计算方法1.原理:达朗贝尔原理,动静法建立方程2.计算工具:微分方程,线性代数,结构力学六、体系振动的自由度---------动力自由度结构具有质量,有质量在运动时就有惯性力。
在进行动力计算时,一般把结构的质量简化为若干质点的质量,整个结构的惯性力就成为各质点的惯性力问题。
1.质点简化的一般要求①简单,②能反映主要的振动特性例如:楼房;质量集中在各层楼板平面内水塔:质量集中在水箱部分梁:无限自由度集中质量(楼房质量集中)(水塔质量集中)(梁的质量集中)2.位移y(t)即指质点的位移y(t),其加速度为y&&)(t3.动力自由度的确定即质点位移数量的确定。
结构动力学习题解析
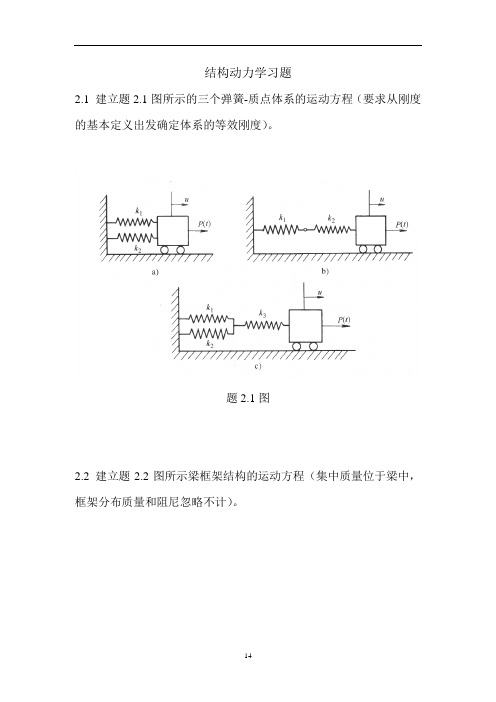
结构动力学习题2.1 建立题2.1图所示的三个弹簧-质点体系的运动方程(要求从刚度的基本定义出发确定体系的等效刚度)。
题2.1图2.2 建立题2.2图所示梁框架结构的运动方程(集中质量位于梁中,框架分布质量和阻尼忽略不计)。
题2.2图2.3 试建立题2.3图所示体系的运动方程,给出体系的广义质量M、广义刚度K、广义阻尼C和广义荷载P(t),其中位移坐标u(t)定义为无重刚杆左端点的竖向位移。
题2.3图2.4 一总质量为m1、长为L的均匀刚性直杆在重力作用下摆动。
一集中质量m2沿杆轴滑动并由一刚度为K2的无质量弹簧与摆轴相连,见题 2.4图。
设体系无摩擦,并考虑大摆角,用图中的广义坐标q1和q2建立体系的运动方程。
弹簧k2的自由长度为b。
题2.4图2.5 如题2.5图所示一质量为m1的质量块可水平运动,其右端与刚度为k的弹簧相连,左端与阻尼系数为c的阻尼器相连。
摆锤m2以长为L的无重刚杆与滑块以铰相连,摆锤只能在图示铅垂面内摆动。
建立以广义坐标u和θ表示的体系运动方程(坐标原点取静平衡位置)。
题2.5图2.6如题2.6图所示一质量为m1的质量块可水平运动,其上部与一无重刚杆相连,无重刚杆与刚度为k2的弹簧及阻尼系数为c2的阻尼器相连,m1右端与刚度为k1的弹簧相连,左端与阻尼系数为c1的阻尼器相连。
摆锤m2以长为L的无重刚杆与滑块以铰相连,摆锤只能在图示铅垂面内摆动。
建立以广义坐标u和θ表示的体系运动方程(坐标原点取静平衡位置,假定系统作微幅振动,sinθ=tanθ=θ)。
计算结果要求以刚度矩阵,质量矩阵,阻尼矩阵的形式给出。
3.1单自由度建筑物的重量为900kN,在位移为3.1cm时(t=0)突然释放,使建筑产生自由振动。
如果往复振动的最大位移为2.2cm(t =0.64s),试求:(1)建筑物的刚度k;(2)阻尼比ξ;(3)阻尼系数c。
3.2 单自由度体系的质量、刚度为m=875t,k=3500kN/m,且不考虑阻尼。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
于是
F0 sin - c A2 0
进一步得:
A F0 sin c ;
(3) 当n 时, sin 1 ,
则
Amax xst 2 ,
得
max 1 2 , 2 max 。
1.4 求图 1-35 中标出参数的系统的固有频率。
(1)此系统相当于两个弹簧串联,弹簧刚度为 k1、简支梁
谷的幅值 Ai 、 Ai1 。
(2)由对数衰减率定义 ln( Ai ) , Ai1
进一步推导有
2 , 1 2
1
结构动力学习题解答
因为 较小, 所以有 。 2
方法二:共振法求单自由度系统的阻尼比。 (1)通过实验,绘出系统的幅频曲线, 如下图:
单自由度系统的幅频曲线 (2)分析以上幅频曲线图,得到:
刚度为
k2
48EI L3
;
等效刚度为 k;有 1 k
1 k1
1 k2
;
m
k 1 48EIk
1 k1
1 k2
48EI k1l 3
L/2
L/2
则固有频率为: k
48EIl 3
;
m
48EI k1l 3 m
(2)此系统相当于两个弹簧串联, 等效刚度为:
k
k1
48EI l3
;
则固有频率为: k k1l 3 48EI
(2) 利用牛顿第二定律 m x F ,得到系统的运动微分方程;
(3) 求解该方程所对应的特征方程的特征根,得到该系统的固有频率。 2、 动量距定理法 适用范围:绕定轴转动的单自由度系统的振动。 解题步骤:(1) 对系统进行受力分析和动量距分析;
(2) 利用动量距定理 J M ,得到系统的运动微分方程;
l
k1
1 2
l
)=
1 2
ml
2
得:
k1 0 , 2m
则
k1 。
2m
m
k1
k1
图 1-33(d)
1.5 求下图所示系统的固有频率。图中匀质轮 A 半径 R,重物 B 的重量为 P/2,弹簧刚度为 k.
解:以 为广义坐标,则
系统的动能为
T
T重物
T轮子
1(m)x 2
2
1 2
I 0 2
A k
1( P )x2 1 ( 1 P R 2 ) x 2 P x 2 P x 2
4
2
由 d T U 0 得系统运动微分方程
dt
得系统的固有频率
3 Mx Kx 0 ; 2
(3) 求解该方程所对应的特征方程的特征根,得到该系统的固有频率。
4、 能量守恒定理法
适用范围:所有无阻尼的单自由度保守系统的振动。
解题步骤:(1)对系统进行运动分析、选广义坐标、写出在该坐标下系统的动能 T 和势能 U
的表达式;进一步写出机械能守恒定理的表达式 T+U=Const
(2)将能量守恒定理 T+U=Const 对时间求导得零,即 d (T U ) 0 ,进一步得到系
2 2g
2 2 g R 4g 4g
图 1-34 B
P x 2
0
2g
系统的势能能为: x
U
U 重物
U 弹簧
Px
1 2
kx 2
;
拉格朗日函数为
L=T-U ;
由拉格朗日方程
dt
(
L x)L x Nhomakorabea0
得
4
结构动力学习题解答
P x kx 0 g
则,
0 =
kg P
kg
所以:系统的固有频率为
P
1.6 求图 1-35 所示系统的固有频率。图中磙子半径为 R,质量为 M,作纯滚动。弹簧刚度
当单自由度系统在正弦激励 F0 sin t 作用下其稳态响应为:
x A sin( t ) ,
其中:
A
F0
x st
;
m
2 n
2 0
4n 2 2
1 2 4 2 2
(1)
arctan2 /1 2
(2)
2
结构动力学习题解答
从实验所得的幅频曲线和相频曲线图上查的相关差数,由上述(1),(2)式求得阻尼比 。
为K 。 解:磙子作平面运动, 其动能 T=T 平动 +T 转动 。
K R
x
M
图 1-35
T平动
1 2
Mx 2 ;
T转动
1 2
I
x R
2
1 2
MR2 2
x R
2
;
而势能
T 1 Mx 2 1 Mx 2 3 Mx 2 ;
2
4
4
系统机械能
U 1 Kx 2 ; 2
T U 3 Mx 2 1 Kx 2 C ;
dt
统的运动微分方程;
(3) 求解该方程所对应的特征方程的特征根,得到该系统的固有频率。
1.2 叙述用衰减法求单自由度系统阻尼比的方法和步骤。 用衰减法求单自由度系统阻尼比的方法有两个:衰减曲线法和共振法。 方法一:衰减曲线法。
求解步骤:(1)利用试验测得单自由度系统的衰减振动曲线,并测得周期和相邻波峰和波
m
ml 3
图 1-33(a)
m
L/2
L/2
k1
图 1-33(b)
3
结构动力学习题解答
(3)系统的等效刚度为
k
k1
3EI l3
k1
3EI l3
则系统的固有频率为 k k1l3 3EI
m
ml 3
m
k1
k1
图 1-33(c)
(4)
由动量距定理 m0 F I0得:
(
1 2
l
k1
1 2
l
1 2
1,2 max / 2 2 / 4 ;
于是
12
(1
2
)
2 n
;
进一步
2 2
(1
2
)
2 n
;
最后
2 1 / 2n / 2n ;
1.3 叙述用正选弦激励求单自由度系统阻尼比的方法和步骤。 用正选弦激励求单自由度系统阻尼比的方法有两个:幅频(相频)曲线法和功率法。
方法一:幅频(相频)曲线法
方法二:功率法:
(1) 单自由度系统在 F0 sin t 作用下的振动过程中,在一个周期内,
弹性力作功为
Wc 0 、
阻尼力做功为
W d c A 2 、
激振力做作功为
W f F0 sin ;
(2) 由机械能守恒定理得,弹性力、阻尼力和激振力在一个周期内所作功为零,
即:
Wc +Wd +W f 0 ;
结构动力学习题解答
第一章 单自由度系统
1.1 总结求单自由度系统固有频率的方法和步骤。 单自由度系统固有频率求法有:牛顿第二定律法、动量距定理法、拉格朗日方程法和能量守 恒定理法。 1、 牛顿第二定律法 适用范围:所有的单自由度系统的振动。 解题步骤:(1) 对系统进行受力分析,得到系统所受的合力;
(3) 求解该方程所对应的特征方程的特征根,得到该系统的固有频率。
3、 拉格朗日方程法:
适用范围:所有的单自由度系统的振动。
解题步骤:(1)设系统的广义坐标为 ,写出系统对于坐标 的动能 T 和势能 U 的表达式;
进一步写求出拉格朗日函数的表达式:L=T-U ;
(2)由格朗日方程
dt
(
L
)
L
=0,得到系统的运动微分方程;
