自测题9 矩阵位移法答案

第九章矩阵位移法习题集

第九章矩阵位移法【练习题】9-1 是非题：1、单元刚度矩阵反映了该单元杆端位移与杆端力之间的关系。

2、单元刚度矩阵均具有对称性和奇异性。

3、局部坐标系与整体坐标系之间的坐标变换矩阵T 是正交矩阵。

4、结构刚度矩阵反映了结构结点位移与荷载之间的关系。

5、用矩阵位移法计算连续梁时无需对单元刚度矩阵作坐标变换。

6、结构刚度矩阵是对称矩阵，即有K i j = K j i ，这可由位移互等定理得到证明。

7、结构刚度方程矩阵形式为：[]{}{}K P ∆=，它是整个结构所应满足的变形条件。

8、在直接刚度法的先处理法中，定位向量的物理意义是变形连续条件和位移边界条件。

9、等效结点荷载数值等于汇交于该结点所有固端力的代数和。

10、矩阵位移法中，等效结点荷载的“等效原则”是指与非结点荷载的结点位移相等。

11、矩阵位移法既能计算超静定结构，也能计算静定结构。

9-2 选择题：1、已知图示刚架各杆EI = 常数，当只考虑弯曲变形，且各杆单元类型相同时，采用先处理法进行结点位移编号，其正确编号是：(0,1,2)(0,0,0)(0,0,0)(0,1,3)(0,0,0)(1,2,0)(0,0,0)(0,0,3)(1,0,2)(0,0,0)(0,0,0)(1,0,3)(0,0,0)(0,1,2)(0,0,0)(0,3,4)A.B.C.D.21341234123412342、平面杆件结构一般情况下的单元刚度矩阵[]k 66⨯，就其性质而言，是： A ．非对称、奇异矩阵； B ．对称、奇异矩阵； C ．对称、非奇异矩阵； D ．非对称、非奇异矩阵。

3、单元i j 在图示两种坐标系中的刚度矩阵相比：A ．完全相同；B ．第2、3、5、6行(列)等值异号；C ．第2、5行(列)等值异号；D ．第3、6行(列)等值异号。

jxi4、矩阵位移法中，结构的原始刚度方程是表示下列两组量值之间的相互关系： A ．杆端力与结点位移； B ．杆端力与结点力； C ．结点力与结点位移； D ．结点位移与杆端力。

结构力学(9.14.1)--矩阵位移法习题2

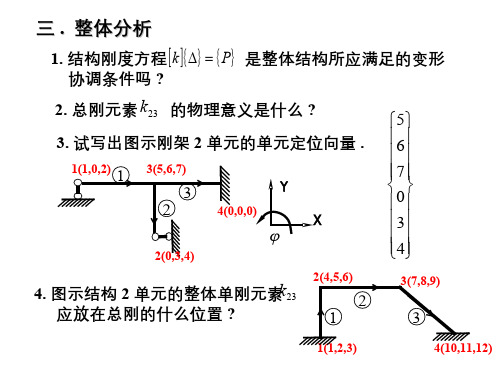
5kN m
8m 8m
8m
三 . 整体分析
12. 试求图示结构 ( 不计轴变 ) 的荷载列阵 ( 先处理法 ).
1(1,0,2) 2(1,0ቤተ መጻሕፍቲ ባይዱ3) 3(1,0,3)
X1
X2
4(0,0,0)
P

X
1
0
X
2

0
四 . 求杆端力
1. 连续梁在一般荷载作用下 , 单元杆端力由下式计算 . 是否正确 ?
6
48

4
2
1(0,0,0)
12
1 6
k

6
48

4(1,0,3)
3
2(0,0,0)
3
1
2

3
例 . 不计轴变 , 作弯矩图
已知 : 各杆长均为 12m, 线刚度均为 12
P 10kN, q 5kN / m
P 10kN, q 5kN / m
解 : 1 6 1 6
k
1

6
1
48 6
6 1
24

6

6
24
6
48

3(1,0,2)
2
1
1 6 1 6 1 0

k
1

6 1
48 6
6 1
24

2
0
63 1
6 24
EI
EI
EA 2l

2 2
l
l
三 . 整体分析
4(1,0,0)
5(1,0,0)

矩阵位移法题目及答案

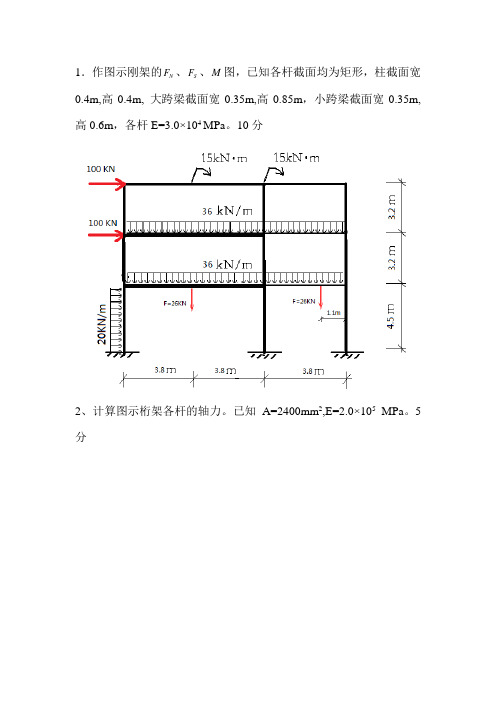
1．作图示刚架的F、S F、M图，已知各杆截面均为矩形，柱截面宽N0.4m,高0.4m, 大跨梁截面宽0.35m,高0.85m，小跨梁截面宽0.35m,高0.6m，各杆E=3.0×104 MPa。

10分2、计算图示桁架各杆的轴力。

已知A=2400mm2,E=2.0×105MPa。

5分3．作图示连续梁的F、M图，已知各梁截面面积A=6.52m,惯性矩SI=5.504m，各杆E=3.45×104MPa。

5分答案1******************************************************************** ** 1 composite beam 2012.10.17 ** ********************************************************************3E10 16 13 9 11 2 0.2975 17.912E-32 3 0.2975 17.912E-33 4 0.21 6.3E-31 5 0.16 2.133E-33 6 0.16 2.133E-34 7 0.16 2.133E-35 6 0.2975 17.912E-36 7 0.21 6.3E-35 8 0.16 2.133E-36 9 0.16 2.133E-37 10 0.16 2.133E-38 9 0.2975 17.912E-39 10 0.21 6.3E-38 11 0.16 2.133E-39 12 0.16 2.133E-310 13 0.16 2.133E-3 0 10.93.8 10.97.6 10.911.4 10.90 7.77.6 7.711.4 7.70 4.57.6 4.511.4 4.50 07.6 011.4 0111 0112 0113 0121 0122 0123 0131 0132 0133 041 100E3 0 02 0 0 -15E33 0 0 -15E35 100E3 0 0712 2 -26E3 3.813 2 -26E3 2.77 4 -36E3 7.68 4 -36E3 3.812 4 -36E3 7.613 4 -36E3 3.814 3 20E3 4.5第一题结果******************************************************************* * * * 1 composite beam 2012.10.17 * * * *******************************************************************The Input DataThe General InformationE NM NJ NS NLC3.000E+10 16 13 9 1The Information of Membersmember start end A I1 12 2.975000E-01 1.791200E-022 23 2.975000E-01 1.791200E-023 34 2.100000E-01 6.300000E-034 15 1.600000E-01 2.133000E-035 36 1.600000E-01 2.133000E-036 47 1.600000E-01 2.133000E-037 5 6 2.975000E-01 1.791200E-028 6 7 2.100000E-01 6.300000E-039 5 8 1.600000E-01 2.133000E-0310 6 9 1.600000E-01 2.133000E-0311 7 10 1.600000E-01 2.133000E-0312 8 9 2.975000E-01 1.791200E-0213 9 10 2.100000E-01 6.300000E-0314 8 11 1.600000E-01 2.133000E-0315 9 12 1.600000E-01 2.133000E-0316 10 13 1.600000E-01 2.133000E-03The Joint Coordinatesjoint X Y1 .000000 10.9000002 3.800000 10.9000003 7.600000 10.9000004 11.400000 10.9000005 .000000 7.7000006 7.600000 7.7000007 11.400000 7.7000008 .000000 4.5000009 7.600000 4.50000010 11.400000 4.50000011 .000000 .00000012 7.600000 .00000013 11.400000 .000000The Information of SupportsIS VS111 .000000112 .000000113 .000000121 .000000122 .000000123 .000000131 .000000132 .000000133 .000000( NA= 357 )( NW= 1167 )Loading Case 1The Loadings at JointsNLJ= 4ILJ PX PY PM1 100000.0000 .0000 .000002 .0000 .0000 -15000.000003 .0000 .0000 -15000.00000 5 100000.0000 .0000 .00000The Loadings at MembersNLM= 7ILM ITL PV DST12 2 -26000.0000 3.80000013 2 -26000.0000 2.7000007 4 -36000.0000 7.6000008 4 -36000.0000 3.80000012 4 -36000.0000 7.60000013 4 -36000.0000 3.80000014 3 20000.0000 4.500000The Results of CalculationThe Joint Displacementsjoint u v phi1 1.845349E-02 -1.982711E-04 -1.263100E-042 1.841771E-02 -3.424398E-04 -8.180773E-063 1.838193E-02 -5.043591E-04 -1.356524E-044 1.836317E-02 -3.892198E-04 -1.683554E-045 1.608566E-02 -2.069957E-04 -9.278065E-046 1.601139E-02 -5.147233E-04 6.593305E-057 1.599555E-02 -3.701310E-04 -4.819689E-048 1.132049E-02 -1.535800E-04 -1.283845E-039 1.131820E-02 -3.849935E-04 3.869225E-0510 1.130585E-02 -2.796765E-04 -9.193725E-0411 7.105234E-18 -1.638186E-17 -1.781240E-1712 9.610834E-18 -4.106598E-17 -2.156936E-1713 7.783932E-18 -2.983216E-17 -1.882119E-17The Terminal Forcesmember N(st) Q(st) M(st) N(en) Q(en) M(en)1 84035.890 -13086.980 -41569.990 -84035.890 13086.980 -8160.5532 84035.890 -13086.980 -6839.447 -84035.890 13086.980 -42891.1003 31099.080 -28633.300 -52776.720 -31099.080 28633.300 -56029.8104 -13086.980 15964.110 41569.990 13086.980 -15964.110 9515.1395 -15546.320 52936.810 80667.820 15546.320 -52936.810 88729.9806 28633.300 31099.080 56029.810 -28633.300 -31099.080 43487.2307 87221.910 93210.620 -62622.290 -87221.910 180389.400 -268657.0008 26256.560 29751.550 -2861.126 -26256.560 107048.500 -144003.0009 80123.640 28742.190 53107.150 -80123.640 -28742.190 38867.85010 194594.600 113902.200 182788.200-194594.600-113902.200 181698.70011 135681.800 57355.640 100515.700-135681.800 -57355.640 83022.30012 2689.851 83695.000 -146729.300 -2689.851 215905.000 -355668.70013 20483.680 160.171 -42824.000 -20483.680 162639.800 -245087.30014 163818.600 26052.340 107861.500-163818.600-116052.300 211874.00015 410659.800 96108.340 216794.000-410659.800 -96108.340 215693.50016 298321.600 77839.320 162065.000-298321.600 -77839.320 188211.900( NA= 357 )单位（N m）( NW= 1195 )第二题答案******************************************************************* * * * 2 composite beam 2012.10.17 * * * ******************************************************************* 2E11 14 9 4 11 2 2.4E-3 1E-102 3 2.4E-3 1E-103 4 2.4E-3 1E-104 5 2.4E-3 1E-101 8 2.4E-3 1E-101 6 2.4E-3 1E-102 6 2.4E-3 1E-103 6 2.4E-3 1E-103 7 2.4E-3 1E-104 7 2.4E-3 1E-105 7 2.4E-3 1E-105 9 2.4E-3 1E-106 8 2.4E-3 1E-107 9 2.4E-3 1E-100 62 64 66 68 62 36 30 08 081 082 091 092 051 0 -50E3 02 0 -50E3 03 0 -50E3 04 0 -50E3 05 -10E3 -50E3 0第二题结果******************************************************************* * * * 2 composite beam 2012.10.17 * * * *******************************************************************The Input DataThe General InformationE NM NJ NS NLC2.000E+11 14 9 4 1The Information of Membersmember start end A I1 12 2.400000E-03 1.000000E-102 23 2.400000E-03 1.000000E-103 34 2.400000E-03 1.000000E-104 45 2.400000E-03 1.000000E-105 1 8 2.400000E-03 1.000000E-106 1 6 2.400000E-03 1.000000E-107 2 6 2.400000E-03 1.000000E-108 3 6 2.400000E-03 1.000000E-109 3 7 2.400000E-03 1.000000E-1010 4 7 2.400000E-03 1.000000E-1011 5 7 2.400000E-03 1.000000E-1012 5 9 2.400000E-03 1.000000E-1013 6 8 2.400000E-03 1.000000E-1014 7 9 2.400000E-03 1.000000E-10The Joint Coordinatesjoint X Y1 .000000 6.0000002 2.000000 6.0000003 4.000000 6.0000004 6.000000 6.0000005 8.000000 6.0000006 2.000000 3.0000007 6.000000 3.0000008 .000000 .0000009 8.000000 .000000The Information of SupportsIS VS81 .00000082 .00000091 .00000092 .000000( NA= 270 )( NW= 907 )Loading Case 1The Loadings at JointsNLJ= 5ILJ PX PY PM1 .0000 -50000.0000 .000002 .0000 -50000.0000 .000003 .0000 -50000.0000 .000004 .0000 -50000.0000 .000005 -10000.0000 -50000.0000 .00000The Loadings at MembersNLM= 0The Results of CalculationThe Joint Displacementsjoint u v phi1 -1.052370E-04 -9.375000E-04 -7.026900E-052 -1.746814E-04 -1.193735E-03 1.087907E-043 -2.441259E-04 -8.137530E-04 -3.230397E-054 -3.552370E-04 -1.302888E-03 -1.022944E-045 -4.663480E-04 -9.375000E-04 1.412285E-046 3.860367E-04 -8.812350E-04 1.226822E-047 -7.938921E-04 -9.903881E-04 -6.211760E-058 -3.833334E-18 -1.325000E-17 -2.257494E-049 2.833334E-18 -1.175000E-17 3.510750E-04The Terminal Forcesmember N(st) Q(st) M(st) N(en) Q(en) M(en)1 16666.660 .009 .007 -16666.660 -.009 .0112 16666.660 -.009 -.008 -16666.660 .009 -.0113 26666.660 .011 .011 -26666.660 -.011 .0104 26666.660 -.010 -.012 -26666.660 .010 -.0075 75000.000 -.001 -.003 -75000.000 .001 -.0046 -30046.240 -.002 -.004 30046.240 .002 -.0027 49999.980 -.002 -.003 -49999.980 .002 -.0038 39060.150 -.002 -.005 -39060.150 .002 -.0039 21032.390 .002 .004 -21032.390 -.002 .00310 49999.980 .002 .002 -49999.980 -.002 .00311 -30046.240 .002 .005 30046.240 -.002 .00212 75000.000 .001 .003 -75000.000 -.001 .00413 69106.410 .003 .008 -69106.410 -.003 .00414 51078.650 -.004 -.009 -51078.650 .004 -.004( NA= 270 )( NW= 907 )第三题答案******************************************************************** ** 3 composite beam 2012.10.17 ** ******************************************************************** 3.45E10 4 5 6 11 2 6.5 5.52 3 6.5 5.53 4 6.5 5.54 5 6.5 5.50 040 060 080 0120 011 012 013 022 042 052 013 0 -320E3 -100E341 4 -10.5E3 402 4 -10.5E3 203 4 -10.5E3 204 4 -10.5E3 40第三题结果******************************************************************* * * * 3 composite beam 2012.10.17 * * * *******************************************************************The Input DataThe General InformationE NM NJ NS NLC3.450E+10 4 5 6 1The Information of Membersmember start end A I1 12 6.500000E+00 5.500000E+002 23 6.500000E+00 5.500000E+003 34 6.500000E+00 5.500000E+004 45 6.500000E+00 5.500000E+00The Joint Coordinatesjoint X Y1 .000000 .0000002 40.000000 .0000003 60.000000 .0000004 80.000000 .0000005 120.000000 .000000The Information of SupportsIS VS11 .00000012 .00000013 .00000022 .00000042 .00000052 .000000( NA= 66 )( NW= 299 )Loading Case 1The Loadings at JointsNLJ= 1ILJ PX PY PM3 .0000 -320000.0000 -100000.00000The Loadings at MembersNLM= 4ILM ITL PV DST1 4 -10500.0000 40.0000002 4 -10500.0000 20.0000003 4 -10500.0000 20.0000004 4 -10500.0000 40.000000The Results of CalculationThe Joint Displacementsjoint u v phi1 0.000000E+00 3.713943E-18 4.951923E-172 0.000000E+00 -2.916827E-17 -5.219418E-053 0.000000E+00 -1.405865E-03 1.038816E-064 0.000000E+00 -3.431731E-17 4.276883E-055 0.000000E+00 6.771635E-18 5.239688E-05The Terminal Forcesmember N(st) Q(st) M(st) N(en) Q(en) M(en)1 .000 172860.600 904807.700 .000 247139.400-2390385.0002 .000 359543.300 2390385.000 .000-149543.300 2700481.0003 .000-170456.700-2800481.000 .000 380456.700-2708654.0004 .000 277716.300 2708654.000 .000 142283.700 .000( NA= 66 )( NW= 315 )。

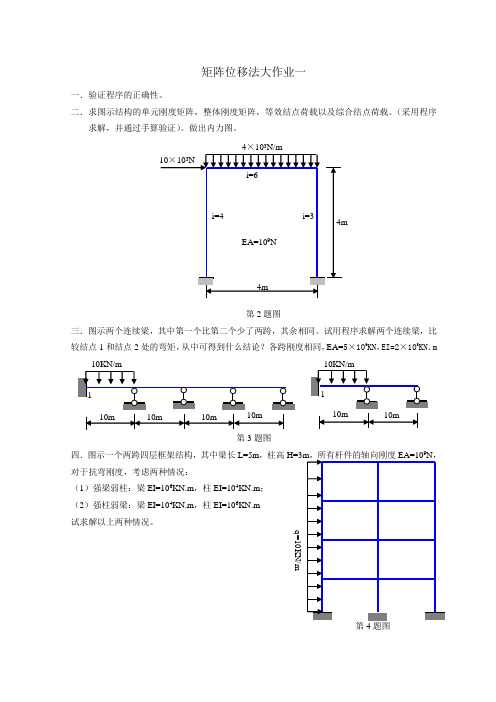
矩阵位移法大作业

①
1
2
ql
②
2
3
③
4
q
1① 2 ② 3 ③
4
y M, x
(a)
(b)
第 3 题图
各杆 EI 、l 相同，杆长也相同，具体数值可自己给定。
四．采用程序计算图示结构
i
跨长 l（m）
层高 h（m）
集中力（KN）
1
6
7
30
2
10
4
100
3
8
3
50
其他：
柱刚度：EA=105KN，EI=1.5×104KN.m2 梁刚度：EA=106KN，EI=1.0×104KN.m2 支座沉降 C=0.01m
四．采用程序计算图示结构，并作出弯矩图。已知各杆 E=3.0×106KN/m2，A1=0.16m2，I1=0.012m4，I2=2I1， A2=2A1，I3=3I1，A3=3A1
第 3 题图
20KN
40KN．m
I1，A1 50KN
40KN
15KN/m I3，A3
25KN
I2，A2 40KN．m
4m
4m
3m
3m
五．编写一段程序，实现“将已知支座位移转化为等效节点荷载”。六．采用程序计算图示结构，并作出最后内力图。已知各杆 E=3.2×106KN/m2，A=0.16m2，I=0.012m4。
36KN
8KN/m
12KN/m
36KN 54KN.m 3m
3m
q=10KN/m
6KN/m
36KN
3m
3m
六．不修改源程序，计算图示结构。
10KN
35KN
6m
15KN

《结构力学习题集》-矩阵位移法习题及答案

第八章矩阵位移法 – 老八校一、判断题：1、单元刚度矩阵反映了该单元杆端位移与杆端力之间的关系。

2、单元刚度矩阵均具有对称性和奇异性。

3、局部坐标系与整体坐标系之间的坐标变换矩阵T 是正交矩阵。

4、结构刚度矩阵反映了结构结点位移与荷载之间的关系。

5、结构刚度方程矩阵形式为：[]{}{}K P ∆=，它是整个结构所应满足的变形条件。

6、图示结构用矩阵位移法计算时（计轴向变形）未知量数目为8个。

7、在直接刚度法的先处理法中，定位向量的物理意义是变形连续条件和位移边界条件。

8、等效结点荷载数值等于汇交于该结点所有固端力的代数和。

9、矩阵位移法中，等效结点荷载的“等效原则”是指与非结点荷载的结点位移相等。

10、矩阵位移法既能计算超静定结构，也能计算静定结构。

11、已知图示刚架各杆EI = 常数，当只考虑弯曲变形，且各杆单元类型相同时，采用先处理法进行结点位移编号，其正确编号是：(0,1,2)(0,0,0)(0,0,0)(0,1,3)(0,0,0)(1,2,0)(0,0,0)(0,0,3)(1,0,2)(0,0,0)(0,0,0)(1,0,3)(0,0,0)(0,1,2)(0,0,0)(0,3,4)A.B.C.D.2134123412341234( )二、计算题：12、用先处理法计算图示结构刚度矩阵的元素133322,,K K K 。

123ll4l5EI2EIEA(0,0,0)(0,0,1)(0,2,3)(0,0,0)(0,2,4)(0,0,0)EI13、用先处理法计算图示刚架结构刚度矩阵的元素153422,,K K K 。

EI ，EA 均为常数。

l14、计算图示结构整体刚度矩阵的元素665544,,K K K 。

E 为常数。

ll1342A , I AA /222A I , 2A15、写出图示结构以子矩阵形式表达的结构原始刚度矩阵的子矩阵[][]K K 2224,。

[][]k k 1112 [][]k k 2122 []k =ii iii单刚分块形式为：16、已知平面桁架单元在整体坐标系中的单元刚度矩阵，计算图示桁架结构原始刚度矩阵[]K 中的元素,,7877K K EA ＝常数。

矩阵位移法方法课习题

已知图示结构的单元编码及局部坐标如图，已知图示结构的单元编码及局部坐标如图，局部坐标单元刚度矩阵相同如（）按结点号顺序写出结点位移编，度矩阵相同如（c）式。求：按结点号顺序写出结点位移编，并求结构刚度矩阵。并求结构刚度矩阵。
2 i
①
3
1
−10 0 0 0 0 10 0 −2 2 0.5 0 0.5 0 0.5 0.2 0 −0.5 0.1 e 6 k = ×10 L(c) 0 10 0 0 −10 0 0 −2 −0.5 0 2 −0.5 0 −0.5 0.2 0 0.5 0.1
3kN/m
① ②
4m
用矩阵位移法求解图示结构。标示整体坐标系，用矩阵位移法求解图示结构。标示整体坐标系，单元局部坐标系；按结点号顺序编写结点位移编码；部坐标系；按结点号顺序编写结点位移编码；写出单元定位向量；求结构结点荷载列阵{F}。定位向量；求结构结点荷载列阵。
4 4m 20kN/m 1 2 4m 3 6m 10 kN . m
T
试求杆14的轴力。试求杆的轴力。 EA = 1kN 的轴力
1kN 1kN 2 4 6 1m 1 3 1m 1m y 5 M, θ x
已知图示结构的结点位移列阵为
{ ∆} = [ 0
0 0 0.841 − 0.5752 − 0.9964 0 0 − 0.7425]
T
试求杆32的杆端力列阵中端的剪力试求杆的杆端力列阵中1端的剪力。的杆端力列阵中端的剪力。
l
y
M, θ x
试求图示结构在所示位移编码情况下的结点荷载列阵
P 1(0,0,0) 2 (0,0,1) q 3 (0,2,3) 4 (0,0,0) l 5 (0,0) l

结构力学大作业(矩阵位移法)

矩阵位移法编程大作业姓名：学号：一、编程原理本程序的原理是基于结构力学矩阵位移法原理，以结构结点位移作基本未知量，将要分析的结构拆成已知节点力—结点力位移关系的单跨梁集合，通过强令结构发生待定的基本未知位移，在各个单跨梁受力分析结果的基础上通过保证结构平衡建立位移法的线性方程组，从而求得基本未知量。

二、程序说明本程序是计算10个节间距的悬索-拱组合体系主塔顶节点水平位移、主塔底截面弯矩、拱顶节点竖向位移、拱顶截面弯矩和轴力的程序。

首先将各杆件的交汇点作为结点，共有20个结点，51个位移，然后根据不同结构单元分别建立单元刚度矩阵，然后转换为整体坐标系下的刚度矩阵，然后将所有杆件的单元刚度矩阵整合成为总体刚度矩阵，在进行整合时连续运用for函数，最终形成51阶的总体刚度矩阵。

然后通过对荷载的分析确定出荷载矩阵，直接写进程序。

这样就可以把20个结点的51个位移求得，然后再利用各个单元的单元刚度矩阵和所得的位移求得单元杆件的内力。

三、算法流程建立各单位在局部结构离散化编号进行单元分析坐标系下的单位刚度方程确定各单位在总体将单元刚度矩阵集合确定综合结点坐标系下的单元矩阵方程成总体刚度矩阵点荷载矩阵建立方程利用杆件单元刚度矩阵输出结果求解位移和所求位移求内力结束四、源代码L=input('输入单节间L：');EIc=input('主塔的抗弯刚度EIc:');EAc=input('主塔的抗压刚度EAc:');EAb=input('悬索和斜索的抗拉刚度EAb:');EAt=input('吊杆的抗拉刚度EAt:');EIa=input('拱的抗弯刚度EIa:');EAa=input('拱的抗压刚度EAa:');q=input('拱上沿轴向均布荷载集度q:');T1=[0,1,0,0,0,0;-1,0,0,0,0,0;0,0,1,0,0,0;0,0,0,0,1,0;0,0,0,-1,0,0;0,0,0,0,0,1;];%主塔的转换矩阵h=(5*L)/2;KcO=[EAc/h,0,0,-EAc/h,0,0;0,12*EIc/(h*h*h),6*EIc/(h*h),0,-12*EIc/(h*h*h),6*EIc/(h*h);0,6*EIc/(h*h),4*EIc/h,0,-6*EIc/(h*h),2*EIc/h;-EAc/h,0,0,EAc/h,0,0;0,-12*EIc/(h*h*h),-6*EIc/(h*h),0,12*EIc/(h*h*h),-6*EIc/(h*h);0,6*EIc/(h*h),2*EIc/h,0,-6*EIc/(h*h),4*EIc/h;];%主塔的单元刚度矩阵x=atan(2*L/h);T2=[cos(x),sin(x),0,0;-sin(x),cos(x),0,0;0,0,cos(x),sin(x);0,0,-sin(x),cos(x);];y=-atan(2*L/h);T21=[cos(y),sin(y),0,0;-sin(y),cos(y),0,0;0,0,cos(y),sin(y);0,0,-sin(y),cos(y);];%斜索的转换矩阵s1=sqrt(2*L*2*L+h*h);KbO1=(EAb/s1)*[1 0 -1 0;0 0 0 0;-1 0 1 0;0 0 0 0;];%斜索的单元刚度矩阵f2(1)=5*L/2;f2(2)=58*L/25;f2(3)=109*L/50;f(4)=52*L/25;f2(5)=101*L/50;f2 (6)=2*L;f2(7)=101*L/50;f2(8)=52*L/25;f2(9)=109*L/50;f2(10)=58*L/25;f2(1 1)=5*L/2;y=zeros(10,1);for i=1:10y(i)=atan((f2(i+1)-f2(i))/L);endT3=zeros(4,40);for i=1:10T3(1:4,4*i-3:4*i)=[cos(y(i)),sin(y(i)),0,0;-sin(y(i)),cos(y(i)),0,0;0,0,cos(y(i)),sin(y(i));0,0,-sin(y(i)),cos(y(i));];end%悬索的转换矩阵s2=zeros(10,1);for i=1:10s2(i)=sqrt((f2(i+1)-f2(i))^2+L^2);endKbO2=zeros(4,40);KbO2(1:4,4*i-3:4*i)=(EAb/s2(i))*[1 0 -1 0;0 0 0 0;-1 0 1 0;0 0 0 0;];end%悬索的单元刚度矩阵f1(1)=0;f1(2)=9*L/20;f1(3)=4*L/5;f1(4)=21*L/20;f1(5)=6*L/5;f1(6)=5*L/4; f1(7)=6*L/5;f1(8)=21*L/20;f1(9)=4*L/5;f1(10)=9*L/20;f1(11)=0;z=zeros(10,1);for i=1:10z(i)=atan((f1(i+1)-f1(i))/L);endT4=zeros(6,60);for i=1:10T4(6*i-5:6*i,6*i-5:6*i)=[cos(z(i)),sin(z(i)),0,0,0,0;-sin(z(i)),cos(z(i)),0,0,0,0;0,0,1,0,0,0;0,0,0,cos(z(i)),sin(z(i)),0;0,0,0,-sin(z(i)),cos(z(i)),0;0,0,0,0,0,1;];end%拱的转换矩阵s3=zeros(10,1);for i=1:10s3(i)=sqrt((f1(i+1)-f1(i))^2+L^2);endKaO=zeros(6,60);for i=1:10KaO(1:6,6*i-5:6*i)=[EAa/s3(i) 0 0 -EAa/s3(i) 0 0;0 12*EIa/(s3(i)*s3(i)*s3(i)) 6*EIa/(s3(i)*s3(i)) 0-12*EIa/(s3(i)*s3(i)*s3(i)) 6*EIa/(s3(i)*s3(i));0 6*EIa/(s3(i)*s3(i)) 4*EIa/s3(i) 0 -6*EIa/(s3(i)*s3(i)) 2*EIa/s3(i);-EAa/s3(i) 0 0 EAa/s3(i) 0 0;0 -12*EIa/(s3(i)*s3(i)*s3(i)) -6*EIa/(s3(i)*s3(i)) 012*EIa/(s3(i)*s3(i)*s3(i)) -6*EIa/(s3(i)*s3(i));0 6*EIa/(s3(i)*s3(i)) 2*EIa/s3(i) 0 -6*EIa/(s3(i)*s3(i)) 4*EIa/s3(i);]; end%拱的单元刚度矩阵T5=[0 1 0 0;-1 0 0 0;0 0 0 1;0 0 -1 0;];%吊杆的转换矩阵s4=zeros(9,1);s4(i)=f2(i+1)-f1(i+1);endKtO=zeros(4,36);for i=1:9KtO(1:4,4*i-3:4*i)=(EAt/s4(i))*[1 0 -1 0;0 0 0 0;-1 0 1 0;0 0 0 0;];end%吊杆的单元刚度矩阵Kc=T1'*KcO*T1;%总体坐标下主塔的单元刚度矩阵Kb1=T2'*KbO1*T2;Kb11=T21'*KbO1*T21;%总体坐标下斜索的单元刚度矩阵Kb2=zeros(4,40);for i=1:10T3O=T3(1:4,4*i-3:4*i);Kb2(1:4,4*i-3:4*i)=T3O'*KbO2(1:4,4*i-3:4*i)*T3O;end%总体坐标下悬索的单元刚度矩阵Ka=zeros(6,60);for i=1:10T4O=T4(6*i-5:6*i,6*i-5:6*i);Ka(1:6,6*i-5:6*i)=T4O'*KaO(1:6,6*i-5:6*i)*T4O;end%总体坐标下拱的单元刚度矩阵Kt=zeros(4,36);for i=1:9KtOO=KtO(1:4,4*i-3:4*i);Kt(1:4,4*i-3:4*i)=T5'*KtOO*T5;end%总体坐标下吊杆的单元刚度矩阵%定义51阶0矩阵K1=zeros(51,51);K2=zeros(51,51);K3=zeros(51,51);K4=zeros(51,51);K5=zero s(51,51);X=zeros(51,51);Y=zeros(51,51);Z=zeros(51,51);%把主塔整合到整体刚度矩阵中：K1(1:3,1:3)=KcO(4:6,4:6);K1(22:24,22:24)=KcO(4:6,4:6);%把斜索整合到整体刚度矩阵中：K2(1:2,1:2)=Kb1(3:4,3:4);K2(22:23,22:23)=Kb11(1:2,1:2);%把悬索整合到整体刚度矩阵中:K3(1:2,1:2)=KbO2(1:2,1:2);K3(1:2,4:5)=KbO2(1:2,3:4);for i=2:10X(2*i:2*i+3,2*i:2*i+3)=KbO2(1:4,4*i-3:4*i);K3=K3+X;end%把拱整合到整体刚度矩阵中：K4(25:27,25:27)=KaO(4:6,4:6);K4(49:51,49:51)=KaO(1:3,55:57);for i=2:9Y(3*i+19:3*i+24,3*i+19:3*i+24)=KaO(1:6,6*i-5:6*i); K4=K4+Y;end%把吊杆整合到整体刚度矩阵中：for i=1:9Z(2*i+2:2*i+3,2*i+2:2*i+3)=KtO(1:2,1:2);Z(2*i+2:2*i+3,3*i+22:3*i+23)=KtO(1:2,3:4);Z(3*i+22:3*i+23,2*i+2:2*i+3)=KtO(3:4,1:2);Z(3*i+22:3*i+23,3*i+22:3*i+23)=KtO(3:4,3:4);K5=K5+Z;endK=K1+K2+K3+K4+K5;%荷载矩阵：P=zeros(51,1);P(26,1)=-q*L/(2*cos(s3(1)));P(27,1)=q*L*L/(12*cos(s3(1)));P(50,1)=-q*L/(2*cos(s3(10)));P(51,1)=-q*L*L/(12*cos(s3(10)));for i=2:9P0=zeros(51,1);P0(3*i+20,1)=-q*L/(2*cos(s3(i)));P0(3*i+21,1)=-q*L*L/(12*cos(s3(i)));P0(3*i+23,1)=-q*L/(2*cos(s3(i)));P0(3*i+24,1)=q*L*L/(12*cos(s3(i)));P=P+P0;endA=K\P;%结构的位移%主塔底截面的弯矩：Ac(4:6,1)=A(1:3,1);Bc=KcO*Ac;Mc=Bc(3,1);%拱顶截面的弯矩和轴力：Aa=A(34:39,1);KaO17=KaO(1:6,25:30);Ba=KaO17*Aa;Ma=Ba(6,1);Fa=Ba(4,1);%输出结果fprintf('主塔顶结点的水平位移%f\n',A(1,1)); fprintf('主塔底截面的弯矩%f\n',Mc);fprintf('拱顶结点的竖向位移%f\n',A(38,1)); fprintf('拱顶截面的弯矩%f\n',Ma);fprintf('拱顶截面的轴力%f\n',Fa);五、试算算例输入单节间L：1主塔的抗弯刚度EIc:1主塔的抗压刚度EAc:1悬索和斜索的抗拉刚度EAb:1吊杆的抗拉刚度EAt:1拱的抗弯刚度EIa:1拱的抗压刚度EAa:1拱上沿轴向均布荷载集度q:1主塔顶结点的水平位移NaN主塔底截面的弯矩NaN拱顶结点的竖向位移0.016046拱顶截面的弯矩3.791098拱顶截面的轴力0.000000。

9矩阵位移法习题.docx

第9章矩阵位移法习题解答习题9・1是非判断题（1）矩阵位移法既可计算超静定结构，又可以计算静定结构。

（T ）（2）矩阵位移法棊木未知量的数冃与位移法棊木未知量的数冃总是相等的。

（|T*） F（3）单元刚度矩阵都具有对称性和奇界性。

（F ）（4）在矩阵位移法中，整体分析的实质是建立各结点的平衡方程。

（T ）（5）结构刚度短阵与单元的编号方式冇关。

（F ）（6）原荷载与对应的等效结点荷载使结构产生相同的内力和变形。

（F ）【解】（1）正确。

（2）错误。

位移法中某些不独立的杆端位移不计入基本未知量。

（3）错谋。

不计结点线位移的连续梁单元的单刚不具奇异性。

（4）正确。

（5）错误。

结点位移分量统-•编码会影响结构刚度矩阵，但单元或结点编码则不会。

（6）错误。

二者只产生相同的结点位移。

习题9.2填空题（1） ______________________________________________________________ 矩阵位移法分析包含三个基本环节，其一是结构的___________________________________ ,其二是_________ 分析，-其三是______ 分析。

（2）已知某单元©的定位向量为[3 5 6 7 8 9]丁，则单元刚度系数紜应叠加到结构刚度矩阵的元素—中去。

（3） ________________________________________________________________________ 将非结点荷载转换为等效结点荷载，等效的原则是____________________________________ o（4）矩阵位移法屮，在求解结点位移之前，主要工作是形成_____________________ 矩阵和_______________ 列阵。

（5）用矩阵位移法求得某结构结点2的位移为J2=[w2V2 ft]T=[O.S 0.3 0.5]丁，单元①的始、末端结点码为3、2,单元定位向量为= [0 0 0 3 4 5]T,设单元与兀轴之间的夹角为« = |,则（6 ）用短阵位移法求得平面刚架某单元在单元坐标系中的杆端力为戸=[7.5 -48 -70.9 -7.5 48 -121.09]7,则该单元的轴力F* _______________________ k N。

矩阵位移法

k22坐k11标局k01成部1k029坐200标时kk20与32，3 整局k0体12部45 单k0k20514
0 k26 k26
To 47
k e ke
刚和有何整k关体3k3系单33 ？刚k0k间454535
k35 00
k3k6 36
0 k56
对称对称
kk5544
kk65k66 66
F e FEe k e e
单元杆端位移矩阵
e 1
2
3
4
T e
单元刚度矩阵(应熟记)
12 6l 12 6l
k
e
EI l3
6l
12
4l 2 6l
6l 12
2l
2
6l
6l 2l 2 6l 4l 2
是转角位移方程的矩阵表示
单元等效结点荷载矩阵
根据单跨梁的载常数，可得
向上满跨均布荷载 q 作用
(F FE )e k e e F e FEe k e e
连续梁单元需要进行坐标转换吗？
连续梁的局部坐标与整体坐标一致，所以不需要转换。
第一种做法
桁架单元如何
进行坐标转换？ T
力的转换
T
F1
F2
F3
F4
T
cos
0
位移的转换
sin
0
0
cos
0 T F1
sin F2
1 2
3. 坐标转换问题
在搞清单元特性后，像位移法一样，需将单元拼装回去。在结点处位移自动满足协调条件的基础上，令全部结点平衡，即可建立求解位移的方程，这是下一节将讨论的内容。
除连续梁外，一般结构单元不全同方位，为保证协调和平衡，应将杆端位移和杆端力都转换成统一的，对整体坐标的量，因此要先解决坐标转换问题。下面先讨论自由式梁单元的转换问题。

《结构力学习题集》(下)-矩阵位移法习题及答案 (2)

第七章矩阵位移法一、就是非题1、单元刚度矩阵反映了该单元杆端位移与杆端力之间得关系。

2、单元刚度矩阵均具有对称性与奇异性。

3、局部坐标系与整体坐标系之间得坐标变换矩阵T 就是正交矩阵。

4、结构刚度矩阵反映了结构结点位移与荷载之间得关系。

5、用矩阵位移法计算连续梁时无需对单元刚度矩阵作坐标变换。

6、结构刚度矩阵就是对称矩阵 ,即有K i j = K j i ,这可由位移互等定理得到证明。

7、结构刚度方程矩阵形式为:,它就是整个结构所应满足得变形条件。

8、在直接刚度法得先处理法中,定位向量得物理意义就是变形连续条件与位移边界条件。

9、等效结点荷载数值等于汇交于该结点所有固端力得代数与。

10、矩阵位移法中,等效结点荷载得“等效原则”就是指与非结点荷载得结点位移相等。

11、矩阵位移法既能计算超静定结构,也能计算静定结构。

二、选择题1、已知图示刚架各杆EI = 常数,当只考虑弯曲变形,且各杆单元类型相同时,采用先处理法进行结点位移编号,其正确编号就是:(0,1,2)(0,0,0)(0,0,0)(0,1,3)(0,0,0)(1,2,0)(0,0,0)(0,0,3)(1,0,2)(0,0,0)(0,0,0)(1,0,3)(0,0,0)(0,1,2)(0,0,0)(0,3,4)A.B.C.D.21341234123412342、平面杆件结构一般情况下得单元刚度矩阵,就其性质而言,就是:A.非对称、奇异矩阵;B.对称、奇异矩阵;C.对称、非奇异矩阵;D.非对称、非奇异矩阵。

3、单元i j 在图示两种坐标系中得刚度矩阵相比:A.完全相同;B.第2、3、5、6行(列)等值异号;C.第2、5行(列)等值异号;D.第3、6行(列)等值异号。

4、矩阵位移法中,结构得原始刚度方程就是表示下列两组量值之间得相互关系:A.杆端力与结点位移;B.杆端力与结点力;C.结点力与结点位移;D.结点位移与杆端力。

矩阵位移法自测题

自测题
一、判断题
1. 在矩阵位移法中整体分析的实质是结点平衡。( √ ) 2.单元刚度矩阵是单元固有的特性，与坐标选取无关。
(√ ) 3. 矩阵位移法中，结构等效节点荷载作用下的内力与
结构在荷载作用下的内力相同。（ ×）应该是位移相同。
4. 结构刚度矩阵是对称矩阵，即有kij=kji ，这可由位移
互等定理得到证明。( × ) 应该是反力互等定理。
5. 设整体坐标下单元刚度矩阵为 ke，杆端力列阵为Fe,
杆端位移列阵为⊿e，杆件固端力列阵为F0e，则有
Fe =ke⊿e+ F0e
(√ )
自测题
二、选择填空
1. 平面杆件结构用后处理法建立的原始刚度方程组。（D ）
A．可求得全部结点位移 B．可求得可动结点的移 C．可求得支座结点位移 D．无法求得结点位移
l 4EI
2 1
l 4
1
4 1
EI
2
3
k
2
4 3
8
3
8 3
EI
4
2
k 3
3 1
3
1
3 2
EI
3
自测题
（3）用单元集成法形成结构总刚度矩阵
各单元的定位向量如下：
1 0 1T
2 1 2T
3 2 3T
按单元定位向量将单元刚度矩阵集成整体刚度矩阵如下：
K
1
2
3
3 4
15.5kN
m
M 43
2i (3) 2
4i (3) 3
30.0kN
m
B. k56
C. k03
D. k58
三、考研题选解
1. 单元i , j 在图示两种坐标系中的刚度矩阵：（ A）

结构力学自测题(第八单元)矩阵位移法

A
q M
10kN/m 2EI 6m
y
l
y
M, x
l
七、图 a 所示结构，整体坐标见图 b，图中圆括号内数码为
结点定位向量(力和位移均按水平、竖直、转动方向顺序排列 )。求等效结点荷载列阵 PE 。(不考虑轴向变形)
于： A． 6 ； C．10 ；
20kN/m M1 1 Y1 2m 2 4m 3 y M, x
e
T K
e
。
(
)
二、选择题（将选中答案的字母填入括弧内） 1、已知图示刚架各杆 EI=常数，当只考虑弯曲变形，且各
杆单元类型相同时，采用先处理法进行结点位移编号，其正确编号是：
是：
附：
EA l 0 0 EA l 0 0
0 12EI l 6 EI l 0 12EI l 6 EI l
2 3 2 3
0 6 EI
2

EA l 0 0 EA l 0 0
0 12EI l 6 EI l
2 3
l 4 EI l 0 6 EI l 2 EI l
(1,0,2) i 6m ② (0,0,0) 6m (a) y M, x (b) i ① (1,0,3)
1 3 1m 1m
y 5
M, x
十、试用矩阵位移法解图示连续梁，绘弯矩图。EI=已知常
数。
50 kN. m B EI 4m 20 kN C 2m D x M,
六、求图示结构的自由结点荷载列阵 P 。
A. 2(0,1,2) 1(0,0,0) 4(0,0,0) 3(0,1,3) C. 2(1,0,2) 1(0,0,0) 4(0,0,0) 3(1,0,3) 1(0,0,0) D. 2(0,1,2) 4(0,0,0) 1(0,0,0) B. 2(1,2,0) 4(0,0,0) 3(0,0,3) y M, x

结构力学习题集矩阵位移法习题及答案老八校

1文档收集于互联网，已整理，word 版本可编辑.第八章矩阵位移法 – 老八校一、判断题：1、单元刚度矩阵反映了该单元杆端位移与杆端力之间的关系。

2、单元刚度矩阵均具有对称性和奇异性。

3、局部坐标系与整体坐标系之间的坐标变换矩阵T 是正交矩阵。

4、结构刚度矩阵反映了结构结点位移与荷载之间的关系。

5、结构刚度方程矩阵形式为：[]{}{}K P ∆=，它是整个结构所应满足的变形条件。

6、图示结构用矩阵位移法计算时（计轴向变形）未知量数目为8个。

7、在直接刚度法的先处理法中，定位向量的物理意义是变形连续条件和位移边界条件。

8、等效结点荷载数值等于汇交于该结点所有固端力的代数和。

9、矩阵位移法中，等效结点荷载的“等效原则”是指与非结点荷载的结点位移相等。

10、矩阵位移法既能计算超静定结构，也能计算静定结构。

11、已知图示刚架各杆EI = 常数，当只考虑弯曲变形，且各杆单元类型相同时，采用先处理法进行结点位移编号，其正确编号是：二、计算题：12、用先处理法计算图示结构刚度矩阵的元素133322,,K K K 。

13、用先处理法计算图示刚架结构刚度矩阵的元素153422,,K K K 。

EI ，EA 均为常数。

14、计算图示结构整体刚度矩阵的元素665544,,K K K 。

E 为常数。

15、写出图示结构以子矩阵形式表达的结构原始刚度矩阵的子矩阵[][]K K 2224,。

16、已知平面桁架单元在整体坐标系中的单元刚度矩阵，计算图示桁架结构原始刚度矩阵[]K 中的元素,,7877K K EA ＝常数。

,cos α=C ,sin α=S ,C C A ⋅= S S D S C B ⋅=⋅=,，各杆EA 相同。

2文档收集于互联网，已整理，word 版本可编辑.17、计算图示刚架结构刚度矩阵中的元素8811,K K （只考虑弯曲变形）。

设各层高度为h ，各跨长度为l h l 5.0,=，各杆EI 为常数。

18、计算图示结构原始刚度矩阵的元素4544,K K 。

第九章矩阵位移法例题

Cy
=
3 5
⎡ 192
[k](4) =
EA
⎢ ⎢
144
3000 ⎢−192
⎢⎣− 144
144 108 − 144 − 108
− 192 − 144 192 144
− 144⎤
− 108⎥⎥
144 ⎥
108
⎥ ⎦
贡献刚度矩阵
⎡192 144 0 0⎤
[K ](4) = EA ⎢⎢144 108 0 0⎥⎥
⎪⎪ ⎨ ⎪
40 0
⎪⎪ ⎬
=
⎪⎪ ⎨
⎪⎪
0 0
⎪⎪ ⎬ ⎪
⎢0 − 3 − 6 0 3 − 6⎥ ⎪ 0 ⎪ ⎪ 60 ⎪ ⎪ 22.74 ⎪
⎢ ⎢⎣0 6
8
0
−6
⎥ 16 ⎥⎦
⎪⎪⎩ 12.033 ⎪⎪⎭
⎪⎪⎩− 40⎪⎪⎭ ⎪⎪⎩−10.98⎪⎪⎭
{ } 单元（2）{δ }(2) = δ (2) = 1 {− 50.081 0 12.033 − 50.081 0 11.382}T EI
结点 4 荷载
荷载贡献
{P}= {0 0 0 20}T
总荷载向量
{P}= {−10 −13.33 13.33 10}T
解结构方程，求出位移向量
{∆} = 1 {− 50.081 −19.350 12.033 11.382}T
EI 求单元内力
{ } 单元（1）{δ }(1) = δ (1) = 1 {− 50.081 0 −19.350 − 50.081 0 12.033}T EI
⎢ ⎢⎣0 6
⎥ 8 0 − 6 16 ⎥⎦
⎪⎪⎩11.382⎪⎪⎭ ⎪⎪⎩ 10 ⎪⎪⎭ ⎪⎪⎩ 2.60 ⎪⎪⎭

《结构力学习题》(含答案解析)

第三章静定结构的位移计算一、判断题：1、虚位移原理等价于变形谐调条件，可用于求体系的位移。

2、按虚力原理所建立的虚功方程等价于几何方程。

3、在非荷载因素(支座移动、温度变化、材料收缩等)作用下，静定结构不产生内力，但会有位移且位移只与杆件相对刚度有关。

4、求图示梁铰C 左侧截面的转角时，其虚拟状态应取：A.;; B.D.C.=1=15、功的互等、位移互等、反力互等和位移反力互等的四个定理仅适用于线性变形体系。

6、已知M p 、M k 图，用图乘法求位移的结果为：()/()ωω1122y y EI +。

M k M p 21y 1y 2**ωω( a )M =17、图a 、b 两种状态中，粱的转角ϕ与竖向位移δ间的关系为：δ=ϕ 。

8、图示桁架各杆E A 相同，结点A 和结点B 的竖向位移均为零。

a a9、图示桁架各杆EA =常数，由于荷载P 是反对称性质的，故结点B 的竖向位移等于零。

二、计算题：10、求图示结构铰A 两侧截面的相对转角ϕA ，EI = 常数。

q l l l /211、求图示静定梁D 端的竖向位移 ∆DV 。

EI = 常数，a = 2m 。

a a a 10kN/m12、求图示结构E 点的竖向位移。

EI = 常数。

l l l /3 2 /3/3q13、图示结构，EI=常数，M =⋅90kN m , P = 30kN 。

求D 点的竖向位移。

P 3m 3m 3m14、求图示刚架B 端的竖向位移。

ql15、求图示刚架结点C 的转角和水平位移，EI = 常数。

q16、求图示刚架中Ｄ点的竖向位移。

EI ＝常数。

l/217、求图示刚架横梁中Ｄ点的竖向位移。

EI＝常数。

18、求图示刚架中D点的竖向位移。

E I = 常数。

qll l/219、求图示结构Ａ、Ｂ两截面的相对转角，EI＝常数。

l/23l/320、求图示结构A、B两点的相对水平位移，E I = 常数。

ll21、求图示结构B点的竖向位移，EI = 常数。

位移法习题与答案

位移法习题与答案位移法是结构力学中常用的一种分析方法，通过计算结构在外力作用下的位移，来求解结构的应力、应变和变形等问题。

在学习位移法时，习题与答案的练习是非常重要的，可以帮助我们加深对位移法的理解和掌握。

下面将给大家介绍一些位移法习题及其答案。

习题一：求解简支梁的弯矩分布已知一根长度为L的简支梁，受到均布载荷q作用，求解弯矩分布。

解答：首先，我们需要根据受力分析确定梁的反力。

对于简支梁，两个支座处的反力相等，且为qL/2。

接下来，我们可以利用位移法求解弯矩分布。

假设梁的弯矩分布为M(x)，则根据位移法的基本原理，可以得到以下方程：d2M(x)/dx2 = -q对该方程进行两次积分，得到：M(x) = -q*x^2/2 + C1*x + C2由于梁两端是简支条件，即位移和转角为零，可以得到边界条件：M(0) = 0M(L) = 0代入上述方程，解得C1 = qL/2，C2 = -qL^2/2。

因此，弯矩分布为：M(x) = -q*x^2/2 + qL/2*x - qL^2/2习题二：求解悬臂梁的挠度已知一根长度为L的悬臂梁，受到集中力F作用在悬臂端点，求解梁的挠度。

解答：首先，我们需要根据受力分析确定梁的反力。

对于悬臂梁，端点处的反力只有一个，即为F。

接下来，我们可以利用位移法求解梁的挠度。

假设梁的挠度为δ(x)，则根据位移法的基本原理，可以得到以下方程：d2δ(x)/dx2 = -F/(EI)对该方程进行两次积分，得到：δ(x) = -F*x^2/(2EI) + C1*x + C2由于梁端点处的位移为零，可以得到边界条件：δ(0) = 0dδ(x)/dx|_(x=L) = 0代入上述方程，解得C1 = 0，C2 = 0。

因此，梁的挠度为：δ(x) = -F*x^2/(2EI)习题三：求解悬臂梁的最大挠度已知一根长度为L的悬臂梁，受到均布载荷q作用，求解梁的最大挠度。

解答：首先，我们需要根据受力分析确定梁的反力。

位移法网上练习题答案

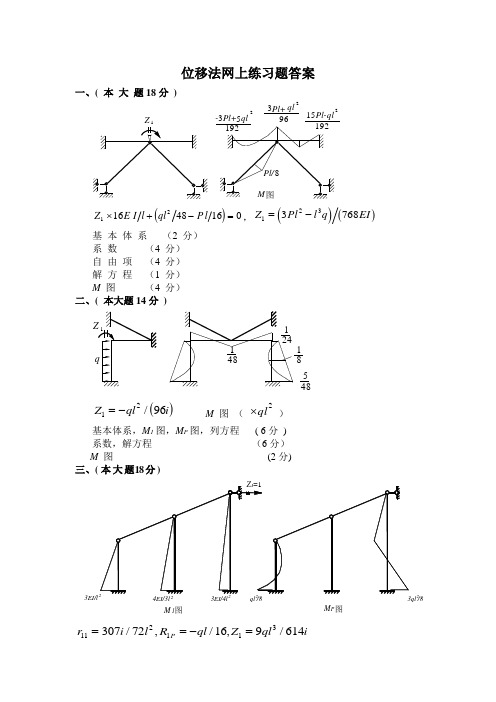
位移法网上练习题答案一、( 本大题18分 )Z2- Pl+ ql 192962Pl+ql Pl-ql 2192Pl/M 35315图8()Z E I l ql Pl 121648160⨯+-=，()()Z Pl l qEI 1233768=-基本体系（2 分）系数（4 分）自由项（4 分）解方程（1 分） M 图（4 分）二、( 本大题14分 )814812414851M 图（ ⨯ql 2）基本体系4分，M 1、M P 图及系数共9分，列方程、解方程 3分M 图 2分。

四、( 本大题13分 )Z( 5分）Z m i 128=/ , Z ml i 256=-/ . ( 8 分）五、( 本大题19分)Pr i h r r i h r i h 11212212222242448===-=/,/,/, （6 分）R P R P P P 12=-=-,,（4 分）()()Z Ph i Z Ph i 1222812==/,/,（4 分）1/21/21/21/21/41/41/41/43/43/4M ( )Ph 图（4 分）六、( 本大题12分 )M1图=114iMP 图4444Z图 M ()kN .m 5228266616812M 图r i 1111=,R P 144=, Zi 14=-/七、( 本大题18分 )Z 1r i 115= , R Pl P 14=/ , Z 1=-Pl / 20i , N P AB =35/1/51/103/10M 图 ()⨯Pl（1/4结构4分，方程2分，M 1图2分，M P 图2分，系数4分，方程解2分，M 图2分）八、( 本大题21分 )Z 2基本体系5 /185 /18/6/62 /92 /9/18/18M 图Pl Pl Pl Pl Pl Pl Pl Pl 简化126036612201812112222Z Z l Z Pl Z l Z l P Z Pl -==-+-==/,////,/简化 1/4结构（ 3 分）基本体系（ 2 分）位移法典型方程（ 2分） M 1图（2分）；M 2图（2分）；M P 图（2分）系数（ 3 分）自由项（ 2 分）解方程（ 1 分） M 图（ 2 分）。

自测题9 矩阵位移法答案

第九章矩阵位移法习题集

结构力学(9.14.1)--矩阵位移法习题2

矩阵位移法题目及答案

矩阵位移法大作业

《结构力学习题集》-矩阵位移法习题及答案

矩阵位移法方法课习题

结构力学大作业(矩阵位移法)

9矩阵位移法习题.docx

矩阵位移法

《结构力学习题集》(下)-矩阵位移法习题及答案 (2)

矩阵位移法自测题

结构力学自测题(第八单元)矩阵位移法

结构力学习题集矩阵位移法习题及答案老八校

第九章 矩阵位移法例题

《结构力学习题》(含答案解析)

位移法习题与答案

位移法网上练习题答案

第九章矩阵位移法例题