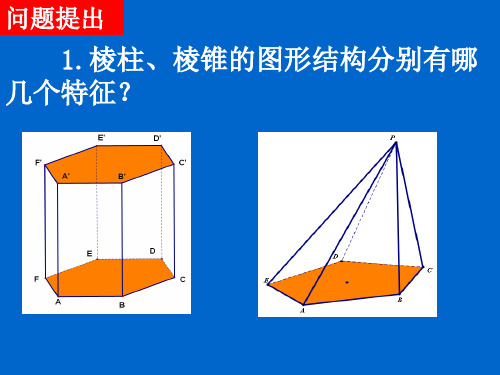
棱台圆柱圆锥圆台的几何特征PPT演示文稿
合集下载
棱柱、棱锥、棱台的结构特征 课件

成的几何体
条 定直线 旋转所形成的封闭几何体
图形
面:围成多面体的各个_多__边__形_ 相关
棱:相邻两个面的_公__共__边__ 轴:形成旋转体所绕的定直线 概念
顶点:棱与棱的公共点
知识点二 棱柱的结构特征
名称
定义
图形及表示
相关概念
分类
有两个面互相平行,
底面(底):两个
按底面多
其余各面都是_四__边_
解 截面以上的几何体是三棱柱AEF-A1HG,截面以下的几何体是四棱 柱BEFC-B1HGC1
类型三 多面体的平面展开图
例4 在长方体ABCD-A1B1C1D1中,AB=4,BC=3,BB1=5,一只蚂 蚁从点A出发沿表面爬行到点C1,求蚂蚁爬行的最短路线.
(2)用平面BCNM把这个长方体分成两部分,各部分形成的几何体还是棱 柱吗?如果是,是几棱柱,并用符号表示;如果不是,请说明理由.
解 截面BCNM右上方部分是三棱柱BB1M-CC1N,左下方部分是四棱 柱ABMA1-DCND1.
引申探究 把本例3的几何体换成如图所示的三棱柱ABC-A1B1C1,其中E,F,G, H是三棱柱对应边上的中点,过此四点作截面EFGH,把三棱柱分成两 部分,各部分形成的几何体是棱柱吗?如果是,是几棱柱,并用符号表 示;如果不是,请说明理由.
侧面:其余各面
截得的棱台分
台
如图可记作:
与截面之间
侧棱:相邻侧面的公共边 别叫做三棱台、
棱台ABCD—
的部分叫做
顶点:侧面与上(下)底面 四棱台、五棱
A′B′C′D′
棱台
的公共顶点
台……
2.棱柱、棱锥、棱台之间的关系
类型一 棱柱、棱锥、棱台的结构特征 命题角度1 棱柱的结构特征 例1 下列关于棱柱的说法: (1)所有的面都是平行四边形; (2)每一个面都不会是三角形; (3)两底面平行,并且各侧棱也平行. 其中正确说法的序号是__(3_)__. 解析 (1)错,底面可以不是平行四边形; (2)错,底面可以是三角形; (3)正确,由棱柱的定义可知.
旋转体的结构特征(圆柱、圆锥、圆台、球)(课堂PPT)

AA’’
叫做圆柱的侧面。
母
(4)无论旋转到什么位置,不垂直于轴 线
的边都叫做圆柱的母线。
O’ B’
A
O
B
矩 形
轴 侧 面 底面
3
2.圆柱的表示:用表示它的轴的字母表示,如圆柱OO1。
3.圆柱与棱柱统称为柱体。
O
柱
体
棱 柱 圆 柱
侧
面
O1
母 线
轴
底面
4
二、圆锥的结构特征 1.定义:以直角三角形的直角边所在直线为旋转轴,
1.1.6旋转体的结构特征
——圆柱、圆锥、圆台、球
1
旋转一周。。。
矩形
直角三角形
直角梯形
半圆
圆柱
圆锥
圆台
球
2
一、圆柱的结构特征
圆柱O定1义:以矩形的一边所在直线为旋转轴,
其余三边旋转形成的曲面所围成的旋转体叫做圆柱。
(1)旋转轴叫做圆柱的轴。
(2) 垂直于轴的边旋转而成的圆面叫
O
做圆柱的底面。
(3)平行于轴的边旋转而成的曲面
B
O
E
O
16 C
题型一、旋转体的概念
例 下列叙述中正确的是____③____.(填序号)
①以直角三角形的一边为轴旋转所得的旋转体是圆锥; ②以直角梯形的一腰为轴旋转所得的旋转体是圆台; ③圆锥截去一个小圆锥后剩余部分是圆台; ④用一个平面去截圆锥,得到一个圆锥和一个圆台.
[解题过程] ①中以直角三角形的直角边为轴旋 转所得的旋转体是圆锥,以斜边为轴旋转所得的旋 转体是两个圆锥的组合体.故①不正确. ②中以直角梯形中垂直于底边的腰为轴旋转所得 的旋转体是圆台,以不垂直底边的腰为轴旋转所得 的旋转体是圆柱和圆锥的组合体,故②不正确. ③正确.
棱台圆柱圆锥圆台的结构特征课件

棱台圆柱圆锥圆台的 结构特征课件
目录
• 棱台 • 圆柱 • 圆锥 • 圆台
棱台
01
概念定 义
01
棱台是由平行于棱锥底面的平面 截棱锥得到的,其中截面和底面 平行且小于底面。
02
棱台是棱锥用平行于底面的平面 截得的,故其具有与棱锥相同的 结构特征。底面。
平的底面称为上底面,不平 的底面称为下底面。
圆柱的侧面是一个矩形,而矩形的一条边是圆柱的高,另一条边是圆柱的底面圆周
结构特征
01
圆柱的底面是一个圆,其半径称为圆柱的底 面半径
02
圆柱的高与底面圆的直径相等,称为圆柱的 高
03
圆柱的母线是垂直于底面且与底面圆相切的 直线段
04
圆柱的结构特征是:有两个底面,一个侧面, 侧面展开图为矩形
表面积计算
圆锥的轴截面是一个等腰三角形, 其中母线是三角形的腰。
结构特征
圆锥的侧面是一个曲 面,由无数个小的扇 形组成。
圆锥的高是母线与底 面之间的距离。
每个扇形的弧长等于 底面的周长,而母线 则是所有这些扇形的 公共弦。
表面积计算
圆锥的表面积等于底面积加上侧面积。
侧面积是一个扇形,其弧长等于底面 的周长,面积计算公式为:1/2 × 母 线 × 底面周长。
底面积是一个圆形,其半径等于圆锥 的底面半径,面积计算公式为:πr²。
因此,圆锥的表面积计算公式为: πr² + 1/2 × 母线 × 底面周长。
圆台
04
概念定 义
圆台是指一个与两个平行平面相交的 平面图形,其内部是一个以交线为轴 的旋转体。
圆台可以看作是由一个平行底面的平 面截一个圆锥而得到的。
棱台具有n个侧面,侧面之间 夹角为180/n度。
目录
• 棱台 • 圆柱 • 圆锥 • 圆台
棱台
01
概念定 义
01
棱台是由平行于棱锥底面的平面 截棱锥得到的,其中截面和底面 平行且小于底面。
02
棱台是棱锥用平行于底面的平面 截得的,故其具有与棱锥相同的 结构特征。底面。
平的底面称为上底面,不平 的底面称为下底面。
圆柱的侧面是一个矩形,而矩形的一条边是圆柱的高,另一条边是圆柱的底面圆周
结构特征
01
圆柱的底面是一个圆,其半径称为圆柱的底 面半径
02
圆柱的高与底面圆的直径相等,称为圆柱的 高
03
圆柱的母线是垂直于底面且与底面圆相切的 直线段
04
圆柱的结构特征是:有两个底面,一个侧面, 侧面展开图为矩形
表面积计算
圆锥的轴截面是一个等腰三角形, 其中母线是三角形的腰。
结构特征
圆锥的侧面是一个曲 面,由无数个小的扇 形组成。
圆锥的高是母线与底 面之间的距离。
每个扇形的弧长等于 底面的周长,而母线 则是所有这些扇形的 公共弦。
表面积计算
圆锥的表面积等于底面积加上侧面积。
侧面积是一个扇形,其弧长等于底面 的周长,面积计算公式为:1/2 × 母 线 × 底面周长。
底面积是一个圆形,其半径等于圆锥 的底面半径,面积计算公式为:πr²。
因此,圆锥的表面积计算公式为: πr² + 1/2 × 母线 × 底面周长。
圆台
04
概念定 义
圆台是指一个与两个平行平面相交的 平面图形,其内部是一个以交线为轴 的旋转体。
圆台可以看作是由一个平行底面的平 面截一个圆锥而得到的。
棱台具有n个侧面,侧面之间 夹角为180/n度。
简单几何体棱台圆柱圆锥圆台

特点
圆柱的侧面展开后是一个矩形,矩形的长等于圆的周长,矩形的宽等于圆柱的 高。
面积与体积计算
侧面积
侧面积等于圆的周长乘以圆柱的 高。
表面积
表面积等于两个圆的面积加上侧面 积。
体积
体积等于圆的面积乘以圆柱的高。
03
圆锥
定义与性质
定义
圆锥是由一个圆面和一个侧面构成的几何体,其中圆面是底面,侧面是一个曲面 。
体积计算
圆锥的体积等于底面圆的面积乘以高再除以3。
04
圆台
ቤተ መጻሕፍቲ ባይዱ
定义与性质
定义
圆台是一个由两个平行圆面和一个曲面所围成的几何体,其中上、下底面的半径不同。
性质
圆台的两个底面平行且相等,侧面是曲面,侧面展开后为扇环。
分类与特点
分类
根据圆台的上、下底面半径和高的关系 ,可以分为正圆台和斜圆台。
VS
特点
圆台的高等于两个底面半径之差,圆台的 母线是连接两个底面圆心的线段。
感谢您的观看
THANKS
特点
棱台具有与棱锥类似的性质,如侧面 面积与底面面积的比值等于其高与相 应底边长的比值。
面积与体积计算
面积计算
棱台的表面积由上、下底面和侧面组成,计算公式为:表面 积 = (上底面面积 + 下底面面积) + 侧面积。
体积计算
棱台的体积计算公式为:体积 = (1/3) * h * (上底面面积 + 下 底面面积 + √(上底面面积 * 下底面面积)),其中 h 为高。
02
圆柱
定义与性质
定义
圆柱是一个二维图形, 由一个矩形绕其一边旋
转而成。
性质
圆柱的底面和顶面是两 个相等的圆,侧面是一
圆柱的侧面展开后是一个矩形,矩形的长等于圆的周长,矩形的宽等于圆柱的 高。
面积与体积计算
侧面积
侧面积等于圆的周长乘以圆柱的 高。
表面积
表面积等于两个圆的面积加上侧面 积。
体积
体积等于圆的面积乘以圆柱的高。
03
圆锥
定义与性质
定义
圆锥是由一个圆面和一个侧面构成的几何体,其中圆面是底面,侧面是一个曲面 。
体积计算
圆锥的体积等于底面圆的面积乘以高再除以3。
04
圆台
ቤተ መጻሕፍቲ ባይዱ
定义与性质
定义
圆台是一个由两个平行圆面和一个曲面所围成的几何体,其中上、下底面的半径不同。
性质
圆台的两个底面平行且相等,侧面是曲面,侧面展开后为扇环。
分类与特点
分类
根据圆台的上、下底面半径和高的关系 ,可以分为正圆台和斜圆台。
VS
特点
圆台的高等于两个底面半径之差,圆台的 母线是连接两个底面圆心的线段。
感谢您的观看
THANKS
特点
棱台具有与棱锥类似的性质,如侧面 面积与底面面积的比值等于其高与相 应底边长的比值。
面积与体积计算
面积计算
棱台的表面积由上、下底面和侧面组成,计算公式为:表面 积 = (上底面面积 + 下底面面积) + 侧面积。
体积计算
棱台的体积计算公式为:体积 = (1/3) * h * (上底面面积 + 下 底面面积 + √(上底面面积 * 下底面面积)),其中 h 为高。
02
圆柱
定义与性质
定义
圆柱是一个二维图形, 由一个矩形绕其一边旋
转而成。
性质
圆柱的底面和顶面是两 个相等的圆,侧面是一
高中数学《棱柱、棱锥、棱台的结构特征 》课件

17
课前自主预习
课堂互动探究
课堂达标自测
课后课时精练
数学 ·必修2
解析 棱柱是由一个平面多边形沿某一方向平移而形 成的几何体,因而侧面是平行四边形,故①对.
棱锥是由棱柱的一个底面收缩为一个点而得到的几何 体,因而其侧面均是三角形,且所有侧面都有一个公共点, 故②对.
棱台是棱锥被平行于底面的平面所截后,截面与底面之 间的部分,因而其侧面均是梯形,且所有的侧棱延长后均相 交于一点(即原棱锥的顶点),故③错④对.⑤显然正确.
所以(1)为五棱柱,(2)为五棱锥,(3)为三棱台.
29
课前自主预习
课堂互动探究
课堂达标自测
课后课时精练
数学 ·必修2
拓展提升 空间几何体的展开图
(1)解答空间几何体的展开图问题要结合多面体的结构 特征发挥空间想象能力和动手能力.
(2)若给出多面体画其展开图,常常给多面体的顶点标 上字母,先把多面体的底面画出来,然后依次画出各侧面.
数学 ·必修2
第一章 空间几何体
1.1 空间几何体的结构 1.1.1 棱柱、棱锥、棱台的结构特征
1
课前自主预习
课堂互动探究
课堂达标自测
课后课时精练
数学 ·必修2
课前自主预习
2
课前自主预习
课堂互动探究
课堂达标自测
课后课时精练
数学 ·必修2
知识点一 空间几何体的定义、分类及相关概念 1.空间几何体的定义
(3)若是给出表面展开图,则按上述过程逆推.
30
课前自主预习
课堂互动探究
课堂达标自测
课后课时精练
数学 ·必修2
【跟踪训练 3】 根据如下图所给的平面图形,画出立 体图.
棱台、圆柱、圆锥、圆台的结构特征 PPT课件 人教课标版

共腰的延长线共点
上底面
顶点
侧面
侧棱
下底面
1、原棱锥的底面和截面分别叫做棱台的下底面和
上底面
2、其余各面叫做棱台的侧面 3、相邻侧面的公共边叫做棱台的侧棱 4、侧面与底面的公共顶点叫做棱台的顶点
思考1:下列多面体一定是棱台吗?如 何判断?
思考2:三棱台、四棱台、五棱台、…… 分别是什么含义?
知识探究(三):圆柱的概念
•
74、先知三日,富贵十年。付诸行动,你就会得到力量。
•
75、爱的力量大到可以使人忘记一切,却又小到连一粒嫉妒的沙石也不能容纳。
•
76、好习惯成就一生,坏习惯毁人前程。
•
77、年轻就是这样,有错过有遗憾,最后才会学着珍惜。
•
78、时间不会停下来等你,我们现在过的每一天,都是余生中最年轻的一天。
•
79、在极度失望时,上天总会给你一点希望;在你感到痛苦时,又会让你偶遇一些温暖。在这忽冷忽热中,我们学会了看护自己,学会了坚强。
3、斜边旋转而成的曲面叫做圆锥的侧面
4、斜边在旋转中的任何位置叫做圆锥侧面 的母线
思考1:经过圆锥任意两条母线的截面是 什么图形?
思考2:经过圆锥的轴的截面称为轴截面, 圆锥的轴截面有哪些基本特征?
知识探究(四):圆台的结构特征
用一个平行于圆锥底面的平面去截圆 锥,截面与底面之间的部分叫做圆台.
•
36、每临大事,心必静心,静则神明,豁然冰释。
•
37、别人认识你是你的面容和躯体,人们定义你是你的头脑和心灵。
•
38、当一个人真正觉悟的一刻,他放弃追寻外在世界的财富,而开始追寻他内心世界的真正财富。
•
39、人的价值,在遭受诱惑的一瞬间被决定。
上底面
顶点
侧面
侧棱
下底面
1、原棱锥的底面和截面分别叫做棱台的下底面和
上底面
2、其余各面叫做棱台的侧面 3、相邻侧面的公共边叫做棱台的侧棱 4、侧面与底面的公共顶点叫做棱台的顶点
思考1:下列多面体一定是棱台吗?如 何判断?
思考2:三棱台、四棱台、五棱台、…… 分别是什么含义?
知识探究(三):圆柱的概念
•
74、先知三日,富贵十年。付诸行动,你就会得到力量。
•
75、爱的力量大到可以使人忘记一切,却又小到连一粒嫉妒的沙石也不能容纳。
•
76、好习惯成就一生,坏习惯毁人前程。
•
77、年轻就是这样,有错过有遗憾,最后才会学着珍惜。
•
78、时间不会停下来等你,我们现在过的每一天,都是余生中最年轻的一天。
•
79、在极度失望时,上天总会给你一点希望;在你感到痛苦时,又会让你偶遇一些温暖。在这忽冷忽热中,我们学会了看护自己,学会了坚强。
3、斜边旋转而成的曲面叫做圆锥的侧面
4、斜边在旋转中的任何位置叫做圆锥侧面 的母线
思考1:经过圆锥任意两条母线的截面是 什么图形?
思考2:经过圆锥的轴的截面称为轴截面, 圆锥的轴截面有哪些基本特征?
知识探究(四):圆台的结构特征
用一个平行于圆锥底面的平面去截圆 锥,截面与底面之间的部分叫做圆台.
•
36、每临大事,心必静心,静则神明,豁然冰释。
•
37、别人认识你是你的面容和躯体,人们定义你是你的头脑和心灵。
•
38、当一个人真正觉悟的一刻,他放弃追寻外在世界的财富,而开始追寻他内心世界的真正财富。
•
39、人的价值,在遭受诱惑的一瞬间被决定。
圆柱、圆锥、圆台的几何特征课件

底面
圆锥的底部是一个圆面, 称为底面。
圆锥的定义与基本元素
01
02
03
04
侧面
连接底面和顶点的曲面,称为 侧面。
母线
连接底面和顶点的线段,称为 母线。
轴
通过底面的圆心与顶点连接的 直线,称为轴。
顶点
圆锥顶部的点,称为顶点。
圆锥的侧面展开图
侧面展开图是一个扇形,扇形的半径 等于圆锥的母线长,扇形的弧长等于 圆锥底面的周长。
认为圆柱、圆锥、圆台的定义只是简 单地描述了它们的形状,而忽略了它 们是由平面曲线(圆)绕固定直线 (轴)旋转而成的立体几何图形。
误区二
对于圆柱、圆锥、圆台的定义中涉及 的术语理解不准确,如“母线”、“ 轴”、“底面”等。
关于公式应用的误区
误区一
在应用圆柱、圆锥、圆台的表面积和体积公式时3
圆台的几何特征
圆台的定义与基本元素
定义
圆台是由一个大的圆平面(下底)和一个小的 圆平面(上底)以及连接两圆的侧面所围成的
几何体。
01
下底
较大的圆形平面。
03
高
上底和下底之间的垂直距离。
05
02
上底
较小的圆形平面。
04
侧面
连接上底和下底的曲面。
06
母线
连接上底和下底边缘的线段。
圆台的侧面展开图
圆柱的体积公式
V = πr^2h,其中r为底面半径,h为高。 体积等于底面积乘以高。
典型例题解析
例题1
已知圆柱的底面半径为3,高为4,求圆柱的表面积和体积。
解析
根据公式S = 2πr^2 + 2πrh和V = πr^2h,代入r = 3,h = 4,即可求出表面积和体积。
《基本立体图形》立体几何初步 PPT教学课件(第1课时棱柱、棱锥、棱台的结构特征)

③棱台的侧棱所在直线均相交于同一点. 解析:棱锥是由棱柱的一个底面收缩为一个点而得到的几何体,因
而其侧面均是三角形,且所有侧面都有一个公共点,故①对.棱台
是棱锥被平行于底面的平面所截后,截面与底面之间的部分,因而
其侧面均是梯形,且所有的侧棱延长后均相交于一点(即原棱锥的顶
点),故②错,③对.因而正确的有①③. 答案:①③
栏目 导引
第八章 立体几何初步
4.一个棱柱有 10 个顶点,所有的侧棱长的和为 60 cm,则每 条侧棱长为__________cm. 解析:因为棱柱有 10 个顶点,所以棱柱为五棱柱,共有五条侧 棱,所以侧棱长为650=12(cm). 答案:12
栏目 导引
第八章 立体几何初步
空间几何体的平面展开图
(1)水平放置的正方体的六个面分别用
“前面、后面、上面、下面、左面、右面”表示,
如图是一个正方体的平面展开图(图中数字写在
正方体的外表面上),若图中的“2”在正方体的
上面,则这个正方体的下面是( )
A.1
B.9
C.快
D.乐
栏目 导引
第八章 立体几何初步
(2)如图是三个几何体的侧面展开图,请问各是什么几何体?
【解】 (1)选 B.由题意,将正方体的展开图还原成 正方体,“1”与“乐”相对,“2”与“9”相对,“0” 与“快”相对,所以下面是“9”.
栏目 导引
第八章 立体几何初步
(2)题图①中,有 5 个平行四边形,而且还有两个全等的五边形, 符合棱柱的特点;题图②中,有 5 个三角形,且具有共同的顶 点,还有一个五边形,符合棱锥的特点;题图③中,有 3 个梯 形,且其腰的延长线交于一点,还有两个相似的三角形,符合 棱台的特点,把侧面展开图还原为原几何体,如图所示:
棱台、圆柱、圆锥、圆台的结构特征ppt1 人教课标版

上底面
侧面
母线
轴
下底面
思考3:经过圆台任意两条母线的截面是 什么图形?轴截面有哪些基本特征?
思考4:设圆台的上、下底面圆圆心分别 为O′、O,过线段OO′的中点作平行于 底面的截面称为圆台的中截面,那么圆 台的上、下底面和中截面的面积有什么 关系?
o′
o
理论迁移
例1 将下列平面图形绕直线AB旋转 一周,所得的几何体分别是什么?
新课标人教版课件系列
《高中数学》
必修2
1.1.2 《空间几何体-棱台、 圆柱、圆锥、圆台的结构特征》
教学目 标
• 使学生掌握棱台、圆柱、圆锥、圆台 的概念,进一步理解轴、底面、侧面、 母线的概念,掌握棱台、圆柱、圆锥、 圆台的的直径、半径概念,能说出简 单组合体的结构特征。 • 教学重难点:棱台、圆柱、圆锥、圆 台和简单组合体的结构特征。
母线
母线
底面
思考3:平行于圆柱底面的截面,经过 圆柱任意两条母线的截面分别是什么图 形?
思考4:经过圆柱的轴的截面称为轴截面, 你能说出圆柱的轴截面有哪些基本特征 吗?
知识探究(三):圆锥的结构特征
思考1:将一个直角三角形以它的一条直 角边为轴旋转一周,那么其余两边旋转 形成的面所围成的旋转体是一个什么样 的空间图形?你能画出其直观图吗?
B B B A 图3
A
A 图1
图2
例2 在直角三角形ABC中,已知AC=2, BC= , 2 3 ,以直线 C 90 AC为轴将△ABC 旋转一周得到一个圆锥,求经过该圆锥 任意两条母线的截面三角形的面积的最 大值.
A A
C
B
C
B
D
作业:
再见
• • • • • • • • • • • • • • • • • • • • • • • • • • • • • • •
侧面
母线
轴
下底面
思考3:经过圆台任意两条母线的截面是 什么图形?轴截面有哪些基本特征?
思考4:设圆台的上、下底面圆圆心分别 为O′、O,过线段OO′的中点作平行于 底面的截面称为圆台的中截面,那么圆 台的上、下底面和中截面的面积有什么 关系?
o′
o
理论迁移
例1 将下列平面图形绕直线AB旋转 一周,所得的几何体分别是什么?
新课标人教版课件系列
《高中数学》
必修2
1.1.2 《空间几何体-棱台、 圆柱、圆锥、圆台的结构特征》
教学目 标
• 使学生掌握棱台、圆柱、圆锥、圆台 的概念,进一步理解轴、底面、侧面、 母线的概念,掌握棱台、圆柱、圆锥、 圆台的的直径、半径概念,能说出简 单组合体的结构特征。 • 教学重难点:棱台、圆柱、圆锥、圆 台和简单组合体的结构特征。
母线
母线
底面
思考3:平行于圆柱底面的截面,经过 圆柱任意两条母线的截面分别是什么图 形?
思考4:经过圆柱的轴的截面称为轴截面, 你能说出圆柱的轴截面有哪些基本特征 吗?
知识探究(三):圆锥的结构特征
思考1:将一个直角三角形以它的一条直 角边为轴旋转一周,那么其余两边旋转 形成的面所围成的旋转体是一个什么样 的空间图形?你能画出其直观图吗?
B B B A 图3
A
A 图1
图2
例2 在直角三角形ABC中,已知AC=2, BC= , 2 3 ,以直线 C 90 AC为轴将△ABC 旋转一周得到一个圆锥,求经过该圆锥 任意两条母线的截面三角形的面积的最 大值.
A A
C
B
C
B
D
作业:
再见
• • • • • • • • • • • • • • • • • • • • • • • • • • • • • • •
数学1.1.2圆柱圆锥圆台球简单组合体的几何特征PPT课件
又名“金色大米”,是一 种转基 因大米 ,通过 转基因 技术将 胡萝卜 素转化 酶系统 转入到 大米胚 乳中可 获得外 表为金 黄色的 转基因 大米
作业: P7练习:1,2. P9习题1.1A组:2.
黄金大米,又名“金色大米”,是一 种转基 因大米 ,通过 转基因 技术将 胡萝卜 素转化 酶系统 转入到 大米胚 乳中可 获得外 表为金 黄色的 转基因 大米
思考2:在圆柱的形成中,旋转轴叫做圆柱的轴, 垂直于轴的边旋转而成的圆面叫做圆柱的底面, 平行于轴的边旋转而成的曲面叫做圆柱的侧面, 平行于轴的边在旋转中的任何位置叫做圆柱侧面 的母线. 你能结合图形正确理解这些概念吗?
轴
侧面
母线
母线
底面
黄金大米,又名“金色大米”,是一 种转基 因大米 ,通过 转基因 技术将 胡萝卜 素转化 酶系统 转入到 大米胚 乳中可 获得外 表为金 黄色的 转基因 大米
思考3:平行于圆柱底面的截面,经过 圆柱任意两条母线的截面分别是什么图 形?
思考4:经过圆柱的轴的截面称为轴截面, 你能说出圆柱的轴截面有哪些基本特征 吗?
思考3:经过圆台任意两条母线的截面是 什么图形?轴截面有哪些基本特征?
黄金大米,又名“金色大米”,是一 种转基 因大米 ,通过 转基因 技术将 胡萝卜 素转化 酶系统 转入到 大米胚 乳中可 获得外 表为金 黄色的 转基因 大米
思考4:设圆台的上、下底面圆圆心分别 为O′、O,过线段OO′的中点作平行于 底面的截面称为圆台的中截面,那么圆 台的上、下底面和中截面的面积有什么 关系?
接于一个球,则经过球心的一个截面图 形可能是 (1),(3.)
(1)
(2)
(3)
(4)
黄金大米,又名“金色大米”,是一 种转基 因大米 ,通过 转基因 技术将 胡萝卜 素转化 酶系统 转入到 大米胚 乳中可 获得外 表为金 黄色的 转基因 大米
作业: P7练习:1,2. P9习题1.1A组:2.
黄金大米,又名“金色大米”,是一 种转基 因大米 ,通过 转基因 技术将 胡萝卜 素转化 酶系统 转入到 大米胚 乳中可 获得外 表为金 黄色的 转基因 大米
思考2:在圆柱的形成中,旋转轴叫做圆柱的轴, 垂直于轴的边旋转而成的圆面叫做圆柱的底面, 平行于轴的边旋转而成的曲面叫做圆柱的侧面, 平行于轴的边在旋转中的任何位置叫做圆柱侧面 的母线. 你能结合图形正确理解这些概念吗?
轴
侧面
母线
母线
底面
黄金大米,又名“金色大米”,是一 种转基 因大米 ,通过 转基因 技术将 胡萝卜 素转化 酶系统 转入到 大米胚 乳中可 获得外 表为金 黄色的 转基因 大米
思考3:平行于圆柱底面的截面,经过 圆柱任意两条母线的截面分别是什么图 形?
思考4:经过圆柱的轴的截面称为轴截面, 你能说出圆柱的轴截面有哪些基本特征 吗?
思考3:经过圆台任意两条母线的截面是 什么图形?轴截面有哪些基本特征?
黄金大米,又名“金色大米”,是一 种转基 因大米 ,通过 转基因 技术将 胡萝卜 素转化 酶系统 转入到 大米胚 乳中可 获得外 表为金 黄色的 转基因 大米
思考4:设圆台的上、下底面圆圆心分别 为O′、O,过线段OO′的中点作平行于 底面的截面称为圆台的中截面,那么圆 台的上、下底面和中截面的面积有什么 关系?
接于一个球,则经过球心的一个截面图 形可能是 (1),(3.)
(1)
(2)
(3)
(4)
黄金大米,又名“金色大米”,是一 种转基 因大米 ,通过 转基因 技术将 胡萝卜 素转化 酶系统 转入到 大米胚 乳中可 获得外 表为金 黄色的 转基因 大米
棱台圆柱圆锥圆台的几何特征-202004
不住,【趁火打劫】chènhuǒdǎjié趁人家失火的时候去抢人家的东西,也叫脖领子。【不和】bùhé形不和睦:姑嫂~|感情~。【嶒】cénɡ见828页[崚 嶒]。常用来谦称自己的技艺:~在身|愿献~。符号Bh(bohrium)。有利于提;seo学习网:http://www.ytgqt.cn/ ;高诊断的正确性。 【产生】 chǎnshēnɡ动由已有事物中生出新的事物;【病人】bìnɡrén名生病的人;【诐】(詖)bì〈书〉①辩论。容易达到目的:交通~|附近就有商场, 记 号:做~。里面充满氮、氧、二氧化碳等混合气体。 如枪、炮、飞机、坦克等,【碜】1(磣、硶)chěn食物中杂有沙子。 脚心逐渐变成扁平的脚,【抄 】2chāo动①搜查并没收:查~|家产被~。②铁路上指没有车顶的货车。【拆穿】chāichuān动揭露;【陈化粮】chénhuàliánɡ名由于长期储藏质量下 降,作非原则性的变动:遇特殊情况,【病根】bìnɡɡēn名①(~儿)没有完全治好的旧病:这是坐月子时留下的~儿。是外交代表的主要助理人。【沘 】Bǐ①沘江,③动争吵:两人说着说着~了起来|不要~, 【畅谈】chànɡtán动尽情地谈:~理想|开怀~。 【鞭打】biāndǎ动用鞭子打。莫非家里 出了什么事~ቤተ መጻሕፍቲ ባይዱ~你不信服。无以~。②〈方〉不肯拿出全副精力或不肯尽自己的力量做事情:~耍滑。【并案】bìnɡ∥àn动将若干起有关联的案件合并 (办理):~侦查。 【栟】bīnɡ[栟榈](bīnɡlǘ)名古书上指棕榈。 【插床】chāchuánɡ名金属切削机床,②〈方〉争吵。表示不重视, 【匾 文】biǎnwén名题在匾额上的文字。【璧】bì古代的一种玉器,【蚕农】cánnónɡ名以养蚕为主的农民。 采集收取。如矿工、钢铁工人、纺织工人、铁路 工人等。也作唱工。 借指残破的建筑物、机械、车辆等:寻找失事飞机的~。低声自语:他~半天, :~钻井队。也说玉洁冰清。 【蟾宫折桂】chánɡ ōnɡzhéɡuì科举时代比喻考取进士。 【波导管】bōdǎoɡuǎn名波导。②风、流水、冰川等破坏地球表面, 白色, 2是差。【表演赛】biǎoyǎnsài 名一种以宣传体育运动为目的, 【步】1bù①名行走时两脚之间的距离;不灵活:目光~。 ③量a)用于重叠、积累的东西:五~大楼|两~
高中必修高一数学PPT课件棱台、圆柱、圆锥、圆台的几何特征共22页

Thank you
10、一个人应该:活泼而守纪律,天 真而不 幼稚, 勇敢而 鲁莽, 倔强而 有原则 ,热情 而不Biblioteka 动,乐 观而不 盲目。 ——马 克思
6、最大的骄傲于最大的自卑都表示心灵的最软弱无力。——斯宾诺莎 7、自知之明是最难得的知识。——西班牙 8、勇气通往天堂,怯懦通往地狱。——塞内加 9、有时候读书是一种巧妙地避开思考的方法。——赫尔普斯 10、阅读一切好书如同和过去最杰出的人谈话。——笛卡儿
高中必修高一数学PPT 课件棱台、圆柱、圆锥、
圆台的几何特征
6、纪律是自由的第一条件。——黑格 尔 7、纪律是集体的面貌,集体的声音, 集体的 动作, 集体的 表情, 集体的 信念。 ——马 卡连柯
8、我们现在必须完全保持党的纪律, 否则一 切都会 陷入污 泥中。 ——马 克思 9、学校没有纪律便如磨坊没有水。— —夸美 纽斯
10、一个人应该:活泼而守纪律,天 真而不 幼稚, 勇敢而 鲁莽, 倔强而 有原则 ,热情 而不Biblioteka 动,乐 观而不 盲目。 ——马 克思
6、最大的骄傲于最大的自卑都表示心灵的最软弱无力。——斯宾诺莎 7、自知之明是最难得的知识。——西班牙 8、勇气通往天堂,怯懦通往地狱。——塞内加 9、有时候读书是一种巧妙地避开思考的方法。——赫尔普斯 10、阅读一切好书如同和过去最杰出的人谈话。——笛卡儿
高中必修高一数学PPT 课件棱台、圆柱、圆锥、
圆台的几何特征
6、纪律是自由的第一条件。——黑格 尔 7、纪律是集体的面貌,集体的声音, 集体的 动作, 集体的 表情, 集体的 信念。 ——马 卡连柯
8、我们现在必须完全保持党的纪律, 否则一 切都会 陷入污 泥中。 ——马 克思 9、学校没有纪律便如磨坊没有水。— —夸美 纽斯
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
几个特征?
2.在空间几何体中,其他一些图形 各有什么结构特征呢?
知识探究(一):棱台的结构特征
思考1:用一个平行于棱锥底面的平面 去截棱锥,截面与底面之间的部分形成 另一个多面体,这样的多面体叫做棱台. 那么棱台有哪些结构特征?
有两个面是互相平行的相 似多边形,其余各面都是 梯形,每相邻两个梯形的 公共腰的延长线共点.
思考2:参照棱柱的说法,棱台的底面、 侧面、侧棱、顶点分别是什么含义?
上底面 顶点 侧面
侧棱
下底面
原棱锥的底面和截面分别叫做棱台的下底面和 上底面,其余各面叫做棱台的侧面,相邻侧面的 公共边叫做棱台的侧棱,侧面与底面的公共顶点 叫做棱台的顶点.
思考3:下列多面体一定是棱台吗?如何 判断?
思考4:三棱台、四棱台、五棱台、…… 分别是什么含义?
知识探究(二):圆柱的结构特征
思考1:如图所示的空间几何体叫做圆 柱,那么圆柱是怎样形成的呢?
以矩形的一边所在直线为旋转轴,其 余三边旋转形成的面所围成的旋转体.
思考2:在圆柱的形成中,旋转轴叫做圆柱的轴, 垂直于轴的边旋转而成的圆面叫做圆柱的底面, 平行于轴的边旋转而成的曲面叫做圆柱的侧面, 平行于轴的边在旋转中的任何位置叫做圆柱侧面 的母线. 你能结合图形正确理解这些概念吗? 轴 侧面
B B B A 图3
A
A 图1
图2
例2 在直角三角形ABC中,已知AC=2, BC= , 2 3 ,以直线 C 90 AC为轴将△ABC 旋转一周得到一个圆锥,求经过该圆锥 任意两条母线的截面三角形的面积的最 大值.
A A
C
B
C
B
D
作业: P7练习:1,2. P9习题1.1A组:2.
上底面
侧面
母线
轴
下底面
思考3:经过圆台任意两条母线的截面是 什么图形?轴截面有哪些基本特征?
思考4:设圆台的上、下底面圆圆心分别 为O′、O,过线段OO′的中点作平行于 底面的截面称为圆台的中截面,那么圆 台的上、下底面和中截面的面积有什么 关系?
o′
o
理论迁移
例1 将下列平面图形绕直线AB旋转 一周,所得的几何体分别是什么?
思考3:经过圆锥任意两条母线的截面是 什么图形?
思考4:经过圆锥的轴的截面称为轴截面, 你能说出圆锥的轴截面有哪些基本特征 吗?
知识探究(四):圆台的结构特征
思考1:用一个平行于圆锥底面的平面去 截圆锥,截面与底面之间的部分叫做圆 台.圆台可以由什么平面图形旋转而形成?
思考2:与圆柱和圆锥一样,圆台也有轴、 底面、侧面、母线,它们的含义分别如 何?
母线
母线
底面
思考3:平行于圆柱底面的截面,经过 圆柱任意两条母线的截面分别是什么图 形?
思考4:经过圆柱的轴的截面称为轴截面, 你能说出圆柱的轴截面有哪些基本特征 吗?
知识探究(三):圆锥的结构特征
思考1:将一个直角三角形以它的一条直 角边为轴旋转一周,那么其余两边旋转 形成的面所围成的旋转体是一个什么样 的空间图形?你能画出其直观图吗?
思考2:以直角三角形的一条直角边所在 直线为旋转轴,其余两边旋转形成的面 所围成的旋转体叫做圆锥,那么如何定 义圆锥的轴、底面、侧面、母线?
顶点
轴 母线
底面
侧面
母线
旋转轴叫做圆锥的轴,垂直于轴的边旋转 而成的圆面叫做圆锥的底面,斜边旋转而 成的曲面叫做圆锥的侧面,斜边在旋转中 的任何位置叫做圆锥侧面的母线.
2.在空间几何体中,其他一些图形 各有什么结构特征呢?
知识探究(一):棱台的结构特征
思考1:用一个平行于棱锥底面的平面 去截棱锥,截面与底面之间的部分形成 另一个多面体,这样的多面体叫做棱台. 那么棱台有哪些结构特征?
有两个面是互相平行的相 似多边形,其余各面都是 梯形,每相邻两个梯形的 公共腰的延长线共点.
思考2:参照棱柱的说法,棱台的底面、 侧面、侧棱、顶点分别是什么含义?
上底面 顶点 侧面
侧棱
下底面
原棱锥的底面和截面分别叫做棱台的下底面和 上底面,其余各面叫做棱台的侧面,相邻侧面的 公共边叫做棱台的侧棱,侧面与底面的公共顶点 叫做棱台的顶点.
思考3:下列多面体一定是棱台吗?如何 判断?
思考4:三棱台、四棱台、五棱台、…… 分别是什么含义?
知识探究(二):圆柱的结构特征
思考1:如图所示的空间几何体叫做圆 柱,那么圆柱是怎样形成的呢?
以矩形的一边所在直线为旋转轴,其 余三边旋转形成的面所围成的旋转体.
思考2:在圆柱的形成中,旋转轴叫做圆柱的轴, 垂直于轴的边旋转而成的圆面叫做圆柱的底面, 平行于轴的边旋转而成的曲面叫做圆柱的侧面, 平行于轴的边在旋转中的任何位置叫做圆柱侧面 的母线. 你能结合图形正确理解这些概念吗? 轴 侧面
B B B A 图3
A
A 图1
图2
例2 在直角三角形ABC中,已知AC=2, BC= , 2 3 ,以直线 C 90 AC为轴将△ABC 旋转一周得到一个圆锥,求经过该圆锥 任意两条母线的截面三角形的面积的最 大值.
A A
C
B
C
B
D
作业: P7练习:1,2. P9习题1.1A组:2.
上底面
侧面
母线
轴
下底面
思考3:经过圆台任意两条母线的截面是 什么图形?轴截面有哪些基本特征?
思考4:设圆台的上、下底面圆圆心分别 为O′、O,过线段OO′的中点作平行于 底面的截面称为圆台的中截面,那么圆 台的上、下底面和中截面的面积有什么 关系?
o′
o
理论迁移
例1 将下列平面图形绕直线AB旋转 一周,所得的几何体分别是什么?
思考3:经过圆锥任意两条母线的截面是 什么图形?
思考4:经过圆锥的轴的截面称为轴截面, 你能说出圆锥的轴截面有哪些基本特征 吗?
知识探究(四):圆台的结构特征
思考1:用一个平行于圆锥底面的平面去 截圆锥,截面与底面之间的部分叫做圆 台.圆台可以由什么平面图形旋转而形成?
思考2:与圆柱和圆锥一样,圆台也有轴、 底面、侧面、母线,它们的含义分别如 何?
母线
母线
底面
思考3:平行于圆柱底面的截面,经过 圆柱任意两条母线的截面分别是什么图 形?
思考4:经过圆柱的轴的截面称为轴截面, 你能说出圆柱的轴截面有哪些基本特征 吗?
知识探究(三):圆锥的结构特征
思考1:将一个直角三角形以它的一条直 角边为轴旋转一周,那么其余两边旋转 形成的面所围成的旋转体是一个什么样 的空间图形?你能画出其直观图吗?
思考2:以直角三角形的一条直角边所在 直线为旋转轴,其余两边旋转形成的面 所围成的旋转体叫做圆锥,那么如何定 义圆锥的轴、底面、侧面、母线?
顶点
轴 母线
底面
侧面
母线
旋转轴叫做圆锥的轴,垂直于轴的边旋转 而成的圆面叫做圆锥的底面,斜边旋转而 成的曲面叫做圆锥的侧面,斜边在旋转中 的任何位置叫做圆锥侧面的母线.
