几何综合之多结论问题(通用版)

合集下载

2019届深圳中考复习《多结论几何综合题》专题试卷含解析

2017届中考复习多结论几何综合题专题试卷一、单选题1、如图，△ABC和△CDE均为等腰直角三角形，点B，C，D在一条直线上，点M是AE的中点，下列结论：①tan∠AEC=；②S△ABC+S△CDE≥S△ACE；③BM⊥DM；④BM=DM．正确结论的个数是（）A、1个B、2个C、3个D、4个2、如图，在Rt△ABC中，AB=AC，D、E是斜边BC上两点，且∠DAE=45°，将△ADC绕点A顺时针旋转90°后，得到△AFB，连接EF，下列结论：①△AED≌△AEF；②=;③△ABC的面积等于四边形AFBD的面积；④BE2+DC2=DE2⑤BE+DC=DE;其中正确的是( )A、①②④B、③④⑤C、①③④D、①③⑤3、如图，将等边△ABC沿射线BC向右平移到△DCE的位置，连接AD、BD ，则下列结论：①AD＝BC；②BD、AC互相平分；③四边形ACED是菱形；④BD⊥DE；其中正确的个数是（）.A、1B、2C、3D、44、如图，把一张长方形纸片ABCD沿对角线BD折叠，使C点落在E处，BE与AD相交于点F，下列结论：①BD=AD2+AB2；②△ABF≌△EDF；③＝④AD=BD•cos45°．其中正确的一组是（）A、①②B、②③C、①④D、③④5、如图，已知正方形ABCD的边长为4，点E、F分别在边AB、BC上，且AE=BF=1，CE、DF交于点O．下列结论：①∠DOC=90°，②OC=OE，③tan∠OCD= ，④S△ODC=S四边形BEOF中，正确的有（）A、1个B、2个C、3个D、4个6、如图，已知正方形ABCD的边长为12，BE=EC，将正方形边CD沿DE折叠到DF，延长EF交AB于G，连接DG，现在有如下4个结论：①△ADG≌△FDG；②GB=2AG；③△GDE∽△BEF；④S△BEF=．在以上4个结论中，正确的有（）A、1B、2C、3D、47、如图，▱ABCD的对角线AC、BD交于点O，AE平分∠BAD交BC于点E，且∠ADC=60°，AB=BC，连接OE．下列结论：①∠CAD=30°；②S▱ABCD=AB•AC；③OB=AB；④OE=BC，成立的个数有（）A、1个B、2个C、3个D、4个8、如图，AD是△ABC的角平分线，DE，DF分别是△ABD和△ACD的高，得到下列四个结论：①OA=OD；②AD⊥EF；③当∠A=90°时，四边形AEDF是正方形；④AE+DF=AF+DE．其中正确的是（）A、②③B、②④C、①③④D、②③④9、如图，G，E分别是正方形ABCD的边AB，BC的点，且AG=CE，AE⊥EF，AE=EF，现有如下结论：①BE=GE；②△AGE≌△ECF；③∠FCD=45°；④△GBE∽△ECH，其中，正确的结论有（）A、1个B、2个C、3个D、4个10、如图，PA=PB，OE⊥PA，OF⊥PB，则以下结论：①OP是∠APB的平分线；②PE=PF③CA=BD；④CD∥AB；其中正确的有（）个．A、4B、3C、2D、111、如图，在Rt△ABC中，AB=CB，BO⊥AC，把△ABC折叠，使AB落在AC上，点B与AC上的点E重合，展开后，折痕AD交BO于点F，连接DE、EF．下列结论：①tan∠ADB=2；②图中有4对全等三角形；③若将△DEF沿EF折叠，则点D不一定落在AC上；④BD=BF；⑤S四边形DFOE=S△AOF，上述结论中正确的个数是（）A、1个B、2个C、3个D、4个12、如图，将等边△ABC绕点C顺时针旋转120°得到△EDC，连接AD，BD．则下列结论：①AC=AD；②BD⊥AC；③四边形ACED是菱形．其中正确的个数是（）A、0B、1C、2D、313、如图，CB=CA，∠ACB=90°，点D在边BC上（与B、C不重合），四边形ADEF为正方形，过点F作FG⊥CA，交CA的延长线于点G，连接FB，交DE于点Q，给出以下结论：①AC=FG；②S△FAB：S四边形CBFG=1：2；③∠ABC=∠ABF；④AD2=FQ•AC，其中正确的结论的个数是（）A 、1B 、2C 、3D 、414、如图，矩形ABCD 中，O 为AC 中点，过点O 的直线分别与AB 、CD 交于点E 、F ，连结BF 交AC 于点M ，连结DE 、BO ．若∠COB=60°，FO=FC ，则下列结论：①FB 垂直平分OC ；②△EOB ≌△CMB ；③DE=EF ；④S △AOE ：S △BCM =2：3．其中正确结论的个数是（）A 、4个B 、3个C 、2个D 、1个15、（2016•攀枝花）如图，正方形纸片ABCD 中，对角线AC 、BD 交于点O ，折叠正方形纸片ABCD ，使AD 落在BD 上，点A 恰好与BD 上的点F 重合，展开后折痕DE 分别交AB 、AC 于点E 、G ，连结GF ，给出下列结论：①∠ADG=22.5°；②tan ∠AED=2；③S △AGD =S △OGD ；④四边形AEFG 是菱形；⑤BE=2OG ；⑥若S △OGF =1，则正方形ABCD 的面积是6+4 ，其中正确的结论个数为（）A 、2B 、3C 、4D 、516、如图，在正方形ABCD 中，E 、F 分别为BC 、CD 的中点，连接AE ，BF 交于点G ，将△BCF 沿BF 对折，得到△BPF ，延长FP 交BA 延长线于点Q ，下列结论正确的个数是（）①AE=BF ；②AE ⊥BF ；③sin ∠BQP= ；④S四边形ECFG=2S △BGE ．A 、4B 、3C 、2D 、117、如图所示，抛物线y=ax 2+bx+c （a≠0）与x 轴交于点A （﹣2，0）、B （1，0），直线x=﹣0.5与此抛物线交于点C ，与x 轴交于点M ，在直线上取点D ，使MD=MC ，连接AC 、BC 、AD 、BD ，某同学根据图象写出下列结论： ①a ﹣b=0；②当﹣2＜x ＜1时，y ＞0； ③四边形ACBD 是菱形； ④9a ﹣3b+c ＞你认为其中正确的是（）A、②③④B、①②④C、①③④D、①②③18、如图，正方形ABCD中，AB=6，点E在边CD上，且CE=2DE．将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连结AG、CF．下列结论：①△ABG≌△AFG；②BG=GC；③EG=DE+BG；④AG∥CF；⑤S△FGC=3.6．其中正确结论的个数是（）A、2B、3C、4D、519、如图，AB是⊙O的直径，弦CD⊥AB于点G，点F是CD上一点，且满足= ，连接AF并延长交⊙O于点E，连接AD，DE，若CF=2，AF=3，给出下列结论：①△ADF∽△AED；②FG=2；③tanE= ；④S△DEF=4 ，其中正确的是（）A、①②③B、②③④C、①②④D、①③④20、如图，在⊙O中，AB是直径，点D是⊙O上一点，点C是弧AD的中点，弦CE⊥AB于点E，过点D的切线交EC的延长线于点G，连接AD，分别交CE、CB 于点P、Q，连接AC，给出下列结论：①∠DAC=∠ABC；②AD=CB；③点P是△ACQ的外心；④AC2=AE•AB；⑤CB∥GD，其中正确的结论是（）A、①③⑤B、②④⑤C、①②⑤D、①③④答案解析部分一、单选题1、【答案】D【考点】等腰三角形的性质，梯形中位线定理，锐角三角函数的定义【解析】【分析】①根据等腰直角三角形的性质及△ABC∽△CDE的对应边成比例知，；然后由直角三角形中的正切函数，得tan∠AEC=，再由等量代换求得tan∠AEC=；②由三角形的面积公式、梯形的面积公式及不等式的基本性质a2+b2≥2ab（a=b时取等号)解答；③、④通过作辅助线MN，构建直角梯形的中位线，根据梯形的中位线定理及等腰直角三角形的判定定理解答．【解答】解：∵△ABC和△CDE均为等腰直角三角形，∴AB=BC，CD=DE，∴∠BAC=∠BCA=∠DCE=∠DEC=45°，∴∠ACE=90°；∵△ABC∽△CDE∴①∴tan∠AEC=，∴tan∠AEC=；故本选项正确；②∵S△ABC=a2，S△CDE=b2，S梯形ABDE=（a+b)2，∴S△ACE=S梯形ABDE-S△ABC-S△CDE=ab，S△ABC+S△CDE=（a2+b2)≥ab（a=b时取等号)，∴S△ABC+S△CDE≥S△ACE；故本选项正确；④过点M作MN垂直于BD，垂足为N．∵点M是AE的中点，则MN为梯形中位线，∴N为中点，∴△BMD为等腰三角形，∴BM=DM；故本选项正确；③又MN=（AB+ED)=（BC+CD)，∴∠BMD=90°，即BM⊥DM；故本选项正确．故选D．【点评】本题综合考查了等腰直角三角形的判定与性质、梯形的中位线定理、锐角三角函数的定义等知识点．在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边．2、【答案】C【考点】全等三角形的判定，勾股定理，相似三角形的判定，旋转的性质【解析】【分析】①根据旋转的性质知∠CAD=∠BAF，AD=AF，因为∠BAC=90°，∠DAE=45°，所以∠CAD+∠BAE=45°，可得∠EAF=45°=∠DAE，由此即可证明△AEF≌△AED；②当△ABE∽△ACD时，该比例式成立；③根据旋转的性质，△ADC≌△ABF，进而得出△ABC的面积等于四边形AFBD 的面积；④据①知BF=CD，EF=DE，∠FBE=90°，根据勾股定理判断．⑤根据①知道△AEF≌△AED，得CD=BF，DE=EF；由此即可确定该说法是否正确；【解答】①根据旋转的性质知∠CAD=∠BAF，AD=AF，∵∠BAC=90°，∠DAE=45°，∴∠CAD+∠BAE=45°．∴∠EAF=45°，∴△AED≌△AEF；故本选项正确；②∵AB=AC，∴∠ABE=∠ACD；∴当∠BAE=∠CAD时，△ABE∽△ACD，∴=；当∠BAE≠∠CAD时，△ABE与△ACD不相似，即≠；∴此比例式不一定成立；故本选项错误；③根据旋转的性质知△ADC≌△AFB，∴S△ABC=S△ABD+S△ABF=S四边形AFBD，即三角形ABC的面积等于四边形AFBD的面积；故本选项正确；④∵∠FBE=45°+45°=90°，∴BE2+BF2=EF2，∵△ADC绕点A顺时针旋转90°后，得到△AFB，∴△AFB≌△ADC，∴BF=CD，又∵EF=DE，∴BE2+DC2=DE2，故本选项正确；⑤根据①知道△AEF≌△AED，得CD=BF，DE=EF，∴BE+DC=BE+BF＞DE=EF，即BE+DC＞DE，故本选项错误；综上所述，正确的说法是①③④；故选C．【点评】此题主要考查了图形的旋转变换以及全等三角形的判定等知识，解题时注意旋转前后对应的相等关系．3、【答案】D【考点】等边三角形的性质，菱形的判定与性质，平移的性质【解析】【解答】∵△ABC、△DCE是等边三角形，∴∠ACB＝∠DCE＝60°，AC ＝CD ，∴∠ACD＝180°－∠ACB－∠DCE＝60°，∴△ACD是等边三角形，∴AD＝AC＝BC ，故①正确；由①可得AD＝BC ，∵AB＝CD ，∴四边形ABCD是平行四边形，∴BD、AC互相平分，故②正确；由①可得AD＝AC＝CE＝DE ，故四边形ACED是菱形，即③正确；∵四边形ACED是菱形，∴AC⊥BD ，∵AC∥DE ，∴∠BDE＝∠COD＝90°，∴BD⊥DE ，故④正确；综上可得①②③④正确，共4个，故选D．【分析】先求出∠ACD＝60°，继而可判断△ACD是等边三角形，从而可判断①是正确的；根据①的结论，可判断四边形ABCD是平行四边形，从而可判断②是正确的；根据①的结论，可判断③正确；根据菱形的对角线互相垂直可得AC⊥BD ，再根据平移后对应线段互相平行可得∠BDE＝∠COD＝90°，进而判断④正确．4、【答案】B【考点】勾股定理，翻折变换（折叠问题），相似三角形的判定与性质，特殊角的三角函数值【解析】【解答】①∵△ABD为直角三角形，∴BD2=AD2+AB2，不是BD=AD2+AB2，故说法错误；②根据折叠可知：DE=CD=AB，∠A=∠E，∠AFB=∠EFD，∴△ABF≌△EDF，故说法正确；③根据②可以得到△ABF∽△EDF，∴＝，故说法正确；④在Rt△ABD中，∠ADB≠45°，∴AD≠BD•cos45°，故说法错误．所以正确的是②③．故选B．【分析】①直接根据勾股定理即可判定是否正确；②利用折叠可以得到全等条件证明△ABF≌△EDF；③利用全等三角形的性质即可解决问题；④在Rt△ABD中利用三角函数的定义即可判定是否正确．此题主要考查了折叠问题，也考查了勾股定理、相似三角形的性质、全等三角形的性质及三角函数的定义，它们的综合性比较强，对于学生的综合能力要求比较高，平时加强训练．5、【答案】C【考点】全等三角形的判定与性质，勾股定理，正方形的性质，锐角三角函数的定义【解析】【解答】解：∵正方形ABCD的边长为4，∴BC=CD=4，∠B=∠DCF=90°，∵AE=BF=1，∴BE=CF=4﹣1=3，在△EBC和△FCD中，∴△EBC≌△FCD（SAS），∴∠CFD=∠BEC，∴∠BCE+∠BEC=∠BCE+∠CFD=90°，∴∠DOC=90°；故①正确；若OC=OE，∵DF⊥EC，∴CD=DE，∵CD=AD＜DE（矛盾），故②错误；∵∠OCD+∠CDF=90°，∠CDF+∠DFC=90°，∴∠OCD=∠DFC，∴tan∠OCD=tan∠DFC= = ，故③正确；∵△EBC≌△FCD，∴S△EBC=S△FCD，∴S△EBC﹣S△FOC=S△FCD﹣S△FOC，即S△ODC=S四边形BEOF．故④正确．故选C．【分析】由正方形ABCD的边长为4，AE=BF=1，利用SAS易证得△EBC≌△FCD，然后全等三角形的对应角相等，易证得①∠DOC=90°正确；②由线段垂直平分线的性质与正方形的性质，可得②错误；易证得∠OCD=∠DFC，即可求得③正确；由①易证得④正确．6、【答案】C【考点】全等三角形的判定与性质，正方形的性质，翻折变换（折叠问题），相似三角形的判定与性质【解析】【解答】由折叠可知，DF=DC=DA，∠DFE=∠C=90°，∴∠DFG=∠A=90°，∴△ADG≌△FDG，①正确；∵正方形边长是12，∴BE=EC=EF=6，设AG=FG=x，则EG=x+6，BG=12﹣x，由勾股定理得：EG2=BE2+BG2，即：（x+6）2=62+（12﹣x）2，解得：x=4∴AG=GF=4，BG=8，BG=2AG，②正确；BE=EF=6，△BEF是等腰三角形，易知△GED不是等腰三角形，③错误；S△GBE=×6×8=24，S△BEF=•S△GBE==，④正确．故选：C．【分析】根据正方形的性质和折叠的性质可得AD=DF，∠A=∠GFD=90°，于是根据“HL”判定△ADG≌△FDG，再由GF+GB=GA+GB=12，EB=EF，△BGE为直角三角形，可通过勾股定理列方程求出AG=4，BG=8，进而求出△BEF的面积，再抓住△BEF是等腰三角形，而△GED显然不是等腰三角形，判断③是错误的．7、【答案】C【考点】等边三角形的判定与性质，含30度角的直角三角形，平行四边形的性质【解析】【解答】∵四边形ABCD是平行四边形，∴∠ABC=∠ADC=60°，∠BAD=120°，∵AE平分∠BAD，∴∠BAE=∠EAD=60°∴△ABE是等边三角形，∴AE=AB=BE，∵AB=BC，∴AE=BC，∴∠BAC=90°，∴∠CAD=30°，故①正确；∵AC⊥AB，∴S▱ABCD=AB•AC，故②正确，∵AB=BC，OB=BD，∵BD＞BC，∴AB≠OB，故③错误；∵CE=BE，CO=OA，∴OE=AB，∴OE=BC，故④正确．故选：C．【分析】由四边形ABCD是平行四边形，得到∠ABC=∠ADC=60°，∠BAD=120°，根据AE平分∠BAD，得到∠BAE=∠EAD=60°推出△ABE是等边三角形，由于AB=BC，得到AE=BC，得到△ABC是直角三角形，于是得到∠CAD=30°，故①正确；由于AC⊥AB，得到S▱ABCD=AB•AC，故②正确，根据AB=BC，OB=BD，且BD＞BC，得到AB≠OB，故③错误；根据三角形的中位线定理得到OE=AB，于是得到OE=BC，故④正确．8、【答案】D【考点】全等三角形的判定与性质，角平分线的性质，正方形的判定【解析】【解答】如果OA=OD，则四边形AEDF是矩形，∠A=90°，不符合题意，∴①不正确；∵AD是△ABC的角平分线，∴∠EAD∠FAD，在△AED和△AFD 中，∴△AED≌△AFD（AAS），∴AE=AF，DE=DF，∴AE+DF=AF+DE，∴④正确；在△AEO和△AFO中，，∴△AE0≌△AF0（SAS），∴EO=FO，又∵AE=AF，∴AO是EF的中垂线，∴AD⊥EF，∴②正确；∵当∠A=90°时，四边形AEDF的四个角都是直角，∴四边形AEDF是矩形，又∵DE=DF，∴四边形AEDF是正方形，∴③正确．综上，可得正确的是：②③④．故选：D．【分析】①如果OA=OD，则四边形AEDF是矩形，∠A=90°，不符合题意，所以①不正确．②首先根据全等三角形的判定方法，判断出△AED≌△AFD，AE=AF，DE=DF；然后根据全等三角形的判定方法，判断出△AE0≌△AFO，即可判断出AD⊥EF．③首先判断出当∠A=90°时，四边形AEDF的四个角都是直角，四边形AEDF是矩形，然后根据DE=DF，判断出四边形AEDF是正方形即可．④根据△AED≌△AFD，判断出AE=AF，DE=DF，即可判断出AE+DF=AF+DE成立，据此解答即可．9、【答案】B【考点】全等三角形的判定与性质，正方形的性质，相似三角形的判定与性质【解析】【解答】∵四边形ABCD是正方形，∴∠B=∠DCB=90°，AB=BC，∵AG=CE，∴BG=BE，由勾股定理得：BE=GE，∴①错误；∵BG=BE，∠B=90°，∴∠BGE=∠BEG=45°，∴∠AGE=135°，∴∠GAE+∠AEG=45°，∵AE⊥EF，∴∠AEF=90°，∵∠BEG=45°，∴∠AEG+∠FEC=45°，∴∠GAE=∠FEC，在△GAE和△CEF中∴△GAE≌△CEF，∴②正确；∴∠AGE=∠ECF=135°，∴∠FCD=135°﹣90°=45°，∴③正确；∵∠BGE=∠BEG=45°，∠AEG+∠FEC=45°，∴∠FEC＜45°，∴△GBE和△ECH不相似，∴④错误；即正确的有2个．故选B．【分析】根据正方形的性质得出∠B=∠DCB=90°，AB=BC，求出BG=BE ，根据勾股定理得出BE=GE，即可判断①；求出∠GAE+∠AEG=45°，推出∠GAE=∠FEC，根据SAS推出△GAE≌△CEF，即可判断②；求出∠AGE=∠ECF=135°，即可判断③；求出∠FEC＜45°，根据相似三角形的判定得出△GBE和△ECH不相似，即可判断④．10、【答案】A【考点】全等三角形的判定与性质，圆心角、弧、弦的关系，相似三角形的判定与性质【解析】【解答】连接OP、OC、OA、OD、OB、CD、AB．∵PC•PA=PD•PB（相交弦定理），PA=PB（已知），∴PC=PD，∴AC=BD；在△AOC和△BOD中，∵∠AOC=∠BOD（等弦对等角），OA=OB（半径），OD=OC（半径），∴△AOC≌△BOD，∴③CA=BD；OE=OF；又∵OE⊥PA，OF⊥PB，∴①OP是∠APB的平分线；∴②PE=PF；在△PCD和△PAB中，PC：PA=PD：PB，∠DPC=∠BPA，∴△PCD∽△PAB，∴∠PDC=PBA，∴④CD∥AB；综上所述，①②③④均正确，故答案选A．【分析】①通过证明△AOC≌△BOD，再根据全等三角形的对应高相等求得OE=OF；再根据角平分线的性质证明OP是∠APB的平分线；②由角平分线的性质证明PE=PF；③通过证明△AOC≌△BOD，再根据全等三角形的对应边相等求得CA=BD；④通过证明△PCD∽△PAB，再根据相似三角形的性质对应角相等证得∠PDC=PBA；然后由平行线的判定得出结论CD∥AB．11、【答案】C【考点】全等三角形的判定与性质，翻折变换（折叠问题），锐角三角函数的定义【解析】【解答】①由折叠可得BD=DE，而DC＞DE，∴DC＞BD，∴tan∠ADB≠2，故①错误；②图中的全等三角形有△ABF≌△AEF，△ABD≌△AED，△FBD≌△FED，（由折叠可知) ∵OB⊥AC，∴∠AOB=∠COB=90°，在Rt△AOB和Rt△COB中，AB="CB" ,BO=BO ，∴Rt△AOB≌Rt△COB（HL)，则全等三角形共有4对，故②正确；③∵AB=CB，BO⊥AC，把△ABC折叠，∴∠ABO=∠CBO=45°，∠FBD=∠DEF，∴∠AEF=∠DEF=45°，∴将△DEF沿EF折叠，可得点D一定在AC上，故③错误；④∵OB⊥AC，且AB=CB，∴BO为∠ABC的平分线，即∠ABO=∠OBC=45°，由折叠可知，AD是∠BAC的平分线，即∠BAF=22.5°，又∵∠BFD为三角形ABF的外角，∴∠BFD=∠ABO+∠BAF=67.5°，易得∠BDF=180°-45°-67.5°=67.5°，∴∠BFD=∠BDF，∴BD=BF，故④正确；⑤连接CF，∵△AOF和△COF等底同高，∴S△AOF=S△COF，∵∠AEF=∠ACD=45°，∴EF∥CD，∴S△EFD=S△EFC，∴S四边形DFOE=S△COF，∴S四边形DFOE=S△AOF，故⑤正确；故正确的有3个．故选C．12、【答案】D【考点】等边三角形的性质，菱形的判定，旋转的性质【解析】【解答】解：∵将等边△ABC绕点C顺时针旋转120°得到△EDC，∴∠ACE=120°，∠DCE=∠BCA=60°，AC=CD=DE=CE，∴∠ACD=120°﹣60°=60°，∴△ACD是等边三角形，∴AC=AD，AC=AD=DE=CE，∴四边形ACED是菱形，∵将等边△ABC绕点C顺时针旋转120°得到△EDC，AC=AD，∴AB=BC=CD=AD，∴四边形ABCD是菱形，∴BD⊥AC，∴①②③都正确，故选D．【分析】根据旋转和等边三角形的性质得出∠ACE=120°，∠DCE=∠BCA=60°，AC=CD=DE=CE，求出△ACD是等边三角形，求出AD=AC，根据菱形的判定得出四边形ABCD和ACED都是菱形，根据菱形的判定推出AC⊥BD．本题考查了旋转的性质，菱形的性质和判定，等边三角形的性质和判定的应用，能灵活运用知识点进行推理是解此题的关键．13、【答案】D【考点】全等三角形的判定与性质，矩形的判定与性质，正方形的性质，相似三角形的判定与性质，等腰直角三角形【解析】【解答】解：∵四边形ADEF为正方形，∴∠FAD=90°，AD=AF=EF，∴∠CAD+∠FAG=90°，∵FG⊥CA，∴∠C=90°=∠ACB，∴∠CAD=∠AFG，在△FGA和△ACD中，，∴△FGA≌△ACD（AAS），∴AC=FG，①正确；∵BC=AC，∴FG=BC，∵∠ACB=90°，FG⊥CA，∴FG∥BC，∴四边形CBFG是矩形，∴∠CBF=90°，S△FAB= FB•FG= S四边形CBFG，②正确；∵CA=CB，∠C=∠CBF=90°，∴∠ABC=∠ABF=45°，③正确；∵∠FQE=∠DQB=∠ADC，∠E=∠C=90°，∴△ACD∽△FEQ，∴AC：AD=FE：FQ，∴AD•FE=AD2=FQ•AC，④正确；故选：D．【分析】本题考查了相似三角形的判定与性质、全等三角形的判定与性质、正方形的性质、矩形的判定与性质、等腰直角三角形的性质；熟练掌握正方形的性质，证明三角形全等和三角形相似是解决问题的关键．由正方形的性质得出∠FAD=90°，AD=AF=EF，证出∠CAD=∠AFG，由AAS证明△FGA≌△ACD，得出AC=FG，①正确；证明四边形CBFG是矩形，得出S△FAB= FB•FG= S四边形CEFG，②正确；由等腰直角三角形的性质和矩形的性质得出∠ABC=∠ABF=45°，③正确；证出△ACD∽△FEQ，得出对应边成比例，得出D•FE=AD2=FQ•AC，④正确．14、【答案】B【考点】全等三角形的判定与性质，线段垂直平分线的性质，等腰三角形的性质，矩形的性质【解析】【解答】解：①∵矩形ABCD中，O为AC中点，∴OB=OC，∵∠COB=60°，∴△OBC是等边三角形，∴OB=BC，∵FO=FC，∴FB垂直平分OC，故①正确；②∵FB垂直平分OC，∴△CMB≌△OMB，∵OA=OC，∠FOC=∠EOA，∠DCO=∠BAO，∴△FOC≌△EOA，∴FO=EO，易得OB⊥EF，∴△OMB≌△OEB，∴△EOB≌△CMB，故②正确；③由△OMB≌△OEB≌△CMB得∠1=∠2=∠3=30°，BF=BE，∴△BEF是等边三角形，∴BF=EF，∵DF∥BE且DF=BE，∴四边形DEBF是平行四边形，∴DE=BF，∴DE=EF，故③正确；④在直角△BOE中∵∠3=30°，∴BE=2OE，∵∠OAE=∠AOE=30°，∴AE=OE，∴BE=2AE，∴S△AOE：S△BCM=S△AOE：S△BOE=1：2，故④错误；所以其中正确结论的个数为3个；故选B【分析】①利用线段垂直平分线的性质的逆定理可得结论；②证△OMB≌△OEB得△EOB≌△CMB；③先证△BEF是等边三角形得出BF=EF，再证▱DEBF得出DE=BF，所以得DE=EF；④由②可知△BCM≌△BEO，则面积相等，△AOE和△BEO属于等高的两个三角形，其面积比就等于两底的比，即S△AOE：S△BOE=AE：BE，由直角三角形30°角所对的直角边是斜边的一半得出BE=2OE=2AE，得出结论S△AOE：S△BOE=AE：BE=1：2．本题综合性比较强，既考查了矩形的性质、等腰三角形的性质，又考查了全等三角形的性质和判定，及线段垂直平分线的性质，内容虽多，但不复杂；看似一个选择题，其实相当于四个证明题，属于常考题型．15、【答案】B【考点】菱形的判定与性质，翻折变换（折叠问题），等腰直角三角形【解析】【解答】解：∵四边形ABCD是正方形，∴∠GAD=∠ADO=45°，由折叠的性质可得：∠ADG= ∠ADO=22.5°，故①正确．∵由折叠的性质可得：AE=EF，∠EFD=∠EAD=90°，∴AE=EF＜BE，∴AE＜AB，∴＞2，故②错误．∵∠AOB=90°，∴AG=FG＞OG，△AGD与△OGD同高，∴S△AGD＞S△OGD，故③错误．∵∠EFD=∠AOF=90°，∴EF∥AC，∴∠FEG=∠AGE，∵∠AGE=∠FGE，∴∠FEG=∠FGE，∴EF=GF，∵AE=EF，∴AE=GF，故④正确．∵AE=EF=GF，AG=GF，∴AE=EF=GF=AG，∴四边形AEFG是菱形，∴∠OGF=∠OAB=45°，∴EF=GF= OG，∴BE= EF= ×OG=2OG．故⑤正确．∵四边形AEFG是菱形，∴AB∥GF，AB=GF．∵∠BAO=45°，∠GOF=90°，∴△OGF时等腰直角三角形．∵S△OGF=1，∴OG2=1，解得OG= ，∴BE=2OG=2 ，GF= ==2，∴AE=GF=2，∴AB=BE+AE=2 +2，∴S正方形ABCD=AB2=（2 +2）2=12+8 ，故⑥错误．∴其中正确结论的序号是：①④⑤．故选B．【分析】①由四边形ABCD是正方形，可得∠GAD=∠ADO=45°，又由折叠的性质，可求得∠ADG的度数；②由AE=EF＜BE，可得AD＞2AE；③由AG=GF＞OG，可得△AGD的面积＞△OGD的面积；④由折叠的性质与平行线的性质，易得△EFG是等腰三角形，即可证得AE=GF；⑤易证得四边形AEFG是菱形，由等腰直角三角形的性质，即可得BE=2OG；⑥根据四边形AEFG是菱形可知AB∥GF，AB=GF，再由∠BAO=45°，∠GOF=90°可得出△OGF时等腰直角三角形，由S△OGF=1求出GF的长，进而可得出BE及AE的长，利用正方形的面积公式可得出结论．此题考查的是四边形综合题，涉及到正方形的性质、折叠的性质、等腰直角三角形的性质以及菱形的判定与性质等知识．此题综合性较强，难度较大，注意掌握折叠前后图形的对应关系，注意数形结合思想的应用．16、【答案】B【考点】全等三角形的判定与性质，正方形的性质，翻折变换（折叠问题），相似三角形的判定与性质【解析】【解答】解：∵E，F分别是正方形ABCD边BC，CD的中点，∴CF=BE，在△ABE和△BCF中，，∴Rt△ABE≌Rt△BCF（SAS），∴∠BAE=∠CBF，AE=BF，故①正确；又∵∠BAE+∠BEA=90°，∴∠CBF+∠BEA=90°，∴∠BGE=90°，∴AE⊥BF，故②正确；根据题意得，FP=FC，∠PFB=∠BFC，∠FPB=90°∵CD∥AB，∴∠CFB=∠ABF，∴∠ABF=∠PFB，∴QF=QB，令PF=k（k＞0），则PB=2k在Rt△BPQ中，设QB=x，∴x2=（x﹣k）2+4k2，∴x= ，∴sin=∠BQP= = ，故③正确；∵∠BGE=∠BCF，∠GBE=∠CBF，∴△BGE∽△BCF，∵BE= BC，BF= BC，∴BE：BF=1：，∴△BGE的面积：△BCF的面积=1：5，∴S四边形ECFG=4S△BGE，故④错误．故选：B．【分析】首先证明△ABE≌△BCF，再利用角的关系求得∠BGE=90°，即可得到①AE=BF；②AE⊥BF；△BCF沿BF对折，得到△BPF，利用角的关系求出QF=QB，解出BP，QB，根据正弦的定义即可求解；根据AA可证△BGE与△BCF相似，进一步得到相似比，再根据相似三角形的性质即可求解．本题主要考查了四边形的综合题，涉及正方形的性质、全等三角形的判定和性质、相似三角形的判定和性质以及折叠的性质的知识点，解决的关键是明确三角形翻转后边的大小不变，找准对应边，角的关系求解．17、【答案】D【考点】二次函数的图象，二次函数的性质，菱形的判定【解析】【解答】解：①∵抛物线y=ax2+bx+c（a≠0）与x轴交于点A（﹣2，0）、B（1，0），∴该抛物线的对称轴为x=﹣=﹣0.5，∴a=b，a﹣b=0，①正确；②∵抛物线开口向下，且抛物线与x轴交于点A（﹣2，0）、B（1，0），∴当﹣2＜x＜1时，y＞0，②正确；③∵点A、B关于x=0.5对称，∴AM=BM，又∵MC=MD，且CD⊥AB，∴四边形ACBD是菱形，③正确；④当x=﹣3时，y＜0，即y=9a﹣3b+c＜0，④错误．综上可知：正确的结论为①②③．故选D．【分析】①由抛物线与x轴的两交点坐标即可得出抛物线的对称轴为x=﹣=﹣0.5，由此即可得出a=b，①正确；②根据抛物线的开口向下以及抛物线与x轴的两交点坐标，即可得出当﹣2＜x＜1时，y＞0，②正确；③由AB关于x=0.5对称，即可得出AM=BM，再结合MC=MD以及CD⊥AB，即可得出四边形ACBD是菱形，③正确；④根据当x=﹣3时，y＜0，即可得出9a﹣3b+c＜0，④错误．综上即可得出结论．本题考查了二次函数的图象、二次函数的性质以及菱形的判定，解题的关键是逐条分析四条结论是否正确．本题属于中档题，难度不大，解决该题型题目时，根据给定的函数图象结合二次函数的性质逐条分析给定的结论是关键．18、【答案】D【考点】全等三角形的判定与性质，正方形的性质，翻折变换（折叠问题）【解析】【解答】解：∵正方形ABCD的边长为6，CE=2DE，∴DE=2，EC=4，∵把△ADE沿AE折叠使△ADE落在△AFE的位置，∴AF=AD=6，EF=ED=2，∠AFE=∠D=90°，∠FAE=∠DAE，在Rt△ABG和Rt△AFG中，∴Rt△ABG≌Rt△AFG（HL），∴GB=GF，∠BAG=∠FAG，∴∠GAE=∠FAE+∠FAG= ∠BAD=45°，所以①正确；设BG=x，则GF=x，C=BC﹣BG=6﹣x，在Rt△CGE中，GE=x+2，EC=4，CG=6﹣x，∵CG2+CE2=GE2，∴（6﹣x）2+42=（x+2）2，解得x=3，∴BG=3，CG=6﹣3=3∴BG=CG，所以②正确；∵EF=ED，GB=GF，∴GE=GF+EF=BG+DE，所以③正确；∵GF=GC，∴∠GFC=∠GCF，又∵Rt△ABG≌Rt△AFG，∴∠AGB=∠AGF，而∠BGF=∠GFC+∠GCF，∴∠AGB+∠AGF=∠GFC+∠GCF，∴∠AGB=∠GCF，∴CF∥AG，所以④正确；过F作FH⊥DC∵BC⊥DH，∴FH∥GC，∴△EFH∽△EGC，∴，EF=DE=2，GF=3，∴EG=5，∴△EFH∽△EGC，∴相似比为：= ，∴S△FGC=S△GCE﹣S△FEC= ×3×4﹣×4×（×3）= =3.6，所以⑤正确．故正确的有①②③④⑤，故选：D．【分析】先计算出DE=2，EC=4，再根据折叠的性质AF=AD=6，EF=ED=2，∠AFE=∠D=90°，∠FAE=∠DAE，然后根据“HL”可证明Rt△ABG≌Rt△AFG，则GB=GF，∠BAG=∠FAG，所以∠GAE= ∠BAD=45°；GE=GF+EF=BG+DE；设BG=x，则GF=x，CG=BC﹣BG=6﹣x，在Rt△CGE中，根据勾股定理得（6﹣x）2+42=（x+2）2，解得x=3，则BG=CG=3，则点G为BC的中点；同时得到GF=GC，根据等腰三角形的性质得∠GFC=∠GCF，再由Rt△ABG≌Rt△AFG得到∠AGB=∠AGF，然后根据三角形外角性质得∠BGF=∠GFC+∠GCF，易得∠AGB=∠GCF，根据平行线的判定方法得到CF∥AG；过F作FH⊥DC，则△EFH∽△EGC，△EFH∽△EGC，由相似比为，可计算S△FGC．本题考查了折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．也考查了三角形全等的判定与性质、勾股定理和正方形的性质．19、【答案】C【考点】垂径定理，圆周角定理，相似三角形的判定与性质，解直角三角形【解析】【解答】解：①∵AB是⊙O的直径，弦CD⊥AB，∴，DG=CG，∴∠ADF=∠AED，∵∠FAD=∠DAE（公共角），∴△ADF∽△AED；故①正确；②∵= ，CF=2，∴FD=6，∴CD=DF+CF=8，∴CG=DG=4，∴FG=CG﹣CF=2；故②正确；③∵AF=3，FG=2，∴AG= = ，∴在Rt△AGD中，tan∠ADG= = ，∴tan∠E= ；故③错误；④∵DF=DG+FG=6，AD= = ，∴S△ADF= DF•AG= ×6×=3 ，∵△ADF∽△AED，∴=（）2，∴= ，∴S△AED=7 ，∴S△DEF=S△AED﹣S△ADF=4 ；故④正确．故选C．【分析】①正确．由AB是⊙O的直径，弦CD⊥AB，根据垂径定理可得：，DG=CG，继而证得△ADF∽△AED；②正确．由= ，CF=2，可求得DF的长，继而求得CG=DG=4，则可求得FG=2；③错误．由勾股定理可求得AG的长，即可求得tan∠ADF的值，继而求得tan∠E=．④首先求得△ADF的面积，由相似三角形面积的比等于相似比的平方，即可求得△ADE的面积，继而求得S△DEF=4 ．20、【答案】D【考点】垂径定理，圆周角定理，相似三角形的判定与性质【解析】【解答】解：∵在⊙O中，点C是的中点，∴= ，∴∠CAD=∠ABC，故①正确；∵≠ ，∴≠ ，∴AD≠BC，故②错误；∵AB是⊙O的直径，∴∠ACB=90°，又∵CE⊥AB，∴∠ACE+∠CAE=∠ABC+∠CAE=90°，∴∠ACE=∠ABC，又∵C为的中点，∴= ，∴∠CAP=∠ABC，∴∠ACE=∠CAP，∴AP=CP，∵∠ACQ=90°，∴∠ACP+∠PCQ=∠CAP+∠PQC=90°，∴∠PCQ=∠PQC，∴PC=PQ，∴AP=PQ，即P为Rt△ACQ斜边AQ的中点，∴P为Rt△ACQ的外心，故③正确；∵AB是⊙O的直径，∴∠ACB=90°，又∵CE⊥AB∴根据射影定理，可得AC2=AE•AB，故④正确；如图，连接BD，则∠ADG=∠ABD，∵≠ ，∴≠ ，∴∠ABD≠∠BAC，∴∠ADG≠∠BAC，又∵∠BAC=∠BCE=∠PQC，∴∠ADG≠∠PQC，∴CB与GD不平行，故⑤错误．故答案为：D．【分析】在同圆或等圆中，同弧或等弧所对的圆周角相等，据此推理可得①正确，②错误；通过推理可得∠ACE=∠CAP，得出AP=CP，再根据∠PCQ=∠PQC，可得出PC=PQ，进而得到AP=PQ，即P为Rt△ACQ斜边AQ的中点，故P为Rt△ACQ 的外心，即可得出③正确；连接BD，则∠ADG=∠ABD，根据∠ADG≠∠BAC，∠BAC=∠BCE=∠PQC，可得出∠ADG≠∠PQC，进而得到CB与GD不平行，可得⑤错误．。

课题：几何多结论

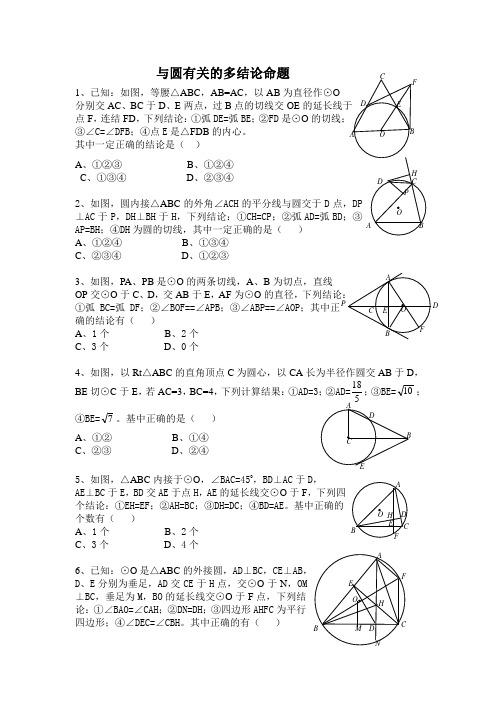
DP与圆有关的多结论命题1、已知：如图，等腰△ABC，AB=AC，以AB为直径作⊙O分别交AC、BC于D、E两点，过B点的切线交OE点F，连结FD，下列结论：①弧DE=弧BE；②FD是⊙O③∠C=∠DFB；④点E是△FDB的内心。

其中一定正确的结论是（）A、①②③B、①②④C、①③④D、②③④2、如图，圆内接△ABC的外角∠ACH的平分线与圆交于D⊥AC于P，DH⊥BH于H，下列结论：①CH=CP；②弧AD=弧BDAP=BH；④DH为圆的切线，其中一定正确的是（）A、①②④B、①③④C、②③④D、①②③3、如图，PA、PB是⊙O的两条切线，A、B为切点，直线OP交⊙O于C、D，交AB于E，AF为⊙O的直径，①弧BC=弧DF；②∠BOF==∠APB；③∠ABP==∠AOP；其中正确的结论有（）A、1个B、2个C、3个D、0个4、如图，以Rt△ABC的直角顶点C为圆心，以CA长为半径作圆交AB于D，BE切⊙C于E，若AC=3，BC=4，下列计算结果：①AD=3；②AD=518；③BE=10；④BE=7。

基中正确的是（）A、①②B、①④C、②③D、②④5、如图，△ABC内接于⊙O，∠BAC=450，BD⊥AC于D，AE⊥BC于E，BD交AE于点H，AE的延长线交⊙O于F，下列四个结论：①EH=EF；②AH=BC；③DH=DC；④BD=AE。

基中正确的个数有（）A、1个B、2个C、3个D、4个6、已知：⊙O是△ABC的外接圆，AD⊥BC，CE⊥AB，D、E分别为垂足，AD交CE于H点，交⊙O于N，OM⊥BC，垂足为M，BO的延长线交⊙O于F点，下列结论：①∠BAO=∠CAH；②DN=DH；③四边形AHFC为平行四边形；④∠DEC=∠CBH。

其中正确的有（）A 、①②③B 、①②③④C 、②③④D 、①③④7、AB 为半圆O 的直径，C 、F 是半圆上的点，且有弧 BC=弧CF ，CE ⊥AB 于E ，PB 是圆的切线，交AC 的延长线于P ，连BF ，交AC 于H ，交CE 于G ，过C 点的切线交PB 于D ，连OG ，下列结论：①CD ∥BF ；②DB=CD ；③BF=2CE ④OG=21AH 。

专题02 几何图形的多结论问题(解析版)

专题二几何图形的多结论问题【专题解读】几何类多结论判断题考查的知识点较多，主要以圆和四边形为核心开放研究型问题，所谓“开放”简单来说就是答案不唯一的，解题的方向不确定，条件或者结论不止一种情况的试题，解答此类试题时，需要对问题全方位、多层次、多角度思考审视，尽量找到解决问题的方法，根据开放性的试题的特点，主要有如下几种类型：条件开放性、结论开放性、选择开放型、综合开放型，属于中考必考题型.（2020•广东二模）如图，已知▱ABCD的对角线AC、BD交于点O，DE平分∠ADC 交BC于点E，交AC于点F，且∠BCD＝60°，BC＝2CD，连结OE．下列结论：①OE∥AB；②S平行四边形ABCD＝BD•CD；③AO＝2BO；④S△DOF＝2S△EOF．其中成立的个数有（C）A．1个B．2个C．3个D．4个【思路点拨】①证明BE＝CE，OA＝OC，根据三角形中位线定理可得结论正确；②证明BD⊥CD，可得结论正确；③设AB＝x，分别表示OA和OB的长，可以作判断；④先根据平行线分线段成比例定理可得：DF＝2EF，由同高三角形面积的比等于对应底边的比可作判断．【自主解答】①∵四边形ABCD是平行四边形，∴AD∥BC，OA＝OC，∴∠ADC+∠BCD＝180°，∵∠BCD＝60°，∴∠ADC＝120°，∵DE平分∠ADC，∴∠CDE＝60°＝∠BCD，∴△CDE是等边三角形，∴CE＝CD，∵BC＝2CD，∴BE＝CE，∵OA＝OC，∴OE∥AB；故①正确；②∵△DEC是等边三角形，∴∠DEC＝60°＝∠DBC+∠BDE，∵BE＝EC＝DE，∴∠DBC＝∠BDE＝30°，∴∠BDC＝30°+60°＝90°，∴BD⊥CD，∴S平行四边形ABCD＝BD•CD；故②正确；③设AB＝x，则AD＝2x，则BD=√3x，∴OB=√32x，由勾股定理得：AO=(√3x2)=√72x，故③不正确；④∵AD ∥EC ，∴AD EC =DF EF =21，∴DF ＝2EF ，∴S △DOF ＝2S △EOF ．故④正确；故选：C ．1．（2020•深圳模拟）在边长为2的正方形ABC D 中，P 为AB 上的一动点，E 为A D 中点，PE 交CD 延长线于Q ，过E 作EF ⊥PQ 交BC 的延长线于F ，则下列结论：①△APE ≌△DQE ；②PQ ＝EF ；③当P 为A B 中点时，CF =√2；④若H 为QC 的中点，当P 从A 移动到B 时，线段EH 扫过的面积为1，其中正确的有（）A ．1个B ．2个C ．3个D ．4个【答案】B【接卸】①∵四边形ABCD 是正方形，∴AB ＝BC ＝CD ＝AD ，∠A ＝∠B ＝∠ADC ＝90°，∴∠A ＝∠EDQ ＝90°，∵E 为A D 中点，∴AE ＝ED ，在△APE 和△DQE 中，{∠A =∠EDQAE =ED ∠AEP =∠DEQ，∴△APE ≌△DQE （ASA ），故①正确；②作PG ⊥CD 于G ，EM ⊥BC 于M ，如图1所示：∴∠PGQ ＝∠EMF ＝90°，∵EF ⊥PQ ，∴∠PEF ＝90°，∴∠PEM +∠MEF ＝90°，∵∠GPE +∠MEP ＝90°，∴∠GPE ＝∠MEF ，在△EFM 和△PQG 中，{∠EMF =∠PGQEM =PG ∠MEF =∠GPQ，∴△EFM ≌△PQG （ASA ），∴EF ＝PQ ，故②正确；③连接QF ，如图2所示：则QF ＝PF ，PB 2+BF 2＝QC 2+CF 2，设CF ＝x ，则（2+x ）2+12＝32+x 2，∴x ＝1，故③错误；④如图3所示：当P 在A 点时，Q 与D 重合，QC 的中点H 在DC 的中点S 处，当P 运动到B 时，QC 的中点H 与D 重合，故EH 扫过的面积为△ESD 的面积为12，故④错误；故选：B ．2．（2020•灌南县一模）如图，正方形ABC D 中，E 、F 分别为BC 、CD 的中点，AF 与DE 交于点G ．则下列结论中：①AF ⊥DE ；②AD ＝BG ；③GE +GF =√2GC ；④S △AGB ＝2S 四边形ECFG ．其中正确的是（）A ．1个B ．2个C ．3个D ．4个【答案】D【解析】∵正方形ABCD ，E ，F 均为中点,∴AD ＝BC ＝DC ，EC ＝DF =12BC,∵在△ADF 和△DCE 中，{AD =DC∠ADF =∠DCE DF =CE，∴△ADF ≌△DCE （SAS ），∴∠AFD ＝∠DEC ，∵∠DEC +∠CDE ＝90°，∴∠AFD +∠CDE ＝90°＝∠DGF ，∴AF ⊥DE ，故①正确；如图1，过点B 作BH ∥DE 交AD 于H ，交AF 于K ，∵AF ⊥DE ，BH ∥DE ，E 是BC 的中点，∴BH ⊥AG ，H 为AD 的中点，∴BH 是AG 的垂直平分线，∴BG ＝AB ＝AD ，故②正确，如图2，延长DE 至M ，使得EM ＝GF ，连接CM ，∵∠AFD ＝∠DEC ，∴∠CEM ＝∠CFG ，又∵E ，F 分别为BC ，DC 的中点，∴CF ＝CE ，∵在△CEM 和△CFG 中，{CE =CF∠CEM =∠CFG EM =FG，∴△CEM ≌△CFG （SAS ），∴CM ＝CG ，∠ECM ＝∠GCF ，∵∠GCF +∠BCG ＝90°，∴∠ECM +∠BCG ＝∠MCG ＝90°，∴△MCG 为等腰直角三角形，∴GM ＝GE +EM ＝GE +GF =√2GC ，故③正确；如图3，过G 点作TL ∥AD ，交AB 于T ，交DC 于L ，则GL ⊥AB ，GL ⊥DC ，设EC ＝x ，则DC ＝2x ，DF ＝x ，由勾股定理得DE =√5x ，由DE ⊥GF ，易证得△DGF ∽△DCE ， ∴DE DF =GF EC =√5x x ，∴S △DEC S △DGF =(√51)2=51， ∴S △DGF =15S △DEC ，∴S 四边形ECFG ＝S △DEC ﹣S △DGF =45S △DEC ，∵S △DEC =12⋅2x ⋅x =x 2，∴S 四边形ECFG =45x 2，S △DGF =15x 2∵DF ＝x ， ∴GL =15x 212x =25x ，∴TG ＝2x −25x =85x ，∴S △AGB =12•AB •TG =12•2x •85x =85x 2，∴S △AGB ＝2S 四边形ECFG 故④正确，故选：D ．3．（2020•东莞市一模）如图，在菱形ABC D 中，∠BAD ＝60°，AC 与BD 交于点O ，E 为CD 延长线上的一点，且CD ＝DE ，连接BE 分别交AC 、AD 于点F 、G ，连接OG ，则下列结论中一定成立的是 ①④ ．（把所有正确结论的序号都填在横线上）①OG =12AB ；②与△EGD 全等的三角形共有5个；③S 四边形ODGF ＞S △ABF ； ④由点A 、B 、D 、E 构成的四边形是菱形．【答案】①④【解析】∵四边形ABCD 是菱形，∴AB ＝BC ＝CD ＝DA ，AB ∥CD ，OA ＝OC ，OB ＝OD ，AC ⊥BD ，∴∠BAG ＝∠EDG ，△ABO ≌△BCO ≌△CDO ≌△AOD ，∵CD ＝DE ，∴AB ＝DE ，在△ABG 和△DEG 中，{∠BAG =∠EDG ∠AGB =∠DGE AB =DE，∴△ABG ≌△DEG （AAS ），∴AG ＝DG ，∴OG 是△ACD 的中位线，∴OG =12CD =12AB ，①正确；∵AB ∥CE ，AB ＝DE ，∴四边形ABDE是平行四边形，∵∠BCD＝∠BAD＝60°，∴△ABD、△BCD是等边三角形，∴AB＝BD＝AD，∠ODC＝60°，∴OD＝AG，四边形ABDE是菱形，④正确；∴AD⊥BE，由菱形的性质得：△ABG≌△BDG≌△DEG，在△ABG和△DCO中，{OD=AG∠ODC=∠BAG=60°AB=DC，∴△ABG≌△DCO（SAS），∴△ABO≌△BCO≌△CDO≌△AOD≌△ABG≌△BDG≌△DEG，②不正确；∵OB＝OD，AG＝DG，∴OG是△ABD的中位线，∴OG∥AB，OG=12AB，∴△GOD∽△ABD，△ABF∽△OGF，∴△GOD的面积=14△ABD的面积，△ABF的面积＝△OGF的面积的4倍，AF：OF＝2：1，∴△AFG的面积＝△OGF的面积的2倍，又∵△GOD的面积＝△AOG的面积＝△BOG的面积，∴S四边形ODGF＝S△ABF；不正确；正确的是①④．故答案为：①④．4．（2020•天河区一模）如图，在正方形ABC D中，对角线AC，BD交于点O，点E，F分别在AB，BD上，且△ADE≌△FDE，DE交AC于点G，连接GF．得到下列四个结论：①∠ADG＝22.5°；②S△AGD＝S△OGD；③BE＝2OG；④四边形AEFG是菱形，其中正确的结论是①③④．（填写所有正确结论的序号）【答案】①③④．【解析】∵四边形ABCD是正方形，∴∠GAD＝∠ADO＝45°，∴由△ADE≌△FDE，可得：∠ADG=12∠ADO＝22.5°，故①正确；∵△ADE≌△FDE，∴AD＝FD，∠ADG＝∠FDG，又∵GD＝GD，∴△ADG≌△FDG（SAS），∴S△AGD＞S△OGD，故②错误；∵△ADE≌△FDE，∴EA＝EF，∵△ADG≌△FDG，∴GA＝GF，∠AGD＝∠FGD，∴∠AGE＝∠FGE．∵∠EFD＝∠AOF＝90°，∴EF∥AC，∴∠FEG＝∠AGE，∴∠FGE＝∠FEG，∴EF＝GF，∴EF＝GF＝EA＝GA，∴四边形AEFG是菱形，故④正确；∵四边形AEFG是菱形，∴AE∥FG，∴∠OGF＝∠OAB＝45°，∴△OGF为等腰直角三角形，∴FG=√2OG，∴EF=√2OG，∵△BFE为等腰直角三角形，∴BE=√2EF=√2×√2OG＝2OG，∴③正确．综上，正确的有①③④．故答案为：①③④．5．（2020•福田区一模）如图，正方形ABC D中，E是BC延长线上一点，在AB上取一点F，使点B关于直线EF的对称点G落在AD上，连接EG交CD于点H，连接BH交EF于点M，连接CM．则下列结论，①∠1＝∠2；②∠3＝∠4；③GD=√2CM；④若AG＝1，GD ＝2，则BM=√5，其中正确的是．.【答案】①②③④【解析】如图1中，过点B作BK⊥GH于K．∵B，G关于EF对称，∴EB＝EG，∴∠EBG＝∠EGB，∵四边形ABCD是正方形，∴AB＝BC，∠A＝∠ABC＝∠BCD＝90°，AD∥BC，∴∠AGB＝∠EBG，∴∠AGB＝∠BGK，∵∠A＝∠BKG＝90°，BG＝BG，∴△BAG≌△BKG（AAS），∴BK＝BA＝BC，∠ABG＝∠KBG，∵∠BKH＝∠BCH＝90°，BH＝BH，∴Rt△BHK≌Rt△BHC（HL），∴∠1＝∠2，∠HBK＝∠HBC，故①正确，∴∠GBH＝∠GBK+∠HBK=1∠ABC＝45°，2过点M作MQ⊥GH于Q，MP⊥CD于P，MR⊥BC于R．∵∠1＝∠2，∴MQ＝MP，∵∠MEQ＝∠MER，∠BCD＝45°，∴MQ＝MR，∴MP＝MR，∴∠4＝∠MCP=12∴∠GBH＝∠4，故②正确，如图2中，过点M作MW⊥AD于W，交BC于T．∵B，G关于EF对称，∴BM＝MG，∵CB＝CD，∠4＝∠MCD，CM＝CM，∴△MCB≌△MCD（SAS），∴BM＝DM，∴MG＝MD，∵MW⊥DG，∴WG＝WD，∵∠BTM＝∠MWG＝∠BMG＝90°，∴∠BMT+∠GMW＝90°，∵∠GMW+∠MGW＝90°，∴∠BMT＝∠MGW，∵MB＝MG，∴△BTM≌△MWG（AAS），∴MT＝WG，∵MC=√2TM，DG＝2WG，∴DG=√2CM，故③正确，∵AG＝1，DG＝2，∴AD＝AB＝TM＝3，EM＝WD＝TM＝1，BT＝AW＝2，∴BM=√BT2+MT2=√22+12=√5，故④正确，故答案为：①②③④．。

初三几何多结论题

几何小综合…一多结论选择题一、以等腰、等腰亘角、等边三黠形为背景1.如图r ^AUC中.AC=HC. f 的内心.川的延长熾变BC F A；MI丄內交力甘于* MN.田艾予&F列鉛论：①AM龍冶②③—产曲AB其中正确的妃＜ )2.如酣AABC中，AB=AC, A£丄眈I £,以"为腰那譽股直梢厶^必MH.舷的延长统龙于M 连CN,下列结论；®CW丄启M ②际土冋応③S MK= .其中正晞的亍散冇()儿】卒乩2个 C 3个 D.斗中N3-如阁"^AfiC中’ AfiMC.点F为冲C的中点，点D为RF延长蜒上一点. 且Z^DC=Zfi4C* 为CD延K:线上•一点『W Al^AE.下列站论r①AQ举莎NBDE； ®CD=2PF；③RF刃F+DE；④九对=巧叭町其中正垠的个数育＜)A. 1个B. 2牛G 3个弘4伞4.如图，GJW?中* AB=AC, ZCAB=9(r.点耐为A匚上点* CD丄咼f于D・点E为CD延长姥上一点” 11 CE=BD，点N为8E的中点”连AE. AN. 下列结稳】■’ I®^CEA=45\ ®AN//BDi ®AN=DM, AM=CM. ^AE = 2-/2AN.:-,：；1 if “.• -：［.；_ . ,7 "其中正碘的有()A. ®@©K. ®@@ C. ®@®三、以梯形为背寰g”如图”梯形AACD中、BC//AD, ZX8C=W\且CX平井/朋6AD二血C、師丄肌于E,BE的延长线交C7）于DE、片材交于M下列皓论：’_ Lyr ®D£=AB；②CD 二忑RE：③AM 丄8：®sinZCflf^ —.AD 英中正确的个数有（1扎1个 E 2个 C 3个D. 41LQ,如酸直角梯^ACBD中.AD//BC r Z4C/?=9（F* AC=BC.ZDR4=22^% 点E为故1上一点"DE交ABF乩点M为NE的中点「F列结论: ①DEg②点開为/UBC的内心，©SZUSC内切囲半径为r, K④拠丄4 AN. .■p■■> 梵中正确的有（1A. ®®乩®®@ C ®® A ①®③©11.如图，協形舫CD申，BC//AD. ZA=90%点E柜朋上，氐3E 於边4, 且ZfiC£=b%点F为CO上一点，航価的廷检找交于帆下列结论；■ 1 节®ZXD£=45% ®AB=BC t®EFLCD・®^ZAW5=30% 则九和芍昵具中正确的有<} M A. ffi@ B. ®@® C ®® 6 ®@®12.如風盘角AHCD中* BC^CD, BC//AD. ZBCD=^f'点E 为AB 上—点"DE的平分线交M的延长线于乩连B仏下列结论t①ZBCM =-ZCDEz②ZCWM眉= —: ®MD=2MB r2 , £空首Affi ,其中正确的有（）A.①®③R、②®④ C.①®④ D.①®④四、以其它四边形为背臺(mpy,菱瞻冲HCD中，ZAZ/C-60%上点，虫F为忧运扯堤上一点.fl. 连际EF. DF、M奄DC于M卜冽结论；①DABE沁CDFt ②E4EF；®ZDF^=60°J牟若<7氐沁・^A1£L 邛英中正确的个数有( )A. 1 t 乩2个<7. 3个 6 4个14.如酥四^A8CD*l^AD - CD. ZADC »为DC延检线上「点川"丄于交SC于妆且Z(MJV=45\ 下列结论；①ZCBD = 45J2 BD-AB = BC@^ J?£*2C£.则矣*护広匚®・Jt中止确的个tt育< >.4.0伞且】个C24" D3个15.如药AfiCL>中…4扫鮎G M力对角线At?上一氐且则下列结论；①ZMBC=2^ACDi@4^-2CM ・AG®S/.AW*=>-S^: ④LinZADAf=3t直中站论正确的亍数址£2儿1 臥2U 3 6 416.如图.零腰拂形AJfD 屮，ADfJRC. AH=CD. ZABC^if, E 是腰CO上-点，连眼AE. AC.HD交于6 若^ACff-6（f t"眈=新’ 下列黠论；（S）CE=CBi@AC=AD+EC:®AE車直平分OUv ④ S27CT.共中正确的结论个数科］> rA. 1 6 R. 2 个G 3 个 D 4 个£> D1、如图0是正方形ABCD勺对角线的交点，E为BC的中点，EF丄AE 交CD于F, AE、EF交对角线于P、Q,则下列结论：①EP=EQ ②厶ABP^ECQ③BP=20P④AE平分/ BAF其中正确的结论有（）A 1个B 、2个C 、3个D 、4个2. 如图，正方形ABCD勺三边中点E、F、G连ED交AF于M,GC 交DE于N,下列结论①GMLCM②CD=CM③四边形MFCG为等腰梯形。

专题06 多结论判断问题2(几何图形的多结论判断)(原卷版)-2021年中考数学选填压轴题专项复习

【2021年中考数学填选重点题型突破】专题六：结论判断问题几何图形的多结论判断【备考指南】结论判断问题是近几年来中考的一个热点问题，往往以压轴题的形式出现在填空题与选择题中．这类问题是由多项选择演变而来，试题中包含多个正确或错误的结论，考生对给定的条件通过综合分析、推理、计算等形式来论证题中所给出的结论的真伪性．试题的题境常以代数结论判断题和几何结论判断题为主，在代数结论判断题中，通常以函数的多结论判断来考察，尤其是以二次函数为主的来考查函数知识，在几何结论判断题中，通过点的运动或图形的三大变换〔平移、旋转、轴对称〕，得出假设干结论。

以考查三角形和四边形性质居多．这类试题的合性很强，难度很大，易错，不易得分，对考生综合运用知识解决问题的能力要求高.解决这类问题，第一要有足够的知识积累和结论储藏〔例如：手拉手模型，半角模型，对角互补模型等〕，并且分析能力较强。

而综合分析所给出的条件是解决此类问题的关健，同时要将已论证出来成立的结论直接应用于后继证明之中，在分析、推理过程中，要以数学思想为魂，注重灵活运用各种方法〔如特殊值法、特殊图形法，反证法、直接测量等〕，同时要注重计算的准确性．【典例引领】例1：〔2021四川遂宁〕如图，在正方形ABCD 中，点E 是边BC 的中点，连接AE 、DE ，分别交BD 、AC 于点P 、Q ，过点P 作PF ⊥AE 交CB 的延长线于F ，以下结论：①∠AED +∠EAC +∠EDB ＝90°，②AP ＝FP ，③AE ＝2AO ， ④假设四边形OPEQ 的面积为4，那么该正方形ABCD 的面积为36，⑤CE •EF ＝EQ •DE ．其中正确的结论有〔〕A. 5个B. 4个C. 3个D. 2个变式训练1：.如图，正方形ABCD 的边长为4，点E 在边AB 上，BE ＝1，∠DAM ＝45°，点F 在射线AM 上，且AF ＝，过点F 作AD 的平行线交BA 的延长线于点H ，CF 与AD 相交于点G ，连接EC 、EG 、EF ．以下结论：①△ECF 的面积为；②△AEG 的周长为8；③EG 2＝DG 2+BE 2；其中正确的选项是〔〕 A ．①②③B ．①③C ．①②D ．②③变式训练2：〔2021山东泰安〕如图，矩形ABCD 中，,AC BD 相交于点O ，过点B 作BF AC 交CD 于点F ，交AC 于点M ，过点D 作//DE BF 交AB 于点E ，交AC 于点N ，连接,FN EM ．那么以下结论：①DN BM =；②//EM FN ；③AE FC =；④当AO AD =时，四边形DEBF 是菱形．其中，正确结论的个数是〔〕A. 1个B. 2个C. 3个D. 4个【强化训练】1．〔2021湖北咸宁〕如图，四边形ABCD 是边长为2的正方形，点E 是边BC 上一动点〔不与点B ，C 重合〕，90AEF ∠=︒，且EF 交正方形外角的平分线CF 于点F ，交CD 于点G ，连接AF ，有以下结论： ①ABE ECG ∽；②AE EF =；③DAF CFE ∠=∠；④CEF △的面积的最大值为1．其中正确结论的序号是_____________．〔把正确结论的序号都填上〕2.〔2021·东营〕如图，在正方形ABCD 中，点P 是AB 上一动点〔不与A 、B 重合〕，对角线AC 、BD 相交于点O ，过点P 分别作AC 、BD 的垂线，分别交AC 、BD 于点E 、F ，交AD 、BC 于点M 、N ，以下结论：①△APE ≌△AME ；②PM+PN=AC ；③222PE PF PO ；④△POF ∽△BNF ；⑤点O 在M 、N 两点的连线上．其中正确的选项是〔〕A. ①②③④B. ①②③⑤C. ①②③④⑤D. ③④⑤3.〔2021浙江绍兴〕将两条邻边长分别为，1的矩形纸片剪成四个等腰三角形纸片〔无余纸片〕，各种剪法剪出的等腰三角形中，其中一个等腰三角形的腰长可以是以下数中的〔填序号〕．①，②1，③﹣1，④，⑤．4.如图，等边三角形ABC 的边长为4,点O 是△ABC 的中心，∠FOG =120∘.绕点o 旋转∠FOG ,分别交线段AB 、BC 于D 、E 两点，连接DE ,给出以下四个结论：①OD =OE ;②S ΔODE =S ΔBDE ;③四边形ODBE 的面积始终等于43√3;④△BDE 周长的最小值为6,上述结论中正确的个数是( ) A ．1 B ．2 C ．3 D ．45..〔2021内蒙古包头〕如图，在Rt ABC 中，90ACB ∠=︒，BC AC >，按以下步骤作图：〔1〕分别以点,A B 为圆心，以大于12AB 的长为半径作弧，两弧相交于,M N 两点〔点M 在AB 的上方〕；〔2〕作直线MN 交AB 于点O ，交BC 于点D ；〔3〕用圆规在射线OM 上截取OE OD ．连接,,AD AE BE ，过点O 作OF AC ⊥，垂足为F ，交AD 于点G ．以下结论：①2CD GF =；②222BD CD AC -=；③2BOE AOG S S =；④假设6,9AC OF OA =+=，那么四边形ADBE 的周长为25．其中正确的结论有〔〕A. 1个B. 2个C. 3个D. 4个6.如图，在正方形ABCD 中，连接AC ，以点A 为圆心，适当长为半径画弧，交AB 、AC 于点M ，N ，分别以M ，N 为圆心，大于MN 长的一半为半径画弧，两弧交于点H ，连结AH 并延长交BC 于点E ，再分别以A 、E 为圆心，以大于AE 长的一半为半径画弧，两弧交于点P ，Q ，作直线PQ ，分别交CD ，AC ，AB 于点F ，G ，L ，交CB 的延长线于点K ，连接GE ，以下结论：①∠LKB =22.5°，②GE ∥AB ，③tan ∠CGF =KB LB，④S △CGE ：S △CAB =1：4．其中正确的选项是〔〕A ．①②③B ．②③④C ．①③④D ．①②④7.〔2021四川达州〕如图，45BOD ∠=︒，BO DO =，点A 在OB 上，四边形ABCD 是矩形，连接AC 、BD 交于点E ，连接OE 交AD 于点F ．以下4个判断：①OE 平分BOD ∠；②OF BD =；③DF =；④假设点G 是线段OF 的中点，那么AEG △为等腰直角三角形．正确判断的个数是〔〕A. 4B. 3C. 2D. 18.〔2021湖北鄂州〕如图，在AOB 和COD △中，OA OB =，OC OD =，OA OC <，36AOB COD ︒∠=∠=．连接AC 、BD 交于点M ，连接OM ．以下结论：①36AMB ︒∠=；②AC BD =；③OM 平分AOD ∠；④MO 平分AMD ∠其中正确的结论个数有〔〕个．A. 4B. 3C. 2D. 19.〔2021四川广元〕如下图，,ABC ECD 均为等边三角形，边长分别为5cm,3cm ，B 、C 、D 三点在同一条直线上，那么以下结论正确的________________．〔填序号〕①AD BE = ②7cm BE = ③CFG △为等边三角形 ④13cm 7CM = ⑤CM 平分BMD ∠ 10.如图，在Rt △ACB 中，∠ACB =90°，AC =BC ，D 是AB 上的一个动点〔不与点A ，B 重合〕，连接CD ，将CD 绕点C 顺时针旋转90°得到CE ，连接DE ，DE 与AC 相交于点F ，连接AE ．以下结论：①△ACE ≌△BCD ；②假设∠BCD =25°，那么∠AED =65°；③DE 2=2CF •CA ；④假设AB =3√2，AD =2BD ，那么AF =53．其中正确的结论是______．〔填写所有正确结论的序号〕11.〔2021深圳〕如图，矩形纸片ABCD 中，AB =6，BC =12.将纸片折叠，使点B 落在边AD 的延长线上的点G 处，折痕为EF ，点E 、F 分别在边AD 和边BC 上。

2019年深圳中考复习《几何多结论》综合题专题

2019年深圳中考复习多结论几何综合题专题一、单选题1、如图，△ABC和△CDE均为等腰直角三角形，点B，C，D在一条直线上，点M是AE的中点，下列结论：①tan∠AEC=CDBC；②S△ABC+S△CDE≥S△ACE；③BM⊥DM；④BM=DM．正确结论的个数是（）A、1个B、2个C、3个D、4个2、如图，在Rt△ABC中，AB=AC，D、E是斜边BC上两点，且∠DAE=45°，将△ADC绕点A顺时针旋转90°后，得到△AFB，连接EF，下列结论：①△AED≌△AEF；②=;③△ABC的面积等于四边形AFBD的面积；④BE2+DC2=DE2⑤BE+DC=DE;其中正确的是( )A、①②④B、③④⑤C、①③④D、①③⑤3、如图，将等边△ABC沿射线BC向右平移到△DCE的位置，连接AD、BD ，则下列结论：①AD＝BC；②BD、AC互相平分；③四边形ACED是菱形；④BD⊥DE；其中正确的个数是（）.A、1B、2C、3D、4 4、如图，把一张长方形纸片ABCD沿对角线BD折叠，使C点落在E处，BE与AD相交于点F，下列结论：①BD=AD2+AB2；②△ABF≌△EDF；③＝④AD=BD•cos45°．其中正确的一组是（）A、①②B、②③C、①④D、③④5、如图，已知正方形ABCD的边长为4，点E、F分别在边AB、BC上，且AE=BF=1，CE、DF交于点O．下列结论：①∠DOC=90°，②OC=OE，③tan∠OCD= ，④S△ODC=S四边形BEOF中，正确的有（）A、1个B、2个C、3个D、4个6、如图，已知正方形ABCD的边长为12，BE=EC，将正方形边CD沿DE折叠到DF，延长EF交AB于G，连接DG，现在有如下4个结论：①△ADG≌△FDG；②GB=2AG；③△GDE∽△BEF；④S△BEF=．在以上4个结论中，正确的有（）A、1B、2C、3D、47、如图，▱ABCD的对角线AC、BD交于点O，AE平分∠BAD交BC于点E，且∠ADC=60°，AB=BC，连接OE．下列结论：①∠CAD=30°；②S▱ABCD=AB•AC；③OB=AB；④OE=BC，成立的个数有（）A、1个B、2个C、3个D、4个8、如图，AD是△ABC的角平分线，DE，DF分别是△ABD和△ACD的高，得到下列四个结论：①OA=OD；②AD⊥EF；③当∠A=90°时，四边形AEDF是正方形；④AE+DF=AF+DE．其中正确的是（）A、②③B、②④C、①③④D、②③④9、如图，G，E分别是正方形ABCD的边AB，BC的点，且AG=CE，AE⊥EF，AE=EF，现有如下结论：①BE=GE；②△AGE≌△ECF；③∠FCD=45°；④△GBE∽△ECH，其中，正确的结论有（）A、1个B、2个C、3个D、4个10、如图，PA=PB，OE⊥PA，OF⊥PB，则以下结论：①OP是∠APB的平分线；②PE=PF③CA=BD；④CD∥AB；其中正确的有（）个．A、4B、3C、2D、111、如图，在Rt△ABC中，AB=CB，BO⊥AC，把△ABC折叠，使AB落在AC 上，点B与AC上的点E重合，展开后，折痕AD交BO于点F，连接DE、EF．下列结论：①tan∠ADB=2；②图中有4对全等三角形；③若将△DEF沿EF折叠，则点D不一定落在AC上；④BD=BF；⑤S四边形DFOE=S△AOF，上述结论中正确的个数是（）A、1个B、2个C、3个D、4个12、如图，将等边△ABC绕点C顺时针旋转120°得到△EDC，连接AD，BD．则下列结论：①AC=AD；②BD⊥AC；③四边形ACED是菱形．其中正确的个数是（）A、0B、1C、2D、313、如图，CB=CA，∠ACB=90°，点D在边BC上（与B、C不重合），四边形ADEF为正方形，过点F作FG⊥CA，交CA的延长线于点G，连接FB，交DE于点Q，给出以下结论：①AC=FG；②S△FAB：S四边形CBFG=1：2；③∠ABC=∠ABF；④AD2=FQ•AC，其中正确的结论的个数是（）A、1B、2C、3D、414、如图，矩形ABCD中，O为AC中点，过点O的直线分别与AB、CD交于点E、F，连结BF交AC于点M，连结DE、BO．若∠COB=60°，FO=FC，则下列结论：①FB垂直平分OC；②△EOB≌△CMB；③DE=EF；④S△AOE：S△BCM=2：3．其中正确结论的个数是（）A、4个B、3个C、2个D、1个15、（2016•攀枝花）如图，正方形纸片ABCD中，对角线AC、BD交于点O，折叠正方形纸片ABCD，使AD落在BD上，点A恰好与BD上的点F重合，展开后折痕DE分别交AB、AC于点E、G，连结GF，给出下列结论：①∠ADG=22.5°；②tan∠AED=2；③S△AGD=S△OGD；④四边形AEFG是菱形；⑤BE=2OG；⑥若S△OGF=1，则正方形ABCD的面积是6+4 ，其中正确的结论个数为（）A、2B、3C、4D、516、如图，在正方形ABCD中，E、F分别为BC、CD的中点，连接AE，BF交于点G，将△BCF沿BF对折，得到△BPF，延长FP交BA延长线于点Q，下列结论正确的个数是（）①AE=BF；②AE⊥BF；③sin∠BQP= ；④S四边形ECFG=2S△BGE．A、4B、3C、2D、117、如图所示，抛物线y=ax2+bx+c（a≠0）与x轴交于点A（﹣2，0）、B（1，0），直线x=﹣0.5与此抛物线交于点C，与x轴交于点M，在直线上取点D，使MD=MC，连接AC、BC、AD、BD，某同学根据图象写出下列结论：①a﹣b=0；②当﹣2＜x＜1时，y＞0；③四边形ACBD是菱形；④9a﹣3b+c＞0你认为其中正确的是（）A、②③④B、①②④C、①③④D、①②③18、如图，正方形ABCD中，AB=6，点E在边CD上，且CE=2DE．将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连结AG、CF．下列结论：①△ABG≌△AFG；②BG=GC；③EG=DE+BG；④AG∥CF；⑤S△FGC=3.6．其中正确结论的个数是（）A、2B、3C、4D、519、如图，AB是⊙O的直径，弦CD⊥AB于点G，点F是CD上一点，且满足= ，连接AF并延长交⊙O于点E，连接AD，DE，若CF=2，AF=3，给出下列结论：①△ADF∽△AED；②FG=2；③tanE= ；④S△DEF=4 ，其中正确的是（）A、①②③B、②③④C、①②④D、①③④20、如图，在⊙O中，AB是直径，点D是⊙O上一点，点C是弧AD的中点，弦CE⊥AB于点E，过点D的切线交EC的延长线于点G，连接AD，分别交CE、CB 于点P、Q，连接AC，给出下列结论：①∠DAC=∠ABC；②AD=CB；③点P是△ACQ的外心；④AC2=AE•AB；⑤CB∥GD，其中正确的结论是（）A、①③⑤B、②④⑤C、①②⑤D、①③④答案解析部分一、单选题1、【答案】D【考点】等腰三角形的性质，梯形中位线定理，锐角三角函数的定义【解析】【分析】①根据等腰直角三角形的性质及△ABC∽△CDE的对应边成比例知，；然后由直角三角形中的正切函数，得tan∠AEC=，再由等量代换求得tan∠AEC=；②由三角形的面积公式、梯形的面积公式及不等式的基本性质a2+b2≥2ab（a=b时取等号)解答；③、④通过作辅助线MN，构建直角梯形的中位线，根据梯形的中位线定理及等腰直角三角形的判定定理解答．【解答】解：∵△ABC和△CDE均为等腰直角三角形，∴AB=BC，CD=DE，∴∠BAC=∠BCA=∠DCE=∠DEC=45°，∴∠ACE=90°；∵△ABC∽△CDE∴①∴tan∠AEC=，∴tan∠AEC=；故本选项正确；②∵S△ABC=a2，S△CDE=b2，S梯形ABDE=（a+b)2，∴S△ACE=S梯形ABDE-S△ABC-S△CDE=ab，S△ABC+S△CDE=（a2+b2)≥ab（a=b时取等号)，∴S△ABC+S△CDE≥S△ACE；故本选项正确；④过点M作MN垂直于BD，垂足为N．∵点M是AE的中点，则MN为梯形中位线，∴N为中点，∴△BMD为等腰三角形，∴BM=DM；故本选项正确；③又MN=（AB+ED)=（BC+CD)，∴∠BMD=90°，即BM⊥DM；故本选项正确．故选D．【点评】本题综合考查了等腰直角三角形的判定与性质、梯形的中位线定理、锐角三角函数的定义等知识点．在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边．2、【答案】C【考点】全等三角形的判定，勾股定理，相似三角形的判定，旋转的性质【解析】【分析】①根据旋转的性质知∠CAD=∠BAF，AD=AF，因为∠BAC=90°，∠DAE=45°，所以∠CAD+∠BAE=45°，可得∠EAF=45°=∠DAE，由此即可证明△AEF≌△AED；②当△ABE∽△ACD时，该比例式成立；③根据旋转的性质，△ADC≌△ABF，进而得出△ABC的面积等于四边形AFBD的面积；④据①知BF=CD，EF=DE，∠FBE=90°，根据勾股定理判断．⑤根据①知道△AEF≌△AED，得CD=BF，DE=EF；由此即可确定该说法是否正确；【解答】①根据旋转的性质知∠CAD=∠BAF，AD=AF，∵∠BAC=90°，∠DAE=45°，∴∠CAD+∠BAE=45°．∴∠EAF=45°，∴△AED≌△AEF；故本选项正确；②∵AB=AC，∴∠ABE=∠ACD；∴当∠BAE=∠CAD时，△ABE∽△ACD，∴=；当∠BAE≠∠CAD时，△ABE与△ACD不相似，即≠；∴此比例式不一定成立；故本选项错误；③根据旋转的性质知△ADC≌△AFB，∴S△ABC=S△ABD+S△ABF=S四边形AFBD，即三角形ABC的面积等于四边形AFBD的面积；故本选项正确；④∵∠FBE=45°+45°=90°，∴BE2+BF2=EF2，∵△ADC绕点A顺时针旋转90°后，得到△AFB，∴△AFB≌△ADC，∴BF=CD，又∵EF=DE，∴BE2+DC2=DE2，故本选项正确；⑤根据①知道△AEF≌△AED，得CD=BF，DE=EF，∴BE+DC=BE+BF＞DE=EF，即BE+DC＞DE，故本选项错误；综上所述，正确的说法是①③④；故选C．【点评】此题主要考查了图形的旋转变换以及全等三角形的判定等知识，解题时注意旋转前后对应的相等关系．3、【答案】D【考点】等边三角形的性质，菱形的判定与性质，平移的性质【解析】【解答】∵△ABC、△DCE是等边三角形，∴∠ACB＝∠DCE＝60°，AC ＝CD ，∴∠ACD＝180°－∠ACB－∠DCE＝60°，∴△ACD是等边三角形，∴AD＝AC＝BC ，故①正确；由①可得AD＝BC ，∵AB＝CD ，∴四边形ABCD是平行四边形，∴BD、AC互相平分，故②正确；由①可得AD＝AC＝CE＝DE ，故四边形ACED是菱形，即③正确；∵四边形ACED是菱形，∴AC⊥BD ，∵AC∥DE ，∴∠BDE＝∠COD＝90°，∴BD⊥DE ，故④正确；综上可得①②③④正确，共4个，故选D．【分析】先求出∠ACD＝60°，继而可判断△ACD是等边三角形，从而可判断①是正确的；根据①的结论，可判断四边形ABCD是平行四边形，从而可判断②是正确的；根据①的结论，可判断③正确；根据菱形的对角线互相垂直可得AC⊥BD ，再根据平移后对应线段互相平行可得∠BDE＝∠COD＝90°，进而判断④正确．4、【答案】B【考点】勾股定理，翻折变换（折叠问题），相似三角形的判定与性质，特殊角的三角函数值【解析】【解答】①∵△ABD为直角三角形，∴BD2=AD2+AB2，不是BD=AD2+AB2，故说法错误；②根据折叠可知：DE=CD=AB，∠A=∠E，∠AFB=∠EFD，∴△ABF≌△EDF，故说法正确；③根据②可以得到△ABF∽△EDF，∴＝，故说法正确；④在Rt△ABD中，∠ADB≠45°，∴AD≠BD•cos45°，故说法错误．所以正确的是②③．故选B．【分析】①直接根据勾股定理即可判定是否正确；②利用折叠可以得到全等条件证明△ABF≌△EDF；③利用全等三角形的性质即可解决问题；④在Rt△ABD中利用三角函数的定义即可判定是否正确．此题主要考查了折叠问题，也考查了勾股定理、相似三角形的性质、全等三角形的性质及三角函数的定义，它们的综合性比较强，对于学生的综合能力要求比较高，平时加强训练．5、【答案】C【考点】全等三角形的判定与性质，勾股定理，正方形的性质，锐角三角函数的定义【解析】【解答】解：∵正方形ABCD的边长为4，∴BC=CD=4，∠B=∠DCF=90°，∵AE=BF=1，∴BE=CF=4﹣1=3，在△EBC和△FCD中，∴△EBC≌△FCD（SAS），∴∠CFD=∠BEC，∴∠BCE+∠BEC=∠BCE+∠CFD=90°，∴∠DOC=90°；故①正确；若OC=OE，∵DF⊥EC，∴CD=DE，∵CD=AD＜DE（矛盾），故②错误；∵∠OCD+∠CDF=90°，∠CDF+∠DFC=90°，∴∠OCD=∠DFC，∴tan∠OCD=tan∠DFC= = ，故③正确；∵△EBC≌△FCD，∴S△EBC=S△FCD，∴S△EBC﹣S△FOC=S△FCD﹣S△FOC，即S△ODC=S四边形BEOF．故④正确．故选C．【分析】由正方形ABCD的边长为4，AE=BF=1，利用SAS易证得△EBC≌△FCD，然后全等三角形的对应角相等，易证得①∠DOC=90°正确；②由线段垂直平分线的性质与正方形的性质，可得②错误；易证得∠OCD=∠DFC，即可求得③正确；由①易证得④正确．6、【答案】C【考点】全等三角形的判定与性质，正方形的性质，翻折变换（折叠问题），相似三角形的判定与性质【解析】【解答】由折叠可知，DF=DC=DA，∠DFE=∠C=90°，∴∠DFG=∠A=90°，∴△ADG≌△FDG，①正确；∵正方形边长是12，∴BE=EC=EF=6，设AG=FG=x，则EG=x+6，BG=12﹣x，由勾股定理得：EG2=BE2+BG2，即：（x+6）2=62+（12﹣x）2，解得：x=4∴AG=GF=4，BG=8，BG=2AG，②正确；BE=EF=6，△BEF是等腰三角形，易知△GED不是等腰三角形，③错误；S△GBE=×6×8=24，S△BEF=•S△GBE==，④正确．故选：C．【分析】根据正方形的性质和折叠的性质可得AD=DF，∠A=∠GFD=90°，于是根据“HL”判定△ADG≌△FDG，再由GF+GB=GA+GB=12，EB=EF，△BGE为直角三角形，可通过勾股定理列方程求出AG=4，BG=8，进而求出△BEF的面积，再抓住△BEF是等腰三角形，而△GED显然不是等腰三角形，判断③是错误的．7、【答案】C【考点】等边三角形的判定与性质，含30度角的直角三角形，平行四边形的性质【解析】【解答】∵四边形ABCD是平行四边形，∴∠ABC=∠ADC=60°，∠BAD=120°，∵AE平分∠BAD，∴∠BAE=∠EAD=60°∴△ABE是等边三角形，∴AE=AB=BE，∵AB=BC，∴AE=BC，∴∠BAC=90°，∴∠CAD=30°，故①正确；∵AC⊥AB，∴S▱ABCD=AB•AC，故②正确，∵AB=BC，OB=BD，∵BD＞BC，∴AB≠OB，故③错误；∵CE=BE，CO=OA，∴OE=AB，∴OE=BC，故④正确．故选：C．【分析】由四边形ABCD是平行四边形，得到∠ABC=∠ADC=60°，∠BAD=120°，根据AE平分∠BAD，得到∠BAE=∠EAD=60°推出△ABE是等边三角形，由于AB=BC，得到AE=BC，得到△ABC是直角三角形，于是得到∠CAD=30°，故①正确；由于AC⊥AB，得到S▱ABCD=AB•AC，故②正确，根据AB=BC，OB=BD，且BD＞BC，得到AB≠OB，故③错误；根据三角形的中位线定理得到OE=AB，于是得到OE=BC，故④正确．8、【答案】D【考点】全等三角形的判定与性质，角平分线的性质，正方形的判定【解析】【解答】如果OA=OD，则四边形AEDF是矩形，∠A=90°，不符合题意，∴①不正确；∵AD是△ABC的角平分线，∴∠EAD∠FAD，在△AED和△AFD 中，∴△AED≌△AFD（AAS），∴AE=AF，DE=DF，∴AE+DF=AF+DE，∴④正确；在△AEO和△AFO中，，∴△AE0≌△AF0（SAS），∴EO=FO，又∵AE=AF，∴AO是EF的中垂线，∴AD⊥EF，∴②正确；∵当∠A=90°时，四边形AEDF的四个角都是直角，∴四边形AEDF是矩形，又∵DE=DF，∴四边形AEDF是正方形，∴③正确．综上，可得正确的是：②③④．故选：D．【分析】①如果OA=OD，则四边形AEDF是矩形，∠A=90°，不符合题意，所以①不正确．②首先根据全等三角形的判定方法，判断出△AED≌△AFD，AE=AF，DE=DF；然后根据全等三角形的判定方法，判断出△AE0≌△AFO，即可判断出AD⊥EF．③首先判断出当∠A=90°时，四边形AEDF的四个角都是直角，四边形AEDF是矩形，然后根据DE=DF，判断出四边形AEDF是正方形即可．④根据△AED≌△AFD，判断出AE=AF，DE=DF，即可判断出AE+DF=AF+DE成立，据此解答即可．9、【答案】B【考点】全等三角形的判定与性质，正方形的性质，相似三角形的判定与性质【解析】【解答】∵四边形ABCD是正方形，∴∠B=∠DCB=90°，AB=BC，∵AG=CE，∴BG=BE，由勾股定理得：BE=GE，∴①错误；∵BG=BE，∠B=90°，∴∠BGE=∠BEG=45°，∴∠AGE=135°，∴∠GAE+∠AEG=45°，∵AE⊥EF，∴∠AEF=90°，∵∠BEG=45°，∴∠AEG+∠FEC=45°，∴∠GAE=∠FEC，在△GAE和△CEF中∴△GAE≌△CEF，∴②正确；∴∠AGE=∠ECF=135°，∴∠FCD=135°﹣90°=45°，∴③正确；∵∠BGE=∠BEG=45°，∠AEG+∠FEC=45°，∴∠FEC＜45°，∴△GBE和△ECH不相似，∴④错误；即正确的有2个．故选B．【分析】根据正方形的性质得出∠B=∠DCB=90°，AB=BC，求出BG=BE，根据勾股定理得出BE=GE，即可判断①；求出∠GAE+∠AEG=45°，推出∠GAE=∠FEC，根据SAS推出△GAE≌△CEF，即可判断②；求出∠AGE=∠ECF=135°，即可判断③；求出∠FEC＜45°，根据相似三角形的判定得出△GBE和△ECH不相似，即可判断④．10、【答案】A【考点】全等三角形的判定与性质，圆心角、弧、弦的关系，相似三角形的判定与性质【解析】【解答】连接OP、OC、OA、OD、OB、CD、AB．∵PC•PA=PD•PB（相交弦定理），PA=PB（已知），∴PC=PD，∴AC=BD；在△AOC和△BOD中，∵∠AOC=∠BOD（等弦对等角），OA=OB（半径），OD=OC（半径），∴△AOC≌△BOD，∴③CA=BD；OE=OF；又∵OE⊥PA，OF⊥PB，∴①OP是∠APB的平分线；∴②PE=PF；在△PCD和△PAB中，PC：PA=PD：PB，∠DPC=∠BPA，∴△PCD∽△PAB，∴∠PDC=PBA，∴④CD∥AB；综上所述，①②③④均正确，故答案选A．【分析】①通过证明△AOC≌△BOD，再根据全等三角形的对应高相等求得OE=OF；再根据角平分线的性质证明OP是∠APB的平分线；②由角平分线的性质证明PE=PF；③通过证明△AOC≌△BOD，再根据全等三角形的对应边相等求得CA=BD；④通过证明△PCD∽△PAB，再根据相似三角形的性质对应角相等证得∠PDC=PBA；然后由平行线的判定得出结论CD∥AB．11、【答案】C【考点】全等三角形的判定与性质，翻折变换（折叠问题），锐角三角函数的定义【解析】【解答】①由折叠可得BD=DE，而DC＞DE，∴DC＞BD，∴tan∠ADB≠2，故①错误；②图中的全等三角形有△ABF≌△AEF，△ABD≌△AED，△FBD≌△FED，（由折叠可知)∵OB⊥AC，∴∠AOB=∠COB=90°，在Rt△AOB和Rt△COB中，AB="CB" ,BO=BO ，∴Rt△AOB≌Rt△COB（HL)，则全等三角形共有4对，故②正确；③∵AB=CB，BO⊥AC，把△ABC折叠，∴∠ABO=∠CBO=45°，∠FBD=∠DEF，∴∠AEF=∠DEF=45°，∴将△DEF沿EF折叠，可得点D一定在AC上，故③错误；④∵OB⊥AC，且AB=CB，∴BO为∠ABC的平分线，即∠ABO=∠OBC=45°，由折叠可知，AD是∠BAC的平分线，即∠BAF=22.5°，又∵∠BFD为三角形ABF的外角，∴∠BFD=∠ABO+∠BAF=67.5°，易得∠BDF=180°-45°-67.5°=67.5°，∴∠BFD=∠BDF，∴BD=BF，故④正确；⑤连接CF，∵△AOF和△COF等底同高，∴S△AOF=S△COF，∵∠AEF=∠ACD=45°，∴EF∥CD，∴S△EFD=S△EFC，∴S四边形DFOE=S△COF，∴S四边形DFOE=S△AOF，故⑤正确；故正确的有3个．故选C．12、【答案】D【考点】等边三角形的性质，菱形的判定，旋转的性质【解析】【解答】解：∵将等边△ABC绕点C顺时针旋转120°得到△EDC，∴∠ACE=120°，∠DCE=∠BCA=60°，AC=CD=DE=CE，∴∠ACD=120°﹣60°=60°，∴△ACD是等边三角形，∴AC=AD，AC=AD=DE=CE，∴四边形ACED是菱形，∵将等边△ABC绕点C顺时针旋转120°得到△EDC，AC=AD，∴AB=BC=CD=AD，∴四边形ABCD是菱形，∴BD⊥AC，∴①②③都正确，故选D．【分析】根据旋转和等边三角形的性质得出∠ACE=120°，∠DCE=∠BCA=60°，AC=CD=DE=CE，求出△ACD是等边三角形，求出AD=AC，根据菱形的判定得出四边形ABCD和ACED都是菱形，根据菱形的判定推出AC⊥BD．本题考查了旋转的性质，菱形的性质和判定，等边三角形的性质和判定的应用，能灵活运用知识点进行推理是解此题的关键．13、【答案】D【考点】全等三角形的判定与性质，矩形的判定与性质，正方形的性质，相似三角形的判定与性质，等腰直角三角形【解析】【解答】解：∵四边形ADEF为正方形，∴∠FAD=90°，AD=AF=EF，∴∠CAD+∠FAG=90°，∵FG⊥CA，∴∠C=90°=∠ACB，∴∠CAD=∠AFG，在△FGA和△ACD中，，∴△FGA≌△ACD（AAS），∴AC=FG，①正确；∵BC=AC，∴FG=BC，∵∠ACB=90°，FG⊥CA，∴FG∥BC，∴四边形CBFG是矩形，∴∠CBF=90°，S△FAB= FB•FG= S四边形CBFG，②正确；∵CA=CB，∠C=∠CBF=90°，∴∠ABC=∠ABF=45°，③正确；∵∠FQE=∠DQB=∠ADC，∠E=∠C=90°，∴△ACD∽△FEQ，∴AC：AD=FE：FQ，∴AD•FE=AD2=FQ•AC，④正确；故选：D．【分析】本题考查了相似三角形的判定与性质、全等三角形的判定与性质、正方形的性质、矩形的判定与性质、等腰直角三角形的性质；熟练掌握正方形的性质，证明三角形全等和三角形相似是解决问题的关键．由正方形的性质得出∠FAD=90°，AD=AF=EF，证出∠CAD=∠AFG，由AAS证明△FGA≌△ACD，得出AC=FG，①正确；证明四边形CBFG是矩形，得出S△FAB= FB•FG= S四边形CEFG，②正确；由等腰直角三角形的性质和矩形的性质得出∠ABC=∠ABF=45°，③正确；证出△ACD∽△FEQ，得出对应边成比例，得出D•FE=AD2=FQ•AC，④正确．14、【答案】B【考点】全等三角形的判定与性质，线段垂直平分线的性质，等腰三角形的性质，矩形的性质【解析】【解答】解：①∵矩形ABCD中，O为AC中点，∴OB=OC，∵∠COB=60°，∴△OBC是等边三角形，∴OB=BC，∵FO=FC，∴FB垂直平分OC，故①正确；②∵FB垂直平分OC，∴△CMB≌△OMB，∵OA=OC，∠FOC=∠EOA，∠DCO=∠BAO，∴△FOC≌△EOA，∴FO=EO，易得OB⊥EF，∴△OMB≌△OEB，∴△EOB≌△CMB，故②正确；③由△OMB≌△OEB≌△CMB得∠1=∠2=∠3=30°，BF=BE，∴△BEF是等边三角形，∴BF=EF，∵DF∥BE且DF=BE，∴四边形DEBF是平行四边形，∴DE=BF，∴DE=EF，故③正确；④在直角△BOE中∵∠3=30°，∴BE=2OE，∵∠OAE=∠AOE=30°，∴AE=OE，∴BE=2AE，∴S△AOE：S△BCM=S△AOE：S△BOE=1：2，故④错误；所以其中正确结论的个数为3个；故选B【分析】①利用线段垂直平分线的性质的逆定理可得结论；②证△OMB≌△OEB得△EOB≌△CMB；③先证△BEF是等边三角形得出BF=EF，再证▱DEBF得出DE=BF，所以得DE=EF；④由②可知△BCM≌△BEO，则面积相等，△AOE和△BEO属于等高的两个三角形，其面积比就等于两底的比，即S△AOE：S△BOE=AE：BE，由直角三角形30°角所对的直角边是斜边的一半得出BE=2OE=2AE，得出结论S△AOE：S△BOE=AE：BE=1：2．本题综合性比较强，既考查了矩形的性质、等腰三角形的性质，又考查了全等三角形的性质和判定，及线段垂直平分线的性质，内容虽多，但不复杂；看似一个选择题，其实相当于四个证明题，属于常考题型．15、【答案】B【考点】菱形的判定与性质，翻折变换（折叠问题），等腰直角三角形【解析】【解答】解：∵四边形ABCD是正方形，∴∠GAD=∠ADO=45°，由折叠的性质可得：∠ADG= ∠ADO=22.5°，故①正确．∵由折叠的性质可得：AE=EF，∠EFD=∠EAD=90°，∴AE=EF＜BE，∴AE＜AB，∴＞2，故②错误．∵∠AOB=90°，∴AG=FG＞OG，△AGD与△OGD同高，∴S△AGD＞S△OGD，故③错误．∵∠EFD=∠AOF=90°，∴EF∥AC，∴∠FEG=∠AGE，∵∠AGE=∠FGE，∴∠FEG=∠FGE，∴EF=GF，∵AE=EF，∴AE=GF，故④正确．∵AE=EF=GF，AG=GF，∴AE=EF=GF=AG，∴四边形AEFG是菱形，∴∠OGF=∠OAB=45°，∴EF=GF= OG，∴BE= EF= ×OG=2OG．故⑤正确．∵四边形AEFG是菱形，∴AB∥GF，AB=GF．∵∠BAO=45°，∠GOF=90°，∴△OGF时等腰直角三角形．∵S△OGF=1，∴OG2=1，解得OG= ，∴BE=2OG=2 ，GF= ==2，∴AE=GF=2，∴AB=BE+AE=2 +2，∴S正方形ABCD=AB2=（2 +2）2=12+8 ，故⑥错误．∴其中正确结论的序号是：①④⑤．故选B．【分析】①由四边形ABCD是正方形，可得∠GAD=∠ADO=45°，又由折叠的性质，可求得∠ADG的度数；②由AE=EF＜BE，可得AD＞2AE；③由AG=GF＞OG，可得△AGD的面积＞△OGD的面积；④由折叠的性质与平行线的性质，易得△EFG是等腰三角形，即可证得AE=GF；⑤易证得四边形AEFG是菱形，由等腰直角三角形的性质，即可得BE=2OG；⑥根据四边形AEFG是菱形可知AB∥GF，AB=GF，再由∠BAO=45°，∠GOF=90°可得出△OGF时等腰直角三角形，由S△OGF=1求出GF的长，进而可得出BE及AE的长，利用正方形的面积公式可得出结论．此题考查的是四边形综合题，涉及到正方形的性质、折叠的性质、等腰直角三角形的性质以及菱形的判定与性质等知识．此题综合性较强，难度较大，注意掌握折叠前后图形的对应关系，注意数形结合思想的应用．16、【答案】B【考点】全等三角形的判定与性质，正方形的性质，翻折变换（折叠问题），相似三角形的判定与性质【解析】【解答】解：∵E，F分别是正方形ABCD边BC，CD的中点，∴CF=BE，在△ABE和△BCF中，，∴Rt△ABE≌Rt△BCF（SAS），∴∠BAE=∠CBF，AE=BF，故①正确；又∵∠BAE+∠BEA=90°，∴∠CBF+∠BEA=90°，∴∠BGE=90°，∴AE⊥BF，故②正确；根据题意得，FP=FC，∠PFB=∠BFC，∠FPB=90°∵CD∥AB，∴∠CFB=∠ABF，∴∠ABF=∠PFB，∴QF=QB，令PF=k（k＞0），则PB=2k在Rt△BPQ中，设QB=x，∴x2=（x﹣k）2+4k2，∴x= ，∴sin=∠BQP= = ，故③正确；∵∠BGE=∠BCF，∠GBE=∠CBF，∴△BGE∽△BCF，∵BE= BC，BF= BC，∴BE：BF=1：，∴△BGE的面积：△BCF的面积=1：5，∴S四边形ECFG=4S△BGE，故④错误．故选：B．【分析】首先证明△ABE≌△BCF，再利用角的关系求得∠BGE=90°，即可得到①AE=BF；②AE⊥BF；△BCF沿BF对折，得到△BPF，利用角的关系求出QF=QB ，解出BP，QB，根据正弦的定义即可求解；根据AA可证△BGE与△BCF相似，进一步得到相似比，再根据相似三角形的性质即可求解．本题主要考查了四边形的综合题，涉及正方形的性质、全等三角形的判定和性质、相似三角形的判定和性质以及折叠的性质的知识点，解决的关键是明确三角形翻转后边的大小不变，找准对应边，角的关系求解．17、【答案】D【考点】二次函数的图象，二次函数的性质，菱形的判定【解析】【解答】解：①∵抛物线y=ax2+bx+c（a≠0）与x轴交于点A（﹣2，0）、B（1，0），∴该抛物线的对称轴为x=﹣=﹣0.5，∴a=b，a﹣b=0，①正确；②∵抛物线开口向下，且抛物线与x轴交于点A（﹣2，0）、B（1，0），∴当﹣2＜x＜1时，y＞0，②正确；③∵点A、B关于x=0.5对称，∴AM=BM，又∵MC=MD，且CD⊥AB，∴四边形ACBD是菱形，③正确；④当x=﹣3时，y＜0，即y=9a﹣3b+c＜0，④错误．综上可知：正确的结论为①②③．故选D．【分析】①由抛物线与x轴的两交点坐标即可得出抛物线的对称轴为x=﹣=﹣0.5，由此即可得出a=b，①正确；②根据抛物线的开口向下以及抛物线与x轴的两交点坐标，即可得出当﹣2＜x＜1时，y＞0，②正确；③由AB关于x=0.5对称，即可得出AM=BM，再结合MC=MD以及CD⊥AB，即可得出四边形ACBD是菱形，③正确；④根据当x=﹣3时，y＜0，即可得出9a﹣3b+c＜0，④错误．综上即可得出结论．本题考查了二次函数的图象、二次函数的性质以及菱形的判定，解题的关键是逐条分析四条结论是否正确．本题属于中档题，难度不大，解决该题型题目时，根据给定的函数图象结合二次函数的性质逐条分析给定的结论是关键．18、【答案】D【考点】全等三角形的判定与性质，正方形的性质，翻折变换（折叠问题）【解析】【解答】解：∵正方形ABCD的边长为6，CE=2DE，∴DE=2，EC=4，∵把△ADE沿AE折叠使△ADE落在△AFE的位置，∴AF=AD=6，EF=ED=2，∠AFE=∠D=90°，∠FAE=∠DAE，在Rt△ABG和Rt△AFG中，∴Rt△ABG≌Rt△AFG（HL），∴GB=GF，∠BAG=∠FAG，∴∠GAE=∠FAE+∠FAG= ∠BAD=45°，所以①正确；设BG=x，则GF=x，C=BC﹣BG=6﹣x，在Rt△CGE中，GE=x+2，EC=4，CG=6﹣x，∵CG2+CE2=GE2，∴（6﹣x）2+42=（x+2）2，解得x=3，∴BG=3，CG=6﹣3=3∴BG=CG，所以②正确；∵EF=ED，GB=GF，∴GE=GF+EF=BG+DE，所以③正确；∵GF=GC，∴∠GFC=∠GCF，又∵Rt△ABG≌Rt△AFG，∴∠AGB=∠AGF，而∠BGF=∠GFC+∠GCF，∴∠AGB+∠AGF=∠GFC+∠GCF，∴∠AGB=∠GCF，∴CF∥AG，所以④正确；过F作FH⊥DC∵BC⊥DH，∴FH∥GC，∴△EFH∽△EGC，∴，EF=DE=2，GF=3，∴EG=5，∴△EFH∽△EGC，∴相似比为：= ，∴S△FGC=S△GCE﹣S△FEC= ×3×4﹣×4×（×3）= =3.6，所以⑤正确．故正确的有①②③④⑤，故选：D．【分析】先计算出DE=2，EC=4，再根据折叠的性质AF=AD=6，EF=ED=2，∠AFE=∠D=90°，∠FAE=∠DAE，然后根据“HL”可证明Rt△ABG≌Rt△AFG，则GB=GF，∠BAG=∠FAG，所以∠GAE= ∠BAD=45°；GE=GF+EF=BG+DE；设BG=x，则GF=x，CG=BC﹣BG=6﹣x，在Rt△CGE中，根据勾股定理得（6﹣x）2+42=（x+2）2，解得x=3，则BG=CG=3，则点G为BC的中点；同时得到GF=GC，根据等腰三角形的性质得∠GFC=∠GCF，再由Rt△ABG≌Rt△AFG得到∠AGB=∠AGF，然后根据三角形外角性质得∠BGF=∠GFC+∠GCF，易得∠AGB=∠GCF，根据平行线的判定方法得到CF∥AG；过F作FH⊥DC，则△EFH∽△EGC，△EFH∽△EGC，由相似比为，可计算S△FGC．本题考查了折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．也考查了三角形全等的判定与性质、勾股定理和正方形的性质．19、【答案】C【考点】垂径定理，圆周角定理，相似三角形的判定与性质，解直角三角形【解析】【解答】解：①∵AB是⊙O的直径，弦CD⊥AB，∴，DG=CG，∴∠ADF=∠AED，∵∠FAD=∠DAE（公共角），∴△ADF∽△AED；故①正确；②∵= ，CF=2，∴FD=6，∴CD=DF+CF=8，∴CG=DG=4，∴FG=CG﹣CF=2；故②正确；③∵AF=3，FG=2，∴AG= = ，∴在Rt△AGD中，tan∠ADG= = ，∴tan∠E= ；故③错误；④∵DF=DG+FG=6，AD= = ，∴S△ADF= DF•AG= ×6×=3 ，∵△ADF∽△AED，∴=（）2，∴= ，∴S△AED=7 ，∴S△DEF=S△AED﹣S△ADF=4 ；故④正确．故选C．【分析】①正确．由AB是⊙O的直径，弦CD⊥AB，根据垂径定理可得：，DG=CG，继而证得△ADF∽△AED；②正确．由= ，CF=2，可求得DF的长，继而求得CG=DG=4，则可求得FG=2；③错误．由勾股定理可求得AG的长，即可求得tan∠ADF的值，继而求得tan∠E=．④首先求得△ADF的面积，由相似三角形面积的比等于相似比的平方，即可求得△ADE的面积，继而求得S△DEF=4 ．20、【答案】D【考点】垂径定理，圆周角定理，相似三角形的判定与性质【解析】【解答】解：∵在⊙O中，点C是的中点，∴= ，∴∠CAD=∠ABC，故①正确；∵≠ ，∴≠ ，∴AD≠BC，故②错误；∵AB是⊙O的直径，∴∠ACB=90°，又∵CE⊥AB，∴∠ACE+∠CAE=∠ABC+∠CAE=90°，∴∠ACE=∠ABC，又∵C为的中点，∴= ，∴∠CAP=∠ABC，∴∠ACE=∠CAP，∴AP=CP，∵∠ACQ=90°，∴∠ACP+∠PCQ=∠CAP+∠PQC=90°，∴∠PCQ=∠PQC，∴PC=PQ，∴AP=PQ，即P为Rt△ACQ斜边AQ的中点，∴P为Rt△ACQ的外心，故③正确；∵AB是⊙O的直径，∴∠ACB=90°，又∵CE⊥AB∴根据射影定理，可得AC2=AE•AB，故④正确；如图，连接BD，则∠ADG=∠ABD，∵≠ ，∴≠ ，∴∠ABD≠∠BAC，∴∠ADG≠∠BAC，又∵∠BAC=∠BCE=∠PQC，∴∠ADG≠∠PQC，∴CB与GD不平行，故⑤错误．故答案为：D．【分析】在同圆或等圆中，同弧或等弧所对的圆周角相等，据此推理可得①正确，②错误；通过推理可得∠ACE=∠CAP，得出AP=CP，再根据∠PCQ=∠PQC，可得出PC=PQ，进而得到AP=PQ，即P为Rt△ACQ斜边AQ的中点，故P为Rt△ACQ 的外心，即可得出③正确；连接BD，则∠ADG=∠ABD，根据∠ADG≠∠BAC，∠BAC=∠BCE=∠PQC，可得出∠ADG≠∠PQC，进而得到CB与GD不平行，可得⑤错误．。

中考数学几何多结论问题

∴正确的有4个．故选D.
3. 如图，P为正方形ABCD的对角线BD上任一
点，过点P作PE⊥BC于点E，PF⊥CD于点F，
连接EF.给出以下4个结论：
①△FPD是等腰直角三角形；②AP＝EF；③
AD＝PD；④∠PFE＝∠BAP.
其中，所有正确的结论是( )
A. ①②
B. ①④
C. ①②④
D. ①③④
∴FH≠FD， ∴S△EFH≠S△EFD， ∴S四边形EFHG＝S△HEG＋S△EFH＝S△AHG＋ S△EFH≠S△DEF＋S△AGH，故③错误，
18. 如图，点E，F分别为正方形ABCD的边BC，
CD上一点，AC，BD交于点O，且∠EAF＝
45°，AE，AF分别交对角线BD于点M，N，
则有以下结论：①△AOM∽△ADF；②EF＝
∵CG＝GF，∴∠CFG＝∠FCG， ∵∠BGF＝∠CFG＋∠FCG，又∵∠BGF＝∠AGB＋∠AGF， ∴∠CFG＋∠FCG＝∠AGB＋∠AGF， ∵∠AGB＝∠AGF，∠CFG＝∠FCG， ∴∠AGB＝∠FCG， ∴AG∥CF， ∴④正确；
8. 如图，在菱形ABCD中，AB＝6，∠DAB＝
60°，AE分别交BC，BD于点E，F，CE＝2，
连接CF，以下结论：①△ABF≌△CBF；②
点E到AB的距离是；③AF＝CF；④△ABF
的面积为 .其中一定成立的有( )个
A. 1
B. 2
C. 3 D. 4
10. 如图，在正方形ABCD中，E，F分别为BC，
CD的中点，连接AE，BF交于点G，将△BCF
11. 如图，正方形ABCD边长为6，E是BC的中
点，连接AE，以AE为边在正方形内部作
∠EAF＝45°，边AF交CD于F，连接EF.则下

2022年九年级数学中考专题十一几何多结论题

专题11 几何多结论选择题一．试题（共14小题）1．如图，矩形ABCD中，AC，BD相交于点O，过点B作BF⊥AC交CD于点F，交AC于点M，过点D作DE ∥BF交AB于点E，交AC于点N，连接FN，EM．则下列结论：①DN＝BM；②EM∥FN；③AE＝FC；④当AO＝AD时，四边形DEBF是菱形．其中，正确的结论是（）A．①③B．①②③C．①③④D．①②③④2．如图，四边形ABCD是平行四边形，点E是边CD上一点，且BC＝EC，CF⊥BE交AB于点F，P是EB延长线上一点，下列结论：①BE平分∠CBF；②CF平分∠DCB；③BC＝FB；④PF＝PC．其中正确结论的个数为（）A．1B．2C．3D．43．如图，在△AOB和△COD中，OA＝OB，OC＝OD，OA＜OC，∠AOB＝∠COD＝36°．连接AC，BD交于点M，连接OM．下列结论：①∠AMB＝36°，②AC＝BD，③OM平分∠AOD，④MO平分∠AMD．其中正确的结论个数有（）个．A．4B．3C．2D．14．如图，在△ABC中，AB＝AC，AD和CE是高，∠ACE＝45°，点F是AC的中点，AD与FE，CE分别交于点G、H，∠BCE＝∠CAD，有下列结论：①图中存在两个等腰直角三角形；②△AHE≌△CBE；③BC•AD=√2AE2；④S△ABC＝4S△ADF．其中正确的个数有（）A ．1B ．2C ．3D ．45．已知如图等腰△ABC ，AB ＝AC ，∠BAC ＝120°，AD ⊥BC 于点D ．点P 是BA 延长线上一点，O 点是线段AD 上一点，OP ＝OC ，下面的结论：①AC 平分∠P AD ；②∠APO ＝∠DCO ；③△OPC 是等边三角形；④AC ＝AO +AP ；⑤S △ABC ＝S 四边形AOCP ．其中正确的序号是．6．如图，分别以Rt △ABC 的斜边AB ，直角边AC 为边向外作等边△ABD 和等边△ACE ，F 为AB 的中点，DE ，AB 相交于点G ，若∠BAC ＝30°，下列结论：①EF ⊥AC ；②四边形ADFE 为菱形；③AD ＝4AG ；④△DBF ≌△EF A ．其中正确结论的个数有（）A ．1B ．2C ．3D ．47．如图，在矩形ABCD 中，AD =√2AB ，AE 平分∠BAD ，DF ⊥AE 于F ，BF 交DE 、CD 于O 、H ，下列结论：①∠DEA ＝∠DEC ；②BF ＝FH ；③OE ＝OD ；④BC ﹣CH ＝2EF ；⑤AB ＝HF ，其中正确结论的个数是（）A ．2个B ．3个C ．4个D ．5个 8．如图，平行四边形ABCD 的对角线AC ，BD 相交于点O ，AE 平分∠BAD ，分别交BC ，BD 于点E ，P ，连接OE ，∠ADC ＝60°，AB =12BC ＝2，下列结论：①∠CAD ＝30°；②BD ＝2√7；③S 四边形ABCD ＝AB •AC ；④OE =14AD ；⑤S △BOE =√32．其中正确的个数有（）个A．2B．3C．4D．59．如图，在等腰Rt△ABC中，AB＝AC，过A作直线交BC于G，BG＜GC，BD⊥AG于D，CE⊥AD于E，F 为BC边中点，则下列结论中：①∠BAD＝∠ACE；②BD＝CE﹣ED；③FE＝FD；④EF⊥DF，其中正确结论的个数为（）A．1个B．2个C．3个D．4个10．如图，已知△ABC和△ADE都是等腰三角形，∠BAC＝∠DAE＝90°，BD，CE交于点F，连接AF．下列结论：①BD＝CE；②BF⊥CF；③AF平分∠CAD；④∠AFE＝45°．其中正确结论的个数有（）A．1个B．2个C．3个D．4个11．如图，矩形ABCD中，O为AC中点，过点O的直线分别与AB、CD交于点E、F，连接BF交AC于点M，连接DE、BO．若∠COB＝60°，FO＝FC，则下列结论：①FB垂直平分OC；②△EOB≌△CMB；③DE＝EF；④S△AOE：S△BCM＝3：2．其中正确结论的个数是（）A．4个B．3个C．2个D．1个12．如图，在平行四边形ABCD中，AD＝2AB，CE⊥AB于点E，点F、G分别是AD、BC的中点，连接CF、EF、FG，下列结论：①CE⊥FG；②四边形ABGF是菱形；③EF＝CF；④∠EFC＝2∠CFD．其中正确的个数是（）A．1个B．2个C．3个D．4个13．如图，AB是⊙O的直径，C，D是⊙O上的点，且OC∥BD，AD分别与BC，OC相交于点E，F，则下列结论：①AD⊥BD；②∠AOC＝∠AEC；③BC平分∠ABD；④AF＝DF；⑤BD＝2OF．其中正确结论的个数是（）A．2B．3C．4D．514．如图，△ABC中，AB＝AC，以AB为直径的⊙O交AC于E，交BC于D，DF⊥AC于F．给出以下五个结论：①BD＝DC；②CF＝EF；③弧AE＝弧DE；④∠A＝2∠FDC；⑤DF是⊙O的切线．其中正确的有（）A．5个B．4个C．3个D．2个专题11 几何多结论选择题参考答案与试题解析一．试题（共14小题）1．【解答】解：∵四边形ABCD 是矩形，∴AB ＝CD ，AB ∥CD ，∠DAE ＝∠BCF ＝90°，OD ＝OB ＝OA ＝OC ，AD ＝BC ，AD ∥BC ， ∴∠DAN ＝∠BCM ，∵BF ⊥AC ，DE ∥BF ，∴DE ⊥AC ，∴∠DNA ＝∠BMC ＝90°，在△DNA 和△BMC 中，{∠DAN =∠BCM ∠DNA =∠BMC AD =BC，∴△DNA ≌△BMC （AAS ），∴DN ＝BM ，∠ADE ＝∠CBF ，故①正确；在△ADE 和△CBF 中，{∠ADE =∠CBF AD =BC ∠DAE =∠BCF，∴△ADE ≌△CBF （ASA ），∴AE ＝FC ，DE ＝BF ，故③正确；∴DE ﹣DN ＝BF ﹣BM ，即NE ＝MF ，∵DE ∥BF ，∴四边形NEMF 是平行四边形，∴EM ∥FN ，故②正确；∵AB ＝CD ，AE ＝CF ，∴BE ＝DF ，∵BE ∥DF ，∴四边形DEBF 是平行四边形，∵AO ＝AD ，∴AO ＝AD ＝OD ，∴△AOD 是等边三角形，∴∠ADO ＝∠DAN ＝60°，∴∠ABD ＝90°﹣∠ADO ＝30°，∵DE ⊥AC ，∴∠ADN ＝∠ODN ＝30°，∴∠ODN ＝∠ABD ，∴DE ＝BE ，∴四边形DEBF 是菱形；故④正确；故选：D ．2．【解答】证明：∵BC ＝EC ，∴∠CEB ＝∠CBE ，∵四边形ABCD 是平行四边形，∴DC ∥AB ，∴∠CEB＝∠EBF，∴∠CBE＝∠EBF，∴①BE平分∠CBF，正确；∵BC＝EC，CF⊥BE，∴∠ECF＝∠BCF，∴②CF平分∠DCB，正确；∵DC∥AB，∴∠DCF＝∠CFB，∵∠ECF＝∠BCF，∴∠CFB＝∠BCF，∴BF＝BC，∴③正确；∵FB＝BC，CF⊥BE，∴B点一定在FC的垂直平分线上，即PB垂直平分FC，∴PF＝PC，故④正确．故选：D．3．【解答】解：∵∠AOB＝∠COD＝36°，∴∠AOB+∠BOC＝∠COD+∠BOC，即∠AOC＝∠BOD，在△AOC和△BOD中，{OA=OB∠AOC=∠BOD OC=OD∴△AOC≌△BOD（SAS），∴∠OCA＝∠ODB，AC＝BD，故②正确；∵∠OAC＝∠OBD，由三角形的外角性质得：∠AMB+∠OBD＝∠OAC+∠AOB，∴∠AMB＝∠AOB＝36°，故①正确；法一：作OG⊥AM于G，OH⊥DM于H，如图所示，则∠OGA＝∠OHB＝90°，∵△AOC≌△BOD，∴OG ＝OH ，∴MO 平分∠AMD ，故④正确；法二：∵△AOC ≌△BOD ，∴∠OAC ＝∠OBD ，∴A 、B 、M 、O 四点共圆，∴∠AMO ＝∠ABO ＝72°，同理可得：D 、C 、M 、O 四点共圆，∴∠DMO ＝∠DCO ＝72°＝∠AMO ，∴MO 平分∠AMD ，故④正确；假设MO 平分∠AOD ，则∠DOM ＝∠AOM ，在△AMO 与△DMO 中，{∠AOM =∠DOMOM =OM ∠AMO =∠DMO，∴△AMO ≌△DMO （ASA ），∴AO ＝OD ，∵OC ＝OD ，∴OA ＝OC ，而OA ＜OC ，故③错误；正确的个数有3个；故选：B ．4．【解答】解：∵CE ⊥AB ，∠ACE ＝45°，∴△ACE 是等腰直角三角形，∵AF ＝CF ，∴EF ＝AF ＝CF ，∴△AEF ，△EFC 都是等腰直角三角形，∴图中共有3个等腰直角三角形，故①错误，∵∠AHE +∠EAH ＝90°，∠DHC +∠BCE ＝90°，∠AHE ＝∠DHC ，∴∠EAH ＝∠BCE ，∵AE ＝EC ，∠AEH ＝∠CEB ＝90°，∴△AHE ≌△CBE ，故②正确，∵S △ABC =12BC •AD =12AB •CE ，AB ＝AC =√2AE ，AE ＝CE ，∴BC •AD =√2CE 2，故③正确，∵AB ＝AC ，AD ⊥BC ，∴BD ＝DC ，∴S △ABC ＝2S △ADC ，∵AF ＝FC ，∴S △ADC ＝2S △ADF ，∴S △ABC ＝4S △ADF ．故选：C ．5．【解答】解：①∵AB＝AC，∠BAC＝120°，AD⊥BC；∴∠CAD=12∠BAC＝60°，∠P AC＝180°﹣∠CAB＝60°，∴∠P AC＝∠DAC，∴AC平分∠P AD故①正确；②由①知：∠APO＝∠ABO，∠DCO＝∠DBO，∵点O是线段AD上一点，∴∠ABO与∠DBO不一定相等，则∠APO与∠DCO不一定相等，故②不正确；③∵∠APC+∠DCP+∠PBC＝180°，∴∠APC+∠DCP＝150°，∵∠APO+∠DCO＝30°，∴∠OPC+∠OCP＝120°，∴∠POC＝180°﹣（∠OPC+∠OCP）＝60°，∵OP＝OC，∴△OPC是等边三角形；故③正确；④如图2，在AC上截取AE＝P A，连接PB，∵∠P AE＝180°﹣∠BAC＝60°，∴△APE是等边三角形，∴∠PEA＝∠APE＝60°，PE＝P A，∴∠APO+∠OPE＝60°，∵∠OPE+∠CPE＝∠CPO＝60°，∴∠APO＝∠CPE，∵OP＝CP，在△OP A和△CPE中，{PA=PE∠APO=∠CPE OP=CP，∴△OP A≌△CPE（SAS），∴AO＝CE，∴AC＝AE+CE＝AO+AP；故④正确；如图3，过点C作CH⊥AB于H，∵∠P AC＝∠DAC＝60°，AD⊥BC，∴CH＝CD，∴S△ABC=12AB•CH，S 四边形AOCP ＝S △ACP +S △AOC =12AP •CH +12OA •CD =12AP •CH +12OA •CH =12H •（AP +OA ）=12CH •AC ， ∴S △ABC ＝S 四边形AOCP ；故⑤正确．本题正确的结论有：①③④⑤故答案为：①③④⑤．6．【解答】解：连接FC ，如图所示：∵∠ACB ＝90°，F 为AB 的中点，∴F A ＝FB ＝FC ，∵△ACE 是等边三角形，∴EA ＝EC ，∵F A ＝FC ，EA ＝EC ，∴点F 、点E 都在线段AC 的垂直平分线上，∴EF 垂直平分AC ，即EF ⊥AC ；∵△ABD 和△ACE 都是等边三角形，F 为AB 的中点，∴DF ⊥AB 即∠DF A ＝90°，BD ＝DA ＝AB ＝2AF ，∠DBA ＝∠DAB ＝∠EAC ＝∠ACE ＝60°． ∵∠BAC ＝30°，∴∠DAC ＝∠EAF ＝90°，∴∠DF A ＝∠EAF ＝90°，DA ⊥AC ，∴DF ∥AE ，DA ∥EF ，∴四边形ADFE 为平行四边形而不是菱形；∵四边形ADFE 为平行四边形，∴DA ＝EF ，AF ＝2AG ，∴BD ＝DA ＝EF ，DA ＝AB ＝2AF ＝4AG ；在△DBF 和△EF A 中，{BD =FE ∠DBF =∠EFA BF =FA，∴△DBF ≌△EF A ；综上所述：①③④正确，故选：C ．7．【解答】解：∵四边形ABCD为矩形，AE平分∠BAD，∴∠BAE＝∠DAE＝∠AEB＝45°，∵∠AFD＝∠ABE＝90°，∴△AFD与△ABE都为等腰直角三角形，即AF＝DF，AB＝BE，∴AE=√2AB，又∵AD=√2AB，∴AD＝AE，∴∠AED＝∠ADE＝67.5°，∴∠DEC＝180°﹣45°﹣67.5°＝67.5°，∴∠DEA＝∠DEC，选项①正确；过F作GM⊥AD，与AD交于G点，与BC交于M点，利用三线合一得到G为AD中点，∴F为BH中点，M为BC中点，∴BF＝FH，选项②正确；∵AD=√2AF，AD=√2AB，∴AF＝AB，∴∠AFB＝67.5°，∴∠OFE＝∠OEF＝67.5°，∴OE＝OF，∴∠ODF＝∠OFD＝22.5°，∴OF＝OD，∴OD＝OE，选项③正确；∴∠DEF＝67.5°﹣45°＝22.5°，∠EDC＝90°﹣67.5°＝22.5°，∴∠EDF＝∠DEC，∵EF⊥DF，EC⊥CD，∴EF＝EC，∵△EFM为等腰直角三角形，∴FM＝ME，∴BC﹣CH＝2CM﹣2FM＝2CM﹣2ME＝2EF，选项④正确；∵AB＝AF，∠BAE＝45°，∴△ABF不是等边三角形，∴AB≠BF，∴即AB≠HF，故⑤错误；综上所述，结论正确的是①②③④．则正确的序号有4个．故选：C．8．【解答】解：①∵AE平分∠BAD，∴∠BAE＝∠DAE，∵四边形ABCD是平行四边形，∴AD∥BC，∠ABC＝∠ADC＝60°，∴∠DAE＝∠BEA，∴∠BAE＝∠BEA，∴AB＝BE＝2，∴△ABE是等边三角形，∴AE＝BE＝2，∵BC＝4，∴EC＝2，∴AE＝EC，∴∠EAC＝∠ACE，∵∠AEB＝∠EAC+∠ACE＝60°，∴∠ACE＝30°，∵AD∥BC，∴∠CAD＝∠ACE＝30°，故①正确；②∵BE＝EC，OA＝OC，∴OE=12AB＝1，OE∥AB，∴∠EOC＝∠BAC＝60°+30°＝90°，Rt△EOC中，OC=√EC2−OE2=√3，∵四边形ABCD是平行四边形，∴∠BCD＝∠BAD＝120°，∴∠ACB＝30°，∴∠ACD＝90°，Rt△OCD中，OD=√OC2+CD2=√7 BD＝2OD＝2√7故②正确③由②知：∠BAC＝90°，∴S▱ABCD＝AB•AC，故③正确；④由②知：OE是△ABC的中位线，∴OE=12AB，∵AB=12BC，∴OE=14BC=14AD，故④正确；⑤∵BE＝EC＝2∴S△BOE＝S△EOC=12OE•OC=√32故⑤正确故选：D．9．【解答】解：如图连接AF．∵AB＝AC，BF＝FC，∴AF⊥BC，∵BD⊥AD，CE⊥AD，∴∠ADB＝∠AEC＝∠BAC＝90°，∵∠CAE+∠BAD＝90°，∠BAD+∠ABD＝90°，∴∠CAE＝∠ABD，故①正确，∴△ABD≌△CAE（AAS），∴BD＝AE，AD＝CE，∴CE﹣ED＝AD﹣DE＝AE＝BD，故②正确，∵∠BAC＝90°，BF＝FC，∴AF＝BF＝FC，∵∠AGF＝∠BGF，∠BDG＝∠AFG＝90°，∴∠DBG＝∠GAF，∵AE＝BD，∴△FBD≌△FEA（SAS），∴EF＝DF，∠AFE＝∠BFD，∴∠AFB＝∠EFD＝90°，∴EF⊥DF，故③④正确．故选：D．10．【解答】解：如图，作AM⊥BD于M，AN⊥EC于N，设AD交EF于O．∵∠BAC＝∠DAE＝90°，∴∠BAD＝∠CAE，∵AB＝AC，AD＝AE，∴△BAD≌△CAE（SAS），∴EC＝BD，∠BDA＝∠AEC，故①正确∵∠DOF＝∠AOE，∴∠DFO＝∠EAO＝90°，∴BD⊥EC，故②正确，∵△BAD≌△CAE，AM⊥BD，AN⊥EC，∴AM＝AN，∴F A平分∠EFB，∴∠AFE＝45°，故④正确，若③成立，则∠EAF＝∠BAF，∵∠AFE＝∠AFB，∴∠AEF＝∠ABD＝∠ADB，推出AB＝AD，由题意知，AB不一定等于AD，所以AF不一定平分∠CAD，故③错误，故选：C．11．【解答】解：①∵矩形ABCD中，O为AC中点，∴OB＝OC，∵∠COB＝60°，∴△OBC是等边三角形，∴OB＝BC，∵FO＝FC，∴FB垂直平分OC，故①正确；②∵△BOC为等边三角形，FO＝FC，∴BO⊥EF，BF⊥OC，∴∠CMB＝∠EOB＝90°，∴BO≠BM，∴△EOB与△CMB不全等；故②错误；③易知△ADE≌△CBF，∠1＝∠2＝∠3＝30°，∴∠ADE＝∠CBF＝30°，∠BEO＝60°，∴∠CDE＝60°，∠DFE＝∠BEO＝60°，∴∠CDE＝∠DFE，∴DE＝EF，故③正确；④易知△AOE≌△COF，∴S△AOE＝S△COF，∵S△COF＝2S△CMF，∴S△AOE：S△BCM＝2S△CMF：S△BCM=2FMBM，∵∠FCO＝30°，∴FM=CM√3，BM=√3CM，∴FMBM=13，∴S△AOE：S△BCM＝2：3，故④错误；所以其中正确结论的个数为2个；故选：C．12．【解答】解：∵四边形ABCD是平行四边形，∴AD∥BC，AD＝BC，∵点F、G分别是AD、BC的中点，∴AF=12AD，BG=12BC，∴AF＝BG，∵AF∥BG，∴四边形ABGF是平行四边形，∴AB∥FG，∵CE⊥AB，∴CE⊥FG；故①正确；∵AD＝2AB，AD＝2AF，∴AB＝AF，∴四边形ABGF是菱形，故②正确；延长EF，交CD延长线于M，∵四边形ABCD是平行四边形，∴AB∥CD，∴∠A＝∠MDF，∵F为AD中点，∴AF＝FD，在△AEF和△DFM中，{∠A=∠FDM AF=DF∠AFE=∠DFM，∴△AEF≌△DMF（ASA），∴FE＝MF，∠AEF＝∠M，∵CE⊥AB，∴∠AEC＝90°，∴∠AEC＝∠ECD＝90°，∵FM＝EF，∴FC＝EF＝FM，故③正确；∴∠FCD＝∠M，∵四边形ABCD是平行四边形，∴AB＝CD，AD∥BC，∵AF＝DF，AD＝2AB，∴DF＝DC，∴∠DCF＝∠DFC，∴∠M＝∠FCD＝∠CFD，∵∠EFC＝∠M+∠FCD＝2∠CFD；故④正确，故选：D．13．【解答】解：∵AB是⊙O的直径，∴∠ADB＝90°，即AD⊥BD，故①正确；∵∠AEC＝∠DAB+∠EBA，∠AOC＝2∠EBA，∴∠AOC≠∠AEC，故②不正确；∵OC∥BD，∴∠OCB＝∠CBD，∵OC＝OB，∴∠OCB＝∠OBC，∴∠OBC＝∠CBD，即BC平分∠ABD，故③正确；∴OC⊥AD，∴AF＝FD，故④正确；∴OF为△ABD的中位线，∴BD＝2OF，故⑤正确，综上可知正确的有4个，故选：C．14．【解答】解：连接OD，AD．∵AB是⊙O的直径，∴∠ADB＝90°（直径所对的圆周角是直角），∴AD⊥BC；而在△ABC中，AB＝AC，∴AD是边BC上的中线，∴BD＝DC（正确）；∵AB是⊙O的直径，∴AD⊥BC，∵AB＝AC，∴DB＝DC，∵OA＝OB，∴OD是△ABC的中位线，即：OD∥AC，∵DF⊥AC，∴DF⊥OD．∴DF是⊙O的切线（正确）；∵DF⊥AC，AD⊥BC，∴∠FDC+∠C＝∠CAD+∠C＝90°，∴∠FDC＝∠CAD，又AB＝AC，∴∠BAD＝∠CAD，∴∠A＝2∠CAD＝2∠FDC（正确）；∵DF是⊙O的切线，∴∠FDE＝∠CAD＝∠FDC，∴∠C＝∠DEC，∴DC＝DE，又DF⊥AC，∴CF＝EF（正确）；̂=DÊ，此时△ABC为等边三角形，当∠EAD＝∠EDA时，AE当△ABC不是等边三角形时，∠EAD≠∠EDA，̂≠DÊ，则AÊ=DÊ（不正确）；∴AE综上，正确结论的序号是①②④⑤，故选：B．。

立体几何结论Microsoft Word 文档

P H M N G EC 'B'D 'CDFA'AB图1立体几何中的若干实用小结论1、三个平面两两相交，其三条交线要么共点，要么互相平行.2、设E ，F ，G 分别是正方体D C B A ABCD ''''-的棱AD ，AB ，B B '的中点，则该正方体过E ，F ，G 三点的截面为正六边形.3、一个四面体有两组对棱互相垂直，则其第三组对棱也互相垂直，且这时每一个顶点在对面三角形所在平面内的射影，都是该三角形的垂心；反之也成立.（特别地，正四面体的三组对棱都互相垂直，且每一个顶点在对面正三角形所在平面内的射影，都是该正三角形的中心）.4、过空间任意一点P ，与两条异面直线a ，b 都平行的平面有0个或1个.5、与两条异面直线a ，b 都相交的两条直线c ，d 不一定是异面直线（注：异面或相交）. 7、平行六面体有12条棱，12条面对角线，4条体对角线. 在这28条直线中，平行直线有 24对，相交直线有180对，异面直线有174对.8、若异面直线AB 与CD 所成的角θ，过点P 的直线l 与直线AB 与CD 所成的角都为γ，则当2θγ=时直线l 只有一条；当22θπγθ-<< 时直线l 只有两条；当2θπγ-=时时直线l 只有三条；当22πγθπ<<-时时直线l 只有四条；9、任意一个四面体PABC 都可补成一个平行六面体B P A C ADB C ''-'，且四面体PABC 的体积等于对应平行六面体B P A C ADB C ''-'的体积的三分之一.（特别地，①任意一个正四面体都可补成一个正方体；②任意一个三组对棱分别相等的四面体都可补成一个长方体③若四面体PABC 满足PB PA ⊥，PC PB ⊥，PA PC ⊥，则该四面体可补成一个长方体B P A C ADB C ''-'，如图3所示.A'C'P'C BAPB'图310、设正四面体的棱长为a ，表面积为S ，体积为V ，相邻两个面所成二面角为α，内切球半径为r ，外接球半径为R ，高为h 则有：① 23a S =；② 3122a V =； ③ 31cos =α，322sin =α，22tan =α；④ a r 126=；⑤ a R 46=；⑥ a h 36=，r h 4=，r R 3= 且球心在高线上分高线长为3：1即R 与r .11、任意一个四面体都有一个内切球和一个外接球.（特别地正三棱锥侧棱为b ,底面边长为a ,内切球半径为r ，外接球半径为R ，高为h 则有：h b R 22=，表S Vr 3=；12、最小角定理：21cos cos cos θθθ=（1θ为最小角，如图）13、特殊棱锥的顶点在底面的射影位置：①棱锥的侧棱长均相等，则顶点在底面上的射影为底面多边形的外心.②棱锥的侧棱与底面所成的角均相等，则顶点在底面上的射影为底面多边形的外心. ③棱锥的各侧面与底面所成角均相等，则顶点在底面上的射影为底面多边形内心. ④棱锥的顶点到底面各边距离相等，则顶点在底面上的射影为底面多边形内心. ⑤三棱锥有两组对棱垂直，则顶点在底面的射影为三角形垂心. ⑥三棱锥的三条侧棱两两垂直，则顶点在底面上的射影为三角形的垂心.⑦每个四面体都有外接球，球心0是各条棱的中垂面的交点，此点到各顶点的距离等于球半径；⑧每个四面体都有内切球，球心I 是四面体各个二面角的平分面的交点，到各面的距离等于半径. [注]：i. 各个侧面都是等腰三角形，且底面是正方形的棱锥是正四棱锥.（×）（各个侧面的等腰三角形不知是否全等）ii. 若一个三棱锥，两条相对棱互相垂直，则第三组相对棱必然垂直.iii. 空间四边形OABC 且四边长相等，则顺次连结各边的中点的四边形一定是矩形. iv. 若是四边长与对角线分别相等，则顺次连结各边的中点的四边是一定是正方形.Or14、向量的常用方法：①利用法向量求点到面的距离定理：如图，设n 是平面α的法向量，AB 是平面α的一条射线，其中α∈A ，则点B 到平面α的距离为||||n n AB ∙.②.异面直线间的距离 nn CD d ∙=(12,l l 是两异面直线，其公垂向量为n ，C D 、分别是12,l l 上任一点，d 为12,l l 间的距离).③.直线AB 与平面所成角sin||||AB marc AB m β⋅=(m 为平面α的法向量).④.利用法向量求二面角的平面角定理：设21,n n 分别是二面角βα--l 中平面βα,的法向量，则21,n n 所成的角就是所求二面角的平面角或其补角大小（21,n n 方向相同，则为补角，21,n n 反方，则为其夹角）.二面角l αβ--的平面角cos||||m n arc m n θ⋅=或cos ||||m narc m n π⋅-（m ，n 为平面α，β的法向量）.（5）证直线和平面平行定理：已知直线⊄a 平面α，α∈∈D C a B A ,,,，且C 、D 、E 三点不共线，则a ∥α的充要条件是存在有序实数对μλ,使CE CD AB μλ+=.（常设CE CD AB μλ+=求解μλ,若μλ,存在即证毕，若μλ,不存在，则直线AB 与平面相交）.α▲nBCAαβ▲n 2n 1αCED AB。

立体几何常见结论

立体几何常见结论1．平面平面的基本性质：掌握三个公理及推论，会说明共点、共线、共面问题。

（1）.证明点共线的问题，一般转化为证明这些点是某两个平面的公共点(依据：由点在线上，线在面内，推出点在面内），这样可根据公理2证明这些点都在这两个平面的公共直线上.（2).证明共点问题,一般是先证明两条直线交于一点，再证明这点在第三条直线上，而这一点是两个平面的公共点，这第三条直线是这两个平面的交线。

（3）。

证共面问题一般先根据一部分条件确定一个平面，然后再证明其余的也在这个平面内，或者用同一法证明两平面重合 2。

空间直线。

(1). 空间直线位置关系三种:相交、平行、异面. 相交直线：共面有且仅有一个公共点；平行直线:共面没有公共点;异面直线：不同在任一平面内,无公共点［注］:①两条异面直线在同一平面内射影一定是相交的两条直线.（×）（也可能两条直线平行，也可能是点和直线等）②直线在平面外，指的位置关系是平行或相交③若直线a 、b 异面，a 平行于平面α，b 与α的关系是相交、平行、在平面α内. ④两条平行线在同一平面内的射影图形是一条直线或两条平行线或两点。

⑤在平面内射影是直线的图形一定是直线.（×）（射影不一定只有直线，也可以是其他图形） ⑥在同一平面内的射影长相等，则斜线长相等。

（×)（并非是从平面外一点．．向这个平面所引的垂线段和斜线段)⑦b a ,是夹在两平行平面间的线段，若b a =,则b a ,的位置关系为相交或平行或异面.⑧异面直线判定定理:过平面外一点与平面内一点的直线和平面内不经过该点的直线是异面直线。

(不在任何一个平面内的两条直线）（2). 平行公理：平行于同一条直线的两条直线互相平行. 等角定理:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等（如右图）。

(直线与直线所成角]90,0[︒︒∈θ）（向量与向量所成角])180,0[ ∈θ推论:如果两条相交直线和另两条相交直线分别平行，那么这两组直线所成锐角（或直角）相等.（3）. 两异面直线的距离:公垂线段的长度.空间两条直线垂直的情况：相交(共面）垂直和异面垂直.[注］：21,l l 是异面直线,则过21,l l 外一点P ，过点P 且与21,l l 都平行平面有一个或没有，但与21,l l 距离相等的点在同一平面内。

第56课几何型综合问题

∵∠FAN＝90°，∠MAN＝45°， ∴∠1＋∠2＝∠FAM＝∠MAN＝45°，
题型分类·深度剖析
∴△AFM≌△ANM(SAS)，∴FM＝NM， ∵∠FBP＝180°－∠FBA＝180°－135°＝45°， ∴∠FBP＋∠PBM＝45°＋45°＝90°， ∴△FBM是直角三角形，∵FB＝DN，FM＝MN， ∴以BM、DN、MN为三边围成的三角形为直角三角形．
图形来表示代数式；第三步：构造合适的几何图形；第四步：利用几何图形的性质来解答代数问题；第五步：反思回顾，查看关键点、易错点，完善解题步骤．
第56课几何型综合问题
易错警示系列
题型分类·深度剖析
批阅笔记在解数学题时，有些代数问题借助于图形来解，可使抽象的问题变得直观，复杂的问题变得简单，常常使人有茅塞顿开之感．
第56课几何型综合问题
第56课几何型综合问题
要点梳理
基础知识·自主学习
几何型综合题考查知识点多，条件隐晦，要求学生有较强的理解能力、分析能力、解决问题的能力，对数学基础知识、数学基本方法有较强的驾驭能力，并有较强的创新意识和创新能力．
几何论证型综合问题，常以相似形、圆的知识为背景，串联其他几何知识．顺利证明几何问题取决于下列因素：①熟悉各种常见问题的基本证明；②能准确添加基本辅助线；③对复杂图形能进行恰当的分解与组合；④善于选择证题的起点并转化问题．
(3)如图3，当点F在CB的延长线上时，线段PC、PG又有怎样的数量关系，写出你的猜想(不必证明)．
第56课几何型综合问题
题型分类·深度剖析
解 (1)提示：如图1，延长GP交DC于点E，利用△PED≌△PGF，得出PE＝PG，DE＝FG， ∴CE＝CG， ∴CP是EG的中垂线，

初中几何多结论问题

专题—几何多结论问题【考题研究】以函数/几何为背景多结论问题自13年以来深圳广州等地每年必考，出现的位置是选择题或者填空题的压轴题.其难度不言自于，对学生综合分析问题的能力要求比较高.【解题策略】常见类型有：(1)代数中的多结论题;特别是有关二次函数中的多结论选填题是综合性比较强的题目，解决此类题目不仅要掌握二次函数的图象与性质、抛物线位置与字母系数的关系、二次函数与方程、不等式的关系等知识，还要学会代入特殊值的方法并结合二次函数的图象去验证一些不等式的正误;(2)几何中的多结论题;几何中的多结论选填题则结合了三角形、四边形、圆的有关性质和判定，是几何中综合性很强的题目，掌握三角形、四边形、圆的有关性质并能熟练的运用才能解决此类问题.具体求解时，一是从题干出发考虑，探求结果;二是题干和选择支联合考虑或从选择支出发探求是否满足题干条件. 事实上，后者在解答选择题时更常用、更有效.常用方法有以下几种：1.直接法从题设条件出发，通过正确的运算、推理或判断，直接得出结论再与选择支对照，从而作出选择的一种方法。

运用此种方法解题需要扎实的数学基础.2.特例法运用满足题设条件的某些特殊数值、特殊位置、特殊关系、特殊图形、特殊数列、特殊函数等对各选择支进行检验或推理，利用问题在某一特殊情况下不真，则它在一般情况下也不真的原理，由此判明选项真伪的方法。

用特例法解选择题时，特例取得愈简单、愈特殊愈好.3.筛选法(也叫排除法、淘汰法)运用选择题中单选题的特征，即有且只有一个正确选择支这一信息，从选择支入手，根据题设条件和各选项之间的关系，通过分析、推理、计算、判断，对选择项进行筛选，将其中与题设相矛盾的干扰逐一排除从而获得正确结论的方法。

使用筛选法的前提是“答案唯一”，即四个选项中有且只有一个答案正确.4.逆推代入法将选择项中给出的答案或其特殊值，代入题干逐一去验证是否满足题设条件，然后选择符合题设条件的择题项的一种方法. 在运用验证法解题时，若能据题意确定代入顺序，则能较大提高解题速度. 5.直观选择法利用函数图像或数学结果的几何意义，将数的问题(如解方程、解不等式、求最值，求取值范围等)与某些图形结合起来，利用直观几性，再辅以简单计算，确定正确答案的方法。

专题02 几何多解问题(解析版)

【2019年中考数学填选重点题型突破】专题二：几何多解问题【备考指南】“几何多解题”是指由于试题条件的不明确性，或题意中含有不确定的参数或图形时，导致结果有多种可能性，从而使答案不唯一．而此类问题因其能更好的体现学生分析问题和解决问题的能力，所以此类问题往往会出现在中考的试卷中，同时，许多考生因忽视问题中的“不确定性”而导致所得出的答案不全，从而失分．应如何解决此类问题呢？解决此类问题最好的方法就是应用分类讨论思想．分类讨论思想就是人们面对比较复杂的问题，有时无法通过统一研究或者整体研究解决，需要把研究的对象按照一定的标准进行分类并逐类进行讨论，再把每一类的结论综合，使问题得到解决．其解题步骤为：（1）根据研究的需要确定同一分类标准；（2）恰当地对研究对象进行分类，分类后的所有子项之间既不能“交叉”也不能“从属”，而且所有子项的外延之和必须与被分类的对象的外延相等，通俗地说就是要做到“既不重复又不遗漏”；（3）逐类逐级进行讨论；（4）综合概括、归纳得出最后结论．【典例引领】例1：已知△ABC中，tan B＝23，BC＝6，过点A作BC边上的高，垂足为点D，且满足BD：CD＝2：1，则△ABC面积的所有可能值为.【答案】8或24【分析】根据高线在△ABC的内部还是外部进行分类讨论.【解答】解：有两种情况：（1）如图1所示：∵BC＝6，BD：CD＝2：1，∴BD＝4，∵AD ⊥BC ，tan B∴AD∴S △ABC •AD 68；（2）如图2所示：∵BC ＝6，BD ：CD ＝2：1，∴BD ＝12，∵AD ⊥BC ，tan B∴AD ＝8，∴S △ABC •AD 6×8＝24；综上，△ABC 面积的所有可能值为8或24，故答案为：8或24.【解题指导】本题考查了三角函数、三角形的面积等知识.确定三角形的高线的位置是解题的关键.变式训练1：某园艺公司对一块直角三角形的花园进行改造，测得两直角边长分别为a ＝6米，b ＝8米.现要将其扩建成等腰三角形，且扩充部分是以b 为直角边的直角三角形，则扩建后的等腰三角形花圃的周长为________米.【答案】32或803或20＋【分析】由于扩充所得的等腰三角形腰和底不确定，若设扩充所得的三角形是△ABD ，则应分为①AB ＝AD ，②AD＝BD ，③ AB ＝BD 这三种情况进行分类讨论.【解答】解：如图所示：在Rt△ABC中，∵AC＝8m，BC＝6m，∴AB＝10m，如图1，当AB＝AD时，CD＝BC＝6m，此时等腰三角形花圃的周长＝10＋10＋6＋6＝32(m)；如图2：当AD＝BD时，设AD＝BD＝xm；Rt△ACD中，BD＝xm，CD＝(x﹣6)m；由勾股定理，得AD2＝DC2＋CA2，即(x﹣6)2＋82＝x2，解得x＝253；此时等腰三角形绿地的周长＝253×2＋10＝803(m).如图3：当AB＝BD时，在Rt△ACD中，AD==∴等腰三角形绿地的周长＝2×10＋20＋【解题指导】本题考查了等腰三角形的性质.明确是哪两条边相等是解题的关键.变式训练2：已知三角形相邻两边长分别为20cm和30cm，第三边上的高为10cm则此三角形的面积为cm².【答案】(或(【分析】根据第三边上的高是在三角形的内部还是外部，即可进行分类解决.【解答】解：设AB＝30cm，AC＝20cm，AD＝10cm，由题意作图，有两种情况：第一种：如图①，在Rt △ABD 中，利用勾股定理BD ==cm ，同理求出CD ＝cm ，则三角形面积＝12BC •AD ＝12(＋10＝()cm 2 第二种：如图②，在Rt △ABD 中，BD ==在Rt △ACD 中，CD =则BC ＝cm所以三角形面积＝12BC •AD ＝12(10＝cm 2故答案为：(或(【解题指导】本题考查了勾股定理、三角形的面积等知识.确定第三边上的高的位置是解题的关键.例2：在菱形ABCD 中，∠A ＝30°，在同一平面内，以对角线BD 为底边作顶角为120°的等腰三角形BDE ，则∠EBC 的度数为 .【答案】105°或45°【分析】根据点E 在BD 的左侧还是右侧，可进行分类讨论，如图当点E 在BD 右侧时，求出∠EBD ，∠DBC 即可解决问题，当点E 在BD 左侧时，求出∠DBE ′即可解决问题.【解答】解：如图，当点E 在BD 右侧时，∵四边形ABCD是菱形，∴AB＝AD＝BC＝CD，∠A＝∠C＝30°，∠ABC＝∠ADC＝150°，∴∠DBA＝∠DBC＝75°，∵ED＝EB，∠DEB＝120°，∴∠EBD＝∠EDB＝30°，∴∠EBC＝∠EBD+∠DBC＝105°，当点E′在BD左侧时，∵∠DBE′＝30°，∴∠E′BC＝∠DBC﹣∠DBE′＝45°，∴∠EBC＝105°或45°，【解题指导】本题考查了菱形的性质.明确点E在BD的两侧这两种情况是解题的关键.变式训练1：如图，在一张长为6cm，宽为5cm的矩形纸片上，现要剪下一个腰长为4cm的等腰三角形(要求：等腰三角形的一个顶点与矩形的一个顶点重合，其余的两个顶点在矩形的边上).则剪下的等腰三角形的面积为_____cm2.【答案】8【分析】根据题意，利用分类讨论，有三种情况(如图所示)，对这三种情况分别进行计算即可得出答案.【解答】解：如图所示，有三种情况：(1)当AE＝AF＝4cm时，△AEF是等腰直角三角形，cm；所以S△AEF•AF4×4＝82(2)如图，当AE＝EF＝4cm时，因为AB＝5，所以BE＝1，所以BF所以S△AEF•BF4(3)如图,当AE＝EF＝4厘米时,因为AD＝6cm，所以DE＝6－4＝2cm，所以DF＝所以S△AEF•DF4综上所述，剪下的等腰三角形的面积为：8【解题指导】本题考查了矩形、等腰三角形的性质、勾股定理等知识.明确等腰三角形的哪两条边长为4cm是解题的关键. 变式训练2：在矩形ABCD中，AD＝5，AB＝4，点E，F在直线AD上，且四边形BCFE为菱形，若线段EF的中点为点M，则线段AM的长为.【答案】5.5或0.5【分析】本题需要分两种情况来进行分类讨论：(1)当点F在射线AD上时，(2)当点E在射线DA上时进行求解，即①当点F在射线AD上时，由矩形的性质得出CD＝AB＝4，BC＝AD＝5，∠ADB＝∠CDF＝90°，由菱形的性质得出CF＝EF＝BE＝BC＝5，由勾股定理求出DF，得出MF，即可求出AM；②同①得出AE＝3，求出ME，即可得出AM的长.【解答】解：分两种情况：①如图1所示：∵四边形ABCD是矩形，∴CD＝AB＝4，BC＝AD＝5，∠ADB＝∠CDF＝90°，∵四边形BCFE为菱形，∴CF＝EF＝BE＝BC＝5，∴DF=＝3，∴AF＝AD＋DF＝8，∵M是EF的中点，∴MF＝12EF＝2.5，∴AM＝AF﹣DF＝8﹣2.5＝5.5；②当点E在射线DA上时，如图2所示：同①得：AE＝3，∵M是EF的中点，∴ME＝2.5，∴AM＝AE﹣ME＝0.5；综上所述：线段AM的长为：5.5，或0.5；故答案为：5.5，或0.5.【解题指导】本题考查了菱形的性质、勾股定理等知识.利用分类讨论确定点F的位置是解题的关键.【强化训练】1．在同一平面内，设a、b、c是三条互相平行的直线，已知a与b的距离为4cm，b与c的距离为1cm，则a与c的距离为________【答案】5cm或3cm【分析】分类讨论：当直线c在a、b之间或直线c不在a、b之间，然后利用平行线间的距离的意义分别求解．【解答】当直线c在a、b之间时，∵a、b、c是三条平行直线，而a与b的距离为4cm，b与c的距离为1cm，∴a与c的距离=4-1=3（cm）；当直线c不在a、b之间时，∵a、b、c是三条平行直线，而a与b的距离为4cm，b与c的距离为1cm，∴a与c的距离=4+1=5（cm），综上所述，a与c的距离为3cm或5cm．故答案为：3cm或5cm ．【解题指导】本题考查了平行线之间的距离，从一条平行线上的任意一点到另一条直线作垂线，垂线段的长度叫两条平行线之间的距离．平行线间的距离处处相等．注意分类讨论．2．已知⊙O的半径为10，圆心O到弦AB的距离为5，则弦AB所对的圆周角的度数是_________【答案】60°或120°【分析】由图可知，OA=10，OD=5．根据特殊角的三角函数值求出∠AOB的度数，再根据圆周定理求出∠C的度数，再根据圆内接四边形的性质求出∠E的度数即可．【解答】由图可知，OA=10，OD=5，在Rt△OAD中，∵OA=10，OD=5，AD=√OA2−OD2=5√3，=√3，∴∠1=60°，∴tan∠1=ADOD同理可得∠2=60°，∴∠AOB=∠1+∠2=60°+60°=120°，∴∠C=60°，∴∠E=180°-60°=120°,即弦AB 所对的圆周角的度数是60°或120°，故答案为：60°或120°．【解题指导】本题考查了圆周角定理、圆内接四边形的对角互补、解直角三角形的应用等，正确画出图形，熟练应用相关知识是解题的关键.3．已知⊙O 的直径CD =10cm ，AB 是⊙O 的弦，AB ⊥CD ，垂足为M ，且AB =8cm ，则AC 的长为________【答案】2√5cm 或4√5cm【分析】先根据题意画出图形，由于点C 的位置不能确定，故应分两种情况进行讨论．【解答】解：连接AC ，AO ，∵⊙O 的直径CD =10cm ，AB ⊥CD ，AB =8cm ，∴AM =12AB =12×8=4（cm ），OD =OC =5cm ，当C 点位置如图1所示时，∵OA =5cm ，AM =4cm ，CD ⊥AB ，∴OM =√OA 2−AM 2=√52−42=3（cm ），∴CM=OC +OM =5+3=8（cm ），∴AC =√AM 2+CM 2=√42+82=4√5（cm ）；当C 点位置如图2所示时，同理可得OM=3cm，∵OC=5cm，∴MC=5-3=2（cm），在Rt△AMC中，AC=√AM2+MC2=√42+22=2√5（cm）．故答案为：2√5cm或4√5cm．【解题指导】本题考查的是垂径定理（垂直于弦的直径平分这条弦，并且平分弦所对的两条弧），根据题意作出辅助线，构造出直角三角形是解答此题的关键．4．如图，已知Rt△ABC中，∠B=90°，∠A=60°，AC=2√3+4，点M、N分别在线段AC、AB上，将△ANM 沿直线MN折叠，使点A的对应点D恰好落在线段BC上，当△D CM为直角三角形时，折痕MN的长为__．或√6【答案】2√3+43【分析】依据△D CM为直角三角形，需要分两种情况进行讨论：当∠CDM=90°时，△CDM是直角三角形；当∠CM D=90°时，△CDM是直角三角形，分别依据含30°角的直角三角形的性质以及等腰直角三角形的性质，即可得到折痕MN的长．【解答】解：分两种情况：①如图，当∠CDM=90°时，△CDM是直角三角形，∵在Rt △ABC 中，∠B =90°，∠A =60°，AC =2√3+4，∴∠C =30°，AB =12AC =√3+2，由折叠可得，∠MDN =∠A =60°，∴∠BDN =30°，∴BN =12DN =12AN ， ∴BN =13AB =√3+23， ∴AN =2BN =2√3+43， ∵∠DNB =60°，∴∠ANM =∠DNM =60°，∴∠AMN =60°，∴AN =MN =2√3+43； ②如图，当∠CM D =90°时，△CDM 是直角三角形，由题可得，∠CDM =60°，∠A =∠MDN =60°，∴∠BDN =60°，∠BND =30°，∴BD =12DN =12AN ，BN =√3BD ，又∵AB =√3+2，∴AN =2，BN =√3，过N 作NH ⊥AM 于H ，则∠ANH =30°，∴AH =12AN =1，HN =√3，由折叠可得，∠AMN =∠DMN =45°，∴△MNH 是等腰直角三角形，∴HM =HN =√3，∴MN =√6，故答案为：2√3+43或√6．【解题指导】本题考查了翻折变换-折叠问题，等腰直角三角形的性质，正确的作出图形是解题的关键．折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等． 5．如图，∠MAN =90°，点C 在边AM 上，AC =4，点B 为边AN 上一动点，连接BC ，△A ′BC 与△ABC 关于BC 所在直线对称，点D ，E 分别为AC ，BC 的中点，连接DE 并延长交A ′B 所在直线于点F ，连接A ′E ．当△A ′EF 为直角三角形时，AB 的长为_____．【答案】4√3或4【分析】当△A ′EF 为直角三角形时，存在两种情况：①当∠A 'EF =90°时，如图1，根据对称的性质和平行线可得：A 'C =A 'E =4，根据直角三角形斜边中线的性质得：BC =2A 'B =8，最后利用勾股定理可得AB 的长；②当∠A 'FE =90°时，如图2，证明△ABC 是等腰直角三角形，可得AB =AC =4．【解答】解：当△A′EF为直角三角形时，存在两种情况：①当∠A'EF=90°时，如图1，.∵△A′BC与△ABC关于BC所在直线对称，∴A'C=AC=4，∠ACB=∠A'CB，∵点D，E分别为AC，BC的中点，∴D、E是△ABC的中位线，∴DE∥AB，∴∠CDE=∠MAN=90°，∴∠CDE=∠A'EF，∴AC∥A'E，∴∠ACB=∠A'EC，∴∠A'CB=∠A'EC，∴A'C=A'E=4，Rt△A'CB中，∵E是斜边BC的中点，∴BC=2A'E=8，由勾股定理得：AB2=BC2-AC2，∴AB=√82−42=4√3；②当∠A'FE=90°时，如图2，.∵∠ADF=∠A=∠DFB=90°，∴∠ABF=90°，∵△A′BC与△ABC关于BC所在直线对称，∴∠ABC=∠CBA'=45°，∴△ABC是等腰直角三角形，∴AB=AC=4；.综上所述，AB的长为4√3或4；故答案为：4√3或4.【解题指导】本题考查了三角形的中位线定理、勾股定理、轴对称的性质、等腰直角三角形的判定、直角三角形斜边中线的性质，并利用分类讨论的思想解决问题．6．在正方形ABCD中，AB=6，连接AC,BD,P是正方形边上或对角线上一点，若PD=2AP，则AP的长为____________ .【答案】2，2√3，√14−√2【分析】根据题意分情况画出符合题意的图形，然后针对每一个图形进行求解即可得.【解答】∵四边形ABCD是正方形，∴AD=AB=6，∠BAD=90°，∠DAC=45°，AC=BD=6√2；如图1，当点P在AD上时，∵AP+PD=AD=6，PD=2AP，∴AP=2；如图2，当点P在AB上时，∵∠P AD=90°，∴AP2+AD2=AP2，∵AD =6，PD =2AP ，∴AP 2+36=4AP 2，∴AP =2√3；如图3，当点P 在AC 上时，作PN ⊥AD 于点N ，设AN =x ，则有DN =6-x ，PN =x ，由勾股定理则有AP =√2x ，PD =√x 2+(6−x )2，∵PD =2AP ，∴√x 2+(6−x )2=2√2x ，∴x =√7−1或x =−√7−1（不符合题意，舍去），∴AP =√2x =√14−√2，当点P 在其余边可对角线上时，不存在可以使PD =2AP 的点，综上，AP 的长为2，2√3 ，√14−√2，故答案为：2，2√3 ，√14−√2.【解题指导】本题考查了正方形的性质，勾股定理的应用等，难度较大，解题的关键是正确画出符合题意的图形.7．如图，在直角△ABC 中，∠C =90°，AC =6，BC =8，P 、Q 分别为边BC 、AB 上的两个动点，若要使△APQ 是等腰三角形且△BPQ 是直角三角形，则AQ =________．【答案】154或307【分析】分两种情形分别求解：①如图1中，当AQ =PQ ，∠QPB =90°时，②当AQ =PQ ，∠PQB =90°时；【解答】解：①如图1中，当AQ =PQ ，∠QPB =90°时，设AQ =PQ =x ，∵PQ ∥AC ，∴△BPQ ∽△BCA ， ∴BQ BA =PQ AC ， ∴10−x 10=x 6， ∴x =154，∴AQ =154．②当AQ =PQ ，∠PQB =90°时，如图2，设AQ =PQ =y ．∵△BQP ∽△BCA ，∴PQ AC =BQ BC ，∴y 6=10−y 8， ∴y =307．综上所述，满足条件的AQ 的值为154或307．【解题指导】本题考查勾股定理、等腰三角形的性质、相似三角形的判定和性质等知识，解题的关键是学会用分类讨论的思想思考问题，学会利用参数构建方程解决问题．8．如图，△ABC 中，∠ACB =90°，sin A =513，AC =12，将△ABC 绕点C 顺时针旋转90°得到△A 'B 'C ，P 为线段A ′B '上的动点，以点P 为圆心，P A ′长为半径作⊙P ，当⊙P 与△ABC 的边相切时，⊙P 的半径为_____．【答案】15625或10213【分析】分两种情形分别求解：如图1中，当⊙P 与直线AC 相切于点Q 时，如图2中，当⊙P 与AB 相切于点T 时，【解答】解：如图1中，当⊙P 与直线AC 相切于点Q 时，连接PQ ．设PQ =P A ′=r ，∵PQ ∥CA ′，∴PQ CA ′=PB ′A ′B ′，∴r 12=13−r 13，∴r =15625．如图2中，当⊙P 与AB 相切于点T 时，易证A ′、B ′、T 共线，∵△A ′BT ∽△ABC ，∴A ′T AC=A ′B AB ， ∴A ′T 12=1713，∴A ′T =20413，∴r =12A ′T =10213．综上所述，⊙P 的半径为15625或10213．【解题指导】本题考查切线的性质、勾股定理、锐角三角函数、相似三角形的判定和性质、平行线分线段成比例定理等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题．9．等腰三角形ABC 中，顶角A 为40∘，点P 在以A 为圆心，BC 长为半径的圆上，且BP =BA ，则∠PBC 的度数为__________．【答案】30∘或110∘【分析】画出示意图，分两种情况进行讨论即可.【解答】如图：分两种情况进行讨论.易证△ABP ≌△ABC ，∴∠ABP =∠BAC =40°,∠ABC =180°−40°2=70°.∴∠PBC =∠ABP +∠ABC =110°.同理：△ABP ′≌△BAC ，∴∠ABP ′=∠BAC =40°,∠ABC =180°−40°2=70°.∴∠P ′BC =∠ABC −∠ABP =30°.故答案为：30∘或110∘【点评】考查全等三角形的判定与性质，等腰三角形的性质等，注意分类讨论思想在数学中的应用.10．如图，△AOB 三个顶点的坐标分别为A （8，0），O （0，0），B （8，﹣6），点M 为OB 的中点．以点O 为位似中心，把△AOB 缩小为原来的12，得到△A ′O ′B ′，点M ′为O ′B ′的中点，则MM ′的长为_____．【答案】52或152【分析】分两种情形画出图形，即可解决问题；【解答】如图，在Rt △AOB 中，OB =√62+82=10，∴OM =5，OM ′=52，①当△A ′OB ′在第三象限时，MM ′=5-52=52；②当△A ″OB ″在第二象限时，MM ′=5+52=152，故答案为：52或152．【解题指导】本题考查不位似变换，坐标与图形的性质等知识，解题的关键是学会用分类讨论的思想思考问题． 11．如果一个正方形被截掉一个角后，得到一个多边形，那么这个多边形的内角和是__________．【答案】180°或360°或540°【分析】剪掉一个多边形的一个角，则所得新的多边形的角可能增加一个，也可能不变，也可能减少一个，根据多边形的内角和定理即可求解.【解答】解： n 边形的内角和是（n -2）•180°，边数增加1，则新的多边形的内角和是（4+1-2）×180°=540°，所得新的多边形的角不变，则新的多边形的内角和是（4-2）×180°=360°，所得新的多边形的边数减少1，则新的多边形的内角和是（4-1-2）×180°=180°，因而所成的新多边形的内角和是540°或360°或180°．故答案为：540°或360°或180°.【解题指导】本题主要考查了多边形的内角和的计算公式，理解：剪掉一个多边形的一个角，则所得新的多边形的角可能增加一个，也可能不变，也可能减少一个，是解决本题的关键.12．Rt △ABC 中，∠ABC =90°，AB =3，BC =4，过点B 的直线把△ABC 分割成两个三角形，使其中只有一个是等腰三角形，则这个等腰三角形的面积是_____．【答案】3.6或4.32或4.8【分析】在Rt △ABC 中，通过解直角三角形可得出AC =5、S △ABC =6，找出所有可能的分割方法，并求出剪出的等腰三角形的面积即可．【解答】在Rt △ABC 中，∠ACB =90°，AB =3，BC =4，∴AB =√AB 2+BC 2=5，S △ABC =12AB •BC =6．沿过点B 的直线把△ABC 分割成两个三角形，使其中只有一个是等腰三角形，有三种情况：①当AB =AP =3时，如图1所示，S 等腰△ABP =AP AC •S △ABC =35×6=3.6；②当AB =BP =3，且P 在AC 上时，如图2所示，作△ABC 的高BD ，则BD =AB·BC AC =3×45=2.4，∴AD=DP=√32−2.42=1.8，∴AP=2AD=3.6，∴S等腰△ABP=APAC •S△ABC=3.65×6=4.32；③当CB=CP=4时，如图3所示，S等腰△BCP=CPAC •S△ABC=45×6=4.8；综上所述：等腰三角形的面积可能为3.6或4.32或4.8，故答案为：3.6或4.32或4.8．【解题指导】本题考查了勾股定理、等腰三角形的性质以及三角形的面积，找出所有可能的分割方法，并求出剪出的等腰三角形的面积是解题的关键．13．如图，若直线L与x轴、y轴分别交于点A、B，并且OB=4，∠ABO=30∘，一个半径为1的⊙O，圆心C从点(0,1)开始沿y轴向下运动，当⊙C与直线L相切时，⊙C运动的距离是__________．【答案】3或7【分析】分圆运动到第一次与AB相切，继续运算到第二次与AB相切两种情况，画出图形进行求解即可得.【解答】设第一次相切的切点为E，第二次相切的切点为F，连接EC′，FC″，在Rt△BEC′中，∠ABC＝30°，EC′＝1，∴BC′＝2EC′＝2，∵BC＝5，∴CC′＝3，同法可得CC″＝7，故答案为：3 或7．【解题指导】本题考查了切线的性质、含30度角的直角三角形的性质，会用分类讨论的思想解决问题是关键，注意数形结合思想的应用.14．如图，正方形ABCD的边长为8，M是AB的中点，P是BC边上的动点，连结PM，以点P为圆心，PM长为半径作⊙P.当⊙P与正方形ABCD的边相切时，BP的长为______．【答案】3或4√3【分析】分两种情况：⊙P与直线CD相切、⊙P与直线AD相切，分别画出图形进行求解即可得.【解答】如图1中，当⊙P与直线CD相切时，设PC=PM=m，在Rt△PBM中，∵PM2=BM2+PB2，∴x2=42+(8−x)2，∴x=5，∴PC=5，BP=BC−PC=8−5=3；如图2中当⊙P与直线AD相切时，设切点为K，连接PK，则PK⊥AD，四边形PKDC是矩形，∴PM=PK=CD=2BM，∴BM=4，PM=8，在Rt△PBM中，PB=√82−42=4√3，综上所述，BP的长为3或4√3．【解题指导】本题考查切线的性质、正方形的性质、勾股定理等知识，会用分类讨论的思想思考问题，会利用参数构建方程解决问题是关键．15．已知等腰三角形的一个外角为130∘，则它的顶角的度数为______．【答案】50∘或80∘【分析】等腰三角形的一个外角等于130°，则等腰三角形的一个内角为50°，但已知没有明确此角是顶角还是底角，所以应分两种情况进行分类讨论即可得．【解答】∵等腰三角形的一个外角为130∘，∴与130°相邻的内角为50°，当50∘为顶角时，其他两角都为65∘、65∘，当50∘为底角时，其他两角为50∘、80∘，所以等腰三角形的顶角为50∘或80∘，故答案为：50∘或80∘．【解题指导】本题考查了等腰三角形的性质、三角形内角和定理，在解决与等腰三角形有关的问题，由于等腰所具有的特殊性质，很多题目在已知不明确的情况下，要进行分类讨论，才能正确解题.16．在ΔABC 中，AB =AC =5√2，∠BAC =90°，点D 在BC 边上，DE ⊥BC ，分别交射线BA 、射线CA 于点E 、F ，若DE =2EF ，则线段BD 的长为_________.【答案】203或4【分析】画出图形，利用勾股定理和一元一次方程进行求解即可.【解答】如图，符合题意的情况有两种。

几何多结论选择题填空题的解题方法

几何多结论选择题填空题的解题方法几何多结论选择题填空题基本方向：①找全等；②找特殊角；③分析数量关系；④确定位置关系；⑤确定图形形状；⑥特殊—一一般——特殊.几何多结论选择题填空题基本方法：①常见辅助线构造基本图形；②②代数方法解决几何计算证明；③面积与线段的比值转化；A定正确的结论有（） A ．①②③ B ．①②④ C ．①③④ D ．②③④考点：等腰直角三角形；等腰三角形的判定与性质；平行四边形的性质．【思路引导】①利用SAS 证明△BAD ≌△CAE ，可得到CE=BD ，②利用平行四边形的性质可得AE=CD ，再结合△ADE 是等腰直角三角形可得到 △ADC 是等腰直角三角形；③利用SAS 证明△BAE ≌△BAD 可得到∠ADB=∠AEB ；④由②△ADC 是等腰直角三角形和四边形ACDE 是平行四边形，可得EF=CF ，AF=DF ，所以得△CFD 为等腰直角三角形且∠CFD=90°，即得CD ≠CF ，即CD ≠EF ．故④CD=EF 错误；所以一定正确的结论有①②③，故选A ．点评：本题主要考查了全等三角形的判定及性质、平行四边形的性质及等腰三角形的判定与性质，注意细心分析，熟练应用全等三角形的判定以及平行四边形的性质及等腰三角形的判定与性质，是解决问题的关键．练习一：1．如图所示，已知△ABC 和△BDE 都是等边三角形，A 、B 、D 三点共线，下列结论：①AE=CD ； ②BF=BG ；③HB 平分∠AHD ；④∠AHC=60°；⑤△BFG 是等边三角形；⑥FG ∥AD ，其中正确的有（） A ．3个 B. 4个 C. 5个 D. 6个2.如图，Rt ABC 中，AC BC ⊥，AD 平分BAC ∠交BC 于点D ，DE AD ⊥交AB 于点E ，M 为AE 的中点，BF ⊥BC 交CM 的延长线于点F ，BD=4，CD=3．下列结论：①AED ADC ∠=∠；②3 4DE DA =；③AC BE 12⋅=；④3BF 4AC =；其中结论正确的个数有（） A ．1个 B ．2个 C ．3个 D ．4个3．如图，点A 在线段BD 上，在BD 的同侧作等腰Rt △ABC 和等腰Rt △ADE ，CD 与BE ，AE分别交于点P ，M.对于下列结论：①△BAE ∽△CAD ；②MP ·MD ＝MA ·ME ；③2CB 2＝CP ·CM.其中正确的是( )A ．①②③B ．①C ．①②D ．②③题型二：以四边形为背景（平行四边形、矩形、菱形）例3.如图，在□ABCD中，CD=2AD，BE⊥AD于点E，F为DC的中点，连结EF、BF，下列结论：①∠ABC=2∠ABF；②EF=BF；③S四边形DEBC=2S△EFB；④∠CFE=3∠DEF，其中正确结论的个数共有（）A．1个 B．2个 C．3个D．4个考点：平行四边形的性质、全等三角形的判定及性质、等腰三角形的性质、菱形的判定、直角三角形的斜边上的中线。

几何多结论选择题

•CPOD E AB•DPBACOEF•ACDFBP O E··BADPO FM E C几何多结论选择题21．已知：如图,△ABC 中，∠A=60º，BC 为定长，以BC 为直径的⊙O 分别交AB 、AC 于点D 、E,连结DE 、OE.下列结论: ①BC ＝2DE ；②D 点到OE 的距离不变；③BD+CE ＝2DE ； ④OE 为△ADE 外接圆的切线.其中正确的结论是 . A.①② B.③④ C.①②③ D.①②④2.已知：如图，⊙O 是△ABC 的外接圆，AD ⊥BC,CE ⊥AB ,D 、E 分别为垂足，AD 交CE 于H 点，交⊙O 于N ，OM ⊥BC ，M 为垂足，BO 延长交⊙O 于F 点，下列结论：其中正确的有 . ①∠BAO=∠CAH ； ②DN=DH; ③四边形AHCF 为平行四边形；④CH •EH=OM •HN. A.①②③ B.②③④ C.①③④ D.①②③④3.已知:如图,P 为⊙O 外一点,PA 、PB 切⊙O 于A 、B 两点，OP 交⊙O 于点C,连结BO 交延长分别交⊙O 及切线PA 于D 、E 两点,连结AD 、BC.下列结论：①AD ∥PO ；②ΔADE ∽ΔPCB;③tan ∠EAD=EAED；④BD 2=2AD •OP.其中正确的有 .A.①②④B.③④C.①③④D.①④4.已知:如图, PA 、PB 为⊙O 的两条切线，A 、B 为切点，直线PO 交⊙O 于C 、D 两点，交AB 于E ，AF 为⊙O 的直径，连结EF 、PF ，下列结论：①∠ABP=∠AOP ；②BC 弧=DF 弧 ;③PC •PD=PE •PO;④∠OFE=∠OPF.其中正确的有 .A.①②③④B.①②③C.①③④D.①②④5.已知:如图,∠ACB=90º,以AC 为直径的⊙O 交AB 于D 点，过D 作⊙O 的切线交BC 于E 点，EF ⊥AB 于F 点，连OE 交DC 于P ，则下列结论:其中正确的有 .①BC=2DE ； ②OE ∥AB; ③DE=2PD ； ④AC•DF =DE•CD .A.①②③B.①③④C.①②④D.①②③④6.已知：如图，M 为⊙O 上的一点,⊙M 与⊙O 相交于A 、B 两点，P 为⊙O 上任意一点，直线PA 、PB 分别交⊙M 于C 、D 两点，直线CD 交⊙O 于E 、F 两点，连结PE 、PF 、BC ，下列结论：其中正•D MB OH AE NFC·B ACDEO•• BAPO 1CEO 2DF• • A EO 1O 2BDCP •P ACB ON DE FM•• DPO2BF E C O 1A 确的有 .①PE=PF ； ②PE 2=PA·PC; ③EA·EB=EC·ED ； ④rRBC PB =（其中R 、r 分别为⊙O 、⊙M 的半径）. A.①②③ B.①②④ C.②④ D.①②③④7已知：如图，⊙O 1、⊙O 2相交于A 、B 两点，PA 切⊙O 1于A ，交⊙O 2于P ，PB 的延长线交⊙O 1于C ，CA 的延长线交⊙O 2于D ，E 为⊙O 1上一点，AE=AC ，EB 延长线交⊙O 2于F ，连结AF 、DF 、PD,下列结论：①PA=PD ；②∠CAE=∠APD; ③DF ∥AP ； ④AF 2=PB •EF.其中正确的有 .A.①②③B.②③④C.①③④D.①②③④ 8.已知:如图,⊙O 1、⊙O 2内切于点A ，P 为两圆外公切线上的一点,⊙O 2的割线PBC 切⊙O 1于D 点,AD 延长交⊙O 2于E 点,连结AB 、AC 、O 1D 、O 2E,下列结论：①PA=PD ；②BE 弧=CE 弧;③PD 2=PB •PC;④O 1D ‖O 2E.其中正确的有 .A.①②④B.②③④C.①③④D.①②③④9.已知:如图, P 为⊙O 外一点，割线PBC 过圆心O,交⊙O 于B 、C 两点，PA 切⊙O 于A 点，CD ⊥PA ，D 为垂足，CD 交⊙O 于F ，AE ⊥BC 于E ，连结PF 交⊙O 于M ，CM 延长交P A 于N ，下列结论： ①AB =AF ；②FD 弧=BE 弧 ;③DF •DC=OE •PE ； ④PN=AN.其中正确的有 .A.①②③④B.②③④C.①③④D. ①②④10.已知：如图，⊙O 1、⊙O 2内切于点P , ⊙O 1的弦AB 切⊙O 2于C 点,PC 的延长线交⊙O 1于D 点,PA 、PB 分别交⊙O 2于E 、F 两点, 下列结论：其中正确的有 .①CE=CF ； ②△APC ∽△CPF;③PC •PD=PA •PB ； ④DE 为⊙O 2的切线. A.①②③ B.②③④ C.①③④ D.①②③④11．如图,直径AB 、CD 相互垂直，P 为⋂BC 上任意一点，连PC 、P A 、PD 、PB ，下列结E54321A BC OPOFE D CBA论：①∠APC =∠DPE ；②∠AED =∠DF A ；③CP DP APBP AP DP+=+，中正确的是( ). （A ）①③. （B ）只有①. （C ）只有②. （D ）①②③.12、如图，等腰Rt △ABC 中，AC ＝BC ，以AC 为直径作⊙O 交AB 于D 点，E 为CD 上的一个动点，过E 作AE 的垂线交BC 的延长线于点F ，连接AE 、BE 、EF ，下列结论：①AE ＝BE ；②BE ＝EF ；③∠EAC ＝∠EFC ；④∠AED ＝AFB.其中正确的个数是（） A.1个 B.2个 C.3个 D.4个13．如图，在⊙O 中，直径AB 垂直弦CD ，E 为BC 弧上一点，下列结论：①∠1=∠2；②∠3=2∠4；③∠3+∠5=180°。

姓名几何多图多结论问题

姓名几何多图多结论问题
1、△ABC中，AB=AC，AB的垂直平分线
2、等腰三角形一腰上的高等于该
与AC所在的直线相交所得锐角为40°，三角形某一条边的长度的一半，则∠B= 则其顶角的度数是
2、已知圆内接△ABC中，AB=AC，4、已知△ABC为等腰三角形，其
圆心O到BC的的距离为3，圆的半径面积为30，一边长是10，则另是7，则腰长AB= 外两边长是
5、已知等腰梯形BCDE中，B C∥DE，BD
6、△ABC中，AB=AC，过△ABC
和CE交于点A，B M⊥CE于M，若某一顶点的直线将△ABC分成
2，则∠CBM的两个等腰三角形，则△ABC的AM=6，AB=2
度数是的顶角的度数是
7、已知ABCD的周长是28，自顶点A 8、已知，在Rt△ABC中，AC=6，
作AE⊥CD于E，AF⊥BC于F，若AE=3，BC=8，点D在边AB上运动，AF=4，则CE-CF= DE平分∠CDB边BC于E，
EM ⊥BD于M，EN⊥CD于
N，若△BME与△CNE相似，
则AD的长是。

初中几何综合：一题多解，展现几何魅力，好的文章值得阅读和分享

初中几何综合：一题多解，展现几何魅力，好的文章值得阅读
和分享
第二问证明线段的数量关系，关键点平行这个条件如何用，我整理了两种思路，一个是共底角旋转出相似，然后结合平行出特殊角45°，最后通过子母型相似求解。

另一种思路是，利用平行构造平行四边形，
证出两三角形全等，结合平行推出直角，再利用正切值不变证出2倍关系，从而证出结论。

第三问同样分享四种思路：分别用了定角定弦，共底角相似，第3种的思路又结合了正切值直接计算，其实也是典型的12345的题型，关键是如何证明求解。

其它三种都证出AD=DP，然后结合内在关系设方程求解即可。

总之整理一题需要大量的思考时间，做完之后在整理在电脑的时间会更多些，同时边整理再边思考，也考虑过一些解法，稍麻烦的就不考虑了。

喜欢研究初中数学的朋友们可以多多交流。

专栏
中考几何综合题型。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1.(本小题10分)如图,正方形ABCD,正方形CGEF的边长分别是2,3,且点B,C,G在同一直线上,M是线段AE中点,连接FM,则FM的长为( )A.B.C.D.2.(本小题10分)如图,在等腰三角形ABC中,∠ABC=90°,D为AC边中点,过点D作DE⊥DF,交AB于点E,交BC于点F.若,则AB的长为( )A. 3B. 6C. 9D. 183.(本小题10分)两个全等的含30°,60°角的三角板ADE和三角板BAC按如图所示放置,E,A,C三点在一条直线上,连接BD,取BD的中点M,连接ME,MC.则△EMC的形状是( )A. 等腰(非直角)三角形B. 直角(非等腰)三角形C. 等腰直角三角形D. 形状不确定4.(本小题10分)如图,在△ABC中,BE,CF分别为边AC,AB上的高,D为BC的中点,DM⊥EF于点M,若BC=10,DM=3,则EF的长为( )A. 6B. 9C. 7D. 85.(本小题10分)如图,在ΔABC中,D是BC边的中点,点E,F分别在边AB,AC上（不与两端点重合）,且DE⊥DF.则下列说法正确的是( )A.B.C.D.6.(本小题10分)如图所示,在△ABC中,,M为BC边的中点,AD平分∠BAC,交BC于点D.若CF⊥AD交AD的延长线于点F,连接FM,则下列说法正确的是( )A.B.C.D.7.(本小题10分)如图,在△ABC中,∠ABC=90°,BD为AC边上的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG,DF.若AG=13,CF=6,则四边形BDFG的周长为( )A.B. 24C. 20D. 168.(本小题10分)如图,在菱形ABCD中,∠A=100°,M,N分别是AB,BC的中点,于点P,则的度数为( )A. 40°B. 45°C. 50°D. 55°9.(本小题10分)如图,在△ABC中,AD是BC边上的中线,分别以AB,AC为直角边向外作等腰直角三角形ABE和等腰直角三角形ACF,连接EF,下列说法正确的是( )A.B. EF=2ADC.D. EF=AD10.(本小题10分)如图,在△ABC中,BE平分∠ABC交AC于点E,CF平分∠ACB交AB于点F,且BE,CF相交于点O,AG⊥BE于点G,AH⊥CF于点H.若AB=9,AC=14,BC=18,则GH的长为( )A.B. 5C. 3D. 6与角相关的模型证明及应用（通用版）单选题(本大题共9小题，共100分)1.(本小题11分)如图,等腰直角三角形ABC的直角边长为3,P为斜边BC上一点,且BP=1,D 为AC上一点.若∠APD=45°,则CD的长为( )A.B.C.D.2.(本小题11分)在△ABC中,∠C=90°,AC=3,BC=4,O是AB上的一点,且,点P是AC 上的一个动点,交线段BC于点Q(不与点B,C重合).若AP=2,则CQ的长为( )A.B.C.D. 23.(本小题11分)如图,在△ABC中,∠B=2∠C,AD⊥BC于点D,M为BC中点.若AB=10,则MD的长为( )A. 3B. 5C. 6D. 84.(本小题11分)如图,在等腰直角三角形ABC中,∠A=90°,AC=8,点O在AC上,且AO=2,点P 是AB上一动点.连接OP,将线段OP绕点O逆时针旋转90°得到线段OD,要使点D恰好落在BC上,则AP的长度为( )A.B. 6C. 5D. 45.(本小题11分)如图,在等腰梯形ABCD中,AD∥BC,AD=6cm,BC=14cm,∠B=60°.P为下底BC 上一点(不与点B,C重合),连接AP,过点P作射线PE交线段DC于点E,使得∠APE=∠B.若DE:EC=5:3,则BP=( )A. 4或6B. 3或8C. 或D. 2或126.(本小题11分)在△ABC中,AB=7,AC=8,且∠A是∠C的2倍,则BC=( )A.B. 10C.D.7.(本小题11分)已知直线,且与的距离为1,与的距离为3,把一块含有45°角的直角三角板如图放置,顶点A,B,C恰好分别落在这三条直线上,且AC与直线交于点D,则线段BD的长度为( )A.B.C.D.8.(本小题11分)如图,△ABC是边长为3的等边三角形,△BDC是等腰三角形,且∠BDC=120°.以D为顶点作一个60°的角,使其两边分别交AB,AC于点M,N,连接MN,则△AMN的周长为( )A. 5B. 6C. 7D. 89.(本小题12分)如图,在平面直角坐标系中,正方形ABCD的顶点A的坐标是(0,2),顶点B 在x轴负半轴上,对角线AC,BD交于点M,,则点D的坐标是( )A.B.C.D.图形面积的计算（通用版）一. 单选题(本大题共8小题，共64分)1.(本小题8分)由7个形状、大小完全相同的正六边形组成的网格如图所示,正六边形的顶点称为格点.已知每个正六边形的边长均为1,△ABC的顶点都在格点上,则△ABC的面积为( )A. 2B.C.D.2.(本小题8分)如图,边长为1的两个正方形互相重合,按住其中一个不动,将另一个绕顶点A顺时针旋转45°,则这两个正方形重叠部分的面积为( )A.B.C.D.3.(本小题8分)如图,四边形ABCD中,AB=2,CD=1,∠A=60°,∠B=∠D=90°,则四边形ABCD的面积为( )A.B.C.D.4.(本小题8分)如图,菱形ABCD和菱形EFGD的边长分别为4和6,∠A=120°,则图中阴影部分的面积为( )A.B.C.D.5.(本小题8分)正方形ABCD,正方形BEFG和正方形RKPF的位置如图所示,点G在线段DK上,且G为BC的三等分点,R为EF中点.若正方形BEFG的边长为4,则△DEK的面积为( )A. 12B. 16C. 20D. 246.(本小题8分)如图,将含60°角的直角三角板ABC绕顶点A顺时针旋转45°度后得到,点B经过的路径为弧.若∠BAC=60°,AC=1,则图中阴影部分的面积为( )A.B.C.D.7.(本小题8分)如图,在矩形ABCD中,AB=4cm,BC=3cm,点P是AB上除A,B外任一点,对角线AC,BD相交于点O,DP,CP分别交AC,BD于点E,F.若△ADE和△BCF的面积之和为,则四边形PEOF的面积为( )A.B.C.D.8.(本小题8分)如图,在中,是斜边的中点,过作于,连接交于;过作于,连接交于;过作于,连接交于;…;如此继续.若分别记,,,…,的面积为,则( )A.B.C.D.二. 填空题(本大题共4小题，共36分)9.(本小题9分)如图，在△ABC中，已知点D，E，F分别为BC，AD，CE的中点，若，则阴影部分的面积为____．10.(本小题9分)如图为△ABC与△D EC重叠的情形，其中点E在BC上，AC与DE交于点F，且AB∥DE．若△ABC与△DEC的面积相等，且EF=9，AB=12，则DF=____．11.(本小题9分)如图，在矩形ABCD中，E是AD的中点，F是CE的中点，若△BDF的面积为6，则矩形ABCD的面积为____．12.(本小题9分)如图，已知正方形ABCD的面积为120，E是AB的中点，F是BC的中点，EC 分别交BD，DF于点G，H．则四边形BGHF的面积为____．几何结构综合检测（通用版）单选题(本大题共8小题，共100分)1.(本小题12分)如图,在平行四边形ABCD中,BC=2AB,CE⊥AB于E,F为AD的中点,若∠AEF=52°,则∠B=( ).A. 52°B. 54°C. 72°D. 76°2.(本小题12分)如图,正方形ABCD的周长为24,△BCE是等边三角形,F是CE的中点,AE,BF 交于点G,连接CG,则CG的长为( )A.B.C.D.3.(本小题12分)如图,平行四边形ABCD中,AB:BC=3:2,∠DAB=60°,E在AB上,且AE:EB=1:2,F是BC的中点,过D分别作DP⊥AF于P,DQ⊥CE于Q,则DP:DQ等于( )A. 3:4B.C.D.4.(本小题12分)如图,在直角梯形ABCD中,∠A=90°,∠B=120°,,AB=6.在边AB 上取点E,在射线DC上取点F,使得∠DEF=120°.若射线EF经过点C,则AE的长为( )A. 2B. 2或4C. 2或5D. 3或55.(本小题13分)如图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=3.点D是BC边上一动点(不与点B,C重合),过点D作DE⊥BC,交AB于点E,将∠B沿直线DE翻折,点B落在直线BC上的点F处.当△AEF为直角三角形时,BD的长为( )A. 1B. 2C. 1或2D. 2或46.(本小题13分)在等腰三角形ABC中,∠ACB=90°,AC=1,过点C作直线l∥AB,P为直线l 上一点,且AP=AB,则点P到BC所在直线的距离是( )A.B. 或C. 或D. 或7.(本小题13分)如图,在等腰直角三角形ABC中,∠BAC=90°,BC=2,点E为线段AB上任意一点(E不与B重合),以CE为斜边作等腰直角三角形CDE,连接AD,下列结论:①∠BCE=∠ACD;②BE=AD;③AD∥BC;④四边形ABCD的面积有最大值,且最大值为.其中正确的结论有( )个.A. 1B. 2C. 3D. 48.(本小题13分)如图,在等腰三角形ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA 延长线上一点,点O是线段AD上一点,OP=OC,下面的结论:①∠APO+∠DCO=30°;②△OPC是等边三角形;③AC=AO+AP;④.其中所有正确结论的序号为( )A. ①②③B. ①②④C. ①③④D. ①②③④角度、长度、周长及面积的计算（北师版）一. 单选题(本大题共13小题，共81分)1.(本小题6分)如图，在△A BC中，AB=AC=9，∠BAC=120°，AD是△ABC的中线．若AE平分∠BAD，交BC于点E，DF∥AB，交AE延长线于点F，则DF的长为( )A.B. 3C.D. 42.(本小题6分)在△ABC中，AB=12，AC=10，BC=9，AD是BC边上的高．将△ABC按如图所示的方式折叠，使点A与点D重合，折痕为EF，则△DEF的周长为( )A.B.C. 11D.3.(本小题6分)如图，在梯形ABCD中，AD∥BC，AD+BC=CD，M是AB的中点．若∠MCB=40°，则∠ADM的度数为( )A. 50°B. 100°C. 40°D. 60°4.(本小题6分)如图，点A，C在直线上，点B在射线AD上，，分别是∠BAE，∠CBD的平分线．若，则∠BAE的度数为( )A. 150°B. 168°C. 135°D. 160°5.(本小题6分)如图，在等边三角形ABC中，D是边AC上一点，连接BD．将△BCD绕点B 逆时针旋转60°得到△BAE，连接ED．若BC=10，BD=9，则△AED的周长是( )A.B. 18C. 19D. 206.(本小题6分)如图，在△ABC中，∠BAC=50°，AD平分∠BAC，交BC于点D，E为AC上一点．若AB=9，AD=6，AE=4，则∠CDE的度数为( )A. 50°B. 35°C. 25°D. 20°7.(本小题6分)如图所示，以Rt△ABC的斜边BC为一边，在△ABC的同侧作正方形BCEF，设正方形的中心为O，连接AO，如果AB=4，，那么AC的长为( )A. 12B. 16C.D.8.(本小题6分)如图，在平行四边形ABCD中，AB=6，AD=9，∠BAD的平分线交BC于点E，交DC的延长线于点F，BG⊥AE于点G．若，则ΔCEF的周长为( )A. 8B.C. 10D.9.(本小题6分)如图，在Rt△ABC中，∠ABC=90°，D为斜边AC上一点，连接BD．E为BD 上一点，过点E作正方形EFGH和正方形EIJK，使得点F，G在BC边上，点H，I在AC边上，点J，K在AB边上．若EF=3，EK=2，则AC的长为( )A.B.C.D.10.(本小题6分)如图，在正方形ABCD内有一折线段，其中AE⊥EF，EF⊥FC，且AE=6，EF=8，FC=10，则该正方形的面积为( )A. 120B. 140C. 150D. 16011.(本小题7分)如图，已知E，F，G，H分别是四边形ABCD的边AB，BC，CD，AD的中点，且AF，CE交于点K，AG，CH交于点L，则的值为( )A.B.C.D.12.(本小题7分)如图，在直角梯形ABCD中，AD∥BC，∠ABC=90°，∠C=60°，，点E是BC边的中点．若△DEF是等边三角形，DF交AB于点G，则△BFG的周长为( )A.B.C.D. 413.(本小题7分)如图，在矩形纸片ABCD中，AB=6，BC=10，将纸片折叠，使点B落在边AD 上的点处，折痕为CE．在折痕CE上存在一点P到边AD的距离与到点B的距离相等，则此相等距离为( )A. 3B. 4C.D. 5二. 填空题(本大题共3小题，共19分)14.(本小题6分)如图，△ABC的外角∠ACD的平分线CP与内角∠ABC的平分线BP交于点P，若∠BPC=40°，则∠CAP=____度．15.(本小题6分)如图，在平行四边形ABCD中，AE⊥BC于点E，AF⊥CD于点F，∠EAF＝45°，且，则平行四边形ABCD的周长为____．16.(本小题7分)如图，在平行四边形ABCD中，M是BC边的中点，且AM=9，BD=12，AD=10，则平行四边形ABCD的面积为____．路径长问题（通用版）一. 单选题(本大题共5小题，共80分)1.(本小题15分)如图，在⊙O中，P是直径AB上一动点，在AB同侧作CA⊥AB，BD⊥AB，且AC=AP，BD=BP，连接CD．当点P从点A移到点B时，CD的中点的位置( )A. 在平分AB的某直线上移动B. 在垂直AB的某直线上移动C. 在弧AB上移动D. 保持固定不移动2.(本小题15分)如图，边长为a的六角螺帽在桌面上滚动（没有滑动）一周，它的中心O 点所经过的路径长为( )A. 6aB. 5aC. 2πaD.3.(本小题15分)如图，正方形ABCD的边长为2，将长为2的线段QR的两端放在正方形相邻的两边上同时滑动．如果点Q从点A出发，按A→B→C→D→A的方向滑动到A停止，同时点R从点B出发，按B→C→D→A→B的方向滑动到B停止，在这个过程中，线段QR的中点M 所经过的路线与正方形围成的图形面积为( )A. 2B. 4-πC. πD. π-14.(本小题15分)如图，在平面直角坐标系中，已知点A（0，2），点P是x轴上一动点，以线段AP为一边，在其一侧作等边三角形APQ．当点P运动到原点O处时，记点Q的位置为B，则当点P从运动到时，点Q运动的路径长为( )A. 2B. 2πC. 4D. 4π5.(本小题20分)如图，在平面直角坐标系中，菱形OABC的顶点A的坐标为（2，0），∠COA=60°，点D是线段AB上一动点（可与端点重合），过点B作BN⊥CD于点N（可与端点重合），当点D从点A运动到点B的过程中，点N运动的路径长为( )A.B.C.D. 2二. 填空题(本大题共1小题，共20分)6.(本小题20分)如图，MN=16，点P，Q在线段MN上，且PM=2，NQ=4．C是线段MN上的动点，分别以CM，CN为斜边在线段MN的同侧作Rt△ACM和Rt△BCN，使∠AMC=∠BCN=30°，连接AB，设AB的中点为D，当点C从点P运动到点Q时，点D的运动路径长为____．。