灰色关联分析详解+结果解读
灰色关联模型

灰色关联分析及理论灰色系统分析“白”指信息完全确知,“黑”指信息完全不确知,“灰”则指信息部分确知,部分不确知,或者说信息不完全。
这是“灰”的基本含义。
对于不同问题,在不同的场合,“灰”可以引伸为别的含义。
如:从表象看:“明”是白,“暗”是黑,那么“半明半暗或若明若暗”就是灰。
从态度看:“肯定”是白,“否定”是黑,那么“部分肯定,部分否定”就是灰。
从性质看:“纯”是白,“不纯”是黑,那么“多种成分”就是灰。
从结果看:“唯一”是白,“无数”是黑,那么“非唯一”就是灰。
从过程看:“新”是白,“旧”是黑,那么“新旧交替”就是灰。
从目标看:“单目标”是白,“无目标”是黑,那么“多目标”就是灰。
类似地可以举出许多例子,就其基本含义而言,“灰”是信息不完全性与非唯一性。
信息不完全性与非唯一性在人们认识与改造客观世界的过程中会经常遇到的。
客观世界是物质世界,也是信息世界。
所谓系统是指:由客观世界中相同或相似的事物按一定的秩序相互关联、相互制约而构成的整体。
例如工程技术系统,社会系统,经济系统等等。
所谓白色系统是指:信息完全明确的系统。
如,一个家庭,其人口、收入、支出、父子、母女上下间的关系等等完全明确;一个工厂。
其职工、设备、技术条件、产值、产量等等信息完全明确。
像家庭、工厂这样的系统就是白色系统。
所谓黑色系统是指:信息完全不明确的系统。
如遥远的某个星球,其重量、体积、是否有生命等等全然不知;湖北原始森林神农架的野人,其生活习性、群体关系,交换信息的方法等等完全不清楚,这样一类的系统都是黑色系统,还有飞碟、百暮三角洲等等目前只能看成黑色系统。
所谓灰色系统是指:介于白色系统与黑色系统之间的系统(Grey System),即系统内部信息和特性是部分已知的另一部分是未知的。
例如人体,其身高、体重、年龄、血压、脉搏、体温等等都是已知的,而人体的穴位的多少,穴位的生物、化学、物理性能;生物信息的传递;温度场;意识流等等尚未确知或者知道不透彻。
灰色关联分析

灰色关联分析灰色关联分析是一种常用于研究和预测多个影响因素之间关联程度的方法。
该分析方法可以通过对各个因素的数值进行比较,得出它们之间的关联强度,从而为决策提供依据。
下面将详细介绍灰色关联分析的原理、应用以及优势。
灰色关联分析的原理基于灰色系统理论,该理论是中国科学家陈纳德于1982年提出的一种对部分已知和部分未知信息进行分析的数学方法。
灰色关联分析将各个影响因素的数据进行标准化处理,然后计算各个因素之间的关联度。
通过对关联度进行排序,即可得出影响因素之间的关联程度大小。
灰色关联分析在各个领域都有广泛的应用,比如经济学、管理学、环境科学等。
在经济学领域,可以使用灰色关联分析来研究不同经济指标之间的关联程度,从而预测未来的经济趋势。
在管理学中,可以利用灰色关联分析来研究不同管理指标之间的关联程度,进而指导管理决策。
在环境科学领域,可以运用灰色关联分析来分析各个环境因素对生态系统的影响程度,以及控制污染等。
灰色关联分析相对于其他分析方法有一些独特的优势。
首先,它不要求数据分布满足正态分布等数学假设,可以对数据进行较好的处理。
其次,灰色关联分析可以处理样本量较小的情况,对于样本量不足的数据分析也有较好的适用性。
此外,由于灰色关联分析能够捕捉到数据之间的内在联系,因此对于某些非线性关系的分析,其结果可能更加准确。
然而,灰色关联分析也存在一些限制和不足之处。
首先,该分析方法依赖于数据的稳定性,对于非稳态的数据可能会导致分析结果不准确。
其次,灰色关联分析无法处理存在时间滞后效应的数据。
此外,该方法对数据的标准化要求较高,如果数据质量较差或者存在异常值,也会影响分析结果。
综上所述,灰色关联分析是一种研究和预测多个影响因素之间关联程度的有效方法。
它的原理基于灰色系统理论,可以在各个领域中广泛应用。
灰色关联分析相对于其他分析方法有一些独特的优势,但也存在一定限制。
在实际应用中,我们应该结合具体情况,合理选择分析方法,并充分考虑其适用性和局限性,以提高分析和决策的准确性。
(整理)灰色关联度分析法
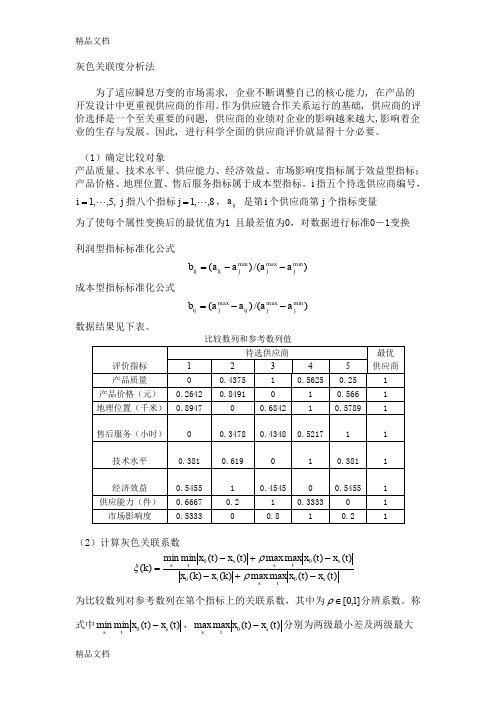
灰色关联度分析法为了适应瞬息万变的市场需求, 企业不断调整自己的核心能力, 在产品的开发设计中更重视供应商的作用。
作为供应链合作关系运行的基础, 供应商的评价选择是一个至关重要的问题, 供应商的业绩对企业的影响越来越大,影响着企业的生存与发展。
因此, 进行科学全面的供应商评价就显得十分必要。
(1)确定比较对象产品质量、技术水平、供应能力、经济效益、市场影响度指标属于效益型指标;产品价格、地理位置、售后服务指标属于成本型指标。
i 指五个待选供应商编号,,5,,1 =i j 指八个指标8,,1j =,ij a 是第i 个供应商第j 个指标变量为了使每个属性变换后的最优值为1 且最差值为0,对数据进行标准0-1变换利润型指标标准化公式)/()(min maxmin j j j ij ij a a a a b --=成本型指标标准化公式)/()(min max max j j ij j ij a a a a b --=数据结果见下表。
(2)计算灰色关联系数)()(max max )()()()(max max )()(min min )(0000t x t x k x k x t x t x t x t x k s tsi s ts s ts -+--+-=ρρξ为比较数列对参考数列在第个指标上的关联系数,其中为]1,0[∈ρ分辨系数。
称式中)()(min min 0t x t x s ts-、)()(max max 0t x t x s ts-分别为两级最小差及两级最大差。
一般来讲,分辨系数ρ越大,分辨率越大;ρ越小,分辨率越小。
在这里ρ取0.5。
(3)计算灰色加权关联度 灰色加权关联度的计算公式为∑==nk i i k w r 1)(ξ这里i r 为第i 个评价对象对理想对象的灰色加权关联度。
关联系数和关联度值(4)评价分析根据灰色加权关联度的大小,对各评价对象进行排序,可建立评价对象的关联序,关联度越大其评价结果越好。
灰色关联度评价方法(10)讲解

01 (t )
x0 (t ) x2 (t )
0.0492 0.0704 0.0785 0.0112 0.0477 0.1392
02 (t )
x0 (t ) x3 (t )
0.0119 0.0289 0.0694 0.0278 0.0006 0.0832
首 页 上 页 下 页 尾 页
式中分辨系数 在(0,1)内取值,一般情况下依据 (6.10)中数据情况多在0.1至0.5取值, 越小越能 提高关联系数间的差异.关联系数 0i (k ) 是不超 过1的正数, 0i (k ) 越小, 0i (k ) 越大,它反映第i 个比较序列Xi与参考序列X0在第k个期关联程度.
首 页 上 页 下 页 尾 页
0i (t )
首 页 上 页 下 页 尾 页
上式可变形为
(min) (max) 0i (t ) 0i (t ) (max) i 1, 2,3; t 2000, , 2005
(6.1)
0i (t )称为序列xi和序列x0在第t期的灰色关联系 数(或简称为关联系数). 由(6.1)式可以看出, 取值的大小可以控制(max) 对数据转化的影响, 取较小的值,可以提高关联 系数间差异的显著性,因而称 为分辨系数. 利用(6.1)对表6-3中绝对差值0i (t ) 进行规范化,取 0.4, 结果见表6-4,以01 (2000)计算为例:
首 页 上 页 下 页 尾 页
表6-1是某地区2000-2005年国内生产总值的统计 资料.现在提出这样的问题:该地区三次产业中, 哪一产业的变化与该地区国内生产总值(GDP)的 变化态势更一致?也就是哪一产业与GDP的关联 度最大呢? 表6-1 某地区国内生产总值统计资料(百万元)
灰色关联分析法原理及解题步骤

灰色关联分析法原理及解题步骤---------------研究两个因素或两个系统的关联度(即两因素变化大小,方向与速度的相对性)关联程度——曲线间几何形状的差别程度灰色关联分析是通过灰色关联度来分析和确定系统因素间的影响程度或因素对系统主行为的贡献测度的一种方法。
灰色关联分析的基本思想是根据序列曲线几何形状的相似程度来判断其联系是否紧密1> 曲线越接近,相应序列之间的关联度就越大,反之就越小 2> 灰色关联度越大,两因素变化态势越一致分析法优点它对样本量的多少和样本有无规律都同样适用,而且计算量小,十分方便,更不会出现量化结果与定性分析结果不符的情况。
灰色系统关联分析的具体计算步骤如下 1》参考数列和比较数列的确定参考数列——反映系统行为特征的数据序列比较数列——影响系统行为的因素组成的数据序列2》无量纲化处理参考数列和比较数列(1) 初值化——矩阵中的每个数均除以第一个数得到的新矩阵(2) 均值化——矩阵中的每个数均除以用矩阵所有元素的平均值得到的新矩阵(3) 区间相对值化3》求参考数列与比较数列的灰色关联系数ξ(Xi) 参考数列X0比较数列X1、X2、X3……………比较数列相对于参考数列在曲线各点的关联系数ξ(i)称为关联系数,其中ρ称为分辨系数,ρ?(0,1),常取0.5.实数第二级最小差,记为Δmin。
两级最大差,记为Δmax。
为各比较数列Xi曲线上的每一个点与参考数列X0曲线上的每一个点的绝对差值。
记为Δoi(k)。
所以关联系数ξ(Xi)也可简化如下列公式:4》求关联度ri关联系数——比较数列与参考数列在各个时刻(即曲线中的各点)的关联程度值,所以它的数不止一个,而信息过于分散不便于进行整体性比较。
因此有必要将各个时刻(即曲线中的各点)的关联系数集中为一个值,即求其平均值,作为比较数列与参考数列间关联程度的数量表示,关联度ri公式如下:5》排关联序因素间的关联程度,主要是用关联度的大小次序描述,而不仅是关联度的大小。
灰色关联分析法讲解

“非唯一性”
目标非唯一 灰靶思想
目标可约束
目标可接近 信息可扩充 方案可改善 关系可协调 思维可多向 认识可深化 途径可优化
灰色系统理论研究灰元、灰数、灰关系 灰数——指信息不完全的数。
灰关联分析法
(一)什么是灰色系统
灰色系统理论是1982年由邓聚龙创立的一门边缘性学科 (interdisciplinary)
灰色系统用颜色深浅反映信息量的多少。说一个系统是黑色的, 就是说这个系统是黑洞洞的,信息量太少;说一个系统是白色的, 就是说这个系统是清楚的,信息量充足。
这种处于黑白之间的系统,就是灰色系统,或说信息不完全的系 统,成为灰色系统或简称会系统(grey system)。
如“这个人的年龄18岁左右” “今天的气温10 - 15度之间” 灰元——指信息不完全的元素。如“货币”是灰元。
货币的两种功能:流通手段和价值尺度 灰关系——指信息不完全的关系。例:多种经济成份并存、一国两制
换轨思维
例1:小司马光灵机一动,换个角度处置眼前的危急场面。其实, 他砸碎的不完全是一口现实生活中看得见摸得着的缸,同时也打破 了一种旧的思维模式。当我们打破旧思维,再将我们的思路重新组 装的时候,结果一定是一幅好风光。 爱迪生是美国的大发明家。他的一切发明都是和他的思维活跃分不 开的。
例2:一天,爱迪生在实验室里工作,急需知道一个灯泡容量的数 据。由于手头忙不开,他便递给助手一个没有上灯口的玻璃灯泡, 吩咐助手把灯泡的容量数据量出来。过了很久,爱迪生手头的活早 已干完,助手仍未将数据送来。爱迪生只好亲自去找助手,一进门, 就看到助手正忙于计算,桌上演算纸已经推了一大迭。爱迪生忙问: “还需多长时间?”助手说:“一半还没完呢。”爱迪生明白了。 原来,他的助手用软尺测量灯泡的周长、斜度,正在用复杂的公式 计算呢!小伙子还把程序说给爱迪生听,证明自己的思路没错。爱 迪生不等他说完,便拍拍他的肩膀说:“别白忙了,小伙子,瞧我 这么干。”说着,他往灯泡里面注满了水,交给助手:“把这里的 水倒在量杯里,马上告诉我它的容量。”助手听到后,脸马上就红 了。
灰色关联分析

灰⾊关联分析
灰⾊关联分析法
对于有m个评价对象,n个评价指标的问题,⽤灰⾊关联分析来选择,可以针对⼤量的不确定因素以及相互关系,⽤定性和定量有机结合的⽅式,使原本复杂的决策问题变得更加清晰简单,⽽且计算⽅便,主要是排除了决策者的主观任意性,得出的结论很客观,有⼀定的参考价值。
主要步骤
1. 确定评价对象和评价标准。
(以⼀个评价对象为例)
评价对象为x={x(k)|k=1,2,3,...,n},评价标准为x0={x(k)|k=1,2,3,...,n}
k是指该评价对象的第k个评价指标
2. 确定各个评价指标的权重
主要是为了最后对求出的各个指标的灰⾊关联系数进⾏总和,若⽆权重也可以直接求平均值
3. 计算灰⾊关联系数
将每⼀个评价对象的评价指标都与评价标准相减并求绝对值,即
令c=|x(k)−x0(k)|
那么我们可以得到⼀个新的矩阵C
取C中的每⼀列中的最⼩值在每⼀⾏中的最⼩值,即两级最⼩差
a=min i min j c ij
再取每⼀列中的最⼤值在每⼀⾏中的最⼤指,即两级最⼤差
b=max i max j c ij
灰⾊关联系数为
ξi(j)=a+ρb c ij+ρb
式中,ρ⼀般取0.5,ρ属于0到1.
4. 计算灰⾊加权关联度
就是计算每⼀个评价对象的灰⾊关联度的加权和
r i=
n
∑
j=1w i∗ξi(j)
灰⾊关联度越⼤则效果越好Processing math: 100%。
灰色关联度分析GreyRelationalAnalysis是其中的一种

( X0 ) 考試成績 考 詴 成 績 出席率 ( X1 ) 出 席 ( X2 ) 率
評分項
實例參考 ( 一 ) 六、綀習題
Hale Waihona Puke 周世傑 周阿舍 100 100 90 100% 90
100%
說明 劉阿華 蕭阿薔 蕭阿薔 劉阿華
95 95 80 90% 80
90%
60 以周阿 60 50 舍為基 80% 50
80% 準點
1、標準化
姓名 評分項目
周阿舍 1 1 1
劉阿華 0.95 0.89 0.90
蕭阿薔 0.60 0.50 0.80
總成績(X0) 考詴成績(X1) 出席率(X2)
2、對應差數列表
差值 姓名 差式
周阿舍 0 0
劉阿華 0.06 0.05
蕭阿薔 0.1 0.2
min
k
max
k
| X 0 k X 1 k |
灰色關聯度可分成「局部性灰色關 聯度」與「整體性灰色關聯度」兩 類。主要的差別在於「局部性灰色 關聯度」有一參考序列,而「整體 性灰色關聯度」是任一序列均可為 參考序列。
二.直觀分析
依據因素數列繪製曲線圖,由曲 線圖直接觀察因素列間的接近程 度及數值關係,表一某老師給學 生的評分表數據資料為例,繪製 曲線圖如圖一所示,由曲線圖大 約可直接觀察出該老師給分總成 績主要與考詴成績關聯度較高。
第五章 灰色關聯度分析
目錄
壹、何謂灰色關聯度分析 5-2 貳、灰色聯度分析實例詳說與練習 5-8
負責組員 工教行政碩士班二年級 周世傑591701017 陶虹沅591701020 林炎瑩591701025
壹、何謂灰色關聯度分析
灰色关联分析法(灰色综合评价法)

灰色关联分析法对于两个系统之间的因素,其随时间或不同对象而变化的关联性大小的量度,称为关联度。
在系统发展过程中,若两个因素变化的趋势具有一致性,即同步变化程度较高,即可谓二者关联程度较高;反之,则较低。
因此,灰色关联分析方法,是根据因素之间发展趋势的相似或相异程度,亦即“灰色关联度”,作为衡量因素间关联程度的一种方法。
应用于综合评价(灰色综合评价)步骤:(1) 确定比较对象(评价对象)和参考数列(评价标准)。
设评价对象有m 个,评价指标有n 个,参考数列为{}00()|1,2,,x x k k n ==⋅⋅⋅,比较数列为{}()|1,2,,,1,2,,i i x x k k n i m ==⋅⋅⋅=⋅⋅⋅。
(2) 对参考数列和比较数列进行无量纲化处理由于系统中各因素的物理意义不同,导致数据的量纲也不一定相同,不便于比较,或在比较时难以得到正确的结论。
因此在进行灰色关联度分析时,一般都要进行无量纲化的数据处理。
设无量纲化后参考数列为{}00()|1,2,,x x k k n ''==⋅⋅⋅,无量纲化后比较数列为{}()|1,2,,,i i x x k k n ''==⋅⋅⋅1,2,,i m =⋅⋅⋅。
(3) 确定各指标值对应的权重。
可用层次分析法等确定各指标对应的权重[]12,,,n w w w w =⋅⋅⋅,其中(1,2,,)k w k n =⋅⋅⋅为第k 个评价指标对应的权重。
(4) 计算灰色关联系数:0000min min ()()max max ()()()()()max max ()()s s s t s t i i s s tx t x t x t x t k x k x k x t x t ρξρ''''-+-=''''-+- 为比较数列i x 对参考数列0x 在第k 个指标上的关联系数,其中[]0,1ρ∈为分辨系数,称0min min ()()s s t x t x t ''-、0max max ()()s s tx t x t ''-分别为两级最小差及两级最大差。
灰色关联分析法讲解

系统
白色系统 灰色系统 黑色系统
“信息不完全”是灰的基本含义,在不同场合可引申为
白
黑
灰
从表象看 从过程看 从性质看 从信息看 从结果看 从态度看 从方法看
明朗 新 纯
完全 唯一的解
肯定 严厉
暗 旧 不纯 不完全 无数的解 否定 放纵
若明若暗 新旧交替 多种成分 部分完全 非唯一性
扬弃 宽容
“信息不完全”,一般指:
灰关联分析法
(一)什么是灰色系统
灰色系统理论是1982年由邓聚龙创立的一门边缘性学科 (interdisciplinary)
灰色系统用颜色深浅反映信息量的多少。说一个系统是黑色的, 就是说这个系统是黑洞洞的,信息量太少;说一个系统是白色的, 就是说这个系统是清楚的,信息量充足。
这种处于黑白之间的系统,就是灰色系统,或说信息不完全的系 统,成为灰色系统或简称会系统(grey system)。
K X0(K) X1(K) X2(K) | X0(K)- X1(K)| | XO(K)- X2(K)| ————————————————————————————————————
11
1
1
0
0
2 1.1
1.6
2.2
0.5
1.1
3 1.2
1.7
1.8
0.5
0.6
4 1.5
2.1
2. 0
0.6
0.5
————————————————————————————————————
(3)苏联高级官员利加乔夫在一次向全国发布的电视讲话中,破天荒省略 了按照惯例必须向安德罗波夫问候习惯。
(4)他驱车经过苏军参谋部及国防部时发现大楼里以往这时仅是少数窗户 有灯光,而当时几百间房间里灯火通明。 杜德尔把这些现象联系起来,最后得出结论:安德罗波夫已去世
灰色关联度分析法

灰色关联度分析法引言灰色关联度分析法是一种用于揭示变量之间关联程度的方法。
它可以在缺乏足够数据的情况下,通过对变量之间的相关性进行评估,帮助分析人员做出决策。
在本文中,我们将介绍灰色关联度分析法的原理和应用,并探讨其在实际问题中的价值和局限性。
一、灰色关联度分析法的原理灰色关联度分析法是在灰色系统理论基础上发展起来的一种关联性分析方法。
灰色关联度分析法的核心思想是通过模糊度量的方法,将样本数据的数量化描述量和次序特征结合起来,通过计算变量间的关联度,得出它们之间的相关性。
具体而言,灰色关联度分析法的步骤主要包括以下几个方面:1. 数据标准化:将原始数据进行归一化处理,以消除变量之间的量纲差异,使其具有可比性。
2. 确定参考序列:在给定的多个序列中,根据研究目标和实际需求,选择一个作为参考序列,其他序列将与之进行比较。
3. 计算关联度指数:通过计算每个序列与参考序列之间的关联度指数,来评估它们之间的关联程度。
关联度指数的计算通常有多种方法,如灰色关联度、相对系数法等。
4. 判别等级:根据关联度指数的大小,将序列划分为几个等级,以便更直观地评估变量之间的关联程度。
二、灰色关联度分析法的应用灰色关联度分析法在许多领域和问题中都有广泛的应用。
下面将介绍一些典型的应用情况:1. 经济领域:灰色关联度分析法可以用于评估经济指标之间的关联性,识别影响经济发展的主要因素,帮助政府和企业做出相应的调整和决策。
2. 工业制造业:在工业制造领域,灰色关联度分析法可以用于优化生产工艺,提高产品质量,降低成本。
通过分析不同因素对产品质量的影响程度,可以找出关键因素,并制定相应的改进措施。
3. 市场调研:在市场调研中,灰色关联度分析法可以用于分析消费者行为和市场趋势,预测产品的需求量和销售额。
通过对多个变量之间的关联性进行评估,可以为企业的市场营销决策提供有价值的参考和支持。
4. 环境管理:在环境管理领域,灰色关联度分析法可以用于评估各种环境因素对生态系统的影响程度,为环境保护和可持续发展提供科学依据。
数学建模——灰色关联度分析讲解

依照问题的要求,我们自然选取铅球运动员专项 成绩作为参考数列,将上表中的各个数列的初始化数 列代入(1) 、 (2) ,易计算出各数列的关联度,如下表 所示。
灰色关联度分析的运用
因 素 分 析 优 势 分 析 综 合 评 价
二、铅球运动员专项成绩的因素分析 通过对某健将级女子铅球运动员的跟踪调查,获 得其 1982~1986 年每年最好成绩及 16 项专项素质和 身体素质的时间序列资料,见下表。
指 铅球专项成绩 4 公斤前抛 4 公斤后抛 4 公斤原地 立定跳远 高翻 抓举 卧推 3 公斤前抛 3 公斤后抛 3 公斤原地 3 公斤滑步 立定三级跳远 全蹲 挺举 30 米起跑 100 米
4、在第 4 列中 r 24=0.809 最大,表明科技对工业影响 最大,而 r 34=0.588 比较小,表明从全面来衡量,还没 有使科技投资与农村经济挂上钩,即科技投资针对的 不是农村需要的科技,r 64=0.584 更小, 表明科技对建 筑业的作用比农业还差; 5、第 3 列的元素普遍比较大,表明农业是个综合性行 业,需要其它方面的配合,例如: r 32=0.828 表明工业 发展能够较大地促进农业的发展。另外,r 35=0.735 表 明农业发展与交通发展也是密切相关的。
关联度
关联度是事物之间、因素之间关联性大小的量度。它 定量地描述了事物或因素之间相互变化的情况,即变 化的大小、方向与速度等的相对性。如果事物或因素 变化的态势基本一致,则可以认为它们之间的关联度 较大,反之,关联度较小。
基本思想:
灰色关联度分析法

灰色关联度分析法
灰色关联度分析法(Grey Relational Analysis,GRA)是一种多属性
决策分析的统计方法,是一个在变量未知情况下实现系统模型和控制
不确定性的有用工具。
灰色关联度分析法主要用于研究和分析影响多
维度多属性数据测量结果的各种因素之间的相关关系。
它对模糊数据
进行综合处理,可以把多维评价分解成基本的准则来实现。
灰色关联度分析法的原理是利用灰色关联度的基本定义来衡量某种系
统的相关程度,灰色关联度通过确定系统的相似度和差异度来计算相
关程度,以此作为最终判断结果。
首先,将所有系统样本的信息表示
成一维度序列,并计算各时间点的灰色关联度。
其次,将灰色关联度
转化成定量指标,以此确定每一种系统的相关程度。
最后,根据定量
指标的值,把每一种系统分成几个类,以便于进一步分析和研究。
灰色关联度分析法可以应用于多种领域,例如工程设计、产品设计、
资源调配等。
例如,当进行工程设计时,可以利用灰色关联度分析法,通过灰色关联度来考虑多种参数和因素,以便最大限度地满足工程项
目的要求。
总之,灰色关联度分析法是一种有效的多属性决策分析方法,在许多
领域得到了广泛的应用,对于多维度和多属性问题具有显著优势。
有
效地利用灰色关联度分析法,能够更好地实现系统模型和控制不确定性,有助于优化效率和提高决策水平。
数据分析知识:如何进行数据分析的灰色关联分析

数据分析知识:如何进行数据分析的灰色关联分析灰色关联分析是一种用于处理灰色系统问题的数学分析方法,常用于实现数据关联度分析,在数据分析的过程中具有广泛的应用。
一、灰色系统的基本概念灰色系统学是我国科学家为处理灰色系统问题而发明发展起来的,特别是在现代科技和管理中,灰色预测及灰色控制等灰色系统的应用也得到了长足的发展。
灰色系统最基本的两个变量是“系统输入序列”和“系统输出序列”,其中输入序列代表被测参数的原始数据序列,而输出序列则表示对输入序列的观测序列。
灰色模型中输入序列被视为“灰色”,而输出序列则被看做是“白色”,也就是说有一部分数据的可靠度高,有一部分数据的可靠度没有那么高,这也是该模型与其他预测模型之间最大的不同。
二、灰色关联分析原理及其应用灰色关联分析是利用灰色系统理论,按照客观规律,定量分析它们之间的联系和预测分析的一种方法,通常用于实现数据的关联分析,在数据分析的过程中具有广泛的应用。
在灰色关联分析方法中,选择一组参考序列和一组待测序列,对它们进行运算,以得出它们之间关联程度。
在比较两组序列时,灰色关联方法可以把两组序列进行交叉比较,再根据一定的准则对相关系数进行修正,从而得到更为精确的结果。
三、灰色关联分析步骤1、选择指标序列:根据研究的具体需要,选择所需的指标序列,包括生产指标、销售指标、财务指标等。
2、建立数据矩阵:将所需的指标序列按表格的形式进行收集和整理,既可形成行数据矩阵,也可形成列数据矩阵。
3、数据序列标准化:对数据矩阵进行标准化处理,一般采用最大值归一化法、平均值归一化法等方法。
4、计算灰色关联系数:在计算灰色关联系数时,可选取单一灰色关联度(包括一阶灰色关联度和二阶灰色关联度)、多因素灰色关联度等。
5、灰色关联函数的优化:通过建立优化模型,对数据序列进行灰色关联函数的优化,提高关联分析的准确性和可靠性。
6、结果判断:根据实际需求对关联分析的结果进行判断,判断结果是否符合实际情况,对结果进行修正和调整。
灰色关联度分析解法及详细例题解答

灰色关联度分析解法及详细例题解答1.地梭梭生长量与气候因子的关联分析下表为1995年3年梭梭逐月生长量(X0)、月平均气温(X1)、月降水量(X2)、月日照(X3)时数和月平均相对湿度(X4)的原始数据,试排出影响梭梭生长的关联序,并找出主要的影响因子。
1 2 3 4 5 6 7 8 9 10 11 12X0(cm) 0.01 0.5 1.5 10.8 13 16.3 18 19.3 14.8 10.3 8 1X1(℃) 4.2 7.4 10 16.1 21.1 23.9 24.7 24.5 22 18 13.1 6.8 X2(mm) 17 10.8 17.4 19.7 248.7 72.2 96.9 269.5 194.8 58.1 4.9 12.6 X3(hour) 54.5 73.8 84.7 137 149.6 109.5 101.6 164.6 81.6 84 79.3 66.5 X4(%) 81 79 75 75 77 79 83 86 83 82 81 82灰色系统理论提出了灰色关联度的概念,它是提系统中两个因素关联性大小的量度,关联度的大小直接反映系统中的各因素对目标值的影响程度。
运用灰色关联分析法进行因素分析的一般步骤为:第一步:确定分析数列。
确定反映系统行为特征的参考数列和影响系统行为的比较数列。
反映系统行为特征的数据序列,称为参考数列。
(Y)设参考数列(又称母序列)为Y = {Y (k)| k = 1,2,Λ,n};影响系统行为的因素组成的数据序列,称比较数列。
(X)比较数列(又称子序列)Xi = {Xi(k)| k = 1,2,Λ,n},i = 1,2,Λ,m。
第二步,变量的无量纲化由于系统中各因素列中的数据可能因量纲不同,不便于比较或在比较时难以得到正确的结论。
因此为了保证结果的可靠性,在进行灰色关联度分析时,一般都要进行数据的无量纲化处理。
第三步,计算关联系数。
X0(k)与xi(k)的关联系数记,则,称为分辨系数。
灰色关联度分析解法及详细例题解答

灰⾊关联度分析解法及详细例题解答1.地梭梭⽣长量与⽓候因⼦的关联分析下表为1995年3年梭梭逐⽉⽣长量(X0)、⽉平均⽓温(X1)、⽉降⽔量(X2)、⽉⽇照(X3)时数和⽉平均相对湿度(X4)的原始数据,试排出影响梭梭⽣长的关联序,并找出主要的影响因⼦。
灰⾊系统理论提出了灰⾊关联度的概念,它是提系统中两个因素关联性⼤⼩的量度,关联度的⼤⼩直接反映系统中的各因素对⽬标值的影响程度。
运⽤灰⾊关联分析法进⾏因素分析的⼀般步骤为:第⼀步:确定分析数列。
确定反映系统⾏为特征的参考数列和影响系统⾏为的⽐较数列。
反映系统⾏为特征的数据序列,称为参考数列。
(Y)设参考数列(⼜称母序列)为Y = {Y(k)|k= 1,2,Λ,n};影响系统⾏为的因素组成的数据序列,称⽐较数列。
(X)⽐较数列(⼜称⼦序列)Xi = {Xi(k)|k= 1,2,Λ,n},i= 1,2,Λ,m。
第⼆步,变量的⽆量纲化由于系统中各因素列中的数据可能因量纲不同,不便于⽐较或在⽐较时难以得到正确的结论。
因此为了保证结果的可靠性,在进⾏灰⾊关联度分析时,⼀般都要进⾏数据的⽆量纲化处理。
第三步,计算关联系数。
X0(k)与x i(k)的关联系数记,则,称为分辨系数。
ρ越⼩,分辨⼒越⼤,⼀般ρ的取值区间为(0,1),具体取值可视情况⽽定。
当时,分辨⼒最好,通常取ρ =0.5。
ξi(k)继⽐较数列xi的第k个元素与参考数列xo的第k个元素之间的关联系数。
第四步,计算关联度因为关联系数是⽐较数列与参考数列在各个时刻(即曲线中的各点)的关联程度值,所以它的数不⽌⼀个,⽽信息过于分散不便于进⾏整体性⽐较。
因此有必要将各个时刻(即曲线中的各点)的关联系数集中为⼀个值,即求其平均值,作为⽐较数列与参考数列间关联程度的数量表⽰,关联度ri公式如下:第五步,关联度排序关联度按⼤⼩排序,如果r1在算出Xi(k)序列与Y(k)序列的关联系数后,计算各类关联系数的平均值,平均值ri就称为Y(k)与Xi(k)的关联度。
灰色关联度分析讲解

第五章灰色关联度分析目录壹、何谓灰色关联度分析-------------------- 5-2贰、灰色联度分析实例详说与练习--------------- 5-8第五章灰色关联度分析壹、何谓灰色关联度分析一.关联度分析灰色系统分析方法针对不同问题性质有几种不同做法,灰色关联度分析(Grey Relational Analysis) 是其中的一种。
基本上灰色关联度分析是依据各因素数列曲线形状的接近程度做发展态势的分析。
灰色系统理论提出了对各子系统进行灰色关联度分析的概念,意图透过一定的方法,去寻求系统中各子系统(或因素)之间的数值关系。
简言之,灰色关联度分析的意义是指在系统发展过程中,如果两个因素变化的态势是一致的,即同步变化程度较高,则可以认为两者关联较大;反之,则两者关联度较小。
因此,灰色关联度分析对于一个系统发展变化态势提供了量化的度量,非常适合动态(Dynamic)的历程分析。
灰色关联度可分成「局部性灰色关联度」与「整体性灰色关联度」两类。
主要的差别在于「局部性灰色关联度」有一参考序列,而「整体性灰色关联度」是任一序列均可为参考序列。
二.直观分析依据因素数列绘制曲线图,由曲线图直接观察因素列间的接近程度及数值关系,表一某老师给学生的评分表数据数据为例,绘制曲线图如图一所示,由曲线图大约可直接观察出该老师给分总成绩主要与考试成绩关联度较高。
表一某一老师给学生的评分表单位:分/%由曲线图直观分析,是可大略分析因素数列关联度,可看出考试成绩与总成绩曲线形状较接近,故较具关联度,但若能以量化分析予以左证,将使分析结果更具有说服力。
三.量化分析量化分析四步曲:1.标准化(无量纲化):以参照数列(取最大数的数列)为基准点,将各数据标准化成介于0至1之间的数据最佳。
2.应公式需要值,产生对应差数列表,内容包括:与参考数列值差(绝对值)、最大差、最小差、Z (Zeta)为分辨系数,0VZV1,可设Z = 0.5(采取数字最终务必使关联系数计算:E i (k)小于1为原则,至于分辨系数之设定值对关联度并没影响,请参考p14例)3.关联系数E i (k)计算:应用公式i(k)mi n maxAoi(k)+』max 计算比较数列X上各点k与参考数列X参照点的关联系数,最后求各系数的平均值即是X与X o的关联度r i。
Matlab学习系列28.-灰色关联分析

28. 灰色(huīsè)关联分析一、灰色系统理论(lǐlùn)简介若系统的内部信息是完全已知的,称为白色(báisè)系统;若系统的内部信息是一无所知(一团漆黑),只能从它同外部的联系来观测研究,这种系统便是黑色系统;灰色系统介于二者之间,灰色系统的一部分信息是已知的,一部分是未知的。
灰色系统(xìtǒng)理论以“部分信息已知、部分信息未知”的“小样本(yàngběn)”、“贫信息”不确定型系统为研究对象,其特点是:(1)认为不确定量是灰数,用灰色数学来处理不确定量,使之量化,灰色系统理论只需要很少量的数据序列;(2)观测到的数据序列看作随时间变化的灰色量或灰色过程,通过鉴别系统因素之间发展趋势的相似或相异程度,即进行关联度分析;(3)通过累加生成和累减生成逐步使灰色量白化,从而建立相应于微分方程解的模型,从而预测事物未来的发展趋势和未来状态。
二、灰色关联度分析1. 要定量地研究两个事物间的关联程度,可以用相关系数和相似系数等,但这需要足够多的样本数或者要求数据服从一定概率分布。
在客观世界中,有许多因素之间的关系是灰色的,分不清哪些因素之间关系密切,哪些不密切,这样就难以找到主要矛盾和主要特性。
灰因素关联分析,目的是定量地表征诸因素之间的关联程度,从而揭示灰色系统的主要特性。
关联分析是灰色系统分析和预测的基础。
关联分析源于几何直观,实质上是一种曲线间几何形状的分析比较,即几何形状越接近,则发展变化趋势越接近,关联程度越大。
如下图所示:xt曲线A与B比较平行,则认为A与B的关联程度大;曲线C与A随时间变化的方向很不一致,则认为A与C的关联程度较小;曲线A与D相差最大,则认为两者的关联程度最小。
2. 关联度分析是分析系统中各因素关联程度的方法步骤:(1) 计算(jì suàn)关联系数设参考(cānkǎo)序列为比较(bǐjiào)序列为比较(bǐjiào)序列X i对参考(cānkǎo)序列X0在k时刻的关联系数定义为:其中,和分别称为两级最小差、两级最大差,称为分辨系数,越大分辨率越大,一般采用对单位不一,初值不同的序列,在计算关联系数之前应首先进行初值化,即将该序列的所有数据分别除以第一数据,将变量化为无单位的相对数值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
灰色关联分析
1、作用
对于两个系统之间的因素,其随时间或不同对象而变化的关联性大小的量度,称为关联度。
在系统发展过程中,若两个因素变化的趋势具有一致性,即同步变化程度较高,即可谓二者关联程度较高;反之,则较低。
因此,灰色关联分析是指对一个系统发展变化态势的定量描述和比较的方法,其基本思想是通过确定参考数据列和若干个比较数据列的几何形状相似程度来判断其联系是否紧密,它反映了曲线间的关联程度。
2、输入输出描述
输入:特征序列为至少两项或以上的定量变量,母序列(关联对象)为 1 项定量变量。
输出:反应考核指标与母序列的关联程度。
3、案例示例
案例:分析 09-18 年内,影院数量,观影人数,票价、电影上线数量这些因素对全年电影票房的影响。
其中电影票房是母序列,影院数量,观影人数,票价、电影上线数量是特征序列。
4、案例数据
灰色关联分析案例数据
5、案例操作
Step1:新建分析;
Step2:上传数据;
Step3:选择对应数据打开后进行预览,确认无误后点击开始分析;
step4:选择【灰色关联分析】;
step5:查看对应的数据数据格式,【灰色关联分析】要求特征序列为定量变量,且至少有一项;要求母序列为定量变量,且只有一项。
step6:设置量纲处理方式(包括初值化、均值化、无处理)、分辨系数(ρ越
小,分辨力越大,一般ρ的取值区间为 ( 0 ,1 ),具体取值可视情况而定。
当ρ≤ 0.5463 时,分辨力最好,通常取ρ = 0.5 )
step7:点击【开始分析】,完成全部操作。
6、输出结果分析
输出结果 1:灰色关联系数
图表说明:关联系数代表着该子序列与母序列对应维度上的关联程度值(数字越大,代表关联性越强)。
输出结果 2:关联系数图
分析:输出结果 1 和输出结果 2 是一样的,输出结果 1 用了表格形式来呈现关联系数,输出结果 2 用了图表形式来呈现关联系数。
图表很直观地展现了,大多数年份的银幕数量和电影上线数量对票房影响更大。
输出结果 3:关联系数图
分析:针对本次 4 个评价项,银幕数量评价最高(关联度为:0.882),其次是电影上线数量(关联度为:0.873)。
这说明对票房影响最大的是银幕数量,其次是电影上线数量、票价,观影人数对电影票房的影响程度较小。
7、注意事项
在选择量纲处理方式时,一般地,初值化方法适用于稳定递增或递减的数据,而均值化适合没有明显升降趋势现象的数据;
灰色关联分析时,数据一定需要大于 0,原因在于如果小于 0 进行计算时会出现‘抵消’现象,并不符合灰色关联分析的计算原理。
如果出现小于 0 数据,建议作为空值处理或者填补;
母序列是指标的参照对比项,比如研究 5 个指标与母序列的关联程度,通常研究者需要自己提供母序列数据。
