第八章 图论原理
合集下载
第八章图论

有向图是一个有序二元组(V,A),记为 D=(V,A),其中 V=(v1,v2,…….vp)是 p 个点 的集合,A={a1,a2,……aq}是 q 条弧的集合,并且 ai 是一个有序二元组,记为 aij=(vi,vj)≠ (vj,vi),vi,vj∈V,并称 aij 是以 vi 为始点,vj 为终点的弧, i, j 的顺序不能颠倒,图中弧的方 向用箭头标识。
27
Dijkstra标号法原理
方法的每一步是去修改 T 标号,并且把某一个具有 T 标号的点改变 为具有 P 标号的点,从而使 D 中具有标号的顶点数为多一个.这样至多
树与最小树问题
某企业的组织机构如下所示
生产计划科
行政办公室技术科工 设艺 计组 组
供销科Βιβλιοθήκη 财务科厂长 行政科
车间铸 锻造 压车 车间 间
生产办公室
二车间 三车间 四车间
18
树的概念和性质
树的定义
定义 无圈的连通图,称为树,记作 T=(V,ET)。
树的性质
v1
v3 7 v5
24
矩阵法举例
例 8.2 下面是一个求最小树的问题。用矩阵法求解
V3
7
V6
1
4
1
2
9
V1
3
3
V4
10
V7 3
V9
7
V2
4
8
6
5
V5
2
V8
25
最短路问题
最短路问题,就是从给定的网络图中找出一点到各点或任意两 点之间距离最短的一条路
最短路问题在实际中具有广泛的应用,如管道铺设、线路选择 等问题,还有些如设备更新、投资等问题也可以归结为求最短 路问题
27
Dijkstra标号法原理
方法的每一步是去修改 T 标号,并且把某一个具有 T 标号的点改变 为具有 P 标号的点,从而使 D 中具有标号的顶点数为多一个.这样至多
树与最小树问题
某企业的组织机构如下所示
生产计划科
行政办公室技术科工 设艺 计组 组
供销科Βιβλιοθήκη 财务科厂长 行政科
车间铸 锻造 压车 车间 间
生产办公室
二车间 三车间 四车间
18
树的概念和性质
树的定义
定义 无圈的连通图,称为树,记作 T=(V,ET)。
树的性质
v1
v3 7 v5
24
矩阵法举例
例 8.2 下面是一个求最小树的问题。用矩阵法求解
V3
7
V6
1
4
1
2
9
V1
3
3
V4
10
V7 3
V9
7
V2
4
8
6
5
V5
2
V8
25
最短路问题
最短路问题,就是从给定的网络图中找出一点到各点或任意两 点之间距离最短的一条路
最短路问题在实际中具有广泛的应用,如管道铺设、线路选择 等问题,还有些如设备更新、投资等问题也可以归结为求最短 路问题
离散数学第8章 图论及其应用

重要课题。
38
第八章 图论及其应用 例如图8-5中(a)与(b)均有6个结点,5条边;3个1度结点
,2个2度结点,1个3度结点。 满足上述3个条件,然而并不同构。
因为在图8-5(a)中的结点x应和图8-5(b)中结点y对应, 它们的度数均为3,而图8-5(a)中的结点x与两个度数为1 的结点邻接,图8-5(b)中结点y仅与一个度数为1的结点
E={e1,e2,e3,e4,e5,e6,e7},
e1=(a,b),e2=(a,c),e3=(b,d),e4=(b,c),e5=(d,c),e6=(a,d),
e7=(b,b)
则图G可用图(a)或(b)表示。
一个图G可用一个图形来
表示且表示形式不唯一
6
第八章 图论及其应用
有向图与无向图
• 在图G中,如果每条边都是有向边,则称该图为有向图; • 若每条边都是无向边,则称该图为无向图; • 如果有些边是有向边,另一些边是无向边,图G称为混合
•
(1)
(2)
37
第八章 图论及其应用 图之间的同构关系具有自反性、对称性和传递性.
若两图同构,则两图必然满足: (1)有相同结点数目; (2)有相同边数; (3)度数相同的结点数目相同; (4)有相同重数的边数相同,等等。
但这仅仅是必要条件而不是充分条件。
寻找一种简单 有效的方法来 判定图的同构, 至今仍是图论 中悬而未决的
• 若边e所对应的结点对是有序对〈a,b〉,则称e是有向边。a叫 边e的始点,b叫边e的终点,统称为e的端点。 • 若边e所对应的结点对是无序对(a,b) ,则称e是无向边。 • 这时统称e关联顶点a和b,端点a和b是邻接的。
5
第八章 图论及其应用
例 设G=〈V,E〉,其中V={a,b,c,d},
38
第八章 图论及其应用 例如图8-5中(a)与(b)均有6个结点,5条边;3个1度结点
,2个2度结点,1个3度结点。 满足上述3个条件,然而并不同构。
因为在图8-5(a)中的结点x应和图8-5(b)中结点y对应, 它们的度数均为3,而图8-5(a)中的结点x与两个度数为1 的结点邻接,图8-5(b)中结点y仅与一个度数为1的结点
E={e1,e2,e3,e4,e5,e6,e7},
e1=(a,b),e2=(a,c),e3=(b,d),e4=(b,c),e5=(d,c),e6=(a,d),
e7=(b,b)
则图G可用图(a)或(b)表示。
一个图G可用一个图形来
表示且表示形式不唯一
6
第八章 图论及其应用
有向图与无向图
• 在图G中,如果每条边都是有向边,则称该图为有向图; • 若每条边都是无向边,则称该图为无向图; • 如果有些边是有向边,另一些边是无向边,图G称为混合
•
(1)
(2)
37
第八章 图论及其应用 图之间的同构关系具有自反性、对称性和传递性.
若两图同构,则两图必然满足: (1)有相同结点数目; (2)有相同边数; (3)度数相同的结点数目相同; (4)有相同重数的边数相同,等等。
但这仅仅是必要条件而不是充分条件。
寻找一种简单 有效的方法来 判定图的同构, 至今仍是图论 中悬而未决的
• 若边e所对应的结点对是有序对〈a,b〉,则称e是有向边。a叫 边e的始点,b叫边e的终点,统称为e的端点。 • 若边e所对应的结点对是无序对(a,b) ,则称e是无向边。 • 这时统称e关联顶点a和b,端点a和b是邻接的。
5
第八章 图论及其应用
例 设G=〈V,E〉,其中V={a,b,c,d},
运筹学 第八章 图论 - 全

(a)明显为二部图,(b)也是二部图,但不明显,改画为(c) 时即可看出。
2017/7/13 11
图与网络的基本知识
次,奇点,偶点,孤立点 与某一个点vi相关联的边的数目称为 点vi的次(也叫做度),记作d(vi)。 右图中d(v1)=4,d(v3)=5,d(v5)=1。次 为奇数的点称作奇点,次为偶数的
2017/7/13
18
图与网络的基本知识
有向图 无向图
道路
回路
链
圈
道路(边的方向一致)
2017/7/13 19
图与网络的基本知识
连通图
定义10 一个图中任意两点间至少有一条链相连,则称此图为 连通图。任何一个不连通图总可以分为若干个连通子图,每 一个称为原图的一个分图(连通分支)。
连通图
2017/7/13
边,对余下的图重复这个步骤,直至无圈为止。
2、避圈法:每次增加一条边,且与已有边不构成圈,直至恰 有n-1条边为止。
2017/7/13
24
树
例1、下图是某建筑物的平面图,要求在其内部从每一房间都能走到 别的所有的房间,问至少要在墙上开多少门? 试给出一个开门的方案。
三
七
Байду номын сангаас
三 八 一 四 二 五
七 八 九 六
无向图
2017/7/13
有向图
8
图与网络的基本知识
环, 多重边, 简单图 如果边e的两个端点相重,称该边为 环。如右图中边e1为环。如果两个点 之间边多于一条,称为多重边,如右
v2 e5
多重边
e2
e1 v1
环
e3 v3
e4
图中的e4和e5,对无环、无多重边的
图论详细讲解

e1
e2
V1
e3
e4
V4 e5
e8 e6
V5
39
V3 本书由天疯上传于世界工厂网-下载中心
2.树和最小支撑树
取一个圈(v1,v2,v3,v1),在一个圈中去 掉边e3 。在剩下的图中,再取一个圈 (v1,v2,v4,v3,v1),去掉边e4 。再从圈 (v3,v4 v5,v3)中去掉边e6 。再从圈 (v1,v2,v5,v4,v3,v1 )中去掉边e7, 这样,剩下的图不含圈,于是得到一个 支撑树,如图8.12所示。
v3
15
1.图的基本概念与基本定理
图8.5是一个有向图D=(V,A) 其中V={v1,v2,v3,v4,v5,v6,v7} A={(v1,v2),(v,v3),(v3,v2), (v3,v4),(v2,v4),(v4,v5), (v4,v6),(v,v3),(v5,v4), (v5,v6),(v6,v7)}
19
1.图的基本概念与基本定理
定理8.1 所有顶点次数之和 等于所有边数的2倍。
定理8.2 在任一图中,奇 点的个数必为偶数。
1.图的基本概念与基本定理
图的连通性:
链: 由两两相邻的点及其相关联的 边构成的点边序列;如: v0 ,e1 ,v1 ,e2 ,v2 ,e3 ,v3 ,…,vn-1, en , vn ; v0 ,vn分别为链的起点和终点; 简单链:链中所含的边均不相同; 初等链:链中所含的点均不相同,也 称通路;
本书由天疯上传于世界工厂网-下载中心
9
1.图的基本概念与基本定理
北京 太原 石家庄
天津 塘沽 济南 青岛郑州 Nhomakorabea徐州 连云港
南京 上海
10
重庆
武汉
e2
V1
e3
e4
V4 e5
e8 e6
V5
39
V3 本书由天疯上传于世界工厂网-下载中心
2.树和最小支撑树
取一个圈(v1,v2,v3,v1),在一个圈中去 掉边e3 。在剩下的图中,再取一个圈 (v1,v2,v4,v3,v1),去掉边e4 。再从圈 (v3,v4 v5,v3)中去掉边e6 。再从圈 (v1,v2,v5,v4,v3,v1 )中去掉边e7, 这样,剩下的图不含圈,于是得到一个 支撑树,如图8.12所示。
v3
15
1.图的基本概念与基本定理
图8.5是一个有向图D=(V,A) 其中V={v1,v2,v3,v4,v5,v6,v7} A={(v1,v2),(v,v3),(v3,v2), (v3,v4),(v2,v4),(v4,v5), (v4,v6),(v,v3),(v5,v4), (v5,v6),(v6,v7)}
19
1.图的基本概念与基本定理
定理8.1 所有顶点次数之和 等于所有边数的2倍。
定理8.2 在任一图中,奇 点的个数必为偶数。
1.图的基本概念与基本定理
图的连通性:
链: 由两两相邻的点及其相关联的 边构成的点边序列;如: v0 ,e1 ,v1 ,e2 ,v2 ,e3 ,v3 ,…,vn-1, en , vn ; v0 ,vn分别为链的起点和终点; 简单链:链中所含的边均不相同; 初等链:链中所含的点均不相同,也 称通路;
本书由天疯上传于世界工厂网-下载中心
9
1.图的基本概念与基本定理
北京 太原 石家庄
天津 塘沽 济南 青岛郑州 Nhomakorabea徐州 连云港
南京 上海
10
重庆
武汉
离散数学 第八章 图论

C
A
B
D 图2
此图实际上是反 映了客观事物 之间的相互关系
10
离散数学
本世纪40年代,一个数学游戏也使用类似的方法得到 了解决:某人挑一担菜、并带一只狗、一只羊,要从河 的北岸到南岸。由于船小,只允许带狗、羊、菜三者中 的一种过河;而由于明显的原因,当人不在场时狗与羊、 羊与菜不能呆在一起。问此人应采取怎样的办法才能将 这三样东西安全地带过河去? 方法一:不对称状态空间法 将人(person)、狗(dog)、羊(sheep)、菜(cabbage)中任意 几种在一起的情况看作是一种状态,则北岸可能出现的 状态共有十六种,其中 安全状态有下面十种: (人,狗,羊,菜),(空); (P,D,S,C) ,() ; (人,狗,羊), (菜); (P,D,S,) ,(C) ; (人,狗,菜),(羊); (P,D,C) ,(S) ;
7
离散数学
但当地的居民和游人做了不少的尝试,却都没有取得成 功。于是,有好事者便向当时居住在该城的大数学家欧 拉请教。 1736年,瑞士的数学家L.Euler解决了这个问题。他将 四块陆地表示成四个结点,凡陆地间有桥相连的,便在 两点间连一条线,这样图1就转化为图2了。此时,哥尼 斯堡七桥问题归结为:在图2 所示的图中,从 A, B, C, D 任一点出发,通过每条边一次且仅一次而返回出发点 的回路是否存在?后人称如此的问题为Euler环游。 欧拉断言这样的回路是不存在的。理由是:从图2中 的任一结点出发,为了要回到原来的出发点,要求与每 个结点相关联的边数均为偶数。这样才能保证从一条边 进入某结点后,可从另一条边出去,而不经过已走过的
v3
1 2
v1
1 1 1
v4 v2
2 1
图论的基本概念性术语和一些特殊图: 图3 (1)(n,m)图: |V| = n,|E| = m,即有n个结点和m条边的图称 为 ( n, m ) 图。 (2)无向边:(undirected edges简edges)在定义3下,若边 (u, , v)与边(v, ,u)表示同一条边,则称此边为无 向边。 22
A
B
D 图2
此图实际上是反 映了客观事物 之间的相互关系
10
离散数学
本世纪40年代,一个数学游戏也使用类似的方法得到 了解决:某人挑一担菜、并带一只狗、一只羊,要从河 的北岸到南岸。由于船小,只允许带狗、羊、菜三者中 的一种过河;而由于明显的原因,当人不在场时狗与羊、 羊与菜不能呆在一起。问此人应采取怎样的办法才能将 这三样东西安全地带过河去? 方法一:不对称状态空间法 将人(person)、狗(dog)、羊(sheep)、菜(cabbage)中任意 几种在一起的情况看作是一种状态,则北岸可能出现的 状态共有十六种,其中 安全状态有下面十种: (人,狗,羊,菜),(空); (P,D,S,C) ,() ; (人,狗,羊), (菜); (P,D,S,) ,(C) ; (人,狗,菜),(羊); (P,D,C) ,(S) ;
7
离散数学
但当地的居民和游人做了不少的尝试,却都没有取得成 功。于是,有好事者便向当时居住在该城的大数学家欧 拉请教。 1736年,瑞士的数学家L.Euler解决了这个问题。他将 四块陆地表示成四个结点,凡陆地间有桥相连的,便在 两点间连一条线,这样图1就转化为图2了。此时,哥尼 斯堡七桥问题归结为:在图2 所示的图中,从 A, B, C, D 任一点出发,通过每条边一次且仅一次而返回出发点 的回路是否存在?后人称如此的问题为Euler环游。 欧拉断言这样的回路是不存在的。理由是:从图2中 的任一结点出发,为了要回到原来的出发点,要求与每 个结点相关联的边数均为偶数。这样才能保证从一条边 进入某结点后,可从另一条边出去,而不经过已走过的
v3
1 2
v1
1 1 1
v4 v2
2 1
图论的基本概念性术语和一些特殊图: 图3 (1)(n,m)图: |V| = n,|E| = m,即有n个结点和m条边的图称 为 ( n, m ) 图。 (2)无向边:(undirected edges简edges)在定义3下,若边 (u, , v)与边(v, ,u)表示同一条边,则称此边为无 向边。 22
图论基本概念(new)

八. 完全图 定义:G是个简单图, 如果每对不同结点之间都有边相连 则称G是个无向完全图. 如果G有n个结点, 则记作Kn. o o K2 o K3 o o o o K4 o o o o o o K5 o
定理4 完全图Kn, 有边数 1 n (n 1) 2 证明: 因为Kn中每个结点都与其余n-1个结点关联, 即每 个结点的度均为n-1, 所以Kn的所有结点度数总和为 n(n-1), 设边数为|E|, 于是n(n-1)=2|E| 1 所以|E|= 2 n ( n 1)
二. 无向图结点v的度(degree): 1.定义:G是个无向图, v∈V(G), 结点v所关联边 数,称之为结点v的度. 记作 d(v).
ob ao 奇点:度为奇数的点。 偶点:度为偶数的点。 od co 2.无向图的结点度序列: 令G=<V,E>是无向图, V={v1,v2,v3,…,vn}, 则称: (d(v1), d(v2),d(v3), …,d(vn)) 为图G的结点度序 列.
4
(1)
(2)
(3)
(4)
练习:请画出K4的所有不同构的生成子图.
v1
o
e5
e2
e3 e6
o v2
o v3
如果图是个简单图, 则路可以只用结点序列表示. ao od 如右图中, 路:abcad
bo oc
2. 回路:如果一条路的起点和终点是一个结点,则 称此路是一个回路. o v0
e1 e4 e6 v1
例 设G是一个图,若δ≥2,则G含有圈。
证明:因为δ≥2,所以从任意一点u出发到另一 点v恒可以向前延伸,又由于G是有限图,所以延 伸到某一点后,再往下延伸时,必然要和已走过 的顶点重合,即G有圈。 例:设G是简单图,若G中每个点的度至少为3, 则G中必含带弦的圈(初级回路). 例:在简单图中,证明:若n≥4且m≥2n-3,则G 中必含带弦的圈.
第八章图论

3. 图的结点与边之间的关系 定义 如果边e={vi,vj}是G的边, 则称结点vi 和vj邻接的, 边e和结点vi ,边e和结点vj称为关联的。 没有与边关联的结点称为孤立点。 关联于同一结点的相异边称为邻接的。 不与任何边邻接的边称为孤立边。
例1
在上图中显然e1和e2, e1与e4是邻接的, 结点v1和v2,v2和v4等是邻接的, 没有孤立点和孤立边。
例2.如下图中:
图(a)是伪图。图(b)是有向多重 图。 最右第三个图是简单图有权图。
三、结点的度
1.定义 图G中关联于结点vi的边的总数称为 结点vi的度, 用deg(vi)表示。
2.定理1(握手定理) 图G的所有结点的度的总和为边数 的二倍。即若G为具有n结点的(n,m)图, 则有: n deg(vi ) 2m
例8 如下图
(a)是连通图。 (b)是一个具有三个分图 的非连通图。 结论: (1)一个图的分图必是连通的; (2)一个连通图一定只能有一个分图。
例11 对于图的连通性,常常由于删除了 图中的结点和边而影响了图的连通性。
在连通图(a)中删除边e后, 则变成了不连通 的图(b)。
8.2 图的矩阵表示
2. 有向图的定义 定义 设G=(V,E), V是一个有限非空集合, E是V中不同元素的有序对偶的集合, 则称G是一有向图。在有向图G中 若vi≠vj,则(vi,vj)和(vj,vi)表示两条 不同的边,且用一个从结点vi指向vj 的箭头表示边(vi,vj)。
定义 具有n个结点和m条边的图称为(n,m)图。 (n,0)图称为零图。(1,0)图称为平凡图。
三、边割集、点割集 定义3 设图G=<V,E>是连通图,若有E的子集S, 使得在图G中删去了S的所有边后, 得到的子图G-S变成具有两个分图的不连通图, 删去了S的任一真子集后所得子图仍是连通图, 则称S是G的一个边割集。 注:割边是边割集的一个特例。
离散数学第8章图论剖析

例1 设 V ={v1,v2,v3,v4,v5},
E = {v1, v2}, {v1, v3}, {v2, v3}, {v2,v4}, {v3, v4},{v3, v5}, {v4 , v5}
则 G=(V,E)是一个图。
2. 图的表示方法
(1) 图解表示法
例2 下图(a).(b)分别给出了例1中图G的图解表示。
若中有相同的结点,设为ur= uk(r<k),则子路ur+1…uk可以从 中删去而形成一条较短的路= viu1…ur uk+1…uh–1 vj,仍连接vi到 vj。 若中还有相同的结点,那么重复上述过程又可形成一条
更短的路,…。这样,最后必得到一条真路,它连接vi到vj, 并短于前述任一非真路。因此,只有真路才能是短程。
将邻接矩阵A看作是布尔矩阵,矩阵的乘法运算和加法 运算中,元素之间的加法与乘法采用布尔运算(参看第 2章2.4节,P34)
1.由A,计算 A(2) , A(3), …, A(n) ; 2.计算 C=A+A(2)+…+ A(n) ; C便是所要求的连接矩阵。
例4 根据例1图的邻接矩阵A,用布尔运算的方法,求 其连接矩阵。
则称H是G的分图。
注: (2)的言外之意是:H是G的最大连通子图。
例
解 (b)显然不是G的分图,因为(b)不连通;
(c)也不是G的分图; (d)是G的分图; (e)是G的分图。
1.割点:如果在图G中删去结点v(及与其相关联的所 有边后),图G的分图数增加,则称结点v是G的割点。 2.割边:如果在图G中删去边{ vi,vj}后,图G的分 图数增加,则称边{ vi,vj}是G的割边。 例10 下图中v4 ,v6均是割点;
1 0
离散数学第八章一些特殊的图知识点总结

图论部分 第八章、一些特殊的图 8.1 二部图 二部图:定义 设无向图 G=<V,E>, 若能将 V 划分成 V1 和 V2 (V1V2=V, V1V2=), 使得 G 中的每条边的两个端 点都一个属于 V1, 另一个属于 V2, 则称 G 为二部图, 记为<V1,V2,E>, 称 V1 和 V2 为互补顶点子集. 完全二部图:又若 G 是简单图, 且 V1 中每个顶点都与 V2 中每个顶点相邻, 则称 G 为完全二部图, 记为 Kr,s, 其中 r=|V1|, s=|V2|. 注意: n 阶零图为二部图.
得证 m=k+1 时结论也成立. 证毕.
欧拉公式的推广
设 G 是有 p (p2) 个连通分支的平面图, 则
nm+r=p+1
证 设第 i 个连通分支有 ni 个顶点, mi 条边和 ri 个面.
对各连通分支用欧拉公式,
ni mi + ri = 2, 求和并注意 r = r1+…+rp+ p1, 即得
极大平面图: 定义 若 G 是简单平面图, 并且在任意两个不相邻的顶点之 间加一条新边所得图为非平面图, 则称 G 为极大平面图. 性质
• 若简单平面图中已无不相邻顶点,则是极大平面图. 如 K1, K2, K3, K4 都是极大平面图.
• 极大平面图必连通. • 阶数大于等于 3 的极大平面图中不可能有割点和桥.
8.2 欧拉图
欧拉通路: 图中行遍所有顶点且恰好经过每条边一次的通路. 欧拉回路: 图中行遍所有顶点且恰好经过每条边一次的回路.
欧拉图: 有欧拉回路的图. 半欧拉图: 有欧拉通路而无欧拉回路的图. 几点说明: 上述定义对无向图和有向图都适用. 规定平凡图为欧拉图. 欧拉通路是简单通路, 欧拉回路是简单回路. 环不影响图的欧拉性.
得证 m=k+1 时结论也成立. 证毕.
欧拉公式的推广
设 G 是有 p (p2) 个连通分支的平面图, 则
nm+r=p+1
证 设第 i 个连通分支有 ni 个顶点, mi 条边和 ri 个面.
对各连通分支用欧拉公式,
ni mi + ri = 2, 求和并注意 r = r1+…+rp+ p1, 即得
极大平面图: 定义 若 G 是简单平面图, 并且在任意两个不相邻的顶点之 间加一条新边所得图为非平面图, 则称 G 为极大平面图. 性质
• 若简单平面图中已无不相邻顶点,则是极大平面图. 如 K1, K2, K3, K4 都是极大平面图.
• 极大平面图必连通. • 阶数大于等于 3 的极大平面图中不可能有割点和桥.
8.2 欧拉图
欧拉通路: 图中行遍所有顶点且恰好经过每条边一次的通路. 欧拉回路: 图中行遍所有顶点且恰好经过每条边一次的回路.
欧拉图: 有欧拉回路的图. 半欧拉图: 有欧拉通路而无欧拉回路的图. 几点说明: 上述定义对无向图和有向图都适用. 规定平凡图为欧拉图. 欧拉通路是简单通路, 欧拉回路是简单回路. 环不影响图的欧拉性.
概率论-第十九讲--图的基本概念
8
简单图:无自回路的线图。
一、图的基本概念
多重图
多重图
线图
简单图
9
一、图的基本概念
定义2: 赋权图G一个三重组<V,E,g>或四重组<V,E,f,g>, V:一个非空的结点集合, E:边的集合, f:定义在V上的函数, g:定义在E上的函数。 3 e1 4 b 6 8 7 e2 5 c a 如左图所示: V={a,b,c}, e3 E={e1,e2,e3}, f(a)=3, f(b)=4, f(c)=5, g(e1)=6, g(e2)=7, g(e3)=8。
15
三、图的同构
例2: (a)
存在同构f: f(a)=1 或f(a)=1 f(d)=2 f(d)=6 f(b)=5 f(b)=5 f( f)=6 f(f )=4 f(c)=3 f(c)=3 f(e)=4 f(e)=2
(b)
不同构
两图同构的必要条件(不是充分条件) * 结点数相同; * 边数相同; * 度数相同的结点数相等。
1
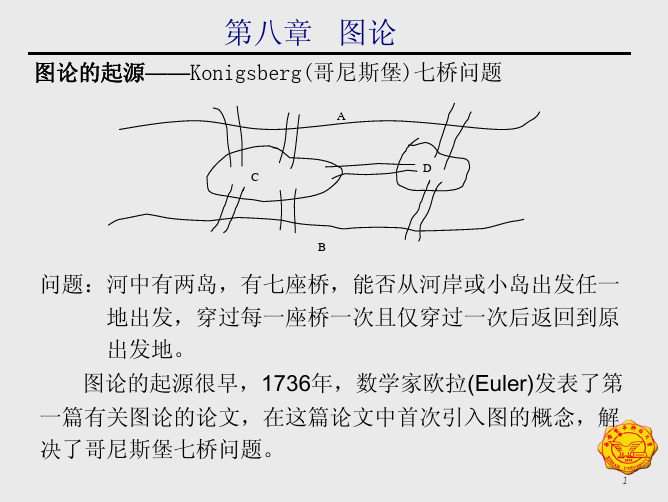
图论的起源——Konigsberg(哥尼斯堡)七桥问题
图 1 如果用结点代表陆地,用边代表桥,哥尼斯堡七桥问题 就等价在于图1(b)中找到这样一条路径,它经过每条边一次 且仅一次。
2
图论的应用 计算机科学与技术 运筹学 物理学 信息论 网络理论
3
8.1
一、图的基本概念
图的基本概念
定义1:一个图G是一个三重组〈V(G),E(G),ΦG〉, V(G):一个非空的结点(或叫顶点)集合; E(G):边的集合;
ΦG :从边集E到结点偶对集合上的函数。
4
一、图的基本概念
例1:图G为
则该图可表示为 G=〈V(G),E(G),ΦG〉: V(G)={a,b,c,d}; E(G)={e1,e2,e3,e4, e5,e6,e7}; ΦG(e1)=(a,b),ΦG(e2)=(a,c),ΦG(e3)=(b,d),ΦG(e4)=(b,c), ΦG(e5)=(d,c),ΦG(e6)=(a,d),ΦG(e7)=(b,b)。 简记 G=<V,E>=<{a,b,c,d},{(a,b),(a,c),(b,d),(b,c),(d,c),(a,d),(b,b)}> 5
简单图:无自回路的线图。
一、图的基本概念
多重图
多重图
线图
简单图
9
一、图的基本概念
定义2: 赋权图G一个三重组<V,E,g>或四重组<V,E,f,g>, V:一个非空的结点集合, E:边的集合, f:定义在V上的函数, g:定义在E上的函数。 3 e1 4 b 6 8 7 e2 5 c a 如左图所示: V={a,b,c}, e3 E={e1,e2,e3}, f(a)=3, f(b)=4, f(c)=5, g(e1)=6, g(e2)=7, g(e3)=8。
15
三、图的同构
例2: (a)
存在同构f: f(a)=1 或f(a)=1 f(d)=2 f(d)=6 f(b)=5 f(b)=5 f( f)=6 f(f )=4 f(c)=3 f(c)=3 f(e)=4 f(e)=2
(b)
不同构
两图同构的必要条件(不是充分条件) * 结点数相同; * 边数相同; * 度数相同的结点数相等。
1
图论的起源——Konigsberg(哥尼斯堡)七桥问题
图 1 如果用结点代表陆地,用边代表桥,哥尼斯堡七桥问题 就等价在于图1(b)中找到这样一条路径,它经过每条边一次 且仅一次。
2
图论的应用 计算机科学与技术 运筹学 物理学 信息论 网络理论
3
8.1
一、图的基本概念
图的基本概念
定义1:一个图G是一个三重组〈V(G),E(G),ΦG〉, V(G):一个非空的结点(或叫顶点)集合; E(G):边的集合;
ΦG :从边集E到结点偶对集合上的函数。
4
一、图的基本概念
例1:图G为
则该图可表示为 G=〈V(G),E(G),ΦG〉: V(G)={a,b,c,d}; E(G)={e1,e2,e3,e4, e5,e6,e7}; ΦG(e1)=(a,b),ΦG(e2)=(a,c),ΦG(e3)=(b,d),ΦG(e4)=(b,c), ΦG(e5)=(d,c),ΦG(e6)=(a,d),ΦG(e7)=(b,b)。 简记 G=<V,E>=<{a,b,c,d},{(a,b),(a,c),(b,d),(b,c),(d,c),(a,d),(b,b)}> 5
第八章图论原理

第八章图论原理
图论
• 图论是用图的方法研究客观世界的一门科 学.
• 用“结点”表示事物, 用“边”表示事物 之间联系, 而由结点与边所构成的图表示 所研究的客观对象.
• 图论研究图的逻辑结构与性质,是研究图 的抽象性质的一种数学.
图论
• 图论在语言学、逻辑学、物理学、化学、 电气工程、计算机网络、计算机科学及数 学的其他分支中有广泛应用.
8.1.2 图的基本概念
• 有序结点对所对应的边称为有向边,无序结点对 所对应的边称为无向边
• 有向图:图中的所有边均为有向边 • 无向图:图中的所有边均为无向边
8.1.2 图的基本概念
• 有向边lk={vi,vj}中, vi称为lk的起点, vj称为lk的终点 • 不管lk是有向还是无向, 均称lk与vi和vj相关联, 而vi
• 如果有V’⊂V, E⊂E’, 则称G’是G的真子图. • 如果有V’=V, E⊆E’, 则称G’是G的生成子图.
8.1.2 图的基本概念
• (n,m)图: 一个具有n个结点、m条边所组成的图
• 零图: 由一些孤立点组成的图, 即(n,0)图
• 平凡图: 由一个孤立结点组成的图, 即(1,0)图
• 解: 其资源分配图:
8.2.1 通路与回路
• 例8.4 用有向图刻画过程间的调用关系,来判断某过 程是否是递归的. 一个过程集合P={P1,P2,P3,P4,P5} 调用关系: P1调用P2; P2调用P4; P3调用P1; P4调用P5; P5调用P2;
• 某过程是递归的充分必要条件是包括此过程在内的结 点构成一个回路.
• 定义8.6
一个有向图, 如果忽略其边的方向后得到的无向 图是连通的, 则称此有向图为连通图; 否则, 称为 非连通图.
图论
• 图论是用图的方法研究客观世界的一门科 学.
• 用“结点”表示事物, 用“边”表示事物 之间联系, 而由结点与边所构成的图表示 所研究的客观对象.
• 图论研究图的逻辑结构与性质,是研究图 的抽象性质的一种数学.
图论
• 图论在语言学、逻辑学、物理学、化学、 电气工程、计算机网络、计算机科学及数 学的其他分支中有广泛应用.
8.1.2 图的基本概念
• 有序结点对所对应的边称为有向边,无序结点对 所对应的边称为无向边
• 有向图:图中的所有边均为有向边 • 无向图:图中的所有边均为无向边
8.1.2 图的基本概念
• 有向边lk={vi,vj}中, vi称为lk的起点, vj称为lk的终点 • 不管lk是有向还是无向, 均称lk与vi和vj相关联, 而vi
• 如果有V’⊂V, E⊂E’, 则称G’是G的真子图. • 如果有V’=V, E⊆E’, 则称G’是G的生成子图.
8.1.2 图的基本概念
• (n,m)图: 一个具有n个结点、m条边所组成的图
• 零图: 由一些孤立点组成的图, 即(n,0)图
• 平凡图: 由一个孤立结点组成的图, 即(1,0)图
• 解: 其资源分配图:
8.2.1 通路与回路
• 例8.4 用有向图刻画过程间的调用关系,来判断某过 程是否是递归的. 一个过程集合P={P1,P2,P3,P4,P5} 调用关系: P1调用P2; P2调用P4; P3调用P1; P4调用P5; P5调用P2;
• 某过程是递归的充分必要条件是包括此过程在内的结 点构成一个回路.
• 定义8.6
一个有向图, 如果忽略其边的方向后得到的无向 图是连通的, 则称此有向图为连通图; 否则, 称为 非连通图.
图论原理

点中的每一个均与其余n-1个结点邻接。
p1
kn
p2
完全图中m=?
p4
p3
m n(n 1) / 2
图的基本概念
6、补图:设有一图 G V , E ,对图 G' V , E ' ,如果 有 G V , E ' E 是完全图且 E E 。
'
p1
p2
p3 p5
第八章 图论原理
图论
欧拉
C
C
A
B
A
B
D
D
?
欧拉图
§8.1 图的基本概念
图的基本概念
欧拉
C
(B,C)
图G是由非空结点集合
V {v1 , v2 ,, vn }
A
B
以及边集合
E {l1, l2 ,, lm}
D
G=<V,E>
li (vi1 , vi 2 )
图的基本概念
例 1 有 4 个城市 v1 , v2 , v3 , v4 ,其中 v1 与 v2 间; v1 与 v4 间;
连通性 1 1
6
2
5
2
4 3
5
3
(a)
4
(b)
一个无向图G,如果它的任何两结点间均是可达
的,则称图G为连通图;否则,称为非连通图。
连通性
一个有向连通图G,
弱连通:如果忽略边的方向后其无向图是连通的
单向连通:如果其任何两点间至少存在一向是可达的
强连通:如果其任何两点间均是互相可达的
a
a
a
b
(a)
c
deg(E)=4
§8.4
p1
kn
p2
完全图中m=?
p4
p3
m n(n 1) / 2
图的基本概念
6、补图:设有一图 G V , E ,对图 G' V , E ' ,如果 有 G V , E ' E 是完全图且 E E 。
'
p1
p2
p3 p5
第八章 图论原理
图论
欧拉
C
C
A
B
A
B
D
D
?
欧拉图
§8.1 图的基本概念
图的基本概念
欧拉
C
(B,C)
图G是由非空结点集合
V {v1 , v2 ,, vn }
A
B
以及边集合
E {l1, l2 ,, lm}
D
G=<V,E>
li (vi1 , vi 2 )
图的基本概念
例 1 有 4 个城市 v1 , v2 , v3 , v4 ,其中 v1 与 v2 间; v1 与 v4 间;
连通性 1 1
6
2
5
2
4 3
5
3
(a)
4
(b)
一个无向图G,如果它的任何两结点间均是可达
的,则称图G为连通图;否则,称为非连通图。
连通性
一个有向连通图G,
弱连通:如果忽略边的方向后其无向图是连通的
单向连通:如果其任何两点间至少存在一向是可达的
强连通:如果其任何两点间均是互相可达的
a
a
a
b
(a)
c
deg(E)=4
§8.4
第八章 图论(第1-3节)

集合。
由点和弧所构成的图,称为有向图,记为 D = ( V, A )
,式中 V 是有向图的点集合G ; A 是有向图 G 的弧集
合。
第10页
无向图
有向图
第11页
5. 无向图中顶点数、边数的表示方式
顶点数:p(G),简记为p。
边 数:q(G),简记为q。
6. 有向图中顶点数、弧数的表示方式
顶点数:p(D),简记为p。
边 数:q(D),简记为q。
第12页
二、图的引申概念
1. 端点、始点、终点 无向图 G = ( V, E ) 中,边 e = [ u, v ]∈ E,称
顶点 u 和 v 是边 e 的端点,也称顶点 u 和 v 是
相邻的。 u e v
第13页
有向图 D = ( V, A ) 中,弧 a = ( u, v )∈ A,称
第42页
3. 简单链和简单路
若链
v
i1
, e i , v i , e i ,..., v i
1 2 2
k 1
, ei
k 1
,vi
k
中,边
e i , e i ,..., e i
1 2
k 1
均不相同,则称之为简单链。
注:简单链中边无相同的,但可有相同的点。
第43页
若路
v
i1
, a i , v i , a i ,..., v i
第49页
v1
a4
v5
a5
a6 a1 a3
v4
v2
a2 v3
(v1,a1,v2,a2,v3,a6,v1)不是一个回路。
第50页
5. 初等圈和初等回路
若圈 v i1 , e i1 , v i 2 , e i 2 ,..., v i k 1 , e i k 1 , v i1
第八章 图论8.1

A
B C
G
F
E
A
H
D
B
D
C
首页
上页
返回
下页
结束
铃
回到“七桥问题”
3 5 3
奇点的个数为4个,所以不能一笔画出。
3
首页
上页
返回
下页
结束
铃
知道了一笔画的规律后,亲自体验一下,来看看下面图 形能否一笔画出
4个奇点
0个奇点
首页
上页
返回
下页
结束
铃
例1 公路连接问题 某一地区有若干个主要城市,现准备修建高速公路把这 些城市连接起来,使得从其中任何一个城市都可以经高速公 路直接或间接到达另一个城市。假定已经知道了任意两个城 市之间修建高速公路的成本,那么应如何决定在哪些城市间 修建高速公路,使得总成本最小? 例2 中国邮递员问题(CPP-Chinese postman problem) 一名邮递员负责投递某个街区的邮件。如何为他(她)设 计一条最短的投递路线(从邮局出发,经过投递区内每条街道 至少一次,最后返回邮局)?由于这一问题是我国管梅谷教授 1960年首先提出的,所以国际上称之为中国邮递员问题。
V
+ d ( ) d ( ) E
V
首页
上页
返回
下页
结束
铃
首页
上页
返回
下页
结束
铃
§ 8.1 图的基本概念
4. 多重图、简单图和完全图
定义8.1.8(1)设u和v是无向图G=(V, E)的 两个顶点。如果G中有两条或两条以上的边 分别以u和v为端点, 则称这些边是平行边。 (2)设u和v是有向图D=(V, E)的 两个顶点。如果D中有两条或两条以上的边 分别以u和v为端点, 且它们的起点相同,终 点也相同,则称这些边是有向平行边,简 称平行边。
离散数学第八章(第1讲)

(2)无向图,有向图
a
d
每一条边都是无向边的图称无向图。
b
c
每一条边都是有向边的图称有向图。 a
d
b
c
例:将右图用二元组表示为: G=〈V,E〉 其中V={a,b,c,d} E={<a,b>,<b,a>,<b,d>,<d,a>,<d,d>,<c,c>} 则:G=〈V,E〉= 〈 {a,b,c,d} , {<a,b>,<b,a>,<b,d>,<d,a>,<d,d>,<c,c>} 〉
A
最大度,记为:△(G)=max{d(v)| vV} B
E
最小度,记为:δ(G)=min{d(v)| vV}
D
C
定理1 (握手定理) :每个图中,结点度数的总和等于边 数的两倍。即
deg(v) 2 E
vV
证:∵每条边必关联两个结点,而一条边给于关联的每 个结点的度数为1。 故上述定理成立。
例:在一次10周年同学聚会上,想统计所有人握手的 次数之和,应该如何建立该问题的图论模
a
h
b
c
g
d h
b
c
g
d
a
h
f (a)
f e
e
(b)
f (c)
(13)生成子图:如果G的子图包含G的所有结点,则称 该子图为G的生成子图。
如下图,(b)、(c)都是(a)的生成子图。
v1
v4
v1
v4
v1
v4
v2
v3
(a)
v2
v3
v2
(b)
08图论模型剖析

0 1 0 1 v1 1 0 1 1 v2 0 1 0 1 v3 1 1 1 0 v4
对有向图G=(V,E) ,其邻接矩阵 A (aij ) ,其中:
1 aij 0
若( vi,v j) E 若( vi,v j) E
基 本 概 念
定义 在无向图 G=(V ,E, )中:
c
x
x1 j 1 v j V s.t. x ji 1 ,i 1 v j V x 0或1 ij
8.2
最短通路问题
8.2.1 问题的背景与提出
在各种网络的铺设、网络的输送、线路的安排等 问题中,经常涉及到确定一条最短路.如在输送网络 中,考虑最小运输路线、最省运输费用、最少运输时 间等,这些都是最短通路问题.最短通路问题有非常 广泛的背景和应用,它也是图论或组合优化中的一个 重要问题.1959年,E.W.Dijkstra给出了该问题的一个 解法.
1956年Kruskal给出了一种求最优树的算法,称为避 圈法,算法如下: 1. 选择边 e1 ,使得w(e1 ) 尽可能小; 2. 若已选边 e1 , e2, ...,ei ,则从边集
E \ {e1 , e2, ...,ei } 中选取 ei 1 ,使
(1) G[{e1 , e2 ,...,ei 1}] 为无圈图;
节点间的连线,表示 有关联 一般用 eij 表示
节点和边的集合 一般用 G(V,E) 表示 点集 V={v1,v2,…, vn} 边集E={eij }
图 (Graph)
所有边都没有方向的图称为无向图,如上图 在无向图中 eij=eji,或 (vi, vj)=(vj, vi) 当所有边都有方向时,称为有向图,用G(V,A) 表示 在有向图中,有向边又称为弧,用 aij表示,i, j 的顺序是不能颠倒的,图中弧的方向用箭头标 识 图中既有边又有弧,称为混合图
离散数学第8章图论

§8-1-1 图
定义8-1.1 一个图G定义为一个三元组<V,E, φ>,记作G=<V,E,φ>。其中: V是一个非空有限集合,其中元素v称为图G 的顶点或结点; E是和V没有公共元素的有限集合,E可以是 空集,其元素e称为图G的边; φ称为关联函数,是从E到V中的有序对或无 序对的映射。
由定义可知,图G中的每条边都与图中的无序或
图8-1(b)表示有向图G=<V,E,φ>,其中: V = { v1,v2,v3,v4 } E= { e1,e2,e3,e4 }
e1 v1 , v2
:
e2 v1 , v3 e3 v1 , v3 e4 v3 , v3
在图 G=<V , E> 中,如果任何两结点间不多 于一条边(对于有向图中,任何两结点间不 多于一条同向弧),并且任何结点无环,则 图 G 称为简单图;若两结点间多于一条边 (对于有向图中,两结点间多于一条同向弧) 图 G 称为多重图,并把联结两结点之间的 多条边或弧,称为平行边或平行弧,平行 边或弧的条数称为重数。
哈密顿问题
1859年,英国数学家哈密顿发明了一种游戏:用一 个规则的实心十二面体,它的20个顶点标出世界 著名的20个城市,要求游戏者找一条沿着各边通 过每个顶点刚好 一次的闭回路,即「绕行世界」。 用图论的语言来说,游戏的目的是在十二面体的 图中找出一个生成圈。这个问题后来就叫做哈密 顿问题。由於运筹学、计算机科学和编码理论中 的很多问题都可以化为哈密顿问题,从而引起广 泛的注意和研究。
1872年,英国当时最著名的数学家凯利正式向伦 敦数学学会提出了这个问题,于是四色猜想成了 世界数学界关注的问题。世界上许多一流的数学 家都纷纷参加了四色猜想的大会战。1878~1880 年两年间,著名律师兼数学家肯普和泰勒两人分 别提交了证明四色猜想的论文,宣布证明了四色 定理。但后来数学家赫伍德以自己的精确计算指 出肯普的证明是错误的。不久,泰勒的证明也被 人们否定了。于是,人们开始认识到,这个貌似 容易的题目,其实是一个可与费马猜想相媲美的 难题(当n>2时,xn+yn=zn,n为奇素数,X,Y,Z 没有正整数解。)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8.1.1 图
• 著名的柯尼斯堡七桥问题。在柯尼斯堡的普莱格 尔河上有七座桥将河中的岛及岛与河岸联结起来, 如下图所示,A、B、C,D表示陆地。
• 问题是要从这四块陆地中任何一块开始,通过每 一座桥正好一次,再回到起点。
8.1.1 图
• 欧拉在1736年解决了这个问题,他用抽象分析 法将这个问题化为第一个图论问题:即把每一块 陆地用一个点来代替,将每一座桥用联接相应的 两个点的一条线来代替,从而相当于得到一个 「图」。欧拉证明了这个问题没有解,并且推广 了这个问题,给出了对於一个给定的图可以某种 方式走遍的判定法则。这项工作使欧拉成为图论 〔及拓扑学〕的创始人。
• 解: 图中的结点集为:V={v1,v2,v3,v4} 边集为E={l1,l2,l3} l1={v1,v2}, l2={v1,v4}, l3={v2,v3}, -------无序结点对 这个图可以用G=<V,E>表示
8.1.2 图的基本概念
• 例8.2 有4个程序p1,p2,p3,p4, 它们间有一些调用 关系:p1调用p2;p2能调用p3;p1能调用p4, 试将 此事实用图的方式表示.
• (a)(b)同构,(c)(d)同构
8.1.4 图中结点的次数
• 定义8.3
• 在有向图中, 以结点v为起点的边的条数称为v的 引出次数, 记以deg(v); 以v为终点的边的条数叫v 的引入次数, 记以deg(v); v的引入次数与引出次 数之和称为v的次数或全次数, 记为deg(v).
• 在无向图中, 结点v的次数或全次数是与v相关联 的边的条数, 也用deg(v)表示.
• 在计算机科学中,图论在形式语言、数据 结构、分布式系统、操作系统及数据库研 究中均有很重要的应用.
• 本篇结构
– 第八章 介绍图论一般原理 – 第九章 介绍一些常用的图如平面图、两步图
以及树等
第八章 图论原理
• 本章主要介绍图论的基本原理,包括图论 中的基本概念、基本方法以及图论的矩阵 计算等内容.
• 一个图与其补图是互补的 • 一个图的补图的补图还是自己
8.1.3 图的同构
• 定义8.2
设有图G=<V,E>与G’=<V’,E’>, 如果它们的结点 间存在一一对应关系, 而且这种对应关系也反映 在表示边的结点对中(如果是有向边, 则对应的结 点对还保持相同的顺序), 则称此两图是同构的.
8.1.3 图的同构
• 如果有V’⊂V, E⊂E’, 则称G’是G的真子图. • 如果有V’=V, E⊆E’, 则称G’是G的生成子图.
8.1.2 图的基本概念
• (n,m)图: 一个具有n个结点、m条边所组成的图
• 零图: 由一些孤立点组成的图, 即(n,0)图
• 平凡图: 由一个孤立结点组成的图, 即(1,0)图
8.1.2 图的基本概念
• 有序结点对所对应的边称为有向边,无序结点对 所对应的边称为无向边
• 有向图:图中的所有边均为有向边 • 无向图:图中的所有边均为无向边
8.1.2 图的基本概念
• 有向边lk={vi,vj}中, vi称为lk的起点, vj称为lk的终点 • 不管lk是有向还是无向, 均称lk与vi和vj相关联, 而vi
和vj称为邻接的. • 若干条边关联于同一个结点, 则这些边称为邻接
的.
8.1.2 图的基本概念
• 一条边若与两个相同的结点相关联, 则称为环, 即 lk={vi,vi}
• 不与任何结点相邻的结点称为孤立点
8.1.2 图的基本概念
• 图G=<V,E>与G’=<V’,E’>间如果有V’⊆V, E⊆E’, 则称G’是G的子图.
• 解: 图中的结点集为:V={p1,p2,p3,p4} 边集为E={c1,c2,c3} c1={p1,p2}, c2={p2,p3}, c3={p1,p4}, -----有序结点对 这个图可以用G=<V,E>表示
8.1.2 图的基本概念
• 一般,用带有箭头的边表示有序结点对,而用不 带箭头的边表示无序结点对.
图论
图论
• 图论是用图的方法研究客观世界的一门科 学.
• 用“结点”表示事物, 用“边”表示事物 之间联系, 而由结点与边所构成的图表示 所研究的客观对象.
• 图论研究图的逻辑结构与性质,是研究图 的抽象性质的一种数学.
图论
• 图论在语言学、逻辑学、物理学、化学、 电气工程、计算机网络、计算机科学及数 学的其他分支中有广泛应用.
• 任一图的所有结点的次数之和必为偶数, 且必为 图中边数的两倍, 因为每条边必与两个结点相关 联.
8.1.4 图中结点的次数
• 题(8.1) 设V={u,v,w,x,y}, 画出图G=<V,E>:
1) E = {(u,v),(u,x),(v,w),(v,y)(x,y)}
2) E = {(u,v),(v,w),(w,x),(w,y)(x,y)}
8.1.2 图的基本概念
• 定义 8.1
图G是由非空结点集合V={v1,v2,…,vn}以及边集合 E={l1,l2,…,lm}所组成, 其中每条边可用一个节点 对表示, 亦即
li = (vi1,vi2), i = 1,2,…,m 这样一个图G可用G = <V,E>表示
8.1.2 图的基本概念
• 例8.1 有4个城市: v1,v2,v3,v4, 其中v1与v2间; v1与 v4间; v2与v3间有直达长话线路相连, 将此试试用 图的方式表示
• 完全图: 一个(n,m)图G如果其n个结点(n≥2)中的 每一个均与其中n-1个结点邻接, 可记为Kn. m=n(n-1)/2
8.1.2 图的基本概念
8.1.2 图的基本概念
• 补图: 设有一图G=(V,E), 对图G’=(V,E’), 如果有 G=(V,EE')是完全图且E∩E’= Ø 则称G’是G的补图.
8.1.1 图
• 起源:
• 历史上图论曾经被好多位数学家各自独立地建立 过。关于图论的文字记载最早出现在欧拉1736 年的论着中,他所考虑的原始问题有很强的实际 背景。
Leonhard Euler , (1707—1783),瑞士数学 家、力学家、天文学家、 物理学家,图论的创始人, 变分法的奠基人,复变函 数论的先驱者,理论流体 力学的创始人。
