一般常数项级数
合集下载
常数项级数的概念和性质
∞
lim u n = lim ( S n − S n −1 )
n →∞ n →∞
= lim S n − lim S n −1
n →∞ n →∞
= S −S =0
例4. 判别 ∑ ( −1)
n =1
∞
n −1
n 的敛散性. n +1
(−1) n −1 n = 1, 解：由于 lim | u n |= lim n →∞ n →∞ n +1
一、问题的提出
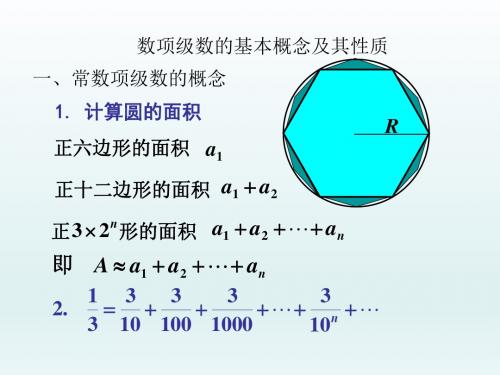
1. 计算圆的面积 正六边形的面积 a1 正十二边形的面积 a1 + a 2
n 正 3 × 2 形的面积 a1 + a 2 + L + a n
R
即 A ≈ a1 + a2 +L+ an 1 3 3 3 3 2. = + + +L+ n +L 3 10 100 1000 10
二、常数项级数的概念
n =1 ∞
S n = ∑ u k = u1 + u 2 + L + u n ,
k =1
n
称为常数项级数的部分和. 若 lim S n = S 存在，则称级数 ∑ u n 收敛， n →∞
n =1 ∞
∑ S称为级数的和： u n = S .
n =1
∞
观察雪花分形过程
设三角形 周长为 P1 = 3, 3 ; 面积为 A1 = 4 第一次分叉： 第一次分叉：
1.常数项级数的定义 1.常数项级数的定义 设有数列{un}:u1, u2, …, un, …, 则称表达式
∑u
n =1
∞
n
= u1 + u 2 + L + u n + L
常数项级数的概念和
n(n 2
1)
.
ln im snln im n(n21), ∴所给级数是发散的. 3
定 义 如 果 级un数 的 部 分{和 sn}有 数极 列 s， 限
n1
则 称 级 un数 收 敛 ， 并 un且 s.
n1
n1
例2 判定级数1 的收敛 . 性
课堂练习 判别级数1 的敛散. 性
P255.4(3)
n2 n 3
解ln im un
1 lim
3 nn
级数
1 发散.
lim
n
1
1
3n
1 1 0. 1
|q|1,
该级数收敛,
并且
4
n
n0 5
1
1
4
5.
5
9
二、收敛级数的基本性质
性质1 设常k数 0,则kun与un有相同的敛
n1
n1
证 设u n的部sn 分 u 1 和 u 2 为 u n;
n 1
则knu 的 部n 分 k1 u 和 k2u 为 knu ksn . n 1
( u 1 u 2 u n ) ( v 1 v 2 v n ) snn,
ln i m nln i (m snn)s,
(un vn)收敛，且其和s为 ．
n1
11
性质2 如果级 数 un、 vn分别收敛s、 于 , 和
例3 讨 论 等a比 nq aa 级 qa数 2q anq
n0
第三节 一般常数项级数
满足莱布尼兹定理条件，故级数收敛，且为条件收敛。 满足莱布尼兹定理条件，故级数收敛，且为条件收敛。
上页 下页 返回
例3：判定级数 ∑ ：
∞
n =1
x 的敛散性。 的敛散性。 n
∞
n
高等数学
xn xn | , 记 un = | 解： 考察正项级数 ∑ | |, n n=0 n
n→ ∞
lim
un +1 un
则交错级数收敛，其和 s ≤ u1 , 余项满足 | Rn | ≤ un+1 则交错级数收敛， 4. 检验条件（1）常用的方法 检验条件（ ）
un+1 是否成立？ ≤ 1 是否成立？ （1）比值法： 考察 ）比值法： un 是否成立？ （2）差值法： 考察 un+1 un ≤ 0 是否成立？ ）差值法：
上页 下页 返回
定理7（莱布尼兹定理） 定理 （莱布尼兹定理）如果交错级数
n =1
高等数学
∑ (1)
∞
n1
= u1 u 2 + u 3 u 4 + L + ( 1) n1 u n + L un
满足条件： 满足条件：
n→∞
(1) un ≥ un +1 ( n = 1, 2 , L), ( 2 ) lim un = 0
原级数绝对收敛， 从而收敛， 当 | x | < 1 时，原级数绝对收敛， 从而收敛，
xn 发散，且是用比值法判别的， | x | > 1 时， ∑ | | 发散，且是用比值法判别的， n n =1 xn 所以原级数 ∑ n =1 n
∞
∞
发散。 发散。
上页 下页 返回
例3：判定级数 ∑ ：
∞
上页 下页 返回
例3：判定级数 ∑ ：
∞
n =1
x 的敛散性。 的敛散性。 n
∞
n
高等数学
xn xn | , 记 un = | 解： 考察正项级数 ∑ | |, n n=0 n
n→ ∞
lim
un +1 un
则交错级数收敛，其和 s ≤ u1 , 余项满足 | Rn | ≤ un+1 则交错级数收敛， 4. 检验条件（1）常用的方法 检验条件（ ）
un+1 是否成立？ ≤ 1 是否成立？ （1）比值法： 考察 ）比值法： un 是否成立？ （2）差值法： 考察 un+1 un ≤ 0 是否成立？ ）差值法：
上页 下页 返回
定理7（莱布尼兹定理） 定理 （莱布尼兹定理）如果交错级数
n =1
高等数学
∑ (1)
∞
n1
= u1 u 2 + u 3 u 4 + L + ( 1) n1 u n + L un
满足条件： 满足条件：
n→∞
(1) un ≥ un +1 ( n = 1, 2 , L), ( 2 ) lim un = 0
原级数绝对收敛， 从而收敛， 当 | x | < 1 时，原级数绝对收敛， 从而收敛，
xn 发散，且是用比值法判别的， | x | > 1 时， ∑ | | 发散，且是用比值法判别的， n n =1 xn 所以原级数 ∑ n =1 n
∞
∞
发散。 发散。
上页 下页 返回
例3：判定级数 ∑ ：
∞
常数项级数的应用
常数项级数的应用在数学中，常数项级数是一种由常数项组成的数学级数。
常数项级数在各个领域的应用非常广泛，从物理学到工程学，从经济学到计算机科学。
本文将介绍常数项级数的定义和性质，并探讨其在实际应用中的一些例子。
1. 常数项级数的定义常数项级数是指一个无穷序列的和，其中每一项都是常数。
具体地，常数项级数的一般形式为：$$ S = a_0 + a_1 + a_2 + a_3 + \\ldots $$其中，a i表示第i项的常数。
2. 常数项级数的性质常数项级数有许多重要的性质，下面列举其中几个常见的性质。
2.1 收敛与发散常数项级数可能收敛或发散。
当常数项级数的部分和有一个有限的极限值时，我们称该级数收敛。
如果常数项级数的部分和趋向于无穷大，我们称该级数发散。
2.2 收敛级数的性质如果一个常数项级数收敛，那么它有以下性质：•唯一性：常数项级数的和是唯一确定的。
•加法性：如果两个常数项级数收敛，那么它们的和也收敛，并且和的值等于两个级数的和之和。
•数乘性：如果一个常数项级数收敛，那么把每一项乘以同一个常数，所得到的级数也收敛，并且和的值等于原级数的和乘以该常数。
2.3 绝对收敛与条件收敛如果一个常数项级数的每一项的绝对值都收敛，那么我们称该级数是绝对收敛的。
如果一个常数项级数是收敛的但不是绝对收敛的，那么我们称该级数是条件收敛的。
2.4 收敛级数的收敛方法常数项级数有多种判定方法来确定其是否收敛。
其中一些重要的方法包括比值判别法、根值判别法和积分判别法。
3. 常数项级数的应用常数项级数在实际应用中发挥着重要作用。
下面我们将介绍一些常见的应用。
3.1 数值逼近常数项级数可以用来进行数值逼近。
通过适当选择常数项的值，我们可以使用有限个项的和来近似表达无穷级数。
这在计算机科学、物理学和工程学中非常常见。
3.2 统计学常数项级数在统计学中有广泛的应用。
例如，在统计模型中，我们经常需要计算概率分布的累积分布函数（CDF）。
常数项级数的概念和..
n1
n1
如果 {sn } 没有极限， 则称级数 un 发散．
n1
例1 证明级数 1 2 3 n 是发散的.
证 这级数的部分和为
sn 1 2 3 n
n(n 1) . 2
lim
n
sn
lim
n
n(n 1) 2
,
∴所给级数是发散的.
3
定 义 如 果 级 数 un 的 部 分 和 数 列{sn } 有 极 限s，
3
7
a aq aq2
aqn
aqn
n0
| q | 1时, 收敛,
|
q
|
1
时,
发散.
并且 aqn
a
( q 1). (P250例 1)
n0
1q
课堂练习
判定级数
5 3
52 32
53 33
(1)n
5n 3n
的敛散性.
解 为等比级数，公 比q 5 . 3
| q | 1, 该级数发散.
n0
(a 0, q为 公 比) 的 收 敛 性.
解
若q
q
1,
1时, sn
则 lim q n n
a aq aq2 aqn1
0，
lim
n
sn
a， 1q
1 qn
a
.
1q
级数收敛.
若 q 1,
则 lim q n n
，
lim
n
sn
，级数发散．
q 1时,
若q 1,
则
lim
n
sn
lim na
n
，级数发散，
若
q
1,
则lim n
常数项级数的概念和性质
n
sn
存在(不存在)
余项 rn s sn un1 un2 uni
i 1
即 sn s
误差为 rn
(lim n
rn
0)
例 1 讨论等比级数(几何级数)
aqn a aq aq2 aqn (a 0)
n0
的收敛性.
解 如果q 1时
sn a aq aq2 aqn1
设
un
是正项级数,如果lim n
n
un
n1
(为数或 ), 则 1时级数收敛;
1时级数发散; 1时失效.
例如, 设级数 1 ,
nn
n1
n
un
n
1 nn
1 n
0 (n )
级数收敛.
习惯塑造人生
从自己旳经历谈什么事先做起来 • 教育就是养成习惯——叶圣陶.
• 一种人不想做某事，能够找出千万条理由，下 决心做一件事情时，有一条理由就足够了。
1111
发散
四、级数收敛旳必要条件
设收敛级数
S
un ,
n1
则必有 lim
n
un
0.
证: un Sn Sn1
lim
n
un
lim
n
S
n
lim
n
Sn1
S
S
0
可见: 若级数旳一般项不趋于0 , 则级数必发散 .
例如, 1 2 3 4 (1)n1 n , 其一般项为
2345
n 1
un
(1)n1
(1) lim nsin 1
n
n
n1
3
n
;
n sin 1
lim n 1,
n 1
sn
存在(不存在)
余项 rn s sn un1 un2 uni
i 1
即 sn s
误差为 rn
(lim n
rn
0)
例 1 讨论等比级数(几何级数)
aqn a aq aq2 aqn (a 0)
n0
的收敛性.
解 如果q 1时
sn a aq aq2 aqn1
设
un
是正项级数,如果lim n
n
un
n1
(为数或 ), 则 1时级数收敛;
1时级数发散; 1时失效.
例如, 设级数 1 ,
nn
n1
n
un
n
1 nn
1 n
0 (n )
级数收敛.
习惯塑造人生
从自己旳经历谈什么事先做起来 • 教育就是养成习惯——叶圣陶.
• 一种人不想做某事，能够找出千万条理由，下 决心做一件事情时，有一条理由就足够了。
1111
发散
四、级数收敛旳必要条件
设收敛级数
S
un ,
n1
则必有 lim
n
un
0.
证: un Sn Sn1
lim
n
un
lim
n
S
n
lim
n
Sn1
S
S
0
可见: 若级数旳一般项不趋于0 , 则级数必发散 .
例如, 1 2 3 4 (1)n1 n , 其一般项为
2345
n 1
un
(1)n1
(1) lim nsin 1
n
n
n1
3
n
;
n sin 1
lim n 1,
n 1
常数项级数的概念和性质
的说法．从数学的角度上看，这就是
111 248
1 2n
1．
1.1 常数项级数的概念
再如，计算半径为 R 的圆面积 A，具体做法如下：如图所示，作圆的内接正六 边形，算出这六边形的面积 a1 ，它是圆面积 A 的一个粗糙的近似值．为了比较准确 地计算出 A 的值，我们以这个六边形的每一边为底分别作一个顶点在圆周上的等腰 三角形，算出这六个等腰三角形的面积之和为 a2 ，那么 a1 a2 （即内接正十二边形 的面积）就是 A 的一个较好的近似值．同样地，再在正十二边形的每一边上分别作 一个顶点在圆周上的等腰三角形，算出这十二个等腰三角形的面积之和为 a3 ，那么 a1 a2 a3 （即内接正二十四边形的面积）是 A 的一个更好的近似值．如此继续下 去，内接正 n 边形的面积就逐步逼近圆的面积，即
高等数学
常数项级数的概念和性质
无穷级数是高等数学的一个重要组成部分，是表示函数、研究函数性质以 及用简单函数逼近复杂函数进行数值计算的有力工具．无穷级数在自然科学、 工程技术和数学的许多分支中都有着广泛的应用．像其他数学理论一样，无穷 级数理论也是在科学技术的发展和推动下，逐渐形成和完善起来的．早在魏晋 时代，我国数学家刘徽就已经用无穷级数的思想来计算圆的面积了．直到19世 纪，极限理论的建立，才给无穷级数奠定了理论基础．
a
；如果| q |
1，则级数 aqn
n0
1 q
n0
发散．
1.1 常数项级数的概念
例 2 证明级数
1 2 3 n 是发散的．
证明 此级数的部分和为
Sn 1 2 3
n n(n 1) ． 2
显然，
lim
n
Sn
，因此所给级数是发散的．
常数项级数的概念和性质
则式子 u1 u2 u3 un
称为(常数项)无穷级数，简称(常数项)级数。
记作
u ， 即 u
n
Hale Waihona Puke nn 1n 1
u1 u2 un
其中 un 称为级数的一般项（或通项），
问题： un 存在不存在？ (即有没有和数)
n 1
2 . 部分和数列 一数列中有限项相加总是有和数的，
用 Sn 近似代替 S 产生的误差为 | rn | ,
且因为 n 时, Sn S， 所以 rn 0 .
例
题
例1. 讨论等比级数 (几何级数) 的敛散性：
aq n 1 a aq aq 2 ... aq n ...
(a 0, q为公比）
n 1
n 1
, un Sn Sn1 ,
n 1
un
{ Sn }
现通过研究 { Sn } 来研究级数。
3. 级数的收敛和发散
定义： 设级数
n
un ， 对应的部分和数列 Sn ，
n 1
若 lim S n S 存在， 则称
un 收敛 ,
n 1
(C)
convergence
n 1 n 1
则
(un vn ) s un vn .
n 1
收敛级数可逐项相加减。
推论： 若
则
un (C ) , vn ( D) , n 1
n 1
(un vn )
n 1
( D) .
推论： (C) + (D) => (D)
12-1常数项级数的概念和性质
n1
n1
n1
即 收敛级数可以逐项相加与逐项相减．
例6 若级数 an 与 bn 均发散，
n1
n1
则级数 (an bn )是否必发散？ (1987)
n1
解 结论是错误的．
例如级数 ln n 1 及 ln n 1 均发散，
n1
n
n1
n
但级数 [ln n 1 ln n 1] 0 是收敛的．
23
n
n1 n
n
2. 级数的部分和与部分和数列
n
设有级数 un，其前 n 项的和 sn ui
n1
i 1
称为级数的部分和． 它所构成的数列 sn
s1 u1， s2 u1 u2，，sn u1 u2 un，
称为级数的部分和数列．
3. 级数的敛散性
aqn a aq aq2 aqn (a 0) 的敛散性．
n0
解
当
|
当 q 1 时，sn q | 1时，lim qn
n
a
aq 0，
aq2 lim
n
sn
1
aqn1 a. q
a1 qn 1q
收敛
当综当当上q|qq所|述111时ln时i时m， ，，ssansnqn不 lninm存a当nqa在 n，|aq．| 发a，1ln散i时m,lns收inm(敛s1n于)n.11a发a.q散发.a0散nn为为偶奇数数，
第十二章质
一、常数项级数的概念
1. 常数项级数的定义
设有数列 un：u1，u2，，un，，按其次序求和
u1 u2 u3 un un 称为(常数项)级数．
常数项级数考研辅导
P157例4
收敛, 性质 5 如果级数 un 收敛,则 lim un = 0 n→ ∞ n=1 注意 ∞
∑
∞
1 (1)仅仅是必要条件,不是充分条件. 如∑ 仅仅是必要条件, 仅仅是必要条件 不是充分条件. n =1 n
(2)如果级数的一般项不趋于零,则级数发散. 如果级数的一般项不趋于零,则级数发散. 如果级数的一般项不趋于零
∞n =1 n =1 n
∞
n= 2
∞
∑ u 收敛时 , Sn 可看成是和的近似值 .
∞
= s − s n= u n + 1 + u n + 2 + ⋯ = ∑ u n + i ∞ i =1 即当 ∑ u n 收敛时 , lim rn = 0
(2) un ＝ Sn－ Sn－1
n=1
n→ ∞
( 3 ) lim u n 存在 ⇔
∑u
n =1 ∞
∞
n
的 和 . 并 写 成
s = u1 + u2 + ⋯ + u3 + ⋯＝∑ un
n =1
极限不存在, 如果 sn 极限不存在,则称无穷级数
P1771(2)
考研辅导
发散. ∑ un 发散. n =1
∞
收敛， 收敛， 例1 已知数列 {nan } 收敛， n(an − an−1 ) 收敛， ∑ 证明： 收敛。 证明：级数 ∑ an 收敛。 注 (1)当 (1)当 余项 rn
n=1 n =1
P155例3
例4 讨论下列级数的敛散性。 讨论下列级数的敛散性。 ∞ ∞ ln n n ln n (2) (1 − ) (1)∑ p n n= 2 n n =1
∑
解(2)un = e
收敛, 性质 5 如果级数 un 收敛,则 lim un = 0 n→ ∞ n=1 注意 ∞
∑
∞
1 (1)仅仅是必要条件,不是充分条件. 如∑ 仅仅是必要条件, 仅仅是必要条件 不是充分条件. n =1 n
(2)如果级数的一般项不趋于零,则级数发散. 如果级数的一般项不趋于零,则级数发散. 如果级数的一般项不趋于零
∞n =1 n =1 n
∞
n= 2
∞
∑ u 收敛时 , Sn 可看成是和的近似值 .
∞
= s − s n= u n + 1 + u n + 2 + ⋯ = ∑ u n + i ∞ i =1 即当 ∑ u n 收敛时 , lim rn = 0
(2) un ＝ Sn－ Sn－1
n=1
n→ ∞
( 3 ) lim u n 存在 ⇔
∑u
n =1 ∞
∞
n
的 和 . 并 写 成
s = u1 + u2 + ⋯ + u3 + ⋯＝∑ un
n =1
极限不存在, 如果 sn 极限不存在,则称无穷级数
P1771(2)
考研辅导
发散. ∑ un 发散. n =1
∞
收敛， 收敛， 例1 已知数列 {nan } 收敛， n(an − an−1 ) 收敛， ∑ 证明： 收敛。 证明：级数 ∑ an 收敛。 注 (1)当 (1)当 余项 rn
n=1 n =1
P155例3
例4 讨论下列级数的敛散性。 讨论下列级数的敛散性。 ∞ ∞ ln n n ln n (2) (1 − ) (1)∑ p n n= 2 n n =1
∑
解(2)un = e
高等数学高数课件 12.3一般常数项级数
,
而
n1
1 2n
发散,
故
| un
n1
|
n1
n n2 +
1
发散.
于是级数
(1)n1
n1
n n2 + 1
是条件收敛的.
例9 判别下列级数的敛散性 .
(1)n
(1) n2 n + (1)n
(2)
(1)n
n2 n + (1)n
解: (1) (1)n (1)n n 1
n + (1)n
n 1 n 1
绝对收敛与条件收敛
根据这个定理, 我们可以将许多一般常数项级数的
收敛性判别问题转化为正项级数的收敛性判别问题.
为此先给出以下定义.
定义1 设 un 为一般常数项级数, 则
n1
(1) 当 | un |收敛时, 称 un为绝对收敛;
n1
n1
(2) 当 | un |发散, 但 un 收敛时, 称 un
解
这是一个交错级数,
令
un
(1)n
(
nn+1 n + 1)!
,
考察级数 | un | 是否绝对收敛, 采用比值审敛法:
n1
lim | un+1 | n | un |
lim1 n
+
1 n
n
e
1,
所以原级数非绝对收敛.
由 lim |un+1 | 1, n |un |
可知当 n 充分大时,
有 |un+1||un |,
可知当 n 充分大时,
有 |un+1||un |,
故
lim
n
un
数项级数的基本概念及其性质
2
n1
a aq n a aqn , 1 q 1 q 1 q
a sn 当q 1时, lim q 0 lim n 1 q 收敛 n
n n lim q lim sn 当q 1时, n n
发散
如果 q 1时
k 1
k
1 dx ， x
1 sn 1 2
2
1 n
31 1 如: dx ， 2 2x
31 n 1 1 1 dx dx dx 1 x 2 x n x n 1 1 n dx ln( n 1) 级数发散 . 1 x
5 1 5 1 n n 2 n1 n( n 1) n1 2 n1 n( n 1)
5 1 1 5 n 1 n1 n( n 1) n 1 n
1 1 1 令 g n 5 ), 5(1 k 1 n1 k 1 k
1. 级数的定义:
一般项 (常数项)无穷级数
un u1 u2 u3 un n1
级数的部分和
部分和数列
sn u1 u2 un ui
i 1
n
s1 u1 , s2 u1 u2 , s3 u1 u2 u3 ,, sn u1 u2 un ,
n (2) cos 2 n 1
(4)
(1)
n 1
n
以上四个都是发散的，你判断对了吗？
例6 证明级数是发散的：
n ln 1 2ln 2 n ln n 1 2 3 n 1
证 级数的通项
n1
a aq n a aqn , 1 q 1 q 1 q
a sn 当q 1时, lim q 0 lim n 1 q 收敛 n
n n lim q lim sn 当q 1时, n n
发散
如果 q 1时
k 1
k
1 dx ， x
1 sn 1 2
2
1 n
31 1 如: dx ， 2 2x
31 n 1 1 1 dx dx dx 1 x 2 x n x n 1 1 n dx ln( n 1) 级数发散 . 1 x
5 1 5 1 n n 2 n1 n( n 1) n1 2 n1 n( n 1)
5 1 1 5 n 1 n1 n( n 1) n 1 n
1 1 1 令 g n 5 ), 5(1 k 1 n1 k 1 k
1. 级数的定义:
一般项 (常数项)无穷级数
un u1 u2 u3 un n1
级数的部分和
部分和数列
sn u1 u2 un ui
i 1
n
s1 u1 , s2 u1 u2 , s3 u1 u2 u3 ,, sn u1 u2 un ,
n (2) cos 2 n 1
(4)
(1)
n 1
n
以上四个都是发散的，你判断对了吗？
例6 证明级数是发散的：
n ln 1 2ln 2 n ln n 1 2 3 n 1
证 级数的通项
数项级数基本知识点
一．常数项级数的概念
设有数列｛U n ｝，则称u 1+u 2+...+u n +...为（常数项）无穷级数，简称（常数项）级数，记为∑Un ∞n=1，其中U n 称为级数的通项或一般项 令S n =u 1+u 2+...+u n （n=1,2,...），则称数列｛S n ｝为级数∑Un ∞n=1的部分和数列，
如果部分和数列｛S n ｝有极限S ,即
lim n→∞
Sn
则称级数∑Un ∞n=1收敛，这时极限S 叫做级数∑Un ∞n=1的和，即
S=∑Un ∞n=1
如果｛S n ｝没有极限，则称级数∑Un ∞n=1发散 讨论几何级数（等比级数） [1] =aq n-1
∑[1]∞n=1=a + aq + aq 2 + ...+ aq n-1+...的敛散性，其中a ≠0，q 是
级数的公比
解析：如果 |q|≠1，则部分和： 【2】=q n
∑[1]∞n=1
=a + aq + aq 2 + ...+ aq n-1+...=a （1−【2】）
1−q
级数（6--1）
二．收敛级数的基本性质
三．级数收敛的必要条件
定理1为必要条件，不是充分条件
四．正项级数的判别法
1.比较判别法
（比较判别法的极限形式）
2.比值判别法
例题：
3.其他判别法
五．交错级数的判别法
六．绝对收敛与条件收敛。
8.1常数项级数的概念和性质
n1
称为几何级数(又称为等比级数), 其中a 0, q 0.
试讨论该级数的敛散性.
解 该级数的前n项部分和为
Sn
a
aq
aqn1
a aqn 1q
(q 1)
(1)当 q
1时,
有
lim
n
S
n
a, 1q
所以级数 (8 1) 收敛, 且其和为 a . 1q
(2)当 q 1时,
有
lim
n
n1
un 同时收敛或同时发散, 且同时收敛时, 有
n1
cun c un .
n1
n1
性质8.2 若级数 un 与级数 vn 都收敛, 则级数
n1
n1
(un vn ) 收敛 , 且有
n1
(un vn ) un vn .
n1
n1
n1
级数 un 发散, vn 收敛, 必有 （un vn数发散.
(3)当q 1 时, Sn na ( n 时 );
当q 1时,
Sn
a [1 2
(1)n1 ],
n 时, Sn 的极限不存在,
故当 q 1时, 级数 (8 1) 发散.
综上讨论 , 当 q 1 时收敛于 q ,当 q 1 时发散. 1q
例2 判断级数
并不存在和数 S .
练习：讨论下列级数的敛散性；若收敛，求其值。
1
1.
;
n1 (2n 1)(2n 1)
n
2. ln ;
n1 n 1
3.
ln(1
1
);
n1
n
(ln 2)n
4. n1
2n
;
5. (1)n1 5n
n1
称为几何级数(又称为等比级数), 其中a 0, q 0.
试讨论该级数的敛散性.
解 该级数的前n项部分和为
Sn
a
aq
aqn1
a aqn 1q
(q 1)
(1)当 q
1时,
有
lim
n
S
n
a, 1q
所以级数 (8 1) 收敛, 且其和为 a . 1q
(2)当 q 1时,
有
lim
n
n1
un 同时收敛或同时发散, 且同时收敛时, 有
n1
cun c un .
n1
n1
性质8.2 若级数 un 与级数 vn 都收敛, 则级数
n1
n1
(un vn ) 收敛 , 且有
n1
(un vn ) un vn .
n1
n1
n1
级数 un 发散, vn 收敛, 必有 （un vn数发散.
(3)当q 1 时, Sn na ( n 时 );
当q 1时,
Sn
a [1 2
(1)n1 ],
n 时, Sn 的极限不存在,
故当 q 1时, 级数 (8 1) 发散.
综上讨论 , 当 q 1 时收敛于 q ,当 q 1 时发散. 1q
例2 判断级数
并不存在和数 S .
练习：讨论下列级数的敛散性；若收敛，求其值。
1
1.
;
n1 (2n 1)(2n 1)
n
2. ln ;
n1 n 1
3.
ln(1
1
);
n1
n
(ln 2)n
4. n1
2n
;
5. (1)n1 5n
n1
高等数学11-1 无穷级数的概念与性质
1 sin 1 n 1 0, 解. （1）因为 lim n sin lim n n n 1 / n 所以级数发散.
17/21
常数项级数的概念与性质
1 ln n 3 (2) n 3 n 1 3n 1 1 因调和级数 解 发散, 由性质1知, 发散. n 1 n n 1 3n ln n 3 l n3 而级数 n 是以 r 为公比的等比级数, 3 n 1 3
常数项级数的概念与性质
一、常数项级数的概念
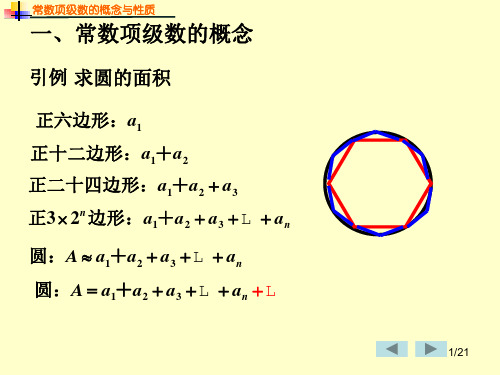
引例 求圆的面积
正六边形：a1 正十二边形：a1＋a2 正二十四边形：a1＋a2 a3
正3 2n 边形：a1＋a2 a3
圆：A a1＋a2 a3 圆：A a1＋a2 a3 an
an
an
1/21
常数项级数的概念与性质
n 1 n 1
n 1
n 1
n 1
n 1
12/21
常数项级数的概念与性质
性质3 添加或去掉有限项不影响一个级数的敛散性 .
注：
仅讨论级数 un 的敛散性时， 可简记为 un ，
n1
但求收敛级数的和时，需指明从哪一项开始！
13/21
常数项级数的概念与性质
性质4 设级数 un 收敛, 则对其各项任意加括号所得
n
矛盾！ 级数发散 .
9/21
常数项级数的概念与性质
小结：判断级数敛散性步骤：
（1）求出级数的前n项和（部分和）Sn；
（2）讨论 lim Sn 的存在性.
n
10/21
常数项级数的概念与性质
二、收敛级数的基本性质
性质1 设常数 k 0, 则 un与 kun
第三节一般常数项级数
定理 若
u
n 1
n
收敛,则
u
n 1
n 收敛.
1 证明 令 vn ( un un ) ( n 1,2,), 2 且 vn un , v n收敛, 显然 vn 0,
又 un ( 2v n un ),
n 1 n 1
un 收敛.
n
由比值判别法，级数 un 发散，从而题设
n 1
级数不是绝对收敛.
又因为
un1 un
lim
n
un 1 un
1
,所以当
n 充分大时，
un 0散.
例5 判定级数
1
n 1
2
n
1 1 的敛散性. 1 n 2 n
lim
n
un1 un
n+1 n+1！ n 1 n 1 lim lim n 1 n n+1 1！ n n n n n 2
n 2 n 2
1 lim 1 e 1. n n
u1
n
数列 s2 n是有界的 ,
lim u2 n1 0,
n
lim s2 n s u1 .
lim s2 n1 lim( s2 n u2 n1 ) s,
n n
级数收敛于和s, 且s u1 .
余项 rn (un1 un 2 ),
第三节
一般常数项级数
一、交错级数 二、一般常数项级数
一、交错级数
定义: 正、负项相间的级数称为交错级数.
( 1) n 1
u
n 1
n
收敛,则
u
n 1
n 收敛.
1 证明 令 vn ( un un ) ( n 1,2,), 2 且 vn un , v n收敛, 显然 vn 0,
又 un ( 2v n un ),
n 1 n 1
un 收敛.
n
由比值判别法，级数 un 发散，从而题设
n 1
级数不是绝对收敛.
又因为
un1 un
lim
n
un 1 un
1
,所以当
n 充分大时，
un 0散.
例5 判定级数
1
n 1
2
n
1 1 的敛散性. 1 n 2 n
lim
n
un1 un
n+1 n+1！ n 1 n 1 lim lim n 1 n n+1 1！ n n n n n 2
n 2 n 2
1 lim 1 e 1. n n
u1
n
数列 s2 n是有界的 ,
lim u2 n1 0,
n
lim s2 n s u1 .
lim s2 n1 lim( s2 n u2 n1 ) s,
n n
级数收敛于和s, 且s u1 .
余项 rn (un1 un 2 ),
第三节
一般常数项级数
一、交错级数 二、一般常数项级数
一、交错级数
定义: 正、负项相间的级数称为交错级数.
( 1) n 1
常数项级数与幂级数的收敛性
常数项级数与幂级数的收敛性在数学中，级数是由一系列数按照一定次序进行加法运算得到的结果。
本文将讨论两种重要的级数，即常数项级数和幂级数的收敛性。
一、常数项级数的收敛性常数项级数是指以常数项为公差得到的级数。
常数项级数的一般形式可以写作\[S = a_0 + a_1 + a_2 + a_3 + \ldots\]其中，\(a_0, a_1, a_2, \ldots\)为常数项。
我们来研究常数项级数的收敛性。
1. 收敛性的定义常数项级数收敛是指级数的部分和\(S_n = a_0 + a_1 + \ldots + a_n\)当\(n\)趋向于无穷大时有极限存在，即\[\lim_{{n \to \infty}} S_n = S\]这个极限称为常数项级数的和。
2. 收敛判别法常数项级数的收敛性常用的判别法有以下几种：2.1. 正项级数判别法如果常数项级数中的每一项都是非负数，且满足\(a_1 \leq a_2 \leq a_3 \leq \ldots\)，那么级数收敛与否可以通过判断部分和序列\(S_n\)是否有上界来决定。
即如果存在一个实数\(M\)使得对于任意正整数\(n\)，都有\(S_n \leq M\)，那么级数收敛。
2.2. 比较判别法比较判别法分别有以下两种情况：2.2.1. 当级数\(S = a_0 + a_1 + a_2 + \ldots\)中的每一项\(a_n\)都是非负数且满足\(a_n \leq b_n\)，其中级数\(T = b_0 + b_1 + b_2 + \ldots\)收敛时，级数\(S\)也收敛。
2.2.2. 当级数\(S = a_0 + a_1 + a_2 + \ldots\)中的每一项\(a_n\)都是非负数且满足\(a_n \geq b_n\)，其中级数\(T = b_0 + b_1 + b_2 + \ldots\)发散时，级数\(S\)也发散。
2.3. 比值判别法比值判别法是判断正项级数的收敛性的一种方法。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
(莱布尼茨定理)
练习题
判别下列级数是否收敛?如果是收敛的,是绝对收敛还
是条件收敛?
1、
n1
( 1) n1
n 3 n1
；
2、 1 1 1 1 ； ln 2 ln 3 ln 4 ln 5
3、
(1)n .
n2 n ln n
练习题答案
一、1、绝对收敛； 2、条件收敛； 3、条件收敛.
lim n
s2n
s
u1 .
lim
n
u2n1
0,
lim n
s2n1
lim(
n
s2n
u2n1 )
s,
级数收敛于和 s, 且s u1.
余项 rn (un1 un2 ),
rn un1 un2 ,
满足收敛的两个条件, rn un1 .
定理证毕.
例 1 判别级数 (1)n n 的收敛性.
一、交错级数
定义: 正、负项相间的级数称为交错级数.
(1)n1un或 (1)nun (其中un 0)
n1
n1
证明 un1 un 0, s2n (u1 u2 ) (u3 u4 ) (u2n1 u2n )
又 s2n u1 (u2 u3 ) (u2n2 u2n1 ) u2n u1
1，
1 n
n2
因为
先判断
lim n
n
un
lim
n
1 2
1
1 n
n
e 1 2
由根值判别法，级数 un n1
发散，故
lim
n
un
0，
从而题设级数发散.
小结
任意项级数
1. 若 Sn S ,则级数收敛;
审 2. 当 n , un 0, 则级数发散;
3.按基本性质;
敛 4.绝对收敛
法 5.交错级数
例4
判定级数
（
n1
1）n
nn1
n+1！
的敛散性.
解
级数为交错级数.un
（
1）n
nn1 ，先判断
n+1！
级数 un =
n1
n1
nn1
n+1 ！是否收敛.
因为
lim
n
un1 un
lim
n
n+1n2 n+1 1！
n+1！
nn1
lim
n
n
n
1
n
n 12 nn 2
lim
n
1
1 n
n
收敛.
（
1）n1
ln
n
n2
n
二、一般常数项级数
定义: 正项和负项任意出现的级数称为任意项级数.
证明
令
vn
1 2 (un
un
)
(n 1,2, ),
显然 vn 0, 且 vn un , vn收敛,
n1
又 un (2vn un ), un 收敛.
n1
n1
n1
上定理的作用： 任意项级数
n2 n 1
解
(
x
x ) 1
2
(1 x) x( x 1)2
0
( x 2)
故函数 x 单调递减, x1
un un1 ,
又
lim
n
un
lim
n
n
n 1
0.
原级数收敛.
例2 判定级数
（1）n1ຫໍສະໝຸດ lnnn2
n
的敛散性.
解 级数为交错级数.令 f (x) ln x ，则
x
f
(
x)
1
ln x2
x
0(
x
3)
即当 x 3 时，f (x) 0 ，所以在[3， ）上，
f (x) 单调减少.于是当 n 3 时，f (n) f (n 1)，
即 un un1，(n 3, 4,L ) ,又利用洛必达法则
有
ln n
ln x
1
lim lim lim 0.
n n x x x x
所以，由莱布尼兹定理知，级数
e
1.
由比值判别法，级数 un 发散，从而题设 n1
级数不是绝对收敛.
又因为
lim un1 u n
n
1
,所以当
n
充分大时，
un1 un
,
故
lim
n
un
0
,从而题设级数发
散.
例5
判定级数
n1
1n
1 2n
1
1 n
n2
的敛散性.
解级数级n1数un为=n交1 21n错1级n1 数n2 ,是u否n 收敛1 n.21n
正项级数
定义:若 un 收敛, 则称 un 为绝对收敛;
n1
n1
若 un 发散,而 un 收敛, 则称 un 为条件收敛.
n1
n1
n1
例3
判别级数
n1
s
i n
nn
2
的收敛性.
解
sin n n2
1 n2
,
而 1 收敛, n2
n1
sin n 收敛,
n2
n1
故由定理知原级数绝对收敛.
练习题
判别下列级数是否收敛?如果是收敛的,是绝对收敛还
是条件收敛?
1、
n1
( 1) n1
n 3 n1
；
2、 1 1 1 1 ； ln 2 ln 3 ln 4 ln 5
3、
(1)n .
n2 n ln n
练习题答案
一、1、绝对收敛； 2、条件收敛； 3、条件收敛.
lim n
s2n
s
u1 .
lim
n
u2n1
0,
lim n
s2n1
lim(
n
s2n
u2n1 )
s,
级数收敛于和 s, 且s u1.
余项 rn (un1 un2 ),
rn un1 un2 ,
满足收敛的两个条件, rn un1 .
定理证毕.
例 1 判别级数 (1)n n 的收敛性.
一、交错级数
定义: 正、负项相间的级数称为交错级数.
(1)n1un或 (1)nun (其中un 0)
n1
n1
证明 un1 un 0, s2n (u1 u2 ) (u3 u4 ) (u2n1 u2n )
又 s2n u1 (u2 u3 ) (u2n2 u2n1 ) u2n u1
1，
1 n
n2
因为
先判断
lim n
n
un
lim
n
1 2
1
1 n
n
e 1 2
由根值判别法，级数 un n1
发散，故
lim
n
un
0，
从而题设级数发散.
小结
任意项级数
1. 若 Sn S ,则级数收敛;
审 2. 当 n , un 0, 则级数发散;
3.按基本性质;
敛 4.绝对收敛
法 5.交错级数
例4
判定级数
（
n1
1）n
nn1
n+1！
的敛散性.
解
级数为交错级数.un
（
1）n
nn1 ，先判断
n+1！
级数 un =
n1
n1
nn1
n+1 ！是否收敛.
因为
lim
n
un1 un
lim
n
n+1n2 n+1 1！
n+1！
nn1
lim
n
n
n
1
n
n 12 nn 2
lim
n
1
1 n
n
收敛.
（
1）n1
ln
n
n2
n
二、一般常数项级数
定义: 正项和负项任意出现的级数称为任意项级数.
证明
令
vn
1 2 (un
un
)
(n 1,2, ),
显然 vn 0, 且 vn un , vn收敛,
n1
又 un (2vn un ), un 收敛.
n1
n1
n1
上定理的作用： 任意项级数
n2 n 1
解
(
x
x ) 1
2
(1 x) x( x 1)2
0
( x 2)
故函数 x 单调递减, x1
un un1 ,
又
lim
n
un
lim
n
n
n 1
0.
原级数收敛.
例2 判定级数
（1）n1ຫໍສະໝຸດ lnnn2
n
的敛散性.
解 级数为交错级数.令 f (x) ln x ，则
x
f
(
x)
1
ln x2
x
0(
x
3)
即当 x 3 时，f (x) 0 ，所以在[3， ）上，
f (x) 单调减少.于是当 n 3 时，f (n) f (n 1)，
即 un un1，(n 3, 4,L ) ,又利用洛必达法则
有
ln n
ln x
1
lim lim lim 0.
n n x x x x
所以，由莱布尼兹定理知，级数
e
1.
由比值判别法，级数 un 发散，从而题设 n1
级数不是绝对收敛.
又因为
lim un1 u n
n
1
,所以当
n
充分大时，
un1 un
,
故
lim
n
un
0
,从而题设级数发
散.
例5
判定级数
n1
1n
1 2n
1
1 n
n2
的敛散性.
解级数级n1数un为=n交1 21n错1级n1 数n2 ,是u否n 收敛1 n.21n
正项级数
定义:若 un 收敛, 则称 un 为绝对收敛;
n1
n1
若 un 发散,而 un 收敛, 则称 un 为条件收敛.
n1
n1
n1
例3
判别级数
n1
s
i n
nn
2
的收敛性.
解
sin n n2
1 n2
,
而 1 收敛, n2
n1
sin n 收敛,
n2
n1
故由定理知原级数绝对收敛.