有理函数积分法

合集下载

有理函数的积分

§6.3 有理函数的积分法（1）【导语】【正文】一、有理函数的积分设()n P x 与()m Q x 分别是n 次和m 次多项式，则称()()m n Q x P x 为有理函数；当m n <时，()()m n Q x P x 称为真分式；当m n ≥时，()()m n Q x P x 称为假分式． A ax b +，()k A ax b +，2Bx C px qx r +++，2()kBx Cpx qx r +++称为最简分式（部分分式）．定理6（多项式除法定理）任意一个假分式都可以表示成一个多项式与一个真分式之和．当m n ≥时，设()()()()()m n n Q x R x S x P x P x =+，则 ()()d ()d d ()()m nn Q x R x x S x x x P x P x =+∫∫∫． Remark 有理函数的积分问题转化为真分式的积分问题！（一）分母为一次重因式的真分式的积分法例1 求积分2353d (2)x x x ++∫．解令 232353(2)2(2)(2)x A B Cx x x x +=++++++．将右端通分得22323353(2)(2)(2)2(2)(2)(2)x A B C A x B x Cx x x x x +++++=++=+++++．比较两端分子对应项的系数得5,40,42 3.A A B A B C =+=++=解得 5,20,23.A B C ==− =所以23235352023(2)2(2)(2)x x x x x +=−+++++，于是2353d (2)x x x ++∫2352023d d d 2(2)(2)x x x x x x =−++++∫∫∫ 220235ln 222(2)x C x x =++−+++．（二）分母为不同一次因式乘积的真分式的积分法对于d ()()cx dx x a x b +−−∫，可令()()cx d A Bx a x b x a x b+=+−−−−，等式右端通分得()()()()()()cx d A B A x b B x a x a x b x a x b x a x b +−+−=+=−−−−−−．比较两端分子对应项的系数得待定系数A 和B 满足的一次方程组，求出,A B 的值．于是d d d ln ||ln ||()()cx dA Bx x x A x a B x b C x a x b x a x b +=+=−+−+−−−−∫∫∫．例2 求积分2d (3)(5)x x x x −−−∫．解令2(3)(5)35x A Bx x x x −=+−−−−．等式右端通分得2()(53)(3)(5)35(3)(5)x A B A B x A B x x x x x x −+−+=+=−−−−−−．比较两端分子对应项的系数得1,53 2.A B A B +=+=解得12A =−，32B =．所以13222(3)(5)35x x x x x −−=+−−−−．于是2d (3)(5)x x x x −−−∫113113d(3)d(5)ln 3ln 5232522x x x x C x x =−−+−=−−+−+−−∫∫．（三）分母为二次多项式(没有实根)的真分式的积分法1．积分21d x x px q++∫假设240p q −<，则22211d d 4()24x x p q p x px q x =−++++∫∫．记2pu x =+，A21d x x px q ++∫221d u u A =+∫1arctan uA A=C ．2．积分2d (0)ax bx a x px q+≠++∫假设240p q −<，则2222(2)()d d d 2bb x x p p ax b a a a x a x x x px q x px q x px q+++−+==++++++∫∫∫ 222d()21()d 22a x px q a bp x x px q a x px q +++−++++∫∫ 2221ln()d 22a a bx px q p x ax px q+++− ++ ∫．（四）分母为二次重因式的真分式的积分法例3 求积分322221d (1)x x x x x −+++∫．解令3211222222221(1)1(1)A x B A x B x x x x x x x x ++−+=+++++++．等式右端通分得32321122111121122222222()()21(1)1(1)(1)A x B A x B A x A B x A A B x B B x x x x x x x x x x +++++++++−+=+=++++++++．比较两端分子对应项的系数得111121121,2,0,1.A A B A A B B B = +=− ++= += 解得11221,3,2,4.A B A B ==− = = 所以 32222222132(2)(1)1(1)x x x x x x x x x x −+−+=+++++++．对于积分23d 1x x x x −++∫，有2231(21)7d d 121x x x x x x x x −+−=++++∫∫221d(1)7212x x x x ++−++∫217ln(1)22x x C ++−．对于积分222(2)d (1)x x x x +++∫，有2222222222(2)(21)3d(1)1d d 3d (1)(1)(1)(1)x x x x xx x x x x x x x x x +++++==+++++++++∫∫∫∫222113d 13(1)[()]24x x x x =−+++++∫，其中22212d 133[()]3()244x x C x x =++++∫．（Remark 对于22d ()n nxI a x =+∫，有122222122()n nn n x I I na na a x +−=++）于是32222222132(2)d d d (1)1(1)x x x x x x x x x x x x x −+−+=+++++++∫∫∫222112ln(1)32(1)4x x x C x x x ++−+++++．（五）分母为一次因式与二次因式乘积的真分式的积分法对于积分22d ()()bx cx d xx a x px q ++−++∫2(40)p q −<，令 222()()bx cx d A Bx Cx a x px q x a x px q+++=+−++−++．等式右端通分后，根据分子相等得恒等式22()()()bx cx d A x px q Bx C x a ++≡++++−．比较两端对应项的系数得待定系数,,A B C 满足的一次方程组，求出,,A B C 的值．于是22d ()()bx cx dxx a x px q ++−++∫22d d ln ||d A Bx C Bx C x x A x a x x a x px q x px q +++=−+−++++∫∫∫．Remark1 在上述积分问题中牵扯到的简单积是：（1）d Ax ax b+∫ln Aax b C a++；（2）()d kAxax b +∫11(1)()k A C a k ax b −+−+；(0,1)k k >≠ （3）22d (40)Bx Cx q pr px qx r+−<++∫“2211211d d 2211x x x x x x x x x ++=+++++∫∫”（4）22d (40,0,1)()kBx Cx q pr k k px qx r +−<>≠++∫“2211211d d 22(1)(1)k k x x x x x x x x x ++=+++++∫∫．Remark2A ax b +，()k A ax b +，2Bx C px qx r +++，2()kBx Cpx qx r +++称为最简分式．定理7 设()()Q x P x 是一真分式，则其可表示成最简分式之和，且表示形式唯一．设 221122111222()()()()()k l P x a x b a x b p x q x r p x q x r =++++++ ，则12211222222()()()()k k A A A Q x AP x a x b a x b a x b a x b =++++ ++++112222222111222222222()()l l l B x C B x C B x C Bx Cp x q x r p x q x r p x q x r p x q x r +++++++++ +++++++++ ．【本讲总结与下讲预告】。

44有理函数的积分知识讲解

44有理函数的积分知识讲解有理函数意为有理数的函数，即可以表示为$p(x)/q(x)$的函数，其中$p(x)$和$q(x)$均为多项式函数。

有理函数积分是指对有理函数进行积分运算，是高等数学中一个非常重要的内容。

下面将介绍有理函数积分的知识。

一、分式分解要求有理函数的积分，首先要进行分式分解。

分式分解是将一个有理函数分解成多个个简单的有理函数的和的过程，即对于一个形如$p(x)/q(x)$的有理函数进行分解，使得分解式的分母均为一次多项式或既约二次多项式。

分式分解的基本方法是：用二次多项式的因式作分子的一次式，二次多项式必须既约，即无重根。

若$q(x)$的某个根是$k$，则$(x-k)$是$q(x)$的因式；若二次多项式$(x^2+px+q)$有两个不同实根$x_1,x_2$，则分式分解式可写成两个部分的和形式，即分子为$k_1/(x-x_1)$，分母为$(x-x_1)$，分子为$k_2/(x-x_2)$，分母为$(x-x_2)$。

二、基本积分公式有理函数的积分可以根据基本积分公式进行求解。

常用的基本积分公式有以下几种：1. $\int \frac{1}{x} dx = \ln |x| + C$2. $\int \frac{1}{x^2+a^2} dx=\frac{1}{a}\arctan(\frac{x}{a})+C$三、换元积分法针对部分比较复杂的有理函数，可以采用换元积分法进行求解。

具体方法是：先将分式分解为几个部分，其中一个部分是含有根式的二次函数，用$t=\sqrt{x^2+a^2}$进行代换，然后进行简化，并根据基本积分公式计算积分。

四、分步积分法对于含有较多项的有理函数，可以采用分步积分法进行求解。

具体方法是：将原式中的有理函数分解为两个有理函数的和，其中一个有理函数是原式的导数的因式，另一个有理函数则是原式的乘积。

然后，用分部积分法求解原式的积分。

总之，有理函数积分是高等数学中的一个非常重要的内容，可以通过分式分解、基本积分公式、换元积分法和分步积分法进行求解。

高数讲义第四节有理函数的积分全

例9
求积分
1
x
1 xdx x
解令 1 x t 1 x t2,
x
x
x
t
1 2
, 1
dx
2tdt t2 1
2,
例9
求积分
1
x
1 xdx x
解
令 1 x t x
x
xt2211a12,dxdx
1
2a
ln
x2tdat tx2 a1
2
C,
1 x
1
x
xdx
t
2
1t
t
2
2t
12
dt
2
x
2)
1
A 2x
Bx 1
C x2
解：令：
x
1 (1
x)
2
A x
B 1 x
C (1 x)
2
1 A(1 x)2 B x(1 x) C x
取 x1, 得 C 1; 取 x0, 得 A1;
再取 x 2 , 得 1 (1 2)2 B2(1 2) 2 , B 1 ;
1 x (1 x) 2
t
3
1 t 1
1dt
6
(t
2
t
1
t
1
)dt 1
2t 3 3t 2 6t 6 ln | t 1 | C
2 x 1 33 x 1 36 x 1 6 ln(6 x 1 1) C.
说明无理函数去根号时, 取根指数的最小公倍数.
例11 求积分
x 3x 1
dx. 2x 1
解先对分母进行有理化
f (x) 为真分式 , 当 m n 时
f (x) 为假分式

有理函数积分法

第21讲理函数的不定积分一、有理函数的不定积分有理函数是指由两个多项式函数的商所表示的函数，其一般形式为mm mn n n xxx x x Q x P x R βββααα++++++==-- 110110)()()(， (1)其中，m 为n 非负整数，n ααα,,,10 与m βββ ,,10都是常数，且00≠α，00≠β．若n m >，则称它为真分式；若n m ≤，则称它为假分式．由多项式的除法可知，假分式总能化为一个多项式与一个真分式之和．由于多项式的不定积分是容易求得的，因此只需研究真分式的不定积分，故设(1)为一有理真分式．根据代数知识，有理真分式必定可以表示成若干个部分分式之和(称为部分分式分解)．因而问题归结为求那些部分分式的不定积分．为此，先把怎样分解部分分式的步骤简述如下(可与例1对照着做)：第一步对分母()x Q 在实系数内作标准分解： ()()()()()tt t s q p x q x p xa x a x x Q μμλλ++++--=21121121，（2）其中()t iji ,,2,1,1,0 ==μλβ均为自然数，而且.,,2,1,04;2211t j q p m j j si tj ji =-=+∑∑==μλ第二步根据分母的各个因式分别写出与之相应的部分分式：对于每个形如()ka x -的因式，它所对应的部分分式是 ()();221kka x A a x A ax A -++-+-对每个形如()kq px x ++2的因式，它所对应的部分分式是()().22222211kkk q px xC x B q px xC x B qpx x C x B ++++++++++++把所有部分分式加起来，使之等于()x R ．(至此，部分分式中的常数系数i i i C B A ,,尚为待定的.)第三步确定待定系数：一般方法是将所有部分分式通分相加，所得分式的分母即为原分母()x Q ，而其分子亦应与原分子()x P 恒等．于是，按同幂项系数必定相等，得到一组关于待定系数的线性方程，这组方程的解就是需要确定的系数．例1 对()8425109422345234-+--+-++-=x x x x x x x x x x R 作部分分式分解解按上述步骤依次执行如下：()=x Q 84252345-+--+x x x x x ()()().12222+-+-=x x x x部分分式分解的待定形式为()().122222210+-++++++-=x x C Bx x A x A x A x R （3）用()x Q 乘上式两边，得一恒等式()()1210942220234+-+≡-++-x x x A x x x x +()()()()()121222221+--++-+-x x x A x x x x A+()()()222+-+x x C Bx （4）然后使等式两边同幂项系数相等，得到线性方程组：⎪⎪⎪⎩⎪⎪⎪⎨⎧-=---=--+=+----=+++-=++常数项的系数，的系数，的系数，的系数 .1082449483442433123,22102122103210410C A A A x C B A A x C B A A A x C B A A A x B A A 求出它的解：1,1,1,2,1210=-=-===C B A A A ，并代人(3)式，这便完成了)(x R 的部分分式分解：.11)2(12221)(22+---+-++-=x x x x x x x R上述待定系数法有时可用较简便的方法去替代．例如可将x 的某些特定值(如0)(=x Q 的根)代人(4)式，以便得到一组较简单的方程，或直接求得某几个待定系数的值．对于上例，若分别用2=x 和2-=x 代人(4)式，立即求得1120-==A A 和，于是（4）式简化成为)1)(2)(2(161232134+-+-=-+-x x x x A x x x .)2)(2)((2+-++x x C Bx为继续求得C B A ,,1，还可用x 的三个简单值代人上式，如令1,1,0-=x ，相应得到⎪⎩⎪⎨⎧=+-=++=+.83,233,42111C B A C B A C A 由此易得1,1,21=-==C B A ．这就同样确定了所有待定系数．一旦完成了部分分式分解，最后求各个部分分式的不定积分．由以上讨论知道，任何有理真分式的不定积分都将归为求以下两种形式的不定积分：⎰-I ka x dx)()(；()⎰<-+++I I )04()(22q p dx q px x M Lx k．对于()I ，已知()()⎪⎩⎪⎨⎧>+--=+-=--⎰.1,11,1,ln )(1k C a x k k C a x a x dx k k对于()II ，只要作适当换元(令2p x t +=)，便化为()⎰⎰++=+++dt rtNLt dx q px xMLx kk222)(⎰⎰+++=,)()(2222kkr t dt N dt r t t L （5）其中.2,422L p M N pq r-=-=．当1=k 时，（5）式右边两个不定积分分别为⎰++=+C r t dt rtt)ln(212222，.a r c t a n 122C rtr rtdt+=+⎰ （6）当2≥k 时，（5）式右边第一个不定积分为C r t k dt r t tk k++-=+⎰-12222))(1(21)(.对于第二个不定积分，记 ,)(122⎰-+=k k r tdtI 可用分部积分法导出递推公式如下：dt r t t r t rI kk ⎰+-+=)()(1222222⎰+-=-dt r ttrI rkk )(11222212⎰⎪⎪⎭⎫ ⎝⎛+-+=--122212)(1)1(211k k r t td k r I r.)()1(2111122212⎥⎦⎤⎢⎣⎡-+-+=---k k k I r t tk r I r 经整理得到.)1(232))(1(2121222----++-=k k k I k r k r t k r tI （7）重复使用递推公式(7)，最终归为计算1I ，这已由(6)式给出. 把所有这些局部结果代回(5)式，并令2p x t +=，就II ）的计算．例2 求.)22(1222dx x xx ⎰+-+解：在本题中，由于被积函数的分母只有单一因式，因此，部分分式分解能被简化为222222)22()12()22()22(1+--++-=+-+x x x x x x x x .)22(12221222+--++-=x x x x x现分别计算部分分式的不定积分如下：.)1arctan(1)1()1(22122C x x x d x x dx +-=+--=+-⎰⎰dx x xx dx x xx ⎰⎰+-+-=+--2222)22(1)22()22(12++-+-=⎰222)22()22(x xx x d []⎰+--221)1()1(x x d.)1(221222⎰+++--=tdtx x由递推公式（7）,求得其中⎰⎰+++=+121)1(2)1(2222tdtt t t dt .)1arctan(21)22(2122C x x x x +-++--=于是得到.)1a r c t a n (23)22(23)22(12222C x x x x dx x xx +-++--=+-+⎰二、三角函数有理式的不定积分⎰dx x x R )cos ,(sin 是三角函数有理式的不定积分。

简单有理函数的积分

简单有理函数的积分
有理函数积分拆项原则求abc：通分，x^2+1=a（x-1）（x+3）+b（x+3）+c（x-1）^2，代入x＝1求得b，代入x＝-3求得c，再随便代入一个其它数字，求得a。

有理函数是通过多项式的加减乘除得到的函数。

在数学中，理性函数就是可以由有理分数定义的任何函数，即为代数分数，使分子和
分母都就是多项式。

多项式的系数不须要就是有理数，它们可以在任何字段k中展开。

变量的情况可以在涵盖k的任何字段l中展开。

函数的域就是变量，分母不为零，代码区
为l。

代数几何定义编辑语音
设v为不容向量丛簇，座标环k[v]为整环，故存有商域k（v），称作v的函数域，
其元为v上的一个有理函数。

一个有理函数h可以写成如下形式：h=f/g，这里f和g都是多项式函数。

有理函数
是特殊的亚纯函数，它的零点和极点个数有限。

有理函数的积分

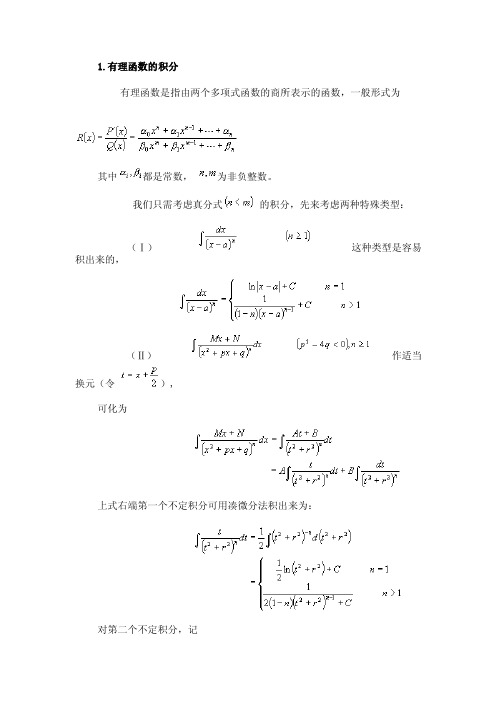
1.有理函数的积分有理函数是指由两个多项式函数的商所表示的函数，一般形式为其中都是常数，为非负整数。

我们只需考虑真分式的积分，先来考虑两种特殊类型：（Ⅰ）这种类型是容易积出来的，（Ⅱ）作适当换元（令）,可化为上式右端第一个不定积分可用凑微分法积出来为：对第二个不定积分，记用分部积分法可导出递推公式：整理得重复使用递推公式，最终归结为计算而可积出来为这样就可完成对不定积分（Ⅱ）的计算。

对任一个有理函数而言，均可写成一个多项式与一个有理真分式的和，而多项式的积分问题已经解决，下面主要考虑有理真分式(不妨设)的积分问题。

为叙述简便，不妨设．其方法是将化成许多简单分式（即类型（Ⅰ）、（Ⅱ））的代数和然后逐项积分。

由于类型（Ⅰ）、（Ⅱ）总是可“积出来”的，从面有理函数总是可以“积出来”。

下面简述分解有理真分式（）的步骤：第一步按代数学的结论，将分母分解成实系数的一次因式与二次因式的乘幂之积。

其中均为自然数。

第二步根据因式分解结构，写出的部分分式的待定形式：对于每个形如的因式，所对应的部分分式为对于每个形如的因式，所对应的部分分式为把各个因式所对应的部分分式加起来，就完成了对的部分分式分解。

第三步确定待定系数：通分后比较分子上的多次式的系数，得待定系数的线性方程组，由此解得待定系数的值。

例8.13 求2.三角函数有理式和积分由及常数经过有限次四则运算所得的函数称为关于的有理式（或三角函数有理式）。

用表示对于这种函数的不定积分我们总可通过代换，化为以为变量的有理函数的积分。

理由是，，，又，故从而上面的讨论说明：三角函数有理式也总是可以“积出来”的，但对具体问题而言，用上述方法往往计算量太大，因此，有时要考虑用其它简便方法。

（1）如果是的奇函数时，即则设即可。

例如求（1）；（2）．（2）如果是的奇函数时，即则设即可。

例如求．（3）如果是关于与的偶函数时，即则设即可。

例如求（1）；（2）．（4）请研究被积函数为（为自然数）时的情况。

有理函数积分法(3)

2
2
( x2 px q)n
dx
类型4
A
2
(x2
2x px
p
q)n dx
(B
p 2
A)
1 ( x2 px q)n dx
A
2
(x2
1 px
q)n d ( x 2
px
q)
(B
p 2
A)
1 ( x2 px q)n dx
A 1 2 1n
(x2
1 px q)n1
(B p A) 2
arctan
x
2 x (1 x2 )2 dx
arctanx
1 2x 2
2 (1 x2 )2
dx
arctanx 1 2
2x (1 x2 )2 dx
2 (1 x 2 )2 dx
arctanx
1 2
1
1 x2
2
1 (1 x 2 )2 dx
15
1 x x2 ( x2 1)2
13
例4
求
1
3
x x
3
dx.
解
1
3
x x
3
dx
(
1
1
x
1
x1 x x2
)dx
1
3
ln1
x
1
x1 x x
2
dx
ln1
x
(2x 1) 2 1 x x2 2dx
ln1
x
1 2
1
2x x
1 x2 dx
3 2
1
1 x
x2 dx
ln 1 x 1 ln1 x x2 3
( x 1)( x 2)2

有理函数积分法

第21讲理函数的不定积分一、有理函数的不定积分有理函数是指由两个多项式函数的商所表示的函数，其一般形式为mm m nn n x x x x x Q x P x R βββααα++++++==-- 110110)()()(， (1) 其中，m 为n 非负整数，n ααα,,,10 与m βββ ,,10都是常数，且00≠α，00≠β．若n m >，则称它为真分式；若n m ≤，则称它为假分式．由多项式的除法可知，假分式总能化为一个多项式与一个真分式之和．由于多项式的不定积分是容易求得的，因此只需研究真分式的不定积分，故设(1)为一有理真分式．根据代数知识，有理真分式必定可以表示成若干个部分分式之和(称为部分分式分解)．因而问题归结为求那些部分分式的不定积分．为此，先把怎样分解部分分式的步骤简述如下(可与例1对照着做)：第一步对分母()x Q 在实系数内作标准分解： ()()()()()t t t s q p x q x p xa x a x x Q μμλλ++++--=21121121 ，（2）其中()t i j i ,,2,1,1,0 ==μλβ均为自然数，而且.,,2,1,04;2211t j q p m j j si tj j i=-=+∑∑==μλ第二步根据分母的各个因式分别写出与之相应的部分分式：对于每个形如()ka x -的因式，它所对应的部分分式是()();221kk a x A a x A a x A -++-+- 对每个形如()kq px x ++2的因式，它所对应的部分分式是()().22222211kkk qpx xC x B qpx x C x B q px x C x B ++++++++++++把所有部分分式加起来，使之等于()x R ．(至此，部分分式中的常数系数i i i C B A ,,尚为待定的.)第三步确定待定系数：一般方法是将所有部分分式通分相加，所得分式的分母即为原分母()x Q ，而其分子亦应与原分子()x P 恒等．于是，按同幂项系数必定相等，得到一组关于待定系数的线性方程，这组方程的解就是需要确定的系数．例1 对()8425109422345234-+--+-++-=x x x x x x x x x x R 作部分分式分解解按上述步骤依次执行如下：()=x Q 84252345-+--+x x x x x ()()().12222+-+-=x x x x部分分式分解的待定形式为()().122222210+-++++++-=x x CBx x A x A x A x R （3）用()x Q 乘上式两边，得一恒等式()()1210942220234+-+≡-++-x x x A x x x x +()()()()()121222221+--++-+-x x x A x x x x A+()()()222+-+x x C Bx （4）然后使等式两边同幂项系数相等，得到线性方程组：⎪⎪⎪⎩⎪⎪⎪⎨⎧-=---=--+=+----=+++-=++常数项的系数，的系数，的系数，的系数 .1082449483442433123,22102122103210410C A A A x C B A A x C B A A A x C B A A A x B A A 求出它的解：1,1,1,2,1210=-=-===C B A A A ，并代人(3)式，这便完成了)(x R 的部分分式分解：.11)2(12221)(22+---+-++-=x x x x x x x R 上述待定系数法有时可用较简便的方法去替代．例如可将x 的某些特定值(如0)(=x Q 的根)代人(4)式，以便得到一组较简单的方程，或直接求得某几个待定系数的值．对于上例，若分别用2=x 和2-=x 代人(4)式，立即求得1120-==A A 和，于是（4）式简化成为)1)(2)(2(161232134+-+-=-+-x x x x A x x x .)2)(2)((2+-++x x C Bx为继续求得C B A ,,1，还可用x 的三个简单值代人上式，如令1,1,0-=x ，相应得到⎪⎩⎪⎨⎧=+-=++=+.83,233,42111C B A C B A C A 由此易得1,1,21=-==C B A ．这就同样确定了所有待定系数．一旦完成了部分分式分解，最后求各个部分分式的不定积分．由以上讨论知道，任何有理真分式的不定积分都将归为求以下两种形式的不定积分：⎰-I k a x dx )()(； ()⎰<-+++II )04()(22q p dx q px x M Lx k．对于()I ，已知()()⎪⎩⎪⎨⎧>+--=+-=--⎰.1,11,1,ln )(1k C a x k k C a x a x dx k k 对于()II ，只要作适当换元(令2px t +=)，便化为()⎰⎰++=+++dt r t NLt dx q px x M Lx kk 222)(⎰⎰+++=,)()(2222k k r t dt N dt r t t L （5）其中.2,422L pM N p q r -=-=．当1=k 时，（5）式右边两个不定积分分别为⎰++=+C r t dt r t t )ln(212222， .arctan 122C rtr r t dt +=+⎰ （6）当2≥k 时，（5）式右边第一个不定积分为C r t k dt r t t k k++-=+⎰-12222))(1(21)(. 对于第二个不定积分，记 ,)(122⎰-+=k k r t dtI 可用分部积分法导出递推公式如下：dt r t t r t r I k k ⎰+-+=)()(1222222⎰+-=-dt r t t r I r kk )(11222212 ⎰⎪⎪⎭⎫ ⎝⎛+-+=--122212)(1)1(211k k r t td k r I r .)()1(2111122212⎥⎦⎤⎢⎣⎡-+-+=---k k k I r t tk r I r 经整理得到.)1(232))(1(2121222----++-=k k k I k r k r t k r t I （7）重复使用递推公式(7)，最终归为计算1I ，这已由(6)式给出. 把所有这些局部结果代回(5)式，并令2p x t +=，就完成了对不定积分（II ）的计算．例2 求.)22(1222dx x x x ⎰+-+ 解：在本题中，由于被积函数的分母只有单一因式，因此，部分分式分解能被简化为222222)22()12()22()22(1+--++-=+-+x x x x x x x x .)22(12221222+--++-=x x x x x 现分别计算部分分式的不定积分如下：.)1arctan(1)1()1(22122C x x x d x x dx +-=+--=+-⎰⎰dx x x x dx x x x ⎰⎰+-+-=+--2222)22(1)22()22(12++-+-=⎰222)22()22(x x x x d []⎰+--221)1()1(x x d.)1(221222⎰+++--=t dtx x由递推公式（7）,求得其中⎰⎰+++=+121)1(2)1(2222t dt t t t dt .)1arctan(21)22(2122C x x x x +-++--=于是得到 .)1arctan(23)22(23)22(12222C x x x x dx x x x +-++--=+-+⎰ 二、三角函数有理式的不定积分⎰dx x x R )cos ,(sin 是三角函数有理式的不定积分。

简单有理分式函数的积分

简单有理分式函数的积分
一、有理函数的积分
有理函数是指有理式所表示的函数，它包括有理整式和有理分式两类：
有理整式 f(x)=a0xn+a1xn－1+…+an－1x+an;
有理分式
其中m，n都是非负整数，a0,a1,…,an及b0,b1,…,bn都是实数，并且a0≠0,b0≠0.
一、有理函数的积分
1=A(1+x2)+(Bx+C)(1+x)，
一、有理函数的积分
整理得 1=(A+B)x2+(B+C)x+A+C.（4-19）
比较式（4-19）两端x的同次幂的系数及常数，有
一、有理函数的积分
3. 有理函数积分举例【例1】
去分母,得 2x3+x－1=(Ax+B)(x2+1)+(Cx+D) =Ax3+Bx2+(A+C)x+(B+D),
三、积分表的使用
同时还应了解，求函数的不定积分与求函数的导数的区别.求一个函数的导数总可以循着一定的规则和方法去做，而求一个函数的不定积分却没有统一的规则可循，需要具体问题具体分析，灵活应用各类积分方法和技巧.
实际应用中常常利用积分表来计算不定积分.求不定积分时可按被积函数的类型从表中查到相应的公式，或经过少量的运算和代换将被积函数化成表中已有公式的形式.
二、可化为有理函数的积分
二、可化为有理函数的积分
二、可化为有理函数的积分
【例3】
二、可化为有理函数的积分
【例4】
二、可化为有理函数的积分
二、可化为有理函数的积分
2. 简单无理函数的积分

有理函数和三角函数有理式的积分法

§3-7 阅读(有理函数和三角函数有理式的积分法)在前面几节中，读者都已经遇到过许多有理函数的积分和三角函数有理式的积分在前面几节中，读者都已经遇到过许多有理函数的积分和三角函数有理式的积分..在那里，因为被积函数都很特殊，因为被积函数都很特殊，所以用所以用所以用“拼凑的方法”“拼凑的方法”就求出了它们的积分就求出了它们的积分..这一节讨论的是一般情形下，如何求它们的积分当你遇到那些简单或特殊的情形时，当然不必用这里的一般方法，而仍用以前那种“拼凑方法”就行了法，而仍用以前那种“拼凑方法”就行了. .1.有理函数的积分法有理函数的积分()d ()p x x q x ò[ [其中其中()p x 和()q x 都是多项式都是多项式] ] 总可以积出来，即可把它表示成初等函数总可以积出来，即可把它表示成初等函数..积分方法的要点是：第一，若有理函数()()p x q x 中，分子()p x 的次数不低于分母()q x 的次数，则称它为假分式假分式..在这种情形下，就用多项式除法（见下面例2727）），先把它变成一个多项式与一个真分式之和，即()()()()()p x r x s x q x q x =+ [ [其中分子其中分子()r x 的次数低于分母()q x 的次数的次数] ] 于是，()d ()p x x q x ò()()d d ()r x s x x x q x =+òò右端第一项是多项式的积分右端第一项是多项式的积分((用分项积分法可以积出来用分项积分法可以积出来))，所以就变成求有理函数真分式的积分()d ()r x x q x ò. . 关于多项式除法，请看下面的例题关于多项式除法，请看下面的例题关于多项式除法，请看下面的例题. . 例27 例如求有理函数假分式的积分522d 36x x x x -++ò首先像做整数除法那样，做多项式除法：由此可得63225++-x x x 3212323336x x x x +æö=-+ç÷+èø其次再逐项积分，即(余式) 23+x (被除式) （除式）255336000202x x x x x ++++-+++xx x x 40220233-+-+-+-（商式）31233x x -5342222212321132d d d d 33123363636x x x x x x x x x x x x x x x -+++æö=-+=-+ç÷+++èøòòòò这样就变成求这样就变成求((右端最后一个右端最后一个))有理函数真分式的积分有理函数真分式的积分. .第二，第二，对于真分式对于真分式()()r x q x ，先把分母上的多项式()q x 分解成一次因式或没有实根的二次因式的乘积二次因式的乘积((根据代数基本定理，这是可能的).).然后用待定系数法然后用待定系数法然后用待定系数法((或拼凑方法或拼凑方法))把()()r x q x 化成不超出下面这些“最简分式”的和：化成不超出下面这些“最简分式”的和：22,,,()()n m A B Cx D Ex Fx a x b x px q x rx s ++--++++(n 和m 为正整数为正整数)) (分子比分母上的基因式低一次分子比分母上的基因式低一次) )这样，根据分项积分法，有理函数真分式的积分就化为最简分式的积分这样，根据分项积分法，有理函数真分式的积分就化为最简分式的积分. . 我们用例子来说明上述方法我们用例子来说明上述方法我们用例子来说明上述方法. .⑴分母为一次重因式的真分式的积分法例28 例如求例如求2353d (2)x x x ++ò，可令，可令2323532(2)(2)(2)x A B C x x x x +=++++++将右端通分，将右端通分，并比较两端分子，并比较两端分子，并比较两端分子，即即C x B x A x ++++º+)2()2(3522，则得三元线性方程组则得三元线性方程组ïîïíì=++=+=（常数项）的系数）（的系数）（3240452C B A x B A x A ，解得解得ïîïíì=-==23205C B A 于是得于是得3232)2(23)2(2025)2(35+++-+=++x x x x x 因此，因此， 2353d (2)x x x ++ò2352023d d d 2(2)(2)x x x x x x =-++++òòò220235ln 222(2)x x x =++-++【注1】上面求待定系数的方法是比较两端x 的同次项系数，下面是求待定系数的另一个方法：根据2253(2)(2)x A x B x C +º++++，则，则第一步，让2x =-，得23C =；第二步，在2253(2)(2)x A x B x C +º++++两端关于x 求导数，得102(2)x A x B º++. 再令2x =-，得20B =-；第三步，在102(2)x A x B º++两端关于x 求导数，则得102A =，即5A =.【注2】把真分式2353(2)x x ++化成最简分式之和的另一个方法是依次用多项式除法化成最简分式之和的另一个方法是依次用多项式除法: :25323(510)22x x x x +=-+++,222253510232023522(2)(2)(2)x x x x x x x +-=+=-++++++ 232353520232(2)(2)(2)x x x x x +=-+++++ ( (你看懂了吗你看懂了吗你看懂了吗?) ?)⑵分母为不同一次因式乘积的真分式的积分法例如求d ()()cx d x x a x b +--ò，可令，可令 bx Ba x Ab x a x d cx -+-=--+))((（A 和B 为待定系数）为待定系数）然后根据恒等式()()cx d A x b B x a +º-+-，求出待定系数A 和B .于是，于是，d ()()cx d x x a x b +=--òd d ln ||ln ||A B x x A x a B x b x a x b +=-+---òò例29 求2d (3)(5)x x x x ---ò.解设53)5)(3(2-+-=---x Bx A x x x (B A ,为待定常数为待定常数) ) 则得)3()5(2-+-º-x B x A x ，即，即2)35()(-º+-+x B A x B A 比较两端常数项和x 的系数，则得线性方程组的系数，则得线性方程组îíì=+=+1235BA B A 解得23,21=-=B A ( (求求B A 和的另一个方法见下注的另一个方法见下注).).).因此，因此，因此， 523321)5)(3(2-+--=---x x x x x 从而得从而得2d(3)(5)x x x x ---ò113113d(3)d(5)ln 3ln 5232522x x x x x x =--+-=--+---òò【注】在式2(5)(3)x A x B x -º-+-中，让3x =，则得12A =-，所以12A =-；再让5x =，则得32B =，所以32B =.⑶分母为二次多项式(没有实根)的真分式的积分法例如例如[[注意注意,,分母没有实根2(40)p q -<]，22222111(1)d d d 424x x ux px q u A p q px ==+++-æö++ç÷èøòòò24,22q p p u x A æö-ç÷=+=ç÷èø(套用积分公式)1arctan u A A =2222arctan 44q q x p p p+-=-2222(2)(2)d (0)d d 2b bx p p x ax ba a ax a ax x x px qx px qx px qæö++-+ç÷+èø¹==++++++òòò222d()21d 22ax px q a b p x a x px q x px q++æö=+-ç÷++++èøòò2221ln()d 22aa bx px q p x a x px q æö=+++-ç÷++èøò(套用前一题的结果套用前一题的结果).). ⑷分母为二次重因式的真分式的积分法例30 例如求积分例如求积分322221d (1)x x x x x -+++ò.若用待定系数法，就令若用待定系数法，就令322222221(1)1(1)x xAx B Cx D x x x x x x -+++=+++++++若不用待定系数法，可依次用多项式除法：若不用待定系数法，可依次用多项式除法：第一步，3222212(2)(3)11x x x x x x x x -++=-+++++；第二步，32222222132(2)(1)1(1)x x x x x x x x x x -+-+=+++++++于是，于是，32222222132(2)d d d (1)1(1)x x x x xx x x x x x x x -+-+=+++++++òòò其中右端第一个积分其中右端第一个积分22222231(21)71d(1)7d d d 1212121322x x x x x x x x x x x x x x -+-++==-++++++æöæö++ç÷ç÷èøèøòòòò217221ln(1)arctan 2233x x x +=++-×而第二个积分而第二个积分2222222222(2)(21)3d(1)1d d 3d (1)(1)(1)(1)x x x x xxx x x x x x x x x +++++==+++++++++òòòò2222113d (1)1322x x x x =-+++éùæöæöêú++ç÷ç÷êúèøèøëûò[套积分公式⒇] ⑸分母为一次因式与二次因式乘积的真分式的积分法例如，求22d ()()bx cx d x x a x px q ++-++ò时，可令时，可令 q x p x C x B a x Aq x p x a x d x c x b ++++-=++-++222))((然后根据恒等式然后根据恒等式22()()()bx cx d A x px q Bx C x a ++º++++-求出待定系数A 、B 和C . 于是，于是，22d ()()bx cx dx x a x px q ++-++ò2ln ||d Bx C A x a x x px q +=-+++ò (注意2xpx q ++没有实根没有实根,,即240p q -<)2.三角函数有理式的积分法所谓“三角函数有理式”，是指由常数和简单三角函数x sin 与x cos 经过有限次的有理运算经过有限次的有理运算((加、减、乘、除加、减、乘、除))得到的函数，记成)cos ,(sin x x R .下面介绍的是形如积分的是形如积分(sin ,cos )d R x x x ò的积分法的积分法..例如积分例如积分2cos d 2sin cos x x x x +ò，1d 2sin cos 1x x x -+ò，1d (0)cos x ab a b x ¹+ò等.实际上，我们在前面几节中曾多次遇到这种类型的积分我们在前面几节中曾多次遇到这种类型的积分..这里介绍的是一般方法这里介绍的是一般方法..你在做题时．．．．．，还是要具体问题具体分析．．．．．．．．．．．，未必就一定要用这里介绍的方法．．．．．．．．．．．．．．（因为一般情形下，这里介绍的方法要麻烦一些）方法要麻烦一些）. .令2tan xt =(称它为半角替换或万能替换称它为半角替换或万能替换))，则，则2222122tan12tan22sec 2tan22cos2tan22cos2sin2sin t t x x xx xx x x x +=+==== 22222222112tan12tan 1)2tan 1(2cos 2sin 2cos cos t t x x x x x x x +-=+-=-=-= t t t x d 12)arctan 2(d d 2+==于是，于是，(sin ,cos )d R x x xò2222212,d 111t t R t t t t-æö=ç÷+++èøò这样，三角函数有理式的积分就变成有理函数的积分三角函数有理式的积分就变成有理函数的积分..在有些情形下，像前面做过的那样，不必用半角替换，而用其它三角替换会更简单必用半角替换，而用其它三角替换会更简单..例如例如()i 当(sin ,cos )(sin ,cos )R x x R x x -=-时，令cos t x =； ()ii 当(sin ,cos )(sin ,cos )R x x R x x -=-时，令sin t x =； ()iii 当(sin ,cos )(sin ,cos )R x x R x x --=时，令tan t x =.习题1.求下面的原函数：⑴25d (3)x x x --ò； ⑵⑵325d (2)x x x --ò；⑶23354d (1)x x x x -+-ò； ⑷⑷3223242d 21x x x x x x -++-+ò. 答案：⑴323ln -+-x x；⑵2)2(2122-+--x x ；⑶2)1(1111ln 3-----x x x ； ⑷171ln 94232---++x x x x .2.求下面的原函数：求下面的原函数：⑴x x x x d )3)(2(73ò---； ⑵⑵x x x x d 2152ò-++； ⑶⑶x x x x x x d )2)(2(2342ò+---. 答案：⑴3ln 22ln -+-x x ；⑵1ln 22ln 3-++x x ；⑶2ln 252ln ln 21++-+x x x . 3.求下面的原函数：求下面的原函数：⑴x x x x x d )1)(2(23222ò++-+； ⑵⑵x x x x x d )32)(1(2ò+++； ⑶⑶x x x d 134ò+. 答案：⑴x x arctan )1ln(2-+；⑵21arctan 21)32ln(411ln 212++++++-x x x x ；⑶312arctan 311)1(ln 6121222--+-++x x x x x . 4.根据提示，请把下面的演算做到底：根据提示，请把下面的演算做到底：⑴tan 21d 2sin cos 1x t x x x æö=ç÷èø====-+ò⑵(cos )1d (2cos )sin t x x x x ======+ò⑶2(sin )cos d 2sin cos t x xx x x ======+ò⑷3(tan )3sin d sin cos t x xx x x======+ò答案：⑴22tan2tan ln21+x x ；⑵32)cos 1()cos 1()cos 2(ln 61x x x +-+；⑶12sin 1ln 222sin 1x x +--+；⑷÷÷øöççèæ---+-x x x x x x x sin 3sin cos 2arctan 31cos sin 1)cos (sin ln 612.。

几种特殊函数的积分

2 2
p p x px q x q , 2 4 p 令 x t 2
记 x 2 px q t 2 a 2 ,
则
Mx N Mt b,
p2 2 a q , 4
Mp b N , 2
Mx N 2 dx n ( x px q ) Mt b 2 dt 2 dt 2 n 2 n (t a ) (t a )
真分式化为部分分式之和的待定系数法
x3 x3 A B 例1 2 , x 5 x 6 ( x 2)( x 3) x 2 x 3
x 3 A( x 3) B( x 2), x 3 ( A B ) x ( 3 A 2 B ),
1 dx . 例4 求积分 2 x( x 1) 1 1 1 1 dx 解 2 2 dx x ( x 1) x ( x 1) x 1 1 1 1 dx dx dx 2 x ( x 1) x 1
1 ln x ln x 1 C. x 1
三、简单无理函数的积分
ax b 讨论类型 R( x, ax b ), R( x , ), cx e
n
n
解决方法作代换去掉根号.
1 1 x 例10 求积分 dx x x
解
1 x 2 1 x 令 t t , x x
1 sin x dx. 例9 求积分 sin 3 x sin x A B A B 解 sin A sin B 2 sin cos 2 2 1 sin x 1 sin x sin 3 x sin x dx 2 sin 2 x cos x dx 1 sin x dx 2 4 sin x cos x 1 1 1 1 dx dx 2 2 4 sin x cos x 4 cos x

有理函数积分法解决不定积分

有理函数积分法解决不定积分有理函数积分法是解决不定积分的一种重要方法。

它的思路是将被积函数化为有理函数的形式，再利用有理函数积分的技巧求解积分。

本文将从以下几个方面进行介绍：一、什么是有理函数有理函数是指可以表示为分子是多项式函数，分母是非零多项式函数的函数。

例如，$\dfrac{1}{x^2+1}$就是一个有理函数，它的分子是常数函数$1$，分母是$x^2+1$这个二次多项式函数。

二、有理函数积分法的框架有理函数积分法的框架是将被积函数拆分成基本有理函数之和的形式，即：$$ \frac{N(x)}{D(x)}=A(x)+\frac{R(x)}{S(x)} $$其中，$A(x)$是整式函数，$R(x)$和$S(x)$均为非零多项式函数，且$S(x)$的次数大于$R(x)$的次数。

$R(x)/S(x)$是真分式函数，可以用部分分式分解的方法化为基本有理函数之和的形式。

例如，对于$\dfrac{1}{x(x-2)}$这个被积函数，可以进行部分分式分解，得到：$$ \frac{1}{x(x-2)}=\frac{1}{2x}-\frac{1}{2(x-2)} $$这样，原来的被积函数就被化为了基本有理函数之和的形式。

三、基本有理函数的积分下面我们来介绍几种常见的基本有理函数的积分。

1. $\int \dfrac{1}{x-a}\mathrm{d}x=\ln|x-a|+C$，其中$a$为常数。

2. $\int \dfrac{1}{x^2-a^2}\mathrm{d}x=\frac{1}{2a}\ln\left|\frac{x-a}{x+a}\right|+C$，其中$a$为常数。

3. $\int\dfrac{1}{x^2+a^2}\mathrm{d}x=\frac{1}{a}\arctan\frac{x}{a}+C $，其中$a$为常数。

4. $\int \dfrac{1}{x^2-a^2}\mathrm{d}x=\frac{1}{2a}\ln\left|\frac{x+a}{x-a}\right|+C$，其中$a$为常数。

有理函数积分法范文

有理函数积分法范文一、有理函数的基本概念有理函数是指多项式函数与有理函数的商，即R(x)=P(x)/Q(x)，其中P(x)和Q(x)都是多项式函数，且Q(x)不等于零。

有理函数的特点是在有理函数定义域内，有理函数都是连续的。

有理函数有两类基本类型：真分式和带余商。

如果多项式P(x)的次数小于Q(x)的次数，即P(x)的次数是m，Q(x)的次数是n且m<n，则有理函数R(x)是一个真分式。

如果多项式P(x)的次数大于等于Q(x)的次数，即P(x)的次数是m，Q(x)的次数是n且m≥n，则有理函数R(x)是带余商。

二、有理函数积分的基本方法1.真分式的积分如果R(x)是一个真分式，即R(x)=P(x)/Q(x)，其中P(x)的次数小于Q(x)的次数，那么有理函数积分的方法如下：(1) 当Q(x)的次数是1时，即Q(x) = x-a，则有理函数积分公式为：∫R(x)dx = ln，x-a，+C。

(2) 当Q(x)的次数大于1时，即Q(x) = (x-a)^m，其中m>1，那么有理函数积分公式为：∫R(x)dx = A1ln，x-a， + A2ln，x-a，^2 + …+ Amln，x-a，^m + C，其中A1，A2，…，Am为常数。

2.带余商的积分如果R(x)是一个带余商，即R(x)=P(x)/Q(x)，其中P(x)的次数大于等于Q(x)的次数，那么有理函数积分的方法如下：(1) 当P(x)的次数是Q(x)的次数加上1时，即P(x)的次数是n+1，Q(x)的次数是n，那么有理函数积分公式为：∫R(x)dx =∫(S(x)+P(x)/Q(x))dx = S(x) + ∫P(x)/Q(x)dx其中S(x)是带余商的部分。

(2)当P(x)的次数大于Q(x)的次数加上1时，即P(x)的次数大于n+1，Q(x)的次数是n，那么可以使用多项式除法将有理函数R(x)分解成S(x)和Q(x)的部分分式之和，然后分别对每个部分分式进行积分。

【考研数学】高数有理分式积分法

第四节1•基本积分法: 直接积分法;换元积分法;分部积分法•初等函数求导初等函数积分一、有理函数的积分二、可化为有理函数的积分举例有理函数的积分本节内容:第四章n1m>时,为真分式为假分式;n简单分式:形如3456789解:(1) 用拼凑法111-)1(--x x10112C +42-=B已知1⎡1=1213原式x x 22⎰+=)22(21+x 如何求变形方法同例3, 并利用上一节课件例1415⎰+++=x x x x x d 4552243⎰++x x 52416原式⎰+=x x 2(2)22(2++x x172arctan2211xx -=21-221 ln 21-+x x 21++x x C+比较系数定a , b , c , d . 得化为部分分式. 即令比较系数定A , B , C , D..此解法较繁18xcos-x sinxA=xsin)(cos++⎰x(sinR,20212223⎰=原式xxd 2cos 1⎰=tan d 12425xb cos +⎢⎣⎡2+b a a sin 22ba +x ba +tan(12226=Ct +-31C x +cos 22728uu d 1)1(32⎰+-=29为去掉被积函数分母中的根式6 ,t x =令30t t td )1(222--内容小结31 1. 可积函数的特殊类型有理函数分解多项式及部分分式之和三角函数有理式万能代换简单无理函数三角代换根式代换2.特殊类型的积分按上述方法虽然可以积出,但不一定要注意综合使用基本积分法,简便计算.简便,32:1.⎰-=233()(d 31a x 原式a x a x a +--=33333ln 61ax ax a -+33333ln 61作业33P218 1-2434⎰11t551t -=t -d x =511113x x +35前式令arctan21u=; 后式配元13cos x+cos x2tanxu =2d u ⋅1。

有理函数积分法

有理函数积分法
有理函数积分法（Rational Function Integration Method）是指利用N个数有关的定积分的方法，由于所运用的有理函数特性它可以进行快速的求解。

有理函数积分法的基本思想是通过将积分根据要求积分区间（即要进行积分的函数那部分）划分成多个子区间并将积分分解成多个有理函数求解，再把多个有理函数的结果加在一起得到最终的积分结果。

有理函数积分法的流程有如下步骤：
首先，根据需要，将要求积分的函数的这部分划分成多个子区间，以便于分解成多个有理函数；其次，将每个子区间内的有理函数求解；然后，将每个子区间内的有理函数求解出来的结果相加得到最终的结果；最后，根据最终的结果检查，以确保结果是正确的。

有理函数积分法的优点是可以迅速求解定积分，但其也存在一定的缺点，例如它对函数的区间分解要求较高，而且需要有较好的数学模型和计算能力。

因此，当积分难度较大时，有理函数积分法的常规方法得不到较好的解决方案。

有理函数积分

万能代换
t 的有理函数的积分
x x 2 tan 2 tan x x 2 , 2 sin x 2sin cos 2 x 2 2 2 x 1 tan sec 2 2 2 x 2 x 1 tan 1 tan 2 x 2 x 2 2, cos x cos sin 2 2 2 x 2 x 1 tan sec 2 2 x x 2arctan u （万能置换公式）令 u tan 2
Mx N 3. 2 dx x px q Mx N 4. 2 dx n ( x p x q)
变分子为
M 2
(2 x p)分 2 n ( x px q )
2 p p 2 x px q x q , 2 4 2

x dx 使用凑微分法比较简单 3 x 1
尽量使分母简单——降幂、拆项、同乘等
2
基本思路
化部分分式，写成分项积分可考虑引入变量代换
例2. 求积分
解：

1 dx . 2 x( x 1)

1 1 1 1 dx dx 2 2 x( x 1) x 1 x ( x 1)
2 2u 2 1 u sin x , cos x du , dx 2 2 2 1 u 1 u 1 u
2u 1 u 2 2 R(sin x ,cos x ) dx R 1 u2 , 1 u2 1 u2 du.
1 sin x dx . 例8. 求 sin x(1 cos x) x 解: 令 t tan , 则 2 x cos x x 2 sin 2 2 tan 2t 2 2 sin x 2 x cos 2 x 1 tan 2 x 1 t 2 sin 2 2 2