第三章机电系统数学模型
电机数学模型(完整版)

电机数学模型以二相导通星形三相六状态为例,分析BLDC的数学模型及电磁转矩等特性。
为了便于分析,假定:a)三相绕组完全对称,气隙磁场为方波,定子电流、转子磁场分布皆对称;b)忽略齿槽、换相过程和电枢反应等的影响;c)电枢绕组在定子内表面均匀连续分布;d)磁路不饱和,不计涡流和磁滞损耗。
(1)为定子相绕组电压(V);为定子相绕组电流(A);为定子相绕。
(2)(3)(4)图.无刷直流电机的等效电路无刷直流电机的电磁转矩方程与普通直流电动机相似,其电磁转矩大小与磁通和电流幅值成正比(5)所以控制逆变器输出方波电流的幅值即可以控制BLDC电机的转矩。
为产生恒定的电磁转矩,要求定子电流为方波,反电动势为梯形波,且在每半个周期内,方波电流的持续时间为120°电角度,梯形波反电动势的平顶部分也为120°电角度,两者应严格同步。
由于在任何时刻,定子只有两相导通,则:电磁功率可表示为:(6)电磁转矩又可表示为:(7)无刷直流电机的运动方程为:(8)其中为电磁转矩;为负载转矩;B为阻尼系数;为电机机械转速;J为电机的转动惯量。
传递函数:无刷直流电机的运行特性和传统直流电机基本相同,其动态结构图可以采用直流电机通用的动态结式中:K1K2,T m为电机时间常数,,基于BLDC系统模型的建立在提出在(FFT)模块化,在Matlab/Simulink建立独立的功能模块:BLDC本体模块、电流滞环控制模块、速度控制模块、参考电流模块、转矩计算模块和电压逆变模块,对这些功能模块进行有机整合,即可搭建出无刷直流电机系统的仿真模型。
在建模过程中,梯形波反电动势的求取方法一直是较难解决的问题[27,28],本文采用分段线性法成功地化解了这一难点,克服了建模方法存在的不足。
Matlab6.5针对电气传动控制领域所设计的工具箱SimPowerSystemToolbox2.3已提供了PMSM的电机模型,但没有给出BLDC的电机模型。
【DOC】第3章机电一体化技术与系统中微型计算机控制系统及接

第3章:机电一体化技术与系统中微型计算机控制系统及接口设计 3.1 控制系统的一般设计思路3.1.1专用与通用、硬件与软件的权衡与抉择1. 专用与通用的抉择 专用控制系统:适合于大批量生产的而且较成熟的机电一体化产品。
通用控制系统:适合还在不断改进,结构还不十分稳定的产品。
2. 硬件与软件的权衡根据经济性和可靠性的标准权衡决定。
例:分立元件组成硬件------软件 利用LSI 芯片组成电路-----软件3.1.2 控制系统的一般设计思路 设计步骤为:确定系统整体控制方案;确定控制算法;选用微型计算机;系统总体设计;软件设计等。
1、确定系统整体控制方案(1)应了解被控对象的控制要求,构思控制系统的整体方案。
(2)考虑执行元件采用何种方式。
(3)要考虑是否有特殊控制要求。
(4)考虑微机在整个控制系统中的作用,是设定计算、直接控制还是数据处理,微机应承担哪些任务,为完成这些任务,微机应具备哪些功能,需要哪些输入/输出通道、配备哪些外围设备。
(5)应初步估算其成本。
2、确定控制算法建立该系统的数学模型,确定其控制算法。
数学模型:就是系统动态特性的数学表达式。
它反映了系统输入、内部状态和输出之间的数量和逻辑关系。
控制算法:所谓计算机控制,就是按照规定的控制算法进行控制,因此,控制算法的正确与否直接影响控制系统的品质,甚至决定整个系统的成败。
例如:机床控制中常使用的逐点比较法的控制算法和数字积分法的控制算法;直线算法:a a xy yx F -= 或K x y T T ee Y X==∆∆ 圆弧算法:222R Y X F i i i -+= 或yxT T Y X =∆∆ 直接数字控制系统中常用的PID 调节的控制算法;位置数字伺服系统中常用的实现最少拍控制的控制算法;另外,还有各种最优控制的控制算法、随机控制和自适应控制的控制算法。
3、选择微型计算机 (1)较完善的中断系统 (2)足够的存储容量(3)完备的输入/输出通道和实时时钟(4)特殊要求:字长、速度、指令4、系统总体设计设计中主要考虑硬件与软件功能的分配与协调、接口设计、通道设计、操作控制台设计、可靠性设计等问题。
机电一体化系统设计第三章计算流体力学(CFD)简介

4
数值求解
基于离散和数值方法求解Navier-Stokes方程组。
5
后处理
分析和可视化模拟结果,评估流体行为和性能。
CFD工具的选择和使用
商业软件
流行的商业CFD软件包,如ANSYS Fluent和OpenFOAM。
开源软件
开放源代码的CFD软件,如SU2和OpenFOAM。
使用技巧
合理选择工具,灵活使用模拟参数和求解方法,优化模型和网格。
机电一体化系统设计第三 章计算流体力学(CFD)简 介
本章介绍机电一体化系统设计第三章,包括计算流体力学的定义、应用范围、 模拟步骤、工具选择和使用、分析的意义和价值,以及CFD的未来发展趋势。
计算流体力学的定义
计算流体力学(CFD)是一种利用数值方法进行流体动力学问题求解的数值 模拟技术。它可以模拟流体的流动行为和相应的物理现象。
CFD的应用范围
CFD广泛应用于工程领域,如航空航天、汽车、能源、建筑等。它可以用于 流体流动分析、热传递和传质分析、气动性能仿真等方面。
CFD模拟的步骤
1
几何建模
使用CAD软件创建物体的几何模型。
2
网格划分
将几何模型划分为小的有限体积或有限元网。
3
物理建模
定义边界条件和流体参数,如速度、压力和温度。
CFD分析的意义和价值
1 性能评估
通过模拟和分析,可以评估设计的性能并提出改进意见。
2 节省成本
CFD分析可以在实际制造前模拟和优化设计,以降低产品开发和测试的成本。
3 提高效率
通过CFD优化流体系统,可以提高流体传输效率和能源利用效率。
CFD的未来发展趋势
CFD在大数据、人工智能和高性能计算的支持下,将在精度、效率和应用范 围上都取得更大突破。同时,深度学习和自动化技术将进一步改进CFD模拟 和预测的准确性。
机械控制工程理论基础课程教学大纲

“机械控制工程理论基础”课程教学大纲英文名称:Elements of Mechanical Control Theory课程编号:MACH3435学时:56(理论学时:40 实验学时:16 课外学时:20)学分:3适用对象:机械类、动力类本科生先修课程:高等数学,理论力学,电工电子技术使用教材及参考书:[1] 董霞、陈康宁、李天石.机械控制理论基础.西安交通大学出版社,2005.ISBN 7-5605-2041-3.[2] 董景新等.控制工程基础(第二版).清华大学出版社,2003.ISBN: 9787302063872[3] [美] Katsuhiko Ogata著,卢伯英、于海勋译.现代控制工程(第三版).电子工业出版社,2000.ISBN 7-5053-5395-0/TN.1247.一、课程性质和目的性质:专业基础目的:1.培养学生从动态和系统的角度建立机械系统数学模型的能力;2.培养学生对机械控制系统进行动态分析的能力;3.培养学生对机械控制系统的设计能力和综合能力;4.培养学生使用计算机仿真能力;5.培养学生系统分析能力和综合能力。
二、课程内容简介机械控制理论是研究“控制论”在“机械工程”中应用的科学,本课程主要介绍机械控制工程的基本概念、机电系统数学模型的建立、机电控制系统的时域分析和频域分析、机电控制系统的稳定性分析和机电控制系统的设计和校正。
通过课程教学和实验,培养学生对机电控制系统进行动态分析的能力和综合能力。
三、教学基本要求1.了解机电系统的数学模型并掌握基本的建模方法;2.掌握机电控制系统时域分析方法;3. 掌握机电控制系统的频域分析方法;4. 掌握机电控制系统稳定性分析方法;5. 初步掌握机械控制系统设计和校正方法。
四、教学内容及安排第一章:绪论1.理解“机械工程控制”的基本含义,本课程的特点,以及学习本课程的目的与任务;2.初步建立系统、反馈、控制、闭环系统等的基本概念。
电机数学模型(完整版)

电机数教模型之阳早格格创做以二相导通星形三相六状态为例,分解BLDC的数教模型及电磁转矩等个性.为了便于分解,假定:a)三相绕组真足对于称,气隙磁场为圆波,定子电流、转子磁场分散皆对于称;b)忽略齿槽、换相历程战电枢反应等的效率;c)电枢绕组正在定子内表面匀称连绝分散;d)磁路不鼓战,不计涡流战磁滞耗费.则三相绕组的电压仄稳圆程可表示为:(1)式中:为定子相绕组电压(V);为定子相绕组电流(A);为定子相绕组电动势(V);L为每相绕组的自感(H);M为每相绕组间的互感(H);p为微分算子p=d/dt.三相绕组为星形连交,且不中线,则有(2)(3)得到最后电压圆程:(4)无刷曲流电机的电磁转矩圆程与一般曲流电效果相似,其电磁转矩大小与磁通战电流幅值成正比(5)所以统制顺变器输出圆波电流的幅值即不妨统制BLDC 电机的转矩.为爆收恒定的电磁转矩,央供定子电流为圆波,反电动势为梯形波,且正在每半个周期内,圆波电流的持绝时间为120°电角度,梯形波反电动势的仄顶部分也为120°电角度,二者应庄重共步.由于正在所有时刻,定子惟有二相导通,则:电磁功率可表示为:(6)电磁转矩又可表示为:(7)无刷曲流电机的疏通圆程为:(8)其中为电磁转矩;为背载转矩;B为阻僧系数;为电机板滞转速;J为电机的转化惯量.传播函数:无刷曲流电机的运止个性战保守曲流电机基本相共,其动背结构图不妨采与曲流电机通用的动背结构图,如图所示:由无刷曲流电机动背结构图可供得其传播函数为:式中:K1为电动势传播系数,,Ce 为电动势系数;K2为转矩传播函数,,R 为电效果内阻,Ct 为转矩系数;Tm 为电机时间常数,,G 为转子沉量,D 为转子曲径.鉴于MATLAB的BLDC系统模型的建坐正在Matlab中举止BLDC建模仿真要收的钻研已受到广大关注,已有提出采与节面电流法对于电机统制系统举止分解,通过列写m文献,建坐BLDC仿真模型,那种要收真量上是一种真足分解法,果而那一模型前提上建改统制算法大概增加、简略关环便隐得很不便当;为了克服那一缺累,提出正在Matlab/Simulink中构制独力的功能模块,通过模块拉拢举止BLDC建模,那一要收可瞅性佳,正在本有建模的前提上增加、简略关环大概改变统制战术皆格外便利,但是该要收采与赶快傅坐叶变更(FFT)要收供与反电动势,使得仿真速度受节制.本文提出了一种新式的BLDC 建模要收,将统制单元模块化,正在Matlab/Simulink建坐独力的功能模块:BLDC本量模块、电流滞环统制模块、速度统制模块、参照电流模块、转矩估计模块战电压顺变模块,对于那些功能模块举止有机调整,即可拆建出无刷曲流电机系统的仿真模型.正在建模历程中,梯形波反电动势的供与要收背去是较深刻决的问题[27,28],本文采与分段线性法乐成天弥合了那一易面,克服了建模要收存留的缺累. Matlab6.5针对于电气传动统制范围所安排的工具箱SimPowerSystemToolbox2.3已提供了PMSM的电机模型,但是不给出BLDC的电机模型.果此,本文正在分解无刷曲流电机数教模型的前提上,借帮于Matlab强盛的仿真建模本收,正在Matlab/Simulink中建坐了BLDC统制系统的仿真模型.BLDC建模仿真系统采与单关环统制规划:下即为BLDC建模的真足统制框图,其中主要包罗:BLDC 本量模块、电流滞环统制模块、速度统制模块、参照电流模块、转矩估计模块战电压顺变模块.BLDC本量结构(1)BLDCM本量模块正在所有统制系统的仿真模型中,BLDCM本量模块是最要害的部分,该模块根据BLDC电压圆程式(4)供与BLDC三相相电流,结构框图如图所示正在所有统制系统的仿真模型中,BLDC本量模块是最要害的部分,该模块根据BLDC电压圆程式(24)供与BLDC三相相电流,而要赢得三相相电流旗号ia,ib,ic,必须最先供得三差异电动势旗号ea,eb,ec统制框图如图211所示.而BLDC建模历程中,梯形波反电动势的供与要收背去是较深刻决的问题,反电动势波形不睬念会制成转矩脉动删大、相电流波形不睬念等问题,宽沉时会引导换相波折,电机得控.果此,赢得理念的反电动势波形是BLDC仿真建模的关键问题之一.本文采与了分段线性法,如图212所示,将一个运止周期0°~360°分为6个阶段,每60°为一个换相阶段,每一相的每一个运止阶段皆可用一段曲线举止表示,根据某一时刻的转子位子战转速旗号,决定该时刻各相所处的运奇迹态,通过曲线圆程即可供得反电动势波形.分段线性法简朴易止,且粗度较下,不妨较佳的谦脚建模仿果然安排央供.果而,本文采与分段线性法建坐梯形波反电动势波形.理念情况下,二相导通星形三相六状态的BLDC定子三差异电动势的波形如图212所示.图中,根据转子位子将运止周期分为6个阶段:0~π/3,π/3~2π/3,2π/3~π,π~4π/3,4π/3~5π/3,5π/3~2π.以第一阶段0~π/3为例,A差异电动势处于正背最大值Em,B差异电动势处于背背最大值Em,C差异电动势处于换相阶段,由正的最大值Em沿斜线程序变更到背的最大值Em.根据转子位子战转速旗号,便不妨供出各差异电动势变更轨迹的曲线圆程,其余5个阶段,也是如许.据此程序,不妨推得转子位子战反电动势之间的线性关系,如表21所示,进而采与分段线性法,办理了正在BLDC本量模块中梯形波反电动势的供与问题.转子位子战反电动势之间的线性关系表表中:K为反电动势系数(V/(r/min),pos为角度旗号,w为转速旗号,转数per=fix(pos/(2*pi))*2*pi,fix函数是真止与整功能.根据上式,用M文献编写反电势系数的S函数如下:反电动势 S 函数(emf.m)%============================================ =============%BLDCM模型中反电动势函数%============================================ =============function [sys,x0,str,ts] =emf(t,x,u,flag)switch flagcase 0, %初初化树坐[sys,x0,str,ts]=mdlInitializeSizes;case 3, %输出量估计sys = mdlOutputs(t,x,u);case {1,2,4,9} %已定义标记sys = [];otherwise%过得处理error(['unhandled flag = ',num2str(flag)]);end%============================================ =============%mdlInitializeSizes 举止初初化,树坐系统变量的大小%============================================ =============function [sys,x0,str,ts]=mdlInitializeSizes()sizes = simsizes; %与系统默认树坐sizes.NumContStates = 0;sizes.NumDiscStates = 0;sizes.NumOutputs = 3;sizes.NumInputs = 2;sizes.DirFeedthrough = 1;sizes.NumSampleTimes = 1;sys = simsizes(sizes);x0 = [];str = [];ts = [1 0];%============================================ =============%mdlOutputs 估计系统输出%============================================ =============function sys=mdlOutputs(t,x,u)global k;global Pos;global w;k=0.060; % V/(r/min)反电动势系数w=u(1); % 转速(rad/s)Pos=u(2); % 角度(rad)if Pos>=0 & Pos<=pi/3sys=[k*w,k*w,k*w*((Pos)/(pi/6)+1)];elseif Pos>=pi/3 & Pos<=2*pi/3sys=[k*w,k*w*((Pospi/3)/(pi/6)1),k*w];elseif Pos>=2*pi/3 & Pos<=pisys=[k*w*((2*pi/3Pos)/(pi/6)+1),k*w,k*w];elseif Pos>=pi & Pos<=4*pi/3sys=[k*w,k*w,k*w*((Pospi)/(pi/6)1)];elseif Pos>=4*pi/3 & Pos<=5*pi/3sys=[k*w,k*w*((4*pi/3Pos)/(pi/6)+1),k*w];else Pos>=5*pi/3 & Pos<=2*pisys=[k*w*((Pos5*pi/3)/(pi/6)1),k*w,k*w];end转矩估计模块根据BLDC数教模型中的电磁转矩圆程式,不妨建坐图5.7所示的转矩估计模块,模块输进为三相相电流与三差异电动势,通过加、乘模块即可供得电磁转矩旗号Te .转矩估计模块结构框图及其启拆形式转速估计模块根据疏通圆程式(2.4),由电磁转矩、背载转矩以及摩揩转矩,通过加乘、积分关节即可得到转速旗号,供得的转速旗号通过积分便可得到电机转角旗号,如图转速估计模块结构框图及其启拆形式电流滞环统制模块正在那个仿真模块中采与滞环统制本理去真止电流的安排,使得本量电流随跟定电流的变更.模块结构框图如图5.10所示[40],输进为三相参照电流战三相本量电流,输出为PWM顺变器统制旗号.电流滞环统制模块结构框图及其启拆参照电流模块参照电流模块的效率是根据电流幅值旗号Is战位子旗号给出三相参照电流,输出的三相参照电流曲交输进电流滞环统制模块,用于与本量电流比较举止电流滞环统制.转子位子战三相参照电流之间的对于应关系如表所示,参照电流模块的那一功能可通过S函数编程真止,步调如下参照电流 S 函数(mod.m)function [sys,x0,str,ts] =mod(t,x,u,flag)switch flagcase 0,[sys,x0,str,ts]=mdlInitializeSizes;case 3, sys = mdlOutputs(t,x,u);case 2, sys = [];case 9, sys = [];otherwiseerror(['unhandled flag = ',num2str(flag)]);endfunction [sys,x0,str,ts]=mdlInitializeSizes()sizes = simsizes;sizes.NumContStates = 0; sizes.NumDiscStates = 0; sizes.NumOutputs = 1; sizes.NumInputs = 1; sizes.DirFeedthrough = 1; sizes.NumSampleTimes = 1; sys = simsizes(sizes);x0 = [];str = [];ts = [1 0];function sys=mdlOutputs(t,x,u) global Pos;global w;global Theta;Theta=u;b=fix(Theta/(2*pi));%与整if Theta==0sys=0;else if (Theta/(2*pi))==bsys=2*pi;elsesys=Thetab*2*pi;endendPos=sys; %位子表5.2 转子位子战三相参照电流之间的对于应关系表5.2.5 位子估计模块电机转角旗号到电机位子旗号的变更可通过S函数编程真止,步调如下位子估计 S 函数(is.m)function [sys,x0,str,ts] =is(t,x,u,flag)switch flagcase 0,[sys,x0,str,ts]=mdlInitializeSizes;case 3, sys = mdlOutputs(t,x,u);case 2, sys = [];case 9,sys = [];otherwiseerror(['unhandled flag = ',num2str(flag)]); endfunction [sys,x0,str,ts]=mdlInitializeSizes() sizes = simsizes;sizes.NumContStates = 0;sizes.NumDiscStates = 0;sizes.NumOutputs = 3;sizes.NumInputs = 2;sizes.DirFeedthrough = 1;sizes.NumSampleTimes = 1;sys = simsizes(sizes);x0 = [];str = [];ts = [1 0];function sys=mdlOutputs(t,x,u)global Is;global Pos;Is=u(1); %电流Pos=u(2);%位子if Pos>=0& Pos<=pi/3sys=[Is,Is,0];elseif Pos>=pi/3& Pos<=2*pi/3sys=[Is,0,Is];elseif Pos>=2*pi/3& Pos<=pisys=[0,Is,Is];elseif Pos>=pi& Pos<=4*pi/3sys=[Is,Is,0];elseif Pos>=4*pi/3& Pos<=5*pi/3sys=[Is,0,Is];else Pos>=5*pi/3& Pos<=2*pisys=[0,Is,Is];end5.2.6 电压顺变器模块顺变器对于BLDC去道,最先是功率变更拆置,也便是电子换背器,每一个桥臂上的一个功率器件相称于曲流电效果的一个板滞换背器,还共时兼有PWM电流安排器功能.对于顺变器的建模,本文采与Simulink的SimPowerSystem工具箱提供的三相齐桥IGBT模块.由于正在Matlab新版本(如Matlab7.0)中SimPowerSystem工具箱战Simulink工具箱不不妨随便贯串的,中间必须加上受控电压源(大概者受控电压源、电压表、电流表).本文给IGBT的A、B、C三相加三个电压表,输出的Simulink旗号不妨与BLDC曲交连交,如图5.11所示.顺变器根据电流统制模块所统制PWM旗号,程序导通战关断,爆收圆波电流输出.电压顺变器模块结构框图及其启拆鉴于Matlab/Simulink建坐了BLDC统制系统的仿真模型,并对于该模型举止了BLDC单关环统制系统的仿真.仿真中,BLDC电机参数树坐为:定子相绕组电阻R=1Ω,定子相绕组自感L=0.02H,互感M=0.061H,转化惯量J=0.005kg·m2,阻僧系数B= 0.0002N·m·s/rad,额定转速n=1000r/min,极对于数p=1,220V曲流电源供电.总体模型:存留问题:仿真速度缓,且示波器值均为0。
机电一体化系统设计第三章

39
第3章 控制系统设计
(3) 离散系统的时间响应
图3.37离散系统的时间响应
40
第3章 控制系统设计
3.5.4 离散系统的性能分析
图3.38平面的映射关系
Bem N1 Bm N BL 2
2
J em
N1 Jm N JL 2
c (s) r ( s ) R B s (1 T s )(1 T s ) K K s K AK N 1 a em a em b i s i
图3.26 理想采样开关后所得的采样脉冲序列 18
第3章 控制系统设计
19
第3章 控制系统设计
20
第3章 控制系统设计
(2)信号采样的数学描述 1)脉冲函数的采样性质 ●脉冲函数…如图所示,其数学表达式为
……
…………………………………………………… (3.59)
●脉冲强度
……………………………………………………(3.60)
(3)保持器 保持器:将离散的采样信号恢复到原连续信号的装置。 理想的保持器如图3.28所示频谱的低通滤波器。
零阶保持器:将前一个采样时刻的采 样值………保持到下一个采样时刻 ………,如图3.29所示。
3.28 理想保持器的频谱
3.29应用零阶保持器恢复的信号
31
第3章 控制系统设计
零阶保持器:将前一个采样 时刻的采样值………保持到 下一个采样时刻……..…,如 图3.29所示。零阶保持器的时 域函数: …………………………(3.71) ………. 零阶保持器的传递函数 …………………………(3.73) ……… 零阶保持器的频谱特性如图 所示。
第3章 控制系统设计
1. 直流电动机
电机数学模型(完整版)

机电数学模型之迟辟智美创作以二相导通星形三相六状态为例,分析BLDC的数学模型及电磁转矩等特性.为了便于分析,假定:a)三相绕组完全对称,气隙磁场为方波,定子电流、转子磁场分布皆对称;b)忽略齿槽、换相过程和电枢反应等的影响;c)电枢绕组在定子内概况均匀连续分布;d)磁路不饱和,不计涡流和磁滞损耗.则三相绕组的电压平衡方程可暗示为:(1)式中:为定子相绕组电压(V);为定子相绕组电流(A);为定子相绕组电动势(V);L为每相绕组的自感(H);M为每相绕组间的互感(H);p为微分算子p=d/dt.三相绕组为星形连接,且没有中线,则有(2)(3)获得最终电压方程:(4)无刷直流机电的电磁转矩方程与普通直流电念头相似,其电磁转矩年夜小与磁通和电流幅值成正比(5)所以控制逆变器输出方波电流的幅值即可以控制BLDC 机电的转矩.为发生恒定的电磁转矩,要求定子电流为方波,反电动势为梯形波,且在每半个周期内,方波电流的继续时间为120°电角度,梯形波反电动势的平顶部份也为120°电角度,两者应严格同步.由于在任何时刻,定子只有两相导通,则:电磁功率可暗示为:(6)电磁转矩又可暗示为:(7)无刷直流机电的运动方程为:(8)其中为电磁转矩;为负载转矩;B为阻尼系数;为机电机械转速;J为机电的转动惯量.传递函数:无刷直流机电的运行特性和传统直流机电基秘闻同,其静态结构图可以采纳直流机电通用的静态结构图,如图所示:由无刷直流机电静态结构图可求得其传递函数为:式中:K1为电动势传递系数,,Ce 为电动势系数;K2为转矩传递函数,,R 为电念头内阻,Ct 为转矩系数;Tm 为机电时间常数,,G 为转子重量,D 为转子直径.基于MATLAB的BLDC系统模型的建立在Matlab中进行BLDC建模仿真方法的研究已受到广泛关注,已有提出采纳节点电流法对机电控制系统进行分析,通过列写m文件,建立BLDC仿真模型,这种方法实质上是一种整体分析法,因而这一模型基础上修改控制算法或添加、删除闭环就显得很不方便;为了克服这一缺乏,提出在Matlab/Simulink中构造自力的功能模块,通过模块组合进行BLDC建模,这一方法可观性好,在原有建模的基础上添加、删除闭环或改变控制战略都十分便捷,但该方法采纳快速傅立叶变换(FFT)方法求取反电动势,使得仿真速度受限制.本文提出了一种新型的BLDC建模方法,将控制单位模块化,在Matlab/Simulink建立自力的功能模块:BLDC本体模块、电流滞环控制模块、速度控制模块、参考电流模块、转矩计算模块和电压逆变模块,对这些功能模块进行有机整合,即可搭建出无刷直流机电系统的仿真模型.在建模过程中,梯形波反电动势的求取方法一直是较难解决的问题[27,28],本文采纳分段线性法胜利地化解了这一难点,克服了建模方法存在的缺乏.Matlab6.5针对电气传动控制领域所设计的工具箱SimPowerSystemToolbox2.3已提供了PMSM的机电模型,但没有给出BLDC的机电模型.因此,本文在分析无刷直流机电数学模型的基础上,借助于Matlab强年夜的仿真建模能力,在Matlab/Simulink中建立了BLDC控制系统的仿真模型.BLDC建模仿真系统采纳双闭环控制方案:下即为BLDC建模的整体控制框图,其中主要包括:BLDC 本体模块、电流滞环控制模块、速度控制模块、参考电流模块、转矩计算模块和电压逆变模块.BLDC本体结构(1)BLDCM本体模块在整个控制系统的仿真模型中,BLDCM本体模块是最重要的部份,该模块根据BLDC电压方程式(4)求取BLDC三相相电流,结构框图如图所示在整个控制系统的仿真模型中,BLDC本体模块是最重要的部份,该模块根据BLDC电压方程式(24)求取BLDC三相相电流,而要获得三相相电流信号ia,ib,ic,必需首先求得三相反电动势信号ea,eb,ec控制框图如图211所示.而BLDC建模过程中,梯形波反电动势的求取方法一直是较难解决的问题,反电动势波形不理想会造成转矩脉动增年夜、相电流波形不理想等问题,严重时会招致换相失败,机电失控.因此,获得理想的反电动势波形是BLDC仿真建模的关键问题之一.本文采纳了分段线性法,如图212所示,将一个运行周期0°~360°分为6个阶段,每60°为一个换相阶段,每一相的每一个运行阶段都可用一段直线进行暗示,根据某一时刻的转子位置和转速信号,确定该时刻各相所处的运行状态,通过直线方程即可求得反电动势波形.分段线性法简单易行,且精度较高,能够较好的满足建模仿真的设计要求.因而,本文采纳分段线性法建立梯形波反电动势波形.理想情况下,二相导通星形三相六状态的BLDC定子三相反电动势的波形如图212所示.图中,根据转子位置将运行周期分为6个阶段:0~π/3,π/3~2π/3,2π/3~π,π~4π/3,4π/3~5π/3,5π/3~2π.以第一阶段0~π/3为例,A相反电动势处于正向最年夜值Em,B相反电动势处于负向最年夜值Em,C相反电动势处于换相阶段,由正的最年夜值Em沿斜线规律变动到负的最年夜值Em.根据转子位置和转速信号,就可以求出各相反电动势变动轨迹的直线方程,其它5个阶段,也是如此.据此规律,可以推得转子位置和反电动势之间的线性关系,如表21所示,从而采纳分段线性法,解决了在BLDC本体模块中梯形波反电动势的求取问题.转子位置和反电动势之间的线性关系表表中:K为反电动势系数(V/(r/min),pos为角度信号,w为转速信号,转数per=fix(pos/(2*pi))*2*pi,fix函数是实现取整功能.根据上式,用M文件编写反电势系数的S函数如下:反电动势 S 函数(emf.m)%============================================ =============%BLDCM模型中反电动势函数%============================================ =============function [sys,x0,str,ts] =emf(t,x,u,flag)switch flagcase 0, %初始化设置[sys,x0,str,ts]=mdlInitializeSizes;case 3, %输出量计算sys = mdlOutputs(t,x,u);case {1,2,4,9} %未界说标识表记标帜sys = [];otherwise%毛病处置error(['unhandled flag = ',num2str(flag)]);end%============================================ =============%mdlInitializeSizes 进行初始化,设置系统变量的年夜小%============================================ =============function [sys,x0,str,ts]=mdlInitializeSizes()sizes = simsizes; %取系统默认设置sizes.NumContStates = 0;sizes.NumDiscStates = 0;sizes.NumOutputs = 3;sizes.NumInputs = 2;sizes.DirFeedthrough = 1;sizes.NumSampleTimes = 1;sys = simsizes(sizes);x0 = [];str = [];ts = [1 0];%============================================ =============%mdlOutputs 计算系统输出%============================================ =============function sys=mdlOutputs(t,x,u)global k;global Pos;global w;k=0.060; % V/(r/min)反电动势系数w=u(1); % 转速(rad/s)Pos=u(2); % 角度(rad)if Pos>=0 & Pos<=pi/3sys=[k*w,k*w,k*w*((Pos)/(pi/6)+1)];elseif Pos>=pi/3 & Pos<=2*pi/3sys=[k*w,k*w*((Pospi/3)/(pi/6)1),k*w];elseif Pos>=2*pi/3 & Pos<=pisys=[k*w*((2*pi/3Pos)/(pi/6)+1),k*w,k*w];elseif Pos>=pi & Pos<=4*pi/3sys=[k*w,k*w,k*w*((Pospi)/(pi/6)1)];elseif Pos>=4*pi/3 & Pos<=5*pi/3sys=[k*w,k*w*((4*pi/3Pos)/(pi/6)+1),k*w];else Pos>=5*pi/3 & Pos<=2*pisys=[k*w*((Pos5*pi/3)/(pi/6)1),k*w,k*w];end转矩计算模块根据BLDC数学模型中的电磁转矩方程式,可以建立图5.7所示的转矩计算模块,模块输入为三相相电流与三相反电动势,通过加、乘模块即可求得电磁转矩信号Te .转矩计算模块结构框图及其封装形式转速计算模块根据运动方程式(2.4),由电磁转矩、负载转矩以及摩擦转矩,通过加乘、积分环节即可获得转速信号,求得的转速信号经过积分就可获得机电转角信号,如图转速计算模块结构框图及其封装形式电流滞环控制模块在这个仿真模块中采纳滞环控制原理来实现电流的调节,使得实际电流随跟定电流的变动.模块结构框图如图5.10所示[40],输入为三相参考电流和三相实际电流,输出为PWM逆变器控制信号.电流滞环控制模块结构框图及其封装参考电流模块参考电流模块的作用是根据电流幅值信号Is和位置信号给出三相参考电流,输出的三相参考电流直接输入电流滞环控制模块,用于与实际电流比力进行电流滞环控制.转子位置和三相参考电流之间的对应关系如表所示,参考电流模块的这一功能可通过S函数编程实现,法式如下参考电流 S 函数(mod.m)function [sys,x0,str,ts] =mod(t,x,u,flag)switch flagcase 0,[sys,x0,str,ts]=mdlInitializeSizes;case 3, sys = mdlOutputs(t,x,u);case 2, sys = [];case 9, sys = [];otherwiseerror(['unhandled flag = ',num2str(flag)]);endfunction [sys,x0,str,ts]=mdlInitializeSizes()sizes = simsizes;sizes.NumContStates = 0; sizes.NumDiscStates = 0; sizes.NumOutputs = 1; sizes.NumInputs = 1; sizes.DirFeedthrough = 1; sizes.NumSampleTimes = 1; sys = simsizes(sizes);x0 = [];str = [];ts = [1 0];function sys=mdlOutputs(t,x,u) global Pos;global w;global Theta;Theta=u;b=fix(Theta/(2*pi));%取整if Theta==0sys=0;else if (Theta/(2*pi))==bsys=2*pi;elsesys=Thetab*2*pi;endendPos=sys; %位置表5.2 转子位置和三相参考电流之间的对应关系表5.2.5 位置计算模块机电转角信号到机电位置信号的转换可通过S函数编程实现,法式如下位置计算 S 函数(is.m)function [sys,x0,str,ts] =is(t,x,u,flag)switch flagcase 0,[sys,x0,str,ts]=mdlInitializeSizes;case 3, sys = mdlOutputs(t,x,u);case 2, sys = [];case 9,sys = [];otherwiseerror(['unhandled flag = ',num2str(flag)]); endfunction [sys,x0,str,ts]=mdlInitializeSizes() sizes = simsizes;sizes.NumContStates = 0;sizes.NumDiscStates = 0;sizes.NumOutputs = 3;sizes.NumInputs = 2;sizes.DirFeedthrough = 1;sizes.NumSampleTimes = 1;sys = simsizes(sizes);x0 = [];str = [];ts = [1 0];function sys=mdlOutputs(t,x,u)global Is;global Pos;Is=u(1); %电流Pos=u(2);%位置if Pos>=0& Pos<=pi/3sys=[Is,Is,0];elseif Pos>=pi/3& Pos<=2*pi/3sys=[Is,0,Is];elseif Pos>=2*pi/3& Pos<=pisys=[0,Is,Is];elseif Pos>=pi& Pos<=4*pi/3sys=[Is,Is,0];elseif Pos>=4*pi/3& Pos<=5*pi/3sys=[Is,0,Is];else Pos>=5*pi/3& Pos<=2*pisys=[0,Is,Is];end5.2.6 电压逆变器模块逆变器对BLDC来说,首先是功率变换装置,也就是电子换向器,每一个桥臂上的一个功率器件相当于直流电念头的一个机械换向器,还同时兼有PWM电流调节器功能.对逆变器的建模,本文采纳Simulink的SimPowerSystem工具箱提供的三相全桥IGBT模块.由于在Matlab新版本(如Matlab7.0)中SimPowerSystem工具箱和Simulink工具箱不成以随便相连的,中间必需加上受控电压源(或者受控电压源、电压表、电流表).本文给IGBT的A、B、C三相加三个电压表,输出的Simulink信号可以与BLDC直接连接,如图5.11所示.逆变器根据电流控制模块所控制PWM信号,顺序导通和关断,发生方波电流输出.电压逆变器模块结构框图及其封装基于Matlab/Simulink建立了BLDC控制系统的仿真模型,并对该模型进行了BLDC双闭环控制系统的仿真.仿真中,BLDC机电参数设置为:定子相绕组电阻R=1Ω,定子相绕组自感L=0.02H,互感M=0.061H,转动惯量J=0.005kg·m2,阻尼系数B= 0.0002N·m·s/rad,额定转速n=1000r/min,极对数p=1,220V直流电源供电.总体模型:存在问题:仿真速度慢,且示波器值均为0。
第三章 机电一体化系统数学模型

1 0 x k x 2 m
1 m
状态变量图
u
1 x 0 B 1 1 u x2 m m
2 x
∫
B m
1 x2 x
∫
x1
1
y
K m
3.由微分方程写出状态方程
设系统微分方程如下:
用向量和矩阵写成如下形式的状态方程:
1 0 x x 2 0 n a0 x 1 0 0 1 0 x1 0 0 x2 0 u an1 xn b0
--数学模型
11
第四章 机电一体化系统的建模与仿 真
(1)基本概念:
通过输入与输出间信息传递关系,描述系统动态特性
dny d n1 y d mx d m1 x an n an1 n1 a0 y bm m bm1 m1 b0 x dt dt dt dt 式中n m
第三章 机电一体化系统数学模型
本章的学习内容: 模型的基本概念 数学模型的表现形式
微分方程 传递函数 状态空间描述 数学模型的建立方法 系统微分方程的建立 机电系统传递函数的建立 状态空间表达式的建立
数学模型的建立
例:如图所式的质量-弹簧-阻尼组成的机械动 力学系统,其输入量为作用力f(t),输出量为 质量块的位移y(t) 。 (1)应用达朗贝尔原理,系统的运动方程为 M y(t)
1 0 x k x 2 m
1 x 0 B 1 1 u x2 m m
第三章 机电能量转换基础

输出的机械能 电源输入能量 = (耦合场内增加的储能) + − 电阻损耗能量 + 机械能量损耗
dWelec = dWm + dWmech
(3-33)
式中,dWelec为时间dt内电源输入的净能量;dWm为时 间dt内耦合场储能增量;dWmech为时间dt内转换为机 械能的总量。
3.2 变压器电势与速度电势 3.2.1 电磁感应定律与电动势
dφ u = −e = N dt
注意,只有线圈的 磁通和电势正方向 的规定符合右手螺 旋关系,上式才取 负号。这种电动势 正方向的规定被用 于本书的内容中。
图3-7 交流感应电动势的方向
3.2.2 变压器电势与运动电势
研究一个简单的,以磁场作为耦合场的机电装置—电磁铁, 如图3-8所示。该装置由固定铁心、可动衔铁组成,磁链 随电流和衔铁的位置而变化,即ψ=ψ(i,x)
3.4 机电能量转换的基本原理 3.4.1 典型的机电能量转换装置
通常把电能转换为机械能的装置称为电动机,把机械 能转换为电能的装置称为发电机。直流电机可作为一个三 端口装置(二电端口和一机械端口)对待,如图3-13所示,图 中T为转矩, 为角速度。电磁铁可作为一个两端口装置(一 电端口和一机械端口)对待,如图3-14所示,图中x为位移,f 为电磁力。 在以磁场作为耦合场的机电装置中,以电磁铁为例,机 电能量转换的过程大体为:当装置的可动部分发生位移x时, 气隙磁场将发生变化,由此引起线圈内磁链的变化,以及气 隙内磁场储能的变化。由位移引起的磁场储能的变化将产 生磁场力f,并使部分磁能释放出来变为机械能;由磁链变化 引起的的线圈内感应电势e将从电源吸收电能;这样,通过 耦合磁场的作用,电能将变为机械能或反之。
电机数学模型(完整版)

电机数学模型以二相导通星形三相六状态为例,分析 BLDC 的数学模型及电磁转矩等特 性。
为了便于分析,假定:a)三相绕组完全对称,气隙磁场为方波,定子电流、转子磁场分布皆对称; b)忽略齿槽、换相过程和电枢反应等的影响; C)电枢绕组在定子内表面均匀连续分布;⅛t J ⅛∙堵为定子相绕组电动势(V); L 为每相绕组的自感(H) ; M 为每相绕组间的互感(H) ; P 为微分算子P=d/dt 。
三相绕组为星形连接,且没有中线,则有i a + ⅛ + i c =OMi a +Mi b +Mi r =O得到最终电压方程:U ir O OI f -M O Oe√⅛ =O r O+ O L-M O P⅛ + ebΛ O r..Q O L-Mθc .图•无刷直流电机的等效电路无刷直流电机的电磁转矩方程与普通直流电动机相似, 其电磁转矩大小与磁 通和电流幅值成正比⅛-e√M P Jb+ ≡t L-* -* 1* -(1)—I :为定子相绕组电流(A);d)磁路不饱和,不计涡流和磁滞损耗式中:=.鬲乩为定子相绕组电压(V);Tβ=[e l i1+e b⅛+⅛]^所以控制逆变器输出方波电流的幅值即可以控制BLDC电机的转矩。
为产生恒定的电磁转矩,要求定子电流为方波,反电动势为梯形波,且在每半个周期内,方波电流的持续时间为120°电角度,梯形波反电动势的平顶部分也为120°电角度,两者应严格同步。
由于在任何时刻,定子只有两相导通,贝U:电磁功率可表示为:电磁转矩又可表示为:无刷直流电机的运动方程为:血(8) 其中I为电磁转矩;为负载转矩;B为阻尼系数;起为电机机械转速;J为电机的转动惯量。
传递函数:无刷直流电机的运行特性和传统直流电机基本相同,其动态结构图可以采用直流电机通用的动态结构图,如图所示:图2.无刷直流电机动态结构图由无刷直流电机动态结构图可求得其传递函数为… K I… K2n(s) = ~~—U(S) ---------- T L1 + T m s l+‰s L式中:Ki为电动势传递系数,【;:• L : , Ce为电动势系数;⅛K2为转矩传递函数,• - 一一,R为电动机内阻,Ct为转矩系数;⅛⅛Tm为电机时间常数,’1 .. ―一,G为转子重量,D为转子直径。
4.1机电一体化系统的数学模型及其表现形式

机电一体化系统数学模型及其表现形式 1.数学模型 物理模型 完全根据相似原理 真实系统按比例放大或缩小
数学模型 数学方程 分静态模型(与时间无关)和动态模型(与时间有关)
描述模型 抽象,不能或很难用数学方法描述 智能用语言描述
有缘学习更多+谓ygd3076考证资料或关注桃报:奉献教育(店铺)
机电一体化系统数学模型及其表现形式
2.数学模型的表现形式 2.3传递函数
对线性定常系统: a0 y(n) a1 y(n1) an1 y ' an y b0u(m)
bmu
在零初始条件下,两边同时进行拉普拉斯变换 (a0s(n) an1s an )Y (s) (b0s(m) bm1u bm )U(s)
传递函数
G(s)
Y (s) U(s)
b0 s(m) a0 s( n )
bm1u bm an1s an
连续系统的传递函数模型
sys=tf(num,den)
有缘学习更多+谓ygd3076考证资料或关注桃报:奉献教育(店铺)
机电一体化系统数学模型及其表现形式
2.数学模型的表现形式
2.3传递函数
例2:用MATLAB建立系统传递函数模型:
机电一体化系统数学模型及其表现形式
机电一化系统的 数学模型及其表现形式
机电一体化系统数学模型及其表现形式 1.数学模型
数学模型
仿真求解
动态性能分析
设计技术指标
设计结果
建模是系统分析与设计的基础,仿真是系统分析与设计的重要手段
系统模型是对系统的特征与变化规律的一种定量抽象,是人们用 以认识事物的一种手段(或工具)
该系统的动力学模型 my(t) y(t) ky(t) ku(t)
北航机电控制工程基础(自动控制原理)第三章2-时域分析法-一阶系统分析二阶系统分析
北京航空航天大学
机电控制工程基础
Fundamentals of Mechatronic Control Engineering
(3 )调节时间Regulation time :t s 根据调节时间的定义,当t≥ts时 |h(t)-h(∞)|≤ h(∞) ×Δ%。
e nt
1 2
sin(d t
tg1
1 2
袁松梅教授 Tel:82339630 Email:yuansm@
北京航空航天大学
• 定性分析 (1) 平稳性Stability ---> % ---> %
机电控制工程基础
Fundamentals of Mechatronic Control Engineering
d n 1 2
1 1
s1,2 n n 2 1 s1,2 n
欠阻尼 underdamping
0
1
s1,2
n
jn
1 2
零阻尼 undamping
0
s1,2 jn
负阻尼
0
negative damping
s1,2 n n 2 1
两个不等负实根 两个相等负实根 两个负实部共轭复根 两个纯虚根 正实部特征根
北京航空航天大学
机电控制工程基础
Fundamentals of Mechatronic Control Engineering
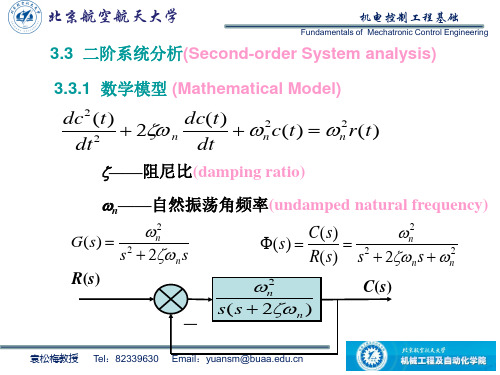
3.3 二阶系统分析(Second-order System analysis)
3.3.1 数学模型 (Mathematical Model)
dc2 (t) dt2
2 n
dc(t) dt
dtp 0, ,2 ,
得:
tp
电机数学模型(完整版)

电机数学模型以二相导通星形三相六状态为例,分析BLDC 的数学模型及电磁转矩等特性。
为了便于分析,假定:a)三相绕组完全对称,气隙磁场为方波,定子电流、转子磁场分布皆对称; b)忽略齿槽、换相过程和电枢反应等的影响; c)电枢绕组在定子内表面均匀连续分布; d)磁路不饱和,不计涡流和磁滞损耗。
则三相绕组的电压平衡方程可表示为:(1)式中:为定子相绕组电压(V);为定子相绕组电流(A);为定子相绕组电动势(V);L 为每相绕组的自感(H);M 为每相绕组间的互感(H);p 为微分算子p=d/dt 。
三相绕组为星形连接,且没有中线,则有(2) (3)得到最终电压方程:(4)L-ML-M L-Mrr ri a i b i ce ae ce b图.无刷直流电机的等效电路无刷直流电机的电磁转矩方程与普通直流电动机相似,其电磁转矩大小与磁通和电流幅值成正比(5)所以控制逆变器输出方波电流的幅值即可以控制BLDC 电机的转矩。
为产生恒定的电磁转矩,要求定子电流为方波,反电动势为梯形波,且在每半个周期内,方波电流的持续时间为120°电角度,梯形波反电动势的平顶部分也为120°电角度,两者应严格同步。
由于在任何时刻,定子只有两相导通,则:电磁功率可表示为:(6)电磁转矩又可表示为:(7)无刷直流电机的运动方程为:(8)其中为电磁转矩;为负载转矩;B 为阻尼系数;为电机机械转速;J 为电机的转动惯量。
传递函数:无刷直流电机的运行特性和传统直流电机基本相同,其动态结构图可以采用直流电机通用的动态结构图,如图所示:Ct365/(GD^2s)Ce1/RU(s)+-+-T L (s)T C (s)I(s)N(s)图2.无刷直流电机动态结构图由无刷直流电机动态结构图可求得其传递函数为:式中:K1为电动势传递系数,,Ce 为电动势系数;K2为转矩传递函数,,R 为电动机内阻,Ct 为转矩系数;T m为电机时间常数,,G 为转子重量,D 为转子直径。
第三章 机电系统的速度控制

串电阻调速
异步电机调速
n 60 f (1 s) p
• 因此异步电动机的调速方法大致可分为改变转差率、极对 数和电源频率三种。
• 改变极对数调速的方法在第一章双速电机控制一节中已经 介绍。
• 改变转差率的方法又可以通过调定子电压、转子电阻、转 子电压以及定转子供电频率差等方法来实现,从而得出很 多种调速方法。会使电机特性变软。
3.直流调速系统的控制方式 主电路构成不同,控制方法不同 :移相控制、PWM控制等
电机调速系 统中通常为:
闭环控制方式 开环控制
闭环控制
单闭环 双闭环 多环控制
速度环 速度环和电流环
加位置环等
4.工作象限
n
n
n
n
a)单象限运行
0
T
0
T
0
T
0
T b)电压可反向的二象限运行
c) 电流可反向的二象限运行
Ud
M
优点:静止装置、经济、可靠 缺点:功率因数低、对电网谐波污染
直流脉宽调制(PWM)系统
原理电路图
控制思路
Ud
控制原理
制动时的能量传递关系 工作象限
i0 Ea
u0
VD u0
Ud
驱动 VT
0 Ton
T
U0
t
a) a)原理电路图
n
n
b)
b)斩波器输出电压波形
U0
u0
Ton T
Ud
tU d
越高(S值越小),则允许的调速范围就越小。
例如,某一开环V-M调速系统,额定 转速nN =1000r/min ,额定负载下的稳态速 降 △nN =50r/min,当要求静差率S=0.33 时,允许的调速范围为:
机电系统建模与仿真--ch3(1)共28页文档

s s
ms2
1 Bs
K
第三章 机械传动系统的数字仿真分析
——面向数学模型的仿真分析
• 集中参数系统的控制方框图(4):单轮汽车支 承系统简化模型
第三章 机械传动系统的数字仿真分析 ——面向数学模型的仿真分析
• 集中参数系统的控制方框图(4):轴系传动
第三章 机械传动系统的数字仿真分析 ——面向数学模型的仿真分析
由代数方程解出因变量的拉氏变换;
对因变量的拉氏变换作拉氏反变换,即得到 因变量的时域函数。
第一章:概述——关于拉氏变换
例1:自由振动方程 x&& 2n x& n2 x 0, 1
初始条件 x0 a, x&0 b
s2X s sx0 x&0 2n sX s x0 n2X s 0
No X s
逆向+正向+终点判别
第三章 机械传动系统的数字仿真分析 ——面向数学模型的仿真分析
• 基于MATLAB函数的仿真实例:匀速驱动的四连 杆机构
A=B,=A1B
A
r3 sin3
r3
cos3
=[3, 4]T
r4 sin4
r4
cos
4
B
2r22r2sicnos22 22r222rc2ossin2 2323r23r3csoisn334242rr44csoisn44
a1 a2 an
s p1 s p2
s pn
第三章 机械传动系统的数字仿真分析——面 向数学模型的仿真分析
常见函
数的拉
氏变换
(及z 变换)
第三章 机械传动系统的数字仿真分析— —面向数学模型的仿真分析
4. 应用拉氏变换求解线性常微分方程
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.1 数学模型的基本概念
一、 传递函数
对于线性连续系统,描述其动态特性的数学模型为一组线性微分 方程。
系统的传递函数:当初始条件为零时(即当t≤0时, 输入量、输出量及其各阶导数均为 零),输出量拉氏变换与输入量的拉 氏变换之比。
二、方框图
方框图是为了方便求解输入输出量之间的关系所引入的一种方法。
3.2 机械传动系统数学模型
例3
3.3 电气传动系统数学模型
例3:对于图3-11所示的网络 ,求输入与输出之间的传递函 数。
3.4 机电系统模型相似法
力——电流相似
力——电压相似
连接点:指若干个机械元件相互连接的地方。规定同一个 刚体上的所有点都属于同一个连接点。
拉普拉斯变换与反变换
一、拉普拉斯变换是什么
二、几种常用函数的拉氏变换
三、拉氏变换的主要运算定理
第三章 机电一体化产品的数学模型
机电一体化系统数学模型:用数学的方法去阐述系统中 输入、输出及各变量之间的 相互关系。 建立系统数学模型的理论依据:
机械传动系统:牛顿第二定律
电路系统:基尔霍夫电压、电流定律
