圆的基本性质练习(含答案)
人教版九年级数学上册 圆的基本性质 专题训练(含答案)

人教版九年级数学上册 圆的基本性质 专题训练一、单选题1.如图,AB 是⊙O 的直径,若⊙BAC=35°,则⊙ADC=( )A .35°B .55°C .70°D .110°2.如图,两弦AB 、CD 相交于点E ,且AB CD ⊥,若30A ∠=︒,则弧BD 的度数为( ).A .30°B .50︒C .60︒D .70︒ 3.如图,四边形ABCD 为⊙O 的内接四边形,若110ADC ∠=︒,则AOC ∠的度数是( )A .110︒B .120︒C .130︒D .140︒ 4.下列说法中,正确的是( )A .经过半径的端点并且垂直于这条半径的直线是这个圆的切线B .平分弦的直径垂直于弦,并且平分弦所对的两条弧C .90°的圆周角所对的弦是直径D .如果两个圆周角相等,那么它们所对的弦相等.5.已知在⊙O 中,弦AB 的长为8,圆心O 到AB 的距离为3,则⊙O 的面积是( ) A .9π B .16π C .25π D .64π 6.如图,点A 、B 、C 是⊙O 上的三点,若056=∠OBC ,则A ∠的度数是( ).A .28︒B .30︒C .34︒D .56︒7.如图,在同圆中,弧AB 等于弧CD 的2倍,试判断AB 与2CD 的大小关系是( )A .2AB CD > B .2AB CD <C .2AB CD = D .不能确定 8.如图所示,⊙O 的半径为13,弦的长度是24,ON AB ⊥,垂足为N ,则ON =( )A .5B .7C .9D .119.如图,⊙ABC 内接于⊙O ,若⊙OAB =26°,则⊙C 的大小为( )A .26°B .52°C .60°D .64°10.已知⊙ABC 内接于⊙O ,连接AO 并延长交BC 于点D ,若⊙B =60°,⊙C =50°,则⊙ADB 的度数是( )A .70°B .80°C .82°D .85°11.如图,⊙O 是正五边形ABCDE 的外接圆,点P 是弧BE 的一点,则⊙CPD 的度数是( )A .30°B .36°C .45°D .72°12.如图, BC 是O e 的直径,AB 切⊙O 于点B ,8AB BC ==,点D 在⊙O 上,DE AD ⊥交BC 于E ,3BE CE =,则AD 的长是( )A B C . D .二、填空题13.如图,⊙O 中,直径20cm CD =,弦AB CD ⊥于点M ,:3:2OM MD =,则AB 的长是________cm .14.如图,⊙O 经过原点,并与两坐标轴分别交于A ,D 两点,已知30OBA ∠=︒,点A 的坐标为()2,0,则点D 的坐标为________.15.如图,将⊙O 沿弦AB 折叠,使弧AB 经过圆心O ,则⊙OAB=_______°.16.若⊙O 的半径为4cm ,弦AB =4cm ,则点O 到AB 的距离为_____cm .17.如图,量角器的0度刻度线为AB ,将一矩形直尺与量角器部分重叠,使直尺一边与量角器相切于点C ,直尺另一边交量角器于点A ,D ,量得10AD cm =,点D 在量角器上的读数为60o ,则该直尺的宽度为____________cm .18.如图,AB 是半圆O 的直径,C 为半圆上一点,AB =10,BC =6,过O 作OE ⊙AB 交AC 于点E ,则OE 的长为_____.19.如图,四边形ABCD 内接于⊙O ,延长CO 交圆于点E ,连接BE .若110A ∠=︒,70E ∠=︒ ,则OCD ∠=__________度.20.如图,若AB 是⊙O 的直径,CD 是⊙O 的弦,⊙ABD =58°,则⊙BCD =_____.三、解答题21.如图,已知⊙O 的直径6AB =,E 、F 为AB 的三等分点,M 、N 为»AB 上两点,且MEB NFB ∠=∠60︒=,求EM FN +的值.22.如图,已知AB 、MD 是⊙O 的直径,弦CD⊙AB 于E .(1)若CD=16cm ,OD=10cm ,求BE 的长;(2)若⊙M=⊙D ,求⊙D 的度数.23.如图,BC 为⊙O 的直径,AD BC ⊥,垂足为D ,点A 是弧BF 的中点,BF 和AD 相交于E ,求证:AE BE =.24.如图,AB 为⊙O 的直径,AC 切O e 于点A ,连结BC 交O 于点D ,E 是⊙O 上一点,且与点D 在AB 异侧,连结DE(1)求证:C BED ∠=∠;(2)若50C ∠=︒,2AB =,则»BD的长为(结果保留π)25.如图,AD 是⊙O 直径,B ,C 是圆上点且在AD 同侧.(1)如果30COD ︒∠=,则ACO ∠=________°.(2)如果2BOC COD ∠=∠,45BAD ∠=︒,求BAC ∠度数.26.如图,AB 是⊙O 的一条弦,C 、D 是⊙O 上的两个动点,且在AB 弦的异侧,连接CD .(1)若AC=BC,AB平分⊙CBD,求证:AB=CD;(2)若⊙ADB=60°,⊙O的半径为1,求四边形ACBD的面积最大值.参考答案1.B2.C3.D4.C5.C6.C7.B8.A9.D10.B11.B12.A13.1614.(0, 15.3016.1718.154 19.50° 20.32°.21 22.(1)4cm ;(2)30° 23.略 24.(1)略;(2)59π 25.(1)15(2)30BAC ∠=︒26.(1)略;(2.。
圆的基本性质 单元能力测试(含答案)

第7题第8题第三章 圆的基本性质能力提升测试卷一、选择题(共10小题,每小题3分,共30分)1. 如图,在⊙O 中,弦AB ∥CD ,若︒=∠40ABC ,则=∠BOD ( ) A. ︒20 B. ︒40 C. ︒50 D. ︒802.如图,点A 、B 、C 在⊙O 上,∠ACB =30°,则sin ∠AOB 的值是( ) A . B .C .D .3.用圆心角为120°,半径为6cm 的扇形纸片卷成一个圆锥形无底纸帽(如图所示),则这个纸帽的高是( ) A .cm B .3cm C .4cm D .4cm4.如图,AD 为⊙O 的直径,作⊙O 的内接正三角形ABC ,甲、乙两人的作法分别是:甲:1、作OD 的中垂线,交⊙O 于B ,C 两点,2、连接AB ,AC ,△ABC 即为所求的三角形 乙:1、以D 为圆心,OD 长为半径作圆弧,交⊙O 于B ,C 两点。
2、连接AB ,BC ,CA .△ABC 即为所求的三角形。
对于甲、乙两人的作法,可判断( )A .甲、乙均正确B .甲、乙均错误C .甲正确、乙错误D .甲错误,乙正确第4题 第5题 5.如图,已知BD 是⊙O 直径,点A 、C 在⊙O 上,⌒AB =⌒BC,∠AOB =60°,则∠BDC 的 度数是( )A.20°B.25°C.30°D. 40°6.如图,AB 为⊙O 的直径,弦CD ⊥AB 于E ,已知CD =12,则⊙O 的直径为( ) A. 8 B. 10 C.16 D.20第1题 第2题 第3题DCB AO第9题7.如图所示,扇形AOB的圆心角为120︒,半径为2,则图中阴影部分的面积为( )334.-πA2334.-πB3234.-πC34.πD8.如图,AB是⊙O的直径,弦CD⊥AB,垂足为M,下列结论不成立的是()A.CM=DM B.CB=DB C.∠ACD=∠ADC D.OM=MD9.如图,AB是⊙O的直径,弦CD⊥AB,垂足为M,下列结论不成立的是()A.CM=DM B.CB=DB C.∠ACD=∠ADC D.OM=MD10.如图所示,圆O的弦AB垂直平分半径OC,则四边形OACB()A、是正方形B、是长方形C、是菱形D、以上答案都不对二、填空题(共6小题,每小题4分,共24分)如图所示的圆面图案是用相同半径的圆与圆弧构成的.若向圆面投掷飞镖,则飞镖落在黑色区域的概率为.12.如图,AB是⊙O的弦,OC⊥AB于C.若AB=23,0C=1,则半径OB的长为________.13.如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=2.将△ABC绕顶点A顺时针方向旋转至△AB′C′的位置,B,A,C′三点共线,则线段BC扫过的区域面积为.14.如图,“凸轮”的外围由以正三角形的顶点为圆心,以正三角形的边长为半径的三段等弧组成. 已知正三角形的边长为1,则凸轮的周长等于_________.15.如图所示,AB为⊙O的直径,AC为弦,OD∥BC交AC于点D,若AB=20cm,∠A=30°,则AD=cm.16.如图,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交AB于E,交⊙O于D.则AD=_____________.三、解答题(共7题,共66分)17、(本题8分)如图所示,已知F是以O为圆心,BC为直径的半圆上任一点,A是弧BF的A BCO第10题第11题第12题第13题第14题第15题第16题中点,AD ⊥BC 于点D .求证:AD =12BF .18(本题8分).如图,⊙O 的直径AB 和弦CD 相交于点E ,∠CEA =30°, 求CD 的长.19.(本题8分)如图所示,OA 、OB 、OC都是圆O 的半径,∠AOB =2∠BOC . 求证:∠ACB =2∠BAC .20、(本题10分)如图,弧AC 是劣弧,M 是弧AC 中点,B 为弧AC 上任意一点,自M 向BC 弦引垂线,垂足为D ,求证:AB +BD =DC 。
浙教版九年级上册数学第3章 圆的基本性质 含答案

浙教版九年级上册数学第3章圆的基本性质含答案一、单选题(共15题,共计45分)1、下列命题:①任意三点确定一个圆;②平分弦(不是直径)的直径垂直于弦;③相等的圆心角所对的弦相等;④长度相等的弧是等弧.其中真命题的有()A. 个B. 个C. 个D. 个2、如图,一个半径为r(r<1)的圆形纸片在边长为10的正六边形内任意运动,则在该六边形内,这个圆形纸片不能接触到的部分的面积是()A.πr 2B.C. r 2D. r 23、如图,点A,B,C都在⊙O上,若∠C=30°,则∠AOB的度数为()A.30°B.60°C.150°D.120°4、如图,在⊙O中,∠ACB=34°,则∠AOB的度数是().A.17°B.34°C.56°D.68°5、如图,在矩形ABCD中,已知AB=4,BC=3,矩形在直线l上绕其右下角的顶点B向右旋转90°至图①位置,再绕右下角的顶点继续向右旋转90°至图②位置,…,以此类推,这样连续旋转2015次后,顶点A在整个旋转过程中所经过的路程之和是()A.2015πB.3019.5πC.3018πD.3024π6、下列说法中:1)圆心角相等,所对的弦相等2)过圆心的线段是直径3)长度相等的弧是等弧4)弧是半圆5)三点确定一个圆6)平分弦的直径垂直于弦,并且平分弦所对的弧7)弦的垂直平分线必经过圆心正确的个数有()A.1个B.2个C.3个D.4个7、如图,一条公路的转弯处是一段圆弧,点O是这段弧所在圆的圆心,,点C是的中点,D是AB的中点,且,则这段弯路所在圆的半径为()A. B. C. D.8、将正方体骰子(相对面上的点数分别为1和6、2和5、3和4)放置于水平桌面上,如图6-1.在图6-2中,将骰子向右翻滚90°,然后在桌面上按逆时针方向旋转90°,则完成一次变换.若骰子的初始位置为图6-1所示的状态,那么按上述规则连续完成10次变换后,骰子朝上一面的点数是()A.6B.5C.3D.29、如图,用一块直径为1m的圆桌布平铺在对角线长为1m的正方形桌面上,若四周下垂的最大长度相等,则桌布下垂的最大长度x为()A. -1B.C.D.2-10、如图,在64方格纸中,格点三角形甲经过旋转后得到格点三角形乙,则其旋转中心是()A.点MB.格点NC.格点PD.格点Q11、如图,已知A,B,C,D是⊙O上的点,AB⊥CD,OA=2,CD=2 ,则∠D 等于()A. B. C. D.12、圆内接四边形ABCD,∠A,∠B,∠C的度数之比为3∶4∶6,则∠D的度数为( )A.60°B.80°C.100°D.120°13、如图,AB为⊙O的直径,C,D为⊙O上两点,若∠BCD=38°,则∠ABD的大小为()A.76°B.52°C.50°D.38°14、下列命题:(1)经过三点一定可以作圆;(2)任一个三角形一定有一个外接圆,而且只有一个外接圆;(3)任意一个圆一定有一个内接三角形,而且只有一个内接三角形;(4)三角形的外心到三角形三个顶点的距离相等.上述结论中正确的有( )A.1个B.2个C.3个D.4个15、下列命题中,正确的是()①平分弦的直径垂直于弦;②圆内接平行四边形必为矩形;③90°的圆周角所对的弦是直径;④不在同一条直线上的三个点确定一个圆;⑤相等的圆周角所对的弧相等.A.①②③B.②③④C.②③④⑤D.①②③④⑤二、填空题(共10题,共计30分)16、如图,BC是⊙O的直径,A、D是⊙O上的两点,若∠ABC=25°,则∠D的度数是________°.17、如图1,折线段AOB将面积为S的⊙O分成两个扇形,大扇形、小扇形的面积分别为S1、S2,若=0.618,则称分成的小扇形为“黄金扇形”.生活中的折扇(如图2)大致是“黄金扇形”,则“黄金扇形”的圆心角约为________°.(精确到0.1)18、如图,四边形ABCD是菱形,⊙O经过点A、C、D,与BC相交于点E,连接AC、AE.若∠D=78°,则∠EAC=________°.19、如图,将一块含30°角的直角三角版和半圆量角器按如图的方式摆放,使斜边与半圆相切.若半径OA=4,则图中阴影部分的面积为________.(结果保留π)20、如图,A、B、C是⊙O上的三点,∠AOB=76°,则∠ACB的度数是________.21、问题背景:如图1,将△ABC绕点A逆时针旋转60°得到△ADE,DE与BC交于点P,可推出结论:PA+PC=PE问题解决:如图2,在△MNG中,MN=6,∠M=75°,MG=.点O是△MNG 内一点,则点O到△MNG三个顶点的距离和的最小值是________22、如图,⊙O中,直径CD⊥弦AB于E,AM⊥BC于M,交CD于N,连AD.AB=,ON=1,则⊙O的半径长为________.23、如图,等边△AOB中,点B在x轴正半轴上,点A坐标为(1,),将△AOB绕点O顺时针旋转15°,此时点A对应点A′的坐标是________.24、如图,将△ABC绕点A逆时针旋转65°得△ADE,若∠E=70°,AD⊥BC,则∠BAC=________.25、如图,点A,B,C均在6×6的正方形网格格点上,过A,B,C三点的外接圆除经过A,B,C三点外还能经过的格点数为________.三、解答题(共5题,共计25分)26、圆锥的底面半径为3cm,侧面展开图是圆心角为120º的扇形,求圆锥的全面积。
浙教版数学九年级上册 第3章 圆的基本性质(含答案)

第3章 圆的基本性质班级 学号 得分 姓名一、选择题(本大题有10小题,每小题3分,共30分)1. 下列三个命题:①圆既是轴对称图形又是中心对称图形;②垂直于弦的直径平分弦;③相等的圆心角所对的弧相等.其中真命题是( )A. ①②B. ②③C. ①③D. ①②③2. 如图,AB 是⊙O 的直径,C,D 是⊙O 上位于AB 异侧的两点,下列四个角中一定与∠ACD 互余的是 ( )A. ∠ADCB. ∠ABDC. ∠BACD. ∠BAD3.如图,点A,B,C,D,E 均在⊙O 上,∠BAC=15°,∠CED=30°,则∠BOD 的度数为( )A. 45°B. 60°C. 75°D. 90°4.如图,AB 是圆O 的弦,OC⊥AB,交圆O 于点C,连结OA,OB,BC,若∠ABC=20°,则∠AOB 的度数是( )A. 40°B. 50°C. 70°D. 80°5. 如图,点A ,B ,S 在圆上,若弦AB 的长度等于圆半径 2₂倍,则∠ASB 的度数是( )A. 22.5°B. 30°C. 45°D. 60°6.(2020·中考)如图,在等腰△ABC 中, AB =AC =25,BC =8,,按下列步骤作图:①以点 A 为圆心,适当的长度为半径作弧,分别交 AB ,AC 于点E ,F ,再分别以点 E ,F 为圆心,大 12₂EF 的长为半径作弧相交于点H ,作射线AH ;②分别以点 A ,B为圆心,大 12₂AB 的长为半径作弧相交于点M ,N ,作直线MN ,交射线AH 于点O ;③以点O 为圆心线段OA 的长为半径作圆,则⊙O 的半径为( )A.25B. 10C. 4D. 57. 如图,在⊙O 中,AE 是直径,半径OC 垂直于弦AB 于点 D,连结BE,若 AB =27,CD =1,则BE 的长是( )A. 5B. 6C. 7D. 88.已知⊙O 中,弦AB 的长等于半径,P 为弦AB 所对的弧上一动点,则∠APB 的度数为( )A. 30°B. 150°C. 30°或150°D. 60°或120°9. 已知⊙O 的直径CD=10cm,AB 是⊙O 的弦,AB⊥CD,垂足为M,且AB=8cm,则AC 的长为…… ( ) A.25cm B.45cmC.25cm 或 45cmD.23cm 或 43cm10. 如图,AB为⊙O的直径,AC交⊙O于点E,BC交⊙O于点D,CD=BD,∠C=70°,现给出以下三个结论:①∠A=45°;②AC=AB;③AE=BE.其中正确的有( )A. 1个B. 2 个C. 3个D. 0个二、填空题(本大题有6小题,每小题4分,共24分)11. 如图,一次函数y= kx+b的图象与x轴,y轴分别相交于A,B两点,⊙O经过A,B两点,已知AB=2,则 kb的值为 .12. 如图,AB是⊙O的直径,点C,D在圆上,∠D=65°,则∠BAC等于度.13. 如图,已知矩形ABCD的边AB=3,AD=4.(1)以点 A为圆心,4为半径作圆A,则点B,C,D与圆A 的位置关系分别是;(2)若以A点为圆心作圆A,使B,C,D三点中至少有一个点在圆内,且至少有一个点在圆外,则圆A的半径r的取值范围是 .14. 如图,BC是半圆O 的直径,D,E是BC上两点,连结BD,CE 并延长交于点A,连结OD,OE.如果∠A=70°,那么∠DOE的度数为 .15. 如图所示,AB是⊙O的直径,弦CD⊥AB于点H,∠A=30∘,CD=23,则⊙O的半径是 .16. 如图所示,⊙O的直径AB=16cm,P是OB 中点,∠ABP=45°,则CD= cm.三、解答题(本大题有8小题,共66分)17.(6分)如图,点A,B,C都在⊙O上,OC⊥OB,点A 在劣弧BC上,且OA=AB,求∠ABC的度数.18. (6分)如图,在同一平面内,有一组平行线l₁,l₂,l₃,,相邻两条平行线之间的距离均为4,点O在直线l₁上,⊙O与直线l₃的交点为A,B,AB=12,求⊙O的半径.19.(6分)如图,在△ABC的外接圆上AB,BC,CA三弧的度数比为12:13:11.在劣弧BC上取一点D,过点D分别作直线AC,直线AB的平行线,分别交 BC于E,F两点,求∠EDF的度数.20. (8分)如图,△ABC内接于⊙O,AB=AC,,D在弧AB 上,连结CD交AB 于点E,B 是弧CD 的中点,求证:∠B=∠BEC.21.(8分)已知:如图,点M是/AB的中点,过点M的弦MN交AB 于点C,设⊙O的半径为4cm,. MN=43cm.(1)求圆心 O到弦MN的距离;(2)求∠ACM的度数.22.(10分)如图,已知方格纸中每个小正方形的边长为1个单位,Rt△ABC的三个顶点A(-2,2),B(0,5),C(0,2).(1)将△ABC以C 为旋转中心旋转180°,得到△A₁B₁C,请画出△A₁B₁C;(2)平移△ABC,使点 A的对应点.A₂的坐标为(−2,−6),请画出平移后对应的图形△A₂B₂C₂;(3)若将△A₁B₁C绕某一点旋转可得到△A₂B₂C₂.请直接写出旋转中心的坐标.23.(10分)如图,已知AB是⊙O的直径,C是圆周上的动点,P 是ABC的中点.(1)求证:OP//BC;(2)如图,连结PA,PC交直径AB于点D,当(OC=DC时,求∠A的度数.24.(12分)我们学习了“弧、弦、圆心角的关系”,实际上我们还可以得到“圆心角、弧、弦,弦心距之间的关系”如下:圆心角、弧、弦、弦心距之间的关系:在同圆或等圆中,如果两个圆心角,两条弧,两条弦或两条弦的弦心距中有一组量相等,那么它们对应的其余各组量也相等弦心距指从圆心到弦的距离如图(1)中的 OC,OC′,弦心距也可以说成圆心到弦的垂线段的长度 l请直接运用圆心角、弧、弦、弦心距之间的关系解答下列问题.如图(2),点O是∠EPF的平分线上一点,以点O为圆心的圆与角的两边分别交于点A,B,C,D.(1)求证:AB=CD.(2)若角的顶点 P 在圆上或圆内,上述结论还成立吗? 若不成立,请说明理由;若成立,请加以证明.第3章 圆的基本性质1. A2. D3. D4. D5. C6. D7. B8. C9. C 10. A 11. 1212. 25 13. (1)B 在圆内、C 在圆外、D 在圆上(2)3<r<5 14. 40° 15. 2 16. 1417. 解:∵OA=OB,OA=AB,∴OA=OB=AB,即△OAB 是等边三角形,∴∠AOB=60°,∵OC⊥OB,∴∠COB= 90°,∴∠COA = 90°- 60°= 30°,∴∠ABC=15°.18. 解:如图,连结 OA,过点O 作OD⊥AB 于点 D.∵ AB =12,∴AD =12AB =12×12=6.相邻两条平行线之间的距离均为4,∴OD=8.在 Rt△AOD 中,∵AD =6,OD =8,∴OA =AD 2+OD = 62+82=10.∴⊙O 的半径为 10.19. 解: ∵AB ,BC ,CA 三弧的度数比为12:13:11,∴ ABm.1212+13+11×360∘=120∘,AC−m m 1112+13+11×360∘=110∘,∴∠ACB =12×120∘= 0∘,∠ABC =12×110∘=55∘,∵ACED,AB DF,∴∠FED=∠ACB=60°,∠EFD=∠ABC= 55°,∴∠EDF =180°−60°−55°=65°20. 证明:∵B 是弧 CD 的中点, ∴BC =BD ,∴∠BCE = =∠BAC.:∠BEC =180°−∠BCE,∠ACE ,=180°-∠BAC--∠B,∴∠BEC=∠ACB,∵AB=AC,∴∠B=∠ACB,∴∠B=∠BEC.21. 解:(1)连结 OM.∵点 M 是. AB 的中点,∴OM⊥AB.过点 O 作OD⊥MN 于点 D,由垂径定理,得 MD =12MN =23cm,在Rt△ODM 中,OM=4cm, MD =23cm,∴OD =OM 2−MD 2=2(cm ).故圆心 O 到弦MN 的距离为 2cm. (2)∵OD=2cm,OM=4cm,∴∠M=30°,∴∠ACM=60°.22. 解:(1)(2)图略.(3)旋转中心的坐标为(0,-2).23. (1)证明:连结AC,延长 PO 交AC 于点 H,如图,∵P 是 ABC 的中点,∴PH⊥AC,∵A B 是⊙O 的直径,∴∠ACB=90°,∴BC⊥AC,∴OP∥BC. (2)解:∵P 是 ABC 的中点, P C,∴∠PAC=∠PCA,:OA=OC, ∴ ∠OA C= ∠OCA,∴∠PAO=∠C O=CD 时,设∠DCO=x,则∠OPC=x,∠PAO=x,∴∠POD =2x,∴∠ODC=∠POD+∠OP C=3x,∵CD=CO,∴∠DOC=∠ODC=3x.在△POC 中,x+x+5x=180°,解得 x =180∘7,即 ∠PAO =180∘7.24. (1)证明:过点 O 作OM⊥AB 于点M,ON⊥CD 于点 N,连结OB,OD,则∠OMB=∠OND=90°,∵PO 平分∠EPF,∴O M=ON,∵OM⊥AB,ON⊥CD,∴AB=CD.(2)成立.当点 P 在圆上时如图;作OM⊥PB,ON⊥PD,垂足分别为M,N,∵PC平分∠EPF,∴OM=ON,∵OM⊥AB,ON⊥CD,∴PB=PD;当点P 在圆内时:过点 O作OM⊥AB,ON⊥CD,∵PO平分∠BPF,∴OM=ON.∵OM⊥AB,ON⊥CD,∴AB=CD.。
八年级数学圆的性质练习题及答案

八年级数学圆的性质练习题及答案1. 单选题1) 设O为平面内一个圆的圆心,AB为圆上一条弧,点C是弧AB 的中点,则在一个平面内以下哪些命题是真的?a) 点C在弧AB的弦上。
b) ∠CAB = 90°。
c) ∠CAB = ∠CBO。
d) ∠C = ∠CAB/2。
答案:a) 和 c)2) 平面上有一个不经过圆心的直线与一个圆相交,交点有0个,1个以及2个,那么圆的位置是什么关系?a) 圆心在直线上。
b) 圆心在直线的一侧。
c) 圆的圆心在直线的对面。
d) 圆的圆心在直线所在直线的垂直平分线上。
答案:c)2. 填空题1) 设AB为直径的圆,点C为圆上一点,则直线AC的度数为_________。
答案:90°2) 在平面上给出一条弧,求出它平分的角的度数,圆心的角度数为_________。
答案:360°3. 解答题1) 已知O为圆心,AB为圆上一条弧,点P为圆弧上一点,连接OP并延长交圆于点C。
如果∠ACB=70°,求∠APB的度数。
解答:由于OP与圆弧AB相交于点P,而OP与圆相交于点C,所以∠BAC=∠BPC。
又∠ACB=70°,则∠BAC=70°,所以∠APC=140°。
因为角度补角原理,得到∠APB=360°-140°=220°。
2) 圆内接于四边形ABCD,如果∠ABC=85°,∠BCD=120°,求证:∠BAD+∠ADC=180°。
解答:由于圆内接于四边形ABCD,所以∠ABC=∠ADC,∠BCD=∠BAD。
又已知∠ABC=85°,∠BCD=120°,所以∠BAD+∠ADC=85°+120°=205°。
根据角度和为180°的原理可知,∠BAD+∠ADC不等于180°。
所以命题不成立。
3) 平面内有一个圆心为O,半径为r的圆,点P为圆上一点,直线l经过点P且与圆相交于A、B两点。
第3章 圆的基本性质 浙教版数学九年级上册测试(含答案)

浙教版数学九年级上册第三章圆的基本性质一、选择题1.下列说法正确的是( )A.三个点可以确定一个圆B.半圆(或直径)所对的圆周角是直角C.相等的圆心角所对的弧相等D.长度相等的弧是等弧2.已知一个扇形的面积是24π,弧长是2π,则这个扇形的半径为( )A.24B.22C.12D.63.如图,点A、B、C在⊙O上,∠C=40∘,则∠AOB的度数是( )A.50∘B.60∘C.70∘D.80∘4.如图,AB是⊙O的直径,弦CD⊥AB于点E,若BE=5,AE=1,则弦CD的长是()A.5B.5C.25D.65.将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A,B的读数分别为86°,30°,则∠ACB的度数是( )A.28°B.30°C.36°D.56°6.如图,AB为⊙O的直径,点C在⊙O上,若∠OCA=50°,AB=4,则BC的长为( )A .103πB .109πC .59πD .518π7.如图, AB 是半圆O 的直径,点C ,D 在半圆O 上.若 ∠ABC =50° ,则 ∠BDC 的度数为( )A .90°B .100°C .130°D .140°8. 如图,正六边形ABCDEF 内接于⊙O ,若⊙O 的周长等于6π,则正六边形的边长为( )A .3B .6C .3D .239.如图,正五边形ABCDE 内接于⊙O ,阅读以下作图过程:①作直径AF ;②以点F 为圆心,FO 为半径作圆弧,与⊙O 交于点M ,N ;③连接AM ,MN ,AN .结论Ⅰ:△AMN 是等边三角形;结论Ⅱ:从点A 开始,以DN 长为半径,在⊙O 上依次截取点,再依次连接这些分点,得到正十八边形.对于结论Ⅰ和结论Ⅱ,下列判断正确的是( )A .Ⅰ和Ⅱ都对B .Ⅰ和Ⅱ都不对C.Ⅰ不对Ⅱ对D.Ⅰ对Ⅱ不对10.如图,抛物线y=x2﹣8x+15与x轴交于A、B两点,对称轴与x轴交于点C,点D(0,﹣2),点E (0,﹣6),点P是平面内一动点,且满足∠DPE=90°,M是线段PB的中点,连接CM.则线段CM的最大值是( )A.3B.412C.72D.5二、填空题11.如图,在⊙O中,弦AB,CD相交于点P.若∠A=40°,∠APD=75°,则∠B= °.12.如图,AB、AC是⊙O的弦,OM⊥AB,ON⊥AC,垂足分别为M、N.如果MN=2.5,那么BC= .13.如图,四边形ABCD内接于⊙O ,若四边形ABCD的外角∠DCE=65°,则∠BAD的度数是 .14.如图,四边形ABCD是菱形,⊙O经过点A、C、D,与BC相交于点E,连接AC、AE.若∠D=70°,则∠EAC的度数为 .15.我国魏晋时期数学家刘徽在《九章算术注》中提到了著名的割圆术:“割之弥细,所失弥少.割之又割,以至于不可割,则与圆周合体,而无所失矣”.“割圆术”孕育了微积分思想,他用这种思想得到了圆周率π的近似值为3.1416.如图,⊙O的半径为1,运用“割圆术”,以圆内接正六边形面积近似估计⊙O,若用圆内接正十二边形作近似估计,可得π的估计值为 .的面积,可得π的估计值为33216.如图,点M(2,0)、N(0,4),以点M为圆心5为半径作⊙M交y轴于A、B两点,点C为⊙M上一动点,连接CN,取CN中点D,连接AD、BD,则A D2+B D2的最大值为 .三、解答题17.如图,四边形ABCD为⊙O的内接四边形,AC是⊙O的直径,AD=BD,∠CAB=32°.求∠ACD的度数.18.如图,OC为⊙O的半径,弦AB⊥OC于点D,OC=10,CD=4,求AB的长.19.如图,正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求解答下列问题:(1)△A1B1C1与△ABC关于坐标原点O成中心对称,则B1的坐标为__________;(2)BC与B1C1的位置和数量关系为___________;(3)将△ABC绕某点逆时针旋转90°后,其对应点分别为A2(―1,―2),B2(1,―3),C2(0,―5),则旋转中心的坐标为___________.20.如图,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于点D,(1)求∠ACB的度数;(2)求BC的长;(3)求AD,BD的长.21.如图,AB是⊙O的直径,C是⏜BD的中点,CE⊥AB于点E,BD交CE于点F.(1)求证:CF=BF.(2)若CD=6,AC=8,求⊙O的半径及CE的长.22.如图所示,AB为☉O的直径,AC是☉O的一条弦,D为BC的中点,作DE⊥AC于点E,交AB的延长线于点F,连接DA.(1)若AB=90 cm,则圆心O到EF的距离是多少?说明你的理由.(2)若DA=DF=63,求阴影部分的面积(结果保留π).23.如图,AB是⊙O的直径,弦CD⊥AB与点E,已知AB=10,AE=8,点P为AB上任意一点,(点P不与A、B重合),连结CP并延长与⊙O交于点Q,连QD,PD,AD.(1)求CD的长.(2)若CP=PQ,直接写出AP的长.(3)①若点P在A,E之间(点P不与点E重合),求证:∠ADP=∠ADQ.②若点P在B,E之间(点P不与点E重合),求∠ADP与∠ADQ满足的关系.答案解析部分1.【答案】B2.【答案】A3.【答案】D4.【答案】C5.【答案】A6.【答案】B7.【答案】D8.【答案】C9.【答案】D10.【答案】C11.【答案】3512.【答案】513.【答案】65°14.【答案】15°15.【答案】316.【答案】49217.【答案】61°18.【答案】1619.【答案】(1)(2,2);(2)平行且相等;(3)(0,―1).20.【答案】(1)∠ACB=90°(2)BC=8cm(3)BD=AD=52cm21.【答案】(1)证明:∵AB是⊙O的直径,∴∠ACB=90°,∴∠A=90°-∠ABC.∵CE⊥AB,∴∠ECB=90°-∠ABC,又∵C是BD的中点,∴CD=BC,∴∠DBC=∠A,∴∠ECB=∠DBC,∴CF= BF;(2)解:∵BC=CD,∴BC=CD=6.在Rt△ABC中,AB= BC2+AC2=62+82=10,∴⊙O的半径为5;∵S△ABC= 12AB×CE= 12BC×AC,∴CE= BC×ACAB =6×810=245.22.【答案】(1)解:如图所示,连接OD,∵D为BC的中点,∴∠CAD=∠BAD.∵OA=OD,∴∠BAD=∠ADO.∴∠CAD=∠ADO.∴OD∥AE.∵DE⊥AC,∴OD⊥EF.∴OD的长是圆心O到EF的距离.∵AB=90 cm,∴OD=12AB=45 cm.(2)解:如图所示,过点O作OG⊥AD交AD于点G.∵DA=DF,∴∠F=∠BAD.由(1),得∠CAD=∠BAD,∵∠F+∠BAD+∠CAD=90°,∴∠F=∠BAD=∠CAD=30°.∴∠BOD=2∠BAD=60°,OF=2OD.∵在Rt△ODF中,OF2-OD2=DF2,∴(2OD)2-OD2=(63)2,解得OD=6.在Rt△OAG中,OA=OD=6,∠OAG=30°,AG=OA2―O G2=33,AD=23,S△AOD=1×63×3=93.2+93=6π+93.∴S阴影=S扇形OBD+S△AOD=60π×6236023.【答案】(1)解:连接OD,∵直径AB=10,AE=8,∴BE=2.∴OE=5-2=3.又∵AB⊥CD,在Rt△PED中,P D2=P E2+E D2∴ED=52―32=4∴CD=2ED=8(2)解:若CP=PQ,则点P与点O重合,或点P与点E重合.所以AP=5或8(3)解:①连接AC,由图可知∠ACQ=∠ADQ,因为AB是⊙O的直径,AB⊥CD,所以CE=DE,即AB是CD的垂直平分线,所以AC=AD,PC=PD,因为AP=AP,所以∠ACP=∠ADP ,所以∠ADP=∠ADQ .②∠ADP+∠ADQ=180°.理由如下:连接AC ,因为AB 是直径,AB ⊥CD ,所以AC=AD ,CE=DE ,所以△ACP ≌△ADP (SSS ),所以∠ACP=∠ADP ,因为∠ACP=12ADQ ,∠ADQ=12ACQ ,所以∠ACP+∠ADQ=12(ADQ +ACQ )=180°.。
圆的有关性质练习及答案(供参考)

1° ° D CB A O圆的有关性质【知识要点】 1.圆的定义:(1)动态定义:在一个平面内,线段OA 绕它固定的一个端点O 旋转一周,另一个端点A 所形成的图形叫做圆。
(2)静态定义:在平面内到定点(圆心O )的距离等于定长(半径r )所有点的集合叫做圆:2.圆的相关概念弦:直径:弧:半圆弧:优弧:劣弧:等弧:同心圆:3.垂径定理及推论:垂直于弦的直径平分弦,并且平分弦所对的两条弧。
由此得到推论:(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。
(2)弦的垂直平分线,经过圆心, 并且平分弦所对的两条弧。
4.圆的轴对称性:(1)圆是轴对称图形;(2)经过圆心的每一条直线都是它的对称轴;(3)圆的对称轴有无数条。
5..圆的旋转不变性圆是以圆心为对称中心的中心对称图形6.圆心角、弧、弦关系定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对弦的弦心距相等。
7.弧的度数等于它所对的圆心角的度数。
8..圆周角定理及推论:在同圆或等圆中,同弧或等弧所对的圆周角相等,并等于这条弧所对的圆心角的一半.推论:(1)半圆(或直径)所对的圆周角是直角.90°的圆周角所对的弦是直径.(2)三角形的一边上的中线等于这边的一半,则这个三角形是直角三角形9:三角形:圆内接三角形;圆:三角形的外接圆 四边形:圆内接四边形圆:四边形的外接圆 定理:圆内接四边形的对角互补【基础和能力训练】 一、选择题1.平行四边形的四个顶点在同一圆上,则该平行四边形一定是( )A.正方形 B.菱形 C.矩形 D.等腰2.(2014•毕节地区)如图,已知⊙O 的半径为13,弦AB 长为24,则点O 到AB 的距离是( ) A 6 B 5 C 4 D 33. ( 2014•珠海)如图,线段AB 是⊙O 的直径, 弦CD 丄AB ,∠CAB =20°,则∠AOD 等于( ) A 160° B 150° C 140° D 120°4.(2015湖南常德)如图,四边形ABCD 为⊙O 的内接四边形,已知∠BOD =100°,则∠BCD 的度数为( ) A 、50° B 、80° C 、100° D 、130°5.(2015上海)如图,已知在⊙O 中,AB 是弦,半径OC ⊥AB ,垂足为点D ,要使四边形OACB 为菱形,还需要添加一个条件,这个条件可以是( )A 、AD =BD ;B 、OD =CD ;C 、∠CAD =∠CBD ;D ∠OCA =∠OCB .6. 如图:是小明完成的.作法是:取⊙O 的直径AB ,在⊙O 上任取一点C 引弦CD ⊥A B.当C 点在半圆上移动时(C 点不与A 、B 重合),∠OCD 的平分线与⊙O 的交点P 必( ) A 。
初中数学:圆的基本性质测试题(含答案)

初中数学:圆的基本性质测试题(含答案)一、选择题(每小题4分,共24分)1.如图G -3-1,在⊙O 中,AB ︵=AC ︵,∠AOB =40°,则∠ADC 的度数是( ) A .40° B .30° C .20° D .15°2.在同圆或等圆中,下列说法错误的是( ) A .相等的弦所对的弧相等 B .相等的弦所对的圆心角相等 C .相等的圆心角所对的弧相等 D .相等的圆心角所对的弦相等G -3-1G -3-23.如图G -3-2,在两个同心圆中,大圆的半径OA ,OB ,OC ,OD 分别交小圆于点E ,F ,G ,H ,∠AOB =∠GOH ,则下列结论中,错误的是( )A .EF =GH B.EF ︵=GH ︵ C .∠AOC =∠BOD D.AB ︵=GH ︵4.已知正六边形的边长为2,则它的外接圆的半径为( )A.1 B. 3 C.2 D.2 35.在如图G-3-3所示的暗礁区,两灯塔A,B之间的距离恰好等于圆的半径,为了使航船(S)不进入暗礁区,那么S对两灯塔A,B的视角∠ASB必须( ) A.大于60° B.小于60°C.大于30° D.小于30°G-3-3G-3-46.如图G-3-4,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论:①AD⊥BD;②∠AOC=∠AEC;③BC 平分∠ABD;④AF=DF;⑤BD=2OF;⑥△CEF≌△BED.其中一定成立的是( ) A.②④⑤⑥ B.①③⑤⑥C.②③④⑥ D.①③④⑤二、填空题(每小题4分,共24分)7.如图G-3-5,AB是⊙O的直径,AC=BC,则∠A=________°.G-3-5G-3-68.如图G-3-6,在⊙O的内接四边形ABCD中,点E在DC的延长线上.若∠A=50°,则∠BCE=________°.9.如图G-3-7,AB是⊙O的直径,C是⊙O上的一点.若BC=6,AB=10,OD⊥BC于点D,则OD的长为________.G-3-7G-3-810.用一条宽相等的足够长的纸条,打一个结,然后轻轻拉紧、压平就可以得到如图G-3-8所示的正五边形ABCDE,其中∠BAC=________°.11.如图G-3-9,⊙O的半径为4,△ABC是⊙O的内接三角形,连结OB,OC.若∠BAC和∠BOC互补,则弦BC的长度为________.G-3-9图G-3-1012.如图G-3-10,已知正六边形ABCDEF内接于半径为4的⊙O,则B,D 两点间的距离为__________.三、解答题(共52分)13.(12分)如图G-3-11所示,⊙O的直径AB长为6,弦AC长为2,∠ACB 的平分线交⊙O于点D,求四边形ADBC的面积.图G-3-1114.(12分)如图G-3-12,∠BAC的平分线交△ABC的外接圆于点D,∠ABC 的平分线交AD于点E,连结DB.(1)求证:DE=DB;(2)若∠BAC=90°,BD=4,求△ABC的外接圆半径.图G -3-1215.(12分)作图与证明:如图G -3-13,已知⊙O 和⊙O 上的一点A ,请完成下列任务:(1)作⊙O 的内接正六边形ABCDEF ;(2)连结BF ,CE ,判断四边形BCEF 的形状,并加以证明.图G -3-1316.(16分)如图G -3-14,正方形ABCD 内接于⊙O ,E 为CD ︵上任意一点,连结DE ,AE .(1)求∠AED的度数;(2)如图②,过点B作BF∥DE交⊙O于点F,连结AF,AF=1,AE=4,求DE 的长.图G-3-14详解详析1.C 2.A 3.D 4.C 5.D6.D [解析] ∵AB是⊙O的直径,∴∠D=90°,即AD⊥BD,∴①正确;∵OC∥BD,∴∠C=∠CBD.又∵OB=OC,∴∠C=∠OBC,∴∠OBC=∠CBD,即BC平分∠ABD,∴③正确;∵∠D=90°,OC∥BD,∴∠CFD=∠D=90°,即OC⊥AD,∴AF=DF,∴④正确;又∵AO=BO,∴OF是△ABD的中位线,∴OF=12BD,即BD=2OF,∴⑤正确.故选D.7.45 [解析] ∵AB是⊙O的直径,∴∠C=90°.∵AC=BC,∴△ABC是等腰直角三角形,∴∠A=∠B=12(180°-∠C)=45°.8.509.4 [解析] ∵AB是⊙O的直径,∴∠ACB=90°.∵BC=6,AB=10,∴AC =102-62=8.∵OD⊥BC于点D,∴DB=DC.又∵OA=OB,∴OD=12AC=4.10.3611.4 3 [解析] ∵∠BAC+∠BOC=180°,2∠BAC=∠BOC,∴∠BOC=120°,∠BAC=60°.过点O作OD⊥BC于点D,则∠BOD=12∠BOC=60°.∵OB=4,∴OD=2,∴BD=OB2-OD2=42-22=2 3,∴BC=2BD=4 3.12.4 3 [解析] 如图,连结OB,OC,OD,BD,BD交OC于点P,∴∠BOC=∠COD=60°,∴∠BOD =120°,BC ︵=CD ︵, ∴OC ⊥BD . ∵OB =OD , ∴∠OBD =30°. ∵OB =4,∴PB =OB ·cos ∠OBD =32OB =2 3, ∴BD =2PB =4 3.13.解:∵AB 是⊙O 的直径, ∴∠ACB =∠ADB =90°. 在Rt △ABC 中,AB =6,AC =2, ∴BC =AB 2-AC 2=62-22=4 2. ∵∠ACB 的平分线交⊙O 于点D , ∴∠DCA =∠BCD , ∴AD ︵=BD ︵, ∴AD =BD ,∴在Rt △ABD 中,AD =BD =3 2,∴四边形ADBC 的面积=S △ABC +S △ABD =12AC ·BC +12AD ·BD =12×2×4 2+12×32×3 2=9+4 2.故四边形ADBC的面积是9+4 2.14.解:(1)证明:连结CD,∵AD平分∠BAC,∴∠BAD=∠CAD.又∵∠CBD=∠CAD,∴∠BAD=∠CBD.∵BE平分∠ABC,∴∠CBE=∠ABE,∴∠DBE=∠CBE+∠CBD=∠ABE+∠BAD.又∵∠BED=∠ABE+∠BAD,∴∠DBE=∠BED,∴DE=DB.(2)∵∠BAC=90°,∴BC是圆的直径,∴∠BDC=90°.∵AD平分∠BAC,BD=4,∴BD=CD=4,∴BC=BD2+CD2=4 2.∴△ABC的外接圆半径为2 2.15.解:(1)如图①,首先作直径AD,然后分别以A,D为圆心,OA长为半径画弧,分别交⊙O 于点B ,F ,C ,E ,连结AB ,BC ,CD ,DE ,EF ,AF ,则正六边形ABCDEF 即为所求.(2)四边形BCEF 是矩形.证明:如图②,连结OE ,∵六边形ABCDEF 是正六边形,∴AB =AF =DE =DC =FE =BC ,∴AB ︵=AF ︵=DE ︵=DC ︵,∴BF ︵=CE ︵,∴BF =CE ,∴四边形BCEF 是平行四边形.∵六边形ABCDEF 是正六边形,∴∠DEF =∠EDC =120°.∵DE =DC ,∴∠DEC =∠DCE =30°,∴∠CEF =∠DEF -∠DEC =90°,∴平行四边形BCEF 是矩形.16.解:(1)如图①,连结OA ,OD .∵四边形ABCD是正方形,∴∠AOD=90°,∴∠AED=12∠AOD=45°.(2)如图②,连结CF,CE,CA,过点D作DH⊥AE于点H.∵BF∥DE,AB∥CD,∴∠ABF=∠CDE.∵∠CFA=∠AEC=90°,∠AED=∠BFC=45°,∴∠DEC=∠AFB=135°.又∵CD=AB,∴△CDE≌△ABF,∴AF=CE=1,∴AC=AE2+CE2=17,∴AD=22AC=342.∵∠DHE=90°,∴∠HDE=∠HED=45°,∴DH=EH,设DH=EH=x,在Rt△ADH中,∵AD2=AH2+DH2,∴344=(4-x)2+x2,解得x=32或x=52,∴DE=2DH=3 22或5 22.。
2.3_圆的基本性质水平测试题(含答案)

圆的基本性质一、选择题1、下面三个命题:①圆既是轴对称图形,又是中心对称图形;②垂直于弦的直径平分这条弦;③相等的圆心角所对的弧相等。
其中是真命题的是 ( )A.①②;B. ①③;C. ②③;D. ①②③。
2、已知⊙O 的半径为5cm ,P 为该圆内一点,且OP=1cm ,则过点P 的弦中,最短的弦长为( )A 、8cm ;B 、6cm ;C 、; D 、。
3.如图1,CD 是O 的直径,A B ,是O 上的两点,若20ABD ∠=,则ADC ∠的度数为( )A .40B .50 C .60 D .70图1 图2 图34、如图2,点A 、B 、D 、C 是⊙O 上的四个点,且∠BOC=110°,则∠BAC 的度数是( )A.110°B.70°C.100°D.55°5、如图3,正方形ABCD 的四个顶点分别在⊙O 上,点P 在劣弧CD 上不同于点C 得到任意一点,则∠BPC 的度数是( )A 、45 ;B 、60 ;C 、75 ;D 、90。
6、如图4,AD 平分∠BAC ,则图中相似三角形有( )A 、2对;B 、3对;C 、4对;D 、5对。
图4D二、精心填一填(每小题3分,共24分)7、如图,已知AB是⊙O的直径,弦CD与AB相交于点E。
若______,则CE=DE(只须填上一个适合的条件即可)。
8、已知AB、CD为⊙O的两条弦,圆心O到它们的距离分别为OM、ON,如果AB>CD,那么OM____ON。
(填“>、=、<”中的一种)9、在⊙O中,AB是直径,CD是弦,若AB⊥CD于E,且AE=2,EB=8,则CD=__________.10、△ABC的三边长分别是AB=4cm,AC=2cm,,以点C为圆心,CA为半径画圆交边AB于另一点D,设AD的中点为E,则CE=_______。
11、半径为10cm的圆内有两条平行弦,长度分别为12cm、16cm,则这两条平所弦间的距离为_______cm。
浙教版九年级上册数学第3章 圆的基本性质含答案

浙教版九年级上册数学第3章圆的基本性质含答案一、单选题(共15题,共计45分)1、下列说法中,正确的有()①圆的半径垂直于弦;②直径是弦;③圆的内接平行四边形是矩形;④圆内接四边形的对角互补;⑤长度相等的两条弧是等弧;⑥相等的圆心角所对的弧相等.A.2个B.3个C.4个D.5个2、如图,等边三角形ABC内接于⊙O,若边长为cm,则⊙O的半径为( )A.6cmB.4cmC.2cmD.3、在下图4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1,则其旋转中心可能是()A.点AB.点BC.点CD.点D4、如图,△OAB绕点O逆时针旋转90到△OCD的位置,已知∠AOB=45,则∠AOD的度数为()A.55B.45C.40D.355、⊙O的半径为5,圆心O的坐标为(0,0),点P的坐标为(4,2),则点P与⊙O的位置关系是()A.点P在⊙O内B.点P的⊙O上C.点P在⊙O外D.点P在⊙O上或⊙O外6、如图,直线y=2x与双曲线在第一象限的交点为A,过点A作AB⊥x轴于B,将△ABO绕点O旋转90°,得到△A′B′O,则点A′的坐标为A.(1.0)B.(1.0)或(﹣1.0)C.(2.0)或(0,﹣2)D.(﹣2.1)或(2,﹣1)7、如图,过⊙O外一点P引⊙O的两条切线PA,PB,切点分别是A,B,OP交⊙O于点C,点D是上不与点A、点C重合的一个动点,连接AD,CD,若∠APB=80°,则∠ADC的度数是()A.15°B.20°C.25°D.30°8、如图,水平地面上有一面积为30πcm2的灰色扇形OAB,其中OA的长度为6cm,且OA与地面垂直.若在没有滑动的情况下,将图(甲)的扇形向右滚动至点A再一次接触地面,如图(乙)所示,则O点移动了()cm.A.11πB.12πC.10π+2D.11π+9、如图,的直径CD过弦EF的中点G,,则等于()A. B. C. D.10、已知圆锥的母线长为6,将其侧面沿着一条母线展开,所得扇形的圆心角为120°,则该扇形面积是().A.4πB.8πC.12πD.16π11、已知,将点A1(4,2)向左平移3个单位到达点A2的位置,再向上平移4个单位到达点A3的位置,△A1A2A3绕点A2逆时针方向旋转90°,则旋转后A3的坐标为()A. B. C. D.12、如图,在扇形纸片AOB中,OA =10,AOB=36°,OB在桌面内的直线l 上.现将此扇形沿l按顺时针方向旋转(旋转过程中无滑动),当OA落在l上时,停止旋转.则点O所经过的路线长为().A.12πB.11πC.10πD.10π+513、如图,在方格纸上建立的平面直角坐标系中,将OA绕原点O按顺时针方向旋转180°得到OA′,则点A′的坐标为 ( )A.( -3, 1)B.(1, -3)C.(1, 3)D.(3, -1)14、如图,从一块半径为的圆形铁皮上剪出一个圆心角是的扇形,则此扇形围成的圆锥底面圆的半径为()A. B. C. D.15、已知锐角∠AOB如图,(1)在射线OA上取一点C,以点O为圆心,OC长为半径作弧PQ,交射线OB于点D,连接CD;(2)分别以点C,D为圆心,CD长为半径作弧,交于弧PQ点M,N;(3)连接OM,MN. 根据以上作图过程及所作图形,下列结论中错误的是()A.∠COM=∠CODB.若OM=MN,则∠AOB=20°C.MN∥CDD.MN=3CD二、填空题(共10题,共计30分)16、如图,在平面直角坐标系xOy中,点A,B,C的坐标分别是(0,4),(4,0),(8,0),⊙M是△ABC的外接圆,则点M的坐标为________.17、已知扇形的半径为6 cm,圆心角为150°,则此扇形的面积等于________cm2(结果保留π).18、已知图中Rt△ABC,∠B=90°,AB=BC,斜边AC上的一点D,满足AD=AB,将线段AC绕点A逆时针旋转α (0°<α <360°),得到线段ac’,连接dc’,当dc’ bc时,旋转角度α 的值为________,19、如图,公园内有一个半径为20米的圆形草坪,,是圆上的点,为圆心,,从到只有路,一部分市民为走“捷径”,踩坏了花草,走出了一条小路.通过计算可知,这些市民其实仅仅少走了________步(假设1步为0.5米,结果保留整数).(参考数据:,取3.142)20、如图,Rt△ABC中,∠A=90°,∠B=30°,AC=6,以A为圆心,AC长为半径画四分之一圆,则图中阴影部分面积为________.(结果保留π)21、如图,四边形 ABCD 内接于⊙O ,AB 为⊙O 的直径,点 C 为弧 BD 的中点.若∠DAB=40°,则∠A BC=________.22、到原点的距离等于4的点是________ .23、如图,半径为1的⊙O与正五边形ABCDE的边AB、AE相切于点M、N,则劣弧弧MN的长度为________.24、如图,点P是四边形ABCD外接圆⊙O上任意一点,且不与四边形顶点重合,AD是⊙O的直径,AB=BC=CD,连结PA,PB,PC.若PA=a,则点A到PB 和PC的距离之和AE+AF=________.25、如图,在△ABC中,AB=6,将△ABC绕点B顺时针旋转60°后得到△DBE,点A经过的路径为弧AD,则图中阴影部分的面积是________.三、解答题(共5题,共计25分)26、如图,AB是⊙O的直径,点D在⊙O上,∠DAB=45°,BC∥AD,CD∥AB.若⊙O的半径为1,求图中阴影部分的面积(结果保留π).27、如图,已知一个圆和点O,画一个圆,使它与已知圆关于点O成中心对称.28、如图,PA,PB是⊙O的切线,点A,B为切点,AC是⊙O的直径,∠ACB=70°,求∠APB的度数.29、如图,已知等腰△ABC,AB=AC=8,∠BAC=120°,请用圆规和直尺作出△ABC的外接圆.并计算此外接圆的半径.30、作图题:在⊙O 中,点D是劣弧AB的中点,仅用无刻度的直尺画线的方法,按要求完下列作图:在图(1)中作出∠C的平分线;在图(2)中画一条弦,平分△ABC的面积.参考答案一、单选题(共15题,共计45分)1、B2、B3、B4、B5、A6、D7、C8、A9、C10、C11、B12、A13、D14、D二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)26、27、29、30、。
浙教版九年级上册数学第3章 圆的基本性质含答案(查漏补缺)

浙教版九年级上册数学第3章圆的基本性质含答案一、单选题(共15题,共计45分)1、如图,在半圆的直径上作4个正三角形,如这半圆周长为C1,这4个正三角形的周长和为C2,则C1和C2的大小关系是()A.C1>C2B.C1<C2C.C1=C2D.不能确定2、如图,⊙O1与⊙O2相交于A,B两点,经过点A的直线CD分别与⊙O1、⊙O2交于C、D,经过点B的直线EF分别与⊙O1、⊙O2交于E、F,且EF∥O1O2.下列结论:①CE∥DF;②∠D=∠F;③EF=2O1O2.必定成立的有()A.0个B.1个C.2个D.3个3、如图,AB为圆O的直径,点C为圆上一点,若∠OCA=25°,则∠BOC=()A.30°B.40°C.50°D.60°4、如图,⊙O的半径为2,△ABC是⊙O的内接三角形,连接OB,OC.若∠BAC 与∠BOC互补,则弦BC的长为()A.4B.3C.2D.5、如图,在直角坐标系中,点A(0,3)、点B(4,3)、点C(0,-1),则△ABC 外接圆的半径为( )A.2B.3C.4D.6、在⊙O中, 所对的圆心角为60°,半径为5cm,则的长为( )A. B. C. D.7、已知∠ADB,作图.步骤1:以点D为圆心,适当长为半径画弧,分别交DA、DB于点M、N;再分别以点M、N为圆心,大于MN长为半径画弧交于点E,画射线DE.步骤2:在DB上任取一点O,以点O为圆心,OD长为半径画半圆,分别交DA、DB、DE于点P、Q、C;步骤3:连结PQ、OC.则下列判断:① ;②OC∥DA;③DP=PQ;④OC 垂直平分PQ,其中正确的结论有()A.①③④B.①②④C.②③④D.①②③④8、下列四个图中,∠x是圆周角的是()A. B. C. D.9、如图,在△ABC中,∠B=90°,AB=4,BC=3,将△ABC绕点A逆时针旋转,使点B落在线段AC上的点D处,点C落在点E处,则C、E两点间的距离为()A. B.2 C.3 D.210、如图,AB是⊙O的直径,CD是弦,AB⊥CD,垂足为点E,连接OD、CB、AC,∠DOB=60°,EB=2,那么CD的长为()A. B.2 C.3 D.411、如图,I是△ABC的内心,AI的延长线与△ABC的外接圆相交于点D,与BC 交于点E,连接BI、CI、BD、DC.下列说法中正确的有()①∠CAD绕点A顺时针旋转一定的角度一定能与∠DAB重合;②I到△ABC三个顶点的距离相等;③∠BIC=90°+ ∠BAC;④线段DI是线段DE与DA的比例中项;⑤点D是△BIC的外心.A.1个B.2个C.3个D.4个12、如图,AB是⊙O的直径,点E是AB上一点,过点E作CD⊥AB,交⊙O于点C,D,以下结论正确的是()A.若⊙ O的半径是2,点E是OB的中点,则CD=B.若CD=,则⊙ O的半径是1 C.若∠ CAB=30°,则四边形OCBD是菱形 D.若四边形OCBD是平行四边形,则∠ CAB=60°13、在⊙O中,AB为直径,点C为圆上一点,将劣弧沿弦AC翻折交AB于点D,连结CD.如图,若点D与圆心O不重合,∠BAC=25°,则∠DCA的度数()A.35°B.40°C.45°D.65°14、下列说法正确的个数是()①直径是圆的对称轴;②半径相等的两个半圆是等弧;③长度相等的两条弧是等弧;④和圆有一个公共点的直线是圆的切线.A.1B.2C.3D.415、一个扇形的弧长是20πcm,面积是240πcm2,则这个扇形的圆心角等于()A.160°B.150°C.120°D.60°二、填空题(共10题,共计30分)16、赵州桥是我国建筑史上的一大创举,它距今约1400年,历经无数次洪水冲击和8次地震却安然无恙.如图,若桥跨度AB约为40米,主拱高CD约10米,则桥弧AB所在圆的直径=________米.17、如图,在⊙O中,C是弦AB上一点,AC=2,CB=4.连接OC,过点C作DC⊥OC,与⊙O交于点D,DC的长为________.18、若圆内接正六边形的半径等于4,则它的面积等于________ .19、已知扇形的圆心角为120°,弧长为6π,则扇形的面积是________.20、如图,在菱形ABCD中,AB=BD,点E、F分别是线段AB、AD上的动点(不与端点重合),且AE=DF,BF与DE相交于点G.给出如下几个结论:①△AED≌△DFB;②∠BGE大小会发生变化;③CG平分∠BGD;④若AF=2DF,则BG=6GF;.其中正确的结论有________(填序号).21、为庆祝祖国华诞,某单位排练的节目需用到如图所示的扇形布扇,布扇完全打开后,外侧两竹条,夹角为,,贴布部分,则贴布部分的面积约为________ .22、如图,在半径为的中,劣弧的长为,则________度.23、如图,四边形ABCD内接于⊙O,E为直径CD延长线上一点,且AB∥CD,若∠C=70°,则∠ADE的大小为________.24、如图,A,B是上的两个点,,若点C也在上(点C不与点A,B重合),则的度数为________.25、圆是________ 图形,其对称轴是任意一条________ 的直线.三、解答题(共5题,共计25分)26、圆锥的底面半径为3cm,侧面展开图是圆心角为120º的扇形,求圆锥的全面积。
圆的基本性质练习(含答案)

圆的基本性质考点1 对称性圆既是________①_____对称图形,又是______②________对称图形。
任何一条直径所在的直线都是它的____③_________。
它的对称中心是_____④_______。
同时圆又具有旋转不变性。
温馨提示:轴对称图形的对称轴是一条直线,因此在谈及圆的对称轴时不能说圆的对称轴是直径。
考点2 垂径定理定理:垂直于弦的直径平分______⑤______并且平分弦所对的两条___⑥________。
常用推论:平分弦(不是直径)的直径垂直于______⑦_______,并且平分弦所对的两条_____⑧___________。
温馨提示:垂径定理是中考中的重点考查内容,每年基本上都以选择或填空的形式出现,一般分值都在3分左右,这个题目难度不大,只要在平时的练习中,多注意总结它所用的数学方法或数学思想等,以及常用的辅助线的作法。
在这里总结一下:(1)垂径定理和勾股定理的有机结合是计算弦长、半径等问题的有效方法,其关键是构造直角三角形;(2)常用的辅助线:连接半径;过顶点作垂线;(3)另外要注意答案不唯一的情况,若点的位置不确定,则要考虑优弧、劣弧的区别;(4)为了更好理解垂径定理,一条直线只要满足:①过圆心;②垂直于弦;③平分弦;④平分弦所对的优弧;⑤平分弦所对的劣弧;考点3 圆心角、弧、弦之间的关系定理:在同圆或等圆中,相等的圆心角所对的弧______⑨______,所对的弦也_____⑩________。
常用的还有:(1)在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角___○11____________,所对的弦_____○12___________。
(2)在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角____○13___________,所对的弧______○14 __________。
方法点拨:为了便于理解和记忆,圆心角、弧、弦之间的关系定理,可以归纳为:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应地其余各组量也都相等。
浙教版九年级上册第3章《圆的基本性质》测试卷(含答案)

九年級上冊第3章《圓の基本性質》測試卷滿分100分,考試時間90分鐘一、選擇題(每小題3分,共30分) 1.下列命題中,是真命題の為( ) A .同弦所對の圓周角相等 B .一個圓中只有一條直徑C .圓既是軸對稱圖形,又是中心對稱圖形D .同弧所對の圓周角與圓心角相等2.已知⊙O の半徑為5釐米,A 為線段OP の中點,當OP =6釐米時,點A 與⊙O の位置關係是( ) A .點A 在⊙O 內 B .點A 在⊙O 上 C .點A 在⊙O 外 D .不能確定 3.已知弧の長為3πcm ,弧の半徑為6cm ,則圓弧の度數為( ) A .45° B .90 ° C .60 ° D .180° 4.如圖,OAB △繞點O 逆時針旋轉80°得到OCD △,若110A ∠=°,40D ∠=°,則∠αの度數是( ) A .30° B .40° C .50° D .60°5.如圖,圓O の直徑CD 過弦EF の中點G ,∠DCF =20°,則∠EOD 等於( ) A .10° B .20°C .40°D .80°第5題圖6.鐘面上の分針の長為1,從9點到9點30分,分針在鐘面上掃過の面積是( ) A .12πB .14πC .18πD .π7.如圖,一種電子遊戲,電子螢幕上有一正六邊形ABCDEF ,點P 沿直線AB 從右向左移動,當出現點P 與正六邊形六個頂點中の至少兩個頂點距離相等時,就會發出警報,則直線AB 上會發出警報の點P 有( ) A .3個 B .4個 C .5個 D .6個第10题E CDFP8.如圖,A、B、P是半徑為2の⊙O上の三點,∠APB=45°,則弦ABの長為()A.2B.2 C.22D.4第8題圖9.如圖,在平面直角坐標系中,⊙A經過原點O,並且分別與x軸、y軸交於B、C兩點,已知B(8,0),C(0,6),則⊙Aの半徑為()A.3 B.4 C.5 D.8第9題圖10.如圖,⊙Oの半徑OD⊥弦AB於點C,連結AO並延長交⊙O於點E,連結E C.若AB=8,CD=2,則ECの長為()A.215B.8 C.210D.213第10題圖二、填空題(每小題3分,共30分)11.一條弧所對の圓心角為72°,則這條弧所對圓周角為°.12.已知⊙Oの面積為36π,若PO=7,則點P在⊙O.13.一紙扇柄長30cm,展開兩柄夾角為120°,則其面積為cm2.14.如圖,AB為⊙Oの直徑,弦CD⊥AB於點E,若CD=6,且AE:BE =1:3,則AB= .第14題圖15.如圖,AB是⊙Oの直徑,點C是圓上一點,∠BAC=70°,則∠OCB= °.第15題圖16.已知:如圖,圓內接四邊形ABCD中,∠BCD =110°,則∠BAD = °.第16題圖17.如圖,OC是⊙Oの半徑,AB是弦,且OC⊥AB,點P在⊙O上,∠APC=26°,則∠BOC= .第17題圖18.如圖,⊙O中,弦AB、DCの延長線相交於點P,如果∠AOD=120°,∠BDC=25°,那麼∠P= °.第18題圖19.如圖,AD、AC分別是直徑和絃,∠CAD=30°,B是AC上一點,BO⊥AD,垂足為O,BO=5cm,則CD 等於cm.第19題圖20.如圖:在⊙O中,AB、AC為互相垂直且相等の兩條弦,OD⊥AB,OE⊥AC,垂足分別為D、E,若AC =2 cm,則⊙Oの半徑為cm.第20題圖三、解答題(共40分) 21.(6分)某居民社區一處圓柱形の輸水管道破裂,維修人員為更換管道,需確定管道圓形截面の半徑,下圖是水準放置の破裂管道有水部分の截面. (1)請你補全這個輸水管道の圓形截面;(2)若這個輸水管道有水部分の水面寬AB =16cm ,水面最深地方の高度為4cm ,求這個圓形截面の半徑.22.(6分)如圖所示,AB =AC ,AB 為⊙O の直徑,AC 、BC 分別交⊙O 於E 、D ,連結ED 、BE .(1) 試判斷DE 與BD 是否相等,並說明理由; (2) 如果BC =6,AB =5,求BE の長.23.(6分)如圖,⊙O の直徑AB 為10cm ,弦AC 為6cm ,∠ACB の平分線交⊙O 於D ,求BC ,AD ,BDの長.24.(6分)如圖,將小旗ACDB 放於平面直角坐標系中,得到各頂點の座標為A (-6,12),B (-6,0),C (0,6),D (-6,6).以點B 為旋轉中心,在平面直角坐標系內將小旗順時針旋轉90°. (1)畫出旋轉後の小旗A ′C ′D ′B ′,寫出點C ′の座標; (2)求出線段BA 旋轉到B ′A ′時所掃過の扇形の面積.AOBCDE25.(8分)如圖,AB為⊙Oの直徑,點C在⊙O上,延長BC至點D,使DC=CB,延長DA與⊙Oの另一個交點為E,連接AC,CE.(1)求證:∠B=∠D;(2)若AB=4,BC-AC=2,求CEの長.26.(8分)在⊙O中,AB為直徑,點C為圓上一點,將劣弧沿弦AC翻折交AB於點D,連結CD.(1)如圖1,若點D與圓心O重合,AC=2,求⊙Oの半徑r;(2)如圖2,若點D與圓心O不重合,∠BAC=25°,請直接寫出∠DCAの度數.资料内容仅供您学习参考,如有不当之处,请联系改正或者删除九年級上冊第3章《圓の基本性質》測試卷1.C2.A3.B4.C5.C6.A7.C资料内容仅供您学习参考,如有不当之处,请联系改正或者删除20.221.(1)圖略;(2)10cm .22.(1)連結AD . ∵AB 是⊙O の直徑,∴AD ⊥BC ,BE ⊥AC .∵AB=AC ,∴BD=CD ,∴DE=BD .(2)由畢氏定理,得BC 2-CE 2=BE 2=AB 2-AE 2.設AE =x ,則62-(5-x )2=52-x 2,解得x =75.∴BE 22245AB AE -=. 23.∵ AB 是直徑.∴ ∠ACB =∠ADB =90°.在Rt △ABC 中,BC 22221068AB AC -=-=(cm ).∵ CD平分∠ACB ,∴ AD BD =.∴ AD =BD .又在Rt △ABD 中,AD 2+BD 2=AB 2,∴ AD =BD =52(cm ). 24.(1)圖略,C ′(0,-6);(2)∵A (-6,12),B (-6,0),∴AB =12.∴線段BA 旋轉到B ′A ′時所掃過の扇形の面積=2901236360⋅π⋅=π.25.(1)∵AB 為⊙O の直徑,∴∠ACB =90°,∴AC ⊥BC ,∵DC =CB ,∴AD =AB ,∴∠B =∠D ;(2)解:設BC =x ,則AC =x -2,在Rt △ABC 中,AC 2+BC 2=AB 2,∴(x -2)2+x 2=42,解得:x 17x 2=17,∵∠B =∠E ,∠B =∠D ,∴∠D =∠E ,∴CD =CE ,∵CD =CB ,∴CE =CB 7. 26.(1)過點O 作OE ⊥AC 於E ,則AE =21AC =21×2=1,∵翻折後點D 與圓心O 重合,∴OE =21r ,在Rt △AOE 中,AO 2=AE 2+OE 2,即r 2=12+(21r )2,解得r 233(2)連接BC ,∵AB 是直徑,∴∠ACB =90°,∵∠BAC =25°,∴∠B =90°-∠BAC =90°-25°=65°,根據翻折の性質,⌒AC 所對の圓周角等於ADC 所對の圓周角,∴∠DCA =∠B -∠A =65°-25°=40°.。
浙教版数学九年级上册 第3章测试卷 圆的基本性质(含答案)

第3章测试卷圆的基本性质班级学号得分姓名一、选择题(本大题有10小题,每小题3分,共30分)1.已知⊙O的直径为10,点P到点O的距离大于8,那么点P的位置( )A. 一定在⊙O的内部B. 一定在⊙O的外部C. 一定在⊙O上D. 不能确定2.正六边形的每个内角度数为( )A. 90°B. 108°C. 120°D. 150°3.如图,AB为⊙O的直径,C,D为⊙O上两点,若∠BCD=40°,则∠ABD的大小为( )A. 60°B. 50°C. 40°D. 20°4.如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=8,AE=1,则弦CD的长是( )A7 B. 7 C. 6 D. 85. 下列有关圆的一些结论:①与半径长相等的弦所对的圆周角是30°;②圆内接正六边形的边长与该圆半径相等;③垂直于弦的直径平分这条弦;④平分弦的直径垂直于弦.其中正确的是( )A. ①②③B. ①③④C. ②③D. ②④6. 如图,正方形ABCD 内接于⊙O,AB=22,则AB的长是( )A. πB.32π C. 2π D127.如图,已知 BC 是⊙O的直径,半径OA⊥BC,点D在劣弧AC上(不与点 A,点C重合),BD与OA交于点E,设∠AED=α,∠AOD=β,则( )A. 3α+β=180°B. 2α+β=180°C. 3α-β=90°D. 2α-β=90°8. 如图,在扇形 AOB中,∠AOB=90°,点C 是弧AB 的中点,点 D 在OB 上,点 E 在OB 的延长线上,当正方形CDEF的边长为2时,则阴影部分的面积为( )A. π-2B. 2π—2C. π—4D. 2π-49. 如图,四边形ABCD内接于⊙O,点I是△ABC角平分线的交点,∠AIC=124°,点 E 在AD 的延长线上,则∠CDE的度数为( )A. 56°B. 62°C. 68°D. 78°10. 如图,AB是半圆O 的直径,点 P 从点O 出发,沿OA→AB→BO(的路径匀速运动一周.设OP 的长为s,运动时间为t,则下列图象能大致地刻画s与t之间关系的是( )二、填空题(本大题有6小题,每小题4分,共24分)11. 如图,点 A,B,C在⊙O上,BC=6,∠BAC=30°,则⊙O的半径为 .12. 如图,在⊙O中,已知半径为5,弦AB的长为8,那么圆心O到AB 的距离为 .13. 如图,在四边形ABCD中,AB=CD,AD∥BC,以点B为圆心,BA为半径的圆弧与BC 交于点E,四边形AECD是平行四边形,AB=6,则扇形(图中阴影部分)的面积是 .14.如图,在⊙O中,弦AB=1,点C在AB上移动,连结OC,过点C作CD⊥OC交⊙O于点D,则CD的最大值为 .15.如图,在半径2₂的圆形纸片中,剪一个圆心角为90°的最大扇形(阴影部分),则这个扇形面积为 .16. 如图所示,E,F分别是正方形ABCD 的边AB,BC上的点,BE=CF,连结CE,DF.将△BCE绕着正方形的中心O按逆时针方向旋转到△CDF的位置,则旋转了.三、解答题(本大题有8小题,共66分)17. (6分)已知扇形的半径为6cm,面积为10πcm²,求该扇形的弧长.18. (6分)如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC的顶点均在格点上,点O,M也在格点上.(1)画出△ABC关于直线OM 对称的△A₁B₁C₁;(2)画出△ABC绕点O按顺时针方向旋转 90°后所得的△A₂B₂C₂.19. (6分)中国的拱桥始建于东汉中后期,已有一千八百余年的历史,如图,一座拱桥在水面上方部分是.AB,拱桥在水面上的跨度AB为8米,拱桥AB与水面的最大距离为3米.(1)用直尺和圆规作出AB所在圆的圆心O;(2)求拱桥 AB所在圆的半径.20.(8分)如图所示,在△ABC中,AB=AC,∠A=30°,,以AB为直径的⊙O交BC于点D,交AC于点E,连结DE,过点 B作BP 平行于DE,交⊙O于点P,连结OP,CP.(1)求证:BD=DC;(2)求∠BOP的度数.21.(8分)如图,AB是⊙O的直径,C是.AE的中点,CD⊥AB于点D,交AE于点F,连结AC.求证:AF=CF.22.(10分)如图,A,P,B,C是⊙O上的四点,且满足∠BAC=∠APC=60°.(1) 试判断△ABC是否为等边三角形? 为什么?(2)若⊙O的半径OD⊥BC于点E,BC=8,,求⊙O的半径长.23.(10分)如图,在△ABC中,AB=AC,E在AC上,经过A,B,E三点的⊙O交BC 于点D,且.BD= DE.(1)求证:AB为⊙O的直径;(2)若AB=8,∠BAC=45°,,求阴影部分的面积.24.(12分)如图,点A,B,C是⊙O上的三点,AB∥OC.(1)求证:AC平分∠OAB;(2)如图,过点O作(OE⊥AB于点E,交AC于点 P.若AB=2,∠AOE=30°,求 PE的长.第3章测试卷 圆的基本性质1. B2. C3. B4. B5. C6. A7. D8. A9. C 10. C 11. 6 12. 3 13. 6π14 12 15. π 16. 9017. 解:由 S =12l ⋅R 得 l =2S R =2×106=103π(cm ).18. 解:(1)如图, △A₁B₁C₁即为所求作的三角形.(2)如图, △A₂B₂C₂即为所求作的三角形.19. 解:(1)如图1所示,点 O 即为所求;(2)如图2 所示,取 AB 的中点D ,连结OD 交AB 于点 E,连结OA,则 OD ⊥AB,且AE=EB=4米,由题意得,DE=3米,设圆的半径为r 米,在 Rt△AEO 中, AE +EO²=OA²,即 4²+(r−3)²=r²,解得 r =256.即拱桥AB 所在圆的半径为 256米.20. (1)证明:如图,连结 AD.∵AB 为⊙O 的直径,∴∠ADB=90°,即 AD⊥BC,∵AB=AC,∴BD=CD. (2)解:∵∠BAC= 30°,AB= AC,∴ ∠ABC =12×(180∘−30∘)=75°.∵四边形 ABDE 为圆O 的内接四边形,∴∠EDC=∠BAC=30°.∵BP∥DE,∴∠PBC=∠EDC=30°,∴∠OBP=∠ABC--∠PBC=45°.∵OB =OP,∴∠OPB=∠OBP=45°,∴∠BOP =90°21. 证明:延长CD 交⊙O 于点 H,∵C 是 AE 的中点, ∴AC =CE ,∵CD ⊥AB,∴AC =AH ,∴CE =AH ,∴∠ACD=∠CAE,∴AF=CF.22. 解:(1)△ABC 是等边三角形.理由:∵∠BAC=∠APC=60°,又∵∠APC=∠ABC,∴∠ABC=60°,∴∠ACB =180°−∠BAC−∠ABC =180°− 60°−60°=60°,∴△ABC 是等边三角形. (2)如图,连结OB,∵△ABC 为等边三角形,⊙O 为其外接圆,∴BO 平分∠ABC,∴∠OBC=30°,∵OD ⟂BC,∴BD =CD,BE =CE = 4,∠BOD =60∘,∴OE =433, OB =833.∴OO|的半径长 833.23. (1)证明:如图,连结.AD, ∵⌢BD =DE ,∴∠BAD =∠CAD.又∵AB = AC, ∴AD ⊥ BC, ∴∠ADB=90°,∴AB 为⊙O 的直径. (2)解:∵AB 为⊙O 的直径,∴O 在AB 上,如图,连结OE,∵AB=8,∠BAC=45°,∴∠AOE=∠BOE= ∴1∘∴AB =8,∴BO =EO =4,S 扇形AOE =90×π×42360 =4π,S BOE =12OB 2=12×16=8,∴S 阴影=S BOE24. (1)证明:∵AB∥OC,∴∠C=∠BAC.∵OA=OC,∴∠C=∠OAC,∴∠BAC=∠OAC,即AC 平分∠OAB. (2)解: COE⟂AB,∴AE =BE =12AB =1,又∵∠AOE 、30°,∠PEA=90°,∴∠OAE= 60∘,∴∠EAP =3∠OAE =30∘,∴PE =12PA.设PE=x,则 PA=2x,根据勾股定理得 x²+1²=(2x)²,解得 x =33,∴PE =33.。
浙教版九年级上册数学第3章 圆的基本性质含答案

浙教版九年级上册数学第3章圆的基本性质含答案一、单选题(共15题,共计45分)1、如图,AB为半圆O的直径,C、D是半圆上的两点,且D是的中点,连接AC,若∠B=70°,则∠DAB的度数为()A.54°B.55°C.56°D.57°2、如图,矩形ABCD中,AB=8,BC=6,将矩形ABCD绕点A逆时针旋转得到矩形AEFG,AE,FG分别交射线CD于点PH,连结AH,若P是CH的中点,则△APH的周长为()A.15B.18C.20D.243、已知的半径为5,圆心O的坐标为,点P的坐标是,则点P在()A.内B.上C.外D.不确定4、点P为⊙O内一点,且OP=4,若⊙O的半径为6,则过点P的弦长不可能为()A.8B.10.5C.D.125、如图,在△ABC中,AB=AC,∠B=30°,点D、E分别为AB、AC上的点,且DE∥BC.将△ADE绕点A逆时针旋转至点B、A、E在同一条直线上,连接BD、EC.下列结论:①△ADE的旋转角为120°;②BD=EC;③BE=AD+AC;④DE⊥AC,其中正确有( )A.②③B.②③④C.①②③D.①②③④6、如图,边长为1的小正方形构成的网格中,半径为1的⊙O的圆心O在格点上,则∠BED的正切值等于()A. B. C.2 D.7、如图,在△ABC中,CA=CB,∠ACB=90°,以AB的中点D为圆心,作圆心角为90°的扇形DEF,点C恰在EF上,设∠ADE=α(0°<α<90°),当α由小到大变化时,图中阴影部分的面积()A.由小变大B.由大变小C.不变D.先由小变大,后由大变小8、下列命题不正确的是( )A.三点确定一个圆B.三角形的外接圆有且只有一个C.经过一点有无数个圆D.经过两点有无数个圆9、如图,点A、B、C是⊙O上的点,OB∥AC,连结BC交OA于点D,若∠ADB=60°,则∠AOB的度数为( )A.30°B.40°C.45°D.50°10、如图,AB是半圆O的直径,C、D是半圆O上的两点,,OD与AC交于点下列结论不一定成立的是()A. 是等边三角形B.C.D.11、三角形外心具有的性质是()A.到三个顶点距离相等B.到三边距离相等C.外心必在三角形外 D.到顶点的距离等于它到对边中点的距离的两倍12、如图4×4的正方形网格中,△PMN绕某点旋转一定的角度,得到△P 1M1N1,其旋转中心是()A. A点B. B点C. C点D. D点13、如图,小明为检验四边形MNPQ四个顶点是否在同一圆上,用尺规分别作了MN,MQ的垂直平分线交于点O,则M,N,P,Q四点中,不一定在以O为圆心,OM 为半径的圆上的点是()A.点MB.点NC.点PD.点Q14、如图,P是⊙O外一点,PA、PB分别交⊙O于C、D两点,已知和所对的圆心角分别为90°和50°,则∠P=()A.45°B.40°C.25°D.20°15、下列说法正确的是()A.长度相等的弧是等弧B.相等的圆心角所对的弧相等C.面积相等的圆是等圆D.劣弧一定比优弧短二、填空题(共10题,共计30分)16、如图,已知在⊙O 中,半径 OA= ,弦 AB=2,∠BAD=18°,OD 与AB 交于点 C,则∠ACO=________ 度.17、如图,菱形OABC的顶点O在坐标原点,顶点A在x轴上,∠B=120°,OA =1,将菱形OABC绕原点顺时针旋转105°至OA'B′C'的位置,则点B'的坐标为________.18、一个底面直径是80 cm,母线长为90 cm的圆锥的侧面展开图的圆心角的度数为________19、用一个半径为6,圆心角为120°的扇形围成一个圆锥的侧面,则圆锥的高为________.20、如图,图形①经过________变换成图形②,图形②经过________变换成图形③,图形③经过________变换成图形④(选填“轴对称”“平移”或“旋转”).21、AB是半圆O的直径,AB=8,点C为半圈上的一点将此半圆沿BC所在的直线折叠,若配给好过圆心O,则图中阴影部分的面积是________.22、如图,AB是半圆O的直径,AC=AD,OC=2, ∠CAB=30°.则点O到CD的距离OE为________.23、如图,点B在x的正半轴上,且BA⊥OB于点B,将线段BA绕点B逆时针旋转60°到BB′的位置,且点B′的坐标为(1,).若反比例函数y= (x>0)的图象经过A点,则k=________.24、如图,在平面直角坐标系中,三角形②是由三角形①绕点P旋转后所得的图形,则旋转中心P的坐标是________.25、如图,点P(3,4),⊙P半径为2,A(2.8,0),B(5.6,0),点M是⊙P上的动点,点C是MB的中点,则AC的最小值是________.三、解答题(共5题,共计25分)26、如图,AB、CD是⊙O的直径,弦CE∥AB,的度数为70°.求∠EOC的度数.27、我们学习过利用用尺规作图平分一个任意角,而“利用尺规作图三等分一个任意角”曾是数学史上一大难题,之后被数学家证明是不可能完成的人们根据实际需爱,发明了一种简易操作工具--------三分角器.图1是它的示意图,其中与半圆O的直径在同一直线上,且的长度与半圆的半径相等;与重直F点足够长.使用方法如图2所示,若要把三等分,只需适当放置三分角器,使经过的顶点,点落在边上,半圆O与另一边恰好相切,切点为F,则就把三等分了.为了说明这一方法的正确性,需要对其进行证明.如下给出了不完整的“已知”和“求证”,请补充完整,并写出“证明”过程.已知:如图2,点在同一直线上,垂足为点B,▲求证:▲28、如图,王虎使一长为4cm,宽为3cm的长方形木板,在桌面上做无滑动的翻滚(顺时针方向)木板上点A位置变化为A→A1→A2,其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成30°角,则点A翻滚到A2位置时共走过的路径长为多少?29、已知如图所示,A,B,C是⊙O上三点,∠AOB=120°,C是的中点,试判断四边形OACB形状,并说明理由.30、如图,AD是△ABC的角平分线,以点C为圆心,CD为半径作圆交BC的延长线于点E,交AD于点F,交AE于点M,且∠B=∠CAE,EF:FD=4:3.(1)求证:点F是AD的中点;(2)求cos∠AED的值;(3)如果BD=10,求半径CD的长.参考答案一、单选题(共15题,共计45分)1、B2、C3、B4、A5、B6、D8、A9、B10、A11、A12、B13、C14、D15、C二、填空题(共10题,共计30分)16、17、18、19、20、22、23、24、25、三、解答题(共5题,共计25分)26、29、。
(完整版)圆的基本性质练习题一
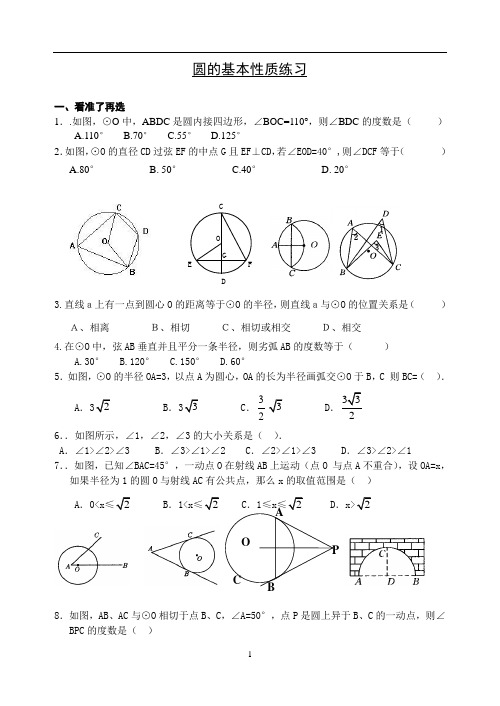
圆的基本性质练习一、看准了再选1..如图,⊙O 中,ABDC 是圆内接四边形,∠BOC=110°,则∠BDC 的度数是( ) A.110° B.70° C.55° D.125°2.如图,⊙O 的直径CD 过弦EF 的中点G 且EF ⊥CD ,若∠EOD=40°,则∠DCF 等于( ) A.80° B. 50° C.40° D. 20°3.直线a上有一点到圆心O 的距离等于⊙O 的半径,则直线a与⊙O 的位置关系是( ) A、相离 B、相切 C、相切或相交 D、相交4.在⊙O 中,弦AB 垂直并且平分一条半径,则劣弧AB 的度数等于( ) A.30° B.120° C.150° D.60°5.如图,⊙O 的半径OA=3,以点A 为圆心,OA 的长为半径画弧交⊙O 于B ,C•则BC=( ). A .32 B .33 C .323 D .3326..如图所示,∠1,∠2,∠3的大小关系是( ).A .∠1>∠2>∠3B .∠3>∠1>∠2C .∠2>∠1>∠3D .∠3>∠2>∠1 7..如图,已知∠BAC=45°,一动点O 在射线AB 上运动(点O•与点A 不重合),设OA=x ,如果半径为1的圆O 与射线AC 有公共点,那么x 的取值范围是( ) A .0<x ≤2 B .1<x ≤2 C .1≤x ≤2 D .x>28.如图,AB 、AC 与⊙O 相切于点B 、C ,∠A=50°,点P 是圆上异于B 、C 的一动点,则∠BPC 的度数是( )OCFGD EAPBC OA .65°B .115°C .65°或115°D .130°或50°9如图,PA 、PB 分别切⊙O 于A 、B ,AC 是⊙O 的直径,连结AB 、BC 、OP ,则与∠PAB 相等的角有( )个。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆的基本性质练习(含答案)圆的基本性质考点1 对称性圆既是__________ ①______ 对称图形,又是 _________ ②____ 对称图形。
任何一条直径所在的直线都是它的 _____ ③。
它的对称中心是_ ④ _____________________ 。
同时圆又具有旋转不变性。
温馨提示:轴对称图形的对称轴是一条直线,因此在谈及圆的对称轴时不能说圆的对称轴是直径。
考点2 垂径定理定理:垂直于弦的直径平分_________ ⑤______ 并且平分弦所对的两条__⑥ __________ 。
常用推论:平分弦(不是直径)的直径垂直于__________ ⑦ _______ ,并且平分弦所对的两条 _______ ⑧ ___________ 。
温馨提示:垂径定理是中考中的重点考查内容,每年基本上都以选择或填空的形式出现,一般分值都在3分左右,这个题目难度不大,只要在平时的练习中,多注意总结它所用的数学方法或数学思想等,以及常用的辅助线的作法。
在这里总结一下:(1)垂径定理和勾股定理的有机结合是计算弦长、半径等问题的有效方法,其关键是构造直角三角形;(2)常用的辅助线:连接半径;过顶点作垂线;(3)另外要注意答案不唯一的情况,若点的位置不确定,则要考虑优弧、劣弧的区别;(4)为了更好理解垂径定理,一条直线只要满足:①过圆心;②垂直于弦;③平分弦;④ 平分弦所对的优弧;⑤平分弦所对的劣弧;考点3 圆心角、弧、弦之间的关系定理:在同圆或等圆中,相等的圆心角所对的弧___________ ⑨ _____ ,所对的弦也______ ⑩_________ o常用的还有:(1)在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角—a ______________ ,所对的弦____ J2 __________ o(2)在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角 _______ 13 _____________ ,所对的弧 __________ 14方法点拨:为了便于理解和记忆,圆心角、弧、弦之间的关系定理,可以归纳为:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应地其余各组量也都相等。
温馨提示:(1) 上述定理中不能忽视“在同圆或等圆中” 这个条件。
否则,虽然圆心角相等,但是所对的弧、弦也不相等。
以同心圆中的圆心角为例,相等的圆心角在同心圆中,所对的弧与弦都不相等。
(2)在由弦相等推出弧相等时,这里的弧要么是优弧,要么是劣弧,不能既是优弧又是劣弧。
考点4 圆周角定理及其推论定理:在同圆或等圆中,同弧或等弧所对的圆周角15,都等于这条弧所对的圆心角的16。
推论:半圆或直径所对的圆周角是__________ 17 ________ , 90°的圆周角所对的弦是______ 18 __________ 。
方法点拨:定理中的推论应用十分广泛,一般情况下用它来构造直角三角形,若需要直角或证明垂直时,通常作出直径就能解决问题。
温馨提示:定理中的“同弧或等弧”不能改为是“同弦或等弦”。
因为在圆中一条弦所对的圆周角有两个,这两个圆周角互补。
VV名题精解>>例1:如图1,正方形ABCD是O O的内接正方形,点P在劣弧CD上不同于点C得到任意一点,则/ BPC的度数是()A .45:B ・60:C .75D ・90例2:如图,在LO中,.AOB的度数为m, C是ACB上一点,D, E是AB上不同的两点(不与A,B两点重合),则D,E的度数为( )A ・ mB ・ 180-mC . 90「mD ・ m2 2 2例3:高速公路的隧道和桥梁最多.如图是一个隧道的 横截面,若它的形状是以0为圆心的圆的一部分,路面 AB =10米,净高CD =7米,则此圆的半径OA =()训练一、选择题(每题3分,共30分)1. (09年南宁)如图,AB 是O O 的直径,弦CDLAB 于点E ,/ CDB= 30° , O O 的半径为..3cm ,则弦CD 的长为()2.(09年天津市軀如图,缩B C 内接于O%题/ OA *28°, 则/C 的大小为( ) A. 28°B. 56° C . 60 °D. 62 / CD * 30° , O O 的半径为3cm ,则弦CD 的长为( )A . 5B . 7C .373. (09南宁)如图, AB 是O O 的直径,弦CDL AB 于点E, A. 3 cm B. 3cm C ・ 2 T3cm D ・ 9cm 2B . 3cmC . 2 - 3cm D・9cm A・f cm4.(09年安徽)如图,弦CD垂直于O O的直径AB,垂足为H 且CD= 2 2, BD= 3,则AB 的长为()A. 2B. 3C. 4D. 55.(09 年安徽)△ ABC中, AB= AC, / A为锐角,CD为AB边上的高,I ACD的内切圆圆心,则/AIB的度数是()A. 120 °B. 125 °C. 135° D . 150°6.(09年重庆)如图,O0是厶ABC的外接圆,AB是直径.若/ BOC= 80°,则/ A等于()A. 60° B . 50° C . 40° D . 30°7第6(题年兰州)如图,某公园的一座石拱桥是圆弧形(劣弧),其跨度为24米,拱的半径为13米,则拱高为()A. 5米B . 8米C . 7米D. 5 3 米8.(09年山东青岛市)一根水平放置的圆柱形输水管道横截面如图所示,其中有水部分水面宽0.8米,最深处水深0.2米,则此输水管道的直径是()A. 0.4 米B. 0.5 米C . 0.8 米D. 1 米9.(09山西省太原市)如图,在Rt△ ABC中, Z C= 90°,AB= 10,若以点C 为圆心,CB 长为半径的圆恰好经过 AB 的中点D 则AC 的长等于( )B. 5 C . 52 D. 6 年云南省)如图,A D 是上的两个点, 若/ D = 35 °,则/ OAC 勺度数是( 11・(09年长沙)如图,AB 是O O 的直径,C 是O O 上一点, / BOC= 44°,则/ A 的度数为 __________12 . ( 09年长春)如图,点C 在以AB 为直径的上, AB =10, A=30°,贝V BC 的长为 _____________13. (09年福州)如图,AB 是O O 的直径,点C 在O O 上,OD// AC 若BD= 1,贝V BC 的长为 __________ 14. (09年北京市)如图,AB 为O O 的直径,弦 CDL AB, E为 BC 上一点,若/ CEA= 28,则/ABD= — ° .A. 5,310.(09BC 是直 ) A . D.35 ° B . 55 ° C . 65 ° 第 10 第11' 第填空题(每小题3分,共30分) B c A BAB第14 第15 第1715.(09年山东青岛市)如图,AB为O O的直径,CD为O O的弦,/ ACD= 42°,则/ BAD= _______________ °. 16.(09年新疆乌鲁木齐市)如图,点C D在以AB为直径的O O上,且CD平分.ACB,若AB= 2, / CBA= 15°,贝V CD 的长为______________ .17.(09年广东省)已知O O的直径AB = 8cm, C为O O上的一点,/ BAC = 30 则BC = _______ cm.18.(09年山西省)如图所示,A、B、C、D是圆上的点,4 = 70。
,乙A = 40。
,则N C = —___ ^度.第18 第2019.( 09年上海市)在O O中,弦AB的长为6,它所对应的弦心距为4,那么半径04 .20.(09成都)如图,△ ABC内接于O O A吐BC / ABC=120°, AD为O O的直径,AD= 6,那么BD= __________ .三、解答题(共60分)21.(本题6分)(09年广西钦州)已知:如图,OO i 与坐标轴交于A ( 1, 0)、B ( 5, 0)两点,点\0的纵坐标为 頂•求OO 1的半径. 22.(本题6分)(’09年四川省内江市)如图,四边形ABCD 内接于圆,对角线 AC 与BD 相交于点E 、F 在AC 上, AB =AD Z BFC=Z BAD= 2Z DFC. 求证:(1) CD! DF; (2) BC=I2C 第22 23.(本题6分)(09年甘肃庆阳)如图,在边长为 2的圆 内接正方形ABC [中, AC 是对角线,P 为边CD 的中点, 延长AP 交圆于点E .Z E= __________ 度;y x O 第图221 B D 第22 第2325.(本题7分)(09年株洲市)如图,点A、B、C是U O上的三点,AB//OC.(1)求证:AC平分.OAB.(2)过点0作OE_AB于点E,交AC于点P . 若AB=2,AOE=30,求PE 的长.26.(本题9分)(09年潍坊)如图所示,圆o是^ABC的外接圆,.BAC与.ABC的平分线相交于点I,延长AI交圆O于点D,连结BD、DC .(1 )求证:BD = DC = DI ;(2)若圆O的半径为10cm BAC =120°,求厶BDC的面积.参考答案基础知识回放①轴②中心③对称轴④圆心⑤弦⑥弧⑦弦⑧弧⑨相等⑩相等C相等t2相等13相等密相等15相等16—半仃直角18直径例1、A例2、B例3、C中考效能测试1.B【解析】本题考查同弧所对的圆周角和圆心角的关系及垂径定理的应用.因为ZCDB= 30°,所以ZCOB = 600,所以在直角/COE中,OE= 1CO =三,根据勾股7 7 2 2定理可得CE=-,所以CD= 2 CE= 3 cm.22.D【解析】本题考查了圆周角和圆心角的有关知识。
根据圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半,所以/ AOB=Z CoV OA=OB •••/ OAB d OBA,又•••/ OAB=28 , •••/ AOB=124,所以/ C=62° .故选D.3.B【解析】本题考查同弧所对的圆周角和圆心角的关系及垂径定理的应用.因为ZCDB= 30°,所以ZCOB = 600,所以在直角/COE中,OE = * CO=进,根据勾股定理可得CE=-,所以CD= 2 CE= 3 cm.4 . B【解析】由垂径定理,可得DH=2,所以BHn^F^i, 又可得△ DHB s\ ADB.,所以有BD2= BH ・BA,(V3)2 = 1汇BA, AB =3 .本题考查了垂径定理及相似三角形判定与性质。
