化工热力学第二章 流体的p-V-T关系和状态方程
合集下载
化工热力学第二章 流体的pVT关系
南阳理工学院
生化学院
化工热力学
第二章
流体的PVT关系 关系 流体的
（3）理想气体状态方程的变型
G G pV = RT ........... n = M M
气体密度：ρ = G = pM .......... ( Kg / m3 ) 气体密度：
V RT
p1V1 p2V2 = = nR T1 T2
( ∂ P ∂V )T=T = 0 C 2 (∂ P ∂V2 )T=TC = 0
化工热力学
第二章
流体的PVT关系 关系 流体的
∂V = βV ∂T p
∂V = − κV ∂p T
dV = β dT − κdp V
对于液体，由于其具有不可压缩性，体积膨胀系数和等温 对于液体，由于其具有不可压缩性， 压缩系数是温度和压力的弱函数， 压缩系数是温度和压力的弱函数，其数值可以从文献或工具书 中查到。因此，在液体的温度和压力变化不大时， 中查到。因此，在液体的温度和压力变化不大时，可以将体积 膨胀系数和等温压缩系数当作常数，则 膨胀系数和等温压缩系数当作常数，
南阳理工学院
生化学院
化工热力学
第二章
流体的PVT关系 关系 流体的
2.1 纯物质的 纯物质的p-V-T关系 关系
流体的PVT数据是化工生产﹑工程设计和科学 数据是化工生产﹑ 流体的 数据是化工生产 研究最为基本的数据， 研究最为基本的数据，它们是化工热力学的基础 数据。这些数据是可以直接测量的， 数据。这些数据是可以直接测量的，也可以通过 关联计算得到。要进行关联计算，首先，我们就 关联计算得到。要进行关联计算，首先， 要搞清楚纯物质PVT之间有何种数学关系。 之间有何种数学关系。 要搞清楚纯物质 之间有何种数学关系 三维立体图2-1是典型的纯物质的 关系图。 三维立体图 是典型的纯物质的PVT关系图。 是典型的纯物质的 关系图
化工热力学-流体的 p-V-T 关系
Z
Z
Z
1
q
Z
或
Z
0.026196
Z
Z
0.026196
1.026196 Z 6.6060 0.026196
将 Z= 代入上式右边，迭代计算后得到收敛值Z=0.04331。
V l ZRT 0.043318.314350 133.3 cm3mol1
p
0.9457
为了比较计算结果，在例2/5-1的情况下，运用四种立方型状态 方程所计算得到的V v及V l 值列表如下：
第二章 流体的 p-V-T 关系
（一）纯流体的三维相图
自由度与相律
（二）纯流体的二维相图
异戊烷的p-V图
p-T相图
T-V图
（三）纯流体 pVT 行为的模型化
→ 什么是状态方程？
f p,V,T 0
dV
V T
p
dT
V p
T
dp
V=V(T,p)
p=p(T,V )
（四）理想气体
只有在Zc相等的条件下，对比态原理才能成立
以ω为第三参数的对应状态原理
Z f pr ,Tr ,
偏心因子
Pitzer： 物质对比饱和蒸汽压的对数，与对比温度的倒数呈 下列线性关系
log
prS
a 1
1 Tr
prS
pS pc
球形分子虽然临界参数相差很大，但在Tr=0.7时，对比蒸气压 logprS = -1 。
ZC 3/8 1/3 1/3 0.30740
临界压缩因子Zc
VDW: 3/8 RK/SRK: 1/3 PR: 0.3047
立方型状态方程的数值求解
p
RT
V b
V
化工热力学第二章liyibing
Z 1 B V
(2-9) (2-10a) (2-10b)
1 B/ p
1 Bp RT
实践表明，当温度低于临界温度、压力不高于1.5MPa时，用二阶舍项的维里 方程可以很精确地表示气体的p-V-T关系，当压力高于5.0MPa时，需要用更多阶 的维里方程。
2.2.3 立方型状态方程
立方型状态方程是指方程可展开为体积 (或密度) 的三次方形式。这类方程能够 解析求解，精度较高，又不太复杂，很受工程界欢迎。
等温线在两相区的水平段随温度的升高而逐渐变短，到 临界温度时最后缩成一点C。临界等温线在图2-3中临界点 为水平拐点，其斜率和曲率均为零，数学上表示为
( )
2 p
p V T Tc
0
(2-1)
( V 2 )T Tc 0
(2-2)
式 ( 2-1)、( 2-2 ) 对于不同物质均成立，它们对状态方程 等的研究意义重大。
为了提高 RK 方程对极性物质及饱和液体p-V-T 计算的精确度，Soave 对RK 方程进行了改进，成为 RKS (或SRK，或Soave)方程。它将RK 方程中与温度有 关的a/T0.5 改为a(T)，方程形式为
p RT a(T ) V b V (V b)
2
(2-14) V
1
B
C
2
D
3
式中，B(B′)、C(C′)、D(D′)、分别称为第二、第三、第四、… … 维里 (Virial) 系数。 当式 ( 2-5 ) - ( 2-7 ) 取无群级数时，不同形式的维里系数之间存在着下述关系:
B / B RT
C B2 C (RT ) 2
2.2.3.2 Redlich-Kwong 方程
(2-9) (2-10a) (2-10b)
1 B/ p
1 Bp RT
实践表明，当温度低于临界温度、压力不高于1.5MPa时，用二阶舍项的维里 方程可以很精确地表示气体的p-V-T关系，当压力高于5.0MPa时，需要用更多阶 的维里方程。
2.2.3 立方型状态方程
立方型状态方程是指方程可展开为体积 (或密度) 的三次方形式。这类方程能够 解析求解，精度较高，又不太复杂，很受工程界欢迎。
等温线在两相区的水平段随温度的升高而逐渐变短，到 临界温度时最后缩成一点C。临界等温线在图2-3中临界点 为水平拐点，其斜率和曲率均为零，数学上表示为
( )
2 p
p V T Tc
0
(2-1)
( V 2 )T Tc 0
(2-2)
式 ( 2-1)、( 2-2 ) 对于不同物质均成立，它们对状态方程 等的研究意义重大。
为了提高 RK 方程对极性物质及饱和液体p-V-T 计算的精确度，Soave 对RK 方程进行了改进，成为 RKS (或SRK，或Soave)方程。它将RK 方程中与温度有 关的a/T0.5 改为a(T)，方程形式为
p RT a(T ) V b V (V b)
2
(2-14) V
1
B
C
2
D
3
式中，B(B′)、C(C′)、D(D′)、分别称为第二、第三、第四、… … 维里 (Virial) 系数。 当式 ( 2-5 ) - ( 2-7 ) 取无群级数时，不同形式的维里系数之间存在着下述关系:
B / B RT
C B2 C (RT ) 2
2.2.3.2 Redlich-Kwong 方程
化工热力学_02流体的p-V-T关系
0.90008.314 (200 273.15)106 1.013106
349（5 cm3 mol1）
(3)Z
1
B V
C V2
pV B C
RT
1 V
V2
1.013106 V 8.314106 (200 273.15)
1
388 V
26000 V2
迭代计算得：V 3426cm3 mol 1, Z 0.8848
（2） Z 1 Bp RT
（3）
Z
1
B V
C V2
（1）理想气体方程
V
RT P
8.314
106 （200 1.013106
273.15）
388（3 cm3
mol
1）
(2)Z 1 Bp RT
Z
1
(388) 1.013 106 8.314106 (200 273.15)
0.9000
V
ZRT p
b 0.08664 RTC pC
0.08664
8.314 304.2 7.376 106
2.97075105 m3 mol 1
p
RT V b
T
a 0.5V (V
b)
8.314 285
6.4675
(6.011 0.297075) 104 2850.5 6.011104 (6.011 0.297075) 104
2.2.3 立方型状态方程（两常数状态方程）
立方型状态方程可以展开成为V的三 次方形式。
2.2.3.1 Van der Waals(vdW)方程
(1) vdW 方程是后续立方型方程的基础
RT a
p
其中 a V2
化工热力学 第二章 流体的压力,体积,温度的关系：状态方程式
5
m 3 kmol
1 3
0.08664 a PC 2 b 0.42748 R
a 0.08664 1 TC b 0.42748 R
2 3
VC 3.847 b
化工热力学
第二章
流体的PVT关系
化工热力学
第二章
流体的PVT关系C 6a 4 3 VC b VC
两式相比得:
2
2a VC b TC 3 R VC
2
2 VC b VC 3
VC 3b
27 R 2TC a 64 PC
2
2a 4b 8a TC 3 R 27b 27bR
化工热力学
第二章
流体的PVT关系
(a)、求蒸汽的摩尔体积 将RK方程两端乘
V b 整理成：
P
aV b T PV V b
1 2
RT V b P
写成迭代形式：
RT Vi 1 b P
aVi b T PVi Vi b
1 2
化工热力学
化工热力学
3
第二章
2
流体的PVT关系
0 .5
PVi RTVi ab / T Vi 1 2 0.5 Pb bRT a / T
如令： b 2 C
3
bRT a ，则上式写成： 1 P PT 2
取初值：
RT 2 ab CVi 1 Vi Vi 1 P PT 2
2P 0 V 2 T Tc
27 R T a 64 PC
2
2 C
RTC b 8PC
化工热力学
第二章
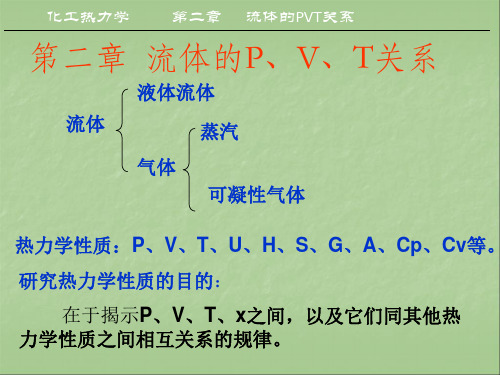
m 3 kmol
1 3
0.08664 a PC 2 b 0.42748 R
a 0.08664 1 TC b 0.42748 R
2 3
VC 3.847 b
化工热力学
第二章
流体的PVT关系
化工热力学
第二章
流体的PVT关系C 6a 4 3 VC b VC
两式相比得:
2
2a VC b TC 3 R VC
2
2 VC b VC 3
VC 3b
27 R 2TC a 64 PC
2
2a 4b 8a TC 3 R 27b 27bR
化工热力学
第二章
流体的PVT关系
(a)、求蒸汽的摩尔体积 将RK方程两端乘
V b 整理成：
P
aV b T PV V b
1 2
RT V b P
写成迭代形式：
RT Vi 1 b P
aVi b T PVi Vi b
1 2
化工热力学
化工热力学
3
第二章
2
流体的PVT关系
0 .5
PVi RTVi ab / T Vi 1 2 0.5 Pb bRT a / T
如令： b 2 C
3
bRT a ，则上式写成： 1 P PT 2
取初值：
RT 2 ab CVi 1 Vi Vi 1 P PT 2
2P 0 V 2 T Tc
27 R T a 64 PC
2
2 C
RTC b 8PC
化工热力学
第二章
化工热力学-GG-第2章 p-V-T关系和状态方程-144
2p
在C点 V 2 T 0 在C点
0
重要！
• 超临界流体（SuperCritical Fluid, SCF） – 在T>Tc和p>pc区域内，气体、液体变得不可区分，形成的 一种特殊状态的流体，称为超临界流体。 – 多种物理化学性质介于气体和液体之间 ,并兼具两者的优 点。具有液体一样的密度、溶解能力和传热系数 ,具有气 体一样的低粘度和高扩散系数。 – 物质的溶解度对T、p的变化很敏感 ，特别是在临界状态 附近 ， T、p微小变化会导致溶质的溶解度发生几个数量 级的突变 ，超临界流体正是利用了这一特性，通过对T、 p的调控来进行物质的分离。
难测!
但存在问题： 1) 有限的p-V-T数据，无法全面了解流体的p-V-T 行为 2) 离散的p-V-T数据，不便于求导和积分，无法获得数据点 以外的p-V-T 和H，U，S，G数据
如何解决？
引言
如何解决？
只有建立能反映流体p-V-T关系的解析形式才能解决。 这就是状态方程Equation of State(EOS)的由来。 EOS反映了体系的特征，是推算实验数据之外信息和其 它物性数据不可缺少的模型。 流体p-V-T数据+状态方程EOS是计算热力学性质最重要 的模型之一。 EOS+CPig可推算所有的热力学性质。
OD 是AO的延长线，是过冷水和水蒸气的介稳平衡线。因为 在相同温度下，过冷水的蒸气压大于冰的蒸气压，所以OD线 在OB线之上。过冷水处于不稳定状态，一旦有凝聚中心出现， 就立即全部变成冰。
O点 是三相点（triple point），气-液-固三相共存。 三相点的温度和压力皆由系 统自定。
610Pa
（0.6~2） ×10-3 （1~3） ×10-4
在C点 V 2 T 0 在C点
0
重要！
• 超临界流体（SuperCritical Fluid, SCF） – 在T>Tc和p>pc区域内，气体、液体变得不可区分，形成的 一种特殊状态的流体，称为超临界流体。 – 多种物理化学性质介于气体和液体之间 ,并兼具两者的优 点。具有液体一样的密度、溶解能力和传热系数 ,具有气 体一样的低粘度和高扩散系数。 – 物质的溶解度对T、p的变化很敏感 ，特别是在临界状态 附近 ， T、p微小变化会导致溶质的溶解度发生几个数量 级的突变 ，超临界流体正是利用了这一特性，通过对T、 p的调控来进行物质的分离。
难测!
但存在问题： 1) 有限的p-V-T数据，无法全面了解流体的p-V-T 行为 2) 离散的p-V-T数据，不便于求导和积分，无法获得数据点 以外的p-V-T 和H，U，S，G数据
如何解决？
引言
如何解决？
只有建立能反映流体p-V-T关系的解析形式才能解决。 这就是状态方程Equation of State(EOS)的由来。 EOS反映了体系的特征，是推算实验数据之外信息和其 它物性数据不可缺少的模型。 流体p-V-T数据+状态方程EOS是计算热力学性质最重要 的模型之一。 EOS+CPig可推算所有的热力学性质。
OD 是AO的延长线，是过冷水和水蒸气的介稳平衡线。因为 在相同温度下，过冷水的蒸气压大于冰的蒸气压，所以OD线 在OB线之上。过冷水处于不稳定状态，一旦有凝聚中心出现， 就立即全部变成冰。
O点 是三相点（triple point），气-液-固三相共存。 三相点的温度和压力皆由系 统自定。
610Pa
（0.6~2） ×10-3 （1~3） ×10-4
化工热力学第2章流体的PVT关系
时，这种流体就处于对比状态。
例如：H2 和N2这两种流体
对于H2
状态点记为1，P1 V1 T1
Tr1 =T1/TcH2
Pr1=P1/PcH2
对于N2
状态点记为2，P2 V2 T2
Tr2 =T2/TcN2
Pr2=P2/PcN2
当Tr1=Tr2 ，Pr1=Pr2 时，此时就称这两种流体处
一.P-T图
P
Pc
3液
相
固
相
2
1
密 流 区 C
气相
Tc T
1-2线 汽固平衡线（升华线）
2-c线 汽液平衡线（汽化线） 2-3线 液固平衡线（熔化线） C点临界点，2点三相点 P<Pc,T<Tc的区域，属汽体 P<Pc,T>Tc的区域，属气体 P＝Pc,T＝Tc的区域，两相 性质相同
P>Pc,T>Tc的区域，密流区
压缩因 子，方 程的计 算值和 实测值 的符合 程度是 判断方 程的优 劣标志 之一。
2. R-K Equation (1949年，Redlich and Kwong)
(1) R-K Eq的一般形式：
P
RT V-b
-
a T0.5V(V
b)
(2-11)
① R-K Equation中常数值不同于范德华方程中的a、b值， 不能将二者混淆。 在范德华方程中，修正项为a/V2，没有考虑温度的影响 在R-K方程中，修正项为，考虑了温度的影响。 ② R-K Equation中常数a、b值是物性常数，具有单位。
为表征物质分子的偏心度，既非球型分子偏离球对称的 程度，简单流体为0
R-K Eq经过修改后，应用范围扩宽。 SRK Eq：可用于两相PVT性质的计算，对烃类计算，其 精确度很高。
例如：H2 和N2这两种流体
对于H2
状态点记为1，P1 V1 T1
Tr1 =T1/TcH2
Pr1=P1/PcH2
对于N2
状态点记为2，P2 V2 T2
Tr2 =T2/TcN2
Pr2=P2/PcN2
当Tr1=Tr2 ，Pr1=Pr2 时，此时就称这两种流体处
一.P-T图
P
Pc
3液
相
固
相
2
1
密 流 区 C
气相
Tc T
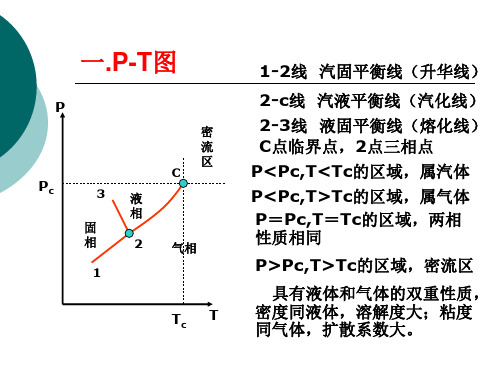
1-2线 汽固平衡线（升华线）
2-c线 汽液平衡线（汽化线） 2-3线 液固平衡线（熔化线） C点临界点，2点三相点 P<Pc,T<Tc的区域，属汽体 P<Pc,T>Tc的区域，属气体 P＝Pc,T＝Tc的区域，两相 性质相同
P>Pc,T>Tc的区域，密流区
压缩因 子，方 程的计 算值和 实测值 的符合 程度是 判断方 程的优 劣标志 之一。
2. R-K Equation (1949年，Redlich and Kwong)
(1) R-K Eq的一般形式：
P
RT V-b
-
a T0.5V(V
b)
(2-11)
① R-K Equation中常数值不同于范德华方程中的a、b值， 不能将二者混淆。 在范德华方程中，修正项为a/V2，没有考虑温度的影响 在R-K方程中，修正项为，考虑了温度的影响。 ② R-K Equation中常数a、b值是物性常数，具有单位。
为表征物质分子的偏心度，既非球型分子偏离球对称的 程度，简单流体为0
R-K Eq经过修改后，应用范围扩宽。 SRK Eq：可用于两相PVT性质的计算，对烃类计算，其 精确度很高。
P-V-T关系和状态方程
一、立方型状态方程
发展路线 1： van der Waals(1873)→ Ridlich-Kwong(1949)→ Wilson(1965) → Soave(1972) →
Peng-Robinson(1976) 特点：
◎可以表示成为 V 的三次方——能用解析法求解。 ◎一般由引力相和斥力相组成：
P＝Prep＋Patt
一般情况下，Prep＞0，而 Patt＜0
a(T)是 T 的函数， f (V)是 V 的二次函数
（一）方程形式
1、van der Waals 方程
（1）方程形式
P RT a 或 V b V 2
a (P )(V b) RT
V2
（2）两点修正：①实际气体分子占有一定的体积；②分子间存在作用力。
2、状态方程体积根的求解 （1）图解法（例 2—2） （2）解析求根（略） （3）数值求根：
牛顿迭代法：
（4）试差法 例 2-8、2-9（略）
②
V (n1) V (n) f (V (n) ) f (V (n) )
二、多常数状态方程
1、virial 方程
（1）方程形式
密度型： 压力型：
Z 1 B C V V2
§2.2 状态方程（EOS）
EOS 是计算热力学性质最重要的模型之一，它能推算实验数据之外信息和其它物性数据（H，S， G）。
EOS 是物质 P-V-T 关系的解析式；能反映物质的微观特征或宏观的 P-V-T 特征。 ◎状态方程（EOS）的定义：根据相律，纯物质在单相区的自由度 F = C-P+2 为 2，因此 P，V， T 中任意两个指定后，状态就确定了。
2、BWR 方程：8 个常数的状态方程。
化工热力学2流体的P-V-T关系
2P V 2
T Tc
0
肇庆学院
《化工热力学》 流体的P-V-T关系
2.2 气体的状态方程（Equation of state）
纯流体的状态方程（EOS）是描述流体P-V-T 性质的关系式。由相律可知，对纯流体有：
f(P,V,T)=0
混合物的状态方程中还包括混合物的组成（通 常是摩尔分数）
Tc T
超临界流体既不同于液体，又不同于气体，密度可以接近 液体，但又具有气体的体积可变性和传递性质，可以作为特殊 的萃取溶剂和反应介质。
肇庆学院
《化工热力学》 流体的P-V-T关系
图2.3 纯物质的P-V图
肇庆学院
《化工热力学》 流体的P-V-T关系
特性：高于Tc的的等温线光滑，无转折点。
T2 T1
2.2.1 理想气体方程（Ideal Gas EOS）
pV=RT
Z=PV/RT=1
p为气体压力；V为摩尔体积； T为绝对温度；R为通用气体常数
R=8.314 (m3·Pa)/(mol·K)
肇庆学院
《化工热力学》 流体的P-V-T关系
2.2.1 理想气体方程 理想气体方程的应用： （1）在较低压力和较高温度下可用理想气体方程 进行计算。 （2）为判断真实气体状态方程的正确程度提供了 一个标准：当P 0或V ∞时，任何状态方程都 还原为理想气体方程。
流体的P-V-T关系
（1）用一个状态方程即可精确地代表相当广泛范围 内的P、V、T实验数据，借此可精确地计算所需的P、
V、T数据， 从而大大减少实验测定的工作量。
（2）用状态方程可计算不能直接从实验测定的其他
热力学性质。
（3）用状态方程可进行相平衡计算
肇庆学院
化工热力学第二章.
第2章流体的p-V-T关系
主要内容
1) 流体的压力p、摩尔体积V 和温度T是物质最基
本的性质；
2)p、V、T 性质可以通过实验直接测量；
3)pVT+c p ig能推算其它不能直接从实验测量的热力
学性质如H、S、U、G等。
1
）
c
A B
对任何气体，
根据气体的临界参数，即可求出Z
计算常数需要
同时适用于汽液两相，
(1)
(2) EOS
(3)
与立方型状态方程相比，多参数状态方程的优多参数方程的基础是
能同时适用于汽、液两相
在计算和关联烃类混合物时极有价值；计算结果明显高于立方型状态方程；
该方程的数学规律性较弱，给方程的求解。
化工热力学讲义-1-第二章-流体的p-V-T关系
pVT性质实验装置简介
装置组成
高压容器、温度计、压力计、体积测量系统等。
工作原理
通过改变流体的压力、体积和温度，测量相应 的物理量变化。
适用范围
适用于气体、液体等多种流体的pVT性质测定。
实验步骤和数据处理
02
01
03
实验步骤 1. 准备实验装置，检查各部件完好。 2. 将待测流体注入高压容器中，密封容器。
p-v-t关系
p-v-t关系是指流体的压力、体积和温度之间的关系。对于理想气体， 其p-v-t关系符合理想气体状态方程，即pV=nRT，其中p为压力，V 为体积，T为温度，n为摩尔数，R为气体常数。对于实际气体，其 p-v-t关系需要考虑分子间的相互作用力和分子本身的体积等因素， 因此需要使用更复杂的状态方程来描述。
THANK YOU
感谢聆听
02
流体的压缩性与膨胀性
压缩因子及计算方法
01
压缩因子的定义
表示实际气体与理想气体偏差程 度的物理量，用Z表示。
02
压缩因子的计算方 法
通过实验测定不同温度、压力下 的气体体积，利用状态方程计算 得到。
03
压缩因子与气体性 质的关系
不同气体的压缩因子不同，与气 体的分子结构、相互作用力等因 素有关。
行提供依据。
管道压力损失计算
在管道输送过程中，流体的 压力和体积会发生变化，通 过流体的p-v-t关系可以计算 出管道的压力损失，以便优
化管道设计和运行参数。
管道泄漏检测
利用流体的p-v-t关系，可以 实时监测管道内流体的状态 变化，从而及时发现管道泄 漏等异常情况。
化学反应过程中的体积变化问题
反应体积变化预测
反应器压力控制
《化工热力学》第2章pvt关系和状态方程课后习题答案
习题解答一、是否题1.纯物质由蒸汽变成液体，必须经过冷凝的相变化过程。
（错。
可以通过超临界流体区。
）2.当压力大于临界压力时，纯物质就以液态存在。
（错。
若温度也大于临界温度时，则是超临界流体。
）3.由于分子间相互作用力的存在，实际气体的摩尔体积一定小于同温同压下的理想气体的摩尔体积，所以，理想气体的压缩因子Z=1，实际气体的压缩因子Z<1。
（错。
如温度大于Boyle温度时，Z＞1。
）4.纯物质的三相点随着所处的压力或温度的不同而改变。
（错。
纯物质的三相平衡时，体系自由度是零，体系的状态已经确定。
）5.在同一温度下，纯物质的饱和液体与饱和蒸汽的吉氏函数相等。
（对。
这是纯物质的汽液平衡准则。
）6.纯物质的平衡汽化过程，摩尔体积、焓、热力学能、吉氏函数的变化值均大于零。
（错。
只有吉氏函数的变化是零。
）7.气体混合物的virial系数，如B，C…，是温度和组成的函数。
（对。
）二、选择题指定温度下的纯物质，当压力低于该温度下的饱和蒸汽压时，则气体的状态为(C。
参考P－V图上的亚临界等温线。
) A.饱和蒸汽B.超临界流体C. 过热蒸汽2.T 温度下的过冷纯液体的压力P （A 。
参考P －V 图上的亚临界等温线。
）A. >()T P sB. <()T P sC. =()T P s3.能表达流体在临界点的P-V 等温线的正确趋势的virial 方程，必须至少用到（A 。
要表示出等温线在临界点的拐点特征，要求关于V 的立方型方程） A. 第三virial 系数 B. 第二virial 系数 C. 无穷项D. 只需要理想气体方程4.当0®P 时，纯气体的()[]P T V P RT ,-的值为（D 。
因()[]0lim lim ,lim 000=÷øöçè涶÷øöçè涶=-=®®®B T T P T P P P Z P Z RT P T V P RT ，又） A. 0B. 很高的T 时为0C. 与第三virial 系数有关D. 在Boyle 温度时为0三、填空题1、表达纯物质的汽平衡的准则有()()()()s ls v s l s v V T G V T G T G T G ,,==或（吉氏函数）、vap vap s V T H dT dP D D =（Claperyon 方程）、()ò-=svslV V slsv s V V P dV V T P ),(（Maxwell 等面积规则）。
化工热力学 第二章 流体的PVT关系
V
0.125
误差
（2.150 1.875）107
1.875 107
100%
14.67%
误差高达14.67%!!!
[研究理想气体的实际意义]
*自然界中虽然不存在真正的理想气体，但工程上常 见的气体，当它们所处的压力足够低，温度足够高 时，所表现出来的性质都与理想气体十分相近，完 全可以把这时的气体当作理想气体来处理，并不会 引起太大的误差。 例如：在大气环境下的空气、氮气以及常压高温条 件下的燃烧烟气等均可视为理想气体。 *为真实气体状态方程的正确程度提供一个判断标准
§2.2.2 理想气体的状态方程
理想气体EOS只适合压力非常低的气体,不适合真 实气体。
例2:将1kmol甲烷压缩储存于容积为0.125m3,温度
为323.16K的钢瓶内.问此时甲烷产生的压力多大?
其实验值为1.875x107Pa.
解: P nRT 1000 8.314 323.16 2.150107 Pa
❖ 是第一个同时能计算汽，液两相和临界点的方程
2.范德华方程常数a、b的确定
对于Van der Waals方程
P
RT V b
a V2
（1）
应用临界条件，即
p
2 p
( V
)Tc
0, ( V 2 )Tc
0
（2）
❖ 临界等温线在C 点的斜率等于零
❖ 临界等温线在C 点的曲率等于零
把van der Waals方程代入上述条件， 即可得
①立方型：vdW方程，Redlich-Kwong方程 ②多参数高次型： Virial方程 ③理论方程：从分子理论和统计力学推导
2、两类经验状态方程的发展史：
❖ （1）立方型状态方程（Van der Waals型）
化工热力学第二章 流体的p-V-T关系
由纯物质临界性质计算
a
0.42748R
T2 2.5 c
/
pc
(2-7a)
b 0.08664 RTc / pc
(2-7b)
RK方程(Zc=1/3=0.333)适用非极性和弱极性化合 物，计算准确度比van der Waals方程(Zc=3/8=0.375) 有很大提高，但对多数强极性化合物有较大偏差。
下一内容
回主目录
19
理想气体是极低压力和较高温度下各种真实 气体的极限情况，实际上并不存在。理想气体方 程除了在工程设计中可用作近似估算外，更重要 的是为判断真实气体状态方程的正确程度提供了 一个标准。
当 P 0 或者 V 时，
任何真实气体状态方程都应还原为理想气 体方程。使用状态方程时，应注意通用气体常 数R的单位必须和p, V, T的单位相适应。
2.2
上一内容
下一内容
回主目录
15
一个优秀的状态方程应是形式简单， 计算方便，适用范围广，计算不同热力 学性质均有较高的准确度。但已发表的 数百个状态方程中，能符合这些要求的 为数不多。因此有关状态方程的深入研 究尚在继续进行。
2.2
上一内容
下一内容
回主目录
16
状态方程的分类：
分为三类：非解析型状态方程 密度为三次方的立方型方程 非立方型方程
p 0 V T TC
(2-1)
2 p V 2
T
TC
0
(2-2)
上一内容
图2-3
下一内容
回主目录
2.1
9
式 (2-1) 和 式 （ 2-2 ） 提 供 了 经 典的临界点定义。 Martin 和 侯 虞 钧 在研究气体状态方 程时发现，在临界 点P对V的三阶和 四阶导数也是零或 是很小的数值。
第2章p-V-T关系和状态方程
等温线（T=Tc、T>Tc、T<Tc）
临界等温的数学特征
P V T 0 在C点
2P V 2 T 0 在C点
13
2.3状态方程（EOS）
EOS是特指p-V-T的解析函数关系； EOS是由经典热力学推算其它性质时所必
需的模型； EOS应反映物质的微观特征或宏观的p-V-
2
2-1 引 言
推算热力学性质时需要输入流体最基本的性质以及表达系统特
征的模型。流体最基本的性质有两大类，一类是p、V、T、组成
和热容数据，另一类是热数据（如标准生成焓和标准生成熵等）。 后者已在物理化学中进行过详细介绍。
状态方程不仅本身是重要的p-V-T关系式，而且是推算热力学 性质不可缺少的模型之一。欲得到热力学性质与p-V-T 和Cpig的
这样就可以从纯物质的Tc ,pc和计算SRK常数
25
SRK方程的特点
在临界点同RK，Zc =1/3（偏大）；
计算常数需要Tc, Pc和，a是温度的函数；
除了能计算气相体积之外，能用于表达 蒸汽压（汽液平衡），是一个适用于汽、 液两相的EOS，但计算液相体积误差较 大；
为了改善计算液相体积的准确性，Peng Robinson提出了PR方程。
17
关于vdW常数和临界压缩因子Zc
临界等 温线在 C点的 斜率和 曲率等 于零
P V
T ,c
RTc
Vc b2
2a Vc3
0
2P V 2
T ,c
2RTc
Vc b3
6a Vc4
0
18
解方程组得方程常数
9 a 8 RTcVc
临界等温的数学特征
P V T 0 在C点
2P V 2 T 0 在C点
13
2.3状态方程（EOS）
EOS是特指p-V-T的解析函数关系； EOS是由经典热力学推算其它性质时所必
需的模型； EOS应反映物质的微观特征或宏观的p-V-
2
2-1 引 言
推算热力学性质时需要输入流体最基本的性质以及表达系统特
征的模型。流体最基本的性质有两大类，一类是p、V、T、组成
和热容数据，另一类是热数据（如标准生成焓和标准生成熵等）。 后者已在物理化学中进行过详细介绍。
状态方程不仅本身是重要的p-V-T关系式，而且是推算热力学 性质不可缺少的模型之一。欲得到热力学性质与p-V-T 和Cpig的
这样就可以从纯物质的Tc ,pc和计算SRK常数
25
SRK方程的特点
在临界点同RK，Zc =1/3（偏大）；
计算常数需要Tc, Pc和，a是温度的函数；
除了能计算气相体积之外，能用于表达 蒸汽压（汽液平衡），是一个适用于汽、 液两相的EOS，但计算液相体积误差较 大；
为了改善计算液相体积的准确性，Peng Robinson提出了PR方程。
17
关于vdW常数和临界压缩因子Zc
临界等 温线在 C点的 斜率和 曲率等 于零
P V
T ,c
RTc
Vc b2
2a Vc3
0
2P V 2
T ,c
2RTc
Vc b3
6a Vc4
0
18
解方程组得方程常数
9 a 8 RTcVc
化工热力学第二章 流体的p-V-T关系和状态方程
甲烷 乙烷 丙烷 正丁烷 正戊烷 正己烷
-82.62 32.18 96.59 151.9 196.46 234.4
45.36 48.08 41.98 37.43 33.32 29.80
-161.45 -88.65 -42.15 -0.5 36.05 68.75
55.6 52.0 50.5 49.6 49.1 48.4
二氧化碳
水 氨
CO2
H2 O NH3
72.9
217.6 112.5
31.2
374.2 132.4
0.433
0.332 0.235
乙烷
乙烯 氧化二氮 丙烷 戊烷 丁烷
C2H6
C 2 H4 N2O C 3 H8 C5H12 C4H10
48.1
49.7 71.7 41.9 37.5 37.5
32.2
9.2 36.5 96.6 196.6 135.0
③汽液两相平衡区 F=C-P+2=1
②过热蒸汽区
什么是正 常沸点？
①饱和液相线
（泡点线）
②饱和汽相线 （露点线 ）
ห้องสมุดไป่ตู้
恒温线
临界点—p-V-T中最重要的性质
• 1）Tc、pc 是纯物质能够呈现汽液平衡时的最高温度 和最高压力。 • 要使气体液化温度绝对不能超过Tc 。 • 气体“液化”的先决条件是T<Tc，否则无论施加多大 的压力都不可能使之液化。 • 2）临界等温的数学特征：等于临界温度的等温线在 临界点出现水平拐点。 P V TC 0 在C点 重要！ 2 P V 2 TC 0 在C点
• 【例2-3】 在4L的刚性容器中装有50℃、2kg水的饱和 汽液混合物，已知50℃水的饱和液相体积Vsl=1.0121 ， 饱和汽相体积Vsv=12032；水的临界体积Vc=3.111 。现 在将水慢慢加热，使得饱和汽液混合物变成了单相，问： 此单相是什么相？ 如果将容器换为400L，最终答案是 什么？
化工热力学讲义-2-第二章-流体的p-V-T关系
h 0.2387
Z 1 1 0.5335 0.2387 0.8829 1 0.2387 0.2387 1 0.2387
即Z1和Z0之间相差颇大，需进行第二次迭代。
第二次迭代：取 Z 2 Z 1 0.8829
则：p
ZRT V
0.8829 8.314 323.16 1.25 104
2.3.1两参数对比态原理
一、原理的导出
令：Tr T T，C
pr
p p，C
Vr
V VC
1 r
式中：Tr、pr、Vr、ρr称为对比温度、对比压力、对比摩尔体积、对比密度。
对于van der Waals方程，上节课中已经推导并得到：
a
9 8
RVCT，C
b VC，同时： 3
pC
3 8
RTC VC
将以上各值代入van der Waals方程，得：
分析：BpC 是无因次的，可以看作对比第二维里系数。 RTC
以下要解决的是该系数的计算问题：对于指定的气体来说，B仅仅 是温度的函数，B的普遍化关系只与对比温度有关，与压力无关。
因此Pitzer提出如下关联式：
BpC B 0 B1
RTC 式中B0、B1只是对比温度的函数，由下列关系式确定：
B0
Z Z 0 Z 1
式中Z0、Z1则是（pr、Tr）的复杂函数，和ω无关。根据 实验数据得到的Z0、Z1和（pr、Tr）的函数关系见P15页 图2-7（a）（b）和图2-8（a）（b）。工程计算时，具体数 据参见附录三
二、SRK、PR、PT方程的普遍化
SRK、PR两方程式中显然引入了Pitzer提出的偏心因子概念， 对它们的普遍化（见第9页表2-3）显示，它们是基于Pitzer提 出的三参数对应态原理。具体推导过程略。
Z 1 1 0.5335 0.2387 0.8829 1 0.2387 0.2387 1 0.2387
即Z1和Z0之间相差颇大，需进行第二次迭代。
第二次迭代：取 Z 2 Z 1 0.8829
则：p
ZRT V
0.8829 8.314 323.16 1.25 104
2.3.1两参数对比态原理
一、原理的导出
令：Tr T T，C
pr
p p，C
Vr
V VC
1 r
式中：Tr、pr、Vr、ρr称为对比温度、对比压力、对比摩尔体积、对比密度。
对于van der Waals方程，上节课中已经推导并得到：
a
9 8
RVCT，C
b VC，同时： 3
pC
3 8
RTC VC
将以上各值代入van der Waals方程，得：
分析：BpC 是无因次的，可以看作对比第二维里系数。 RTC
以下要解决的是该系数的计算问题：对于指定的气体来说，B仅仅 是温度的函数，B的普遍化关系只与对比温度有关，与压力无关。
因此Pitzer提出如下关联式：
BpC B 0 B1
RTC 式中B0、B1只是对比温度的函数，由下列关系式确定：
B0
Z Z 0 Z 1
式中Z0、Z1则是（pr、Tr）的复杂函数，和ω无关。根据 实验数据得到的Z0、Z1和（pr、Tr）的函数关系见P15页 图2-7（a）（b）和图2-8（a）（b）。工程计算时，具体数 据参见附录三
二、SRK、PR、PT方程的普遍化
SRK、PR两方程式中显然引入了Pitzer提出的偏心因子概念， 对它们的普遍化（见第9页表2-3）显示，它们是基于Pitzer提 出的三参数对应态原理。具体推导过程略。
第2章 PVT2化工热力学资料
P
液固平衡线
液体区
临界等容线
超临界流体区(SF)
（T>Tc和P>Pc）
固体区 汽固平衡线
临界点
汽液平衡线
气体区
三相点F=C-P+2=0
水的三相点：0.0098℃
7
T
P-T 图的点、线和面（区域）
❖ 点 临界点
❖ 三相点
❖ 线 VLE线
❖ SLE线
❖ SVE线）
❖ 区域 V
❖
G
❖
L
❖
S
❖
SF （T>Tc和P>Pc）
37.43 33.32 29.80
-0.5 36.05 68.75
燃烧值，kJ/g 55.6 52.0 50.5
3(T降低)
2
11
V
2.2.4超临界流体（Supercritical Fluid, SCF）
P-V-T相图中最重要的性质之一
临界点：气液两相共存的最高温度或最高压力。 超临界流体区（T>Tc和P>Pc） Tc—临界温度；Pc —临界压力；Vc —临界体积 临界等温的数学特征
P V T 0 在C点
第二章 流体的P-V-T关系
2.1 引言 2.2 纯流体的P-V-T 特性 2.3 气体状态方程（EOS） 2.4 对应状态原理及其应用 2.5 真实气体混合物P-V-T关系
1
2.1引言
流体包括：Gas Vapor Solid Liquid Supercritial fluid 等 化工数据一般分为： ❖ 基础物性数据（分子量、临界数据、偏心因子等） ❖ 热LL力E等学）性质数据（P、V、T、CP、CV、H 、S、G、VLE和 ❖ 迁移性质数据（D、λ、μ等） ❖ 热力学性质数据分为 ： ❖ 可直接测量性质P、V、T、CP和CV等 ❖ 难直接测量性质H 、S、G等 ❖ 难应用直热接力测学量关性系质式可计由算可得直到接。测因量此性P质VTP数、据V、是T基、础C，P和本C章V首等
液固平衡线
液体区
临界等容线
超临界流体区(SF)
（T>Tc和P>Pc）
固体区 汽固平衡线
临界点
汽液平衡线
气体区
三相点F=C-P+2=0
水的三相点：0.0098℃
7
T
P-T 图的点、线和面（区域）
❖ 点 临界点
❖ 三相点
❖ 线 VLE线
❖ SLE线
❖ SVE线）
❖ 区域 V
❖
G
❖
L
❖
S
❖
SF （T>Tc和P>Pc）
37.43 33.32 29.80
-0.5 36.05 68.75
燃烧值，kJ/g 55.6 52.0 50.5
3(T降低)
2
11
V
2.2.4超临界流体（Supercritical Fluid, SCF）
P-V-T相图中最重要的性质之一
临界点：气液两相共存的最高温度或最高压力。 超临界流体区（T>Tc和P>Pc） Tc—临界温度；Pc —临界压力；Vc —临界体积 临界等温的数学特征
P V T 0 在C点
第二章 流体的P-V-T关系
2.1 引言 2.2 纯流体的P-V-T 特性 2.3 气体状态方程（EOS） 2.4 对应状态原理及其应用 2.5 真实气体混合物P-V-T关系
1
2.1引言
流体包括：Gas Vapor Solid Liquid Supercritial fluid 等 化工数据一般分为： ❖ 基础物性数据（分子量、临界数据、偏心因子等） ❖ 热LL力E等学）性质数据（P、V、T、CP、CV、H 、S、G、VLE和 ❖ 迁移性质数据（D、λ、μ等） ❖ 热力学性质数据分为 ： ❖ 可直接测量性质P、V、T、CP和CV等 ❖ 难直接测量性质H 、S、G等 ❖ 难应用直热接力测学量关性系质式可计由算可得直到接。测因量此性P质VTP数、据V、是T基、础C，P和本C章V首等
化工热力学(第二版)第二章
2 用状态方程可计算不能直接从实验测定的 其它热力学性质。 3 用状态方程可进行相平衡和化学反应平衡计 算。
2.2.2 理想气体方程
PV RT PV Z 1 RT
P为气体压力；V为摩尔体积； T为绝对温度；R为通用气体常数。
理想气体方程的应用 1 在较低压力和较高温度下可用理想气体 方程进行计算。 2 为真实气体状态方程计算提供初始值。 3 判断真实气体状态方程的极限情况的正 确程度，当 P 0 或者 V 时，任何 的状态方程都还原为理想气体方程。
2 流体的 P-V-T关系
2.1 纯物质的P-V-T关系
2.2 气体的状态方程
2.3 对比态原理及其应用
2.4 真实气体混合物的P-V-T关系 2.5 液体的P-V-T性质
2.1 纯物质的P-V-T关系
液 固 固 液 汽液临界点 气源自固临界点 气汽
凝固时收缩
凝固时膨胀
图2-1 纯物质的P-V-T相图
3
PV RTV ab / T Vk 1 2 0.5 Pb bRT a / T
T Tr Tc P Pr Pc
RK方程可以表示成压缩因子Z的三次方表达式：
Z Z A B B Z AB 0
3 2 2
PV Z RT
2 Soave - Redlich - Kwong ( SRK )方程
RT a P V b V V b
2 2 c
ap Pr A 2 2 0.42748 2 T RT Tr bP Pr B 0.08664 RT Tr
SRK方程可以表示成压缩因子Z的三次方表达式：
Z 3 Z 2 A B B 2 Z AB 0
3 Peng - Robinson ( PR )方程
2.2.2 理想气体方程
PV RT PV Z 1 RT
P为气体压力；V为摩尔体积； T为绝对温度；R为通用气体常数。
理想气体方程的应用 1 在较低压力和较高温度下可用理想气体 方程进行计算。 2 为真实气体状态方程计算提供初始值。 3 判断真实气体状态方程的极限情况的正 确程度，当 P 0 或者 V 时，任何 的状态方程都还原为理想气体方程。
2 流体的 P-V-T关系
2.1 纯物质的P-V-T关系
2.2 气体的状态方程
2.3 对比态原理及其应用
2.4 真实气体混合物的P-V-T关系 2.5 液体的P-V-T性质
2.1 纯物质的P-V-T关系
液 固 固 液 汽液临界点 气源自固临界点 气汽
凝固时收缩
凝固时膨胀
图2-1 纯物质的P-V-T相图
3
PV RTV ab / T Vk 1 2 0.5 Pb bRT a / T
T Tr Tc P Pr Pc
RK方程可以表示成压缩因子Z的三次方表达式：
Z Z A B B Z AB 0
3 2 2
PV Z RT
2 Soave - Redlich - Kwong ( SRK )方程
RT a P V b V V b
2 2 c
ap Pr A 2 2 0.42748 2 T RT Tr bP Pr B 0.08664 RT Tr
SRK方程可以表示成压缩因子Z的三次方表达式：
Z 3 Z 2 A B B 2 Z AB 0
3 Peng - Robinson ( PR )方程
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第二章 内 容
§2.1 纯流体的p-V-T相图 §2.2 气体状态方程（EOS） §2.3 对应态原理和普遍化关联式 §2.4 液体的p-V-T性质 §2.5 真实气体混合物p-V-T关系
§2.6 状态方程的比较和选用
§2.1 纯流体的p-V-T相图
§2.1.1 T –V 图 §2.1.2 p-V 图 §2.1.3 p-T 图 §2.1.4 p-V-T 立体相图 §2.1.5 纯流体p-V-T关系的应用及思考
§2.1.4 P-V-T立体相图
P-V-T立体相图
§2.1.4 P-V-T立体相图
水的P-V-T立体相图
【例2-1】 将下列纯物质经历的过程表 示在p-V图上：
1）过热蒸汽等温冷凝为过冷液体； 2）过冷液体等压加热成过热蒸汽； 3）饱和液体恒容加热； 4）在临界点进行的恒温膨胀
P
C
1）过热蒸汽等温冷凝为过冷液体； 2）过冷液体等压加热成过热蒸汽； 3）饱和蒸汽可逆绝热膨胀； 4）饱和液体恒容加热； 5）在临界点进行的恒温膨胀
• 1）由于刚性容器体积保持不变， 因此加热过程在等容线上变化，到 达B1时，汽液共存相变为液相单相； 继续加热，当T>Tc，则最终单相为 超临界流体，即C1点。
• 2）当水慢慢加热后，则状态从位 于汽液共存区的A2，变为汽相单相 B2，继续加热，当T>Tc，则最终单 相为临界流体C2。
§2.1 纯流体的P-V-T相图
P-T图
液相区
8atm下变成液体
气相区
1atm下变成气体
液化气的p-T 图
-82.62 ℃
室温10~40℃
乙烯、丙烯、 丁烯能做液化 气吗？
96.59℃
TC = 196.46 Tb =36.05 ℃
物质 甲烷 乙烷 丙烷 正丁 烷 正戊 烷 正己 烷 Ⅹ 32.18 ℃ Ⅹ
151.9℃
√ √
Ⅹ Ⅹ
• 【例2-3】 在4L的刚性容器中装有50℃、2kg水的饱和 汽液混合物，已知50℃水的饱和液相体积Vsl=1.0121 ， 饱和汽相体积Vsv=12032；水的临界体积Vc=3.111 。现 在将水慢慢加热，使得饱和汽液混合物变成了单相，问： 此单相是什么相？ 如果将容器换为400L，最终答案是 什么？
甲烷 乙烷 丙烷 正丁烷 正戊烷 正己烷
-82.62 32.18 96.59 151.9 196.46 234.4
45.36 48.08 41.98 37.43 33.32 29.80
Hale Waihona Puke -161.45 -88.65 -42.15 -0.5 36.05 68.75
55.6 52.0 50.5 49.6 49.1 48.4
P-V-T关系的用途
• 1.流体的p-V-T关系可直接用于设计，如： – 1) 输送管道直径的选取。 – 2）储罐的体积、承受压力。 • 2.利用可测的热力学性质（T，P，V，CP）计算不可 测的热力学性质（H，S，G，f，φ，α，γ）。 • 而2点的意义比1点要大得多。（将在第3、4章介绍） 有了p-V-T关系，热力学的大多数问题均可得到解 决。
超临界流体萃取过程简介
溶液+萃取质A 原料A+B 萃取质A
萃取
萃取残质B
循环萃取剂
分离
新鲜萃取剂
利用超临界CO2流体技术从植物/动物中提 取纯天然的高附加值的物质
高附加值的天然产品 （从樱桃核中提取）
O CH
苯甲酮
OH CH2
苯甲醇
有樱桃味 US$120/Ib 无樱桃味 US$14/Ib
US$140/Ib US$14/Ib
5 4 1
3(T降低)
2
V
【例2-2】
： 现有一过程，从pV 图的状态点 a( 过 热蒸气 ) 出发，到达 状态点d（过冷液体） 可以有两种途径： ① 均 相 途 径 (a→b→c→d) ； ② 非 均 相 途 径 (a→b’→ c’→d) 。 请在 p-T 图上画出 对应的路径。
A
B
C
D
【例2-2】
室内压力 1atm
4. 超临界流体萃取技术
1）定义：在T>Tc和P>Pc区域内，气体、液体变得不可区 分，形成的一种特殊的流体，称为超临界流体。
超临界流体区
（T>Tc和P>Pc）
• 2）特点：超临界流体兼具气体和液体两者的优点。
– 具有液体一样的溶解能力和密度等 ； – 具有气体一样的低粘度和高扩散系数。 – 在临界状态附近 ，溶质在超临界流体中的溶解度 对T、P的变化很敏感 ；
§2.1.1 T –V 图
在常压下加热水
T 5
2 1
3
4 v
临界点
§2.1.1 T -V图
气体
液体
液体和蒸汽
饱和液相线 （泡点线） 饱和汽相线 （露点线）
§2.1.2 P-V图
P 0.2Mpa P 1Mpa T =150 C
o
P 0.4762Mpa T =150o C
P 0.4762Mpa T =150 C
§2.2 状态方程
• 从§2.1可知，流体的p-V-T数据是多么的重要。 • 毫无疑问，流体的p-V-T数据是可以直接测定的。现已 积累了大量水、空气、氨和氟里昂等的 p-V-T数据。 • 但测定数据费时耗资，而且测定所有流体的所有p-V-T 数据是不现实的，特别是高温高压下的p-V-T数据测定 不但技术上相当困难而且非常危险。 • 仅从有限的p-V-T测定数据不可能全面地了解流体的pV-T行为。 • 流体的p-V-T数据更重要作用是通过它推算内能、焓、 熵等信息。 • 需要P-V-T关系的解析形式！——状态方程！
0.203
0.218 0.450 0.217 0.232 0.228
• 将萃取原料装入萃取釜。采用CO2为超临界溶剂。 • CO2气体经热交换器冷凝成液体； • 用加压泵把压力提升到工艺过程所需的压力(应高于CO2的 pc)，同时调节温度 ，使其成为超临界CO2流体。 • CO2流体作为溶剂从萃取釜底部进入，与被萃取物料充分接 触，选择性溶解出所需的化学成分。 • 含溶解萃取物的高压CO2流体经节流阀降压到低于CO2的pc 以下进入分离釜，由于CO2溶解度急剧下降而析出溶质，自 动分离成溶质和CO2气体二部分，前者为过程产品，定期从 分离釜底部放出，后者为循环CO2气体，经过热交换器冷凝 成CO2液体再循环使用。 • 整个分离过程是利用CO2流体在超临界状态下对有机物有极 高的溶解度，而低于临界状态下对有机物基本不溶解的特性， 将CO2流体不断在萃取釜和分离釜间循环，从而有效地将需 要分离提取的组分从原料中分离出来。
– 甲烷：Tc= -82.62℃，pc=4.536 MPa, 。
• 问：室温下能否通过加压使天然气变成LNG ？ • 气体“液化”的先决条件是物质T<Tc。
临界点——最重要的性质
2. 制冷剂的选择
• 在选择氟里昂替代品时，离不开p-V-T数 据。 • 制冷剂工作特点:低压饱和蒸汽室温下饱 和液体交替变化。 对制冷剂的要求： 1)临界温度要高，否则在常温或普通低温范 围内不能被液化； 2) 在冷凝温度下的蒸汽压也不宜过高； 3)为了使蒸发压力高于大气压力。 • 制冷剂的选择离不开p-V-T数据。
– 对于高沸点、低挥发性、易热解的物质也能轻而易举萃 取出来，这是传统分离方法做不到的；
– 最初，用超临界CO2成功地从咖啡中提取咖啡因；现在 非常多用于中药提取领域。 – 从红豆杉树皮叶中获得的紫杉醇是抗癌药物； – 从银杏叶中提取银杏黄酮；从蛋黄中提取的卵磷脂 。
各种溶剂的临界特性
流体名称 分子式 临界压力 (bar) 临界温度 (℃ ) 临界密度 (g/cm3)
③汽液两相平衡区 F=C-P+2=1
②过热蒸汽区
什么是正 常沸点？
①饱和液相线
（泡点线）
②饱和汽相线 （露点线 ）
恒温线
临界点—p-V-T中最重要的性质
• 1）Tc、pc 是纯物质能够呈现汽液平衡时的最高温度 和最高压力。 • 要使气体液化温度绝对不能超过Tc 。 • 气体“液化”的先决条件是T<Tc，否则无论施加多大 的压力都不可能使之液化。 • 2）临界等温的数学特征：等于临界温度的等温线在 临界点出现水平拐点。 P V TC 0 在C点 重要！ 2 P V 2 TC 0 在C点
4区
临界等容线
液固平衡线
液体区
（T>Tc和P>Pc）
超临界流体区
临界点 固体区
汽液平衡线
气体区
三相点F=C-P+2=0
汽固平衡线
水的三相点：0.0098℃
P-T图的特征、相关概念
• p-T图最能表达温度、压力变化所引起的相态变化， 因此p-T图常被称之为相图。
• 单相区
• 两相平衡线（饱和曲线） – 汽化曲线、熔化曲线、升华曲线 • 三相点(Tt,Pt)和临界点(Tc,Pc,Vc) • 等容线 – 临界等容线V=Vc、V>Vc、V<Vc
o
P 0.4762Mpa T =150o C
T =150o C
Ps (T1 ) P s (T2 )
T Tc Tc T1 Tc T2 Tc
§2.1.2 P-V图
临界点
在C点 1点、 4区 2 P V 22 T线、 0 在C点
④
P
V T 0
超临界流体区 （T>Tc和P>Pc） ①过冷液体区L
各章之间的联系
第2章 流体的PVT关系 ( p-V-T, EOS) 第5章 相平衡
ˆ p i xi pyi
V i s i s i
给出物质 有效 利用 极限
第3章 纯流体的热力学 性质(H,S,U，难测； 由EOS+Cp得到）