苏科版九年级数学上册直线与圆、圆与圆的位置关系专题练习

合集下载

苏科版九年级数学上册直线与圆、圆与圆的位置关系专题练习

初中数学试卷直线与圆、圆与圆的地点关系专题练习一、选择题1 ．如图，⊙ O 内切于△ABC ，D 、E、F 为三个切点，若DEF=52 0，则 A 的度数为()A. 76 0B．680C．52 0D．38 02 ．同一平面内两圆的半径是R 和 r ，圆心距是 d ，若以R、 r 、d 为边长，能围成一个三角形，则这两个圆的位置关系是( )A ．外离B．相切C．订交D．内含3 ．如图，等腰梯形 ABCD 的腰 AD 的长为 3 ，⊙O 为其内切圆，则它的中位线长是( )A ． 3 B． 4 C． 5 D ．6则OC的长为()A ． 3 B． 2 C．23 D ． 22 2 3二、填空题5 ．如图， AB 是⊙ O 的直径， CD 与⊙ O 相切于点 C，BAC=50 0，则ACD=________ 0．6 ．如图， AB 是⊙ O 的直径， AM 为弦， MAB=30 0，过 M 点的⊙ O 的切线交 AB 延伸线于点 N ．若 ON=12 cm ，则⊙ O 的半径为 _________cm．7 ．两圆相切，圆心距为9 cm ，已知此中一圆的半径为 5 cm ，则另一圆的半径为 _______cm.8 ．半径分别为 13 、15 的⊙ O 1，与⊙ O 2订交于 A、B 两点，它们的公共弦 AB 的长为 24 ，则这两个圆的圆心距为．三、解答题9 ．如图， PA、 PB 是⊙ O 的切线，点A、 B 为切点， AC 是⊙ O 的直径，ACB=70 0．求P 的度数．10 ．如图， AB 是⊙ O 的直径， F 是 BA 的延伸线上的一点，EF AB ，垂足为 F，直线 EA 交⊙ O 于点 C，过 C 作⊙ O 的切线交直线EF 于点 D ． DC 与 DE 相等吗 ?为何 ?11 ．如图， AB 为⊙ O 的直径， C 为⊙ O 上一点， CD 切⊙ O 于点 C，且DAC=BAC ．(1)试判断 AD 与 CD 的地点关系，并说明原因．(2)若 AD=4 ，AB=6 ，求 AC．12 ．如图， O 为原点，点 A 的坐标为 (4 ， 3) ，⊙ A 的半径为 2 ．过点 A 作直线 l 平行于 x 轴，交 y 轴于点 B，点 P 在直线 l 上运动．(1)当点 P 在⊙ A 上时，请你直接写出它的坐标．(2)设点 P 的横坐标为 12 ，试判断直线 OP 与⊙ A 的地点关系，并说明原因．13 ．如图，在直角梯形ABCD 中，AD ∥BC，B=90 0，AB=8 cm，AD=24 cm，BC=26 cm ， AB 为⊙ O 的直径．动点P 从 A 点开始沿 AD 边向点 D 以 l cm ／s 的速度运动，动点 Q 从点 C 开始沿 CB 边向点 B 以 3 cm ／ s 的速度运动， P、Q 两点同时出发，当此中一点抵达端点时，另一点也随之停止运动，设运动时间为t s ，求：(1)t 分别为何值时，四边形PQCD 为平行四边形、等腰梯形?(2)t 分别为何值时，直线PQ 与⊙ O 订交、相切、相离?参照答案1． A2．C3．A4．C5． 406 ． 67．4 或 148．4 或 149．P为 40010 ． DC=DE连结OC(图略)．则有OC=OA，OAC=OCA ．又 Q CD是⊙O的切线,DCA+OCA=900．依据 EF AB ，EAF+E=90 0．E=DCA ．DC=DE11 ． (1)AD CD 连结 OC ，则 OA=OC ．OCA= BAC ．OCA= DAC ．AD ∥OC ．又 CD 切⊙O 于点 C, OC CD ．AD CD(2) 连结 BC．由题意得△ ADC ∽△ACB ． AC 2 =AD ·AB ．AC=2 6 12 ．(1) 点 P 的坐标是 (2，3) 或(6 ，3)(2) 连结 OP，过点 A 作 AC OP ，垂足为 C(图略 ) ，则 AP=PB-AB=12-4=8 ， OB=3 ，OP= 122 32 153 ,Q ACP= OBP=90 0，APC= OPB,APC ∽ OPB ．AC AP AC 8, AC=241.9 2．OB,3 153 153OP直线 OP与⊙A订交13 ． (1) 当 t=6 时， rain PQCD 为平行四边形；当t=7 时，四边形 PQCD 为等腰梯形 .2或 8时，直线 PQ 与⊙O 相切；0 t 2 26时，直线 PQ 与⊙ O 相(2) 当 t= 或 8 t3 3 32t 8 时，直线PQ与⊙O相离交；当3。

苏科版九年级上25直线与圆的位置关系(1)同步练习含答案.docx

第2章对称图形一一圆2.5直线与圆的位置关系（1）【基础提优】1. 已知。

O 的半径是6,点O 到直线/的距离为5,则直线/与0O 的位置关系是（）A.相离B.相切C.相交D.无法判断2. 已知直线I 与半径为r 的相交，且点0到直线/的距离为6,则r 的取值范围是（）A.相交B.相切 6. 如图，在矩形ABCD 中，AB=6, BO4,若OO 是以AB 为直径的圆，则直线DC 与O 0的位置关系是DAB 7. 已知的半径为3 cm,圆心0到直线/的距离是4 cm,则直线/与的位置关系是 __________ • 12 8. 如图，已知0P 的半径为2,圆心P 在反比例函数y =—上运动，当OP 与兀轴相切时, x9. 如图，0P 的圆心为P （-3, 2）,半径为3,直线MN 过点M （5, 0）且平行于y 轴，点N 在点A. r<6B. r=6C. r>63. 在 RtAABC 中，ZC=90°与直线AB 相切，则厂的值为（ A. 4. A. 5. 是,AC=3cm, BC=4cm, ）2cm B ・ 2.4cm C. 3cmD.心6 以点C 为圆心，/•为半径作圆，若D. 4cm 若OO 的半径为2,直线/上有一点P 满足P0=2,则直线/与的位置关系是（）相切 B.相离己知OO 的面积为9兀cm 2,（）C.相离或相切D.相切或相交若点O 到直线1的距离为7： cm,贝ij 直线I 与OO 的位置关D.无法确定C.相离 XM的上方.（1）在图中作LBOP关于y轴对称的。

卩，根据作图直接写出OP，与直线MN的位置关系；（2）若点N在（1）中的（DP，上，求PN的长.【拓展捉优】圆心0在等腰直角三角形ABC 的内部，ZBAC= 90°, OA=1,3. 如图，直线y =——x + >/3与x 轴、y 轴分别相交于A, B 两点，圆心P 的坐标为(1, 0), (DP 与y 轴相切于点O.若将(DP 沿兀轴向左移动，当OP 与该直线相交时，横坐标为整数的点P 的个数是( )1.如图，在 RtAABC 屮，ZC=90°, ZB=30°, BC=4 cm,以点C 为圆心，2 cm 的长为半D.相切或相交B. 3C. 4D. 5相交 2.如图，OO 过点B, C. A. 24. 如图，已知＜30是以平面直角坐标系的原点0为圆心，半径为1的圆，ZAOB=45°,点 P 在兀轴上运动（点P 与点0不重合）,若过点P 且与0B 平行的直线与OO 有公共点，设D. A >V25. 在平面直角坐标系xOy 中，以点P （・3, 4）为圆心，广为半径的圆与两坐标轴恰有四个公共点，则尸的取值范围是 _________________ . 6. 如图，已知ZAPB=30°, 0是射线PB±的一点，0P=5cm,若以点0为圆心，1.5cm 为半径的（DO 沿BP 方向以lcm/s 的速度移动，则O0移动__________ s 后与PA 相切. 7. 如图，公路MN 与公路PQ 在点P 处交汇，且ZQPN=30。

苏科版九年级数学上册2.5 直线与圆的位置关系2.5.1直线与圆的位置关系(word版含答案)

2.5 直线与圆的位置关系2.5.1直线与圆的位置关系一、选择题（共6小题；共30分）1. 如图所示，已知∠BAC=45∘，一动点O在射线AB上运动（点O与点A不重合），设OA=x，如果半径为1的⊙O与射线AC有公共点，那么x的取值范围是( )A. 0<x≤√2B. 1<x≤√2C. 1≤x<√2D. x>√22. 在平面直角坐标系中，以点(3,2)为圆心，3为半径的圆一定( )A. 与x轴相切，与y轴相切B. 与x轴相切，与y轴相交C. 与x轴相交，与y轴相切D. 与x轴相交，与y轴相交3. 设⊙O的半径为r，圆心O到直线l的距离为d，若直线l与⊙O有交点，则d与r的关系为( )A. d=rB. d<rC. d>rD. d≤r4. 如图，△ABC中，AB=6，AC=8，BC=10，D，E分别是AC，AB的中点，则以DE为直径的圆与BC的位置关系是( )A. 相交B. 相切C. 相离D. 无法确定5. 如图，⊙O的半径为1，正方形ABCD的对角线长为6，OA=4．若将⊙O绕点A按顺时针方向旋转360∘，在旋转过程中，⊙O与正方形ABCD的边只有一个公共点的情况一共出现( )A. 3次B. 4次C. 5次D. 6次6. 在Rt△ABC中，∠C=90∘，BC=3cm，AC=4cm，以点C为圆心，以2.5cm为半径画圆，则⊙C与直线AB的位置关系是( )A. 相交B. 相切C. 相离D. 不能确定二、填空题（共8小题；共40分）7. 如图，在矩形ABCD中，AB=6，BC=4，⊙O是以AB为直径的圆，则直线DC与⊙O的位置关系是．8. 如图，在Rt△ABC中，∠C=90∘，AC=3，BC=4，若以点C为圆心，R为半径所作的圆与斜边AB有两个交点，则R的取值范围是．9. 已知直线l与半径为4的⊙O相交，则点O到直线l的距离d可取的整数值是．10. 如图，给定一个半径为2的圆，圆心O到水平直线l的距离为d，即OM=d．我们把圆上到直线l的距离等于1的点的个数记为m．如d=0时，l为经过圆心O的一条直线，此时圆上有四个到直线l的距离等于1的点，即m= 4．由此可知：（1）当d=3时，m=；（2）当m=2时，d的取值范围是．11. Rt△ABC中，∠C=90∘，AC=5，BC=12，如果以点C为圆心，r为半径，且⊙C与斜边AB仅有一个公共点，那么半径r的取值范围是．12. 如图，△ABC为等边三角形．AB=6，动点O在△ABC的边上从点A出发沿着A→C→B→A的路线匀速运动一周，速度为每秒1个长度单位，以O为圆心，√3为半径的圆在运动过程中与△ABC的边第二次相切时是出发后第秒．13. 如图所示，在平面直角坐标系xOy中，半径为2的⊙P的圆心P的坐标为(−3,0)，将⊙P沿x轴正方向平移，使⊙P与y轴相切，则平移的距离为．14. 如图，已知∠APB=30∘，OP=3cm，⊙O的半径为1cm，若圆心O沿着BP的方向在直线BP上移动．（1）当圆心O移动的距离为1cm时，则⊙O与直线PA的位置关系是；（2）若圆心O的移动距离是d cm，当⊙O与直线PA相交时，则d的取值范围是．三、解答题（共2小题；共30分）15. 在同一平面内，已知点O到直线l的距离为5，以点O为圆心，r为半径画圆．探究、归纳：（1）当r=时，⊙O上有且只有一个点到直线l的距离等于3；（2）当r=时，⊙O上有且只有三个点到直线l的距离等于3；（3）随着r的变化，⊙O上到直线l的距离等于3的点的个数有什么变化，并求出相对应的r的值或取值范围（不必写出计算过程）．16. 已知到直线l的距离等于a的所有点的集合是与直线l平行且距离为a的两条直线l1，l2（如图①）．（1）在图②的平面直角坐标系中，画出到直线y=x+2√2的距离为1的所有点的集合的图形．并写出该图形与y轴交点的坐标．（2）试探讨在以坐标原点O为圆心，r为半径的圆上，到直线y=x+2√2的距离为1的点的个数与r的关系．（3）如图③，若以坐标原点O为圆心，2为半径的圆上有两个点到直线y=x+ b的距离为1，则b的取值范围为．答案第一部分1. A2. C3. D 【解析】当d=r时，直线与圆相切，则直线l与⊙O有一个交点；当d<r时，直线与圆相交，则直线l与⊙O有两个交点，∴若直线l与⊙O有交点，则d与r的关系为d≤r．4. A 【解析】过点A作AM⊥BC于点M，交DE于点N，由AB2+AC2=BC2，得∠BAC=90∘，∴AM⋅BC=AC⋅AB，=4.8．∴AM=6×810∵D，E分别是AC，AB的中点，BC=5，∴DE∥BC，DE=12AM，∴AN=MN=12∴MN=2.4．∵以DE为直径的圆的半径为 2.5，∴r=2.5>2.4，∴以DE为直径的圆与BC的位置关系是相交．5. B【解析】如图，∵⊙O的半径为1，正方形ABCD的对角线长为6，OA=4，∴⊙O与正方形ABCD的边AB，AD只有一个公共点的情况各有1次，与边BC，CD只有一个公共点的情况各有1次．∴在旋转过程中，⊙O与正方形ABCD的边只有一个公共点的情况一共出现4次．6. A 【解析】过C作CD⊥AB于D，如图所示：∵在Rt△ABC中，∠C=90，AC=4，BC=3，∴AB=2+BC2=5，∵△ABC的面积=12AC×BC=12AB×CD，∴3×4=5CD，∴CD=2.4<2.5，即d<r，∴以2.5为半径的⊙C与直线AB的关系是相交．第二部分7. 相离8. 2.4<R≤3【解析】过点C作CD⊥AB交AB于点D．∵BC>AC，∴要使以点C为圆心，R为半径所作的圆与斜边AB有两个交点，则圆的半径应大于CD的长，小于或等于AC的长，由勾股定理知，AB=√AC2+BC2=5．∵S△ABC=12AC⋅BC=12CD⋅AB，即12×3×4=12×5×CD，∴CD=2.4，即R的取值范围是 2.4<R≤3．9. 0，1，2，3【解析】∵直线l与半径为4的⊙O相交，∴点O到直线l的距离d的取值范围为0≤d<4，∴d可取的整数值是0，1，2，3．10. 1，1<d<3【解析】（1）当d=3时，d>r，∴直线l与⊙O相离，此时圆上只有一个到直线l的距离等于1的点，∴m=1；（2）当d=3时，m=1；当d=1时，m=3，∴当m=2时，d的取值范围是1<d<3．11. r=60或5<r≤1213【解析】根据勾股定理求得直角三角形的斜边是2+122=13．当圆和斜边相切时，则半径即是斜边上的高，等于60；13当圆和斜边相交，且只有一个交在斜边上时，可以让圆的半径大于短直角边而小于或等于长直角边，则5<r≤12．故半径r的取值范围是r=60或5<r≤12．1312. 4【解析】根据题意，该圆在运动过程中与△ABC的边第二次相切时是与BC边相切．作OD⊥BC于D，则OD=√3．在Rt△OCD中，∠C=60∘，OD=√3，∴OC=2，∴OA=6−2=4，∴4÷1=4（秒），∴以O为圆心，√3为半径的圆在运动过程中与△ABC的边第二次相切时是出发后第4秒．13. 1或5【解析】当⊙P位于y轴的左侧且与y轴相切时，平移的距离为1；当⊙P位于y轴的右侧且与y轴相切时，平移的距离为5．14. 相切，1<d<5【解析】（1）如图①，当圆心O向左移动1cm时，POʹ=PO−OʹO=3−1=2(cm)，作OʹC⊥PA于C，∴∠P=30∘，POʹ=1(cm)．∴OʹC=12∵圆的半径为1cm，∴⊙O与直线PA的位置关系是相切．（2）如图②，当圆心O由Oʹ向左继续移动时，PA与圆相交，当移动到Oʺ时，相切，此时OʺP= POʹ=2cm，∴点O移动的距离d的范围满足1<d<5时相交．第三部分15. （1）2（2）8（3）当0<r<2时，⊙O上没有点到直线l的距离等于3；当r=2时，⊙O上有1个点到直线l的距离等于3；当2<r<8时，⊙O上有2个点到直线l的距离等于3；当r=8时，⊙O上有3个点到直线l的距离等于3；当r>8时，⊙O上有4个点到直线l的距离等于3．16. （1）如图，与y轴交点的坐标为(0,√2)和(0,3√2)．（2）（线定圆动）当0<r<1时，0个；当r=1时，1个；当1< r<3时，2个；当r=3时，3个；当3<r时，4个．（3）（圆定线动）−3√2<b<−√2或√2<b<3√2。

苏科版九年级数学(上册) 直线与圆的位置关系一课一练【含答案】

苏科版九年级数学（上册）直线与圆的位置关系一课一练一、单选题1．在中，，以点为圆心，为半径作圆．若与边只有ABC 9045C AC AB ︒∠===，，C R C AB 一个公共点，则的取值范围是（）R A ．B ．C ．或D ．或125R =34R 03R <<4R >34R < 125R =2．如图，PA 切⊙O 于点A ，PB 切⊙O 于点B ，如果∠APB=60°，⊙O 半径是3，则劣弧AB 的长为（）A ．B ．πC ．2πD ．4π2π3．在中，，，，以C 为圆心作与AB 相切，则的半径Rt ABC △90C ∠=︒10AB =8AC =C C 长为（）A ．8B ．4C ．9.6D ．4.84．已知⊙O 的半径是5，直线l 是⊙O 的切线，那么点O 到直线l 的距离是( )A ．2.5B ．3C ．5D ．105．已知某直线到圆心的距离为，圆的周长为，请问这条直线与这个圆的公共点的个数为（ 5cm 10cm π）A ．0B ．1C ．2D ．无法确定6．如图，在中，，点在线段上（不与、重合），若为的ABC 40B C ∠=∠=︒D BCB C O ADC 内心，则不可能是（）AOC ∠A ．B ．C ．D ．100︒120︒140︒150︒7．如图，△ABC 的内切圆⊙O 与BC 、CA 、AB 分别相切于点D 、E 、F ，且AB ＝5，BC ＝13，CA ＝12，则阴影部分(即四边形AEOF)的面积是()A ．4B ．6.25C ．7.5D ．98．已知⊙O 分别与△ABC 的BC 边，AB 的延长线，AC 的延长线相切，则∠BOC等于（）A ．（∠B+∠C ）B ．90°+∠AC ．90°-∠AD ．180°-∠A1212129．如图，AB 是⊙O 的直径，点P 在BA 的延长线上，PA ＝AO，PD 与⊙O 相切于点D ，BC ⊥AB 交PD 的延长线于点C，若⊙O 的半径为1，则BC 的长是（）A ．1.5B ．2CD 10．如图，AB 是⊙O 的直径，C ，D 在⊙O上，且BC=CD ，过点C 作CE ⊥AD ，交AD 延长线于E ，交AB 延长线于F 点．若AB=4ED ，则cos ∠ABC 的值是（　）A ．B ．C ．D ．12131415二、填空题11．如图，⊙O 的半径OC =5cm ，直线l ⊥OC ，垂足为H ，且l 交⊙O 于A 、B 两点，AB =8cm ，则l沿OC 所在直线向下平移 __________cm 时与⊙O 相切．12．如图，已知，M 为OB 边上任意一点，以M 为圆心，2cm 为半径作，当30AOB ∠=︒M ________cm时，与OA 相切.OM =M 13．以正方形的边为直径作半圆，过点作直线切半圆于点，交边于点，若ABCD AB O C F AB E的周长为，则直角梯形周长为___________．CDE ∆12ABCE 14．如图，已知Rt △ABC 中，AC =5，BC =12，∠ACB =90°，P 是边AB 上的动点，Q 是边BC上的动点，且∠CPQ =90°，则线段CQ 的取值范围是____．15．在Rt △ABC 中，∠C=90°，AC=4，BC=3，若以C 为圆心，R 为半径作的圆与直线AB 相切,则R=______.16．已知⊙O的半径OA＝5cm，延长OA到B，AB＝2cm，以OB为一边作∠OBC＝45°，那么BC所在直线与⊙O的位置关系是_____．17．如图，△ABC是⊙O的内接三角形，AB是⊙O的直径，I是△ABC的内心，则∠BIA的度数是_______°．18．等腰直角△ABC中, ∠C=90度，斜边AB=6,则此三角形的内心与外心之间的距离是_________.三、解答题19．在Rt△ABC中，∠C=90°，AC=3cm，BC=4cm，以C为圆心，r为半径的圆与AB有何位置关系？(1) r=2cm；(2) r=2.4cm；(3) r=3cm．20．已知：如图，⊙O内切于△ABC，∠BOC=105°，∠ACB=90°，AB=20cm．求BC、AC的长．21．已知：如图，△ABC三边BC=a，CA=b，AB=c，它的内切圆O的半径长为r．求△ABC的面积S．22．如图，在锐角△ABC 中，BC ＝5，sin ∠BAC ＝，点I 为三角形ABC 的内心，AB ＝BC ，求AI 的45长．23．如图，以平行四边形的顶点为圆心，长为半径作，分别交于两点，ABCD A ABA ,BC AD ,E F 交的延长线于点．BA G （1）求证：；EF FG =（2）连接，若，求的度数．AE 140EAG ︒∠=D ∠24．已知：如图，⊙O 是Rt △ABC 的内切圆，∠C=90°．(1)若AC=12cm，BC=9cm，求⊙O的半径r；(2)若AC=b，BC=a，AB=c，求⊙O的半径r．25．如图，AB是⊙O的直径，点P是弦AC上一动点（不与A，C重合），过点P作PE⊥AB，垂足为 ACE，射线EP交于点F，交过点C的切线于点D．（1）求证：DC=DP；AC（2）若∠CAB=30°，当F是的中点时，判断以A，O，C，F为顶点的四边形是什么特殊四边形？说明理由．26．如图，⊙O与四边形ABCD的各边依次切于M，N，G，H．（1）猜想AB+CD与AD+BC有何数量关系，并证明你的猜想；（2）若四边形ABCD 增加条件AD ∥BC 而成为梯形，梯形的中位线长为m ，其他条件不变，试用m 表示梯形的周长．27．如图，都为⊙O 的切线，切点分别为，且．52,,,APB PA PB DE ︒∠=,,A B F 6PA =（1）求的周长；PDE △（2）求的度数．DOE ∠28．如图，在Rt △ABC 中，∠BAC ＝90°，CD 平分∠ACB ，交AB 于点D ，以点D 为圆心，DA 为半径的⊙D 与AB 相交于点E.(1)判断直线BC 与⊙D 的位置关系，并证明你的结论.(2)若AC＝3，BC＝5，求BE的长.答案1．D如图，过点作于点．C CD AB ⊥D ，．9045ACB AC AB ︒∠=== ，，3BC ∴=①如果以点为圆心，为半径的圆与斜边相切，则．此时C R AB CD R =．1112225CD AB AC BC R CD ⋅=⋅∴==，②当时，圆与边也只有一个公共点．34R < AB 综上，或．34R < 125R =故选D．2．C解：连接OA ，OB ．则OA ⊥PA ，OB ⊥PB∵∠APB=60°∴∠AOB=120°∴劣弧AB 的长是：120π32π.180⨯=故选C ．3．D解：如图，过点C 作CD ⊥AB 于点D ，∵，，，90C ∠=︒10AB =8AC =∴，6BC ==∵S △ABC ，1122AC BC CD AB =⋅=⋅∴，4.8AC BC CD AB ⋅==则以C 为圆心CD 为半径作与AB 相切.C 故选D.4．C根据圆与直线的位置关系可得：当直线与圆相切时，圆心到直线的距离等于半径；当直线与圆相交时，圆心到直线的距离小于半径；当直线与圆相离时，圆心到直线的距离大于半径.5．B解：∵圆的周长为10πcm ，∴圆的半径为5cm ，∵圆心到直线l 的距离为5cm ，∴d=r ，∴直线与圆相切，∴直线l 和这个圆的公共点的个数为1个．故选：B ．6．A∵中，，ABC 40B C ∠=∠=︒∴∠BAC=180º﹣∠B﹣∠C=100º，∵为的内心，O ADC ∴∠OAC=∠DAC ，∠ACO=∠ACB=20º，1212∴∠AOC=180º﹣∠OAC﹣∠ACO=160º﹣∠DAC ，12∵点在线段上（不与、重合），D BC B C ∴0º﹣∠DAC﹣100º，即0º﹣∠DAC﹣50º，12∴110º﹣∠AOC﹣160º，故∠AOC 不可能是100º，故选：A ．7．A∵AB=5，BC=13，CA=12，∴AB 2+AC 2=BC 2，∴△ABC 为直角三角形，且∠BAC=90°，∵⊙O 为△ABC 内切圆，∴∠AFO=∠AEO=90°，且AE=AF ，∴四边形AEOF 为正方形，设⊙O 的半径为r ，∴OE=OF=r ，∴S 四边形AEOF =r²，连接AO ，BO ，CO，∴S △ABC =S △AOB +S △AOC +S △BOC ，∴，11()22AB AC BC r AB AC ++=⋅∴r=2，∴S 四边形AEOF =r²=4，故选A.8．C设⊙O 分别与△ABC 的BC 边，AB 的延长线，AC 的延长线相切，切点分别为D ，E ，F ，∴OE ⊥AB ，OF ⊥AC ，∠BOD ＝∠EOD ，∠COD ＝∠FOD ，1212∴∠EOF ＝180°－∠A ，∴∠BOC ＝∠BOD ＋∠COD＝(∠EOD ＋∠FOD )12＝∠EOF12＝×(180°－∠A )12＝90°－∠A ．12故选C ．9．D连接OD ，如图所示∵PC 切⊙O 于D ∴∠ODP ＝90°∵⊙O 的半径为1，PA ＝AO ，AB 是⊙O 的直径 ∴PO ＝1+1＝2，PB ＝1+1+1＝3，OD ＝1∴由勾股定理得：PD==∵BC ⊥AB ，AB 过O ∴BC 切⊙O 于B ∵PC 切⊙O 于D ∴CD ＝BC设CD ＝CB ＝x 在Rt △PBC 中，由勾股定理得：PC 2＝PB 2+BC 2即解得：x即BC222)3x x =+故选：D10．A连接OC 、AC，∵CE ⊥AD ，∴∠EAC+∠ECA=90°，∵OC=OA ，∴∠OCA=∠OAC ，又∵BC=CD ，∴∠OAC=∠EAC ，∴∠OCA=∠EAC ，∴∠ECA+∠OCA=90°，∴EF 是⊙O 的切线，∴∠ECD=∠EAC ，又∵BC=CD ，∴∠EAC=∠BAC ，∴∠ECD=∠BAC ，又∵AB 是直径，∴∠BCA=90°，在△BAC 和△DCE 中，∠BCA=∠DEC=90°，∠ECD=∠CAB ，∴△CDE ∽△ABC ，∴ ＝，CDDE A B B C 又∵AB=4DE ，CD=BC ，∴，=14BC AB BCAB∴BC=AB ，12∴cos ∠ABC= =．BC AB 12故选：A ．11．2∵直线和圆相切时，OH =5，又∵在直角三角形OHA 中，HA =AB ÷2 =4，OA =5，∴OH =3．∴需要平移5-3=2cm ．故答案是：2．12．4解：如图，过M 作MN ⊥OA 于点N ，∵MN=2cm ，，30AOB ∠=︒∴OM=4cm ，则当OM=4cm 时，与OA相切.M 故答案为4.13．212设正方形ABCD 的边长为a则，AB BC CD AD a ====90BAD ABC D ∠=∠=∠=︒由圆的切线的判定得：AD 、BC 均为圆O 的切线由切线长定理得：,AE FE FC BC a===的周长为CDE 12，即12DE CE CD ∴++=12DE FE FC CD +++=，即12DE AE BC CD ∴+++=12AD BC CD ++=，解得312a ∴=4a =设，则AE x =3,3DE AD AE x CE FE FC x =-=-=+=+在中，，即Rt CDE △222CD DE CE +=2223(3)(3)x x +-=+解得34x =315,344AE CE x ∴==+=则直角梯形周长为ABCE 1532133442AB BC CE AE +++=+++=故．21214．≤CQ ≤12．203∵Rt △ABC 中，AC =5，BC =12，∠ACB =90°，∴AB =13，①当半圆O 与AB 相切时，如图，连接OP ，则OP ⊥AB ，且AC =AP =5，∴PB =AB ﹣AP =13﹣5=8；设CO =x ，则OP =x ，OB =12﹣x ；在Rt △OPB 中，OB 2=OP 2+OB 2，即(12﹣x )2=x 2+82，解之得x =，103∴CQ =2x =；203即当CQ =且点P 运动到切点的位置时，△CPQ 为直角三角形．203②当＜CQ ≤12时，半圆O 与直线AB 有两个交点，当点P 运动到这两个交点的位置时，△CPQ 为直203角三角形；③当0＜CQ ＜时，半圆O 与直线AB 相离，即点P 在AB 边上运动时，均在半圆O 外，∠CPQ ＜90°，203此时△CPQ 不可能为直角三角形；∴当≤CQ ≤12时，△CPQ 可能为直角三角形．203故≤CQ ≤12．20315．2.4解：过C 作CD ⊥AB 于D.∵ AB 2＝AC 2＋BC 2，AC ＝3，BC ＝4，∴ AB 2＝32＋42＝25，∴ AB ＝5，根据三角形面积，得AC ·BC ＝CD ·AB∴CD ＝2.4.∵直线AB 和⊙C相切，∴ R ＝CD ＝2.4.16．相交过O 作OC ⊥BC ，在Rt △OBC 中，∠B=45°，OB=5+2=7，∴5，∴BC 所在直线与⊙O 的位置关系是相交，故答案为相交．17．135∵AB 是⊙O 的直径∴=90ACB ∠︒∴90CAB CBA ∠+∠=︒∵I 是△ABC 的内心∴IA 、IB 是角平分线∴()1452IAB IBA CAB CBA +=+=︒∠∠∠∠∴()180135AIB IAB IBA =︒-+=︒∠∠∠故135．18．3如图，∵AB=6，AC=BC ，∠ABC=90°∴CO 1= AO 1= BO 1=3AC=BC=∵O 2是内心，∴11()22AB CDAB AC BC r ⋅=++∴-3即O 1O 2-3故-319．（1）相离（2）相切（3）相交∵∠C ＝90°，AC ＝3cm ，BC ＝4cm ，∴AB ＝5cm.作CD ⊥AB 于D , 则 AC ·BC ＝ AB ·CD , CD ＝ cm.(1) ∵CD ＝2.4cm ＞r ＝2cm, ∴直线AB 与⊙C 相离.(2) ∵CD ＝2.4cm ＝r ＝2.4cm, ∴直线AB 与⊙C 相切.(3) ∵CD ＝2.4cm ＜r ＝3cm, ∴直线AB 与⊙C 相交.20．BC 、AC 的长分别是10cm 、cm.解：∵圆O 内切于△ABC ，∴∠ABO=∠CBO ，∠BCO=∠ACO ，∵∠ACB=90°，∴∠BCO=×90°=45°，12∵∠BOC=105°，∴∠CBO=180°−45°−105°=30°，∴∠ABC=2∠CBO=60°，∴∠A=30°，∴BC=AB=×20=10cm ，1212∴==∴BC 、AC 的长分别是10cm 、21．S=(a+b+c)r12如图，设△ABC 与⊙O 相切与点D 、E 、F ．连接OA 、OB 、OC 、OD 、OE 、OF ．则OD ⊥AB ，OE ⊥AC ，OF ⊥BC ．∵S △AOB =AB•OD=cr ，同理，S △OBC =ar ，S △OAC =br ．12121212∵S △ABC =S △AOB +S △OBC +S △OAC ，即S=cr+ar+br=(a+b+c)r1212121222．AI .连结CI ，BI ，且延长BI 交AC 于点F ，过点I 作IG ⊥BC 于点G ，IE ⊥AB 于点E .∵AB ＝BC ＝5，点I 为△ABC 的内心，∴BF ⊥AC ，AF ＝CF .在Rt △ABF 中，∵sin ∠BAC ＝，∴BF ＝4.∴AF＝3，∴AC ＝6.∵点I 是△ABC 的内心，45BF AB ＝IE ⊥AB ，IF ⊥AC ，IG ⊥BC ，∴IE ＝IF ＝IG .∴S △ABC ＝AB ＋AC ＋BC )·IF ＝AC ·BF ，∴IF ＝1212，∴AI.6436562AC BF AB AC BC ⨯ ＝＝＋＋＋＋23．（1）详见解析；（2）70°（1）证明：连接．AE∵四边形是平行四边形，ABCD ，//AD BC ∴，，EAF AEB ∴∠=∠GAF B ∠=∠，AE AB = ，B AEB ∴∠=∠，EAF GAF ∴∠=∠.EF FG ∴=（2）解：为的直径，，GB A 140EAG ︒∠=，40BAE ︒∴∠=，70B AEB ︒∴∠=∠=∵四边形是平行四边形，ABCD ．70D B ︒∴∠=∠=24．（1）r=3cm. (2) r=（a+b-c ）．12（1）如图,连接OD ，OF ；在Rt △ABC 中，∠C=90°，AC=12cm ，BC=9cm ；根据勾股定理=15cm ；四边形OFCD 中，OD=OF ，∠ODC=∠OFC=∠C=90°；则四边形OFCD 是正方形；由切线长定理，得：AD=AE ，CD=CF ，BE=BF ；则CD=CF=（AC+BC-AB ）；12即：r=（12+9-15）=3cm ．12（2）当AC=b ，BC=a ，AB=c ，由以上可得： CD=CF=（AC+BC-AB ）；12即：r=（a+b-c ）．则⊙O 的半径r 为：（a+b-c ）．121225．（1）证明见解析；（2）菱形，理由见解析．解：（1）连接BC、OC，∵AB是⊙O的直径，∴∠OCD=90°，∴∠OCA+∠OCB=90°，∵∠OCA=∠OAC，∠B=∠OCB，∴∠OAC+∠B=90°，∵CD为切线，∴∠OCD=90°，∴∠OCA+∠ACD=90°，∴∠B=∠ACD，∵PE⊥AB，∴∠APE=∠DPC=∠B，∴∠DPC=∠ACD，∴AP=DC；（2）以A，O，C，F为顶点的四边形是菱形．理由如下：∵∠CAB=30°，∴∠B=60°，∴△OBC为等边三角形，∴∠AOC=120°，连接OF，AF，AC∵F是的中点，∴∠AOF=∠COF=60°，∴△AOF与△COF均为等边三角形，∴AF=AO=OC=CF，∴四边形OACF为菱形．26．（1）AB+CD=AD+BC，证明详见解析；（2）4m.(1)AB+CD=AD+BC证明：由切线长定理，得：AM=AH，BN=BM，CN=CG，DG=DH，所以AB+CD=AM+BM+CG+DG=AH+BN+CN+DH=AD+BC，即AB+CD=AD+BC(2)AD∥BC，在梯形ABCD中，由梯形的中位线定理得，AD+BC=2m，梯形的周长=AB+CD+AD+BC=2(AD+BC)=2×2m=4m27．（1）12；（2）64°解：（1）∵PA 、PB 、DE 都为⊙O 的切线，∴DA=DF ，EB=EF ，PA=PB=6，∴DE=DA+EB ，∴PE+PD+DE=PA+PB=12，即△PDE 的周长为12；（2）连接OF，∵PA 、PB 、DE 分别切⊙O 于A 、B 、F 三点，∴OB ⊥PB ，OA ⊥PA ，∠BOE=∠FOE=∠BOF ，∠FOD=∠AOD=∠AOF ，1212∵∠APB=52°，∴∠AOB=360°-90°-90°-52°=128°，∴∠DOE=∠FOE+∠FOD=（∠BOF+∠AOF ）=∠BOA=64°．121228．(1)直线BC 与⊙D 相切，理由见解析；(2)BE=1.(1)直线BC 与⊙D 相切，理由：过D 作DF ⊥BC 于F ，∴∠CFD ＝∠A ＝90°，∵CD 平分∠ACB ，∴DA ＝DF ，∴直线BC 与⊙D 相切；(2)∵∠BAC ＝90°，AC ＝3，BC ＝5，∴AB 4，在Rt △ACD 与Rt △FCD 中,AD DF CD CD =⎧⎨=⎩∴Rt △ACD ≌Rt △FCD(HL)，∴CF ＝AC ＝3，∴BF ＝2，∵BF 是⊙D 的切线，∴BF 2＝BA•BE ，∴.22214BF BE AB ===。

九年级数学苏科版上册课时练第2单元《2.5直线与圆的位置关系》(1) 练习试题试卷含答案

课时练2.5直线与圆的位置关系一、选择题1.圆的直径为13cm，如果圆心与直线的距离是d，则（）A.当d=8cm时，直线与圆相交B.当d=4.5cm时，直线与圆相离C.当d=6.5cm时，直线与圆相切D.当d=13cm时，直线与圆相切2.已知在直角坐标平面内，以点P（﹣2，3）为圆心，2为半径的圆P与x轴的位置关系是（）A.相离B.相切C.相交D.相离、相切、相交都有可能3.直线l上的一点到圆心的距离等于半径，则直线与圆的位置关系一定是（）A.相离B.相切C.相交D.相切或相交4.如图，△ABC中，AB=3，AC=4，BC=5，D、E分别是AC、AB的中点，则以DE为直径的圆与BC的位置关系是（）A.相切B.相交C.相离D.无法确定5.已知⊙O的半径为4，点O到直线m的距离为3，则直线m与⊙O公共点的个数为（）A.0个B.1个C.2个D.3个6.如图，两个圆的圆心都是点O，AB是大圆的直径，大圆的弦BC所在直线与小圆相切于点D．则下列结论不一定成立的是（）A.BD=CDB.AC⊥BCC.AB=2ACD.AC=2OD7.如图，⊙O的半径OC=5cm，直线l⊥OC，垂足为H，且l交⊙O于A，B两点，AB=8cm，若l沿OC所在直线平移后与⊙O相切，则平移的距离是()A.1cmB.2cmC.8cmD.2cm或8cm8.如图，CD是⊙O的直径，弦AB⊥CD于点G，直线EF与⊙O相切于点D，则下列结论中不一定正确的是()A.AG=BGB.AB∥EFC.AD∥BCD.∠ABC=∠ADC9.如图，等腰直角三角形ABC中，AB=AC=8，O为BC的中点，以O为圆心作半圆，使它与AB，AC都相切，切点分别为D，E，则⊙O的半径为()A.8B.6C.5D.410.如图，△ABC是一张三角形纸片，⊙O是它的内切圆，点D、E是其中的两个切点，已知CD=6cm，小明准备用剪刀沿着与⊙O相切的一条直线MN剪下一块三角形（△CMN），则剪下的△CMN的周长是（）A.9cmB.12cmC.15cmD.18cm二、填空题11.在平面直角坐标系中，⊙C的圆心为C（a，0），半径长为2，若y轴与⊙C相离，则a 的取值范围为.12.如图，已知Rt△ABC的斜边AB=8，AC=4.以点C为圆心作圆，当⊙C与边AB只有一个交点时，则⊙C的半径的取值范围是.13.已知圆O的半径为5，AB是圆O的直径，D是AB延长线上一点，DC是圆O的切线，C是切点，连接AC，若∠CAB=30°，则BD的长为．14.如图，若以平行四边形一边AB为直径的圆恰好与对边CD相切于点D，则∠C=____度.15.如图，在⊙O中，弦AB=OA，P是半径OB的延长线上一点，且PB=OB，则PA与⊙O的位置关系是_________.16.如图，直线AB、CD相交于点O，∠AOC=30°，半径为1cm的⊙P的圆心在射线OA上，开始时，PO=6cm.如果⊙P以1cm/s的速度沿由A向B的方向移动，那么当⊙P的运动时间t(秒)满足条件时，⊙P与直线CD相交.三、解答题17.如图，已知∠APB=30°，OP=3cm，⊙O的半径为1cm，若圆心O沿着BP的方向在直线BP 上移动.（1）当圆心O移动的距离为1cm时，则⊙O与直线PA的位置关系是什么？（2）若圆心O的移动距离是d，当⊙O与直线PA相交时，则d的取值范围是什么？18.如图，AB为⊙O直径，E为⊙O上一点，∠EAB的平分线AC交⊙O于C点，过C点作CD ⊥AE的延长线于D点，直线CD与射线AB交于P点.（1）判断直线DP与⊙O的位置关系，并说明理由；（2）若DC=4，⊙O的半径为5，求PB的长.19.如图，△ABD是⊙O的内接三角形，E是弦BD的中点，点C是⊙O外一点且∠DBC=∠A，连接OE延长与圆相交于点F，与BC相交于点C．（1）求证：BC是⊙O的切线；（2）若⊙O的半径为6，BC=8，求弦BD的长．20.已知：△ABC内接于⊙O，过点A作直线EF．（1）如图①，AB为直径，要使EF为⊙O的切线，还需添加的条件是（只需写出三种情况）：①；②；③．（2）如图②，AB是非直径的弦，∠CAE=∠B，求证：EF是⊙O的切线．（3）如图③，AB是非直径的弦，∠CAE=∠ABC，EF还是⊙O的切线吗？若是，请说明理由；若不是，请解释原因．参考答案1.C.2. A.3. D.4. B.5. C.6.C．7.D.8.C9.D10.B11.a＜﹣2或a＞2.12.r=2或4＜r≤4.13.5．14.4515.相切16.4＜t＜8.17.解：（1）如图，当点O向左移动1cm时，PO′=PO﹣O′O=3﹣1=2cm，作O′C⊥PA于C，∵∠P=30度，∴O′C=PO′=1cm，∵圆的半径为1cm，∴⊙O与直线PA的位置关系是相切；（2）如图：当点O由O′向右继续移动时，PA与圆相交，当移动到C″时，相切，此时C″P=PO′=2，∵OP=3，∴OO'=1，OC''=OP+C''P=3+2=5∴点O移动的距离d的范围满足1cm＜d＜5cm时相交，故答案为：：1cm＜d＜5cm.18.解：（1）直线DP与⊙O相切.理由如下：连接OC，如图，∵AC是∠EAB的平分线，∴∠EAC=∠OAC∵OA=OC，∴∠ACO=∠OAC，∴∠ACO=∠DAC，∴OC∥AD，∵CD⊥AE，∴OC⊥CD，∴DP是⊙O的切线；（2）作CH⊥AB于H，如图，∵AC是∠EAB的平分线，CD⊥AD，CH⊥AB，∴CH=CD=4，∴OH==3，∵OC⊥CP，∴∠OCP=∠CHO=90°，而∠COP=∠POC，∴△OCH∽△OPC，∴OC：OP=OH：OC，∴OP==，∴PB=OP﹣OB=﹣5=.19.（1）证明：连接OB，如图所示：∵E是弦BD的中点，∴BE=DE，OE⊥BD，=，∴∠BOE=∠A，∠OBE+∠BOE=90°，∵∠DBC=∠A，∴∠BOE=∠DBC，∴∠OBE+∠DBC=90°，∴∠OBC=90°，即BC⊥OB，∴BC是⊙O的切线；（2）解：∵OB=6，BC=8，BC⊥OB，∴OC==10，∵△OBC的面积=OC•BE=OB•BC，∴BE===4.8，∴BD=2BE=9.6，即弦BD的长为9.6．20.（1）当AB⊥EF或∠BAE=90°可判断EF为⊙O的切线；当∠ABC=∠EAC，∵AB为直径，∴∠ACB=90°，∴∠ABC+∠CAB=90°，∴∠EAC+∠CAB=90°，∴AB⊥EF，∴EF为⊙O的切线；故答案为AB⊥EF、∠BAE=90°、∠ABC=∠EAC；（2）证明：如图2，作直径AD，连结CD，∵AD为直径，∴∠ACD=90°，∴∠D+∠CAD=90°，∵∠D=∠B，∠CAE=∠B，∴∠CAE=∠D，∴∠EAC+∠CAD=90°，∴AD⊥EF，∴EF为⊙O的切线；（3）如图3，作直径AD，连结CD，BD，∵AD为直径，∴∠ABD=90°，∵∠CAE=∠ABC，∴∠DAE+∠DAC=∠ABD+∠DBC，而∠DAC=∠DBC，∴∠DAE=∠ABD=90°，∴AD⊥EF，∴EF为⊙O的切线．。

苏科版九年级上册数学圆章节2.5 直线与圆的位置关系(3) (含答案)

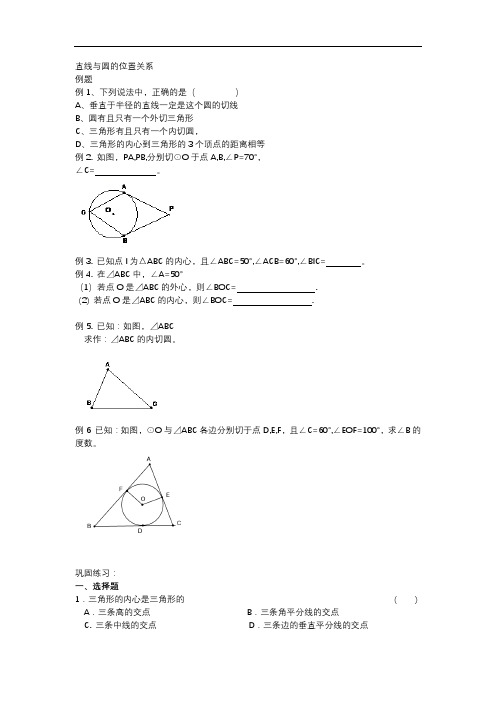
直线与圆的位置关系例题例1、下列说法中，正确的是（）A、垂直于半径的直线一定是这个圆的切线B、圆有且只有一个外切三角形C、三角形有且只有一个内切圆，D、三角形的内心到三角形的3个顶点的距离相等例2. 如图，PA,PB,分别切⊙O于点A,B,∠P=70°，∠C= 。

例3. 已知点I为△ABC的内心，且∠ABC=50°,∠ACB=60°,∠BIC= 。

例4. 在⊿ABC中，∠A=50°（1）若点O是⊿ABC的外心，则∠BOC= .(2) 若点O是⊿ABC的内心，则∠BOC= .例5. 已知：如图，⊿ABC求作：⊿ABC的内切圆。

例6 已知：如图，⊙O与⊿ABC各边分别切于点D,E,F，且∠C=60°,∠EOF=100°，求∠B的度数。

巩固练习：一、选择题1．三角形的内心是三角形的( ) A．三条高的交点B．三条角平分线的交点C. 三条中线的交点D．三条边的垂直平分线的交点2．如图，点O是△ABC的内切圆的圆心，若∠BOC=1260，则∠BAC的度数为( )A．720B．540C．630D．3603．如图，☉O是△ABC的内切圆，切点分别是D、E、F，已知∠A=1000，∠C=300，则∠DFE的度数为( )A．550B．600 C. 650D．7004．如图，☉I是△ABC的内切圆，切点分别为D、E、F，则△DEF是( )A．钝角三角形B．直角三角形C．锐角三角形D．它的形状不能确定二、填空题5．已知点I为△ABC的内心，且∠ABC＝50°，∠ACB＝60°，则∠BIC＝________．6．在△ABC中，∠A＝50°．(1)若点O是△ABC的外心，则∠BOC＝_______．(2)若点O是△ABC的内心，则∠BCC＝_______．7．三角形的面积为15，周长为30，则它的内切圆半径为__________．8．定义1：与四边形四边都相切的圆叫做四边形的内切圆．定义2：一组邻边相等，另两边也相等的凸四边形叫做筝形．探究：任意筝形是否一定存在内切圆?答案：________ (填“是”或“否”)．三、解答题9．如图是一块三角形木板余料．现要从中裁出一块圆形的木板，怎样裁剪才能使这块圆形木板的面积尽可能大?10．如图，PA、PB是⊙O的切线，切点分别是A、B，直线EF也是⊙O的切线，切点为Q，分别交PA、PB于点E、F，已知PA＝12 cm，∠P＝70°．(1)求△PEF的周长；(2)求∠EOF的度数．11．等腰三角形的腰长为10 cm，底边长为12 cm，求它的内切圆的半径．12．如图，AB是☉O的直径，AE平分 BAC交☉O于点E，过E作☉O的切线ME交AC于点D．试判断△AED的形状，并说明理由．13．如图①，⊙O是边长为6的等边三角形ABC的外接圆，点D在BC上运动（不与点B、C重合），过点D作DE∥BC，DE交AC的延长线于点E，连接AD、CD．(1)在图①中，当AD＝210时，求AE的长；(2)当点D为弧BC的中点时（如图②），①DE与⊙O的位置关系是_______；②求△ADC的内切圆半径r．巩固练习答案1. B 2．A 3．C 4．C5．125°6．(1)100°(2)115°7．18．是9．作出这个三角形木板余料的内切圆即可10．(1)24 cm (2)∠EOF＝55°11．3 cm12．∆AED为直角三角形连接BE(图略)．AB是直径，∴∠BEA= 900．∴∠B+∠BAE= 900。

苏教版九年级数学上册第二章 2.5 直线与圆的位置关系同步练习题(含答案解析)

2.5直线与圆的位置关系一、选择题（本大题共8小题，每小题3分，共24分）在每小题所给出的四个选项中，只有一项是符合题目要求的．1．（2019秋•宿豫区期中）下列关于三角形的外心说法正确的是（）A．三角形的外心一定在它的外部B．三角形的外心是它三边垂直平分线的交点C．三角形的外心到它的三边距离相等D．三角形的外心与它的内心不可能重合2．（2019秋•宿豫区期中）已知⊙O的直径为8，点P在直线l上，且OP＝4，则直线l与⊙O的位置关系是（）A．相离B．相切C．相交D．相切或相交3．（2019秋•邗江区校级期中）直线l与半径为r的⊙O相交，且点O到直线l的距离为3，则r的取值范围是（）A．r＜3 B．r＝3 C．r＞3 D．r≥34．（2019秋•睢宁县期中）如图，AB是半圆的直径，P是AB延长线上的一点，PC切半圆于点C，若∠CAB ＝29°，则∠P等于（）A．29°B．30°C．31°D．32°5．（2019秋•东台市期中）如图所示，在Rt△ABC中，∠ACB＝90°，AC＝3，BC＝4，以C为圆心，r为半径的圆与边AB有公共点，则r的取值范围为（）A．r B．r＝3或r＝4 C．r≤3 D．r≤46．（2019秋•西城区校级期中）如图，小明同学测量一个光盘的直径，他只有一把直尺和一块三角板，他将直尺、光盘和三角板如图放置于桌面上，并量出AB＝3cm，则此光盘的半径是（）A．3cm B．3cm C．6cm D．6cm7．（2019秋•江宁区期中）如图，AB、BC、CD、DA都是⊙O的切线，已知AD＝2，BC＝5，则AB+CD的值是（）A．14 B．12 C．9 D．78．（2019秋•锡山区期中）如图，在平面直角坐标系xOy中，点P的坐标为（0，﹣6），⊙P的半径为2，⊙P沿y轴以2个单位长度/s的速度向正方向运动，当⊙P与x轴相切时⊙P运动的时间为（）A．2s B．3s C．2s或4s D．3s或4s二、填空题（本大题共6小题，每小题3分，共18分．不需写出解答过程，请把答案直接填写在横线上）9．（2019秋•睢宁县期中）如图，P A、PB是⊙O的切线，切点分别是A、B，C在AB上，过C的切线分别交P A、PB于点D、E．若PB＝10，则△PDE的周长为．10．（2019秋•亭湖区校级期中）若直角三角形两边分别为6和8，则它内切圆的半径为．11．（2019秋•宝应县期中）如图，在平面直角坐标系中，已知C（3，4），以点C为圆心的圆与y轴相切，点A、B在x轴上，且OA＝OB．点P为⊙C上的动点，∠APB＝90°，则AB长度的最小值为．12．（2019秋•沛县期中）如图，⊙O是△ABC的内切圆，切点分别为D、E、F，∠B＝50°，∠C＝60°，则∠EDF＝．13．（2019秋•镇江期中）如图，AB是⊙O的直径，CD与⊙O相切于点C，∠BCD＝25°，∠ABC＝°．14．（2019秋•建邺区期中）如图，△ABC为等边三角形，AB＝4，以点A为圆心，半径为1作⊙A．M为BC边上的一动点，过点M作⊙A的一条切线，切点为N，则MN的最小值是．三、解答题（本大题共6小题，共58分．解答时应写出文字说明、证明过程或演算步骤）15．（2020春•锡山区期中）如图，AC是⊙O的直径，AB是⊙O的一条弦，AP是⊙O的切线．作BM＝AB 并与AP交于点M，延长MB交AC于点E，交⊙O于点D，连接AD．（1）求证：AB＝BE；（2）若⊙O的半径R＝2.5，MB＝3，求AD的长．16．（2019秋•宿豫区期中）如图，AB是⊙O的直径，C为⊙O上的一点，点D为的中点，DE⊥AC于点E．（1）求证：DE是⊙O的切线；（2）若AE＝8，DE＝4，求⊙O的半径．17．（2019秋•新北区期中）如图，已知AB是⊙P的直径，点C在⊙P上，D为⊙P外一点，且∠ADC＝90°，直线CD为⊙P的切线．（1）试说明：2∠B+∠DAB＝180°（2）若∠B＝30°，AD＝2，求⊙P的半径．18．（2019秋•建湖县期中）如图，AB为⊙O直径，P A、PC分别与⊙O相切于点A、C，PE⊥P A，PE交OC的延长线于点E．（1）求证：OE＝PE；（2）连接BC并延长交PE于点D，P A＝AB，且CE＝9，求PE的长．19．（2019秋•宝应县期中）如图，直线AB经过⊙O上的点C，直线AO与⊙O交于点E和点D，OB与⊙O 交于点F连接DF、DC．已知OA＝OB，CA＝CB．（1）求证：直线AB是⊙O的切线；（2）求证：∠FDC＝∠EDC；（3）已知：DE＝10，DF＝8，求CD的长．20．（2019秋•东海县期中）小明在学习“圆的对称性”时知道结论：垂直于弦的直径一定平分这条弦，请尝试解决下面的问题：如图，在Rt△ACB中，∠ACB＝90°，圆O是△ACB的外接圆．点D是圆O上一点，过点D作DE⊥BC，垂足为E，且BD平分∠ABE．（1）判断直线ED与圆O的位置关系，并说明理由．（2）若AC＝12，BC＝5，求线段BE的长．答案解析一、选择题（本大题共8小题，每小题3分，共24分）在每小题所给出的四个选项中，只有一项是符合题目要求的．1．（2019秋•宿豫区期中）下列关于三角形的外心说法正确的是（）A．三角形的外心一定在它的外部B．三角形的外心是它三边垂直平分线的交点C．三角形的外心到它的三边距离相等D．三角形的外心与它的内心不可能重合【分析】分别根据三角形外心内心逐项判断即可．【解析】A．三角形的外心还可以在三角形的边上或三角形的内部，故错误；B．三角形的外心是它三边垂直平分线的交点，正确；C．根据三角形的外心到三个顶点的距离相等，故此选项错误；D．只有等边三角形的外心与内心重合，故错误．故选：B．2．（2019秋•宿豫区期中）已知⊙O的直径为8，点P在直线l上，且OP＝4，则直线l与⊙O的位置关系是（）A．相离B．相切C．相交D．相切或相交【分析】根据垂线段最短，得圆心到直线的距离小于或等于4，再根据数量关系进行判断．若d＜r，则直线与圆相交；若d＝r，则直线于圆相切；若d＞r，则直线与圆相离．【解析】如图所示：根据题意可知，圆的半径r＝4．因为OP＝4，当OP⊥l时，直线和圆是相切的位置关系；当OP与直线l不垂直时，则圆心到直线的距离小于4，所以是相交的位置关系．所以l与⊙O的位置关系是：相交或相切，故选：D．3．（2019秋•邗江区校级期中）直线l与半径为r的⊙O相交，且点O到直线l的距离为3，则r的取值范围是（）A．r＜3 B．r＝3 C．r＞3 D．r≥3【分析】直线和圆有三种位置关系：已知⊙O的半径为r，圆心O到直线l的距离是d，①当d＝r时，直线l和⊙O相切，②当d＜r时，直线l和⊙O相交，③当d＞r时，直线l和⊙O相离，根据以上内容得出即可．【解析】∵直线l与半径为r的⊙O相交，且点O到直线l的距离为3，∴r＞3，故选：C．4．（2019秋•睢宁县期中）如图，AB是半圆的直径，P是AB延长线上的一点，PC切半圆于点C，若∠CAB ＝29°，则∠P等于（）A．29°B．30°C．31°D．32°【分析】连接OC，根据圆周角定理和切线的性质即可得到结论．【解析】连接OC，∴∠CAB＝29°，∴∠COP＝2∠CAB＝58°，∵PC切半圆于点C，∴∠OCP＝90°，∴∠P＝90°﹣58°＝32°，故选：D．5．（2019秋•东台市期中）如图所示，在Rt△ABC中，∠ACB＝90°，AC＝3，BC＝4，以C为圆心，r为半径的圆与边AB有公共点，则r的取值范围为（）A．r B．r＝3或r＝4 C．r≤3 D．r≤4【分析】作CD⊥AB于D，由勾股定理求出AB，由三角形的面积求出CD，由AC＞BC，可得以C为圆心，r或4为半径所作的圆与斜边AB只有一个公共点；若⊙C与斜边AB有公共点，即可得出r的取值范围．【解析】作CD⊥AB于D，如图所示：∵∠C＝90°，AC＝3，BC＝4，∴AB5，∵△ABC的面积AB•CD AC•BC，∴CD，即圆心C到AB的距离d，∵AC＜BC，∴以C为圆心，r或4为半径所作的圆与斜边AB只有一个公共点，∴若⊙C与斜边AB有公共点，则r的取值范围是r≤4．故选：D．6．（2019秋•西城区校级期中）如图，小明同学测量一个光盘的直径，他只有一把直尺和一块三角板，他将直尺、光盘和三角板如图放置于桌面上，并量出AB＝3cm，则此光盘的半径是（）A．3cm B．3cm C．6cm D．6cm【分析】先画图，根据题意求出∠OAB＝60°，再根据直角三角形的性质和勾股定理求得OB，从而得出光盘的半径．【解析】设圆心为O，∵∠CAD＝60°，∴∠CAB＝120°，∵AB和AC与⊙O相切，∴∠OAB＝∠OAC，∴∠OAB∠CAB＝60°，∵AB＝3cm，∴OA＝6cm，∴由勾股定理得OB＝3cm，∴光盘的半径是3cm．故选：B．7．（2019秋•江宁区期中）如图，AB、BC、CD、DA都是⊙O的切线，已知AD＝2，BC＝5，则AB+CD的值是（）A．14 B．12 C．9 D．7【分析】根据切线长定理，可以证明圆的外切四边形的对边和相等，由此即可解决问题．【解析】∵AB、BC、CD、DA都是⊙O的切线，∴可以假设切点分别为E、H、G、F，∴AF＝AE，BE＝BH，CH＝CG，DG＝DF，∴AD+BC＝AF+DF+BH+CH＝AE+BE+DG+CG＝AB+CD，∵AD＝2，BC＝5，∴AB+CD＝AD+BC＝7，故选：D．8．（2019秋•锡山区期中）如图，在平面直角坐标系xOy中，点P的坐标为（0，﹣6），⊙P的半径为2，⊙P沿y轴以2个单位长度/s的速度向正方向运动，当⊙P与x轴相切时⊙P运动的时间为（）A．2s B．3s C．2s或4s D．3s或4s【分析】由题意可求OP＝2，分圆心P在x轴下方和x轴上方两种情况讨论可求解．【解析】∵⊙P与x轴相切∴OP＝2当点P在x轴下方，即点P（0，﹣2）∴t2s当点P在x轴上方，即点P（0，2）∴t4s故选：C．二、填空题（本大题共6小题，每小题3分，共18分．不需写出解答过程，请把答案直接填写在横线上）9．（2019秋•睢宁县期中）如图，P A、PB是⊙O的切线，切点分别是A、B，C在AB上，过C的切线分别交P A、PB于点D、E．若PB＝10，则△PDE的周长为20．【分析】根据切线长定理求出AP＝BP，DA＝DC，CE＝BE，代入求出△PDE的周长为2PB，代入即可．【解析】∵P A、PB、DE是圆O的切线，切点分别是A、B、C，∴AP＝BP，DA＝DC，CE＝BE，∴△PED的周长是：PD+DE+PE＝PD+DC+CE+PE＝PD+DA+PE+BE＝P A+PB＝2PB＝20．答：△PED的周长是20．故答案为：20．10．（2019秋•亭湖区校级期中）若直角三角形两边分别为6和8，则它内切圆的半径为2或1．【分析】首先证明四边形ODCF为正方形；求出AB的长度；证明AF＝AE，BD＝BE，分两种情况，问题即可解决．【解析】如图，⊙O内切于直角△ABC中，切点分别为D、E、F；半径为r，连接OD、OF；则OD⊥BC，OF⊥AC；OD＝OF；∵∠C＝90°，∴四边形ODCF为正方形，∴CD＝CF＝r；①当AC＝8，BC＝6时，由勾股定理得：AB2＝AC2+BC2＝36+64＝100，∴AB＝10；由切线长定理得：AF＝AE，BD＝BE；∴CD+CF＝AC+BC﹣AB＝6+8﹣10＝4，∴r＝2；②当AB＝8，AC＝6，则BC2，∴r（26﹣8）1；它的内切圆半径为2或1．故答案为：2或 111．（2019秋•宝应县期中）如图，在平面直角坐标系中，已知C（3，4），以点C为圆心的圆与y轴相切，点A、B在x轴上，且OA＝OB．点P为⊙C上的动点，∠APB＝90°，则AB长度的最小值为4．【分析】连接OC，交⊙C上一点P，以O为圆心，以OP为半径作⊙O，交x轴于A、B，此时AB的长度最小，根据勾股定理和题意求得OP＝2，则AB的最小长度为4．【解析】连接OC，交⊙C上一点P，以O为圆心，以OP为半径作⊙O，交x轴于A、B，此时AB的长度最小，∵C（3，4），∴OC5，∵以点C为圆心的圆与y轴相切．∴⊙C的半径为3，∴OP＝OC﹣3＝2，∴OP＝OA＝OB＝2，∵AB是直径，∴∠APB＝90°，∴AB长度的最小值为4，故答案为：4．12．（2019秋•沛县期中）如图，⊙O是△ABC的内切圆，切点分别为D、E、F，∠B＝50°，∠C＝60°，则∠EDF＝55°．【分析】连接OE，OF．由三角形内角和定理可求得∠A＝70°，由切线的性质可知：∠OF A＝90°，∠OEA＝90°，从而得到∠A+∠EOF＝180°，故可求得∠EOF＝110°由圆周角定理可求得∠EDF＝55°．【解析】如图所示，连接OE，OF．∵∠B＝50°，∠C＝60°，∴∠A＝180°﹣50°﹣60°＝70°．∵AB是圆O的切线，∴∠OF A＝90°．同理∠OEA＝90°．∴∠A+∠EOF＝180°．∴∠EOF＝110°．∴∠EDF＝55°，故答案为：55°．13．（2019秋•镇江期中）如图，AB是⊙O的直径，CD与⊙O相切于点C，∠BCD＝25°，∠ABC＝65°．【分析】连接OC，如图，根据切线的性质得OC⊥CD，利用互余得到∠OCB＝65°，然后根据等腰三角形的性质得到∠B的度数．【解析】连接OC，如图，∵CD切⊙O于点C，∴OC⊥CD，∴∠OCD＝90°，∴∠OCB＝90°﹣∠BCD＝90°﹣25°＝65°，∵OB＝OC，∴∠B＝∠OCB＝65°．故答案为：65．14．（2019秋•建邺区期中）如图，△ABC为等边三角形，AB＝4，以点A为圆心，半径为1作⊙A．M为BC边上的一动点，过点M作⊙A的一条切线，切点为N，则MN的最小值是．【分析】作AD⊥BC于D，过D作⊙A的一条切线，切点为E，连接AE，由等边三角形的性质和勾股定理得出AD2，由切线的性质得出AE⊥DE，由勾股定理求出DE，当点M与D重合时，N与E重合，此时MN最小．【解析】作AD⊥BC于D，过D作⊙A的一条切线，切点为E，连接AE，如图所示：∵△ABC是等边三角形，AD⊥BC，∴BC＝AB＝4，BD＝CD BC＝2，∴AD2，∵DE是⊙A的一条切线，∴AE⊥DE，AE＝1，∴DE，当点M与D重合时，N与E重合，此时MN最小，故答案为：．三、解答题（本大题共6小题，共58分．解答时应写出文字说明、证明过程或演算步骤）15．（2020春•锡山区期中）如图，AC是⊙O的直径，AB是⊙O的一条弦，AP是⊙O的切线．作BM＝AB 并与AP交于点M，延长MB交AC于点E，交⊙O于点D，连接AD．（1）求证：AB＝BE；（2）若⊙O的半径R＝2.5，MB＝3，求AD的长．【分析】（1）根据切线的性质得出∠EAM＝90°，等腰三角形的性质∠MAB＝∠AMB，根据等角的余角相等得出∠BAE＝∠AEB，即可证得AB＝BE；（2）连接BC，证明△ABC∽△EAM，由比例段求出AM的长，则答案可求出．【解答】（1）证明：∵AP是⊙O的切线，∴∠EAM＝90°，∴∠BAE+∠MAB＝90°，∠AEB+∠AMB＝90°．又∵AB＝BM，∴∠MAB＝∠AMB，∴∠BAE＝∠AEB，∴AB＝BE；（2）解：连接BC，∵AC是⊙O的直径，∴∠ABC＝90°，∴∠ABC＝∠EAM，在Rt△ABC中，AC＝5，BM＝AB＝3，∴BC4，∵BE＝AB＝BM，∴EM＝6，由（1）知，∠BAE＝∠AEB，∴△ABC∽△EAM，∴，∠AMB＝∠C，即，∴AM，又∵∠C＝∠D，∴∠AMB＝∠D，∴AD＝AM．16．（2019秋•宿豫区期中）如图，AB是⊙O的直径，C为⊙O上的一点，点D为的中点，DE⊥AC于点E．（1）求证：DE是⊙O的切线；（2）若AE＝8，DE＝4，求⊙O的半径．【分析】（1）连接AD．证明OD∥AE，可得∠E＝90°，则∠ODE＝90°得出DE⊥OD即可；（2）设⊙O的半径为r．过点O作OF⊥AE于F，则OF＝DE＝4，EF＝OD＝r，AF＝8﹣r（8﹣r）2+42＝r2解方程即可得出答案．【解答】（1）证明：连接AD．∵点D为弧BC的中点，∴，∴∠EAD＝∠DAB，∵OA＝OD，∴∠ADO＝∠DAB，∴∠EAD＝∠ADO，∴OD∥AE，∵DE⊥AC，∴∠E＝90°，∴∠ODE＝90°，∴DE⊥OD∴DE是⊙O的切线；（2）解：设⊙O的半径为r．过点O作OF⊥AE于F，则OF＝DE＝4，EF＝OD＝r，AF＝8﹣r，∵在Rt△AFO中，AF2+OF2＝OA2，∴（8﹣r）2+42＝r2，∴r＝5，∴⊙O的半径为5．17．（2019秋•新北区期中）如图，已知AB是⊙P的直径，点C在⊙P上，D为⊙P外一点，且∠ADC＝90°，直线CD为⊙P的切线．（1）试说明：2∠B+∠DAB＝180°（2）若∠B＝30°，AD＝2，求⊙P的半径．【分析】（1）根据切线的性质和圆周角定理，可得∠APC＝∠PCB+∠B＝2∠B，证得∠DAB+∠APC＝180°，则结论得证；（2）连接AC，证得△ACP是等边三角形，可得AC＝P A，∠ACP＝60°，可求出AC长，P A长，则⊙P 的半径可求出．【解析】（1）连接CP，∵PC＝PB，∴∠B＝∠PCB，∴∠APC＝∠PCB+∠B＝2∠B，∵CD是⊙OP的切线，∴∠DCP＝90°，∵∠ADC＝90°，∴∠DAB+∠APC＝180°∴2∠B+∠DAB＝180°；（2）解：连接AC，∵∠B＝30°，∴∠APC＝60°，∵PC＝P A，∴△ACP是等边三角形，∴AC＝P A，∠ACP＝60°，∴∠ACD＝30°，∴AC＝2AD＝4，∴P A＝4．即⊙P的半径为4．18．（2019秋•建湖县期中）如图，AB为⊙O直径，P A、PC分别与⊙O相切于点A、C，PE⊥P A，PE交OC的延长线于点E．（1）求证：OE＝PE；（2）连接BC并延长交PE于点D，P A＝AB，且CE＝9，求PE的长．【分析】（1）欲证明OE＝PE，只要证明∠EOP＝∠EPO即可；（2）设OA＝r．在Rt△PCE中，利用勾股定理构建方程求出r，即可解决问题．【解答】（1）证明：连接OP．∵P A、PC分别与⊙O相切于点A，C∴P A＝PC，OA⊥P A，∵OA＝OC，OP＝OP，∴△OP A≌△OPC（SSS），∴∠AOP＝∠POC，∵EP⊥P A，∴EP∥BA，∴∠EPO＝∠AOP，∴∠EOP＝∠EPO，∴OE＝PE．（2）设OA＝r．∵OB＝OC，∴∠OBC＝∠OCB，∵OB∥ED，∴∠EDC＝∠B，∵∠OCB＝∠ECD，∴∠ECD＝∠EDC，∴EC＝ED＝9，∵EO＝EP，∴OC＝DP＝r，∵PC是⊙O的切线，∴OC⊥PC，∴∠OCP＝∠PCE＝90°，在Rt△PCE中，∵PE2＝PC2+EC2，∴（9+r）2＝92+（2r）2，解得：r＝6或0（舍弃），∴PE＝15．19．（2019秋•宝应县期中）如图，直线AB经过⊙O上的点C，直线AO与⊙O交于点E和点D，OB与⊙O 交于点F连接DF、DC．已知OA＝OB，CA＝CB．（1）求证：直线AB是⊙O的切线；（2）求证：∠FDC＝∠EDC；（3）已知：DE＝10，DF＝8，求CD的长．【分析】（1）欲证明直线AB是⊙O的切线，只要证明OC⊥AB即可．（2）首先证明OC∥DF，再证明∠FDC＝∠OCD，∠EDC＝∠OCD即可．（3）作ON⊥DF于N，延长DF交AB于M，在Rt△CDM中，求出DM、CM即可解决问题．【解答】（1）证明：连接OC．∵OA＝OB，AC＝CB，∴OC⊥AB，∵点C在⊙O上，∴AB是⊙O切线．（2）证明：∵OA＝OB，AC＝CB，∴∠AOC＝∠BOC，∵OD＝OF，∴∠ODF＝∠OFD，∵∠AOB＝∠ODF+∠OFD＝∠AOC+∠BOC，∴∠BOC＝∠OFD，∴OC∥DF，∴∠CDF＝∠OCD，∵OD＝OC，∴∠ODC＝∠OCD，∴∠ADC＝∠CDF．（3）解：作ON⊥DF于N，延长DF交AB于M．∵ON⊥DF，∴DN＝NF＝4，在Rt△ODN中，∵∠OND＝90°，OD＝5，DN＝4，∴3，∵∠OCM+∠CMN＝180°，∠OCM＝90°，∴∠OCM＝∠CMN＝∠MNO＝90°，∴四边形OCMN是矩形，∴ON＝CM＝3，MN＝OC＝5，在RT△CDM中，∵∠DMC＝90°，CM＝3，DM＝DN+MN＝9，∴CD3．20．（2019秋•东海县期中）小明在学习“圆的对称性”时知道结论：垂直于弦的直径一定平分这条弦，请尝试解决下面的问题：如图，在Rt△ACB中，∠ACB＝90°，圆O是△ACB的外接圆．点D是圆O上一点，过点D作DE⊥BC，垂足为E，且BD平分∠ABE．（1）判断直线ED与圆O的位置关系，并说明理由．（2）若AC＝12，BC＝5，求线段BE的长．【分析】（1）直线ED与⊙O相切．连接OD．根据圆的性质和等边对等角可得∠ODB＝∠OBD，等量代换得到∠ODB＝∠DBE，根据平行线的判定和性质得到∠DEC＝∠ODE＝90°，再根据垂直的定义和性质可得OD⊥DE，根据切线的判定即可求解；（2）如图，延长DO交AC于点H，连结CO，构建直角△ABC的中位线OH，运用三角形中位线定理和勾股定理分别求得OH＝HO BC、AB＝13，结合图形找到相关线段间的和差关系求得线段BE的长度即可．【解析】（1）如图，连接OD．∵OB＝OD，∴∠ODB＝∠OBD，又∵∠OBD＝∠DBE，∴∠ODB＝∠DBE，∴OD∥BE，又∵DE⊥BC，∴∠DEC＝90°，∴∠ODE＝90°，∴OD⊥DE，又∵OD为半径，∴直线ED与⊙O相切；（2）如图，延长DO交AC于点H，连结CO，∵OD∥BE，∠ODE＝90°，∴∠OHC＝90°，即OH⊥AC，又∵OA＝OC，∴AH＝CH，又由O是AB的中点，∴HO是△ABC的中位线，∴HO BC．∵AC为直径，∴∠ACB＝90°，∴AC＝12，BC＝5，∴AB13，∴OA＝OD AB．∴HD＝HO+OD＝9由四边形CEDH是矩形，∴CE＝HD＝9，∴CE＝9，∴BE＝CE﹣BC＝4．。

专题2.3 直线与圆的位置关系(专项拔高卷)学生版-2024-2025学年九年级数学上册真题汇编章节

2024-2025学年苏科版数学九年级上册同步专题热点难点专项练习专题2.3 直线与圆的位置关系（专项拔高卷）考试时间：90分钟试卷满分：100分难度：0.52姓名：___________班级：___________考号：___________题号一二三总分得分评卷人得分一．选择题（共10小题，满分20分，每小题2分）1．（2分）（2022秋•金华期末）AB为⊙O的直径，延长AB到点P，过点P作⊙O的切线，切点为C，连接AC，∠P＝40°，D为圆上一点，则∠D的度数为（）A．20°B．25°C．30°D．40°2．（2分）（2022秋•阳谷县期末）如图是“光盘行动”的宣传海报，图中餐盘与筷子可看成直线和圆的位置关系是（）A．相切B．相交C．相离D．平行3．（2分）（2022秋•河西区校级期末）如图，AB是⊙O的切线，B为切点，AO与⊙O交于点C，若∠BAO＝35°，则∠OCB的度数为（）A．42.5°B．55.5°C．62.5°D．75°4．（2分）（2023春•青山区校级月考）如图，不等边△ABC内接于⊙O，I是其内心，BI⊥OI，AC＝14，BC ＝13，△ABC内切圆半径为（）A．4 B．C．D．5．（2分）（2022秋•大荔县期末）如图，点O是△ABC的内心，也是△DBC的外心．若∠A＝84°，则∠D的度数为（）A．42°B．66°C．76°D．82°6．（2分）（2023•沙坪坝区校级模拟）如图，AB是⊙O的直径，E为⊙O上一点，BD垂直平分OE交⊙O于点D，过点D的切线与BE的延长线交于点C．若，则AB的长为（）A．4 B．2 C．D．7．（2分）（2023•哈尔滨）如图，AB是⊙O的切线，A为切点，连接OA，点C在⊙O上，OC⊥OA，连接BC并延长，交⊙O于点D，连接OD，若∠B＝65°，则∠DOC的度数为（）A．45°B．50°C．65°D．75°8．（2分）（2023•遵义一模）如图，AB是半圆O的直径，点P为BA延长线上一点，PC是⊙O的切线，切点为C，过点B作BD⊥PC交PC的延长线于点D，连接BC．若CD＝2，BD＝4，则⊙O的半径为（）A．3 B．2 C．2.5 D．29．（2分）（2023•江岸区模拟）如图，AB为⊙O直径，C为圆上一点，I为△ABC内心，AI交⊙O于D，OI ⊥AD于I，若CD＝4，则AC为（）A．B．C．D．510．（2分）（2022•成县校级模拟）如图，⊙O与∠A＝90的Rt△ABC的三边AB、BC、AC分别相切于点D、E、F，若BE＝10，CF＝3，则⊙O的半径为（）A．5 B．4 C．3 D．2评卷人得分二．填空题（共10小题，满分20分，每小题2分）11．（2分）（2023•柯桥区校级模拟）如图AB、AC、BD是圆O的切线，切点分别为P、C、D，若AB＝5，BD ＝2，则AC的长是．12．（2分）（2022秋•启东市校级期末）如图，AB为⊙O的直径，CB为⊙O的切线，AC交⊙O于D，∠C＝38°．点E在AB右侧的半圆上运动（不与A、B重合），则∠AED的大小是．13．（2分）（2022秋•河西区校级期末）如图，在Rt△OAB中，∠AOB＝90°，OA＝8，AB＝10，⊙O的半径为4，点P是AB上的一动点，过点P作⊙O的一条切线PQ，Q为切点，则PQ的最小值为．14．（2分）（2023•青海）如图，MN是⊙O的切线，M是切点，连接OM，ON．若∠N＝37°，则∠MON的度数是．15．（2分）（2022秋•建昌县期末）如图，点O是△ABC的内心，∠A＝60°，OB＝3，OC＝6，，则⊙O的半径为．16．（2分）（2023•西陵区模拟）木工师傅可以用角尺测量并计算出圆的半径．如图，用角尺的较短边紧靠⊙O于点A，并使较长边与⊙O相切于点C．记角尺的直角顶点为B，量得AB＝8cm，BC＝16cm，则⊙O的半径等于cm．17．（2分）（2023•安岳县二模）如图，AB、CD是⊙O的两条直径，EA切⊙O于点A，交CD的延长线于点E．若∠ABC＝75°，则∠E的度数为．18．（2分）（2022•宜宾）我国古代数学家赵爽的“弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形（如图所示）．若直角三角形的内切圆半径为3，小正方形的面积为49，则大正方形的面积为．19．（2分）（2022秋•鼓楼区校级月考）在Rt△ABC中，∠ACB＝90°，BC＝6，AC＝8，直线l经过△ABC的内心O，过点C作CD⊥l，垂足为D，连接AD，则AD的最小值是．20．（2分）（2022秋•滨湖区校级期中）如图，AC是矩形ABCD的对角线，⊙O是△ABC的内切圆，现将矩形ABCD按如图所示的方式折叠，使点D与点O重合，折痕为FG，点F、G分别在AD、BC上，连结OG、DG，若OG⊥DG，且⊙O的半径长为1，则BC﹣AB的值，CD+DF的值．评卷人得分三．解答题（共8小题，满分60分）21．（6分）（2023•鞍山二模）如图，在△ABC中，以AB为直径作⊙O，⊙O恰好经过点C，点D为半圆AB 中点，连接CD，过D作DE∥AB交AC延长线于点E．（1）求证：DE为⊙O切线：（2）若AC＝4，，求⊙O的半径长．22．（6分）（2023•槐荫区模拟）如图，AB为⊙O的直径，C为⊙O上一点，⊙O的切线BD交OC的延长线于点D．（1）求证：∠DBC＝∠OCA；（2）若∠BAC＝30°，AC＝2．求CD的长．23．（8分）（2022秋•嘉祥县校级期末）已知BC是⊙O的直径，点D是BC延长线上一点，AB＝AD，AE是⊙O的弦，∠AEC＝30°．（1）求证：直线AD是⊙O的切线；（2）若AE⊥BC，垂足为M，⊙O的半径为10，求AE的长．24．（8分）（2022秋•平阴县期末）如图，AB为⊙O的直径，PQ切⊙O于E，AC⊥PQ于C，交⊙O于D．（1）求证：AE平分∠BAC；（2）若，∠BAC＝60°，求⊙O的半径．25．（8分）（2023•宛城区二模）如图①，中国古代的马车已经涉及很复杂的机械设计（相对当时的生产力），包含大量零部件和工艺，所彰显的智慧让人拜服．如图②是马车的侧面示意图，AB为车轮⊙O的直径，过圆心O的车架AC一端点C着地时，地面CD与车轮⊙O相切于点D，连接AD，BD．（1）徽徽猜想∠C+2∠BDC＝90°，徽徽的猜想正确吗？请说明理由；（2）若，BC＝2米，求车轮的直径AB的长．26．（8分）（2023•晋安区校级模拟）如图，以AB边为直径的⊙O经过点P，C是⊙O上一点，连接PC交AB 于点E，且∠ACP＝60°，PA＝PD．（1）证明：PD是⊙O的切线．（2）若点C是弧AB的中点，已知AB＝2，求CE•CP的值．27．（8分）（2022秋•惠阳区校级期末）（1）如图1，在菱形ABCD中，点E，F分别为边CD，AD的中点，连接AE，CF．求证：AE＝CF．（2）如图2，AB是⊙O的直径，CA与⊙O相切于点A，连接CO交⊙O于点D，CO的延长线交⊙O于点E，连接BE，BD，∠ABD＝25°，求∠C的度数．28．（8分）（2023•绥江县二模）如图1，在四边形ABCD中，AD＝CD＝6，∠B＝60°，以AB为直径所作的⊙O经过点C，且与AD相切于A点，连接AC．（1）求证：CD是⊙O的切线；（2）⊙E是△ACD的外接圆，不与A、D重合的点F在⊙E的劣弧AD上运动（如图2所示）．若点P、Q 分别为线段AC、CD上的动点（不与端点重合），当点F运动到每一个确定的位置时，△FPQ的周长有最小值m，随着点F的运动，m的值也随之变化，求m的最大值．。

苏科版九年级上2.5直线与圆的位置关系(3)同步练习含答案.doc

第 2 章对称图形——圆2.5直线与圆的位置关系（3）【基础提优】1．如图，△A．70°ABC 的内心为点B． 60°O，∠ BOC=110°，则∠C． 50°A 的度数是（D． 40°）第1题第2题2．如图，⊙ O 是 Rt△ ABC 的内切圆， D， E， F 分别为切点，∠ACB=90°，则∠ EDF 的度数为（）A．25°B． 30°C． 45°D． 60°3．已知在△ ABC 中，内切圆⊙ I 和 BC ， CA ，AB 边分别相切于点 D， E， F，则点 I 是△ABC （）A ．三条高的交点B ．三个内角平分线的交点C．三边中线的交点 D ．三边垂直平分线的交点4．下列说法中，正确的是（）A ．垂直于半径的直线一定是这个圆的切线B．圆有且只有一个外切三角形C．三角形有且只有一个内切圆D．三角形的内心到三角形的三个顶点的距离相等5．如图，在△ ABC 中，⊙ I 是△ ABC 的内切圆，与边BC、 CA 、AB 分别相切于点D、 E、F，则∠ FDE 与∠ A 的关系为．第5题第6题6．如图， PA、PB 分别切⊙ O 于点 A 、B，并与⊙ O 的切线分别相交于cm，则△ PCD 的周长等于．7．在△ ABC 中，如果∠ A= m°，点 I 是内心，那么∠BIC= D、C 两点，已知．PA=78．已知⊙ O 分别切△ ABC 的三边 AB ， BC ， CA 于点 D， E， F，若 BC= a， AC= b， AB= c，∠C=90°，则⊙ O 的半径为．9．如图，某市有一块由三条马路围成的三角形绿地，现准备在其中建一小亭供人们休息，要求小亭中心到三条马路的距离相等，试确定小亭的中心位置．（不写作法，保留作图痕迹）10．如图，点I 是△ ABC于点 E．求证： BD=ID ．的内心，∠BAC 的平分线与△ABC 的外接圆相交于点D，交BC 【拓展提优】1．已知三角形的面积为A．2B．1 15，周长为30，则它的内切圆半径为（C．1.5 D ． 2.5）2．下列四边形中，一定有内切圆的是（A ．平行四边形B．菱形3．如图，⊙ O 是边长为 2 的等边三角形）C．矩形D．直角梯形ABC 的内切圆，则图中阴影部分的面积是（）A ．πB ．3C． 2π D ． 3 π3 3第 3 题4．如图， EB 、EC 是⊙ O 的切线，B、C 是切点，第 4 题A 、 D 是⊙ O 上的两点，如果∠E=46°，∠DCF=32°，那么∠ A 的度数为（）A ．64°B．96°C． 99° D ．104 °5．如图， O 是正方形 ABCD 的对角线 BD 上一点，⊙ O 与边 AB ，BC 都相切，点 E ， F 分别在 AD ，DC 上，现将△ DEF 沿着 EF 对折，折痕 EF 与⊙ O 相切，此时点 D 恰好落在圆心 O 处．若DE=2 ，则正方形ABCD的边长是（）A ． 3B ．4C ． 22D ．2 2第 5 题第 6 题6．如图， AB 是⊙ O 的直径， AM 和 BN 是它的两条切线，切点分别为 A ，B ，DE 切⊙ O 于点 E ，交 AM 于点 D ，交 BN 于点 C ，OD=6cm ， OC=8cm ，则 CD 的长为．7．已知点 I 为△ ABC 的内心， AB=8 ， BC=5 ，AC=7 ，则内切圆⊙ I 的半径 r =．8．阅读材料：如图 1，△ ABC 的周长为 l ，内切圆⊙ O 的半径为 r ，连结 OA 、 OB 、 OC ，△ABC 被划分为三个小三角形，用 S △ ABC 表示△ ABC 的面积．因为 S△ABC =S△OAB +S △ OBC +S △OCA ，又因为 11 BC ?r ，S △OCA =1 CA?r ，S△OAB = AB ?r ，S△OBC =2 2 1 1 1 1 2l?r （可作为三角形内切圆半径公式）．所以 S △ABC = AB?r+ BC?r+2CA?r =222（1）利用公式计算边长分别为 5、 12、13 的三角形内切圆的半径；（2）若四边形 ABCD 存在内切圆（与各边都相切的圆，如图 2）且面积为 S ，各边长分别为 a 、 b 、 c 、d ，试推导四边形的内切圆半径公式；（3）若一个 n 边形（ n 为不小于 3 的整数）存在内切圆，且面积为 S ，各边长分别为 a 1、a 2、 a 3、、 a n ，合理猜想其内切圆半径公式（不需说明理由）．参考答案【基础提优】1-4 DCBC5．∠ A+2 ∠ FDE=180°6． 14 cmm7．(90)2ab8．a b c9．图略（画三角形的三条内角平分线，交点即为所求）10．证明略【拓展提优】1-5 BBDCC6． 10 cm7． 38．（ 1）r 2 2S；（ 3）r2S；（ 2）ra na b c d a1 a2。

苏科版九年级数学上册直线与圆的位置关系练习题2(1)

2.5 直线与圆的位置关系（2）1、如图，△ABC内接于⊙O，AB是⊙O的直径，∠CAD＝∠ABC．判断直线AD与⊙O的位置关系，并说明理由．拓展：如果A B不是直径，其余条件不变，上面的结论还成立吗？2、如图，AB是⊙O的直径，弦AD平分∠ABC，过点D的切线交AC于点E，DE与AC 有怎样的位置关系？为什么？从中你有什么启发？3．如图，AB是⊙O的直径，∠ABC＝45°，AB＝AC．判断直线AC与⊙O的位置关系，并说明理由．BOA C拓展提升4、如图：在△ABC中AB＝BC，以AB 为直径的⊙O 与AC交于点D，过D作DF⊥BC，交AB的延长线于E，垂足为F．求证：直线DE是⊙O的切线．达标检测1.下列直线是圆的切线的是（）A．与圆有公共点的直线B．到圆心的距离等于半径的直线2C．垂直于圆的半径的直线D．过圆直径外端点的直线2．如图，⊙M与x轴相交于点A（2，0），B（8，0），与y轴相切于点C，则圆心M•的坐标是_______．3．如图3，AB是⊙O的直径，点D在AB的延长线上，过点D作⊙O的切线，切点为C，若∠A=25°，则∠D=______．4．如图，已知AB是⊙O的直径，AC是弦，CD切⊙O于点C，交AB•的延长线于点D，∠ACD=120°，BD=10．（1）求证：CA=CD；（2）求⊙O的半径．5．如图，A是以BC为直径的⊙O上一点，AD⊥BC于点D，过点B作⊙O的切线，与CA的延长线相交于点E，G是AD的中点，连结OG并延长与BE相交于点F，延长AF•与CB的延长线相交于点P．（1）求证：BF=EF；（2）求证：PA是⊙O的切线；（3）若FG=BF，且⊙O的半径长为2，求BD和FG的长度．专项训练二概率初步一、选择题1．(徐州中考)下列事件中的不可能事件是( )A．通常加热到100℃时，水沸腾B．抛掷2枚正方体骰子，都是6点朝上C．经过有交通信号灯的路口，遇到红灯D．任意画一个三角形，其内角和是360°2．小张抛一枚质地均匀的硬币，出现正面朝上的可能性是( )A．25% B．50% C．75% D．85%3．(2016·贵阳中考)2016年5月，为保证“中国大数据产业峰会及中国电子商务创新发展峰会”在贵阳顺利召开，组委会决定从“神州专车”中抽调200辆车作为服务用车，其中帕萨特60辆、狮跑40辆、君越80辆、迈腾20辆，现随机从这200辆车中抽取1辆作为开幕式用车，则抽中帕萨特的概率是( )A.110B.15C.310D.254．(金华中考)小明和小华参加社会实践活动，随机选择“打扫社区卫生”和“参加社会调查”其中一项，那么两人同时选择“参加社会调查”的概率为( )A.14B.13C.12D.345．在一个不透明的袋中装着3个红球和1个黄球，它们只有颜色上的区别，随机从袋中摸出2个小球，两球恰好是一个黄球和一个红球的概率为( )A.12B.13C.14D.166．现有两枚质地均匀的正方体骰子，每枚骰子的六个面上都分别标有数字1、2、3、4、5、6.同时投掷这两枚骰子，以朝上一面所标的数字为掷得的结果，那么所得结果之和为9的概率是( )A.13B.16C.19D.1127．分别转动图中两个转盘一次，当转盘停止转动时，两个指针分别落在某个数所表示的区域，则两个数的和是2的倍数或3的倍数的概率等于( )A.316B.38C.58D.1316第7题图第8题图8．(2016·呼和浩特中考)如图，△ABC是一块绿化带，将阴影部分修建为花圃，已知AB＝15，AC＝9，BC＝12，阴影部分是△ABC 的内切圆，一只自由飞翔的小鸟将随机落在这块绿化带上，则小鸟落在花圃上的概率为( ) A.16 B.π6 C.π8 D.π5二、填空题9．已知四个点的坐标分别是(－1，1)，(2，2)，⎝ ⎛⎭⎪⎫23，32，⎝⎛⎭⎪⎫－5，－15，从中随机选取一个点，在反比例函数y ＝1x 图象上的概率是________．10．(黄石中考)如图所示，一只蚂蚁从A 点出发到D ，E ，F 处寻觅食物．假定蚂蚁在每个岔路口都可能随机选择一条向左下或右下的路径(比如A 岔路口可以向左下到达B 处，也可以向右下到达C 处，其中A ，B ，C 都是岔路口)．那么，蚂蚁从A 出发到达E 处的概率是________．11．(贵阳中考)现有50张大小、质地及背面图案均相同的《西游记》任务卡片，正面朝下放置在桌面上，从中随机抽取一张并记下卡片正面所绘人物的名字后原样放回，洗匀后再抽．通过多次试验后，发现抽到绘有孙悟空这个人物卡片的频率约为0.3.估计这些卡片中绘有孙悟空这个人物的卡片张数约为________．12．(荆门中考)荆楚学校为了了解九年级学生“一分钟内跳绳次数”的情况，随机选取了3名女生和2名男生，则从这5名学生中，选取2名同时跳绳，恰好选中一男一女的概率是________．13．(重庆中考)点P的坐标是(a，b)，从－2，－1，0，1，2这五个数中任取一个数作为a的值，再从余下的四个数中任取一个数作为b的值，则点P(a，b)在平面直角坐标系中第二象限内的概率是________．14．★从－1，1，2这三个数字中，随机抽取一个数记为a，那么，使关于x的一次函数y＝2x＋a的图象与x轴、y轴围成的三角形的面积为14，且使关于x的不等式组⎩⎪⎨⎪⎧x＋2≤a，1－x≤2a有解的概率为________．三、解答题15．(南昌中考)在一个不透明的袋子中装有仅颜色不同的10个小球，其中红球4个，黑球6个．(1)先从袋子中取出m(m＞1)个红球，再从袋子中随机摸出1个球，将“摸出黑球”记为事件A，请完成下列表格：(2)先从袋子中取出m个红球，再放入m个一样的黑球并摇匀，随机摸出1个黑球的概率等于45，求m的值．16．(菏泽中考)锐锐参加我市电视台组织的“牡丹杯”智力竞答节目，答对最后两道单选题就顺利通关，第一道单选题有3个选项，第二道单选题有4个选项，这两道题锐锐都不会，不过锐锐还有两个“求助”可以用(使用“求助”一次可以让主持人去掉其中一题的一个错误选项)．(1)如果锐锐两次“求助”都在第一道题中使用，那么锐锐通关的概率是________；(2)如果锐锐两次“求助”都在第二道题中使用，那么锐锐通关的概率是________；(3)如果锐锐将每道题各用一次“求助”，请用树状图或者列表来分析他顺利通关的概率．17．(丹东中考)甲、乙两人进行摸牌游戏．现有三张形状大小完全相同的牌，正面分别标有数字2，3，5.将三张牌背面朝上，洗匀后放在桌子上．(1)甲从中随机抽取一张牌，记录数字后放回洗匀，乙再随机抽取一张．请用列表法或画树状图的方法，求两人抽取相同数字的概率；(2)若两人抽取的数字之和为2的倍数，则甲获胜；若抽取的数字之和为5的倍数，则乙获胜．这个游戏公平吗？请用概率的知识加以解释．18．一只不透明的袋子中装有4个质地、大小均相同的小球，这些小球分别标有数字3，3，5，x，甲、乙两人每次同时从袋中各随机摸出1个球，并计算摸出的这2个球上数字之和，记录后将小球放回袋中搅匀，进行重复实验．实验数据如下表：(1)如果实验继续进行下去，根据上表数据，出现“和为8”的频率稳定在它的概率附近，估计出现“和为8”的概率是________；(2)如果摸出的这两个小球上数字之和为9的概率是13，那么x的值可以取4吗？请用列表法或画树状图法说明理由；如果x的值不可以取4，请写出一个符合要求的x的值．参考答案与解析1．D 2.B 3.C 4.A 5.A 6.C 7.C8．B 解析：∵AB ＝15，BC ＝12，AC ＝9，∴AB 2＝BC 2＋AC 2，∴△ABC 为直角三角形，∴△ABC 的内切圆半径为12＋9－152＝3，∴S △ABC ＝12AC ·BC ＝12×12×9＝54，S 圆＝9π，∴小鸟落在花圃上的概率为9π54＝π6.9.12 10.12 11.15 12.35 13.15 14.13 15．解：(1)4 2或3(2)根据题意得6＋m 10＝45，解得m ＝2，所以m 的值为2.16．解：(1)14 解析：第一道肯定能对，第二道对的概率为14，所以锐锐通关的概率为14；(2)16 解析：锐锐两次“求助”都在第二道题中使用，则第一道题对的概率为13，第二道题对的概率为12，所以锐锐能通关的概率为12×13＝16；(3)锐锐将每道题各用一次“求助”，分别用A ，B 表示剩下的第一道单选题的2个选项，a ，b ，c 表示剩下的第二道单选题的3个选项，树状图如图所示．共有6种等可能的结果，锐锐顺利通关的只有1种情况，∴锐锐顺利通关的概率为16.17．解：(1)所有可能出现的结果如下表，从表格可以看出，总共有9种结果，每种结果出现的可能性相同，其中两人抽取相同数字的结果有3种，所以两人抽取相同数字的概率为13；(2)不公平．从表格可以看出，两人抽取数字之和为2的倍数有5种，两人抽取数字之和为5的倍数有3种，所以甲获胜的概率为59，乙获胜的概率为13.∵59＞13，∴甲获胜的概率大，游戏不公平．2 3 5 2 2 2 3 2 5 2 32 33 35 318．解：(1)0.33(2)当x 为4时，数字和为9的概率为212＝16≠13，所以x 不能取4；当x ＝6时，摸出的两个小球上数字之和为9的概率是13.。

苏科版九年级上2.5直线与圆的位置关系专题练习(3)含答案

《直线与圆的位置关系》专题练习（3）1．（2016•大连）如图，AB是⊙O的直径，点C、D在⊙O上，∠A=2∠BCD，点E在AB 的延长线上，∠AED=∠ABC（1）求证：DE与⊙O相切；（2）若BF=2，DF=，求⊙O的半径．2．（2016•锦州）如图，已知△ABC，∠ACB=90°，AC＜BC，点D为AB的中点，过点D 作BC的垂线，垂足为点F，过点A、C、D作⊙O交BC于点E，连接CD、DE．（1）求证：DF为⊙O的切线；（2）若AC=3，BC=9，求DE的长．3．（2016•兰州）如图，△ABC是⊙O的内接三角形，AB是⊙O的直径，OD⊥AB于点O，分别交AC、CF于点E、D，且DE=DC．（1）求证：CF是⊙O的切线；（2）若⊙O的半径为5，BC=，求DE的长．4．（2016•宿迁）如图1，在△ABC中，点D在边BC上，∠ABC：∠ACB：∠ADB=1：2：3，⊙O是△ABD的外接圆．（1）求证：AC是⊙O的切线；（2）当BD是⊙O的直径时（如图2），求∠CAD的度数．5．（2016•菏泽）如图，直角△ABC内接于⊙O，点D是直角△ABC斜边AB上的一点，过点D作AB的垂线交AC于E，过点C作∠ECP=∠AED，CP交DE的延长线于点P，连结PO交⊙O于点F．（1）求证：PC是⊙O的切线；（2）若PC=3，PF=1，求AB的长．6．（2016•荆州）如图，A、F、B、C是半圆O上的四个点，四边形OABC是平行四边形，∠FAB=15°，连接OF交AB于点E，过点C作OF的平行线交AB的延长线于点D，延长AF交直线CD于点H．（1）求证：CD是半圆O的切线；（2）若DH=6﹣3，求EF和半径OA的长．7．（2016•本溪）如图，△ABC中，AB=AC，点E是线段BC延长线上一点，ED⊥AB，垂足为D，ED交线段AC于点F，点O在线段EF上，⊙O经过C、E两点，交ED于点G．（1）求证：AC是⊙O的切线；（2）若∠E=30°，AD=1，BD=5，求⊙O的半径．8．（2016•茂名）如图，在△ABC中，∠C=90°，D、F是AB边上的两点，以DF为直径的⊙O与BC相交于点E，连接EF，过F作FG⊥BC于点G，其中∠OFE=∠A．（1）求证：BC是⊙O的切线；（2）若sinB=，⊙O的半径为r，求△EHG的面积（用含r的代数式表示）．9．（2016•宜宾）如图1，在△APE中，∠PAE=90°，PO是△APE的角平分线，以O为圆心，OA为半径作圆交AE于点G．（1）求证：直线PE是⊙O的切线；（2）在图2中，设PE与⊙O相切于点H，连结AH，点D是⊙O的劣弧上一点，过点D作⊙O的切线，交PA于点B，交PE于点C，已知△PBC的周长为4，tan∠EAH=，求EH的长．10．（2016•西宁）如图，D为⊙O上一点，点C在直径BA的延长线上，且∠CDA=∠CBD．（1）求证：CD是⊙O的切线；（2）过点B作⊙O的切线交CD的延长线于点E，BC=6，．求BE的长．11．（2016•凉山州）阅读下列材料并回答问题：材料1：如果一个三角形的三边长分别为a，b，c，记，那么三角形的面积为．①古希腊几何学家海伦（Heron，约公元50年），在数学史上以解决几何测量问题而闻名．他在《度量》一书中，给出了公式①和它的证明，这一公式称海伦公式．我国南宋数学家秦九韶（约1202﹣﹣约1261），曾提出利用三角形的三边求面积的秦九韶公式：．②下面我们对公式②进行变形：=====．这说明海伦公式与秦九韶公式实质上是同一公式，所以我们也称①为海伦﹣﹣秦九韶公式．问题：如图，在△ABC中，AB=13，BC=12，AC=7，⊙O内切于△ABC，切点分别是D、E、F．（1）求△ABC的面积；（2）求⊙O的半径．12．（2016•桂林）已知任意三角形的三边长，如何求三角形面积？古希腊的几何学家海伦解决了这个问题，在他的著作《度量论》一书中给出了计算公式﹣﹣海伦公式S=（其中a，b，c是三角形的三边长，p=，S为三角形的面积），并给出了证明例如：在△ABC中，a=3，b=4，c=5，那么它的面积可以这样计算：∵a=3，b=4，c=5∴p==6∴S===6事实上，对于已知三角形的三边长求三角形面积的问题，还可用我国南宋时期数学家秦九韶提出的秦九韶公式等方法解决．如图，在△ABC中，BC=5，AC=6，AB=9（1）用海伦公式求△ABC的面积；（2）求△ABC的内切圆半径r．13．已知：AB为⊙O的直径，P为AB延长线上的任意一点，过点P作⊙O的切线，切点为C，∠APC的平分线PD与AC交于点D．（1）如图1，若∠CPA恰好等于30°，求∠CDP的度数；（2）如图2，若点P位于（1）中不同的位置，（1）的结论是否仍然成立？说明你的理由．14．如图，已知AB是⊙O的直径，弦CD与AB交于点E，过点A作⊙O的切线与CD长线交于点F，AC=8，CE：ED=6：5，AE：EB=2：3．求：（1）AB的长度；（2）tan∠ECB的值．15．如图，点P在y轴上，⊙P交x轴于A、B两点，连结BP并延长交⊙P于C，过点C的直线y=2x+b交x轴于D，且⊙P的半径为，AB=4．（1）求点B、P、C的坐标；（2）求证：CD是⊙P的切线．16．已知等边三角形ABC，AB=12，以AB为直径的半圆与BC边交于点D，过点D作DF ⊥AC，垂足为F，过点F作FG⊥AB，垂足为G，连接GD，（1）求证：DF与⊙O的位置关系并证明；（2）求FG的长．17．如图一，AB是⊙O的直径，AC是弦，直线EF和⊙O相切于点C，AD⊥EF，垂足为D．（1）求证：∠CAD=∠BAC；（2）如图二，若把直线EF向上移动，使得EF与⊙O相交于G，C两点（点C在点G的右侧），连接AC，AG，若题中其他条件不变，这时图中是否存在与∠CAD相等的角？若存在，找出一个这样的角，并证明；若不存在，说明理由．18．完成下列各题：（1）如图，在矩形ABCD中，AF=BE，求证：DE=CF；（2）如图，AB是⊙O的直径，CA与⊙O相切于点A，连接CO交⊙O于点D，CO的延长线交⊙O于点E，连接BE，BD，∠ABD=25°，求∠C的度数．19．（2016•扬州）如图1，以△ABC的边AB为直径的⊙O交边BC于点E，过点E作⊙O 的切线交AC于点D，且ED⊥AC．（1）试判断△ABC的形状，并说明理由；（2）如图2，若线段AB、DE的延长线交于点F，∠C=75°，CD=2﹣，求⊙O的半径和BF的长．20．如图，在△ABC中，已知AB=BC=CA=4cm，AD⊥BC于D，点P、Q分别从B、C两点同时出发，其中点P沿BC向终点C运动，速度为1cm/s；点Q沿CA、AB向终点B运动，速度为2cm/s，设它们运动的时间为x（s）．（1）求x为何值时，PQ⊥AC；（2）设△PQD的面积为y（cm2），当0＜x＜2时，求y与x的函数关系式；（3）当0＜x＜2时，求证：AD平分△PQD的面积；（4）探索以PQ为直径的圆与AC的位置关系，请写出相应位置关系的x的取值范围（不要求写出过程）．21．（2015•德阳）如图，已知BC是⊙O的弦，A是⊙O外一点，△ABC为正三角形，D 为BC的中点，M为⊙O上一点，并且∠BMC=60°．（1）求证：AB是⊙O的切线；（2）若E，F分别是边AB，AC上的两个动点，且∠EDF=120°，⊙O的半径为2，试问BE+CF 的值是否为定值？若是，求出这个定值；若不是，请说明理由．22．（2015•厦门）已知四边形ABCD内接于⊙O，∠ADC=90°，∠DCB＜90°，对角线AC 平分∠DCB，延长DA，CB相交于点E．（1）如图1，EB=AD，求证：△ABE是等腰直角三角形；（2）如图2，连接OE，过点E作直线EF，使得∠OEF=30°，当∠ACE≥30°时，判断直线EF与⊙O的位置关系，并说明理由．23．如图，在△ABC中，AB=AC，∠A=30°，以AB为直径的⊙O交BC于点D，交AC于点E，连接DE，过点B作BP平行于DE，交⊙O于点P，连接EP、CP、OP．（1）BD=DC吗？说明理由；（2）求∠BOP的度数；（3）求证：CP是⊙O的切线；如果你解答这个问题有困难，可以参考如下信息：为了解答这个问题，小明和小强做了认真的探究，然后分别用不同的思路完成了这个题目．在进行小组交流的时候，小明说：“设OP交AC于点G，证△AOG∽△CPG”；小强说：“过点C作CH⊥AB于点H，证四边形CHOP是矩形”．24．等腰直角△ABC和⊙O如图放置，已知AB=BC=1，∠ABC=90°，⊙O的半径为1，圆心O与直线AB的距离为5．现△ABC以每秒2个单位的速度向右移动，同时△ABC的边长AB、BC又以每秒0.5个单位沿BA、BC方向增大．（1）当△ABC的边（BC边除外）与圆第一次相切时，点B移动了多少距离？（2）若在△ABC移动的同时，⊙O也以每秒1个单位的速度向右移动，则△ABC从开始移动，到它的边与圆最后一次相切，一共经过了多少时间？（3）在（2）的条件下，是否存在某一时刻，△ABC与⊙O的公共部分等于⊙O的面积？若存在，求出恰好符合条件时两个图形移动了多少时间？若不存在，请说明理由．25．如图1在平面直角坐标系中，⊙O1与x轴切于A（﹣3，0）与y轴交于B、C两点，BC=8，连AB．（1）求证：∠ABO1=∠ABO；（2）求AB的长；（3）如图2，过A、B两点作⊙O2与y轴的正半轴交于M，与O1B的延长线交于N，当⊙O2的大小变化时，得出下列两个结论：①BM﹣BN的值不变；②BM+BN的值不变．其中有且只有一个结论正确，请判断正确结论并证明．26．如图，在△ABC中，∠ACB=90°，∠ABC=30°，BC=6cm，点D、E从点C同时出发，分别以1cm/s和2cm/s的速度沿着射线CB向右移动，以DE为一边在直线BC的上方作等边△DEF，连接CF，设点D、E运动的时间为t秒．（1）△DEF的边长为（用含有t的代数式表示），当t=秒时，点F落在AB上；（2）t为何值时，以点A为圆心，AF为半径的圆与△CDF的边所在的直线相切？（3）设点F关于直线AB的对称点为G，在△DEF运动过程中，是否存在某一时刻t，使得以A、C、E、G为顶点的四边形为梯形？若存在，请直接写出t的值；若不存在，请说明理由．27．在半径为4的⊙O中，点C是以AB为直径的半圆的中点，OD⊥AC，垂足为D，点E 是射线AB上的任意一点，DF∥AB，DF与CE相交于点F，设EF=x，DF=y．（1）如图1，当点E在射线OB上时，求y关于x的函数解析式，并写出函数定义域；（2）如图2，当点F在⊙O上时，求线段DF的长；（3）如果以点E为圆心、EF为半径的圆与⊙O相切，求线段DF的长．28．如图1，在平面直角坐标系中，以坐标原点O为圆心的⊙O的半径为﹣1，直线l：y=﹣x﹣与坐标轴分别交于A、C两点，点B的坐标为（4，1），⊙B与x轴相切于点M．（1）求点A的坐标及∠CAO的度数；（2）⊙B以每秒1个单位长度的速度沿想x轴负方向平移，同时，直线l绕点A以每秒钟旋转30°的速度顺时针匀速旋转，当⊙B第一次与⊙O相切时，请判断直线l与⊙B的位置关系，并说明理由：（3）如图2，过A、O、C三点作⊙O1，点E是⊙O1上任意一点，连接EC、EA、EO．①若点E在劣弧OC上，试说明：EA﹣EC=EO；②若点E在优弧OAC上，①的结论中EC、EA、EO的关系式是否仍然成立？若成立，请你说明理由？若不成立，请你直接写出正确的结论．29．在Rt△ABC中，∠A=90°，AB=AC=4，O是BC边上的点且⊙O与AB、AC都相切，切点分别为D、E．（1）求⊙O的半径；（2）如果F为上的一个动点（不与D、E），过点F作⊙O的切线分别与边AB、AC相交于G、H，连接OG、OH，有两个结论：①四边形BCHG的周长不变，②∠GOH的度数不变．已知这两个结论只有一个正确，找出正确的结论并证明；（3）探究：在（2）的条件下，设BG=x，CH=y，试问y与x之间满足怎样的函数关系，写出你的探究过程并确定自变量x的取值范围，并说明当x=y时F点的位置．参考答案与解析1．（2016•大连）如图，AB是⊙O的直径，点C、D在⊙O上，∠A=2∠BCD，点E在AB 的延长线上，∠AED=∠ABC（1）求证：DE与⊙O相切；（2）若BF=2，DF=，求⊙O的半径．【分析】（1）连接OD，由AB是⊙O的直径，得到∠ACB=90°，求得∠A+∠ABC=90°，等量代换得到∠BOD=∠A，推出∠ODE=90°，即可得到结论；（2）连接BD，过D作DH⊥BF于H，由弦且角定理得到∠BDE=∠BCD，推出△ACF与△FDB都是等腰三角形，根据等腰直角三角形的性质得到FH=BH=BF=1，则FH=1，根据勾股定理得到HD==3，然后根据勾股定理列方程即可得到结论．【解答】（1）证明：连接OD，∵AB是⊙O的直径，∴∠ACB=90°，∴∠A+∠ABC=90°，∵∠BOD=2∠BCD，∠A=2∠BCD，∴∠BOD=∠A，∵∠AED=∠ABC，∴∠BOD+∠AED=90°，∴∠ODE=90°，即OD⊥DE，∴DE与⊙O相切；（2）解：连接BD，过D作DH⊥BF于H，∵DE与⊙O相切，∴∠BDE=∠BCD，∵∠AED=∠ABC，∴∠AFC=∠DBF，∵∠AFC=∠DFB，∴△ACF与△FDB都是等腰三角形，∴FH=BH=BF=1，则FH=1，∴HD==3，在Rt△ODH中，OH2+DH2=OD2，即（OD﹣1）2+32=OD2，∴OD=5，∴⊙O的半径是5．【点评】本题考查了切线的判定和性质，等腰三角形的判定，直角三角形的性质，勾股定理，正确的作出辅助线是解题的关键．2．（2016•锦州）如图，已知△ABC，∠ACB=90°，AC＜BC，点D为AB的中点，过点D 作BC的垂线，垂足为点F，过点A、C、D作⊙O交BC于点E，连接CD、DE．（1）求证：DF为⊙O的切线；（2）若AC=3，BC=9，求DE的长．【分析】（1）连接DO并延长交AC于M，证出，由垂径定理得出DM⊥AC，证出DM∥BC，由已知得出DF⊥DO，即可得出DF为⊙O的切线；（2）由（1）得出DF=AC=1.5，CF=BF=BC=4.5，作ON⊥CE于N，连接OA，由垂径定理得出CN=EN=CE，AM=CM=ON=DF=1.5，设⊙O的半径为r，在△AOM中，由勾股定理求出半径，得出CN=EN=OM=2，CE=4，求出EF=4.5﹣4=0.5，再由勾股定理求出DE 即可．【解答】（1）证明：连接DO并延长交AC于M，如图1所示：∵∠ACB=90°，AC＜BC，点D为AB的中点，∴CD=AB=AD，∴，∴DM⊥AC，∴DM∥BC，∵DF⊥BC，∴DF⊥DO，∴DF为⊙O的切线；（2）解：由（1）得：AC∥DF，∵点D为AB的中点，∴DF=AC=1.5，CF=BF=BC=4.5，作ON⊥CE于N，连接OA，如图2所示：则CN=EN=CE，AM=CM=ON=DF=1.5，设⊙O的半径为r，在△AOM中，由勾股定理得：r2+（4.5﹣r）2=r2，解得：r=2.5，∴CN=EN=OM=4.5﹣2.5=2，∴CE=4，∴EF=4.5﹣4=0.5，∴DE===．【点评】本题考查了切线的判定、直角三角形斜边上的中线性质、勾股定理，垂径定理等知识；熟练掌握切线的判定，由勾股定理求出半径是解决问题（2）的关键．3．（2016•兰州）如图，△ABC是⊙O的内接三角形，AB是⊙O的直径，OD⊥AB于点O，分别交AC、CF于点E、D，且DE=DC．（1）求证：CF是⊙O的切线；（2）若⊙O的半径为5，BC=，求DE的长．【分析】（1）连接OC，欲证明CF是⊙O的切线，只要证明∠OCF=90°．（2）作DH⊥AC于H，由△AEO∽△ABC，得=求出AE，EC，再根据sin∠A=sin∠EDH，得到=，求出DE即可．【解答】证明：连接OC，∵OA=OC，∴∠A=∠OCA，∵OD⊥AB，∴∠A+∠AEO=90°，∵DE=DC，∴∠DEC=∠DCE，∵∠AEO=∠DEC，∴∠AEO=∠DCE，∴∠OCE+∠DCE=90°，∴∠OCF=90°，∴OC⊥CF，∴CF是⊙O切线．（2）作DH⊥AC于H，则∠EDH=∠A，∵DE=DC，∴EH=HC=EC，∵⊙O的半径为5，BC=，∴AB=10，AC=3，∵△AEO∽△ABC，∴=，∴AE==，∴EC=AC﹣AE=，∴EH=EC=，∵∠EDH=∠A，∴sin∠A=sin∠EDH，∴=，∴DE===．，【点评】本题考查切线的性质、相似三角形的判定和性质、三角函数等知识，解题的关键是添加辅助线，构造相似三角形，属于中考常考题型．4．（2016•宿迁）如图1，在△ABC中，点D在边BC上，∠ABC：∠ACB：∠ADB=1：2：3，⊙O是△ABD的外接圆．（1）求证：AC是⊙O的切线；（2）当BD是⊙O的直径时（如图2），求∠CAD的度数．【分析】（1）连接AO，延长AO交⊙O于点E，则AE为⊙O的直径，连接DE，由已知条件得出∠ABC=∠CAD，由圆周角定理得出∠ADE=90°，证出∠AED=∠ABC=∠CAD，求出EA⊥AC，即可得出结论；（2）由圆周角定理得出∠BAD=90°，由角的关系和已知条件得出∠ABC=22.5°，由（1）知：∠ABC=∠CAD，即可得出结果．【解答】（1）证明：连接AO，延长AO交⊙O于点E，则AE为⊙O的直径，连接DE，如图所示：∵∠ABC：∠ACB：∠ADB=1：2：3，∠ADB=∠ACB+∠CAD，∴∠ABC=∠CAD，∵AE为⊙O的直径，∴∠ADE=90°，∴∠EAD=90°﹣∠AED，∵∠AED=∠ABD，∴∠AED=∠ABC=∠CAD，∴∠EAD=90°﹣∠CAD，即∠EAD+∠CAD=90°，∴EA⊥AC，∴AC是⊙O的切线；（2）解：∵BD是⊙O的直径，∴∠BAD=90°，∴∠ABC+∠ADB=90°，∵∠ABC：∠ACB：∠ADB=1：2：3，∴4∠ABC=90°，∴∠ABC=22.5°，由（1）知：∠ABC=∠CAD，∴∠CAD=22.5°．【点评】本题考查了切线的判定、圆周角定理、角的互余关系；熟练掌握切线的判定方法，由圆周角定理得出直角是解决问题的关键．5．（2016•菏泽）如图，直角△ABC内接于⊙O，点D是直角△ABC斜边AB上的一点，过点D作AB的垂线交AC于E，过点C作∠ECP=∠AED，CP交DE的延长线于点P，连结PO交⊙O于点F．（1）求证：PC是⊙O的切线；（2）若PC=3，PF=1，求AB的长．【分析】（1）连接OC，欲证明PC是⊙O的切线，只要证明PC⊥OC即可．（2）延长PO交圆于G点，由切割线定理求出PG即可解决问题．【解答】解：（1）如图，连接OC，∵PD⊥AB，∴∠ADE=90°，∵∠ECP=∠AED，又∵∠EAD=∠ACO，∴∠PCO=∠ECP+∠ACO=∠AED+∠EAD=90°，∴PC⊥OC，∴PC是⊙O切线．（2）延长PO交圆于G点，∵PF×PG=PC2，PC=3，PF=1，∴PG=9，∴FG=9﹣1=8，∴AB=FG=8．【点评】本题考查切线的判定、切割线定理、等角的余角相等等知识，解题的关键是熟练运用这些知识解决问题，学会添加常用辅助线，属于中考常考题型．6．（2016•荆州）如图，A、F、B、C是半圆O上的四个点，四边形OABC是平行四边形，∠FAB=15°，连接OF交AB于点E，过点C作OF的平行线交AB的延长线于点D，延长AF交直线CD于点H．（1）求证：CD是半圆O的切线；（2）若DH=6﹣3，求EF和半径OA的长．【分析】（1）连接OB，根据已知条件得到△AOB是等边三角形，得到∠AOB=60°，根据圆周角定理得到∠AOF=∠BOF=30°，根据平行线的性质得到OC⊥CD，由切线的判定定理即可得到结论；（2）根据平行线的性质得到∠DBC=∠EAO=60°，解直角三角形得到BD=BC=AB，推出AE=AD，根据相似三角形的性质得到，求得EF=2﹣，根据直角三角形的性质即可得到结论．【解答】解：（1）连接OB，∵OA=OB=OC，∵四边形OABC是平行四边形，∴AB=OC，∴△AOB是等边三角形，∴∠AOB=60°，∵∠FAD=15°，∴∠BOF=30°，∴∠AOF=∠BOF=30°，∴OF⊥AB，∵CD∥OF，∴CD⊥AD，∵AD∥OC，∴OC⊥CD，∴CD是半圆O的切线；（2）∵BC∥OA，∴∠DBC=∠EAO=60°，∴BD=BC=AB，∴AE=AD，∵EF∥DH，∴△AEF∽△ADH，∴，∵DH=6﹣3，∴EF=2﹣，∵OF=OA，∴OE=OA﹣（2﹣），∵∠AOE=30°，∴==，解得：OA=2．【点评】本题考查了切线的判定，平行四边形的性质，直角三角形的性质，等边三角形的判定和性质，连接OB构造等边三角形是解题的关键．7．（2016•本溪）如图，△ABC中，AB=AC，点E是线段BC延长线上一点，ED⊥AB，垂足为D，ED交线段AC于点F，点O在线段EF上，⊙O经过C、E两点，交ED于点G．（1）求证：AC是⊙O的切线；（2）若∠E=30°，AD=1，BD=5，求⊙O的半径．【分析】（1）根据等腰三角形的性质得到∠B=∠ACB，∠OCE=∠E，推出∠ACO=90°，根据切线的判定定理即可得到结论；（2）根据已知条件得到∠CFO=30°，解直角三角形得到DF==，EF=3OE=4，即可得到结论．【解答】（1）证明：∵AB=AC，∴∠B=∠ACB，∵OC=OE，∴∠OCE=∠E，∵DE⊥AB，∴∠BDE=90°，∴∠B+∠E=90°，∴∠ACB+∠OCE=90°，∴∠ACO=90°，∴AC⊥OC，∴AC是⊙O的切线；（2）解：∵∠E=30°，∴∠OCE=30°，∴∠FCE=120°，∴∠CFO=30°，∴∠AFD=∠CFO=30°，∴DF==，∵BD=5，∴DE=5，∵OF=2OC，∴EF=3OE=4，∴OE=，即⊙O的半径=．【点评】本题考查了切线的判定，直角三角形的性质，等腰三角形的性质，熟练掌握切线的判定定理是解题的关键．8．（2016•茂名）如图，在△ABC中，∠C=90°，D、F是AB边上的两点，以DF为直径的⊙O与BC相交于点E，连接EF，过F作FG⊥BC于点G，其中∠OFE=∠A．（1）求证：BC是⊙O的切线；（2）若sinB=，⊙O的半径为r，求△EHG的面积（用含r的代数式表示）．【分析】（1）首先连接OE，由在△ABC中，∠C=90°，FG⊥BC，可得FG∥AC，又由∠OFE=∠A，易得EF平分∠BFG，继而证得OE∥FG，证得OE⊥BC，则可得BC是⊙O 的切线；（2）由在△OBE中，sinB=，⊙O的半径为r，可求得OB，BE的长，然后由在△BFG中，求得BG，FG的长，则可求得EG的长，易证得△EGH∽△FGE，然后由相似三角形面积比等于相似比的平方，求得答案．【解答】（1）证明：连接OE，∵在△ABC中，∠C=90°，FG⊥BC，∴∠BGF=∠C=90°，∴FG∥AC，∴∠OFG=∠A，∴∠OFE=∠OFG，∴∠OFE=∠EFG，∵OE=OF，∴∠OFE=∠OEF，∴∠OEF=∠EFG，∴OE∥FG，∴OE⊥BC，∴BC是⊙O的切线；（2）解：∵在Rt△OBE中，sinB=，⊙O的半径为r，∴OB=r，BE=r，∴BF=OB+OF=r，∴FG=BF •sinB=r ，∴BG==r ，∴EG=BG ﹣BE=r ，∴S △FGE =EG •FG=r 2，EG ：FG=1：2，∵BC 是切线，∴∠GEH=∠EFG ，∵∠EGH=∠FGE ，∴△EGH ∽△FGE ，∴=（）2=，∴S △EHG =S △FGE =r 2．【点评】此题考查了切线的判定、相似三角形的判定与性质以及三角函数等知识．注意准确作出辅助线是解此题的关键．9．（2016•宜宾）如图1，在△APE 中，∠PAE=90°，PO 是△APE 的角平分线，以O 为圆心，OA 为半径作圆交AE 于点G ．（1）求证：直线PE 是⊙O 的切线；（2）在图2中，设PE 与⊙O 相切于点H ，连结AH ，点D 是⊙O 的劣弧上一点，过点D 作⊙O 的切线，交PA 于点B ，交PE 于点C ，已知△PBC 的周长为4，tan ∠EAH=，求EH 的长．【分析】（1）作OH ⊥PE ，由PO 是∠APE 的角平分线，得到∠APO=∠EPO ，判断出△PAO ≌△PHO ，得到OH=OA ，用“圆心到直线的距离等于半径”来得出直线PE 是⊙O 的切线；（2）先利用切线的性质和△PBC的周长为4求出PA=2，再用三角函数求出OA，AG，然后用三角形相似，得到EH=2EG，AE=2EH，用勾股定理求出EG，最后用切割线定理即可．【解答】证明：（1）如图1，作OH⊥PE，∴∠OHP=90°，∵∠PAE=90，∴∠OHP=∠OAP，∵PO是∠APE的角平分线，∴∠APO=∠EPO，在△PAO和△PHO中，∴△PAO≌△PHO，∴OH=OA，∵OA是⊙O的半径，∴OH是⊙O的半径，∵OH⊥PE，∴直线PE是⊙O的切线．（2）如图2，连接GH，∵BC，PA，PB是⊙O的切线，∴DB=DA，DC=CH，∵△PBC的周长为4，∴PB+PC+BC=4，∴PB+PC+DB+DC=4，∴PB+AB+PC+CH=4，∴PA+PH=4，∵PA，PH是⊙O的切线，∴PA=PH，∴PA=2，由（1）得，△PAO≌△PHO，∴∠OFA=90°，∴∠EAH+∠AOP=90°，∵∠OAP=90°，∴∠AOP+∠APO=90°，∴∠APO=∠EAH，∵tan∠EAH=，∴tan∠APO==，∴OA=PA=1，∴AG=2，∵∠AHG=90°，∵tan∠EAH==，∵△EGH∽△EHA，∴===，∴EH=2EG，AE=2EH，∴AE=4EG，∵AE=EG+AG，∴EG+AG=4EG，∴EG=AG=，∵EH是⊙O的切线，EGA是⊙O的割线，∴EH2=EG×EA=EG×（EG+AG）=×（+2）=，∴EH=．【点评】此题是切线的性质和判定题，主要考查了切线的判定和性质，相似三角形的性质和判定，勾股定理，三角函数，解本题的关键是用三角函数求出OA．10．（2016•西宁）如图，D为⊙O上一点，点C在直径BA的延长线上，且∠CDA=∠CBD．（1）求证：CD是⊙O的切线；（2）过点B作⊙O的切线交CD的延长线于点E，BC=6，．求BE的长．【分析】（1）连OD，OE，根据圆周角定理得到∠ADO+∠ODB=90°，而∠CDA=∠CBD，∠CBD=∠ODB，于是∠CDA+∠ADO=90°；（2）根据已知条件得到△CDA∽△CBD由相似三角形的性质得到，求得CD=4，由切线的性质得到BE=DE，BE⊥BC根据勾股定理列方程即可得到结论．【解答】（1）证明：连结OD，∵OB=OD，∴∠OBD=∠BDO，∵∠CDA=∠CBD，∴∠CDA=∠ODB，又∵AB是⊙O的直径，∴∠ADB=90°，∴∠ADO+∠ODB=90°，∴∠ADO+∠CDA=90°，即∠CDO=90°，∴OD⊥CD，∵OD是⊙O半径，∴CD是⊙O的切线（2）解：∵∠C=∠C，∠CDA=∠CBD∴△CDA∽△CBD∴∵，BC=6，∴CD=4，∵CE，BE是⊙O的切线∴BE=DE，BE⊥BC∴BE2+BC2=EC2，即BE2+62=（4+BE）2解得：BE=．【点评】本题考查了切线的判定与性质：过半径的外端点与半径垂直的直线是圆的切线；也考查了圆周角定理的推论以及三角形相似的判定与性质．11．（2016•凉山州）阅读下列材料并回答问题：材料1：如果一个三角形的三边长分别为a，b，c，记，那么三角形的面积为．①古希腊几何学家海伦（Heron，约公元50年），在数学史上以解决几何测量问题而闻名．他在《度量》一书中，给出了公式①和它的证明，这一公式称海伦公式．我国南宋数学家秦九韶（约1202﹣﹣约1261），曾提出利用三角形的三边求面积的秦九韶公式：．②下面我们对公式②进行变形：=====．这说明海伦公式与秦九韶公式实质上是同一公式，所以我们也称①为海伦﹣﹣秦九韶公式．问题：如图，在△ABC中，AB=13，BC=12，AC=7，⊙O内切于△ABC，切点分别是D、E、F．（1）求△ABC的面积；（2）求⊙O的半径．【分析】（1）由已知△ABC的三边a=3，b=12，c=7，可知这是一个一般的三角形，故选用海伦﹣秦九韶公式求解即可；（2）由三角形的面积=lr，计算即可．【解答】解：（1）∵AB=13，BC=12，AC=7，∴p==16，∴==24；（2）∵△ABC的周长l=AB+BC+AC=32，∴S=lr=24，∴r==．【点评】此题考查了三角形面积的求解方法．此题难度不大，注意选择适当的求解方法是关键．12．（2016•桂林）已知任意三角形的三边长，如何求三角形面积？古希腊的几何学家海伦解决了这个问题，在他的著作《度量论》一书中给出了计算公式﹣﹣海伦公式S=（其中a，b，c是三角形的三边长，p=，S 为三角形的面积），并给出了证明例如：在△ABC中，a=3，b=4，c=5，那么它的面积可以这样计算：∵a=3，b=4，c=5∴p==6∴S===6事实上，对于已知三角形的三边长求三角形面积的问题，还可用我国南宋时期数学家秦九韶提出的秦九韶公式等方法解决．如图，在△ABC中，BC=5，AC=6，AB=9（1）用海伦公式求△ABC的面积；（2）求△ABC的内切圆半径r．【分析】（1）先根据BC、AC、AB的长求出P，再代入到公式S=即可求得S的值；（2）根据公式S=r（AC+BC+AB），代入可得关于r的方程，解方程得r的值．【解答】解：（1）∵BC=5，AC=6，AB=9，∴p===10，∴S===10；故△ABC的面积10；（2）∵S=r（AC+BC+AB），∴10=r（5+6+9），解得：r=，故△ABC的内切圆半径r=．【点评】本题主要三角形的内切圆与内心、二次根式的应用，熟练掌握三角形的面积与内切圆半径间的公式是解题的关键．13．已知：AB为⊙O的直径，P为AB延长线上的任意一点，过点P作⊙O的切线，切点为C，∠APC的平分线PD与AC交于点D．（1）如图1，若∠CPA恰好等于30°，求∠CDP的度数；（2）如图2，若点P位于（1）中不同的位置，（1）的结论是否仍然成立？说明你的理由．【分析】（1）连接OC，则∠OCP=90°，根据∠CPA=30°，求得∠COP，再由OA=OC，得出∠A=∠ACO，由PD平分∠APC，即可得出∠CDP=45°．（2）由PC是⊙O的切线，得∠OCP=90°．再根据PD是∠CPA的平分线，得∠APC=2∠APD．根据OA=OC，可得出∠A=∠ACO，即∠COP=2∠A，在Rt△OCP中，∠OCP=90°，则∠COP+∠OPC=90°，从而得出∠CDP=∠A+∠APD=45°．所以∠CDP的大小不发生变化．【解答】解：（1）连接OC，∵PC是⊙O的切线，∴OC⊥PC∴∠OCP=90°．∵∠CPA=30°，∴∠COP=60°∵OA=OC，∴∠A=∠ACO=30°∵PD平分∠APC，∴∠APD=15°，∴∠CDP=∠A+∠APD=45°．（2）∠CDP的大小不发生变化．∵PC是⊙O的切线，∴∠OCP=90°．∵PD是∠CPA的平分线，∴∠APC=2∠APD．∵OA=OC，∴∠A=∠ACO，∴∠COP=2∠A，在Rt△OCP中，∠OCP=90°，∴∠COP+∠OPC=90°，∴2（∠A+∠APD）=90°，∴∠CDP=∠A+∠APD=45°．即∠CDP的大小不发生变化．【点评】本题考查了切线的性质以及角平分线的性质、等腰三角形的性质，要注意各个知识点的衔接．14．如图，已知AB是⊙O的直径，弦CD与AB交于点E，过点A作⊙O的切线与CD长线交于点F，AC=8，CE：ED=6：5，AE：EB=2：3．求：（1）AB的长度；（2）tan∠ECB的值．【分析】（1）设CE=6k，ED=5k，AE=2a，BE=3a，过点O作OH⊥CD垂足为H，则CH=HD，由△OHE∽△FAE，得=求出EF=，由CE•ED=BE•AE求出k、a关系，得EF=10k，得到DE=DC，得△DEA、△BCE都是等腰三角形，在RT△ABC中利用勾股定理即可解决问题．（2）根据tan∠ECB=tan∠AEF=，求出AF、AE即可．【解答】解：（1）设CE=6k，ED=5k，AE=2a，BE=3a，过点O作OH⊥CD垂足为H，则CH=HD，∴EH=0.5k，OE=0.5a，∵AF是切线，∴∠FAE=90°=∠OHE，∵∠OEH=∠FEA，∴△OHE∽△FAE，∴=即=，∴EF=，∵CE•ED=BE•AE，∴6k•5k=3a•2a，∴a2=5k2，∴EF=10k，∴点D是EF中点，∴AD=ED=DF=5k，∴△DEA、△BCE都是等腰三角形，∴BC=BE=3a，∵AB是直径，∴∠ACB=90°，∴BC2+AC2=AB2，∴（3a）2+82=（5a）2，∴a=2，∴AB=5a=10．（2）∵a=2，∴k=，∵AF2=DF•FC=80k2=64，∴AF=8，∴tan∠ECB=tan∠AEF===2．【点评】本题考查切线的性质、垂径定理、直角三角形斜边中线性质、等腰三角形的性质、勾股定理等知识，解题的关键是设两个参数，想办法求出EF的长，发现点D是EF中点这个突破口，题目比较难，属于中考压轴题．15．如图，点P在y轴上，⊙P交x轴于A、B两点，连结BP并延长交⊙P于C，过点C的直线y=2x+b交x轴于D，且⊙P的半径为，AB=4．（1）求点B、P、C的坐标；（2）求证：CD是⊙P的切线．【分析】（1）连结AC，由于BC是圆P的直径，那么∠CAB=90°．解Rt△ABC，得出AC==2，由垂径定理得出OB=OA=2，根据三角形中位线定理得出OP=AC=1，从而求出点B、P、C的坐标；（2）将C（﹣2，2）代入y=2x+b，利用待定系数法求出过点C的直线解析式为y=2x+6，得到D（﹣3，0），AD=1．再利用SAS证明△ADC≌△OPB，得出∠DCA=∠B，然后证明∠BCD=90°，根据切线的判定定理证明CD是⊙P的切线．【解答】（1）解：连结AC．∵BC是⊙P的直径，∴∠CAB=90°．在Rt△ABC中，∵∠CAB=90°，BC=2，AB=4，∴AC==2，∵OP⊥AB，∴OB=OA=2，∴OP=AC=1，∴P（0，1），B（2，0），C（﹣2，2）；（2）证明：将C（﹣2，2）代入y=2x+b，得﹣4+b=2，解得b=6∴y=2x+6，当y=0时，则x=﹣3，∴D（﹣3，0），∴AD=1．在△ADC和△OPB中，，∴△ADC≌△OPB（SAS），∴∠DCA=∠B．∵∠B+∠ACB=90°，∴∠DCA+∠ACB=90°，即∠BCD=90°，∴CD是⊙P的切线．【点评】本题考查了切线的判定，垂径定理，勾股定理，全等三角形的判定与性质等知识点．要证某线是圆的切线，已知此线过圆上某点，连接圆心与这点（即为半径），再证垂直即可．16．已知等边三角形ABC，AB=12，以AB为直径的半圆与BC边交于点D，过点D作DF ⊥AC，垂足为F，过点F作FG⊥AB，垂足为G，连接GD，（1）求证：DF与⊙O的位置关系并证明；（2）求FG的长．【分析】（1）连接OD，证∠ODF=90°即可．（2）利用△ADF是30°的直角三角形可求得AF长，同理可利用△FHC中的60°的三角函数值可求得FG长．【解答】（1）证明：连接OD，∵以等边三角形ABC的边AB为直径的半圆与BC边交于点D，∴∠B=∠C=∠ODB=60°，∴OD∥AC，∵DF⊥AC，∴∠CFD=∠ODF=90°，即OD⊥DF，∵OD是以边AB为直径的半圆的半径，∴DF是圆O的切线；（2）∵OB=OD=AB=6，且∠B=60°，∴BD=OB=OD=6，∴CD=BC﹣BD=AB﹣BD=12﹣6=6，∵在Rt△CFD中，∠C=60°，∴∠CDF=30°，∴CF=CD=×6=3，∴AF=AC﹣CF=12﹣3=9，∵FG⊥AB，∴∠FGA=90°，∵∠FAG=60°，∴FG=AFsin60°=．【点评】本题主要考查了直线与圆的位置关系、等边三角形的性质、垂径定理等知识，判断直线和圆的位置关系，一般要猜想是相切，那么证直线和半径的夹角为90°即可；注意利用特殊的三角形和三角函数来求得相应的线段长．17．如图一，AB是⊙O的直径，AC是弦，直线EF和⊙O相切于点C，AD⊥EF，垂足为D．（1）求证：∠CAD=∠BAC；（2）如图二，若把直线EF向上移动，使得EF与⊙O相交于G，C两点（点C在点G的右侧），连接AC，AG，若题中其他条件不变，这时图中是否存在与∠CAD相等的角？若存在，找出一个这样的角，并证明；若不存在，说明理由．【分析】（1）连接OC，根据切线的性质定理以及等角的余角相等即可证明；（2）构造直径所对的圆周角，根据等弧所对的圆周角相等以及等角的余角相等，发现∠BAC=∠GAD，再根据等式的性质即可证明∠BAG=∠DAC．【解答】（1）证明：如图一，连接OC，则OC⊥EF，且OC=OA，易得∠OCA=∠OAC．∵AD⊥EF，∴OC∥AD．∴∠OCA=∠CAD，∴∠CAD=∠OAC．即∠CAD=∠BAC．（2）解：与∠CAD相等的角是∠BAG．证明如下：如图二，连接BG．∵四边形ACGB是⊙O的内接四边形，∴∠ABG+∠ACG=180°．∵D，C，G共线，∴∠ACD+∠ACG=180°．∴∠ACD=∠ABG．∵AB是⊙O的直径，∴∠BAG+∠ABG=90°∵AD⊥EF∴∠CAD+∠ACD=90°∴∠CAD=∠BAG．【点评】此题运用了切线的性质定理、圆周角定理的推论．注意根据等角的余角相等是证明角相等的一种常用方法．18．完成下列各题：（1）如图，在矩形ABCD中，AF=BE，求证：DE=CF；（2）如图，AB是⊙O的直径，CA与⊙O相切于点A，连接CO交⊙O于点D，CO的延长线交⊙O于点E，连接BE，BD，∠ABD=25°，求∠C的度数．。

专题05 直线与圆的位置关系(原卷版)21-22年九年级数学上学期专题(苏科版)

（1）如图1，点P是AC延长线上一点，∠APB＝∠ADC，求证：BP与⊙O相切；
（2）如图2，点G在CD上，OF⊥AC于点F，连接AG并延长交⊙O于点H，若CD为⊙O的直径，当∠CGB＝∠HGB，BG＝2OF＝6时，求⊙O半径的长．
30．（2020•乌兰浩特市一模）如图，在△ABC中，E是AC边上的一点，且AE＝AB，∠BAC＝2∠CBE，以AB为直径作⊙O交AC于点D，交BE于点F．
（1）求证：EF＝BF；
（2）求证：BC是⊙O的切线．
（3）若AB＝4，BC＝3，求DE的长．
2021-2022学年苏科版数学九年级全册压轴题专题精选汇编
专题05直线与圆的位置关系
一．选择题
1．（2020•江岸区模拟）如图，正方形ABCD的每一条边都与⊙O相切，E、F为切点，BD与⊙O交于H，求＝（）
A． B． C． D．
2．（2020•肥城市三模）如图，AB是⊙O的直径，点C在⊙O上，过点C的切线与BA的延长线交于点D，点E在上（不与点B，C重合），连接BE，CE．若∠D＝40°，则∠BEC的度数为（）
25．（2020•浙江自主招生）如图，在边长为8的正方形ABCD中，点O为AD上一动点（4＜OA＜8），以O为圆心，OA的长为半径的圆交边CD于点M，连接OM，过点M作⊙O的切线交边BC于N．在动点O逐渐向点D运动（OA逐渐增大）的过程中，△CMN的周长如何变化？说明理由．
26．（2020•浙江自主招生）如图所示，在△ABC中，CD为∠ACB的平分线，以CD为弦作一与AB相切的圆，分别交CA，CB于点M，N．
A．3B． C． D．
二．填空题
9．（2020秋•香坊区期末）如图，菱形OABC的顶点A、B、C在⊙O上，过点B作⊙O的切线交OA的延长线于点D，若⊙O的半径为5，则线段BD的长为．

苏科版九年级数学上《25直线与圆的位置关系》专题练习含答案初三数学试题.docx

《直线与圆的位置关系》专题练习（2）1. （2016*百色）如图，己知AB 为（30的直径，AC 为＜30的切线，0C 交（DO 于点D, BD 的延长线交AC 于点E. （1）求证：Z1=ZCAD ；（2）若AE=EC=2,求OO 的半径.2. （2016・济南）（1）如图1,在菱形ABCD 中，CE=CF,求证：AE=AF.（2）如图2, AB 是的直径，PA 与G ＞0相切于点A, 0P 与OO 交于点C,连接CB, ZOPA=40°,求ZABC 的度数.3. （2016*曲靖）如图，在RtAABC ZBAC=90°, O 是AB 边上的一点，以0A 为半径的＜30与边BC 相切于点E. （1）若 AC=5, BC=13,求OO 的半径；（2）过点E 作弦EF 丄AB 于M,连接AF,若ZF=2ZB,求证：四边形ACEF 是菱形.4. （2016*南通）已知：如图，AM 为。

0的切线，A 为切点, 于点D, BD 交OO 于点C, OC 平分ZAOB.B（1）求ZAOB的度数；（2）当OO的半径为2cm,求CD的长.5. (2016*十堰)如图1, AB 为半圆O 的直径，D 为BA 的延长线上一点，DC 为半圆O 的切线，切点为C.(1) 求证：ZACD=ZB ；(2) 如图2, ZBDC 的平分线分别交AC, BC 于点E, F ； ① 求tanZCFE 的值；② 若AC=3, BC=4,求CE 的长.6.丄AO 交AC 于点P,交EC 的延长线于点D. (1) 求证：APCD 是等腰三角形；(2) CG 丄AB 于H 点，交OO 于G 点，过B 点作BF 〃EC,交OO 于点F,交CG 于Q 点, 3(2016-武汉)如图，点C 在以AB 为直径的OO±, AD 与过点C 的切线垂直，垂足为点 AD交图2E 是AB 延长线上一点，EC 切OO 于点C, OP7. D,＜30于点E.(1)求证：AC平分ZDAB；4 AF(2)连接BE交AC于点F,若COS ZCAD=5,求FC的值.D r8.(2016*江西)如图，AB是(DO的雙，点P是弦AC ±一动点(不与A, C重合)，过点P作PE丄AB,垂足为E,射线EP交AC于点F,交过点C的切线于点D.(1)求证：DC=DP；(2)若ZCAB=30°,当F是AC的中点时，判断以A, 0, C, F为顶点的四边形是什么特殊四边形？说明理由.9.(2016*烟台)如图，AABC内接于©0, AC为OO的直径，PB是(30的切线，B为切点，0P 丄BC,垂足为E,交于D,连接BD.(1)求证：BD平分ZPBC；(2)若＜90的半径为1, PD=3DE,求0E及AB的长.10.(2016*北京)如图，AB为OO的直径，F为弦AC的中点，连接OF并延长交AC于点D,过点D作＜30的切线，交BA的延长线于点E.(1)求证：AC〃DE；(2)连接CD,若0A二AE二a,写出求四边形ACDE面积的思路.11.(2016*南平)如图，PA, PB是OO的切线，A, B为切点，点C在PB上，OC〃AP, CD丄AP于D(1)求证：0C二AD；(2)若ZP=50°, G＞0的半径为4,求四边形AOCD的周长(精确到0」)D12. (2016・孝感)如图，在RtAABC ZC=90°,点O 在AB ±,经过点A 的(DO 与BC 相切于点D,与AC, AB 分别相交于点E, F,连接AD 与EF 相交于点G. (1) 求证：AD 平分ZCAB ；(2) 若 0H 丄AD 于点 H, FH 平分ZAFE, DG=1. ①试判断DF 与DH 的数量关系，并说明理由； ⑥求。

苏科新版九年级上25直线与圆的位置关系同步训练含答案解析.docx

2016年苏科新版九年级数学上册同步训练：2.5直线与圆的位置关系一、选择题（共3小题）1.如图，AC是矩形ABCD的对角线，OO是AABC的内切圆，现将矩形ABCD按如图所示的方式折叠, 使点D与点O重合，折痕为FG•点F, G分别在边AD, BC ±,连结OG, DG.若OG丄DG, FLO0的A. CD+DF二4B. CD・DF二2逅・3 C・BC+AB=2A/5+4 D. BC ・ AB=22.若等峻直角三角形的外接圆半径的长为2,则其内切圆半径的长为（）A. V2B. 2^2-2C. 2-V2D. V2-23.将正方形ABCD绕点A按逆时针方向旋转30。

,得正方形ABQD], B】C]交CD于点E, AB=V3,则V5+1 R 3_馅r V5+1 n3_忑二、填空题（共4小题）4.边长为1的正三角形的内切圆半径为__________ .5.如图，AABC的内心在x轴上，点B的坐标是（2, 0），点C的坐标是（0,・2），点A的坐标是（・3,b）,反比例函数y=Z （x<0）的图象经过点A,X则k= ___________ .结果落在区域D屮每一个点都是等可能的，用A表示“实验结果落在D中的某个小区域M屮〃这个事件，那么事件A发生的概率P A二与.如图，现在等边AABC内射入一个点则该点落在AABC内切圆中的概率是____________ .7.如图，在边长为2的正三角形屮，将其内切圆和三个角切圆（少角两边及三角形内切圆都相切的圆）的内部挖去，则此三角形剩下部分（阴影部分）的面积为三、解答题（共10小题）8.如图，0是厶ABC的内心，BO的延长线和AABC的外接圆相交于点D,连接DC, DA, OA, OC,舛边形OADC为平行以边形.（1）求证：ABOC^ACDA；（2）若AB=2,求阴影部分的面积.9.如图，AD是。

0的切线，切点为A, AB是OO的弦.过点B作BC〃AD,交OO于点C,连接AC, 过点C 作CD〃AB,交AD于点D.连接AO并延长交BC于点M,交过点C的肓线于点P,且ZBCP= ZACD.(1)判断直线PC与(DO的位置关系，并说明理由；(2)若 AB二9, BC=6.求PC 的长.P C10.如图，AB是OO的直径，AM和BN是OO的两条切线，E是0O ±一点，D是AM ±一点,连接DE 并延长交BN于点C,且OD〃BE, OF/7BN.(1)求证：DE与相切；(2)求证:OF二£C D.AD M11.如图，AB是(DO直径，D为OO±一点，AT平分ZBAD交OO于点T,过T作AD的垂线交AD的延长线于点C.(1)求证：CT为OO的切线；(2)若OO半径为2, CT二灵，求AD的长.12.如图，在平面直角坐标系中，以点0为圆心，半径为2的圆My轴交于点A,点P (4, 2)是(DO外一点，连接AP,直线PB与相切于点B,交x轴于点C.(1)证明PA是OO的切线；13.如图，AABC内接于OO, AB是直径，OO的切线PC交BA的延长线于点P, OF〃BC交AC于点E,交PC于点F,连接AF.(1)判断AF与OO的位置关系并说明理由；14.如图，AB是。

2.5 直线与圆的位置关系苏科版数学九年级上册堂堂练(含答案)

2.5直线与圆的位置关系—2023-2024学年苏科版数学九年级上册堂堂练1.已知的直径为4，点O到直线m的距离为3，则直线m与的位置关系是( )A.相离B.相交C.相切D.不确定2.已知的半径为5，直线EF经过上一点P（点E，F在点P的两旁），下列条件能判定直线EF与相切的是( )A. B.C.点O到直线EF的距离是4D.3.如图，PA，PB分别切于点A，B，，CD切于点E，分别交PA，PB 于C，D两点，则的周长是( )A.10B.18C.20D.224.如图, PA,PB是的切线, A,B为切点, 若, 则的度数为 ( )A. B. C. D.5.如图，是等边的内切圆，分别切AB，BC，AC于点E，F，D，P是上一点，则的度数是( )A.65°B.60°C.58°D.50°6.如图，已知是直角，在射线BC上取一点O，以O为圆心，长为半径画圆，射线BA绕点B顺时针旋转_______________时与圆O相切.7.如图，直线l是的切线，A为切点，B为直线l上一点，连接OB交于点C.若，，则OC的长为_________.8.如图,AB为圆O的切线,B为切点,过点B作BC⊥OA,垂足为点E,交圆O于点C,延长CO与AB的延长线交于点D.（1）求证:AC为圆O的切线;（2）若,,求线段AD和AC的长.答案以及解析1.答案：A解析：由的直径为4，则圆的半径为2，点O到直线m的距离为3，可知圆心到直线的距离大于半径，所以直线m与的位置关系是相离；故选A.2.答案：D解析：根据切线的判定定理可求得需要满足的条件.点P在上，只需要即可.故选D.3.答案：C解析：，PB是的切线，.又是的切线，，，的周长.4.答案：B解析：PA,PB是的切线, ，, 即，.5.答案：B解析：如图，连接OE，OF.是的内切圆，E，F是切点，，，，是等边三角形，，，，故选B.6.答案：60°或120°解析：将射线BA绕点B顺时针旋转60°时，记为射线BE，作，垂足为D.在中，，，即OD为的半径，与相切.射线BA绕点B顺时针旋转120°时，同理可证.7.答案：6解析：直线l是的切线，A为切点，OA为半径，，，，，，故答案为：6.8.解析:（1）证明:连接OB,则,如图所示:,,OA是CB的垂直平分线,,在和中,,.AB为圆O的切线,B为切点,,,即,AC是圆O的切线.（2）解:,,,,,,设,则,,,解得,,.。

苏科版九年级数学上册直线与圆、圆与圆的位置关系 专题练习