数学期望与方差
数学期望和方差

12
9
7 50
10
15 50
12
11
10 50
12
10 50
则这 50 个零件的平均直径为
D k P( X k ) kpk 10.14
k 8 k 8
称之为这 5 个数字的加权平均,数学期望的 概念源于此.
第四章
数学期望和方差
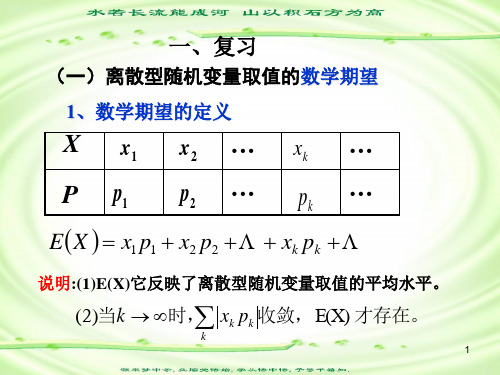
数学期望的定义
定义1.1 设离散型随机变量X 的概率分布为
证明 令g ( x ) x f ( x ).
g(x)是奇函数.
t f ( t )dt g ( t )dt .
( x ) f ( x )dx (令t x )
( x ) f ( x )dx f ( x )dx
E ( X ) xf ( x)dx
注意:随机变量的数学期望的本质就是加权 平均数,它是一个数,不再是随机变量。
第四章
数学期望和方差
常见连续型分布的数学期望 (5)指数分布E()
随机变量X的密度为:
第四章
数学期望和方差
第四章
数学期望和方差
定理1 设X的数学期望有限, 概率密度f (x) 关于
8 8
9 10 11 12 7 15 10 10 50
则这 50 个零件的平均直径为
8 8 9 7 1015 1110 1210 50 10.14cm
第四章
数学期望和方差
换个角度看,从这50个零件中任取一个,它 的尺寸为随机变量X , 则X 的概率分布为 X P 8
对称, f ( x ) f ( x ), 则E ( X ) .
数学期望和方差

第四章 数学期望和方差
本 章 内 容
随机变量的平均取值 —— 数学 期望 随机变量取值平均偏离平均值的 情况 —— 方差 描述两个随机变量之间的某种关
系的数 —— 协方差与相关系数
第四章 数学期望和方差
§4.1 数学期望
引例:测量 50 个圆柱形零件直径(见下表)
尺寸(cm) 8 9 10 11 12 数量(个) 8 7 15 10 10 50
E(X) kC n kpk(1p)nk
k0
n
k
n!
pk(1p)nk
k1 k!(nk)!
nn p(n 1 )!p k 1 (1 p )(n 1 ) (k 1 )
k 1 (k 1 )(n ! k )!
n1
npCn k1pk(1p)(n1)k np
k0
第四章 数学期望和方差
(3)泊松分布
E i n1aiXiC i n1aiE (Xi)C
当X ,Y 相互独立时,
E (X Y ) = E (X )E (Y ) .
第四章 数学期望和方差
注:性质 4 的逆命题不成立,即 若E (X Y) = E(X)E(Y),X ,Y 不一定相互独立.
反例
pij X -1
Y
-1
18
0
18
第四章 数学期望和方差
若X ≥0,且EX 存在,则EX ≥0.
证明:设 X 为连续型,密度函数为f (x), 则 由X ≥0 得:
f(x)0, x0,
所以
E Xxf(x )d xxf(x )d x 0 .
0
推论: 若 X ≤Y,则 EX ≤EY.
证明:由已知 Y-X≥0,则 E(Y-X) ≥0. 而E(Y-X)=E(Y)-E(X), 所以,E(X) ≤E(Y).
常用分布的数学期望及方差

方差的性质
方差具有可加性
对于两个独立的随机变量X和Y,有Var(X+Y) = Var(X) + Var(Y)。
方差具有对称性
对于一个常数a和随机变量X,有Var(aX) = |a|^2 * Var(X)。
方差具有非负性
对于随机变量X,有Var(X) >= 0,其中 Var(X) = 0当且仅当X是一个常数。
05 数学期望与方差的应用
在统计学中的应用
描述性统计
数学期望和方差用于描述一组数据的中心趋势和 离散程度,帮助我们了解数据的基本特征。
参数估计
通过样本数据的数学期望和方差,可以对总体参 数进行估计,如均值和方差的无偏估计。
假设检验
在假设检验中,数学期望和方差用于构建检验统 计量,判断原假设是否成立。
常见分布的数学期望
均匀分布的数学期望为
$E(X) = frac{a+b}{2}$,其中a和b是均匀分布的下限和上 限。
柯西分布的数学期望为
$E(X) = frac{pi}{beta} sinh(frac{1}{beta})$,其中β是柯西 分布的参数。
拉普拉斯分布的数学期望为
$E(X) = frac{beta}{pi} tan(frac{pi}{beta})$,其中β是拉普 拉斯分布的参数。
03
泊松分布
正态分布是一种常见的连续型随机变量 分布,其方差记作σ²。正态分布的方差 描述了随机变量取值的分散程度。
二项分布是一种离散型随机变量分布, 用于描述在n次独立重复的伯努利试验 中成功的次数。其方差记作σ²,且σ² = np(1-p),其中n是试验次数,p是单次 试验成功的概率。
泊松分布是一种离散型随机变量分布, 用于描述在一段时间内随机事件发生的 次数。其方差记作σ²,且σ² = λ,其中 λ是随机事件发生的平均速率。
数学期望与方差

第四章 随机变量Biblioteka 数字特征第一节 随机变量的 数学期望
一、数学期望的概念
二、随机变量函数的数学期望 三、数学期望的性质
四、应用实例
下 回
停
一、数学期望的概念
1. 问题的提出 1654年, 一个名叫德.梅尔的贵族就“两个 赌徒约定赌若干局, 且谁先赢 c 局便算赢家, 若 在一赌徒胜a局 (a<c), 另一赌徒胜b局(b<c)时便 终止赌博, 问应如何分赌本” 为题求教于帕斯 卡, 帕斯卡与费马通信讨论这一问题, 于1654 年 共同建立了概率论的第一个基本概念 — 数学 期望
0 . 3 0 .1 0 . 6
8 9 10
乙射手
0 .2 0 .5 0 .3
试问哪个射手技术较好?
解 运动员的水平是通过其平均水平来衡量的, 因而甲、乙两射手的平均水平分别为
甲 : 8 0.3 9 0.1 10 0.6 9.3(环) , 乙 : 8 0.2 9 0.5 10 0.3 9.1(环), 故甲射手的技术比较好.
若级数 xk pk 绝对收敛, 即 xk pk , 则称
级数 xk pk 的和为随机变量 X 的数学期望,
k 1 k 1
k 1
PX xk pk , k 1,2,.
记为EX, 即 E X
k 1
xk pk .
比如
X的分布律为
正态分布 指数分布
1 λ
λe λx , x 0 p x x0 0,
数学期望和方差

数学期望和方差
第四章 数学期望和方差
分布函数能够完整地描述随机变量的统计特 性,但在实际问题中,随机变量的分布函数较 难确定,而它的一些数字特征较易确定.并且 在很多实际问题中,只需知道随机变量的某些 数字特征也就够了.
另一方面,对于一些常用的重要分布,如二 项分布、泊松分布、指数分布、正态分布等, 只要知道了它们的某些数字特征,就能完全确 定其具体的分布.
8 8
9 10 11 12 7 15 10 10 50
则这 50 个零件的平均直径为
8 8 9 7 1015 1110 1210 50 10.14cm
第四章
数学期望和方差
换个角度看,从这50个零件中任取一个,它 的尺寸为随机变量X , 则X 的概率分布为 X P 8
x
| x| 但 | x | f ( x ) dx dx 发散. 2 (1 x )
它的数学期望不存在.
注:虽然f(x)是偶函数,但不能用定理1.1.
第四章
数学期望和方差
§4.2 数学期望的性质
设已知随机变量X的分布,我们需要计算的不 是X的数学期望, 而是X的某个函数的数学期望, 比如说g(X)的数学期望. 那么应该如何计算呢? 更一般的,已知随机向量(X1 , X2 …,Xn ) 的联合分布, Y= g(X1, X2 …,Xn ) 是 (X1 , X2 …,Xn ) 的函数, 需要计算Y 的数学期 望,应该如何计算呢? 我们下面就来处理这个 问题.
8 50
12
9
7 50
10
15 50
12
11
10 50
12
10 50
则这 50 个零件的平均直径为
各个分布的数学期望和方差

各个分布的数学期望和方差
当数据分布比较分散(即数据在平均数附近波动较大)时,各个数据与平均数的差的
平方和较大,方差就较大;当数据分布比较集中时,各个数据与平均数的差的平方和较小。
因此方差越大,数据的波动越大;方差越小,数据的波动就越小。
样本中各数据与样本平均数的差的平方和的平均数为样本方差;样本方差的算术平方
根为样本标准差。
样本方差和样本标准差都是衡量一个样本波动大小的量,样本方差或样
本标准差越大,样本数据的波动就越大。
方差和标准差为测算线性趋势最重要、最常用的指标,它就是测算数值型数据线性程
度的最重要的方法。
标准差为方差的算术平方根,用s则表示。
连续型随机变量的数学期望与方差
(1)D( )
E[
E( )]2
[x
E( )]2
p( x)dx
(2)方差的简便计算公式
D( )=E( 2) E(2 )
x2 p(x)dx
x p( x)dx
例2 随机变量的概率密度函数
6x(1 x),当0 x 1
p(x)
0
当x 0或x 1时
求随机变量的方差。
12
4、方差的性质 设 k ,b,c均为常数,则有
E( ) xp(x)dx
15
2、数学期望的性质
(1)EaX b aEX b
(2)EaX aEX
(3)EX b EX b
(4)Eb b
(5)EX Y EX EY
(6)E( f ( )) f (x)p(x)dx
(6)E f ( ) f (xk )PK
k
16
(二)连续型随机变量ξ取值的方差
(1)D(c) 0
(2)D(k ) k 2D( ) (3)D( b) D( )
(4)D(k b) k 2D( )
13
下页
三、练习
• 课本第90页 第6题
14
四、小结 (一)连续型随机变量ξ取值的数学期望
1、连续型随机变量的数学期望的定义 p(x) 设连续型随机变量 的密度函数为
若积分 xp(x绝)d对x 收敛,则 的数学期望为:
x0 x1 x2 L xn
xi xi1 xi
b i
【xi
,
xi
)
+1
y p(x)
o
x0b0 x1 xi bi xi1
xn x
6
连续型随机变量ξ的概率分布
ξ 【x0 , x1)【x1, x2)
数学期望与方差

x
4,
x x
0 0
则 P{X 1}
1
pX (x)d x
寿命不超过1年的概率 =出售的设备在售出
11
-
e
x 4
dx
1
1
e4
04
一年之内调换的概率
PX
1
1
e4
寿命超过1年的概率 =不需调换的概率
因此出售一台设备净赢利Y 的分布律为
Y 100 100 300
内容小结
1. 数学期望是一个实数, 而非变量, 它是一种
加权平均, 与一般的平均值不同, 它从本质上
体现了随机变量 X 取可能值的真正的平均值.
2. 数学期望的性质
10 EC C;
20 ECX CX ;
30
E
n
ai
i 1
Xi
k1 k![(n 1) (k 1)]!
n1
np
(n 1)!
p qi (n1)i
i0 i![(n 1) i]!
n1
np Cni 1 p i q n1i i0
np np( p q)n1
(3) Poisson 分布: X ~ P()
E( X ) k k e e k1
10 100
X
X ki.
k 1 i1
17
例5.(续)
而X ki服从 p ek 的( 0 — 1)分布,E( X ki ) ek . i 1,2,,100, 所以
10 100
10
E(X )
E( X ki ) 100ek
常见分布的数学期望和方差

e x , x 0
f (x) 0, x0
E( X )
xf ( x)dx
x ex dx
0
x de x
0
xex
0
exdx
0
1
ex
0
1
.
14
2. 指数分布 X ~ E() .
E( X )
1
,D( X )
1
2
E( X 2 ) x 2 f ( x) dx x 2 ex dx
一、常见离散型分布的数学期望和方差
1. 0-1分布 X 0 1
P 1 p p
E( X ) 0(1 p) 1 p p . E( X 2 ) 02 (1 p) 12 p p , D( X ) E( X 2 ) [E( X )]2 p p2 p(1 p) .
E( X ) p D( X ) p(1 p)
2
方 差
正态 分布
f (x)
1
e , ( x )2 2 2
x
2
( 0)
2
例1
设X
~
N
(
1
,
2 1
)
,Y
~
N
(2ຫໍສະໝຸດ ,2 2)
,且X ,Y
相互
独立,则 E( XY )
, D( XY )
.
解 E( XY ) 12 ,
D( XY ) E[( XY )2 ] [E( XY )]2
[D( X ) (EX )2 ][D(Y ) (EY )2 ] (12 )2
D. D(2 X 1) 4np(1 p)
解选
例2 设(D随).机变量X ,Y 相互独立且分布相同,则 X Y
与 2X 的关系是则( ).
数学期望与方差的运算性质

数学期望与方差的运算性质教程一:复习公式离散随机变量(),(,)(,)(,)(,)i j ij i j ij i jP X Y a b p Eh X Y h a b p ==→=∑连续随机变量()()()2,~,(,)(,),R f x y Eg g x y f x y dxdy ξηξη→=⎰⎰二:期望运算性质()E aX bY c aEX bEY c ++=++应用例题、袋中装有m 个不同色小球,有返回取球n 次,出现X 种不同颜色,求EX 解答:用i X ⎧=⎨⎩1第i颜色球在n次取球中出现0第i颜色球在n次取球中没出现,则m X X X ++= 1由于()()1101,111,n ni i P X P X m m ⎛⎫⎛⎫==-==-- ⎪ ⎪⎝⎭⎝⎭()111/ni EX m =--,()⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛--==++=∑=nmi i m m m EX X X E EX 11111三、协方差:若,EX EY θμ==,()()cov(,)X Y E X Y θμ=--⎡⎤⎣⎦称为随机变量X 、Y 的协方差.covariance()()cov(,)X Y E X Y θμ=--⎡⎤⎣⎦()()()()()()()()()()()EYEX XY E XY E XY E Y E X E XY E E Y E X E XY E Y X XY E ⨯-=-=+--=+--=+-+-+=+--=θμθμθμμθθμθμθμθμθμθμ 例题:害虫一生产卵个数X 服从参数为λ的Poisson分布,若每个卵能孵化成下一代的概率都是p ,假定害虫后代个数为Y ,求cov(,)X Y解答:(,)()()(1)!i i jj ji j i e P X i Y j P X i P Y j X i C p p i λλ-≥-=======-!(1)(1)!!()!!()!i i j i j j i j e i e p p p p i j i j j i j λλλλ----=-=---000(,)(1)!()!i ij i ji j i i j e EXY ijP X i Y j ij p p j i j λλ-∞∞-=≤======--∑∑∑∑000(,)(1)!()!iij i j i j i i j e EX iP X i Y j i p p j i j λλ-∞∞-=≤======--∑∑∑∑000(,)(1)!()!iij i j i j i i j e EY jP X i Y j j p p j i j λλ-∞∞-=≤======--∑∑∑∑clear clcsyms i j p lamda positiveEXY=symsum(symsum(i*j*exp(-lamda)*lamda^i/gamma(j+1)/gamma(i-j+1)*p^j*(1-p)^(i-j),j,0,i),i,0,inf)EX=symsum(symsum(i*exp(-lamda)*lamda^i/gamma(j+1)/gamma(i-j+1)*p^j*(1-p)^(i-j),j,0,i),i,0,inf)EY=symsum(symsum(j*exp(-lamda)*lamda^i/gamma(j+1)/gamma(i-j+1)*p^j*(1-p)^(i-j),j,0,i),i,0,inf)cov=simple(EXY-EX*EY); cov EXY =p*lamda*(lamda+1) EX = lamda EY = lamda*p cov = lamda*p可以看到,协方差不为0 例题:P180 3.4.8()[0,1][0,2],~(,)1/3()(,)f x y x y I x y ξη⨯=+,求(238)Var X Y -+syms x y positivemoment1=int(int((2*x-3*y+8)*1/3*(x+y),x,0,1),y,0,2); moment2=int(int((2*x-3*y+8)^2*1/3*(x+y),x,0,1),y,0,2); Var=moment2-moment1^2 Var = 245/81协方差计算公式()()()(),cov(,)EX a EY bX Y E X EX E Y EY E X a E Y b ===--=--()()()()E XY aY bX ab E XY aE Y bE X ab =--+=--+ ()E XY ab ba ab =--+ ()()()E XY E X E Y =-注: Y=X时得到什么公式?例题:若随机变量,X Y 独立,求它们的协方差解答:,EX EY θμ==,因为,X Y 独立,所以X Y θμ--、也相互独立()()()()cov(,)0X Y E X Y E X E Y θμθμ=--=-⨯-=⎡⎤⎣⎦注:相互独立随机变量协方差为0的逆命题不成立,如,假定随机变量~(1,1)X U -,则显然2cov(,)0X X =,但是2X X 、不独立 四、协方差和方差性质1:协方差是方差推广,方差是特殊协方差cov(,)()X X Var X =,cov(,)0X c =,cov(,)cov(,)X Y Y X =1111cov(,)cov(,)m n m ni i j j i j i j i j i j c X d Y c d X Y =====∑∑∑∑特殊地11111()cov(,)cov(,)mmmmmi i i i j i i i i j Var X X X X X =======∑∑∑∑∑111cov(,)cov(,)cov(,)m m m i j i j i i i j i j i X X X X X X ===≠⎡⎤==+⎢⎥⎣⎦∑∑∑∑1cov(,)()mi j i i j i X X Var X =≠⎡⎤=+⎢⎥⎣⎦∑∑11cov(,)()mmi j i i i j i X X Var X ==≠⎡⎤=+⎢⎥⎣⎦∑∑∑12cov(,)()mi j i i j iX X Var X =>=+∑∑特别地121212()()()2cov(,)Var X X Var X Var X X X +=++121212112212()cov(,)cov(,)cov(,)Var X X X X X X X X X X X X -=--=-+-- 11122122cov(,)cov(,)cov(,)cov(,)X X X X X X X X =+-+-+-- 11122122cov(,)cov(,)cov(,)cov(,)X X X X X X X X =+-+-+-- 1122122()cov(,)cov(,)cov(,)Var X X X X X X X =---- 1121222()cov(,)cov(,)cov(,)Var X X X X X X X =--+ 1212()()2cov(,)Var X Var X X X =+-这个结论说明,一般,和的方差并不等于方差之和 定理:若随机变量1,,n X X 相互独立,则111()2cov(,)()()nnni i j i i i i i j iVar X X X Var X Var X ===>=+=∑∑∑∑。
条件数学期望与条件方差

(3)E[ E( X | Y )] EX
Proof (1)(2)性质与普通数学期望证明是一样的
xp X Y ( x y ) pY ( y )dxdy
EX
定理2. X,Y为r.v.,EX, EY, Eg(Y )存在, 则 (1) X, Y独立,有E(Y|X)=EY; (2) E(g(X)Y|X)=g(X)E(Y|X);
(3) E(c|X)=c;
(4) E(g(X)|X)= g(X); (5) E{Y-E(Y|X)}2E{Y- g(X)}2;
定义 设随机变量X与Y的联合分布律为
P{X xi , Y y j } =pij , i, j 1, 2,
E ( X | Y y j )= xi
i 1
pij p. j
, j 1, 2,
E (Y | X xi )= y j
i 1
pij pi.
, i 1, 2,
1 212 (1 2 )
1 21 1 2
[ x 1 ( y 2 ) y) 1 同理E (Y X x) 2
1 2 2 1
( y 2 ) ( x 1 )
二、条件方差 1、定义
E{[Y E(Y | X )]2 | X }存在, 称之为随机变量X
条件下随机变量Y的条件方差,记为 D(Y | X ) 2、条件方差的性质
D(Y | X ) E{Y | X E (Y | X ) }
正态分布数学期望和方差

正态分布数学期望和方差
正态分布的期望和方差:求期望:ξ,期望:Eξ=x1p1+x2p2+……+xnpn。
方差;s²,方差公式:s²=1/n[(x1-x)²+(x2-x)²+……+(xn-x)²](x上有“-”)。
正态分布,也称“常态分布”,又名高斯分布,最早由A。
棣莫弗在求二项分布的渐近公式中得到。
C。
F。
高斯在研究测量误差时从另一个角度导出了它。
P。
S。
拉普拉斯和高斯研究了它的性质。
是一个在数学、物理及工程等领域都非常重要的概率分布,在统计学的许多方面有着重大的影响力。
方差
方差是在概率论和统计方差衡量随机变量或一组数据时离散程
度的度量。
概率论中方差用来度量随机变量和其数学期望(即均值)之间的偏离程度。
统计中的方差(样本方差)是每个样本值与全体样本值的平均数之差的平方值的平均数。
在许多实际问题中,研究方差即偏离程度有着重要意义。
方差是衡量源数据和期望值相差的度量值。
概率论 第五章数学期望和方差

=
1 5λ
.
(b)Z = max(X1, X2, . . . , X5) 表示 5 台计算机都被感染病毒的时间, P (Z > z) = 1 − P (Z ≤ z) = 1 − P (X1 ≤ z, . . . , X5 ≤ z) = 1 − P (X1 ≤ z)5 = 1 − (1 − exp(−zλ))5, 故 5 台计算机都被病毒感染前的时间期望为
exp?t2exp?t20即得y?e120bey112020vary11202400537解设过生日的分摊的费用为x不过生日的分摊的费用为y则2x5y?要使得分摊公平故在这六次生日中每人分摊的费用是相等的即5?6xy4?6由以上两式可解得x?42y4?21
第五章 数学期望和方差
5.1 解 因为这个家庭是随机抽取的, 故这个小区的每个家庭的年平均收入也为 a 元.
EX
=
9
E(
i=1
Xi)
=
9 i=1
E(Xi)
=
9
×
(1
−
838 938
).
5.17 解 (a) 设 Xi 表示第 i 台计算机被感染病毒前的时间, i = 1, 2, 3, 4, 5
则 P (Xi > y) =
∞ y
λ
exp(−xλ)dx
=
exp(−yλ),
Y = min(X1, X2, X3, X4, X5) 表示首台计算机被感染病毒前的时间,
5.2 解 所以 E(X)
设X = [3 ×
表示盈利金额, 则 P (X = 3 × 106 × 0.8 − 1) =
106
×
0.8
−
1]
×
1 107
概率论中的期望与方差

概率论中的期望与方差概率论是一门研究随机现象的数学理论。
在概率论中,期望和方差是两个重要的概念。
本文将围绕这两个概念展开阐述,并探讨它们在概率论中的应用。
一、期望的定义与性质期望是对随机变量的平均值的度量,反映了随机变量的平均水平。
设随机变量X的分布律为P(X=x),则X的期望E(X)定义为∑[x·P(X=x)]。
期望具有线性性质,即对于任意常数a和b,E(aX+b)=aE(X)+b。
期望在概率论中有着广泛的应用。
在统计学中,期望被用于描述样本均值的性质。
在金融领域,期望被用于计算资产收益的预期值。
在工程学中,期望被用于评估系统的性能。
二、方差的定义与性质方差用于衡量随机变量的离散程度。
设随机变量X的分布律为P(X=x),则X的方差Var(X)定义为∑[(x-E(X))^2·P(X=x)]。
方差的算术平方根称为标准差。
方差的计算是概率论中的重要内容。
方差衡量了随机变量与其期望之间的差异程度,越大表示随机变量值的分散程度越大。
方差的应用包括金融学中的风险度量、质量控制中的异常度量等。
三、期望与方差的关系期望和方差是概率论中两个紧密相关的概念。
根据方差的定义可得,Var(X)=E[(X-E(X))^2]。
这说明方差是对随机变量离散程度的度量,同时也可以看作是随机变量与其期望之差的平方的期望。
期望和方差之间存在一定的关系。
例如,对于两个独立随机变量X和Y,有Var(X+Y)=Var(X)+Var(Y)。
这个性质被称为方差的可加性。
另外,若常数a和b分别为aX和bY的系数,则Var(aX+bY)=a^2·Var(X)+b^2·Var(Y)。
四、期望与方差的应用期望和方差在概率论中有着广泛的应用。
以期望为例,它可以用于计算随机变量的平均值,进而评估随机事件的结果。
在统计学中,期望被用于估计总体参数,如样本均值是总体均值的无偏估计。
方差的应用也是多种多样的。
在金融学中,方差被用于度量资产的风险程度。
常见分布的数学期望与方差

If X
P ( ), then
D(X )
二、常见的连续型随机变量的数学期望与方差
1.均匀分布的方差
分布密度
1 f (x) b a 0 a x b 其 它
E(X )
3 b a 2
1 2
(a b)
2
方差
E(X
2
)
b a
x
2
b a
2
dx
”;此后十年间,航空事业获得较快发展。
筹办航空事宜
处
三、从驿传到邮政 1.邮政
(1)初办邮政: 1896年成立“大清邮政局”,此后又设
邮传部 邮传正式脱离海关。
,
(2)进一步发展:1913年,北洋政府宣布裁撤全部驿站; 1920年,中国首次参加 万国邮联大会 。
2.电讯 (1)开端:1877年,福建巡抚在 办电报的开端。 (2)特点:进程曲折,发展缓慢,直到20世纪30年代情况才发生变 化。 3.交通通讯变化的影响
2
1
2
常见分布及其期望和方差列表
分布名称 数学期望E(X) 方差D(X)
p np
0-1分布
二项分布 泊松分布
pq
npq
a b 2
(b a ) 12
2
均匀分布
正态分布 指数分布
1
2
1
2
历史ⅱ岳麓版第13课交通与通讯 的变化资料
精品课件欢迎使用
[自读教材· 填要点] 一、铁路,更多的铁路 1.地位
铁路是
交通运输 建设的重点,便于国计民生,成为国民经济
发展的动脉。 2.出现 1881年,中国自建的第一条铁路——唐山 路建成通车。 1888年,宫廷专用铁路落成。 至胥各庄铁 开平
数学期望和方差.ppt

第四章 数学期望和方差
(2) 二项分布
X的取值为0,1,…,n. 且
P(X=k)=
n
Cnk
pk
(1-p)n-k,
k= 0, 1, …, n.
E(X) kC n kpk(1p)nk
k0
n
k
n!
pk(1p)nk
k1 k!(nk)!
nn p(n 1 )!p k 1 (1 p )(n 1 ) (k 1 )
k 1 e
k 1 ( k 1)!
k e k0 k!
(4)几何分布
第四章 数学期望和方差
X的可能取值为1,2,…, 且 P(X=k)= qk-1 p, k= 1,2,…. p+q=1.
第四章 数学期望和方差
E (X ) kkp kpk q 1p kq k 1
第四章 数学期望和方差
解:设X为停止检查时,抽样的件数,则X 的可能取值为1,2,…,n,且
P{Xk} q qn k 1 1,p,
k1,2,,n1; kn.
其中 q1p,于是
n1
E(X) kqk1pnqn1
k1
第四章 数学期望和方差
n1
E(X) kqk1(1q)nqn1
k 1 (k 1 )(n ! k )!
n1
npCn k1pk(1p)(n1)k np
k0
第四章 数学期望和方差
(3)泊松分布
X的可能取值为0,1,2,…,且
P(Xk)ke,k0,1,2,,
k!
k
E(X) kk p k
k0
《数学期望与方差》课件

对于二项分布,可以直接使用公式计算期望 值。
方差的计算技巧
定义法
根据方差的定义,利用概率和数学公 式进行计算。
性质法
利用方差的非负性、方差的加法性质 和方差的常数性质简化计算。
随机变量函数的方差
通过随机变量函数的概率分布计算方 差。
二项分布方差
对于二项分布,可以直接使用公式计 算方差值。
Excel计算
在Excel中,可以使用"DEVSQ"函数来计算方差,该函数会自动处理数据点的数 量和每个数据点与均值之差的平方。
方差的应用
数据分析
方差可以用来分析数据的分散程度,从而了解数据的稳定 性、可靠性等方面的情况。
质量控制
在生产过程中,方差可以用来衡量产品质量的一致性和稳 定性,通过控制生产过程中各种因素的影响,降低产品质 量的波动。
风险评估
在金融和投资领域,方差被用来评估投资组合的风险,通 过计算投资组合收益率的方差和标准差等指标,投资者可 以了解投资组合的风险情况。
社会科学研究
在社会学、心理学、经济学等社会科学研究中,方差可以 用来分析调查数据的分散程度,从而了解群体内部的差异 和分布情况。
数学期望与方差的
03
关系
数学期望与方差的联系
方差的期望值性质
Var(E(X|Y))=E(Var(X|Y))。
方差的非负性质
Var(X)≥0,当且仅当X是常数 时等号成立。
期望与方差的性质和定理在实际问题中的应用
在金融领域,期望和方差用于评估投资 组合的风险和预期收益。通过计算期望 收益和方差,投资者可以了解投资组合
的预期表现和风险水平。
在统计学中,期望和方差用于描述数据 的集中趋势和离散程度。例如,在计算 平均数和标准差时,期望和方差是重要
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
n
(n 1)! np k p k 1q ( n1)( k 1) k![(n 1) (k 1)]! k 1
(n 1)! np p i q ( n1)i i 0 i![(n 1) i ]!
n 1
i i n 1i np C n p q 1 i 0
X
k 1 i 1
10 100
ki .
17
例5.(续)
而X ki 服从 p e k 的( 0 — 1)分布, E ( X ki ) e k . i 1,2,,100, 所以
10 100 10
E ( X ) E ( X ki ) 100e
k 1 i 1 k 1
解 设每张彩票中奖的数额为随机变量X, 则
X 10000 p 1 105
5000
1000
100
10
0
2 105
10 105 100 105 1000 105 p0
X 10000 p 1 105
5000
1000
100
10
0
2 105
10 105 100 105 1000 105 p0
每张彩票平均能得到奖金 1 2 E X 10000 5 5000 5 0 p0 10 10 0.5(元). 每张彩票平均可赚 2 0.5 0.3 1.2(元).
引例1 分赌本问题(产生背景)
A、B两人赌技相同, 各出赌金100元, 并约定 先胜三局者为胜, 取得全部 200元. 由于出现意外 情况, 在 A 胜 2 局、B 胜1局时, 不得不终止赌博, 如果要分赌金, 该如何分配才算公平?
分析 假设继续赌两局, 则结果有以下四种情况:
AA A胜B负 A胜B负 AB A胜B负 B胜A负 BA B胜A负 A胜B负 BB B胜A负 B胜A负
性质2和3
E (3 X 2 XY Y 5) 3 E ( X ) 2 E ( XY ) E (Y ) E (5)
3 10 2 E( X ) E(Y ) 3 5
30 2 10 3 3 5 92
12
性质4
数学期望不存在的实例
B. 数学期望的性质
E (C ) = C E (aX ) = a E (X )
E ( X + Y ) = E (X ) + E (Y )
E ai X i C ai E ( X i ) C i1 i1
n n
当X ,Y 相互独立时,
E ( X Y ) = E (X )E (Y ) .
但
E ( XY ) 0;
2 P( X 0) P(Y 0) 8
P( X 0, Y 0) 0
2
10
若X ≥0,且EX 存在,则EX ≥0。
证明:设 X 为连续型,密度函数为f (x), 则 由X ≥0 得:
f ( x) 0,
x0,
0
所以
EX x f ( x)dx x f ( x)dx 0 .
n 1
np( p q) n1
np
(3) Poisson 分布: X ~ P( )
E( X ) k
k 0
k
k!
e
e
(k 1)!
k 1
k 1
e e
(4) 正态分布: X ~ N (, )
2
E( X )
Remark 分布完全描述了随机变量的规律,而期望只 刻画了它的一个重要特征——“位置”特征.随 机变量以期望为“中心”而随机取值. 已知分布律可求均值.但不同的分布可有相 同的均值.
把已赌过的三局(A 胜2局、B 胜1局)与上述结果 相结合, 即A、B赌完五局: 前三局: 后二局: A胜2局B胜1局 AA
AB
A胜
BA
BB B胜
故有, 在赌技相同的情况下, A、B最终获胜的 可能性大小之比为 3:1. 1 3 即A 应获得赌金的 , 而 B 只能获得赌金的 . 4 4 因此, A 能“期望”得到的数目应 为 3 1 200 0 150(元 ), 4 4 而B 能“期望”得到的数目, 则为 1 3 200 0 50(元). 4 4
变除法为乘法和加法
Def. 1
设离散型随机变量 X 的分布律为
P{X ak } pk , k 1, 2,
E ( X ) ak P{X ak } ak pk
k k
称为 X 的数学期望或均值 Def. 2 设连续型随机变量 X 的分布密度函数为 f ( x)
其数学期望定义为 E( X )
数学期望和方差是常用的随机变量的两个数字特征
一、数学期望(mathematical expectation)
1.数学期望的概念
e.g. 小组 8 个人,英语得 90 分的 3 人,80 分的 4 人, 60 分的 1 人,求平均分数
.
90 3 80 4 60 1 3 4 1 90 80 60 3 4 1 8 8 8Leabharlann xf ( x)dx
e. g. 1
概率为
1 甲、乙两人赌博,甲赢的概率为 ,输的 3 2
,但甲赢一次可从乙处得 3 元,而输
3 一次要付给乙 1 元,求甲的平均赢利。
e. g. 2 某同学假期回家探亲,有三种方法:坐汽车, 240 元;坐火车,300 元;坐飞机,980 元.由于
各种原因,该同学采用三种路线的概率分别为: 0.3, 0.5, 0.2 。试写出差旅费 X 的概率分布,并计 算差旅费的平均值。
E ( X ) 8 0.3 2 0.7 1(万元), 存入银行的利息: 10 5% 0.5(万元), 故应选择投资.
内容小结
1. 数学期望是一个实数, 而非变量, 它是一种 加权平均, 与一般的平均值不同, 它从本质上 体现了随机变量 X 取可能值的真正的平均值. 2. 数学期望的性质 10 E C C ; 0 2 E CX C X ; n n 0 ai E X i ; 3 E a X i i i 1 i 1 0 4 X ,Y独立 E XY E X E Y .
8
注
性质 4 的逆命题不成立,即
若E (X Y) = E(X)E(Y),X ,Y 不一定相互独立.
反例
Y -1 pij X -1
18 18 18
0
18
1
18 18 18
p• j
38 28 38
0
1 pi•
0
18
38
28
38
9
XY P
-1
0
1
28
48
28
E ( X ) E (Y ) 0; E ( XY ) E ( X ) E (Y )
k
100 e
k 1
10
k
100e (1 e 1 e
10
)
18
例6. 某厂家的自动生产线, 生产一件正品的 概率为 p (0<p<1),生产一件次品的概率为 q=1-p。生产一件产品的成本为c元,正品的 价格为s元,次品不能出售。这样,厂家生产 一件正品获利s-c元, 生产一件次品亏损c 元(假定每个产品的生产过程是相互独立的 )。 若生产了N件产品,问厂家所获利润的 期望值是多少?
Y
100
1 e 4
100 300
1 1 e 4
p
则 EY 100e
1 4
1 200 1 e 4 33.64元 . .
发行彩票的创收利润
某一彩票中心发行彩票10万张, 每张2元. 设头等奖1个, 奖金 1万元, 二等奖2个, 奖金各 5千元; 三等奖10个, 奖金各1千元; 四等奖100 个, 奖金各1百元; 五等奖1000个, 奖金各10元. 每张彩票的成本费为0.3元, 请计算彩票发行单 位的创收利润.
20
四、应用实例
厂家的销售策略
1 某设备寿命X(以年计)服从 λ 的指数分布. 4 按规定: 出售的设备在售出的一年内损坏可予 以调换. 若出售一台设备赢利100元, 调换一台 设备厂方需花费300元. 求厂方出售一台设备净 赢利Y的数学期望.
1 x 4 e ,x0 p x 解 依题设, 有 X 4 x0 0,
例8 设离散型随机变量X的分布律为
k 2 1 k pk P X 1 k , k 1,2, k 2 求EX. k 1 解 由于 xk pk 1 lnk . k k 1 k 1
1 但是 xk pk . k k 1 k 1
因此彩票发行单位发行10万张彩票的创收利润为 100000 1.2 120000元 .
如何确定投资决策方向?
某人现有10万元现金, 想投资于 某项目, 为期一年. 欲估成功的机会 为30%, 并可获利8万元, 失败的机会 为70%, 将损失2万元 . 若存入银行 , 同期间的利率为 5 %, 哪一种方案可 使投资的效益较大? X 8 2 解 设X为投资利润, 则 p 0 .3 0.7
则 P{ X 1}
p X ( x ) d x 寿命不超过1年的概率 =出售的设备在售出 x 1 11 一年之内调换的概率 4 4 e dx 1 e 04 1 寿命超过1年的概率 P X 1 e 4 =不需调换的概率
1
因此出售一台设备净赢利Y 的分布律为
