高中提前招生数学试卷
重点高中提前招生(数学)

综合素质测试科学素养答题卷(数学) 共 8 页 第 1 页重点高中提前招生(数学部分)参考公式:二次函数y=ax 2+bx+c 的顶点坐标是(-ab 2,ab ac 442)一、选择题(本题有6小题,每小题4分,共24分.请选出各题中一个符合题意的正确选项,不选、多选、错选,均不给分)1.如图,数轴上表示1,2的对应点分别为A ,B ,点B 关于点A 的对称点为C ,则点C 所表示的数是 (A )2-2(B )2-2(C )1-2(D )2-12.数学老师布置10道选择题作为课堂练习,课代表将全班同学的答题情况绘制成条形统计图(如图),根据此图可知,每位同学答对的题数所组成样本的中位数和众数分别为 (A )8,8 (B )8,9 (C )9,9(D )9,83.小华和小明到同一早餐店买馒头和豆浆.已知小华买了5个馒头和6杯豆浆;小明买了7个馒头和3杯豆浆,且小华花的钱比小明少1元.关于馒头与豆浆的价钱,下列叙述正确的是 (A )4个馒头比6杯豆浆少2元 (B )4个馒头比6杯豆浆多2元 (C )12个馒头比9杯豆浆少1元(D )12个馒头比9杯豆浆多1元4.如图,C 为线段AE 上一动点(不与点A ,E 重合),在AE 同侧分别作正三角形ABC 和正三角形CDE ,AD 与BE 交于点O ,AD 与BC 交于点P ,BE 与CD 交于点Q ,连结PQ .现有五个结论:①AD =BE ;②PQ ∥AE ;③AP =BQ ;④DE =DP ;⑤∠AOE =120°. 其中一定成立的结论有 (A )2个 (B )3个(C )4个(D )5个5.如图,在矩形ABCD 中,AB =8,BC =4,将矩形沿AC 折叠,使点D与点D'重合,则重叠部分ΔAFC 的面积为 (A )6(B )8(第4题图)(第5题图)C(第1题图)(第2题图)综合素质测试科学素养答题卷(数学) 共 8 页 第 2 页(C )10 (D )126.如图,正方形ABCD 的边长是3cm ,一个边长为1cm 的小正方形沿着正方形ABCD的边AB →BC →CD →DA →AB 连续地翻转,那么这个小正方形第一次回到起始位置时,它的方向是二、填空题(本题有4小题,每小题4分,共16分) 7.如图,D ,E ,F 分别是等边三角形ΔABC 三边的中点,且ΔDEF 的面积为93,则ΔABC 的周长为 ▲ .8.下表为2008年北京奥运会官方票务网站公布的几种球类比赛的门票价格:小明准备用8000元预订10张表中比赛项目的门票,其中男篮门票数与足球门票数相同,且乒乓球门票的费用不超过男篮门票的费用,则他能预订足球门票 ▲ 张.9.如图,已知一次函数y =3x +b 和y =ax -3的 图象交于点P (-2,-5),则根据图象可得不 等式3x +b >ax -3的解集是 ▲ .10.如图,在平面直角坐标系中,⊙A 的圆心在x 轴上,半径为1,直线l 的解析式为y =x -2.若⊙A 沿x 轴向右运动,在运动过程中,⊙A 与直线l 会有两个切点,则这两个切点之间的距离是 ▲ .(第6题图)(A) (B) (C)(D)A BCDE F(第7题图)(第10题图)(第9题图)综合素质测试科学素养答题卷(数学) 共 8 页 第 3 页三、解答题(本题有4小题,第11小题6分,第12小题7分,第13题11分,第14小题11分,共35分)11.(1)已知a ,b 为实数,且1=ab ,设11+++=b b a a M ,1111+++=b a N ,请比较M ,N 的大小,并说明理由;(2)一天,小明爸爸的同事来家做客,已知爸爸的年龄比小明年龄的平方大5岁,爸爸同事的年龄是小明年龄的4倍,请你计算一下:小明爸爸与他的同事,谁的年龄大?12.如图,已知在直角坐标系中的正方形ABCD 的边长为4.现做如下实验:转盘被划分成4个相同的小扇形,并分别标上数字1,2,3,4. 分别转动两次转盘,转盘停止后,指针所指向的数字作为直角坐标系中M 点的坐标(第一次作横坐标,第二次作纵坐标),指针如果指向分界线上,则重新转动转盘.(1)请你用树状图或列表的方法,求点M 落在正方形ABCD 内(包含边线)的概率; (2)将正方形ABCD 平移整数个单位,则是否存在某种平移,使点M 落在正方形ABCD面上的概率为43?若存在,指出一种具体的平移过程;若不存在,请说明理由.13.已知抛物线32++-=mx x y 与x 轴的一个交点A (3,0),另一个交点为B ,与y 轴的交点为C ,顶点为D .(1)请分别求出点B ,C ,D 的坐标;(第12题图)综合素质测试科学素养答题卷(数学) 共 8 页 第 4 页(2)请在图中画出抛物线的草图. 若点E (-2,n )在直线BC 上,试判断点E 是否在经过点D 的反比例函数的图象上,把你的判断过程写出来;(3)若过点A 的直线L 与x 轴所夹锐角α的正切值满足tan α≤31,试求直线L 与抛物线另一个交点横坐标的取值范围.14.如图,在Rt △PQO 中,∠POQ =90°,∠Q =30°,OP =43.在菱形ABCD 中,点A在边PQ 上运动,B ,C 在边QO 上运动(点B 在点C 的左侧),且∠ABC =60°,设BQ 的长为x .(1)试用含x 的代数式表示菱形ABCD 的边长; (2)当点D 在线段OP 上时,求x 的值;(3)设菱形ABCD 与△OPQ 重合部分的面积为y ,求y 关于x 的函数关系式;(4)连结PD ,OD ,对于不同的x 值,请你比较线段OD 与PD 的大小关系,直接写出结论.(第14题图)(第13题图)综合素质测试科学素养答题卷(数学) 共 8 页 第 5 页综合素质测试科学素养答题卷数学部分一、选择题(本大题共有6小题,每小题4分,共24分)二、填空题(本大题共有4小题,每小题4分,共16分)7. ; 8. ; 9. ; 10. .三、解答题(本大题共有4小题,共35分)11.(本题6分) 解:学校: 姓名: 准考证号:解:(第12题图)综合素质测试科学素养答题卷(数学)共8 页第6 页13.(本题11分)Array解:(第13题图)综合素质测试科学素养答题卷(数学)共8 页第7 页综合素质测试科学素养答题卷(数学) 共 8 页 第 8 页14.(本题11分) 解:(第14题图1)(第14题图3)QP(第14题图2)。
省重点中学高一提前招生考试数学试卷及答案(共4份)

省重点中学高一提前招生考试数学试卷满分:120分 时间:90分钟一、选择题(本题有10个小题,每小题3分,共30分)(1)如果一元一次不等式组⎩⎨⎧>>a x x 3的解集为x >3,则a 的取值范围是A .a >3B .a ≥3C .a <3D .a ≤3(2)若实数x 满足12223-=++x x x ,则9932x x x x ++++ =A .1-B .0C .1D .99(3)如果从一卷粗细均匀的电线上截取1米长的电线, 称得它的质量为a 克,再称得剩余电线的质量为b 克,那么原来这卷电线的总长度是A .a b 1+米B .(a b +1)米C .(a+b a +1)米D .(b a +1)米(4)若实数n 满足2)45()46(22=-+-n n ,则代数式)45)(46(n n --的值是A .1-B .21-C .21D .1(5)已知方程2(21)10x k x k +++-=的两个实数根12,x x 满足1241x x k -=-,则实数k 的值为 A .—3,0 B .1,43-C .1,13- D .1,0 (6)如图,矩形AOBC 的面积为16,反比例函数xky =的图象经过矩形的对角线的交点P ,则反比例函数的解析式是A .x y 1= B .x y 2=C .x y 4=D .x y 8= (7)设213a a +=,213b b +=,且a b ≠,则代数式3311ba +的值为A .24-B .18-C .18D .24(8)当x 分别取值201,191,181,…31,21,1,2,3,…,18,19,20时,计算代数式2211x x +-的值,将所得的结果相加,其和等于A .-20B .0C .1D .20(9)如图,∠ACB =60○,半径为2的⊙O 切BC 于点C ,若将⊙O 在CB 上向右滚动,则当滚动到⊙O 与CA 也相切时,圆心O 移动的水平距离为A .32B .4C .πD .2π(10)方程813222=++y xy x 的整数解(,)x y 的组数为A .7B . 6C .5D .4(第9题)二、填空(本题有7个小题,其中11题6分,其余每小题4分,共30分) (11)直接写出下列关于x 的方程的根:①015722=-+x x ; ②24)3)(2)(1(=+++x x x x ;③41122=+++x x xx ;④01)2(2=+--+a x a x ; (12)已知三个数a 、b 、c 的积为负数,和为正数,且x =a a +b b +c c +ab ab +ac ac +cb bc,则ax 3+bx 2+cx +1=_________.(13)若化简16812+---x x x 的结果为52-x ,则x 的取值范围是 . (14)如图,DE 是△ABC 的中位线,点P 是DE 的中点,CP 的延长线交AB 于点Q ,那么:DPQ ABC S S ∆∆=______________. (15)若实数a 、b 满足b >a >0,且ab b a 422=+,则ba b a +-= . (16)若实数b a ,满足0111=+--ba b a ,则=+ab b a 22. (17)桌面上有三颗球,相互靠在一起。
(完整)重点高中提前招生数学试卷.doc

数学试卷 (满分 100 分)一、选择题(每小题均给出了代号为 A 、B 、 C 、 D 的四个结论,其中只有一个是正确的,请将正确答案的代号填在题后的括号内,每题4 分,共 28 分,选择题的答案写在答卷上)1x 11是方程 mx 2m2 0的根,则 xm 的值为 ().若mA .0B . 1C .- 1D . 22.内角的度数为整数的正n 边形的个数是( )A .24B . 22C .20D . 183.某商场五一期间举行优惠销售活动,采取“满一百元送二十元,并且连环赠送”的酬宾方式,即顾客每消费满100 元( 100元可以是现金,也可以是购物券,或二者合计)就送20 元购物券,满 200 元就送40 元购物券,依次类推,现有一位顾客第一次就用了16000 元购物,并用所得购物券继续购物,那么他购回的商品大约相当于它们原价的( )A .90%B .85%C . 80%D . 75%4x 1是完全平方数,则它前面的一个完全平方数是 ().设 x 为正整数,若A . xB x 2 x 1C . x 2 x 1 1D . x 2 x 1 2.5.横坐标、 纵坐标都是整数的点叫做整点,6x 3( )函数 y的图象上整点的个数是2x 1A .3 个B . 4 个C . 6 个D . 8 个D6、如图,四边形BDCE 内接于以 BC 为直径的⊙ A ,已知:BC 10, cos BCD 3 ,BCE 30 ,则线段 DE 的长5B是 ()CAA 、 89B 、7 3C 、 4+3 3D 、 3+4 37、某学校共有 3125 名学生,一次活动中全体学生被排成E一个 n 排的等腰梯形阵,且这 n 排学生数按每排都比前一排多一人的规律排列,则当 n 取到最大值时,排在这等腰梯形阵最外面的一周的学生总人数是()A.296B.221C.225D.641数学答题卷一、 (每 4 分,共 28 分,每 4 分,共 28 分)1 2 3 4 5 6 7二、填空 (本 共 8 小 ,每小 4 分,共 32 分)8. 算: 1+ 2-3+ 4+ 5- 6+ 7+ 8- 9+⋯+ 97+ 98-99+ 100= .9.若抛物 y2x 2px 4 p 1 中不管 p 取何 都通 定点, 定点坐10.已知 数 x 足 ( x 2 x)24(x 2 x)120 , 代数式 x 2 x 1 的11.若方程5x 3 y 2 3kx a, 且 | k | <3, a b 的取 范 是3x y k 4的解b,y12、若 任意 数 x 不等式 axb 都成立,那么 a 、 b 的取 范13、 1x 2 , x2 1 x 2的最大 与最小 之差 x214.有八个球 号是①至⑧,其中有六个球一 重,另外两个球都 1 克, 了找出 两个 球, 用天平称了三次, 果如下:第一次①+②比③+④重, 第二次⑤ +⑥比⑦+⑧ ,第三次① +③+⑤和② +④ +⑧一 重.那么,两个 球的 号是__15.在 2× 3 的矩形方格 上,各个小正方形的 点 格点。
高中提前招生考试数学试卷(含答案)

市高中提前招生考试试卷一、选择题(每小题4分,共40分)2. 如果从一卷粗细均匀的电线上截取1米长的电线, 称得它的质量为a 克,再称得剩余电线的质量为b 克, 那么原来这卷电线的总长度是……………( ) A .b+1a 米; B .(b a +1)米; C .(a+b a +1)米; D .(a b+1)米3. 国家质检总局出台了国内销售的纤维制品甲醛含量标准, 从2003年1月1 日起正式实施.该标准规定:针织内衣. 床上用品等直接接触皮肤的制品,甲醛含量应在百万分之七十五以下. 百万分之七十五用科学记数法表示应写成………( ) A .75×10-7; B .75×10-6; C .7.5×10-6; D .7.5×10-54. 已知⊙O 1半径为3cm ,⊙O 2的半径为7cm, 若⊙O 1和⊙O 2的公共点不超过1 个, 则两圆的圆心距不可能为………………………( ) A .0cm ; B .4cm ; C .8cm ; D .12cm5. 如图所示的两个圆盘中,指针落在每一个数上的机会均等,那么两个指针同时落在偶数上的概率是……( ) A .1925 ; B .1025 ; C .625 ; D .5256. 在四边形ABCD 中,对角线AC 与BD 相交于点E ,若AC 平分∠DAB ,AB=AE , AC=AD. 那么在下列四个结论中:(1) AC ⊥BD ;(2)BC=DE ; (3)∠DBC=12 ∠DAB ;(4) △ABE 是正三角形,正确的是……………( )A .(1)和(2);B .(2)和(3);C .(3)和(4);D .(1)和(4) 7. 红星学校准备开办一些学生课外活动的兴趣班,结果反应热烈。
各种班的计划招生人若计划招生人数和报名人数的比值越大,表示学校开设该兴趣班相对学生需要的满足程度就越高,那么根据以上数据,满足程度最高的兴趣班是------( ) A .计算机班; B .奥数班;C .英语口语班;D .音乐艺术班8. 抛物线y=ax 2+2ax+a 2+2的一部分如图所示,那么该抛 物线在y 轴右侧与x 轴交点的坐标是……………( )A .(12 ,0);B .(1, 0);C .(2, 0);D .(3, 0)9. 如图是一张简易活动餐桌,现测得OA=OB=30cm , OC=OD=50cm ,现要求桌面离地面的高度为40cm ,那么 两条桌腿的张角∠COD 的大小应为…………………( ) A .100°;B .120°;C .135°;D .150°.10. 下列四个图形中,每个小正方形都标上了颜色. 若要求一个正方体两个相对面上的颜色都一样,那么不可能是这一个正方体的展开图的是-------( )二、填空题(每小题5分,共30分)11. 如图是2006年1月的日历,李钢该月每周都要参加1次足球赛,共参加5次.按照原定的安排,其中去1次的是星期日、星期一和星期六,去2次的是星期三.那么李钢参加比赛的日期数的总和是 .12. 若不等式组112x x a -≤≤⎧⎨<⎩有解,那么a 必须满足 .13. 已知A 、B 、C 、D 点的坐标如图所示, E 是图中两条虚线的交点, 若△ABC 和△ADE 相似, 则E 点的坐标是___________________.14. 等腰△ABC 的底边BC=8cm ,腰长AB=5cm ,一动点P 在底边上从点B 开始向点C 以0.25cm/秒的速度运动, 当点P 运动到PA 与腰垂直的位置时,点P 运动的时间应为 秒.15. 请你将一根细长的绳子,沿中间对折,再沿对折后的绳子中间再对折,这样连续对折5次,最后用剪刀沿对折5次后的绳子的中间将绳子剪断,此时绳子将被剪成 段.A .B .C .D .16. 假设一家旅馆一共有30个房间,分别编以1~30三十个号码,现在要在每个房间的钥匙上刻上数字,要求所刻的数字必须使服务员很容易辨认是哪一个房间的钥匙,而使局外人不容易猜到. 现在有一种编码的方法是:在每把钥匙上刻上两个数字,左边的一个数字是这把钥匙原来的房间号码除以5所得的余数,而右边的一个数字是这把钥匙原来的房间号码除以7所得的余数. 那么刻的数是36的钥匙所对应的原来房间应该是号.三、解答题19. 严先生能言善辨,他说,他能证明图中的直角等于钝角。
高中提前招生数学试卷

高中提前招生数学试卷1.已知关于x 的方程m x +2=2(m —x )的解满足|x -21|-1=0,则m 的值是 ( ) A .10或52 B .10或-52 c .-10或52 D .-10或52- 2.设直角三角形的三边长分别为a 、b 、c ,若c -b =b -a >0,则 ( )A .1/2B .1/3C .1/4D .1/53.某工厂第二季度的产值比第一季度的产值增长了x %,第三季度的产值又比第二季度的产值增长了x %,则第三季度的产值比第一季度的产值增长了 ( )A .2x %B . 1+2x %C .(1+x %)x %D .(2+x %)x %4.甲从一个鱼摊上买了三条鱼,平均每条a 元,又从另—个鱼摊上买了两条鱼,平均每条b 元,后来他又以每条2b a +元的价格把鱼全部卖给了乙,结果发现赔了钱,原因是 ( )A .a >bB .a <bC .a =bD .与a 和b 的大小无关5.若D 是△ABC 的边AB 上的一点,∠ADC=∠BCA ,AC=6,DB=5,△ABC 的面积是S ,则△BCD 的面积是 ( )A .S 53B . S 74C .S 95D .S 1166.如图,AE ⊥AB 且AE=AB ,BC ⊥CD 且BC=CD ,请按照图中所标注的数据,计算图中实线所围成的图形的面积S 是( )A .50B .62C .65D .687.如图,两个标有数字的轮子可以分别绕轮子的中心旋转,旋转停止时,每个轮子上方的箭头各指着轮子上的一个数字,若左图轮子上方的箭头指着的数字为a ,右图轮子上方的箭头指着的数字为b ,数对(a ,b )所有可能的个数为n ,其中a +b 恰为偶数的不同数对的参数为m ,则m/n 等于 ( )A .21B .61C .125D .438.如图,甲、乙两动点分别从正方形ABCD 的顶点,A 、C 同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行,若乙的速度是甲的速度的4倍,则它们第2000次相遇在边 ( )A .AB 上 B .BC 上 C .CD 上 D .DA 上9.已知2+x a 与2-x b 和等于442-x x ,则a = ,b =10.如图,AD 是△ABC 的中线,E 是AD 上的一点,且AE=31AD ,CE 交AB 于点F 。
省重点高中高一新生提前招生考试数学试卷及答案(共5份)

18.解:按颜色把 8 个扇形分为红 1、绿 1、黄 1、红 2、绿 2、黄 2、绿 3、黄
3,所有可能结果的总数为 8。
( 1)指针指向红色可能结果为
21
2,∴ P(指针指向红色) =
。
84
( 2)指针指向黄色或绿色可能结果为
6,∴ P(指针指向黄色或绿色)
63
=
。
84
a2 4
1
a2a2 a3
19.解:
2
3 m2
=
4
x1
x 2 ቤተ መጻሕፍቲ ባይዱ即
9 m 4 = 3 m 2。解之得
16
4
此时
3m2 4
2
32 3
43
1 。 点 C 的坐标为
OC 1。
m 2 3。 3
0, 1 。
又 x2
2
x1
2
x1 x2
4 x1 x2
2
m4
3 m2 4
4 m 2,
m > 0 , x 2 x1
2m 4 3 ,即 AB 3
4 3。 3
1
∴ ∠PDF= ∠ DFA= ∠ DFP。∴ PD=PF。
∴ PA=PF。即 P 是线段 AF 的中点。
( 3)∵∠ DAF= ∠DBA ,∠ ADB= ∠ FDA ,∴△ FDA ∽△ ADB 。
AD AF
∴
。
DB AB
15
AD AF ∴在△ ADB 中, tan ABD
2
3 。
DB AB 10 4
D. 12 3
10.二次函教 y x2 2x 5 有
A .最大值 5 B.最小值 5 C.最大值 6 D .最小值 6
重点高中提前招生数学练习卷(有答案)

重点高中提前招生数学练习卷班级 姓名 成绩一、选择题(每小题4分,共32分)1.若0<x <1,则x -1,x ,x 2的大小关系是( C )A .x -1<x <x 2B . x <x 2<x -1C .x 2<x <x -1D .x 2<x -1<x 【解析】用特殊值法,例如,取x =12.2.匀速行驶的城际列车,若将速度提高25%,则相同距离的 行车时间可节省k %,那么k 的值是( D )A .35B .30C .25D .20【解析】设距离为s ,原速为v ,则(s v -s 1.25v )÷sv =20%,∴k =20.3.如图,将△ADE 绕正方形ABCD 的顶点A 顺时针旋转90°, 得△ABF ,连接EF 交AB 于H ,则下列结论错误的是( C )A .AE ⊥AFB .EF ∶AF =2∶1C .AF 2=FH •FED .FB ∶FC =HB ∶EC4.用0,l ,2,3,4,5,6,7,8这九个数字组成若干个一位数或两位数(每个数字都只用一次),然后把所得的数相加,它们的和不可能是( C ) A. 36 B. 117 C. 115 D. 153【解析】由于a +b +c +d +e +f +g +h +i =36,当组成的数中含有两位数时(如a 为十位数字),它们的和为10a +b +c +d +e +f +g +h +i =9a +(a +b +c +d +e +f +g +h +i) =36+9a 为9的倍数.同理,当多个数为十位数字时(如a ,b ,c 为十位数字),它们的和为10a +10b +10c +d +e +f +g +h +i =9a +9b +9c +(a +b +c +d +e +f +g +h +i)=36+9a +9b +9c 仍为9的倍数. ∵115不是9的倍数,∴C 答案不可能.5.如图,四边形ABMN ,BCPQ 是两个全等的矩形(AB ≤BC ),点R 在线段AC 上移动,则满足∠NRP =90°的点R 有( C )A. 1个B. 2个C. 1个或2个D. 无数多个 【解析】设AB =a ,BC =b ,AR =x. ∵∠A =∠C =∠NRP =90°,∴△ANR ∽△CRP , ∴AN RC =AR CP ,即b a +b -x =x a ,∴x 2-(a +b)x +ab =0, 解得x 1=a ,x 2=b. ∴当a <b 时点R 有2个,当a =b 时点R 有1个,故选C.6. 实数a ,b ,c 满足a +b +c =0,且abc >0,则1a +1b +1c的值是( B )A. 正数B. 负数C. 零D. 不能确定【解析】将等式a +b +c =0两边平方,得a 2+b 2+c 2+2ab +2bc +2ca =0, ∴ab +bc +ca =-12(a 2+b 2+c 2)<0. ∵abc >0,∴1a +1b +1c =ab +bc +caabc<0.7.在△ABC 中,点D ,E 分别在AB ,AC 上,CD 与BE 相交于点F ,已知△BDF 的面积为10,△BCF 的面积为20,△CEF 的面积为16,则四边形ADFE 的面积等于( D ) A .22 B .24 C .36 D .44 【解析】如图,由题意得x y +16=1020,y x +10=1620, ∴⎩⎨⎧2x =y +16,5y =4x +40,解得⎩⎨⎧x =20,y =24.∴四边形ADFE 的面积为44.8.某医院内科病房有护士15人,每2人一班,轮流值班,每8小时换班一次,某两人同值一班后,到下次两人再同班,最长需要( B )A .30天B .35天C .56天D .448天 【解析】15人每2人一班,轮流值班,有15×142=105种排法.每8小时换班一次,一天须排3班,某两人同值一班后,到下次两人再同班,最长需要105÷3=35(天). 二、填空题(每小题5分,共40分)9.已知∠A 为锐角,且4sin 2A -4sin A cos A +cos 2A =0,则tan A = . 【答案】12【解析】由题意得(2sin A -cos A )2=0,∴2sin A -cos A =0,∴sinA cosA =12. ∴tan A =sinA cosA =12.10.在某海防观测站的正东方向12海里处有A ,B 两艘船相遇,然后A 船以每小时12海里的速度往南航行,B 船以每小时3海 里的速度向北漂移.则经过 小时后,观测站及A ,B 两 船恰成一个直角三角形. 【答案】211.一个样本为l ,3,2,2,a ,b ,c .已知这个样本唯一的众数 为3,平均数为2,则这个样本的方差为 . 【答案】87【解析】这个样本为l ,3,2,2,3,3,0.∴方差为87.12.如图,直角坐标系中,沿着两条坐标轴摆着三个相同的长方 形,其长、宽分别为4,2,则通过A ,B ,C 三点的拋物线对应的 函数关系式是 . 【答案】y =-512x 2-12x +20313. 在一个木制的棱长为3的正方体的表面涂上颜色,将它的棱三等分,然后从等分点把正方体锯开,得到27个棱长为l 的小正方体,将这些小正方体充分混合后,装入口袋,从这个口袋中任意取出一个小正方体,则这个小正方体的表面恰好涂有两面颜色的概率是 . 【答案】4914. 如图,在边长为2的正方形ABCD 的四边上分别取点E ,F ,G ,H ,当四边形EFGH 各边的平方和EF 2+FG 2+GH 2+HE 2取得最小值时,四边形EFGH 的面积为 . 【答案】2【解析】设AE =a ,BF =b ,CG =c ,DH =d ,∴EF 2+FG 2+GH 2+HE 2=(2-a)2+b 2+(2-b)2+c 2+(2-c)2+d 2+(2-d)2+a 2 =2a 2+2b 2+2c 2+2d 2-4a -4b -4c -4d +16 =2[(a -1)2+(b -1)2+(c -1)2+(d -1)2+4] 当a =b =c =d =1时,四边形EFGH 恰好是 正方形ABCD 的中点四边形, ∴四边形EFGH 的面积为2.15.点P ,Q 从点A (2,0)同时出发,沿正方形BCDE 的边匀速运动,点P 以每秒1个单位的速度按逆时针方向运动,点Q 以每秒2个单位的速度按顺时针方向运动,则P ,Q 两点第11次相遇时的坐标是 . 【答案】(-43,-2)【解析】∵P ,Q 第一次相遇时,点P 所走的路程为周长的13,∴第3次相遇时点P 回到A 处.以此类推,第6次、第9次相遇时点P 均在A 处. 第11次相遇时,点P 从A 处出发,走了周长的23,其坐标为(-43,-2).16. 已知2,a ,b 分别为三角形三边,且a ,b 为方程(3x 2-4x -1)(3x 2-4x -5)=12的根,则三角形周长为 .【答案】163,203【解析】解方程(3x 2-4x -1)(3x 2-4x -5)=12,设3x 2-4x =y ,则(y -1)(y -5)=12, 解得y =-1或y =7.当y =-1时,3x 2-4x +1=0,解得x 1=1,x 2=13,当y =7时,3x 2-4x -7=0,解得x 3=-1,x 4=73.其中能与2组成三角形只有2种:(2,1,73),(2,73,73),∴周长为163或203.三、解答题(共58分)17.(10分)已知a =12+3, 求1-2a +a 2a -1-a 2-2a +1a 2-a 的值.【解】由已知得a =2- 3.原式=(1-a)2a -1-(a -1)2a(a -1). a =2-3<1,∴(a -1)2=1-a.∴原式=a -1+1a=2-3-1+2+3=3.18.(10分)在凸四边形ABCD 中,∠A -∠B =∠B -∠C =∠C -∠D >0,且四个内角中有一个角为84°,求其余各角的度数.【解】设∠A -∠B =∠B -∠C =∠C -∠D =x , 则∠C =∠D +x ,∠B =∠D +2x ,A =∠D +3x ,∵∠A +∠B +∠C +∠D =6x +4∠D =360°,∴∠D +32x =90°.若∠D =84°,则x =4°,∴∠A =96°,∠B =92°,∠C =88°; 若∠C =84°,则2x +4∠C =360°,x =12°,∴∠A =108°,∠B =96°,∠D =72°. 若∠B =84°,则-2x +4∠B =360°,x =-12°(舍去). 若∠A =84°,则-6x +4∠A =360°,x =-4(舍去).. ∴各角的度数为∠A =96°,∠B =92°,∠C =88°,∠D =84°;或∠A =108°,∠B =96°,∠C =84°,∠D =72°.19.(12当比赛进行到12 (1)试判断甲队胜、平、负各几场?(2)若每一场每名参赛队员均得出场费500元,设甲队中一位参赛队员所得的奖金与出场费的和为W (元),试求W 的最大值.【解】(1)设甲队胜x 场,平y 场,负z 场,则⎩⎨⎧x +y +z =12,3x +y =19,∴⎩⎨⎧y =19-3x ,z =2x -7,依题意知x≥0,y≥0,z≥0,且x ,y ,z 均为整数,∴⎩⎪⎨⎪⎧x ≥019-3x ≥0,2x -7≥0,∴解得72≤x ≤193,∴甲队胜、平、负的场数有三种情况:当x =4时,y =7,z =1; 当x =5时,y =4,z =3; 当x =6时,y =1,z =5.(2)∵W =(1500+500)x +(700+500)y +500z =-600x +19300. 当x =4时,W 最大值=-600×4+19300=16900(元) ∴W 的最大值为16900元.20.(12分)对于平面直角坐标系 xOy 中的点P (a ,b ),若点P'的坐标为(a +bk ,ka +b )(k 为常数,k ≠0),则称点P'为点P 的“k 属派生点”.例如:P (1,4)的“2属派生点”为P'(1+42,2×1+4),即P'(3,6).(1)①点P (-1,-2)的“2属派生点”P'的坐标为___________. ②若点P 的“k 属派生点”为P'(3,3),请写出一个符合条件的点P 的坐标____________. (2)若点P 在x 轴的正半轴上,点P 的“k 属派生点”为P'点,且△OPP'为等腰直角三角形,则k 的值为 .(3)如图, 点Q 的坐标为(0,43),点A 在函数y =-43x(x <0)的图象上,且点A 是点B 的“-3属派生点”,当线段BQ 最短时,求B 点坐标. 【解】(1)①(-2,-4);②答案不唯一,只需横、纵坐标之和为3即可,如(1,2).(2)±1. (3)设B (a ,b ),则A (a -b3,-3a +b ). ∵点A 在反比例函数y =-43x的图象上, ∴(a -b3)(-3a +b)=-4 3.∴(3a -b)2=12.∴b =3a -23或b =3a +2 3.∴B 在直线y =3x -23或y =3x +23上.过Q 作y =3x +23的垂线Q B 1,垂足为B 1,求得B 1(32,723). ∵点Q 到直线y =3x -23的距离大于Q B 1,∴B 1即为所求的B 点,∴B (32,723).21.(14分)已知:矩形ABCD (字母顺序如图)的边长AB =3,AD =2,将此矩形放在平面直角坐标系xOy 中,使AB 在x 轴的正半轴上,矩形的其它两个顶点在第一象限,且直线y =32x -1经过这两个顶点中的一个. (1)求矩形的各顶点的坐标.(2)以AB 为直径作⊙M ,经过A ,B 两点的抛物线y =ax 2+bx +c 的顶点是P 点. ①若点P 位于⊙M 外,且在矩形ABCD 内部,求a 的取值范围.②过点C 作⊙M 的切线交AD 于F 点,当PF ∥AB 时,试判断抛物线与y 轴的交点Q 是位于直线y =32x -1的上方?还是下方?还是正好落在此直线上?并说明理由.【解】(1)设A (m ,0)(m >0),则有B (m +3,0);C (m +3,2),D (m ,2); 若C 点过直线y =32x -1;则2=32( m +3)-1,解得m =-1(舍去);若点D 过直线y =32x -1,则2=32m -1,m =2(符合题意).∴A (2,0),B (5,0),C (5,2),D (2,2). (2)①∵⊙M 以AB 为直径,∴M (72,0),设抛物线y =a(x -2)( x -5)=ax 2-7ax +10a , ∴抛物线顶点P (72,-94a ).∵顶点同时在⊙M 内和在矩形ABCD 内部, ∴32<-94a <2,∴-89<a <-23. ②设切线CF 与⊙M 相切于Q ,交AD 于F (如图所示). 设AF =n ,由切线长定理得FQ =AF =n ,∴CF =n +2.由勾股定理得DF 2+DC 2=CF 2,∴32+(2-n)2=( n +2)2,解得n =98,∴F (2,98).当PF ∥AB 时,P 点纵坐标为98,∴-94a =98,∴a =-12.∴抛物线的解析式为y =-12x 2+72x -5,与y 轴的交点为Q (0,-5).∵直线y =32x -1与y 轴交点(0,-1),∴Q 在直线y =32x -1下方.。
各地重点高中提前招生试题精选(一)(附答案详解)

各地重点高中提前招生数学试题精选(一)一.选择题(共6小题)1.(2016•黄冈校级自主招生)设实数a,b,c满足a+b+c=3,a2+b2+c2=4,则++=()A.0 B.3 C.6 D.92.(2017•江阴市自主招生)已知三个关于x的一元二次方程ax2+bx+c=0,bx2+cx+a=0,cx2+ax+b=0恰有一个公共实数根,则的值为()A.0 B.1 C.2 D.33.(2017•雨城区校级自主招生)若关于x的方程﹣=﹣1无解,则m 的值是()A.m=B.m=3 C.m=或1 D.m=或34.(2014•武侯区校级自主招生)若实数abc满足a2+b2+c2=9,代数式(a﹣b)2+(b﹣c)2+(c﹣a)2的最大值是()A.27 B.18 C.15 D.125.(2017•诸暨市校级自主招生)如图,直线y=x+m交双曲线y=于A、B两点,交x轴于点C,交y轴于点D,过点A作AH⊥x轴于点H,连结BH,若OH:HC=1:5,S=1,则k的值为()△ABHA.1 B.C.D.第5题第6题6.(2017•奉化市自主招生)如图,已知动点P在函数y=(x>0)的图象上运动,PM⊥x轴于点M,PN⊥y轴于点N,线段PM、PN分别与直线AB:y=﹣x+1交于点E,F,则AF•BE的值为()A.4 B.2 C.1 D.二.填空题(共6小题)7.(2016•黄冈校级自主招生)若a4+b4=a2﹣2a2b2+b2+6,则a2+b2=.8.(2013•清浦区校级自主招生)当﹣4≤x≤1时,不等式始终成立,则满足条件的最小整数m=.9.(2016•湖北校级自主招生)已知抛物线y=ax2+bx+c与双曲线y=有三个交点A(﹣3,m),B(﹣1,n),C(2,p),则不等式ax3+bx2+cx﹣k2>0的解集为.10.(2016•黄冈校级自主招生)已知y=x2+mx﹣6,当1≤m≤3时,y<0恒成立,那么实数x的取值范围是.11.(2017•镜湖区校级自主招生)如图,在矩形ABCD中,E是BC边上的点,且CE=2BE,△DEF的面积等于2,则此矩形的面积等于.第11题第12题12.(2017•奉化市自主招生)在Rt△ABC中,∠ACB=90°,在斜边AB上分别截取AD=AC,BE=BC,DE=6,点O是△CDE的外心,如图所示,则点O到△ABC的三边的距离之和是.三.解答题(共5小题)13.(2017•启东市校级自主招生)已知:关于x的方程①x2﹣(m+2)x+m﹣2=0有两个符号不同的实数根x1,x2,且x1>|x2|>0;关于x的方程②mx2+(n﹣2)x+m2﹣3=0有两个有理数根且两根之积等于2.求整数n的值.14.(2017•镜湖区校级自主招生)方程x2﹣kx+k﹣2=0有两个实数根x1,x2,且0<x1<1,2<x2<3,求k的取值范围.15.(2017•余姚市校级自主招生)已知:实数x满足﹣≥x﹣,并且关于x的函数y=2|x﹣a|+a2的最小值为4,求常数a的值.16.(2017•江阴市自主招生)如图,在直角坐标系中,一次函数y=x+3的图象与x轴、y轴分别交于A、B,平行四边形ABCD中,D(6,0),函数y=x+m图象过点E(4,0),与y轴交于G,动点P从O点沿y轴正方向以每秒2个单位的速度出发,同时,以P为圆心的圆,半径从6个单位起以每秒1个单位的速度缩小,设运动时间为t.(1)若⊙P与直线EG相切,求⊙P的面积;(2)以CD为边作等边三角形CDQ,若⊙P内存在Q点,求t的取值范围.17.(2012•怀化校级自主招生)如图,已知锐角△ABC及其外接圆⊙O,AM是BC边的中线.分别过点B,C作⊙O的切线,两条切线相交于点X,连接AX.求证:.各地重点高中提前招生数学试题精选(一)答案与解析一.选择题(共6小题)1.(2016•黄冈校级自主招生)设实数a,b,c满足a+b+c=3,a2+b2+c2=4,则++=()A.0 B.3 C.6 D.9【解析】由a2+b2+c2=4,得到a2+b2=4﹣c2,b2+c2=4﹣a2,a2+c2=4﹣b2,且a+b+c=3,代入得:原式=++=2﹣c+2﹣a+2﹣b=6﹣(a+b+c)=6﹣3=3,故选:B.2.(2017•江阴市自主招生)已知三个关于x的一元二次方程ax2+bx+c=0,bx2+cx+a=0,cx2+ax+b=0恰有一个公共实数根,则的值为()A.0 B.1 C.2 D.3【解析】x0是它们的一个公共实数根,则ax02+bx0+c=0,bx02+cx0+a=0,cx02+ax0+b=0.把上面三个式子相加,并整理得(a+b+c)(x02+x0+1)=0.因为,所以a+b+c=0.于是=故选:D.3.(2017•雨城区校级自主招生)若关于x的方程﹣=﹣1无解,则m 的值是()A.m=B.m=3 C.m=或1 D.m=或3【解析】去分母得:3﹣2x+mx﹣2=﹣x+3,整理得:(m﹣1)x=2,当m﹣1=0,即m=1时,方程无解;当m﹣1≠0时,x﹣3=0,即x=3时,方程无解,此时=3,即m=,故选:C.4.(2014•武侯区校级自主招生)若实数abc满足a2+b2+c2=9,代数式(a﹣b)2+(b﹣c)2+(c﹣a)2的最大值是()A.27 B.18 C.15 D.12【解析】∵a2+b2+c2=(a+b+c)2﹣2ab﹣2ac﹣2bc,∴﹣2ab﹣2ac﹣2bc=a2+b2+c2﹣(a+b+c)2①∵(a﹣b)2+(b﹣c)2+(c﹣a)2=2a2+2b2+2c2﹣2ab﹣2ac﹣2bc;又(a﹣b)2+(b﹣c)2+(c﹣a)2=3a2+3b2+3c2﹣(a+b+c)2=3(a2+b2+c2)﹣(a+b+c)2②①代入②,得3(a2+b2+c2)﹣(a+b+c)2=3×9﹣(a+b+c)2=27﹣(a+b+c)2,∵(a+b+c)2≥0,∴其值最小为0,故原式最大值为27.故选:A.5.(2017•诸暨市校级自主招生)如图,直线y=x+m交双曲线y=于A、B两点,交x轴于点C,交y轴于点D,过点A作AH⊥x轴于点H,连结BH,若OH:HC=1:5,S=1,则k的值为()△ABHA.1 B.C.D.【解析】设OH=a,则HC=5a,∴C(6a,0)代入y=﹣x+m,得m=3a,设A点坐标为(a,n)代入y=﹣x+m,得n=﹣a+3a=a,∴A(a,a),代入y=得,∴k=a2,∴y=,解方程组,可得:,,∴A点坐标为(a,a),B点坐标为(5a,a),∴AH=a,=×a×(5a﹣a)=5a2,∴S△ABH=1,∵S△ABH∴5a2=1,即a2=,∴k=×=.故选:B.6.(2017•奉化市自主招生)如图,已知动点P在函数y=(x>0)的图象上运动,PM⊥x轴于点M,PN⊥y轴于点N,线段PM、PN分别与直线AB:y=﹣x+1交于点E,F,则AF•BE的值为()A.4 B.2 C.1 D.【解析】作FG⊥x轴,∵P的坐标为(a,),且PN⊥OB,PM⊥OA,∴N的坐标为(0,),M点的坐标为(a,0),∴BN=1﹣,在直角三角形BNF中,∠NBF=45°(OB=OA=1,三角形OAB是等腰直角三角形),∴NF=BN=1﹣,∴F点的坐标为(1﹣,),同理可得出E点的坐标为(a,1﹣a),∴AF2=(1﹣1+)2+()2=,BE2=(a)2+(﹣a)2=2a2,∴AF2•BE2=•2a2=1,即AF•BE=1.故选:C.二.填空题(共6小题)7.(2016•黄冈校级自主招生)若a4+b4=a2﹣2a2b2+b2+6,则a2+b2=3.【解析】有a4+b4=a2﹣2a2b2+b2+6,变形后(a2+b2)2﹣(a2+b2)﹣6=0,(a2+b2﹣3)(a2+b2+2)=0,又a2+b2≥0,即a2+b2=3,故答案为3.8.(2013•清浦区校级自主招生)当﹣4≤x≤1时,不等式始终成立,则满足条件的最小整数m=4.【解析】∵﹣4≤x≤1,∴4+x≥0,1﹣x≥0,∴不等式两边平方得:m2>5+2∵当x=﹣1.5时,最大为2.5,∴m2>10∴满足条件的最小的整数为4.故答案为4.9.(2016•湖北校级自主招生)已知抛物线y=ax2+bx+c与双曲线y=有三个交点A(﹣3,m),B(﹣1,n),C(2,p),则不等式ax3+bx2+cx﹣k2>0的解集为﹣3<x<﹣1或x>2.【解析】∴抛物线y=ax2+bx+c与双曲线y=有三个交点A(﹣3,m),B(﹣1,n),C(2,p),∴xy1=ax3+bx2+cx,xy2=k2,∴xy1﹣xy2=ax3+bx2+cx﹣k2,∴不等式ax3+bx2+cx﹣k2>0的解集为:﹣3<x<﹣1或x>2,故答案为:﹣3<x<﹣1或x>2.10.(2016•黄冈校级自主招生)已知y=x2+mx﹣6,当1≤m≤3时,y<0恒成立,那么实数x的取值范围是﹣3<x<.【解析】∵1≤m≤3,y<0,∴当m=3时,x2+3x﹣6<0,由y=x2+3x﹣6<0,得<x<;当m=1时,x2+x﹣6<0,由y=x2+x﹣6<0,得﹣3<x<2.∴实数x的取值范围为:﹣3<x<.故本题答案为:﹣3<x<.11.(2017•镜湖区校级自主招生)如图,在矩形ABCD中,E是BC边上的点,且CE=2BE,△DEF的面积等于2,则此矩形的面积等于16.【解析】∵四边形ABCD是矩形,∴AD∥BC,AD=BC,∴△AFD∽△EFB,∴AD:BE=DF:BF,∵CE=2BE,∴DF:BF=3:1,=2,∵S△DEF=,∴S△BEF=2+=∴S△BED=∴S△DEC∴S △DBC =S △DEB +S △DEC ==8,∴S 矩形fBCD =2S △DBC =16. 故答案为:16. 12.(2017•奉化市自主招生)在Rt △ABC 中,∠ACB=90°,在斜边AB 上分别截取AD=AC ,BE=BC ,DE=6, 点O 是△CDE 的外心,如图所示,则点O 到△ABC 的三边的距离之和是 9 .【解析】由题意点O 是EC 、CD 垂直平分线的交点, ∵AD=AC ,BE=BC ,∴EC 的垂直平分线经过B 且平分∠B ,CD 的垂直平分线经过A 且平分∠A , ∴O 是△ABC 的内心,则r=(AC +BC ﹣AB )=(AD +BE ﹣AB )=DE=3,∴点O 到△ABC 的三边的距离之和是3r=9, 故答案为9.三.解答题(共5小题) 13.(2017•启东市校级自主招生)已知:关于x 的方程①x 2﹣(m +2)x +m ﹣2=0有两个符号不同的实数根x 1,x 2,且x 1>|x 2|>0;关于x 的方程②mx 2+(n ﹣2)x +m 2﹣3=0有两个有理数根且两根之积等于2.求整数n 的值. 【解析】由方程①知: ∵x 1•x 2<0,x 1>|x 2|>0, ∴x 1>0,x 2<0,∵△=(m ﹣2)2+8>0,∴x 1+x 2=m +2>0,x 1•x 2=m ﹣2<0, ∴﹣2<m <2, 由方程②知:,∴m 2﹣2m ﹣3=0, ∴m=3(舍去),m=﹣1(2分) 代入②得:x 2﹣(n ﹣2)x +2=0, ∵方程的两根为有理数, ∴△=(n ﹣2)2﹣8=k 2, ∴(n ﹣2)2﹣k 2=8,(n ﹣2+k )(n ﹣2﹣k )=8, ∵n ﹣2+k 和n ﹣2﹣k 奇偶性相同, ∴或或或,解得n=5或n=﹣1.14.(2017•镜湖区校级自主招生)方程x2﹣kx+k﹣2=0有两个实数根x1,x2,且0<x1<1,2<x2<3,求k的取值范围.【解析】∵方程x2﹣kx+k﹣2=0有两个实数根x1,x2,且0<x1<1,2<x2<3,∴二次函数y=x2﹣kx+k﹣2如图所示,∴x=0,y=k﹣2>0;x=1,y=1﹣k+k﹣2<0;x=2,y=4﹣2k+k﹣2<0;x=3,y=9﹣3k+k﹣2>0,而△=k2﹣4(k﹣2)=(k﹣2)2+4>0,∴2<k<3.5,即k的取值范围为2<k<3.5.15.(2017•余姚市校级自主招生)已知:实数x满足﹣≥x﹣,并且关于x的函数y=2|x﹣a|+a2的最小值为4,求常数a的值.【解析】﹣≥x﹣,解得:x≥1,当x=a时,y=a2=4,最小解得:a=±2,∵x≥1,∴a=2,当x>a时,y=2x+a2﹣2a,∴当x=1时,y最小=2+a2﹣2a=4,解得:a==1±,∵x≥1,∴a<1,∴a=1﹣,∴x<a时,y=﹣2(x﹣a)+a2=﹣2x+a2+2a无最小值,综上所述:a=2或a=1﹣时,y=2|x﹣a|+a2的最小值为4.16.(2017•江阴市自主招生)如图,在直角坐标系中,一次函数y=x+3的图象与x轴、y轴分别交于A、B,平行四边形ABCD中,D(6,0),函数y=x+m图象过点E(4,0),与y轴交于G,动点P从O点沿y轴正方向以每秒2个单位的速度出发,同时,以P为圆心的圆,半径从6个单位起以每秒1个单位的速度缩小,设运动时间为t.(1)若⊙P与直线EG相切,求⊙P的面积;(2)以CD为边作等边三角形CDQ,若⊙P内存在Q点,求t的取值范围.【解析】(1)函数y=x+m图象过点E(4,0),∴m=﹣3,G(0,﹣3),⊙P与直线EG相切,作PH⊥EG于H,如图1,则PH=6﹣t,P(0,2t),由Rt△PHG∽Rt△EOG可得:=,即=,解得t=,所以⊙P半径为6﹣=,⊙P面积为:π•()2=π;(2)如图2,由y=x+3图象与x轴、y轴分别交于A、B,∴A(﹣3,0),B(0,3),C(9,3),∵tanA==,∴∠A=60°.以CD为边作等边三角形CDQ,∠D=∠A=60°,CD=AB=6,∴Q1(3,3),Q2(12,0),显然Q2(12,0)不可能在⊙P内,若Q1(3,3)在⊙P内,则可得:PQ1<r(半径),∵P(0,2t),r=6﹣t,即:9+(2t﹣3)2<(6﹣t)2,t2﹣(4﹣4)t<0,∵t>0,∴t﹣(4﹣4)<0即t<4(﹣1),∴t的取值范围为0<t<4(﹣1).17.(2012•怀化校级自主招生)如图,已知锐角△ABC及其外接圆⊙O,AM是BC边的中线.分别过点B,C作⊙O的切线,两条切线相交于点X,连接AX.求证:.【解析】证明:设AX与⊙O相交于点A1,连接OB,OC,OA1.又M为BC 的中点,所以,连接OX,它过点M.∵OB⊥BX,OX⊥BC,∴XB2=XM•XO.①又由切割线定理得XB2=XA1•XA.②由①,②得,∴△XMA∽△XA1O,∴.又∵∠BOC=2∠BAC,∴∠BOX=∠BAC,∴.。
2023年全国重点高中提前招生数学考试全真试卷1

重点高中招生试卷1一、选择题(每小题5分,共30分) 1.设3232-++=a ,则aa 1+的整数部分为( ) A.2 B.3 C.4 D.52.如图,在边长为1的正方形ABCD 中,E 、F 分别为线段AB 、AD 上的动点,若EF 为折线翻折,A 点落在正方形ABCD 所在A '点的位置,那么A '所有可能位置形成的区域面积为( )A.21B.4πC.12-D.12-π 3.正整数构成的数列 ,,,,21n a a a ,满足:①数列递增,即<<<<n a a a 21;②21--+=n n n a a a (3≥n ),则称为“类斐波拉契数列”.例如: ,29,18,11,7,4,3,则满足595=a 的“类斐波拉契数列”有( )A.1种B.2种C.3种D.4种 4.如图,已知梯形ABCO 的底边AO 在x 轴上,BC//AO ,AB ⊥AO ,过点C 的双曲线x ky =交OB 于D ,且OD:DB=1:2,若△OBC 的面积等于3,则k 的值为( )A.2B.43C.524D.无法确定 5.如图,在等边△ABC 中,M ,N 分别是边AB ,AC 的中点,D 为MN 上任意一点,BD ,CD 的延长线分别交AC ,AB 于点E ,F.若3111=+BF CE ,则△ABC 的边长为( )A.12B.9C.6D.36.如图,已知抛物线12+-=x y 的顶点为P ,点A 是第一象限内该二次函数图像上一点,过点A 作x 轴的平行线交二次函数图像于点B ,分别过点B 、A 作x 轴的垂线,垂足分别为C 、D ,连接PA 、PD ,PD 交AB 于点E ,则△PAD 与△PEA( )A.始终不相似 B 始终相似 C.只有AB=AD 时相似 D.无法确定二、填空题(每小题5分,共30分)7.关于x ,y 的方程组⎪⎩⎪⎨⎧==+-1x y y x yx y x 的解是________ 8.已知2)2(2013)2(3-=-+-x x ,2)2(2013)2(3=-+-y y ,则y x +=_______9.若关于x 的方程0)6)(4(2=+--m x x x 的三个根恰好可以组成某直角三角形的三边长,则m=___________10.如图,矩形ABCD 中,AB=10,BC=12,M 为AB 中点,N 为BC 边上一动点,将△MNB 沿MN 折叠,得到'MNB ∆,则'CB 的最小值为 11.在平面四边形ABCD 中,∠A=∠B=∠C=75°,BC=2,则AD 的取值范围是__________12.如图,△ABC 中,,8,53sin ,90==︒=∠AC A ACB 将△ABC 绕点C 顺时针旋转90°,得到C B A ''∆,P 为线段''B A 上的动点,以点P 为圆心,'PA 长为半径作⊙P ,当⊙P 与△ABC 的边相切时,⊙P 的半径为三、解答题(每小题12分,共60分)13.已知1x ,2x 是方程02)12(22=+++-k x k x 的两个实数根,试求2221)2()2(-+-x x 的最小值14.如图,在平面直角坐标系中已知四边形ABCD 为菱形,且A(0,3),B(-4,0)(1)求过点C 的反比例函数表达式;(2)设直线l 与(1)中所求函数图象相切,且与x 轴,y 轴的交点分别为M ,N ,O 为坐标原点. 求证:△OMN 的面积为定值.15.如图,在边长为1的正方形ABCD 中,以点A 为圆心,AB 为半径作圆,E 是BC 边上的一个动点(不运动至B ,C),过点E 作弧BD 的切线EF ,交CD 于F ,H 是切点,过点E 作EG ⊥EF ,交AB 于点G ,连接AE. (1)求证:△AGE 是等腰三角形;(2)设BE=x ,△BGE 与△CEF 的面积比y S S CEF BGE =∆∆,求y 关于x 的函数关系式,并写出自变量x 的取值范围; (3)在BC 边上(点B ,C 除外)是否存在一点E ,使得GE=EF ,若存在,求出此时BE 的长,若不存在,请说明理由.16.如图1是实验室中的一种摆动装置,BC 在地面上,支架ABC 是底边为BC 的等腰直角三角形,BC=10,摆动臂AD 可绕点A 旋转,AD=2 (1)在旋转过程中,①当A ,D ,B 三点同一直线上的,求BD 的长; ②当A ,D ,B 三点为同一直角三角形的顶点时,求BD 的长;(2)若摆动臂AD 顺时针旋转90°,点D 的位置由△ABC 外的点1D 转到其内的点2D 处,如图2,此时C AD 1∠=135°,2CD =1,求2BD (3)如图3,若连接(2)中的21D D ,将(2)中21D AD ∆的形状和大小保持不变,把21D AD ∆绕点A 在平面内自由旋转,分别取21D D ,2CD ,BC 的中点M ,P ,N ,连接MP ,PN ,NM ,M 随着21D AD ∆绕点A 在平面内自由旋转,△MPN 的面积是否发生变化,若不变,请直接写出△MPN 的面积;若变化,△MPN 的面积是否存在最大与最小?若存在,请直接写出△MPN 面积的最大与最小值.17.如图,已知抛物线c bx x y 222++=(bc 是常数,且c<0)与x 轴分别交于点AB(点A 位于点B 的左侧),与y 轴的负半轴交于点C ,点A 的坐标为)0,1(-.(1)点B 的坐标为(结果用含c 的代数式表示); (2)连接BC ,过点A 作直线AE//BC ,与抛物线c bx x y 222++=交于点E ,点D 是x 轴上的一点,其坐标为(2,0). 当C ,D ,E 三点在同一直线上时,求抛物线的解析式;(3)在(2)条件下,点P 是x 轴下方的抛物线上的一个动点,连接PB ,PC ,设所得△PBC 的面积为S. ①求S 的取值范围;②若∆PBC 的面积S 为整数,则这样的∆PBC 共有____个。
中考提前招生数学试卷

一、选择题(每题4分,共40分)1. 下列各数中,有理数是()A. √9B. πC. √-4D. 2/32. 如果a=3,b=-2,那么a-b的值是()A. 1B. -1C. 5D. -53. 下列方程中,无解的是()A. 2x + 5 = 0B. 3x - 6 = 0C. 5x - 15 = 0D. x^2 - 1 = 04. 在等腰三角形ABC中,AB=AC,若∠B=40°,则∠C的度数是()A. 40°B. 50°C. 60°D. 70°5. 下列函数中,y与x成反比例关系的是()A. y = 2x + 3B. y = 3/xC. y = 3x^2D. y = x^36. 若a、b、c是等差数列,且a+b+c=12,a+c=8,则b的值为()A. 2B. 4C. 6D. 87. 在平面直角坐标系中,点P(2,3)关于原点的对称点是()A. (2,3)B. (-2,-3)C. (2,-3)D. (-2,3)8. 下列图形中,不是轴对称图形的是()A. 正方形B. 等边三角形C. 长方形D. 梯形9. 若等比数列的首项为2,公比为3,则该数列的前5项和为()A. 124B. 153C. 189D. 24310. 下列命题中,正确的是()A. 平行四边形一定是矩形B. 相似三角形一定是全等三角形C. 对角线相等的四边形一定是菱形D. 对角线互相平分的四边形一定是平行四边形二、填空题(每题4分,共40分)11. 若a=5,b=-3,则a^2 + b^2 = ________。
12. 等差数列的前三项分别为3,5,7,则第10项是 ________。
13. 若二次函数y=ax^2+bx+c的图象开口向上,且顶点坐标为(-1,2),则a________(填“>0”或“<0”)。
14. 在平面直角坐标系中,点A(1,2),点B(-3,4),则线段AB的中点坐标是________。
重点高中提前招生数学模拟试卷.docx
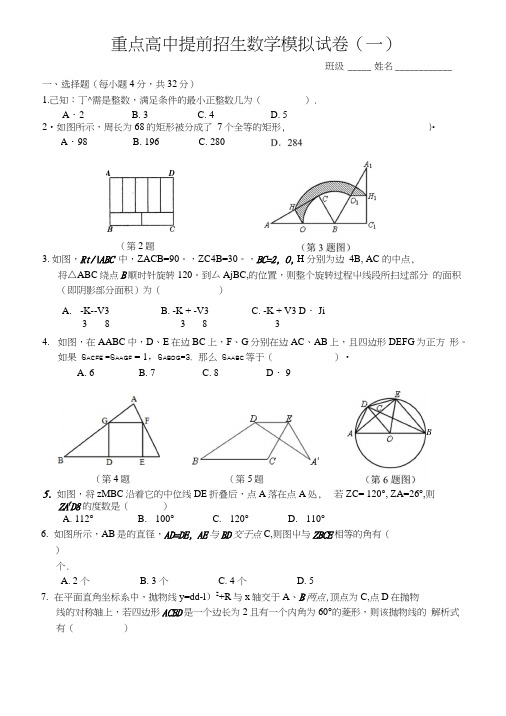
重点高中提前招生数学模拟试卷(一)班级 _____ 姓名 ____________一、选择题(每小题4分,共32分)1.己知:丁^需是整数,满足条件的最小正整数几为().2•如图所示,周长为68的矩形被分成了 7个全等的矩形,3. 如图,Rt/\ABC 中,ZACB=90。
,ZC4B=30。
,BC=2, O, H 分别为边 4B, AC 的中点,将△ABC 绕点B 顺时针旋转120。
到厶AjBC,的位置,则整个旋转过程屮线段所扫过部分 的面积(即阴影部分面积)为()A. -K--V3B. -K + -V3C. -K + V3 D ・ Ji3 8 3 8 34. 如图,在AABC 中,D 、E 在边BC 上,F 、G 分别在边AC 、AB 上,且四边形DEFG 为正方 形。
如果 S ACFE =S AAGF = 1,S ABDG =3,那么 S AABC 等于()•A. 6B. 7C. 8 D ・ 9ZA fD8的度数是( ) 6. 如图所示,AB 是的直径,AD=DE, AE 与BD 交于点C,则图屮与ZBCE 相等的角有()个.A. 2 个B. 3 个C. 4 个D. 57. 在平面直角坐标系中,抛物线y=dd-l )2+R 与x 轴交于A 、B 两点,顶点为C,点D 在抛物线的对称轴上,若四边形ACBD 是一个边长为2且有一个内角为60°的菱形,则该抛物线的 解析式有()A ・2 B. 3 C. 4 D. 5 )•A ・98B. 196C. 2805. 如图,将zMBC 沿着它的中位线DE 折叠后,点A 落在点A 处, 若ZC= 120°, ZA=26°,则 A. 112° B. 100° C. 120°D. 110° AD(第2题图) (第4题图) (第5题图) BA. 2个B. 3个C. 4个D. 5个8. 方程一肘+4加?+2”莎+2”+5 = 0的正整数解有(A 」B.2C.4D.无穷二、填空题(每小题5分,共40分)9. 如图,乐器上一根弦固定在乐器面板上4、B 两点,支撑点C 是靠近点B 的黄金分割点,若AB=80cm,则AC= ______________ cm.(结果保留根号)10. 如图,四边形ABCD 中,AB=4, BC = 7, CD=2, AD=x,则x 的取值范围是 ___________________11. 已知〃M 是关于兀的方程『_2血+。
重点高中高一提前招生选拔考试数学试卷及答案(共5份)

重点高中提前招生选拔考试数学试卷(本卷满分100分,时间120分钟)一、选择题(每题4分,共40分) 1.下列运算正确的是( )A.a 5.a 6= a 30B. (a 5)6= a 30C.a 5+a 6= a 11D.a 5÷a 6=65 2.抛物线2)8x (y 2+--=的顶点坐标是( )A .(2,8)B .(8,2)C .(—8,2)D .(—8,—2)3.在平面内有线段AB 和直线L,点A 、B 到直线L 的距离分别是4㎝、6㎝.则线段AB 的中点C到直线l 的距离是 ( )A .1或5B .3或5C .4D .54.已知:3223222⨯=+; 8338332⨯=+;154415442⨯=+;245524552⨯=+,……;809980992⨯=+,若ab10a b 102⨯=+(a,b 为正整数)则a+b 的值不可能是( ) A .109 B .218 C .326 D .4365.无论m 为何实数,直线y=2x+3m 与y=-x+5的交点不可能在( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限6.已知a 、b 、c 为△ABC 的三条边,且满足a 2+ab -ac -bc=0,b 2+bc -ba -ca=0,则 △ABC 是( )A .等边三角形 B.直角三角形C.等腰三角形D.等腰三角形或直角三角形7.若关于x 的不等式组 x ≥3a -2 无解,则函数y=(a -3)x 2-x -41的图象与 x<a+4 x 轴的交点个数为( )A.0B.1C.2D.1或28.将任意一张凸四边形的纸片对折,使它的两个不相邻的顶点重合,然后剪去纸片 的不重合部分,展开纸片,再一次对折,使另外的两个顶点重合,再剪去不重合 的部分后展开,此时纸片的形状是( )A.正方形B.长方形C.菱形D.等腰梯形9.如图,点M 是正方形ABCD 的CD 边上的中点, 点P 按A →B →C →M 的顺序在正方形的边上运动, 设AB=1,点P 经过的路程为x ,△APM 的面积为y ,则y 关于x 的函数是( )CP10.为了迎接2010年亚运会的到来,某足球协会举办了一次足球联赛,其记分规则及奖励方案如下表:当比赛进行到12轮结束(每队均需比赛12场)时,A 队共积19分,若每 赛一场每名参赛队员均得出场费500元,设A 队其中一名参赛队员所得的奖金与 出场费的和为W (元),试求W 的最大值是( ) .16300 B. 16900 C. 15700 D. 17500二、填空题(每题5分,共30分)11.一盒子内放有3个红球、6个白球和5个黑球,它们除颜色外都相同,搅匀后任意摸出1个球是白球的概率为 .12.某校七年级2班的男生人数是女生人数的1.8倍,在一次数学测试中,全班成绩 的平均分是75分,其中女生的平均分比男生的平均分高20%,则女生的平均分是 ___________分。
省重点高中高一提前招生考试数学试卷及答案(共6份)

省重点高中高一提前招生考试数学试卷考试用时100分钟,满分为120分一、选择题(本大题5小题,每小题3分,共15分)在每小题列出的四个选项中,只有一个是正确的,请把答题卡上对应题目所选的选项涂黑. 1.-2的倒数是A .2B .-2C .12D .-122.据中新社北京2010年12月8日电,2010年中国粮食总产量达到546 400 000吨,用科学记数法表示为A .5.464×107吨B .5.464×108吨C .5.464×109吨D .5.464×1010吨 3.将左下图中的箭头缩小到原来的12,得到的图形是4.在一个不透明的口袋中,装有5个红球3个白球,它们除颜色外都相同,从中任意摸 出一个球,摸到红球的概率为 A .51 B .31 C .85 D .835.正八边形的每个内角为A .120ºB .135ºC .140ºD .144º二、填空题(本大题5小题,每小题4分,共20分)请将下列各题的正确答案填写在答题卡相应的位置上.6.已知反比例函数=ky x的图象经过(1,-2),则=k ______▲______. 7.使2-x 在实数范围内有意义的x 的取值范围是______▲______. 8.按下面程序计算:输入3=x ,则输出的答案是______▲______.9.如图,AB 与⊙O 相切于点B ,AO 的延长线交⊙O 于点C .若∠A=40º,A .B .D .则∠C=______▲______.10.如图(1),将一个正六边形各边延长,构成一个正六角星形AFBDCE ,它的面积为1;取△ABC 和△DEF 各边中点,连接成正六角星形A 1F 1B 1D 1C 1E 1,如图(2)中阴影部分;取△A 1B 1C 1和 △D 1E 1F 1各边中点,连接成正六角星形A 2F 2B 2D 2C 2E 2,如图(3)中阴影部分;如此下去…,则正六角星 形A 4F 4B 4D 4C 4E 4的面积为______▲______.三、解答题(一)(本大题5小题,每小题6分,共30分) 11.计算:20245sin 18)12011(-︒+-.12.解不等式组:213821x >x +-⎧⎨-≤-⎩ ①②,并把解集在数轴上表示出来.13.已知:如图,E ,F 在AC 上,AD//CB 且AD=CB ,∠D=∠B .求证:AE=CF .14.如图,在平面直角坐标系中,点P 的坐标为(-4,0),⊙P 的半径为2,将⊙P 沿x 轴向右平移4个单位长度得⊙P 1. (1)画出⊙P 1,并直接判断⊙P 与⊙P 1的位置关系; (2)设⊙P 1与x 轴正半轴,y 轴正半轴的交点分别为A ,B ,求劣弧AB 与弦AB 围成的图形的面积(结果保留π). 15.已知抛物线c x x y ++=221与x 轴没有交点. (1)求c 的取值范围;(2)试确定直线1+=cx y 经过的象限,并说明理由. 四、解答题(二)(本大题4小题,每小题7分,共28分)16.某品牌瓶装饮料每箱价格26元.某商店对该瓶装饮料进行“买一送三”促销活动,若BCDAFE(1)E(2)(3)整箱购买,则买一箱送三瓶,这相当于每瓶比原价便宜了0.6元.问该品牌饮料一箱有多少瓶? 17.如图,小明家在A 处,门前有一口池塘,隔着池塘有一条公路l ,AB 是A 到l 的小路. 现新修一条路AC 到公路l. 小明测量出∠ACD=30º,∠ABD=45º,BC=50m. 请你帮小明计算他家到公路l 的距离AD 的长度(精确到0.1m ;参考数据:414.12≈,732.13≈).18.李老师为了解班里学生的作息时间表,调查了班上50名学生上学路上花费的时间,他发现学生所花时间都少于50分钟,然后将调查数据整理,作出如下频数分布直方图的一部分(每组数据含最小值不含最大值).请根据该频数分布直方图,回答下列问题:(1)此次调查的总体是什么? (2)补全频数分布直方图;(3)该班学生上学路上花费时间在30分钟以上(含30分钟)的人数占全班人数的百分比是多少?19.如图,直角梯形纸片ABCD 中,AD//BC ,∠A=90º,∠C=30º.折叠纸片使BC 经过点D ,点C 落在点E 处,BF 是折痕,且BF=CF=8. (1)求∠BDF 的度数; (2)求AB 的长.五、解答题(三)(本大题3小题,每小题9分,共27分)20.如下数表是由从1开始的连续自然数组成,观察规律并完成各题的解答.1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36…………………………(1)表中第8行的最后一个数是______________,它是自然数_____________的平方,第8行共有____________个数;(2)用含n 的代数式表示:第n 行的第一个数是___________________,最后一个数是________________,第n 行共有_______________个数;(3)求第n 行各数之和.21.如图(1),△ABC 与△EFD 为等腰直角三角形,AC 与DE 重合,AB=AC=EF=9,∠BAC=∠DEF=90º,固定△ABC ,将△DEF 绕点A 顺时针旋转,当DF 边与AB 边重合时,旋转中止.现不考虑旋转开始和结束时重合的情况,设DE ,DF(或它们的延长线)分别交BC(或它的延长线) 于G ,H 点,如图(2) (1)问:始终与△AGC 相似的三角形有 及 ;(2)设CG=x ,BH=y ,求y 关于x 的函数关系式(只要求根据图(2)的情形说明理由) (3)问:当x 为何值时,△AGH 是等腰三角形.∴当x =9x =时,△AGH 是等腰三角形。
2024初升高自主招生数学试卷(一)及参考答案

—1—2024初升高自主招生数学模拟试卷(一)1.方程43||||x x x x -=实数根的个数为()A .1B .2C .3D .42.如图,△ABC 中,点D 在BC 边上,已知AB =AD =2,AC =4,且BD :DC =2:3,则△ABC 是()A .锐角三角形B .直角三角形C .钝角三角形D .等腰三角形3.已知G 是面积为24的△ABC 的重心,D 、E 分别为边AB 、BC 的中点,则△DEG 的面积为()A .1B .2C .3D .44.如图,在Rt △ABC 中,AB =35,一个边长为12的正方形CDEF 内接于△ABC ,则△ABC 的周长为()A .35B .40C .81D .845.已知2()6f x x ax a =+-,()y f x =的图象与x 轴有两个不同的交点(x 1,0),(x 2,0),且1212383(1)()1)(16)(16)a a x x a x a x -=-++----,则a 的值是()A .1B .2C .0或12D .126.如图,梯形ABCD 中,AB //CD ,AB =a ,CD =b .若∠ADC =∠BFE ,且四边形ABFE 的面积与四边形CDEF 的面积相等,则EF 的长等于()A .2a b+B .abC .2ab a b +D .222a b +—2—7.在△ABC 中,BD 平分∠ABC 交AC 于点D ,CE 平分∠ACB 交AB 于点E .若BE +CD =BC ,则∠A 的度数为()A .30°B .45°C .60°D .90°8.设23a =,26b =,212c =.现给出实数a 、b 、c 三者之间所满足的四个关系式:①2a c b +=;②23a b c +=-;③23b c a +=+;④21b ac -=.其中,正确关系式的个数是()A .1B .2C .3D .49.已知m 、n 是有理数,方程20x mx n ++=2,则m +n =.10.正方形ABCD 的边长为5,E 为边BC 上一点,使得BE =3,P 是对角线BD 上的一点,使得PE +PC 的值最小,则PB =.11.已知x y ≠,22()()3x y z y z x +=+=.则2()z x y xyz +-=.12.如图,四边形ABCD 的对角线相交于点O ,∠BAD =∠BCD =60°,∠CBD =55°,∠ADB =50°.则∠AOB 的度数为.13.两个质数p 、q 满足235517p q +=,则p q +=.14.如图,四边形ABCD 是矩形,且AB =2BC ,M 、N 分别为边BC 、CD 的中点,AM 与BN 交于点E .若阴影部分的面积为a ,那么矩形ABCD 的面积为.第12题图第14题图15.设k 为常数,关于x 的方程2223923222k k x x k x x k --+=---有四个不同的实数根,求k 的取值范围.—3—16.已知实数a 、b 、c 、d 互不相等,并且满足1111a b c d x b c d a+=+=+=+=,求x 的值.17.已知抛物线2y x =与动直线(21)y t x c =--有公共点(x 1,y 1),(x 2,y 2),且2221223x x t t +=+-.(1)求t 的取值范围;(2)求c 的最小值,并求出c 取最小值时t 的取值.—4—18.如图,已知在⊙O 中,AB 、CD 是两条互相垂直的直径,点E 在半径OA 上,点F 在半径OB 延长线上,且OE=BF ,直线CE 、CF 与⊙O 分别交于点G 、H ,直线AG 、AH 分别与直线CD 交于点N 、M .求证:1DM DN MC NC-=.参考答案。
重点高中提前招生数学试卷

)bx重点高中提前招生数学试卷一、选择题(每小题5分)1、方程1116x y+=的正整数解的个数是()A 7个B 8个C 9 个D 10个2、如图,A,B的坐标为(2,0),(0,1)若将线段AB平移至11A B,则a b+的值为()A.2 B.3 C.4 D.53、解关于x的不等式⎩⎨⎧-<>axax,正确的结论是()A、无解B、解为全体实数C、当a>0时无解D、当a<0时无解4、某一天的不同时刻老板把信交给秘书打字,每次都将信放在秘书信堆的最上面,秘书有时间就将信堆最上面的那封信取来打。
假定共有5封信,且老板以1、2、3、4、5的顺序交来,在下列各顺序中,哪一顺序不可能是秘书打字的顺序?(A、12345B、54321C、23541D、235145、二次函数2y ax bx c=++的图象如图所示,)2,(nQ是图象上的一点,且BQAQ⊥,则a的值为().A.13- B.12- C.-1 D.-26、如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连结AO,如果AB=4,AO=26,那么AC的长等于()(A) 12(B) 16 (C) (D)7、函数y=(m2-1)x2-(3m-1)x+2的图象与x轴的交点情况是( )A、当m≠3时,有一个交点B、1±≠m时,有两个交点C、当1±=m时,有一个交点 D、不论m为何值,均无交点8、已知函数f(x)=x2+λx,p、q、r为⊿ABC的三边,且p﹤q﹤r,若对所有的正整数p、q、r都满足f(p)﹤f(q)﹤f(r),则λ的取值范围是()A、λ﹥-2B、λ﹥-3C、λ﹥-4D、λ﹥-5二、填空题(每小题5分)9、若关于x的分式方程3131+=-+xax在实数范围内无解,则实数=a_____.10、若222a b c bc=+-则的值是ABCEFOc ba b a c+++第13题图11、在Rt △ABC 中,∠C =900,AC =3,BC =4.若以C 点为圆心, r 为半径 所作的圆与斜边AB 只有一个公共点,则r 的取值范围是____________ .12、在平面直角坐标系中,横坐标与纵坐标都是整数的点(y x ,)称为整点,如果将二次函数43982-+-=x x y 的图像与x 轴所围成的封闭图形染成红色,则此红色区域内部及其边界上的整点个数有 个。
江苏某重点高中提前招生数学试卷

江苏省某重点高中提前招生数学试题(考试时间:120分钟满分150分)一、选择题(每小题3分,共27分.)1.新亚商城春节期间,开设一种摸奖游戏,中一等奖的机会为20万分之一,用科学记数法表示为:A. 2×10–5B. 5×10–6C. 5×10–5 D. 2×10–62.下列各式中,正确的是:A.=9 B.a2·a3=a6 C.(-3a2)3=-9a6 D. a5+a3=a83.若等腰梯形的三边长分别为3,8,11,则这个等腰梯形的周长是:A.25B.30C.25或30D.25或30或334.如图,△ABC中,∠A=60°,BC为定长,以BC为直径的⊙O分别交AB、AC 于点D、E.连结DE, 已知DE=EC.下列结论:①BC=2DE;②BD+CE=2DE.其中一定正确的有:A.2个B.1个 C.0个D.无法判断5.如图,在四边形ABCD中,M、N分别是CD、BC的中点,且AM⊥CD,AN⊥BC,已知∠MAN=74°,∠DBC=41°,则∠ADC度数为:A.45° B.47° C.49°D.51°6.小明从家骑车上学,先上坡到达A地后再下坡到达学校,所用的时间与路程如图所示.如果返回时,上、下坡速度仍然保持不变,那么他从学校回到家需要的时间是:A.8.6分钟B.9分钟C.12分钟 D.16分钟7.已知不等腰三角形三边长为、、,其中、两边满足,那么这个三角形的最大边c的取值范围是:A.B.C.D.8.平面内一个正五边形与一个正方形的边长正好相等,在它们相接的地方,形成一个完整的“苹果”图案(如图).如果让正方形沿着正五边形的四周滚动,并且始终保持正方形和正五边形有两条边邻接,那么第一次恢复“苹果”的图形时,正方形要绕五边形转:A.1圈B.2圈C.3圈D.4圈9.如图,四边形ABCD是直角梯形,AB∥CD,AD⊥AB,点P是腰AD上的一个动点,要使PC+PB最小,则点P应该满足 :A.PB=PC B.PA=PD C.∠BPC=90° D.∠APB =∠DPC二、填空题 (每小题4分,共36分)10. 如果点P()关于原点的对称点为(-2,3),则▲ .11.如果,则代数式x3+2x2-6x+3的值为▲ .12.有2名男生和2名女生,王老师要随机地、两两一对地为他们排座位,一男一女排在一起的概率是▲ .13.已知关于的分式方程的解为正数,则a的范围为▲ .14. 如图,正比例函数y=-x与反比例函数y=-的图象相交于A、C两点,AB⊥x轴于B,CD⊥x轴于D,则四边形ABCD的面积为▲ .15.如图是圆锥的主视图(单位:cm),则其表面积为___▲___cm2(结果保留π)16.已知抛物线y=ax2+bx+c的部分图象如图,则下列说法:①对称轴是直线x=1;②当-1<x<3时,y<0;③方程ax2+bx+c+5=0无实数根.其中正确的说法是(只填写序号) ▲ .17. 正方形ABCD中,AB=1,分别以A、C为圆心作两个半径为R、r(R>r)的圆,当R、r满足条件▲时,⊙A与⊙C有2个交点.18.已知△ABC为等腰三角形,由A点作BC边的高恰好等于BC边长的一半,则∠BAC的度数为▲ .三、解答题 (本大题共9题,计87分.解答应写明演算步骤、证明过程或必要的文字说明.)得分评卷人19. (本题8分)如图,向口ABCD的外侧画正方形ADGH和正方形DCEF,连结BH、BE和HE,①试猜想△BHE的形状为三角形.②向口ABCD的内侧画正方形ADGH和正方形DCEF,连结BH、BE和HE,请画出图形.判断△BHE的形状,并给出证明.得分评卷人20.(本题8分)如图,Rt△ABC中,∠C=90°,按题目所给条件及要求将相应的直角三角形,分割成若干个全等的并且分别与原三角形相似的三角形.画出图形并在图形下方简要说明操作方法.第(1)图,AC=BC,将ΔABC分割成2个三角形;第(2)图,AB=2AC,将ΔABC分割成3个三角形;第(3)图,将ΔABC分割成4个三角形;第(4)图,BC=2AC,将ΔABC分割成5个三角形;得分评卷人21. (本题9分)如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m),围成中间隔有一道篱笆的长方形花圃.设花圃的宽AB为xm,面积为Sm2.⑴求S与x的函数关系式;⑵如果要围成面积为45m2的花圃,AB的长是多少米?⑶能围成面积比45m2更大的花圃吗?如果能,请求出最大面积,并说明围法;如果不能,请说明理由.得分评卷人22. (本题8分)星光旅行社“五一”前为了了解市区居民“五一”外出旅游情况,采用下列调查方式:①到机关单位随机选取200名在职人员进行调查;②到不同的社区随机选取200名居民进行调查;③到大学城随机选取200名在校学生进行调查.⑴上述调查方式最合理的是_____________________;⑵将最合理的调查方式得到的数据制成扇形统计图(如图1),则在这个调查的200个人中“五一”外出旅游的有____________人;⑶请补全频数分布直方图(如图2).(4)请估计市区2 0万居民“五一”外出旅游时间不少于3天的人数.答人。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中提前招生数学试卷 1.已知关于x 的方程m x +2=2(m —x )的解满足|x -2
1|-1=0,则m 的值是 ( ) A .10或52 B .10或-52 c .-10或52 D .-10或5
2- 2.设直角三角形的三边长分别为a 、b 、c ,若c -b =b -a >0,则 ( )
A .1/2
B .1/3
C .1/4
D .1/5
3.某工厂第二季度的产值比第一季度的产值增长了x %,第三季度的产值又比第二季度的产值增长了x %,则第三季度的产值比第一季度的产值增长了 ( )
A .2x %
B . 1+2x %
C .(1+x %)x %
D .(2+x %)x %
4.甲从一个鱼摊上买了三条鱼,平均每条a 元,又从另—个鱼摊上买了两条鱼,平均每条b 元,后来他又以每条
2b a +元的价格把鱼全部卖给了乙,结果发现赔了钱,原因是 ( )
A .a >b
B .a <b
C .a =b
D .与a 和b 的大小无关
5.若D 是△ABC 的边AB 上的一点,∠ADC=∠BCA ,AC=6,DB=5,△ABC 的面积是S ,则△BCD 的面积是 ( )
A .S 53
B . S 74
C .S 95
D .S 11
6 6.如图,AE ⊥AB 且AE=AB ,BC ⊥CD 且BC=CD ,请按照图中
所标注的数据,计算图中实线所围成的图形的面积S 是( )
A .50
B .62
C .65
D .68
7.如图,两个标有数字的轮子可以分别绕轮子的中心旋转,旋转停止时,每个轮子上方的箭头各指着轮子上的一个数字,若左图轮子上方的箭头指着的数字
为a ,右图轮子上方的箭头指着的数字为b ,数对(a ,b )所有可能
的个数为n ,其中a +b 恰为偶数的不同数对的参数为m ,则m/n 等
于 ( )
A .21
B .61
C .125
D .4
3 8.如图,甲、乙两动点分别从正方形ABCD 的顶点,A 、C 同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行,若乙的速度是甲的速度的4倍,则它们第2000次相遇在边 ( )
A .A
B 上 B .B
C 上 C .C
D 上 D .DA 上
9.已知2+x a 与2-x b 和等于442-x x ,则a = ,b = 10.如图,AD 是△ABC 的中线,E 是AD 上的一点,且AE=3
1AD ,CE 交AB 于点F 。
若AF=1.2c m ,则AB= c m 。
11.在梯形ABCD 中,AB ∥CD ,AC .BD 相交于点O ,若AC=5,BD=12,中位线长为
213,△AOB 的面积为S 1,△COD 的面积为S 2,则21S S +=
12.已知矩形A 的边长分别为a 和b ,如果总有另一矩形B ,使得矩形B 与矩形A 的周长之比与面积之比都等于k ,则k 的最小值为 。
13.如图,AB ∥EF ∥CD ,已知 AC+BD=240,BC=100,EC+ED=192,求CF 。
14.已知x 、y 均为实数,且满足x y+x +y=17,x 2y+x y 2=66,求x 4+x 3y+x 2y 2+x y 3+y 4的值。
15.将数字1,2,3,4,5,6,7,8分别填写到八边形ABCDEFGH 的8个顶点上,并且以S 1,S 2,…,S 8分别表示(A ,B ,C ),(B ,C ,D ),…,(H ,A ,B )8组相邻的三个顶点上的数字之和。
(1)试给出一个填法,使得S 1,S 2,…,S 8都大于或等于12;
(2)请证明任何填法均不可能使得S 1,S 2,…,S 8都大于或等于13。
高中提前招生数学试卷
参考答案
1.A
2.C
3.D
4.A
5.C
6.A
7.C
8.A
9.2;2
10.6
11.30 12.2)(4b a ab + 13.因为AB ∥EF ∥CD ,所以由平行线分线段成比例定理,得:
BC AC BF AF CF CE ==①,BC
BD BF BE CF DE ==② ①+②,得BC
BD AC BF BE AE CF DE CE +=+=+③ 由③中取适合已知条件的比例式,得BC
BD AC CF DE CE +=+ 将已知条件代入比例式中,得100
240192=CF , 所以,CF=80
14.由已知xy+x+y=17,xy (x+y )=66,
所以xy 和x+y 是方程t 2-17t +66=0①的两个实数根,
解方程①,得t 1=6,t 2=11,
即xy =6,x +y =11或xy =11,x +y =6,
当xy =6,x +y =11时,x 、y 是方程u 2-11u +6=0②的两个根,
因为Δ1=(-11)2-4·6=121-24>0,所以方程②有实数根,
这时,x 2+y 2=(x +y )2-2x y =112-2·6=121-12=109
当xy =11,x +y =6时,x 、y 是方程v 2-6v +11=0③的两个根。
因为Δ2=(-6)2-4·11=36-44<0,所以方程③没有实数根,
所以x 4+x 3y +x 2y 2+xy 3+y 4的值为12499。
15.(1)不难验证,如图所示填法满足S1,S2,…S8都大于或等于12。
(2)显然,每个顶点出现在全部8组3个相邻顶点组的3个组中,
所以有S1+S2+…+S8=(1+2+3+…+8)·3=108
如果每组三数之和都大于或等于13,因13·8=104,所以至
多有108-104=4个组的三数之和大于13。
由此我们可得如下结论:
(1)相邻两组三数之和一定不相等。
设前一组为(i,j,k),
后一组为(j,k,l)。
若有i+j+k=j+k+l,则l=i,这不符合填写
要求;
(2)每组三数之和都小于或等于14。
因若有一组三数之和大于或等于15,则至多还有另外两个组,其三数之和大于13,余下5个组三数之和等于13,必有相邻的两组相等,这和上述结论(1)不符。
因此,相邻两组三数之和必然为13或14。
不妨假定1填在B点上,A点所填为i,C点所填为j。
(I)若S1=i+1+j=13,
则S2=1+j+l=14,S3=j+l+k=13,因j>1,这是不可能的。
(II)若S1=i+1+j=14,
则S2=1+j+(i-1)=13,S3=j+(i-1)+2=14,S4=(i-1)+2+(j-1)=13,这时S5=14,只能是S5=2+(j-1)+i,i重复出现。
所以不可能有使得每组三数之和均大于或等于13的填法。
