第八章复杂应力状态强度理论
应力状态和强度理论

7.10 强度理论概述 低碳钢在拉伸、压缩和扭转时 低碳钢在拉伸、压缩和扭转时, 当试件的应力达 到屈服点后, 就会发生明显的塑性变形, 到屈服点后 就会发生明显的塑性变形 使其失 去正常的工作能力, 去正常的工作能力 这是材料破坏的一种基本形 塑性屈服。 叫做塑性屈服 式, 叫做塑性屈服。 铸铁拉伸或扭转时, 铸铁拉伸或扭转时 在未产生明显的塑性变形的 情况下就突然断裂, 材料的这种破坏形式, 情况下就突然断裂 材料的这种破坏形式 叫做 脆性断裂。 脆性断裂 。 石料压缩时的破坏也是这种破坏形 式。
混凝土压缩时的力学性能 使用标准立方体试块测定
端面未润滑时的破 端面润滑时的 坏形式 破坏形式
(三)最大剪应力(第三强度)理论 最大剪应力(第三强度) 认为构件的屈服是由最大剪应力引起的。 认为构件的屈服是由最大剪应力引起的。当最 最大剪应力引起的 大剪应力达到单向拉伸试验的极限剪应力时, 大剪应力达到单向拉伸试验的极限剪应力时, 构件就破坏了。 构件就破坏了。 σ1 −σ3 σ s = =τs τ max = τ s τ max =
[
]
1+µ 2 = τ E
E ∴G= 2(1+µ )
7.10 强度理论概述
1.材料破坏的基本形式
在前面的实验中, 在前面的实验中 曾接触过一些材料的 破坏现象, 破坏现象 如果以低碳钢和铸铁两种材料 为例, 它们在拉伸(压缩 压缩)和扭转试验时的破 为例 它们在拉伸 压缩 和扭转试验时的破 坏现象虽然各有不同, 坏现象虽然各有不同 但都可把它归纳为 两类基本形式, 塑性屈服和脆性断裂。 两类基本形式 即塑性屈服和脆性断裂。
第一类强度理论-----脆性断裂的理论 脆性断裂的理论 第一类强度理论
第一强度理论---第一强度理论 最大拉应力理论 第二强度理论---第二强度理论 最大伸长线应变理论
材料力学应力状态分析强度理论

断裂力学用于研究材料发生断裂时的力学行为,包括断裂韧性和断裂韧性指标。
断裂模式分析
通过对材料断裂模式的分析,了解材料在受到外力作用时如何发生破裂。
材料的强度
应力。 材料在受力过程中开始产生塑性变形的应力值。
材料在受到大幅度应力作用时发生破裂的强度。
由强度理论推导的材料设计
根据材料的强度特性,可以进行材料设计,以确保材料在使用过程中不超过其强度极限。
考虑材料疲劳的应力分析
1
疲劳寿命评估
扭转应力分析
扭转应力是材料在受扭转力作 用下的应力分布,对材料的扭 转能力和疲劳寿命影响较大。
应力分布分析
1 梁的应力分布
梁的应力分布分析可以 帮助了解梁在受力过程 中的强度和变形情况。
2 压力容器的应力分析 3 板的应力分布
压力容器的应力分析是 为了确保容器在承受压 力时不会发生破裂或变 形。
板的应力分布分析可用 于评估板在受力状态下 的强度和变形性能。
材料力学应力状态分析强 度理论
材料力学应力状态分析强度理论是研究材料受力情况及其强度特性的理论体 系,包括弹性理论、横向状态分析、应力分布分析等内容。
弹性理论
基本原理
材料在受力过程中 会发生变形,弹性 理论用于描述材料 的弹性性质和应变 的产生与传递。
弹性模量
弹性模量是衡量材 料对应力的响应能 力,不同材料具有 不同的弹性模量。
应力-应变关 系
弹性理论可以通过 应力-应变关系来描 述材料受力后的变 形情况。
限制条件
弹性理论是在一定 条件下适用的,需 要考虑材料的线性 弹性和小变形假设。
横向状态分析
横向力
横向状态分析用于研究材料在 受横向力作用下的变形和应力 分布。
化工设备设计基础第8章内压薄壁圆筒与封头的强度设计

Sc pcDi
2[]t- pc
计算壁厚公式
考虑腐蚀裕量C2,得到圆筒的设计壁厚
Sd 2[p]ctD-i pc C2
设计壁厚公式
设计壁厚加上钢板厚度负偏差C1,再根据钢板标准规格向上圆整确定 选用钢板的厚度,即名义壁厚(Sn),即为图纸上标注厚度。
一、强度计算公式
1.圆筒强度计算公式的推导 1.2 无缝钢管作筒体(外径DO为基准)
内径为基准 外径为基准
内径为基准 外径为基准
一、强度计算公式
3.球形容器厚度计算及校核计算公式
3.1厚度计算公式
Sc
pcDi
4[]t -
p
计算壁厚
Sd 4[p]ctD i-pc C2
设计壁厚
3.2校核计算公式
t pcDi Se[]t
4S e
[pw]
4[]tSe
Di Se
已有设备强度校核
确定最大允许工作压 力
常温容器 中温容器 高温容器
[]
minnss
,b
nb
[]t
minnsst
,bt
nb
[]t
minnsst
, D t , nt
nD nn
二、设计参数的确定
3.许用应力和安全系数
3.2安全系数
安全系数的影响因素: ①计算方法的准确性、可靠性和受力分析的的精确程度; ②材料的质量和制造的技术水平; ③ 容器的工作条件以及容器在生产中的重要性和危险性。
当
0
n
[]
二、强度理论及其相应的强度条件
复杂应力状态的强度条件,要解决两方面的问题: 一是根据应力状态确定主应力; 二是确定材料的许用应力。
内压薄壁容器的主应力:
材料力学-第8章应力状态与强度理论

第8章 应力状态与强度理论及其工程应用
强度理论概述
关于脆性断裂的强度理论
第8章 应力状态与强度理论及其工程应用
关于脆性断裂的强度理论
零件或构件在载荷作用下,没有明显的破坏 前兆(例如明显的塑性变形)而发生突然破坏的 现 象 , 称 为 断 裂 失 效 ( failure by fracture or rupture)。
Mechanics of materials
材料力学
材料力学
第 8章
基础篇之八
应力状态与强度理论 及其工程应用(B)
第8章 应力状态与强度理论及其工程应用
什么是“失效”;怎样从众多的失效现象中寻找失效 规律;假设失效的共同原因,从而利用简单拉伸实验结果, 建立一般应力状态的失效判据,以及相应的设计准则,以 保证所设计的工程构件或工程结构不发生失效,并且具有 一定的安全裕度。这些就是本章将要涉及的主要问题。
2 1 3
max 1 ( 1 0)
= b
o max b
失效判据 强度条件
1 b
1
b
nb
第8章 应力状态与强度理论及其工程应用
关于脆性断裂
第二强度理论又称为最大拉应变准则(maximum tensile strain criterion),它也是关于无裂纹脆性材 料构件的断裂失效的理论。
第8章 应力状态与强度理论及其工程应用
关于脆性断裂的强度理论
根据第二强度理论,无论材料处于什么应力状态, 只要发生脆性断裂,其共同原因都是由于微元的最大 拉应变达到了某个共同的极限值。
max
o max
(1 0)
第8章 应力状态与强度理论及其工程应用
第八章-2强度理论.

(2)
剪切破坏—— 塑性屈服(流动)和剪断:最大切应力引起的破坏,
例如低碳钢拉、扭,铸铁受压。
强度理论:构件失效的原因的假说。 意义:无论何种应力状态,也无论何种材料,只要失效形式相同, 则失效原因就相同的,从而可由简单应力状态的实验结果,来建立复杂 应力状态的强度条件。 关于断裂的强度理论:最大拉应力理论和最大伸长线应变理论。 关于屈服的强度理论:最大切应力理论和形状改变比能理论。
莫尔强度理论强度条件:
1
[ ] [ ]
3 [ ]
试验表明,这一理论适用于脆性材料的剪断破坏。 若[][]莫尔强度理论强度即为第三强度理论
强度理论的适用条件: 1. 脆性材料多发生脆性断裂,因而应选用第一、第二强度理
论或莫尔强度理论; 2.塑性材料多发生屈服,应选用第三或第四强度理论。
1 [ ]
铸铁拉伸
铸铁扭转
5
2. 最大伸长拉应变理论(第二强度理论)
最大拉应变是材料发生脆性断裂的破坏因素。无论材料处于什么应力 状态,只要构件内一点处的e1达到极限值eu , 材料发生脆性断裂。
eu——极限拉应变,由单向拉伸实验测得。
断裂条件
e1 e u
许用拉应变
[e ]
b eu E e u b [ ]
一、 问题的提出 1. 杆件基本变形下的强度条件 拉压 max
FN max [ ] A
正应力强度条件
M max [ ] 弯曲 max W
剪切 扭转
max [ ]
max k
max
FQ A
[ ]
切应力强度条件
高等教育出版社简明材料力学第二版 第八章 应力状态分析和强度理论分析

1 150 MPa, 2 75 MPa,
3 0
2018/10/12 15
8-2 二向和三向应力状态的实例
火车车轮与钢轨的接 触点也是三向应力状态
A
滚 珠 轴 承
2 A
3
1
2018/10/12
16
第八章
应力状态分析和强度理论
§8-1 应力状态的概述 单向拉伸时斜截面上的应力 §8-2 二向和三向应力状态的实例 §8-3 二向应力状态分析 §8-4 二向应力状态的应力圆 §8-5 三向应力状态简介 §8-6 广义胡克定律 §8-7 复杂应力状态下的应变能密度 §8-8 强度理论概述 §8-9 四种常用强度理论
则斜截面面积为: A Aα = cos α F F cosα F pα cos σ cosα Aα A A
σ σα = pα cosα =σ cos α τ α = pα sin α = σ sin α cos α = sin 2α 2
2
直杆拉伸应力分析结果表明:即使同一点不同方向面 上的应力也是各不相同的,此即应力的面的概念。
10
第八章
应力状态分析和强度理论
§8-1 应力状态的概述 单向拉伸时斜截面上的应力 §8-2 二向和三向应力状态的实例 §8-3 二向应力状态分析 §8-4 二向应力状态的应力圆 §8-5 三向应力状态简介 §8-6 广义胡克定律 §8-7 复杂应力状态下的应变能密度 §8-8 强度理论概述 §8-9 四种常用强度理论
8-3 二向应力状态分析
考虑到切应力互等定理:τxy=τyx
xy
x y
yx
x y
x y
应力状态分析和强度理论

03
弹性极限
材料在弹性范围内所能承受的最大应力状态,当超过这一极限时,材料会发生弹性变形。
01
屈服点
当物体受到一定的外力作用时,其内部应力状态会发生变化,当达到某一特定应力状态时,材料会发生屈服现象。
02
强度极限
材料所能承受的最大应力状态,当超过这一极限时,材料会发生断裂。
应力状态对材料强度的影响
形状改变比能准则
04
弹塑性材料的强度分析
屈服条件
屈服条件是描述材料在受力过程中开始进入屈服(即非弹性变形)的应力状态,是材料强度分析的重要依据。
根据不同的材料特性,存在多种屈服条件,如Mohr-Coulomb、Drucker-Prager等。
屈服条件通常以等式或不等式的形式表示,用于确定材料在复杂应力状态下的响应。
最大剪切应力准则
总结词
该准则以形状改变比能作为失效判据,当形状改变比能超过某一极限值时发生失效。
详细描述
形状改变比能准则基于材料在受力过程中吸收能量的能力。当材料在受力过程中吸收的能量超过某一极限值时,材料会发生屈服和塑性变形,导致失效。该准则适用于韧性材料的失效分析,尤其适用于复杂应力状态的失效判断。
高分子材料的强度分析
01
高分子材料的强度分析是工程应用中不可或缺的一环,主要涉及到对高分子材料在不同应力状态下的力学性能进行评估。
02
高分子材料的强度分析通常采用实验方法来获取材料的应力-应变曲线,并根据曲线确定材料的屈服极限、抗拉强度等力学性能指标。
03
高分子材料的强度分析还需要考虑温度、湿度等环境因素的影响,因为高分子材料对环境因素比较敏感。
02
强度理论
总结词
该理论认为最大拉应力是导致材料破坏的主要因素。
应力状态和强度理论

第八章 应力状态和强度理论授课学时:8学时主要内容:斜截面上的应力;二向应力状态的解析分析和应力圆。
三向应力简介。
$8.1应力状态概述 单向拉伸时斜截面上的应力1.应力状态过构件上一点有无数的截面,这一点的各个截面上应力情况的集合,称为这点的应力状态2.单向拉伸时斜截面上的应力 横截面上的正应力AN =σ斜截面上的应力ασαcos cos ===AP A P p a a斜截面上的正应力和切应力为ασασ2cos cos ==a a pασατ2sin 2sin ==a a p可以得出 0=α时σσ=max4πα=时 2m a x στ=过A 点取一个单元体,如果单元体的某个面上只有正应力,而无剪应力,则此平面称为主平面。
主平面上的正应力称为主应力。
主单元体 若单元体三个相互垂直的面皆为主平面,则这样的单元体称为主单元体。
三个主应力中有一个不为零,称为单向应力状态。
三个主应力中有两个不为零,称为二向应力状态。
三个主应力中都不为零,称为三向应力状态。
主单元体三个主平面上的主应力按代数值的大小排列,即为321σσσ≥≥。
PPaaα$8.2二向应力状态下斜截面上的应力1. 任意斜截面上的应力在基本单元体上取任一截面位置,截面的法线n 。
在外法线n 和切线t 上列平衡方程αασαατσc o s )c o s (s i n )c o s (dA dA dA x xy a -+0sin )sin (cos )sin (=-+αασαατdA dA y yxαασααττsin )cos (cos )cos (dA dA dA xxy a --0sin )sin (cos )sin (=++ααταασdA dA yx y根据剪应力互等定理,yx xy ττ=,并考虑到下列三角关系 22sin 1sin ,22cos 1cos 22αααα-=+=,ααα2sin cos sin 2=简化两个平衡方程,得ατασσσσσα2sin 2cos 22xy yx yx --++=ατασστα2cos 2sin 2xy yx +-=2.极值应力将正应力公式对α取导数,得⎥⎦⎤⎢⎣⎡+--=ατασσασα2cos 2sin 22xy y x d d 若0αα=时,能使导数0=ασαd d ,则 02cos 2sin 200=+-ατασσxy yxyx xytg σστα--=220上式有两个解:即0α和 900±α。
第8章(强度理论)

断裂失效断裂失效屈服失效屈服失效断口处材料颗粒状断口处材料颗粒状断口处材料片状断口处材料片状材料失效单向应力状态的试验结果单向应力状态的试验结果关于材料破坏规律的假说,一般假设材料不同应力状态下同种失效由同种因素引起的。
关于材料破坏规律的假说,一般假设材料不同应力状态下同种失效由同种因素引起的。
引起失效的因素已知引起失效的因素已知同种失效引起的因素是相同的同种失效引起的因素是相同的建立复杂应力状态下的强度条件建立复杂应力状态下的强度条件强度理论一、最大拉应力理论(第一强度理论)材料发生断裂是最大拉应力引起,即最大拉应力达到某一极限值时材料发生断裂。
材料发生断裂是最大拉应力引起,即最大拉应力达到某一极限值时材料发生断裂。
1.第一强度理论的计算准则单向应力状态max bσσ=最大拉应力最大拉应力b σ=复杂应力状态max u σσ=材料断裂失效材料断裂失效bσ=引起失效的因素max 1σσ=1bσσ=max u σσ=?=1bσσ=[]1σσ≤2.第一强度理论的的应用与局限材料无裂纹脆性断裂失效形式(脆性材料二向或三向受拉状态;最大压应力值不超过最大拉应力值或超过不多)。
材料无裂纹脆性断裂失效形式(脆性材料二向或三向受拉状态;最大压应力值不超过最大拉应力值或超过不多)。
没考虑σ2、σ3 对材料的破坏影响,对无拉应力的应力状态无法应用。
没考虑σ2、σ3 对材料的破坏影响,对无拉应力的应力状态无法应用。
第一强度理论的断裂准则第一强度理论的强度条件二、最大拉应变理论(第二强度理论)材料发生断裂是最大拉应变引起,即最大拉应变达到某一极限值时材料发生断裂。
材料发生断裂是最大拉应变引起,即最大拉应变达到某一极限值时材料发生断裂。
1.第二强度理论的计算准则b max E σε=单向应力状态b σσ=最大拉应变最大拉应变b E σ=材料断裂失效材料断裂失效引起失效的因素max u εε=?=123max ()E σµσσε−+=b u E σε==123b()σµσσσ−+=b max Eσε=单向应力状态b σσ=最大拉应变最大拉应变b E σ=材料断裂失效材料断裂失效引起失效的因素max u εε=?=复杂应力状态材料断裂失效材料断裂失效2.第二强度理论的的应用与局限123b()σµσσσ−+=[]123()σµσσσ−+≤与极少数的脆性材料在某些受力形式下的实验结果吻合。
材料力学课件 第八章应力状态与强度理论

单向应力状态(Unidirectional State of Stress): 一个主应力不为零的应力状态。
x B x
zx
xz
x
x
A
§8–2 平面应力状态下的应力分析
y
y
y
xy x
等价 y
x
xy
x z
Ox
一、解析法
30
x
y
2
sin 2
x cos2
80 (40) sin(2 30 ) 60 cos(2 30 ) 2
21.96MPa
确定主平面方位,将单元体已知应力代入 8.3,得
20 45
tan 20
2 x x y
2 (60) 80 (40)
1
0 22.5
0 即为最大主应力1 与 x 轴的夹角。主应力为
x
各侧面上剪应力均为零的单元体。
z
z
2
3
主平面(Principal Plane):
剪应力为零的截面。 x
主应力(Principal Stress ):
主平面上的正应力。
1
主应力排列规定:按代数值大小,
1 2 3
三向应力状态( Three—Dimensional State of Stress): 三个主应力都不为零的应力状态。
解:由于主应力1 ,2 ,3 与主应变1 ,2 ,3 一一对应,故由已知数据可知,
已知点处于平面应力状态且 2 0 。由广义胡克定律
1
1 E
(1
3 )
3
1 E
( 3
1)
联立上式
8应力状态和强度理论

3
40
max 1 3 3) 40 .3MPa min 2
1
20 14.9o 30
1
单位:MPa
3
例3 简支梁如图所示.已知mm 截面上 A 点的弯曲 正应力和切应力分别为 =-70MPa, =50MPa . 确定: A 点的主应力及主平面的方位 . m A
y =60 MPa
xy = -50MPa =-30°
45 135
0
22.5 67.5
因为 x < y ,所以 0= -22.5° 与 min 对应
x y 2 2 max x y 80.7 MPa ( ) xy 2 2 60.7 MPa min
若 0 时,能使 d 0 d
x y
2
sin 2 0 x cos 2 0 0
最大正应力和最小正应力所在平面就是主平面 , 最大正应力和最小正应力就是两个主应力。
tan 2 0
2 xy
x y
0 、 0 90 , 它们确定两个互相垂直
(
x y
2
) (
2 2
x y
2
2
2 ) 2 xy
( x a) y 0 R 2
2
因为 x ,y ,xy 皆为已知量, 所以上式是一个以 , 为变量的圆周方程。当斜截面随方位角 变化时, 其上的应力 , 在 - 直角坐标系内的轨迹是一个圆 。 1. 圆心的坐标
即:最大和最小剪应力所在平面与 主平面的夹角为45
例2 图示单元体,试求:①a=30o斜截面上的应力; ②主应力并画出主单元体;③极值切应力。
强度理论分析
工程上常见的断裂破坏主要有三种类型:
无裂纹结构或构件的突然断裂.
由脆性材料制成的构件在绝大多数受力情形下都发生突 然断裂,如受拉的铸铁等构件的断裂.
具有裂纹构件的突然断裂.
这类断裂经常发生在由塑性材料制成的,且由于各种 原因而具有初始裂纹的构件.
构件的疲劳断裂.
构件在交变应力作用下,即使是塑性材料,当经历一定次 数的应力交变之后也会发生脆性断裂.
r3 1 3
r4
1 2
(1
2 )2
( 2
3)2
(3
1)2
在大多数应力状态下,脆性材料将发生脆性断裂.故应选用 第一强度理论;
而在大多数应力状态下,塑性材料将发生屈服和剪断.故应选 用第三强度理论或第四强度理论.
但材料的破坏形式不仅取决于材料的力学行为,而且与所处的 应力状态,温度和加载速度有关.
强度理论:关于材料强度失效主要原因的假说。
“材料无论处于复杂应力状态还是处于简单应力 状态,引起失效的因素是相同的”。
(与应力状态无关)
简单应力状态 复杂应力状态
失效因素f
失效条件
实验测量fjx
计算fmax
Fmax= fjx
这样:一方面由简单应力状态(拉压)的实验,测出引起材料失效的那 个因素的极限值,另一方面计算实际受力构件上处于复杂应力状态下的 危险点处的相应因素,从而建立材料处于复杂应力状态下的强度条件。
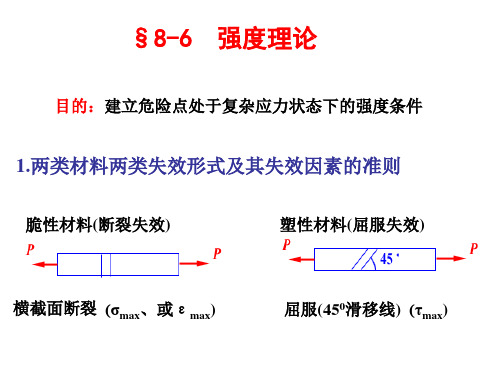
§8-6 强度理论
目的:建立危险点处于复杂应力状态下的强度条件
1.两类材料两类失效形式及其失效因素的准则
脆性材料(断裂失效)
塑性材料(屈服失效)
横截面断裂 (σmax、或εmax)
屈服(450滑移线) (τmax)
材料力学 强度理论与组合变形

第八章强度理论与组合变形§8-1 强度理论的概念1.不同材料在同一环境及加载条件下对“破坏”(或称为失效)具有不同的抵抗能力(抗力)。
例1常温、静载条件下,低碳钢的拉伸破坏表现为塑性屈服失效,具有屈服极限σ,s铸铁破坏表现为脆性断裂失效,具有抗拉强度σ。
图9-1a,bb2.同一材料在不同环境及加载条件下也表现出对失效的不同抗力。
例2常温静载条件下,带有环形深切槽的圆柱形低碳钢试件受拉时,不再出现塑性变形,而沿切槽根部发生脆断,切槽导致的应力集中使根部附近出现两向和三向拉伸型应力状态。
图(9-2a,b)例3 常温静载条件下,圆柱形铸铁试件受压时,不再出现脆性断口,而出现塑性变形,此时材料处于压缩型应力状态。
图(9-3a )例4 常温静载条件下,圆柱形大理石试件在轴向压力和围压作用下发生明显的塑性变形,此时材料处于三向压缩应力状态下。
图9-3b3.根据常温静力拉伸和压缩试验,已建立起单向应力状态下的弹性失效准则,考虑安全系数后,其强度条件为 []σσ≤ ,根据薄壁圆筒扭转实验,可建立起纯剪应力状态下的弹性失效准则,考虑安全系数后,强度条件为 []ττ≤ 。
建立常温静载一般复杂应力状态下的弹性失效准则——强度理论的基本思想是: 1)确认引起材料失效存在共同的力学原因,提出关于这一共同力学原因的假设; 2)根据实验室中标准试件在简单受力情况下的破坏实验(如拉伸),建立起材料在复杂应力状态下共同遵循的弹性失效准则和强度条件。
3)实际上,当前工程上常用的经典强度理论都按脆性断裂和塑性屈服两类失效形式,分别提出共同力学原因的假设。
§8-2四个强度理论1.最大拉应力准则(第一强度理论)基本观点:材料中的最大拉应力到达材料的正断抗力时,即产生脆性断裂。
表达式:u σσ=+max复杂应力状态321σσσ≥≥, 当01>σ, 1m a xσσ=+简单拉伸破坏试验中材料的正断抗力b u σσσ==1,032==σσ 最大拉应力脆断准则: b σσ=1(9-1a)相应的强度条件:[]bb n σσσ=≤1(9-1b)适用范围:虽然只突出 1σ 而未考虑 32,σσ 的影响,它与铸铁,工具钢,工业陶瓷等多数脆性材料的实验结果较符合。
强度理论

B :1 2 120MPa, 3 200MPa
二、关于塑性屈服破坏的强度理论
1、最大切应力理论(第三强度理论)
最大切应力τmax 是引起材料屈服破坏的主要原因。
屈服条件: τmax = τs
σ1 - σ3 = σs
强度条件: σ1 - σ3 ≤ [σ ] ➢ 能解析塑性材料的屈服破坏。——Tresca屈服准则
➢ 用这一理论计算结果偏于安 全,在工程中广泛应用。
n
强度条件为:
1
t c
3
t
可以解析铸铁受压破坏并不是与横截面成45。的截面。
适用于 脆性材t料 c
塑性材料 t c 即为第三强度理论
➢ 能解析三向均匀受压不破坏;一定条件下能解析三向均 匀受拉发生破坏。
τ
α
2α
O2
O O1
点圆
铸
σ
铁
压
缩
σbc
σbt
§8-4 强度理论的应用
强度理论的统一公式:
力,但也与同一截面上的正应力有关。 由三向应力圆可知,最大切应力和较大的切应力均在
主应力σ1、σ3 所作的应力圆上。 按材料在破坏时的主应力σ1、 σ3 所作的应力圆,就 代表在极限应力状态下的应力圆——极限应力圆。
τ
极限应力图
τ
包络线
破坏
σ
O2
O O3
O1
σ
包络线
未破坏
σbc
σbt
O3 N O3O1 O2 P O2O1
例2. 已知一锅炉的内径D0=1000mm,壁厚δ=10mm,
如图所示。锅炉材料为低碳钢,其容许应力[σ]=170MPa。
应力状态及强度理论

/
2
低碳钢
低碳钢 : σ s 240MPa; τs 200MPa
灰口铸铁 : σ Lb 98 ~ 280MPa σ yb 640 ~ 960MPa; τb 198 ~ 300MPa
铸铁
30° 40
图示单元体中应力单位为MPa
20
①求斜截面上旳应力
30
解 : x 30 y 40
60°
y
二、应力圆旳画法
y
Ox
C O
B(y ,yx)
x
xy
建立应力坐标系,如下图所示, (注意选好百分比尺)
在坐标系内画出点A( x,xy) 和B(y,yx)
x
A(x ,xy)
AB与 轴旳交点C便是圆心。
以C为圆心,以AC为半径画
圆——应力圆;
y
n 三、单元体与应力圆旳相应关系
x
xy
面上旳应力( , ) 应力圆上一点( , )
y
y
主单元体:
x
六个面上剪应力均为零旳单元体。
z
z
2
主平面:
剪应力为零旳截面。 x
主应力:
主平面上旳正应力。
1
主应力排序规则:按代数值大小排序:
3
σ1 σ2 σ3
三向应力状态: 三个主应力都不为零旳应力状态。(即三对平行平面上旳应
力均不为零)
二向应力状态: 一种主应力为零旳应力状态。(即仅一对平行平面上旳应力为零)
y
一、应力圆
x
y
xy
Ox
x
y
y
xy
σα
σx
σy 2
σx
σy 2
cos2α
τ xy sin2α
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
F
M
① 判定组合变形的类型 属弯拉扭组合变形 ②画每个基本变形内力图, 确定危险截面(忽略剪力)。
M
()
x
()
T
FN
()
x x
③ 根据危险截面应力分布图,确定危险点 A P 对于弯拉扭组合圆截面轴, 危险截面上的危险点同时作用有 最大弯曲正应力、轴向拉伸正应 力和最大扭转切应力: A
F
M A
max s
2
s
n
3、实用范围:实用于破坏形式为屈服的构件。
二、畸变能理论(第四强度理论) :
认为材料的屈服主要是由畸变能引起的。不论材料处于何 种应力状态,只要畸变能密度达到材料单向拉伸屈服时的畸变 能密度,材料即发生屈服破坏。 1、屈服条件: 1 1 2 2 2 3 2 3 1 2 s 2 2、强度条件: 1 2 2 2 1 2 2 3 3 1 3、实用范围:实用于破坏形式为屈服的构件。对大多数塑性金 属材料来说,畸变能理论比最大切应力理论更符合试验结果。
P
M
二、强度理论:是关于“材料发生强度失效起因”的假说
。 三、材料的破坏形式:⑴ 屈服; ⑵ 断裂 。 四、常用的四个强度理论: 1、第一强度理论:最大拉应力理论。 2、第二强度理论:最大拉应变理论。 3、第三强度理论:最大切应力理论。 4、第四强度理论:畸变能理论。
§8–2
关于断裂的强度理论
一、最大拉应力理论(第一强度理论)
1、断裂条件: 1 2 3 b 2、强度条件: 1 2 3
1 1 1 2 3 , E
1u
b
E
n 3、实用范围:实用于破坏形式为脆断的构件。例如,某
=
b
些脆材在二向拉-压应力状态下,且压应力值大于拉应力值 时。砖、石、水泥预制件压缩时。
r3
= M 2 T 2 W
2 2
B P L/2 4kN.m
M T
4000 +2800 32
0.08
3
97.2MPa
x
r4
M 2 0.75T 2 W 4000 0.75 2800 32
2 2
x
2.8kN.m
=
0.08
3
=93.1MPa
该轴满足强度要求。
例3 图示平面直角拐杆,P=4kN,a =160mm,材料的 [σ] = 80MPa。试按第三强度理论设计AB段的直径d。 解:A截面为危险截面
M Pa, T Pa
z x y
M 2 T 2 W W =
d 3
32
2
M T
2
2
( 2 Pa)
内表面
2
外表面
pD 1 2
pD 2 4
1
薄壁圆筒筒壁任意点的应力状态如图, 三个主应力为:
pD pD , 3=0 1 ,2 4 2
2
一般薄壁圆筒是用塑性材料制作, 应按第三或第四强度理论进行强度计算, 相应的强度条件分别为:
r3
x X
T 120N m
③强度计算:
(Nm) M Tn (Nm)
120 Mn
x x
(N m) M (Nm) M
r3
M 2 T2 W
Mmax 71.3
5.5
40.6
x X
32 71.32 1202 3.14 0.033 (10.84 )
97.5MPa
安全
二、圆轴弯拉(压)扭组合强度计算 PWM NhomakorabeaM
d
3
T
T
32
,WP
d
3
16
r 3 1 3 M 4 T
2
2
M 2 T 2 1 ( ) 4( ) W WP W
WP
r4
M T
2 2
d 3
16
2W
1 2 2 2 1 2 2 3 3 1 2
2
2
W
[ ]
r4
M 2 0.75T 2 W
[ ]
例2 传动轴AB直径d=80mm,轴长L=2m,[σ]=100MPa, 轮缘挂重P=8kN,与转矩m相平衡,轮直径D=0.7m。 试分别用第三、第四强度理论校核轴的强度。
y m x z A
L/2
解: ①外力分析: ②内力分析: ③强度计算:
26.2MPa = -16.2MPa
1=26.2MPa, 2 0, 3 16.2MPa
脆材拉压应力状态下,最大压应力值小于最大拉应力值时, 宜采用 第一强度理论进行强度计算。
1
该点满足强度条件。
§8–3
关于屈服的强度理论
一、最大切应力理论(第三强度理论) :
应用强度理论进行强度计算的步骤:
1、外力分析:确定所需的外力值。 2、内力分析:画内力图,确定可能的危险截面。 3、应力分析:画危面应力分布图,确定危险点并画出 危险点的单元体,求主应力。 4、强度分析:选择适当的强度理论,计算相当应力,
然后进行强度计算。
§8–4
弯扭组合,弯拉(压)扭组合
一、圆轴弯扭组合强度计算 P
x
M
① 判定组合变形的类型 属弯扭组合变形 ②画每个基本变形内力图, 确定危险截面(忽略剪力)。
M
()
x
T
()
x
③画危险截面应力分布图,找危险点
A
对于弯扭组合圆截面轴,危险截面 上的危险点同时作用有最大弯曲正 应力和最大扭转切应力:
A
B
M
A
M T T , T , W WP 2W
§8–1 引
言
§8–2 关于断裂的强度理论
§8–3 关于屈服的强度理论 §8-4 弯扭组合,弯拉(压)扭组合
§8-5 承压薄壁圆筒的强度计算
§8–1 引 一、引子:
言
1、简单应力状态是根据试验现象和试验结果建立强度条件。 P P M
P
2、杆件危险点处于复杂应力 状态时,将发生怎样的破 坏?怎样建立强度条件?
例1 某灰口铸铁构件危险点处的应例状态如图,若许用拉应力 为[σ]=30 MPa,试校核该点的强度。(图中应力单位MPa ) y
20 10 15
解: x 10MPa, y 20MPa, xy 15MPa x
max 10 20 -10-20 2 2 +(- 15 ) min 2 2
认为材料的屈服主要是由最大切应力引起的。不论材料处 于何种应力状态,只要最大切应力达到材料单向拉伸屈服时的 极限切应力,材料即发生屈服破坏。 1 3 max s max , 2 1、屈服条件: 1 3 s 2、强度条件: 1 3
2
四种强度理论强度条件的统一形式
r
b , 0.2 , s
n
四种强度理论的相当应力:
r1 1
r2 1 2 3
r3 1 3
r4
1 2 2 2 1 2 2 3 3 1 2
该轴满足强度条件。
例5 图示空心圆杆,内径 d=24mm,外径D=30mm, P1=600N,[]=100MPa, DB 0.4m,DD 0.6m 。 试用第三强度理论校核 此杆的强度。 解: ①外力分析: 弯扭组合变形 DB DD P P 1 2z 2 2 求得 P2 z 400N A
2 Pa
d 3
32 2 Pa
48.7 103 m
取d=49mm。
例4 齿轮轴如图,齿轮受到水平径向力F=1.82kN和铅垂切向力 P=5kN的作用,齿轮节圆直径D=0.4m,轴直径d=50mm,轴长L=0.6m。 轴材料[σ]=100MPa,试用第三强度理论校核轴的强度。 m y 解: ①外力分析: D x ②内力分析: z A
杆件满足强度要求。
§8–5 承压薄壁圆筒的强度计算
y
"
D
'
p p l
p
p A O B
x
'
p D x
1、纵向应力
X 0 2 D p D 4
pD 4
'
y
2、环向应力:
z
O
Y 0
"
"
p D
l 2 p Dl
1
pD 2
W
M
()
x
600N.m
T
T 60016 24.46MPa 3 W p 0.05
T
FN
500N.m
④强度计算:
()
40kN
x x
r 4 ( M N ) 2 3 T 2
()
40.76 20.382 3 24.462 74.38MP a
其强度。 解:由广义虎克定律得: y A x
E 2.1 7 x 2 ( x y ) ( 1 . 88 0 . 3 7 . 37 ) 10 94.4MPa 2 10.3 1 E y 2 ( y x ) 2.1 2 (7.370.31.88)10 7 183 .1MPa 10.3 1
M+ N
M+ N
T
M
T
M FN T , N , T , W A WP
