第9章 静电场的基本规律
新人教版必修3第九章静电场及其应用1.电荷

规律:近端感应异种电荷,远端感应同种电荷
【例1】 如图所示,左边是一个原先不带电的导体,右边C是后来靠近导体 的带正电的金属球。若用绝缘工具沿图示某条虚线将导体切开,将导体分为 A、B两部分,这两部分所带电荷量的数值分别为QA、QB,则下列结论正确 的有( ) A.沿虚线d切开,A带负电,B带正电,且QB>QA B.只有沿虚线b切开,才有A带正电,B带负电,且QB=QA C.沿虚线a切开,A带正电,B带负电,且QB>QA D.沿任意一条虚线切开,都有A带正电,B带负电,且QB=QA,而QA、QB 的值与所切的位置有关
1.如图所示,在感应起电现象中,带负电物 体靠近带绝缘底座的导体N处时,M处将( )
A.带正电 B.带负电 C.不带电 D.以上答案均有可能
验电器(静电计)➢作用:①检②验粗物略体判是断否物带体电带,电的多
少
➢结构:金属球、金属杆、金属箔等
➢原理:同种电荷互相排斥
实验:
Ⅲ、接触起电
接触起电:带电物体接触另一个物体,
–+ +
+
–+
+
–
+ +–
+
+ –
++ –
+
–
+
+– –
+
– +
–– – + –+
–+ –+
+ +–– – + –
– + +
++
–+ –+
2021高中物理必修三第九章静电场及其应用9-3专2-1.等量点电荷电场特点

方法究
【例1】 (多选)(2020·广东中山一中高二 期末)两个带等量正电荷的点电荷,O点 为两电荷连线的中点,a点在连线的中 垂线上,若在a点由静止释放一个电子 ,如图所示,关于电子的运动,下列说 法正确的是( AC )
A.电子在从a点向O点运动的过程中,加速度可能先增大再减小 B.电子在从a点向O点运动的过程中,加速度一定越来越小,速度一定越来越大 C.电子运动到O点时,加速度为零,速度最大 D.电子通过O点后,速度越来越小,加速度一直增大
首页
知识梳理
2.等量异种点电荷的电场(电场线分布如图2): (1)两点电荷连线上,沿电场线方向电场强度先变小再变大,中点处电场强度最小。 (2)两点电荷连线的中垂线上电场强度方向都相同,总与中垂线垂直且指向负点电荷 一侧,沿中垂线从中点到无限远处,电场强度一直减小,中点处电场强度最大。 (3)关于中心点对称的点,电场强度等大同向。
第九章 静电场及其应用 专题拓展课二 等量电荷电场和带电粒子(体)运动分析
1.等量点电荷电场特点
知识梳理
1.等量同种点电荷的电场(电场线分布如图1): (1)两点电荷连线上,中点O处电场强度为零,向两侧电场强度逐渐增大。 (2)两点电荷连线的中垂线上由中点O到无限远,电场强度先变大后变小。 (3)关于中心点O点的对称点,电场强度等大反向。
答案 C
首页
首页
方法探究
解析 等量异种电荷形成的电场的电场线如图所示。 在+Q 和-Q 的连线上,从+Q 到-Q 电场强度先变小后变大, 由对称性可知 a 点的电场强度等于 b 点的电场强度; 在+Q 和-Q 连线的中垂线上从 O 点向 M 点或 N 点电场强度均变小, 则检验电荷沿 MN 由 c 移到 d,电场力先增大后减小。故选项 C 正确。
大学物理第九章课后习题答案

题库
第九章 静电场的基本规律
一、 填空 1. 电荷分为 和 ,一般把用 摩擦过的玻璃棒上所带的电 荷称为 , 把用毛皮摩擦过的 上所带的电荷称为 。 2. 物体所带电荷的多寡程度的物理量称为 。 3. 物体所带的电荷量不是以连续值出现,而是以不连续的量值出现的,这称 为 。 4. 试探电荷满足的两个条件是 , 。 5. 穿过电场中某曲面的电场线条数称为电场对该曲面的 。 6. 静电场的电场线起始于, ,终止于 , 是 (填 “闭合” 或 “不闭合” ) 的曲线, 在没有电荷的空间里, 电场线既不会 , 也不会 。 7. 高斯定理的表达式是 。 8. 电场中电势相等的点所构成的曲面称为 。 点电荷的等势面是以点电 荷为球心的一系列 。 9. 沿等势面移动电荷,电场力做功为 ,等势面和电场线处处 。 10. 沿电场线方向,电势 (填“升高”或“降低” ) 。 二、 简答 1. 2. 3. 4. 5. 简述真空中点电荷满足的库仑定律的内容及矢量表达式。 简述研究电场性质时,试探电荷需满足的两个条件。 简述电场线怎样描述电场的性质,以及静电场的电场线的特点。 简述高斯定理。 简述等势面具有的性质。
s
q内
0
。
8. 等势面,同心球面。 9. 零,正交。 10. 降低。 二、 简答 1. 答:内容:真空中两个点电荷之间的相互作用力沿其连线方向,同号相斥, 异号相吸;作用力的大小与两电荷的电荷量的乘积成正比,与两电荷之间的距离 的平方成反比。 矢量表达式: F =
q1 q 2 r0 。 4πε 0 r 2
� q j 2π 2 ε 0 R 2
联立①②, 可得 Q = 3 q 3
① ②
∴在三角形的中心应放置一电量为 − 的合力为零. 5.
人教版高二物理必修第三册第九章静电场及其应用全章知识点梳理

人教版高二物理必修第三册第九章静电场及其应用全章知识点梳理1.对感应起电的理解当金属导体A和B彼此接触时,它们都不带电。
此时贴在它们下面的金属箔是闭合的。
当带正电荷的球C移近导体A时,A和B上的金属箔都张开了,这表示A和B上都带有电荷。
如果把A和B分开,然后移去球C,可以看到A和B 仍带有电荷。
当A和B接触时,金属箔就不再张开,表明它们不再带电了。
这说明A和B所带的电荷是等量的,互相接触时,等量的正、负电荷发生了中和。
因此,感应起电的本质是在导体C上的电荷作用下,导体A和B上的自由电荷发生定向移动,由B端移至A端,从而引起A端带负电,B端带正电。
此时,如果将A和B分离,导体A和B则成为带等量异种电荷的带电体。
2.元电荷与电荷守恒定律元电荷是电子、质子或正电子所带的电荷量,都是e。
所有带电体的电荷量等于e或者是e的整数倍。
因为物体的带电荷量通常较小,因此可用元电荷的整数倍方便地表示。
例如,电子的带电荷量为-1.60×10^-19C。
电荷守恒定律的另一种表达是:一个与外界没有电荷交换的系统,电荷的代数和总是保持不变。
例如,接触带电时不带电物体与带电物体接触后,电荷在两物体上重新分配,但总电荷量不变。
摩擦起电实质上是电子在不同物体间的转移。
当接触带电时,两个完全相同的导体球相互接触,则电荷量平分。
如果两导体球带同种电荷,会把总电荷量平分;如果带异种电荷,则先中和然后再把剩余电荷量平分。
3.库伦定律点电荷是一种物理模型,只有电荷量,没有大小、形状等其他因素。
它类似于力学中的质点,但在实际中并不存在。
当带电体间的距离比它们自身的大小大得多,以至于带电体的形状和大小对相互作用力的影响很小时,就可以忽略形状、大小等次要因素,只保留对问题有关键作用的电荷量,带电体就能看成点电荷。
需要注意的是,点电荷与元电荷是不同的概念。
元电荷是最小的电荷量,其数值等于一个电子或一个质子所带电荷量的绝对值。
点电荷是一种带电个体,其大小和形状不影响其带电荷量,但其带电荷量必定是元电荷的整数倍。
第九章电荷与真空中的静电场

第九章电荷与真空中的静电场第九章电荷与真空中的静电场9.1 电荷库仑定律⼀、电荷对物质电性质的最早认识:摩擦起电和雷电电荷的基本认识包括:电荷类型:正电荷(丝绸摩擦玻璃棒)负电荷(⽑⽪摩擦橡胶棒)电性⼒:同号相斥、异号相吸电量:物体带电荷数量的多少2.电荷所遵循的基本实验规律:1)电荷是量⼦化的在⾃然界中,电荷总是以基本单元的整数倍出现,近代物理把电荷的这种不连续性称为电荷的量⼦化。
⼀个电⼦或质⼦所带电量既为⼀个基本电量单元,其电量为:e = 1.602 10-19 C(库仑)所有带电体的电量均为:q=ne n=±1, ±2, ±3,2)电荷遵从守恒定律电荷守恒定律是⾃然科学中的基本定律之⼀。
电荷既不能创造,也不会被消灭,它只能从⼀个物体转移到另⼀个物体(如摩擦起电),或从物体的⼀部分转移到另⼀部分(如静电感应)。
在任何物理过程中,电荷的代数和是恒定不变的。
9.2 电场电场强度⼀、电场电场强度静电场:存在于电荷周围的,可以对其它电荷施加作⽤⼒的物质,称之为电场,⽽由相对于观察者静⽌的电荷激发的电场则称为 “静电场”场的物质性体现在:给电荷施加⼒(动量),移动电荷做功(能量) 场与实物的共同性:1客观存在;2遵循守恒定律;3不能创⽣场是客观存在的特殊物质,与普通实物⼀样具有能量、质量、动量等,不同的是,场可以与实物共占空间,具有“可侵⼊性”⼆.电场强度— 描述电场各点对电荷作⽤强弱的物理量定义:电场中某点,单位正电荷所受到的电场⼒为该点电场的电场强度,简称场强. 单位:⽅向:某点电场强度E 与该点正电荷受⼒⽅向相同9.3 电通量真空中静电场⾼斯定理1. 电场线电场线(E )线:描述电场空间分布情况的⼀组曲线规定:电场强度的⽅向:曲线在某点的切线⽅向电场强度的⼤⼩:曲线的疏密程度(通过垂直于电场线单位0q F E =1m V -?⾯积的电场线数)。
2. 电通量定义:通过电场中任⼀⾯积的电场线数⽬称为通过该⾯的电通量匀强电场穿过垂直均匀电场的平⾯的电通量通过⼀均匀电场中任⼀平⾯的电通量⾼斯定理:在真空中,通过任意闭合曲⾯S 的电通量等于该曲⾯内所包围的⾃由电荷的代数和除以真空电容率点电荷置于任⼀闭合曲⾯内:由于电场线的连续性,穿过该曲⾯的电⼒线根数与包围同⼀电荷的球⾯相同,当所有电荷均位于曲⾯外时:与曲⾯相切的电⼒线对曲⾯的通量没有贡献,穿过曲⾯的所有电场线都将穿出曲⾯,⽽电场线穿⼊曲⾯为负,穿出为正真空中的⾼斯定理:在真空中,通过任意闭合曲⾯S的电通量等于该曲⾯内所包围的⾃由电荷的代数和除以真空电容率⾼斯定理表明静电场是有源场,电荷就是静电场的源。
第9章-静电场中的导体和电介质

E 加上外电场后 外 E外
把金属导体置于外电场 中,自由电子将产生宏 观定向运动,导体中电 荷按照外电场特性和导 体形状形成特定的分布
在外电场作用下,引起 导体中电荷重新分布而呈 现出的带电现象,称为
静电感应现象 Electrostatic Induction
问:这种静电感应的过程是否会一直进行下去?
辨析
0 一块无限大均匀带电导体薄板,电荷面密度为 0
问:在它附近一点的场强=?
解:由无限大带电均匀平面两侧的场强公式,得
二、导体处于静电平衡状态时的场强分布
导体外部近表面处场强 E
方向:与该处导体表面垂直
E
0
n
大小:与该处导体表面电荷面密度 成正比。 E(nˆ )
0
S
ES
S 0
ΔS
P
E
0
E内=0
讨论:导体表面附近的场强公式
E
0
指导体表面附近场点近旁的导体电荷面密度
一、静电感应 导体的静电平衡条件
无外电场时
无外电场时,导体中 自由电子在金属内作无 规则热运动,而没有宏 观定向运动,整个导体 呈现电中性
无外电场时
导体的静电感应过程
E 外
加上外电场后
导体的静电感应过程
E 外
+
加上外电场后
导体的静电感应过程
E 外
+
+
加上外电场后
导体的静电感应过程
E 外
+ +
E 外
+ + + + +
最新人教版高中物理必修第三册同步课件第9章 静电场及其应用本章整合

?
1.同一直线上的三个自由点电荷都处于平衡状态时,每个电
荷受到的合力均为零,根据平衡方程可得,电荷间的关系为“两
同夹异”“两大夹小”“近小远大”。
2.对于三个自由电荷的平衡问题,只需对其中两个电荷列平
衡方程,不必对第三个电荷列平衡方程。
?
【变式训练4】 光滑固定斜面(足够长)倾角为37°,一带正电
电场线的分布情况。一带电粒子在电场中运动的轨迹如图中
虚线所示。若不考虑其他力,则下列判断正确的是(
)
A.若粒子从A运动到B,则粒子带正电;
若粒子从B运动到A,则粒子带负电
B.不论粒子是从A运动到B,还是从B
运动到A,粒子必带负电
C.若粒子从B运动到A,则其加速度减小
D.若粒子从B运动到A,则其加速度增大
由牛顿第二定律得 F 合=ma,所以 a=3 m/s2,方向沿斜面向下。
(3)由运动学公式,知 v=at=3×2 m/s=6 m/s
2
x=at =×3×22 m=6 m。
已在图中标出,且电荷均匀分布,各圆环间彼此绝缘。坐标原点 O 处
电场强度最大的是(
答案:B
)
?
解析:每个 圆环在 O 点产生的电场强度大小相等,设为 E。根据电
场的叠加原理和对称性,得 A、B、C、D 各图中 O 点的电场强度大
小分别为 EA=E、EB= E、EC=E、ED=0,故 B 正确。
A. ,方向向上
B.
,方向向上
C. ,方向水平向左
D.不能确定
?
解析:先把带电圆环分成若干个小部分,每一小部分可视为
一个点电荷,各点电荷对检验电荷的库仑力在水平方向上的
第9章导体和电介质中的静电场(精)

第第九九章章导导体体和和电电介介质质中中的的静静电电场场引言:一、导体、电介质、半导体导体:导电性能很好的材料;例如:各种金属、电解质溶液。
电介质(绝缘体):导电性能很差的材料;例如:云母、胶木等。
半导体:导电性能介于导体和绝缘体之间的材料;二、本章内容简介三、本章重点和难点1. 重点(1)导体的静电平衡性质;(2)空腔导体及静电屏蔽;(3)电容、电容器;2. 难点导体静电平衡下电场强度矢量、电势和电荷分布的计算;第一节静电场中的导体一、静电感应静电平衡1. 静电感应(1)金属导体的电结构从微观角度来看,金属导体是由带正电的晶格点阵和自由电子构成,晶格不动,相当于骨架,而自由电子可自由运动,充满整个导体,是公有化的。
例如:金属铜中的自由电子密度为:nCu=8⨯1028(m-3)。
当没有外电场时,导体中的正负电荷等量均匀分布,宏观上呈电中性。
(2)静电感应当导体处于外电场E0中时,电子受力后作定向运动,引起导体中电荷的重新分布。
结果在导体一侧因电子的堆积而出现负电荷,在另一侧因相对缺少负电荷而出现正电荷。
这就是静电感应现象,出现的电荷叫感应电荷。
2. 静电平衡不管导体原来是否带电和有无外电场的作用,导体内部和表面都没有电荷的宏观定向运动的状态称为导体的静电平衡状态。
(a)自由电子定向运动(b)静电平衡状态3. 静电平衡条件(静电平衡态下导体的电性质)(1)导体内部任何一点处的电场强度为零;导体表面处电场强度的方向,都与导体表面垂直。
(2)在静电平衡时,导体内上的电势处处相等,导体是一个等势体。
E证明:假设导体表面电场强度有切向分量,即τ≠0,则自由电子将沿导体表面有宏观定向运动,导体未达到静电平衡状态,和命题条件矛盾。
dUdU =0,=0E内=0,Eτ=0dldτ因为,所以,即导体为等势体,导体表面为等势面。
二、静电平衡时导体上电荷的分布1. 实心导体(1)处于静电平衡态的实心导体,其内部各处净电荷为零,电荷只能分布于导体外表面。
4.4静电场的基本规律
对于非匀强电场:
Ψe
E dS
S
EcosdS
S
dS E
S
电场强度通量单位:N∙m2C-1 或 V∙m
静电场的基本规律
二. 闭合曲面的电场强度通量
当曲面为闭合曲面,数学上规定其 面元的法线方向取向外为正。
1. 对于点电荷的电场:
+q处于球形闭合曲面S的中心:
Ψe
通过高斯面的电场强度通量只与闭合面内的电荷有关,但高 斯面上的电场强度为空间全部电荷激发的总电场强度。
静电场的基本规律
四. 静电场的环路定理
在静电场中,沿闭合路径移动q0,电场
L1
dl q0E dl
a
b q0Edl
a ( L1 )
静电场的基本规律
一. 电场强度通量
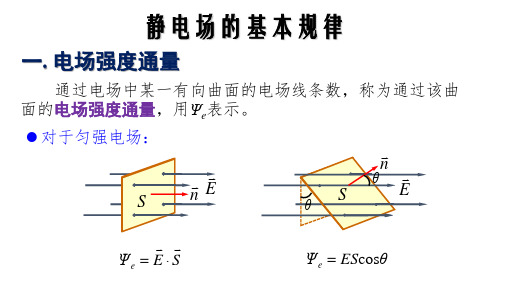
通过电场中某一有向曲面的电场线条数,称为通过该曲
面的电场强度通量,用Ψe表示。
对于匀强电场:
S
n
E
n
θ
S
E
θ
Ψe ES
Ψe EScosθ
静电场的基本规律
一. 电场强度通量
通过电场中某一有向曲面的电场线条数,称为通过该曲
面的电场强度通量,用Ψe表示。
a q0Edl
b( L2 )
b a(L1) q0Edl
b
a(L2 ) q0Edl
0
b
L2 E
静电场的环路定理:静电场中电场强度沿任一闭合环路的线
积分恒等于零。
E dl 0
S
S
静电场的基本规律
二. 闭合曲面的电场强度通量
高中物理必修三第九章 静电场及其应用 电场 电场强度

2.在静电场中的某一点A放一个试探电荷q=-1×10-10 C,q受到的静电 力为1×10-8 N, 方向向左 ,则 A点 的场 强 的 大小 为_1_0_0__N_/_C_ ,方向 ___向__右___;如果从A点取走q,A点场强大小为_1_0_0__N_/_C_.
解析 由题意知,q=-1×10-10 C,F=1×10-8 N, 由场强的定义知A点的场强的大小为: E=|Fq|=11××1100--180 N/C=100 N/C, 场强方向与负电荷在A点所受静电力方向相反,所以A点的场强方向向右; 电场强度是反映电场性质的物理量,与有无试探电荷无关,把这个试探 电荷取走,A点的电场强度不变,大小仍为100 N/C.
图2 答案 200 N/C 方向与F1方向相反 解析 由场强公式可得 EB=|Fq11|=42..00× ×1100- -68 N/C=200 N/C, 因为B处是负电荷,所以B处场强方向与F1方向相反.
(2)如果换成一个q2=+4.0×10-7 C 的电荷放在B点, 其受力多大?此时B处场强多大? 答案 8.0×10-5 N 200 N/C
2.电场强度 (1)定义:放入电场中某点的试探电荷所受的 静电力 跟它的 电荷量 的比 值,叫作该点的电场强度.
F (2)定义式:E= q . (3)单位:牛每库(N/C) .
(4)方向:电场强度是矢量,电场中某点的电场强度的方向与正电荷在该 点所受的静电力的方向 相同 ,与负电荷在该点所受静电力的方向 相反 .
三、点电荷的电场 电场强度的叠加
1.真空中点电荷的电场 Q
(1)场强公式:E= kr2 . (2)方向:如果以电荷量为Q的点电荷为中心作一个球面,当Q为正电荷 时,E的方向沿半径 向外 ;当Q为负电荷时,E的方向沿半径 向内 . 2.电场强度的叠加 场强是矢量,如果场源是多个点电荷时,电场中某点的电场强度为各个 点电荷 单独 在该点产生的电场强度的 矢量和 .
第九章静电场第一节静电现象电荷

规律: 近端 感应异种电荷, 远端 感应同种电荷
感应起电
两个带电体如何进行电荷分配
电荷的分配原则:
两个形状、大小相同的导体,接触后再分开,二者带等量电荷;若两导体原来带异种 电荷,则电荷中和后,余下的电荷再平分。
摩擦起电、接触起电、感应起电从本质上都源于物质的原子中的电子在不同物体间或者在同一物体的不同部分之 间发生了转移,它们之间电荷的总量并没有发生变化。
总结
自然界只有两种电荷,分别叫做正电荷与负电荷。
用丝绸摩擦过的玻璃棒带正电荷;用毛皮摩擦过的硬橡 胶棒带负电荷。
电荷的性质: ①同种电荷相互排斥,异种电荷相互吸引; ②任何带电体都能吸引轻小物体
另外,带电物体可以吸引轻小物体。
当两个物体互相摩擦时,一些束缚得不紧的电子往往从一 个物体转移到另一个物体,于是原来呈电中性的物体由于 得到电子而带负电,失去电子的物体则带正电.如毛皮摩 擦橡胶棒,橡胶棒得到电子带负电;丝绸摩擦玻璃棒,玻 璃棒失去电子带正电.其本质都是发生了电子的转移。
多选4.关于元电荷,下列说法中正确的是( BCD) A、元电荷实质上指电子和质子本身 B、所有带电体的电荷量一定等于元电荷的整数倍 C、元电荷的数值通常取作e=1.6×10-19C D、电荷量e的数值最早是由美国科学家密立根用实验测得的
5.使带电的金属球靠近不带电的验电器,验电器的箔片张开.下列各图表示验电器上感应电荷的分布情况,正确的 是( B )
自然界的闪电,属 于人类早期观察并记录 的静电现象。
除了闪电,人类也 通过观察发现被摩擦之 后的琥珀可以吸引轻小 物体。
秋冬季节,天气干 燥的情况下,我们在日 常生活中也经常会遇到 跟一些人“来电”的情况。
生活中的静电现象是十分常见的。 比如左图所示的三种情况。你还 能想到其他的现象吗?
电磁学静电场中的基本规律

λdl 取电荷元dq则 取电荷元 则 dE = 4 0R2 πε
由对称性 ∫ dEx = 0
Y
dl
λdl E = ∫ dEy = ∫ cosθ 2 4πε0R
λRcosθ λ α = 2∫ dθ = si n 2 4 0R 2 0R 2 πε πε 0
2
R
α
θ dθ
X
α
r dE O
方向: 方向:沿Y轴负向 轴负向
dq = λdl q dl = 2a π
dq r a x
y p
v z d E⊥
v d E//
dq dE = 4 0r2 πε
v v dE// = dEi
x v dE
v v v dE⊥ = dEy j +dEzk
位置发生变化时, 当dq位置发生变化时,它所激发的电场 位置发生变化时 矢量构成了一个圆锥面。 矢量构成了一个圆锥面。
2 1
x
θ θ2
dl
2 2 E = Ex + Ey
方向
λ λ (cosθ1 −cosθ2) Ex = (sin θ2 −sinθ1) Ey = 4 0a πε 4πε0a
θ 1 →0, 讨论 当直线长度 L→∞ 或a →0 θ 2 →π
Ex = 0
λ E = Ey = 2πε a πε 0
5. 选择积分变量
θ1
a
r
l
dl
r、、是 量 而 积 只 一 变 θ l 变 , 线 分 要 个 量
选θ作为积分变量 作为积分变量
l = actg(π−θ) = −actgθ
∴d l = acsc θd θ
2
r = a +l
2 2 2 2
大学物理第九章导体和介质中的静电场

第九章导体与介质中的静电场Electrostatic field in conductor and dielectric §9-1,2静电场中的导体§9-3电容器的电容§9-6电介质中的高斯定理§9-8 静电场的能量§9-1,2静电场中的导体一、导体的静电平衡( electrostatic equilibrium )1.导体绝缘体半导体1)导体(conductor)导电能力极强的物体(存在大量可自由移动的电荷)2)绝缘体(电介质,dielectric)导电能力极弱或不能导电的物体3)半导体(semiconductor)导电能力介于上述两者之间的物体EE E E iii E e E q F 导体静电平衡条件:导体内任一点的电场强度都等于零Ei E E2. 导体的静电平衡条件导体的内部和表面都没有电荷作任何宏观定向运动的状态.导体的静电平衡状态:静电感应E* 推论(静电平衡状态)证:在导体上任取两点p , ql d E V V i qpq pqp V V 0i Epq导体静电平衡条件:2)导体表面任一点场强方向垂直于表面1)导体为等势体,导体表面为等势面否则其切向分量将引起导体表面自由电子的运动,与静电平衡相矛盾。
3.导体上电荷的分布1)当带电导体处于静电平衡状态时,导体内部处处没有净电荷存在, 电荷只能分布于导体的表面上.qdV iiV证明:在导体内任取体积元dV由高斯定理体积元d v 任取导体带电只能在表面!iiqS d E 01 ,0 i E dVn e En e E E S d e E S d E nS E 0S2).导体表面附近的场强方向与表面垂直,大小与该处电荷的面密度成正比.ne ES结论:孤立的带电导体,外表面各处的电荷面密度与该处曲率半径成反比,410R Q V RRrr R ,44,22rRr R rR q Q r R R rQq1)导体表面凸出而尖锐的地方(曲率较大)电荷面密度较大2)导体表面平坦的地方(曲率较小)电荷面密度较小3)导体表面凹进去的地方(曲率为负)电荷面密度更小rq V r 041rq R Q V V R r 004141l d E 导体内,0l d E 腔沿电场线l d E (违反环路定理)在静电平衡状态下,导体空腔内各点的场强等于零,空腔的内表面上处处没有电荷分布.ld E l d E l d E导体内腔沿电场线二、空腔导体(带电荷Q )1 腔内无电荷,导体的电荷只能分布在外表面。
高中物理必修三第九章 静电场及其应用 静电的防止与利用

规律总结
求处于静电平衡状态的导体的感应电荷产生的场强的方法是: (1)先求出外电场场强E外的大小和方向. (2)由于导体处于静电平衡状态,则满足静电平衡条件E合=0. (3)由E外+E感=0,求出感应电场E感的大小和方向.
针对训练 长为l的导体棒原来不带电,现将一带电荷量为+q的点电荷 放在距棒左端R处,如图3所示.当棒达到静电平衡后,棒上的感应电荷在
4kq 棒内中点P处产生的电场强度大小等于_(_2_R_+__l_)_2 ,方向为__向__左__.
图3
解析 导体棒在点电荷+q的电场中发生静电感
应,左端感应出负电荷,右端感应出正电荷,
棒中任意一点都受两个电场的影响,
即外电场(+q在该点形成的电场E0)和附加电场(棒上感应电荷在该点形 成的电场E′), 达到静电平衡状态时 E′=-E0.E′=-E0=-R+kq2l 2=-(2R4+kql)2, 负号代表E′和E0方向相反,即方向向左.
二、尖端放电 1.空气的电离:在一定条件下,导体尖端电荷 密度 很大,导体尖端周围 的强电场使空气中残留的带电粒子发生剧烈运动,并与空气分子碰撞从 而使空气分子中的正负电荷 分离 的现象. 2.尖端放电:所带电荷与导体尖端的电荷符号相反的粒子,由于被 吸引 , 而与尖端上的电荷 中和 ,相当于导体从尖端 失去电荷 的现象. 3.尖端放电的应用与防止: (1)应用: 避雷针 是利用尖端放电避免雷击的一种设施. (2)防止:高压设备中导体的表面尽量 光滑 会减少电能的损失.
(4)用金属网把验电器罩起来,再使带电金属球靠近验电器,则验电器箔
片能张开.( × )
(5)电工穿的高压作业服是用铜丝编织的,目的是铜丝衣服有屏蔽作用,
使体内场强为零.( √ )
02 重点探究
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第九章 静电场的基本规律
9-2 库仑定律
一.点电荷之间的作用力
点电荷(理想模型):当带电体的线度(形状、大小)d<< r(带电体之间的距离)时,就可以把带电体视为点电荷。
真空中的库仑定律:真空中的两个点电荷 q1 和q 2之间的相互作
(1)在给定电场中的同一点,分别放入电荷不同的试探电
荷q 0结果发现 q0所受电场力的大小随 q0电荷的增减而增减,
但
F q0
比值不变。
(2)对于电场中不同的点,比值 F 一
般情况下并不相同。
q0
第九章 静电场的基本规律
电场强度:
E
F
q0
在数值和方向上等于处在该点的单位正电荷所受到的库
仑力的大小和方向。
E 2E c os
ql
3
4 0 y 2
l2 4
2
其中,
cos
l
2( y 2
l2
1
)2
4
E
4
q 0(y2
l2 4
)
在 y l / 2 处,
E ql
4 0 y 3
第九章 静电场的基本规律
电偶极子:若两电荷间的距离远小于它们到场点的距离,这样的电
荷系统称为电偶极子。
电偶极矩矢量(
pr )p
第九章 静电场的基本规律
返回主目录
第九章 静电场的基本规律
9-1 电荷 电场
一. 电荷 电荷量
1.带电体:处于带电状态的物体称为带电体。
自然界的电荷
正电荷:与丝绸摩擦过的玻璃棒上相同的电荷 负电荷:与毛皮摩擦过的橡胶棒上相同的电荷
电力:带电体之间的相互作用力;同种电荷相排斥,异种电荷相吸引。
电荷(电荷量):表示物体所带电荷的多寡程度的物理量。
N E S
N kE S
这样,场强的大小就可以用电场线的疏密程度反映出来。
第九章 静电场的基本规律 几种简单电场的电场线图:
正点电荷
负点电荷
第九章 静电场的基本规律
两个等值异号点电荷
两个等值同号点电荷
第九章 静电场的基本规律
静电场的电场线的两条最重要的性质:
(1)电场线起始于正电荷(或来自于无穷远), 终止于负电荷(或伸向无穷远)。在没有电荷的 空间里,电场线既不会相交也不会中断。
点电荷系的场强公式:
q1 qn
设点电荷系 r … r 处于真空中,各点电荷到场点P的 矢径分别为 r1 … rn 由场强叠加原理,P点的总场强为,
E
1
4 0
n i1
qi ri2
r0i
第九章 静电场的基本规律
若点电荷系处在无限大的均匀电介质中
E
1
4
n i 1
qi ri2
r0i
第九章 静电场的基本规律
ql 其中
l
的大小为两电荷之间的距
离,方向由负电荷指向正电荷。电偶极矩矢量
描述了电偶极子本身的特性。
基于此,上面的结果可记为,
在延长线上, 在中垂线上,
r E
2 pr
4
0
x3
p
E
4 0 y 3
第九章 静电场的基本规律
例题2 真空中一均匀带电直线,常为L,带电荷为Q,求直线外 一点P处的场强。P 点到直线的距离为a,到直线两端点的连线与 直线的夹角分别为θ1和θ2 。 解:建立如图所示的坐标系,此为电荷连续 分布问题。
四.连续分布电荷的场强
虽然电荷是量子化的,但从宏观来说,一般带电体可 以忽略电荷的量子性,视其电荷分布为连续分布。
任意带电体可连续分割为无数电荷为dq的微小带电体的
集合,则 dq(视为点电荷)在场点P处的场强为
1 dq
dE 4 0 r 2 r0
由场强叠加原理,带电体在P处的总场场强为
E
dE
叠加原理的内容:对多个点电荷的系统,其中任一点电荷 所受的静电力等于其它点电荷单独存在时作用于该电荷上 的静电力的矢量和。
如图所示:有n个点电荷组成的系统,另有点电荷q受到这 n个点电荷的作用,根据叠加原理,则点电荷q所受库仑力为
F F1 F2 Fi Fn
第九章 静电场的基本规律
三.电介质中的库仑定律
和中垂线上一点的场强。
解:建立如图所示的坐标系
(1)其连线的延长线上任一点的场强:
在延长线上任取一 P,+q和-q 产生的场强方向相反,大小分别为
E
q
4 0 (x
l )2 2
, E
q
4 0 (x
l )2 2
第九章 静电场的基本规律
则 P点的合场强的大小为,
E
E
E
q
4 0
(
x
l 2
)2
q
40 (x
代入得,
dEx
sind 4 0a
dE y
cosd 4 0a
r a
s in
第九章 静电场的基本规律
两式积分得,
Ex
dEx
4 0 a
2 sin d
1
4 0 a
cos1
cos 2 )
E y
dE y
4 0 a
2 cosd
1
4
0
a
(cos
2
cos1 )
P 点处的总场强大小为,
E Ex2 Ey2
在SI中,场强单位: N C 1
匀强电场:电场中各点场强的大小和方向都相同。
电场力: F qE
★ 试探电荷应满足下列条件:
(1)必须是几何线度足够小的点电荷,以便能用它来确定电场中每一点 的性质。
(2)电量必须充分小,其引入电场后对原电荷及电场的分布的影响可以
忽略。
第九章 静电场的基本规律
二.点电荷的电场
r E 的方向
若q
0,
Er 沿rr0方向
若q 0, Er沿rr0反方向
如果点电荷q放置在无限大的均匀电介质中,电介
质的介电常数为 ,则空间各点的场强为,
1 q
E 4 r 2 r0
第九章 静电场的基本规律
三.场强叠加原理
在点电荷系的电场中,试探电荷 q0 所受的电场力等于
各个点电荷单独存在时对 q0的作用力的矢量和,
电荷的线密度,为小线元,带电体在点P激发的场
强为
r
E
r dE
L
dl r 40r 2 r0
★ 注意:在具体计算中,应建立
r
适当坐标系,写出dE在各坐标轴
方向上的分量式,分别积分计算
的各分量,在合成矢量 Er 。
第九章 静电场的基本规律
五.电场求解问题举例
l 例题1 一对等量异号点电荷-q和+q,相距为 ,求其连线的延长线
若均匀带电直线是无限长的,即θ1=0,
θ2= π,则
Ey 0
E
Ex
2 0a
第九章 静电场的基本规律 六.电场的图示法—电场线
电场线:在电场中做一些有方向的曲线,让曲线上每点的 切线方向和该点的场强方向一致,这样的曲线叫做电场线。
电场线密度:通过与该点电场方向垂直的单位面积上的电 场线条数。
在作电场线时,使电场中任一点的电场线密度与该点的场 强大小成正比,即
(2)电场线不构成闭合曲线(或者说电场线上各 点的电位沿电场线方向不断减小)。
第九章 静电场的基本规律
9-3 高斯定理
一.电通量 电通量:穿过电场中某曲面的电场线条数。用 e
表示。 (1)电场对开曲面的电通量
如下图(a)所示,设电场为匀强电场,根据电场线密 度的定义,穿过垂直于电场方向的平面S的电通量为
e ES
(a)
(b)
第九章 静电场的基本规律
F F1 F2 Fi Fn
由场强的定义,可得,
E
F
F1
F2
Fn
q0 q0 q0
q0
即
E E1 E2 En
第九章 静电场的基本规律
上式表明:电场中任一点处的总场强等于各点电荷单独存 在时在该点所产生的场强的矢量和,即场强叠加原理。
利用叠加原理,原则上可以计算任何带电体系所产生的电 场的场强分布。
r0
第九章 静电场的基本规律 (2)电荷分布为面分布的带电体在空间激发的场强
对于电荷的面分布,可取 dq dS ,其中
为电荷的面密度,dS为小面元, 带电体在点激发
的场强为
E
dE
S
dS 4 0r 2
r0
第九章 静电场的基本规律
(3)电荷分布为线分布的带电体在空间激发的场
强对于电荷的线分布,可取 ,dq dl 其中 为
dq
4 0r 2 r0
第九章 静电场的基本规律
在实际问题中,带电体按其形状特点,其电荷分布可简 化为体分布、面分布和线分布。
(1)电荷分布为体分布的带电体在空间激发的场强对于
电荷的体分布,可取 ,dq dV 其中
为电荷的体密度,dV 为物理小体元,带电体
在点激发的场强为
E
dE
V
dV 4 0r 2
第九章 静电场的基本规律
四.电场
“超距作用”观点:一个带电体所受到的电力是由另一 个带电体直接给予的。这种作用既不需要中间物质进行 传递,也不需要时间,而是从一个带电体立即到达另一 个带电体。
电荷
电场
“场”作用观点:两个电荷之间相互作用是由
电场传递的,需要时间。
电荷
电场
电荷
第九章 静电场的基本规律
4 0
0 的介电常F1数2 为,是q1表对表F征q1现2的2真的0为方空作斥8向特用.力8:性5力,当的,方1r0物q12向1理1为与2沿(量由Cqr1。2q22同方1指N号向向1时;方 m,当2 )
