最新解析几何专题二(焦点弦及焦点三角形)
抛物线焦点弦的性质及应用

抛物线焦点弦的性质及应用抛物线是一种具有特殊性质的二次曲线,它的焦点弦性质是指过焦点parabola. 抛物线上任意一点的切线与从焦点引出的该点的法线的交点,这些交点都在焦点所在的直线上。
抛物线焦点弦的性质和应用如下:1. 焦点弦与顶点:抛物线的焦点弦通过抛物线的顶点,且与抛物线的对称轴垂直相交。
2. 焦点弦的长度:焦点弦的长度等于抛物线焦点到对称轴的距离的两倍。
3. 焦点弦的切线方程:焦点弦的切线方程可由抛物线的切线方程推导得到,即通过抛物线上一点(x1,y1)的切线方程为y = mx + (1 - m²) a/4,其中m为切线的斜率,a为焦点到对称轴的距离。
4. 焦点弦的法线方程:焦点弦的法线方程可由切线方程得到,即过抛物线上一点(x1,y1)的法线方程为y = -x/m + (x1/m + y1)。
5. 焦点弦的性质应用:抛物线焦点弦的性质在物理学、工程学和几何学等领域有广泛的应用。
在物理学中,抛物线焦点弦的性质可以用于描述光线的反射和聚焦。
例如,在反射望远镜中,抛物面用于反射并聚焦光线,使观察者能够看到远处的物体。
在工程学中,抛物线焦点弦的性质可以用于设计抛物面反射器、喇叭等产品。
抛物面反射器可以将声音或者电磁波线聚焦在焦点处,以达到提高功率传输效果的目的。
类似地,喇叭的设计也借鉴了抛物线焦点弦的性质,使声音能够更好地聚焦并扩散。
在几何学中,抛物线焦点弦的性质可以用于求解问题。
例如,已知抛物线上一点的坐标和抛物线焦点的坐标,可以通过焦点弦性质来求解该点在抛物线上的位置。
另外,抛物线焦点弦的性质还可以进一步推广到三维空间中的抛物面。
三维空间中的抛物面也具有焦点弦的性质,可以用于描述反射、聚焦和求解问题等。
综上所述,抛物线焦点弦是抛物线特有的性质之一,它的性质和应用在物理学、工程学和几何学等领域有重要的应用。
深入理解和应用这些性质可以帮助我们更好地解决各种问题,并且进一步推广到更高维度的几何形状中。
高考解析几何复习专题

交点法探究:
①判别式;②根与系数关系:两根和、两根积(横坐标关系与纵坐标关系转换); ③数量关系转换(长度、角度、斜率、面积、向量关系或不等关系等转换); ④位置关系转换(平行或垂直或相交等)
x1 x2 x1x2
y1 y2 y1 y2
问 题
繁 与 简
关于交点法:交点法中的曲线与方程
关联特征转换典型题例关联特征转换非交点法应用题例数学语言转换数形特征转换圆锥曲线概念与基本量关系向量与数量关系转换已知点ab是椭圆的左右顶点f为左焦点点p是椭圆上异于ab的任意一点直线ap与过点b且垂直于x交于点m直线bpmn1求证
高考数学复习专题
解析几何-交点法
(高考全国卷解答题20题探究)
解析几何专题-交点法 1.数学思想:方程(组)思想 2. 问题特征:直线与圆锥曲线-相交弦 3. 途径方法:两式两线两法
焦半
|
PF
|
x0
p 2
, (P(x0,
y0 ) C
:
y2
2 px)
径:
注意:①抛物线方程有四种形式;
②焦半径对应四种不同表示方式
七、圆锥曲线问题类型
问题类型
一、求曲线或轨迹方程问题--方程(组)思想应用 (1)点与曲线-方程思想;(2)向量关系-特征转化; (3)特征量或特征量关系;(4)位置特征关系转化
4、路径选择、计算方法
交点法小练与思考 练习1 若直线
与椭圆
恒有公共点,
求实数 的取值范围
直线与曲线
练习2
已知椭圆
x
2
2
y2 1
1 的左右焦点分别为 F1、F2 ,若过点 P(0,-2)、F1 的直线交
椭圆于 A,B 两点,求 ABF2 的面积
21-22版:专题突破二 焦点弦的性质(步步高)

专题突破二 焦点弦的性质抛物线的焦点弦是考试的热点,有关抛物线的焦点弦性质较为丰富,对抛物线焦点弦性质进行研究获得一些重要结论,往往能给解题带来新思路,有利于解题过程的优化.一、焦点弦性质的推导例1 抛物线y 2=2px (p >0),设AB 是抛物线的过焦点的一条弦(焦点弦),F 是抛物线的焦点,A (x 1,y 1),B (x 2,y 2)(y 1>0,y 2<0),A ,B 在准线上的射影为A 1,B 1.证明:(1)x 1x 2=p 24,y 1y 2=-p 2; (2)若直线AB 的倾斜角为θ,则|AF |=p 1-cos θ,|BF |=p 1+cos θ; (3)|AB |=x 1+x 2+p =2p sin 2θ(其中θ为直线AB 的倾斜角),抛物线的通径长为2p ,通径是最短的焦点弦;(4)1|AF |+1|BF |=2p为定值; (5)S △OAB =p 22sin θ(θ为直线AB 的倾斜角); (6)以AB 为直径的圆与抛物线的准线相切;(7)A ,O ,B 1三点共线,B ,O ,A 1三点也共线.考点 抛物线中过焦点的弦长问题题点 与弦长有关的其它问题证明 (1)①当AB ⊥x 轴时,不妨设A ⎝⎛⎭⎫p 2,p ,B ⎝⎛⎭⎫p 2,-p , ∴y 1y 2=-p 2,x 1x 2=p 24. ②当AB 的斜率存在时,设为k (k ≠0),则直线AB 的方程为y =k ⎝⎛⎭⎫x -p 2, 代入抛物线方程y 2=2px ,消元得y 2=2p ⎝⎛⎭⎫y k +p 2,即y 2-2py k-p 2=0,∴y 1y 2=-p 2,x 1x 2=p 24. (2)当θ≠90°时,过A 作AG ⊥x 轴,交x 轴于G ,由抛物线定义知|AF |=|AA 1|,在Rt △AFG 中,|FG |=|AF |cos θ,由图知|GG 1|=|AA 1|,则p +|AF |cos θ=|AF |,得|AF |=p 1-cos θ, 同理得|BF |=p 1+cos θ; 当θ=90°时,可知|AF |=|BF |=p ,对于|AF |=p 1-cos θ,|BF |=p 1+cos θ亦成立, ∴|AF |=p 1-cos θ,|BF |=p 1+cos θ. (3)|AB |=|AF |+|BF |=x 1+x 2+p=p 1-cos θ+p 1+cos θ=2p sin 2θ≥2p , 当且仅当θ=90°时取等号. 故通径为最短的焦点弦.(4)由(2)可得,1|AF |+1|BF |=1-cos θp +1+cos θp =2p. (5)当θ=90°时,S △OAB =12×2p ×p 2=p 22, 故满足S △OAB =p 22sin θ; 当θ≠90°时,设直线AB :y =tan θ⎝⎛⎭⎫x -p 2, 原点O 到直线AB 的距离d =⎪⎪⎪⎪p 2tan θ1+tan 2θ=p 2sin θ,S △OAB =d 2|AB |=p 4sin θ×2p sin 2θ=p 22sin θ. (6)如图:⊙M 的直径为AB ,过圆心M 作MM 1垂直于准线于点M 1,则|MM 1|=|AA 1|+|BB 1|2=|AF |+|BF |2=|AB |2, 故以AB 为直径的圆与准线相切.(7)设直线AB 的方程:x =my +p 2,代入y 2=2px 得y 2-2pmy -p 2=0.由(1)可得y 1y 2=-p 2.因为BB 1∥x 轴,∴B 1⎝⎛⎭⎫-p 2,y 2,即B 1⎝⎛⎭⎫-p 2,-p 2y 1, 1OB k =-p 2y 1-p 2=2p y 1=y 21x 1×1y 1=y 1x 1=k OA , 所以OB 1→∥OA →且公共点为O ,所以直线AB 1过点O .所以A ,O ,B 1三点共线,同理得B ,O ,A 1三点共线.二、焦点弦性质的应用例2 (1)设F 为抛物线C :y 2=3x 的焦点,过F 且倾斜角为30°的直线交C 于A ,B 两点,O 为坐标原点,则△OAB 的面积为( )A.334B.938C.6332D.94考点 抛物线中过焦点的弦长问题题点 与弦长有关的其它问题答案 D解析 方法一 由题意可知,直线AB 的方程为y =33⎝⎛⎭⎫x -34, 代入抛物线的方程可得4y 2-123y -9=0,设A (x 1,y 1),B (x 2,y 2),则y 1+y 2=33,y 1y 2=-94, 故所求三角形的面积为12×34×(y 1+y 2)2-4y 1y 2=94. 方法二 运用焦点弦倾斜角相关的面积公式,则S △OAB =p 22sin θ=942sin 30°=94. (2)已知F 为抛物线C :y 2=4x 的焦点,过F 作两条互相垂直的直线l 1,l 2,直线l 1与C 交于A ,B 两点,直线l 2与C 交于D ,E 两点,则|AB |+|DE |的最小值为( )A .16B .14C .12D .10考点 抛物线中过焦点的弦长问题题点 与弦长有关的其它问题答案 A解析 方法一 抛物线C :y 2=4x 的焦点为F (1,0),由题意可知l 1,l 2的斜率存在且不为0.不妨设直线l 1的斜率为k ,l 1:y =k (x -1),l 2:y =-1k(x -1), 由⎩⎪⎨⎪⎧y 2=4x ,y =k (x -1),消去y 得k 2x 2-(2k 2+4)x +k 2=0, 设A (x 1,y 1),B (x 2,y 2),则x 1+x 2=2k 2+4k 2=2+4k2, 由抛物线的定义可知,|AB |=x 1+x 2+2=2+4k 2+2=4+4k2. 同理得|DE |=4+4k 2,∴|AB |+|DE |=4+4k 2+4+4k 2=8+4⎝⎛⎭⎫1k 2+k 2≥8+8=16, 当且仅当1k 2=k 2,即k =±1时取等号, 故|AB |+|DE |的最小值为16.方法二 运用焦点弦的倾斜角公式,注意到两条弦互相垂直,设直线AB 的倾斜角为θ,则θ≠π2且θ≠0, 因此|AB |+|DE |=2p sin 2θ+2p sin 2⎝⎛⎭⎫π2+θ =4sin 2θ+4cos 2θ=4sin 2θcos 2θ=16sin 22θ≥16. 当且仅当θ=π4或34π时,等号成立. 点评 上述两道题目均是研究抛物线的焦点弦问题,涉及抛物线焦点弦长度与三角形面积,从高考客观题快速解答的要求来看,常规解法显然小题大做了,而利用焦点弦性质,可以快速解决此类小题.跟踪训练 过抛物线y 2=2x 的焦点F 作直线交抛物线于A ,B 两点,若|AB |=2512,|AF |<|BF |,则|AF |=________.考点 抛物线中过焦点的弦长问题题点 与弦长有关的其它问题答案 56解析 由于y 2=2x 的焦点坐标为⎝⎛⎭⎫12,0,由题意知A ,B 所在直线的斜率存在,设A ,B 所在直线的方程为y =k ⎝⎛⎭⎫x -12,A (x 1,y 1),B (x 2,y 2),x 1<x 2, 将y =k ⎝⎛⎭⎫x -12代入y 2=2x ,得k 2⎝⎛⎭⎫x -122=2x , ∴k 2x 2-(k 2+2)x +k 24=0. ∴x 1x 2=14. 而|AB |=x 1+x 2+p =x 1+x 2+1=2512, ∴x 1+x 2=1312.又|AF |<|BF |,∴x 1=13,x 2=34. ∴|AF |=x 1+p 2=13+12=56.1.过抛物线y =2x 2的焦点且垂直于它的对称轴的直线被抛物线截得的弦长为( )A .2B .1 C.14 D.12考点题点答案 D2. 直线l 过抛物线y 2=4x 的焦点,与抛物线交于A ,B 两点,若|AB |=8,则直线l 的方程为( )A .y =-x +1B .y =x -1C .y =-x +1或y =x -1D .以上均不对考点题点答案 C 解析 由焦点弦长|AB |=2p sin 2α(α为直线AB 的倾斜角), ∴8=4sin 2α,sin 2α=12, 则tan α=±1,又直线过抛物线焦点,∴直线l 的方程为y =-x +1或y =x -1.故选C.3.直线l 过抛物线y 2=-2px (p >0)的焦点,且与该抛物线交于A ,B 两点,若线段AB 的长是8,AB 的中点到y 轴的距离是2,则此抛物线的方程是( )A .y 2=-12xB .y 2=-8xC .y 2=-6xD .y 2=-4x 答案 B解析 设A (x 1,y 1),B (x 2,y 2),根据抛物线的定义可知|AB |=-(x 1+x 2)+p =8.又AB 的中点到y 轴的距离为2,∴-x 1+x 22=2,∴x 1+x 2=-4,∴p =4,∴所求抛物线的方程为y 2=-8x .故选B.4.过抛物线y 2=4x 的焦点作直线交抛物线于点A (x 1,y 1),B (x 2,y 2),若|AB |=7,则AB 的中点M 到抛物线准线的距离为________________.考点题点答案 72 解析 抛物线的焦点为F (1,0),准线方程为x =-1.由抛物线定义知|AB |=|AF |+|BF |=x 1+x 2+p ,即x 1+x 2+2=7,得x 1+x 2=5,于是弦AB 的中点M 的横坐标为52,又准线方程为x =-1,因此点M 到抛物线准线的距离为52+1=72. 5.过抛物线焦点F 的直线与抛物线相交于A ,B 两点,若点A ,B 在抛物线准线上的射影分别为A 1,B 1,则∠A 1FB 1为________.考点题点答案 90°解析 设抛物线方程为y 2=2px (p >0),如图.∵|AF |=|AA 1|,|BF |=|BB 1|,∴∠AA 1F =∠AF A 1,∠BFB 1=∠FB 1B .又AA 1∥Ox ∥B 1B ,∴∠A 1FO =∠F A 1A ,∠B 1FO =∠FB 1B ,∴∠A 1FB 1=12∠AFB =90°.。
焦点三角形问题(解析版)

第一篇圆锥曲线专题01焦点三角形问题焦点三角形的边角关系如下:三条边:122F F c =122PF PF a+==22a c +三角形周长ce a=222a b c =+三个角:随着动点P 的移动,三个角都在变化,可能为锐角,直角和钝角,这里我们只研究顶角P ∠,利用余弦定理,P ∠又和三边a,b,c 的大小有关系三角形的面积:12S ah =底为定值,面积最大时高最大1sin 2S ab c =面积和三边长有关系一、与焦点三角形边长有关的问题焦点三角形中三边长涉及a,c ,因此最直观的是可以根据三边关系求出离心率的值或取值范围,前提是三边之间存在可以转化的关系。
若单独分析三角形的两个腰长,则若能够构成三角形,则需满足1a c PF a c-≤≤+例1椭圆22221x y a b+=的右焦点为F ,其右准线与x 轴的交点为A ,在椭圆上存在一点P ,满足线段AP 的垂直平分线过点F ,则椭圆的离心率的取值范围是________.例2.已知12,F F 是椭圆22221x y a b+=的左右焦点,若在其右准线上存在点P ,使得线段1PF 的中垂线过点2F ,则椭圆的离心率的取值范围是________.【解析】求离心率的范围问题,需要根据条件列出不等式,在含有动点的题目中,需要找出动态的量和常量之间的大小关系。
题目中:2122PF F F c==因为点P 在右准线上下移动,2PF 虽然是常量,但由于不知道a,b,c 的关系,因此还是相对的变量。
本题的定值为22a F H c c=-在2RT PHF 中,222,2a PF F H c c c >≥-解得:313e ≤<例3.设12,F F 是双曲线2214x y -=的左右焦点,点P 在双曲线上,且满足1290F PF ︒∠=,则12PF F ∆的面积是________.方法一:方法二:此题目有更简单的做法,方法一只是为了巩固焦半径的知识,设12,PF x PF y ==则有:4x y -=,又因为2220x y +=解得:2xy =,因此面积等于1.上面两题都是关于焦点三角形中两条腰长的问题,在焦点三角形中两腰长之和为2a ,底边为2c ,因此三边之间暗含离心率的关系,因此在一些出现焦点三角形求离心率的问题中一般腰长和底边之间都存在一个可以互相转化的关系,通过这个关系可以求出离心率。
焦点三角形的性质(经典!必看)

(1)由题设2|F
F2|=|PF1|+|PF2|
2a=4,又2c=2,∴b=3
422yx=1.
设∠F
PF2=θ,则∠PF2F1=60°-θ
1e
60sin(
3sin)60sin(120sin)180sin(21oooo,
5sinθ=3(1+cosθ)
1bbPFPFSPFF
),0(1
222ba
yax左右两焦点分别为,,21FF设焦点三角
1FPF,若21PFF最大,则点P为椭圆短轴的端点。
),(
oyxP,由焦半径公式可知:oexaPF1,oexaPF1
1PFF中,
122121212cosPFPFFFPFPF21221221242)(PFPFcPFPFPFPF
(余)弦定理、内角和定理、面积公式等.
1 椭圆上一点P到焦点
1,FF的距离之差为2,试判断21FPF的形状.
:由1
1622yx椭圆定义:
||,5||.2||||,8|||
12121PFPFPFPFPFPF.
又4||
1FF,故满足:,||||||2122122PFFFPF故21FPF为直角三角形.
sin)180sin(1221PFPFFFo
sin)sin(2121PFPFFF
sin(2)sin(21cFF,sinsin2sinsin21aPFPF
sin)sin(ace。
F
(-1,0)、F2(1,0),P为椭圆上一点,且|F1F2|是|PF1|和|PF2|
求椭圆的方程;
若点P在第三象限,且∠PF
.
),0(1
222ba
怎样解答与焦点三角形有关的问题

焦点三角形是指由椭圆或双曲线上一点与两个焦点构成的三角形.焦点三角形较为特殊,其一条边为椭圆的长轴或双曲线的实轴.与焦点三角形有关的问题经常出现在解析几何试题中.下面结合实例来探讨一下与焦点三角形有关的问题的解法.一、根据椭圆或双曲线的定义求解解答椭圆和双曲线中焦点三角形问题,首先要明确这两种圆锥曲线的几何特征和定义.椭圆的定义:平面内与两个定点F1、F2的距离的和等于常数(大于|F1F2|)的点的轨迹.若P为椭圆上一点,根据椭圆的定义可得|PF1|+|PF2|=2a.双曲线的定义:平面内与两个定点F1、F2的距离的差的绝对值等于常数(小于|F1F2|)的点的轨迹,用代数式可表示为||PF1|-|PF2||=2a.若∠F1PF2=θ,根据椭圆的定义可知(1)4c2=|PF1|2+|PF2|2-2|PF1||PF2|·cosθ;(2)S△PF1F2=|PF1||PF2|·sinθ;(3)焦点三角形的周长为2(a+c).对于双曲线,也有类似的性质.例1.已知双曲线的中心在原点,两个焦点F1,F2的坐标分别为()5,0和()-5,0,点P在双曲线上,且PF1⊥PF2,ΔABC的面积为2,则双曲线的方程为.解:设||PF1=r1,||PF2=r2,根据双曲线的第一定义可知,||r1-r2=2a,因为PF1⊥PF2,所以r21+r22=||F1F22,可得ìíîïïïïr21+r22=20,SΔABC=12r1r2=2,||r1-r2=2a,解得a2=3,而c=5,所以b2=2,可得双曲线方程:x23-y22=1.此题比较简单,根据题目中的垂直关系,利用双曲线的定义和三角形的面积公式即可建立关于||PF1、||PF2的方程组,解方程组就可以求出双曲线的方程.例2.已知椭圆C1与双曲线C2有相同的焦点F1,F2,曲线C1和C2的一个交点为P,且PF1⊥PF2,则C1的离心率e1与C2的离心率e2一定满足的关系是().A.e1+e2=2B.1e1+1e2=2C.e21+e22=2D.1e21+1e22=2解:设椭圆C1的方程为x2a21+y2b21=1,双曲线C2的方程为x2a22-y2b22=1,点P在第一象限,半焦距为c.则||PF1+||PF2=2a1,||PF1-||PF2=2a2,所以||PF1=a1+a2,||PF2=a1-a2,因为PF1⊥PF2,||PF12+||PF22=4c2,所以a21+a22=2c2,所以æèçöø÷a1c2+æèçöø÷a2c2=2,即1e21+1e22=2.解答本题,需利用椭圆与双曲线的定义,借助勾股定理建立关于||PF1、||PF2的方程,然后将其转化为a、c的方程,根据圆锥曲线离心率公式e=c a,得到e1、e2的关系式.二、根据正余弦定理求解若三角形ABC的三个内角的对边为a、b、c,则有正弦定理:asin A=b sin B=c sin C=2R.余弦定理:a2=b2+c2-2bc cos A;b2=c2+a2-2ca cos B;c2=a2+b2-2ab cos C.在解答与焦点三角形有关的问题时,可根据正余弦定理建立关于焦点三角形三边的关系式,通过解方程求考点透视36丈丈丈丈数列求和问题是高考数学试题中的“常客”.这类问题的命题形式多变,侧重于考查等差、等比数列的性质、通项公式、前n 项求和公式.解答此类问题的常用方法有分类讨论法、并项求和法、倒序相加法、裂项相消法等.本文主要介绍分类讨论法、倒序相加法和裂项相消法.一、分类讨论法有时数列中出现几类具有不同特征的项,此时需采用分类讨论法来求数列的和.运用分类讨论法求数列的和,需根据数列中各项的特点,对n 进行分类讨论,如分奇数项、偶数项,分整数项、分数项,分正数项、负数项等.运用该方法解题,需仔细观察数列的通项公式的结构或数列中各项的特点,并确定分类的标准,然后逐类进行讨论,求出各类数列的和,最后综合所得的结果即可解题.例1.已知数列{a n }的前n 项和为S n ,S 2=4,a n +1=2S n +1.(1)求{a n }的通项公式;(2)求数列{|a n -n -2|}的前n 项和.解:(1)数列n 的通项公式是a n n -1.(过程略)(2)设b n =||3n -1-n -2,则b 1=2,b 2=1,当n ≥3时,3n -1>n +2,可得b n =3n -1-n -2,n ≥3,设数列{b n }的前n 项和为T n ,则T 1=2,T 2=3.当n ≥3时,T n =3+9()1-3n -21-3-()n +7()n -22=3n-n 2-5n +112,故T n =ìíîïï2,(n =1)3n -n 2-5n +112.()n ≥2数列{b n }的通项公式中含有绝对值,经分析可知,当n =1、2时和当n ≥3时数列的前n 项和式不一样,因此需采用分类讨论法,分别讨论当n =1、2时和当n ≥3时数列的通项公式和前n 项和,最后综合所有情况即可.二、倒序相加法倒序相加法是求数列前n 项和的常用方法之一,考点透视。
解析几何中焦点相关的常用结论

抛物线焦点弦的性质及应用在直线与抛物线的关系中,过抛物线焦点的直线与抛物线的关系尤为重要,它有一些重要且实用的性质.这些性质通常是解决相关问题的切人点,起着举足轻重的工具性作用,有必要认真领会、系统掌握.但教材中对其相关性质并没有明确而规范的逐一落列,只能靠教学者自身提炼、总结和归纳.现将其有关性质进行探讨和研究设抛物线的方程为y 2=2px(P >0),过焦点F(p2,0)作倾斜角为θ的直线,交抛物线于P 、Q 两点,则线段PQ 称抛物线的焦点弦,(如图1).抛物线的焦点弦具有以下性质.性质1:已知过抛物线22(0)y px p =>的焦点F 的直线交抛物线于1122(,),(,)A x y B x y 两点,则12AB x x p =++例1、过抛物线24y x =的焦点做直线交抛物线于1122(,),(,)A x y B x y 两点,如果126x x +=,那么AB =变式:过抛物线24y x =的焦点做直线交抛物线于,A B 两点,如果8AB =,O 为坐标原点,则OAB ∆的重心的横坐标是性 质2: A 、B 两点的横坐标之积,纵坐标之积为定值。
即x 1x 2=42p , y 1y 2=-p 2证明:当直线AB 斜率存在时,设AB 的方程为:y=k(x -2p ),代入抛物线得4k 2x 2-4p(k 2+2)x+k 2p 2=0,设A (x 1,y 1)、B (x 2,y 2),由韦达定理得x 1x 2=42p 为定值;而|y 1y 2|=12px ·12px =212x x p =2p ·2p =p 2. ∴y 1y 2=-p 2。
当直线AB 斜率不存在时,易证上式结论成立。
例1:过抛物线焦点的一条直线与它交于两点P 、Q ,通过点P 和抛物线顶点的直线交准线于点M ,求证:直线MQ 平行与抛物线的对称轴.证明:为了方便比较,可将P 点横坐标及Q 点纵坐标均用P 点的纵坐标y 1表示.∴P(y 212p ,y 1),Q(x 2,y 2),但y 1y 2=-p 2,∴y 2=﹣p 2y 1,P M 方程是:y=2p y 1x,当x=﹣p 2时,y=﹣p 2y 1即为M 点的纵坐标,这样M 点与Q 点的纵坐标相同,故MQ ∥Ox.例2:设抛物线y 2=2px (p>0)的焦点为F ,经过点F 的直线交抛物线于A 、B ,点C 在抛物线的准线上,且BC//x 轴,则直线AC 经过原点O证明:设A (x 1,y 1),B(x 2,y 2),则C(-2p ,y 2),直线AB 的方程为:y=k(x -2p),代入抛物线得: y 2-22p y kp-=0, ∴y 1y 2=-p 2. K co =py 22-,K ao =11x y ,∴K co - K ao =11x y p y 22+=2112y p y ⋅p y 22+=121222y p y y p ⋅+=0,即K co =K ao ,∴A 、C 、O 三点共线,即直线AC 经过原点O 。
双曲线微专题二 焦点三角形问题

双曲线微专题二:双曲线中焦点三角形问题题型一 焦点三角形的周长问题12PF F ∆由两焦点和双曲线上一点形成,我们把这种三角形叫焦点三角形. 求焦点三角形的周长时,通常会利用双曲线的第一定义.例1:椭圆y 249+x 224=1与双曲线y 2-x 224=1有公共点P ,则P 与双曲线两焦点连线构成三角形的周长为( )解:由已知得椭圆与双曲线具有共同的焦点F 1(0,5)和F 2(0,-5),又由椭圆的定义可得1214PF PF +=又1210F F =因此P 与双曲线两焦点连线构成三角形的周长为24。
整理:已知双曲线x 2a 2-y 2b 2=1(a >0,b >0),其焦点为F 1、F 2,过F 1作直线交双曲线同一支于A 、B 两点,且|AB |=m ,则△ABF 2的周长是4a +2m简要证明:由双曲线的定义知,|AF 2|-|AF 1|=2a ,(1)|BF 2|-|BF 1|=2a ,(2) 又|AF 1|+|BF 1|=|AB |=m ,(3)∴由(1),(2),(3)得|AF 2|+|BF 2|=4 a+m . 故△ABF 2的周长为|AF 2|+|BF 2|+|AB |=4 a+2m .例2:已知双曲线的左、右焦点分别为F 1,F 2,在左支上过F 1的弦AB 的长为5,若2a =8,那么△ABF2的周长是( ) A .16B .18C .21D .26解:如图所示,由双曲线的定义知,|AF 2|-|AF 1|=8,(1)|BF 2|-|BF 1|=8,(2)又|AF 1|+|BF 1|=|AB |=5,(3)∴由(1),(2),(3)得|AF 2|+|BF 2|=21.故△ABF 2的周长为|AF 2|+|BF 2|+|AB |=26.答案 D练习:1.如果12,F F 分别是双曲线191622=−y x 的左、右焦点,AB 是双曲线左支上过点1F 的弦,且||6AB =,则2ABF ∆的周长是 .(28)2.若12,F F 分别是双曲线22x y 1m 7−=的左、右焦点,AB 是双曲线左支上过点1F 的弦,且||4=AB ,2ABF ∆的周长是20,则m= 答案:题型二 焦点三角形的面积问题求焦点三角形的面积时,通常会利用双曲线的定义、正弦定理、余弦定理等,焦点三角形的面积主要有两种求法:1212121211sin =2c |y |22PF F PF F P S r r F PF S =∠ 和。
专题2 焦长焦比体系

专题2 有凤来仪——焦长与焦比体系第一讲 椭圆焦长以及焦比问题4a 体:过椭圆22221(0)x y a b a b +=>>的左焦点1F 的弦AB 与右焦点2F 围成的三角形2ABF △的周长是4a ;焦长公式:A 是椭圆22221(0)x y a b a b+=>>上一点,1F 、2F 是左、右焦点,12AF F ∠为α,AB 过1F ,c 是椭圆半焦距,则:(1)21||cos b AF a c α=-;(2)21||cos b BF a c α=+;(3)2222222222||cos sin ab ab AB a c b c αα==-+.图1-1-1证明 (1)如图1-1-1所示,12||||2AF AF a ;12||||2BF BF a ,故22||||||4AB AF BF a ; (2)设1||AF m ,1||BF n ,2||2AF a m ,2||2BF a n ,由余弦定理得 222(2)(2)2(2)cos mc a m m c ;整理得21||cosb AF ac ①同理:222(2)(2)2(2)cos(180)nc a n n c ;整理得21||cosb BF ac ②①+②得,则过焦点的弦长:2222222222||cos sin ab ab AB m na cbc ③焦比定理 过椭圆22221x y a b +=的左焦点1F 的弦21||cos b AF a c α=-,21||cos b BF a c α=+,令11||||AF F B ,即221coscoscos1b b e ac a c ④,代入焦长公式①可得21(1)||2b AF a⑤.推论 根据公式1cos1e ,利用tan k α=把角度替换掉可以得到e =注意:1.整个焦长体系只需要记住上面~①⑤的公式,其他要熟悉推导,涉及到的面积问题记住是焦长当底即可;当直线过右焦点,或者上焦点、下焦点时,要熟悉此时的公式会如何变化,详见后面记忆方法处. 2.学习焦长焦比体系要非常熟悉推导过程[定义+余弦定理+abc 平方关系],在处理解答题的时候,若用本模块公式到必须给出必要证明. 3.公式1cos1e 和21(1)||2b AF a这两个公式属于结论公式,一般用上能很快解题,所以在解小题的时候要优先考虑这两个公式.和角度相关优先想第一个,只和长度相关优先想第二个.4.焦长公式利用极坐标或第二定义都能更快证明,这个问题大家可以自己去掌握,解答题中的证明建议以余弦定理的方式为主;其他证法本文不在阐述,读者可以自己去掌握.[长短记忆法: 画图,看长短来记忆.当焦点在x 轴上的时候,焦长为2cos b a c ,其中为焦长所在直线的倾斜角或者其补角,为方便判断,一般选用锐角记为.例如上图,如果记12AF F ∠为,那么根据草图1||AF 为长边,则分母小即可得到21||cosb AF ac ,不管交于左右都是如此,交于y 轴的话需要把cos 换成sin .焦比公式,如果1cos1e ,为两个焦长之比,可以选=长短也可以=短长,但是公式里面要正负对齐,如果选的是锐角,那么左侧是正的,右侧也要为正的,此时=长短;反之选钝角,右侧=短长最后一个公式一样的,2(1)2b a,代入的=长短算出来的就是长边,如果代入的=短长,算出来就是短边][口诀记忆法:椭圆的焦点在x 轴的时候,直线过左焦点时,为上减下加;交于右支时,相反,上加下减; 同理,焦点在y 轴时,直线过上焦点时,为左减右加;过下焦点时,相反,为左加右减. 备注:此方法的角度选择均为直线的倾斜角.简短口诀为, “右下焦点对应上加下减,左加右减;反之颠倒.” 此方法角度均选直线的倾斜角.交于y 轴的话分母需要把cos 换成sin例:上图中1||AF 在左侧,如果直线过右焦点的时候焦长为上加下减,过左焦点的时候是颠倒的,1||AF 在上方,所以分母为减.]【例1】(张家口期中)椭圆22:1164x y E +=的左焦点为1F ,过1F 的直线交椭圆于A ,B 两点,则2ABF ∆的周长为( ) A .4B .8C .12D .16【例2】(乐山期中)已知椭圆22:143x y C +=的左、右焦点分别为1F 、2F ,过2F 且倾斜角为4π的直线l 交椭圆C 于A 、B 两点,则△1F AB 的内切圆半径为 .【例3】(天心月考)已知椭圆2222:1(0)x y C a b a b +=>>的离心率12e =,3(1,)2D 为椭圆上一点.(1)求椭圆C 的方程;(2)已知F 为椭圆C 的右焦点,过点F 的直线l 交椭圆(异于椭圆顶点)于A 、B 两点,试判断11||||AF BF +是否为定值?若是,求出该定值;若不是,说明理由.【例4】(唐山模拟)设1F ,2F 分别是椭圆2222:1(0)x y E a b a b+=>>的左、右焦点,过2F 的直线交椭圆于A ,B 两点,且120AF AF =,222AF F B =,则椭圆E 的离心率为( )A .23B .34C D 【例5】(2019•新课标△)已知椭圆C 的焦点为1(10)F -,,2(10)F ,,过2F 的直线与C 交于A ,B 两点.若22||2||AF F B =,1||||AB BF =,则C 的方程为( )A .2212x y +=B .22132x y +=C .22143x y +=D .22154x y +=【例6】(浙江模拟)已知1F 、2F 为椭圆2222:1(0)x y C a b a b+=>>的左、右焦点,过左焦点1F 的直线交椭圆于M 、N 两点,若2MF x ⊥轴,且14MN NF =-,则椭圆的离心率为( ) A .13B .12CD【例7】(南通月考)已知椭圆C ;22221(0)x y a b a b+=>>的左右顶点为A ,B ,点P 为椭圆C 上不同于A ,B 的一点,且直线PA ,PB 的斜率之积为12-.(1)求椭圆的离心率;(2)设(10)F -,为椭圆C 的左焦点,直线l 过点F 与椭圆C 交与不同的两点M ,N ,且3MF FN =,求直线l 的斜率.注意 在解答题当中不能直接使用焦长公式以及涉及的结论,用到的公式必须要证明过程.在上面的解法二中,可以发现过焦点问题能够使用焦长体系能够轻松破解,但要注意不是所有考题都是焦长体系,要会鉴别,也要了解普通方法如何处理.第二讲 双曲线的焦点三角形问题周长问题:双曲线22221x y ab (00)a b >>,,的两个焦点为1F 、2F ,弦AB 过左焦点1F (A 、B 都在左支上),||AB l =,则2ABF △的周长为42a l (如图)图1-2-1 图1-2-2 图1-2-3设A 是双曲线22221x y a b (00)a b >>,上一点,设12AF F ∠为α,直线AB 过点1F .(1)直线和渐近线平行时,此时1=cose (2)当AB 交双曲线于一支时,则21; cos b AF a c α=+21; cos b BF a c α=- 2222222222||cos sin ab ab AB a c b c αα==-+,22222||cos ab AB a c,2221cos 01cos a c e令11||||BF F A ,即221coscos cos1b b e ac a c ,代入弦长公式可得21(1)||2b BF a. 当AB 交双曲线于两支时,21; cos b AF a c α=+21; cos b BF c aα=-22222||cos ab AB c a , 2221coscosac e(图1-2-3),令11||||BF F A ,221cos(1)coscos1b b ec aa c ,代入弦长公式可得21(1)||2b BF a.=长(其中)短[总结:焦点在x 轴上的时候,直线和双曲线交于单支的时候,公式形式和椭圆完全一样; 直线和双曲线交于双支的时候,公式形式有所变化,具体参考上面书写] 因为双曲线的部分考题会涉及渐近线,不过焦点的时候更要注意,注意鉴别.【例8】(全国期中)已知1F ,2F 是双曲线22221x y a b-=的左、右焦点,过1F 作直线交双曲线左支于点A ,B ,若||AB m =,则2ABF △的周长为 .【例9】(和平期中)已知F 为双曲线22221(00)x y a b a b-=>>,的左焦点,定点A 为双曲线虚轴的一个端点,过F ,A 两点的直线与双曲线的一条渐近线在y 轴右侧的交点为B ,若3AB FA =,则此双曲线的离心率为 .【例10】(浏阳月考)已知双曲线2222:1(0)x y C a b a b-=>,的左、右焦点分别为1F ,2F ,过2F 的直线与双曲线C 的右支相交于P ,Q 两点,若223PF F Q =,若1PQF △是以Q 为顶角的等腰三角形,则双曲线的 离心率e =( )A .3B .2C D 【例11】(宁夏模拟)F 是双曲线2222:1(0,0)x y C a b a b-=>>的右焦点,过点F 向C 的一条渐近线引垂线,垂足为A ,交另一条渐近线于点B .若2AF FB =,则C 的离心率是( )AB .2C D 【例12】(江油期中)已知A ,B ,C 是双曲线22221(0,0)x y a b a b-=>>上的三个点,直线AB 经过原点O ,AC 经过右焦F ,若BF AC ⊥,且3AF CF =,则该双曲线的离心率为( )A B .52C D .23第三讲 抛物线焦长公式及性质图1-3-1 图1-3-2 重要结论 1.||||1cos 1cos p pAF BF αα==-+. 2.1222||sin pAB x x p. 3.22sin AOBp S α=△. 4.设||||AF BF λ=,则11cos ;||12AF p λλαλ-+==+. 5.设AB 交准线于点P ,则||cos ||AF PA α=;||cos ||BF PB α=.证明1.||||||||||||cos 1cos AC AF p AF p ED AC AF θθ=⎧⇒=⎨==--⎩,同理||1cos pBF α=+.2.22||||||1cos 1cos sin pp pAB AF BF . 3.设O 到AB 的距离为d ,则 sin 2pd α=,故22112||sin22sin 22sinAOBp pp S AB d △. 4.||1cos 1cos ||1cos 1AF BF αλλλααλ+-=⇒=⇒=-+,1||1cos 2p AF p λα+==-.5.||2A p AF x =+,||2B pBF x =+,||cos ||AF PA α=,||cos ||BF PB α=.关于抛物线22x py 的焦长公式及定理(A 为直线与抛物线右交点,B 为左交点,90α<为AB 倾斜角)1.||1sin p AF α=-;||1sin pBF α=+.2.1222||cos pAB y y p. 3.22cosAOBp S △.4.设||||AF BF λ=,则1sin 1λαλ-=+;1||2AF p λ+=.5.设AB 交准线于点P ,||||sin ;sin ||||AF BF PA PB αα==. [总结:抛物线焦点在x 轴的时候的,焦长为1cos p ,1cos 1λαλ-=+,焦长也12p λ+,记忆方法参考椭圆模块;当焦点在y 轴上的时候cos 换成sin]【例13】(天河一模)已知抛物线2:8C y x =的焦点为F ,直线2)y x =-与C 交于A ,(B A 在x 轴上方)两点,若AF mFB =,则实数m 的值为( )AB .3C .2D .32【例14】(岳阳模拟)已知抛物线的方程为24y x =,过其焦点F 的直线与抛物线交于A 、B 两点,且||3AF =,O 为坐标原点,则AOF △的面积和BOF △的面积之比为( )A .12B C D .2【例15】(赤峰一模)如图,过抛物线22(0)y px p =>焦点F 的直线l 交抛物线于点A 、B ,交其准线于点C ,若||2||BC BF =,且||3AF =,则此抛物线的方程为( )A .23y x =B .29y x =C .232y x =D .292y x =【例16】(2017•新课标△)已知F 为抛物线2:4C y x =的焦点,过F 作两条互相垂直的直线1l ,2l ,直线1l 与C 交于A 、B 两点,直线2l 与C 交于D 、E 两点,则||||AB DE +的最小值为( )A .16B .14C .12D .10【例17】(德州期末)已知抛物线22(0)y px p =>的焦点为F ,过F 的直线l 交抛物线于1(A x ,1)y ,2(B x ,2)y 两点(点A 在第一象限),则下列结论中正确的是( ) A .2124p x x =B .114||||AF BF p+=C .若直线l 的倾斜角为3π,则||3||AF BF =D .若直线的倾斜角为6π,则||4AB p =第四讲 过焦点的面积最值问题4a 体面积:222222222||122sin 2sin 22cos sin ABFAB h ab ab c S c a c b c αααα===-+△. 22222||sin 2sin AOB AB h ab c S b c αα==+△, 222222222222||122sin 22sin 22cos sin sin sin ABF AB h ab ab c ab cS c b a c b c c αααααα==⋅⋅==-++△分母属于一个对勾函数模型,取得最值得条件在于b 与c 的大小比较,或者说离心率范围. ①当cb ,即22e时,22sin2sinb c bc ,当仅当sinbc时等号成立,此时22max22ABF ab c S ab bc△. ②当cb ,即22e 时,22222sinsinb c bca,当sin1时等号成立,此时22max 2ABF b cS a△. 【例18】(宝安期末)设椭圆中心在坐标原点,焦点在x 轴上,一个顶点坐标为(20),. (1)求这个椭圆的方程;(2)若这个椭圆左焦点为1F ,右焦点为2F ,过1F 且斜率为1的直线交椭圆于A 、B 两点,求2ABF ∆的面积.【例19】(武进期末)已知F 为椭圆22:132x y C +=的左焦点,过F 作两条互相垂直的直线1l ,2l ,直线1l 与C 交于A ,B 两点,直线2l 与C 交于D ,E 两点,则四边形ADBE 的面积最小值为( )A .4B .277C .9625D .195【例20】(南关期末)已知椭圆2222:1(0)x y C a b a b+=>>,且过点.椭圆C 的左、右焦点分别为1F,2F ,过1F 的直线交椭圆于B ,D 两点,过2F 的直线交椭圆于A ,C 两点,且AC BD ⊥. (1)求椭圆C 的标准方程; (2)求四边形ABCD 面积的最小值.第五讲 过焦点的弦与其中垂线的性质1.设椭圆焦点弦AB 的中垂线与长轴的交点为D ,则||FD 与||AB 之比是离心率的一半(如图1-5-1) 2.设双曲线焦点弦AB 的中垂线与焦点所在轴的交点为D ,则||FD 与||AB 之比是离心率的一半(如图1-5-2) 3.设抛物线焦点弦AB 的中垂线与对称轴的交点为D ,则||FD 与||AB 之比是离心率的一半(如图1-5-3)图1-5-1 图1-5-2 图1-5-31.证明 根据椭圆焦长公式:2cos b BF a c α=-||,2cos b AF a c α=+||,22222cos ab AB a c α=-||,222222||||||||||cos cos cos ||||||2222cos b b AB AF BF BF AF b c a c a c CF AF AF a c αααα-+--+=-=-===-2222||||cos cos CF b cDF a c αα==-,故22||||222DF b c c e AB a ab ===. 2.证明 当直线AB 与双曲线交于一支时,证明过程同椭圆一致;当直线AB 与双曲线交于两支时,2||cos b BF c a α=-,2||cos b AF c a α=+,22222||cos ab AB c a α=-,2222cos ||cos b c CF c a αα=-,其余过程与椭圆一致. 3.证明 抛物线22(0)y px p =>焦点弦公式:||1cos pAF α=+;||1cos p BF α=-;22||sin p AB α=.2||||||||||cos ||||||222sin AB AF BF BF AF p CF AF AF αα+-=-=-==,2||||cos sin CF pDF αα==,故||1||2DF AB =. 证明思路要记住是用上焦长公式,用上直角三角形的条件,表示DF 即可.【例21】(河南模拟)已知F 是椭圆2222:1(0)x y C a b a b+=>>的左焦点,AB 是椭圆C 过F 的弦,AB 的垂直平分线交x 轴于点P .若2AF FB =,且P 为OF 的中点,则椭圆C 的离心率为 .【例22】(2015•江苏卷)如图,在平面直角坐标系xOy 中,已知椭圆)0(12222>>=+b a by a x,且右焦点F 到左准线l 的距离为3.(1)求椭圆的标准方程;(2)过F 的直线与椭圆交于A ,B 两点,线段AB 的垂直平分线分别交直线l 和AB 于点P ,C ,若2||||PC AB =,求直线AB 的方程.【例23】(类似题2)已知双曲线 22221(0,0)x y a b a b-=>> 的左右焦点分别为 12,F F , 过2F 的直线交双曲线于,P Q 两点且1PQ PF ⊥, 若154||123PQ PF λλ=≤≤,, 则双曲线离心率e 的取值范围为 ( )A.(1 B.(1 C. D.)+∞。
焦点弦长公式二级结论

焦点弦长公式二级结论在数学的奇妙世界里,焦点弦长公式可是一个相当重要的“秘密武器”。
咱们今天就来好好聊聊这个焦点弦长公式的二级结论,瞧瞧它到底有啥神奇之处。
还记得我以前教过的一个学生小明,他呀,脑袋瓜挺聪明,但就是遇到稍微复杂点的数学题就容易犯迷糊。
有一次在课堂上讲到抛物线的时候,我提到了焦点弦长公式,他那迷茫的小眼神儿就一直盯着我,好像在说:“老师,这是啥呀,我咋听不懂呢?”咱们先来说说啥是焦点弦长公式。
对于抛物线 $y^2 =2px$ ($p>0$),过焦点的弦与抛物线交于 $A(x_1,y_1)$ ,$B(x_2,y_2)$ 两点,那么焦点弦长 $|AB| = x_1 + x_2 + p$ 。
这个公式看似简单,可里面蕴含的学问大着呢!比如说,在解决一些与抛物线相关的问题时,如果能巧妙地运用这个公式,那解题的速度和效率可就大大提高啦。
咱们来通过一道具体的题目感受一下。
已知抛物线 $y^2 = 8x$ 的焦点为 $F$,过 $F$ 的直线与抛物线交于 $A$ 、 $B$ 两点,若 $|AF| =6$ ,求 $|BF|$ 。
这时候,咱们就可以用焦点弦长公式啦。
因为抛物线方程为 $y^2 =8x$ ,所以 $p = 4$ 。
设 $A(x_1,y_1)$ ,$B(x_2,y_2)$ ,由焦点弦长公式可得 $|AB| = x_1 + x_2 + 4$ 。
又因为 $|AF| = x_1 + 2 = 6$ ,所以$x_1 = 4$ 。
将 $x_1 = 4$ 代入抛物线方程 $y^2 = 8x$ ,可得 $y_1 = ±4\sqrt{2}$ 。
因为直线过焦点,所以直线斜率存在。
不妨设直线方程为 $y = k(x -2)$ ,将点 $A(4, ±4\sqrt{2})$ 代入,可求得直线方程。
然后联立直线方程和抛物线方程,就可以求出点 $B$ 的横坐标 $x_2$ ,进而求出$|BF|$ 。
抛物线的焦半径、焦点弦、焦点三角形面积的夹角公式课件-高二数学人教A版(2019)选择性必修第一册

2、掌握抛物线焦点三角形面积公式 夹角式 .
学习重难点:
重点:理解公式的推导过程&识记结论并解决相关问题.
难点:公式的灵活使用.
思&议
问题1:如图所示,过抛物线 2 = 2 > 0 的焦点的直线交抛物线于
, 两点(其中点位于轴上方),若该直线的倾斜角为. 试用, 表示:
1 焦半径 和 ;
2 焦点弦长 ;
3 焦点三角形面积△ .
思&议
问题2:由问题1的结果,你能进一步用, 表示下面的量吗?
4
1
+
1
; 5
; 6
∙ .
思&议
问题3:如图所示, , 为抛物线 = > 的两条互相垂直
的焦点弦,由问题1的结果,你能用表示出
圆锥曲线的方程
微专题 — 抛物线的焦半径、焦点弦、焦点三角形面积的夹角公式
引
以开口朝右的抛物线: = > 为例,前面我们学习过
抛物线焦半径、焦点弦的坐标公式:
= +
;
= +
;
= + + .
也学习过抛物线焦点三角形面积的坐标公式:△ =
=
;
1+
2
= 2 ;
2
△ =
;
2
1
1
2
+
= ;
1+
=
;
1−
2
∙ = 2 .
8
1
《焦点三角形》教学设计

《椭圆中焦点三角形》教学设计一、教学背景(一)课标要求2020年修订版《普通高中数学课程标准》明确指出:椭圆中焦点三角形内容属于(二)考情分析本节是二轮复习的专题课,是椭圆知识的延续。
焦点三角形蕴含着椭圆很多耳目一新的几何性质,这些性质浑然一体,相得益彰。
在全国各地的高考模拟试题及高考试题中以焦点三角形为载体的问题,更是层出不穷,精彩纷呈。
椭圆中的焦点三角形问题,以焦点三角形作为载体来研究椭圆的性质是高考的常考考点,涉及平面几何、三角函数、解三角形、解析几何、平面向量等多领域的知识与方法,它是研究高中生数学认知状况的一个重要观测点.故值得我们去探究与总结。
(三)学情分析学生已经复习了直线与圆,椭圆的定义,标准方程和简单性质,以及解三角形的有关知识,所以学生对椭圆的焦点三角形有了一定的认识,这是复习“椭圆的焦点三角形问题”的重要基础与能力起点,因此本节课希望学生在已有认知基础上,系统的对椭圆的焦点三角形问题有一个更高、更深刻的认识,关注其本质特征和内在联系,从而在认知能力和解题能力上有一个新的提升.二、教学分析(一)教学目标1.理解椭圆焦点三角形的概念,会根据图形去探索、归纳并且推导焦点三角形的性质。
2.通过焦点三角形的顶角问题、面积问题、离心率问题,从直观想象、定性描述到定量刻画的自然跨越,培养学生识图能力和数形转化能力。
3.能在具体的问题情境中,识别焦点三角形模型,并运用有关知识解决相应的问题。
(二)教学重难点重点:理解焦点三角形与顶角问题、面积问题、离心率有关的性质。
难点:对椭圆的性质与解三角形知识间的关联的理解和应用,领悟其中蕴含的数学思想方法。
(三)学法分析问题研究,小组讨论合作学习等途径解决问题。
(四)教法分析问题引导,实例研究,归纳提炼,变式训练等形式,培养学生的兴趣,调动学生学习的积极性。
三、德育目标在知识形成和解题教学中,引导学生多角度挖掘知识,充分发挥典型题的探索价值,培养学生的自主学习能力、创新精神和实践能力.三、教学过程分析(一)教学流程1.高考所需,引入新课;2.师生互动,探究问题;3.总结提炼,变式训练;4.讲练结合,巩固新知;5.小结归纳,融会贯通;6.布置作业,提高升华.(二)教学过程环节1:高考所需,引入新课.1.(2021全国甲卷理科)已知21F F ,为椭圆1416:22=+y x C 的两个焦点,Q P ,为C 上关于坐标原点对称的两点,且||||21F F PQ =,则四边形21QF PF 的面积为________.2.(2019全国Ⅲ卷理科)设21F F ,是椭圆12036:22=+y x C 的两个焦点,M 为C 上一点,且在第一象限.若21F MF △为等腰三角形,则M 的坐标为__________.【设计意图】学生感悟高考,凸显本专题在高考中的意义。
中点弦、焦点三角形、椭圆系lyt

关于圆锥曲线的中点弦问题直线与圆锥曲线相交所得弦中点问题,是解析几何中的重要内容之一,也是高考的一个热点问题。
这类问题一般有以下三种类型:(1)求中点弦所在直线方程问题;(2)求弦中点的轨迹方程问题;(3)求弦中点的坐标问题。
其解法有代点相减法、设而不求法、参数法、待定系数法及中心对称变换法等。
一、求中点弦所在直线方程问题例1 过椭圆141622=+y x 内一点M (2,1)引一条弦,使弦被点M 平分,求这条弦所在的直线方程。
解法一:设所求直线方程为y-1=k(x-2),代入椭圆方程并整理得:016)12(4)2(8)14(2222=--+--+k x k k x k又设直线与椭圆的交点为A(11,y x ),B (22,y x ),则21,x x 是方程的两个根,于是14)2(82221+-=+k k k x x , 又M 为AB 的中点,所以214)2(422221=+-=+k k k x x , 解得21-=k , 故所求直线方程为042=-+y x 。
解法二:设直线与椭圆的交点为A(11,y x ),B (22,y x ),M (2,1)为AB 的中点, 所以421=+x x ,221=+y y ,又A 、B 两点在椭圆上,则1642121=+y x ,1642222=+y x ,两式相减得0)(4)(22212221=-+-y y x x , 所以21)(421212121-=++-=--y y x x x x y y ,即21-=AB k , 故所求直线方程为042=-+y x 。
解法三:设所求直线与椭圆的一个交点为A(y x ,),由于中点为M (2,1), 则另一个交点为B(4-y x -2,),因为A 、B 两点在椭圆上,所以有⎩⎨⎧=-+-=+16)2(4)4(1642222y x y x , 两式相减得042=-+y x ,由于过A 、B 的直线只有一条,故所求直线方程为042=-+y x 。
解析几何知识点大总结

解析几何知识点大总结第一局部:椭圆椭圆,即点集M={P| |PF 1|+|PF 2|=2a ,2a >|F 1F 2|=2c};这里两个定点F 1,F 2叫椭圆的焦点,两焦点间的距离叫椭圆的焦距2c 。
(c F F a 2221==时为线段21F F ,c F F a 2221=<无轨迹)。
2.标准方程: 222ca b =-①焦点在x 轴上:12222=+by a x (a >b >0); 焦点F (±c ,0)②焦点在y 轴上:12222=+bx a y (a >b >0); 焦点F (0, ±c )注意:①在两种标准方程中,总有a >b >0,222c b a +=并且椭圆的焦点总在长轴上;②一般形式表示:221x y m n+=或者 ),0,0(122n m n m ny mx ≠>>=+ 二.椭圆的简单几何性质: 1.范围(1)椭圆12222=+by a x (a >b >0) 横坐标-a ≤x ≤a ,纵坐标-b ≤x ≤b(2)椭圆12222=+bx a y (a >b >0) 横坐标-b ≤x ≤b,纵坐标-a ≤x ≤a2.对称性椭圆关于x 轴y 轴都是对称的,这里,坐标轴是椭圆的对称轴,原点是椭圆的对称中心,椭圆的对称中心叫做椭圆的中心 3.顶点(1)椭圆的顶点:A 1(-a ,0),A 2(a ,0),B 1(0,-b ),B 2(0,b )(2)线段A 1A 2,B 1B 2 分别叫做椭圆的长轴长等于2a ,短轴长等于2b ,a 和b 分别叫做椭圆的长半轴长和短半轴长。
4.离心率(1)我们把椭圆的焦距与长轴长的比22c a,即a c称为椭圆的离心率,记作e (10<<e ),22221()b e a a==-c e 越接近于0 (e 越小),椭圆就越接近于圆;e 越接近于1 (e 越大),椭圆越扁;注意:离心率的大小只与椭圆本身的形状相关,与其所处的位置无关。
第一讲 用椭圆定义解题2 —焦点三角形(课件)-高考数学二轮专题之椭圆小题突破

+
= 上的任意一点,点
F1,F2分别为该椭圆的上下焦点,设α=∠PF1F2,
β=∠PF2F1,则sinα+sinβ的最大值为
.
(2)已知点P为椭圆
+
= 上的任意一点,点F1,F2分别为该椭圆的上下焦
点,设α=∠PF1F2,β=∠PF2F1,则sinα+sinβ的最大值为
则2c>2a-2c且4c>2a-2c,得
1
1
e ,e ,
3
2
则2a-2c >2c且4c>2a-2c,得
1
1
e ,
3
2
(7)已知椭圆方程为
+
= (a> ),A,B是
上、下顶点,P为椭圆上的一个动点,且∠APB的最
大值为120°,若M(0, ),N(0,− ),则
|PF1|=λ|PF2|(1≤λ≤3),∠F1PF2= ,,则椭圆离心率的取值范围为
解:
PF1 PF2 PF2 PF2 1 PF2 2a
PF1 PF2 2 PF2 PF2 2 1 PF2 4c 2
2 1
c2
2 1
1
a
PI
2
(5)已知椭圆C:
+ = > > 的左、右
焦点分别为F1,F2,若C上存在一点P,使得∠F1PF2
=120°,且△F1PF2内切圆的半径大于 a,则C的
【知识梳理】解析几何的20个微专题(附高考数学真题讲析)
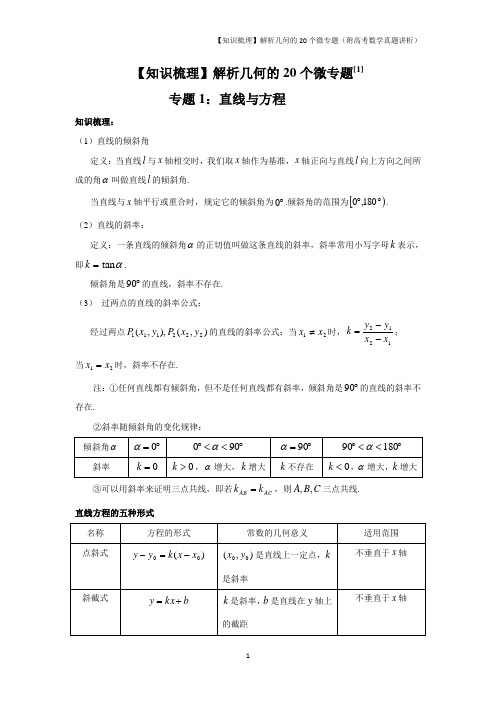
【知识梳理】解析几何的20个微专题[1]专题1:直线与方程知识梳理: (1)直线的倾斜角定义:当直线l 与x 轴相交时,我们取x 轴作为基准,x 轴正向与直线l 向上方向之间所成的角α叫做直线l 的倾斜角.当直线与x 轴平行或重合时,规定它的倾斜角为︒0.倾斜角的范围为[)︒︒180,0. (2)直线的斜率:定义:一条直线的倾斜角α的正切值叫做这条直线的斜率,斜率常用小写字母k 表示,即=k αtan .倾斜角是︒90的直线,斜率不存在. (3) 过两点的直线的斜率公式:经过两点),(),,(222111y x P y x P 的直线的斜率公式:当21x x ≠时,1212x x y y k --=;当21x x =时,斜率不存在.注:①任何直线都有倾斜角,但不是任何直线都有斜率,倾斜角是︒90的直线的斜率不存在.②斜率随倾斜角的变化规律:③可以用斜率来证明三点共线,即若AC AB k k =,则C B A ,,三点共线. 直线方程的五种形式注意:①求直线方程的方法主要有两种:一是直接法,根据已知条件,选择适当的直线方程的形式,直接写出直线方程;二是待定系数法,先设出直线方程,再根据条件求出待定系数,最后代入求出直线方程.但使用直线方程时,一定要注意限制条件,以免解题过程中丢解.②截距与距离的区别:截距可为一切实数,纵截距是直线与y 轴交点的纵坐标,横截距是直线与x 轴交点的横坐标,而距离是一个非负数.直线与直线位置关系1.两条直线的交点若直线1l :0111=++C y B x A 和2l :0222=++C y B x A 相交,则交点坐标是方程组⎩⎨⎧=++=++0222111C y B x A C y B x A 的解. 2.两条直线位置关系的判定 (1)利用斜率判定若直线1l 和2l 分别有斜截式方程1l :11b x k y +=和2l :22b x k y +=,则 ①直线1l ∥2l 的等价条件为2121,b b k k ≠=. ②直线1l 与2l 重合的等价条件为2121,b b k k ==.③直线1l 与2l 相交的等价条件为21k k ≠;特别地,1l ⊥2l 的等价条件为121-=⋅k k .若1l 与2l 斜率都不存在,则1l 与2l 平行或重合.若1l 与2l 中的一条斜率不存在而另一条斜率为0,则1l 与2l 垂直.(2)用直线一般式方程的系数判定设直线1l :0111=++C y B x A ,2l :0222=++C y B x A ,则 ①直线1l ∥2l 的等价条件为0012211221≠-=-C B C B B A B A 且. ②直线1l 与2l 重合的等价条件为0012211221=-=-C B C B B A B A 且.③直线1l 与2l 相交的等价条件为01221≠-B A B A ;特别地, 1l ⊥2l 的等价条件为02121=+B B A A .注:与0=++CBy Ax 平行的直线方程一般可设为0=++m By Ax 的形式,与0=++C By Ax 垂直的直线方程一般可设为0=+-n Ay Bx 的形式.(3)用两直线联立的方程组的解的个数判定设直线1l :0111=++C y B x A ,2l :0222=++C y B x A ,将这两条直线的方程联立,得方程组⎩⎨⎧=++=++00222111C y B x A C y B x A ,若方程组有惟一解,则1l 与2l 相交,此解就是1l ,2l 交点的坐标;若方程组无解,此时1l 与2l 无公共点,则1l ∥2l ;若方程组有无数个解,则1l 与2l 重合.3. 直线系问题(1)设直线1l :0111=++C y B x A 和2l :0222=++C y B x A若1l 与2l 相交,则0)(222111=+++++C y B x A C y B x A λ表示过1l 与2l 的交点的直线系(不包括2l );若1l ∥2l ,则上述形式的方程表示与与2l 平行的直线系.(2)过定点),(00y x 的旋转直线系方程为))((00R k x x k y y ∈-=-(不包括0x x =);斜率为0k 的平行直线系方程为)(0R b b x k y ∈+=.注:直线系是具有某一共同性质的直线的全体,巧妙地使用直线系,可以减少运算量,简化运算过程. 距离公式与对称问题 1.距离公式(1)两点间的距离公式平面上的两点),(),,(222111y x P y x P 间的距离=21P P 212212)()(y y x x -+-.特别地,原点)0,0(O 与任一点),(y x P 的距离=OP 22y x +.若x P P //21轴时,=21P P 21x x -;若y P P //21轴时,=21P P 21y y -. (2)点到直线的距离公式已知点),(000y x P ,直线l :0=++C By Ax ,则点0P 到直线l 的距离=d 2200BA CBy Ax +++.已知点),(000y x P ,直线l :a x =,则点0P 到直线l 的距离=d a x -0. 已知点),(000y x P ,直线l :b y =,则点0P 到直线l 的距离=d b y -0. 注:用此公式求解点到直线距离问题时,直线方程要化成一般式. (3)两条平行直线间的距离公式已知两平行直线1l :0111=++C y B x A 和2l :0222=++C y B x A ,若点),(000y x P 在1l 上,则两平行直线1l 和2l 的距离可转化为),(000y x P 到直线2l 的距离.已知两平行直线1l :01=++C By Ax 和2l :02=++C By Ax ,则两直线1l 和2l 的距离=d 2221BA C C +-.注:用此公式求解两平行直线间的距离时,直线方程要化成一般式,并且y x ,项的系数必须对应相等. 2.对称问题 (1)中心对称 ①点关于点的对称点),(00y x P 关于),(b a A 的对称点为)2,2(001y b x a P --. ②直线关于点的对称在已知直线上取两点,利用中点坐标公式求出它们关于已知点对称的两点的坐标,再由两点式求出直线的方程,或者求出一个对称点,再利用1l ∥2l ,由点斜式求出直线的方程,或者在所求直线上任取一点),(y x ,求出它关于已知点的对称点的坐标,代入已知直线,即可得到所求直线的方程. (2)轴对称①点关于直线的对称点),(00y x P 关于b kx y +=的对称点为),(111y x P ,则有⎪⎪⎩⎪⎪⎨⎧++⋅=+-=⋅--b x x k y y k x x y y 22101010101,由此可求出11,y x .特别地, 点),(00y x P 关于a x =的对称点为),2(001y x a P -,点),(00y x P 关于b y =的对称点为)2,(001y b x P -. ②直线关于直线的对称此类问题一般转化为点关于直线的对称问题来解决,有两种情况:一是已知直线与对称直线相交,一是已知直线与对称直线平行. 本章知识结构专题2:圆的标准方程与一般方程知识梳理:⑴.圆的一般方程的概念:当 时,二元二次方程220x y Dx Ey F ++++=叫做圆的一般方程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题二:圆锥曲线焦点弦、焦点△知识专题【焦半径——椭圆】θ取弦与焦点轴的锐角为121212::=2:=2a ex;a ex;|AB |a e(x x );|AB |a e(x x )ρρ=+=-++-+左焦半径右焦半径左焦弦右焦弦【焦半径——双曲线】θ取弦与焦点轴的锐角为 (1) 单支焦点半径112::=-2(a ex );|AB |a e(x x );ρ=-+-+左焦半径左焦弦 1122::=ex a;|AB |e(x x )a;ρ=-+-右焦半径右焦弦(2) 双支焦点半径1122::=a ex;|AB |a e(x x );ρ=+++异支左焦半径异支左焦弦 1122::=a ex;|AB |a e(x x );ρ=--+异支右焦半径异支右焦弦【焦半径——抛物线】θ取弦与焦点轴的锐角为1212==y x |AB |x x p;y |AB |y p ++++焦点在轴上焦点在轴上::【焦点弦有关推论——椭圆】θ取弦与焦点轴的锐角为1、过椭圆、双曲线的一焦点F 交椭圆或双曲线(单支)于A,B 两点,则2、过双曲线的焦点F 的直线分别与两支交于A,B ,与焦点轴夹角为)2(πθ<21122cos a cos |AF ||BF |p b θθ•+==3、过抛物线的焦点F 直线交抛物线于A,B 两点,与焦点轴夹角为)2(πθ<112|AF ||BF |p+= 4、已知点是离心率为的椭圆或双曲线的焦点,过点的弦与的焦点所在的轴的夹角为θ,且。
(1) 当焦点内分弦时,有(2) 当焦点外分弦时(此时曲线为双曲线),有【椭圆焦三角形 面积】q 为动点到原点的距离,,m,n 为弦长,α为弦夹角【椭圆】222122()S (a c )tanb tanαα=-=22()S b mn b =-3()S (a c )(a c )(a q )(a q )=+-+-【双曲线焦△ 面积】q 为动点到原点的距离,,m,n 为弦长,α为弦夹角212b ()S tanα=22()Sb mn b =-3()S (a c )(a c )(a q )(a q )=+-+-【抛物线焦点弦与原点△ 面积】θ取弦与焦点轴的锐角为【焦点△顶角】椭圆:双曲线一、焦半径与焦点弦 2πθ取弦与焦点轴小于的夹角22221x y a b+=焦点弦,准线图【焦半径——椭圆】 分析:如上左图,11:22|F A ||F B |a b e;e;p =-c =|AM ||BN |c c==根据椭圆第二定义准线与对应焦点距离11111|F A |epx e |F A |e |AM |e(p |F A |cos )|F A ||AM |e cos θθθ=⇒==+⇒=-设焦点弦与轴成角;11111|F B |epe |F B |e |BN |e(p |F B |cos )|F B ||BN |e cos θθ=⇒==-⇒=+12222111::=ep ep ep;;|AB |e cos e cos e cos ρρθθθ==-+-小结:长半焦短半焦焦点弦分析:如上右图,1:22|F A |a b e;p =-c =|AM |c c=根据椭圆第二定义准线与对应焦点距离11111|F A |epx e |F A |e |AM |e(p |F A |cos )|F A ||AM |e cos θθθ=⇒==-⇒=+设焦点弦与轴成角;11111|F B |epe |F B |e |BN |e(p |F B |cos )|F B ||BN |e cos θθ=⇒==+⇒=-12222111::=ep ep epx ;;|AB |e cos e cos e cos ρρθθθ==-+-焦点在轴上结论:长半焦短半焦焦点弦22221y x a b += 22221y x a b+=分析:如上左图,1:22|F A |a b e;p =-c =|AM |c c=根据椭圆第二定义准线与对应焦点距离11111|F A |epx e |F A |e |AM |e(p |F A |cos )|F A ||AM |e cos θθθ=⇒==-⇒=+设焦点弦与轴成角;11111|F B |epe |F B |e |BN |e(p |F B |cos )|F B ||BN |e cos θθ=⇒==+⇒=-分析:如上右图,1:22|F A |a b e;p =-c =|AM |c c=根据椭圆第二定义准线与对应焦点距离11111|F A |epe |F A |e |AM |e(p |F A |cos )|F A ||AM |e cos θθ=⇒==+⇒=-11111|F B |epe |F B |e |BN|e(p |F B |sin )|F B ||BN |e sin θθ=⇒==-⇒=+AB MN2b p c=2a x c=θ【焦半径——双曲线】内部焦点半径 2)x(y πθ取弦与或轴小于的夹角22221y x a b -=12222:=111ep ep ep;;|AB |e cos e cos e cos ρρθθθ==-+-:短结论:长半焦半焦焦点弦外部焦点半径 2πθ取弦与焦点轴小于的夹角AF12a x c=F2MBNAF12a x c=-F2MBN121212::=2:=2a ex;a ex;|AB |a e(x x );|AB |a e(x x )ρρ=+=-++-+左焦半径右焦半径左焦弦右焦弦21a a a |F A |e |AM |e(x )a ex c ==+=+21b ba |F B |e |BN |e(x )a ex c ==+=+22a aa |F A |e |AM |e(x )a ex c==-=-22b ba |F B |e |BN |e(x )a ex c==-=-ABM N2b p c=2a x c=θM‘MBAAM’M分析:如上左图, 122|F A |a b e;p =c =|AM |c c=-:根据第二定义准线与对应焦点距离 11111|F A |x e |F A |e |AM |e(|AM'|p )|AM |epe(|F A |cos p )|F A |e cos θθθ=⇒==-=-⇒=-设焦点弦与轴成角;11111|F B |epe |F B |e |BN |e(p |F B |cos )|F B ||BN |e cos θθ=⇒==-⇒=+ 11222111ep ep ep|AB ||AF ||BF |e cos e cos e cos θθθ⇒=-=-=-+- 分析:如上右图,22221|F A |epe |F A |e |AM |e(|AM'|p )e(|F A |cos p )|F A ||AM |e cos θθ=⇒==-=-⇒=-22221|F B |epe |F B |e |BN |e(p |F B |cos )|F B ||BN |e cos θθ=⇒==-⇒=+11222111ep ep ep|AB ||AF ||BF |e cos e cos e cos θθθ⇒=-=-=-+- 12222111焦点在轴上结论:=ep ep epx ;;|AB |e cos e cos e cos ρρθθθ==-+-:长半焦半焦焦点弦:短同理可以推出:(也可从旋转的角度得出以下结论)12222111:短ep ep epy ;;|AB |e cos e cos e cos ρρθθθ==-+-:=焦点在轴上结论:长半焦半焦焦点弦θM‘MN’NBABθN‘N【焦半径——抛物线】2)x(yπθ取弦与或轴小于的夹角从上图容易得出以下结论122211p p p;;|AB|cos cos sinρρθθθ==-+:=:短结论:长半焦半焦焦点弦从上图分析12在轴上=x|AB||AM||B N|(|AM'||M'M|)(|BN'||N'N|)|AB|x x p −−−→=+=+++⇒++焦点定义:12在轴上=y|AB||AM||B N|(|AM'||M'M|)(|BN'||N'N|)|AB|y y p −−−→=+=+++⇒++焦点定义:【焦半径与焦点弦有关推论】21a aa|F A|e|AM|e(x)a exc==+=+22a aa|F A|e|AM|e(x)a exc==-+=-122:==a b a ba b a ba ex;a ex|AB|a ex a ex e(x x)|AB|a ex a ex a e(x x)ρρ=+=-+--=--+-=-+异左焦半径异右焦半径异左异右AB F2a x c=-2b p c=MN Fθ ABMN2b p c=2a x c=θ【推论1】——常用来求定值过椭圆、双曲线的一焦点F 交椭圆或双曲线(单支)于A,B 两点,则21122a |AF ||BF |b ep+== 过双曲线的一焦点F 的直线分别与两支交于A,B ,与焦点轴夹角为)2(πθ<21122cos a cos |AF ||BF |p b θθ•+==过抛物线的一焦点F 直线交抛物线于A,B 两点,与焦点轴夹角为)2(πθ<112|AF ||BF |p+= 【推论2】2πθ取弦与焦点轴小于的夹角————常用来求定角或斜率已知点是离心率为的椭圆或双曲线的焦点,过点的弦与的焦点所在的轴的夹角为θ,且。
(3) 当焦点内分弦时,有(4) 当焦点外分弦时(此时曲线为双曲线),有θM‘ MNB A【(1)分析证明】11111AF BFAM NB AM NB ()BF ()e e cos e cos AB AF BF ()BF e()BF ()λλθθλλλ-----====⇒=++++ 【(2)分析证明】11111AF BFAM'AM NB ()BF ()e e cos e cos AB AF BF ()BF e()BF ()λλθθλλλ++++====⇒=---- 【焦半径与焦点弦有关例题】例1 (2009年高考福建卷理科第13题)过抛物线的焦点作倾斜角为的直线,交抛物线于两点,若线段的长为8,则___【解】 由抛物线焦点弦的弦长公式为得,,解得。
例2(2010年高考辽宁卷理科第20题)已知椭圆的右焦点为,经过且倾斜角为的直线与椭圆相交于不同两点,已知。
(1)求椭圆的离心率;(2)若,求椭圆方程。
【解】(1)这里,,由定理1的公式得,解得。
(2)将,代入焦点弦的弦长公式得,,解得,即,所以①,又,设,代入①得,所以,所以,故所求椭圆方程为。
例3(2007年重庆卷第16题)过双曲线的右焦点作倾斜角为的直线,交双曲线于两点,则的值为___【解】易知均在右支上,因为,离心率,点准距,因倾斜角为,所以。
