高三文科数学考前训练(4)

合集下载

高三文科生冲刺数学试卷

一、选择题（本大题共12小题，每小题5分，共60分）1. 已知函数f(x) = ax^2 + bx + c（a≠0），若f(1) = 2，f(2) = 5，则f(3)的值为（）A. 8B. 9C. 10D. 112. 在△ABC中，若∠A=60°，∠B=45°，则sinC的值为（）A. √3/2B. 1/2C. √2/2D. 1/√23. 已知等差数列{an}的首项a1=3，公差d=2，则第10项an的值为（）A. 21B. 23C. 25D. 274. 下列命题中正确的是（）A. 若a+b=0，则a和b一定互为相反数B. 若a²+b²=0，则a和b一定同时为0C. 若ab=0，则a和b至少有一个为0D. 若a²+b²=1，则a和b一定同时为15. 已知复数z = 2 + 3i，则|z|的值为（）A. 5B. 6C. 7D. 86. 函数y = log₂(x-1)的定义域为（）A. x > 1B. x ≥ 1C. x < 1D. x ≤ 17. 若不等式2x-3 > x+1的解集为A，则A的表示为（）A. x > 4B. x ≥ 4C. x < 4D. x ≤ 48. 已知直线l的方程为x - 2y + 3 = 0，则直线l的斜率为（）A. 1/2B. 2C. -1/2D. -29. 若向量a = (2, 3)，向量b = (-1, 2)，则向量a·b的值为（）A. 7B. -7C. 1D. -110. 在直角坐标系中，点P(2, -3)关于y轴的对称点为（）A. (2, 3)B. (-2, -3)C. (-2, 3)D. (2, -3)11. 已知函数y = (1/2)x² - x + 1，若y的最大值为3，则x的值为（）A. 1B. 2C. 3D. 412. 若等比数列{an}的首项a1=1，公比q=2，则第5项an的值为（）A. 16B. 32C. 64D. 128二、填空题（本大题共8小题，每小题5分，共40分）13. 已知等差数列{an}的首项a1=5，公差d=2，则第n项an=______。

高三数学考前适应性模拟训练4 文 A 试题

2021届高三考前适用性模拟训练数学文〔4〕一、选择题：本大题一一共12小题，每一小题5分，一共60分。

在每一小题给出的四个选项里面，只有一项是哪一项符合题目要求的。

1．集合{},3M m =-,{}22730,N x x x x =++<∈Z ,假如MN ≠∅,那么m 等于A ．1-B ．2-C ．2-或者1-D ．32- 2．设复数21z i=+(其中i 为虚数单位)，那么23z z +的虚部为 A ．2i B ．0 C ．10- D ．2 3．设,R x y ∈，那么“229x y +≥〞是“3x >且3y ≥〞的 A ．充分不必要条件 B ．必要不充分条件 C ．充分必要条件 D ．即不充分也不必要条件4．函数2log ,0()31,0x x x f x x ->⎧=⎨+≤⎩，那么()31((1))log 2f f f +的值是A ．5B ． 3C ．1-D ．725．过点〔1，0〕且与直线053=-+y x 平行的直线方程是A ．013=++y xB ．013=-+y xC ．033=--y xD ．033=-+y x 6．函数x x x f cos sin 41)(=是 A. 最小正周期为π2的偶函数B. 最小正周期为π2的奇函数C. 最小正周期为π的偶函数D. 最小正周期为π的奇函数7．实数y x ，满足⎪⎩⎪⎨⎧≤≥+≥+-1003x y x y x ，那么y x z 2+-=的最小值是A ．7B ．－3C ．23D ．38．一个简单几何体的主视图，左视图如下图，那么其俯视图不可能为①长方形；②直角三角形；③圆；④椭圆．其中正确的选项是A ．①B ．②C ．③D ．④9．函数⎩⎨⎧<≥+=)1(,)1(,ln 1)(3x x x x x f ，那么)(x f 的图象为A ． B.C. D.10．在ABC ∆中，a =7，b =2，A=60°，那么c = A .1 B.2 C.3 D .411．圆0241022=+-+x y x 的圆心是双曲线)0(19222>=-a y ax 的一个焦点，那么此双曲线主视图左视图第8题图的渐近线方程为A ．x y 34±= B ．x y 43±= C ．x y 53±= D ．x y 54±= 12．函数]2,1[,13)(2-∈--=x x x x f ，任取一点]2,1[0-∈x ，使1)(0≥x f 的概率是 A.32 B. 95 C. 41 D. 94第二卷〔非选择题一共90分〕二、填空题：〔本大题一一共4小题，每一小题4分，一共16分，把答案填在答题卡的相应位置。

2011届深圳中学高三年级数学基础练习4(文科)

深圳中学2011届高三数学基础练习题4（文科）命题人：郭本龙一、选择题：本大题共10小题，每小题5分，共50分. 在每小题给出的四个选项中，只有一项是符合题目要求的. 1．函数214y x x =-在它的图象上点M 处的切线平行于x 轴，则点M 的坐标为（A ） (2,1)- （B ）(0,0) （C ）3(1,)4-（D ）(4,0)2.设定义在R 上的函数()f x 满足()()217f x f x ⋅+=，若()12f =，则()2007f = （A ）17 （B ）2 （C ）172（D ）2173．已知偶函数()f x 在区间[0,)+∞单调增加，则满足(21)f x -＜1()3f 的x 取值范围是（A ）（13，23） (B) ［13，23） (C)（12，23） (D) ［12，23）4．已知函数xy a b =+的图象过第二、三、四象限，那么（A ）1,1a b >>- （B ）1,1a b ><- （C ）01,1a b <<>- （D ）01,1a b <<<-5．为了得到函数3lg10x y +=的图像，只需把函数lg y x =的图像上所有的点A ．向左平移3个单位长度，再向上平移1个单位长度B ．向右平移3个单位长度，再向上平移1个单位长度C ．向左平移3个单位长度，再向下平移1个单位长度D ．向右平移3个单位长度，再向下平移1个单位长度6．若函数3()3f x x x a =-+有3个不同的零点,则实数a 的取值范围是（A ） ()2,2- （B ） []2,2- （C ） (),1-∞- （D ）()1,+∞7．某公司在广州、深圳两地销售同一款汽车，利润（单位：万元）分别为21 5.060.15L x x =-和22L x =，其中x 为销售量（单位：辆）。

若该公司在广州、深圳共销售了15辆车，则能获得的最大利润为（）万元（A ）45.606 （B ）45.6 （C ）45.56 （D ）45.518．已知函数5)(23-+-=x x kx x f 在R 上单调递增, 则实数k 的取值范围是（A ）),31(∞+（B ）]31,0(（C ）)31,0(（D ）),31[∞+9．下列函数()f x 中，满足“对任意1x ，2x ∈（0，+∞），当1x <2x 时，都有1()f x >2()f x 的是 A ．()f x =1xB. ()f x =2(1)x - C .()f x =xe D ()ln(1)f x x =+10．已知函数224,0()4,0x x x f x x x x ⎧+≥⎪=⎨-<⎪⎩若2(2)(),f a f a ->则实数a 的取值范围是A (,1)(2,)-∞-⋃+∞B (1,2)-C (2,1)-D (,2)(1,)-∞-⋃+∞二、填空题：本大题共4小题，每小题5分，共20分.11．已知直线y x b =+与曲线232y x x =++相切，则实数b 的取值为．12．若函数()log (21)a f x x =-在区间(,)a +∞上是单调减函数，则实数a 的取值范围是．13．若函数21144(log )2log 5y x x =-+在定义域[2,4]上有最大值a ，最小值b ，则a b -=.14．曲线xy e =在点2(2,)e 处的切线与坐标轴所围三角形的面积为．填空题答案填在下面：11． 12．13． 14．班级姓名学号得分11. 1 12.1,12⎡⎫⎪⎢⎣⎭13.7414.22e11. 1 12.1,12⎡⎫⎪⎢⎣⎭13.7414.22e。

高三文科数学第二次月考模拟训练(4)

高三文科数学第二次月考选填题模拟训练（4）满分：75分时间：45分钟一、选择题：（本大题9小题，每小题5分，共45分。

）1.若复数()()2321a a a i -++-是纯虚数，则实数a 的值为（）A.1B.2C.1或2D.1- 2.若集合1{|23},{|21}x M x x N x +=-<<=≥，则()R C M N ＝（）A. (3,)+∞B. (1,3)-C. [1,3)-D. [3,)+∞ 3.下列命题中是假命题的是（）A.x x x sin ),2,0(>∈∀πB.0x R ∃∈,2cos sin 00=+x xC.x R ∀∈,03>xD.0lg ,00=∈∃x R x4.如图所示的程序框图．若输出15S =，则图中① 处可以填入（）A. 4n >？B. 8n >？C. 16n >？D. 16n <？ 5.下列四个函数中，最小正周期为π，且图象关于直线12π=x 对称的是（）A ．)32sin(π+=x y B ．)3sin(π-=x y C ．)32sin(π-=x y D ．)32sin(π+=x y6.函数x e e y x x sin )(⋅-=-的图象大致是（）A B C D7.在某次测量中得到的A 样本数据如下:82, 84, 84, 86, 86, 86, 88, 88, 88, 88.若B 样本数据恰好是A 样本数据都加2后所得数据,则A ,B 两样本的下列数字特征对应相同的是（）A ．众数B ．平均数C ．中位数D ．标准差 8.若将函数x x y cos 3sin +=（R ∈x ）的图象向左平移m （0>m ）个单位后，所得图象关于原点对称，则m 的最小值是（）A ．6πB ．3π C ．32π D ．65π9.若点(,)P a b 在函数23ln y x x =-+的图象上，点(,)Q c d 在函数2y x =+的图象上，则22()()a c b d -+-的最小值为（）A B ．2 C ．D ．8二、填空题：（本大题共6小题，每小题5分，满分30分）10.如果1cos()2A π+=-，那么sin()2A π+= .11.=-++10lg 333log 120tan 33ln0e _________.12.设a ∈{1, 2, 3}, b ∈{2, 4, 6}，则函数y ＝xab1log 是减函数的概率为。

高三文科数学练习题推荐

高三文科数学练习题推荐数学是高中阶段其中一门重要的学科，也是许多文科生头疼的科目之一。

对于高三文科学生来说，数学的学习更显得关键和困难。

为了帮助高三文科生提高数学成绩，下面将推荐一些适合高三文科生练习的数学题目。

1. 解析几何：在高考数学中，解析几何是比较重要的一个章节。

要掌握解析几何的基本概念和定理，并能够灵活运用。

推荐练习题目如下：1. 已知点A(-3, 2)和点B(4, -1)，求线段AB的中点坐标。

2. 已知直线L的斜率为2/3，经过点(-1, 2)，求直线L的方程。

3. 已知圆心为原点O，半径为5，点P(3, 4)在圆上，求点P到原点的距离。

2. 概率与统计：概率与统计是高等数学中的一个重要章节，也是高三数学练习题中的热点之一。

推荐练习题目如下：1. 有三个盒子，每个盒子中都装有红、蓝、黄三种颜色的球各10个，从三个盒子中每个盒子抽一个球，求三个球中至少有两个球颜色相同的概率。

2. 一枚硬币抛掷三次，事件A表示出现两个正面，事件B表示至少一次出现反面，求事件A和事件B同时发生的概率。

3. 有五个筛子，分别标有1至6的数字，从中任选一个筛子，投掷一次，求投掷出奇数的概率。

3. 数列与数学归纳法：数列与数学归纳法是高三数学的基础，也是高考数学当中的热点内容。

推荐练习题目如下：1. 若数列{an}满足an+1 = 2an + 3，a1 = 1，求a5的值。

2. 若数列{bn}满足bn+1 = 3bn - 2，b1 = 2，求b6的值。

3. 若数列{cn}满足cn+1 = cn + 3n，c1 = 1，求c7的值。

4. 导数与微分：导数与微分是高三数学中较难的内容之一，也是高考数学的重点和难点。

推荐练习题目如下：1. 求函数f(x) = 2x^3 - 3x^2 + 1的导函数f'(x)。

2. 已知函数f(x) = x^2 - 4x + 1，求f(x)在x = 2处的切线方程。

3. 求函数f(x) = e^x - x的导函数f'(x)。

高三文科数学专题学习：考前强化训练

1.古典概型（五步）2.随机抽样
3.频率分布直方图与茎叶图（画图与识图、前者会估计三数）
4.6数. 字设特x征是：一三组数数（据众x1数, x、2, 中,位xn数的、平平均均数数,则）用两差（标准差、方差
s2
1[( n
x1
x)2
(
x2
x)2
ቤተ መጻሕፍቲ ባይዱ
(xn x)2 ]
5.线性来回衡归量直这线组方数程据与的独波立动性大检小验,并（称四为步这）组
立几部分
不能正确理解：三角形与平面（截面）的关系！
N
1.观察几何体的结构（柱、锥、台、组合体）； 2.注意线线、线面、面面平行（垂直）的转化； 3.求几何体的体积注意高的说明（线面垂直证明）； 4.利用定理证明，注意检查条件是否具备。 5.熟悉折叠问题、存在性问题、函数最值问题等题型。
D1
C1
.
15．(坐标系CD与参数方程选做题)
C D
在极坐标系 O ( 0, 0 2π) 中，点
O
A
A(2,
) 2
关于直线
l
:
cos
1 的对称点
B
的极坐标为 2 2, .
4
互化公式：x cos , y sin;
2 x2 y2, tan y x 0
x
三角部分
高三文数考前强化训练
第一课时
选做题部分
记得涂所选题号，切记！
选做题（请考生在以下两小题中任选一题做答，若两小题都做，
则按第 14 题记分）
14．（几何证明选讲选做题）如图，过点 C 作 ABC 的外接圆 O
的切线交 BA 的延长线于点 D .若 CD 3 ， AB AC 2，

2022版优化方案高考数学(浙江版·文科)二轮专题复习练习：专题4 立体几何第1讲 Word版含答案

[A卷]1．(2021·宁波市高三模拟) 用一个平行于水平面的平面去截球，得到如图所示的几何体，则它的俯视图是()解析：选B.由题意知，用平行于水平面的平面去截球所得的底面圆是看不见的，所以在俯视图中该部分应当是虚线圆，结合选项可知选B.2．下列命题中，错误的是()A．圆柱的轴截面是过母线的截面中面积最大的一个B．用一个平面去截棱锥，底面与截面之间的部分组成的几何体叫棱台C．圆台的全部平行于底面的截面都是圆D．圆锥全部的轴截面都是全等的等腰三角形解析：选B.依据棱台的定义，用一个平行于棱锥底面的平面去截棱锥，底面与截面之间的部分组成的几何体叫棱台．3．(2021·台州市高三调考)一个空间几何体的三视图如图所示，其体积为()A．16B．32C．48 D．96解析：选A.由题意作出直观图P-ABCD如图所示，则该几何体是一个四棱锥，底面是一个直角梯形，其面积为12×(2＋4)×4＝12，高为4，因此其体积V＝13×12×4＝16.4．(2021·高考全国卷Ⅰ)圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体，该几何体三视图中的正视图和俯视图如图所示．若该几何体的表面积为16＋20π，则r＝()A．1 B．2C．4 D．8解析：选B.如图，该几何体是一个半球与一个半圆柱的组合体，球的半径为r，圆柱的底面半径为r，高为2r，则表面积S＝12×4πr2＋πr2＋4r2＋πr·2r＝(5π＋4)r2.又S＝16＋20π，所以(5π＋4)r2＝16＋20π，所以r2＝4，r＝2，故选B.5．如图是一个体积为10的空间几何体的三视图，则图中x的值为()A．2 B．3C．4 D．5解析：选A.依据给定的三视图可知，该几何体对应的直观图是一个长方体和四棱锥的组合体，所以几何体的体积V＝3×2×1＋13×3×2×x＝10，解得x＝2.故选A.6. 如图，水平放置的三棱柱的侧棱长为1，且侧棱AA1⊥平面A1B1C1，正视图是边长为1的正方形，俯视图为一个等边三角形，则该三棱柱的侧视图的面积为()A．2 3 B． 3C.32D．1解析：选C.由直观图、正视图以及俯视图可知，侧视图是宽为32，长为1的长方形，所以面积S＝32×1＝32.故选C.7．一平面截一球得到直径为2 5 cm的圆面，球心到这个平面的距离是2 cm，则该球的体积是() A．12πcm3B．36πcm3C．646πcm3D．108πcm3解析：选B.由于球心和截面圆心的连线垂直于截面，由勾股定理得，球半径R＝22＋（5）2＝3，故球的体积为43πR3＝36π(cm3)．8．(2021·石家庄市第一次模拟)一个几何体的三视图如图所示，则该几何体的体积是()A．64B．72C．80D．112解析：选B.由三视图可知该几何体是一个组合体，下面是一个棱长为4的正方体；上面是一个三棱锥，三棱锥的高为3.故所求体积为43＋13×12×4×4×3＝72.9．已知某组合体的正视图与侧视图相同(其中AB＝AC，四边形BCDE为矩形)，则该组合体的俯视图可以是________(把正确的图的序号都填上)．解析：几何体由四棱锥与四棱柱组成时，得①正确；几何体由四棱锥与圆柱组成时，得②正确；几何体由圆锥与圆柱组成时，得③正确；几何体由圆锥与四棱柱组成时，得④正确．答案：①②③④10．把一个圆锥截成圆台，已知圆台的上、下底面半径的比是1∶4，母线长是10 cm，则圆锥的母线长为________ cm.解析：作出圆锥的轴截面如图，设SA＝y，O′A′＝x，利用平行线截线段成比例，得SA′∶SA＝O′A′∶OA，则(y－10)∶y＝x∶4x，解得y＝403.所以圆锥的母线长为403cm.答案：40311．(2022·高考课标全国卷Ⅱ改编)正三棱柱ABC-A1B1C1的底面边长为2，侧棱长为 3，D为BC中点，则三棱锥AB1DC1的体积为________．解析：由题意可知AD⊥BC，由面面垂直的性质定理可得AD⊥平面DB1C1，又AD＝2sin 60°＝3，所以V AB1DC1＝13AD·S△B1DC1＝13×3×12×2×3＝1，故选C.答案：112．一个四棱锥的侧棱长都相等，底面是正方形，其正(主)视图如图所示，则该四棱锥的侧面积为________，体积为________．解析：由题意可知该四棱锥为正四棱锥，底面边长为2，高为2，侧面上的斜高为22＋12＝5，所以S 侧＝4×⎝⎛⎭⎫12×2×5＝45，V＝13×22×2＝83.答案：458313．(2021·南昌市第一次模拟)如图，在正四棱柱ABCD -A 1B 1C 1D 1中，点P 是平面A 1B 1C 1D 1内一点，则三棱锥P -BCD 的正视图与侧视图的面积之比为________．解析：依据题意，三棱锥P -BCD 的正视图是三角形，且底边为正四棱柱的底面边长、高为正四棱柱的高，侧视图是三角形，且底边为正四棱柱的底面边长、高为正四棱柱的高，故三棱锥P -BCD 的正视图与侧视图的面积之比为1∶1. 答案：1∶114．如图是某空间几何体的三视图，则该几何体的体积为________．解析：由三视图可知，该几何体是棱长为2，2，1的长方体挖去一个半径为1的半球，所以长方体的体积为2×2×1＝4，半球的体积为12×43π×13＝2π3，所以该几何体的体积是4－2π3.答案：4－2π315．如图，正方体ABCD -A 1B 1C 1D 1的棱长为1，E ，F 分别为线段AA 1，B 1C 上的点，则三棱锥D 1EDF的体积为________．解析：由于B 1C ∥平面ADD 1A 1，所以F 到平面ADD 1A 1的距离d 为定值1，△D 1DE 的面积为12D 1D ·AD ＝12，所以V D 1EDF ＝V F D 1DE ＝13S △D 1DE ·d ＝13×12×1＝16.答案：16[B 卷]1．一个锥体的正视图和侧视图如图所示，下面选项中，不行能是该锥体的俯视图的是( )解析：选C.依据三视图中“正俯长一样，侧俯宽一样，正侧高一样”的规律，C 选项的侧视图宽为32，不符合题意，故选C.2．(2021·邢台市摸底考试)已知一个几何体的三视图是三个全等的边长为1的正方形，如图所示，则该几何体的体积为( )A.16 B.13 C.23D ．56解析：选D.依题意得，题中的几何体是从棱长为1的正方体ABCD -A ′B ′C ′D ′中截去三棱锥A ′ABD 后剩余的部分，因此该几何体的体积等于13－13×⎝⎛⎭⎫12×12×1＝56，故选D. 3．(2022·高考湖南卷)一块石材表示的几何体的三视图如图所示．将该石材切削、打磨，加工成球，则能得到的最大球的半径等于( )A ．1B ．2C ．3D ．4解析：选B.由三视图可知该几何体是一个直三棱柱，如图所示．由题意知，当打磨成的球的大圆恰好与三棱柱底面直角三角形的内切圆相同时，该球的半径最大，故其半径r ＝12×(6＋8－10)＝2.因此选B.4．(2021·高考山东卷)在梯形ABCD 中，∠ABC ＝π2，AD ∥BC ，BC ＝2AD ＝2AB ＝2.将梯形ABCD 绕AD所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )A.2π3 B ．4π3 C.5π3D ．2π 解析：选C.过点C 作CE 垂直AD 所在直线于点E ，梯形ABCD 绕AD 所在直线旋转一周而形成的旋转体是由以线段AB 的长为底面圆半径，线段BC 为母线的圆柱挖去以线段CE 的长为底面圆半径，ED 为高的圆锥，如图所示，该几何体的体积为V ＝V 圆柱－V 圆锥＝π·AB 2·BC －13·π·CE 2·DE ＝π×12×2－13π×12×1＝5π3，故选C.5．(2021·郑州市第一次质量猜测)某三棱锥的三视图如图所示，且三个三角形均为直角三角形，则xy 的最大值为( )A ．32B ．327C ．64D ．647解析：选C.依题意，题中的几何体是三棱锥P -ABC (如图所示)，其中底面ABC 是直角三角形，AB ⊥BC ，P A ⊥平面ABC ， BC ＝27，P A 2＋y 2＝102，(27)2＋P A 2＝x 2，因此xy ＝x 102－[x 2－（27）2]＝x128－x 2≤x 2＋（128－x 2）2＝64，当且仅当x 2＝128－x 2，即x ＝8时取等号，因此xy 的最大值是64，故选C.6．(2021·山西省第三次四校联考)在半径为10的球面上有A ，B ，C 三点，假如AB ＝83，∠ACB ＝60°，则球心O 到平面ABC 的距离为( )A ．2B ．4C ．6D ．8解析：选C.设A ，B ，C 三点所在圆的半径为r ，圆心为P .由于∠ACB ＝60°，所以∠APB ＝120°.在等腰三角形ABP 中，AP ＝43sin 60°＝8，所以r ＝8，所以球心O 到平面ABC 的距离为102－82＝6，故选C.7．如图是一个几何体的三视图，则该几何体的表面积是( )A ．5＋ 3B ．5＋2 3C ．4＋2 2D ．4＋2 3解析：选A.该几何体的直观图如图．表面积S ＝1×1＋12×1×1×2＋2×12×(1＋2)×1＋12×6×2＝5＋3，所以选A.8．在三棱锥P -ABC 中，P A ⊥平面ABC ，AC ⊥BC ，D 为侧棱PC 上的一点，它的正视图和侧视图如图所示，则下列命题正确的是( )A ．AD ⊥平面PBC ，且三棱锥D -ABC 的体积为83B ．BD ⊥平面P AC ，且三棱锥D -ABC 的体积为83C ．AD ⊥平面PBC ，且三棱锥D -ABC 的体积为163D ．BD ⊥平面P AC ，且三棱锥D -ABC 的体积为163解析：选C.由正视图可知，P A ＝AC ，且点D 为线段PC 的中点，所以AD ⊥PC .由侧视图可知，BC ＝4.由于P A ⊥平面ABC ，所以P A ⊥BC .又由于BC ⊥AC ，且AC ∩P A ＝A ，所以BC ⊥平面P AC ，所以BC ⊥AD .又由于AD ⊥PC ，且PC ∩BC ＝C ，所以可得AD ⊥平面PBC ，V D ABC ＝13×12×P A ×S △ABC ＝163.9．某几何体的正视图与俯视图如图所示，若俯视图中的多边形为正六边形，则该几何体的侧视图的面积为________．解析：侧视图由一个矩形和一个等腰三角形构成，矩形的长为3，宽为2，面积为3×2＝6.等腰三角形的底边为3，高为3，其面积为12×3×3＝32，所以侧视图的面积为6＋32＝152.答案：15210．(2021·洛阳市高三班级统考)如图是某几何体的三视图，则该几何体的外接球的表面积为( )解析：由三视图知，该几何体可以由一个长方体截去一个角后得到，该长方体的长、宽、高分别为5、4、3，所以其外接球半径R 满足2R ＝42＋32＋52＝52，所以该几何体的外接球的表面积为S ＝4πR 2＝4π×⎝⎛⎭⎫5222＝50π.答案：50π 11．(2021·绍兴市高三诊断性测试)若某几何体的三视图如图所示，则该几何体的体积为________，最长的侧棱长为________．解析：依据三视图及有关数据还原该几何体，得该几何体是底面为直角梯形的四棱锥P -ABCD ，如图，过点P 作PH ⊥AD 于点H ，连接CH .底面面积S 1＝（1＋2）×12＝32，V ＝13×32×1＝12，最长的侧棱长为PB ＝ 3.答案：12312．设甲、乙两个圆柱的底面积分别为S 1，S 2，体积分别为V 1，V 2，若它们的侧面积相等，且S 1S 2＝94，则V 1V 2的值是________．解析：设两个圆柱的底面半径和高分别为r 1，r 2和h 1，h 2，由S 1S 2＝94，得πr 21πr 22＝94，则r 1r 2＝32.由圆柱的侧面积相等，得2πr 1h 1＝2πr 2h 2，即r 1h 1＝r 2h 2，则h 1h 2＝23，所以V 1V 2＝πr 21h 1πr 22h 2＝32.答案：3213．(2021·洛阳市统考)已知点A ，B ，C ，D 均在球O 上，AB ＝BC ＝6，AC ＝23，若三棱锥D -ABC 体积的最大值为3，则球O 的表面积为________．解析：由题意可得，∠ABC ＝π2，△ABC 的外接圆半径r ＝3，当三棱锥的体积最大时，V D ABC ＝13S △ABC ·h (h为D 到底面ABC 的距离)，即3＝13×12×6×6h ⇒h ＝3，即R ＋R 2－r 2＝3(R 为外接球半径)，解得R ＝2，所以球O 的表面积为4π×22＝16π.答案：16π 14．(2021·杭州市联谊学校高三其次次联考)一个等腰直角三角形的三个顶点分别在正三棱柱ABC -A 1B 1C 1的三条侧棱上，已知正三棱柱的底面边长为2，则该三角形的斜边长为________．解析：如图，在正三棱柱ABC -A 1B 1C 1中，△ABC 为正三角形，边长为2，△DEF 为等腰直角三角形，DF 为斜边，设DF 的长为x ，则DE ＝EF ＝22x ，作DG ⊥BB 1，GH ⊥CC 1，EI ⊥CC 1，垂足分别为G ，H ，I ，则EG ＝DE 2－DG 2＝x 22－4，FI ＝EF 2－EI 2＝x 22－4，FH ＝FI ＋HI ＝FI ＋EG＝2x 22－4.连接DH ，在Rt △DHF 中，DF 2＝DH 2＋FH 2，即x 2＝4＋⎝⎛⎭⎫2x 22－42，解得x ＝23，即该三角形的斜边长为2 3.答案：2 3 15．(2021·浙江省名校新高考联盟第一次联考)如图，ABEDFC 为多面体，平面ABED 与平面ACFD 垂直，点O 在线段AD 上，OA ＝1，OD ＝2，△OAB ，△OAC ，△ODE ，△ODF 都是正三角形，则BC ＝________，四棱锥F-OBED的体积为________．解析：取AO的中点M，连接CM，BM，由△OAB，△OAC是正三角形，OA＝1，可知CM⊥AO，BM⊥AO，且BM＝CM＝32，又平面ABED⊥平面ACFD，所以CM⊥平面ABED，所以CM⊥BM，故BC＝62.过点F作FQ⊥OD于点Q，由于平面ABED⊥平面ACFD，所以FQ⊥平面ABED，FQ就是四棱锥F-OBED的高．易知FQ＝3，又S△OBE＝12×1×2×32＝32，S△OED＝12×2×2×32＝3，所以S四边形OBED＝32＋3＝332，故V四棱锥F-OBED＝13×332×3＝32.答案：6232。

高三文科数学训练

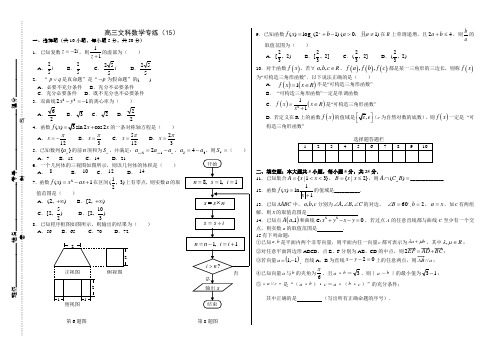
高三文科数学专练（15）一、选择题（共10小题，每小题5分，共50分）1．已知复数i z 2-=，则11+z 的虚部为（）A ．i 52B ．52C ．i 552 D ．552 2． “p q ∨是真命题”是“p ⌝为假命题”的( )A ．必要不充分条件B ．充分不必要条件C ．充分必要条件D ．既不充分也不必要条件 3．双曲线1222-=-y x 的离心率为（）A ．26 B ．3 C ．2 D ．22 4．函数()2cos2f x x x =+的一条对称轴方程是（）A ．12x π=-B ．3x π=C ．512x π=D ．23x π=5．已知数列}{n a 的前n 项和为n S ，并满足：n n n a a a -=++122，354a a -=，则=7S （）A ．7B ．12C ．14D ．216．一个几何体的三视图如图所示，则该几何体的体积是（） A ． 8 B ． 10 C ． 12 D ． 147．函数1)(2+-=ax x x f 在区间)3,21(上有零点，则实数a 的取值范围是（）A ．),2(+∞B ．),2[+∞C ．)25,2[ D ．)310,2[ 8．已知程序框图如图所示，则输出的结果为（） A ．56 B ．65 C ．70 D ．729．已知函数)12(log )(-+=b x f x a )10(≠>a a ，且在R 上单调递增，且42≤+b a ，则ab 的取值范围为（）A ．)2,32[ B ．]2,32[ C ．]2,32( D ．)2,32( 10．对于函数()f x ，若∀,,a b c R ∈，()()(),,f a f b f c 都是某一三角形的三边长，则称()f x 为“可构造三角形函数”．以下说法正确的是（）A ． ()()1f x x R =∈不是“可构造三角形函数”B ． “可构造三角形函数”一定是单调函数C ．()()211f x x R x =∈+是“可构造三角形函数” D ．若定义在R 上的函数()f x 的值域是e ⎤⎦（e 为自然对数的底数），则()f x 一定是 “可构造三角形函数”二、填空题：本大题共5小题，每小题5分，共25分．11．已知集合}31|{<<=x x A ，}2|{≤=x x B ，则=⋂)(B C A R _____________. 12．函数11ln)(+=x x f 的值域是__________． 13．已知ABC ∆中，c b a ,,分别为C B A ∠∠∠,,的对边，60=∠B ,2=b ，x a =，如c 有两组解，则x 的取值范围是14．已知点(),1A a 和曲线C:220x y x y +--=，若过点A 的任意直线都与曲线C 至少有一个交点，则实数a 的取值范围是．15有下列命题：①已知b a ,是平面内两个非零向量，则平面内任一向量c 都可表示为b a μλ+，其中R ∈μλ,； ②对任意平面四边形ABCD ，点E 、F 分别为AB 、CD 的中点，则BC AD EF +=2； ③若向量=a ()1,1-，直线A ，B 为直线02=--y x 上的任意两点，则a AB //；④已知向量a 与b 的夹角为6π，且a ·b ＝3，则｜a －b ｜的最小值为13-； ⑤“c a //”是“（a ·b ）·c ＝a ·（b ·c ）”的充分条件；其中正确的是（写出所有正确命题的序号）．班级_______________姓名_________________考号_____________________得分_____________………………………………………………密…………………………封…………………………线………………………………………………22 1 1 2正视图侧视图俯视图三、解答题：本大题共2个小题，共25分． 16．（本小题满分12分）已知向量a ＝)1),4(cos(πθ-，b ＝)0,3(，其中)45,2(ππθ∈，若a ·b ＝1．（Ⅰ）求θsin 的值；（Ⅱ）求θ2tan 的值．17．（本小题满分13分）已知函数x ax x a x f ln 22)1()(2--+=．（Ⅰ）求证：0=a 时，1)(≥x f 恒成立；（Ⅱ）当]1,2[--∈a 时，求)(x f 的单调区间．专练15参考答案一、选择题：本大题共10小题．每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．二、填空题：本大题共5小题，每小题5分，共25分． 11．)3,2( 12．(],0-∞ 13．)334,2( 14．1][0， 15．②④⑤ 三、解答题：本大题共六个小题，共75分．解答应写出文字说明、证明过程和演算步骤． 16．（12分）【答案解析】（Ⅰ）由已知得：31)4cos(=-πθ，322)4sin(=-πθ θsin ＝]4)4sin[(ππθ+-＝4cos )4sin(ππθ-+4sin )4cos(ππθ-＝624+． ……6分（Ⅱ）由31)4cos(=-πθ得32cos sin =+θθ，两边平方得：92cos sin 21=+θθ 即972sin －=θ，∵),4(4πππθ∈-，且0)4cos(>-πθ，)2,4(4πππθ∈-∴)43,2(ππθ∈∴)23,(2ππθ∈∴ 从而9242cos －=θ 8272tan =∴θ． ……12分17.（13分）【答案解析】（Ⅰ）0=a 时，x x x f ln 2)(2-=，),0(+∞∈xxx x x x x f )1)(1(222)(-+=-='，令0)(='x f ，解得：)1(1舍去-==x x当)1,0(∈x 时，0)(<'x f ，)(x f 在)1,0(上单调递减；当),1(+∞∈x 时，0)(>'x f ，)(x f 在),1(+∞上单调递增。

2022-2023学年河南省高三下学期阶段性测试(四)文科数学试题 Word版含答案

2022—2023学年高中毕业班阶段性测试（四）文科数学一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合{}0A x x =≥，{}1B x x =≠，则A B ⋂=（） A ．{}0x x ≥B ．{}1x x >C ．{}011x x x ≤<>或D ．{}01x x ≤<2．若()12i 112i z +=+，则z =（） A ．34i +B ．34i -C ．43i +D ．43i -3．已知函数()f x 在R 上的导函数为()f x '，则“()00f x '=”是“0x 是()f x 的极值点”的（） A ．充分必要条件 B ．既不充分也不必要条件 C ．充分不必要条件D ．必要不充分条件4．已知向量a ，b 的夹角为56π，且3a =，1b =，则2a b +=（）A ．1B C ．2D5．已知函数()f x 是奇函数，且当0x ≥时，()f x x =，则()4f -=（）A ．4-B ．2-C ．2D ．46．若1cos 2cos sin sin 2cos θθθθθ--=，则tan 4πθ⎛⎫+= ⎪⎝⎭（）A ．3B ．2C D ．17．已知A 为抛物线C ：24y x =上在第一象限内的一个动点，()1,0M -，O 为坐标原点，F 为C 的焦点，若tan 3AMO ∠=，则直线AF 斜率的绝对值为（）A ．2B ．C ．13D ．438．若棱长均相等的正三棱柱的体积为O 的表面上，则球O 的表面积为（） A ．283π B ．1129π C ．6πD ．1123π 9．下表为某外来生物物种入侵某河流生态后的前3个月繁殖数量y （单位：百只）的数据，通过相关理论进行分析，知可用回归模型()1aty ea +=∈R 对y 与t 的关系进行拟合，则根据该回归模型，预测第6个月该物种的繁殖数量为（）第t 个月 1 2 3繁殖数量y1.4e2.2e2.4eA ．3e 百只 B ． 3.5e百只 C ．4e 百只D ． 4.5e百只10．函数()31123f x x x=+-的零点个数为（） A ．1B ．2C ．3D ．411．在ABC △中，角A ，B ，C 的对边分别为a ，b ，c ，若2A B =，则3a cb-的取值范围为（） A ．(]3,4B ．712,35⎛⎤⎥⎝⎦ C ．133,4⎛⎤⎥⎝⎦D ．(]2,512．已知双曲线()222210,0x y a b a b -=>>的左顶点为A ，点0,2b B ⎛⎫⎪⎝⎭，直线AB 与双曲线的两条渐近线分别交于P ，Q 两点，若线段PQ 的垂直平分线经过双曲线的右顶点，则双曲线的离心率为（） A ．2B ．3C ．52D ．233二、填空题：本题共4小题，每小题5分，共20分．13．在区间[]2,3-上随机取一个数x ，则1x >的概率为______．14．已知实数x ，y 满足约束条件10,10,240,x y x x y -+≤⎧⎪+≥⎨⎪-+≥⎩则3z x y =+的最大值为______．15．已知函数()()cos ,0,2f x A x A πωϕωϕ⎛⎫=+>≤⎪⎝⎭的部分图象如图所示，将()f x 的图象向右平移4T（T 为()f x 的最小正周期）个单位长度得到()g x 的图象，则()0g =______．16．已知圆锥内有一个内接圆柱，圆柱的底面在圆锥的底面内，当圆柱与圆锥体积之比最大时，圆柱与圆锥的底面半径之比为______．三、解答题：共70分．解答应写出文字说明，证明过程或演算步骤．第17～21题为必考题，每个试题考生都必须作答．第22，23题为选考题，考生根据要求作答．（一）必考题：共60分．17．（12分）已知数列{}n a 的前n 项和252n n nS -=．（Ⅰ）求{}n a 的通项公式；（Ⅱ）设10,10,2,10,n n n a n b b n -≤⎧=⎨>⎩求数列{}n b 的前30项和．18．（12分）某超市为改善某产品的销售状况并制订销售策略，统计了过去100天该产品的日销售收入（单位：万元）并分成六组制成如图所示的频率分布直方图．（Ⅰ）求a 的值并估计过去100天该产品的日销售收入的平均值x ；（同一区间数据以中点值作代表）（Ⅱ）该超市过去100天中有30天将该商品降价销售，在该商品降价的30天中有18天该产品的日销售收入不低于0.6万元，判断能否有97.5%的把握认为该商品的日销售收入不低于0.6万元与该日是否降价有关．附：()()()()()22n ad bc K a b c d a c b d -=++++，其中n a b c d =+++．()20P K k ≥0.050 0.025 0.010 0k3.8415.0246.63519．（12分）如图，在四棱锥P -ABCD 中，PC BC ⊥，PA PB =，APC BPC ∠=∠．（Ⅰ）证明：PC AD ⊥；（Ⅱ）若AB CD ∥，PD AD ⊥，3PC =，且点C 到平面P AB 的距离为62，求AD 的长．20．（12分）已知函数()32213f x x x ax =-+-，a ∈R ．（Ⅰ）若曲线()y f x =在点()0,1-处的切线斜率为4-，求()f x 的单调区间；（Ⅱ）若存在唯一的()00,2x ∈，满足()()01f x f =-，求a 的取值范围． 21．（12分）已知椭圆()2222:10x y C a b a b +=>>的离心率为23，且3⎫⎪⎪⎭为C 上一点．（Ⅰ）求C 的标准方程；（Ⅱ）点A ，B 分别为C 的左、右顶点，M ，N 为C 上异于A ，B 的两点，直线MN 不与坐标轴平行且不过坐标原点O ，点M 关于原点O 的对称点为M '，若直线AM '与直线BN 相交于点P ，直线OP 与直线MN 相交于点Q ，证明：点Q 位于定直线上．（二）选考题：共10分．请考生在第22，23题中任选一题作答，如果多做，则按所做的第一题计分． 22．[选修4-4：坐标系与参数方程]（10分）在直角坐标系xOy 中，曲线C 的参数方程为2224,4824t x t t y t ⎧=⎪⎪+⎨-⎪=⎪+⎩（t 为参数），以坐标原点O 为极点，x 轴正半轴为极轴建立极坐标系，直线l 的极坐标方程为cos sin 4ρθρθ+=．（Ⅰ）求曲线C 的普通方程；（Ⅱ）若P 为C 上一动点，求P 到l 的距离的取值范围． 23．[选修4-5：不等式选讲]（10分）已知函数()112222f x x x =++-．（Ⅰ）求不等式()3f x <的解集；（Ⅱ）设()f x 的最小值为M ，若正实数a ，b 满足221a b M a b +=++，证明：32a b +≥．2022—2023学年高中毕业班阶段性测试（四）文科数学·答案一、选择题：本题共12小题，每小题5分，共60分．1．答案 C命题意图本题考查集合的交运算．解析 {}011A B x x x ⋂=≤<>或． 2．答案 A命题意图本题考查复数的四则运算．解析 ()()()()112i 12i 112i 1520i34i 12i 12i 12i 5z +-+-====-++-，则34i z =+．3．答案 D命题意图本题考查极值点的概念以及充分必要条件的判断．解析由极值点的定义，若0x 为()f x 的极值点，则有()00f x '=，而由()00f x '=不一定推得0x 为()f x 的极值点，例如()3f x x =，故“()00f x '=”是“0x 是()f x 的极值点”的必要不充分条件． 4．答案 A命题意图本题考查平面向量的运算．解析 ()22222443431ab a ba ab b +=+=+⋅+=+⨯=． 5．答案 C命题意图本题考查奇函数的概念．解析因为()f x 是奇函数，所以()()44f f -=-，又()442f ==-，所以()42f -=． 6．答案 A命题意图本题考查三角恒等变换．解析由题意()2112sin 1tan 2sin cos θθθθ--=-，即1tan 2θ=，1tantan 142tan 3141tan tan 142πθπθπθ++⎛⎫+===⎪⎝⎭--． 7．答案B命题意图本题考查抛物线的性质．解析设211,4y A y ⎛⎫ ⎪⎝⎭，1210tan 314AMy AMO k y -∠===+，解得1y 或1y =12A ⎛ ⎝或(2,A ，又()1,0F ，所以0112AF k ==--AF k ==AF k =． 8．答案 D命题意图本题考查三棱柱的外接球．解析设该正三棱柱棱长为x ，底面三角形的外接圆半径为r ，则21sin 602x x ︒⋅⋅=，∴4x =，则r =O 半径为R ，则22216284233x R r ⎛⎫=+=+=⎪⎝⎭，228112=4=4=33S R πππ⨯表． 9．答案 C命题意图本题考查回归分析．解析由题意，1aty e+=两边取自然对数得ln 1y at =+，令ln u y =，则1u at =+．()1231ln ln ln 23u y y y =++⨯=，()123123t t t t =++⨯=，∵回归直线必过样本点的中心，∴221a =+，得12a =，∴12tu =+，则12t y e +=．当6t =时，4y e =．10．答案 B命题意图本题考查函数零点问题．解析易知()f x 的定义域为{}0x x ≠，()422211x f x x x x -'=-=，令()0f x '<，解得10x -<<或01x <<，∴()f x 在()1,0-和()0,1上单调递减，令()0f x '>，解得1x <-或1x >，∴()f x 在(),1-∞-和()1,+∞上单调递增．当1x =-时，()f x 取得极大值()10103f -=-<，易知()f x 在(),0-∞上没有零点；当1x =时，()f x 取得极小值()2103f =-<，且1820381f ⎛⎫=> ⎪⎝⎭，()7206f =>，可知()f x 在()0,+∞上有2个零点．综上所述，()f x 的零点个数为2． 11．答案 C命题意图本题考查解三角形．解析 ∵2A B =，∴sin sin 22sin cos A B B B ==且0,3B π⎛⎫∈ ⎪⎝⎭，()3sin sin sin33sin 4sin C A B B B B =+==-，由正弦定理可得333sin sin 6sin cos 3sin 4sin sin sin a c A C B B B Bb B B---+==()226cos 41cos 34cos 6cos 1B B B B =+--=-++，令1cos ,12B t ⎛⎫=∈ ⎪⎝⎭，则23461a c t t b -=-++，由二次函数性质知2134613,4t t ⎛⎤-++∈ ⎥⎝⎦，∴3133,4a c b -⎛⎤∈ ⎥⎝⎦． 12．答案 B命题意图本题考查双曲线的性质和离心率的求法．解析不妨设点P 在直线b y x a =上，由题可知(),0A a -，∴2AB b k a =，∴:22AB b bl y x a =+，由,22,b by x a b y x a⎧=+⎪⎪⎨⎪=⎪⎩得,,P P x a y b =⎧⎨=⎩∴(),P a b ，同理,33a b Q ⎛⎫- ⎪⎝⎭，∴PQ 的中点为2,33a b ⎛⎫ ⎪⎝⎭，PQ 的垂直平分线方程为2233b a a y x b ⎛⎫-=-- ⎪⎝⎭，将0,y x a=⎧⎨=⎩代入整理得222b a =，则e ==二、填空题：本题共4小题，每小题5分，共20分． 13．答案35命题意图本题考查几何概型的计算．解析在区间[]2,3-上随机取一个数x ，若1x >，则[)(]2,11,3x ∈--⋃，所以1x >的概率为()()12313325-++-=+．14．答案 9命题意图本题考查线性规划．解析根据不等式组作出可行域如图中阴影部分所示，当目标函数表示的直线经过点()2,3时，3z x y =+取得最大值9．15．答案 3命题意图本题考查三角函数的图象和性质．解析由图可知2A =，22362T πππ=-=，∴T π=，22πωπ==．由()226k K πϕπ⨯+=∈Z ，及2πϕ≤，得3πϕ=-，∴()2cos 23f x x π⎛⎫=-⎪⎝⎭，∴()52cos 22cos 2436g x x x πππ⎡⎤⎛⎫⎛⎫=--=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦，∴()502cos36g π==- 16．答案23命题意图本题考查导数的应用．解析设圆锥的底面半径为R ，圆锥的轴截面为等腰三角形，底边长为2R ，设其底角为α，则圆锥的高为tan R α，圆锥的体积为3tan 3R πα．设圆锥内接圆柱的底面半径为r ，高为h ，则tan tan r R hR R αα-=，即()tan h R r α=-，则圆柱的体积为()()2223tan tan r h r R r Rr r ππαπα=-=-，()0,r R ∈．圆柱与圆锥体积之比为23233r r R R ⎛⎫- ⎪⎝⎭，设()01r t t R =<<，()23f t t t =-，则()()22323f t t t t t '=-=-．由()0f t '=，得23t =，当203t <<时，()0f t '>，当213t <<时，()0f t '<，所以当23t =时，()f t 取得最大值，即圆柱与圆锥体积之比最大，此时23r R =．三、解答题：共70分．解答应写出文字说明，证明过程或演算步骤． 17．命题意图本题考查数列求通项和数列求和．解析（Ⅰ）111522a S -===-，当2n ≥时，有252n n n S -=，()()211512n n n S ----=，两式相减得()()()2215151322n a n n n n n n ⎡⎤=---+-=-≥⎣⎦，当1n =时，12a =-符合上式，故3n a n =-．（Ⅱ）设数列{}n b 的前n 项和为n T ，则()()()301210111220212230T b b b b b b b b b =++⋅⋅⋅++++⋅⋅⋅++++⋅⋅⋅+．由题意得1210121010b b b a a a S ++⋅⋅⋅+=++⋅⋅⋅+=，()11122012101022b b b b b b S ++⋅⋅⋅+=++⋅⋅⋅+=，()21223011122010102224b b b b b b S S ++⋅⋅⋅+=++⋅⋅⋅+=⨯=，∴()230107710501752T S ==-=． 18．命题意图本题考查频率分布直方图和独立性检验．解析（Ⅰ）依题意有()1.5 2.5 2.00.80.20.11a +++++⨯=，得 3.0a =．0.350.150.450.250.550.300.650.200.750.080.850.020.537x =⨯+⨯+⨯+⨯+⨯+⨯=．（Ⅱ）依题意作2×2列联表：()221001858121218.36730707030K ⨯⨯-⨯=≈⨯⨯⨯．因为18.367 5.024>，所以有97.5%的把握认为该商品的日销售收入不低于0.6万元与该日是否降价有关． 19．命题意图本题考查线线垂直的证明，以及点到面距离的求法．解析（Ⅰ）如图，连接AC ，∵PA PB =，APC PBC ∠=∠，PC PC =，∴PAC PBC ≌△△， ∴90PCA PCB ∠=∠=︒，即PC AC ⊥．∵PC BC ⊥，AC BC C ⋂=，PC ⊥平面ABCD ，又AD ⊂平面ABCD ，∴PC AD ⊥．（Ⅱ）取AB 的中点E ，连接PE ，CE ．∵PA PB =，∴PE AB ⊥，由（Ⅰ）知AC BC =，∴CE AB ⊥， ∵PE CE E ⋂=，∴AB ⊥平面PCE ，又AB ⊂平面P AB ，∴平面PAB ⊥平面PCE ．过C 作CH PE ⊥于H ，则CH ⊥平面P AB ，由条件知6CH =．易知PC CE ⊥，设CE m =，则23PE m + 由1122PC CE PE CH ⋅=⋅2633m m =+，得3m =，∴3CE = ∵PD AD ⊥，AD PC ⊥，PC PD P ⋂=，∴AD ⊥平面PCD ，∴AD CD ⊥，又∵AB CD ∥，∴AD AB ⊥，∴四边形AECD 为矩形，∴3AD CE ==20．命题意图本题考查导数的几何意义，以及函数与方程的综合问题．解析（Ⅰ）()222f x x x a '=-+，由题意知()04f a '==-．所以()()()2224212f x x x x x '=--=+-，则当1x <-或2x >时，()0f x '>，当12x -<<时，()0f x '<，所以()f x 的单调递增区间为(),1-∞-和()2,+∞，单调递减区间为()1,2-．（Ⅱ）由()()01f x f =-，得()()010f x f --=，即()()()323200021113x x a x ⎡⎤⎡⎤-----+--⎡⎤⎣⎦⎣⎦⎣⎦()()()()()20000002111113x x x x x a x =+-+--+++ ()()200011253503x x x a =+-++=．根据已知，可得方程20025350x x a -++=在区间()0,2内仅有一个实根，设函数()22535g x x x a =-++，其图象的对称轴为()50,24x =∈，所以只需()()()258350,00,20,a g g ∆=-+>⎧⎪>⎨⎪<⎩或0∆=，解得513a -<<-或58a =-，即a 的取值范围是55,138⎛⎫⎧⎫--⋃-⎨⎬ ⎪⎝⎭⎩⎭．21．命题意图本题考查椭圆方程和定直线的证明．解析（Ⅰ）设椭圆C 的焦距为()20c c >，由题意得222222,371019,c a a ba b c ⎧=⎪⎪⎪+=⎨⎪⎪=+⎪⎩，解得229,5,a b ⎧=⎪⎨=⎪⎩∴C 的标准方程为22195x y +=．（Ⅱ）由题可知()3,0A -，()3,0B ，设()11,M x y ，()22,N x y ，则()11,M x y '--，设:MN l x my n =+．联立22,1,95x my n x y =+⎧⎪⎨+=⎪⎩消去x 得()()2225910590m y mny n +++-=，∴1221059mn y y m -+=+，()21225959n y y m -=+，1122,3,3AM BN y k x y k x '⎧=⎪-⎪⎨⎪=⎪-⎩∴()11:33AM y l y x x '=+-，()22:33BN yl y x x =--，又∵点P 为直线AM '和BN 的交点，∴112233,33,P P P P x y y y x y x y -⎧⋅=+⎪⎪⎨-⎪⋅=-⎪⎩故可得1212332P P x x x y y y ⎛⎫--=+⎪⎝⎭121233P my n my n y y y ⎛⎫+-+-=+ ⎪⎝⎭()121223P y y m n y y y ⎡⎤+=+-⎢⎥⎣⎦()()2102359P mn m n y n ⎡⎤-⎢⎥=+-⋅-⎢⎥⎣⎦， ∴33P P m x y n =+，故3:3OP m l x y n =+．联立3:,3:,OP MN m l x y n l x my n ⎧=⎪+⎨⎪=+⎩消去y 得3Q x =-，因此，点Q 位于定直线3x =-上．22．命题意图本题考查极坐标与参数方程．解析（Ⅰ）()2222164t x t =+，()()22222444t y t -=+， ∴()()()()2222222222216441444t t t y x t t +-++===++，又22282162244t y t t -==-+>-++， ∴曲线C 的普通方程为()22124y x y +=≠-．（Ⅱ）设P 到l 的距离为d ．令cos ,sin ,x y ρθρθ=⎧⎨=⎩得直线l 的直角坐标方程为40x y +-=，设()cos ,2sin P αα，[)0,2απ∈且32πα≠，则d ==1tan 2ϕ=， ∴d的取值范围是22⎡⎢⎣⎦． 23．命题意图本题考查不等式的证明．解析（Ⅰ）由题意知()14,,4111,,4414,.4x x f x x x x ⎧-<-⎪⎪⎪=-≤<⎨⎪⎪≥⎪⎩令()3f x =，得34x =-或34，结合图象可知()3f x <的解集为3344x x ⎧⎫-<<⎨⎬⎩⎭．（Ⅱ）由题意可知2121a b a b +=++，∴4121121a b -+-=++， ∴41221a b +=++．令2m a =+，1n b =+，则412m n +=，()()141141333535432222n m a b m n m n m n m n ⎛⎫⎛⎫+=+-=++-=++-≥+-= ⎪ ⎪⎝⎭⎝⎭，当且仅当23m n ==，即1a =，12b =时等号成立．。

文科数学高三练习题

文科数学高三练习题1. (4x + 3) / (x - 2) = 3解：首先将等式两边都乘以 (x - 2)，得到：4x + 3 = 3(x - 2)展开并整理得：4x + 3 = 3x - 6将变量移到一边，常数移到另一边，得：4x - 3x = -6 - 3化简得：x = -9因此，方程的解为 x = -9。

2. 已知函数 f(x) = 2x^2 + 3x - 2，求函数 f(x) 在 x = 1 处的导数。

解：导数的定义为函数在某一点处的斜率，即切线的斜率。

对于f(x) = 2x^2 + 3x - 2，我们需要求出 x = 1 处的导数。

首先将函数 f(x) = 2x^2 + 3x - 2 求导，得到：f'(x) = 4x + 3然后将 x = 1 代入导函数，得到：f'(1) = 4(1) + 3计算得：f'(1) = 7因此，函数 f(x) 在 x = 1 处的导数为 7。

3. 已知一道三角函数题为：tan(x) = 2，求 x 的取值范围。

解：首先我们知道，tan 函数的周期为π，即tan(x) = tan(x + kπ)，其中 k 为整数。

根据题目中的条件 tan(x) = 2，我们可以找到一个特解 x = arctan(2)。

然后我们需要找到 tan(x) = 2 的解集。

由于 tan 函数的图像在某些区间上是单调递增或递减的，我们可以通过观察来判断。

在第一象限，tan 函数是单调递增的，因此 x = arctan(2) 是最小正解。

利用 tan 函数的周期性，我们可以得到其他解为x = arctan(2) + kπ，其中 k 为整数。

综上，x 的取值范围为x = arctan(2) + kπ，其中 k 为整数。

4. 已知集合 A = {1, 2, 3, 4, 5}，集合 B = {3, 4, 5, 6, 7}，求A ∩ B 和A ∪ B。

解：A ∩ B 表示集合 A 和集合 B 的交集，即同时包含于 A 和 B 的元素。

高三文科数学复习题

高三文科数学复习题高三文科数学复习题高三文科数学复习是每位文科生必经的一道坎。

在这个阶段，数学的复习显得尤为重要，因为数学作为一门基础学科，对于文科生来说，既是挑战又是必修。

在这篇文章中，我将为大家列举一些高三文科数学复习题，希望能够帮助大家更好地备考。

一、函数与方程1. 已知函数 f(x) = 2x + 3，求 f(4) 的值。

2. 解方程 2x + 5 = 15。

3. 已知函数 f(x) = x^2 + 3x + 2，求 f(-1) 的值。

4. 解方程 x^2 + 5x - 6 = 0。

二、数列与数列求和1. 求等差数列 2，5，8，11，... 的第 10 项。

2. 求等差数列 3，6，9，12，... 的前 10 项和。

3. 求等比数列 2，4，8，16，... 的第 5 项。

4. 求等比数列 3，6，12，24，... 的前 5 项和。

三、概率与统计1. 一个骰子投掷一次，求出现奇数的概率。

2. 一副扑克牌中，红桃牌有 13 张，黑桃牌有 13 张，方块牌有 13 张，梅花牌有 13 张。

从中随机抽取一张牌，求抽到红桃牌的概率。

3. 一本书有 100 页，其中有 20 页有错别字。

随机翻到一页，求翻到错别字的概率。

4. 一组数据为：2，4，6，8，10。

求平均数、中位数、众数。

四、几何与三角函数1. 已知正方形 ABCD 的边长为 6cm，求对角线 AC 的长度。

2. 已知三角形 ABC，AB = 5cm，BC = 6cm，AC = 7cm。

判断三角形 ABC 是否为等腰三角形。

3. 已知 sinA = 3/5，求 cosA 的值。

4. 已知直角三角形 ABC，AB = 3cm，AC = 4cm。

求角 B 的正弦值和余弦值。

五、函数与导数1. 求函数 f(x) = x^2 + 3x + 2 的导数。

2. 求函数 f(x) = 2x^3 - 4x 的导数。

3. 求函数 f(x) = 3x^2 - 6x + 2 的极值点。

陕西省榆林市米脂中学2021-2022学年高三上学期第四次模拟文科数学试题(含答案解析)

陕西省榆林市米脂中学2021-2022学年高三上学期第四次模拟文科数学试题学校:___________姓名：___________班级：___________考号：___________一、单选题1．已知全集{1U =，2，3，4，5}，{2A =，4，5}，{3B =，5}，则()U A B =⋃ð（）A ．{3}B ．{2，4}C ．{1，2，3，4}D ．{1，2，4，5}2．命题p ：“x ∃∈R ，()214204x a x +-+≤”，则p ⌝为（）A ．x ∀∈R ，()214204x a x +-+>B ．x ∀∈R ，()214204x a x +-+≤C ．x ∃∈R ，()214204x a x +-+≥D ．x ∃∈R ，()214204x a x +-+>3．下列四个函数中，在区间π0,2⎛⎫ ⎪⎝⎭上为增函数的是（）A ．sin y x =-B ．cos y x =C ．tan y x=D ．tan y x=-4．若函数()1,012,02x x f x x ⎧⎪=⎨+<⎪⎩，则()()1f f -=（）A ．－2B ．－1C ．0D ．15．已知函数()()1xf x a a a =->，则函数()f x 的图像不经过（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限6．若命题p ：函数()()log 11a f x x =-+（0a >且1a ≠的图像过定点()2,1，命题q ：函数()2xg x =的值域为[)0,∞+，则下列命题是真命题的是（）A ．p q ∧B ．p q ∨C ．()p q⌝∧D ．()()p q ⌝∧⌝7．函数()()sin x xf x e e x -=+的图象可能是（）A．B．C．D．8．已知x∈R，则“x>”是“22x>”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件9．若0.70.5a=，0.50.7b=，0.11.1c=，则a，b，c的大小关系是（）A．a b c>>B．c b a>>C．c a b>>D．a c b>>10．函数()()πsin0,2f x xωϕωϕ⎛⎫=+><⎪⎝⎭的图象如图所示，将函数()f x的图象向右平移π6个单位长度，得到函数()g x的图象，则（）A．()sin2g x x=B．()cos2g x x=C．()2πsin23g x x⎛⎫=+⎪⎝⎭D．()2πcos23g x x⎛⎫=+⎪⎝⎭11．给出定义：若函数()f x在区间D上可导，即()f x'存在，且导函数()f x'在D上也可导，则称()f x在D上存在二阶导函数.记()()()f x f x''''=，若()0f x''<在D上恒成立，则称()f x在D上为凸函数.若()2ln5axg x x=+在()0,1上是凸函数，则实数a可取的最大整数值为（）A．0B．1C．2D．312．已知定义在()0,+¥的函数()f x满足：()()()0,,0x f xx f x'+∞-∀∈<，其中()f x¢为()f x的导函数，则不等式()()()(231)123x f x x f x-+>+-的解集为（）A ．3,42⎛⎫ ⎪⎝⎭B ．()4,+∞C ．()1,4-D ．(),4-∞二、填空题13．函数()()1lg 12f x x x =++-的定义域为______.14．若1tan 42⎛⎫-=- ⎪⎝⎭πα，则tan 2α=______.15．设()f x 是定义域为R 的奇函数，且()()1f x f x +=-，则()21f -=______.16．数学中处处存在着美，机械学家莱洛沷现的莱洛三角形就给人以对称的美感．莱洛三角形的画法：先画等边三角形ABC ，再分别以点A ，B ，C 为圆心，线段AB 长为半径画圆弧，便得到莱洛三角形．若线段AB 长为2，则莱洛三角形的面积是________．三、解答题17．设函数()()sin cos R f x x x x =∈.(1)求函数()f x 的最小正周期；(2)求函数π6f x ⎛⎫- ⎪⎝⎭图象的对称中心的坐标.18．已知函数()32f x ax bx =+在1x =时取得极大值3.(1)求a ，b 的值；(2)求曲线()y f x =在点()()1,1f --处的切线方程.19．某商场经营一批进价是每件30元的商品，在市场试销中发现，该商品销售单价x (不低于进价，单位：元)与日销售量y (单位：件)之间有如下关系：x 4550y2712(1)确定x 与y 的一个一次函数关系式y ＝f (x )(注明函数定义域)．(2)若日销售利润为P 元，根据(1)中的关系式写出P 关于x 的函数关系式，并指出当销售单价为多少元时，才能获得最大的日销售利润？20．已知ABC 中，a ，b ，c 分别为角A ，B ，C 的对边，()sin 2b A a B =-.(1)求B ；(2)若D 为BC 边的中点AD =，BC =ABC 的面积.21．已知函数()232log f x x =-，()2log g x x =.(1)当[]2,8x ∈时，求函数()()()1h x f x g x =+⋅⎡⎤⎣⎦的值域(2)如果对任意的[]2,8x ∈，()()22f x fk gx ⋅>⋅恒成立，求实数k 的取值范围.22．已知函数()e 1xf x ax =--，其中e 为自然对数的底数.(1)求()f x 的单调区间：(2)若函数()f x 在区间()0,1上存在零点，求实数a 的取值范围.参考答案：1．D【分析】根据并集和补集的知识求得正确答案.【详解】全集{1U =，2，3，4，5}，{3B =，5}，{1U B ∴=ð，2，4}，{2A = ，4，5}，(){1U A B ∴=⋃ð，2，4，5}，故选：D 2．A【分析】根据命题的否定的定义，直接选出答案即可.【详解】写出命题的否定，则“x ∃∈R ，()214204x a x +-+≤”的否定为，p ⌝为：x ∀∈R ，()214204x a x +-+>故选：A 3．C【分析】根据正弦、余弦、正切函数的单调性判断即可.【详解】对A ，因为sin y x =在π0,2⎛⎫ ⎪⎝⎭上递增，所以sin y x =-在π0,2⎛⎫ ⎪⎝⎭上单调递减，故A 错误；对B ，cos y x =在π0,2⎛⎫ ⎪⎝⎭上单调递减，故B 错误；对C ，tan y x =在π0,2⎛⎫ ⎪⎝⎭上单调递增，故C 正确；对D ，由C 知，tan y x =-在π0,2⎛⎫ ⎪⎝⎭上单调递减，故D 错误.故答案为：C 4．C【分析】首先求()1f -，再代入求()()1f f -的值.【详解】()111212f --=+=，所以()()()1110f f f -===.故选：C 5．B【分析】根据函数()1xy a a =＞的单调性和函数平移规则分析.【详解】()1xy a a =＞是单调递增的函数，经过()0,1，渐近线为0y =，当0x =时，()000f a a =-＜，()10f a a =-=，渐近线为y a=-，所以图像如下图：故选：B.6．B【分析】根据函数过点可以判断命题p 的真假，由函数的值域可以判断命题q ，然后逐项判断命题的真假即可.【详解】命题p :当2x =时，()()2log 2111a f =-+=，函数过定点()2,1，所以p 为真命题；命题q ：由x ∈R ,所以()20xg x =>，所以值域为：()0,∞+，所以命题q 为假命题，选项A:p 为真命题，q 为假命题，故p q ∧为假命题，所以A 错误；选项B:p 为真命题，q 为假命题，故p q ∨为真命题，所以B 正确；选项C:p 为真命题，p ⌝为假命题，故()p q ⌝∧为假命题，所以C 错误；选项D:p 为真命题，q 为假命题，所以p ⌝为假命题，q ⌝为真命题故()()p q ⌝∧⌝为假命题，故选：B.7．B【分析】分析函数()f x 的奇偶性及2f π⎛⎫⎪⎝⎭与2的大小关系，结合排除法可得出合适的选项.【详解】函数()()sin x xf x e e x -=+的定义域为R ，()()()()()sin sin x x x x f x e e x e e x f x---=+-=-+=-，即函数()f x 为奇函数，排除CD 选项；2222f e e e πππ-⎛⎫=+>> ⎪⎝⎭，排除A 选项.故选：B.8．A【分析】利用充分性和必要性的定义求解即可.【详解】由22x >解得x >或x <所以“x >是“22x >”的充分不必要条件，故选：A 9．B【分析】根据指数函数和幂函数的单调性，将a ，b ，c 与中间值0，1进行比较，即可得出.【详解】解：0.5x y = 在R 上是减函数，0.70.50.50.05<∴<，0.5y x = 在[)0,∞+上是增函数，0.7x y =在R 上是减函数，0.50.500.50.70.71∴<<=，则0.70.50.50.7<，即01a b <<<，又 1.1x y =在R 上是增函数，0.101.111.1>=∴，即1c >，综上所述，可知c b a >>，故选：B.10．A【分析】先由图像中周期求得ω，再由点代入求得ϕ，从而利用三角函数图像平移求得()g x 的解析式即可.【详解】结合图像，易得17πππ41234T =-=，则πT =，所以由2πT ω=得2ππω=，所以2ω=，又0ω>，所以2ω=，则()()sin 2f x x ϕ=+，又因为7π,112⎛⎫- ⎪⎝⎭落在()f x 上，所以7πsin 2112ϕ⎛⎫⨯+=- ⎪⎝⎭，即7πsin 16ϕ⎛⎫+=- ⎪⎝⎭，所以7π3π2π,Z 62k k ϕ+=+∈，得ππ,Z k k ϕ=+∈23，因为π2ϕ<，所以当且仅当0k =时，π3ϕ=满足要求，所以()πsin 23f x x ⎛⎫=+ ⎪⎝⎭，因为将函数()f x 的图象向右平移π6个单位长度，得到函数()g x 的图象，所以()ππsin 2sin 263x g x x ⎡⎤⎛⎫-+= ⎪⎢⎥⎣⎦=⎝⎭.故选：A.11．C【分析】根据题意求得()g x ''，将问题转化为()0g x ''<在()0,1x ∈恒成立，解出不等式即可得到结果.【详解】因为()215a g x x x '=+，()2215a g x x ''=-由凸函数的定义可得，()0g x ''<在()0,1x ∈恒成立，即22215052a a x x-<⇒<在()0,1x ∈恒成立，且当1x =时，2min 5522x ⎛⎫< ⎪⎝⎭，所以52a ≤，则实数a 可取的最大整数值为2故选:C.12．A【分析】先构造函数()()f x g x x=，由()()()0,,0x f x x f x '+∞-∀∈<可得()g x 在()0,+¥上单调递增，则所求的不等式等价于()()123123f x f x x x +->+-，列出不等式组，解出x 的范围即可.【详解】设()()()()()2,f x xf x g x g x f x x x ''==-，因为()()()0,,0x f x x f x '+∞-∀∈<，所以在()0,+¥上()0g x ¢>，所以()g x 在()0,+¥上单调递增，由已知，()f x 的定义域为()0,+¥，所以10,230x x +>->，所以()()23 11 2)()3(x f x x f x -+>+-等价于()()123123f x f x x x +->+-，即(()13)2g g x x >-+，所以10230123x x x x +>⎧⎪->⎨⎪+>-⎩，解得342x <<，所以原不等式的解集是3,42⎛⎫⎪⎝⎭.故选：A.13．()()1,22,-⋃+∞【分析】根据函数的解析式，列出函数有意义时满足的不等式，求得答案.【详解】函数()()1lg 12f x x x =++-需满足1020x x +>⎧⎨-≠⎩，解得1x >-且2x ≠，故函数()()1lg 12f x x x =++-的定义域为()()1,22,-⋃+∞，故答案为：()()1,22,-⋃+∞14．34-##0.75-【分析】展开1tan 42⎛⎫-=- ⎪⎝⎭πα，求出tan α，再代入22tan tan 21tan ααα=-，即可求解．【详解】解：πtantan π1tan 14tan π41+tan 21+tan tan 4ααααα--⎛⎫-===- ⎪⎝⎭，解得tan 3α=，所以222tan 236t 4an 2==1tan 1383ααα==---⨯-，故答案为：34-.15．0【分析】结合函数的奇偶性、周期性等知识求得正确答案.【详解】依题意，()f x 是定义域为R 的奇函数，()00f =，由()()1f x f x +=-令0x =得()()100f f ==，()()()()()()21111f x f x f x f x f x f x +=++=--=-+=--=，所以()f x 是周期为2的周期函数，所以()()()212111210f f f -=-+⨯==.故答案为：016．2π-##2π-【分析】由题意，可先求解出正三角形扇形面积，再利用莱洛三角形与扇形之间的关系转化即可求解.【详解】由已知得2π3AB BC AC ===，则AB =BC =AC =2，故扇形的面积为2π3，由已知可得，莱洛三角形的面积扇形面积的3倍减去三角形面积的2倍，∴所求面积为22π3222π3⨯-=-故答案为：2π-或2π-+．17．(1)π(2)ππ,026k ⎛⎫+ ⎪⎝⎭，Z k ∈【分析】（1）利用正弦函数的倍角公式化简()f x ，再由最小正周期公式即可得解；（2）结合（1）中结论求得π6f x ⎛⎫- ⎪⎝⎭，再结合正弦函数的对称性即可得解.【详解】（1）因为()1sin cos sin 22f x x x x ==，所以2ππ2T ==，故函数()f x 的最小正周期为π.（2）由（1）知()1sin 22f x x =，所以π1πsin 2623f x x ⎛⎫⎛⎫-=- ⎪ ⎪⎝⎭⎝⎭，令π2π3x k -=，Z k ∈，则ππ26k x =+，Z k ∈，所以函数π6f x ⎛⎫- ⎪⎝⎭图象的对称中心的坐标为ππ,026k ⎛⎫+ ⎪⎝⎭，Z k ∈.18．(1)6,9a b =-=(2)36210x y ++=【分析】（1）解方程组(1)3(1)320f a b f a b =+=⎧⎨=+='⎩即可求解；（2）只需求出()1f '-，()1f -，再利用点斜式写直线方程即可.【详解】（1）()232f x ax bx '=+，由题意可得(1)3(1)320f a b f a b =+=⎧⎨=+='⎩，解得69a b =-⎧⎨=⎩，检验：()21818f x x x '=-+，令()0f x '=，解得0x =或1x =，当()(),01,x ∞∞∈-⋃+时，()0f x '<，()f x 单调递减；当()0,1x ∈时，()0f x ¢>，()f x 单调递增，满足题意；（2）由（1）得()3269f x x x =-+，所以()21818f x x x '=-+.所以()115f -=，()136f '-=-.所以所求切线方程为()15361y x -=-+，即36210x y ++=.19．(1)f (x )＝－3x ＋162，x ∈[30，54]；(2)P=-3(x-42)2+432,x ∈[30,54]，销售单价为42元.【分析】（1）设出函数的解析式，进而根据表格中的数据求得答案；（2）先求出P ，然后根据二次函数求最值的方法解得答案.【详解】（1）因为f (x )是一次函数，设f (x )＝ax ＋b ，由表格得方程组452735012162a b a a b b +==-⎧⎧⇒⎨⎨+==⎩⎩，所以y ＝f (x )＝－3x ＋162.又y ≥0，所以30≤x ≤54，故所求函数关系式为f (x )＝－3x ＋162，x ∈[30，54]．（2）由题意得，P ＝(x －30)y ＝(x －30)(162－3x )232524860x x =-+-()[]2342432,30,54x x =--+∈.当x ＝42时，最大的日销售利润P ＝432，即当销售单价为42元时，获得最大的日销售利润．20．(1)π6B =(2)【分析】（1）利用正弦定理、辅助角公式化简已知条件，从而求得B .（2）利用余弦定理求得AB ，进而求得三角形ABC 的面积【详解】（1）在ABC 中由正弦定理及已知条件，可得()sin sin sin 2A B A B =，∵()0,πA ∈，∴sin 0A >，∴sin 2B B =-，∴πsin 13B ⎛⎫+= ⎪⎝⎭.∵()0,πB ∈，∴ππ4π333B <+<.∴πππ,326B B +==.（2）∵D 为BC 边的中点，BC =，∴BD =.在ABD △中，由余弦定理得2222cos AD AB BD AB BD B =+-⋅⋅，∴2π7326AB AB =+-，∴2340AB AB --=，解得4AB =或1AB =-（舍去）.∴11sin 4sin 3022ABC S AB BC B =⋅⋅=⨯⨯︒=△21．(1)[]6,2-(2)9,4⎛⎫-∞- ⎪⎝⎭【分析】（1）()()2222log 1h x x =--+，[]2log 1,3x ∈，计算得到值域.（2）令2log t x =，[]1,3t ∈，题目转化为3341k t t ⎛⎫⎛⎫<-- ⎪⎪⎝⎭⎝⎭对任意的[]1,3t ∈恒成立，[]31,3t ∈，计算最值得到答案.【详解】（1）()()()2222242log log 2log 1h x x x x =-=-+-，[]2,8x ∈，[]2log 1,3x ∈，设[]2log 1,3m x =∈，()()2221m k m --=+，()()max 12k m g ==，()()min 36k m g ==-，故函数()h x 的值域为[]6,2-.（2）()()22f x f k g x ⋅>⋅，即()()()222234log 3log log x x k x -->，令2log t x =，[]1,3t ∈，()()2343t t k t -->⋅对任意的[]1,3t ∈恒成立.3341k t t ⎛⎫⎛⎫<-- ⎪⎪⎝⎭⎝⎭对任意的[]1,3t ∈恒成立，[]1,3t ∈，设[]31,3n t =∈.设()()()2594124F n n n n ⎛⎫=--=-- ⎪⎝⎭，()min 5924F n F ⎛⎫==- ⎪⎝⎭，故94k <-.实数k 的取值范围为9,4⎛⎫-∞- ⎪⎝⎭.22．(1)见解析(2)()1,e 1-【分析】(1)对函数求导，分0a ≤和0a >两种情况进行讨论，利用导函数的正负来判断函数的单调区间即可求解；(2)结合（1）的结论，分三种情况进行讨论，根据条件和零点存在性定理即可求解.【详解】（1）∵()e 1x f x ax =--，∴()e x f x a '=-，当0a ≤时，()0f x ¢>恒成立，所以()f x 的单调递增区间为(),-∞+∞，无单调递减区间.当0a >时，令()'0f x <，得ln x a <：令()'0f x >，得ln x a >，所以()f x 的单调递减区间为(),ln a -∞，单调递增区间为()ln ,a +∞.综上：当0a ≤时，函数()f x 的单调递增区间为(),-∞+∞，无单调递减区间；当0a >时，函数()f x 的单调递减区间为(),ln a -∞，单调递增区间为()ln ,a +∞.（2）由（1）知()e x f x a '=-.当1a ≤时，函数()f x 在区间()0,1上单调递增且()00f =，所以函数()f x 在区间()0,1上不存在零点.所以当e a ≥时，()f x 在区间()0,1上单调递减且()00f =，所以函数()f x 在区间()0,1上不存在零点.所以当1e a <<时，函数()f x 在区间()0,ln a 上单调递减，在()ln ,1a 上单调递增，又∵()00f =，()1e 1f a =--，∴当e 10a --≤，即e 1e a -≤<时，函数()f x 在区间()0,1上不存在零点；当e 10a -->，即1e 1a <<-时，函数()f x 在区间()0,1上存在零点.综上，实数a 的取值范围为()1,e 1-.【点睛】用导数求函数的单调区间或判断函数的单调性问题时应注意如下几方面：(1)在利用导数讨论函数的单调区间时，首先要确定函数的定义域；(2)不能随意将函数的2个独立的单调递增（或递减）区间写成并集形式；(3)利用导数解决含参函数的单调性问题时，一般将其转化为不等式恒成立问题，解题过程中要注意分类讨论和数形结合思想的应用.。

高三数学一轮强化训练4文科试题

本卷贰O 贰贰年贰月捌日编写；出题人：令狐学复；欧阳化语；令狐理总。

海兴县中学2021届高三文科数学一轮强化训练04本卷贰O 贰贰年贰月捌日编写；出题人：令狐学复；欧阳化语；令狐理总。

一选择题〔本大题一一共10小题，每一小题5分，满分是50分。

在每一小题给出的四个选项里面，只有一项是哪一项符合题目要求的〕1、程度放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面〞表示，如图是一个正方体的外表展开图，假设图中“爱〞在正方体的后面，那么这个正方体的前面是〔〕 A 我 B 们 C 必 D 赢 2、2(sin cos )1y x x =+-是 ( )2π的偶函数 2π的奇函数ππ的奇函数3、假设函数)(),(x g x f 的定义域都是R ，那么)()(x g x f >，x ∈R 的充要条件是〔〕 A. 有一个x ∈R,使)()(x g x f > B. 有无数多个x ∈R,使)()(x g x f > C. 对任意的x ∈R,使1)()(+>x g x f D. 不存在x ∈R 使)()(x g x f ≤4、假设复数22i z x yi i -==++，x ，y R ∈，那么yx= ( ) A. 43- B. 34 C. 34- D. 435、椭圆12222=+by a x )0(>>b a ，直线b kx y 2+=与椭圆交于不同的两点A 、B ，设AOB S k f ∆=)(，那么函数)(k f 为〔〕A 奇函数B 偶函数C 既不是奇函数又不是偶函数D 无法判断6、在等差数列中，假设是a 2+4a 7+a 12=96，那么2a 3+a 15等于A. 96B.48 C. 24D. 127、在ABC ∆所在的平面上有一点P ，满足PA PB PC AB ++=，那么PBC ∆与ABC ∆的面积之比是A ．13 B ．12 C ．23 D ．348、某公司租地建仓库，每月士地占用费y 1与仓库到车站的间隔成反比，而每月库存货物费y 2与到车我们爱拼必赢本卷贰O 贰贰年贰月捌日编写；站的间隔成正比，假如在间隔车站10公里处建仓库，这这两项费用y 1和y 2分别为2万元和8万元，那么要使这两项费用之和最小，仓库应建在离车站A 5公里处B 4公里处C 3公里处D 2公里处9、程度地面上A 、B 两地立有高分别20米和40米的旗杆，地面上P 对两旗杆顶端的仰角相等，那么P 点的轨迹是〔〕A 椭圆B 抛物线C 圆D 双曲线 10、.函数1()lg ()2xf x x =-有两个零点21,x x ，那么有A. 021<x xB. 121=x xC. 1021<<x xD. 121>x x二、填空题：本大题一一共5小题，考生答题4小题，每一小题5分，满分是20分。

湖南省高考数学模拟试卷(四)文(含解析)-人教版高三全册数学试题

2016年某某省高考数学模拟试卷（文科）（四）一、选择题（本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）1．设复数z满足1+z=（1﹣z）i，则|z|=（）A．B．1 C．D．22．设全集为R，集合A={x|x2﹣9＜0}，B={x|﹣1＜x≤5}，则A∩（∁R B）=（）A．（﹣3，0）B．（﹣3，﹣1） C．（﹣3，﹣1] D．（﹣3，3）3．已知，则a，b，c的大小关系是（）A．a＞c＞b B．c＞a＞b C．a＞b＞c D．c＞b＞a4．阅读如图的程序框图，运行相应的程序，则输出S的值为（）A．﹣10 B．6 C．14 D．185．以下茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩（单位：分）．已知甲组数据的中位数为15，乙组数据的平均数为16.8，则x，y的值分别为（）A．2，5 B．5，5 C．5，8 D．8，86．已知等差数列{a n}前四项中第二项为606，前四项和S n为3834，则该数列第4项为（）A．2004 B．3005 C．2424 D．20167．圆柱被一个平面截去一部分后与半球（半径为r）组成一个几何体，该几何体三视图中的正视图和俯视图如图所示．若该几何体的表面积为16+20π，则r=（）A．1 B．2 C．4 D．88．已知向量满足，，，则与的夹角为（）A．B．C．D．9．已知圆C：x2+y2﹣4x﹣4y=0与x轴相交于A，B两点，则弦AB所对的圆心角的大小（）A．B．C．D．10．将的图象上各点的横坐标缩短到原来的一半，纵坐标不变，再将图象上所有点向左平移个单位，则所得函数图象的一条对称轴为（）A．B．C．D．11．已知四面体P﹣ABC的外接球的球心O在AB上，且PO⊥平面ABC，2AC=AB，若四面体P﹣ABC的体积为，则该球的体积为（）A．B．2πC．D．12．已知双曲线﹣=1 （a＞0，b＞0）的一条渐近线过点（2，），且双曲线的一个焦点在抛物线y2=4x的准线上，则双曲线的方程为（）A．﹣=1 B．﹣=1C．﹣=1 D．﹣=1二、填空题：本大题共4小题，每小题5分，共20分，把答案填在答题卷的横线上．. 13．曲线y=e﹣x+1在点（0，2）处的切线与直线y=0和x=0围成三角形的面积为．14．已知等比数列{a n}中，a3+a5=8，a1a5=4，则=．15．若不等式组表示的平面区域为三角形，且其面积等于，则m的值为．16．已知函数，若|f（x）|≥ax，则a的取值X围是．三、解答题：本大题共5小题，满分60分，解答应写出文字说明、证明过程或演算步骤17．设△ABC的内角A，B，C的对边分别为a，b，c，a=btanA．（Ⅰ）证明：sinB=cosA；（Ⅱ）若sinC﹣sinAcosB=，且B为钝角，求A，B，C．18．某城市100户居民的月平均用电量（单位：度）以[160，180），[180，200），[200，220），[220，240）[240，260），[260，280），[280，300]分组的频率分布直方图如图（1）求直方图中x的值；（2）求月平均用电量的众数和中位数；（3）在月平均用电量[240，260），[260，280），[280，300]的四组用户中，用分层抽样的方法抽取11户居民，则越平均用电量在[220，240）的用户中应抽取多少户？19．在边长为5的菱形ABCD中，AC=8，现沿对角线BD把△ABD折起，折起后使∠ADC的余弦值为．（1）求证：平面ABD⊥平面CBD；（2）若M是AB的中点，求三棱锥A﹣MCD的体积．20．已知抛物线C1：x2=4y的焦点F也是椭圆C2： +=1（a＞b＞0）的一个焦点，C1与C2的公共弦的长为2，过点F的直线l与C1相交于A，B两点，与C2相交于C，D两点，且与同向．（Ⅰ）求C2的方程；（Ⅱ）若|AC|=|BD|，求直线l的斜率．21．已知函数f（x）=lnx﹣．（Ⅰ）求函数f（x）的单调增区间；（Ⅱ）证明；当x＞1时，f（x）＜x﹣1；（Ⅲ）确定实数k的所有可能取值，使得存在x0＞1，当x∈（1，x0）时，恒有f（x）＞k （x﹣1）．四.请考生在第（22）、（23）（24）三题中任选一题作答，如果多做，则按所做的第一题记分，作答时用2B铅笔在答题卡上把所选题目的题号涂黑，把答案填在答题卡上．[选修4-1几何证明选讲]22．如图所示，已知⊙O1与⊙O2相交于A、B两点，过点A作⊙O1的切线交⊙O2于点C，过点B作两圆的割线，分别交⊙O1、⊙O2于点D、E，DE与AC相交于点P．（Ⅰ）求证：AD∥EC；（Ⅱ）若AD是⊙O2的切线，且PA=6，PC=2，BD=9，求AD的长．[选修4-4坐标系与参数方程]23．在平面直角坐标系xOy中，以原点O为极点，x轴的非负半轴为极轴建立极坐标系，已知点A的极坐标为（，），直线l的极坐标方程为ρcos（θ﹣）=a，且点A在直线l上．（1）求a的值及直线l的直角坐标方程；（2）若圆C的参数方程为（α为参数），试判断直线l与圆C的位置关系．[选修4-5不等式选讲]24．已知函数f（x）=|x﹣1|+|x﹣3|+|x﹣a|．（Ⅰ）当a=1时，求不等式f（x）＜4的解集；（Ⅱ）设函数f（x）的最小值为g（a），求g（a）的最小值．2016年某某省高考数学模拟试卷（文科）（四）参考答案与试题解析一、选择题（本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）1．设复数z满足1+z=（1﹣z）i，则|z|=（）A．B．1 C．D．2【考点】复数求模．【专题】转化思想；综合法；数系的扩充和复数．【分析】由1+z=（1﹣z）i，可得z=，再利用复数的运算法则、共轭复数的定义、模的计算公式即可得出．【解答】解：∵1+z=（1﹣z）i，∴z====i，则|z|=1．故选：B．【点评】本题考查了复数的运算法则、共轭复数的定义、模的计算公式，考查了推理能力与技能数列，属于基础题．2．设全集为R，集合A={x|x2﹣9＜0}，B={x|﹣1＜x≤5}，则A∩（∁R B）=（）A．（﹣3，0）B．（﹣3，﹣1） C．（﹣3，﹣1] D．（﹣3，3）【考点】交、并、补集的混合运算．【专题】集合．【分析】根据补集的定义求得∁R B，再根据两个集合的交集的定义，求得A∩（∁R B）．【解答】解：∵集合A={x|x2﹣9＜0}={x|﹣3＜x＜3}，B={x|﹣1＜x≤5}，∴∁R B={x|x≤﹣1，或 x＞5}，则A∩（∁R B）={x|﹣3＜x≤﹣1}，故选：C．【点评】本题主要考查集合的表示方法、集合的补集，两个集合的交集的定义和求法，属于基础题．3．已知，则a，b，c的大小关系是（）A．a＞c＞b B．c＞a＞b C．a＞b＞c D．c＞b＞a【考点】对数值大小的比较．【专题】转化思想；综合法；函数的性质及应用．【分析】根据指数的运算求出a的X围，根据对数的运算性质得到b，c的X围，比较即可．【解答】解： ==＞2，＜0，0＜＜1，即a＞2，b＜0，0＜c＜1，即a＞c＞b，故选：A．【点评】本题考查了指数以及对数的运算性质，是一道基础题．4．阅读如图的程序框图，运行相应的程序，则输出S的值为（）A．﹣10 B．6 C．14 D．18【考点】程序框图．【专题】图表型；算法和程序框图．【分析】模拟执行程序框图，依次写出每次循环得到的i，S的值，当i=8时满足条件i＞5，退出循环，输出S的值为6．【解答】解：模拟执行程序框图，可得S=20，i=1i=2，S=18不满足条件i＞5，i=4，S=14不满足条件i＞5，i=8，S=6满足条件i＞5，退出循环，输出S的值为6．故选：B．【点评】本题主要考查了循环结构的程序框图，正确写出每次循环得到的i，S的值是解题的关键，属于基础题．5．以下茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩（单位：分）．已知甲组数据的中位数为15，乙组数据的平均数为16.8，则x，y的值分别为（）A．2，5 B．5，5 C．5，8 D．8，8【考点】茎叶图．【专题】概率与统计．【分析】求乙组数据的平均数就是把所有乙组数据加起来，再除以5．找甲组数据的中位数要把甲组数据按从小到大的顺序排列，位于最中间的一个数为中位数．据此列式求解即可．【解答】解：乙组数据平均数=（9+15+18+24+10+y）÷5=16.8；∴y=8；甲组数据可排列成：9，12，10+x，24，27．所以中位数为：10+x=15，∴x=5．故选：C．【点评】本题考查了中位数和平均数的计算．平均数是指在一组数据中所有数据之和再除以数据的个数．将一组数据从小到大依次排列，把中间数据（或中间两数据的平均数）叫做中位数．6．已知等差数列{a n}前四项中第二项为606，前四项和S n为3834，则该数列第4项为（）A．2004 B．3005 C．2424 D．2016【考点】等差数列的前n项和；等差数列的通项公式．【专题】等差数列与等比数列．【分析】根据等差数列前n项和公式和通项公式之间的关系进行推导即可．【解答】解：已知a2=606，S4=3834，则S3=a1+a2+a3=3a2=1818即a4=S4﹣S3=3834﹣1818=2016，故选：D【点评】本题主要考查等差数列的前n项和公式和通项公式的应用，比较基础．7．圆柱被一个平面截去一部分后与半球（半径为r）组成一个几何体，该几何体三视图中的正视图和俯视图如图所示．若该几何体的表面积为16+20π，则r=（）A．1 B．2 C．4 D．8【考点】由三视图求面积、体积．【专题】立体几何．【分析】通过三视图可知该几何体是一个半球拼接半个圆柱，计算即可．【解答】解：由几何体三视图中的正视图和俯视图可知，截圆柱的平面过圆柱的轴线，该几何体是一个半球拼接半个圆柱，∴其表面积为：×4πr2+×πr22r×2πr+2r×2r+×πr2=5πr2+4r2，又∵该几何体的表面积为16+20π，∴5πr2+4r2=16+20π，解得r=2，故选：B．【点评】本题考查由三视图求表面积问题，考查空间想象能力，注意解题方法的积累，属于中档题．8．已知向量满足，，，则与的夹角为（）A．B．C．D．【考点】数量积表示两个向量的夹角．【专题】平面向量及应用．【分析】设与的夹角为θ，由数量积的定义代入已知可得cosθ，进而可得θ【解答】解：设与的夹角为θ，∵，，，∴=||||cosθ=1×2×cosθ=，∴cosθ=﹣，∴θ=故选：D【点评】本题考查数量积与向量的夹角，属基础题．9．已知圆C：x2+y2﹣4x﹣4y=0与x轴相交于A，B两点，则弦AB所对的圆心角的大小（）A．B．C．D．【考点】直线与圆的位置关系．【专题】综合题；直线与圆．【分析】根据条件令x=0，求出AB的长度，结合三角形的勾股定理求出三角形ACB是直角三角形即可得到结论．【解答】解：当y=0时，得x2﹣4x=0，解得x=0或x=4，则AB=4﹣0=4，半径R=2，∵CA2+CB2=（2）2+（2）2=8+8=16=（AB）2，∴△ACB是直角三角形，∴∠ACB=90°，即弦AB所对的圆心角的大小为90°，故选：C．【点评】本题主要考查圆心角的求解，根据条件求出先AB的长度是解决本题的关键．10．将的图象上各点的横坐标缩短到原来的一半，纵坐标不变，再将图象上所有点向左平移个单位，则所得函数图象的一条对称轴为（）A．B．C．D．【考点】正弦函数的图象．【专题】三角函数的图像与性质．【分析】由条件利用y=Asin（ωx+φ）的图象变换规律，可得所得图象对应的函数解析式，再根据正弦函数的图象的对称性，求得所得函数图象的一条对称轴．【解答】解：将的图象上各点的横坐标缩短到原来的一半，纵坐标不变，可得函数y=sin（2x+）的图象；再把所得图象象左平移个单位，则所得函数图象对应的解析式为y=sin[2（x+）+]=sin（2x+），令2x+=kπ+，求得 x=﹣，k∈z，故所得函数的图象的对称轴方程为 x=﹣，k∈z．结合所给的选项，故选：A．【点评】本题主要考查y=Asin（ωx+φ）的图象变换规律，正弦函数的图象的对称性，属于基础题．11．已知四面体P﹣ABC的外接球的球心O在AB上，且PO⊥平面ABC，2AC=AB，若四面体P﹣ABC的体积为，则该球的体积为（）A．B．2πC．D．【考点】棱柱、棱锥、棱台的体积．【专题】计算题；空间位置关系与距离．【分析】设该球的半径为R，则AB=2R，2AC=AB=，故AC=R，由于AB是球的直径，所以△ABC在大圆所在平面内且有AC⊥BC，由此能求出球的体积．【解答】解：设该球的半径为R，则AB=2R，2AC=AB=，∴AC=R，由于AB是球的直径，所以△ABC在大圆所在平面内且有AC⊥BC，在Rt△ABC中，由勾股定理，得：BC2=AB2﹣AC2=R2，所以Rt△ABC面积S=×BC×AC=，又PO⊥平面ABC，且PO=R，四面体P﹣ABC的体积为，∴V P﹣ABC==，即R3=9，R3=3，所以：球的体积V球=×πR3=×π×3=4π．故选D．【点评】本题考查四面体的外接球的体积的求法，解题时要认真审题，仔细解答，注意合理地化空间问题为平面问题．12．已知双曲线﹣=1 （a＞0，b＞0）的一条渐近线过点（2，），且双曲线的一个焦点在抛物线y2=4x的准线上，则双曲线的方程为（）A．﹣=1 B．﹣=1C．﹣=1 D．﹣=1【考点】双曲线的标准方程．【专题】计算题；圆锥曲线的定义、性质与方程．【分析】由抛物线标准方程易得其准线方程，从而可得双曲线的左焦点，再根据焦点在x轴上的双曲线的渐近线方程渐近线方程，得a、b的另一个方程，求出a、b，即可得到双曲线的标准方程．【解答】解：由题意， =，∵抛物线y2=4x的准线方程为x=﹣，双曲线的一个焦点在抛物线y2=4x的准线上，∴c=，∴a2+b2=c2=7，∴a=2，b=，∴双曲线的方程为．故选：D．【点评】本题主要考查双曲线和抛物线的标准方程与几何性质，考查学生的计算能力，属于基础题．二、填空题：本大题共4小题，每小题5分，共20分，把答案填在答题卷的横线上．. 13．曲线y=e﹣x+1在点（0，2）处的切线与直线y=0和x=0围成三角形的面积为 2 ．【考点】利用导数研究曲线上某点切线方程．【专题】计算题；方程思想；转化法；导数的概念及应用．【分析】求函数的导数，利用导数求出函数的切线方程，结合三角形的面积公式进行求解即可．【解答】解：函数的导数f′（x）=﹣e﹣x，则f′（0）=﹣1，则切线方程为y﹣2=﹣x，即y=﹣x+2，切线与x轴的交点为（2，0），与y轴的交点为（0，2），∴切线与直线y=0和x=0围成三角形的面积S=，故答案为：2【点评】本题主要考查三角形面积的计算，求函数的导数，利用导数的几何意义求出切线方程是解决本题的关键．14．已知等比数列{a n}中，a3+a5=8，a1a5=4，则= 9 ．【考点】等比数列的性质．【专题】等差数列与等比数列．【分析】由等比数列的性质可得a1a5=a32=4，解出a3，分别可得q2，而=q4，代入可得答案．【解答】解：由等比数列的性质可得a1a5=a32=4，解得a3=2，或a3=﹣2，当a3=2时，可得a5=8﹣a3=6，q2==3当a3=﹣2，可得a5=8﹣a3=10，q2==﹣5，（舍去）∴=q4=32=9故答案为：9【点评】本题考查等比数列的性质，涉及分类讨论的思想，属基础题．15．若不等式组表示的平面区域为三角形，且其面积等于，则m的值为 1 ．【考点】二元一次不等式（组）与平面区域．【专题】数形结合；综合法；不等式的解法及应用．【分析】作出不等式组对应的平面区域，求出三角形各顶点的坐标，利用三角形的面积公式进行求解即可．【解答】解：作出不等式组对应的平面区域如图：若表示的平面区域为三角形，由，得，即A（2，0），则A（2，0）在直线x﹣y+2m=0的下方，即2+2m＞0，则m＞﹣1，则A（2，0），D（﹣2m，0），由，解得，即B（1﹣m，1+m），由，解得，即C（，）．则三角形ABC的面积S△ABC=S△ADB﹣S△ADC=|AD||y B﹣y C|=（2+2m）（1+m﹣）=（1+m）（1+m﹣）=，即（1+m）×=，即（1+m）2=4解得m=1或m=﹣3（舍）．【点评】本题主要考查线性规划以及三角形面积的计算，求出交点坐标，结合三角形的面积公式是解决本题的关键．16．已知函数，若|f（x）|≥ax，则a的取值X围是[﹣2，0]．【考点】绝对值不等式的解法；指、对数不等式的解法．【专题】不等式的解法及应用．【分析】由题意可得，当x＞0时，log2（x+1）＞0恒成立，则此时应有a≤0．当x≤0时，|f（x）|=x2﹣2x≥ax，再分x=0、x＜0两种情况，分别求得a的X围，综合可得结论．【解答】解：由于函数，且|f（x）|≥ax，①当x＞0时，log2（x+1）＞0恒成立，不等式即log2（x+1）≥ax，则此时应有a≤0．②当x≤0时，由于﹣x2+2x 的取值为（﹣∞，0]，故不等式即|f（x）|=x2﹣2x≥ax．若x=0时，|f（x）|=ax，a取任意值．若x＜0时，有a≥x﹣2，即a≥﹣2．综上，a的取值为[﹣2，0]，故答案为[﹣2，0]．【点评】本题主要考查绝对值不等式的解法，对数不等式的解法，体现了分类讨论的数学思想，属于中档题．三、解答题：本大题共5小题，满分60分，解答应写出文字说明、证明过程或演算步骤17．设△ABC的内角A，B，C的对边分别为a，b，c，a=btanA．（Ⅰ）证明：sinB=cosA；（Ⅱ）若sinC﹣sinAcosB=，且B为钝角，求A，B，C．【考点】正弦定理．【专题】解三角形．【分析】（Ⅰ）由正弦定理及已知可得=，由sinA≠0，即可证明sinB=cosA．（Ⅱ）由两角和的正弦函数公式化简已知可得sinC﹣sinAcosB=cosAsinB=，由（1）sinB=cosA，可得sin2B=，结合X围可求B，由sinB=cosA及A的X围可求A，由三角形内角和定理可求C．【解答】解：（Ⅰ）证明：∵a=btanA．∴=tanA，∵由正弦定理：，又tanA=，∴=，∵sinA≠0，∴sinB=cosA．得证．（Ⅱ）∵sinC=sin[π﹣（A+B）]=sin（A+B）=sinAcosB+cosAsinB，∴sinC﹣sinAcosB=cosAsinB=，由（1）sinB=cosA，∴sin2B=，∵0＜B＜π，∴sinB=，∵B为钝角，∴B=，又∵cosA=sinB=，∴A=，∴C=π﹣A﹣B=，综上，A=C=，B=．【点评】本题主要考查了正弦定理，三角形内角和定理，两角和的正弦函数公式的应用，属于基础题．18．某城市100户居民的月平均用电量（单位：度）以[160，180），[180，200），[200，220），[220，240）[240，260），[260，280），[280，300]分组的频率分布直方图如图（1）求直方图中x的值；（2）求月平均用电量的众数和中位数；（3）在月平均用电量[240，260），[260，280），[280，300]的四组用户中，用分层抽样的方法抽取11户居民，则越平均用电量在[220，240）的用户中应抽取多少户？【考点】用样本的数字特征估计总体的数字特征．【专题】计算题；数形结合；整体思想；定义法；概率与统计．【分析】（1）由直方图的性质可得（0.002+0.0095+0.011+0.0125+x+0.005+0.0025）×20=1，解方程可得；（2）由直方图中众数为最高矩形上端的中点可得，可得中位数在[220，240）内，设中位数为a，解方程（0.002+0.0095++0.011）×20+0.0125×（a﹣220）=0.5可得；（3）可得各段的用户分别为25，15，10，5，可得抽取比例，可得要抽取的户数．【解答】解：（1）由直方图的性质可得（0.002+0.0095+0.011+0.0125+x+0.005+0.0025）×20=1，解方程可得x=0.0075，∴直方图中x的值为0.0075；（2）月平均用电量的众数是=230，∵（0.002+0.0095+0.011）×20=0.45＜0.5，∴月平均用电量的中位数在[220，240）内，设中位数为a，由（0.002+0.0095+0.011）×20+0.0125×（a﹣220）=0.5可得a=224，∴月平均用电量的中位数为224；（3）月平均用电量为[220，240）的用户有0.0125×20×100=25，月平均用电量为[240，260）的用户有0.0075×20×100=15，月平均用电量为[260，280）的用户有0.005×20×100=10，月平均用电量为[280，300）的用户有0.0025×20×100=5，∴抽取比例为=，∴月平均用电量在[220，240）的用户中应抽取25×=5户【点评】本题考查频率分布直方图，涉及众数和中位数以及分层抽样，属基础题．19．在边长为5的菱形ABCD中，AC=8，现沿对角线BD把△ABD折起，折起后使∠ADC的余弦值为．（1）求证：平面ABD⊥平面CBD；（2）若M是AB的中点，求三棱锥A﹣MCD的体积．【考点】平面与平面垂直的判定；棱柱、棱锥、棱台的体积．【专题】空间位置关系与距离．【分析】（Ⅰ）由已知条件推导出AO⊥平面BCD，由此能证明平面ABD⊥平面CBD．（Ⅱ）分别以OA，OC，OD所在直线为坐标轴建系，利用向量法能求出三棱锥A﹣MCD的体积．【解答】（Ⅰ）证明：菱形ABCD中，记AC，BD交点为O，AD=5，∴OA=4，OD=3，翻折后变成三棱椎A﹣BCD，在△ACD中，AC2=AD2+CD2﹣2AD•CD•cos∠ADC=25+25﹣2×，在△AOC中，OA2+OC2=32=AC2，∴∠AOC=90°，即AO⊥OC，又AO⊥BD，OC∩BD=O，∴AO⊥平面BCD，又AO⊂平面ABD，∴平面ABD⊥平面CBD．（Ⅱ）解：由（Ⅰ）知OA，OC，OD两两互相垂直，分别以OA，OC，OD所在直线为坐标轴建系，则A （0，0，4），B（0，﹣3，0），C（4，0，0），D（0，3，0），M（0，﹣，2），=（4，，﹣2），=（4，0，﹣4），=（4，﹣3，0），设平面ACD的一个法向量=（x，y，z），则由，得，令y=4，得=（3，4，3），∵=（），∴A到平面ACD的距离d===．∵在边长为5的菱形ABCD中，AC=8，∴S△ACD==12，∴三棱锥A﹣MCD的体积V===．【点评】本题考查平面与平面垂直的证明，考查三棱锥的体积的求法，解题时要认真审题，注意向量法的合理运用．20．已知抛物线C1：x2=4y的焦点F也是椭圆C2： +=1（a＞b＞0）的一个焦点，C1与C2的公共弦的长为2，过点F的直线l与C1相交于A，B两点，与C2相交于C，D两点，且与同向．（Ⅰ）求C2的方程；（Ⅱ）若|AC|=|BD|，求直线l的斜率．【考点】直线与圆锥曲线的关系；椭圆的标准方程．【专题】开放型；圆锥曲线的定义、性质与方程．【分析】（Ⅰ）通过C1方程可知a2﹣b2=1，通过C1与C2的公共弦的长为2且C1与C2的图象都关于y轴对称可得，计算即得结论；（Ⅱ）设A（x1，y1），B（x2，y2），C（x3，y3），D（x4，y4），通过=可得（x1+x2）2﹣4x1x2=（x3+x4）2﹣4x3x4，设直线l方程为y=kx+1，分别联立直线与抛物线、直线与椭圆方程，利用韦达定理计算即可．【解答】解：（Ⅰ）由C1方程可知F（0，1），∵F也是椭圆C2的一个焦点，∴a2﹣b2=1，又∵C1与C2的公共弦的长为2，C1与C2的图象都关于y轴对称，∴易得C1与C2的公共点的坐标为（±，），∴，又∵a2﹣b2=1，∴a2=9，b2=8，∴C2的方程为+=1；（Ⅱ）如图，设A（x1，y1），B（x2，y2），C（x3，y3），D（x4，y4），∵与同向，且|AC|=|BD|，∴=，∴x1﹣x2=x3﹣x4，∴（x1+x2）2﹣4x1x2=（x3+x4）2﹣4x3x4，设直线l的斜率为k，则l方程：y=kx+1，由，可得x2﹣4kx﹣4=0，由韦达定理可得x1+x2=4k，x1x2=﹣4，由，得（9+8k2）x2+16kx﹣64=0，由韦达定理可得x3+x4=﹣，x3x4=﹣，又∵（x1+x2）2﹣4x1x2=（x3+x4）2﹣4x3x4，∴16（k2+1）=+，化简得16（k2+1）=，∴（9+8k2）2=16×9，解得k=±，即直线l的斜率为±．【点评】本题是一道直线与圆锥曲线的综合题，考查求椭圆方程以及直线的斜率，涉及到韦达定理等知识，考查计算能力，注意解题方法的积累，属于中档题．21．已知函数f（x）=lnx﹣．（Ⅰ）求函数f（x）的单调增区间；（Ⅱ）证明；当x＞1时，f（x）＜x﹣1；（Ⅲ）确定实数k的所有可能取值，使得存在x0＞1，当x∈（1，x0）时，恒有f（x）＞k （x﹣1）．【考点】导数在最大值、最小值问题中的应用；利用导数研究函数的单调性．【专题】综合题；开放型；导数的综合应用．【分析】（Ⅰ）求导数，利用导数大于0，可求函数f（x）的单调增区间；（Ⅱ）令F（x）=f（x）﹣（x﹣1），证明F（x）在[1，+∞）上单调递减，可得结论；（Ⅲ）分类讨论，令G（x）=f（x）﹣k（x﹣1）（x＞0），利用函数的单调性，可得实数k 的所有可能取值．【解答】解：（Ⅰ）∵f（x）=lnx﹣，∴f′（x）=＞0（x＞0），∴0＜x＜，∴函数f（x）的单调增区间是（0，）；（Ⅱ）令F（x）=f（x）﹣（x﹣1），则F′（x）=当x＞1时，F′（x）＜0，∴F（x）在[1，+∞）上单调递减，∴x＞1时，F（x）＜F（1）=0，即当x＞1时，f（x）＜x﹣1；（Ⅲ）由（Ⅱ）知，k=1时，不存在x0＞1满足题意；当k＞1时，对于x＞1，有f（x）＜x﹣1＜k（x﹣1），则f（x）＜k（x﹣1），从而不存在x0＞1满足题意；当k＜1时，令G（x）=f（x）﹣k（x﹣1）（x＞0），则G′（x）==0，可得x1=＜0，x2=＞1，当x∈（1，x2）时，G′（x）＞0，故G（x）在（1，x2）上单调递增，从而x∈（1，x2）时，G（x）＞G（1）=0，即f（x）＞k（x﹣1），综上，k的取值X围为（﹣∞，1）．【点评】本题考查导数知识的综合运用，考查函数的单调性，考查不等式的证明，正确构造函数是关键．四.请考生在第（22）、（23）（24）三题中任选一题作答，如果多做，则按所做的第一题记分，作答时用2B铅笔在答题卡上把所选题目的题号涂黑，把答案填在答题卡上．[选修4-1几何证明选讲]22．如图所示，已知⊙O1与⊙O2相交于A、B两点，过点A作⊙O1的切线交⊙O2于点C，过点B作两圆的割线，分别交⊙O1、⊙O2于点D、E，DE与AC相交于点P．（Ⅰ）求证：AD∥EC；（Ⅱ）若AD是⊙O2的切线，且PA=6，PC=2，BD=9，求AD的长．【考点】圆的切线的性质定理的证明；直线与圆相交的性质；直线与圆的位置关系；与圆有关的比例线段．【专题】计算题；证明题．【分析】（I）连接AB，根据弦切角等于所夹弧所对的圆周角得到∠BAC=∠D，又根据同弧所对的圆周角相等得到∠BAC=∠E，等量代换得到∠D=∠E，根据内错角相等得到两直线平行即可；（II）根据切割线定理得到PA2=PB•PD，求出PB的长，然后再根据相交弦定理得PA•PC=BP•PE，求出PE，再根据切割线定理得AD2=DB•DE=DB•（PB+PE），代入求出即可．【解答】解：（I）证明：连接AB，∵AC是⊙O1的切线，∴∠BAC=∠D，又∵∠BAC=∠E，∴∠D=∠E，∴AD∥EC．（II）∵PA是⊙O1的切线，PD是⊙O1的割线，∴PA2=PB•PD，∴62=PB•（PB+9）∴PB=3，在⊙O2中由相交弦定理，得PA•PC=BP•PE，∴PE=4，∵AD是⊙O2的切线，DE是⊙O2的割线，∴AD2=DB•DE=9×16，∴AD=12【点评】此题是一道综合题，要求学生灵活运用直线与圆相切和相交时的性质解决实际问题．本题的突破点是辅助线的连接．[选修4-4坐标系与参数方程]23．在平面直角坐标系xOy中，以原点O为极点，x轴的非负半轴为极轴建立极坐标系，已知点A的极坐标为（，），直线l的极坐标方程为ρcos（θ﹣）=a，且点A在直线l上．（1）求a的值及直线l的直角坐标方程；（2）若圆C的参数方程为（α为参数），试判断直线l与圆C的位置关系．【考点】参数方程化成普通方程．【专题】计算题；规律型；转化思想；直线与圆．【分析】（1）利用点在直线上，代入方程求出a，利用极坐标与直角坐标的互化，求出直线的直角坐标方程．（2）化简圆的参数方程与直角坐标方程，求出圆心与半径，利用圆心到直线的距离与半径比较即可得到直线与圆的位置关系．【解答】解：（1）点A的极坐标为（，），直线l的极坐标方程为ρcos（θ﹣）=a，且点A在直线l上．可得： cos（﹣）=a，解得a=．直线l的极坐标方程为ρcos（θ﹣）=，即：ρcosθ+ρsinθ=2，直线l的直角坐标方程为：x+y﹣2=0．（2）圆C的参数方程为（α为参数），可得圆的直角坐标方程为：（x﹣1）2+y2=1．圆心（1，0），半径为：1．因为圆心到直线的距离d==＜1，所以直线与圆相交．【点评】本题考查参数方程与极坐标方程与直角坐标方程的互化，直线与圆的位置关系的应用，考查计算能力．[选修4-5不等式选讲]24．已知函数f（x）=|x﹣1|+|x﹣3|+|x﹣a|．（Ⅰ）当a=1时，求不等式f（x）＜4的解集；（Ⅱ）设函数f（x）的最小值为g（a），求g（a）的最小值．【考点】绝对值不等式的解法；分段函数的应用．【专题】函数的性质及应用．【分析】（1）化简函数f（x）的解析式，画出函数的f（x）的图象，数形结合求得不等式f（x）＜4的解集．（2）由条件利用绝对值的意义求得g（a）的最小值．【解答】解：（1）当a=1时，f（x）=2|x﹣1|+|x﹣3|=，由图可得，不等式f（x）＜4的解集为（，3）．（2）函数f（x）=|x﹣1|+|x﹣3|+|x﹣a|表示数轴上的x对应点到a、1、3对应点的距离之和，可得f（x）的最小值为g（a）=，故g（a）的最小值为2．【点评】本题主要考查绝对值的意义，绝对值不等式的解法，体现了转化、分类讨论的数学思想，属于中档题．。

高三绝密冲刺模拟卷--文科数学(附答案解析)

绝密冲刺卷--文科数学第Ⅰ卷一、选择题：本大题共12小题，每小题5分，在每小题的四个选项中，只有一项符合题目要求。

1．已知集合{|20}A x x =-<，{|}B x x a =<，若A B A = ，则实数a 的取值范围是（） A ．(,2]-∞- B ．[2,)+∞ C ．(,2]-∞ D ．[2,)-+∞ 2．若复数iia z 21-+=（a ∈R ，i 是虚数单位）是纯虚数，则|a+2i|等于（） A. 2 B. 22 C. 4 D. 8 3．函数()2x f x x =+的零点所在的一个区间是（）A ．(2,1)--B ．(1,0)-C ．(0,1)D ．(1,2) 4．已知函数()sin cos f x x x =-，且()()2f x f x '=，则tan 2x 的值是（）A.43-B.43C.34-D.345．在两个变量y 与x 的回归模型中，分别选择了四个不同的模型，它们的相关指数R 2如下，其中拟合效果最好的为（）A.模型①的相关指数为0.976B.模型②的相关指数为0.776C.模型③的相关指数为0.076D.模型④的相关指数为0.3516．已知各项不为0的等差数列{}n a 满足26780a a a -+=，数列{}n b 是等比数列，且77b a =，则2811b b b ⋅⋅等于（）A ．1B ．2C ．4D ．87. 若函数,1()(4)2,12x a x f x ax x ⎧>⎪=⎨-+≤⎪⎩在(),-∞+∞上单调递增，则a 的取值范围是（） A ．[)4,8 B ．()1,+∞ C ．()4,8 D ．()1,8 8．某几何体的三视图如图所示，且该几何体的体积是 1.5，则正视图中的x 的值是A.2B.4.5C.1.5D.39. ,0002,⎪⎩⎪⎨⎧≤≤≤-≥++=k y y x y x y x y x z 满足、其中实数设若z 的最大值为6，z 的最小值为A.0B.-1C.-2D.-310. 我国南宋数学家秦九韶（约公元1202﹣1261年）给出了求n （n ∈N *）次多项式0111a x a x a x a n n n n ++⋯++--，当0x x =时的值的一种简捷算法．该算法被后人命名为“秦九韶算法”，例如，可将3次多项式改写为0123012233))((a x a x a x a a x a x a x a +++=+++然后进行求值．运行如图所示的程序框图，能求得多项式( )的值．A.432234++++x x x xB.5432234++++x x x xC.3223+++x x xD.43223+++x x x11．已知函数R x x x x f ∈+=,)(3，若当20πθ≤≤时，0)1()sin (>-+m f m f θ恒成立，则实数m 的取值范围是（）A ．)1,0(B ．)0,(-∞C ．⎪⎭⎫ ⎝⎛∞-21, D ．)1,(-∞12．如图，已知双曲线22221x y a b-=（0a >，0b >）的左右焦点分别为1F 、2F ，12||8F F =，P 是双曲线右支上的一点，直线2F P 与y 轴交于点A ，△1APF 的内切圆在边1PF 上的切点为Q ，若||2PQ =，则该双曲线的离心率为（）A．2 D ．3第Ⅱ卷本卷包括必考题和选考题两部分。