动量矩定理作业答案
第十一章动量矩定理习题解答

习 题11-1 质量为m 的质点在平面Oxy 内运动,其运动方程为:t b y t a x ωω2sin ,cos ==。
其中a 、b 和w 均为常量。
试求质点对坐标原点O 的动量矩。
t a xv x ωωsin -== t b y v y ωω2cos 2== x mv y mv L y x O +-=)cos 2cos 22sin sin (t a t b t b t a m ωωωωωω⨯+⨯=)cos 2cos 22sin (sin t t t t mab ωωωωω⨯+⨯=)cos 2cos 2cos sin 2(sin t t t t t mab ωωωωωω⨯+⨯=)2cos (sin cos 22t t t mab ωωωω+=t mab ωω3cos 2=11-2 C 、D 两球质量均为m ,用长为2 l 的杆连接,并将其中点固定在轴AB 上,杆CD 与轴AB 的交角为θ,如图11-25所示。
如轴AB 以角速度w 转动,试求下列两种情况下,系统对AB 轴的动量矩。
(1)杆重忽略不计;(2)杆为均质杆,质量为2m 。
图11-25(1)θθ222sin 2)sin (2ml l m J z =⨯= θω22sin 2l m L z = (2)θθ2202sin 32d )sin (2ml x x l m J lz ==⎰杆 θ22sin 38ml J z = θω22sin 38l m L z =11-3 试求图11-26所示各均质物体对其转轴的动量矩。
各物体质量均为m 。
图11-26(a) ω231ml L O =(b) 22291)6(121ml l m ml J O =+= ω291ml L O -= (c) 2222452312121ml l m l m J O =⨯⨯+⨯⨯= ω2245ml L O = (d) 2222321mR mR mR J O =+= ω223mR L O =11-4 如图11-27所示,均质三角形薄板的质量为m ,高为h ,试求对底边的转动惯量J x 。
《理论力学》第十章--动量矩定理试题及答案
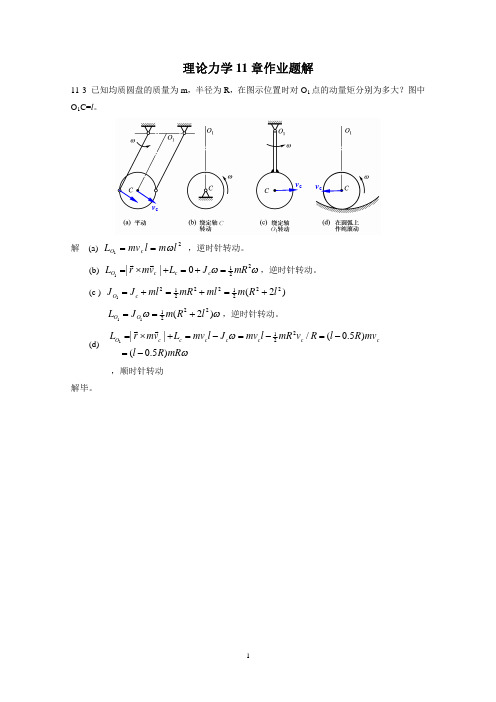
理论力学11章作业题解11-3 已知均质圆盘的质量为m ,半径为R ,在图示位置时对O 1点的动量矩分别为多大?图中O 1C=l 。
解 (a) 21l m l mv L c O w == ,逆时针转动。
(b) w w 2210||1mR J L v m r L c c c O =+=+´=rr ,逆时针转动。
(c ) )2(2221222121l R m ml mR ml J J c O +=+=+=w w )2(222111l R m J L O O +==,逆时针转动。
(d)ww mR R l mv R l R v mR l mv J l mv L v m r L c c c c c c c O )5.0()5.0(/||2211-=-=-=-=+´= r r,顺时针转动解毕。
v cv cv c11-5 均质杆AB 长l 、重为G 1,B 端刚连一重G 2的小球,弹簧系数为k ,使杆在水平位置保持平衡。
设给小球B 一微小初位移0d 后无初速度释放,试求AB 杆的运动规律。
解 以平衡位置(水平)为0=j ,顺时针转为正。
平衡时弹簧受力为:)5.0(312G G F s +=弹簧初始变形量:k G G k F s st /)5.0(3/12+==d在j 角时弹簧的拉力为(小位移):3/)5.0(3)3/(12l k G G l k F st s j j d ++=+=¢系统对A 点的动量矩:j j j&&&221233l gG G l l g G J L A A +=×+= 对点的动量矩定理)(/å=Ei A A F M dt dL r :j j 93/5.033221221kl l F lG lG l g G G s -=¢-+=+&& 0)3(321=++j jG G gk &&,令)3(3212G G gkp +=则有02=+j jp &&,其解为: )cos()sin(pt B pt A +=j由初始条件0| ,/|000====t t l jd j &得l B A / ,00d ==。
理论力学课后习题答案第9章动量矩定理及其应用

(1)
(2)
对A:
(3)
又:
以O为基点:
(→)
(↓)(4)
由上四式联立,得(注意到 )
法2:对瞬心E用动量矩定理(本题质心瞬心之距离为常数)
又
可解得:
9-11图示匀质圆柱体质量为m,半径为r,在力偶作用下沿水平面作纯滚动。若力偶的力偶矩M为常数,滚动阻碍系数为 ,求圆柱中心O的加速度及其与地面的静滑动摩擦力。
解:对轮C:
对轮B和重物A:
运动学关系:
9-5图示电动绞车提升一质量为m的物体,在其主动轴上作用一矩为M的主动力偶。已知主动轴和从动轴连同安装在这两轴上的齿轮以及其它附属零件对各自转动轴的转动惯量分别为J1和J2;传动比r2:r1=i;吊索缠绕在鼓轮上,此轮半径为R。设轴承的摩擦和吊索的质量忽略不计,求重物的加速度。
(7)
将(5)、(6)、(7)代入(2)、(3)、(4)得
(8)
(9)
(10)
解得: ,与(1)式相同。
9-15圆轮A的半径为R,与其固连的轮轴半径为r,两者的重力共为W,对质心C的回转半径为,缠绕在轮轴上的软绳水平地固定于点D。均质平板BE的重力为Q,可在光滑水平面上滑动,板与圆轮间无相对滑动。若在平板上作用一水平力F,试求平板BE的加速度。
解:初始静止,杆开始运动瞬时, 必沿支承处切向,即沿AB方向,所以 此时沿AB方向,如图(a),以D为基点:
由
(1)
由AB作平面运动:
(2)
(3)
(4)
由(3),
解(1)、(2)、(4)联立
9-19如图所示,足球重力的大小为4.45N,以大小 =6.1m/s,方向与水平线夹40 角的速度向球员飞来,形成头球。球员以头击球后,球的速度大小为 =9.14m/s,并与水平线夹角为20 角。若球-头碰撞时间为0.15s。试求足球作用在运动员头上的平均力的大小与方向。
第12章 动量矩定理(田)

第十二章 动量矩定理一、填空题1.如下(1)图所示,在提升重为G的物体A时,可在半径为r的鼓轮上作用一力偶M。
已知鼓轮对轴O的转动惯量为I,某瞬时鼓轮的角加速度为α,则该瞬时,系统对轴O的动量矩定理可写成______________。
2.如下(2)图所示,轮B由系杆AB带动在固定轮A上无滑动滚动,两圆的半径分别为R,r。
若轮B的质量为m,系杆的角速度为ω,则轮B对固定轴A的动量矩大小是_______________。
3.图(3)中匀质圆盘在光滑水平面上作直线平动,图(4)中匀质圆盘沿水平直线作无滑动滚动。
设两圆盘的质量皆为m,半径皆为r,轮心O速度皆为v,则图示瞬时,它们各自对轮心O和对与地面接触点D的动量矩分别为:(3)LO =___________ ;LD =_____________________; (4)LO =_____________;LD =_____________________。
二、选择题1.如下图(1)所示,已知两个匀质圆轮对转轴转动惯量分别为I A,I B,半径分别为RA,RB,作用在A轮上的转矩为M,则系统中A轮角加速度的大小为( )。
22A 22B 2A AB A A 222A DC I I M B A BA B A B A A B B R I R I MR I MR I R I MR +==+=+=αααα、;、;、;、 2.如下图(2)所示,两匀质细杆OA和BC的质量均为m = 8kg,长度均为l = 0.5m,固连成图所示的T字型构件,可绕通过点O的水平轴转动。
当杆OA处于图示水平位置时,该构件的角速度ω = 4rad/s。
则该瞬时轴O处反力的铅垂分力NOy的大小为( )。
A.NO=24.5N;B.NO=32.3N;C.NO=73.8N;D.NO=156.8N3.如果把下图(3)中重为G A 的物体换为图(4)所示的力G A ,在这两种情况下,若把匀质滑轮的角加速度ε1和ε2的大小比较,则有( )。
理论力学课后习题答案

第11章 动量矩定理一、是非题(正确的在括号内打“√”、错误的打“×”)1. 质点系对某固定点(或固定轴)的动量矩,等于质点系的动量对该点(或轴)的矩。
(×)2. 质点系所受外力对某点(或轴)之矩恒为零,则质点系对该点(或轴)的动量矩不变。
(√)3. 质点系动量矩的变化与外力有关,与内力无关。
(√)4. 质点系对某点动量矩守恒,则对过该点的任意轴也守恒。
(√)5. 定轴转动刚体对转轴的动量矩,等于刚体对该轴的转动惯量与角加速度之积。
(×)6. 在对所有平行于质心轴的转动惯量中,以对质心轴的转动惯量为最大。
(×)7. 质点系对某点的动量矩定理e 1d ()d nOO i i t ==∑L M F 中的点“O ”是固定点或质点系的质心。
(√)8. 如图所示,固结在转盘上的均质杆AB ,对转轴的转动惯量为20A J J mr =+ 2213ml mr =+,式中m 为AB 杆的质量。
(×)9. 当选质点系速度瞬心P 为矩心时,动量矩定理一定有e 1d()d nP P i i t ==∑L M F 的形式,而不需附加任何条件。
(×)10. 平面运动刚体所受外力对质心的主矩等于零,则刚体只能做平动;若所受外力的主矢等于零,刚体只能作绕质心的转动。
(×)图二、填空题1. 绕定轴转动刚体对转轴的动量矩等于刚体对转轴的转动惯量与角速度的乘积。
2. 质量为m ,绕z 轴转动的回旋半径为ρ,则刚体对z 轴的转动惯量为2ρm J z =。
3. 质点系的质量与质心速度的乘积称为质点系的动量。
4. 质点系的动量对某点的矩随时间的变化规律只与系统所受的外力对该点的矩有关,而与系统的内力无关。
5. 质点系对某点动量矩守恒的条件是质点系所受的全部外力对该点之矩的矢量和等于零,质点系的动量对x 轴的动量矩守恒的条件是质点系所受的全部外力对x 轴之矩的代数和等于零。
梁坤京理论力学第十二章动量矩定理课后答案

动量矩定理12-1 质量为m 的点在平面Oxy 内运动,其运动方程为: x a cos t y bsin2 t 式中a 、b 和 为常量。
求质点对原点 O 的动量矩。
解:由运动方程对时间的一阶导数得原点的速度V xdxsin t dt aV y dy 2b cos2 t 质点对点 O 的动量矩为L O M o (mV x ) M 0(mV y )mv x y mv y x m ( a sin t) bsin2 t m 2b cos2 t acos t 2mab cos 3 t 12-3 如图所示,质量为m 的偏心轮在水平面上作平面运动。
轮子轴心为A,质心为C, AC = e ;轮子半径为 R,对轴心A 的转动惯量为J A ; C 、A 、B 三点在同一铅直线上。
(1 )当轮子只 滚不滑时,若 V A 已知,求轮子的动量和对地面上 B 点的动量矩。
(2)当轮子又滚又滑时, 若V A 、 已知,求轮子的动量和对地面上 B 点的动量矩。
解:(1)当轮子只滚不滑时 B 点为速度瞬心。
轮子角速度V A R质心C 的速度V CBCR e轮子的动量p mv Cmv A (方向水平向右)R对B 点动量矩L B J B2 2 2由于 J B J C m (R e) J A me m (R e) 故 L B J A me 2 m (R e )2食 (2)当轮子又滚又滑时由基点法求得 C 点速度。
V C V A V CA V A e 轮子动量 p mv C m(v A e) (方向向右) 对B 点动量矩L B mv C BC J Cm(v A 2e) (R e) (J A me) mv A (R e) (J A mRe) 12-13 如图所示,有一轮子,轴的直径为 50 mm 无初速地沿倾角 20的轨道滚下,设 只滚不滑,5秒内轮心滚动的距离为 s =3m 。
试求轮子对轮心的惯性半径。
解:取轮子为研究对象,轮子受力如图( a )所示,根据刚体平面运动微分方程有 ma C mgsi n F ( 1) J C = Fr ( 2)因轮子只滚不滑,所以有 a c = r ( 3) ® 12将式(3)代入式(1)、(2)消去F 得到mr sinm?g上式对时间两次积分,并注意到 t = 0时 0, 0,则 mgrt 2 sin mgrt 2s in 2(J C mr 2) 2(m 2 mr 2) 把 r = 0.025 m 及 t = 5 s 时,s 'grt 2sin f gt 2sin-r r「s r 1grt 2sin 2( 2 r 2) r 3 m 代入上式得0.0259.8 52si n202 30.09 m 90 mm12-17 图示均质杆 AB 长为I ,放在铅直平面内,杆的一端 A 靠在光滑铅直墙上,另一端 B 放在光滑的水平地板上,并与水平面成 °角。
第12章 动量矩定理(田)

第十二章 动量矩定理一、填空题1.如下(1)图所示,在提升重为G的物体A时,可在半径为r的鼓轮上作用一力偶M。
已知鼓轮对轴O的转动惯量为I,某瞬时鼓轮的角加速度为α,则该瞬时,系统对轴O的动量矩定理可写成______________。
2.如下(2)图所示,轮B由系杆AB带动在固定轮A上无滑动滚动,两圆的半径分别为R,r。
若轮B的质量为m,系杆的角速度为ω,则轮B对固定轴A的动量矩大小是_______________。
3.图(3)中匀质圆盘在光滑水平面上作直线平动,图(4)中匀质圆盘沿水平直线作无滑动滚动。
设两圆盘的质量皆为m,半径皆为r,轮心O速度皆为v,则图示瞬时,它们各自对轮心O和对与地面接触点D的动量矩分别为:(3)LO =___________ ;LD =_____________________; (4)LO =_____________;LD =_____________________。
二、选择题1.如下图(1)所示,已知两个匀质圆轮对转轴转动惯量分别为I A,I B,半径分别为RA,RB,作用在A轮上的转矩为M,则系统中A轮角加速度的大小为( )。
22A 22B 2A AB A A 222A DC I I M B A BA B A B A A B B R I R I MR I MR I R I MR +==+=+=αααα、;、;、;、 2.如下图(2)所示,两匀质细杆OA和BC的质量均为m = 8kg,长度均为l = 0.5m,固连成图所示的T字型构件,可绕通过点O的水平轴转动。
当杆OA处于图示水平位置时,该构件的角速度ω = 4rad/s。
则该瞬时轴O处反力的铅垂分力NOy的大小为( )。
A.NO=24.5N;B.NO=32.3N;C.NO=73.8N;D.NO=156.8N3.如果把下图(3)中重为G A 的物体换为图(4)所示的力G A ,在这两种情况下,若把匀质滑轮的角加速度ε1和ε2的大小比较,则有( )。
高中物理动量定理解题技巧讲解及练习题(含答案)及解析

高中物理动量定理解题技巧讲解及练习题(含答案)及解析一、高考物理精讲专题动量定理1.如图1所示,水平面内的直角坐标系的第一象限有磁场分布,方向垂直于水平面向下,磁感应强度沿y 轴方向没有变化,与横坐标x 的关系如图2所示,图线是双曲线(坐标是渐近线);顶角=53°的光滑金属长导轨MON 固定在水平面内,ON 与x 轴重合,一根与ON 垂直的长导体棒在水平向右的外力作用下沿导轨MON 向右滑动,导体棒在滑动过程中始终保持与导轨良好接触,已知t=0时,导体棒位于顶角O 处;导体棒的质量为m=4kg ;OM 、ON 接触处O 点的接触电阻为R=0.5Ω,其余电阻不计,回路电动势E 与时间t 的关系如图3所示,图线是过原点的直线,求:(1)t =2s 时流过导体棒的电流强度的大小;(2)在1~2s 时间内导体棒所受安培力的冲量大小;(3)导体棒滑动过程中水平外力F (单位:N )与横坐标x (单位:m )的关系式.【答案】(1)8A (2)8N s (3)32639Fx【解析】【分析】【详解】(1)根据E-t 图象中的图线是过原点的直线特点,可得到t =2s 时金属棒产生的感应电动势为4VE由欧姆定律得24A 8A0.5E I R(2)由图2可知,1(T m)xB 由图3可知,E 与时间成正比,有E=2t (V )4E ItR因=53°,可知任意t 时刻回路中导体棒有效切割长度43x L又由F BIL安所以163F t安即安培力跟时间成正比所以在1~2s 时间内导体棒所受安培力的平均值163233N8N2F故8N sI F t 安(3)因为43v EBLv Bx所以1.5(m/s)vt 可知导体棒的运动时匀加速直线运动,加速度21.5m/sa又212xat ,联立解得32639Fx【名师点睛】本题的关键首先要正确理解两个图象的数学意义,运用数学知识写出电流与时间的关系,要掌握牛顿运动定律、闭合电路殴姆定律,安培力公式、感应电动势公式.2.如图所示,粗糙的水平面连接一个竖直平面内的半圆形光滑轨道,其半径为R=0.1 m ,半圆形轨道的底端放置一个质量为m=0.1 kg 的小球B ,水平面上有一个质量为M=0.3 kg 的小球A 以初速度v 0=4.0 m/ s 开始向着木块B 滑动,经过时间t=0.80 s 与B 发生弹性碰撞.设两小球均可以看作质点,它们的碰撞时间极短,且已知木块A 与桌面间的动摩擦因数μ=0.25,求:(1)两小球碰前A 的速度;(2)球碰撞后B,C 的速度大小;(3)小球B 运动到最高点C 时对轨道的压力;【答案】(1)2m/s(2)v A =1m/s ,v B =3m/s (3)4N ,方向竖直向上【解析】【分析】【详解】(1)选向右为正,碰前对小球A 的运动由动量定理可得:–μMg t =M v –M v 0解得:v =2m/s(2)对A 、B 两球组成系统碰撞前后动量守恒,动能守恒:AB Mv Mv mv 222111222ABMvMvmv解得:v A =1m/sv B =3m/s(3)由于轨道光滑,B 球在轨道由最低点运动到C 点过程中机械能守恒:2211222BCmvmvmg R在最高点C 对小球B 受力分析,由牛顿第二定律有:2CNvmgF m R解得:F N =4N 由牛顿第三定律知,F N '=F N =4N小球对轨道的压力的大小为3N ,方向竖直向上.3.如图所示,光滑水平面上有一轻质弹簧,弹簧左端固定在墙壁上,滑块A 以v 0=12 m/s的水平速度撞上静止的滑块B 并粘在一起向左运动,与弹簧作用后原速率弹回,已知A 、B的质量分别为m 1=0.5 kg 、m 2=1.5 kg 。
第五章 刚体力学基础 动量矩参考答案

第五章 刚体力学基础 动量矩班级______________学号____________姓名________________一、选择题1、力kNj i F )53(+=,其作用点的矢径为m j i r )34(-=,则该力对坐标原点的力矩大小为 ( B )(A)m kN ⋅-3; (B )m kN ⋅29; (C)m kN ⋅19; (D)m kN ⋅3。
2、圆柱体以80rad /s 的角速度绕其轴线转动,它对该轴的转动惯量为24m kg ⋅。
由于恒力矩的作用,在10s 内它的角速度降为40rad /s 。
圆柱体损失的动能和所受力矩的大小为( D ) (A)80J ,80m N ⋅;(B)800J ,40m N ⋅;(C)4000J ,32m N ⋅;(D)9600J ,16m N ⋅。
3、 一匀质圆盘状飞轮质量为20kg ,半径为30cm ,当它以每分钟60转的速率旋转时,其动能为 ( D )(A)22.16π J ; (B)21.8πJ ;(C )1.8J ; (D )28.1πJ 。
4、如图所示,一轻绳跨过两个质量均为m 、半径均为R 的匀质圆盘状定滑轮。
绳的两端分别系着质量分别为m 和2m 的重物,不计滑轮转轴的摩擦。
将系统由静止释放,且绳与两滑轮间均无相对滑动,则两滑轮之间绳的张力。
( D )(A)mg ; (B)3mg /2; (C)2mg ; (D)11mg /8。
5、一根质量为m 、长度为L 的匀质细直棒,平放在水平桌面上。
若它与桌面间的滑动摩擦系数为μ,在t =0时,使该棒绕过其一端的竖直轴在水平桌面上旋转,其初始角速度为0ω,则棒停止转动所需时间为 (A )(A)μωg L 3/20; (B) μωg L 3/0; (C) μωg L 3/40; (D) μωg L 6/0。
6、关于力矩有以下几种说法,其中正确的是 ( B )(A )内力矩会改变刚体对某个定轴的角动量(动量矩); (B )作用力和反作用力对同一轴的力矩之和必为零;(C )角速度的方向一定与外力矩的方向相同;(D )质量相等、形状和大小不同的两个刚体,在相同力矩的作用下,它们的角加速度一定相等。
动量定理练习题含答案及解析

动量定理练习题含答案及解析一、高考物理精讲专题动量定理1.如图所示,粗糙的水平面连接一个竖直平面内的半圆形光滑轨道,其半径为R =0.1 m ,半圆形轨道的底端放置一个质量为m =0.1 kg 的小球B ,水平面上有一个质量为M =0.3 kg 的小球A 以初速度v 0=4.0 m / s 开始向着木块B 滑动,经过时间t =0.80 s 与B 发生弹性碰撞.设两小球均可以看作质点,它们的碰撞时间极短,且已知木块A 与桌面间的动摩擦因数μ=0.25,求:(1)两小球碰前A 的速度;(2)球碰撞后B ,C 的速度大小;(3)小球B 运动到最高点C 时对轨道的压力;【答案】(1)2m/s (2)v A =1m /s ,v B =3m /s (3)4N ,方向竖直向上【解析】【分析】【详解】(1)选向右为正,碰前对小球A 的运动由动量定理可得:–μ Mg t =M v – M v 0解得:v =2m /s(2)对A 、B 两球组成系统碰撞前后动量守恒,动能守恒:A B Mv Mv mv =+222111222A B Mv Mv mv =+ 解得:v A =1m /s v B =3m /s(3)由于轨道光滑,B 球在轨道由最低点运动到C 点过程中机械能守恒:2211222B C mv mv mg R '=+ 在最高点C 对小球B 受力分析,由牛顿第二定律有: 2C N v mg F m R'+= 解得:F N =4N由牛顿第三定律知,F N '=F N =4N小球对轨道的压力的大小为3N ,方向竖直向上.2.半径均为52m R =的四分之一圆弧轨道1和2如图所示固定,两圆弧轨道的最低端切线水平,两圆心在同一竖直线上且相距R ,让质量为1kg 的小球从圆弧轨道1的圆弧面上某处由静止释放,小球在圆弧轨道1上滚动过程中,合力对小球的冲量大小为5N s ⋅,重力加速度g 取210m /s ,求:(1)小球运动到圆弧轨道1最低端时,对轨道的压力大小;(2)小球落到圆弧轨道2上时的动能大小。
动量矩定理作业参考答案及解答

g (顺时针), 2r
FOx = 0,
1 FOy = mg (↑) 2
6.如题图所示,有一轮子,轴的直径为 50mm,无初速的沿倾角θ=20°的轨道
滚下,设只滚不滑,5s 内轮心滚过的距离为 s=3m。试求轮子对轮心的惯性半径。
s
提示:本题用刚体平面运动微分方程求解。注意到轮心加速度可由式 1 s = at 2 求得,且轮心加速度 a 与轮子角加速度α关系 a = rα ,其中 r 为轮轴的 2 半径。 解:
a mg
Ff × r = mρ α
2
由以上两式消去 Ff 得 ρ 2 =
r ( g sin θ − a )
α
=
r 2 t 2 g sin θ − r 2 = 8113(mm) 2 2s
ρ= & 90mm
r 2 t 2 g sin θ − r 2 = 8113(mm) 2 , ⇒ 2s
答案: ρ 2 =
整个系统对轴 O 的动量矩守恒
p 1 p LO = L1 + L2 = r 2 1 ω + 2 r (ωr − at ) = 0 2 g g
解得
ω=
2aP2 t , r (2 P2 + P1 )
α=
2aP2 dω = dt r (2 P2 + P1 )
答案: ω =
2aP2 t , r (2 P2 + P1 )
vB
A
ωB
B
D
1 1)对杆分析,杆对轴 A 的动量矩 L A1 = m2 R 2ω 3 2)对轮分析
ω B R = ωl
ωB =
齿轮对轮心 B 的动量矩为 齿轮对轴 A 的动量矩为
ωl
理论力学答案(第七章后)

第七章 点的合成运动一、是非题7.1.1动点的相对运动为直线运动,牵连运动为直线平动时,动点的绝对运动必为直线运动。
( × )7.1.2无论牵连运动为何种运动,点的速度合成定理r e a v v v +=都成立。
( ∨ )7.1.3某瞬时动点的绝对速度为零,则动点的相对速度和牵连速度也一定为零。
( × )7.1.4当牵连运动为平动时,牵连加速度等于牵连速度关于时间的一阶导数。
( ∨ )7.1.5动坐标系上任一点的速度和加速度就是动点的牵连速度和牵连加速度。
( × )7.1.6不论牵连运动为何种运动,关系式a a +a a r e =都成立。
( × )7.1.7只要动点的相对运动轨迹是曲线,就一定存在相对切向加速度。
( × )7.1.8在点的合成运动中,判断下述说法是否正确:(1)若r v 为常量,则必有r a =0。
( × )(2)若e ω为常量,则必有e a =0. ( × )(3)若e r ωv //则必有0=C a 。
( ∨ )7.1.9在点的合成运动中,动点的绝对加速度总是等于牵连加速度与相7.1.10当牵连运动为定轴转动时一定有科氏加速度。
( × )二、 填空题7.2.1 牵连点是某瞬时 动系上与7.2.2 v e 与v r 共线 情况下,动点绝对速度的大小为r e a v v v +=,在 情况下,动点绝对速度的大小为a v =v e 、v r ,应按___ ____ __ 计算v a三、选择题:7.3.1 动点的牵连速度是指某瞬时牵连点的速度,它相对的坐标系是( A )。
A 、 定参考系B 、 动参考系C 、 任意参考系7.3.2 在图示机构中,已知t b a s ωsin +=, 且t ωϕ=(其中a 、b 、ω均为常数),杆长为L ,若取小球A 为动点,动系固结于物块B ,定系固结于地面,则小球的牵连速度v e 的大小为( B )。
11 动量矩定理习题解答

R
O ve
r o B
vr
[解]
研究整体,由于∑Mz (F)= 0,且系统初始静止, 所以 Lz = 0,即 L z 盘+ L z 人 = 0 式中 Lz 盘= J z =
1P 2 R 2g
L z 人= 解得
ds Q (v -v )r, v = rω , vr at e r e dt g
解:重物 A 和 B 速度 v A vB r ,
LO m1v A r m2 vB r J O 1 m1r r m2 r r m3r 2 2
A
B (c)
vA
vB
m1 g
m2 g
1 2 m1 m2 m3 r 2
…….. ①
对 B 轮,有
…….. ②
P aB P FT1 g
…….. ③
FT1 FT1
…….. ④
再以轮与绳相切点 D 为基点,则轮心 B 的加速度
v B v D v BD ,式中 v D r A , v BD r B
∴ v B r A r B , 对上式求导得轮心 B 的加速度为
Fx maCx , FNA maCx , Fy maCy , FNB mg maCy , M C ( F ) J C , FNB l cos FNA l sin 1 ml 2 2 2 12
l 2 FNA 2 ( sin cos )m, l 2 FNB mg ( cos sin )m, 2 l l 1 2 FNB 2 cos FNA 2 sin 12 ml
A
动量矩定理

动量矩定理一、是非题1. 平动刚体各点的动量对一轴的动量矩之和可以用质心对该轴的动量矩表示。
( √ )2. 质点系对于任意动点的动量矩对时间的导数,等于作用于质点系的所有外力对于同一点的矩的矢量和。
( × )3. 因为质系的动量为C v p m =,所以质系对O 点的动量矩为()C O O mv M L =。
( × )4. 质点系的内力不能改变质点系的动量与动量矩。
( √ )5. 刚体的质量是刚体平动时惯性大小的度量,刚体对某轴的转动惯量则是刚体绕该轴转动时惯性大小的度量。
( √ )6. 定轴转动刚体各点的动量对转轴上一点的动量矩之矢量和角速度矢量的数量积是负的值。
( × )动量矩7. 均质圆柱绕其对称轴作定轴转动,则圆柱惯性力系对于空间中平行于转轴的任意一轴的力矩之和,都是同一值。
( √ )动量矩8. P 为刚体作平面运动的速度瞬心,有动量矩定量)(d d )e (i P pM t L F ∑=。
( √ )动量矩 9. 均质平面正多边形,对平面内过其形心的任一轴的转动惯量均相等。
( √ )动量矩10. 如果质点系的质心速度为零,则质点系对任一固定点的动量矩都一样。
( √ )动量矩11. 图示无重刚杆焊接在z 轴上,与z 轴夹角90≠β,两球A 、B 焊接在杆两端,两球质量相同,且OB AO =,系统绕z 轴以不变的角速度ω转动,试判断下述说法是否正确:(1)系统对O 点的动量矩守恒,对z 轴的动量矩不守恒。
( × )(2)系统对O 点的动量矩不守恒,对z 轴的动量矩守恒。
( √ )(3)系统对O 点及z 轴的动量矩都守恒。
( × )(4)系统对O 点及z 轴的动量矩都不守恒。
( × )12. 图中,若两轮的转动惯量皆为J ,质心都在各自转轴上,轮I 的半径为R ,轮Ⅱ的半径为r ,两轮接触处无相对滑动,轮I 的角速度为ω 。
试判断下述说法是否正确:(1)系统对1O 轴的动量矩为零。
动量矩定理10
FxA
N Ff F
F F yA f'
N'
X0
ω
Y0
Ff
fN
f
Fl b
,
J
0
Ff r
Ff r fFlr 2 fFl , d d d
J0 J0b mrb
d dt d
2 fFl , d d d
mrb
d dt d
0 d
2 fFl mrb
0
d
2mrb n
4 fFl
FN
a 60 Ff
mgr2 sin 600 r2 fmg cos 60o r2FT mar2 (4)
(3) (4) : a
3r 2 2
fr R
2 r2
r
g
1.29
m
s2
习题12.21 如图所示,两根质量均为8kg的均质细杆固
连成T字形,可绕通过O点的水平轴转动,当OA处于水 平位置时,T形杆具有角速度ω=4rad/s。求该瞬时轴承 O处的约束反力。
Fox mg
c
(b)
m
l
2
macy
Fiye mg Foy
(c)
联立(a)、(b)、(c)解得
Fox 0
Foy
1 4
mg
(2)杆落至任意角φ时,所受的外力有:重力mg、
o处约束反力 FOn 、FO
杆运动的角速度、角加
速度均未知。欲求O处 约束力,必先求质心加
0.25m 0.25m
解:由题意知T字形刚体质心在C0点, 2m=16kg
C0 0.375m
由质心运动定理知
F 0x
ω an
C aτ
2man Fox
动量矩定理

动量矩定理 习 题例1:单摆将质量为m 的小球用长为l 的线悬挂于水平轴上,使其在重力作用下绕悬挂轴O 在铅直平面内摆动。
线自重不计且不可伸长,摆线由偏角0ϕ时从静止开始释放,求单摆的运动规律。
解:将小球视为质点。
其速度为ϕ&l v =且垂直于摆线。
摆对轴的动量矩为()ϕϕ&&2ml l ml mv m o =⋅= 又 ()o T m o =,则外力对轴O 之矩为()ϕsin mgl F m o -=注意:在计算动量矩与力矩时,符号规定应一致(在本题中规定逆时针转向为正)。
根据动量矩定理,有()ϕϕsin 2mgl ml tx-=&d d即 0sin =+ϕϕl g&& (a)当单摆做微幅摆动时,ϕϕ≈sin ,并令lgn =2ω 则式(a )成为 02=+ϕωϕn && (b )解此微分方程,并将运动初始条件带入,即当t=0时,0ϕϕ=,00=ϕ&,得单摆微幅摆动时的运动方程为tn ωϕϕcos 0=©由此可知,单摆的运动是做简谐振动。
其振动周期为gl T nπωπ22==C例2:双轴传动系统中,传动轴Ⅰ与Ⅱ对各自转轴的转动惯量为1J 与2J ,两齿轮的节圆半径分别为1R 与2R ,齿数分别为1z 与2z ,在轴Ⅰ上作用有主动力矩1M ,在轴Ⅱ上作用有阻力矩2M ,如图所示。
求轴Ⅰ的角加速度。
解:轴Ⅰ与轴Ⅱ的定轴转动微分方程分别为 1111R P M J τε-= (a ) 2222R P M J τε+-= (b)又122112z zR R i ===εε(c )以上三式联立求解,得 221211i J J iM M +-=ε例3:质量为m 半径为R 的均质圆轮置放在倾角为α的斜面上,在重力的作用下由静止开始运动,设轮与斜面间的静、动滑动摩擦系数分别为f 、f ',不计滚动摩阻。
试分析轮的运动。
解:取轮为研究对象,根据平面运动微分方程有F mg ma c -=αsin (a ) N mg +-=αcos 0 (b) FR J c =ε (c) 由式(b )得 αcos mg N = (d) 情况一: 设接触处绝对光滑。
高考物理动量定理解题技巧及练习题(含答案)

高考物理动量定理解题技巧及练习题(含答案)一、高考物理精讲专题动量定理1.如图甲所示,平面直角坐标系中,0≤x ≤l 、0≤y ≤2l 的矩形区域中存在交变匀强磁场,规定磁场垂直于纸面向里的方向为正方向,其变化规律如图乙所示,其中B 0和T 0均未知。
比荷为c 的带正电的粒子在点(0,l )以初速度v 0沿+x 方向射入磁场,不计粒子重力。
(1)若在t =0时刻,粒子射入;在t <02T 的某时刻,粒子从点(l,2l )射出磁场,求B 0大小。
(2)若B 0=02c v l ,且粒子从0≤l ≤02T 的任一时刻入射时,粒子离开磁场时的位置都不在y 轴上,求T 0的取值范围。
(3)若B 0= 02c v l ,00l T v π=,在x >l 的区域施加一个沿-x 方向的匀强电场,在04T t =时刻入射的粒子,最终从入射点沿-x 方向离开磁场,求电场强度的大小。
【答案】(1)00v B cl =;(2)00l T v π≤;(3)()20421v E n cl π=+()0,1,2n =L . 【解析】【详解】设粒子的质量为m ,电荷量为q ,则由题意得q c m= (1)粒子在磁场中做匀速圆周运动,设运动半径为R ,根据几何关系和牛顿第二定律得:R l =2000v qv B m R=解得00v B cl= (2)设粒子运动的半径为1R ,由牛顿第二定律得20001v qv B m R = 解得12l R = 临界情况为:粒子从0t =时刻射入,并且轨迹恰好过()0,2l 点,粒子才能从y 轴射出,如图所示设粒子做圆周运动的周期为T ,则002m l T qB v ππ== 由几何关系可知,在02T t =内,粒子轨迹转过的圆心角为 θπ=对应粒子的运动时间为1122t T T ππ== 分析可知,只要满足012T t ≥,就可以使粒子离开磁场时的位置都不在y 轴上。
联立解得0T T ≤,即00lT v π≤;(3)由题意可知,粒子的运动轨迹如图所示设粒子的运动周期为T ,则002m l T qB v ππ== 在磁场中,设粒子运动的时间为2t ,则 21144t T T =+ 由题意可知,还有00244T T t =+ 解得0T T =,即00lT v π=设电场强度的大小为E ,在电场中,设往复一次所用的时间为3t ,则根据动量定理可得302Eqt mv =其中3012t n T ⎛⎫=+ ⎪⎝⎭()0,1,2n =L 解得()20421v E n cl π=+()0,1,2n =L2.汽车碰撞试验是综合评价汽车安全性能的有效方法之一.设汽车在碰撞过程中受到的平均撞击力达到某个临界值F 0时,安全气囊爆开.某次试验中,质量m 1=1 600 kg 的试验车以速度v 1 = 36 km/h 正面撞击固定试验台,经时间t 1 = 0.10 s 碰撞结束,车速减为零,此次碰撞安全气囊恰好爆开.忽略撞击过程中地面阻力的影响.(1)求此过程中试验车受到试验台的冲量I 0的大小及F 0的大小;(2)若试验车以速度v 1撞击正前方另一质量m 2 =1 600 kg 、速度v 2 =18 km/h 同向行驶的汽车,经时间t 2 =0.16 s 两车以相同的速度一起滑行.试通过计算分析这种情况下试验车的安全气囊是否会爆开.【答案】(1)I0 = 1.6×104 N·s ,1.6×105 N;(2)见解析【解析】【详解】(1)v1 = 36 km/h = 10 m/s,取速度v1 的方向为正方向,由动量定理有-I0 =0-m1v1 ①将已知数据代入①式得I0 = 1.6×104 N·s ②由冲量定义有I0 = F0t1 ③将已知数据代入③式得F0 = 1.6×105 N ④(2)设试验车和汽车碰撞后获得共同速度v,由动量守恒定律有m1v1+ m2v2 = (m1+ m2)v⑤对试验车,由动量定理有-Ft2 = m1v-m1v1 ⑥将已知数据代入⑤⑥式得F= 2.5×104 N ⑦可见F<F0,故试验车的安全气囊不会爆开⑧3.如图甲所示,物块A、B的质量分别是m A=4.0kg和m B=3.0kg.用轻弹簧拴接,放在光滑的水平地面上,物块B右侧与竖直墙壁相接触.另有一物块C从t=0时以一定速度向右运动,在t=4s时与物块A相碰,并立即与A粘在一起不分开,C的v-t图象如图乙所示.求:(1)C的质量m C;(2)t=8s时弹簧具有的弹性势能E p1(3)4—12s内墙壁对物块B的冲量大小I【答案】(1) 2kg (2) 27J (3) 36N s×【解析】【详解】(1)由题图乙知,C与A碰前速度为v1=9m/s,碰后速度大小为v2=3m/s,C与A碰撞过程动量守恒m C v1=(m A+m C)v2解得C的质量m C=2kg.(2)t=8s时弹簧具有的弹性势能E p1=12(m A+m C)v22=27J(3)取水平向左为正方向,根据动量定理,4~12s内墙壁对物块B的冲量大小I=(m A+m C)v3-(m A+m C)(-v2)=36N·s4.如图,一轻质弹簧两端连着物体A和B,放在光滑的水平面上,某时刻物体A获得一大小为的水平初速度开始向右运动。
高考物理动量定理答题技巧及练习题(含答案)

高考物理动量定理答题技巧及练习题(含答案)一、高考物理精讲专题动量定理1.如图甲所示,平面直角坐标系中,0≤x ≤l 、0≤y ≤2l 的矩形区域中存在交变匀强磁场,规定磁场垂直于纸面向里的方向为正方向,其变化规律如图乙所示,其中B 0和T 0均未知。
比荷为c 的带正电的粒子在点(0,l )以初速度v 0沿+x 方向射入磁场,不计粒子重力。
(1)若在t =0时刻,粒子射入;在t <02T 的某时刻,粒子从点(l,2l )射出磁场,求B 0大小。
(2)若B 0=02c v l ,且粒子从0≤l ≤02T的任一时刻入射时,粒子离开磁场时的位置都不在y 轴上,求T 0的取值范围。
(3)若B 0=02c v l ,00l T v π=,在x >l 的区域施加一个沿-x 方向的匀强电场,在04T t =时刻入射的粒子,最终从入射点沿-x 方向离开磁场,求电场强度的大小。
【答案】(1)00v B cl =;(2)00l T v π≤;(3)()20421v E n cl π=+()0,1,2n =L . 【解析】 【详解】设粒子的质量为m ,电荷量为q ,则由题意得qc m=(1)粒子在磁场中做匀速圆周运动,设运动半径为R ,根据几何关系和牛顿第二定律得:R l =2000v qv B m R=解得0v B cl=(2)设粒子运动的半径为1R ,由牛顿第二定律得20001v qv B m R =解得12l R =临界情况为:粒子从0t =时刻射入,并且轨迹恰好过()0,2l 点,粒子才能从y 轴射出,如图所示设粒子做圆周运动的周期为T ,则002m lT qB v ππ== 由几何关系可知,在02T t =内,粒子轨迹转过的圆心角为 θπ=对应粒子的运动时间为1122t T T ππ== 分析可知,只要满足012T t ≥,就可以使粒子离开磁场时的位置都不在y 轴上。
联立解得0T T ≤,即00lT v π≤;(3)由题意可知,粒子的运动轨迹如图所示设粒子的运动周期为T ,则002m lT qB v ππ== 在磁场中,设粒子运动的时间为2t ,则21144t T T =+由题意可知,还有00244T T t =+ 解得0T T =,即00lT v π=设电场强度的大小为E ,在电场中,设往复一次所用的时间为3t ,则根据动量定理可得302Eqt mv =其中3012t n T ⎛⎫=+ ⎪⎝⎭()0,1,2n =L解得()2421v E n cl π=+()0,1,2n =L2.如图所示,质量M =1.0kg 的木板静止在光滑水平面上,质量m =0.495kg 的物块(可视为质点)放在的木板左端,物块与木板间的动摩擦因数μ=0.4。
高考物理动量定理解题技巧分析及练习题(含答案)

高考物理动量定理解题技巧分析及练习题(含答案)一、高考物理精讲专题动量定理1.如图甲所示,平面直角坐标系中,0≤x ≤l 、0≤y ≤2l 的矩形区域中存在交变匀强磁场,规定磁场垂直于纸面向里的方向为正方向,其变化规律如图乙所示,其中B 0和T 0均未知。
比荷为c 的带正电的粒子在点(0,l )以初速度v 0沿+x 方向射入磁场,不计粒子重力。
(1)若在t =0时刻,粒子射入;在t <02T 的某时刻,粒子从点(l,2l )射出磁场,求B 0大小。
(2)若B 0=02c v l ,且粒子从0≤l ≤02T的任一时刻入射时,粒子离开磁场时的位置都不在y 轴上,求T 0的取值范围。
(3)若B 0=02c v l ,00l T v π=,在x >l 的区域施加一个沿-x 方向的匀强电场,在04T t =时刻入射的粒子,最终从入射点沿-x 方向离开磁场,求电场强度的大小。
【答案】(1)00v B cl =;(2)00l T v π≤;(3)()20421v E n cl π=+()0,1,2n =L . 【解析】 【详解】设粒子的质量为m ,电荷量为q ,则由题意得qc m=(1)粒子在磁场中做匀速圆周运动,设运动半径为R ,根据几何关系和牛顿第二定律得:R l =2000v qv B m R=解得0v B cl=(2)设粒子运动的半径为1R ,由牛顿第二定律得20001v qv B m R =解得12l R =临界情况为:粒子从0t =时刻射入,并且轨迹恰好过()0,2l 点,粒子才能从y 轴射出,如图所示设粒子做圆周运动的周期为T ,则002m lT qB v ππ== 由几何关系可知,在02T t =内,粒子轨迹转过的圆心角为 θπ=对应粒子的运动时间为1122t T T ππ== 分析可知,只要满足012T t ≥,就可以使粒子离开磁场时的位置都不在y 轴上。
联立解得0T T ≤,即00lT v π≤;(3)由题意可知,粒子的运动轨迹如图所示设粒子的运动周期为T ,则002m lT qB v ππ== 在磁场中,设粒子运动的时间为2t ,则21144t T T =+由题意可知,还有00244T T t =+ 解得0T T =,即00lT v π=设电场强度的大小为E ,在电场中,设往复一次所用的时间为3t ,则根据动量定理可得302Eqt mv =其中3012t n T ⎛⎫=+ ⎪⎝⎭()0,1,2n =L解得()2421v E n cl π=+()0,1,2n =L2.如图所示,一光滑水平轨道上静止一质量为M =3kg 的小球B .一质量为m =1kg 的小球A 以速度v 0=2m/s 向右运动与B 球发生弹性正碰,取重力加速度g =10m/s 2.求:(1)碰撞结束时A 球的速度大小及方向; (2)碰撞过程A 对B 的冲量大小及方向.【答案】(1)-1m/s ,方向水平向左(2)3N·s ,方向水平向右 【解析】【分析】A 与B 球发生弹性正碰,根据动量守恒及能量守恒求出碰撞结束时A 球的速度大小及方向;碰撞过程对B 应用动量定理求出碰撞过程A 对B 的冲量; 解:(1)碰撞过程根据动量守恒及能量守恒得:0A B mv mv Mv =+2220111222A B mv mv Mv =+ 联立可解得:1m/s B v =,1m/s A v =- 负号表示方向水平向左 (2)碰撞过程对B 应用动量定理可得:0B I Mv =- 可解得:3I N s =⋅ 方向水平向右3.半径均为52m R =的四分之一圆弧轨道1和2如图所示固定,两圆弧轨道的最低端切线水平,两圆心在同一竖直线上且相距R ,让质量为1kg 的小球从圆弧轨道1的圆弧面上某处由静止释放,小球在圆弧轨道1上滚动过程中,合力对小球的冲量大小为5N s ⋅,重力加速度g 取210m /s ,求:(1)小球运动到圆弧轨道1最低端时,对轨道的压力大小; (2)小球落到圆弧轨道2上时的动能大小。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
动量矩定理作业参考答案及解答
1.如题图所示,均质细圆环质量为m 1,半径为R ,其上固接一质量为m 2的均质细杆AB ,系统在铅垂面以角速度ω 绕O 轴转动,已知∠CAB =60°,分别计算系统对轴O 和轴C 的动量矩。
解: 先计算系统对轴O 的动量矩。
环对其质心的转动惯量
211R m J C =
由转动惯量的平行移轴定理,环对转轴点O 的转动惯量
2112112R m J R m J C O =+=
杆对其质心 22212
1
R m J C =
由转动惯量的平行移轴定理,杆对转轴点O 的转动惯量
2222)23(R R m J J C O +
+==)36
11
(222m m R + 所以 222121)3611
2(R m m m J J J O O O ++=+= 对轴O 的动量矩为 ==ωO O J L )3611
2(2212m m m R ++ω
再计算系统对轴C 的动量矩。
环对其质心动量矩为 ωω2111R m J L C C == 点C 不是杆AB 的质心,故杆AB 对轴C 的动量矩为
)23
65(2
3)231(12)(222222222
+=⋅++=+=ωωωωR m R R m R m v m M J L C C C C
系统对轴C 的动量矩为 )2
3
65(221221m m m R L L L C C C ++=+=ω
答案:)36112(2212m m m R L O ++
=ω ; )2
365(2212m m m R L C ++=ω
2.行星齿轮机构如题图所示,齿轮D 固定,轮心为A ;行星齿轮B 质量为m 1,半径为R ,对质心B 的回转半径为ρ ;曲柄AB 可看作均质细杆,其质量为m 2,长为l 。
当杆AB 以ω 转动时,求系统对轴A 的动量矩。
提示:本题主要工作是齿轮B 对轴A 的动量矩计算。
齿轮B 作平面运动,先求出齿轮B 的角速度,根据平面运动刚体对轴的动量矩的计算式计算。
注意各项的正负号。
解: 先计算系统对轴A 的动量矩。
对杆分析,杆对轴A 的动量矩 ω22131
R m L A =
对轮分析 l R B ωω=
R
l
B ωω=
(顺时针)
齿轮对轮心B 的动量矩为 R
l
m m L B B 212
1ρωωρ−=−=
齿轮对轴A 的动量矩为 212l m L L B A +=ω 系统对轴A 的动量矩为 =+=21A A A L L L ωρ)3
(212
122R l m l m l m −+
再计算系统对轴B 的动量矩。
杆AB 对轴B 的动量矩为 ωω
ωω62212)(2222221l m l m l l m v m M J L C B C B −=−=+=
齿轮对轮心B 的动量矩为 R
l
m m L B B 212
11ρω
ωρ−=−=
系统对轴B 的动量矩 ωρ)6
(212221R l
m l m L L L B B B +−=+=
这里负号表示动量矩转向顺时针
答案:ωρ)3(212
122R l m l m l m L A −+=; ωρ6
(2122R l m l m L B +−=
3.均质水平圆盘重为P 1,半径为r ,可绕通过其中心O 的铅垂轴旋转。
一重为P 2的人按AB =s =22
1at 的规律沿盘缘行走。
设开始时圆盘是静止的,求圆盘的角速度及角加速度。
提示:整个系统对轴O 的动量矩守恒。
注意人按AB =s =22
1at 的规律沿盘缘行走是指相对运动规律。
解: 以整个系统为研究对象,由于∑=0)(F O M ,故整个系统对轴O 的动量矩守恒。
人相对圆盘的速度大小为
at v dt
ds
==r 人绝对速度的大小为 at r dt
ds
r v −=−=ωωa
整个系统对轴O 的动量矩守恒 0)(2121221=−+=+=at r r g p g p
r L L L O ωω
解得 )
2(2 ,)2(2122122P P r aP dt d P P r t aP +==+=
ω
αω
答案:)
2(2 ,)2(2122122P P r aP P P r t aP +=+=
αω
4.如题图所示,均质细圆环的质量为m ,半径为r ,C 为质心。
圆环在铅垂平面内,可绕位于圆环周缘的光滑固定轴O 转动。
圆环于OC 水平时,由静止释放,求释放瞬时圆环的角加速度及轴承O 的反力。
提示:先用刚体定轴转动微分方程求出角加速度,然后用质心运动定理求轴承O 的反力。
解:
圆环对轴O 的转动惯量为
22mr J O =
由定轴转动微分方程 ∑=)(F O O M J α
得 mgr
mr =α2
2 )(2顺时针r
g
=α 再用质心运动定理
0 :=Ox F x
2
:mg mr mg F y Oy −
=−=−α 解得
)( 2
1
↑=mg F Oy
答案:)( 2
1
,0 ),(2↑===mg F F r g Oy Ox 顺时针α
5.重物A 质量为m 1,系在绳子上,绳子跨过不计质量的固定滑轮D ,并绕在鼓轮B 上,如题图8所示。
由于重物下降,带动了轮C ,使它沿水平轨道滚动而不滑动。
设鼓轮半径为r ,轮C 的半径为R ,两者固连在一起,总质量为m 2,对于其水平轴O 的回转半径为ρ 。
求轮C 的角加速度。
提示:分别取物块A 和轮C αα)(,
r R a A R a O A O +==的加速度物块的加速度轮心
1) 取鼓轮和轮一起为研究对象,鼓轮和轮一起做平面运动,设轮C 受到的摩擦
力为F f ,绳子受到的拉力为F T ,受力如图
分别用质心运动定理和刚体平面运动微分方程得 组合轮O
T
2
2
2f T 2
2f
T 2)()( F R r R m J RF rF m J F F a m D O O +=+=−==−=αρααρα或
重物A T 11F g m a m A −= 将运动学关系αα)(,r R a R a A O +==代入上述动力学方程解得
2
2
2211)()()(m R r R m g
m r R ρα++++=
答案:2
22211)()()(m R r R m g
m r R ρα++++=
1g
a A
6. 一均质杆AB 质量为m ,长为l ,其两端由两条等长的绳子系住在水平位置平衡,如图所示。
如右边绳子突然被剪断,试求绳子突然被剪断瞬时另一根绳子的张力和杆的角加速度。
如将两条等长的绳子换成刚度系数为k 的弹簧,试求右边弹簧被突然去掉瞬时杆的角加速度。
解: 绳子突然被剪断瞬时,其受力和运动学图见右下。
由刚体平面运动微分方程得 4312 , 23 , 22
lF ml J mg F ma F ma C Cy Cx ==−=
=αα 由于此为二自由度系统,故α , , Cy Cx a a 之间必存在一运动学关系。
以点A 为基点,质心C 为动点,有运动学关系
t
CA A Cy Cx a a a a +=+ 得
2
,21 , 23t
t αl a a a a a a CA CA A Cy A Cx =−−==
或消去A a 有 αl a a a CA Cy Cx 2
3
33t
−
=−=+ 将此运动学关系与前面的动力学方程联立解之得
mg F l g 13
3
2 , 1318==
α 当将绳子换成刚度系数为k 的弹簧时,
由于右边弹簧被突然去掉瞬时,左边弹簧的拉力与未去掉前相同,即
mg F 3
3=,由412 43 2lmg
ml lF J C =
⇒=αα 得 l
g
3=
α
C
A
A x
y
A。
