渐开线齿廓及其啮合特点

合集下载

简述渐开线齿廓的啮合特点

简述渐开线齿廓的啮合特点渐开线齿廓是一种常见的齿轮啮合方式，其特点是具有曲率变化的齿廓。

在渐开线齿轮啮合中，两个齿轮的齿廓曲线是相互匹配的，使得齿轮之间可以顺畅地啮合，并传递动力。

渐开线齿廓的啮合特点可以从以下几个方面来描述：1. 齿廓曲线的特殊性：渐开线齿廓是一种特殊的曲线，具有曲率变化的特点。

与其他齿轮啮合方式相比，渐开线齿廓的曲率变化更加平滑，使得齿轮在啮合过程中的运动更加稳定。

这种平滑的曲线使得渐开线齿廓具有较高的传动效率和较低的噪声。

2. 齿廓的中心扩展：渐开线齿廓的中心扩展是指齿廓曲线中心的轨迹不是一个点，而是一个曲线。

这种中心扩展使得齿轮在啮合过程中可以实现相对滑动，减小了啮合时的摩擦和磨损，提高了齿轮的寿命和可靠性。

同时，中心扩展还可以使得渐开线齿轮在高速运动时具有更好的动平衡性能。

3. 齿廓的变位特性：渐开线齿轮的齿廓变位是指齿廓曲线在垂直于齿轮轴线方向上的变化。

齿廓变位可以使得齿轮在啮合过程中实现平稳的传动，减小冲击和振动。

同时，齿廓变位还可以改变齿轮的传动特性，如变速、变转矩等，提高了齿轮传动的灵活性和适应性。

4. 齿廓的接触特性：渐开线齿轮的齿廓接触是指齿轮齿廓之间的接触区域。

由于渐开线齿廓的特殊曲线形状，齿轮在啮合过程中的接触区域相对较大，使得齿轮传递的载荷分布更加均匀，减小了齿轮的磨损和损伤。

同时，齿廓接触还可以改善齿轮的传动效率和承载能力，提高齿轮传动的可靠性。

总的来说，渐开线齿廓具有曲率变化、中心扩展、变位特性和接触特性等特点，在齿轮传动中具有重要的应用价值。

通过合理设计和制造渐开线齿轮，可以实现高效稳定的传动，提高齿轮传动的可靠性和使用寿命。

渐开线和渐开线齿廓啮合传动的特点7月4

一、回顾上节课内容
1、齿轮传动的特点
作用：传递空间任意两轴（平行、相交、交错）的旋转运动，或将转动转换为移动。优点： ①传动比准确、传动平稳。 ②载荷和速度范围大，载荷：0~几万千瓦，速度：0~高达300 m/s。 ③效率高(η→0.99)、使用寿命长、工作安全可靠。 ④可实现平行轴、相交轴和交错轴之间的传动。缺点：要求较高的制造和安装精度，加工成本高、不适宜远距离传动(如单车)。动画1
BK－发生线，
渐开线 k rk 发生线 B O
A r
b
θk
rb －基圆 θ k－AK段的展角
纯滚动对纯滚动运动而言，物体与平面之接触点於接触那一瞬间为静止的，没有任何的滑动。接触点为相对速度瞬心点（瞬时速度相等的重合点）。
基圆
动画
:怎样由一条渐开线得到渐开线齿轮的齿廓呢？
2.渐开线的特性（1）发生线沿基圆滚过的长度，等于基圆上被滚过的圆弧长度。
2、分类：按传动时两轮轴的相对位置分
直齿圆柱齿轮传动平面齿轮机构（轴平行）
斜齿圆柱齿轮传动
人字齿轮传动
外啮合齿轮传动内啮合齿轮传动齿轮与齿条传动
轴相交--圆锥齿轮传动(直齿、斜齿、曲线齿）空间齿轮机构轴交错--交错轴斜齿轮传动蜗杆传动.
3.齿廓曲线的选择
渐开线摆线变态摆线
圆弧抛物线
:渐开线各点的曲率半径有无变化？怎样变化？
课堂练习1:
1）K点离基圆越远，曲率半径BK 越大 ,渐开线越趋于平直。 2）K点离基圆越近，曲率半径BK越小 ,渐开线越弯曲。 3）当K点与基圆上的点A重合时，曲率半径等于。 0
K
（3）渐开线形状取决于基圆的大小

渐开线齿廓啮合的特点

渐开线齿廓啮合的特点
渐开线齿廓是一种常见的齿轮啮合形式，在机械传动中具有重要
的作用。

渐开线齿廓啮合的特点在于，既能保持齿轮的高传动效率，
又能有效减少齿面接触应力和噪声，具有平稳、可靠的传动特性，被
广泛应用于各种机械传动装置中。

渐开线齿廓的设计和制造需要涉及到齿廓的数学计算、加工精度
等诸多方面。

一般而言，渐开线齿廓是利用曲线发生器（如伯努利曲线）来生成的，其曲率半径呈指数增长或递减的特点使得齿轮相对位
置的微小变化不会对啮合产生影响。

同时，渐开线齿廓还需要考虑齿
顶高度、齿宽、齿数等因素，以保证其在实际应用中能够满足传动要求。

在渐开线齿廓的啮合过程中，齿轮的动力学特性也有所改变。

在
轴向载荷和转矩作用下，齿轮会产生变形和扭曲，从而对齿面接触应
力和噪声产生影响。

为了减小这些负面影响，可以采用齿轮优化设计、表面处理、润滑和降噪等多种手段，使齿轮的运转更加平稳、可靠、
低噪声。

总之，渐开线齿廓啮合具有很多独特的特点和优点，但也需要充
分注意其设计和制造的细节问题。

只有在实际应用中能够兼顾传动效率、安全可靠和降噪等多个方面，才能够更好地满足各种机械传动装
置的需求。

渐开线齿廓的啮合特点

渐开线齿廓的啮合特点
1. 渐开线齿廓的啮合能保证传动比恒定呢，就好比我们跑步的速度一直稳定，不会突然变快或变慢，你想想看，要是齿轮传动比不稳定，那机器不就乱套啦！
2. 渐开线齿廓的啮合具有可分性呀，这就像搭积木，哪怕把积木拆开再组合，依然能搭出原来的样子，多厉害！你说要是没这可分性，齿轮维修得多麻烦！
3. 它的齿廓间相对滑动小哦，这就如同轻轻滑过的微风，不会造成太多磨损，那不是能让齿轮更耐用嘛！
4. 渐开线齿廓的啮合使得同时啮合的齿数多呢，就好像一群小伙伴一起用力推东西，力量更大更稳定，多棒啊！
5. 渐开线齿廓能实现平稳传动哟，你想想那种丝滑的感觉，就像坐顺滑的滑梯一样，要是不平稳，那多吓人！
6. 渐开线齿廓还具有中心距可变性呀，这不就像是有弹性的绳子，可以拉长缩短都没问题，要是没这特性，很多情况都没法应用啦！
7. 渐开线齿廓的重合度大呢，就好像我们重叠很多东西来增加厚度，这样传动更可靠呀，多牛！
8. 渐开线齿廓的安装和制造都比较方便哦，可不是嘛，就像搭简单的拼图一样，容易操作，多好呀！
9. 渐开线齿廓的这些啮合特点，让它在各种机械中都大显身手呢，真的是超级厉害！所以啊，渐开线齿廓真的是机械传动里不可或缺的重要角色呀！。

机械设计基础知识点详解

机械设计基础知识点详解绪论1、机器的特征：（1）它是人为的实物组合；（2）各实物间具有确定的相对运动；（3）能代替或减轻人类的劳动去完成有效的机械功或转换机械能。

第一章平面机构的自由度和速度分析要求：握机构的自由度计算公式，理解的基础上掌握机构确定性运动的条件，熟练掌握机构速度瞬心数的求法。

1、基本概念运动副：凡两个构件直接接触而又能产生一定相对运动的联接称为运动副。

低副：两构件通过面接触组成的运动副称为低副。

高副：两构件通过点或线接触组成的运动副称为高副。

复合铰链：两个以上的构件同时在一处用回转副相联构成的回转副。

局部自由度：机构中常出现的一种与输出构件运动无关的自由度，称为局部自由度或多余自由度。

虚约束：对机构运动不起限制作用的重复约束称为虚约束或称消极约束。

瞬心：任一刚体相对另一刚体作平面运动时，其相对运动可看作是绕某一重合点的转动，该重合点称为瞬时回转中心或速度瞬心，简称瞬心。

如果两个刚体都是运动的，则其瞬心称为相对速度瞬心；如果两个刚体之一是静止的，则其瞬心称为绝对速度瞬心。

2、平面机构自由度计算作平面运动的自由构件具有三个自由度，每个低副引入两个约束，即使构件失去两个自由度；每个高副引入一个约束，使构件失去一个自由度。

计算平面机构自由度的公式：F=3n-2PL -PH机构要具有确定的运动，则机构自由度数必须与机构的原动件数目相等。

即，机构具有确定运动的条件是F>0,且F等于原动件个数。

3、复合铰链、局部自由度和虚约束(a)K个构件汇交而成的复合铰链应具有(K-1)个回转副。

(b)局部自由度虽然不影响整个机构的运动，但滚子可使高副接触处的滑动摩擦变成滚动摩擦，减少磨损，所以实际机械中常有局部自由度出现。

(c)虚约束对机构运动虽不起作用，但是可以增加构件的刚性和使构件受力均衡，所以实际机械中虚约束随处可见。

4、速度瞬心如果一个机构由K个构件组成，则瞬心数目为N=K(K-1)/2瞬心位置的确定：(a)已知两重合点相对速度方向，则该两相对速度向量垂线的交点便是两构件的瞬心。

渐开线齿廓的形成与啮合特点

渐开线齿廓的形成与啮合特点
形成原理：
渐开线齿廓是由齿轮齿侧面的直线（称为侧面线）和齿根圆的一部分（称为基圆）组成。

侧面线与基圆的交点构成了齿槽的啮合点。

渐开线齿
廓的形成主要是通过给定齿数、压力角和齿轮传动比等参数，利用特定的
公式计算而得。

啮合特点：
1.线接触。

渐开线齿廓的啮合面积较小，只有一个点或一小段线接触，这样能够实现对点接触的要求，减小了齿轮的摩擦和接触磨损，提高了传
动效率。

2.平稳传动。

渐开线齿廓具有相对平滑的啮合传动特性，能够减小振
动和冲击，使传动更加平稳。

3.轴向移动。

渐开线齿廓的特点使得齿轮在转动过程中能够自动沿轴
向方向进行微小的移动，可以自动适应齿轮间隙的变化。

这样能够保证齿
轮的啮合正常，并且减小了噪声和振动。

4.高承载能力。

渐开线齿廓的啮合传动是通过多点接触来实现的，使
得载荷能够均匀分布在齿面上，提高了齿轮的承载能力。

5.较小的齿根强度。

由于渐开线齿廓的齿根圆的一部分构成了齿轮的
齿槽，在齿根处可能出现较大的应力集中，降低了齿根的强度。

因此在设
计中需要合理选择齿廓参数，以确保齿轮的强度和可靠性。

6.减小中心距误差的影响。

由于渐开线齿轮通过自动的轴向移动来适应齿间隙变化，可以减小中心距误差对齿轮啮合性能的影响，提高传动的准确性。

总之，渐开线齿廓的形成和啮合特点使得其广泛应用于各种机械传动中，能够实现平稳、高效、可靠的传动效果。

07-4第三十六讲渐开线齿廓的啮合特性(精)

O1 ω1 rb1 N1 P N2 rb2 ω2 O2 K C2 C1
= rb2 /rb1
——基圆之反比。
实际安装中心距略有变化时，不影响i12，这一特性称为运动可分性，对加工和装配很有利。
由于上述特性，工程上广泛采用渐开线作为齿轮的齿廓曲线。
JM
返回
第三十六讲渐开线齿廓的啮合特性
1、渐开线齿廓能保证定传动比传动两齿廓在任意点K啮合时，过K作两齿廓的法线N1N2，是基圆的切线，为定直线。两轮中心连线也为定直线，故交点 P必为定点。
N2 ω1 rb1 N1 P K C2 C1
K’
i12=ω 1/ω 2=O2P/ O1P=const
rb2
ω2 O2
工程意义：i12为常数可减少因速度变化所产生的附加动载荷、振动和噪音，延长齿轮的使用寿命，提高机器的工作精度。 2、齿廓间正压力方向不变 N1N2是啮合点的轨迹，称为啮合线该线又是接触点的法线，正压力总是沿法线方向，故正压力方向不变。该特性对传动的平稳性有利。
JM
返回
3、运动可ห้องสมุดไป่ตู้性 △ O1N1P≌△O2N2P 故传动比又可写成： i12=ω 1/ω 2=O2P/ O1P

认识渐开线齿轮

认识渐开线齿轮渐开线齿轮是一种常见的机械传动元件，它具有精密的结构和良好的传动性能，在工业生产和机械制造中得到了广泛的应用。

本文将从渐开线齿轮的定义、结构特点、工作原理、应用领域等方面进行介绍，希望能够帮助读者更好地认识和理解渐开线齿轮。

一、定义。

渐开线齿轮是一种齿轮传动装置，它的齿轮齿面呈渐开线形状，具有一定的曲线曲率。

这种齿轮的特点是在传动过程中，齿轮与齿轮之间的啮合点在传动时不断移动，从而减小了啮合冲击和噪音，提高了传动的平稳性和可靠性。

二、结构特点。

1. 渐开线齿轮的齿面呈渐开线形状，具有一定的曲线曲率，能够减小啮合冲击和噪音，提高传动的平稳性和可靠性。

2. 渐开线齿轮的齿数较多，齿轮齿面的啮合面积大，传动效率高。

3. 渐开线齿轮的齿轮齿面硬度高，耐磨性好，使用寿命长。

4. 渐开线齿轮的制造工艺复杂，成本较高，适用于对传动精度要求较高的场合。

三、工作原理。

渐开线齿轮的工作原理是通过齿轮的啮合传递动力，实现机械传动的目的。

当两个渐开线齿轮啮合时，它们的啮合点会不断移动，从而减小了啮合冲击和噪音，提高了传动的平稳性和可靠性。

同时，渐开线齿轮的齿数较多，齿轮齿面的啮合面积大，传动效率高，能够满足对传动精度要求较高的场合。

四、应用领域。

渐开线齿轮广泛应用于各种机械传动系统中，特别是在对传动精度和可靠性要求较高的场合。

例如，汽车变速箱、工程机械、风力发电机、船舶设备等领域都需要使用渐开线齿轮进行传动。

此外，渐开线齿轮还常用于精密仪器、航空航天等领域，满足了对传动精度和可靠性要求较高的场合。

总之，渐开线齿轮作为一种重要的机械传动元件，具有精密的结构和良好的传动性能，在工业生产和机械制造中得到了广泛的应用。

通过本文的介绍，相信读者对渐开线齿轮有了更深入的认识和理解，希望能够为相关领域的工程师和技术人员提供一些参考和帮助。

齿轮机构的齿廓啮合基本规律特点和类型

第八节直齿圆锥齿轮传动
圆锥齿轮传动用来传递相交两轴的运动和动力。
分直齿圆锥齿轮和曲齿圆锥齿轮
返回
一、传动比和几何尺寸计算
1)分度圆：d1=mz1， d2=mz2 2)齿顶高：ha=m，齿根高：hf=1.2m
3)传动比：i12= d2/d1 = z2/z1
=ctg δ1=tg δ2
1 2 2 d1 d 2 2 注意：分度圆锥角：δ1=arcctg i12， δ2= 900-δ1 齿顶角：θa1= θa2=arctg ha/R，齿根角： θf1= θf2=arctg hf/R 锥距： R
图5-20 背锥及当量齿数
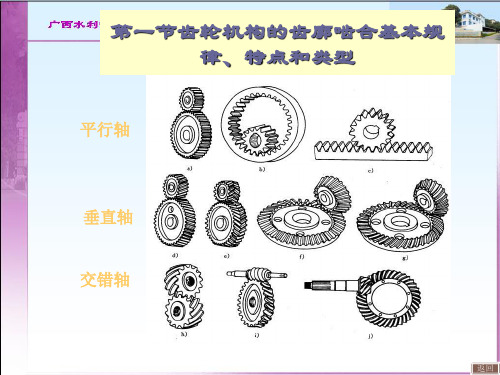
平行轴
垂直轴
交错轴
返回
一、齿轮机构的特点和类型
（一）平行轴线齿轮传动
返回
（二）空间齿轮传动
5
返回
齿轮传动的基本要求
传动准确和平稳（任意瞬时传动比恒定）------由齿
轮轮廓和制造精度决定。
传动比
1 i12 2
承载能力强（足够强度、刚度、耐磨）--------由齿
轮尺寸、材料和工艺决定。
返回
三、正确啮合条件
mn1= mn2 =m αn1= αn2=200 β1= -β2外啮合 (mt1= mt2 ) (αt1= αt2) （ β1=β2内啮合）
返回
四、当量齿数
图5-18 斜齿圆柱齿轮的当量齿数
zmt 2 d z zv 2 3 pn pn cos pt cos cos3
5、分度圆---圆周上的 P/ π =m（模数）为标准值 GB1357-87，压力角α亦为标准值的圆。 d=m Z，α=200，标准齿轮 P=s+e，s=e= π m/2

渐开线齿廓及其啮合特点

渐开线齿廓及其啮合特点如下：
齿廓形状：渐开线的形状是一个圆的渐开线，这个圆在一个平面上沿一个直线作纯滚动。

因此，渐开线齿廓的特点是各齿廓在各圆上的压力角不同。

标准规定分度圆上的压力角为α，其标准值为20°。

啮合特点：
（1）定传动比：渐开线齿轮的啮合角是不变的，因此齿轮的传动比也是恒定的。

这意味着齿轮在转动过程中不会出现速度波动，传动效率高。

（2）可分性：渐开线齿轮的传动比也可以表示为基圆半径的反比。

当两轮的中心距略有改变时，只要两齿轮的基圆半径相应改变，其传动比仍能维持不变。

这一特点对渐开线齿轮的制造和安装都非常有利。

（3）齿廓间正压力方向不变：在齿轮传动过程中，齿廓间的正压力方向始终与接触点的公法线方向一致，并随啮合角的改变而改变。

齿轮的齿廓曲线教学提纲

标准齿轮(standard gears)：
一个标准齿轮的基本参数值确定之后，其主要尺寸和齿廓形状就完全确定了。
m、α、ha* 、c* 取标准值，且e=s的齿轮。
B
二、齿条(the rack)
2)齿廓是直线，各点法线和速度方向线分别平行，压力角处处相等，且等于齿形角，
3)齿距处处相等: p=πm
o1
ω1
§10－2 齿轮的齿廓曲线
1.齿廓啮合基本定律
得： i12 ＝ω1/ω2＝O2P /O1P
齿廓啮合基本定律(fundamental law of gearing): 互相啮合的一对齿轮在任一位置时的传动比，都与连心线O1O2被其啮合齿廓的在接触处的公法线所分成的两段成反比。
在齿轮1上：
在齿轮2上：
kk’=pb1
kk’= pb2
i12 = --
ω1
ω2
传动比：
= --
db2
db1
= --
d’2
d’1
= --
d2
d1
= --
Z2
Z1
啮合过程
为了便于润滑、制造和装配误差，以及受力受热变形膨胀所引起的挤压现象，实际上侧隙不为零，由公差保证。
2.中心距(centre distance) a及啮合角(working pressure angle) α’
根据三心定律可知：P点为相对瞬心。
n
n
P
o2
ω2
k
由： v12 ＝O1P ω1
v12
＝O2P ω2
传动比：i主从=ω主/ω从
节圆
如果要求传动比为常数，则应使O2P/O1P为常数。
节圆(the pitch circle)：设想在P点放一只笔，则笔尖在两个齿轮运动平面内所留轨迹。

渐开线齿轮原理

渐开线齿轮原理一、引言渐开线齿轮是一种常见的机械传动元件，它通过齿轮的啮合来传递动力和运动。

渐开线齿轮原理的理解对于机械工程师和设计师来说至关重要。

本文将介绍渐开线齿轮的原理及其应用。

二、渐开线齿轮的定义渐开线齿轮是一种特殊形状的齿轮，其齿廓曲线为渐开线。

渐开线齿轮的齿廓曲线具有独特的性质，使得齿轮的啮合更加平稳，传动效率更高。

三、渐开线齿轮的原理1. 渐开线的定义：渐开线是一种特殊的曲线，其特点是在任意一点处的切线与该点到一个固定点的距离成正比。

在渐开线齿轮中，齿廓曲线正是由这样的渐开线构成。

2. 渐开线齿轮的齿廓曲线：渐开线齿轮的齿廓曲线是由渐开线与圆弧段组成的。

渐开线部分使得齿轮的啮合过程更加平稳，而圆弧段则用来实现齿轮的啮合。

四、渐开线齿轮的特点1. 平稳的啮合：由于渐开线齿轮的齿廓曲线特殊，使得齿轮的啮合过程更加平稳，减小了齿轮的噪声和振动。

2. 高效的传动：渐开线齿轮的齿廓曲线使得齿轮的传动效率更高，能够减小能量损失，提高传动效率。

3. 大扭矩传递能力：渐开线齿轮由于齿廓曲线的特殊性质，使得齿轮的接触面积更大，从而增加了齿轮的扭矩传递能力。

五、渐开线齿轮的应用1. 机械传动：渐开线齿轮广泛应用于各种机械传动系统中，如汽车变速器、工业机械等。

其平稳的啮合特性和高效的传动性能使其成为理想的传动元件。

2. 纺织机械：渐开线齿轮在纺织机械中的应用也非常广泛。

纺织机械中需要传递大扭矩和保持稳定的运动，渐开线齿轮能够满足这些要求。

3. 风力发电：在风力发电机组中，渐开线齿轮用于传递风力发电机的转动力和转速，保证风能转化为电能的高效率和稳定性。

六、总结渐开线齿轮作为一种常见的机械传动元件，具有平稳的啮合特性、高效的传动性能和大扭矩传递能力。

它在各种机械传动系统中得到广泛应用，如汽车变速器、工业机械、纺织机械和风力发电等领域。

了解渐开线齿轮的原理和特点对于机械工程师和设计师来说非常重要，能够帮助他们设计出更加高效和稳定的机械传动系统。

机械原理复习资料6

渐开线直齿圆柱齿轮的啮合传动(3/6) 渐开线直齿圆柱齿轮的啮合传动
（2）啮合角渐开线齿轮传动的啮合角α′就等于其节圆压力角。当两轮按标准中心距安装时，则 a′= a；当两轮实际中心距 a′与标准中心距 a 不同时，则：若 a′＞a 时， r1′＞r1，r2′＞r2； c′＞0，c＞c*m；α′＞α。若 a′＜a 时，两轮将无法安装。（3）齿轮传动的中心距与啮合角的关系 a′cosα′= a cosα
§10-8 斜齿圆柱齿轮传动
1、螺旋角β 2、端面参数—— 来计算法面参数 ——标准值
斜齿圆柱齿轮传动(3/5) 斜齿圆柱齿轮传动
3、斜齿轮的正确啮合的条件 mn1=mn2= m αn1= αn2 = α β1=-β2 (外啮合) β1=β2 (内啮合)
4、斜齿轮传动的标准中心距为 a = (d1+d2)/2 = mt(z1+z2)/2 = mn(z1+z2)/(2 cosβ ) 斜齿轮的中心距与 m Z β 有关
Hale Waihona Puke §10-9 圆锥齿轮传动圆锥齿轮传动是用来传递两相交轴之间的运动和动力的，一般。 Σ = 90 。通常取圆锥齿轮大端的参数为标准值，
渐开线直齿圆柱齿轮的啮合传动(4/6) 渐开线直齿圆柱齿轮的啮合传动
3．连续传动条件重合度 εα = B1B2 /pb ≥1 重合度εα 的计算 εα= [z1(tanαa1 － tanα′) +z2(tanαa2 － tanα′)]/(2π) 结论重合度εα 与模数m无关，而随着齿数z的增多而增大，还随啮合角α′减少和齿顶高系数ha*的增大而加大，
§10-5 渐开线直齿圆柱齿轮的啮合传动
1．齿轮正确啮合的条件 m1 = m2 = m α1 = α2 = α

第8章齿轮机构及其设计1、本章的教学要求1）了解齿轮机构的类型及

第8章齿轮机构及其设计1、本章的教学要求1）了解齿轮机构的类型及应用。

2）了解齿廓啮合基本定律。

3）深入理解渐开线圆柱齿轮的啮合特性及渐开线直齿轮的正确啮合条件、连续传动条件等。

4）熟悉渐开线齿轮各部分名称、基本参数及各部分几何尺寸的计算。

5）了解渐开线齿廓的范成切齿原理及根切现象；渐开线标准齿轮的最少齿数；渐开线齿轮的变位修正和变位齿轮传动的概念。

6）了解斜齿圆柱齿轮齿廓曲面的形成、啮合特点，并能计算标准斜齿圆柱齿轮的几何尺寸。

7）对蜗轮蜗杆的传动特点有所了解。

2、本章讲授的重点本章讲授的重点是渐开线直齿圆柱齿轮外啮合传动的基本理论和设计计算。

对于其他类型的齿轮及其啮合传动，除介绍它们与直齿圆柱齿轮啮合传动的共同特点外，则着重介绍它们的特点。

3、本章的教学安排本章为10学时。

其中讲授8学时，安排两个实验（2学时）：齿轮范成实验和齿轮基本参数测绘。

4、教学手段利用多媒体课件和传统教学方法相结合的手段。

5、注意事项1）渐开线标准直齿圆柱齿轮各部分的名称和几何尺寸计算，是本章最基本的内容，要求学生必须熟悉和掌握。

特别注意关于“分度圆”的概念。

要注意模数、压力角、齿顶高系数和顶隙系数都已标准化。

2）注意搞清一些比较容易混淆的概念：分度圆与节圆；啮合角与压力角；正确啮合条件与连续传动条件。

注意说明我们研究一对齿轮的中心距时，是从无侧隙为出发点的，而实际上一对齿轮传动时，为了便于在相互啮合的齿廓间进行润滑，及避免轮齿因摩擦发热而膨胀所引起的挤轧现象，在两轮的齿侧之间是有空隙的，但这种侧隙一般都很小，通常是由齿形公差来保证的。

而按名义尺寸而言，两轮的齿侧间隙为零。

3）注意提示学生，对于齿轮的变位修正目的，必须有一个全面的认识。

齿轮的变位修正，除了对于Z < Z min 的齿轮可以避免根切外，对于Z > Z min 的齿轮仍然可以进行变位修正，其主要目的是通过变位修正，可以提高承载能力，改善齿轮的工作性能，或满足中心距要求等。

《机械基础》(赵学主编)教案：3-2 渐开线齿廓

＝＝
而∵△ ∽△
＝，即＝
∴ ＝＝＝＝常量
渐开线齿轮传动的传动比等于主动轮和从动轮基圆半径的反比。由于两啮合齿轮的基圆半径是定值，所以渐开线齿轮传动的传动比能保持恒定不变。
2、中心距的可分离性
由于齿轮传动的传动比仅与两轮基圆半径有关，而与两轮的中心距无关，所以对于基圆半径已确定的齿轮副，其传动比大小不受两轮安装时中心距误差的影响，这一啮合特性称为渐开线齿轮传动的可分离性。
使用挂图进行讲解：渐开线、渐开线基圆。
以渐开线作为齿廓曲线的齿轮称为渐开线齿轮。
2、渐开线的性质
（1）发生线沿基圆上滚过的线段长度NK等于基圆上被滚过的弧长NC；
（2）渐开线上任意一点的法线必定与基圆相切；
（3）渐开线的形状取决于基圆的大小；基圆越大，渐开线越平直；如图4－4。（4）渐开线上各点的曲率半径不相等；离基圆越远，则曲率半径越大，渐开线越趋于平直；
（5）渐开线上各点处的齿形角不相等。
（6）基圆内无渐开线；
由图3－13所示，在直角三角形ONK中，＝＝
三、渐开线齿廓的啮合特性
通过对图4－6讨论，阐明节点、节圆和啮合角的概念。节点、节圆和啮合角只有在一对齿轮啮合时才存在，单个齿轮不存在。
渐开线齿廓啮合具有以下特性：
1、能保证瞬时传动比的恒定
齿轮传动时，两轮在P点的线速度相同，即：＝
二、渐开线的形成及性质
三、Байду номын сангаас开线齿廓的啮合特性
教学
反思
注意各种知识点的实际应用，注重在实践中应用所学理论知识。
关
键
掌握渐开线的性质及啮合性质。
教学内容
教法
学法
时间
分配
组织教学：

渐开线标准齿轮的啮合

O1 ω1
B2 N1
K
定义：实际啮合线B1B2 与基圆齿距Pb比值。
ω2
重合度的大小表示一对齿轮传动过程
中，同时在啮合线上轮齿啮合的对数它，是齿
O2
轮承载能力大小和平稳性好坏的一个重要指
标。
渐开线标准齿轮的啮合
第三节连续传动条件及重合度
二、连续传动条件及重合度
2、连续传动条件为保证连续传动，要求： B1B2≥ pb
3、重合度 ε
pb
N2 B1
O1 ω1
B2 N1
K
连续传动条件是： ε≥1 （理论上）
ω2
为保证可靠工作，工程上要求：ε≥>[1ε] 1.1～1.4
表 [ε]的推荐值：
O2
使用场合一般机械制造业汽车拖拉机金属切削机
[ε]
1.4
1.1～1.2
1.3
总结
1.正确啮合的条件 m1 m2 m
1 2
已经从B2点进入啮合。 B1B2 > pb
当前一对齿到B1点将要
NN B1
22
脱离啮合时，后一对齿正好从B2点进入啮合。 B1B2 = pb
渐开线标准齿轮的啮合
第三节连续传动条件及重合度
二、连续传动条件及重合度 2、连续传动条件
为保证连续传动，要求： B1B2≥ pb
3、重合度 ε
pb
N2 B1
N1N2——理论上可能的最
长啮合线段--理论啮合线段。
B2
NN
11
设设设计计计：：：潘潘潘存存存云云云
NN B1
22
N1、N 2 －啮合极限点
渐开线标准齿轮的啮合
第三节连续传动条件及重合度

机械原理-渐开线齿轮啮合传动满足的条件_二__连续传动条件

B1
PB2 B2 N1 PN1 rb1 (tan a1 tan )
B1 B2 rb1 (tan a1 tan ) rb 2 (tan a 2 tan )
zm pb m cos , rb cos 2
rb1 a1
'
ra1
重合度的意义：表明同时参与啮合的轮齿对数的平均值。
重合度不仅是齿轮传动的连续性条件，而且是衡量齿轮承载能力和传动平稳性的重要指标。
双齿啮合区
K K'
双齿啮合区
单齿啮合区
小
结
连续传动条件
一对齿轮的啮合过程: ——实际啮合线段 ——理论啮合线段连续传动条件：
B1B2 1 pb
重合度计算公式：
1
o1
o2
ra 2
' a 2 rb 2
P K
B2
2
N2
1 [ z1 (tan a1 tan ) 2 z2 (tan a 2 tan )]
式中
N1
B1
rb1 a1
'
ra1
1
o1
rb1 arccos r1 rb1 a1 arccos ra1 rb 2 a 2 arccos ra 2
第 7 章齿轮机构及其设计
齿轮机构的应用、特点与分类
齿廓啮合基本定律
渐开线的性质与方程
渐开线齿轮的尺寸参数
渐开线齿廓的啮合特点
渐开线齿轮啮合传动满足的条件（一）
渐开线齿轮啮合传动满足的条件（二）渐开线齿轮啮合传动满足的条件（三）
第 7 章齿轮机构及其设计
齿轮与齿条啮合传动

第三节渐开线齿廓的形成及特点

O1
N1
C
N
K
O2
二、渐开线齿廓的啮合特点 ——满足齿廓啮合基本定律
渐开线齿轮的传动比
基圆的公切线是一条定直线，与连心线只能交于固定点C，因此能实现传动比恒定的传动。
O1
N1
C
N
i
O2 C O1C
K
N
r '2 r '1 rb 2 rb 1
N2
O2
二、渐开线齿廓的啮合特点 ——满足齿廓啮合基本定律
二、渐开线齿廓的啮合特点 ——中心距可分性
当齿轮制成后，基圆半径rb已确定，传动比i=rb2 /rb1, 即使有制造、安装的误差或轴承磨损导致中心距变更时，其传动比仍保持不变，这一特性称为中心距可分性。它给齿轮的制造和安装带来了很大的方便。由于上述特性，工程上广泛采用渐开线齿廓曲线。
i
O2C O1C

r '2 r '1

rb 2 rb1
渐开线齿轮的传动比等于节圆半径的反比，也等于基圆半径的反比。啮合点一定在公切线 N1N2 上移动， N1N2 称为啮合线。过节点作的圆称为节圆,一对齿轮啮合时才出现节圆,单个齿轮没有节圆,也就不存在节点。一对齿轮传动时，相当于它的一对节圆作纯滚动。
二、渐开线齿廓的啮合特点 ——中心距可分性
齿轮工、车工和铣工配换交换齿轮时，都凭目测安装，安装中心距与设计中心距可能会有误差，这对齿轮传动质量会有影响吗？
1 r rb 2 i12 2 r rb1
' 2 ' 1
齿轮制成后，基圆半径已定，即使中心距稍有变动，传动比仍不变。
二、渐开线齿廓的啮合特点

一对渐开线齿廓啮合时,接触点在啮合线上移动的距离( )对应时间内基圆转过的弧

一对渐开线齿廓啮合时,接触点在啮合线上移动的距离( )对应
时间内基圆转过的弧
渐开线是一种特殊的齿廓，它能够实现牙轮间的精确啮合运动。

在啮合时，接触点会在啮合线上移动，这一过程中基圆也会转动。

接下来我们将详细介绍接触点移动距离与基圆转动弧的相关参考内容。

渐开线的特点是，牙轮齿廓与圆周的半径不同，因此，在啮合时切线速度不同。

而在接触点处，切向速度一定，且沿着啮合线移动。

因此，我们可以通过计算接触点移动的距离，来确定基圆转动的弧长。

当两个渐开线齿轮啮合时，接触点的运动可以简化为一个圆周运动。

如果齿轮转速为w，那么接触点在单位时间内的移动距离v可以表示为v=wr，其中r是接触点到齿轮中心的距离。

同时，基圆的转动弧长也是基于齿轮转速w来计算的。

如果
齿轮的模数为m，喉部圆的半径为r，那么基圆半径为rm。

因此，在一个周期内，基圆转过的弧长s可以表示为s=2πrm。

接触点在啮合线上移动距离与基圆转动弧的关系如下：接触点在单位时间内移动的距离与基圆转一周所需时间相等。

因此，接触点在啮合过程中的轨迹和基圆在旋转时的轨迹是相同的。

这种精确的啮合方式，不仅可以保持齿轮精确的传动比，还能够减小齿轮间的摩擦和磨损。

这样，渐开线齿轮更能够满足高精度传动的要求。

总之，渐开线齿廓的特殊设计使得齿轮之间的啮合更为精确和稳定。

接触点在啮合过程中的移动距离和基圆在转动时所需的弧长具有相同的参考内容，这种关系为我们分析和控制齿轮之间的传动提供了有效的理论支撑。