机械刚体动力学26页PPT
合集下载
《刚体动力学 》课件

牛顿第二定律
物体的加速度与作用在物 体上的力成正比,与物体 的质量成反比。
牛顿第三定律
对于任何两个相互作用的 物体,作用力和反作用力 总是大小相等,方向相反 ,作用在同一条直线上。
刚体的平动
刚体的平动是指刚体在空间中 的位置随时间的变化而变化, 而刚体的形状和大小保持不变
的运动。
刚体的平动具有三个自由度 ,即三个方向的平动。
05
刚体的动力学方程
刚体的动力学方程
牛顿第二定律
刚体的加速度与作用力成正比,与刚体质量 成反比。
刚体的转动定律
刚体的角加速度与作用力矩成正比,与刚体 对转动轴的转动惯量成反比。
刚体的动量方程
刚体的动量变化率等于作用力对时间的积分 。
刚体的自由度与约束
自由度
描述刚体运动的独立变量,如平动自由度和转动 自由度。
约束
限制刚体运动的条件,如固定约束、滑动约束等 。
约束方程
描述刚体运动受约束的数学表达式。
刚体的动力学方程的求解方法
解析法
通过代数运算求解动力学方程,适用于简单问 题。
数值法
通过迭代逼近求解动力学方程,适用于复杂问 题。
近似法
通过近似模型求解动力学方程,适用于实际问题。
06
刚体动力学中的问题与实例 分析
人工智能和机器学习的发展将为刚体 动力学的研究提供新的思路和方法, 有助于解决复杂动力学问题。
感谢您的观看
THANKS
船舶工程
在船舶工程中,刚体动力学 用于研究船舶的航行稳定性 、推进效率以及船舶结构的 安全性等。
兵器科学与技术
在兵器科学与技术领域,刚 体动力学用于研究弹药的发 射动力学、火炮的射击精度 和稳定性等。
刚体定轴转动的动能定理 ppt课件

dt 12
dt
考虑到 t
dr g cost 7lg cos(12 v0 t)ຫໍສະໝຸດ dt 224 v0
7l
上页 下页 返回 结束
第七章 刚体力学 作业: P256 7.4.2 7.5.1
上页 下页 返回 结束
O
上页 下页 返回 结束
第七章 刚体力学
[解](1)由机械能守恒得
m ghc
1 2
I 2
hc
1 2
l
I 1 ml2 3
联立得
3g
l
O Ep=0 C
v l 3gl
上页 下页 返回 结束
(2)根据质心运动定理
FN W mac
分量式
FNn
m
g
m
vc2 rc
mvM
l 2
I
2mu
l 2
1 ml 2
12
1 2
ml 2
解得
mvMl 2
ml 2 12 ml 2 2
6m(2gh)1 2 (m 6m)l
M
N
C
B
l
h A
l/2
上页 下页 返回 结束
第七章 刚体力学 演员N以u起跳,达到的高度,由机械能守恒:
h u 2 l 2 2 ( 3m )2 h
第七章 刚体力学
角动量守恒条件:
M 0
刚体所受的合外力矩为零
若I不变,ω不变; 若I变,ω也变,但 L I 不变.
内力矩不改变系统的角动量.
在冲击等问题中,因内力矩远大于外力矩 ,此时, 角动量守恒。
《刚体动力学》课件

动量定理公式:Ft=mv
单击此处输入你的项正文,文字是您思想的提炼。
应用场景:碰撞、打击、爆炸等 角动量定理 角动量定理
定义:角动量是物体转动惯量和角速度的乘积 单击此处输入你的项正文,文字是您思想的提炼。
角动量定理公式:L=Iω
单击此处输入你的项正文,文字是您思想的提炼。
应用场景:行星运动、陀螺仪等
刚体的滚动和滑动摩擦
刚体滚动:刚体在平面内绕固定点转动,滚动摩擦力产生的原因和影响
刚体滑动摩擦:刚体在平面内滑动时产生的摩擦力,滑动摩擦系数与接触面材料和粗糙度等因素 的关系
刚体滚动和滑动摩擦的应用实例:例如,汽车轮胎与地面之间的滚动摩擦力,以及机械零件之间 的滑动摩擦力等
刚体滚动和滑动摩擦的实验研究:通过实验研究刚体滚动和滑动摩擦力的影响因素和规律,为实 际应用提供理论支持
04
刚体动力学基本原理
牛顿第二定律
定义:物体加速度的大小跟作用 力成正比,跟物体的质量成反比
应用:解释物体运动状态变化的 原因
添加标题
添加标题
公式:F=ma
添加标题
添加标题
注意事项:只适用于宏观低速运 动的物体
动量定理和角动量定理
定义:动量是物体质量与速度的乘积
单击此处输入你的项正文,文字是您思想的提炼。
刚体动力学研究内容
刚体的定义和性质 刚体运动的基本形式 刚体动力学的基本方程 刚体动力学的研究方法
刚体动力学发展历程
早期发展:古代力学对刚体的研究 经典力学时期:牛顿、伽利略等经典力学大师对刚体动力学的研究 弹性力学时期:弹性力学的发展对刚体动力学的影响 现代发展:计算机技术和数值模拟方法在刚体动力学中的应用
课程内容:刚体 的平动、转动、 碰撞等动力、力学等相关专 业的本科生和研 究生
单击此处输入你的项正文,文字是您思想的提炼。
应用场景:碰撞、打击、爆炸等 角动量定理 角动量定理
定义:角动量是物体转动惯量和角速度的乘积 单击此处输入你的项正文,文字是您思想的提炼。
角动量定理公式:L=Iω
单击此处输入你的项正文,文字是您思想的提炼。
应用场景:行星运动、陀螺仪等
刚体的滚动和滑动摩擦
刚体滚动:刚体在平面内绕固定点转动,滚动摩擦力产生的原因和影响
刚体滑动摩擦:刚体在平面内滑动时产生的摩擦力,滑动摩擦系数与接触面材料和粗糙度等因素 的关系
刚体滚动和滑动摩擦的应用实例:例如,汽车轮胎与地面之间的滚动摩擦力,以及机械零件之间 的滑动摩擦力等
刚体滚动和滑动摩擦的实验研究:通过实验研究刚体滚动和滑动摩擦力的影响因素和规律,为实 际应用提供理论支持
04
刚体动力学基本原理
牛顿第二定律
定义:物体加速度的大小跟作用 力成正比,跟物体的质量成反比
应用:解释物体运动状态变化的 原因
添加标题
添加标题
公式:F=ma
添加标题
添加标题
注意事项:只适用于宏观低速运 动的物体
动量定理和角动量定理
定义:动量是物体质量与速度的乘积
单击此处输入你的项正文,文字是您思想的提炼。
刚体动力学研究内容
刚体的定义和性质 刚体运动的基本形式 刚体动力学的基本方程 刚体动力学的研究方法
刚体动力学发展历程
早期发展:古代力学对刚体的研究 经典力学时期:牛顿、伽利略等经典力学大师对刚体动力学的研究 弹性力学时期:弹性力学的发展对刚体动力学的影响 现代发展:计算机技术和数值模拟方法在刚体动力学中的应用
课程内容:刚体 的平动、转动、 碰撞等动力、力学等相关专 业的本科生和研 究生
《大学物理期末复习》刚体动力学课件

总结词
掌握弹性力对刚体运动的影响
详细描述
弹性力是刚体动力学中另一个重要的问题。解决这类问题需要掌握弹性力的计算方法, 包括胡克定律和弹性常数的概念,以及弹性力在不同运动状态下对刚体运动的影响。同 时,还需要考虑弹性力与刚体质量、加速度等因素的关系,以及弹性力对刚体振动和稳
定性的影响。
01
02
03
阻尼振动定义
刚体在受到阻尼作用下的 振动状态。
阻尼振动特点
振动的能量逐渐减小,最 终趋向于静止状态。
阻尼振动方程
通过求解刚体的运动方程 ,可以得到阻尼振动的解 。
05
刚体动力学中的常见问题 与解决方法
刚体在非惯性系中的运动问题
总结词
理解非惯性系中刚体的运动规律
详细描述
刚体在非惯性系中的运动问题主要涉及到相对运动和科里奥利力。解决这类问题需要理解非惯性系中 刚体的运动规律,掌握科里奥利力的计算方法,以及如何应用这些概念来分析具体的物理现象。
在实际应用中,可以通过合理设计结构、选择合适的材料、加强维护保养等方式来提高刚体的平衡与稳 定性。
刚体的平衡与稳定问题也是物理学中的一个重要研究领域,对于深入理解力学原理、发展新的技术手段 等方面具有重要意义。
04
刚体的振动与阻尼
刚体的自由振动
自由振动定义
刚体在没有任何外力作用下的振动状态。
自由振动特点
振动的周期和振幅与初始条件有关,不受外力影响。
自由振动方程
通过求解刚体的运动方程,可以得到自由振动的解。
刚体的受迫振动
1 2
受迫振动定义
刚体在外力作用下的振动状态。
受迫振动特点
振动的周期和振幅与外力有关,与初始条件无关 。
掌握弹性力对刚体运动的影响
详细描述
弹性力是刚体动力学中另一个重要的问题。解决这类问题需要掌握弹性力的计算方法, 包括胡克定律和弹性常数的概念,以及弹性力在不同运动状态下对刚体运动的影响。同 时,还需要考虑弹性力与刚体质量、加速度等因素的关系,以及弹性力对刚体振动和稳
定性的影响。
01
02
03
阻尼振动定义
刚体在受到阻尼作用下的 振动状态。
阻尼振动特点
振动的能量逐渐减小,最 终趋向于静止状态。
阻尼振动方程
通过求解刚体的运动方程 ,可以得到阻尼振动的解 。
05
刚体动力学中的常见问题 与解决方法
刚体在非惯性系中的运动问题
总结词
理解非惯性系中刚体的运动规律
详细描述
刚体在非惯性系中的运动问题主要涉及到相对运动和科里奥利力。解决这类问题需要理解非惯性系中 刚体的运动规律,掌握科里奥利力的计算方法,以及如何应用这些概念来分析具体的物理现象。
在实际应用中,可以通过合理设计结构、选择合适的材料、加强维护保养等方式来提高刚体的平衡与稳 定性。
刚体的平衡与稳定问题也是物理学中的一个重要研究领域,对于深入理解力学原理、发展新的技术手段 等方面具有重要意义。
04
刚体的振动与阻尼
刚体的自由振动
自由振动定义
刚体在没有任何外力作用下的振动状态。
自由振动特点
振动的周期和振幅与初始条件有关,不受外力影响。
自由振动方程
通过求解刚体的运动方程,可以得到自由振动的解。
刚体的受迫振动
1 2
受迫振动定义
刚体在外力作用下的振动状态。
受迫振动特点
振动的周期和振幅与外力有关,与初始条件无关 。
大学物理第三章刚体力学PPT课件

精选
7
F is iin fis iin m ir i
两边同乘ri,得
F ir i siin fir i siin m ir i2
上式左边第一项为外力Fi对转轴的力矩,而第二项是 内力fi 对转轴的力矩。对刚体的所有质点都可写出类 似上式的方程,求和得
F ir is ii n fir is ii n ( m ir i 2 )
密度为,则dm=dx,有:
Ox
dx
l
J0r2dm ll2 2x2dx1l32 1 1m 22 l
(2)当转轴通过棒的一端A并与棒垂直时:
JAr2dm0 lx2dx3 l31 3m2l
精选
12
例2 求质量为m、半径为R、厚 为h的均质圆盘对通过盘心并与 盘面垂直的轴的转动惯量。
解:如图所示,将圆盘看成许多薄圆环组成。取任一 半径为r,宽度为dr的薄圆环,它的转动惯量为:
转动惯量与刚体的大小形状、质量分布以及转
轴的位置等有关。
精选
9
一般的情况下刚体质量是连 续分布的,把它分割成无限多个 微小部分,其中质量为dm的小块 到转轴的垂直距离为r,则它对该 转轴的转动惯量为
dJr2dm
r dm
积分得到整个刚体对相应转轴的转动惯量为
J r2dm
精选
10
常见刚体的转动惯量
MF 2dF 2rsin
精选
5
若F位于转动平面内,则上式简化为
MFd Fsri n
力矩是矢量,在定轴转动中, 力矩的方向沿着转轴,其指向 可按右手螺旋法则确定:右手 四指由矢径r的方向经小于的 角度转向力F方向时,大拇指的 指向就是力矩的方向。根据矢 量的矢积定义,力矩可表示为:
M rF
机械动力学基础PPT学习教案

其偏心的质量可能分布在几个不同的回转平
面内在,这如种图情况所下示,凸即使轮转轴子。的质
心位于回转轴线上,满足了静平衡的
条件,但由于各偏心质量所产生的离
心惯性力不在同一回转平面内,因而
将形成惯性力偶矩,仍会在支承中引
起附加的动载荷和造成机械振动。这
类转子的不平衡状态称为动不平衡,
而对其平衡称为动平衡。 第10页/共42页
为了使该空间力系及由其各力构成的惯性力偶矩得以平 衡,我们可以根据转子的结构情况,选定两个平衡基面Ⅰ和 Ⅱ。根据理论力学中一个力可以分解为与其相平行的两个分 力的原理,将上述各个离心惯性力分别分解到平衡基面Ⅰ和
Ⅱ上。当转子以等角速度 回转时,这些偏心质量所产生的
离心惯性力 P1 、P2 、P3 将形成一个空间力系。
Wd = Wr + W f + E
第16页/共42页
2.稳定运行阶段
机械系统速度波动及调节
起动阶段完成之后,机械进入稳定运行阶段。此时,机械原
动件以平均角速度 m 作稳定运转。此时E =0
一般情况下,在该阶段机械原动件的角速度 会出现不大 的周期性波动,即在一个周期T内,各个瞬时 略有升降,但
p 的方向随转子的转动而发生周期性变化。 对于转子的平衡,我们首先在设计时就需要根据转子的 结构和质量分布等情况进行平衡计算,使其在工作时的惯性力 在理论上达到平衡。至于因制造不精确和材质不均匀等因素而 导致的不平衡,则需要利用实验的方法加以平衡。
第5页/共42页
刚性转子的平衡
一) 转子的平衡计算
的角加速度d 减小,从而使机械的运转趋于平稳。
dt
第22页/共42页
机械系统速度波动及调节
产生周期性速度波动的原因
《物理刚体力学》课件

体质量乘以角速 度乘以旋转半径。
角动量守恒的条 件:刚体在运动 过程中,不受外 力矩作用,或者 外力矩的矢量和 为零。
角动量守恒的应用: 在物理学、工程学 等领域,角动量守 恒定律被广泛应用 于分析刚体的运动 状态和设计机械设 备。
刚体的振动与波 动
体育器材:篮球架、足球 门、单杠等体育器材的结 构和支撑
医疗设备:手术床、轮椅、 担架等医疗设备的支撑和 连接
电子产品:手机、电脑、 电视等电子产品的外壳和 框架
刚体在体育运动中的应用
篮球:篮球架、篮球板等设备都是 刚体,它们需要承受运动员的撞击 和冲击。
田径:田径运动中的起跑器、跳高 杆等设备也是刚体,它们需要承受 运动员的撞击和冲击。
刚体在工程中的应用:设计、制造和维护各种机械设备,如汽车、飞机、桥梁等
刚体在生物力学中的应用:研究人体骨骼、肌肉等组织的力学性能,为医疗、康复等领域提 供科学依据
感谢您的观看
汇报人:PPT
添加标题
添加标题
添加标题
添加标题
转动惯量:刚体转动时,其转动惯 量与质量、形状、转动轴的位置有 关。
转动定律的局限性:转动定律只适 用于刚体,不适用于非刚体。
刚体的转动惯量
定义:刚体转动惯量是刚体转动时,其角动量与角速度的比值 公式:I=mr^2,其中m是刚体质量,r是刚体到转轴的距离 应用:刚体的转动惯量在物理学、工程学等领域有广泛应用 影响因素:刚体的形状、质量分布、转轴位置等因素都会影响其转动惯量
消失
基本假设:物体 在受到外力作用 时,其运动状态 保持不变,即物 体在受到外力作 用时,其速度、 加速度和位置保
持不变
局限性:刚体 力学只适用于 刚体,不适用 于流体、弹性 体等非刚体物
角动量守恒的条 件:刚体在运动 过程中,不受外 力矩作用,或者 外力矩的矢量和 为零。
角动量守恒的应用: 在物理学、工程学 等领域,角动量守 恒定律被广泛应用 于分析刚体的运动 状态和设计机械设 备。
刚体的振动与波 动
体育器材:篮球架、足球 门、单杠等体育器材的结 构和支撑
医疗设备:手术床、轮椅、 担架等医疗设备的支撑和 连接
电子产品:手机、电脑、 电视等电子产品的外壳和 框架
刚体在体育运动中的应用
篮球:篮球架、篮球板等设备都是 刚体,它们需要承受运动员的撞击 和冲击。
田径:田径运动中的起跑器、跳高 杆等设备也是刚体,它们需要承受 运动员的撞击和冲击。
刚体在工程中的应用:设计、制造和维护各种机械设备,如汽车、飞机、桥梁等
刚体在生物力学中的应用:研究人体骨骼、肌肉等组织的力学性能,为医疗、康复等领域提 供科学依据
感谢您的观看
汇报人:PPT
添加标题
添加标题
添加标题
添加标题
转动惯量:刚体转动时,其转动惯 量与质量、形状、转动轴的位置有 关。
转动定律的局限性:转动定律只适 用于刚体,不适用于非刚体。
刚体的转动惯量
定义:刚体转动惯量是刚体转动时,其角动量与角速度的比值 公式:I=mr^2,其中m是刚体质量,r是刚体到转轴的距离 应用:刚体的转动惯量在物理学、工程学等领域有广泛应用 影响因素:刚体的形状、质量分布、转轴位置等因素都会影响其转动惯量
消失
基本假设:物体 在受到外力作用 时,其运动状态 保持不变,即物 体在受到外力作 用时,其速度、 加速度和位置保
持不变
局限性:刚体 力学只适用于 刚体,不适用 于流体、弹性 体等非刚体物
刚体运动学转动惯量定轴转动PPT课件
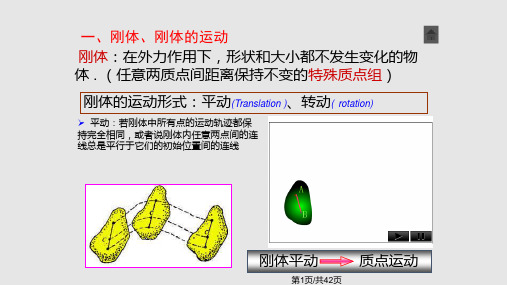
2π 2π
(2)t 6s时,飞轮的角速度
0
t
5
π
π 6
6
4
π
rad s1
(3)t 6s时,飞轮边缘上一点的线速度大小
v r 0.2 4π m s2 2.5 m s2
该点的切向加速度和法向加速度
at
r
0.2 (
π) 6
0.105 m s2
an r 2 0.2 (4π2 ) 31.6(m s2 )
面密度: , 面元:dS 体密度: , 体元:dV
注意
刚体对轴的转动惯量 J
与刚体总质量有关 与刚体质量分布有关 与转轴的位置有关
dm dm
dm
只有对于几何形状规则、质量连续且均匀分布 的刚体,才能用积分计算出刚体的转动惯量
第15页/共42页
注意:此
几
处的m是 挖掉后的
种
刚体质量。
常
公式是对 的
见
dr
r
R
角量系统
习题训练
例2 在高速旋转的微型电机里,有一圆柱形转子
可绕垂直其横截面通过中心的轴转动 . 开始时,它的角
速度0 0 ,经300s 后,其转速达到 18000r·min-1 . 已
知转子的角加速度与时间成正比 . 问在这段时间内,转
子转过多少转?
解 由题意,令 ct
d
,即
ct
,积
第11页/共42页
三、定轴转动刚体的角动量
转轴 ,z角速度
刚体上任一质点
转轴与其转动平面交点m
绕 圆周运动半径为
i
O
mi O
ri
z
转动
平面
o ri
vi
mi
(2)t 6s时,飞轮的角速度
0
t
5
π
π 6
6
4
π
rad s1
(3)t 6s时,飞轮边缘上一点的线速度大小
v r 0.2 4π m s2 2.5 m s2
该点的切向加速度和法向加速度
at
r
0.2 (
π) 6
0.105 m s2
an r 2 0.2 (4π2 ) 31.6(m s2 )
面密度: , 面元:dS 体密度: , 体元:dV
注意
刚体对轴的转动惯量 J
与刚体总质量有关 与刚体质量分布有关 与转轴的位置有关
dm dm
dm
只有对于几何形状规则、质量连续且均匀分布 的刚体,才能用积分计算出刚体的转动惯量
第15页/共42页
注意:此
几
处的m是 挖掉后的
种
刚体质量。
常
公式是对 的
见
dr
r
R
角量系统
习题训练
例2 在高速旋转的微型电机里,有一圆柱形转子
可绕垂直其横截面通过中心的轴转动 . 开始时,它的角
速度0 0 ,经300s 后,其转速达到 18000r·min-1 . 已
知转子的角加速度与时间成正比 . 问在这段时间内,转
子转过多少转?
解 由题意,令 ct
d
,即
ct
,积
第11页/共42页
三、定轴转动刚体的角动量
转轴 ,z角速度
刚体上任一质点
转轴与其转动平面交点m
绕 圆周运动半径为
i
O
mi O
ri
z
转动
平面
o ri
vi
mi
机械系统的动力学分析ppt课件

)
2
min
m (1
)
2
则得:
2 max
2 min
2
2 m
三、机械的调速
2、周期性速度波动的调节 讨论:
max min m
(1)由公式可知,若ωm一定,当δ↓,则ωmax-ωmin↓, 机械运转愈平稳;反之,机械运转愈不平稳。设计时为
使机械运转平稳,要求其速度不均匀系数不超过允许值。
即:
δ ≤[δ ]
为了便于讨论机械系统在外力作用下作 功和动能变化,将整个机械系统个构件的运 动问题根据能量守恒原理转化成对某个构件 的运动问题进行研究。为此引入等效转动惯 量(质量)、等效力(力矩)、等效构件的 概念,建立系统的单自由度等效动力学模型。
§17-2 机械的运转和速度波动的调节
二、机械系统动力学的等效量和运动方程 1、机械的运动方程式的一般表达式
计计算和强度计算的重要依据。 方法:图解法和解析法
§17-1 平面机构力分析
二、平面机构动态静力分析 1、构件惯性力的确定 1)作平面复合运动的构件
2)作平面移动的构件 惯性力P1=—mαs
3)绕定轴转动的构件 惯性力偶矩MI1
§17-2 机械的运转和速度波动的调节
一、机械的运转
机械运转中的功能关系
三、机械的调速
3、飞轮的设计原理 由于机械中其他运动构件的动能比飞轮的动能小
很多,一般近似认为飞轮的动能就等于整个机械所具
有的动能。即飞轮动能的最大变化量△Emax应等于机
械最W大m盈ax 亏 J功(E△mmWaaxx maxE。mmina)xmEax m2inmin12JJ(m2m2ax
2 min
Me = M1-F3(v3/ω1)
《刚体运动学》课件

总结词
理解定轴转动的定义和性质是掌握刚体运动学的基础。
详细描述
定轴转动是指刚体绕某一固定轴线旋转的刚体运动,具有角速度和角加速度两个重要的物理量。刚体在定轴转动 时,其上任意一点都以相同的角速度和角加速度绕轴线旋转。
定轴转动的合成与分解
总结词
掌握定轴转动的合成与分解是解决刚体动力学问题的关键。
详细描述
合成与分解的方法
通过选择合适的参考系和坐标系,利用矢量合成 和分解的方法进行计算。
刚体的定点平面运动
定义:刚体绕某一固定点在平 面内作圆周运动或椭圆运动。
描述参数:刚体的位置、速度 和加速度可以用定点、角位移 、角速度和角加速度等参数描
述。
动力学方程:根据牛顿第二定 律和刚体的转动定理,建立定 点平面运动的动力学方程。
在物理学中的应用
01
力学
刚体运动学是力学的一个重要分支,用于研究刚体的运动规律和力学性
质。通过刚体运动学分析,可以了解物体在不同力场作用下的运动状态
和变化规律。
02
天体物理学
在天体物理学中,刚体运动学用于研究天体的运动和演化。通过对天体
的刚体运动进行分析,可以了解天体的轨道、速度和加速度等运动参数
要点二
分解
空间运动的分解是指将一个复杂的运动分解为若干个简单 的运动。
刚体的定点空间运动
定义
刚体的定点空间运动是指刚体绕一个固定点在空间中的 旋转运动。
性质
定点空间运动具有旋转轴、旋转角速度和旋转中心等物 理量,其运动状态可以通过这些物理量来描述。
06
刚体运动学的应用
在工程中的应用
机械工程
刚体运动学在机械工程中广泛应用于机构分析和设计,如连杆机构、凸轮机构和齿轮机构等。通过刚体运动学分析, 可以确定机构的运动轨迹、速度和加速度,优化机构设计。
理解定轴转动的定义和性质是掌握刚体运动学的基础。
详细描述
定轴转动是指刚体绕某一固定轴线旋转的刚体运动,具有角速度和角加速度两个重要的物理量。刚体在定轴转动 时,其上任意一点都以相同的角速度和角加速度绕轴线旋转。
定轴转动的合成与分解
总结词
掌握定轴转动的合成与分解是解决刚体动力学问题的关键。
详细描述
合成与分解的方法
通过选择合适的参考系和坐标系,利用矢量合成 和分解的方法进行计算。
刚体的定点平面运动
定义:刚体绕某一固定点在平 面内作圆周运动或椭圆运动。
描述参数:刚体的位置、速度 和加速度可以用定点、角位移 、角速度和角加速度等参数描
述。
动力学方程:根据牛顿第二定 律和刚体的转动定理,建立定 点平面运动的动力学方程。
在物理学中的应用
01
力学
刚体运动学是力学的一个重要分支,用于研究刚体的运动规律和力学性
质。通过刚体运动学分析,可以了解物体在不同力场作用下的运动状态
和变化规律。
02
天体物理学
在天体物理学中,刚体运动学用于研究天体的运动和演化。通过对天体
的刚体运动进行分析,可以了解天体的轨道、速度和加速度等运动参数
要点二
分解
空间运动的分解是指将一个复杂的运动分解为若干个简单 的运动。
刚体的定点空间运动
定义
刚体的定点空间运动是指刚体绕一个固定点在空间中的 旋转运动。
性质
定点空间运动具有旋转轴、旋转角速度和旋转中心等物 理量,其运动状态可以通过这些物理量来描述。
06
刚体运动学的应用
在工程中的应用
机械工程
刚体运动学在机械工程中广泛应用于机构分析和设计,如连杆机构、凸轮机构和齿轮机构等。通过刚体运动学分析, 可以确定机构的运动轨迹、速度和加速度,优化机构设计。
演示文稿第七章刚体力学

M滚 FN —滚动摩擦因数,由实验测定.
第26页,共34页。
FN
FNO
W
FP
M滚
FN
O W FP
M滚 使物体角速度减小,则接触面各点有向前滑动趋势,从而 产生反向摩擦力(滚动摩擦)使物体减速.
滚动阻力因数´: / r, r是轮半径.
表7.2 是常见汽车轮在几种典型路面上的´ 值
第27页,共34页。
O
第10页,共34页。
[解] (1)由机械能守恒得
mghc
1 2
I 2
hc
1 2
l
I 1 ml 2 3
联立得
v l 3gl
FN
en
et
Ep=0
C
W
(2)根据质心运动定理
FN W mac
分量式
FNn
mg
m
vc2 rc
FNt mact
第11页,共34页。
杆处于铅直位置时不受力矩作用,由转动定理
如何理解滚动摩擦 << 滑动摩擦 ?
F
M滚
FN
C
W
Ff
F' A C
设滚子匀速滚动,则阻力和阻力矩分别为
Ff F FN W Ff r M滚 0 M滚 FN
联立得
F
Ff
r
FN
r
W
W
若滚子匀速平动 F FN W
表7.2与表3.2相比,有 F F
第28页,共34页。
§7.6 刚体的平衡
第20页,共34页。
[P239 例题2]质量为m的汽车在水平路面上急刹车,前后轮均 停止转动. 前后轮相距L,与地面的摩擦因数为 .汽车质心离 地面高度为h,与前轮轴水平距离为l .求前后车轮对地面的压力
《刚体力学》课件

刚体的转动
总结词
刚体的转动是指刚体绕着某一定点(称为转动中心)的旋转运动。
详细描述
刚体的转动是指刚体绕着某一定点(称为转动中心)的旋转运动。在转动过程中,刚体上任意一点绕着转动中心 作圆周运动,且该圆周运动的半径与刚体上该点到转动中心的距离相等。转动刚体的角速度、角加速度等都是标 量,其方向与转动方向相关。转动刚体的速度和加速度都是矢量,其方向垂直于转动平面。
《刚体力学》ppt课件
目录
• 刚体运动学 • 刚体动力学 • 刚体的平衡 • 刚体的转动惯量 • 刚体的角动量
01
刚体运动学
刚体的平动
总结词
刚体的平动是指刚体在空间中的移动,其上任意两点在同一直线上,且该直线与该刚体的转动轴平行 。
详细描述
刚体的平动是指刚体在空间中的移动,其上任意两点在同一直线上,且该直线与该刚体的转动轴平行 。平动刚体的运动轨迹是一条直线或一个平面图形,其上任意两点的相对位置保持不变。平动刚体的 速度和加速度都是矢量,其方向与平动刚体的移动方向一致。
描述了刚体绕质心转动的动量表现,是刚体动力学中的一个重要概念。
详细描述
动量矩是描述刚体绕质心转动的动量表现的一个物理量。在刚体动力学中,动量 矩是一个非常重要的概念,它与力矩、角速度和时间等物理量密切相关。根据动 量矩的定义,刚体的动量矩等于刚体的质量与角速度的乘积。
刚体的动能
总结词
描述了刚体运动过程中能量的表现形式 ,是刚体动力学中的一个重要概念。
刚体的定点运动
总结词
刚体的定点运动是指刚体绕着通过定点(称为动点) 且垂直于定直线(称为转动轴)的轴线的旋转运动。
详细描述
刚体的定点运动是指刚体绕着通过定点(称为动点) 且垂直于定直线(称为转动轴)的轴线的旋转运动。 在定点运动过程中,刚体上任意一点绕着动点作圆周 运动,且该圆周运动的半径与刚体上该点到动点的距 离相等。定点运动的角速度、角加速度等都是标量, 其方向垂直于转动平面。定点运动的刚体上任意一点 的线速度和角速度都与该点到转动轴的距离成正比。
《机械动力学》课件

求解方法
02
通过迭代法、图形解法、近似解法等求解。
应用领域
03
在化学、生物、经济等领域中广泛应用,如化学反应动力学、
生态学模型等。
离散化方法
定义
将连续的时间或空间离散化,将微分方程法、龙格-库塔法、改进的欧拉法等。
应用领域
在数值计算、计算机模拟等领域中广泛应用,如天气预报、流体 动力学模拟等。
模型建立提供依据。
实验结果与结论
实验结果
实验结果是通过实验观察和数据分析得出的结论,包括对机械系统动力学行为的描述和 解释。
实验结论
实验结论是对实验结果进行总结和归纳,指出实验的局限性和未来改进的方向,同时对 理论分析和模型建立提供支持和验证。
06 机械动力学的未来发展与挑战
新材料与新结构的应用
智能优化
利用人工智能技术进行机械系统优化设计,实现自适应 调整和智能控制,提高机械设备的稳定性和可靠性。
谢谢聆听
能量守恒定律
总结词
描述能量总量保持不变的定律
VS
详细描述
能量守恒定律指出,能量不能被创造或消 灭,只能从一种形式转化为另一种形式。 在机械动力学中,这个定律用于分析各种 运动形式的能量转化和守恒问题。
动能定理
总结词
描述物体动能变化与外力做功关系的定理
详细描述
动能定理指出,合外力对物体做的功等于物 体动能的增量。这个定理是分析机械运动状 态变化的重要工具,特别是在计算速度、加 速度和力之间的关系时非常有用。
要点一
新材料
随着科技的进步,新型材料如碳纤维、钛合金等在机械动 力学中得到广泛应用,这些材料具有高强度、轻量化的特 点,能够显著提升机械设备的性能和效率。
《刚体动力学》PPT课件
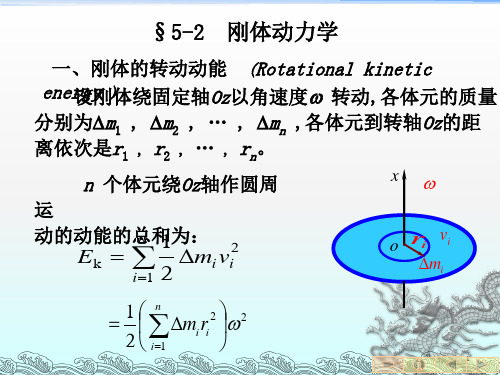
ox
l x
2
为转轴, 如图所示。在距离转轴为x 处取棒元dx,
其质量为
m dm dx
l
7
根据式(5-4), 应有
J
l / 2 l / 2
x
2
m l
dx
1 3
m l
x3
l /2 l / 2
1 ml2 8.3 102 kg m2 12
棒的转动动能为
Ek
1 2
J 2
1 0.083 632 J 2
(2) 闸瓦对飞轮施加的 摩擦力矩所作的功。
d
闸瓦
N
解:为了求得飞轮从制 飞轮
f
动到停止所转过的角度
和摩擦力矩所作的功A, 必须先求得摩擦力、摩擦力矩
和飞轮的角加速度。
27
闸瓦对飞轮施加的摩擦力的大小等于摩擦系数与
正压力的乘积
f N 0.50 500 N 2.5 102 N
方向如图所示。摩擦力相对z 轴的力矩就是摩擦
1.7 102J
8
例2 计算质量为m,长为l 的细棒绕一端的转动惯量。
解: J r2dm
z
dm dx m dx
l
Oo
dm
r2 x2
x dx
x
J l x2 m dx 1 m x3 l
0l
3l 0
J 1 ml2 3
对质量均匀分布的门对门轴的转动惯量也相同。
9
例5-3 如图半圆形匀质细杆,半径为 R,
cosi
因为dsi = ri d, 并且cosi = sini , 所以
dAi Firi sini d Mzid 19
dAi Firi sini d Mzid
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
谢谢!
机械刚体动力学
61、奢侈是舒适的,否则就不是奢侈 。——CocoCha nel 62、少而好学,如日出之阳;壮而夺帅也,匹夫不可夺志也。 ——孔 丘 64、人生就是学校。在那里,与其说好 的教师 是幸福 ,不如 说好的 教师是 不幸。 ——海 贝尔 65、接受挑战,就可以享受胜利的喜悦 。——杰纳勒 尔·乔治·S·巴顿
6、法律的基础有两个,而且只有两个……公平和实用。——伯克 7、有两种和平的暴力,那就是法律和礼节。——歌德
8、法律就是秩序,有好的法律才有好的秩序。——亚里士多德 9、上帝把法律和公平凑合在一起,可是人类却把它拆开。——查·科尔顿 10、一切法律都是无用的,因为好人用不着它们,而坏人又不会因为它们而变得规矩起来。——德谟耶克斯
