2015中环杯6年级答案
第 16届中环杯六年级选拔赛答案

第16届中环杯六年级选拔赛答案1. 计算:18110347535357⨯+⨯+⨯=________.【答案】232. 一项工作,甲单独完成需要6天,乙单独完成需要3天,那么甲、乙合作需要______天完成这项工作【答案】23. 某校六(1)班里的男生数量与女生数量之比为8:5。
某天,有12个男生代表六(1)班出去参加足球比赛了,班里剩下的男生数量与女生数量相等,则(1)班里一共有________个学生【答案】524. 下图是由黑色正六边形和白色正六边形组成的,整个图形往各个方向不断地重复下去。
整个平面上黑色正六边形数量占总体的______%.【答案】12.5 5. 将分数11024000化为有限小数,小数点后一共有________个数码【答案】136. 将+、-号填入下面算式的空格内:123456,可以得到_____种不同的值【答案】227. 在一个森林中,青蛙都是绿色或者蓝色的。
从去年到今年,蓝色青蛙的数量增加了60%,绿色青蛙的数量减少了60%。
今年蓝色青蛙与绿色青蛙的数量比与去年绿色青蛙与蓝色青蛙的数量比相同。
那么,今年青蛙的总数量比去年减少了________%【答案】208. 下图是五个半圆互相外切(如果两个圆只有一个交点,并且两圆圆心的距离等于两圆半径之和,就称这两个圆外切),每个半圆的半径均为2,那么阴影部分的周长为______(答案保留π)【答案】6π9. 从一个34⨯的正方形网格的左上角走到右下角,要求满足下面两个条件:(1)每次走动都走到相邻的小正方形内(所谓相邻就是指有一条公共边的两个小正方形)。
(2)所有小正方形都走到过,并且只能走到一次(左上角的小方格除了出发的时候,不能再次进入;右下角的小方格除了到达的时候,也不能重复进入)。
不同的走法有______种【答案】410. 如果将1234569910034343434⨯⨯⨯⨯⨯⨯⨯⨯ 化为qp的形式,其中,p q 为互质的正整数,p 的值为________. 【答案】7211. 四种瓷砖的尺寸为300300mm mm ⨯、300600mm mm ⨯、600600mm mm ⨯、600900mm mm ⨯。
15届中环杯B卷

列第十个图形需要
颗小石子遥
BBA A
伊
BA
A 99A
11A A
1阴A 阴A
第7题
第8题
二尧 填空题 B院渊每题 8 分袁共 32 分冤
9. 有一个正整数 n袁它的数码和与 n+1 的数码和都 可被 7 整除遥 那么袁 满足上述条件的 n 的最小值是
A
B
第 11 题
遥
10. 在某个年度里袁 每个月的某个相同的日期数都
第4题
格子里的字母连起来袁得到 BA NA NA 遥 不同的走法有 种渊注意袁同一个格子可以反复进入冤遥
7. 已知在图中的乘法算式中袁相同字母代表相同数字袁不同字母代
BA N A NA
表不同数字遥 那么袁A +B=
遥
NA N
8. 小恩在沙滩上用小石子排列出一些有趣的图形袁如图所示袁前四
第6题
个图形所用的小石子数分別是 1尧5尧12尧22遥 按此规律继续下去袁那么袁排
D
不是星期日遥 那么袁这个日期数可能是 渊如果是 25 号袁只需要填数字25冤遥
G AH
11. 如图 A袁一个 2伊10 的方格表用 1伊1 和 1伊2 的小
磁砖去覆盖 渊注意院 这里的 1伊2 小瓷砖必须横过来占 2
格尧竖过来占 1 格袁如图 B 所示袁不能旋转使用冤袁要求不
重不漏袁有
种不同的覆盖方法遥
10. 小黑尧小白各买了一些草莓遥 小黑买了 24 个袁如果小黑给
小白 9 个草莓袁小白的草莓数就是小黑的 4 倍遥 现在要使小黑的草
莓数是小白的 2 倍袁小白要吃掉自己的
个草莓遥
第9题
PDF created with pdfFactory Pro trial version
第 14 届“中环杯”中小学生思维能力训练活动六年级决赛答案

2 2 n 2 2 1 2 6 2 n n n 1 2 1 n n 1 2n 1 2 2 2 2 2 6 6 n n 1 2n 1 n n 2 n 1 6 6 n n 1 2n 1 n 2 6 2
3. 【答案】 8 【解答】设钱老师买了 x 本数学书, y 本物理书,根据题意,我们有
x y 7 7 6 y x y ,所以我们只要找到最小的 y ,使得 y 与 y 之间包含一个正整数即 y 6 6 x y 13 49 可。简单尝试一下,发现 6 ~ 7 之间没有任何正整数,而 7 ~ 之间含有数字 8 ,所以 x 8 6
n n 1 2
2
所以 12 2 22 32 2 42 52 2 62 2 202
20 212 4410 2
而前面还有一个 4410 x ,所以当 0 x 1 时,可以取到最小值。我们就取 x 0 ,此时
4410 x x 1 2 22 x 2 32 x 3 2 4 2 x 4 2 20 2 x 20 13 2 23 33 2 43 2 203 13 23 33 43 203 23 43 203 1 2 20 23 13 23 103
x 30 y 15
即加热 30 秒后往外倒 15 秒水,最少 45 秒后小明能喝到 30 C 的水 13. 【答案】 670 【解答】设总人数为 x ,每人分到的书的数量为 q ,余下的书的数量为 r ,则 2014 xq r ,由于 x 为三位数,所以 q 2 。如果 q 3 ,则 2014 xq r 3x x 671 ,由于 0 r x ,所以 r 670 ;所以,只要当 q 2 的时候,能够取到大于等于 670 的余数,那么就 不用考虑 q 3 的情况了。显然, 2014 672 2 670 ,此时取到余数 670 ,所以我们只要将 注意力集中在 q 2 的情况即可。 此时 2014 2x r ,由于 0 r x ,从而推出 x 的取值范围为 672 ~ 999 ,随着 x 的增大, r 在 减小,所以当 x 672 时,此时 r 最大,其最大值就是 670 14. 【答案】
2015年第十五届“中环杯”小学生思维能力训练活动初赛试卷(五年级答案及解析

2015年第十五届“中环杯”小学生思维能力训练活动初赛试卷(五年级)-学生用卷一、填空题共20题,共100 分1、已知,其中,是两个互质的正整数,则。
2、老师家里有五个烟囱,这五个烟囱正好从矮到高排成一排,相邻两个烟囱之间的高度差为厘米,其中最高的烟囱又正好等于最矮的两个烟囱的高度之和,则五个烟囱的高度之和是厘米。
3、已知,其中、、、是四个正整数,请你写出满足条件的一个乘法算式:。
4、一个长方体的长、宽分别为厘米、厘米,其体积的数值与表面积的数值相等,则它的高为厘米。
5、一次中环杯比赛,满分为分,参赛学生中,最高分为分,最低分为分(所有的分数都是整数),一共有个学生参加,那么至少有个学生的分数相同。
6、对个蛋黄月饼进行打包,一共有两种打包规格:大包装里每包有个月饼,小包装里每包有个月饼。
要求不能剩下月饼,那么一共打了个包。
7、小明和小红在米的环形跑道上跑步,两人从同一起点同时出发,朝相反方向跑,第一次和第二次相遇时间间隔秒,已知小红的速度比小明慢米/秒,则小明的速度为米/秒。
8、、、的因数个数相同,那么在具有这样性质的三个连续自然数、、中,的最小值是。
9、图中的正三角形与正六边形的周长相等,已知正三角形的面积是,则正六边形的面积为。
10、甲、乙、丙在猜一个两位数。
甲说:“它的因数个数为偶数,而且它比大。
”乙说:“它是奇数,而且它比大。
”丙说:“它是偶数,而且它比大。
”如果他们三个人每个人都只说对了一半,那么这个数是。
11、如图,正方形和正方形,他们的四对边互相平行,连接并延长交于点。
已知,三角形面积,三角形,则的长度为。
12、将个桃子分给若干个孩子,这些孩子得到的桃子数量是一些连续的正整数,则获得桃子数量最多的那个孩子最多可以得到个桃子。
13、定义,比如,若(其中为正整数,且)是完全平方数,比如时,,就是一个完全平方数,则所有满足条件的的和为。
14、小明将若干枚棋子放入如图所示的方格的小正方形内,每个小正方形内可以不放棋子,也可以放等于或多于枚的棋子。
2022-2023学年小学六年级奥数典型题测评卷14《等积变形》(解析版)

【六年级奥数举一反三—全国通用】测评卷14《等积变形》试卷满分:100分考试时间:100分钟姓名:_________班级:_________得分:_________一.选择题(共5小题,满分15分,每小题3分)1.(2014•迎春杯)如图,大正六边形内部有7个完全一样的小正六边形,已知阴影部分的面积是180平方厘米.那么大正六边形的面积是()平方厘米.A.240 B.270 C.300 D.360【分析】按题意,显然可以将图进行分割,分割后阴影部分有六个面积相等的小正六边形,而空白部分是3个面积相等的小正六边形,利用面积之比不难求得大正六边形的面积.【解答】解:如图所示,将图分割成面积相等的小正三角形,显然,图中的空白部分的面积和等于3个小正六边形.而阴影部分由6个小正六边形组成,所以,大正六边形是由9个小正六边形组成的.一个小正六边形的面积为:180÷6=30(平方厘米),大正六边形的面积为:30×9=270(平方厘米),故选:B.2.(2014•迎春杯)如图,大正方形的边长为14,小正方形的边长为10,阴影部分的面积之和是()A.25 B.40 C.49 D.50【分析】按题意,将图①逆时针旋转90°,阴影部分可拼成一等腰直角三角形,不难求得阴影部分的面积.【解答】解:根据分析,如下图所示,图①逆时针旋转90°,阴影部分可拼成一等腰直角三角形,S=142÷4=49故选:C.3.(2006•创新杯)图中,将两个正方形放在一起,大、小正方形的边长分别为10,6,则图中阴影部分面积为()A.42 B.40 C.38 D.36【分析】由图意可知:阴影部分的面积就等于两个正方形的面积和减去两个空白三角形的面积,利用正方形和三角形的面积公式即可求解.【解答】解:10×10+6×6﹣6×(10+6)÷2﹣10×10÷2=100+36﹣48﹣50=38答:阴影部分的面积是38.故选:C。
第十四届中环杯中小学生思维能力训练活动六年级决赛试卷及解析

12. 【答案】45 【解答】设加热 x 秒,往外倒水 y 秒,小明 x y 秒后可以喝到 30C 的水。
求(注意,要使得 7 | 66666a a 6 ,与题意不符)
7. 【答案】 6
【解答】设小正方形的边长为
x
,则
S1
2
1 2
12
x
12
x
144
x2
,而
S2
x2
,所以
S1
S2
144
。由于
S1
3S2
,所以
S2
1 4
144
36
,从而推出边长为 6
8. 【答案】
3 47 9 36 48 35 7469258 2 76 25 19 1 81 【解答】如图,从大数字开始分配位置,其中安排数字 6 的时候需要分类讨论,其它都是 直接定下来的。
那么袁五人中分数第二高的人的得分是
分遥
10. 4410 x + x -1 +2 伊 22 x -2 +32 x -3 +2 伊42 x -4
小值为
遥
+ 噎 +2 伊202 x - 20
的最
二尧动手动脑题院渊每小题 10 分袁共 50 分袁除第 15 题外袁请给出详细解题步骤遥 冤 11. 解方程院 x-1 + 2x-1 = x-3 遥
A B
2 6
或
A B
6 2
或
A B
3 5
或
A B
5 3
;
(7)当
D
9
时,
A B
1 8
或
A B
8 1
或
A B
2 7
2015~2016学年度新人教版六年级下册数学毕业考试试题及答案

2015-2016学年度第二学期小学六年级质量检测考试数 学 试 题本卷共6页,满分100分,考试时间90分钟。
注意事项:1.答题前,考生务必将自己的姓名、准考证号填写在答题卡上,并将条形码粘贴在答题卡指定的位置上。
2.选择题的答案选出后,必须使用2B 铅笔把答题卡上对应的答案标号涂黑。
如需改动,先用橡皮擦干净后,再选涂其他答案标号。
3.非选择题的答案,必须使用0.5毫米黑色墨水签字笔填写在答题卡对应的答题区域内,写在试卷、草稿纸上无效。
4.考生必须保持答题卡的整洁,考试结束后,上交答题卡。
一、判断题。
对的在答题卡上涂A ,错的涂B 。
(5分) 1、3.6÷0.3=12,所以3.6能被0.3整除。
( ) 2、假分数的倒数比1小。
( ) 3、5620÷70=562÷7,因为562除以7的商是80,余数是2,所以5620除以 70的商也是80,余数是2。
( ) 4、88008000的零都可以不读出来。
( )5、小圆半径2厘米,大圆半径5厘米,大圆面积与小圆面积之比是5:2。
( )二、选择题。
在下列各小题给出的答案中,有且只有一个正确答案,请将正确答案前的字母代号在答题卡上涂黑,涂错或不涂均为零分。
(10分) 6、A =2×2×3×3,那么A 有( )个因数。
A.2B.4C.9D.10 7、下面年份中,二月份是29天的年份是( )。
A.900年B.2015年C.2008年D.2014年 8、圆的面积与它的半径( )。
A.成正比例B.成反比例C.不成比例D.没有关系 9、下面的分数中不能化成有限小数的是( )。
A.1463B.2115C.2415D.3224 10、-2℃比-5℃高( )℃。
A.-3B.3C.7D.-7 11、如果a ÷b = 5(a 、b 是不为0的自然数),那么a 、b 的最大公因数是( )。
A 、aB 、bC 、5 D.0 12、一个比的前项扩大10倍,后项缩小10倍,则比值( )。
上海市六年级中环杯考试试卷大综合

六年级中环杯参考答案(本答案仅供参考)一.1. 2010;2. 2;3. 9;4. 364cm ;5. 14;6. 132160; 7.17600; 8. 136二、1.A 大;A-B=20111; 2. S=12.56;3. 甲:27元; 乙:18.2元; 4.上海市第九届“中环杯”六年级思维训练题1:计算: 。
2:a 、b 、c 、……j 十个字母分别代表0、1、2、……9十个数码中的某一个,已知下列算式:①h ×g=h ,②,③,④,⑤。
其中形如 的数表示十位数字为x ,个位数字是y 的两位数,则j= 。
3: 式中□分别将2、4、6、8填入。
最多可有 个算式。
4:纯循环小数 写成最简分数时,分子与分母之和是58,则。
5:现有自然数带余除法算式A ÷B=C ……8,如果其中A-B+C=2178,则A= 。
6:甲、乙两人在长400米的直路上来回慢跑,速度分别为3米/秒和2.5米/秒。
他们同时在两端相向出发,20分钟内共相遇次。
7:Q比P多20%,R比P少10%,则R比Q少x%,x= 。
8:15名运动员进行乒乓单循环赛,每名运动员与其它运动员赛了一场,如果1号运动员胜了x1场,2号运动员胜了x2场,……15号运动员胜了x15场,则x1+x2+……+x15= 。
9:某地举行篮球赛,规定每个队都要与其它各队比赛一场。
每胜一场得2分,败一场得0分,平一场各得一分。
在计算所有队得分总数时,统计四次得到不同结果:1054,1055,1056,1057。
经复核,其中只有一个数字是正确的,参加篮球赛共有个队。
10:如图:大长方形被两条直线分成三个小长方形和一个正方形,其中上面的两个小长方形的面积之和是13cm2,右面的两个小长方形的面积之和是33cm2,图中四个小图形的边长都是整数,且正方形面积最大,则原长方形面积为cm2。
11:求(共计2008层)的值为。
12:如图,由14个大小相同的正方形组成的图形,试问能不能把它们剪成7个相邻两个方格组成的长方形,说明你的理由。
第15届二年级中环杯决赛真题(2015年)
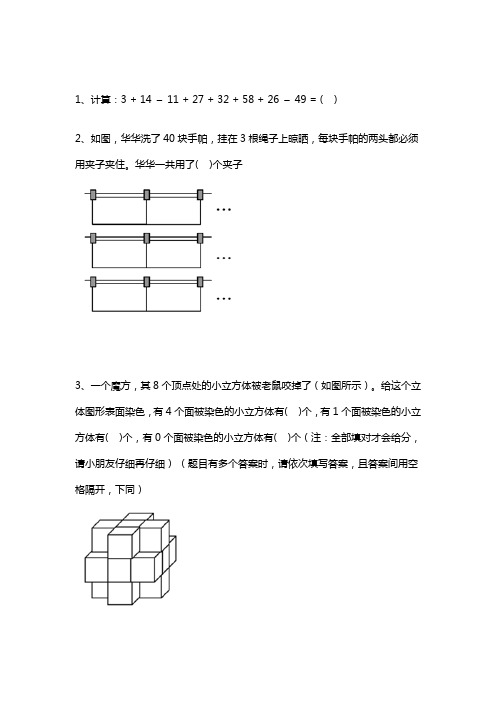
1、计算:3 + 14 –11 + 27 + 32 + 58 + 26 –49 = ( )2、如图,华华洗了40块手帕,挂在3根绳子上晾晒,每块手帕的两头都必须用夹子夹住。
华华一共用了( )个夹子3、一个魔方,其8个顶点处的小立方体被老鼠咬掉了(如图所示)。
给这个立体图形表面染色,有4个面被染色的小立方体有( )个,有1个面被染色的小立方体有( )个,有0个面被染色的小立方体有( )个(注:全部填对才会给分,请小朋友仔细再仔细)(题目有多个答案时,请依次填写答案,且答案间用空格隔开,下同)4、有两根一样长的绳子,第一根用去42 米,第二根用去12 米,第二根剩下来的绳子长度刚好是第一根剩下来绳子长度的4 倍。
原来两根绳子共长( )米。
5、甲、乙、丙三人中有一人是牧师,有一人是骗子,还有一人是赌徒。
牧师从不说谎,骗子总是说谎,赌徒有时说真话有时说谎话。
甲说:“我是牧师。
”乙说:“我是骗子。
”丙说:“我是赌徒。
”那么,三人中,( )是牧师。
6、小明在电脑上玩一种新型飞行棋,如果骰子掷到黑色数字,代表需要后退,掷到红色数字,代表需要前进(例如:黑色2代表后退2步,红色3代表前进3步)。
他掷了5 次,分别是黑色5、红色4、红色2、黑色3、红色1。
走完后发现自己在第6 格。
在第一次掷骰子前,他在第( )格7、一个盒子里有一些大小相同的球,其中白的有8个,黑的有9个,黄的有7个。
不许看球,每次拿一个,至少拿( )次才能保证三种颜色的球都有。
8、阿拉丁在藏宝库里发现了20条项链,其中有的项链只镶有2颗钻石,有的项链镶有5颗钻石,一共有79颗钻石。
那么镶有5颗钻石的项链有( )条9、如图所示,花花被邪恶的巫师关在了由26个正方形房间组成的迷宫里,边与边相邻的房间是互通的。
已知:黑色房间里有怪物,不能进;斜纹房间里住着巫师,只能进,不能出;灰色房间有机关,只能走一次;白色房间是安全的,可以重复走。
巫师告诉花花,走遍所有灰色房间,然后进入斜纹房间就可以离开。
6年级B卷答案

【解答】容易知道1050 250 550 ,它的因数有 5151 2601个, 2030 260 530 ,它的因
数有 6131 1891个,而 1050, 2030 250 530 ,它的因数有 5131 1581个,所以本题的
答案就是 260118911581 2911 个
360
3
4. 在某次宴会中,每位出席参加的男士都与 2 位女士握手,而每位女士则都与 3 位男士 握手。已知此次宴会的总参加人数超过 30 人但不足 40 人,请问:此次宴会总共有 ______位男士参加 【答案】21 【解答】根据“每位出席参加的男士都与 2 位女士握手”、“每位女士则都与 3 位 男士握手”以及总握手次数相等,我们推出男士与女士的人数之比为 3: 2 ,所以总 人数是 5 的倍数。在 30 到 40 之间 5 的倍数的只有 35,所以男士有 3 35 21
成三个数的乘积,这三个数之间的差距应该小于等于 2 。简单凑一下,发现 150 655,接下来分类讨论:
(1)如果 n 6 , 655 适合 n 12 n 的情况,所以有两个相邻的面被染色了;
(2)如果 n 7 , 655 适合 n 22 n 1 的情况,所以有五个面被染色了
满足条件的两串数字 a1, a2 , a3, a4 与 b1,b2 ,b3,b4 有________种不同的安排 【答案】 5353
【解答】(1)我们先对
a1 b1
1
的情况进行分析,此时相当于
a2 a3 a4
b2 b3 b4
,这种的数字串
有 C240 4845 种;
(2)接下来对 a1 1 的情况进行分析,考虑到 a1 a2 a3 a4 ,后面的三个分数相
十三届六年级中环杯决赛答案

8. 答: 1:1 利用沙漏模型,我们知道
CO BO 1 CO OD 。由于 DE 2CO ,所以 OD OA
DE 2 DO 。 利用共边定理我们可以设 SDOA SDOB k SBDE 2SBDO 2k 。
当 x 3 时, 10a b 9a 3b , a 2b , 当 a 2, b 1 ,此时即为 21 3 3 2 1 ; 当 a 4, b 2 ,此时 42 3 3 4 2 ; 当 a 6, b 3 ,此时 63 3 3 6 3 ; 当 a 8, b 4 ,此时 84 3 3 8 4 ; 当 x 4 时, 10a b 16a 4b ax 2 bx ,本种情况舍。
二、动手动脑题: 1. 答:500 套 甲厂生产上衣时间为 乙厂生产上衣时间为
3 5 4
= 35 ,生产裤子时间为5 = 35。
20 3 15
21
2
14
= 35 ,生产裤子时间为7 = 35。 7
2 4
通过比较发现,甲厂适合生产裤子,乙厂适合生产上衣。 甲厂生产裤子有8000 ÷ 5 =20000 (条) , 乙厂生产上衣有10000 ÷ 7 =17500 (件) ,那么甲厂多 20000 - 17500 = 2500 (条) ,占甲厂产量的 2500 ÷ 20000= 8。这部分可以多生产成衣8000 × 8 =1000(套) 。 17500+1000-18000=500(套) ,故现在比过去每月能多生产成衣 500 套。
42, 63,84 2. 答: 16, 21,
第十三届中环杯中小学生思维能力训练活动六年级决赛试卷及解析
第十三届“中环杯”中小学生思维能力训练活动六年级决赛一、填空题(每小题5分,共50分):1.计算:25×43+1.4×1.3+145×13=()。
2.定义n !=n ×(n -1)×…×2×1,比如6!=6×5×4×3×2×1,则15!-13!的最大素因数是()。
3.在9,8,7,6,5,4,3,2,1,0这10个数字之间加入+,-,×,÷以及括号,使得最后的结果是2013,请写出一个你所得到的式子9876543210=2013。
4.一个篮子里有红、橙、黄、绿四种颜色的球。
甲、乙、丙三人开始数这些球,并把他们数到的结果记在了下表中。
很不幸的是,每人都数错了两种颜色球的数量,数对了另两种颜色球的数量。
已知一个人数错了红、橙两色的球,另一个人数错了橙、黄两色的球,第三个人数错了黄、绿两色的球的数量。
那么,篮子中一共有()个球。
5.一个老师正在统计班级的数学平均分。
已知卷子满分是100分,老师每统计到一个同学,就重新计算一次当前的平均分。
当他统计到小明的分数时,平均分上升了1分;当他统计到小红的分数时,平均分又上升了1分;已知小明的分数是91分,那么小红的分数是()分。
6.已知n 位(n 为正整数)自然数N =a 1a 2…a n ,满足2a 1a 2…a n 1:1a 1a 2…a n 2=21:12,则N=()。
7.若x 满足x +41×3×5+x +63×5×7+x +85×7×9+…+x +20122009×2011×2013=10052011,则x =()。
8.如图,在圆O 中,AB 为直径,C 为圆内一点。
作AD//BC 与CO 的延长线交于D 点。
延长OD 至E点,使得DE=2CO 。
第15届中环杯六年级决赛

【答案】21
【解答】设上坡的长度为 x 千米,下坡的长度为 y 千米,则 x y 5 3x 2 y 60 ,
46
这个不定方程的通解为
x
y
2 2t 27 3t
。考虑到
x
、
y
都是正整数,所以
x
y
2 2t 0 27 3t 0
0
t
8
。我们要求的就是
x
y
29
t
的最小值,当
t
取最大值的时
▲ 若 n 3,只有 0,3 或者 0,1,2,3 这 2 种排法,所以 a3 2 ;
▲ 若 n 4 ,只有 0,1,4 或者 0,3,4 或者 0,1,2,3,4 这 3 种排法,所以 a3 3 ;
感觉上,这就是一个斐波那契数列,接下来我们要证明这点:
(1)当 n 为偶数时, n 前面的数可以是 n 1、 n 3 、、1,所以此时 an an1 an3 a1 ;
第 15 届中环杯决赛试题解析(六年级) 一、填空题(本大题共 10 小题,每题 6 分,共 60 分):
1.
计算:
17
3
54
0.4
1 2015
15 3
1
2 3
1 31
________.
8 2015
1 8
2014
4
1 3
2
【答案】2015
【解答】
17
3
54
0.4
1 2015
分)
【答案】1 元 23 分
【解答】设一只鸡蛋的价格为
x
元,则
9x 1100 a 13x 1500 b
。考虑到
0
a
100
2015中环题目

二、填空题B :(每题8分,共32分)9.如图所示,花花被邪恶的巫师关在了由26个正方形房间组成的迷宫里,边与边相邻的房间是互通的。
已知:黑色房间里有怪物,不能进;斜纹房间里住着巫师,只能进,不能出;灰色房间有机关,只能走一次;白色房间是安全的,可以重复走。
巫师告诉花花,走遍所有灰色房间,然后进入斜纹房间就可以离开。
花花只有从(填“A 、B 、C 、D 、E 、F 、G ”中的一个)房间开始走,才能成功离开迷宫。
10.甲、乙、丙、丁四人年龄之和是100岁。
甲32岁,他与乙的年龄之和是另外两个人年龄之和的3倍。
丙比丁大3岁。
那么,这四个人中,年龄最大的人与年龄最小的人,他们的年龄之和是。
11.如图所示,每个小图形代表一个数字(大方框只是起到分割行、列的作用),右边和下边的数字代表该行或者该列所有数之和(每行、每列均有6个数)。
如果“○”代表6,那么,△=。
12.数一数,图中共有个梯形。
三、动手动脑题:(每题10分,共20分)13.如图,把图形分成大小、形状都相同的三部分,并且每部分中都带有一个圆点,请你在图中画出分割线。
14.将1~10分别填入图中的空格内,每个数字只能使用一次。
要求“□”内的数等于它左上角和右上角两个数的差(大减小),“○”里的数等于它左上角和右上角两个数的和。
求:A 的值。
题得分:第十五届“中环杯”小学生思维能力训练活动二年级决赛第十五届“中环杯”小学生思维能力训练活动三年级决赛得分:三尧动手动脑题:(每题10分,共20分)13.5个相同的长方形放在一个正方形内,所有长方形的边都平行于正方形的对应边,正方形的边长为24厘米。
求:单个长方形的面积。
14.D老师将分别写有1、2、……、13这13个数字的13张牌按从小到大的顺序顺时针放在一个圆周上,开始的时候所有牌都是牌面朝上,每次翻动可以将一张牌翻成牌面朝下(一旦变成牌面朝下,这张牌就不能再翻动了)。
D老师翻牌的规则为:若一张牌面朝上的牌上数字为A,并且与这张牌相隔2张的牌也是牌面朝上的,那么D老师就可以翻动写有数字A的这张牌。
第十五届“中环杯”初赛各年级试题

遥
20 个 2
7. 一个物体从高空落下袁已知第一秒下落距离是 5 米袁以后每秒落下的距离都比前一
秒多 10 米袁10 秒末物体落地遥 则物体最初距离地面的高度为
米遥
8. 小明父亲每天上班需要先骑 10 分钟山地自行车袁然后乘坐 40 分钟的地铁遥有一天袁
地铁坏了袁所以他直接骑车上班袁一共花了 3 个半小时遥 那么袁地铁的速度是山地自行车的
这个人有一个头两条腿袁普通狼有一个头四条腿袁变异狼有两个头三条腿遥 所有的人和
狼加起来有 21 个头 57 条腿袁则所有的狼渊包括变异狼冤有
头遥
11. 如图袁从 A 走到 B袁每次走一格袁只能向下或者
向右走遥将一路上的数字全部相加渊如果走到黑格袁就直
接加 5冤袁最后的总和为 51遥 不同的走法有
种遥
每人 70 元遥 他们最少要花
元购买门票遥
5. 到了冰雪宫殿开放的日子袁小朋友们相约一同前往避暑遥 冰雪宫殿
前有个阶梯袁爱丽丝走 20 级台阶用了 120 秒遥用同样的速度走台阶袁爱丽丝
共走了 180 秒袁正好走完所有阶梯遥 到达冰雪宫殿的台阶一共有
级遥
6. 右图中的每个小正方形边长为 5 厘米袁 那么这个图形的周长是 厘米遥
3
7 9 12
16 18 21 噎
246
11 13 15
20 噎
1
5 8 10
14 17 19 噎
第 13 题
A
B
棒中 7
+1杯环中
1中杯环
第 14 题
D
C
第 15 题
影部分面积为
平方厘米遥
16. 将 1~6 填入右图的三个算式中袁每个数恰好使
第十三届中环杯中小学生思维能力训练活动六年级决赛试卷及解析

第十三届“中环杯”中小学生思维能力训练活动六年级决赛一、填空题(每小题5分,共50分):1.计算:25×43+1.4×1.3+145×13=()。
2.定义n !=n ×(n -1)×…×2×1,比如6!=6×5×4×3×2×1,则15!-13!的最大素因数是()。
3.在9,8,7,6,5,4,3,2,1,0这10个数字之间加入+,-,×,÷以及括号,使得最后的结果是2013,请写出一个你所得到的式子9876543210=2013。
4.一个篮子里有红、橙、黄、绿四种颜色的球。
甲、乙、丙三人开始数这些球,并把他们数到的结果记在了下表中。
很不幸的是,每人都数错了两种颜色球的数量,数对了另两种颜色球的数量。
已知一个人数错了红、橙两色的球,另一个人数错了橙、黄两色的球,第三个人数错了黄、绿两色的球的数量。
那么,篮子中一共有()个球。
5.一个老师正在统计班级的数学平均分。
已知卷子满分是100分,老师每统计到一个同学,就重新计算一次当前的平均分。
当他统计到小明的分数时,平均分上升了1分;当他统计到小红的分数时,平均分又上升了1分;已知小明的分数是91分,那么小红的分数是()分。
6.已知n 位(n 为正整数)自然数N =a 1a 2…a n ,满足2a 1a 2…a n 1:1a 1a 2…a n 2=21:12,则N=()。
7.若x 满足x +41×3×5+x +63×5×7+x +85×7×9+…+x +20122009×2011×2013=10052011,则x =()。
8.如图,在圆O 中,AB 为直径,C 为圆内一点。
作AD//BC 与CO 的延长线交于D 点。
延长OD 至E点,使得DE=2CO 。
六年级下册数学试题-能力训练:行程问题 (含部分答案)全国通用

行程问题知识点1:追及与相遇问题三个基本量:路程、速度、时间最原始公式:路程=速度×时间⑴基本相遇追及问题:路程和=速度和×相遇时间;路程差=速度差×追击时间;⑵多次相遇问题:①直线路线上多次相遇:第一次相遇,路程和=1倍全程以后每次相遇,路程和=2倍全程②环形路线上多次相遇:每次相遇,路程和=1圈路线周长每次追及,路程差=1圈路线周长⑶多人相遇问题:每次只同时考虑两个人的相遇或追及过程。
(基础)甲、乙两车同时从A、B两地相向而行,在距B地54千米处相遇。
他们各自到达对方车站后立即返回原地,途中又在距A地42千米处相遇。
求两次相遇地点的距离。
(提高、尖子)甲、乙两人从相距40千米的A,B两地相向往返而行,甲每小时行4千米,甲出发2小时后乙才出发,乙每小时行6千米,两人相遇后继续行走,他们第二次相遇的地点距离A地多少千米?(基础)甲、乙两车分别从A 、B 两地同时相向开出,甲车的速度是50千米/时,乙车的速度是40千米/时,当甲车驶过A 、B 距离的13多50千米时,与乙车相遇。
A 、B 两地相距多少千米?(提高、尖子)甲、乙两列火车的速度比是5∶4,乙车先出发,从B 站开往A 站,当走到离B 站72千米的地方时,甲车从A 站出发开往B 站。
两车相遇的地方离A ,B 两站的距离比是3∶4,那么,A ,B 两站之间的距离是多少千米?甲、乙、丙三人同时从东村到西村去,甲骑自行车,每小时比乙快4千米,比丙快7.5千米,甲走40千米到达西村后立即按原路原速度返回,在距西村10千米处与乙相遇,丙走多少小时和甲相遇?(基础、提高)(第七届“中环杯”学生思维能力训练活动复赛)某人骑车上下班,下班的速度比上班的速度慢16,因此下班比上班多用5分钟,那么上班需要( )分钟。
(尖子)一支解放军部队从驻地乘车赶往某地抗洪抢险,如果行驶1个小时后,将车速提高五分之一,就可比预定时间提前20分钟赶到;如果先按原速度行驶72千米,再将车速提高三分之一,就可比预定时间提前30分钟赶到。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
这个递推式比较麻烦,化简一下:当 n 2k 时, a2 k a2 k 1 a2 k 3 a1 ,而
a2 k 2 a2 k 3 a2 k 5 a1 ,所以推出 a2 k a2 k 1 a2 k 2 ;当 n 2k 1 时, a2 k 1 a2 k a2 k 2 a2 1 ,而 a2 k 1 a2 k 2 a2 k 4 a2 1 ,所以推出 a2 k 1 a2 k a2 k 1 ;
2 ~ 84 中,完全平方数有 4 、 9 、 16 、 25 、 36 、 49 、 64 、 81 ,逐一检验,发现没有
满足条件的数,所以“中环数”的个位数只能是偶数,而且显然不可能是 0 ,接下来 分类讨论: (1)如果 N 的个位数为 2 ,也就是说 N 必须为质数,所以 N 2 ; (2)如果 N 的个位数为 4 ,则 N a3 或 ab ,检验所有以 4 结尾的数,发现 14 、 34 、
将两种情况总结一下,得到 an an 1 an 2 ,构成斐波那契数列,从而知道我们的答 案为 a12 144 二、动手动脑(本大题共 4 小题,每题 10 分,共 40 分): 11. 如图所示,中心的立方体的棱长为 8,在其每个面的中心粘上一个棱长为 4 的立方 体,在所有棱长为 4 的立方体的露出面中心再粘上一个棱长为 2 的立方体。求:这个 立体图形的表面积
【答案】 1248 【解答】我们先不管中心立方体,先考察一个棱长为 4 的立方体带着 5 个棱长为 2 的立方体的表面积:每个棱长为 2 的立方体的一个面可以转移到棱长为 4 的立方体 上,所以整个图形的表面积为 5 42 5 4 22 80 80 160 。将其中的 4 4 16 的部分 转移到中心立方体上,所以最后答案为 160 16 6 6 82 1248 12. 若关于 x, y 的方程组
a 2 ,所以 b 0
分段: (1)当 x 2 时, x 2 5 x 2 x 8 x 2 5 x 2 x 8 5x 16 。由于
ab 111 abc 891 c 7 11
8. 下图是一个捕鱼网,这个网是由一个个节点与一条条绳索构建而成(两个相邻节点之 间都有一条绳索)。每次剪一刀,剪断其中的一条绳索,那么最多能剪______刀,使 得剩下的绳索还能连成一个整体(不会断成两部分或者多个部分)
【答案】 24 【解答】要使得剪的次数最多,那么留下的绳索越少越好。一共有 7 5 35 个节 点,为了使得所有节点还能连接起来,那么至少需要保留 35 1 34 条绳索。原先一 共有 6 5 4 7 58 条绳索,所以最多能剪 58 34 24 刀,最后构造如下:
74 满足要求;
(3)如果 N 的个位数为 6 ,则 N a5 或 a 2 b ,检验所有以 6 结尾的数,发现 76 满足要 求; (4)如果 N 的个位数为 8 ,则 N a7 或 a 3b 或 abc ,检验所有以 8 结尾的数,发现 78 满足要求; 综上所述,满足条件的“中环数”有 6 个 10. 将若干个自然数从小到 大排成一行,若满足下面两个条件,这样的排法称为“中环排法” (1)最左边的数为 0,最右边的数为 12,这行数至少有 2 个; (2)任意两个相邻的自然数中有且只有一个数为偶数(注意:0 也是偶数); 那么,一共有________种“中环排法” 【答案】144 【解答】假设最右边的数为 n ,并设此时满足要求的排法有 an 个。我们先尝试一下
2. 方程
x 133 2 x 267 x 160 5 的解为________. 267 533 80
【答案】 x 400 【解答】观察法,首先 x 400 是方程的解,考虑到一元一次方程只有一个解,所以 答案就是 x 400
3. 9 个鸡蛋的价格为 11 元 a 分, 13 个鸡蛋的价格为 15 元 b 分,其中
0 a 100 ,那么一个 0 b 100
鸡蛋的价格为_______元_______分(注:本题不考虑“角”这个货币单位, 1 元 100 分) 【答案】 1 元 23 分 【解答】设一只鸡蛋的价格为 x 元,则
9 x 1100 a 。考虑到 0 a 100 ,所以 13 x 1500 b
x 4 y 5 3 x 2 y 60 , 6 1 4 3 2 3 2 5 个圆 S 整个圆, 6 5 6
1 4
x 2 2t 。考虑到 x 、 y 都是正整数,所以 y 27 3t
x 2 2t 0 0 t 8 。我们要求的就是 x y 29 t 的最小值,当 t 取最大值的时 y 27 3t 0
第 15 届中环杯决赛试题解析(六年级) 一、填空题(本大题共 10 小题,每题 6 分,共 60 分):
15 2 1 2015 17 3 54 0.4 1 3 1 3 31 计算: ________. 2014 2 1 1 2015 8 4 8 3
候, 29 t 达到最小,此时的最小值为 29 8 21 【说明】考察不定方程 7. 已知 0. a b 0. a b c
33 ,相同的字母代表相同的数字,不同的字母也可以代表相同的数 37
字(比如 a b 1 ),则 abc ________.
【答案】 447 【解答】 0. ab 0. abc
9. 如果一个自然数 N N 1 满足: N 的因数个数就是其个位数字,那么这样的 N 就称为 “中环数”(比如 34 2 17 ,所以它有 4 个因数,正好就是 34 的个位数字,所以 34 就 是一个“中环数”),在 2 ~ 84 中,一共有________个“中环数”
【答案】 6 【解答】如果一个数的因数个数是奇数的话,那么这个数必须是完全平方数。在
a x 1 b x2 3x 5 c x 3 d 0 就是
2 x 1 c x 3 d 0 2 c x 2 3c d 0 。由于这个方程有无数个解,所以
c 2 0 c 2 ,所以 x a 5 x c x d x 2 5 x 2 x 8 ,接下来零点 d 3c 2 0 d 8
▲ 若 n 1 ,只有 0,1 这种排法,所以 a1 1 ; ▲ 若 n 2 ,只有 0,1,2 这种排法,所以 a2 1 ;
▲ 若 n 3 ,只有 0,3 或者 0,1,2,3 这 2 种排法,所以 a3 2 ; ▲ 若 n 4 ,只有 0,1,4 或者 0,3,4 或者 0,1,2,3,4 这 3 种排法,所以
1 2a b c d e 1 8 d 2b c d e 2 1 c 4. 五个数 a, b, c, d , e 满足 ,则 a b c d e ________. 4 1 2c d e 4 b 2 2d e 6 a
1100 9x 1200 123 x 133 ;考虑到 0 b 100 ,所以 1500 13x 1600 116 x 123 ;对 123 x 133 、 116 x 123 取交集得 x 123 ,所以一
只鸡蛋的价格为 1 元 23 分 【说明】考察不等式组
33 ab abc 33 ab ,两边同时乘以 999 ,得 111 abc 891 。 37 99 999 37 11 ab 111 必须也是正整数,所以 11| ab 。其次 11
考虑到 abc,891 都是正整数,所以
891
ab ab 111 abc 110 abc ab0 abc a 4 ,结合 11| ab b 4 ,代入 11 11
a3 3 ;
感觉上,这就是一个斐波那契数列,接下来我们要证明这点: (1)当 n 为偶数时, n 前面的数可以是 n 1 、 n 3 、 、1,所以此时
an an 1 an 3 a1 ;
(2)当 n 为奇数时, n 前面的数可以是 n 1 、 n 3 、 、2 甚至不填,所以此时
【答案】 2 【解答】第一个方程乘以 8 、第二个方程乘以 4 、第三个方程乘以 2 、第四个方程乘 以 1 ,然后全部相加,从而推出 16a 16b 16c 16d 15e 30 a b c d ,所以
abcd e 2
【说明】考察方程组 5. 如图, ABC 是等边三角形, D, E, F 分别是三条边上的中点, AB 2 。所有圆弧的半 径均相同,那么阴影部分面积与 ABC 的面积之差(大减小)为________(答案保留
)
A
D
E
B
F
C
【答案】 【解答】设正三角形的面积为 S ,则阴影部分面积可以分为两大块:其中一大块就 是在 ABC 内部的阴影部分,另一大块就是三个 个圆。显然,在 ABC 内部的阴影 部分面积为 S 个圆,所以阴影部分总面积为: S 个圆 3 所以两者的面积之差就是整个圆,为 r 2 6. 从甲地到乙地的路只有上坡与下坡,上坡与下坡长度的数值都是正整数,单位是千 米。如果上坡的速度是 4 千米,下坡的速度是 6 千米,从甲地到乙地需 5 小时,则 甲、乙两地之间距离的最小值为_______. 【答案】21 【解答】设上坡的长度为 x 千米,下坡的长度为 y 千米,则 这个不定方程的通解为
1.
【答案】2015 【解答】
15 2 1 2015 17 3 54 0.4 1 3 1 3 31 2014 2 1 2015 1 8 4 8 3 2 3 5 20 54 31 5 15 3 8 4 9 3 5 20 54 31 5 3 8 36 5 3 5 20 54 31 3 5 3 28 20 91 31 28 4 5 7 13 31 5 13 31 2015 47
