人教版九年级数学下册百分闯关综合能力检测题及答案

合集下载

九年级下册数学综合能力训练答案

8．函数
2x 1 中自变量 x 的取值范围是 x
.
9．在直角坐标系中，0 为坐标原点，A(1，1)，在 x 轴上确定一点 P，使△AOP 为等腰三角形，则符合条件的点 P 共有个.
PS：双击获取文档，ctrl+a,ctrl+c,然后粘贴到word即可。未能直接提供word文档，抱歉。
九年级下册数学综合能力训练答案
一、选择题（本题共7个小题）
1．在下面四个点中，与点（-3，4）连结的线段和x轴、y轴都不相交的点是…（
）
A．（-2，3）
B．（2，-3）
1 3
C．（2，3）
D．（-2，-3）
）
2．在 ABC 中， C 90 ，AB=15，sinA= ，则 BC 等于…………………………………（
A．45 B．5 C． A．4 3 B．2 3 C．6 D．2 5
）交⊙O 于 C，弦 ( )．
5．如图中的图象（折线 ABCDE）描述了一汽车在某一直线上的行驶过程中，汽车离出发地的距离 s（千米）和行驶时间 t（小时）之间的函数关系，根据图中提供的信息，给出下列说法： ①汽车共行驶了 120 千米；②汽车在行驶途中停留了 0.5 小时； ③汽车在整
(D) 7．已知，如图，⊙O1 与⊙O2 外切于点 C，AB 是一条外公切线，切点为 A、B 连结 AC、BC.设⊙O1 的半径为 R，⊙O2 的半径为 r，若 tan∠ABC= 2 ,则 A． 2 B． 3
R 的值为…………………………（ r
C．2 D．3
） A .O1 B .O2
二、填空题（本题共8个小题）
பைடு நூலகம்
80 千米/时； ④汽车自出发后 3 小时 3 之间行驶的速度在逐渐减少.其中正确的说法共有（） A、1 个 B、2 个 C、3 个 D、4 个

人教版数学九年级上、下册综合达标测试卷(含答案)

人教版数学九年级上、下册综合达标测试卷（本试卷满分120分）一、选择题（本大题共10小题，每小题3分，共30分）1．在Rt△ABC中，∠C=90°，AC=3，BC=4，则tan A的值为（）A．34B．43C．35D．452．（2021·泰州）如图所示几何体的左视图是（）A B C D 第2题图3．一个不透明的袋子里装有黄、红两种颜色的小球，摇匀后每次随机从袋中摸出1个小球，记录下颜色后放回袋中．通过多次试验后，发现摸到红球的频率稳定在0.4，则摸到黄球的概率约为（）A．0.2 B．0.4 C．0.6 D．0.84．如图，将△OAB绕点O顺时针旋转40°得到△OCD，则∠BOD的度数是（）A．33°B．35°C．40°D．45°第4题图第5题图第6题图5．如图，四边形ABCD为⊙O的内接四边形．若四边形OBCD是菱形，则∠BAD的度数为（）A．45°B．60°C．72°D．36°6. （2021·朝阳）如图，O是坐标原点，点B在x轴上，在△OAB中，AO＝AB＝5，OB＝6，点A在反比例函数y＝kx（k≠0）图象上，则k的值（）A．﹣12B．﹣15C．﹣20D．﹣307．若关于x的方程kx2+2x+1＝0有实数根，则实数k的取值范围是（）A．k≠0B．k≤1C．k≥1D．k≤1且k≠08．（2021·深圳）二次函数y＝ax2+bx+1的图象与一次函数y＝2ax+b在同一平面直角坐标系中的图象可能是（）A B C D9．《几何原本》里有一个图形：在△ABC 中，D ，E 是边AB 上的两点（AD ＜AE ），且满足AD ＝BE ．过点D ，E 分别作BC 的平行线，过点D 作AC 的平行线，将△ABC 分成如图的5个部分，其面积依次记为S 1，S 2，S 3，S 4，S 5．若S 2＝18，S 3＝6，则S 4的值为（） A ．9B ．18C ．27D ．54第9题图第10题图10．如图，已知抛物线y ＝-x 2+px+q 的对称轴为直线x ＝-3，过其顶点M 的一条直线y ＝kx+b 与该抛物线的另一个交点为N （-1，1）．若要在坐标轴上找一点P ，使得△PMN 的周长最小，则点P 的坐标为（） A ．（0，2） B ．4,03⎛⎫- ⎪⎝⎭ C ．（0，2）或4,03⎛⎫- ⎪⎝⎭D ．以上都不正确二、填空题（本大题共6小题，每小题3分，共18分）11．已知∠A 是锐角，且1-2sin A=0，则∠A 的度数为． 12．若m 是方程x 2-3x+1=0的一个根，则3m 2-9m-2021的值为．13．（2021·阜新）如图，在6×8的正方形网格中，每个小正方形的边长均为1，点A ，B ，D ，E 均在网格的交点上，则△ABC 与△CDE 的周长比为．第13题图第14题图第16题图14．如图，AB 是⊙O 的直径，半径OA 的垂直平分线交⊙O 于C ，D 两点．若∠C=30°，CD=23，则图中阴影部分的面积是．15．已知抛物线y ＝ax 2+2ax+c 经过点A （3，m ），B （-2，n ），且函数y 有最大值，则m ，n 的大小关系为 . 16．（2021·抚顺）如图，在△ABC 和△DEC 中，∠ACB ＝∠DCE ＝90°，∠BAC ＝∠EDC ＝60°，AC ＝2 cm ，DC ＝1 cm ．下列结论：①△ACD ∽△BCE ；②AD ⊥BE ；③∠CBE+∠DAE ＝45°；④在△CDE 绕点C 旋转的过程中，△ABD 面积的最大值为（23+2）cm 2．其中正确的是．（填序号）三、解答题（本大题共8小题，共72分） 17．（每小题4分，共8分）（1）计算：4sin 45°-2tan 30°cos 30°+cos 45cos 60︒︒；（2）解方程：x 2-4x-5=0.18．（8分）（2021·黑龙江）在正方形网格中，每个小正方形的边长均为1，建立平面直角坐标系xOy ，△ABC 的位置如图所示．（1）在图中以点C 为位似中心，将△ABC 放大至原来的2倍，得到位似图形△A 1B 1C ，作出△A 1B 1C 并写出点A 1的坐标；（2）作出△ABC 绕点C 逆时针旋转90°后的图形△A 2B 2C ；（3）在（2）的条件下，求点B 所经过的路径长．第18题图第19题图19．（8分）（2021·重庆）在如图所示的电路图中，有四个断开的开关A ，B ，C ，D 和一个灯泡L ．（1）若任意闭合其中一个开关，则灯泡L 发亮的概率为；（2）若任意闭合其中两个开关，请用列表法求灯泡L 发亮的概率．20．（8分）（2021·枣庄）2020年7月23日，我国首次火星探测“天问一号”探测器，由长征五号遥四运载火箭在中国文昌航天发射场发射成功，正式开启了中国的火星探测之旅．运载火箭从地面O 处发射，当火箭到达A 处时，地面D 处的雷达站测得AD ＝4000米，仰角为30°，经过3秒后，火箭直线上升到达B 处，此时地面C 处的雷达站测得B 处的仰角为45°．已知点O ，C ，D 在同一条直线上，C ，D 两处相距460米，求火箭从A处到B 处的平均速度．（结果精确到1米/ 1.732 1.414）第20题图第22题图第23题图21.（2021·辽阳）某网店销售一款市场上畅销的蒸蛋器，进价为每个40元，在销售过程中发现，这款蒸蛋器销售单价为60元时，每星期卖出100个．如果调整销售单价，每涨价1元，每星期少卖出2个，现网店决定提价销售，设销售单价为x 元，每星期销售量为y 个．（1）请直接写出y （个）与x （元）之间的函数关系式；（2）当销售单价是多少元时，该网店每星期的销售利润是2400元？（3）当销售单价是多少元时，该网店每星期的销售利润最大？最大利润是多少元？22.（10分）（2021·湘潭）如图，点A（a，2）在反比例函数y＝4x的图象上，AB∥x轴，且交y轴于点C，交反比例函数y＝kx于点B，已知AC＝2BC．（1）求直线OA的解析式；（2）求反比例函数y＝kx的解析式；（3）D为反比例函数y＝kx上一动点，连接AD交y轴于点E，当E为AD的中点时，求△OAD的面积．23．（10分）（2021·柳州）如图，在四边形ABCD中，AD∥BC，AD⊥AB，AD＝AB＝1，，以点A 为圆心，AD长为半径作圆，延长CD交⊙A于点F，延长DA交⊙A于点E，连接BF，交DE于点G．（1）求证：BC为⊙A的切线；（2）求cos ∠EDF的值；（3）求线段BG的长．24．（12分）（2021·黔东南州）如图，抛物线y＝ax2-2x+c（a≠0）与x轴交于点A，B（3，0），与y轴交于点C（0，-3），抛物线的顶点为D．（1）求抛物线的解析式；（2）已知点P在抛物线的对称轴上，点Q在x轴上，若以P，Q，B，C为顶点，BC为边的四边形是平行四边形，求点P，Q的坐标；（3）已知M是x轴上的动点，过点M作x轴的垂线交抛物线于点G，是否存在这样的点M，使得以点A，M，G为顶点的三角形与△BCD相似？若存在，求点M的坐标；若不存在，请说明理由．第24题图人教版数学九年级上、下册综合达标测试卷参考答案一、1．B 2．C 3．C 4．C 5．B 6．A 7．D 8．A 9．C 10．A二、11．30°12．-2024 13．2∶1 14．2π315．m＜n 16．①②④三、17．（1）1．（2）x1＝5，x2＝-1．18. 解：（1）如图，△A1B1C即为所求作，点A1的坐标为（3，-3）．（2）如图，△A2B2C即为所求作．第18题图（3）因为CB B ．19．解：（1）14（2）列表如下：由表格知，任意闭合两个开关，所有机会均等的结果共有12种，其中能使灯泡L 发亮的结果有6种，所以P （灯泡L 发亮）=612=12． 20．解：由题意，知AD ＝4000，CD ＝460，∠ADO ＝30°，∠BCO ＝45°．在Rt △AOD 中，OA ＝12AD ＝2000，OD ＝AD·cos 30°＝在Rt △BOC 中，OB ＝OC ＝OD-CD ＝．所以AB ＝OB-OA ＝2000≈1004．所以1004÷3≈335（米/秒）．答：火箭从A 处到B 处的平均速度约为335米/秒． 21. 解：（1）根据题意，得y=100-2（x-60）=-2x+220.（2）根据题意，得（-2x+220）（x-40）=2400，解得x1=70，x2=80. 答：当销售单价是70元或80元时，该网店每星期的销售利润是2400元．（3）设该网店每星期的销售利润为w 元.根据题意，得w=（-2x+220）（x-40）=-2x2+300x-8800=-2（x-75）2+2450. 当x=75时，w 有最大值，最大值为2450.答：当销售单价是75元时，该网店每星期的销售利润最大，最大利润是2450元． 22.解：（1）将A （a ，2）代入y ＝4x，解得a ＝2.所以A （2，2）. 设直线OA 的解析式为y ＝mx ，将A （2，2）代入，解得m ＝1.所以直线OA 的解析式为y ＝x. （2）由（1）可得AC ＝2.因为AC ＝2BC ，AB ∥x 轴，所以B （﹣1，2）. 将B （﹣1，2）代入y ＝k x ，解得k ＝﹣2.所以反比例函数y ＝k x 的解析式为y ＝﹣2x. （3）因为A （2，2），E 为AD 的中点，点E 在y 轴上，所以x D ＝-2. 将x D ＝-2代入y ＝﹣2x ，解得y D ＝1.所以D （﹣2，1）.所以E 302⎛⎫ ⎪⎝⎭，. 所以S △OAD ＝S △AOE +S △DOE ＝12×32×2+12×32×2=3. 23．（1）证明：因为AD ⊥AB ，所以∠BAD ＝90°．因为AD ∥BC ，所以∠ABC ＝180°﹣∠BAD ＝90°，即AB ⊥BC ．因为AB ＝AD ，即AB 为⊙A 的半径，所以BC 为⊙A 的切线．（2）解：过点D 作DH ⊥BC 于点H ，则∠DHB ＝∠ABH ＝∠BAD ＝90°．所以四边形ABHD 是矩形．又因为AB ＝AD ＝1，所以矩形ABHD 是正方形．所以BH ＝DH ＝AB ＝1．在Rt △DHC 中，，由勾股定理，得，所以cos C=CH CD ==因为AD ∥BC ，所以∠EDF ＝∠C ．所以cos ∠EDF ＝．（3）解：连接EF ．因为DE 是⊙A 的直径，所以∠EFD ＝90°．在Rt △EFD 中，DE ＝2AD ＝2，所以DF ＝DE·cos ∠EDF ．所以CF ＝=因为AD ∥BC ，所以△DFG ∽△CFB ．所以DF DGCF CB =，12DG =+．所以DG=43．所以AG ＝DG ﹣AD=13．在Rt △BAG 中，． 24．解：（1）将点B （3，0），C （0，-3）分别代入y ＝ax 2-2x+c ，得92303a c c -⨯+=⎧⎨=-⎩，，解得13.a c =⎧⎨=-⎩，所以抛物线的解析式为y ＝x 2-2x-3．（2）由抛物线的解析式，知其对称轴为直线x ＝1．设P （1，b ），Q （x ，0）．当以点P ，Q ，B ，C 为顶点，BC 为边的四边形是平行四边形时，点C 向右平移3个单位，向上平移3个单位得到点B ，同样P （Q ）向右平移3个单位，向上平移3个单位可得到点Q （P ）．所以1+3,30x b =⎧⎨+=⎩或+31,03.x b =⎧⎨+=⎩解得34b x =-⎧⎨=⎩，或32.b x =⎧⎨=-⎩，所以点P ，Q 的坐标分别为（1，-3），（4，0）或（1，3），（-2，0）．（3）在y ＝x 2-2x-3中，令y ＝0，解得x 1＝-1，x 2＝3．所以A （-1，0）．因为y ＝x 2-2x-3＝（x-1）2-4，所以顶点D （1，-4）．因为B （3，0），C （0，-3），所以BD 2＝20，CD 2＝2，BC 2＝18．所以BD 2＝CD 2+BC 2．所以△BCD 是直角三角形，且∠BCD ＝90°．由题意，知∠AMG ＝∠BCD ＝90°，所以要使以点A ，M ，G 为顶点的三角形与△BCD 相似，需满足的条件为AM MG BC CD =或AM MGCD BC=．设M （m ，0），则G （m ，m 2-2m-3）． ①当m ＜-12=，解得83m =或m ＝-1；2=，解得m ＝0或m ＝-1．均不符合m ＜-1，所以舍去；②当-1＜m≤3223m m ---=，解得83m =或m ＝-1（舍去）；223m m ---=m ＝0或m ＝-1（舍去）．所以M 8,03⎛⎫⎪⎝⎭或M （0，0）；③当m ＞32103m =或m ＝-1（舍去）； 2m ＝6，m ＝-1（舍去）．所以M 10,03⎛⎫ ⎪⎝⎭或M （6，0）．综上，存在点M 使得以点A ，M ，G 为顶点的三角形与△BCD 相似，点M 的坐标为（0，0），8,03⎛⎫ ⎪⎝⎭，10,03⎛⎫ ⎪⎝⎭或（6，0）．。

人教版数学九年级下册综合达标测试卷(含答案)

人教版数学九年级下册综合达标测试卷（本试题满分120分）一、选择题（本大题10小题，每小题3分，共30分）1. 若△ABC与△DEF的相似比为14，则△ABC与△DEF的周长比为（）A. 14B.13C.12D.1162. 在△ABC中，∠C=90º，若cos B=32，则sin A的值为（）A. 3B.33C.12D.323. 下列立体图形中，主视图是四边形的立体图形的个数是（）A. 1B. 2C. 3D. 4第3题图第4题图第6题图4. 反比例函数y=kx在第一象限的图象如图所示，则k的值是（）A. 1B. 2C. 3D. 45. 在阳光下，一块三角尺的投影不会是（）A. 点B. 与原三角板全等的三角形C. 变形的三角形D. 线段6. 如图，四边形ABCD是平行四边形，点E在BA的延长线上，点F在BC的延长线上，连接EF，分别交AD，CD于点G，H，则下列结论错误的是（）A. EA EGBE EF= B.EG AGGH GD= C.AB BCAE CF= D.FH CFEH AD=7. 已知一次函数y1=ax+b与反比例函数y2=kx的图象如图所示，当y1＜y2时，x的取值范围是（）A. x＜2B. x＞5C. 2＜x＜5D. 0＜x＜2或x＞5第7题图第8题图8. 如图，正方形OABC的边长为8，点P在边AB上，CP交对角线OB于点Q.若S△BPQ=19S△OQC，则OQ的长为（）A. 6B. 62C. 1623D.1639. 如图，小叶与小高欲测量公园内某棵树DE的高度.他们在这棵树正前方的一座凉亭前的台阶上的点A处，测得这棵树顶端D的仰角为30°，朝着这棵树的方向走到台阶下的点C处，测得这棵树顶端D的仰角为60°.已知台阶A处到地面的高度AB为3 m，台阶AC的坡度为1∶3，且B，C，E三点在同一条直线上，则这棵树DE 的高度为（）A. 6 mB. 7 mC. 8 mD. 9 m第9题图第10题图10. 已知两个反比例函数y=kx和y=1x在第一象限内的图象如图所示.点P在y=kx的图象上，PC⊥x轴于点C，交y=1x的图象于点A，PD⊥y轴于点D，交y=1x的图象于点B.当点P在y=kx的图象上运动时，有下列结论：①△ODB与△OCA的面积相等；②四边形PAOB的面积不会发生变化；③PA与PB始终相等；④当A是PC的中点时，B一定是PD的中点.其中一定正确的是（）A. ①②③B. ②③④C. ①②④D. ①③④二、填空题（本大题7小题，每小题4分，共28分）11. 如图是由小正方体组成的几何体的三视图，则该几何体有__________个小正方体组成.第11题图第13题图第14题图第15题图12. 反比例函数y=kx与一次函数y=ax＋b的图象的两个交点分别为A（-1，-4），B（2，m），则a＋2b=__________.13. 如图，已知△ABC是等边三角形，D是边AB上一点，E为边BC上一点.若∠CDE=60°，AD=3，BE=2，则△ABC的边长为__________.14. 如图，在半径为5的⊙O中，弦AB=6，C是优弧AB上一点（不与点A，B重合），则cos C的值为__________.15. 如图，在□ABCD中，E是边AD的中点，EC交对角线BD于点F.若S△DEC=3，则S△BCF =__________.16. 在△ABC中，已知O为AC的中点，点P在边AC上.若5，tan A=12，∠B=120°，BC=23AP=__________.三、解答题（本大题8小题，共72分）17. （6分）计算：tan30°cos30°+sin 260°- sin 245°tan45°.18. （8分）如图，在8×6的网格图中，每个小正方形的边长均为1，点O 和四边形ABCD 的顶点均在小正方形的顶点上.（1）以点O 为位似中心，在网格图中作四边形A 1B 1C 1D 1与四边形ABCD 位似，且相似比为12；（2）根据（1）填空：OD 1∶D 1D=__________.第18题图第19题图19 （8分）如图，一次函数的图象与x 轴，y 轴分别相交于A ，B 两点，且与反比例函数y=kx（k ≠0）的图象在第一象限交于点C.如果点B 的坐标为（0，2），OA=OB ，B 是线段AC 的中点. （1）求点A 的坐标及一次函数的解析式；（2）求点C 的坐标及反比例函数的解析式.20. （10分）学校食堂厨房的桌子上整齐地摆放着若干相同规格的碟子，碟子的个数（个）与碟子的高度（厘米）的关系如下表：（1）当桌子上放有x 个碟子时，请写出此时碟子的高度h ；（用含x 的式子表示）（2）桌子上摆放碟子的三视图如图所示，厨房师傅想把所有的碟子整齐叠成一摞，求叠成一摞后的高度．第20题图第21题图第22题图21. （10分）如图，小东在教学楼距地面9 m 高的窗口C 处，测得正前方旗杆顶部A 点的仰角为37°，旗杆底部B 点的俯角为45°.（1）求旗杆AB 的高；（结果精确到0.01 m ；参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）碟子的个数 1 2 3 4 … 碟子的高度22+1.52+32+4.5…（2）升旗时，国旗上端悬挂在距地面2.25 m处.若国旗随国歌声冉冉升起，并在国歌播放45 s结束时到达旗杆顶端，求国旗匀速上升的速度.22. （10分）如图，四边形ABCD内接于⊙O，AB是⊙O的直径，AC与BD相交于点E，且DC2=CE•CA. （1）求证：BC=CD；（2）分别延长AB，DC交于点P，过点A作AF⊥CD，交CD的延长线于点F.若PB=OB，CD=22，求⊙O的半径.23. （10分）如图，一次函数y=kx+b与反比例函数y=mx（x＞0）的图象交于点P，与x轴交于点A（-4，0），与y轴交于点C（0，1），PB⊥x轴于点B，且AC=BC.（1）求一次函数、反比例函数的解析式；（2）反比例函数的图象上是否存在点D，使四边形BCPD为菱形？如果存在，求出点D的坐标；如果不存在，说明理由.第23题图第24题图24.（12分）如图，在△ABC中，已知AB=AC=5 cm，BC=6 cm.点P从点B出发，沿BA方向匀速运动，速度为1 cm/s；同时，直线QD从点C出发，沿CB方向匀速运动，速度为1 cm/s，且QD⊥BC，与AC，BC分别交于点D，Q.当直线QD停止运动时，点P也停止运动，连接PQ，设运动时间为t s（0＜t＜3）.解答下列问题：（1）当t为何值时，PQ∥AC？（2）设四边形APQD的面积为S cm2，求S与t之间的函数解析式；（3）是否存在某一时刻，使S四边形APQD∶S△ABC=23∶45？若存在，求出t的值；若不存在，请说明理由.人教版数学九年级下册综合达标测试卷一、1. A 2. D 3. B 4. C 5. A 6. C 7. D 8. B 9. D 10. C 二、11. 5 12. -2 13. 9 14.4515. 416. 提示：延长AB ，构造含60º角的直角三角形.三、17. 解：原式+2⎝⎭-2⎝⎭×1=34. 18. 解：（1）如图所示，四边形A 1B 1C 1D 1即为所求.第18题图（2）119. 解：（1）因为OA=OB，B（0，2），所以A（-2，0）.将点A（-2，0），B（0，2）代入y=kx+b，得202k bb-+=⎧⎨=⎩，，解得12.kb=⎧⎨=⎩，所以一次函数的解析式为y=x+2.（2）因为B是线段AC的中点，所以C（2，4）.将点C（2，4）代入y=kx，得k=8，所以反比例函数的解析式为y=8x.20. 解：（1）由题意，得h=2+1.5（x﹣1）=1.5x+0.5.（2）由三视图可知共有12个碟子，所以叠成一摞的高度为1.5×12+0.5=18.5（cm）．21. 解：（1）过点C作CD⊥AB于点D，则∠ADC=∠BDC=90°.因为∠ACD=37°，∠DCB=45°，所以△CDB是等腰直角三角形.由题意，知CD=BD=9 m，所以AD=CD•tan37º≈9×0.75=6.75（m）.所以AB=BD+AD=9+6.75=15.75（m）.答：旗杆AB的高度为15.75 m.（2）由（1）及题意，得（15.75-2.25）÷45=0.3（m/s）.答：国旗匀速上升的速度是0.3 m/s.22.（1）证明：因为DC2=CE•CA，所以DC CACE DC=.因为∠ACD=∠DCE，所以△CAD∽△CDE.所以∠CAD=∠CDE.所以BC DC=.所以BC=DC. （2）解：连接OC.设⊙O的半径为r.由（1），知CD CB=，所以∠BOC=∠BAD.所以OC∥AD.所以2PC PO rCD OA r===2.所以PC=2CD=42.因为四边形ABCD内接于⊙O，所以∠DAB+∠DCB=180º.又∠DCB+∠PCB=180º，所以∠PCB=∠DAB.因为∠CPB=∠APD，所以△PCB∽△PAD.所以PC PBPA PD=4262=，解得r=4.所以⊙O的半径为4.23. 解：（1）将C（0，1），A（-4，0）代入y=kx+b，得140bk b=⎧⎨-+=⎩，，解得141.kb⎧=⎪⎨⎪=⎩，所以一次函数的解析式为y=14x+1.因为AC=BC，CO⊥AB，所以BO=AO=4.所以B（4，0）.因为PB⊥x轴，所以点P的横坐标为4.当x=4时，y=14×4+1=2.所以P（4，2）.将点P（4，2）代入y=mx，得m=8.所以反比例函数的解析式为y=8x.（2）假设存在这样的点D，使四边形BCPD为菱形，连接DC与PB交于点E. 因为四边形BCPD为菱形，所以CE=DE=4.所以CD=8.将x=8代入y=8x，得y=1，所以D（8，1）.所以反比例函数的图象上存在点D，使四边形BCPD为菱形，此时点D的坐标为（8，1）.24. 解：（1）由题意，知BP=t，BQ=6﹣t.因为PQ∥AC，所以△BPQ∽△BAC.所以BP BQBA BC=，即656t t-=，解得t=3011.所以当t=3011s时，PQ∥AC.（2）过点A作AN⊥BC于点N，过点P作PM⊥BC于点M.因为AB=AC=5 cm，BC=6 cm，所以BN=CN=3 cm.所以AN=4（cm）.因为AN⊥BC，PM⊥BC，所以AN∥PM.所以△BPM∽△BAN.所以BP PMBA AN=，即54t PM=，解得PM=45t.所以S△BPQ=12BQ·PM=12（6﹣t）•45t=225t-+125t.在Rt△ANC中，AN=4，CN=3，所以tan C=43.所以tan C=DQQC=43，即DQt=43，得DQ=43t.所以S△CDQ=12CQ·DQ=23t2.因为S△ABC=12BC·AN=12×6×4=12，所以S=S四边形APQD=S△ABC﹣S△CDQ﹣S△BPQ=12﹣23t2﹣221255t t⎛⎫-+⎪⎝⎭=﹣415t2﹣125t+12（0＜t＜3）. （3）存在.由（2），知S四边形APQD=﹣415t2﹣125t+12，S△ABC=12，所以24121215512t t--+=2345，解得t1=2，t2=﹣11（舍去）.所以当t的值为2时，S四边形APQD∶S△ABC=23∶45.。

2022—2023年人教版九年级数学(下册)期末综合能力测试卷及答案

2022—2023年人教版九年级数学(下册)期末综合能力测试卷及答案班级：姓名：一、选择题（本大题共10小题，每题3分，共30分）1．下列二次根式中，最简二次根式的是（）A ．15B ．0.5C ．5D ．502．黄金分割数512-是一个很奇妙的数，大量应用于艺术、建筑和统计决策等方面，请你估算5﹣1的值（）A ．在1.1和1.2之间B ．在1.2和1.3之间C ．在1.3和1.4之间D ．在1.4和1.5之间3．若点1(3,)A y -，2(2,)B y -，3(1,)C y 都在反比例函数12y x =-的图象上，则1y ，2y ，3y 的大小关系是（）A ．213y y y <<B ．312y y y <<C ．123y y y <<D ．321y y y <<4．已知一个多边形的内角和等于900º，则这个多边形是（）A ．五边形B ．六边形C ．七边形D ．八边形5．菱形不具备的性质是（）A ．四条边都相等B ．对角线一定相等C ．是轴对称图形D ．是中心对称图形6．如图是由6个同样大小的正方体摆成的几何体．将正方体①移走后，所得几何体（）A ．主视图改变，左视图改变B ．俯视图不变，左视图不变C ．俯视图改变，左视图改变D ．主视图改变，左视图不变7．如图，抛物线2144y x =-与x 轴交于A 、B 两点，P 是以点C （0,3）为圆心，2为半径的圆上的动点，Q 是线段PA 的中点，连结OQ .则线段OQ 的最大值是（）A ．3B ．412C ．72D ．48．如图，∠ACD 是△ABC 的外角，CE 平分∠ACD ，若∠A=60°，∠B=40°，则∠ECD 等于（）A ．40°B ．45°C ．50°D ．55°9．如图，点E 在CD 的延长线上，下列条件中不能判定AB ∥CD 的是（）A ．∠1=∠2B ．∠3=∠4C ．∠5=∠BD ．∠B +∠BDC =180°10．如图，在平面直角坐标系中，矩形ABCD 的顶点A ，C 分别在x 轴，y 轴的正半轴上，点D （-2，3），AD =5，若反比例函数k y x=（k ＞0，x ＞0）的图象经过点B ，则k 的值为（）A ．163B ．8C ．10D ．323二、填空题（本大题共6小题，每小题3分，共18分）1．计算：124503⨯+＝_____．2．分解因式：2x+xy=_______．3．不等式组34012412xx+≥⎧⎪⎨-≤⎪⎩的所有整数解的积为__________．4．如图，已知△ABC的两边AB=5，AC=8，BO、CO分别平分∠ABC、∠ACB，过点O作DE∥BC，则△ADE的周长等于__________．5．如图，M、N是正方形ABCD的边CD上的两个动点，满足AM BN=，连接AC 交BN于点E，连接DE交AM于点F，连接CF，若正方形的边长为6，则线段CF的最小值是__________．6．如图．在44⨯的正方形方格图形中，小正方形的顶点称为格点.ABC∆的顶点都在格点上,则BAC∠的正弦值是__________．三、解答题（本大题共6小题，共72分）1．解方程：33122 xx x-+=--2．已知a 、b 、c 满足2225(32)0a b c -+-+-=（1）求a 、b 、c 的值．（2）试问：以a 、b 、c 为三边长能否构成三角形，如果能，请求出这个三角形的周长，如不能构成三角形，请说明理由．3．如图，点A 、D 、C 、F 在同一条直线上，AD=CF ，AB=DE ，BC=EF.(1)求证：ΔABC ≌△DEF ；(2)若∠A=55°，∠B=88°，求∠F 的度数.4．如图，BD 是菱形ABCD 的对角线，75CBD ∠=︒，（1）请用尺规作图法，作AB 的垂直平分线EF ，垂足为E ，交AD 于F ；（不要求写作法，保留作图痕迹）（2）在（1）条件下，连接BF ，求DBF ∠的度数．105阳光体育活动．某中学就“学生体育活动兴趣爱好”的问题，随机调查了本校某班的学生，并根据调查结果绘制成如下的不完整的扇形统计图和条形统计图：(1)在这次调查中，喜欢篮球项目的同学有______人，在扇形统计图中，“乒乓球”的百分比为______%，如果学校有800名学生，估计全校学生中有______人喜欢篮球项目．(2)请将条形统计图补充完整．(3)在被调查的学生中，喜欢篮球的有2名女同学，其余为男同学．现要从中随机抽取2名同学代表班级参加校篮球队，请直接写出所抽取的2名同学恰好是1名女同学和1名男同学的概率．6．一商店销售某种商品，平均每天可售出20件，每件盈利40元.为了扩大销售、增加盈利，该店采取了降价措施，在每件盈利不少于25元的前提下，经过一段时间销售，发现销售单价每降低1元，平均每天可多售出2件.（1）若降价3元，则平均每天销售数量为________件；（2）当每件商品降价多少元时，该商店每天销售利润为1200元？参考答案一、选择题（本大题共10小题，每题3分，共30分）1、C2、B3、B4、C5、B6、D7、C8、C9、A10、D二、填空题（本大题共6小题，每小题3分，共18分）1、2、()x x+y．3、04、135、36、三、解答题（本大题共6小题，共72分）1、4x=2、（1）a＝，b＝5，c＝；（2）能；．3、（1）略；（2）37°4、（1）答案略；（2）45°．5、（1）5，20，80；（2）图见解析；（3）3 5.6、（1）26；（2）每件商品降价10元时，该商店每天销售利润为1200元.。

精品解析：人教版九年级数学下册全册综合测试题(解析版)

人教版九年级数学下册全册综合测试题一、选择题(每小题3分，共30分)1.已知反比例函数的图象经过点（﹣1，2），则它的解析式是（）A. y=﹣12xB. y=﹣2xC. y=2xD. y=1x【答案】B 【解析】试题解析：设反比例函数图象设解析式为y＝kx，将点（-1，2）代入y＝kx得，k=-1×2=-2，则函数解析式为y=-2x．故选B．2.下列几何体的主视图既是中心对称图形又是轴对称图形的是（）A. B. C. D.【答案】D【解析】试题分析：先判断主视图的形状，再根据轴对称图形与中心对称图形的概念求解．A、主视图是等腰三角形，是轴对称图形，不是中心对称图形，故错误；B、主视图是等腰三角形，是轴对称图形，不是中心对称图形，故错误；C、主视图是等腰梯形，是轴对称图形，不是中心对称图形，故错误；D、主视图是矩形，是轴对称图形，也是中心对称图形，故正确．故选D．考点：1.中心对称图形；2.轴对称图形；3.简单几何体的三视图．3.如图，已知∠α的一边在x轴上，另一边经过点A(2，4)，顶点为B(－1，0)，则sinα的值是（）A.25B.55C.35D.45【答案】D 【解析】如图：过点A 作垂线AC ⊥x 轴于点C . 则AC =4，BC =3，故由勾股定理得AB =5. sin B =AC AB =45.故选D.4.如图，反比例函数y 1＝1k x 和正比例函数y 2＝k 2x 的图象交于A(－1，－3)、B(1，3)两点．若1kx＞k 2x ，则x 的取值范围是( )A. －1＜x ＜0B. －1＜x ＜1C. x ＜－1或0＜x ＜1D. －1＜x ＜0或x ＞1【答案】C 【解析】【详解】解：已知1k x＞k 2x ，即可知12y y >，观察图象可知，当x ＜－1或0＜x ＜1时12y y >，故选C 5.若函数m 2y x+=的图象在其所在的每一象限内，函数值y 随自变量x 的增大而增大，则m 的取值范围是 A. m ＜﹣2 B. m ＜0C. m ＞﹣2D. m ＞0【答案】A∵函数m 2y x+=的图象在其所在的每一象限内，函数值y 随自变量x 的增大而增大， ∴m+2＜0，解得：m ＜﹣2．故选A ．6.在△ABC 中，2(2cos 2)|1tan |0A B -+-=，则△ABC 一定是（） A. 直角三角形 B. 等腰三角形 C. 等边三角形 D. 等腰直角三角形【答案】D 【解析】试题分析：根据非负数的性质可得：2cosA=2，tanB=1，解得：∠A=45°，∠B=45°，则∠C=90°，则△ABC 是等腰直角三角形.7.小红在观察由一些相同小立方块搭成的几何体时，发现它的主视图、俯视图、左视图均为如图，则构成该几何体的小立方块的个数有( )A. 3个B. 4个C. 5个D. 6个【答案】B 【解析】试题分析：从俯视图发现有3个立方体，从左视图发现第二层最多有1个立方块，则构成该几何体的小立方块的个数有4个；故选B ．考点：由三视图判断几何体．8.如图，某村准备在坡角为α的山坡上栽树，要求相邻两树之间的水平距离为5米，那么这两棵树在坡面上的距离AB 为( )A. 5cosαB.5cos aC. 5sinαD.5sin a【解析】【分析】运用余弦函数求两树在坡面上的距离AB即可．【详解】解：由于相邻两树之间的水平距离为5米，坡角为α，则两树在坡面上的距离AB＝5 cos.故选B．【点睛】此题主要考查了坡度坡角问题，正确掌握三角函数关系是解题关键．9.如图，已知第一象限内的点A在反比例函数y=2x的图象上，第二象限内的点B在反比例函数y=kx的图象上，且OA⊥OB，cosA=3，则k的值为( )A. －3B. －6C. －4D. -23【答案】C【解析】【分析】过A作AE⊥x轴，过B作BF⊥x轴，由OA与OB垂直，再利用邻补角定义得到一对角互余，再由直角三角形BOF中的两锐角互余，利用同角的余角相等得到一对角相等，又一对直角相等，利用两对对应角相等的三角形相似得到三角形BOF与三角形OEA相似，在直角三角形AOB中，由锐角三角函数定义，根据cos∠BAO的值，设出AB与OA，利用勾股定理表示出OB，求出OB与OA的比值，即为相似比，根据面积之比等于相似比的平方，求出两三角形面积之比，由A在反比例函数y=2x上，利用反比例函数比例系数的几何意义求出三角形AOE的面积，进而确定出BOF的面积，再利用k的集合意义即可求出k的值．【详解】过A作AE⊥x轴，过B作BF⊥x轴．∵OA⊥OB，∴∠AOB=90°，∴∠BOF+∠EOA=90°．∵∠BOF+∠FBO=90°，∴∠EOA=∠FBO．∵∠BFO =∠OEA =90°，∴△BFO ∽△OEA ．Rt △AOB 中，cos ∠BAO=AO AB =33．设AB =3，则OA =1，根据勾股定理得：BO =2，∴OB ：OA =2：1， ∴S △BFO ：S △OEA =2：1． ∵A 在反比例函数y =2x上，∴S △OEA =1，∴S △BFO =2，则k =﹣4．故选C ．【点睛】本题属于反比例函数综合题，涉及的知识有：相似三角形的判定与性质，锐角三角函数定义，勾股定理，以及反比例函数k 的几何意义，熟练掌握相似三角形的判定与性质是解答本题的关键． 10.如图，AB 是⊙O 的直径，弦CD ⊥AB 于点G ，点F 是CD 上一点，且满足13CF FD =，连接AF 并延长交⊙O 于点E ，连接AD ，DE ，若CF ＝2，AF ＝3，给出下列结论：①△ADF ∽△AED ；②FG ＝2；③tan E ＝5；④S △DEF ＝45.其中正确的是( )A. ①②③ B . ②③④C. ①②④D. ①③④【答案】C 【解析】试题解析：①∵AB 是⊙O 的直径，弦CD ⊥AB ， ∴AD AC =，DG=CG ， ∴∠ADF=∠AED ，∵∠FAD=∠DAE （公共角）， ∴△ADF ∽△AED ；故①正确； ②∵13CF FD =，CF=2，∴CD=DF+CF=8， ∴CG=DG=4， ∴FG=CG-CF=2；故②正确； ③∵AF=3，FG=2， ∴=∴在Rt △AGD 中，tan ∠ADG=AG DG =∴tan ∠故③错误；④∵DF=DG+FG=6，=，∴S △ADF =12DF•AG=12×∵△ADF ∽△AED ， ∴2ADF AEDS AF SAD=（）， ∴37ADE S =， ∴S △AED∴S △DEF =S △AED-S △ADF 故④正确．故选C ．二、填空题(每小题3分，共24分)11.小亮在上午8时，9时30分，10时，12时四次到室外的阳光下观察向日葵的头茎随太阳转动的情况，无意之中，他发现这四个时刻向日葵影子的长度各不相同，那么影子最长的时刻为________．【答案】上午8时【解析】解：根据地理知识，北半球不同时刻太阳高度角不同影长也不同，规律是由长变短，再变长．故答案为上点睛：根据北半球不同时刻物体在太阳光下的影长是由长变短，再变长来解答此题．12.已知△ABC与△DEF相似且面积比为9︰25，则△ABC与△DEF的相似比为_____________. 【答案】3∶5【解析】试题解析：∵△ABC与△DEF相似且面积比为9：25，∴△ABC与△DEF的相似比为3：5．故答案为3：5．13.若∠A为锐角，且cos A＝14，则∠A的范围是___．【答案】60°＜∠A＜90°【解析】试题解析：∵0＜14＜12，又cos60°=12，cos90°=0，锐角余弦函数值随角度的增大而减小，∴当cosA=14时，60°＜∠A＜90°．故答案为60°＜∠A＜90°．14.如图，A′B′∥AB，B′C′∥BC，且OA′∶A′A＝4∶3，则△ABC与___________是位似图形，相似比是_________．【答案】△A′B′C′；7∶4.【解析】试题解析：∵A′B′∥AB，B′C′∥BC，∴△ABC∽△A′B′C′，∴A B B OAB BO'''＝，B C OBBC OB'''＝，∠A′B′O=∠ABO，∠C′B′O=∠CBO，∴A B B CAB BC＝''''，∠A′B′C′=∠ABC，∴△ABC∽△A′B′C′，相似比=AB ：A′B′=OA ：OA′=（4+3）：4+=7：4． 15.如图,点P ,Q ,R 是反比例函数y ＝2x的图象上任意三点,P A ⊥y 轴于点A ,QB ⊥x 轴于点B ,RC ⊥x 轴于点C ,S 1,S 2,S 3分别表示△OAP ,△OBQ ,△OCR 的面积,则S 1,S 2,S 3的大小关系是_____________．【答案】S 1=S 2=S 3 【解析】分析：本题考查的是反比例函数的k 的几何意义.解析：根据反比例函数的k 的几何意义， S 1=1，,S 2=1，,S 3=1. 故答案为S 1=S 2=S 3.16.某河道要建一座公路桥，要求桥面离地面高度AC 为3 m ，引桥的坡角∠ABC 为15°，则引桥的水平距离BC 的长是__ __m ．(精确到0.1 m ；参考数据：sin 15°≈0.258 8，cos 15°≈0.965 9，tan 15°≈0.267 9)【答案】11.2 【解析】试题解析：Rt △ABC 中，∠ABC=15°，AC=3， ∴BC=AC÷tan15°≈11.2（米）．17.如图，在平行四边形ABCD 中，E ，F 分别是边AD ，BC 的中点，AC 分别交BE ，DF 于点M ，N ，给出下列结论：①△ABM ≌△CDN ；②AM ＝13AC ；③DN ＝2NF ；④S △AMB ＝12S △ABC .其中正确的结论是____．(填序号)【答案】①②③ 【解析】【分析】本题先结合平行四边形性质，根据ASA 得出△ABM ≌△CDN ，从而得出DN=BM ，AM=CN ；再由三角形中位线得出CN=MN ，BM=DN=2NF ，即可判断结果【详解】解：在▱ABCD中，AD∥BC，AD=BC，又E、F分别是边AD、BC的中点，∴BF∥DE，BF=DE，∴四边形BFDE是平行四边形，∴BE∥DF，∴∠AMB=∠ANF=∠DNC，∵∠BAM=∠DCN，AB=CD，∴△ABM≌△CDN；E是AD的中点，BE∥DF，∴M是AN的中点，同理N是CM的中点，∴AM=13 AC，∵DN=BM=2NF；∴S△AMB=12S△ABC不成立，∴正确的结论是①②③．【点睛】解答本题的关键是熟练掌握平行四边形的性质：①平行四边形两组对边分别平行；②平行四边形的两组对边分别相等；③平行四边形的两组对角分别相等；④平行四边形的对角线互相平分．18.如图，在已建立直角坐标系的4×4的正方形方格纸中，△ABC是格点三角形（三角形的三个顶点都是小正方形的顶点），若以格点P、A、B为顶点的三角形与△ABC相似（C点除外），则格点P的坐标是_____．【答案】（1，4）或（3，4）【解析】【详解】试题分析：如图，此时AB 对应P 1A 或P 2B ，且相似比为1：2，故点P 的坐标为：（1，4）或（3，4）.三、解答题(共66分)19.先化简，再求代数式的值．222()111a aa a a ++÷+--，其中a=tan60°﹣sin30°．【答案】原式=2(1)(2)13•(1)(1)1a a a a a a a -++-=+-+（3分）当a= tan600- 2sin300132312⨯=时， (6分) 原式3311=-+分)【解析】【分析】根据分式的运算法则，先进行化简，根据特殊锐角三角函数值求出a,再代入化简式子.【详解】解:原式()()()()2a 2a 2a 1a 1a 1a 1a 13a ⎡⎤-+-=+⋅⎢⎥+-+-⎢⎥⎣⎦()()3a a 1a 1a 13a -=⋅+-，1a 1=+， a tan602cos45=-2322= 31=， ∴原式33113===-+．【点睛】本题考核知识点：分式混合运算，特殊锐角三角函数值.解题关键点：掌握分式运算法则，熟记特殊三角函数值.20.如图，反比例函数的图象经过点A 、B ，点A 的坐标为(1，3)，点B 的纵坐标为1，点C 的坐标为(2，0)．(1)求该反比例函数的表达式；(2)求直线BC 的表达式．【答案】（1）y=3x;(2) y ＝x －2 【解析】试题分析：（1）把点A 的坐标代入反比例函数的解析式，即可求解；（2）根据（1）中的解析式求得点B 的坐标，再进一步运用待定系数法求得一次函数的解析式．试题解析：（1）设所求反比例函数的解析式为k y x=（k≠0）． ∵点A （1，3）在此反比例函数的图象上，∴k 31=，解得k=3． ∴所求反比例函数的解析式为3y x =．（2）设直线BC 的解析式为y=k 1x+b （k 1≠0）．∵点B 的反比例函数3y x =的图象上，点B 的纵坐标为1，设B （m ，1）， ∴31m=，解得m=3．∴点B 的坐标为（3，1）．由题意，得1113k b{02k b =+=+，解得：1k 1{b 2==-．∴直线BC 的解析式为y x 2=-．考点：1.反比例函数与一次函数交点问题；2. 待定系数法的应用；3.曲线上点的坐标与方程的关系． 21.一艘观光游船从港口A 以北偏东60°的方向出港观光，航行80海里至C 处时发生了侧翻沉船事故，立即发出了求救信号，一艘在港口正东方向的海警船接到求救信号，测得事故船在它的北偏东37°方向，马上以40海里每小时的速度前往救援，求海警船到大事故船C 处所需的大约时间．（温馨提示：sin53°≈0.8，cos53°≈0.6）【答案】54小时【解析】【分析】过点C作CD⊥AB交AB延长线于D．先解Rt△ACD得出CD=AC=40海里，再解Rt△CBD中，得出BC=≈50，然后根据时间=路程÷速度即可求出海警船到大事故船C处所需的时间．【详解】解：如图，过点C作CD⊥AB交AB延长线于D．在Rt△ACD中，∵∠ADC=90°，∠CAD=30°，AC=80海里，∴CD=AC=40海里．在Rt△CBD中，∵∠CDB=90°，∠CBD=90°﹣37°=53°，∴BC=≈=50（海里），∴海警船到大事故船C处所需的时间大约为：50÷40=（小时）．考点：解直角三角形的应用-方向角问题22.已知Rt△ABC的斜边AB在平面直角坐标系的x轴上，点C（1，3）在反比例函数y=的图象上，且sin∠BAC=．（1）求k的值和边AC的长；（2）求点B的坐标．【答案】解：（1）∵点C（1，3）在反比例函数y=的图象上∴把C（1，3）代入上式得；3=∴k=3∵sin∠BAC=∴sin∠BAC==∴AC=5；（2）∵△ABC是Rt△，∴∠DAC=∠DCB 又∵sin∠BAC=∴tan∠DAC=∴又∵CD=3∴BD=∴AB=1+=∴B （，0）【解析】试题分析：（1）本题需先根据C 点的坐标在反比例函数y=k x 的图象上，从而得出k 的值，再根据且sin ∠BAC=35，得出AC 的长．（2）本题需先根据已知条件，得出∠DAC=∠DCB ，从而得出CD 的长，根据点B 的位置即可求出正确答案．试题解析：（1）∵点C （1，3）在反比例函数y=kx 的图象上， ∴3=1k，解得k=3，∵sin ∠BAC=35∴sin ∠BAC=3AC =35∴AC=5；∴k 的值和边AC 的长分别是：3，5．（2）①当点B 点A 右边时，如图，作CD ⊥x 轴于D ．∵△ABC 是直角三角形，∴∠DAC=∠DCB ，又∵sin ∠BAC=35，∴tan ∠DAC=34，∴34BDCD ，又∵CD=3，∴BD=94，∴OB=1+94=134，∴B（134，0）；②当点B在点A左边时，如图，作CD⊥x轴于D．∵△ABC是直角三角形，∴∠B+∠A=90°，∠B+∠BCD=90°，∴∠DAC=∠DCB，又∵sin∠BAC=35，∴tan∠DAC=34，∴34 BDCD，又∵CD=3，∴BD=94，BO=BD-1=54，∴B（-54，0）∴点B的坐标是（-54，0），（134，0）．考点：1.解直角三角形；2.待定系数法求反比例函数解析式．23.如图，楼房CD旁边有一池塘，池塘中有一电线杆BE高10米，在池塘边F处测得电线杆顶端E的仰角为45°，楼房顶点D的仰角为75°，又在池塘对面的A处，观测到A，E，D在同一直线上时，测得电线杆顶端E的仰角为30°.(1)求池塘A，F两点之间的距离；(2)求楼房CD的高．【答案】（1）AF ＝3＋10)米；（2）DC ＝(10＋3米.【解析】试题分析：（1）分别解Rt △ABE 与Rt △BEF ，可得AB 与BF 的大小．AF=AB+BF ；（2）设CD=x ．在Rt △FCD 中，可得CF 的值，根据相似三角形的性质，可得比例关系求解．试题解析：（1）在Rt △ABE 中，∵∠A=30°，BE=10， ∴33BE AB =∴3在Rt △EBF 中，∵∠BFE=45°，∴BF=BE=10，∴3；（2）∵BE=10，∠A=30°，∴3CD=x ，设CD=x ．则CF=7523xtan =︒+∵∠EBA=∠DCA=90°，∠A=30°，∴△ABE ∽△ACD ，由相似三角形的性质可得：ABBEAC CD =， 10310103+10+23x +，解得3答：AF 间的距离为（3CD 的高为（3）米．24.如图，在平行四边形ABCD中，对角线AC，BD交于点O. M为AD中点，连接CM交BD于点N，且1ON=.（1）求BD的长；（2）若DCN∆的面积为2，求四边形ABNM的面积.【答案】（1）6；（2）5.【解析】【分析】(1)由四边形ABCD为平行四边形，得到对边平行且相等，且对角线互相平分，根据两直线平行内错角相等得到两对角相等，进而确定出三角形MND与三角形CNB相似，由相似得比例，得到DN：BN=1：2，设OB=OD=x，表示出BN与DN，求出x的值，即可确定出BD的长；(2)由相似三角形相似比为1：2，得到S△MND：S△CND=1：4，可得到△MND面积为1，△MCD面积为3，由S平行四边形ABCD=AD•h，S△MCD=MD•h=AD•h，=4S△MCD，即可求得答案．【详解】(1)∵平行四边形ABCD，∴AD∥BC，AD=BC，OB=OD，∴∠DMN=∠BCN，∠MDN=∠NBC，∴△MND∽△CNB，∴MD DN BC BN=，∵M为AD中点，所以BN=2DN，设OB=OD=x，则有BD=2x，BN=OB+ON=x+1，DN=x﹣1，∴x+1=2（x﹣1），解得：x=3, ∴BD=2x=6；(2)、∵△MND∽△CNB，且相似比为1：2，∴MN：CN=1：2，∴S△MND：S△CND=1：4，∵△DCN的面积为2，∴△MND面积为1，∴△MCD面积为3，设平行四边形AD边上的高为h，∵S平行四边形ABCD=AD•h，S△MCD=12MD•h=14AD•h，∴S平行四边形ABCD=4S△MCD=12，∴S△ABD=6，∴S四边形ABNM= S△ABD- S△MND =6-1=5．【点睛】本题考查相似三角形的性质与判定，解题的关键是熟悉相似三角形的判定与性质与平行四边形的性质.25.如图，点B 在线段AC 上，点D ，E 在AC 的同侧，∠A ＝∠C ＝90°，BD ⊥BE ，AD ＝BC.(1)求证：AC ＝AD ＋CE ；(2)若AD ＝3，AB ＝5，点P 为线段AB 上的动点，连接DP ，作PQ ⊥DP ，交直线BE 于点Q ，当点P 与A ，B 两点不重合时，求DP PQ的值．【答案】（1）详见解析；（2）35. 【解析】试题分析：（1）根据同角的余角相等求出∠1=∠E ，再利用“角角边”证明△ABD 和△CEB 全等，根据全等三角形对应边相等可得AB=CE ，然后根据AC=AB+BC 整理即可得证；（2）过点Q 作QF ⊥BC 于F ，根据△BFQ 和△BCE 相似可得BF QF BC CE ＝，然后求出QF=53BF ，再根据△ADP 和△FPQ 相似可得AD AP PF QF＝，然后整理得到（AP-BF ）（5-AP ）=0，从而求出AP=BF ，最后利用相似三角形对应边成比例可得DP AP PQ QF＝，从而得解．试题解析：（1）∵BD ⊥BE ，∴∠1+∠2=180°-90°=90°，∵∠C=90°，∴∠2+∠E=180°-90°=90°，∴∠1=∠E ，∵在△ABD 和△CEB 中，190E A C AD BC ︒∠∠⎧⎪∠∠⎨⎪⎩＝＝＝＝，∴△ABD ≌△CEB （AAS ），∴AB=CE ，∴AC=AB+BC=AD+CE ；（2）如图，过点Q 作QF ⊥BC 于F ，则△BFQ ∽△BCE ， ∴BFQFBC CE ＝，即 35BFQF＝，∴QF=53BF ，∵DP ⊥PQ ，∴∠APD+∠FPQ=180°-90°=90°， ∵∠APD+∠ADP=180°-90°=90°， ∴∠ADP=∠FPQ ，又∵∠A=∠PFQ=90°，∴△ADP ∽△FPQ ， ∴ADAPPF QF ＝，即35APAP BF QF ＝-+，∴5AP-AP 2+AP•BF=3•53BF ，整理得，（AP-BF ）（AP-5）=0， ∵点P 与A ，B 两点不重合， ∴AP≠5，∴AP=BF ，由△ADP ∽△FPQ 得，DP APPQ QF ＝， ∴35DPPQ ＝．。

人教版九年级数学下册百分闯关习题课件27.1.1相似图形

8．观察图1，图2，并填空：
图1
图2
图2中与(1)相似的图形有_______ ①④；与(2)相似的图形有_____；
与 (3)相似的图形有______．(③⑥ 填序号) ②
9．如果图形甲与图形乙相似，图形乙与图形丙相似，那么图形甲与图形
相似丙______ ．(填“相似”或“不相似”)
10．如图所示，将下列图形分别分成四小块，使它们的形状
尺( B )
A．形状不同 B．形状相同 C．边长不成比例 D．无法比较 4 ．在上生物课时，老师让同学们利用手中的放大镜对蜗牛进相似行观察，同学们在放大镜中看到的蜗牛与实际的蜗牛是 ______ 的．(填“相似”或“不相似”)
5 ．请认真观察下面各组中的两个图形，哪些是形状相同的图形，哪些是形状不同的图形．
27.1 图形的相似
第1课时相似图形
知识点：相似图形 1．相似图形是指( D )
A．形状相同的图形
B．大小相同的图形 C．形状相同，大小不相同的图形 D．形状相同，大小不一定相同的图形 2．下列四组图形中，不是相似图形的是(
D
)
3．小玉的文具袋内有一个塑料的等腰直角三角尺，教室的讲台上有一个木制的大等腰直角三角尺，那么这两个等腰直角三角
解：③、⑤是形状相同的图形，①、②、④、⑥是形状不同的
图形．
6．下列说法正确的是( A．相似图形是全等图形 B．全等图形是相似图形
B )
C．不全等的图形不是相似图形
D．不相似的图形可能是全等图形
7．下列说法正确的有(
) D
①同一底片印出来的不同尺寸的照片是相似的；②放电影时胶片上的图像和它映射到屏幕上的图像是相似的；③放大镜放大后的图形与原来的图形是相似的；④水平观看装在带有水的透明玻璃杯中的金鱼所组成的像与金鱼本身的像是相似的． A．1个 B．2个 C．3个 D．4个

人教版九年级下册数学全册综合检测试卷(含答案解析)

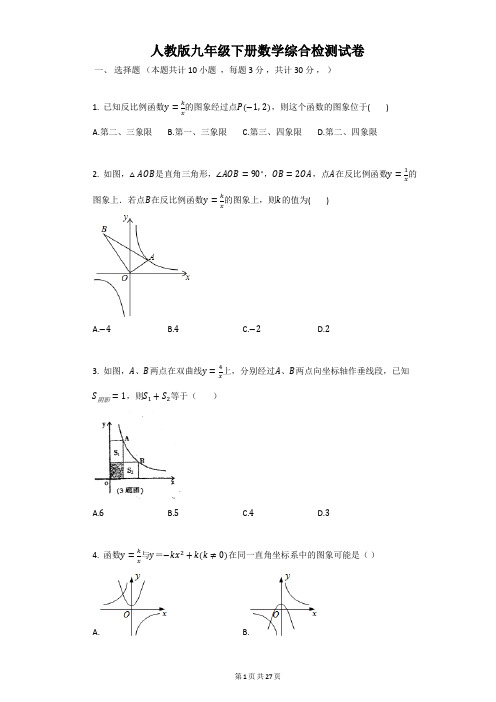
人教版九年级下册数学综合检测试卷一、选择题（本题共计 10 小题，每题 3 分，共计30分，）的图象经过点P(−1, 2)，则这个函数的图象位于( )1. 已知反比例函数y=kxA.第二、三象限B.第一、三象限C.第三、四象限D.第二、四象限2. 如图，△AOB是直角三角形，∠AOB=90∘，OB=2OA，点A在反比例函数y=1的x的图象上，则k的值为( )图象上．若点B在反比例函数y=kxA.−4B.4C.−2D.2上，分别经过A、B两点向坐标轴作垂线段，已知3. 如图，A、B两点在双曲线y=4x=1，则S1+S2等于（）S阴影A.6B.5C.4D.34. 函数y=k与y＝−kx2+k(k≠0)在同一直角坐标系中的图象可能是（）xA. B.C. D.(k≠0)的图象上一点，AB⊥y轴于B，且△5. 如图，已知A点是反比例函数y=kxABO的面积为3，则k的值为( )A.4B.5C.6D.76. 如图，△ABC中，D，E分别是AB，BC上的点，且DE // AC，若S△BDE:S△CDE=1:4，则S△BDE:S△ACD=( )A.1:16B.1:18C.1:20D.1:24(k≠0)，它们在同一坐标系中的图象大致7. 已知关于x的函数y=k(x+1)和y=−kx是（）A. B.C. D.，下列说法正确的是（）8. 关于反比例函数y=−2xA.图象过(1, 2)点B.图象在第一、三象限C.当x>0时，y随x的增大而减小D.当x<0时，y随x的增大而增大(k≠0)图象上的两个点A(x1, y1)，B(x2, y2)，当x1<x2<0时，9. 反比例函数y=kxy1>y2，那么一次函数y=−2kx+k的图象不经过（）A.第一象限B.第二象限C.第三象限D.第四象限上，且P到原点的距离为√5，则符合条件的点P个数为（）10. 已知点P在双曲线y=2xA.1个B.2个C.3个D.4个二、填空题（本题共计 4 小题，每题 3 分，共计12分，）的图象上，当1<x<4时，y的取值范围是________．11. 点A(2, 1)在反比例函数y=kx12. 如图，在平面直角坐标系中，过点M(−3,2)分别作x轴、y轴的垂线与反比例函数y=4的图象交于A、B两点，则四边形MAOB的面积为________．x(k>0)的图象交于A、B两点，点B坐13. 如图，过原点O的直线AB与反比例函数y=kx。

2016《百分闯关》人教版九年级数学下册第2课时图形的相似(2)

四、巩固练习 1．在比例尺为 1∶10 000 000 的地图上，量得甲、乙两地的距离是 30 cm，求两地的实际距离．
3 000 km
2．如图所示的两个直角三角形相似吗？为什么？
相似，因为它们的对应角相等，对应边的比相等．
3．如图所示的两个五边形相似，求未知边 a，b，c，d 的长度．
27．1 图形的相似第2课时图形的相似(2)
知识与技能知道相似图形的两个特征：对应边成比例，对应角相等．掌握判断两个多边形是否相似的方法——“如果两个多边形满足对应角相等、对应边的比相等，那么这两个多边形相似” ．过程与方法经历从生活中的事物中抽象出几何图形的过程，体会由特殊到一般的思想方法，感受图形世界的丰富多彩．
三、例题讲解例如图，四边形 ABCD 和四边形 EFGH 相似，求∠α和∠β的大小以及 EH 的长度 x.
学生通过运用相似多边形的性质正确解答出∠α和∠β的大小以及 EH 的长度 x.
解：四边形 ABCD 和四边形 EFGH 相似，它们的对应角相等．由此可得 ∠α＝∠C＝83°，∠A＝∠E＝118°，在四边形 ABCD 中， ∠β＝360°－(78°＋83°＋118°) ＝81°. 四边形 ABCD 和四边形 EFGH 相似，它们的对应边成比例．由此可得 EH EF x 24 ＝，即 AD AB 21＝18. 解得 x＝28 cm.
现、证明论证获得知识．教师只在关键处进行点拨，不足处
进行补充．鼓励学生大胆猜测、大胆验证．让学生在研究过程中渗透数学思想，有意识地培养学生的解题能力．
情感、态度与价值观在探索中培养学生与他人交流、合作的意识和品质．
重点
知道相似图形的对应角相等、对应边的比相等．

九年级数学下学期期末综合评价新版新人教版(含答案)

九年级数学下册新版新人教版：期末综合评价(时间：120分钟满分：120分)一、选择题(每小题3分，共30分)1．若反比例函数的图象经过点(－1，2)，则它的解析式是BA ．y ＝－12xB ．y ＝－2xC ．y ＝2xD ．y ＝1x2．如图所示的几何体是由一个圆柱体挖去一个长方体后得到的，则它的主视图是BA B C D3．在△ABC 中，(2cos A －2 )2＋|1－tan B |＝0，则△ABC 一定是DA ．直角三角形B ．等腰三角形C ．等边三角形D ．等腰直角三角形4．如图，以坐标原点O 为圆心，1为半径的弧分别交两坐标轴于A ，B 两点，P 是AB 上一点(不与点A ，B 重合)，连接OP ，设∠POB ＝α，则点P 的坐标是DA ．(sin α，sin α)B ．(cos α，cos α)C ．(sin α，cos α)D ．(cos α，sin α)第4题图第7题图5．若点A (x 1，3)，B (x 2，2)，C (x 3，－1)在反比例函数y ＝－|k |x(k ≠0)的图象上，则x 1，x 2，x 3的大小关系是CA ．x 1＜x 2＜x 3B ．x 3＜x 1＜x 2C ．x 2＜x 1＜x 3D ．x 3＜x 2＜x 16．已知两个直角三角形的三边长分别为3，4，m 和6，8，n ，且这两个直角三角形不相似，则m ＋n 的值为AA ．10＋7 或5＋27B ．15C ．10＋7D ．15＋377．小红在观察由一些相同小正方体搭成的几何体时，发现它的主视图、俯视图、左视图均为如图所示，则构成该几何体的小正方体有BA ．3个B ．4个C ．5个D ．6个8．构建几何图形解决代数问题是“数形结合”思想的重要运用，在计算tan 15°时，如图，在Rt △ACB 中，∠C ＝90°，∠ABC ＝30°，延长CB 到点D ，使BD ＝AB ，连接AD ，则∠D ＝15°，所以tan 15°＝AC CD ＝12＋3 ＝2－3（2＋3）（2－3）＝2－3 .类比这种方法，计算tan 22.5°的值为BA ． 2 ＋1B ． 2 －1C ． 2D ．12第8题图第9题图第10题图9．如图，已知第一象限内的点A 在反比例函数y ＝2x的图象上，第二象限内的点B 在反比例函数y ＝k x 的图象上，且OA ⊥OB ，cos A ＝33，则k 的值为B A ．－3 B ．－4 C ．－3 D ．－2310．如图，AB 是⊙O 的直径，弦CD ⊥AB 于点G ，点F 是CD 上一点，且满足CF FD ＝13 ，连接AF 并延长交⊙O 于点E ，连接AD ，DE ，若CF ＝2，AF ＝3，给出下列结论：①△ADF ∽△AED ；②FG ＝2；③tan E ＝52；④S △DEF ＝45 ．其中正确的是C A ．①②③ B ．②③④ C ．①②④ D ．①③④二、填空题(每小题3分，共24分)11．在直角三角形中，sin A 的值为12 ，则cos A 的值等于32． 12．将如图所示的图形剪去一个小正方形，使余下的部分恰好能折成一个正方体，下列序号为1，2，3，6的小正方形不能剪去的是3．(填序号)第12题图第13题图13．如图，海中有一个小岛A ，一艘轮船由西向东航行，在点B 测得小岛A 在北偏东60°方向上，航行12 n mile 到达点C ，这时测得小岛A 在北偏东30°方向上．则小岛A 到航线BC 的距离大约是10.4n mile.(3 ≈1.73，结果用四舍五入法精确到0.1)14．如图，直线l 经过点A (－2，0)和点B (0，1)，点M 在x 轴上，过点M 作x 轴的垂线交直线l 于点C ，若OM ＝2OA ，则经过点C 的反比例函数解析式为y ＝12x．第14题图第15题图15．如图，过y 轴正半轴上的任意一点P ，作x 轴的平行线，分别与反比例函数y ＝－6x和y ＝8x的图象交于点A 和点B ，若点C 是x 轴上任意一点，连接AC ，BC ，则△ABC 的面积为7．16．如图是某圆锥的主视图和左视图，则该圆锥的全面积是36π．第16题图第17题图第18题图17．如图，在已建立平面直角坐标系的4×4的正方形方格中，△ABC 是格点三角形(三角形的三个顶点是小正方形的顶点)，若以格点P ，A ，B 为顶点的三角形与△ABC 相似(全等除外)，则格点P 的坐标是(1，4)或(3，4)．18．(绥化中考)如图，在矩形ABCD 中，P 是边AD 上的一个动点，连接BP ，CP ，过点B 作射线，交线段CP 的延长线于点E ，交边AD 于点M ，且使得∠ABE ＝∠CBP ，如果AB＝2，BC ＝5，AP ＝x ，PM ＝y ，其中2<x ≤5.下列结论：①y 与x 的关系式为y ＝x －4x；②当AP ＝4时，△ABP ∽△DPC ；③当AP ＝4时，tan ∠EBP ＝35.其中正确的结论为①②．(填序号)三、解答题(共66分)19．(8分)先化简，再求值：(1－1a －2 )÷a 2－6a ＋9a 2－2a，其中a ＝2sin 60°＋3tan 45°. 解：原式＝a －2－1a －2 ·a （a －2）（a －3）2 ＝a a －3，当a ＝2sin 60°＋3tan 45°＝2×32 ＋3×1＝3 ＋3时，原式＝3＋33＋3－3＝1＋320．(8分)如图，方格纸中每个小方格都是边长为1个单位长度的正方形，在建立平面直角坐标系后，△ABC 的顶点都在格点上，其坐标分别为A (－4，－4)，B (6，－6)，C (0，－2)，请画出△ABC 并以点O 为位似中心，画出符合条件的△ABC 的所有位似图形，使之与△ABC的相似比为1∶2.解：如图，△ABC ，△A ′B ′C ′和△A ″B ″C ″即为所作21．(9分)如图，在平行四边形ABCD 中，过点D 作DE ⊥AB ，垂足为点E ，连接CE ，F 为线段CE 上一点，且∠DFE ＝∠A .(1)求证：△DFC ∽△CBE ；(2)若AD ＝4，CD ＝6，DE ＝3，求DF 的长．解：(1)证明：∵四边形ABCD 为平行四边形，∴AD ∥BC ，CD ∥AB ，∴∠A ＋∠B ＝180°，∠DCE ＝∠BEC ，∵∠DFE ＝∠A ，∴∠DFE ＋∠B ＝180°，而∠DFE ＋∠DFC ＝180°，∴∠DFC ＝∠B ，而∠DCF ＝∠CEB ，∴△DFC ∽△CBE(2)∵四边形ABCD 为平行四边形，∴CD ∥AB ，BC ＝AD ＝4，∵DE ⊥AB ，∴DE ⊥DC ，∴∠EDC ＝90°，在Rt △DEC 中，CE ＝DE 2＋DC 2 ＝32＋62 ＝35 ，∵△DFC ∽△CBE ，∴DF ∶BC ＝DC ∶CE ，即DF ∶4＝6∶35 ，∴DF ＝85522．(9分)如图，AB 是⊙O 的直径，点E 为⊙O 上一点，点D 是 AE 上一点，连接AE 并延长至点C ，使∠CBE ＝∠BDE ，BD 与AE 交于点F .(1)求证：BC 是⊙O 的切线；(2)若BD 平分∠ABE ，求证：AD 2＝DF ·BD .解：(1)证明：∵AB 是⊙O 的直径，∴∠AEB ＝90°，∴∠EAB ＋∠EBA ＝90°，∵∠CBE ＝∠BDE ，∠BDE ＝∠EAB ，∴∠EAB ＝∠CBE ，∴∠EBA ＋∠CBE ＝90°，即∠ABC ＝90°，∴CB ⊥AB ，∵AB 是⊙O 的直径，∴BC 是⊙O 的切线(2)∵BD 平分∠ABE ，∴∠ABD ＝∠DBE ，∵∠DAF ＝∠DBE ，∴∠DAF ＝∠ABD ，∵∠ADB ＝∠ADF ，∴△ADF ∽△BDA ，∴AD BD ＝DF AD ，∴AD 2＝DF ·BD23．(10分)已知Rt △ABC 的斜边AB 在平面直角坐标系的x 轴上，点C (1，3)在反比例函数y ＝k x 的图象上，且sin ∠BAC ＝35. (1)求k 的值和边AC 的长；(2)求点B 的坐标．解：(1)k ＝3，AC ＝5(2)分两种情况：①当点B 在点A 右侧时，如图①，作CD ⊥AB 于点D ，则AD ＝52－32＝4，∴AO ＝4－1＝3，易得△ACD ∽△ABC ，∴AC AB ＝AD AC ，∴AB ＝AC 2AD ＝254，∴OB ＝AB －AO ＝254 －3＝134 ，∴点B 的坐标为(134，0)；②当点B 在点A 左侧时，如图②，作CD ⊥AB 于点D ，则此时AO ＝4＋1＝5，OB ＝AB －AO ＝254 －5＝54 ，∴点B 的坐标为(－54，0).综上，点B 的坐标为(134 ，0)或(－54，0)24．(10分)如图，一架无人机静止悬浮在空中P 处，小明在山坡A 处测得无人机的仰角为45°，小亮在水平地面C 处测得无人机的仰角为58°，已知山坡AB 的坡度i ＝1∶2.4，斜坡AB 长为52米，水平地面BC 长为62米，求此时无人机离地面的高度PD 的长．(结果精确到整数，参考数据：sin 58°≈0.8，cos 58°≈0.5，tan 58°≈1.6)解：如图，过点A 作AF ⊥BC 于点F ，在Rt △ABF 中，∵山坡AB 的坡度i ＝1∶2.4，∴tan ∠ABF ＝AF BF ＝12.4 ＝512，∴设AF ＝5k 米，则BF ＝12k 米，由勾股定理，得AB ＝13k ＝52，∴k ＝4，∴AF ＝20米，BF ＝48米．过点A 作AE ⊥PD 于点E ，则AE ＝DF ，DE ＝AF ，∵∠P AE ＝45°，∴PE ＝AE ，设AE ＝PE ＝DF ＝x 米，则PD ＝PE ＋DE ＝(x ＋20)米，在Rt △PDC 中，∵∠C ＝58°，∴tan 58°＝PD CD ＝x ＋20CD ≈1.6，∴CD ＝x ＋201.6 .∵BC ＝62，AE ＋CD ＝BF ＋BC ，∴x ＋x ＋201.6＝48＋62，解得x ＝60，∴PD ＝PE ＋DE ＝60＋20＝80(米)，答：此时无人机离地面的高度PD 的长约为80米25．(12分)如图，直线y ＝－34 x ＋6与反比例函数y ＝k x (x ＞0)分别交于点B ，C (AB ＜AC )，经探索研究发现：结论AB ＝CD 始终成立．另一直线y ＝mx (m ＞0)交线段BC 于点E ，交反比例函数y ＝k x(x ＞0)的图象于点F .(1)当BC ＝5时：①求反比例函数的解析式；②若BE ＝3CE ，求点F 的坐标．(2)当BE ∶CD ＝1∶2时，请直接写出k 与m 的数量关系．解：(1)①对于直线y ＝－34x ＋6，令x ＝0，得y ＝6，∴点A (0，6)，∴OA ＝6，令y ＝0，则0＝－34x ＋6，解得x ＝8，∴点D (8，0)，∴OD ＝8，∴由勾股定理，得AD ＝10，∵BC ＝5，∴AB ＋CD ＝AD －BC ＝5，∵AB ＝CD ，∴AB ＝52，如图，过点B 作BG ⊥y 轴于点G ，∴∠AGB ＝90°＝∠AOD ，易得△ABG ∽ADO ，∴AG OA ＝BG OD ＝AB AD ，即AG 6 ＝BG 8 ＝5210，∴AG ＝32 ，BG ＝2，∴OG ＝OA －AG ＝92 ，∴点B (2，92 )，∵点B 在反比例函数y ＝k x(x ＞0)的图象上，∴k ＝2×92 ＝9，∴反比例函数的解析式为y ＝9x .②∵BC ＝5，∴BE ＋CE ＝5，∵BE ＝3CE ，∴BE ＝154 ，∴AE ＝AB ＋BE ＝254，如图，过点E 作EH ⊥y 轴于点H ，∴∠AHE ＝90°＝∠AOD ，易得△HAE ∽△OAD ，∴AH OA ＝EH OD ＝AE AD ，即AH 6 ＝EH 8 ＝25410，∴AH ＝154 ，EH ＝5，∴OH ＝OA －AH ＝94 ，∴点E (5，94)，∵点E 在直线y ＝mx (m ＞0)的图象上，∴94 ＝5m ，解得m ＝920 ，∴直线OE 的解析式为y ＝920x ，联立⎩⎨⎧y ＝9x ，y ＝920x ，解得⎩⎪⎨⎪⎧x ＝－25，y ＝－9510(舍)或⎩⎪⎨⎪⎧x ＝25，y ＝9510，∴点F 的坐标为(25 ，9510 ) (2)∵BE ∶CD ＝1∶2，∴设BE ＝a ，则CD ＝2a ，∴AB ＝CD ＝2a ，∴AE ＝AB ＋BE ＝3a ，AC ＝10－2a .如图，过点C 作CK ⊥y 轴于点K ，易得△KAC ∽△OAD ，∴KA OA ＝KC OD ＝AC AD，即KA 6 ＝KC 8 ＝10－2a 10 ，∴KA ＝30－6a 5 ，KC ＝40－8a 5 ，∴OK ＝OA －KA ＝6－30－6a 5＝6a 5 ，∴点C (40－8a 5 ，65 a )，由(1)知△HAE ∽△OAD ，∴AH OA ＝EH OD ＝AE AD ，即AH 6 ＝EH 8＝3a 10 ，∴AH ＝95 a ，EH ＝125 a ，∴OH ＝OA －AH ＝6－95 a ，∴点E (125 a ，6－95a )，将点E 坐标代入直线y ＝mx (m ＞0)中，得125 am ＝6－95 a ，解得a ＝104m ＋3 ，∴点C 的坐标为(32m ＋84m ＋3，124m ＋3 )，∵点C 在反比例函数y ＝k x (x ＞0)的图象上，∴k ＝32m ＋84m ＋3 ×124m ＋3＝96（4m ＋1）（4m ＋3）2。

九下综合测试(基础过关)-2022-2023学年九年级数学下册单元过关测试定心卷(人教版)(解析版)

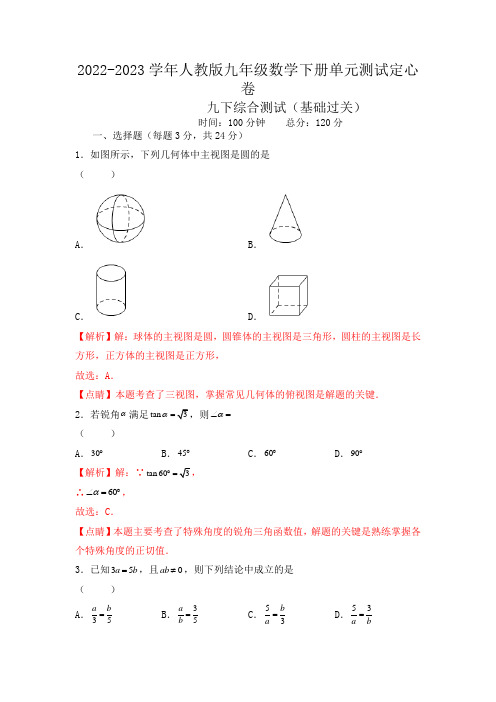
2022-2023学年人教版九年级数学下册单元测试定心卷九下综合测试（基础过关）时间：100分钟总分：120分一、选择题（每题3分，共24分）1．如图所示，下列几何体中主视图是圆的是（）A ．B ．C ．D ．【解析】解：球体的主视图是圆，圆锥体的主视图是三角形，圆柱的主视图是长方形，正方体的主视图是正方形，故选：A ．【点睛】本题考查了三视图，掌握常见几何体的俯视图是解题的关键． 2．若锐角α满足tan 3α=α∠= （） A ．30︒B ．45︒C ．60︒D ．90︒【解析】解：∵tan 603︒= ∴60α∠=︒，故选：C ．【点睛】本题主要考查了特殊角度的锐角三角函数值，解题的关键是熟练掌握各个特殊角度的正切值．3．已知35a b =，且0ab ≠，则下列结论中成立的是（） A ．35ab =B ．35a b =C ．53b a =D ．53a b=【解析】解：A 、等式的左边除以2，右边除以3，等式不成立，故A 错误； B 、等式的两边除以3b ，得到53a b=，故B 错误； C 、等式两边同时除以15，得到53a b =，故C 错误； D 、等式两边同时除以ab ，得到35ba =，故D 正确；故选：D ．【点睛】本题考查了比例的性质，利用了等式的性质2：等式的两边都乘以或除以同一个不为零的数或整式，结果不变．4．已知点(1,2)A -是某反比例函数图象上的一点，则该反比例函数解析式是（） A ．2y x =-B ．2y x=-C ．12y x=-D ．12y x =-【解析】解：设反比例函数表达式为k y x= ∵点(1,2)A -是某反比例函数图象上的一点 ∴21k=-，解得2k =- ∴反比例函数表达式为2y x=-．故选：B ．【点睛】本题主要考查了反比例函数解析式与坐标的关系，解题的关键在于能够熟练掌握反比例函数解析式的求法．5．有阳光的某天下午，小明在不同时刻拍了相同的三张风景照A ，B ，C ，冲选后不知道拍照的时间顺序了，已知投影长度>>A C B l l l ，则A ，B ，C 的先后顺序是（） A ．A 、B 、CB ．A 、C 、BC ．B 、A 、CD ．B 、C 、A【解析】解：由题意可得：都是下午拍摄，影子越长说明太阳倾斜越大， ∵投影长度>>A C B l l l ，∴A ，B ，C 的先后顺序是B 、C 、A ．故选：D ．【点睛】此题主要考查了平行投影，正确掌握平行投影的性质是解题关键．6．若在ABC 中，90?C ∠=，13AB =，12AC =，则cos B 的值是（） A ．125B ．135C ．513D ．1213【解析】解：∵90?C ∠=，13AB =，12AC =， ∴222213125BC AB AC --， ∴5cos 13BC B AB ==，故选：C ．【点睛】本题考查解直角三角形，熟练掌握勾股定理和余弦定义是解题的关键． 7．如图，如果BAD CAE ∠=∠，那么添加下列一个条件后，仍不能确定ABC ADE ∽△△的是（）A ．B D ∠=∠ B ．C AED ∠=∠ C ．AB BC AD DE ⋅=⋅D ．AB AE AD AC ⋅=⋅【解析】解：∵BAD CAE ∠=∠， ∴EAD CAB ∠=∠，A ．若添加B D ∠=∠，可用两角对应相等的两个三角形相似，证明ABC ADE ∽△△，故本选项不符合题意；B ．若添加C AED ∠=∠，可用两角对应相等的两个三角形相似，证明ABC ADE ∽△△，故本选项不符合题意；C ．若添加AB BC AD DE ⋅=⋅，不能证明ABC ADE ∽△△，故本选项符合题意； D ．若添加AB AE AD AC ⋅=⋅，可用两边对应成比例，且夹角相等的两个三角形相似，证明ABC ADE ∽△△，故本选项不符合题意；故选：C ．【点睛】本题主要考查了相似三角形的判定，熟练掌握相似三角形的判定定理是解题的关键．8．已知点A (x 1，m )，B (x 2，n )是直线1y ax b 与双曲线2aby x=的两个交点，若120x x <<，则m ，n 的大小关系是（） A ．m n <B ．m n =C ．m n >D ．不能确定【解析】解：∵120x x <<，∴点A 和点B 都在第二象限或第三象限，当点A 和点B 都在第二象限时，如图，直线1y ax b 经过第一、二、三象限，∴00a b >>，， ∴0ab >，不满足双曲线2aby x=位于第二、四象限，舍去；当点A 和点B 都在第三象限时，如图，直线1y ax b 经过第二、三、四象限，∴00a b <<，， ∴0ab >，满足双曲线2aby x=位于第一、三象限，在每个象限内，在每个象限内，y 随x 的增大而减少， ∵120x x <<，∴m n >．故选：C ．【点睛】本题考查了反比例函数与一次函数的综合题，掌握两函数图象的交点坐标满足两函数解析式是解题的关键．二、填空题（每题3分，共24分） 9．如图，在ABC 中，EF BC ∥，12AE EB =，则ΔΔAEF ABC S S =___________．【解析】解：∵12AE EB =， ∴13AE AB =． ∵EF BC ∥， ∴AEF ABC ∽．∴2AEF ABCS AE SAB ⎛⎫== ⎪⎝⎭213⎛⎫⎪⎝⎭19=．故答案为：9．【点睛】本题考查了相似三角形的判定和性质，解题的关键是掌握相似三角形的面积比等于相似比的平方．10．若::1:3:5a b c =，则2524a b ca b c --=++__．【解析】::1:3:5a b c =，∴设a k =，则3b k =，5c k =， ∴25625301024620279a b c k k k k a b c k k k k -----===-++++．故答案为：109-【点睛】本题主要考查了比例的基本性质，熟练掌握比例的基本性质是解题的关键．11．如图，某仓储中心有一斜坡，斜坡顶部A 处的高AC 为2米，B C 、在同一水平面上，若该斜坡的坡度=1:2i ，则该斜坡的水平宽度BC 为_________米．【解析】∵斜坡AB的坡度=1:2i，∴12 AC BC=∴24BC AC==米，故答案为：4．【点睛】本题考查坡度的概念，熟记坡度是铅垂高与水平宽的比（类似于正切的计算公式）是本题的解题关键．12．如图，是由一些完全相同的小正方体搭成的几何体的主视图和俯视图，则这个几何体最多由______个小正方体搭成．【解析】解：由主视图和俯视图可得：最多由1+3+3=7个小正方体搭成．故答案为：7.【点睛】本题主要考查学生对三视图掌握程度和灵活运用能力，由三视图想象几何体的形状，首先应分别根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状，然后综合起来考虑整体形状．13．如图，点A是反比例函数2(0)y xx=>的图象上任意一点，AB x轴交反比例函数3yx=-的图象于点B，点C在x轴上，连接AC BC、，则ABCS为___________．【解析】如图，连接AO BO ，，设AB 与y 轴交于点D ．∵ABx 轴，∴ABC 和ABO 同底等高， ∴ABCABOS S =．∵ABOBOD AOD SSS =+，3231222BODAODSS -====，， ∴35122ABCS=+=．故答案为：52．【点睛】本题主要考查反比例函数比例系数k 的几何意义．正确的作出辅助线是解题关键．14．如图，ABC 的顶点都在格点上，cos BAC ∠=______．【解析】解：如图所示，作BD AC ⊥于D ，5BC =，22345AB +，221310AC +∴ABC 为等腰三角形， ∴102AC AD ==， ∴10102cos 5AD BAC AB ∠===10【点睛】本题考查了等腰三角形三线合一，解直角三角形，正确构造直角三角形是解题关键．15．如图，四边形OABC 是矩形，四边形ADEF 是正方形，点A 、D 在x 轴的负半轴上，点C 在y 轴的正半轴上，点F 在AB 上，点B 、E 在反比例函数k y x=（k 为常数，0k ≠）的图像上，正方形ADEF 的面积为4，且2BF AF =，则k 值为_____________．【解析】解：∵正方形ADEF 的面积为4， ∴正方形ADEF 的边长为2，∴24BF AF ==，246AB AF BF =+=+=．设B 点坐标为(6)t ，，则E 点坐标(22)t -，， ∵点B 、E 在反比例函数ky x=的图像上， ∴62(2)k t t ==-，解得16t k =-=-，．故答案为：6-．【点睛】本题考查了反比例函数图像上点的坐标特征：反比例函数ky x=（k 为常数，0k ≠）的图像是双曲线，图像上的点()，x y 的横纵坐标的积是定值k ，即xy k =．16．如图，在平面直角坐标系中，△ABC 的顶点A 、B 均在函数6y x=（x ＞0）的图象上，点C 在y 轴正半轴上，AC ＝BC ，∠ACB ＝90°．若点B 的横坐标是点A 横坐标的2倍，则△ABC 的面积为 _____．【解析】解：过点A 作AM ⊥y 轴于点M ，过点B 作BN ⊥y 轴于点N ，设点A 的坐标为6,a a⎛⎫⎪⎝⎭，C （0，c ），则B 32,a a ⎛⎫⎪⎝⎭，∴AM ＝a ，BN ＝2a ，OC ＝c ，CM ＝6c a -，CN ＝3c a-， ∵AC ＝BC ，∠ACB ＝90°，∴∠CAM +∠ACM ＝90°，∠ACM +∠BCN ＝90°， ∴∠CAM ＝∠BCN ， ∵∠CMA ＝∠BNC ＝90°， ∴△CAM ≌△BCN （AAS ）， ∴CM ＝BN ，AM ＝CN ，即6=23=c a a a c a --⎧⎪⎪⎨⎪⎪⎩，解得=1=4a c ⎧⎨⎩或=1=4a c --⎧⎨⎩（舍），∴AM ＝1，CM ＝3， ∴222+10AC AM CM ＝＝， ∴212.52ABCSAC ＝＝．故答案为：2.5【点睛】本题考查了反比例函数的性质，反比例函数图象上点的坐标特征，全等三角形的判定和性质，等腰直角三角形的性质，构造全等三角形是本题的关键．二、解答题（每题8分，共72分）17．如图，是由5个完全相同的小正方体组成的一个几何体，请画出这个几何体的从正面看，从左面看和从上面看的平面图形．（用阴影表示）【解析】如图所示，【点睛】本题主要考查几何体的三视图，解题的关键是对几何体结构的分析，培养学生的空间思维能力．18．如图，在ABC 中，D 、E 在边AB 、AC 上，DE BC ∥，DE =3，AC =5，1EC =，求BC 的长度．【解析】解∵DE BC ∥，∴ADE ABC ∆∆∽，∵5,1AC EC ==，∴4AE AC EC =-=， ∴DE AE BC AC=，即DE AE BC AC =，345BC = ， ∴154BC =．【点睛】本题考查相似三角形的判定与性质．解题的关键是证明ADE ABC ∆∆∽．19．如图所示，点B ，C ，D 在同一条直线上，且BC CD =，点A 和点E 在BD 的同侧，且ACE B D ∠=∠=∠．(1)证明：ABC CDE ∽△△；(2)若2BC =，3AB =，求DE 的长度．【解析】（1）证明：∵180A B ACB ∠=︒-∠-∠，180ECD ACE ACB ∠=︒-∠-∠，ACE B ∠=∠， ∴A ECD ∠=∠，∵B D ∠=∠，∴ABC CDE ∽△△．（2）解：由（1）可知，ABC CDE ∽△△， ∴AB BC CD DE=， ∵BC CD =，2BC =，∴2CD =，∵3AB =，。

人教版九年级数学下册百分闯关习题课件28.2.2.2坡度、方位角与解直角三角形

7．如图，一个小球由地面沿着坡度 i＝1∶2 的坡面向上前进了 10 m，此时小球距离地面的高度为(
D
ห้องสมุดไป่ตู้
)
10 A．5 m B. 3 m C．4 5 m D．2 5 m
8．(2015· 济宁)如图，斜面 AC 的坡度(CD 与 AD 的比)为 1∶2， AC＝3 5米，坡顶有旗杆 BC，旗杆顶端 B 点与 A 点有一条彩带相连．若 AB＝10 米，则旗杆 BC 的高度为( A ) A．5 米 B．6 米 C．8 米 D．(3＋ 5)米
28．2 解直角三角形及其应用
28．2.2 应用举例
第2课时坡度、方位角与解直角三角形
知识点1：利用方向角解直角三角形 1．(2015·南充)如图，一艘海轮位于灯塔P的北偏东55°方向，距离灯塔2海里的点A处，如果海轮沿正南方向航行到灯塔的正东
方向，则海轮航行的距离AB长是(
A．2海里 B．2sin55°海里
解：在 Rt△ADB 中，∵∠ADB＝90°， 1 ∠BAD＝30°，AB＝200，∴BD＝2AB＝100. 在 Rt△CEB 中，∵∠CEB＝90°，∠CBE＝42°，CB＝200，∴CE＝ BC•sin42°≈200×0.67＝134，∴BD＋CE＝100＋134＝234.故缆车从点 A 运行到点 C 的垂直上升的距离约为 234 m
D
)
11 ．如图，河堤横断面是梯形，上底为 4 m ，堤高为 6m ，斜坡 AD的坡度为1∶3，斜坡BC的坡角为45°，则河堤的横断面积为 ( A ) A．96 m2 B．48 m2 C．192 m2 D．84 m2
12．(2015· 十堰)如图，小华站在河岸上的 G 点，看见河里有一小船沿垂直于岸边的方向划过来．此时，测得小船 C 的俯角是∠FDC＝ 30°，若小华的眼睛与地面的距离是 1.6 米，BG＝0.7 米，BG 平行于 AC 所在的直线，迎水坡 i＝4∶3，坡长 AB＝8 米，点 A，B，C，D， F 、 G 在同一平面内，则此时小船 C 到岸边的距离 CA 的长为

第二十九章投影与视图(测能力)——2022-2023学年人教版数学九年级下册单元闯关双测卷

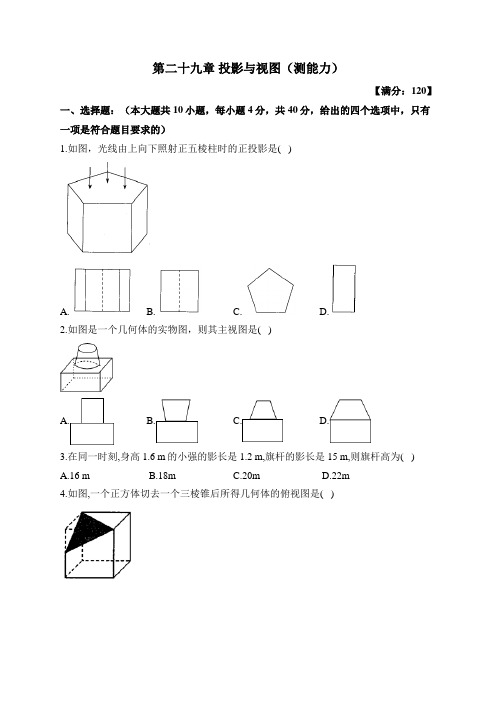
第二十九章投影与视图（测能力）【满分：120】一、选择题：（本大题共10小题，每小题4分，共40分，给出的四个选项中，只有一项是符合题目要求的）1.如图，光线由上向下照射正五棱柱时的正投影是( )A. B. C. D.2.如图是一个几何体的实物图，则其主视图是( )A. B. C. D.3.在同一时刻,身高1.6 m的小强的影长是1.2 m,旗杆的影长是15 m,则旗杆高为( )A.16 mB.18mC.20mD.22m4.如图,一个正方体切去一个三棱锥后所得几何体的俯视图是( )A. B. C. D.5.如图，一个正方体纸盒的六个面上填有不同的数或式，从不同方向看到的情形如图所示，如果相对两个面上的数或式的值互为相反数，则2022+-的值为( )a c x()A.1B.-1C.0D.20226.如图，夜晚，小亮从点A处经过路灯C的正下方沿直线走到点B处，他的影长y随他与点A之间的距离x的变化而变化，那么表示y与x之间的函数关系的图象大致为( )A. B. C. D.7.如图是一个几何体的三视图,根据图中数据计算这个几何体的侧面积是( )A.224πcm D.230πcm15πcm C.212πcm B.28.如图，某剧院舞台上的照明灯P射出的光线形成“锥体”，该“锥体”截面图的“锥角”是60°.已知舞台ABCD是边长为6m的正方形，要使灯光恰好能照射到整个舞台，则照明灯P悬挂的高度是( )m B. C.A.9.用小立方块搭成的几何体，从正面看和从上面看的形状图如下，则组成这样的几何体需要的立方块个数为( )A.最多需要8块，最少需要6块B.最多需要9块，最少需要6块C.最多需要8块，最少需要7块D.最多需要9块，最少需要7块10.如图,路灯距地面8 m,身高1.6 m的小明从点A处沿AO所在的直线行走14 m到,点B 处时,人影的长度( )A.变长3.5mB.变长2.5mC.变短3.5mD.变短2.5m二、填空题（每小题4分，共20分）11.如图所示的几何体中，主视图与左视图都是长方形的是____________.12.如图是某几何体的三视图，根据图中所标的数据求得该几何体的体积为________.13.如图,一位同学身高 1.6AF =米,晚上站在路灯(线段OE )下,他在地面上的影长2AB =米,若他沿着影子的方向移动2米到B 点站立时,影长增加了0.5米,则路灯的高度是________米.14.如图是置于水平地面上的一个球形储油罐，小敏想测量它的半径.在阳光下，他测得球的影子的最远点A 到球罐与地面接触点B 的距离是10米（如图，10AB =米）；同一时刻，他又测得竖直立在地面上长为1米的竹竿的影子长为2米，那么，球的半径是___________米.15.三棱柱的三视图如图所示,EFG △中,8cm,12cm,30EF EG EGF ==∠=︒,则AB 的长为_________cm.三、解答题（本大题共6小题，共计60分，解答题应写出演算步骤或证明过程）16.（8分）画出如图所示何体的三视图.17.（8分）如图所示，阳光透过长方形玻璃投射到地面上，地面上出现一个明亮的平行四边形.已知太阳光线与地面的夹角为30°，AB与A B''在同一平面内，且AB A B''⊥，A B''=米，试求AB的长（结果保留根号）.318.（10分）学校食堂厨房的桌子上整齐地摆放着若干个相同规格的碟子，每一摞碟子的个数与碟子的高度的关系如下表:（1）当桌子上放有x个碟子时，请写出碟子的高度；(用含x的式子表示)（2）分别从三个方向上看，其三视图如图所示，厨房师傅想把它们整齐叠成一摞，求叠成一摞后的高度.19.（10分）在生活中需测量一些球(如足球、篮球…)的直径,某校研究性学习小组,通过实验发现下面的测量方法:如图所示,将球放在水平的桌面上,在阳光的斜射下,得到球的影子长度为AB.设光线,DA CB分别与球相切于点,E F,则线段EF即为球的直径.若测得40cm,30=∠=︒,请你计算球的直径.AB ABC20.（12分）一个长方体的三视图如图所示.若其俯视图为正方形，求这个长方体的表面积.21.（12分）学习投影后,小红、小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时间,身高为1.6 m的小红(AB)的影子BC的长是3,而小颖(EH)刚好在路灯灯泡的正下方H点,并测得6mHB=.(1)请在图中画出形成影子的光线,并确定路灯灯泡所在的位置G;(2)求路灯灯泡的垂直高度GH;(3)如果小红沿线段BH 向小颖(EH )走去,当小红走到BH 中点1B 处时,求其影子11B C 的长;当小红继续走剩下路程的13到2B 处时,求其影子22B C 的长;当小红继续走剩下路程的14到3B 处,…，按此规律继续走下去,当小红走剩下路程的11n 到n B 处时,其影子n n B C 的长为__________m(直接用n 的代数式表示).答案以及解析1.答案：C 解析：如图所示：故选C. 2.答案：C解析：从正面看可得到一个矩形和一个下底和矩形相邻的梯形的组合图. 故选：C. 3.答案：C解析：根据同一时刻物高与影长成正比例可得1.61.215=旗杆高,解得旗杆高为20 m. 4.答案：D解析：俯视图是由上向下观察物体得到的,结合选项可知D 正确.故选D. 5.答案：A 解析：由图可知：a b +与c d +为相对面，a b -与 c d -为相对面，x 与-1为相对面，相对两个面上的数或式的值互为相反数，()a b c d ∴+=-+①， ()a b c d -=--②，1x =，∴①+②得：2a c d c d =---+，22a c =-， 220a c +=， 0a c ∴+=，20222022()(01)1a c x ∴+-=-=.故选：A.6.答案：A解析：夜晚，小亮从点A 处经过路灯的正下方沿直线走到点B 处，其与灯杆的距离先变近后变远，则路灯下的影子先变短，后变长，当小亮走到路灯的正下方时，影长为0，故选项A 中的图象符合题意. 7.答案：B解析：由三视图知,该几何体是底面半径为3 cm 、高为4 cm 的圆锥.∴母线长为()25(cm).π3515πcm S ∴=⨯⨯=圆锥侧.8.答案：A解析：如图，连接AC ，PO ，易知O 在AC 上，PO AC ⊥.60APC ∠=︒，PA PC =，60PAC PCA ∴∠=∠=︒，PA PC AC ∴==，四边形ABCD 是边长为6m 的正方形，AC ∴=，OC ∴=，PC AC ==，PO ∴=，故选A.9.答案：C解析：由主视图可得：这个几何体共有3层，由俯视图可知第一层正方体的个数为4，由主视图可知第二层最少为2块，最多的正方体的个数为3块，第三层只有一块，故：最多为3418++=个，最少为2417++=个，故选C. 10.答案：C解析：设小明在A 处时影长为m,x AO 长为m a ,在B 处时的影长为m y 如图,,////AC OP BD OP ,,ACM OPM BDN OPN ∴∽∽△△△△，,MA AC BN BDMO OP ON OP∴==，则1.6 1.6,8148x y x a y a ==++-， 11, 3.544x a y a ∴==-，3.5x y ∴-=，故人影的长度变短3.5 m.11.答案：（1）（3）（4）解析：图（2）的左视图为三角形，图（5）的主视图和左视图为等腰梯形，主视图与左视图都是长方形的是（1）（3）（4）. 12.答案：136π解析：由三视图知该几何体由大小两个圆柱构成，且处于横放的状态大圆柱的底面直径为8，高为8；小圆柱的底面直径为4，高为2.故该几何体的体积为22π22π488π128π136π⨯⨯+⨯⨯=+=. 13.答案：8解析：设路灯高为x 米,当人在A 点时,影长2AB =米,当人在B 点时,影长20.5 2.5BC =+=(米),所以,x OC x OB BD BC AF AB ==,即 2.5,1.6 2.5 1.62x OC x OC -==,解得8x =,即路灯的高度为8米.14.答案：20) 解析：设半径为r ，竖直立在地面上长为1米的竹竿的影子长为2米，5BC ∴=米.由O 点向AC 作垂线，垂足为D ，则易证ABC ODC ，所以COD A ∠=∠，则 CO 又5CO BO +=，所以102)20)r =÷=米.15.答案：6解析：如图,过点E 作EQ FG ⊥于点Q ,由题意可得,EQ AB =.12,30EG cm EGF =∠=,11sin 126(cm)22AB EQ EG EGF EG ∴==⋅∠==⨯=.16.答案：几何体的三视图如图所示：17.答案：如图，过点A 作//AC A B ''交BB '于C ，则3AC A B ''==，30ACB ∠=︒，90BAC ∠=︒.tan 3AB AC ACB ∴=⋅∠==AB ∴.18.答案：（1）由题意可知，当桌子上放有x 个碟子时，此时碟子的高度为2 1.5(1)(1.50.5)cm x x +-=+.（2）由三视图可知共有12个碟子，所以叠成一摞的高度为1.5120.518.5(cm)⨯+=.19.答案：20 cm解析：如图,过点A 作AG BC ⊥于点G .,DA BC 分别与球相切于点,E F ,,EF DE EF BC ∴⊥⊥,∴四边形AEFG 是矩形,EF AG ∴=.在Rt ABG △中,40cm,30AB ABC =∠=,1sin304020(cm)2AG AB ∴=⋅=⨯=, 20cm EF AG ∴==,即球的直径为20 cm.20.答案：解：连接AB ，则 4.AB CE ==222,,3,AC BC AB AC BC AC BC +==∴== ∴正方形ADBC 的面积为339⨯=，侧面面积为443448AC CE ⋅=⨯⨯=，故这个长方体的表面积为489966++=.21.答案：(1)(2)4.8 m (3)31n n B C n =+ 解析：(1)如图所示.(2)/,,/AB HC GH HC AB GH ⊥⊥∴,,AB BC ABC GHC GH HC ∴∴=∽△△. 1.6m,3m,6m AB BC HB ===, 1.63, 4.8m 63GH GH ∴=∴=+. (3)同(2)得1111A B C GHC ∽△△， 11111A B B C GH HC ∴=. 设11B C 长为m x ,则1.64.83x x =+，解得 1.5x =,即11 1.5m B C =. 同理，22221.64.82B C B C =+，解得221m B C =. 1.614.861n n n n B C B C n ∴=+⋅+, 解得3m 1n n B C n =+.。

人教版九年级数学(下册)期末综合能力测试卷及答案

人教版九年级数学(下册)期末综合能力测试卷及答案班级：姓名：一、选择题（本大题共10小题，每题3分，共30分）1．﹣2020的倒数是（）A ．﹣2020B ．﹣12020C ．2020D ．12020 2．若点A （1+m ，1﹣n ）与点B （﹣3，2）关于y 轴对称，则m+n 的值是（）A ．﹣5B ．﹣3C ．3D ．13．下列结论成立的是（）A ．若|a|＝a ，则a ＞0B ．若|a|＝|b|，则a ＝±bC ．若|a|＞a ，则a ≤0D ．若|a|＞|b|，则a ＞b ．4．今年一季度，河南省对“一带一路”沿线国家进出口总额达214.7亿元，数据“214.7亿”用科学记数法表示为（）A ．2.147×102B ．0.2147×103C ．2.147×1010D ．0.2147×10115．下列说法正确的是（）A ．负数没有倒数B ．﹣1的倒数是﹣1C ．任何有理数都有倒数D ．正数的倒数比自身小6．若三点()1,4，()2,7，(),10a 在同一直线上，则a 的值等于（）A ．-1B ．0C ．3D ．47．如图，将一张含有30角的三角形纸片的两个顶点叠放在矩形的两条对边上，若244∠=，则1∠的大小为（）A ．14B ．16C ．90α-D ．44α-8．填在下面各正方形中四个数之间都有相同的规律，根据这种规律m 的值为（）A ．180B ．182C ．184D ．1869．如图，两个较大正方形的面积分别为225、289，且中间夹的三角形是直角三角形，则字母A 所代表的正方形的面积为（）A ．4B ．8C ．16D ．6410．两个一次函数1y ax b 与2y bx a ，它们在同一直角坐标系中的图象可能是（）A ．B ．C ．D ．二、填空题（本大题共6小题，每小题3分，共18分）181__________．2．因式分解：3269a a a -+=_________.3．已知直角三角形的两边长分别为3、4．则第三边长为________．4．如图，点A 在双曲线1y=x 上，点B 在双曲线3y=x上，且AB ∥x 轴，C 、D 在x 轴上，若四边形ABCD 为矩形，则它的面积为__________．5．如图所示，直线a 经过正方形ABCD 的顶点A ，分别过正方形的顶点B 、D 作BF ⊥a 于点F ，DE ⊥a 于点E ，若DE ＝8，BF ＝5，则EF 的长为__________．6．现有下列长度的五根木棒：3，5，8，10，13，从中任取三根，可以组成三角形的概率为________．三、解答题（本大题共6小题，共72分）1．解方程: 22142x x x +=--2．先化简代数式1﹣1x x-÷2212x x x -+，并从﹣1，0，1，3中选取一个合适的代入求值．3．如图，点A 、D 、C 、F 在同一条直线上，AD=CF ，AB=DE ，BC=EF.(1)求证：ΔABC ≌△DEF ；(2)若∠A=55°，∠B=88°，求∠F 的度数.4．如图，正方形ABCD中，M为BC上一点，F是AM的中点，EF⊥AM，垂足为F，交AD的延长线于点E，交DC于点N．（1）求证：△ABM∽△EFA；（2）若AB=12，BM=5，求DE的长．5．随着科技的进步和网络资源的丰富，在线学习已成为更多人的自主学习选择.某校计划为学生提供以下四类在线学习方式：在线阅读、在线听课、在线答题和在线讨论.为了解学生需求，该校随机对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查，并根据调查结果绘制成如下两幅不完整的统计图.根据图中信息，解答下列问题：（1）求本次调查的学生总人数，并补全条形统计图；（2）求扇形统计图中“在线讨论”对应的扇形圆心角的度数；（3）该校共有学生2100人，请你估计该校对在线阅读最感兴趣的学生人数.61．某企业设计了一款工艺品，每件的成本是50元，为了合理定价，投放市场进行试销．据市场调查，销售单价是100元时，每天的销售量是50件，而销售单价每降低1元，每天就可多售出5件，但要求销售单价不得低于成本．(1)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式；(2)求出销售单价为多少元时，每天的销售利润最大？最大利润是多少？(3)如果该企业要使每天的销售利润不低于4000元，那么销售单价应控制在什么范围内？参考答案一、选择题（本大题共10小题，每题3分，共30分）1、B2、D3、B4、C5、B6、C7、A8、C9、D10、C二、填空题（本大题共6小题，每小题3分，共18分）1、±32、2(3)a a -3、54、25、136、25三、解答题（本大题共6小题，共72分）1、x=-32、-11x +，-14 ． 3、（1）略；（2）37°4、（1）略；（2）4.95、（1）90人，补全条形统计图见解析；.（2）48︒；（3）560人.6、（1）y=﹣5x 2+800x ﹣27500（50≤x ≤100）；（2）当x=80时，y 最大值=4500；（3）70≤x ≤90.。

第27章相似人教版数学九年级下册单元闯关双测卷A及答案

第二十七章相似（测基础）——2022-2023学年人教版数学九年级下册单元闯关双测卷【满分：120】一、选择题：（本大题共10小题，每小题4分，共40分，给出的四个选项中，只有一项是符合题目要求的）1.在比例尺是1:38 000的黄浦江交通游览图上,某隧道长约7cm,它的实际长度约为( )A.266 kmB.26.6kmC.2.66kmD.0.266km2.如图，在中，E是AB的中点，EC交BD于点F，那么EF与CF的比是( )A.1:2B.1:3C.2:1D.3:13.如图，以点O为位似中心，作四边形ABCD的位似图形﹐已知，若四边形ABCD的面积是2，则四边形的面积是( )A.4B.6C.16D.184.如图,小明为了测量一凉亭的高度(顶端A到水平地面的距离),在凉亭的旁边放置一个与凉亭台阶等高的台阶米,三点共线),把一面镜子水平放置在平台上的点G处,测得米,然后沿直线后退到点E处,这时恰好在镜子里看到凉亭的顶端A,测得米,小明身高米,则凉亭的高度约为( )A.8.5米B.9米C.9.5米D.10米5.如图,在矩形中,,在上取一点E,沿将向上折叠,使B点落在上的F点处,若四边形与矩形相似,则( )A. B. C. D.26.如图,已知都与垂直,垂足分别是,且,那么的长是( )A. B. C. D.7.如图,在中,,,则的长为( )A.6B.8C.10D.128.如图，矩形纸片ABCD，，点E，F分别在AD，BC上，把纸片如图沿EF折叠，点A，B的对应点分别为，，连接并延长交线段CD于点G，则的值为( )A. B. C. D.9.如图，是的直径，弦于点E，连接，过点O作于点F.若，则的长度是( )A.3cmB.cmC.2.5cmD.cm10.如图，正方形ABCD中，M为BC上一点，，ME交AD的延长线于点E.若，，则DE的长为( )A.18B.C.D.二、填空题（每小题4分，共20分）11.两个相似三角形对应中线的比为2:3,周长的和是20,则这两个三角形的周长分别为_______.12.如图,四边形与四边形是以O为位似中心的位似图形,满足分别是的中点,则__________.13.如图,小明在A时测得某树的影长为2m,在B时又测得该树的影长为8m,若两次日照的光线互相垂直,则树的高度为__________m.14.如图,的边上有一点D,边的延长线上有一点E,且交于点F,若,则______________.15.如图，在中，，，，点P在边AC上，的半径为1.如果与边BC和边AB都没有公共点，那么线段PC长的取值范围是___________.三、解答题（本大题共6小题，共计60分，解答题应写出演算步骤或证明过程）16.（8分）如图，在中，D为AC边上一点，，，.求证：.17.（8分）如图，AD平分，过点D作于点M，的延长线于点N ，且.（1）求证：.（2）若，,求BD的长.18.（10分）在平面直角坐标系内，的顶点位置如图所示.（1）将作平移变换得到，画出；（2）以点O为位似中心缩小得到，使与的相似比为，且点A与其对应点位于点O的两侧，画出.19.（10分）如图，为了测量一栋楼的高度OE，小明同学先在操场上的A处放一面镜子，向后退到B处，恰好在镜子中看到楼的顶部E，再将镜子放到C处，后退到D 处，恰好再次在镜子中看到楼的顶部E（O，A，B，C，D在同一条直线上），测得m, m，小明的眼睛距地面的高度BF，DG为1.6 m，试确定楼的高度OE.20.（12分）如图，在中，点D，E，F分别在AB，BC，AC边上，，.（1）求证：.（2）设，①若，求线段BE的长；②若的面积是20，求的面积.21.（12分）如图：（1）某学校“智慧方园”数学社团遇到这样一个题目：如图1，在中，点O在线段上，，，，，求的长．经过社团成员讨论发现，过点B作，交的延长线于点D，通过构造就可以解决问题（如图2）．请回答：_______，_______．（2）请参考以上解决思路，解决问题：如图3，在四边形中，对角线与相交于点，，，，求的长．答案以及解析1.答案：C解析：设隧道的实际长度是,根据题意得,解得,.2.答案：A解析：由平行四边形的性质可知：，，点E是AB的中点，，故选A.3.答案：D解析：解：由题意可知，四边形ABCD与四边形相似，由两图形相似面积比等于相似比的平方可知：，又四边形ABCD的面积是2，四边形的面积为18，故选：D.4.答案：A解析：由题意可知.又,，,，米，(米).5.答案：B解析：设,.∵四边形与矩形相似,,即,解得(负值合去),经检验是原分式方程的解.故选B.6.答案：C解析：都与垂直,,,.同理,，,故选C.7.答案：C解析：,四边形是平行四边形,,,故选C.8.答案：A解析：如图，过点F作于点H，由四边形ABCD是矩形，可得四边形ABFH 是矩形，故.令EF与AG的交点为O，则由折叠的性质，得，即，.又，.又，，.9.答案：D解析：如图，连接.是的直径，弦于点，在中，，即，解得，.在中，.,,即.解得.故选D.10.答案：B解析：四边形ABCD是正方形，，，.，，.，，，，，即，解得，.，，，，，即，解得.故选B.11.答案：8和12解析：这两个相似三角形对应中线的比为2:3,∴这两个相似三角形的周长比为2:3.设这两个三角形的周长分别为,则,解得.,即这两个三角形的周长分别为8和12.12.答案：解析：,即四边形与四边形的相似比为,又分别是的中点,.13.答案：4解析：根据题意,画出如下图形.所以.由题意可证得,所以,即.所以.故树的高度为4m.14.答案：24解析：如图,作交于点G....15.答案：解析：在中，，，，.当与AB相切时，设切点为D，如图，连接PD，则，.，，，，，，线段PC长的取值范围是.16.答案：证明见解析解析：，，，，，，又.17.答案：（1）平分，，，，，又，，（2）又，是等腰直角三角形，,即有：.18.答案：（1）如图，为所求作三角形.（2）如图，为所求作三角形.19.答案：如图，设E关于O的对称点为M，延长GC与FA，易知GC、FA的延长线相交于点M，连接GF并延长，交OE于点H.易知，，，，，.答：楼的高度OE为32 m.20.答案：（1）见解析（2）①；②45解析：（1）证明：，，，，；（2）①，，，，解得：；②，∴，，，，.21.答案：(1)75，．(2)解：过点B作交于点E,,,,,,,,在中，即,得在中，即,得.。

2016《百分闯关》人教版九年级数学下册第1课时平行线分线段成比例

解：(1)∵EF∥BC， AE AF ∴EB＝FC. ∵AE＝7，EB＝5，FC＝4， AE·FC 7×4 28 ∴AF＝ EB ＝ 5 ＝ 5 . (2)∵EF∥ BC， AE AF ∴AB＝AC. ∵AB＝10，AE＝6，AF＝5， AB·AF 10×5 25 ∴AC＝ AE ＝ 6 ＝ 3 ， 25 10 ∴FC＝AC－AF＝ 3 －5＝ 3 .
二、共同探究，获取新知师：我们知道两条平行线之间的距离是相等的．如果有三条直线 l3∥l4∥ l5，任意两直线 l1 和 l2 与它们相交且截得的线段 AB＝BC. 我们会得到 DE＝EF， AB DE 即BC＝ EF ＝1. 你们知道为什么吗？生：学生思考、讨论，得出结论．平行线等分线段定理：两条直线被三条平行线所截，如果在其中一条上截得的线段相等，那么在另一条上截得的线段也相等．
重点平行线分线段成比例定理和推论及其应用．难点平行线分线段成比例定理的正确性的说明及推论应用．
一、复习导入师：什么是相似多边形？生：对应角分别相等，对应边成比例的两个多边形．教师用多媒体展示：如图，在△ABC 和△A′B′C′中，如果 ∠A＝∠A′，∠B＝∠B′，∠C＝∠C′， AB BC AC ＝＝＝k. A′B′ B′C′ A′C′
四、巩固练习
A( 1．如图，已知 AB∥CD∥EF，那么下列结论正确的是
AD BC A. DF ＝CE BC DF B.CE＝AD CD BC C. EF ＝BE CD AD D. EF ＝ AF
)
2∶ 3 2．如图，DE∥BC，AB∶DB＝3∶1，则 AE∶AC＝ ________ ．
五、课堂小结师：今天你学习了哪些定理？
学生口述定理．
在思考中，学生总结出当求证的两个比例式的线段不在同一基本型的时候应该怎样解题，并且掌握中间比的找法．对于添加辅助线的证明比例式问题，需要“透析”题目中的条件和证明

人教版九年级数学下册百分闯关综合能力检测题及答案(精品推荐)

第二十八章综合能力检测题时间：120分钟满分：120分一、选择题(每小题3分，共30分) 1．(2015·大庆)sin 60°等于( D ) A.12 B.22 C ．1 D.322．在Rt △ABC 中，∠C ＝90°，a ，b ，c 分别是∠A ，∠B ，∠C 的对边，则下列等式中正确的是( D )A ．cos A ＝a cB ．sin B ＝c bC ．tan B ＝abD ．以上都不正确3．(2015·南通)如图，在平面直角坐标系中，直线OA 过点(2，1)，则tan α的值是( C ) A.55 B. 5 C.12D ．2 第3题图第6题图第7题图4．下列等式成立的是( C )A ．sin45°＋cos45°＝1B ．2tan30°＝tan60°C ．2sin30°＝tan45°D ．sin45°cos45°＝tan45°5．在Rt △ABC 中，∠C ＝90°，∠A ＝45°，a ＋b ＝46，则c 等于( A ) A ．4 3 B ．4 C ．2 6 D ．4 26．如图，一河坝的横断面为等腰梯形ABCD ，坝顶宽10米，坝高12米，斜坡AB 的坡度i ＝1∶1.5，则坝底AD 的长度为( D )A ．26米B ．28米C ．30米D ．46米7．如图所示，在Rt △ABC 中，∠C ＝90°，D 为BC 边上一点，∠DAC ＝30°，BD ＝2，AB ＝23，则AC 的长是( A )A. 3 B ．2 2 C ．3 D.3228．如图是以△ABC 的边AB 为直径的半圆O ，点C 恰好在半圆上，过C 作CD ⊥AB 交AB 于点D.已知cos ∠ACD ＝35，BC ＝4，则AC 的长为( D )A ．1 B.203 C ．3 D.163第8题图第9题图第10题图9．如图，在Rt △ABC 中，∠C ＝90°，∠A ＝30°，E 为AB 边上一点，且AE ∶EB ＝4∶1，EF ⊥AC 于点F ，连接FB ，则tan ∠CFB 的值等于( C )A.33 B.233 C.533D ．5 3 10．如图，学校大门出口处有一自动感应栏杆，点A 是栏杆转动的支点，当车辆经过时，栏杆AE 会自动升起，某天早上，栏杆发生故障，在某个位置突然卡住，这时测得栏杆升起的角度∠BAE ＝127°，已知AB ⊥BC ，支架AB 高1.2米，大门BC 打开的宽度为2米，以下哪辆车可以通过？( C )(栏杆宽度，汽车反光交镜忽略不计)(参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75，车辆尺寸：长×宽×高)A ．宝马Z4(4200 mm×1800 mm×1360 mm)B ．奇瑞QQ(4000 mm×1600 mm×1520 mm)C ．大众朗逸(4600 mm×1700 mm×1400 mm)D ．奥迪A4(4700 mm×1800 mm×1400 mm) 二、填空题(每小题3分，共24分)11．在△ABC 中，∠B ＝45°，cos A ＝12，则∠C 的度数是__75°__．12．将一副三角尺按如图所示叠放在一起，若AB ＝14 cm ，则阴影部分的面积是__492__cm 2.第12题图第14题图第15题图13．已知在Rt △ABC 中，∠C ＝90°，sin A ＝513，则tan B 的值为__125__．14．如图，直线MN 与⊙O 相切于点M ，ME ＝EF 且EF ∥MN ，则cos E ＝__12__．15．如图，等边三角形ABC 中，D ，E 分别为AB ，BC 边上的点，AD ＝BE ，AE 与CD 交于点F ，AG ⊥CD 于点G ，则sin ∠AFG 的值__32__． 16．(2015·德州)如图，某建筑物BC 上有一旗杆AB ，从与BC 相距38 m 的D 处观测旗杆顶部A 的仰角为50°，观测旗杆底部B 的仰角为45°，则旗杆的高度均为__7.2__m ．(结果精确到0.1 m ，参考数据：sin50°≈0.77，cos50°≈0.64，tan50°≈1.19)第16题图第17题图17．一渔船在海岛A 南偏东20°方向的B 处遇险，测得海岛A 与B 的距离为20(3＋1)海里，渔船将险情报告给位于A 处的救援船后，沿北偏西65°方向向海岛C 靠近，同时，从A 处出发的救援船沿南偏西10°方向匀速航行，20分钟后，救援船在海岛C 处恰好追上渔船，那么救援船航行的速度为__2__海里/分．18．已知：在△ABC 中，AC ＝1，AB 与BC 所在直线所成的角中锐角为45°角，AC 与BC 所在直线形成的夹角的余弦值为255(即cos C ＝255)，则BC 边的长是__355或55___．解：点拨：分两种情况：作AD ⊥BC ，垂足为点D.①在△ABC 的内部，∠ABD ＝45°；②在△ABC 外∠ABD ＝45°.这两种情况，解直角△ACD 与直角△ABD ，得到BC 的长．三、解答题(共66分)19．(6分)已知α是锐角，且sin (α＋15°)＝32，计算8－4cos α－(π－3.14)0＋tan α＋⎝⎛⎭⎫13－1的值．解：∵sin (α＋15°)＝32，∴α＝45°，∴原式＝22－4×22－1＋1＋3＝3. 20．(8分)在△ABC 中，∠C ＝90°.(1)已知：c ＝83，∠A ＝60°，求∠B 及a ，b 的值； (2)已知：a ＝36，c ＝63，求∠A ，∠B 及b 的值．解：(1)∠B ＝30°，a ＝12，b ＝43； (2)∠A ＝∠B ＝45°，b ＝3 6.21．(9分)(2015·长春)如图，海面上B ，C 两岛分别位于A 岛的正东和正北方向．一艘船从A 岛出发，以18海里/时的速度向正北方向航行2小时到达C 岛，此时测得B 岛在C 岛的南偏东43°.求A ，B 两岛之间的距离．(结果精确到0.1海里)(参考数据：sin 43°＝0.68，cos 43°＝0.73，tan 43°＝0.93)解：由题意，得AC ＝18×2＝36(海里)，∠ACB ＝43°.在Rt △ABC 中，∵∠A ＝90°，∴AB ＝AC•tan ∠ACB ＝36×0.93≈33.5(海里)．故A ，B 两岛之间的距离约为33.5海里．22．(9分)(2014·重庆)如图，在△ABC 中，CD ⊥AB ，垂足为点D.若AB ＝12，CD ＝6，tan A ＝32，求sin B ＋cos B 的值．解：在Rt △ACD 中，∵∠ADC ＝90°，∴tanA ＝CD AD ＝6AD ＝32，∴AD ＝4，∴BD ＝AB －AD＝12－4＝8.在Rt △BCD 中，∵∠BDC ＝90°，BD ＝8，CD ＝6，∴BC ＝BD 2＋CD 2＝10，∴sinB ＝CD BC ＝35，cosB ＝BD BC ＝45，∴sinB ＋cosB ＝35＋45＝75. 23．(10分)一副三角板如图放置，点C 在FD 的延长线上，AB ∥CF ，∠F ＝∠ACB ＝90°，∠E ＝30°，∠A ＝45°，AC ＝122，试求CD 的长．解：过点B 作BM ⊥DF 于点M.∵∠BCA ＝90°，∠A ＝45°，∴∠ABC ＝45°，∴BC ＝AC ＝12 2.∵AB ∥CF ，∴∠BCM ＝45°.在Rt △BCM 中，BM ＝BC·sin45°＝12.在Rt △BCM 中，∵∠BCM ＝45°，∴∠MBC ＝45°，∴CM ＝BM ＝12.在Rt △BMD 中，∠BDM ＝60°，∴DM ＝BMtan60°＝43，∴CD ＝CM －DM ＝12－4 3.24．(11分)(2015·上海)如图，MN 表示一段笔直的高架道路，线段AB 表示高架道路旁的一排居民楼，已知点A 到MN 的距离为15米，BA 的延长线与MN 相交于点D ，且∠BDN ＝30°，假设汽车在高速道路上行驶时，周围39米以内会受到噪音(XRS )的影响．(1)过点A 作MN 的垂线，垂足为点H ，如果汽车沿着从M 到N 的方向在MN 上行驶，当汽车到达点P 处时，噪音开始影响这一排的居民楼，那么此时汽车与点H 的距离为多少米？(2)降低噪音的一种方法是在高架道路旁安装隔音板，当汽车行驶到点Q 时，它与这一排居民楼的距离QC 为39米，那么对于这一排居民楼，高架道路旁安装的隔音板至少需要多少米长？(精确到1米)(参考数据：3≈1.7)解：(1)连接PA.由题意知，AP ＝39 m ．在Rt △APH 中，PH ＝AP 2－AH 2＝392－152＝36(米)； (2)由题意知，隔音板的长度是PQ 的长度．在Rt △ADH 中，DH ＝AH tan30°＝153(米)．在Rt△CDQ 中，DQ ＝CQ sin30°＝3912＝78(米)．则PQ ＝PH ＋HQ ＝PH ＋DQ －DH ＝36＋78－153≈114－15×1.7＝88.5≈89(米)．故高架道路旁安装的隔音板至少需要89米．25．(13分)如图，某小学门口有一直线马路，交警在门口设有一条宽度为4米的斑马线，为安全起见，规定车头距斑马线后端的水平距离不得低于2米，现有一旅游车在路口遇红灯刹车停下，汽车里司机与斑马线前后两端的视角分别为∠FAE ＝15°和∠FAD ＝30°，司机距车头的水平距离为0.8米，试问该旅游车停车是否符合上述安全标准？(E ，D ，C ，B 四点在平行于斑马线的同一直线上)(参考数据：tan 15°＝2－3，3≈1.732，2≈1.414)解：∵∠FAE ＝15°，∠FAD ＝30°，∴∠EAD ＝15°.∵AF ∥BE ，∴∠AED ＝∠FAE ＝15°，∠ADB ＝∠FAD ＝30°.设AB ＝x ，则在Rt △AEB 中，EB ＝AB tan15°＝xtan15°.∵ED ＝4，ED ＋BD＝EB ，∴BD ＝x tan15°－4.在Rt △ADB 中，BD ＝AB tan30°＝x tan30°，∴x tan15°－4＝xtan30°，即(12－3－133)x ＝4，解得x ＝2，∴BD ＝2tan30°＝2 3.∵BD ＝CD ＋BC ＝CD ＋0.8，∴CD ＝23－0.8≈2×1.732－0.8≈2.7＞2，故符合标准．故该旅游车停车符合规定的安全标准．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。