晶体对称性
晶体的对称性

对称性与人类思维方式的联系
对称性思维方式是人类认知世界的一 种重要方式。人们习惯于将事物进行 对称性的分类、比较和思考,从而更 好地理解和把握事物的本质和内在规 律。
VS
对称性思维方式在科学研究和工程技 术中也发挥着重要作用。科学家们利 用对称性原理探索自然界的奥秘,解 决各种复杂的科学问题。工程师们则 利用对称性设计各种结构,提高产品 的稳定性和可靠性。
晶体的对称性
• 对称性的基本概念 • 晶体中的对称元素 • 对称性和晶体结构 • 对称性在化学中的运用 • 对称性与生物学的关系 • 对称性的哲学思考
01
对称性的基本概念
Hale Waihona Puke 称性的定义对称性是指一个物体或图形在某种变 换下保持不变的性质。在晶体学中, 对称性是指晶体在空间变换下保持不 变的性质。
对称性可以通过对称操作来描述,对 称操作是指将晶体进行刚性旋转、平 移、反演等变换后仍能恢复原状的操 作。
对称性的分类
晶体可以根据其对称性进行分类,常 见的晶体分类包括立方晶系、四方晶 系、六方晶系等。
VS
不同晶系的晶体具有不同的对称性, 晶体的对称性与其内部原子或分子的 排列方式密切相关。
对称操作的数学表达
对称操作可以用数学矩阵来表示,通过矩阵变换可以描述晶体的对称性。
对称操作的数学表达包括旋转矩阵、平移矩阵、反演矩阵等,这些矩阵可以用来描述晶体在空间中的 变换。
02
晶体中的对称元素
点对称元素
定义
01
点对称元素是晶体中以某一点为中心的对称操作,包括旋转、
反演、反映等。
描述
02
点对称元素在晶体中起着关键作用,它们决定了晶体的空间群
对称性在生物医学中的应用
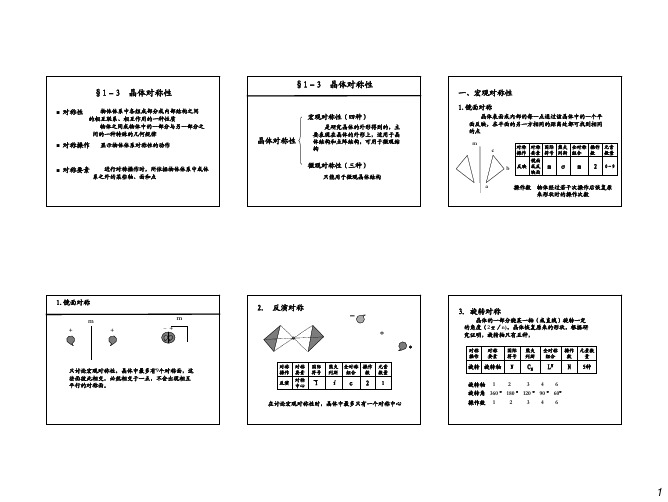
1-3 晶体对称性
2
1 2 3 4 6 2 2 6 4 6
示
平行 斜插纸 纸面 面
二、宏观对称性的组合关系
1. 如果晶体中有两个或两个以上的镜面相交,则每两 个镜面的交线必定是一个对称轴,而对称轴的转角比 定时镜面夹角的二倍。
镜面夹角 180° 90° 60° 45° 30°
旋转轴转 角
360°
180°
120°
90°
Th
Td
O
Oh
晶类(点群)符号 国际符号(全) 国际符号(缩)
1 I(1)
1 I(1)
m
m
2
2
2/m
2/m
3
3
3
3
3m
3m
32
32
32/m
3m
2mm
mm
222
222
2/m2/m2/m
mmm
23
23
2/m3
m3
43m
43m
432
43
4/m32/m
m3m
全对称要素组合
I m(2)
2 2mI
3 3(3I) 33m 332 3323m(3323mI) 23m
三、平移群、布拉菲点阵 例:四方晶系
C→P
F→I
4
晶系 三斜 单斜
菱形
正交
立方
最低对称要素 无
一根二次旋转轴2 或旋转-反演轴2
一根三次旋转轴3 或旋转-反演轴3
三根相互垂直的旋 转轴32或旋转-反 演轴32
四根三次旋转轴43
熊夫列斯符号
C1 Ci(S2) Cs(C1h)
C2 C2h C3 C3i(S6) C3V D3 D3d C2V D2(V) D2h(Vh) T
23晶体的对称性和分类
操作前后晶体保持自身重合的操作,称为对称 操作.
晶体借以进行对称操作的轴、平面或点.称为对 称元素(简称对称素).
6)表示纯转动对称操作(或转动轴);i表示中心反演
(或对称中心);m表示镜面反映(或对称镜面)。
这种表示方法属于国际符号(International
notation)标记法,是海尔曼(Hermann)和毛衮
(Mauguin)制订的,在晶体结构分析中经常使用。
还有一套标记法,是固体物理中惯用的标记, 是熊夫利(Schoenflies)制订的,因此称为熊夫利 符号(Schoenflies notation). 熊夫利符号中Cn 表 示旋转轴;Sn 表示旋转反演轴;Ci 表示中心反 演;Cs 表示镜面反映。
x x
y
y
cos
z
sin
z
y
sin
z
cos
x 1 0 0 x
y0 cos siny z 0 sin cos z
所以,绕x轴旋转的变换矩阵为:
1 0
0
Ax
0
cos
sin
0 sin cos
同理可得绕y轴和绕z轴的变换矩阵
cos 0 sin
Ay
0
1
0
sin 0 cos
cos sin 0
晶体中允许的转动对称轴只能是1、2、3、4和6次轴, 称为晶体的对称性定律
晶体的对称性定律的证明 B
A
如图,A为格点,B为离A最近的 格点之一,则与 平A 行B 的格点
晶体的对称性

反映出晶体外形和其宏 观性质的对称性 当晶体围绕某一轴回转 若通过晶体作一平面,使 当晶体绕某一轴回转到 若晶体中所有的点在经 而能复原时,此轴即为 晶体的各对应点经此平面 一定角度时,再以轴上 过某一点反演后能复原, 回转对称轴。 反映后都能重合一致,则 的一个中心点做反演之 则该点就称为对称中心, 在回转一周的过程中, 该平面称为对称面,用符 用符号i表示 后能复原时,该轴称为 晶体能复原几次,就称 号 m— 表示 回转 反演轴。 几次对称轴。 晶体中实际可能存在的 对称轴有1、2、3、4和 6种,用国际符号1、2、 3、4、6表示。 5次及高于6次的不可能 存在
微观对称元素
( (2 1)螺旋轴 )滑动面
与宏观对称要素配合运用反映出晶 体中原子排列的对称性
螺旋轴是由回转 它是由一个对 轴和平行于轴的 称面加上沿着 平移所构成。晶 此面的平移所 体结构可借绕螺 组成,晶体结 旋轴回转一定角 构可借此面的 度同时沿此轴平 反映并沿此面 移一定距离而得 平移一定距离 而复原。 到重合,从螺旋 轴称为n次螺旋 轴。
晶 系 对 称 要 素
三 单 斜 斜 1 -1 m 2 2/m
正交 2mm 222 2/m 2/m 2/m
四方 -4 4 4/m -4 2 m 4mm 422 4/m 2/m 2/m 1个4或-4
菱方 3 -3 3m 32 -3 2/m
六方 -6 6 6/m -6 2 m 6mm 622 6/m 2/m 2/m 1个6或-6
点群及空间群
点群:晶体形态中全部对称要素的组合称为该晶体 形态的对称型或点群。
晶体的对称性可通过一些对称要素的运用而体现, 各种晶体因其对称性不同所具有的对称要素也不 同。晶体可能存在的对称类型可通过宏观对称要 素在一点上组合应用而得出,但这些组合并不是 任意的例如对称面不能不能与位于此面以外的对 称中心或任意倾斜的对称轴组合。因此,分析了 各种可能组合情况后确定只有32种点群。点群在 宏观上表现为晶体外形的对称。32种点群见表
07-2.3晶体的对称性

定义:点群是指一个晶体中所有点对称元素的集合。 点对称操作的集合称为点群。
晶体可能存在的对称类型可通过宏观对称元素在一点 上组合运用而得出。
点群在宏观上表现为晶体外形的对称。利用组合定律 可导出晶体外形中只能有32种对称点群。
点群可以用对称元素相结合而导出,在不破坏原有对称的
前提下,结合方式有n/m (表示m⊥n,镜面垂直于n次旋转轴), nm (表示m∥n,镜面包含n次旋转轴), n/mm或n/m m(第
晶体绕某一轴回转能复原n次,就称之为n次对称轴。 晶体中实际可能存在的对称轴有五种,并用符号1,
2,3,4,和6来表示。
旋转角 n名称 符号
360 180 120 90 60 度
1
2 3 4 6 次轴
1
2 356
2. 对称面
立方晶系{100} {110}
晶体通过某一平面作 镜像反映而能复原, 则该平面称为对称面 或镜面,用符号m表示。 对称面通常是晶棱或 晶面的垂直平分面或 者为多面角平分面, 且必定通过晶体几何
晶体基本的对称操作有点对称操作和平移对称操作。
在对称操作过程中保持空间至少有一个不动点的操作 称为点对称操作。在一般的对称操作过程中,空间有许多 点在动,但操作前后状态一样。 如旋转,反演,平面反映 均为点对称操作。
用点对称操作ห้องสมุดไป่ตู้组合可以描述有规则几何外形的单晶 体所具有的点对称性,但许多金属单晶体虽然不一定具备 规则的几何外形,但它们相应的点对称性却仍然存在。
180º与P3点重合,再经O点反 演而与P’重合,则称BB‘为2
次旋转—反演轴。
旋转—反演轴有1,2,3,4
和6次五种,分别以国际符号
_ ____
晶体的对称性

晶体对称性
晶体性质
晶体具异向性,并不排斥在某些特定的方向上性质相同。
这是因为在晶体的格子构造中,这些方向质点的排列是一样的,这就是晶体的对称性,表现在晶体外形上,即相等的晶面、晶棱和角顶有规律地重复出现。
晶体的对称性是晶体极其重要的性质。
中文名称
晶体对称性
英文名称
symmetry of crystal
定义
根据晶体其对称元素进行对称操作,能使其等同部分产生规律性的重合特性。
应用学科
材料科学技术(一级学科),材料科学技术基础(二级学科),材料科学基础(三级学科),材料组织结构(四级学科)
晶体的格子构造是晶体实现最小内能的结果。
由于晶体具有最小的内能,所以处于相对稳定的状态,这就是晶体的稳定性。
晶体只有在得到外来能量时,才能破坏其稳定性,有使之向非晶质转化。
这一点可以从晶体的加热曲线得到证明。
固体物理学-晶体对称性

轴为n度旋转—反演轴,又称为n度象转轴。只有1,2,3,4,6。
(2)符号表示
1,2,3,4,6
2.n度象转轴简析
n度象转轴实际上并不都是独立的,通过下面的分析,可以
得到象旋转轴只有 4 是独立的。
Solid State Physics
(1) 1 象转轴—实际上就是对称心i
z ( u轴 )
A
A 点 绕 旋 转 轴 (z 轴 ) 旋
于不同的群。由旋转、中心反演、镜象和旋转--反演点对称操作构成的群,
称作点群。
理论证明,所有晶体只有32种点群,即只有32种不同的点对称操作类型。
这种对称性在宏观上表现为晶体外形的对称及物理性质在不同方向上的对称性。
所以又称宏观对称性。
**在数学分析中需要考虑晶体结构周期性重复的制约。当晶体具有一个以上
如图所示,A和A'等同,如同镜子一样。
2.表示方式
(1)熊夫利符号表示— ;
(2)国际符号表示—m。
z
A
A
y
O
x
x , y, z
A
A
x , y, z
O-xy 相当于镜面。
Solid State Physics
镜面操作的数学描述
如以x3=0面作为对称面,镜象是将图形的任何一点
0 0
0
0
1
|A|=1 or -1
单位矩阵
Solid State Physics
基本对称操作
平移(Translation)
中心反演(Inversion)—具有对称中心
转动(Rotation)—具有对称轴
镜面(Reflection)—具有对称面
平移是一切晶体的内部结构都具有的对称性
晶体对称性

晶体对称性晶体对称性是晶体学研究的一个重要组成部分,它是晶体结构的关键,可以解释晶体的外观、性质以及界面问题。
其中,最常见的是空间群,它用数学表示法确定变换的形式。
接下来,让我们来更多地了解晶体对称性:一、空间群1. 什么是空间群:空间群是一种变换群,也是对称性理论的基础,可以描述物体在特定坐标系中的集合子空间上的空间操作。
举个例子,如果一个物体只可以在空间系中做180°旋转,那么它就只具有一种(即旋转)拓扑群。
2. 空间群划分:空间群可以根据对称性来划分,主要包括有限对称群、无限对称群和单调对称群三类。
其中,有限对称群表示法子群的形状、大小或空间构造不变;无限对称群指的是无限种变换,其轴心、空间点或空间构造不变;而单调的对称群是单一的元素组成的,在该空间群中任何对称性都不变。
二、对称性1. 什么是对称性:对称性是空间群的基础,一般来说,它表示物体在某种坐标下有特定形状和空间操作的属性,也可以用数学表示法来表达这种特征。
2. 对称性的类型:对称性的类型可以分为四大类,分别是正交对称性、立体对称性、平面对称性和点对称性。
其中,正交对称性主要涉及空间中的空间坐标变换,立体对称性是指物体在立体坐标系下的操作,而平面对称性是指物体在平面坐标系下的操作,而点对称性则是指物体在特定空间构造下的操作。
三、晶体对称性1. 晶体对称性是什么:晶体对称性是晶体学研究的一个重要组成部分,它涉及到晶体结构的外观、性质以及界面问题的解释。
2. 晶体对称性的应用:晶体对称性可以用来研究和设计多种材料,如金属、半导体、有机分子晶体、生物晶体等,它们是将材料化学性质同物理性质关联起来,从而更好地理解材料的特性。
此外,晶体对称性也可用于分类、指导结构分析以及材料的设计和合成等。
四、总结从上文可以看出,晶体对称性是一个非常重要的概念,它不仅仅可以用来描述物体的形状、大小和空间结构,而且可以应用于许多不同的领域,如材料的研究与设计等。
晶体的对称性

晶体的对称性晶体因为有了对称,所以才有了他的美丽、永恒,下面重点说下他的对称性一. 对称的概念物体(或图形)中,其相同部分之间的有规律的重复。
例:蝴蝶、花冠、建筑物、面容、服饰等。
二. 晶体对称的特点晶体的对称表现为晶面、晶棱、角顶作有规律的重复——宏观对称。
晶体的对称性是由晶体的格子构造所决定的,研究晶体的对称性对于认识晶体的各项性质和划分晶体具有重要意义。
1.完全性:所有晶体都具有对称性。
(质点在三维空间有规律的重复——格子构造所决定的);2.有限性:晶体的对称要素是有限的。
要受到晶体对称规律的控制:不出现5次或高于6次的对称轴;3.一致性(表里如一):晶体的对称不仅体现在外形上,也体现在物理性质上,即:不仅包含几何意义,还包含物理化学意义。
三。
对称操作(变换)和对称要素的概念对称操作——指能够使对称物体中的各个相同部分作有规律重复的变换动作。
如,旋转、反映、反伸、旋转反伸等。
对称要素——指在进行对称变换时所凭借的几何要素(点、线、面)。
四. 晶体宏观的对称要素1. 对称面(P)对称面为一假想的面,相对应的对称变换是反映,它使图形平分成两个镜像相等的部分。
对称面的寻找:1)垂直并平分晶面;2)垂直并平分晶棱;3)包含晶棱并穿过角顶。
注意:a. 晶体中可以没有对称面,也可以有对称面,但最多只能有9个对称面;b 必须通过晶体中心,其出现的位置多垂直并平分于晶面或晶棱;c 寻找对称面时要尽量避免转动模型,以免造成重复;d 对称面的数目写在前面:如,9P。
2. 对称轴(Ln)对称轴为一假想的直线,相对应的对称操作是围绕此直线的旋转。
旋转一定角度后可使相同(等)部分重复。
轴次(n)——旋转一周重复的次数;基转角(α)——重复时所旋转的最小角度。
二者之间的关系为n = 360°/ α 。
晶体的对称定律(晶体对称的有限性所决定):晶体中只能出现轴次为1、2、3、4、6的对称轴,而不能出现5次或高于6次的对称轴(准晶体则可以出现)。
浅谈晶体物理性质的对称性

浅谈晶体物理性质的对称性
晶体是由规则排列的离子、原子或分子构成的大规模分子结构,具有明显的晶体物理性质的对称性。
这种对称性可分为三种:空间对称性、光学对称性和门梁对称性。
一、空间对称性:
晶体的对称性决定了其外形,因此可以称之为“空间对称性”。
晶体的空间对称性可分为几何对称、点对称和面对称。
几何对称就是晶体位形,由多个元素平面和角组合而成,每一个元都可折叠到一个点。
点对称是指晶体的外形,在任意一整面可看做有规律的点状外形,由来自同一点的元素折叠而成,因此,其空间对称性也可以说是点对称。
面对称是由两个对面的元素折叠而成,因此,其空间对称性也可以说是面对称。
二、光学对称性:
大部分物质都具有双折射特性,即晶格结构中的离子、原子或分子可以阻挡透过去的光线,从而诞生出某种对称的折射现象,这种特性被称为“光学对称性”。
晶体的光学对称性可以表示为反射、折射、旋转等,反射和折射是典型的光学对称现象,旋转则是在一定范围内把光线转动,而不会影响其它属性。
三、门梁对称性:
也叫等值线对称性,指晶体内测得的各种基态的能量在某些轴向上有对称性,即在垂直于该轴的某条波前,能量均为相等的值,而不会随外部环境的变化而而变化,这种对称现象被称为“门梁对称性”。
高中化学竞赛【晶体的对称性】

晶面3
c
晶面2
晶面1
b a
晶面指标示例
例题: 1. 某一立方晶系晶体,晶胞的顶点位置全为
A占据,棱心为B占据, 体心为C占据。①写
出此晶体的化学组成; ②写出A、B、C的
(4)十四种空间点阵形式 立方晶系有立方简单点阵P (立方P ) 、立方
体心点阵I (立方I ) 、立方面心点阵F (立方F );四 方晶系只有四方简单点阵P (四方P ) 、四方体心 点阵I (四方I ); 正交晶系有正交P 、正交I 、正交 F 、正交C (或侧心A和B); 单斜晶系有单斜P 、 单斜C ; 三方、六方、三斜都只有素格子。可见, 晶体只有14种空间点阵型式。见下图。
晶体的对称性
1.晶体的宏观对称性 晶体的宏观对称性就是晶体外型的对称性。
也就是有限物体的对称性。
方铅矿
金绿宝石
(1)晶体的宏观对称元素: 由于习惯原因, 晶体宏观对称元素与分
子对称性中的对称元素名称、符号都不完全 相同。
对称元素 旋转轴n 反映面或镜面m 对称中心i
反轴 n
对应对称操作 旋转L(α) 反映M 倒反I 旋转倒反L(α) I
3.晶面和晶面指标 晶面:晶体中平面点阵所在的平面。 晶面指标: 晶面在三个晶轴上的倒易
截数的互质整数之比。记为: (h*k*l*) 晶面与晶面的交线称为晶棱, 晶棱与
直线点阵对应。
例如, 右图中晶面 1在3个晶轴上的截数 分别:1/2,∞,∞, 因此倒 易截数:2,0,0, 划成互质 整数比后成为: 1:0:0, 因此晶面1的晶面指标 是: (100)。
第一章 晶体的对称性

第一章晶体的对称性§1-1 晶体内部结构的周期性---点阵与晶格大家都知道晶体内部原子(分子、离子和原子团等,以后称质点)的排列是规则的,具有一定的周期性,这是晶体的主要特点。
不同晶体中的质点在空间中的排列规律是不同的,有许多种排列方式。
因此,在对晶体进行研究时,为了归类方便,常将构成晶体的实际质点抽象成纯粹的几何点,并称之为阵点。
这样的阵点在空间中周期性规则排列并有相同的周围环境。
这种阵点的空间排列就称为空间点阵,或晶体点阵,也称布拉法格子,简称点阵或晶格,共有14种。
§1-2 晶体的宏观对称性---点对称操作晶体内部结构不仅具有周期性,还具有比较复杂的对称性。
实际上,晶体宏观性质和外形的对称性都是其内部结构对称性的反映,与其有着密切关系。
应该说,人们最初认识晶体,是从它们丰富多彩又有规则的外部形状开始的,后来才逐步认识到,晶体外形上的规则性及其宏观性质的对称性,是与其内部微观结构的对称性密切相关的。
在本节及以下几节中,通过对晶体的宏观对称性的描述,引进群的初步概念,给出晶体的32个点群,并依据晶体对称性特征,区分晶类和晶系。
1.晶体的宏观对称性。
晶体外形上(宏观上)的规律性,突出表现在晶面的对称排列上。
如:把立方体的岩盐晶体绕其中心轴每转900后,晶体自身就会重合,而把六面柱体的石英晶体绕其柱轴每转600后,晶体亦会自身重合。
这里提到的绕轴转动称旋转操作,是一种点对称操作。
通常把经过某种点对称操作后晶体自身重合的性质称为晶体的宏观对称性。
描述晶体宏观对称性的方法,就是列举使其自身重合的所有点对称操作。
为了明确对称性和对称操作的概念,先给出以下概念:●相等图形。
如花瓣。
●等同图形。
如左右手。
相等图形属于等同图形,但等同图形不一定是相等图形。
●对称图形。
由两个或两个以上的等同图形构成的并在空间有规律排列的图形称对称图形。
2.对称性。
对称图形中各等同部分在空间排列的特殊规律性称对称性。
结构化学晶体结构的对称性和基本定理

点击按钮观察动画.注意:反映滑移操作中
的“反映”是虚操作,可想象而难以实际表现, 故动画 中用幻影逗号的移动来模拟反映,请勿误解!
8.2.2 晶胞
设想把点阵放回晶体中去, 将把晶体切分成并置的平行六面 体小晶块,每个空间格子对应一 个小晶块. 这种小晶块就是晶胞, 是代表晶体结构的最小单元.
晶胞参数
NaCl型晶体
原子的分数坐标: A: 0 0 0
0 1/2 1/2 1/2 0 1/2 1/2 1/2 0 B: 1/2 0 0
0 1/2 0 0 0 1/2 1/2 1/2 1/2 结构基元: A-B (每个晶胞中有4个结构基元)
CsCl型晶体
原子的分数坐标: A: 0 0 0 B: 1/2 1/2 1/2
为什么要考虑带心格子?
立方面心格子,若按左图取素格子只能表现三方对称性;若取右图 所示的复格子就表现出立方对称性(格子选取方式不能改变点阵结构的对 称性,但点阵固有的较高对称性在素格子上可能被掩盖):
14种布拉维格子之一:立方简单(cP)
14种布拉维格子二:立方体心(cI)
14种布拉维格子三:立方面心(cF)
晶胞参数:
a、b、c α、β、γ
晶
胞
两
要
(1)晶胞的大小、型式
素
晶胞的大小可由晶胞参数确定,晶胞的型式是
指素晶胞或复晶胞.
(2)晶胞的内容
晶胞中原子的种类和位置. 表示原子位置要用 分数坐标.
分数坐标
晶胞中原子P 的位置用向量OP=xa+yb+zc代表. x、y、z
就是分数坐标,它们永远不会大于1.
14种布拉维格子之八:正交简单(oP)
14种布拉维格子之九:正交体心(oI)
第03次课 晶体的对称性、晶系和x射线衍射

(2)旋转反演对称操作: 1,2,3,4,6度旋转反演对称操作。 S1,S2,S3,S4,S6(用熊夫利符号表示)
(3)中心反映:i。
(4)镜象反映:m。
独立的对称操作有8种,即1,2,3,4,6,i,m, 4 。
或C1,C2,C3,C4,C6 ,Ci,Cs,S4。
设B1ABA1是晶体中某一晶面上的一个晶列,AB为这一晶列上相邻 的两个格点。
B
A
B1 A
B A1
若晶体绕通过格点A并垂直于纸面
B
的u轴顺时针转角后能自身重合,
则由于晶体的周期性,通过格点B
也有一转轴u。
B1
A
A
B
A1
AB AB 1 2cosθ, AB 是 AB 的整数倍,
cos 0, 1 ,1
晶体中允许的旋转对称轴只能是1,2,3,4,6度轴。
1
2
3
4
6
正五边形沿竖直轴每旋转720恢复原状,但它不能重复排列充 满一个平面而不出现空隙。因此晶体的旋转对称轴中不存在
五次轴,只有1,2,3,4,6度旋转对称轴。
(2)中心反映(i,对称素为点) 取中心为原点,经过中心反映后,图形中任一点
(x1, x2, x3) 变为 (-x1, -x2, -x3)
分别为入射和衍射线方向的单位矢量;
(3)只讨论布拉伐晶格。
设A为任一格点,格矢
S0
A
Rl l1a1 l2 a2 l3 a3
S
Rl
波程差
C O
D
CO OD Rl S 0 Rl S Rl S S0
衍射加强条件为:
Rl S S0 (为整数)
晶体化学(晶体对称性)

划分正当晶胞或单位的原则中,主要做了两方
面的规定:
划分了七个晶系
一、应当尽量选取较规则的形状;
二、应当尽量选取含点阵点少的.
划分出十四种空间 点阵型式
立方 P, I, F
六方 H
晶 三方 R 系 四方 P,I
简单P 型 底心C 式 体心I
正交 P,C(或侧心),I,F
面心F
单斜 P,C
侧心A或B
三斜 P
∴3垂直一平面点阵
3
b3 T3
T1
a1b1
b2 a2
T2
a3
3. 晶体中对称轴的轴次 A
设晶体中有一轴次为 n 的旋转轴,通
过点阵点O垂直纸面
B
则在晶体的空间点阵中,必有一平 面点阵与 n 垂直.
取直线点阵Tm=ma,并设素向量为 a
根据点阵与平移群的关系:
点阵点
平移群
a作用于O必得A点(为点阵点),-a作用于O 得 A'
4
对称操作
倒反
I
反映
M
旋转 旋转 旋转 旋转 旋转 旋转倒反
L(0 ) L(180 ) L(120 ) L(90 ) L(60 ) L(90 )I
二、宏观对称元素的组合和32个点群
晶体宏观对称元素的组合 晶体的独立的宏观对称元素只有八种,但在某一晶体中可以只存在 一个独立的宏观对称元素,也可能有由一种或几种对称元素按照 组合程序及其规律进行合理组合的形式存在。 晶体中,宏观对称元素组合时,必受以下两条的限制:
为什么要考虑带心格子?
立方面心格子,若按左图取素格子只能表现三方对称性;若取右图 所示的复格子就表现出立方对称性(格子选取方式不能改变点阵结构的对 称性,但点阵固有的较高对称性在素格子上可能被掩盖):
晶体的对称性

一个具有21的图形
21所对应的对称操作群为:
L(π )T (t ),[ L(π )T (t )]2 = T (2t ),[ L(π )T (t )]3 = L(π )T (3t ) ⋅ ⋅ ⋅
τ = a = 2t 是基本向量。对称操作有无穷多个。 螺旋轴中的一些对称操作包括在平移群T内。
续表:
特征对 晶胞类型 称元素 序 号 13 14 15 菱面体晶胞 点 熊夫里 斯记号 群 国际记号 对称元素
对称 晶 性的 高低 系 四 方
4
a=b≠c α = β = γ = 90 o
D2d
c4 v
4 mm
42m 422 mmm
4 ,4 m
4 ,2 2 ,2 m
4 , 4 2 ,5 m , i
3 + i = 3, 3 + mh = 6
4
2.晶体的宏观对称元素的组合与32个晶 体学点群
由上述的 8种独立的宏观对称元素按一定的规则 (即对称元素至少要通过一个公共点;组合时不能 出现 5次轴及大于6的对称轴)进行组合,总共有32 种组合形式,称为32个晶体学点群。晶体的宏观外 形不论形状如何,必属于这32个晶体学点群中的某 一个。
描述分子对称性与晶体宏观对称性所常用的对称 元素及相应的对称操作对照表
分子对称性 对称元素 符号 对称轴 Cn 对称面 对称操作 符号 晶体宏观对称性 对称元素 符号 旋转轴 n 反映面 或镜面 对称操作 符号 旋转 反映 倒反
ˆ 旋转 C
n
L(α )
M I
σ
反映 反演
ˆ σ
ˆ i
n
m
对称中心 i 象转轴
7.2 晶体的对称性
晶体的对称性有宏观对称性和微观对称系之 分。前者是指晶体的外形对称性,后者指晶体微 观结构对称性。
晶体对称性

r F ( r ′) 不变 对称物体 r r r 物体 F ( r ′ ) 的一个对称变化 g X = X ′ 相同
[ ]
对称变换的两种理解方法存在着内在的本质上的 联系。分析结构模型时,第一种较为方便; 在进行理论处理时,第二种更为适用。 推论: 1)对称物体必然包含等同部分(包括镜像等同 ); 2)对称变换的反变换也是对称变换。
第四章:晶体的对称性 § 4.2 空间变换
对应于两类四面体的重合过程就是两类基本的度规不变变换。 第一类变换(本征运动): 两个迭合等同四面体的重合过程。 定理一:任何第一类变换都可分解为平移和与之垂 直的转动的迭加(螺旋转动)。 第二类变换(非本征运动): 两个镜象等同四面体的重合过程。 定理二:任何第二类变换都可分解为镜象反射和与 之垂直的转动的迭加(反射转动)。
ABCD 的 A 沿 q 平移至 A ′′′,然后绕 N s转动α ,就与 A ′ B ′C ′D ′ 重合(位向相同,一点重合)。 q D A t s = 0 →简单转动 特例: C α = 0 →平移 Ns B t
s
O
A ′′′ p
α
A′ B′
D′
C′
定理二:总有一个反射转动能使镜像等同四面体重合
′ C C ′的中点作反射面m ; i) 过 A A ′、 BB、
ii)
A ′ B ′C ′D ′ 以 m 为镜面反射至 A ′′ B ′′C ′′D ′′,则 ′ C ′′ 到 m 面的距离相等; B ′、 A、 B、 C 到 m 面的距离分别与 A ′′、 D ′′ D C
A
B
C ′′ A ′′
D
C
A
B
第四章:晶体的对称性 § 4.2 空间变换
固体物理02-晶体的对称性

(1)旋转对称( Cn )
若晶体绕某一固定轴转 以后自身重合,则此轴称为n次 n 旋转对称轴。
2π
绕 z 轴旋转θ角的正交矩阵
cos A(C n ) sin 0 sin cos 0 0 0 1
(2)中心反演( Ci )
取中心为原点,经过中心反演后,图形中任一点
变为
( x, y , z )
( x, y , z )
0 1 0 A(C i ) 0 1 0 0 0 1
中心反演矩阵
(3)镜像( m )
如以 Z=0 面作为对称面,镜象是将图形的任何一点 变为
( x, y , z )
( x, y , z )
sin cos 0
0 0 1
(5)恒等操作( E ): 保持晶体不动
立方体对称性
1. 如(a)图所示3个对称轴, 转动 π/2, π , 3π/2, 共 9 个对称操作 2. 如(b)图所示6个面对角线, 转动 π, 共 6 个对称操作 3. 如(c)图所示4个体对角线, 转动 2π/3, 3π/4, 共 8 个对称操作 4. 恒等操作 5. 以上每个操作都可以再加上中心反演 共 24╳2=48个对称操作
点群的Schönflies符号: 主轴:Cn、Dn、Sn、T 和 O Cn:n次旋转轴; Sn:n次旋转-反演轴; Dn:n次旋转轴加上一个与之垂直的n个二次轴 T: 四面体群; O: 八面体群。
脚标:h、v、d
h:垂直于n次轴(主轴)的水平面为对称面; v:含n次轴(主轴)在内的竖直对称面;
d:垂直于主轴的两个二次轴的平分面为对称面。
闪锌矿结构 InAs, GaAs,InP 等III-V族 元素化合物
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
准 晶
晶体中只有1, 2,3,4,6 次旋转轴,没有 5次轴和大于6 次以上的轴,可 以直观的从只有正方形、长方形、正三角形、正六边形可以重复布满平面, 而 5 边形和 n (>6)边形不能布满平面空间来直观理解。因此固体中不可能存 在 5 次轴曾是大家的共识,然而1984年美国科学家Shechtman在急冷的铝 锰合金中发现了晶体学中禁戒的 20 面体具有的 5 次对称性,这是对传统晶 体观念的一次冲击。
晶体的宏观对称性的描述
原子的周期性排列形成晶格,不同的晶格表现出不同 的宏观对称性 概括晶体宏观对称性的方法是考察晶体在正交变换的 不变性 三维情况下,正交变换的表示:
x x ' a11 y y ' a 12 z z' a 13
−1 ������ = 0 0
0 0 −1 0 0 −1
0 0 −1
1 0 ������(������������) = 0 1 0 0 1 0 ������ = 0 1 0 0 0 0 1
像转操作(Rotary reflection):
������������������������ ������ ������ = ������������������������ 0
目前普遍的认识是:晶体的必要条件是其 构成原子的长程有序,而不是平移对称性, 具有 5 次对称性的准晶体(Quasicrystal) 就是属于原子有严格的位置有序,而无平 移对称性的晶体。它的图像可从二维 Penrose拼图中得到理解。实际是一种准 周期结构,是介于周期晶体和非晶玻璃之 间的一种新的物质形态—准晶态。
(3). 底心单斜
C2 , Cs , C2 h
(4). 简单正交
(5). 底心正交 (6). 体心正交 (7). 面心正交
(8). 三角
(9). 简单四方(四角) (10). 体心四方(四角)
(11). 六角
(12). 简立方
(13). 体心立方 (14). 面心立方
晶系
三斜 单斜
对称性特征
1, 2, 3, 4, 6 1, 2,3, 4,6, i, m, 4
不论任何晶体的宏观对称元 素只有8种独立的对称元素
1 = ������, 2 = ������, 3 = 3 + ������, 6 = 3 + ������
旋转-反演轴的对称操作
1次反轴为对称中心 2次反轴为对称面
3次反轴为3次轴加对称中心
它们有哪些对称操作? 正四面体 正六角拄
(2). 正四面体的对称操作
四个原子位于正四面体的四个 顶角上,正四面体的对称操作 包含在立方体操作之中。 绕三个立方轴转动180度 (3)
绕4个立方体对角线轴 (120 和240度,8) 绕三个立方轴 (90和270度+ 中心反演, 6)
绕6条面对角线轴(180度, 6)
设想有一个对称轴垂直于平面,平面内晶面的格点可以用 来描述 绕通过A的转轴的任意对称操作,转过角度, B点转到B’ 点(B’点必有一个格点) A和B两点等价—以通过B点的 轴顺时针转过, A点转到A’点 (A’点必有一个格点) 观对称性
只能有以下十种对称素
1, 2, 3, 4, 6
群
群
群加上含有n重轴的反演面,共4个
群加上通过n重轴及两根二重轴角平分线 的反演面, 共2个
群只包含旋转反演轴的点群。 其中 共2个
群 — 立方点群, 含有48个对称操作 群 — 正四面体点群, 含有24个对称操作 群 — 立方点群 的24个纯转动操作
群 — 正四面体点群
群—
的12个纯转动操作
群加上中心反演
对称元素为镜面 用 表示
一个物体的全部对称操 作构成一个对称操作群
群的概念
群代表一组“元素”的集合,G {E, A ,B, C, D ……} 这些“元素”被赋予一定的“乘法法则”,
满足如下四个规则:
① 集合 G 中任意两个元素的“乘积”仍为集合内的元素 .
若 A, B G, 则AB=C G. 叫作群的封闭性
对称操作,也就是找出它所具有的对称操作群。
在对称操作中保持不动的轴、面或点,称为对称操
作群的对称元素,比如转动轴,反演中心,反映面
运算法则是连续操作,不动操作是单位元素。
二. 晶体中允许的对称操作
人们早就指出,晶体的外形(宏观)对称性是其原子做周期性 排列的结果。原子排列的周期性用晶体点阵表示,晶体本身对 称操作后不变,其晶体点阵在对称操作后也应该保持不变。晶 体的平移对称性限制了晶体所可能有的点对称操作。
一. 对称性的概念 二. 晶体中允许的对称操作
三. 晶体宏观对称性的表述:点群
四. 七个晶系和14种晶体点阵
五. 晶体的微观对称性:空间群
六. 二维情形 七. 点群对称性和晶体的物理性质
黄昆 书 1.5-1.7 节 阎守胜 书 2.2 节
一. 对称性的概念
一个物体(或图形)具有对称性,是指该物体(或图形)是由两 个或两个以上的部分组成,经过一定的空间操作(线性变换), 各部分调换位置之后整个物体(或图形)保持不变的性质。 对称操作:维持整个物体不变而进行的操作称作对称操作。 即:操作前后物体任意两点间的距离保持不变的操作。 点对称操作:在对称操作过程中至少有一点保持不动的操 作。有限大小的物体,只能有点对称操作。 对称元素:对称操作过程中保持不变的几何要素: 点,反 演中心;线,旋转轴;面,反映面等。
第一章 晶体结构
• • • • • §1.1 晶格 §1.2 晶体的对称性 §1.3 典型的晶体结构和表面结构 §1.4 倒易点阵和布里渊区 §1.5 晶体结构的实验研究
黄昆、韩汝琦《固体物理学》第一章
C. Kittel 《固体物理导论》第一章 阎守胜,固体物理基础,第二章
§1.2 晶体的对称性
−������������������������ ������������������������ 0
0 0 −1
(1). 立方体的对称操作
一个物体在某一个正交变换下保持不变 物体的对称操作越多,其对称性越高 (1). 绕三个立方轴转动 (9) (2). 绕6条面对角线轴转动 (6) (3). 绕4个立方体对角线轴转动 (8) (4). 恒等操作/正交变换 (1) + 中心反演 48个对称操作
4. 一个物体绕某一个转轴转动 2������/������ 加上中心反演的联合
操作,以及其联合操作的倍数不变时, 该轴为物体n重旋
转-反演轴,计为������
立方体
立方轴 为4重轴,计为 4
同时也是4重旋转-反演轴,计为 面对角线 为2重轴,计为2
同时也是2重旋转-反演轴,计为
体对角线轴 为3重轴,计为3
a12 a22 a13
a13 x y a23 z a33
a11 a12 Ai j a21 a22 a 31 a32
a13 a23 a33
—— 其中矩阵是正交矩阵
常见对称操作
绕z固定轴的转动: (Rotation)
彭罗斯瓷砖
1974年Penrose提出的数学游戏
五次对称的黄金分割无理数: 1, 1.618
3D Quasicrystal
AlNiCo 衍射图
二十面体AlPdMn表面的STM图像
三. 晶体学点群
点群:在点对称操作基础上组成的对称操作群 由于点群中的对称操作必须和晶体的平移对称性相容,这种 受限制的点群称为晶体学点群(crystallographic point group). 晶体中只有 8 种独立的对称元素: 1, 2,3, 4,6, i, m, 4
只有C1或Ci 唯一C2或CS
晶胞参数
ab c ab c ==90º ab c = == 90º a=b=c = = 90º a=b c = == 90º a=b c = = 90º=120º
点群的熊夫利Schönflies符号:
主轴:Cn、Dn、Sn、T 和 O Cn: n次旋转轴; Sn: n次旋转-反演轴; Dn: n次旋转轴加上n个与之垂直的二次轴 T: 四面体群; O: 八面体群。 脚标:h、v、d h:垂直于n次轴(主轴)的水平面为对称面;
v:含n次轴(主轴)在内的竖直对称面;
晶体的宏观对称只有32个不同类型
四. 7 种晶系和14种布拉菲格子
— 32种点群描述的晶体对称性 — 对应的只有14种布拉伐格子
— 分为7个晶系 — 单胞的三个基矢 沿晶体的对称轴或对称面
的法向,在一般情况下,它们构成斜坐标系
三个晶轴之间的夹角
14种布拉伐原胞
(1). 简单三斜
C1 , Cs
(2). 简单单斜
② 存在单位元素E, 使得所有元素满足:AE = A ③ 对于任意元素A, 存在逆元素A-1, 有:AA-1=E ④ 元素间的“乘法运算”满足结合律:A(BC)=(AB)C
对称操作群
一个物体全部对称操作的集合,也满足上述群的定 义。因此一个物体的全部对称操作的集合,构成对 称操作群。描述物体的对称性需要找出物体的全部
中心反演(Inversion): 平面反映(Reflection): 恒等操作(Identity operation):
������������������������ ������ ������ = ������������������ = ������������������������ 0 −������������������������ ������������������������ 0 0 0 1
准晶态结构特点:具有长程取向序,没有 长程平移对称性。 其实准晶可以看作是具有平移对称性的六 维超空间在三维真实空间的投影
