机器人学基础_第4章_机器人动力学资料
第四章(机器人学动力学)

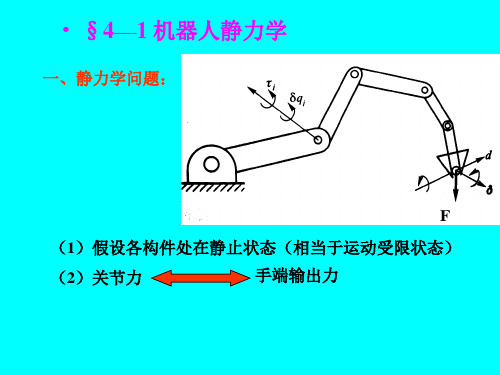
第四章 机器人静力学和动力学
静力学和动力学分析,是机器人操作机设计和动态性能分 析的基础。特别是动力学分析,它还是机器人控制器设计、 动态仿真的基础。 机器人静力学研究机器人静止或缓慢运动式,作用在机器 人上的力和力矩问题。特别是当手端与环境接触时,各关节 力(矩)与接触力的关系。 机器人动力学研究机器人运动与关节驱动力(矩)间的动 态关系。描述这种动态关系的微分方程称为动力学模型。由 于机器人结构的复杂性,其动力学模型也常常很复杂,因此 很难实现基于机器人动力学模型的实时控制。然而高质量的 控制应当基于被控对象的动态特性,因此,如何合理简化机 器人动力学模型,使其适合于实时控制的要求,一直是机器 人动力学研究者追求的目标。 2
3
按静力学方法,把这些力、力矩简化到 Li 的固联坐标系 oi xi yi zi ,可得: Fi Fi 1 G i M i M i 1 r i F i 1 r Ci G i i 1 或 i i i 0
4.1 机器人静力学
一、杆件之间的静力传递 在操作机中,任取两连杆 Li, i 1 。设在杆 Li 1上的 Oi 1 点 L 作用有力矩 M i 1和力 F i 1;在杆 Li 上作用有自重力 G i 〔过质 r 心 Ci );i 和 rCi 分别为由 Oi 到 Oi 1 和 Ci 的向径。 M i 1 F i 1
18
4.4.4 牛顿——欧拉法基本运动方程
刚体的运动可分解为随质心的移动和绕质心的转动。借助于 杆件运动学知识,我们把达朗贝尔原理用于每个杆件,描述机 器人各杆件的运动。达朗贝尔原理可应用于任意瞬时,它实质 上是牛顿第二运动定律的一种变型,可表示为: d mi vi ( Fi ) Fi mi vi 牛顿定理 : dt d I ii Ni I ii i ( I ii ) 欧拉方程 : ( Ni ) dt 式中:mi — 杆i 质量; Fi — 杆i上所有外力合力; N i — 杆i上所有外力对质心的合力矩;
第四章齐次变换

o
x
x w″
u″ y
第26页,此课件共52页哦
z
v ```
7
o′ u ```
w ```
-3 oy
4 x
26
解2:用计算的方法
根据定义1,我们有:
T Trans(4 , 3, 7) R(y, 90 ) R(Z,90 )
0 0 1 4
1 0 0 3
0 1 0 7
0 0 0
1
(2-20)
25
第25页,此课件共52页哦
2.6 相对变换
举例说明:
例1:动坐标系∑0′起始位置与固定参考坐标系∑0重合,动坐标系∑0′做如 下运动:①R(Z,90º) ②R(y,90º) ③Trans(4,-3, 7),求合成矩阵
解1:用画图的方法:
z
w
o(o′ ) v y u x
z
z
w′
v′
v″
o(o′ ) u′ y
ay
Py
nz 0
oz 0
az 0
Pz 1
a z
o
P
n
y
x
9
第9页,此课件共52页哦
2.4坐标系在固定参考坐标系中的表示
nx ox a x Px
F
n
y
oy
ay
Py
nz 0
oz 0
az 0
Pz 1
x
a z
o
P
n
y
• 前三个向量是w=0的方向向量,表示该坐标系 的三个单位向量 n,o,a, 的方向,而第四个w
动坐标系在固定坐标系中的齐次变换有2种情况:
第四章齐次变换
1
第1页,此课件共52页哦
(完整版)机器人学_机器人雅可比矩阵

dy
,
dz
)Rot(k, d)
I 44
k z d
k y d
0
kzd
0
k x d
0
k y d kxd
0
0
dx
dy
dz
0
四. 微分旋转的无序性 当θ→0 时,有sinθ→dθ,cosθ→1.若令δx=dθx,δy=dθy,
δz=dθz,则绕三个坐标轴(p16)的微分旋转矩阵分别为
1 0 0 0
例 :如图3-18所示的平面2R机械手,手爪端点与外界接触,手爪
作用于外界环境的力为
ቤተ መጻሕፍቲ ባይዱ
,若关节无摩擦
力存在,求力 的等效关节力矩
。
解:由前面的推导知
0F [Fx , Fy ]T
所以得:
y0
2
1
x0
图3-18 关节力和操作力关系
例:如图所示的机械手夹扳手拧螺丝,在腕部({Os})装有力/力矩
传感器,若已测出传感器上的力和力矩
只要知道机械手的雅可比J是满秩的方阵,相应的关节速度即
可求出,即
。
上例平面2R机械手的逆雅可比
J
1
1 l1l2s2
l2c12 l1c1 l2c12
l2s12
l1s1
l2s12
于是得到与末端速度
相应的关节速度:
显然,当θ2趋于0°(或180°)时,机械手接近奇异形位,相应的 关节速度将趋于无穷大。
解:因为已知
,可以根据前面的公式求得dA和δA。也可
根据与它一样的另一组表达式(写法不同)求解,即
求得
,
4.2 机器人的静力学
v F
[
v f,
《机器人技术基础》第四章 机器人动力学

人
4.2 机械手动力学方程
动
力
学
4.1.1 拉格朗日方法
机器人是一个具有多输入和多输出的复杂的 运动学系统,存在严重的非线性,需要非常复杂 的方法来处理。
动力学处理方法: Lagrange , Newton-Euler, Gauss,Kane, Screw, Roberson-Wittenburg
2 )
d
dt
L
1
(m1 m2 )l12
m2l22
2m2l1l2
cos
2
1
(
m2
l
2 2
m2l1l2 cos 2 )2
2m2l1l2 si n212 m2l1l2 si n22L1Fra bibliotek(m1
m2 )gl1
s i n1
m2 gl2
s i n (1
2)
4.1.2 拉格朗日方程
⑤求出机器人动力学方程:
)
然后求微分,则其速度就为:
x2 y 2
l1 l1
co s11 sin 11
l2 l2
cos(1 2 )(1 2 ) sin(1 2 )(1 2 )
θ1
关节2
m1
(x1, y1)
l2
θ2 m2
(x2, y2 )
由此可得连杆的速度平方值为:
v22 x22 y22 l1212 l22(12 212 22 ) 2l1l2 cos2(12 12 )
m2 gl2 sin(1 2 )
T2 (m2l22 m2l1l2 cos2 )1 m2l222 m2l1l2 sin 21
m2 gl2 sin(1 2 )
4.1.2 拉格朗日方程
将得到的机器人动力学方程简写为如下形式:
第四章机器人学逆运动学方程ppt课件

这里 其中
f11 = C1 x+S1 y
f12 = - z f13 = - S1 x+C1 y
(4.10) (4.11) (4.12)
x =[ nx ox ax px ]T, y =[ ny oy ay py ]T, z =[ nz oz az pz ]T 由第三章得到的斯坦福机械手运动学方程式(3.48)为
同样比较式(4.48)等号两边矩阵的第2行第1列和第2行第2列元素可知
sin f12 (n)
(4.64)
cos f12 (o)
(4.65)
或
由此可得
sin sin nx cos ny cos sin ox cos oy
tan
1
sin sin
n o
x x
cos ny cos oy
d3 S2 C1 px S1 py C2 pz
(4.24) (4.25)
4
tan 1
C2
S1ax C1ay C1ax S1ay S2az
(4.26)
5
tan 1
C4
C2
C1ax
S1ay S2az S2 C1ax S1ay
S4 S1ax C2az
C1ay
由式(4.36)和式(4.43)可解出Ψ角
cos1 nz
sin
(4.43) (4.44) (4.45)
这里需要指出的是,在我们采用式(4.43)~式(4.45) 来计算θ、φ、Ψ时都是采用反余弦函数,而且式(4.43)和 式(4.45)的分母为sinθ,这会带来如下问题:
1)由于绝对值相同的正负角度的余弦相等,如cosθ= cos(-θ),因此不能确定反余弦的结果是在那个象限;
由于机械手各关节变量的相互耦合,后面计算的关节变量与前 面的关节变量有关,因此当前面关节变量的计算结果发生变化 时,后面关节变量计算的结果也会发生变化,所以逆运动方程 的解不是唯一的,我们应该根据机械手的组合形态和各关节的 运动范围,经过多次反覆计算,从中选择一组合理解。由此可 见,求解机械手的逆运动方程是一个十分复杂的过程。
第4章 机器人的动力学初步

图4-4 质点平移运动 作为回转运动的解析
机器人的静力学
如果I =mr2,则式(4-14) 就改写为
式(4-15)是 质 点 绕 固 定 轴 进 行 回 转 运 动 时 的 运 动 方 程 式 。 与 式 (4⁃ 11)比较,I相当于平移运动时的质量,在旋转运动中称为惯性矩。
机器人的静力学
对于质量连续分布的物体, 求解其惯性矩, 可以将其分割成假想的微小 物体, 然后再把每个微小物体的惯性矩加在一起。这时, 微小物体的质量d m 及其微小体积dV 的关系, 可用密度ρ 表示为 所以, 微小物体的惯性矩dI, 依据I =mr2, 可以写成
行器在笛卡尔空间的轨迹已确定(轨迹已被规划),求解机器人各执行器的驱
动力或力矩,这称为机器人动力学方程的反面求解,简称为逆动力学问题。
概述
不管是哪一种动力学问题都要研究机器人动力学的数学模型,区别在于问
题的解法。人们研究动力学的重要目的之一是对机器人的运动进行有效控制,
以实现预期的运动轨迹。 常用的方法有牛顿.欧拉法、拉格朗日法、凯恩动力学法等。牛顿·欧拉动
原理。
机器人的静力学
如图4⁃1所示,已知作用在杠杆一端的力FA,试用虚功原理求作用于另 一端的力FB。假设杠杆长度LA和LB已知。 按照虚功原理,杠杆两端受力所做的虚功应该是
式中,δ xA 、δ xB是杠杆两端的虚位移。而就虚位移来讲,下式成立
式中, δθ 是绕杠杆支点的虚位移。 把式(4⁃2)代入式(4⁃1)消 δ xA 、δ xB,可得到下式 图4-1 杠杆及作用在两端上的力
机器人动力学方程式
式中, n 为机器人的关节总数。其次我们来考虑把K 作为机器人各关节 速度的函数。这里vCi与ω i 分别表示为
机器人学导论复习资料

第一章绪论1.机器人三守则:1)机器人必须不危害人类,也不允许它眼看人将受害而袖手旁观;2)机器人必须绝对服从于人类,除非这种服从有害于人类;3)机器人必须保护自身不受伤害,除非为了保护人类或是为人类做出牺牲。
2.机器人的定义共同处:1)像人或人的上肢,并能模仿人的动作;2)具有智力或感觉与识别能力;3)是人造的机器或机械电子装置。
3.机器人的主要特点:①通用性:机器人的通用性取决于其几何特性和机械能力。
通用性指的是执行不同的功能和完成多样的简单任务的实际能力。
通用性也意味着,机器人具有可变的几何结构。
②适应性:机器人的适应性是指其对环境的自适应能力,即所设计的机器人能够自我执行未经完全指定的任务,而不管任务执行过程中所发生的没有预计到的环境变化。
这一能力要求机器人认识其环境,即具有人工知觉。
4.机器人系统的结构:一个机器人系统由四个相互作用的部分组成:机械手、环境、任务和控制器。
机械手是具有传动执行装置的机械,它由臂、关节和末端执行装置(工具等)构成,组合为一个互相连接和互相依赖的运动机构。
环境是指机器人所处的周围环境。
我们把任务定义为环境的两种状态(初始状态和目标状态)间的差别。
计算机是机器人的控制器或脑子。
5.机器人的自由度:物体能够对坐标系进行独立运动的数目称为自由度。
物体所能进行的运动包括:沿着坐标轴ox、oy、oz的三个平移运动T1,T2,T3;绕着坐标轴ox、oy、oz的三个旋转运动R1,R2,R3。
自由度是机器人的一个重要技术指标,它是由机器人的结构决定的,并直接影响到机器人的机动性。
6.机器人的分类:①按机械手的几何结构来分:1)柱面坐标机器人2)球面坐标机器人3)关节式球面坐标机器人②按机器人的控制方式分:1)非伺服机器人:工作能力有限,按照预先编好的程序顺序工作2)伺服控制机器人:有更强的工作能力,反馈控制系统③按机器人的智能程度分:1)一般机器人,不具有智能,只具有一般编程能力和操作功能2)智能机器人,具有不同程度的智能,又可分为传感型机器人、交互型机器人、自立型机器人。
机器人技术基础复习要点

机器人技术基础复习要点第一章:绪论1.机器人分类:按开发内容与应用分为工业机器人,操纵型机器人,智能机器人;按发展程度分为第一代,第二代和第三代机器人;按性能指标分为超大型,大型。
中型。
小型和超小型机器人;按结构形式分为直角坐标型机器人,圆柱坐标型机器人,球坐标型机器人和关节坐标型机器人;按控制方式分为点位控制和连续轨迹控制;按驱动方式分为气力驱动式,液力驱动式和电力驱动式。
按机座可动分类分为固定式和移动式。
2.机器人的组成:驱动系统,机械系统,感知系统,控制系统,机器人-环境交互系统,人机交互系统。
3.机器人的技术参数:自由度:是指机器人所具有的独立坐标轴的数目;精度:主要依存于机械误差,控制算法误差与分辨率系统误差;重复定位精度;是关于精度的统计数据;工作范围:指的是机器人手臂末端或手腕中心所能达到的所有店的集合;最大工作速度:不同厂家定义不同,通常在技术参数中加以说明;承载能力:指的是机器人在工作范围内的任何位姿上所能承受的最大质量。
第二章:机器人本体结构1.机器人本体基本结构:传动部件,机身及行走机构,臂部,腕部,手部。
2.机器人本体材料的选择:强度高,弹性模量大,质量轻,阻尼大,经济性好。
3.机身设计要注意的问题:刚度和强度大;动灵活,导套不宜过短,避免卡死;驱动方式适宜;结构布置合理。
4.臂部的基本形式:机器人的手臂由大臂,小臂所组成,手臂的驱动方式主要有液压驱动,气动驱动和电动驱动几种形式,其中电动驱动最为通用;臂部的典型机构有臂部伸缩机构,手臂俯仰运动机构,手臂回转与升降机构。
5.臂部设计需要的注意的问题:足够的承载能力;刚度高;导向性能好,运动迅速,灵活,平稳,定位精度高;重量轻,转动惯性小;合理设计与腕部和机身的连接部位。
6.机器人的平稳性和臂杆平衡方法:机身和臂部的运动较多,质量较大,如果运动速度和负载游较大,当运动状态变化时,将产生冲击和振动。
这将仅影响机器人的精确定位,甚至会使其不能正常运转。
四自由度机器人设计及运动学动力学分析

目录摘要............................................................................................................错误!未定义书签。
Abstract ........................................................................................................错误!未定义书签。
1绪论 (4)1.1 引言 (4)1.2机器人研究现状及发展趋势 (5)1.3本课题的主要研究内容和工作安排 (10)1.3.1课题研究的背景及意义 (10)1.3.2课题研究的内容及安排 (12)2四自由度串联机器人本体结构设计 (13)2.1机器人的总体方案设计 (13)2.1.1抓取机器人功能需求分析及其特点 (13)2.1.2机器人驱动方案的确定 (14)2.1.3机械传动方案的确定 (15)2.1.3机器人基本技术参数设计 (15)2.1.4机器人本体的总体结构 (17)2.2机器人本体基本结构设计 (18)2.2.1大臂和小臂机械结构设计 (18)2.2.2腕部机械结构设计 (20)2.2.3直线组件的设计选择 (20)2.2.4支架结构设计 (21)2.2.5步进电机与减速器的计算和选择 (22)2.2.6机器人传动轴的校核 (25)2.2.7机器人本体的三维模型 (26)2.3本章小结 (27)3四自由度抓取机器人运动学分析及仿真 (28)3.1机器人运动学分析 (28)3.1.1奇次坐标变换 (29)3.1.2 Denavt-Hartenberg(D-H)表示法 (30)3.1.3抓取机器人运动学模型的建立 (32)3.2机器人运动学方程的建立 (33)3.2.1抓取机器人的正运动学分析 (33)3.2.2工业机器人工作空间分析 (35)3.2.3机器人雅可比(Jacobian)关系求解 (38)3.2.4 抓取机器人的逆运动学分析 (41)3.3四自由度串联机器人运动学仿真 (45)3.3.1虚拟样机技术概述 (45)3.3.2本文用到的ADAMS软件模块 (46)3.3.3建立机器人仿真模型 (47)3.3.4机器人位移仿真分析 (49)3.3.5机器人速度仿真分析 (50)3.4 本章小结 (51)4. 轨迹规划及仿真分析............................................................................. 错误!未定义书签。
第04章-机器人动力学剖析

研究机器人动力学的目的
研究机器人动力学的目的是多方面的。 动力学正问题与机器人的仿真有关; 逆问题是为了实时控制的需要,利用动力学模型,实现 最优控制,以期达到良好的动态性能和最优指标。在设计中 需根据连杆质量、运动学和动力学参数、传动机构特征和负
载大小进行动态仿真,从而决定机器人的结构参数和传动方
利用前面的虚功原理来推导机器人的静力学关系式。 如图4-2所示的机械手,要产生图(a)所示的虚位 移,推导出图(b)所示各力之间的关系式。这一推导方 法本身也适用于一般的情况。
图4-2 机械手的虚位移和施加的力
假设 : T m1 手爪的虚位移为 r r1 ,, rm , R 关节的虚位移为 1 ,, n T , R n1 T m1 手爪力为 F f1 ,, f m , R T n1 关节驱动力为 1 ,, n , R 如果施加在机械手上的力作为手爪力的 反力( F 用来表示)时,机械手的虚功可 表示为: T T (4-5) W (F ) r
下面看一个例子来理解一下实际上如何使用虚 功原理。如图4-1所示,已知作用在杠杆一端的 力FA ,试用虚功原理求作用于另一端的力 FB 。假 设杠杆长度 L A ,LB 已知。
图4-1 杠杆及作用在它两端上的力
按照虚功原理,杠杆两端受力所作的虚功应
该是
FAx A FBx B 0
(4 - 1 )
一、虚功原理 在介绍机器人静力学之前,首先要说明一下 静力学中所需要的虚功原理(principle of virtual work)。 约束力不作功的力学系统实现平衡的必要且 充分条件是对结构上允许的任意位移(虚位移) 施力所作功之和为零。这里所指的虚位移 (virtual displacement)是描述作为对象的系统 力学结构的位移,不同于随时间一起产生的实际 位移。为此用“虚”一词来表示。而约束力 (force of constraint)是使系统动作受到制约的 力。
机器人静力学动力学
• 质心速度
.
.
..
x2 l1 cos1 1 l2 cos(1 2 )(12 )
.
.
..
y2 l1 sin1 1 l2 sin(1 2 )(12 )
• 质心速度:
v22
.
y
2
2
.
x22
.
.
..
.
.
..
l12 12 l22 (12 21 2 22 ) 2l1l2 cos2 (12 1 2 )
JT
例题 二自由度平面关节机器人,知端点力,略摩擦、重
力,求关节力矩。 1 0 2 90 F [FX , FY ]T
解:
J
l1s1 l2 s12
l1c1
l2c12
l2 s12
l 2 c12
JT
l1s1 l2 s12 l2 s12
l1c1 l2c12
l 2 c12
1
关节虚位移
q1
q
2
q
qq43
q5
q6
虚位移原理:
W 1q1 2q2 F1 x F2 y F3 z F4
W Tq F TP
W 0
W Tq F TP Tq F T Jq ( J T F )T q 0
( J T F )T 0
JTF
雅可比转置矩阵
• 三、静力学两类问题: • 1、 正向静力学—知各关节驱动力(力矩),求手部
端点能输出的力(力矩) 。
• 2、 逆向静力学—知手部端点作用力(力矩),求关 节需施加的力(力矩)。
• 机器人通常是逆向力学问题。
• §4—2 机器人动力学
• 一、动力学两类问题: • 1、 正向动力学—知各关节驱动力(力矩),求末端
机器人技术基础复习要点

机器人技术基础复习要点第一章:绪论1。
机器人分类:按开发内容与应用分为工业机器人,操纵型机器人,智能机器人;按发展程度分为第一代,第二代和第三代机器人;按性能指标分为超大型,大型。
中型。
小型和超小型机器人;按结构形式分为直角坐标型机器人,圆柱坐标型机器人,球坐标型机器人和关节坐标型机器人;按控制方式分为点位控制和连续轨迹控制;按驱动方式分为气力驱动式,液力驱动式和电力驱动式。
按机座可动分类分为固定式和移动式.2.机器人的组成:驱动系统,机械系统,感知系统,控制系统,机器人—环境交互系统,人机交互系统。
3.机器人的技术参数:自由度:是指机器人所具有的独立坐标轴的数目;精度:主要依存于机械误差,控制算法误差与分辨率系统误差;重复定位精度;是关于精度的统计数据;工作范围:指的是机器人手臂末端或手腕中心所能达到的所有店的集合;最大工作速度:不同厂家定义不同,通常在技术参数中加以说明;承载能力:指的是机器人在工作范围内的任何位姿上所能承受的最大质量。
第二章:机器人本体结构1.机器人本体基本结构:传动部件,机身及行走机构,臂部,腕部,手部.2。
机器人本体材料的选择:强度高,弹性模量大,质量轻,阻尼大,经济性好. 3。
机身设计要注意的问题:刚度和强度大;动灵活,导套不宜过短,避免卡死;驱动方式适宜;结构布置合理。
4.臂部的基本形式:机器人的手臂由大臂,小臂所组成,手臂的驱动方式主要有液压驱动,气动驱动和电动驱动几种形式,其中电动驱动最为通用;臂部的典型机构有臂部伸缩机构,手臂俯仰运动机构,手臂回转与升降机构。
5。
臂部设计需要的注意的问题:足够的承载能力;刚度高;导向性能好,运动迅速,灵活,平稳,定位精度高;重量轻,转动惯性小;合理设计与腕部和机身的连接部位。
6。
机器人的平稳性和臂杆平衡方法:机身和臂部的运动较多,质量较大,如果运动速度和负载游较大,当运动状态变化时,将产生冲击和振动。
这将仅影响机器人的精确定位,甚至会使其不能正常运转。
第四章机器人的动力学

n
1
v Ci
v Ci
1 2
i Ii i )
T
1
[m 2
i 1 n
i
(J L q ) J L q (J A q ) IiJ A q ]
(i) (i) T (i) T T
1
(m 2
i 1
i
q
JL
(i)T
JL q q
(i)
二、机器人静力学关系式推导
以2自由度机械手为例,要产生图a所示的虚位移 , , r , 则图b所示各力 , 和 F 之间的关系:
1 2
1
2
由 虚 功 原 理 知 : 1 1 2 2 F r 0 即: 1
2
1 F 2
当刚体绕过质心的轴线旋转时,角速度ω,角加速度
,惯
性张量
与作用力矩N之间满足欧拉方程:
IC (IC ) N
——欧拉运动方程
Ic R
3 3
是绕重心 c 的惯性矩(转动惯量) N 回转力矩
, I c的各元素表示对应的力
矩元素和加速度元素间
的惯性矩;
回转角速度;
对于对于zz轴轴于是于是12联立可得联立可得对于一般形状连杆对于一般形状连杆除第33分量以外其它分量皆不为分量以外其它分量皆不为00的第1122分量成为改变轴方向的力矩但在固定分量成为改变轴方向的力矩但在固定轴场合与这个力矩平衡的约束力生成轴场合与这个力矩平衡的约束力生成22式中的式中的1122分分量不产生运动
由虚功原理得:
F A x A FB x B 0 即 : F A L A F B L B 0 ( F A L A F B L B ) 0 F A L A FB L B 0 FB LA LB FA
机器人学-第4章_机器人动力学

机械手系统(包括传动装置)的总动能为:
Kt K Ka
1 2
6 i 1
i j 1
i k 1
Trace
Ti qi
Ii
Ti T qk
qj qk
1 2
6
I ai qi2
i 1
(4.20)
4.2.2 动能和位能的计算
23
4.2.2 动能和位能的计算
位能的计算 一个在高度h处质量m为的物体,其位能为:
对拉格朗日函数求导,以得到动 力学方程式。
O3 连杆2
3rp
连杆3 O2
O1 连杆1 0rp
P
连杆4 O4
O
图4.4 四连杆机械手
第四章 机器人动力学
15
4.2.1 速度的计算
连杆3上点P的速度为:
0vp
d dt
(
0
r
p
)
d dt
(T3
3
rp
)
T3 3rp
对于连杆i上任一点的速度为:
v
dr dt
4
4.1.1 刚体的动能与位能
x0 0, x0和x1均为广义坐标,有下式:
M1 x1 c( x1 x0 ) k( x1 x0 ) M1 g F M 0 x0 c( x1 x0 ) k( x1 x0 ) M 0 g F
或用矩阵形式表示为:
M1
0
0 M0
x1 x0
D212 D221 0
重力项
D1 (m1 m2 )gd1 sin1 m2 gd2 sin(1 2 ) D2 m2 gd2 sin(1 2 )
4.1.2 动力学方程的两种求法
10
拉格朗日功能平衡法
表4.1给出这些系数值及其与位置 2的关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Lagrangian formulation is an "energy-based" approach to dynamics.
Ch.4 Manipulator Dynamics
4
Ch.4 Manipulator Dynamics
There are two problems related to the dynamics of a manipulator that we wish to solve.
0 gx0
D
1 2
c(
x&1
x&0 )2
W Fx1 Fx0
F
x0
F
M1
x1
k
c
M0
图4.1 一般物体的动能与位能
4.1 Dynamics of a Rigid Body
8
4.1.1 Kinetic and Potential Energy of a Rigid Body
x0 0, x1 is a generalized coordinate
机器人学基础
第四章 机器人动力学
Fundamentals of Robotics
Ch.4 Manipulator Dynamics
中南大学 蔡自兴,谢 斌 zxcai, xiebin@
2010
Fundamentals of Robotics
1
Contents
Introduction to Dynamics Rigid Body Dynamics Lagrangian Formulation Newton-Euler Formulation Articulated Multi-Body Dynamics
4.1 Dynamics of a Rigid Body
7
4.1 Dynamics of a Rigid Body
4.1.1 Kinetic and Potential Energy of a Rigid Body
K
1 2
M1 x&12
1 2
M0 x&02
P
1 2
k( x1
x0 )2
M1 gx1
M
Ch.4 Manipulator Dynamics
6
4.1 Dynamics of a Rigid Body 刚体动力学
Langrangiຫໍສະໝຸດ n Function L is defined as:
LKP
(4.1)
Kinetic Energy
Potential Energy
Dynamic Equation of the system (Langrangian
Ch.4 Manipulator Dynamics
2
Ch.4 Manipulator Dynamics
Introduction
Manipulator Dynamics considers the forces required to cause desired motion. Considering the equations of motion arises from torques applied by the actuators, or from external forces applied to the manipulator.
Equation):
Fi
d dt
L qi
L qi
,i
1,2,
n
(4.2)
where qi is the generalized coordinates, qi represent corresponding velocity, Fi stand for corresponding torque or force on the ith coordinate.
Forward Dynamics: given a torque vector, Τ, calculate the resulting motion of the manipulator, , &, and && . This is useful for simulating the manipulator.
F
x0
F
d dt
K x1
K x1
D x1
P x1
W x1
M1
x1
k
c
① ②③ ④⑤
M0
① Kinetic Energy due to (angular) velocity ② Kinetic Energy due to position (or angle) ③ Dissipation Energy due to (angular) velocity ④ Potential Energy due to position ⑤ External Force or Torque
Inverse Dynamics: given a trajectory point, , &, and &&,
find the required vector of joint torques, Τ. This formulation of dynamics is useful for the problem of controlling the manipulator.
Ch.4 Manipulator Dynamics
5
Contents
Introduction to Dynamics Rigid Body Dynamics Lagrangian Formulation Newton-Euler Formulation Articulated Multi-Body Dynamics
Ch.4 Manipulator Dynamics
3
Ch.4 Manipulator Dynamics
Two methods for formulating dynamics model:
Newton-Euler dynamic formulation
Newton's equation along with its rotational analog, Euler's equation, describe how forces, inertias, and accelerations relate for rigid bodies, is a "force balance" approach to dynamics.
