经济应用数学试卷

合集下载

经济应用数学基础(一)微积分_试题及答案

；
；；；
3 2 6、函数 f ( x ) = x − x + 1 的极大点是
′ 7、设 f ( x ) = x ( x − 1)( x − 2)……(x − 2006) ，则 f (1) =
x 8、曲线 y = xe 的拐点是
；；；
9、
∫
2
0
x − 1dx
=
� � � � � � � � � � a = i + 3 j − 2 k , b = i − j + λ k 10、设，且 a ⊥ b ，则 λ =
；
⎧ 2x f ( x) = ⎨ ⎩a + x 2、设函数
x<0 x ≥ 0 在点 x = 0 连续，则 a =
；；
4 3、曲线 y = x − 5 在（-1，-4）处的切线方程是
f ( x )dx = x 4、已知 ∫
1 x lim(1 − ) 2 x = 5、 x →∞
3
+C
，则 f ( x ) =
（A）极限不存在（B）极限存在但不连续（C）连续但不可导（D）可导
9．设函数 f ( x ) 在 ( −∞, ∞) 上连续，且 f (0) = 0 ， f ′(0) 存在，则函数（A）在 x = 0 处左极限不存在（B）有跳跃间断点 x = 0 （C）在 x = 0 处右极限不存在（D）有可去间断点 x = 0
ln cos x dx 2 ∫ 3. cos x
4.
∫
x 2 dx
1 − x2
三、求解下列各题（每题 7 分，共 28 分） ⎧ e −2 x , x≤o ⎪ 2 f ( x) = ⎨ x 1 , x >0 ⎪ 2 ∫ f (t )dt ⎩1 + x

《经济应用数学》6套期末考试题AB卷带答案模拟测试题

《经济应用数学》试题 (1)（4）已知 y sin x ，则 y（）.A ．sin xB ．sin xC ． cos xD ．cos xxxxx 年x 月题号一二三四五六总分x（5）设 f (x, y) y , 则f x y ( )' ( , )xxA ． y ln yB ． x 1 xyC． xyD．x 1lnxyy题得分评分人得分评分人一、填空（每题 2 分，共 10 分）三、求下列函数的极限（每题 6 分，共 12 分）班级答12(1)y 4 x的定义域为__________________x 1 (2) 函数 2 2 1 y x x 的单调递增区间是 __________________(1)2xlim2x1xx 21(3) 设函数 z sin( x y) , 则 dz __________________要2(4) 已知 f (x)dx x sin x c, 则 f (x) ___________________学号不(5) 3 sin x 2 dx 1 cosx2 得分评分人 _______ 二、选择题 ( 每题 2分，共 10分）(2) lim x2 x (x 2 cos sin x x) 21 姓名内（1）若 lim f (x) Axx，则 f (x) 在点 x 0 处()线A ．有定义，且 f ( x 0 ) AB ．没有定义C ．有定义，且 f ( ) 可为任意值D ．可以有定义，也可以没有定义x得分评分人四、求导数或微分（每题 6 分，共 24 分）封（2）下列函数中（）是奇函数A． 2 1y x B ．xy e C．y x sin 3x D ．y x c os 1xx cos（1）y 3e x x 求y'密（3）设f (x) 为可导函数，以下各式正确的是（）A． f ( x)dx f (x) B． f ( x)dx f (x) x cos 求dy（2）y e xC ． f ( x)dx f (x)D ． f ( x)dx f (x) C《经济应用数学》试题（1）第1页《经济应用数学》试题（1）第2页(共4 页)得分评分人（3）yy 1 xe ,求d ydx六、应用题（每题9 分，共18 分）11．求由曲线 3 , y x3y x所围成的平面图形的面积.题x ey（4）设0xy e ,求d ydx答班级五、求下列积分和解微分方程（每题 6 分，解微分方程8 得分评分人分，共26分）要学号不2x x cosx 2（1）dxx2．已知某产品的边际成本为 C '(q )4q ( 万元／百台) ，边际收入为R '(q) 60 2q( 万元／百台), 如果该产品的固定成本为10 万元，求：（1）产量为多少时总利润L(q) 最大？姓名内（2） 2sin x dx（2）从最大利润产量的基础上再增产200台，总利润会发生什么变化？线2x（3）xe dx封《经济应用数学》试题(1)参考答案一、填空（每题 2 分，共10分）密（4）xy ' y 3, y 0x 1 1, 2,1 1,2 ；2, 1, ；3,cos x y( ydx xdy )；4, 2x cosx；5,0 二、选择题( 每题2 分，共10 分）1,D 2,D 3,C 4,B 5,A三、求下列函数的极限（每题分，共分）6 121,原式limx 1 x 2 x 1 3x 1 x 1 2，《经济应用数学》试题（1）第3页《经济应用数学》试题（1）第4页(共4 页)2，原式2cos x 112 2x xlim 12xsin x1x《经济应用数学》试题(2)xxxxx年月题号一二三四五六总分四、求导数或微分（每题 6 分，共24 分）班级题答x 11,4,y'=3e +sinx+2 xx x2, y' e (cos x sin x) dy e (cos x sin x) d xydy e' y y 'y e xe y y3,x xdx 1 xexdy e y' ' 0x yy xy e e y yx xdx x e五、求下列积分和解微分方程（每题 6 分，解微分方程8 分，共26 分）得分评分人一、填空（每题 2 分，共10 分）2 x g x x(1) 设函数 f (x) x 6 10, ( ) 3，则f g(x) =________________(2) 曲线 2 1y x 在点(1,0) 处的切线方程为______3 x(3) 函数y ( ) 3 1在定义域内单调___________（递增、减少）f x x要1, 原式2 12(x cos x)dx x sin x 2ln x cx 2(4) 若x s in x是f (x) 的一个原函数，则 f ( x) d x ________学号不2, 原式3, 原式22sin xdx sin xdx cosx cos 41 12 2 2xsin tdt（5）0lim ___________2x 0xxxe d x e c22姓名内4, y 1 xy 3 x, P 1 x Q 3 x得分评分人二、选择题 ( 每题 2 分，共 10 分）线封 1 1 dx3 dxpdxPdxy eQedx cedx cexxx由 yx 1得 c 3特解y 33x六、应用题（每题 9 分，共 18 分） 1, 由对称性141 311 3433S 2 (xx )dx 2xx 1 4 41 x3x c（1）设 f (x) 的定义域为 0,1 , 则 f (x 1) 的定义域为（）A ． 0,1B ． 1,2C ． 1,0D ． 0,2（2）下列函数中（）是奇函数1x2D．y eC y x cos3xy sin．xA y f ( x)B lim f (x) ．x．函数在的一个邻域内有定义xx21y xB ．A ．（3）函数 yf (x) 在点 x 0 处连续，则（）存在；密2,（1） L(q) R(q ) C( q )L '(q ) R '(q) C '(q) 60 6qC ．极限值等于x 处的函数值 f ( x 0 ) 即 lim f ( x)f (x 0 ) 0x xD ． y f (x) 在x 点无定令 L '(q )0 得 q 10义驻点唯一， q 10 百台 1000台为最大值，此时利润最大x（4） f (x dx xe C ，则 f (x)（）)（2）12122A ．x(x 2)eB ．x(x 1)e C ．xxeD ．x(x 1)eL 60 6qdq 60q 3q 12（万元）120000（元）1010《经济应用数学》试题（1）第5页《经济应用数学》试题（1）第6页(共4 页)（5）微分方程y ' y 满足初始条件y(0) 1 的特解为（）A．x x x x y e B．y e 1 C．y e 1 D．y 2 ex cos 3，求dy （3）设y e x得分评分人三、求下列函数的极限（每题 6 分，共12 分）（4） 3 3z x y y x,求z z' , 'x y题(1) 1limx3 x x 2 3答班级得分评分人要(2) limx 0 1 cos2x2x五、求下列积分和解微分方程（每题 6 分，解微分方程8分，共26 分）学号（1）4x(1 x )dx不得分评分人姓名内四、求导数或微分（每题 6 分，共24 分）（2）e sin x cosxdx线（1）设x 1f ( x) ，求 f '( x)x 1 （3） 11xexedx封密 5 x x x x4 3 2（2）y 2x 3 5 4 7 ,求y" （4）1y' y 02x《经济应用数学》试题（1）第7页《经济应用数学》试题（1）第8页(共4 页)得分评分人六、应用题（每题9分，共18 分）1 ，f '( x)1 1x 1 x 112 x 2 x2 2x 1 x x 11．求由曲线y x2 , y x 所围成的平面图形的面积. 4 3 2 3 22, y ' 10 x12 x15 x2x 4 y" 40 x36 x30 x 2xy e x x (cos3 3sin 3 )dy e x x dxx3, ' (cos3 3sin 3 )题' 3 2 3' 3 3 24,z x y yz x xyxy五、求下列积分和解微分方程（每题 6 分，解微分方程8 分，共26 分）班级答要1, 原式2, 原式3, 原式1342 140222 x xdx xx3 20 34xxsinsinsin e dx ec1111x xx d 1 e ln 1 e ln 1 e ln 2e 0学号不2．某企业分批生产某产品，每批产量为q吨，固定成本8万元，总成本函数为34,dyydy 1,dx2x2dxy x11xln y ln cxy ce,dy 1, dx2y x2C(q) 8 q , 其中 k 为待定系数，已知批量 q 9 吨时，总成本 C 62万元。

经济应用数学试卷

四川农业大学网络教育专科考试经济应用数学试卷（课程代码 391006）本试题一共五道大题，共2页，满分100分。

考试时间90分钟.注意:1、答案必须填写在答题纸上，题号不清或无题号的以零分计。

2、答题前，请在答题纸上准确、清楚地填写各项目；3、学号、考点名称、考室号、姓名、身份证号、课程代码、课程名称、培养层次等,不写、乱写及模糊不清者,答题纸作废；4、闭卷考试，若有雷同以零分计。

一、是非题(每小题3分,共15分)1。

y =的间断点为1x =±。

错2。

22sin ()1xf x x =+是奇函数。

对 3。

若lim ()0x af x →=,lim ()0x ag x →=.则一定有()lim0()x af xg x →=。

错 4. 设)(x f 在a x =点处连续，则有()()f x f a '=。

对 5。

若()f x 为边际收益函数（x 为产量），则0()()x F x f x dx =⎰为总收益函数。

对二、填空题（每小题3分,共15分）6.函数1lg 1y x=- [3,1)- ）。

7。

设211sin ,0,(),0.x x f x xk xx ⎧+≠⎪=⎨⎪+=⎩ 在0=x 连续，则k =（ 1 ）.8。

导数6(sin 1)4[]x d e dx dx+=⎰（ 0 ）。

9。

定积分22021xdxx =+⎰（ ln5 ).10. )(x f 一个原函数为sin x ，则⎰=dx x f )('( cos x C -+ ）。

三、选择题（每小题3分，共15分）11. 当2→x 时，2312x x x ++-是（ B ）.A ．无穷小量B ．无穷大量C ．1D ．—1 12。

极限0sin3lim3x xx→= （ A ）A ．1B ．0C ．不存在D ．313．在下列函数中，在0=x 不可导的是( C )。

A ．xe y = B ．x y sin = C ．21xy = D ．x y arcsin = 14．设122=+y x ，则dxdy=（ D ）. A ．21x x - B ．xyC ．y xD ． y x -15。

经济应用数学习题及答案

经济应用数学习题第一章极限和连续填空题1. sin limx xx→∞=0 ；2.函数 x y ln =是由 u y =，v u ln =，x v =复合而成的； 3当 0x → 时，1cos x - 是比 x 高阶的无穷小量。

4. 当 0x → 时，若 sin 2x 与 ax 是等价无穷小量，则 a =25.2lim(1)x x x →∞-=2-e选择题1.02lim5arcsin x xx →= （ C ）（A ） 0 （B ）不存在（C ）25（D ）12.()f x 在点 0x x = 处有定义，是 ()f x 在 0x x =处连续的（ A ）（A ）必要条件（B ）充分条件（C ）充分必要条件（D ）无关条件计算题1.求极限 20c o s 1l i m 2x x x →-解：20cos 1lim 2x x x →-＝414sin lim 0-=-→x x x 2. x x x 10)41(lim -→＝41)41(40)41(lim ---→=-e x x x 3.201lim x x e x x →--112lim 0-=-=→x e x x导数和微分填空题1若 )(x u 与 )(x v 在 x 处可导，则 ])()(['x v x u =2'')]([)()()()(x v x v x u x v x u - 2.设)(x f 在0x 处可导，且A x f =')(0，则hh x f h x f h )3()2(lim000--+→用A 的代数式表示为A 5 ；32)(x e x f =，则xf x f x )1()21(lim--→= 4e - 。

2(12)(1)'()2,lim2'(1)4x x f x f f x xe f ex →--==-=-解选择题1. 设 )(x f 在点 0x 处可导，则下列命题中正确的是（ A ）（A ） 000()()limx x f x f x x x →-- 存在（B ） 000()()lim x x f x f x x x →--不存在（C ） 00()()limx x f x f x x →+-存在（D ） 00()()lim x f x f x x∆→-∆不存在2. 设)(x f 在0x 处可导，且0001lim(2)()4x x f x x f x →=--，则0()f x '等于（ D ）（A ） 4 （B ） –4 （C ） 2 （D ） –2 3. 3设 ()y f x = 可导，则 (2)()f x h f x -- = （ B ）（A ） ()()f x h o h '+ （B ） 2()()f x h o h '-+ （C ） ()()f x h o h '-+ （D ） 2()()f x h o h '+ 4.设 (0)0f = ，且 0()limx f x x → 存在，则 0()lim x f x x→ 等于（ B ）（A ）()f x ' （B ）(0)f ' （C ）(0)f （D ）1(0)2f '5.函数 )(x f e y =，则 ="y （ D ）（A ） )(x f e （B ） )(")(x f e x f（C ） 2)()]('[x f e x f （D ） )}(")]('{[2)(x f x f e x f +6函数 x x x f )1()(-=的导数为（ D ）（A ）x x x )1(- （B ） 1)1(--x x （C ）x x x ln （D ） )]1ln(1[)1(-+--x x xx x7函数 xx x f =)( 在 0=x 处（ D ）（A ）连续但不可导（B ）连续且可导（C ）极限存在但不连续（D ）不连续也不可导计算与应用题1. 设 ln()y xy = 确定 y 是 x 的函数，求 dxdy 解： )(1)(1)][ln(''''xy y xyxy xy xy y +=== )1('''-=+=⋅y x yy xy y y xy2. 2设 x y e y ln = 确定 y 是 x 的函数，求 dxdy 解：''ln (ln )y y y dy y e y y x xdx x e x ⋅=⋅+=- 3. 3求 13cos x y e x -= 的微分解：'131313(3cos sin )(3cos sin )x x x dy y dx e x e x dx e x x dx ---==--=-+4. 4求 2xe y x= 的微分；解：222'222(21)x x x e x e e x y x x --== 22(21)x e x dy dx x -= 5设sin 10()20ax x e x f x xa x ⎧+-≠⎪=⎨⎪=⎩在(,)-∞+∞上连续，求a 的值。

经济数学试题及答案大全

经济数学试题及答案大全一、单项选择题（每题2分，共20分）1. 函数f(x)=x^2-4x+3的零点个数为（）。

A. 0B. 1C. 2D. 3答案：C2. 极限lim(x→0) (sin x)/x的值为（）。

A. 1B. 0C. -1D. 2答案：A3. 以下哪个函数是奇函数（）。

A. y = x^2B. y = x^3C. y = x^4D. y = ln(x)答案：B4. 以下哪个选项是二阶导数（）。

A. f'(x)B. f''(x)C. f'''(x)D. f(x)答案：B5. 以下哪个选项是定积分的基本性质（）。

A. ∫[a,b] f(x)dx = ∫[a,c] f(x)dx + ∫[c,b] f(x)dxB. ∫[a,b] f(x)dx = ∫[b,a] f(x)dxC. ∫[a,b] f(x)dx = -∫[b,a] f(x)dxD. ∫[a,b] f(x)dx = ∫[a,b] f(-x)dx答案：A6. 以下哪个选项是多元函数的偏导数（）。

A. ∂f/∂xB. ∂f/∂yC. ∂f/∂zD. ∂f/∂t答案：A7. 以下哪个选项是线性代数中的矩阵运算（）。

A. 矩阵加法B. 矩阵乘法C. 矩阵转置D. 矩阵求逆答案：B8. 以下哪个选项是概率论中的随机变量（）。

A. X = 5B. X = {1, 2, 3}C. X = [0, 1]D. X = {x | x ∈ R}答案：B9. 以下哪个选项是统计学中的参数估计（）。

A. 点估计B. 区间估计C. 假设检验D. 方差分析答案：A10. 以下哪个选项是计量经济学中的回归分析（）。

A. 简单线性回归B. 多元线性回归C. 时间序列分析D. 面板数据分析答案：A二、填空题（每题2分，共20分）11. 函数f(x)=x^3-3x的导数为_________。

答案：f'(x) = 3x^2 - 312. 极限lim(x→∞) (x^2 - 3x + 2)/(x^2 + 4x + 3)的值为_________。

大学专业试卷经济应用数学二考A

《经济应用数学二》试卷（A ）适用专业：考试日期：考试时间：120分钟；考试方式：闭卷；总分100分一.填空题(21020⨯=分分).1. 设5212,0113A B -⎛⎫⎛⎫==⎪ ⎪⎝⎭⎝⎭, 则A B += , AB = . ２．排列３，２，５，１，４的逆序数为３. 设A 的列向量组为123,,ααα, 且3A =, 1332(2,,)B αααα=+, 则B = .４．行列式11aa aa= ５. 设３阶方阵A 的列向量组123,,ααα，若12,αα线性无关且0A =，则向量组123,,ααα的秩为 .６. 3阶方阵A 的特征值为1, 2, 3, 则A = . 7.向量12(1,1),(2,)T T p p a ==正交, 则a = . ８．设()1234α=,()4321β=, 则,αβ的内积为 .９．设1112344916D =，则212223A A A ++=二.选择题(21020⨯=分分)１．下列矩阵中，不是初等矩阵的是（）Ａ．001010100⎛⎫ ⎪ ⎪ ⎪⎝⎭ Ｂ．100001010⎛⎫ ⎪ ⎪ ⎪⎝⎭ C. 100020001⎛⎫ ⎪⎪ ⎪⎝⎭ D. 100012001⎛⎫ ⎪- ⎪ ⎪⎝⎭2. 设,A B 为n 阶方阵, 则下列结论成立的是( )A. A A λλ=, R λ∈.B. 若0AB ≠, 则111()AB B A ---=.C. 若,A B 均为对称阵, 则AB 为对称阵D. 若0AB =，则0A =或0B =．３．设,1a b A ad bc c d ⎛⎫=-=⎪⎝⎭，则1A -=（）Ａ．d b c a ⎛⎫⎪⎝⎭ Ｂ．d c b a ⎛⎫ ⎪⎝⎭ Ｃ．d b c a -⎛⎫ ⎪-⎝⎭ Ｄ．d c b a -⎛⎫ ⎪-⎝⎭４. 设矩阵20003101A x ⎛⎫ ⎪= ⎪ ⎪⎝⎭与400020002B ⎛⎫⎪= ⎪ ⎪⎝⎭相似, 则x =( ).A. 2B. 3C. 0D. 1５. 设向量组123,,ααα线性无关，则下列向量组线性无关的是（）Ａ．122331,,αααααα--- Ｂ．1213,,αααα+ Ｃ．1212,,23αααα- Ｄ．2323,,2αααα+６. 设A 为(2)n n ≥阶方阵，且0A α=≠，则*A =（）A. 1α- B.α Ｃ．1n α- Ｄ．n α７．若四阶方阵Ａ的秩为3，则（）A ．A 为可逆阵B ．齐次方程组Ax =0有非零解C ．齐次方程组Ax =0只有零解D ．非齐次方程组Ax =b 必有解８．矩阵121200120000--⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦的秩是 ( ).(A) 1; (B) 2; (C) 3; (D) 4.９．设Ａ为n 阶方阵，若行列式50I A -=，则Ａ必有特征值（）Ａ．１Ｂ．－１Ｃ．５Ｄ．０ 1０．下列矩阵不是正交矩阵的是（） A ．⎥⎥⎦⎤⎢⎢⎣⎡--100010001B ．⎪⎪⎭⎫ ⎝⎛11001110121 C ．cos sin sin cos θθθθ-⎛⎫⎪⎝⎭D．1212⎫-⎪⎝三. 计算题（６0分）1．( 12分) 设120231340,240123A B ⎛⎫-⎛⎫ ⎪== ⎪ ⎪-⎝⎭ ⎪-⎝⎭，求（１）TAB ；（２）4A2．(９分) 设25461321X -⎛⎫⎛⎫=⎪ ⎪⎝⎭⎝⎭, 求矩阵X .３. (1５分) λ为何值时, 非齐次线性方程组12312321231x x x x x x x x x λλλλλ++=⎧⎪++=⎨⎪++=⎩ (1) 有唯一解? (2) 无解? (3) 有无穷多解? 并求其全部解.４．（1２分）求向量组123421234,1,3,52012αααα⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪==== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭的秩，并求一个极大无关组．５．(12分) 设110240421A -⎛⎫ ⎪= ⎪ ⎪⎝⎭(1) 求A 的特征值和特征向量(2) 矩阵Ａ能否对角化？若能，求可逆阵Ｐ，使1P AP -为对角阵．。

经济应用数学试题及答案

经济应用数学试题及答案一、选择题（每题2分，共20分）1. 下列函数中，哪一个是偶函数？A. f(x) = x^2B. f(x) = x^3C. f(x) = |x|D. f(x) = sin(x)答案：C2. 在线性规划问题中，目标函数的最优值可能在：A. 可行域的顶点B. 可行域的边界C. 可行域的内部D. 所有上述情况答案：D3. 假设某公司生产两种产品，产品1的利润为每单位10元，产品2的利润为每单位20元。

如果公司每天只能生产100单位的产品，且生产产品1需要2小时，产品2需要1小时，而公司每天有200小时的生产时间。

该公司应该如何分配生产时间以最大化利润？A. 只生产产品1B. 只生产产品2C. 生产50单位产品1和50单位产品2D. 生产100单位产品2答案：D4. 以下哪个选项不是边际成本的概念？A. 增加一单位产量的成本B. 总成本对产量的导数C. 固定成本D. 总成本的增加量除以产量的增加量答案：C5. 假设某公司的成本函数为C(x) = 3x^2 + 2x + 5，其中x是生产量。

该公司要生产多少单位的产品才能使平均成本最小？A. x = 0B. x = 1C. x = 2D. x = 3答案：B6. 在完全竞争市场中，长期均衡时，市场价格等于：A. 边际成本B. 平均成本C. 总成本D. 固定成本答案：B7. 以下哪个选项是关于消费者剩余的描述？A. 消费者支付的价格与他们愿意支付的价格之间的差额B. 消费者实际支付的价格C. 消费者购买的商品数量D. 消费者购买商品的总成本答案：A8. 如果一个市场的需求曲线是线性的，斜率为-2，那么需求的价格弹性是多少？A. 0.5B. -1C. -2D. 2答案：C9. 以下哪个选项不是经济利润的特点？A. 包括正常利润B. 考虑了机会成本C. 等于会计利润D. 可能为负值答案：C10. 在多阶段生产过程中，以下哪个选项不是生产者面临的决策类型？A. 投入品的选择B. 生产技术的选择C. 产品价格的确定D. 产出水平的确定答案：C二、简答题（每题10分，共20分）1. 解释什么是边际效用递减原理，并给出一个生活中的实例。

大专经济数学试题及答案

大专经济数学试题及答案一、单项选择题（每题2分，共20分）1. 以下哪个选项是边际成本的定义？A. 总成本除以产量B. 总成本的增量除以产量的增量C. 总产量的增量除以成本的增量D. 总产量除以总成本答案：B2. 在完全竞争市场中，企业在短期内会如何调整生产？A. 增加产量直到边际成本等于边际收益B. 减少产量直到边际成本等于边际收益C. 增加产量直到边际成本等于平均成本D. 减少产量直到边际成本等于平均成本答案：A3. 以下哪个函数是凹函数？A. f(x) = x^2B. f(x) = -x^2C. f(x) = x^3D. f(x) = -x^3答案：B4. 如果一个商品的需求价格弹性是-2，那么价格上升10%会导致需求量变化多少？A. 下降20%B. 下降10%C. 上升20%D. 上升10%答案：A5. 以下哪个选项是机会成本的定义？A. 为了获得某种资源所放弃的最大价值B. 为了获得某种资源所支付的货币成本C. 为了获得某种资源所支付的非货币成本D. 为了获得某种资源所放弃的所有成本答案：A6. 以下哪个选项是帕累托效率的定义？A. 资源分配使得至少一个人变得更好而其他人不变差B. 资源分配使得至少一个人变得更差而其他人不变好C. 资源分配使得没有人能变得更好而不使其他人变得更差D. 资源分配使得没有人能变得更差而不使其他人变得更好答案：C7. 以下哪个选项是消费者剩余的定义？A. 消费者愿意支付的最高价格与实际支付价格之间的差额B. 消费者实际支付价格与最低愿意支付价格之间的差额C. 消费者愿意支付的最高价格与最低愿意支付价格之间的差额D. 消费者实际支付价格与市场价格之间的差额答案：A8. 以下哪个选项是生产者剩余的定义？A. 生产者愿意接受的最低价格与市场价格之间的差额B. 生产者实际接受价格与市场价格之间的差额C. 生产者愿意接受的最低价格与实际接受价格之间的差额D. 生产者实际接受价格与最低愿意接受价格之间的差额答案：A9. 以下哪个选项是无差异曲线的特点？A. 向下倾斜B. 向上倾斜C. 垂直于价格轴D. 水平于价格轴答案：B10. 以下哪个选项是边际替代率的定义？A. 消费者愿意放弃一种商品以换取另一种商品的数量B. 消费者愿意放弃一种商品以换取另一种商品的比率C. 消费者愿意接受一种商品以换取另一种商品的数量D. 消费者愿意接受一种商品以换取另一种商品的比率答案：B二、计算题（每题10分，共30分）1. 假设某企业的成本函数为C(Q) = 0.5Q^2 + 10Q + 100，求该企业在产量为100单位时的边际成本。

经济应用数学一下考试试题库

《经济应用数学（一）》(下) 考试试题库适用专业: 怀德学院会计、营销、国贸、财务管理、人力、物流专业一、定积分及应用选择题（18题）1. 设)(x f 可导，下列式子正确的是（）A.()()tad f x dx f x dt =⎰ B. ()()xa d f x dx f x dx=⎰ C.)()(x f dx x f dx d ba=⎰ D. )()(x f dx x f ba='⎰2.1(2)f x dx '=⎰（）.A.2[(2)(0)]f f -B. 2[(1)(0)]f f -C.1[(2)(0)]2f f - D. 1[(1)(0)]2f f - 3. 下列定积分的值为负的是（）.A.20sin xdx π⎰B.2cos xdx π-⎰C.233x dx --⎰D.225x dx --⎰4. 设()f x 在[,]a b 上连续.⎰=>=aI a xx f x I 023)0(d )(，则（）⎰⎰⎰⎰aa a ax x xf D x x xf C xx xf B xx xf A 0d )(21.d )(21.d )(.d )(.225. 设等于）（则极限连续⎰-→x a ax x x f ax xx f d lim,)(（） A. af （a ） B. 0C.1D. 不存在 6. 设⎰---aax x f a a x f 等于）（分上的连续函数，则定积为d ],[)(（）⎰⎰⎰---aaa aaxx f D xx f C x f B A d .d .2.0.0）（）（）（7.设()f x 在区间[,]a b 上连续，则下列各式中不成立的是（）.A.()()bbaaf x dx f t dt =⎰⎰ B.()()baabf x dx f x dx =-⎰⎰C. ()0aaf x dx =⎰D. 若()0b af x dx =⎰，则()0f x =8.=-+⎰-dx x f x f x a a)]()([（）.A. ⎰a dx x f 0)(4B. ⎰-+adx x f x f x 0)]()([2C. 0D.以上都不正确.9．设()43422222sin cos ,sin cos 1x M xdx N x x dx x ππππ--==++⎰⎰， 23422(sin cos )P x x x dx ππ-=-⎰，则有（）A.N ＜P ＜M;B.M ＜P ＜N;C.N ＜M ＜P ;D.P ＜M ＜N ．10．下列积分可直接使用牛顿--莱布尼兹公式的有 ( )．A.35201x dx x +⎰;B.1-⎰;C.43022(5)x dx x -⎰; D.11ln eedx x x⎰． 11.下列广义积分收敛的是（）. A.x e dx +∞⎰B.1ln edx x x +∞⎰C.1+∞⎰D.1+∞⎰12.下列广义积分发散的是（）.A.211dx x+∞⎰ B. 0xe dx +∞⎰ C. 211ln dx x x+∞⎰ D. 0x e dx -+∞⎰ 13.下列积分不是广义积分的有（）A. 101dx x⎰ B. 121dx x ⎰C.1⎰D. 10sin xdx x⎰14.下列积分计算过程正确的有（）A. 440201[tan ]1cos dx x xππ==⎰； B. 1112111[]2dx x x --=-=-⎰； C.110[arcsin ]2x π==⎰； D. 因为1x 是奇函数，所以1110dx x -=⎰. 15．由曲线x y cos =和直线0=x ，π=x ，0=y 所围成的图形面积为（）A.cos xdx π⎰;B.0|cos |xdx π⎰;C.cos x dx π⎰;D.2cos xdx π⎰+2cos xdx ππ⎰.16．曲线ln y x =与直线ln ,ln ,0y a y b a b ==<<及y 轴所围成的面积值为（）A.ln ln byae dy ⎰;B.by a e dy ⎰;C.ln ln ln baxdx ⎰; D.ln baxdx ⎰.17.*在区间[,]a b 上0>(),f x 0<'(),f x 0>"(),f x 1=⎰()baS f x dx , 2=-()()S f b b a ,32+=-()()()f a f b S b a , 则由它们的几何意义可得( )A. 123S S S <<B. 213S S S <<C. 321S S S <<D. 231S S S <<18．曲线()y f x =、()y g x =(()()0)f x g x >>及直线,x a x b ==所围成图形绕x 轴旋转而成的旋转体的体积为（）A.120[()()]f x g x dx π-⎰;B.1220[()()]f x g x dx π-⎰;C.1201[()()]2f x g x dx π-⎰;D.1221[()()]2f x g x dx π-⎰. 填空题（17题） 1．比较积分值的大小：10x e dx ⎰___ ____1(1)x dx +⎰2. 比较积分值的大小：10x e dx ⎰____ ___21x e dx ⎰3.02sin limxt x e tdt x→=⎰______________.4.522cosxdx ππ-=⎰___________.5.设0(1)(2)xy t t dt =--⎰，则(0)y '= .6.已知函数20sin xy t dt =⎰，则2y '= .7.若2kx e dx +∞-=⎰，则k = .8. 20x d dx⎰=9. 22x d t dt dx =10 325425sin 81x x dx x x -=++⎰ . 11.42sin 1cos x xdx xππ-=+⎰ . 12.312111x x dx x -++=+⎰ .13.12=⎰.14. 如果()f x 在[],a b 上的最大值与最小值分别为M 与m ，则()abf x dx ⎰有如下估计式:________________________________. 15.由曲线xy 1=与直线x y =及2=x 所围成的图形的面积是 16. 椭圆t b y t a x sin ,cos ==，π20≤≤t 所围图形的面积是17.曲线(),(),(()()0)y f x y g x f x g x ==>>与x 轴及两直线)(,b a b x a x <==围成平面图形绕x 轴旋转产生的旋转体的体积为18. 曲线2y x =、1x =和x 轴所围成的图形绕y 轴旋转产生的旋转体的体积为计算题（基本题38题）1. 设函数()y y x =由方程00cos 0yxte dt tdt +=⎰⎰所确定，求dydx. 2. 设函数()y y x =由方程2200cos 0y x t e dt t dt +=⎰⎰所确定，求dy dx.3.计算 322cos()x x d t dt dxπ⎰；4.计算 203ln(1)limxx t dt x→+⎰；5.求2limxx x →⎰．6* .计算 2220020()limxt xx t e dt te dt→⎰⎰.7. 计算 312x dx --⎰． 8. ⎰-511du u u ; 9.⎰-2ln 01dx e x ;10.⎰-1024dx x ;11.ax ⎰；12.21e ⎰13.22ππ-⎰；14.⎰+10222)1(dx x x ;15⎰-+10232)1(dx x ; 16.计算.sin sin 053⎰-πdx x x17.⎰230arccos xdx ;18.⎰20sin πxdx x ; 19*.⎰>-+aa dx xa x 022)0(.120.1arctan x xdx ⎰；21.⎰-+222sin )(ππxdx x x22.21⎰；23.41⎰；24.1ln e ex dx ⎰；25. 32224x xdx x -++⎰. 26. 0x xe dx +∞-⎰；27. 232cos sin x xdx π⎰28.20sin cos x x dx π-⎰29.12ln(1)(2)x dx x ++⎰30.520cos sin 2d πθθθ⎰31.221t te dt -⋅⎰32.211ln ln ex xdx x++⎰ 33.1201ln 1x x dx x +⎛⎫ ⎪-⎝⎭⎰34.1ln(1)e x x dx -+⎰35 判定dx x x⎰∞+∞-+21的敛散性． 36.求21()-⎰f x dx ,其中22000,(),x e x f x x -⎧≥=⎨<⎩.37.设2301()12x x f x x ⎧≤≤⎪=⎨<≤⎪⎩,，求20()f x dx ⎰.38.计算21()f x dx -⎰，其中0()00x e x f x x -⎧≥=⎨<⎩,,.综合题与应用题（27题）39.求由抛物线x y =，直线y =-x 及y =1围成的平面图形的面积.40. 求椭圆12222=+by a x 所围图形的面积．41.计算曲线x e y =，x e y -=与直线1=x 所围成的图形的面积。

1月浙江自考经济应用数学试题及答案解析

1浙江省2018年1月自考经济应用数学试题课程代码：06956一、单项选择题(本大题共9小题，每小题2分，共18分)在每小题列出的四个备选项中只有一个是符合题目要求的，请将其代码填写在题后的括号内。

错选、多选或未选均无分。

1.若221)1(x x x x f +=+，则f (x )=( )A.x 2B.x 2+2 C.x 2-2D.4421x x x ++2.极限113)2(3)2(lim ++∞→+-+-n n nn n =( )A.21-B.31C.3D.03.函数)1()(12-=-x x e x f x的可去间断点为( )A.0B.1C.0和1D.无可去间断点4.不定积分⎰+-x x x d 9132=( ) A.C xx +-+3arctan 31)9ln(232 B. x x arctan )9ln(2-+ C. 3arctan 31)9ln(232x x ++D. 3arctan)9ln(2x x -+ 5.⎰xt t x2d sind d =( )A.sin 2t B.cos 2x C.2x cos 2x D.sin 2x26.下列级数发散的是( ) A.∑∞=-+-11)1ln(1)1(n n nB.∑∞=-113n n nC.∑∞=--1131)1(n nn D.∑∞=13n nn7.设0≤a n ＜n1(n =1,2,…)，则一定收敛的级数是( ) A.∑∞=1n n aB.∑∞=-1)1(n n n aC.∑∞=1n n aD.∑∞=-12)1(n n na8.设a 是正常数，则级数∑∞=-++-11)1(n n nna n ( )A.发散B.绝对收敛C.条件收敛D.敛散性与a 有关9.设函数)2ln(),(xyx y x f +=，则f y (1,0)=( ) A.1 B.21 C.2D.0二、填空题(本大题共5小题，每小题2分，共10分) 请在每小题的空格中填上正确答案。

经济应用数学》试卷

《经济应用数学》试卷（A ）１、函数1arctan y x=的连续区间是（）Ａ. [1,3]- B. (3,)+∞ C. (,0)(0,3]-∞U D. (,3]-∞ ２、x 12sin lim 2sin x x x x→--=+（）Ａ. 0 B. 1 C. 13 D. 不存在 3、下列等式成立的是（）Ａ.21lim()21x x x e x →∞-=+ B.21lim()21x x x e x →∞+=- C.10021lim()21x x e x →∞-=+ D.10021lim()21x x x e x -→∞+=- ４、当ｘ→０时，变量12-x e 的等价无穷小是（）A. xB.2xC.x 2sinD.2sin x５、(lnd =（） A 12x B 2dx x C D ６、设曲线22y x x =+-在点M 处的切线斜率为3，则点M 的坐标为（）A (0,1)B (1,0)C (0,0)D (1,1)７、函数2ln(1)y x =+的单调增加区间是（）A.(,)-∞+∞B.[0,)+∞C.(,0]-∞D. 以上都不对８、点(0,1)是曲线c bx ax y ++=23的拐点，则有（）A.1,3,1=-==c b aB. 1,0,==c b a 为任意值C. 为任意值c b a ,0,1==D. 1,=c b a 为任意值、９、设函数()f x 的一个原函数是1x 则()f x '=（） A1x B ln x C 32x D 21x - １０、如果x e -是()f x 的一个原函数，则()x f x dx =⎰（）A (1)x e x c --+B (1)x e x c --+C (1)x e x c -++D (1)x e x c --++二、填空（每空3分共30分）１、sin 3x y e =是由复合而成的。

２、设⎩⎨⎧>+≤+=001)(x bax x e x f x ，如果)(x f 在0=x 处可导，则=a ，=b 。

经济应用数学复习题(1)

一单选题1. 设函数y=f(x)的定义域[4,4-]，则)的定义域是 ( A )A. [0,16]B. （0,16）C. [0,16）D. （0,16] 2. 函数211x y x -=+的反函数是 ( C ) A. 11()212x y x x -=≠-+ B. 11()212x y x x +=≠-C. 1(2)2x y x x +=≠-D. 1(2)2x y x x+=≠-+3. 153lim251n n n x +→∞-=⨯+ ( B ) A.35 B. 12 C. 35- D. 12-4. 当x →+∞时，是 (A ) A. 同阶无穷小 B.等价无穷小 C. 高阶无穷小 D.低阶无穷小 5. 设函数f(x)在0x 处可导，则000()()lim x f x x f x x∆→-∆-=∆ ( B )A. 0()f x 'B. 0-()f x 'C. 0-()f xD. 0()f x6. 设某商产品单价为500元时，需求价格弹性0.2η=，它说明在价格500元的基础上上涨1℅，需求将下降 ( C ) A. 0.2B. 20℅C. 0.2℅D. 207. 在区间[]-1,1上满足罗尔定理条件的函数是 ( D )A. sin x yx=B. 2(1)y x =+ C. y x = D. 21y x =+8. 已知函数sin xy e x =，则dy = ( C )A. sin x e xdx +B. cos xe xdx + C. (sin cos )xe x x dx + D. (sin cos )xe x x dx - 9. 已知y=f(x)的一个原函数为sin 2x ,则()f x dx '⎰= ( D )A. sin 2x C +B. 2sin 2x C +C. cos2x C +D. 2cos2x C + 10. 设2,0(),0x x f x x x >⎧=⎨≤⎩，则11()f x dx -=⎰ ( D ) A. 012xdx -⎰B. 1202x dx ⎰C.10201x dx xdx -+⎰⎰ D.10201xdx x dx -+⎰⎰11. 以下各组函数中表示同一函数的一组是( C )A. f(x)= x xC. f(x)=xlg x g(x)= 2lg x12. 设2()arcsin3x f X -=，则函数的定义域是 ( B ) A. （1,5-） B. [1,5-] C. [1,5-） D. （1,5-]13. 设sinx 2()2 x 2x f x x πππ⎧≥⎪⎪=⎨⎪<⎪⎩.则2lim ()x f x π→是( A )A. 1B. 0C. 1-D. 不存在14. 当0x →时，下列变量中是无穷小量的是 ( B )A.sin xx B. sin x x C. 11sin x x D. 1(1)xx+15. 抛物线2x y =上的点)41,21(-处切线的斜率K= ( D )A. 1B. 2C. -2D. -116. 下列各函数在给定区间上满足罗尔定理条件的是 ( A )A.[]23(),1,121f x x =-+ B. [](),0,1x f x xe =C.[](),1,1f x x =- D. []1(),1,ln f x e x=17. 函数xy x e =-在区间(,0)-∞内 ( B )A. 单调递减B. 单调递增C. 不增不减D. 有增有减18.cos xd x =⎰( A )A. cos sin x x x C -+B. cos sin x x x C ++C. cos cos x x x C -+D. cos cos x x x C ++19. 1arcsin xd tdt dx =⎰( C )A. 0C. arcsin xD. arcsin arcsin b a -20. 下列广义积分收敛的是 ( D )A.1+∞⎰B.+∞⎰C.+∞⎰D.211dx x +∞⎰21.函数21log y =+ ( D )A.12-=x y B.122-=x yC.14-=x yD.14x y -=22.1lim(1)1nn n →∞+=+ ( A ) A. e B. 1e - C. 2eD. 123.函数()212y x =+间断点的个数是 ( B )A. 0B. 1C. 2D. 324.关于函数连续与可导的关系，下列叙述正确的是 ( B )A.连续必可导B. 可导必连续C.可导不一定连续D. 连续与可导没有直接关系25.设2()y f x =.则=dy（） ( D )A. 2()xf x dx 'B. 22()f x dxC. 2(2)xf x dx 'D. 22()xf x dx '26.设函数ln y x =在闭区间[1,]e 上满足拉格朗日定理.则定理中的ξ= ( A )A. 1e -B. 1e +C. eD. e -27. 函数2xy e=在2x =时的弹性是( D )A. 2B. 42e C. 44eD. 428.经过第二换元积分法,设tan x t =.则= ( B )A.sec tdt ⎰B. 3sec tdt ⎰C.2sec 1tdt t +⎰D. 3sectdt -⎰29.203sin lim13xx t dt x →=⎰( A )A. 1B. 0C. 12D.1330.2011dx x +∞=+⎰ ( C ) A. 0 B. πC. 2πD. ∞31.函数y =( A ) A.]( 1 , 1- B. ( 1 , 1)-C. ]( 1 , 0-D.(),1(1,)-∞--+∞32. 函数ln(12),(,0]y x x =-∈-∞的反函数是 ( A )A. 12xe y -=B. 12xe y +=C. 12x e y -=D. 12xe y +=-33. 若3222lim1221x an bn n n →∞++=++，则a,b 的值分别是 ( B ) A. 0,1a b == B. 0,2a b == C. 1,2a b == D. 1,0a b ==34. 2201cos lim x xx→-= ( B ) A. 0 B. 1 C. 2 D. 1235. 函数()f x x =在0x =处 ( C )A. 既连续又可导B. 不连续但可导C. 连续但不可导D. 既不连续也不可导36. 函数ln cos y x =，则dydx= ( B ) A. tan x B. tan x - C. cot x D. cot x -37. 函数()f x =[0,1]使罗尔定理成立ξ= ( C ) A. 0 B. 12C.23D. 1 38. 函数ln(1)y x x =-+的单调减区间是 ( A ) A. ()1,0- B. ()1,-+∞ C.()1,1- D. []1,1-39. 设()()F x G x ''=，则下列结论中正确的是 ( D ) A. ()()F x G x = B. ()()1F x G x =+ C. ()()F x dx G x dx ''⎡⎤⎡⎤=⎣⎦⎣⎦⎰⎰ D. ()()dF x dG x =⎰⎰ 40.21(1)dxx x +∞=+⎰( D )A. 0B. ∞C. ln 2D.1ln 2241. 设函数y =的定义域是 ( C )A. (),1(1,)-∞--+∞B. (),1(1,4)-∞--C.(),1(1,4)-∞- D. ()4,1(1,4)--42. 函数2,11xyx x -=≠-+的反函数是 ( A ) A. 21x y x -=+ B. 21xy x +=+C. 21x y x +=-D. 21xy x -=-43. 11(2)3lim(2)3n nn n x ++→∞-+=-+ ( A ) A.13 B. 12 C. 13- D. 12-44. 当0x →时，sin x 与x 是 ( B )A. 同阶无穷小B.等价无穷小C. 高阶无穷小D.低阶无穷小 45. 设()f a '存在且为1，则0(2)()limh f a h f a h→+-= ( D )A. 0B. 1C. 1-D. 246. 设某商产品单价为100元时，需求价格弹性0.1η=，它说明在价格100元的基础上上涨1℅，需求将下降 ( C ) A. 0.1B. 10℅C. 0.1℅D. 1047. 函数lnsin y x =在5,66ππ⎡⎤⎢⎥⎣⎦上满足罗尔定理条件的ξ= ( D ) A. 0 B.4π C. 3π D. 2π48. 已知函数sin 3xy e x =，则dy = ( A )A. []sin33cos3xe x x dx + B. []sin33cos3x e x x dx - C. []sin33cos3xe x x dx -+ D. []sin33cos3x e x x dx -+49.ln xdx ⎰= ( A )A. (ln 1)x x C ++B. (ln 1)x x C -++C. (ln 1)x x C -+D. (1ln )x x C -+ 50.cos x dx π=⎰( C )A. 0B. 1C. 2D. 2-二填空题1. 设f(x)=11x x +-，则f(x+1)= 2xx-+。

经济应用数学(习题参考答案)

习题参考答案第1章函数、极限与连续习题1.11．（1）不同，因为它们的定义域不同；（2）不同，因为它们的定义域和对应法则都不同． 2．（1）[2,1)(1,2]-U ；（2）(3,3)-．3．2,41,1． 4．（1）12,,ln 2+===x v v u u y ；（2）13,sin ,2+===x v v u u y ；（3）x u u y ln 1,5+==；（4）52,sin ,,2+==-==x t t v v u e y u． 5．(100)2000C =，(100)20C =． 6．2214)(x x x R -=． 7.（1）25000；（2）13000；（3）1000． 8．()1052p Q p =+⨯． 9．130,(0700)9100117,(7001000)x x y x x ≤≤⎧=⎨+<≤⎩．习题1.21．（1）0；（2）0；（3）1；（4）0；（5）24；（6）41；（7）1；（8）41；（9）0；（10）∞． 2．（1）无穷大；（2）无穷大；（3）无穷小；（4）无穷小；经济应用数学（5）无穷小；（6）无穷大；（7）无穷大；（8）无穷大．3．（1）2；（2）1；（3）53；（4）4e ；（5）e1；（6）21e ；（7）4；（8）0．4．0lim ()lim ()lim ()1x x x f x f x f x +-→→→===-．习题1.31．（1）32；（2）2sin 2；（3）0；（4）2；（5）21；（6）∞． 2．不连续；图形略． 3．2=k ．因为函数()f x 在其定义域内连续，即在0=x 也联系，则()0lim (0)x f x f →=，即()()0lim lim x x f x f x k ++→→==，0lim ()2x f x -→=，所以2=k ． 4．略．习题1.41．本利和1186.3元，利息186.3元；本利和1164.92元，利息164.92元． 2．1173.51元；xey ⋅-=1.06000，4912.39元，4444.91元，3639.19元，2979.51元．第1章复习题1．（-2，2），图形略． 2．（1）13,-==x u u y ；（2）x u u y 21,3+==；（3）x u u y ln 2,10+==；（4）2,,x v e u e y vu===-；（5）x v v u u y ===,ln ,；（6）x t t w w v v u u y 2,cos ,,lg ,22=====． 3．（1）()1200010C q q =+；（2）()30R q q =；（3）()2012000L q q =-． 4．280,(0900)22450400,(9002000)q q R q q ⎧=⎨+<⎩≤≤≤．习题参考答案5．1,(04)1.5,(410)2,(1020)s P s p <<⎧⎪=⎨⎪<⎩≤≤≤，图形略．6．1-．7．（1）9-；（2）∞；（3）0；（4）0；（5）2；（6）0；（7）5；（8）2；（9）5e ；（10）8-e ． 8．1k =． 9．a π=．10．221R Q Q =++．11．150,(0300)142.52250,(300800)1358250,(8001000)q q R q q q q ⎧⎪=+<⎨⎪+<⎩≤≤≤≤．12．800001000Q P =-．13．3000100Q P =+；平衡状态时，70,10000P Q ==． 14．(600)1000400L =；．第2章导数与微分习题2.11.（1）1-；（2）51． 2.（1）3ln 1x y ='；（2）3132-='x y ；（3）32x y -='；（4）2523--='x y ；（5）2121-='x y ；（6）3734--='x y ；（7）2ln 1x y ='；（8）x y sin -='．3．033633=--+πy x ．4．切线方程：02=-+y x ；法线方程：x y =．经济应用数学5．切线方程：01-=+y x ；法线方程：03=-+y x ．习题2.21．（1）4|2='=x y ；（2）1sin 2|0='=x y ；（3）32|1-='=x y ；（4）213|-=='e y x ；（5）2|21-='=x y ；（6）92|1-='=x y ． 2．（1）x x y 2cos 432+='；（2）xe y x 122+='；（3）2)cos 1(sin cos 1t t t y +++='；（4）xx y ln 121+='；（5）xx x x y 3)12(-+='；（6）)63cos(6+='x y ；（7）x x x x x y tan sec sec 3tan 32++='；（8）x x y 2sin cos 22-='；（9）x e x y x 52cos 42sin 2+⋅='；（10）)sin 2(sec cos 22x x y ⋅='；（11）xx ex x y 221)2ln 1(2⋅++='；（12）xe xe y x e 11++⋅='-． 3．（1）yx y x dx dy 22+-=；（2）)2cos(sin )2cos(2cos y x y x y x y dx dy +++-=． 4．0222=-+y x ．5．（1）x y x y x y x y cos ,sin ,cos ,sin )4(=='''-=''-='；（2）x x x y cos sin 2--=''．6．切线方程：022=--y x ；法线方程：012=-+y x ．习题2.31．（1）dx x x dy )26(2-=；（2）dx x x dy )sin (cos -=；（3）dx xx xdy 2ln 2-=；（4）dx x e x dy x2)1(-=；习题参考答案（5）dx e dy x 2.04.0=；（6）dx x x dy )32(sec )32tan(42++=． 2．（1）221x ；（2）x sin ；（3）||ln x ；（4）x 2．3．11.75．习题2.41．（1）2；（2）1；（3）a cos ；（4）n m ；（5）3；（6）21-；（7）21；（8）∞+．2．（1）1；（2）0．习题2.51．（1）在)2,(-∞内单调增加，在),2(∞+内单调减少，有极大值为7)2(=f ；（2）在),(∞+-∞内单调增加，无极值；（3）在),(∞+-∞内单调增加，无极值；（4）在),1()0,(∞+-∞Y 内单调减少，在)1,0(内单调增加，有极小值为0)0(=f ，有极大值为1)1(-=e f ．2．（1）最大值为69)4(=f ，最小值为61)6(-=-f ；（2）最大值为2)1(=f ，最小值为26)3(-=f ；（3）最大值为2)2(ππ=-f ，最小值为2)2(ππ-=f ．3．当销售量80=x 时，平均成本最低为40)80(=C 元．4．当学费降低15次，即学费降为325元时，这个培训班可获得最大收益，最大收益为422500元．5．当每周泵的销售量33=x 个时，每周取得利润最大约为662.31元．习题2.61．（1）凹区间为)1,(-∞，凸区间为),1(∞+，拐点为)2,1(；（2）凹区间为),2(∞+，凸区间为)2,(-∞，拐点为)3,2(；（3）凹区间为),1(∞+，凸区间为)1,(-∞，拐点为)6,1(；（4）凹区间为)1,1(-，凸区间为),1()1,(∞+--∞Y ，拐点为)2ln ,1(-和)2ln ,1(；（5）凸区间为),0()0,(∞+-∞Y ，无拐点；（6）凹区间为)2,(-∞，凸区间为),2(∞+，无拐点．2．平均成本函数在)80,0(内单调减少，在),80(∞+内单调增加，有极小值为经济应用数学40)80(=C ，在),0(∞+内是凹的．3．收益函数曲线在)6,0[内单调增加，在]80,6(内单调减少，有极大值为44.73)6(=R ，在)80,0(内是凸的．习题2.71．(20)160L =元，(20)8L =元，(20)6L '=元．2．（1）2()0.092S t t t '=++；（2）(5)29.25S =（百万元），(5)9.25S '=（百万元）；（3）(5)29.25S =表明5个月的销售总量为29.58百万元；(5)9.25S '=表明若再多销售1个月，将多销售9.25百万元．3．（1）23780()N x x'=；（2）(10)37.837N '=≈（只），表明当广告费用为1万美元时，若多投入1千美元的广告费，将再多销售船只37只；(20)9.459N '=≈（只），表明当广告费用为2万美元时，若再多投入1千美元的广告费，将多销售船只9只．4．（1）179.9美元；（2）180美元． 5．约108.27元． 6．（1）13EQ P EP =-；（2）11|3P EQ EP ==-，3|1P EQ EP ==-，55|3P EQ EP ==-．7．3EQ P EP P =+，31|2P EQ EP ==．8．（1）24EQ P EP P =--；（2）61|3P EQ EP ==-；（3）因为62|03P ER EP ==>，所以在6P =时，若价格上涨1%，总收益增加0.67%．（4）12P =时，总收益最大，最大总收益是(12)72R =．第2章复习题1．（1）212sin(31)y x x '=-+；（2）41y x '=+；（3）34)1(2xx y -='；（4）2222(1)x x y x -+'=-；（5）222sec tan (1)2sec (1)x x x x xy x +-'=+；（6）sin 22cos 2x y e x '=；习题参考答案（7）2(1)[2cot (1)csc ]y x x x x '=+-+；（8）22ln(1)1x x y x --=-．2．222(24)x d yx x e dx=++．3．（1）21xx y e y ye '=-+；（2）32x y y'=-． 4．求下列函数的微分．（1）2(622)dy x x dx =+-；（2）(sin 22cos2)dy x x x dx =+；（3）222(1)x dy x x edx -=-；（4）2332(1)x dy dx x =-．5．切线方程：870x y --=；法线方程：890x y +-=．6．在(,0)(1,)-∞+∞U 内单调增加，在(0,1)内单调减少，有极大值为(0)0f =，有极小值为3(1)2f =-．7．在(0,24)内单调增加，在(24,)+∞内单调减少，有极大值为(24)6916f =；凹区间为(0,12)，凸区间为(12,)+∞，拐点为(12,3460)．8．生产50000个单位时，获得的利润最大，最大利润为30000)50000(=L ． 9．455100dP x Pdx x P+=-+，其实际含义为：当需求量为x 时，若需求量再增加一个单位，则价格将减少455100dP x Pdx x P+=-+元． 10．280()(2)N t t '=+，其实际意义是：当对一个新工人进行t 天培训后，若再多培训一天，该工人就能多装配280()(2)N t t '=+个元件． 11.（1）生产量3Q =时，平均成本最小为(3)6C =元．（2）边际成本2()15123C Q Q Q '=-+，显然(3)(3)6C C '==元．（3）1Q ECEQ ==0.6，其经济意义为：当生产量1Q =时，若生产量增加1%，则成本将增加0.6%．经济应用数学第3章不定积分与定积分习题3.11．（1）C x +661；（2）C x x ++2717；（3）C x+22ln 1；（4）C x x ++-sin cos ；（5）C x +22ln 81；（6）C x x ++3||ln ；（7）C x +2774；（8）C x x ++23223；（9）C x x +-232931092；（10）C x x x ++-838522325；（11）C x x +-sin 3||ln 2；（12）C x x e x +-+sin 32；（13）C x x x +++65225；（14）C x x x +++-3271344；（15）C x x x++--||ln 21；（16）C x x x x +--+23327323172．2．()f x 2)21(2x e x --=． 3．2ln +=x y （21ex ≥）． 4．2125Q Q R -=． 5．20005212++=x x C ．习题3.21．（1）41(53)20x C ++；（2）31(32)6x C --+；（3）1sin(31)3x C ++；（4）1cos(12)2x C -+；习题参考答案（5）2313x e C ++；（6）2x e C --+；（7）212x e C +；（8）2214x e C --+；（9）21cos(2)2x C -++；（10）322(sin )3x C +；（11）2xeC + ；（12）2xe C --+．2．（1）532224(2)(2)53x x C +-++；（2）26ln(3)x x C ++；（3）5322210(35)(35)4527x x C -+-+；（4）3ln 322x x C --；（5）322(3)633x x C -+-；（623ln(123)x x C --+．3．（1）3311ln 39x x x C -+；（2）221124x x xe e C -+；（3）ln3x x x C -+；（4）1(cos sin )2x x x e C ++．习题3.31.（1）32；（2）52；（3）214a π；（4）0． 2.（1）⎰102dx x ≥⎰13dx x ；（2）⎰10dx e x ≥⎰12dx e x ；（3）⎰10dx e x ≥⎰+1)1(dx x ；（4）⎰20πxdx ≥⎰2sin πxdx ．习题3.41．（1）2243；（2）0；（3）2183740--；（4）e e -3；（5）331-；（6）3340；（7）34；（8）487． 2．245．3．⎰-=503001.030201dx e p x ．经济应用数学 4．146250元．习题3.51．（1）313；（2）431121121）（π--；（3）32---e e ；（4）)1(211--e ；（5）)1(23-e ；（6）)2cos 1(cos 21-．2．（1）52ln 8-；（2）2ln )1ln(1++-e ；（3）35；（4）15216532+-．3．（1）0；（2）0；（3）332π；（4）22π-． 4．（1）121--e ；（2））（251+-πe ．习题3.61．（1）31；（2）2；（3）21；（4）0．2．1．习题3.71．50424.0)(2++=x x x C ．2．4200)(2x x x R -=，17500)100(=R 元，175)100(=R 元/单位．3．t e t S 08.05050)(--=，18.3)6(≈S 辆． 4．约8.97万元． 5.（1）40；（2）总收益为5200美元，平均单位收益为130美元/kg ，总成本为4200美元，总利润是1000美元．习题3.81.（1）一阶；（2）二阶；（3）五阶；（4）四阶．2．（1）C x y +=221；（2）C x y +-=21；（3）)ln(C e y x +=；（4）1-⋅=x C xy ；（5）22332x e C y -⋅+=；（6）)21(122C e x y x +-=-．3.（1）xe e y =；（2）)1(212x y --=．第3章复习题1．（1）C x ++-)1(cos 212；（2）C x +-4)53(121；（3）C x x +++-+)22ln(422；（4）C x x +-)41(ln 44．2．（1）21；（2）24；（3）)25(6-；（4）)3132(313+e ．3．1． 4．40000． 5．约1.53美元．6．10ln0.216-≈，在[0,16]内的全部利润约87.82百元． 7．总成本函数为2()215200C x x x =++；总利润函数为2()442200L x x x =--；11=x 个单位时，获得最大利润，最大利润是42)11(=L ．8.（1）C x y =+-)1)(1(；（2）)(2C e e y x x +-=-；（3）4)1(21+=x y ，．第4章矩阵习题4.1略．习题4.21．11,3,2,7,5-====-=z u w y x ．2．⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡--=111325325310373432316317383Z ． 3．5211114208235-⎡⎤⎢⎥-⎢⎥⎢⎥-⎣⎦4．15461021⎡⎤⎢⎥-⎣⎦5．（1）505176213-⎡⎤⎢⎥⎢⎥⎢⎥-⎣⎦；（2）1235-⎡⎤⎢⎥⎣⎦；（3）[]13161922；（4）20742769-⎡⎤⎢⎥---⎣⎦；（5）123246369⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦；（6）[]70． 8．（1）12190544-⎡⎤⎢⎥-⎣⎦；（2）26751110614-⎡⎤⎢⎥-⎢⎥⎢⎥-⎢⎥⎣⎦；（3）1111580391241424201225218--⎡⎤⎢⎥-⎢⎥⎢⎥--⎢⎥-⎣⎦；（4）5303128⎡⎤⎢⎥-⎣⎦；（5）5313028⎡⎤⎢⎥-⎣⎦．运费耗费 9．420000130000382000119000320001000001122000349000⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦一班二班三班总计 10．[]64601600010540钾氨磷习题4.31．（1）113-1-200-7470000000000⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦，2R =；（2）120001130024000⎡⎤⎢⎥-⎢⎥⎢⎥⎢⎥⎣⎦，3R =；（3）12390236596410022⎡⎤⎢⎥--⎢⎥-⎢⎥⎢⎥-⎢⎥⎣⎦，3R =；（4）1312074800210000--⎡⎤⎢⎥-⎢⎥⎢⎥⎢⎥⎣⎦，3R =． 2．（1）2；（2）2；（3）4；（4）3．3．（1）8=k ；（2）8≠k ，（3）k 不存在．习题4.41．因为AB =BA =E ,所以B 是A 的逆矩阵．2．11,510x y =-=．3．（1）2550291111⎡⎤⎢⎥⎢⎥⎢⎥-⎣⎦；（2）414457568⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦；（3）2015215911-⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦414457568⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦． 4．（1）1-A143153164--⎡⎤⎢⎥=--⎢⎥⎢⎥-⎣⎦；（2）1-A 不存在，（3）15111444411112222111144441111A -⎡⎤--⎢⎥⎢⎥⎢⎥-⎢⎥=⎢⎥⎢⎥--⎢⎥⎢⎥--⎣⎦；（4）1-A 1153222421731222⎡⎤--⎢⎥⎢⎥=-⎢⎥⎢⎥-⎢⎥⎣⎦． 5．A =18315511115511055⎡⎤--⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦． 6．1200020002B AB -⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦．第4章复习题一、1．().,,2,1;,,2,1,,n j m i b a t n s m ij ij ΛΛ=====2．t l m k s n ===,,． 3．()TA 1-． 4．B ，A ． 5．非零行的行数．二、1．(d)； 2．(b)(d)； 3．(a)； 4．(c)(d)．三、1．3071845232⎡⎤⎢⎥-⎢⎥⎢⎥-⎣⎦．2．()3R A =，()1R B =．3．38172777122221935222Z ⎡⎤---⎢⎥⎢⎥⎢⎥=---⎢⎥⎢⎥⎢⎥---⎢⎥⎣⎦．第5章线性方程组习题5.21．（1）123783x x x =⎧⎪=⎨⎪=-⎩；（2）无解；（3）123000x x x =⎧⎪=⎨⎪=⎩；（4）1233252x k x k x k ⎧=⎪⎪⎪=⎨⎪=⎪⎪⎩；（5）1123212331425351622623x k k k x k k k x k x k x k =++-⎧⎪=---+⎪⎪=⎨⎪=⎪⎪=⎩；（6）12342,3,1,0.x x x x =⎧⎪=-⎪⎨=⎪⎪=⎩．2. （1）4m =，1233x k x k x k =-⎧⎪=⎨⎪=⎩；（2）3m =，1233525x k x k x k ⎧=-⎪⎪⎪=⎨⎪=⎪⎪⎩．3．（1）5m ≠；（2）5,2m k =≠-；（3）5,2m k ==-． 4．（1）02p q ≠≠或时方程组无解；（2）02p q ==且时有解，解为11232123314253522263x k k k x k k k x k x kx k =++-⎧⎪=---+⎪⎪=⎨⎪=⎪⎪=⎩5．5=m ，1122123142164555373555x k k x k k x k x k ⎧=--+⎪⎪⎪=-+⎨⎪=⎪⎪=⎩．6．（1）7349121714Z ⎡⎤--⎢⎥⎢⎥⎢⎥=--⎢⎥⎢⎥⎢⎥--⎢⎥⎣⎦；（2）22308Z -⎡⎤=⎢⎥⎣⎦．第5章复习题一、1．111111111,n n m mn m mn m a a a a b aa a ab ⎛⎫⎛⎫⎪ ⎪⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭LL MM MM M LL，无解，有唯一解，有无穷多组解，无解，未知数个数，小于2．（1）无解（2）有无穷多组解（3）有唯一解 3．3124121,2.x x x x x x =++⎧⎨=+⎩二、1. (d)；2. (c)．三、04122112Z ⎡⎤⎢⎥⎢⎥⎢⎥=--⎢⎥⎢⎥⎢⎥-⎣⎦四、1．11221331427188373x k k x k k x k x k =-+⎧⎪=-+-⎪⎨=⎪⎪=⎩；2．1234,321.2x x x ⎧⎪=⎪⎪=-⎨⎪⎪=⎪⎩；3．1231,1,1.x x x =⎧⎪=-⎨⎪=-⎩；4. 1230,0,0.x x x =⎧⎪=⎨⎪=⎩； 5．112321324332x k k k x k x k x k =-+⎧⎪=⎪⎨=⎪⎪=⎩．五、11221231422223x k k x k k x k x k =++⎧⎪=--+⎪⎨=⎪⎪=⎩．第6章线性规划初步习题6.11．设生产1A 产品1x 万瓶，生产2A 产品2x 万瓶，获得利润L 美元．则该问题的数学模型为：12max 80003000L x x =+12121212535003008020000..1249000,0x x x x s t x x x x +⎧⎪+⎪⎨+⎪⎪⎩≤≤≤≥≥其矩阵形式为：max ..0L CX AX B s t X =≤⎧⎨≥⎩其中：[]80003000C =，12x X x ⎡⎤=⎢⎥⎣⎦，5330080124A ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦，50020000900B ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦． 2．设A 需要1x 个单位，B 需要2x 个单位，总费用为F ．则该问题的数学模型为：121212min 20030024.0,0F x x x x s t x x =++⎧⎨⎩≥≥≥其矩阵形式为：min ..0F CX AX B s t X =⎧⎨⎩≥≥ 其中：[]200300C =，12x X x ⎡⎤=⎢⎥⎣⎦，[]12A =，[4]B =．3．设第i 月的进货量为1i x 千件，售货量为2i x 千件（3,2,1=i ），利润为L 美元．则该问题的数学模型为：111221223132max 8969910L x x x x x x =-+-+-+111112211112212231300300..3000(1,2,3;1,2)ij x x x x s t x x x x x x i j ⎧⎪-+⎪⎨-+-+⎪⎪==⎩≤≤≤≥ 其矩阵形式为：max ..0L CX AX B s t X =⎧⎨⎩≤≥其中：[]8969910C =---，111221223132x x x X x x x ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦，100000111000111110A ⎡⎤⎢⎥=-⎢⎥⎢⎥--⎣⎦，300300300B ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦．习题6.21．（1）最优解为12032x x ⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦⎣⎦，最优值为min 3S =-．（2）无最优解．（3）无穷多组最优解为满足8221=+x x 且介于点（2,3）和（4,2）件的线段上的所有点，最优值为16max =S ．第6章复习题1．设生产A 产品1x 个单位，生产B 产品2x 个单位，获得利润L 元．则该问题的数学模型为：12max 800010000L x x =+ 12121212128940058320..642804123500,0x x x x s t x x x x x x +⎧⎪+⎪⎪+⎨⎪+⎪⎪⎩≤≤≤≤≥≥其矩阵形式为：max ..0L CX AX B s t X =⎧⎨⎩≤≥其中：[]800010000C =，12x X x ⎡⎤=⎢⎥⎣⎦，895864412A ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦，400320280350B ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦． 2．设工厂i 给工地j 的砖量为ij x 万块（其中：1,2i =分别表示工厂A 、B ，1,2,3j =分别表示工地甲、乙、丙），总运费为F 元．则该问题的数学模型为：111213212223min 5060706011027F x x x x x x =+++++112112221323111213212223171815..23270(1,2;1,2,3)ij x x x x x x s t x x x x x x x i j +=⎧⎪+=⎪⎪+=⎪⎨++=⎪⎪++=⎪≥==⎪⎩ 其矩阵形式为：min ..0F CX AX B s t X ==⎧⎨≥⎩其中：[5060706011027]C =，⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=232221131211x x x x x x X ，⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=111000000111100100010*********A ，⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=2723151817B3．设第i 个煤矿运往第j 个城市的煤量为ij x 千吨（其中：1,2,3i =分别表示甲、乙、丙三个煤矿，1,2,3,4j =分别表示A 、B 、C 、D 四个城市），总运费为F 元．则该问题的数学模型为：111213142122232431323334min 1211181191111131014137F x x x x x x x x x x x x =+++++++++++习题参考答案·21·41142143131132133134149115..4780)1,2,3;1,2,3,4)j j j j j j i i i i i i i i ij x x x x s t x x x x i j =======⎧=⎪⎪⎪=⎪⎪⎪⎪=⎪⎪⎪=⎪⎨⎪⎪=⎪⎪⎪=⎪⎪⎪=⎪⎪≥==⎪⎩∑∑∑∑∑∑∑ 其矩阵形式为：min ..0F CXAX B s t X ==⎧⎨≥⎩ 其中：[1211181191111131014137]C =，111213142122232431323334x x x x x x X x x x x x x ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦，111100000000000011110000000000001111100010001000010001000100001000100010000100010001A ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦，49115478B ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦． 4．设i A 机床生产j B 工件的数量为ij x （1,2;1,2,3i j ==），总加工费为S 元．则该问题的数学模型为：经济应用数学·22·111213212223min 139********S x x x x x x =+++++ 1121122213231112132122230.40.54001.1 1.26001.3500..0.41018000.5 1.2 1.39000(1,2;1,2,3)ij x x x x x x s t x x x x x x x i j +=⎧⎪+=⎪⎪+=⎪⎨++≤⎪⎪++≤⎪≥==⎪⎩ 其矩阵形式为：min ..0F CXAX B s t AeqX BeqX =⎧⎪=⎨⎪⎩≤≥ 其中：[1391011128]C =，111213212223x x x X x x x ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦，0.4 1.110000000.5 1.2 1.3A ⎡⎤=⎢⎥⎣⎦，800900B ⎡⎤=⎢⎥⎣⎦， 0.4000.5000 1.100 1.2000100 1.3Aeq ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦，400600500Beq ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦5．用图解法求下列各题．（1）最优解为1220x x ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦，最优值为max 4S =．（2）无最优解为．（3）无穷多组最优解为满足121x x +=且介于点（1,0）和点（0,1）间的线段上的所有点．习题参考答案 ·23·第7章随机事件与概率习题7.11．（1）{}0t t Ω=≥；（2）设}{个次品取到正品前抽取了i A i =（0,1,2,3,4i =），则01234{,,,,}A A A A A Ω=；（3）设}{次中得一等奖第i A i =（1,2,i =L ），则12{,,}A A Ω=L ．2．（1）AB ；（2）A ；（3）ABC ABC ABC ⋃⋃；（4）ABC ；（5）A B C ⋃⋃；（6）A B C ⋃⋃或ABC ；（7）ABC 或A B C ⋃⋃；（8）ABC ABC ABC ABC ⋃⋃⋃． 3．（1）321A A A ；（2）321A A A ⋃⋃；（3）321321321A A A A A A A A A ⋃⋃；（4）321321321321A A A A A A A A A A A A ⋃⋃⋃．4.（1）[0,3)；（2）[0,2)；（3）(,0)[2,)-∞⋃+∞；（4）φ．习题7.21．14． 2．（1）13；（2）215；（3）815． 3．（1）61；（2）b ；（3）0.84；（4）1511；（5）0.7；（6）0.6． 4．（1）61；（2）65． 5．（1）158；（2）97． 6．(|)0.3P B S =．7．0.64．8．（1）0.42；（2）0.88；（3）0.46．9.（1）89110；（2）81100．经济应用数学 ·24· 10．35． 11．0.592．12．0.4，0.5，0.6，0.6，0.75．13．0.93．第7章复习题1．12B A A =；12C A A =；1212()()D A A A A =⋃；12E A A =⋃．其中B C D 、、两两互不相容，C 与E 为对立事件．2．因为B A ⊂，所以()()P B P A <．3．（1）2845；（2）145；（3）15；（4）1645；（5）1745；（6）4445． 4．0.97；0.03．5．0.75；0.25．6．（1）0.988；（2）0.012；（3）0.83．7．（1）44%；（2）15%；（3）2.25%；（4）0.25%；（5）13.6%；（6）13.3%．8．（1）0.27；（2）0.15．9．（1）0.45，0.24，0.14；（2）0.83；（3）0.54．10．0.78．11．0.72．12．（1）0.74；（2）0.56．第8章随机变量分布及其数字特征习题8.11．设随机变量0,()1,()X ⎧=⎨⎩没投中投中，则(0)0.6P X ==，(1)0.4P X ==． 2．设取出产品的等级为随机变量X ， X 取1、2、3分别表示产品等级为一、二、三级，则4(1)7P X ==，2(2)7P X ==，1(3)7P X ==．习题参考答案 ·25·习题8.21．（1）是概率分布．因为满足离散型随机变量分布律的性质；（2）25.0)30(==X P ；（3）35.0)25(=≤X P ；（4）4.0)30(=>X P ．2.（1）P (X=100) =0.25；（2）7.0)0(=>X P ；（3）4.0)100(=≥X P ． 3X -12 6 )(X P0.1 0.3 0.6 4． X 01 2 P （X ）2138 1538 119 5．（1） X 01 2 )(X P19 49 49 （2） X 01 2 )(X P115 815 25 6．0.14；0.95．7．0.009；0.998；7，0.617．8.（1）25.0=C ；（2）0.25，0.75；（3）F (X )=0,10.25,130.5,3 4.51,4.5x x x x <-⎧⎪-<⎪⎨<⎪⎪⎩≤≤≥． 9．0.000008．习题8.31.（1）a =3；（2）95． 2.（1）0.2325；（2）0.5479．经济应用数学·26·3.（1）常数k=4；（2）0.5392．4.（1）c=61；（2）127；（3）()F x =20,211,241231,4x x x x <⎧⎪⎪-<⎨⎪⎪⎩≤≥． 5.（1）0.4773；（2）0.0227；（3）0.9545．6． 1.96λ=．7.（1）0.475；（2）0.025．8.（1）0.09176；（2）12475支/周．习题8.41．47． 2．（1）31；（2）32；（3）2435． 3．（1）c =6；（2）61；（3）67． 4．0.3．5．2．6．k =4；α=3．7．（1）445；（2）盈利57500元．习题8.51．163． 2．数学期望为0.3；方差为0.319．3．E (X )=9元；D (X )=3.4．4．（1）31；（2）454；（3）4516． 5.（1）12-；（2）20．6.（1）4.1；（2）3.93，1.98．7．7．8.（1）5；（2）17；（3）0．9．a =0.6，b=1.2， D ( X )=0.08．习题参考答案 ·27·第8章复习题1．1()(1,2,3,4,5,6)6P X k k ===； 0,(1)1,(12)61,(23)31(),(34)22,(45)35,(56)61,(6)x x x F x x x x x <⎧⎪⎪≤<⎪⎪⎪≤<⎪⎪⎪=≤<⎨⎪⎪≤<⎪⎪⎪≤<⎪⎪≥⎪⎩2.（1）0.11；（2）0.96．3.（1）不是；（2）是．4．0.9324．5．0.3935．6．（1）61；（2）21625． 7．（1）K =0.5；（2）1.414．8．（1）0.483；（2）0.983．9．50.85．10．（1）0.1056；（2）0.1056．11．（1）0.5；（2）0.25；（3）43；（4）29． 12．（1）0；（2）1．13．开发该软件．14．（1）()145,()140E X E Y ==，选择中型扩建．（2）()2725,()12400D X D Y ==，选择中型扩建．15.（1） X1 2 3 4 5 P 4% 39% 29% 21% 7%经济应用数学·28·（2）() 2.88E X =；（3）() 1.0256,() 1.013D X D X =≈．16．（1） X1 2 3 4 5 P 7/29 6/29 3/29 6/29 7/29 （2）()3E X =，()11.34D X ≈；（3）略．第9章数理统计初步习题9.1略．习题9.21.（1290,1304）．2.（1271,1323）．3.（2.08, 2.42）．4.（18,20）．5.（17.9,91.1）．习题9.31．产品合格．2．产品合格．3．不正常．4．广告不真实．5．有变化．习题9.41．（1）略；（2）ˆ 6.45 1.58y x =-；（3）变量x 与y 存在显著线性相关关系．2．x 与y 存在显著线性相关关系；ˆ41.320.53yx =+．习题参考答案 ·29· 第9章复习题1．（1）（93.54,136.72）；（26.4,46.84）；（2）略．2．该校3年级男生平均身高与全国一致，身高差异程度没有拉大．3．该生产线不正常．4．这两种药品对血压影响是相同的．5．该基金的风险没有增大．6．（71.15, 80.45）．7．（1）ˆ66.6 1.36y x =+；（2）y 与xx 存在显著线性相关关系．8．（1）y 与x 存在显著线性相关关系；（2）ˆ 4.950.18y x =-+．目录习题参考答案 (1)第1章函数、极限与连续 (1)第1章复习题 (2)第2章导数与微分 (3)第3章不定积分与定积分 (8)第4章矩阵 (11)第4章复习题 (14)第5章线性方程组 (15)第6章线性规划初步 (17)第7章随机事件与概率 (23)第8章随机变量分布及其数字特征 (24)第9章数理统计初步 (28)·I·。

经济应用数学(习题参考答案解析)

则该问题的数学模型为：
其矩阵形式为：
其中：，，，．
2．设工厂给工地的砖量为万块（其中：分别表示工厂A、B，分别表示工地甲、乙、丙），总运费为元．则该问题的数学模型为：
其矩阵形式为：
其中：，
，，
3．设第个煤矿运往第j个城市的煤量为千吨（其中：分别表示甲、乙、丙三个煤矿，分别表示A、B、C、D四个城市），总运费为F元．则该问题的数学模型为：
习题参考答案
第
习题
1．（1）不同，因为它们的定义域不同；
（2）不同，因为它们的定义域和对应法则都不同．
2．（1）；（2）．
3．．
4．（1）；（2）；
（3）；（4）．
5．，．
6．．
7.（1）25000；（2）13000；（3）1000．
8．．
9．．
习题
1．（1）0；（2）0；（3）1；（4）0；（5）24；
习题
1．（1）2；（2）1；（3）；（4）；（5）3；（6）；（7）；（8）．
2．（1）1；（2）0．
习题
1．（1）在内单调增加，在内单调减少，有极大值为；
（2）在内单调增加，无极值；
（3）在内单调增加，无极值；
（4）在内单调减少，在内单调增加，有极小值为，
有极大值为．
2．（1）最大值为，最小值为；
（2）最大值为，最小值为；
（3）最大值为，最小值为．
3．当销售量时，平均成本最低为元．
4．当学费降低15次，即学费降为325元时，这个培训班可获得最大收益，最大收益为422500元．
5．当每周泵的销售量个时，每周取得利润最大约为662.31元．

《经济应用数学》试题(6)

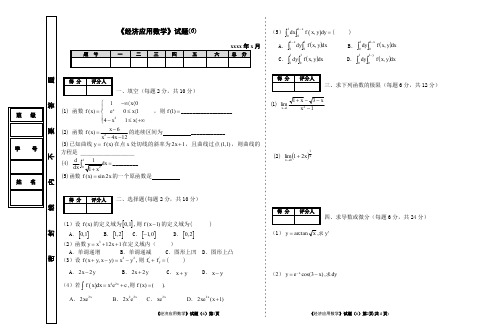
《经济应用数学》试题（6）第1页《经济应用数学》试题（6）第2页(共4页)《经济应用数学》试题(6)月一、填空（每题2分，共10分）(1) 函数210()0141x x f x e x x x -∞〈〈⎧⎪=≤〈⎨⎪-≤〈+∞⎩，则(1)f =__________________(2) 函数26()412x f x x x -=--的连续区间为 ____________(3)已知曲线()y f x =在点x 处切线的斜率为21x +，且曲线过点(1,1)，则曲线的方程是 ___________________(4) 10d dx =⎰_________ (5)函数()sin 2f x x =的一个原函数是二、选择题(每题2分，共10分）（1）设()f x 的定义域为[]0,1,则(1)f x -的定义域为( )A ．[]0,1B ．[]1,2C ．[]1,0- D ．[]0,2（2）函数3121y x x =++在定义域内（）A ．单调递增B ．单调递减C ．图形上凹D ．图形上凸（3）设22(,)f x y x y x y +-=-,则''x y f f +=( )A ．22x y -B ．22x y +C ．x y +D ．x y - （4）若()22x f x dx x e c =+⎰,则()f x =( ).A ．22x xeB ．222x x eC ．2x xeD ．22(1)x xe x +（5）()110,xdx f x y dy -=⎰⎰( )A ．()dx y x f dy x⎰⎰-101, B ．()dx y x f dy x⎰⎰-110, C ．()dx y x f dy ⎰⎰101, D ．()dx y x f dy y⎰⎰-110,三、求下列函数的极限（每题6分，共12分）(1) 131lim 21---+→x xx x(2) ()xx x 1021lim +→四、求导数或微分（每题6分，共24分）（1）x y arctan =,求'y（2）cos(3)x y e x -=-,求dy《经济应用数学》试题（6）第3页《经济应用数学》试题（6）第4页(共4页)（3）arctan x y y +=,求 'y（4）23ln(1)z x y =++,求dz五、求下列积分和解微分方程（每题6分，解微分方程8分，共26分）（1）⎰⎪⎭⎫⎝⎛-dx x x 21（2） ⎰πcos xdx x（3）⎰+dx x2361（4） x e y y 23=+'六、应用题（每题9分，共18分）1．求曲线2y x =-与22y x =-,所围成的平面图形的面积。

经济数学试题及答案

经济数学试题及答案一、选择题1. 某公司的年利润以每年10%的速度增长，如果去年的年利润为100万元，那么两年后的年利润预计为多少？A. 121万元B. 110万元C. 120万元D. 111万元答案：A2. 假设银行的年利率为5%，如果小明存入10000元，一年后他将获得多少利息？A. 500元B. 550元C. 505元D. 450元答案：C3. 某商品的原价为200元，现在打8折出售，打折后的价格是多少？A. 160元B. 180元C. 240元D. 200元答案：A4. 一个投资项目，初始投资为10000元，预计每年可获得2000元的收益，不考虑其他因素，该项目的回收期是多少年？A. 3年B. 4年C. 5年D. 6年答案：B5. 以下哪个公式用于计算复利？A. A = P(1 + r/n)^(nt)B. A = P(1 + r)^tC. A = P + r^tD. A = P(1 - r)^t答案：A二、填空题1. 如果一个贷款的月利率为0.5%，那么年利率为________%。

答案：62. 某公司的股票价格从年初的10元上涨到年末的12元，该股票的年收益率为________%。

答案：203. 某人计划在5年内攒够100000元用于购房首付，如果他每月存入相同的金额，假设年利率为5%，他每月需要存入________元。

答案：1666.67三、计算题1. 张先生向银行贷款150000元，年利率为6%，贷款期限为10年，采用等额本息还款方式，请问张先生每月需要还款多少元？解：根据等额本息还款公式计算，每月还款额 = 贷款本金× 月利率× (1+月利率)^还款期数 / [(1+月利率)^还款期数 - 1]。

月利率为6%/12 = 0.5%，还款期数为10×12=120期。

代入公式得每月还款额 = 150000 × 0.005 × (1+0.005)^120 / [(1+0.005)^120 - 1] ≈ 1572.22元。

经济应用数学基础(一)微积分-试题与答案

。
二、计算下列各题（每题 5 分，共 20 分）
11 lim( − ) 1、 x→1 ln x x −1
2、 y = arcsin 1− 3x ，求 y' ；
3、设函数 y = y(x) 由方程 exy = x − y 所确定，求 dy x=0 ；
4、已知
⎧
⎨ ⎩
y
=
x= cos
sin t t + t sin
高等数学（上）模拟试卷一
一、填空题（每空 3 分，共 42 分）
1、函数 y = 4 − x + lg(x − 1) 的定义域是
；
⎧2x
x<0
f (x) = ⎨
2、设函数
⎩a + x x ≥ 0在点 x = 0 连续，则 a =
；
3、曲线 y = x4 − 5 在（-1，-4）处的切线方程是
；
∫ 4、已知 f (x)dx = x3 + C ，则 f (x) =
；
∫ 4、已知 f (x)dx = x2 + C ，则 f (x) =
；
ห้องสมุดไป่ตู้
lim (1 +
1
x
)3
5、 x→∞ x =
；
6、函数 f (x) = x3 − x2 +1的极大点是
；
7、设 f (x) = x(x −1)(x − 2)……(x −1000) ，则 f '(0) =
；
8、曲线 y = xex 的拐点是
→
a
=
{3,
−4,
0}
，
→
b
=
{k
,
−1,1}

经济应用数学习题及答案

经济应用数学习题第一章极限和连续填空题1. sin limx xx→∞=0 ；2.函数 x y ln =是由 u y =，v u ln =，x v =复合而成的；3当0x →时，1cos x -是比x 高阶的无穷小量。

4. 当0x → 时，若 sin 2x 与 ax 是等价无穷小量，则 a =25.2lim(1)x x x →∞-=2-e选择题1.02lim5arcsin x xx →= （ C ）（A ） 0 （B ）不存在（C ）25（D ）12.()f x 在点0x x =处有定义，是()f x 在0x x =处连续的（A ）（A ）必要条件（B ）充分条件（C ）充分必要条件（D ）无关条件计算题1.求极限 20cos 1lim2x x x →-解：20cos 1lim 2x x x →-＝414sin lim 0-=-→x x x2.x x x 10)41(lim -→＝41)41(40)41(lim ---→=-e x x x 3.201lim x x e x x→--112lim 0-=-=→x e x x导数和微分填空题1若 )(x u 与 )(x v 在x 处可导，则])()(['x v x u =2'')]([)()()()(x v x v x u x v x u - 2.设)(x f 在0x 处可导，且A x f =')(0，则hh x f h x f h )3()2(l i m000--+→用A 的代数式表示为A 5 ；32)(x e x f =，则xf x f x )1()21(lim--→= 4e -。

2(12)(1)'()2,lim2'(1)4x x f x f f x xe f ex →--==-=-解选择题1. 设)(x f 在点 0x 处可导，则下列命题中正确的是（ A ）（A ） 000()()limx x f x f x x x →--存在（B ） 000()()lim x x f x f x x x →--不存在（C ）00()()limx x f x f x x →+-存在（D ）00()()lim x f x f x x∆→-∆不存在2. 设)(x f 在0x 处可导，且0001lim(2)()4x x f x x f x →=--，则0()f x '等于（ D ）（A ） 4 （B ） –4 （C ） 2 （D ）–2 3. 3设()y f x =可导，则 (2)()f x h f x -- = （ B ）（A ）()()f x h o h '+ （B ） 2()()f x h o h '-+ （C ） ()()f x h o h '-+ （D ） 2()()f x h o h '+ 4.设 (0)0f = ，且 0()limx f x x →存在，则0()lim x f x x→等于（ B ）（A ）()f x ' （B ）(0)f ' （C ）(0)f （D ）1(0)2f '5.函数 )(x f e y =，则 ="y （ D ）（A ）)(x f e （B ） )(")(x f e x f（C ） 2)()]('[x f e x f （D ） )}(")]('{[2)(x f x f e x f +6函数 x x x f )1()(-=的导数为（ D ）（A ）x x x )1(- （B ） 1)1(--x x （C ）x x x ln （D ） )]1ln(1[)1(-+--x x xx x7函数xx x f =)( 在 0=x 处（ D ）（A ）连续但不可导（B ）连续且可导（C ）极限存在但不连续（D ）不连续也不可导计算与应用题1. 设 ln()y xy = 确定 y 是 x 的函数，求 dxdy 解： )(1)(1)][ln(''''xy y xy xy xy xy y +=== )1('''-=+=⋅y x yy xy y y xy2. 2设 x y e y ln = 确定y 是 x 的函数，求dx dy 解：''ln (ln )y y y dy y e y y x xdx x e x ⋅=⋅+=- 3. 3求13cos x y e x -=的微分解：'131313(3cos sin )(3cos sin )x x x dy y dx e x e x dx e x x dx ---==--=-+4. 4求2xe y x= 的微分；解：222'222(21)x x x e x e e x y x x --==22(21)x e x dy dx x -=5设sin 10()20ax x e x f x xa x ⎧+-≠⎪=⎨⎪=⎩在(,)-∞+∞上连续，求a 的值。

经济应用数学 试卷

经济应用数学基础(一)微积分_试题及答案

《经济应用数学》6套期末考试题AB卷带答案模拟测试题

经济应用数学 试卷

经济应用数学习题及答案

经济数学试题及答案大全

大学专业试卷经济应用数学二考A

经济应用数学试题及答案

大专经济数学试题及答案

经济应用数学一下考试试题库

1月浙江自考经济应用数学试题及答案解析

经济应用数学》试卷

经济应用数学复习题(1)

经济应用数学(习题参考答案)

经济应用数学(习题参考答案解析)

《经济应用数学》试题(6)

经济数学试题及答案

经济应用数学基础(一)微积分-试题与答案

经济应用数学习题及答案

经济应用数学试卷

经济应用数学试卷