走近毕达哥拉斯树
毕达哥拉斯树定理

毕达哥拉斯树定理:
毕达哥拉斯树定理,也称为勾股定理,是一条描述直角三角形的性质的重要数学定理。
它指出:在一个直角三角形中,斜边的平方等于两条直角边的平方之和。
这个定理不仅在几何学中有重要应用,而且在代数和其他数学领域也有广泛的影响。
证明过程:假设有一个直角三角形,其边长分别为a和b(这两条边构成了直角)。
根据勾股定理,我们可以构建一个类似勾股树的图形来帮助理解这个过程。
在这个图形中,我们从直角三角形的顶点出发,画两条对角线,分别代表直角边ab的长度。
然后,我们会得到两个新的三角形,这两个三角形的边长分别是直角边ab的一半(即\( \sqrt{a} \) 和\( \sqrt{b} \)),并且这两个三角形的斜边长度是相同的。
通过比较这些三角形的面积,我们可以验证勾股定理是否成立。
由于每个三角形的面积是其边长的平方分之一,因此它们的大小相等,从而证明了勾股定理。
1
历史背景:虽然毕达哥拉斯是第一个将勾股定理纳入自己著作并以自己的方式证明的数学家,但这个定理的历史可能更久远。
有证据显示,它在古巴比伦时期的汉谟拉比时代就已存在。
毕达哥拉斯可能是因为它与其他数学概念的联系而被广泛传播。
2
应用实例:在建筑和测量等领域,勾股定理被广泛应用于确定矩形的面积、检查直角的正确性,以及在设计和规划建筑物时保持比例协调。
例如,古埃及人在建造金字塔时会用到勾股定理的知识来确保直角的准确性。
中考数学几何模型专题专题六—勾股定理
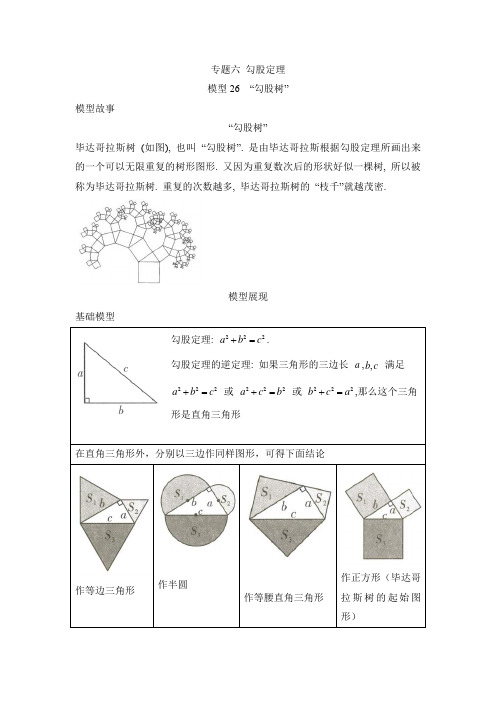
专题六勾股定理模型26 “勾股树”模型故事“勾股树”毕达哥拉斯树(如图), 也叫“勾股树”. 是由毕达哥拉斯根据勾股定理所画出来的一个可以无限重复的树形图形. 又因为重复数次后的形状好似一棵树, 所以被称为毕达哥拉斯树. 重复的次数越多, 毕达哥拉斯树的“枝千”就越茂密.模型展现基础模型勾股定理: 222a b c+=.勾股定理的逆定理: 如果三角形的三边长a,,b c满足222a b c+=或222a c b+=或222b c a+=,那么这个三角形是直角三角形在直角三角形外,分别以三边作同样图形,可得下面结论作等边三角形作半圆作等腰直角三角形作正方形(毕达哥拉斯树的起始图形)怎么用?1. 找模型分别以直角三角形三边为边作相同图形2. 用模型根据勾股定理的关系及等式性质求解, 常用来解决面积问题结论分析:结论: 123S S S +=以作等边三角形为例.证明: 如解图, 过点 D 作 DM AC ⊥ 于点 M ,ACD 是等边三角形, 12AM MC b ∴==, 在 Rt ADM 中, 3tan tan602DM AM DAC AM b ∠=⋅=⋅=, 2111332224S DM AC b b b ∴=⋅⋅=⋅⋅=, 同理可得, 222333,44S a S c ==, ()222212333444S S a b a b ∴+=+=+, Rt ABC 满足 222a b c +=,()222123344S S a b c ∴+=+=.123.S S S ∴+=拓展延伸其余图形的证明, 均是用面积的计算, 然后求和即可, 同学们可以参考给出的证明过程, 自行完成.满分技法以三边分别为边作相同的图形, 解题的基本思想是勾股定理, 但所作图形的性质也是解题的关键.勾股数中常见图形面积公式:1 ;2S =⨯⨯三角形底高2 S =等边三角形边长; 21;2360n r S π=⨯半圆 2 S =正方形边长典例小试例 1 如图,和 AC 为直径的半圆的面积(与模型的作图方法一致), 则123,S S S 和满足的关系式(求面积,可使用结论)为( )A . 123S S S +=B . 123S S S =+C . 123S S S >+D . 123S S S =⋅考什么?圆的面积计算,勾股定理思路点拨满足模型,选填项目中,可直接使用结论,高效解题。
植树问题历史数学文化典故

植树问题历史数学文化典故
植树问题是一个古老的数学问题,最早可以追溯到公元前5世纪的古希腊。
当时,毕达哥拉斯和他的学生们在探讨几何学和自然科学时,提出了在地球上种植树木的最佳方式。
在中国,古代的数学家和科学家也提出了类似的植树问题,比如在北宋时期,沈括在他的《梦溪笔谈》中就提出过类似的问题。
植树问题在历史上有很多著名的例子,比如古希腊数学家毕达哥拉斯提出的“蜜蜂问题”。
这个问题是关于如何在一个正方形的土地上种植12棵树,使得每
棵树之间的距离相等。
这个问题在当时被认为是一个非常困难的问题,但是毕达哥拉斯最终解决了它。
此外,在中国古代的园林设计中,也经常涉及到植树问题。
比如在一个圆形的园林中种植10棵树,如何使得每棵树之间的距离相等。
毕达哥拉斯树课件

contents
目录
• 毕达哥拉斯树简介 • 毕达哥拉斯树的数学原理 • 毕达哥拉斯树的实现方式 • 毕达哥拉斯树的视觉效果和艺术价值 • 毕达哥拉斯树的意义和影响
01
毕达哥拉斯树简介
毕达形 ,由多个直角三角形按照一定 规则堆叠而成。
它以古希腊数学家毕达哥拉斯 命名,因为毕达哥拉斯学派最 早研究了这种几何图形。
。
象征意义
毕达哥拉斯树在艺术中常常被用作 象征,代表着宇宙、生命、和谐等 深刻的意义。
创意表现
毕达哥拉斯树为艺术家提供了无限 的创意空间,可用于表现抽象、具 象等多种艺术风格。
毕达哥拉斯树与其他艺术形式的结合
绘画
雕塑
毕达哥拉斯树在绘画中常被用作背景或装 饰元素,为画面增添层次感和视觉效果。
在雕塑中,毕达哥拉斯树可以作为造型的 灵感来源,创造出立体感十足的作品。
毕达哥拉斯树呈现出一种独特 的分形结构,具有高度的自相 似性。
毕达哥拉斯树的起源和历史
毕达哥拉斯树起源于古希腊数学家毕达哥拉斯的研究,是分形几何学发展史上的重 要里程碑。
中世纪欧洲的艺术家和数学家开始对分形几何学产生兴趣,毕达哥拉斯树成为他们 创作的一部分。
随着计算机技术的发展,毕达哥拉斯树逐渐成为计算机图形学和艺术领域的研究对 象。
建筑
数字艺术
建筑师可以利用毕达哥拉斯树的形状和结 构特点,设计出独特且富有创意的建筑作 品。
在数字艺术中,毕达哥拉斯树可以通过计 算机技术进行动态展示和交互设计,创造 出更加丰富的视觉效果和用户体验。
05
毕达哥拉斯树的意义和影响
毕达哥拉斯树对数学和科学的影响
数学概念
毕达哥拉斯树是数学中分形概念的典型代表,它揭示了简单 数学规则可以产生复杂和精美的结构,对数学的发展产生了 深远的影响。
三角形中的重要模型-弦图模型、勾股树模型(学生版+解析版)

三角形中的重要模型-弦图模型、勾股树模型赵爽弦图分为内弦图与外弦图,是中国古代数学家赵爽发现,既可以证明勾股定理,也可以以此命题,相关的题目有一定的难度,但解题方法也常常是不唯一的。
弦图之美,美在简约,然不失深厚,经典而久远,被誉为“中国数学界的图腾”。
弦图蕴含的割补思想,数形结合思想、图形变换思想更是课堂教学中数学思想渗透的绝佳载体。
一个弦图集合了初中平面几何线与形,位置与数量,方法与思想,小身板,大能量,它就是数学教育里的不老神话。
广受数学教师和数学爱好者研究,近年来也成为了各地中考的热点问题。
模型1、弦图模型(1)内弦图模型:如图1,在正方形ABCD中,AE⊥BF于点E,BF⊥CG于点F,CG⊥DH于点G,DH⊥AE于点H,则有结论:△ABE≌△BCF≌△CDG≌△DAH;S正方形ABCD =4S△EAB+S正方形EFGH。
图1图2图3(2)外弦图模型:如图2,在正方形ABCD中,E,F,G,H分别是正方形ABCD各边上的点,且四边形EFGH是正方形,则有结论:△AHE≌△BEF≌△CFG≌△DGH;S正方形ABCD =4S△EAB+S正方形EFGH。
(3)内外组合型弦图模型:如图3,2S正方形EFGH =S正方形ABCD+S正方形PQMN.1(2023秋·湖北·九年级校联考开学考试)如图,2002年8月在北京召开的国际数学家大会会标其原型是我国古代数学家赵爽的《勾股弦图》,它是由四个全等的直角三角形拼接而成如.如果大正方形的面积是16,直角三角形的直角边长分别为a,b,且a2+b2=ab+10,那么图中小正方形的面积是()A.2B.3C.4D.52(2022·安徽安庆·八年级期末)汉代数学家赵爽为了证明勾股定理,构造了一副“弦图”,后人称其为“赵爽弦图”,如图,大正方形ABCD由四个全等的直角三角形和一个小正方形组成,若∠ADE=∠AED,AD =45,则△ADE的面积为()A.24B.6C.25D.2103(2023·山西八年级期末)如图,图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的,若AC=6,BC=5,将四个直角三角形中的边长为6的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长是()A.24B.52C.61D.764(2022·杭州九年级月考)我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”.如图是由弦图变化得到,它是用八个全等的直角三角形拼接而成,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3.若S1+S2+S3=12,则下列关于S1、S2、S3的说法正确的是()A.S1=2B.S2=3C.S3=6D.S1+S3=85(2023·广东·九年级专题练习)公元三世纪,我国汉代数学家赵爽在注解《周髀算经》题时给出了“赵爽弦图”.将两个“赵爽弦图”(如图1)中的两个正方形和八个直角三角形按图2方式摆放围成正方形MNPQ,记空隙处正方形ABCD,正方形EFGH的面积分别为S1,S2S1>S2,则下列四个判断:①S1+S2=14S四边形MNPQ②DG=2AF;③若∠EMH=30°,则S1=3S2;④若点A是线段GF的中点,则3S1=4S2,其中正确的序号是模型2. 勾股树模型6(2022·福建·八年级期末)如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,如果正方形A、B、C、D的边长分别为3,4,1,2.则最大的正方形E的面积是.7(2022·浙江·乐清市八年级期中)如图,在四边形ABCD中,∠B=∠D=90°,分别以AB,BC,CD,DA为一边向外作正方形甲、乙、丙、丁,若用S甲,S乙,S丙,S丁来表示它们的面积,那么下列结论正确的是()A.S 甲=S 丁B.S 乙=S 丙C.S 甲-S 乙=S 丁-S 丙D.S 甲+S 乙=S 丙+S 丁8(2022·河南八年级期末)如图,正方形ABCD 的边长为2,其面积标记为S 1,以CD 为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S 2,⋯按照此规律继续下去,则S 9的值为()A.126B.127C.128D.1299(2023春·山东菏泽·八年级校考阶段练习)“勾股树”是以正方形一边为斜边向外作直角三角形,再以该直角三角形的两直角边分别向外作正方形,重复这一过程所画出来的图形,因为重复数次后的形状好似一棵树而得名.假设如图分别是第一代勾股树、第二代勾股树、第三代勾股树,按照勾股树的作图原理作图,如果第一个正方形面积为1,则第2023代勾股树中所有正方形的面积为.10(2023·浙江八年级期中)如图,以Rt △ABC 的三边为直径,分别向外作半圆,构成的两个月牙形面积分别为S 1、S 2,Rt △ABC 的面积S 3.若S 1=4,S 2=8,则S 3的值为.11(2022春·浙江温州·九年级校考开学考试)如图1,是数学家毕达哥拉斯根据勾股定理所画的“勾股树”.如图2,在Rt △ABC 中,∠BAC =90°,以其三边为边分别向外作正方形,延长EC ,DB 分别交GF ,AH 于点N ,K ,连接KN 交AG 于点M ,若S 1S 2=916,则tan ∠ACB 为()A.12B.23C.34D.51212(2023·贵州遵义·统考二模)如图1,毕达哥拉斯树,也叫“勾股树”,是由毕达哥拉斯根据勾股定理所画出来的一个可以无限重复的树形图形.在图2中,∠ACB =90°,分别以Rt △ABC 的三条边为边向外作正方形,连接BE ,DG 、BE ,交AC 于点Q ,若∠BAC =30°,BC =2,则四边形EQGD 的面积是.13(2023秋·浙江·八年级专题练习)【背景阅读】勾股定理是人类最伟大的十个科学发现之一,西方国家称之为毕达哥拉斯定理.在我国古书《周髀算经》中就有“若勾三,股四,则弦五”的记载,我国汉代数学家赵爽为了验证勾股定理,创制了一幅“弦图”(如图1),后人称之为“赵爽弦图”,流传至今.【实践操作】(1)请叙述勾股定理;(2)验证勾股定理,人们已经找到了400多种方法,请从下列几种常见的验证方法中任选一种来验证该定理:(以下图形均满足验证勾股定理所需的条件)【探索发现】(3)如图4、5、6,以直角三角形的三边为边或直径,分别向外部作正方形、半圆、等边三角形,这三个图形中面积关系满足S1+S2=S3的有个;(4)如图7所示,分别以直角三角形三边为直径作半圆,设图中两个月形图案(图中阴影部分)的面积分别为S1、S2,直角三角形面积为S3,请判断S1、S2、S3的关系并说明理由.课后专项训练1(2022·云南九年级一模)如图是按照一定规律“生长”的“勾股树”:经观察可以发现:图(1)中共有3个正方形,图(2)在图(1)的基础上增加了4个正方形,图(3)在图(2)的基础上增加了8个正方形,⋯⋯,照此规律“生长”下去,图(6)应在图(5)的基础上增加的正方形的个数是()A.12B.32C.64D.1282(2022·浙江初三期中)勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若图2中阴影部分的面积为2,且AB+AC=8,则BC的长为()图1图2A.42B.6C.254D.1323(2023·浙江·杭州八年级阶段练习)如图,Rt△ABC中,∠BAC=90°,分别以△ABC的三边为边作正方形ABDE,正方形BCFG,正方形ACHI,AI交CF于点J.三个正方形没有重叠的部分为阴影部分,设四边形BGFJ的面积为S1,四边形CHIJ的面积为S2,若S1-S2=12,S△ABC=4,则正方形BCFG的面积为()A.16B.18C.20D.224(2023春·湖北黄冈·八年级统考期中)“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,设直角三角形较长直角边长为a,较短直角边长为b.若ab=8,大正方形的面积为25,则EF 的长为()A.9B.92C.32D.35(2022·四川成都·模拟预测)勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再将较小的两个正方形分别绕直角三角形斜边上的两顶点旋转得到图2.则图2中阴影部分面积等于()A.直角三角形的面积B.最大正方形的面积C.最大正方形与直角三角形的面积和D.较小两个正方形重叠部分的面积6(2023春·广东潮州·九年级校考期末)我国古代数学家赵爽巧妙地用“弦图”证明了勾股定理,标志着中国古代的数学成就.如图所示的“弦图”,是由四个全等的直角三角形和中间的一个小正方形拼成的一个大正方形.直角三角形的斜边长为13,一条直角边长为12,则小正方形ABCD 的面积的大小为()A.144B.100C.49D.257(2023春·湖北武汉·八年级统考期末)大约公元222年我国汉代数学家赵爽为《周髀算经》一书作序时介绍了“勾股圆方图”,亦称“赵爽弦图”,如图,四个全等的直角三角形拼成大正方形ABCD ,中空的部分是小正方形EFGH ,连接EG ,BD 相交于点O ,BD 与HC 相交于点P ,若GO =GP ,则直角三角形的边CG 与BG 之比是()A.12B.25C.2-1D.3-28(2023春·江苏泰州·七年级统考期末)大约在公元222年,赵爽为《周髀算经》一书作序时,介绍了“勾股圆方图”,亦称“赵爽弦图”(如图1).某数学兴趣小组类比“赵爽弦图”构造出图2:△ABC 为等边三角形,AD 、BE 、CF 围成的△DEF 也是等边三角形.已知点D 、E 、F 分别是BE 、CF 、AD 的中点,若△ABC 的面积为14,则△DEF 的面积是()A.1B.2C.3D.49(2023·河北石家庄·校考二模)如图1,毕达哥拉斯树,也叫“勾股树”,是由毕达哥拉斯根据勾股定理所画出来的一个可以无限重复的树形图形.在图2中,∠ACB=90°,分别以Rt△ABC的三条边为边向外作正方形,连接BE,DG,BE交AC于点Q.若∠BAC=30°,BC=2,则四边形EQGD的面积是()B.23C.53+3D.3A.53+3210(2023·江苏扬州·统考中考真题)我国汉代数学家赵爽证明勾股定理时创制了一幅“勾股圆方图”,后人称之为“赵爽弦图”,它是由4个全等的直角三角形和一个小正方形组成.如图,直角三角形的直角边长为a、b,斜边长为c,若b-a=4,c=20,则每个直角三角形的面积为.11(2022秋·四川成都·八年级校考期中)“勾股图”有着悠久的历史,它曾引起很多人的兴趣.1955年希腊发行了以“勾股图”为背景的邮票(如图1),欧几里得在《几何原本》中曾对该图做了深入研究.如图2,在△ABC中,∠ACB=90°,分别以△ABC的三条边为边向外作正方形,连接EB,CM,DG,CM分别与AB,BE相交于点P,Q.若∠ABE=30°,则DGQM的值为.12(2022春·安徽合肥·八年级合肥市第四十二中学校考期中)如图①,在Rt△ACB中∠ACB=90°,分别以AC、BC、AB为边,向形外作等边三角形,所得的等边三角形的面积分别为S1、S2、S3,请解答以下问题:(1)S1、S2、S3满足的数量关系是.(2)现将△ABF向上翻折,如图②,若阴影部分的S甲=6、S乙=5、S丙=4,则S△ACB=.13(2023·湖北孝感·统考三模)“勾股树”是以正方形一边为斜边向外作直角三角形,再以直角三角形的两直角边分别向外作正方形,重复这一过程所画出来的图形,因为重复数次后的形状好似一棵树而得名.假设如图分别是第一代勾股树、第二代勾股树、第三代勾股树,按照勾股树的作图原理作图,则第五代勾股树中正方形的个数为.14(2022·山东临沂·统考二模)中国古代的数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和地位尤其是三国时期的数学家赵爽,不仅最早对勾股定理进行了证明,而且创制了“勾股圆方图”,开创了“以形证数”的思想方法.在图中,小正方形ABCD的面积为1,如果把它的各边分别延长一倍得到正方形A1B1C1D1(如图1),则正方形的面积为;再把正方形A1B1C1D1的各边分别延长一倍得到正方形A2B2C2D2(如图2),如此进行下去,得到的正方形A n B n C n D n的面积为(用含n的式子表示,n为正整数).15(2023·浙江台州·八年级校考期中)如图1,是一个封闭的勾股水箱,其中Ⅰ,Ⅱ,Ⅲ部分是可盛水的正方形,且相互联通,已知∠ACB=90°,AC=6,BC=8,开始时Ⅲ刚好盛满水,而Ⅰ,Ⅱ无水.(1)如图2摆放时,Ⅰ刚好盛满水,而Ⅱ无水,则Ⅲ中有水部分的面积为;(2)如图3摆放时,水面刚好经过Ⅲ的中心O(正方形两条对角线的交点),则Ⅱ中有水部分的面积为.16(2023·湖北黄冈·统考中考真题)如图,是我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”,它是由四个全等的直角三角形和一个小正方形组成的一个大正方形.设图中AF=a,DF=b,连接AE,BE,若△ADE与△BEH的面积相等,则b2a2+a2b2=.17(2023·江苏徐州·统考二模)如图,四个全等的直角三角形拼成“赵爽弦图”,得到正方形ABCD与正方形EFGH.连接AC,若AG平分∠CAD,且正方形EFGH的面积为2,则正方形ABCD的面积为.18(2023·陕西渭南·统考二模)魏朝时期,刘徽利用下图通过“以盈补虚,出入相补”的方法,即“勾自乘为朱方,股自乘为青方,令出入相补,各从其类”证明了勾股定理.如图,四边形ABCD、四边形BFGH和四边形AFMN都是正方形,BF交CD于E,若DE=2,CE=4,则BF的长为.19(2022·宁夏吴忠·统考一模)2002年8月,在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图1),且大正方形的面积是17,直角三角形的较短直角边为a,较长直角边为b.如果将四个全等的直角三角形按如图2的形式摆放,则图2中最大的正方形的面积为31.试求图1中小正方形的面积是为.20(2023·山东济宁·统考二模)勾股定理是人类最伟大的十个科学发现之一,西方国家称之为毕达哥拉斯定理.在我国古书《周髀算经》中就有“若勾三,股四,则弦五”的记载,我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”(如图1),后人称之为“赵爽弦图”,流传至今.勾股定理内容为:如果直角三角形的两条直角边分别为a,b,斜边为c,那么a2+b2=c2.(1)如图2、3、4,以直角三角形的三边为边或直径,分别向外部作正方形、半圆、等边三角形,这三个图形中面积关系满足S1+S2=S3的有个;(2)如图5所示,分别以直角三角形三边为直径作半圆,设图中两个月形图案(图中阴影部分)的面积分别为S1,S2,直角三角形面积为S3,请判断S1,S2,S3的关系并证明;(3)如果以正方形一边为斜边向外作直角三角形,再以该直角三角形的两直角边分别向外作正方形,重复这一过程就可以得到如图6所示的“勾股树”.在如图7所示的“勾股树”的某部分图形中,设大正方形M的边长为定值m,四个小正方形A,B,C,D的边长分别为a,b,c,d,已知∠1=∠2=∠3=∠α,则当∠α变化时,回答下列问题:(结果可用含m的式子表示)①a2+b2+c2+d2=;②b与c的关系为,a与d的关系为.21(2022·湖南·八年级课时练习)如图①,美丽的弦图,蕴含着四个全等的直角三角形.(1)弦图中包含了一大,一小两个正方形,已知每个直角三角形较长的直角边为a,较短的直角边为b,斜边长为c,结合图①,试验证勾股定理.(2)如图②,将这四个直角三角形紧密地拼接,形成飞镖状,已知外围轮廓(粗线)的周长24,OC=3,求该飞镖状图案的面积.(3)如图③,将八个全等的直角三角形紧密地拼接,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1,S2,S3,若S1+S2+S3=40,求S2.22(2023·广东深圳·校联考三模)中华文明源远流长,如图①是汉代数学家赵爽在注解《周髀算经》时给出的图形,人们称之为赵爽弦图,被誉为中国数学界的图腾.2002年北京国际数学家大会依据赵爽弦图制作了会标,该图有4个全等的直角三角形围成几个大正方形和中间一个小正方形,巧妙的证明了勾股定理.问题发现:如图①,若直角三角形的直角边BC=3,斜边AB=5,则中间小正方形的边长CD=,连接BD,△ABD的面积为.知识迁移:如图②,P是正方形ABCD内一点,连接PA,PB,PC,当∠BPC=90°,BP=10时,△PAB的面积为.拓展延伸:如图③,已知∠MBN=90°,以点B为圆心,适当长为半径画弧,交射线BM,BN分别于A,C两点.(1)已知D为线段AB上一个动点,连接CD,过点B作BE⊥CD,垂足为点E;在CE上取一点F,使EF=BE;过点F作GF⊥CD交BC于点G,试判断三条线段BE,DE,GF之间的数量关系,并说明理由.(2)在(1)的条件下,若D为射线BM上一个动点,F为射线EC上一点;当AB=10,CF=2时,直接写出线段DE的长.三角形中的重要模型-弦图模型、勾股树模型赵爽弦图分为内弦图与外弦图,是中国古代数学家赵爽发现,既可以证明勾股定理,也可以以此命题,相关的题目有一定的难度,但解题方法也常常是不唯一的。
人教版勾股定理(5)

勾股定理
如果直角三角形两直角边分别为a、b, 斜边为c,那么
a2 + b2 = c2
即:直角三角形两直角边的平方和等于 斜边的平方。
在西方又称毕达哥拉 斯定理!
15
勾股定理给出了直角三角形三边之间的 A 关系,即两直角边的平方和等于斜边的平方
c2=a2 + b2
b
c a2=c2-b2
b2 =c2-a2
12
证法3: 美国第二十任总统伽菲尔德的证法在
数学史上被传为佳话
a bc
a
c
b
S 梯形
1 (a b)(a b) 2
S梯形
1 2
ab
1 2
ab
1 2
c2
a2 + b2 = c2
13
勾 股
在中国古代,人们把弯曲成直角的 手臂的上半部分称为"勾",下半部分称 为"股"。我国古代学者把直角三角形较 短的直角边称为“勾”,较长的直角边 称为“股”,斜边称为“弦”.
s大正方形=c2 s大正方形=4×
1 2
ab+(b-a)2
=2ab+b2-2ab+b2
=a2+b2
∵s大正方形=s大正方形 ∴c2=a2+b2
c c
a b-a b
中黄实 c b (b-a)2
a
这个图案公元 3 世纪我 国汉代的赵爽在注解《周髀 算经》时就已经给出,人们 称它为“赵爽弦图”.赵爽 根据此图指出:四个全等的 直角三角形(红色)可以如 图围成一个大正方形,中间 的部分是一个小正方形 (黄色).
9 25 34
sA+sB=sC
勾股与弦图

而勾股定理的证明呢,就在《周髀算经》上卷一[2]——
昔者周公问于商高曰:“窃闻乎大夫善数也,请问昔者包牺立周天历度——夫天可不阶而升,地不可得尺寸而度,请问数安从出?”
勾股定理
勾股定理
在我国,把直角三角形的两直角边的平方和等于斜边的平方这一特性叫做勾股定理或勾股弦定理,又称毕达哥拉斯定理或毕氏定理(Pythagoras Theorem)。数学公式中常写作a^2+b^2=c^2
概述
定义
简介
勾股定理指出
勾股数组
推广
勾股定理
定理
勾股定理的来源
毕达哥拉斯树
常见的勾股数
勾、股、弦的比例
《周髀算经》证明步骤
“数之法出于圆方,圆出于方,方出于矩,矩出于九九八十一。”:解释发展脉络——数之法出于圆(圆周率三)方(四方),圆出于方(圆形面积=外接正方形*圆周率/4),方出于矩(正方形源自两边相等的矩),矩出于九九八十一(长乘宽面积计算依自九九乘法表)。
“故折矩①,以为句广三,股修四,径隅五。”:开始做图——选择一个勾三(圆周率三)、股四(四方)的矩,矩的两条边终点的连线应为5(径隅五)。
李国伟:论「周髀算经」“商高曰数之法出于圆方”章。刊於《第二届科学史研讨会汇刊》,台湾,1991年7月,227-234页。
李继闵:商高定理辨证。刊於《自然科学史研究》,1993年第12卷第1期,29-41页。
编辑本段勾股定理
定理
如果直角三角形两直角边分别为A,B,斜边为C,那么A^2+B^2=C^2
勾股定理的来源
毕达哥拉斯树

毕达哥拉斯树★利用几何画板的测量、计算工具,验证勾股定理★利用各类几何图形证明勾股定理你知道毕达哥拉斯树吗?在古希腊数学家之中,毕达哥拉斯是最为人们所熟悉、出类拔萃的大数学家.毕达哥拉斯在西方首次证明了“毕达哥拉斯定理”.在当时的西方引起了轰动,并为此举行了一个“百牛大祭”以表庆贺.请你观察课件(附件06—1),使动态变静止,选取其中的一部分进行观察,毕达哥拉斯树应用的原理是问题一请你选择几何画板中的测量和计算功能验证勾股定理.操作(1)画一任意直角三角形(2)分别度量直角三角形三边长(3)计算a ²,b ²,c ²的值(4)拖动任一顶点改变直角三角形的形状,验证a ²+b ²=c ²问题二见课件(附件06—2)请你在下面给出的图形中适当选取一些图形来验证勾股定理a ²+b ²=c ²操作方法一、取边长为c 的正方形和四个直角三角形拼成一大正方形请你用其他方法也来拼一个。
问题一你知道伽菲尔德证法吗?这位美国第20任总统利用梯形证明了勾股定理a²+b²=c²,请你尝试一下,相信你一定行!问题二见课件(附件06—3)你能理解吗?结论:这个证明的关键是问题一你能利用圆的面积公式设计另一种图形来验明勾股定理吗?问题二1、公元前300年,古希腊数学家帕普斯证明了勾股定理的一个有趣的变形,他将直角三角形三边上的正方形改成平行四边形,请你根据以下的作图方法来画出图形作图方法:对于Rt△ABC,(1)分别以两直角边AB、AC为边,作两个平行四边形;(2)分别延长两个平行四边形中平行于直角边的两边,它们相交于点P;(3)作射线P A,与BC相交于点P,再截取RQ=P A;(4)以BC为一边作平行四边形,使另一组对边平行且等于RQ.结论:斜边上的平行四边形面积等于两条直角边上的平行四边形面积的和.2、你能尝试证明它是真命题吗?。
勾股定理的证明方法和相关故事

证明方法1
• 这个定理有许多证明的方法,其证明的方法可能是 数学众多定理中最多的。路明思(Elisha Scott Loomis)的 Pythagorean Proposition( 《毕达哥 拉斯命题》)一书中总共提到367种证明方式。 有人会尝试以三角恒等式(例如:正弦和余弦函数的 泰勒级数)来证明勾股定理,但是,因为所有的基本 三角恒等式都是建基于勾股定理,所以不能作为勾股 定理的证明(参见循环论证)。 证法1 作四个全等的直角三角形,设它们的两条直角边 长分别为a、b ,斜边长为c. 把它们拼成如图那样的 一个多边形,使D、E、F在一条直线上。 过点C作 AC的延长线交DF于点P. ∵ D、E、F在一条直线 上, 且RtΔGEF ≌ RtΔEBD, ∴ ∠EGF = ∠BED , ∵ ∠EGF + ∠GEF = 90°, ∴ ∠BED + ∠GEF = 90°, ∴ ∠BEG =180°―90°= 90° 又∵ AB = BE = EG = GA = c, ∴ ABEG是一个边长为c的正方形。 ∴ ∠ABC + ∠CBE = 90° ∵ RtΔABC ≌ RtΔEBD, ∴ ∠ABC = ∠EBD. ∴ ∠EBD + ∠CBE = 90° 即 ∠CBD= 90° 又∵ ∠BDE = 90°,∠BCP = 90°, BC = BD = a. ∴ BDPC是一个边长 为a的正方形。 同理,HPFG是一个边长为b的 正方形. 设多边形GHCBE的面积为S,则 A^2+B^2=C^2.
勾股数组
• 满足勾股定理方程 a^2+b^2=c^2;的正整 勾股定 理 • 数组(a,b,c)。例如(3,4, 5)就是一组勾股数组。 由 于方程中含有3个未知数,故勾 股数组有无数多组。 勾股 数组的通式: a=M^2N^2 b=2MN c=M^2+N^2 (M>N,M,N 为正整数)
《走近毕达哥拉斯树》教学反思

《走近毕达哥拉斯树》教学反思“走近毕达哥拉斯树”是人教版五年级上册总复习单元144页带“?”的思考题(图1)。
编者的意图在于让学生借助由一个直角三角形和以这个直角三角形的三条边分别为边长向外作三个正方形组成的图形,通过三个正方形的面积之间的关系发现直角三角形的三边关系。
这个内容看似简单,只要根据直角三角形的三条边求出正方形的面积,实际上蕴藏着直角三角形的三边关系这样一个重要知识,也包含数学上一个非常著名的数学定理----毕达哥拉斯定理这样一种数学文化。
我想,如何让学生得到直角三角形的三边关系?了解毕达哥拉斯定理?如何发展学生的合情推理能力、培养学生的探究精神和丰富学生的数学知识,正是这道题的主要价值。
反思这节课,本人认为有这样几个比较成功的地方:1.导入较新颖。
这是一节探索直角三角形三边关系的思维训练课,纯粹的计算很难调动学生的学习积极性。
于是,我以观察毕达哥拉斯树这一新奇的事物为载体来创设问题情境,让学生一开始就处在兴趣盎然之中。
2.充分体现以学生为主体。
本节课根据学生的认知结构由扶到放,采用“观察--猜想--归纳--验证--应用”的教学方法,这一流程体现了知识发生、形成和发展的过程,让学生体会到观察、猜想、归纳、验证、迁移的思想和数形结合的思想。
3.精心创设问题情境,激发学生思维火花。
探究直角三角形的三边关系这个内容对小学五年级孩子来说有很大的难度,本节课通过精心创设一系列问题情境,激发了学生的求知欲望,激活了学生的思维,让整个课堂充满思维味。
4. 本节课除了探究直角三角形的三边关系外,还通过听历史故事、欣赏图片让学生了解有关勾股定理的历史,感受数学文化的悠久,让数学课堂充满文化味。
这节课带给我的思考:是否能够通过让学生动手摆一摆、算一算来发现围成直角三角形的三个正方形面积之间的关系?让学生更能体会到数形结合的思想。
2024年度美丽的勾股树

水利工程师在设计水坝、桥梁等工程时,需要利用勾股定理来计算水流对结构的作用力。
勾股定理在水利工程中的应用
机械工程师在设计机械零件时,需要利用勾股定理来计算零件的精度和配合间隙。
勾股定理在机械工程中的应用
21
2024/3/24
勾股定理在计算机图形学中的应用
01
计算机图形学中的很多算法都涉及到向量的计算,而勾股定理是向量计算的基础。
17
2024/3/24
勾股树在三角函数中的应用
勾股树可以用来推导三角函数的基本性质和公式,如正弦、余弦、正切等函数的定义和性质。
18
2024/3/24
05
CHAPTER
勾股树在其他领域应用
19
2024/3/24
20
2024/3/24
1
2
3
建筑师在设计建筑时,需要利用勾股定理来计算结构的稳定性和承重能力。
5
2024/3/24
勾股定理是初等几何中的一个基本定理,也是数学中的重要内容之一。
它在数学、物理、工程等领域都有广泛的应用,如计算三角形的面积、求解直角三角形中的未知边长等。
勾股定理及其逆定理是判断一个三角形是否为直角三角形的重要方法,具有极高的实用性和理论价值。
6
2024/3/24
02
CHAPTER
欧拉勾股树
瑞士数学家欧拉对勾股定理做出了重要贡献,以他的名字命名的欧拉勾股树在数学界享有盛誉。
毕达哥拉斯勾股树
古希腊数学家毕达哥拉斯提出的勾股定理,以他的名字命名的勾股树具有深远的历史意义。
中国古代勾股树
中国古代数学家在《周髀算经》等著作中提出了具有中国特色的勾股定理证明方法,相应的中国古代勾股树也独具魅力。
几何画板:如何绘制勾股树

几何画板:如何绘制勾股树————————————————————————————————作者:————————————————————————————————日期:几何画板课件:如何绘制勾股树美丽奇妙的勾股树,又称毕达哥拉斯树,是由毕达哥拉斯根据勾股定理所画出来的一个可以无限重复的图形,因为重复数次后的形状好似一棵树而得名。
下面将讲解利用几何画板绘制勾股树的制作方法。
几何画板制作勾股树的具体的步骤如下:1、用旋转的方法画正方形ABCD(1)绘制出线段AB。
(2)双击点A,把点A标记为旋转中心。
选中点B,选择“变换”—“旋转”命令,将点B旋转90度,得到点D。
(3)双击点D,把点D标记为旋转中心。
选中点A,选择“变换”—“旋转”命令,将点A旋转-90度,得到点C。
(4)绘制出线段AD、DC、BC。
在几何画板中用旋转的方法画正方形ABCD示例2、构造DC的中点E,并以点E为圆心,EC为半径构造圆(1)选中线段DC,选择“构造”—“中点”命令,绘制出DC的中点E。
(2)依次选中点E和点C,选择“构造”—“以圆心和圆周上点绘圆”命令。
构造DC的中点E并构造圆E3、构造圆弧CD,并在弧CD上取点F(1)选中点C、D和圆E,选择“构造”—“圆上的弧”命令。
(2)保持弧的选中状态,选择“构造”—“弧上的点”命令,任意绘制出点F。
构造圆弧CD,并在弧CD上取点F4、构建勾股树动画按钮(1)选择点F,单击“编辑”—“操作类按钮”—“动画”,打开“操作类按钮动画点的属性”对话框,选择“动画”选项卡,将“方向”设为“双向”;“速度”设为“慢速”。
(2)再选择“标签”选项卡,在标签栏输入“勾股数动画按钮”,单击“确定”。
(3)把按钮的位置调整,如下图所示。
构建勾股树动画按钮并调整到相应位置5、隐藏部分对象隐藏圆E、圆弧CD、点E,如下图所示。
隐藏圆E、圆弧CD、点E6、度量出FD的长度,构造出正方形的内部(1)选择动点F和定点D,单击“度量”——“距离”,测出距离FD;(2)选择点A、B、C、D,单击“构造”—“四边形内部”。
毕达哥拉斯树

毕达哥拉斯树简介毕达哥拉斯树(Pythagoras Tree),又称勾股树,是由毕达哥拉斯定理演化而成的一种分形树形结构。
它由一系列相似的形状组成,形状间通过一条边连接。
毕达哥拉斯树提供了一种直观的方式来观察和理解几何学中的重要概念。
毕达哥拉斯树的构造过程1.在画布上绘制一个直角三角形,以直角边作为基准边。
2.将基准边分成两段,按比例分配长度。
这两段长度分别为基准边长度的a和b倍,其中a和b为小于1的正实数。
3.将较长的一段(长度为b倍的边)向内旋转90度,并使其与基准边相连。
4.根据步骤2和3,递归地构造树的各个分支。
毕达哥拉斯树的特性1.自相似性:毕达哥拉斯树的各个部分相互类似,树形结构在不同尺度上具有相似性。
2.分形性:毕达哥拉斯树是一种分形模式,无论放大还是缩小,它的形状都可以被重复和复制。
3.可视化几何学概念:毕达哥拉斯树能够有效地展示几何学中的重要概念,如直角三角形、相似三角形、勾股定理等。
毕达哥拉斯树的应用1.数学教育:毕达哥拉斯树可以作为一种教学工具,帮助学生理解和应用几何学中的概念和原理。
2.计算机图形学:毕达哥拉斯树的分形特性可以用来生成复杂的自然图案,被广泛应用于计算机图形学和图像处理领域。
3.艺术创作:毕达哥拉斯树的美学特点使其成为艺术创作的灵感来源,在艺术作品中常常可以看到毕达哥拉斯树的影子。
代码示例以下是一个使用Python语言生成毕达哥拉斯树的简单代码示例:import turtledef draw_pythagoras_tree(x, y, size, angle):if size <1:returnturtle.penup()turtle.goto(x, y)turtle.pendown()turtle.setheading(angle)turtle.forward(size *100)turtle.right(90)draw_pythagoras_tree(turtle.xcor(), turtle.ycor(), size *0.7, angl e -45)turtle.left(90)draw_pythagoras_tree(turtle.xcor(), turtle.ycor(), size *0.7, angl e +45)turtle.penup()turtle.goto(x, y)turtle.pendown()turtle.setheading(angle)turtle.backward(size *100)def main():turtle.speed(0)draw_pythagoras_tree(0, -200, 2, 0)if__name__=='__main__':main()结论毕达哥拉斯树是一种极具魅力的分形树形结构,可以用于数学教育、计算机图形学和艺术创作。
数学家毕达哥拉斯+勾股定理

7
课堂小结
2、直角三角形ABC中,AB边为13, BC边为12,那AC边为:
A、15 B、12 C、10 D、 5
回答错误哦,你再继续想想! 方法小结:运用勾股定理
a2+b2=c2
我要继续 继续奋斗
为
()
C
A.3 米 B.4 米 C.5米 D.6米
3
4
1 定理简介 21 定理证明 3 视频课堂 4 实际运用 5 拓展内容 6 课后练习 7 课堂小结
数学语言 符号语言
结论变形
勾股定理:直角三角形两直角边的平 方和等于斜边的平方.
1 定理简介 21 定理证明 3 视频课堂 4 实际运用 5 拓展内容 6 课后练习 7 课堂小结
1 定理简介 21 定理证明 3 视频课堂 4 实际运用 5 拓展内容 6 课后练习 7 课堂小结
继续下一题 结束学习
如图,折叠长方形(四个角都是直角,
对边相等)的一边,使点D落在BC边
上的点F处,若AB=8,AD=10.
(1)你能说出图中哪些线段的长?
A
10
D
(2)求EC的长.
8 10
8-x E 8-x x
B 6 F4 C
盛开的水莲
3、在波平如静的湖面上,有一朵美丽的红莲 ,它高
1 定理简介 21 定理证明 3 视频课堂 4 实际运用 5 拓展内容 6 课后练习 7 课堂小结
探索勾股定理视频
勾股定理动画演示
ห้องสมุดไป่ตู้
1 定理简介
21 定理证明 3 视频课堂 4 实际运用 5 拓展内容 6 课后练习 7 课堂小结
勾股定理 (2)

毕达哥拉斯定理一、毕达哥拉斯定理的定义勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方。
这个定理在中国又称为“商高定理”,在外国称为“毕达哥拉斯定理”。
二、毕达哥拉斯定理的由来早在中国商代就由商高发现.据说毕达哥拉斯发现了这个定理后,即斩了百头牛作庆祝,因此又称“百牛定理”.勾股定理指出:直角三角形两直角边(即“勾”“股”短的为勾,长的为股)边长平方和等于斜边(即“弦”)边长的平方.也就是说,设直角三角形两直角边为a和b,斜边为c,那么a的平方+b的平方=c的平方,即;勾股定理现发现约有500种证明方法,是数学定理中证明方法最多的定理之一.勾股定理其实是余弦定理的一种特殊形式.我国古代著名数学家商高说:“若勾三,股四,则弦五.”它被记录在了《九章算术》中.商高是公元前十一世纪的中国人.当时中国的朝代是西周,处于奴隶社会时期.在中国古代大约是西汉的数学著作《周髀算经》中记录着商高同周公的一段对话.周公问商高:“天不可阶而升,地不可将尽寸而度.”天的高度和地面的一些测量的数字是怎么样得到的呢?商高说:“故折矩以为勾广三,股修四,经隅五.”即我们常说的勾三股四弦五.早见于商高的话中,所以人们就把这个定理叫做“商高定理”.欧洲人则称这个定理为毕达哥拉斯定理.毕达哥拉斯(PythAgorAs)是古希腊数学家,他是公元前五世纪的人.希腊另一位数学家欧几里德(Euclid,是公元前三百年左右的人)在编著《几何原本》时,认为这个定理是毕达哥达斯最早发现的,因而国外一般称之为“毕达哥拉斯定理”.并且据说毕达哥拉斯在完成这一定理证明后欣喜若狂,而杀牛百只以示庆贺.因此这一定理还又获得了一个带神秘色彩的称号:“百牛定理”.所以他就把这个定理称为"毕达哥拉斯定理",以后就流传开了.三、思维的勾股定理平方后等于负1的数称为虚数,用表示.的3倍记为、7倍记为,它们都是虚数.1与-1的平方都是1,平方为-1的数原本是没有的,虚数是在‘如果有的话’的前提下提出的概念.由实数和虚数组合成的数叫做复数,复变函数是专门研究复数的数学分支.假设在宇宙的最初(如同霍金所提倡的)时间是虚数,由于加速度为距离除以时间的平方,所以当时间为虚数时,力的符号变为负(反方向).难以逾越的高墙反过来变成了深深的堑壕,在力学上势能(位置能)的符号发生了变化,封闭着能量的口袋在一瞬间消失,从而揭开了宇宙大爆炸的序幕,在此瞬间里时间由虚变实,变成了通常的膨胀.关于大爆炸以前的虚时间难于讲解,示意图也画不出来的,普通的时间尚无法看见,更别提看见虚时间了.我们的意识在一定程度上能够推定时间的经过,如果这时间是虚时间的话将会怎样呢?谁也说不出来.霍金为了避开奇点用数学公式表示了时间的连续性,但是他却回避不了大爆炸前的虚时间的提出,消除了宇宙创生于奇点的困惑.接下来,笔者用比较易懂的狭义相对论的公式,再对虚时间进行一些讲解.狭义相对论认为,光速是不变的,长度及时间随测量方法的不同而不同,时间与长度具有同等的资格.因此狭义相对论的公式是四维公式.设x、y、z为三维空间坐标的互相垂直的三个轴,t为时间.为了使时间成为用长度表示的维,把时间与光速c的乘积ct作为代表第四维的轴.假定光从A点出发沿直线(按狭义相对论观点)到达B点,所需时间为t,则AB间的直线距离为ct.一般地说,时间轴与x、y、z轴中的任何一个轴都不是互相垂直的,长度ct中含有各个轴的成份,光走过的距离ct相当于以x、y、z为三边的立方体的对角线之长,满足三维勾股定理(如图),.也可以写成.如果将相对论的时间记述为三维空间里的一维时间的话,与之和总应该为零.请注意:在数学处理上必须不带任何区别地看待时间与空间.四维几何学很难用我们的常识去理解,在四维几何学里从一开始就把ct 作为一个独立的坐标,而不是光传播于x、y、z三维空间里…….四维空间中的距离并不一定为零,而是一个定数,四个维的平方之和表示四维超立方体对角线的平方(称为扩张的勾股定理),即在四维几何学中,时间与空间之间存在下述关系:,是个定值,与光从A到B的过程有关.这个公式是四维时空间里的物理学公式.在原来的勾股定理中,各边的平方均为正值,只有与时空间有关的时间项的平方为负值,也就是把看作是加上一个负的项.四、毕达哥拉斯定理的证明法.唐初规定它为国子监明算科的教材之一,故改名《周髀算经》.首十一.故折矩,以为句广三,股修四,径隅五.既方之,外半其一矩,环识从何而来.于是商高以勾股定理的证明为例,解释数学知识的由来.边相等的矩),矩出于九九八十一(长乘宽面积计算依自九九乘法表).“故折矩①,以为句广三,股修四,径隅五.”:开始做图——选择一个 勾三(圆周率三)、股四(四方) 的矩,矩的两条边终点的连线应为5(径隅五).“②既方之,外半其一矩,环而共盘,得成三四五.”:这就是关键的证明过程——以矩的两条边画正方形(勾方、股方),根据矩的弦外面再画一个矩(曲尺,实际上用作直角三角),将“外半其一矩”得到的三角形剪下环绕复制形成一个大正方形,可看到其中有 边长三勾方、边长四股方、边长五弦方 三个正方形.“两矩共长③二十有五,是谓积矩.”:此为验算——勾方、股方的面积之和,与弦方的面积二十五相等——从图形上来看,大正方形减去四个三角形面积后为弦方,再是 大正方形 减去 右上、左下两个长方形面积后为 勾方股方之和.因三角形为长方形面积的一半,可推出 四个三角形面积 等于 右上、左下两个长方形面积,所以 勾方+股方=弦方.(二)(欧几里德(Euclid)射影定理证法)如图1,Rt△ABC中,∠ABC=90°,BD是斜边AC上的高,通过证明三角形相似则有射影定理如下:(1) (2) (3)由公式(2)(3)得:;即,这就是勾股定理的结论.图1(三) 爱因斯坦的证明方法至今未见到爱因斯坦12岁时对毕氏定理证明的详细内容,但是按照材料,不难正确地推论出他的方法如下所示.专注到三角形的相似性,从直角三角形的一个顶点向斜边作垂线,设交点为D(见图1).两直角三角形的相似,完全取决于它们的一个锐角,如果有一锐角相等,二者相似;否则,不相似.在图1中,△ABC、△DBC、△DCA彼此都是相似的,因为它们有一锐角是相等的.△ABC与△DBC因相似,二者的两对应边长之比相等,即(1)对△ABC与△ACD,同理有(2)(1) +(2),得到:(3)(四)、(达芬奇的证法)达芬奇的证法三张纸片其实是同一张纸,把它撕开重新拼凑之后,中间那个“洞”的面积前后仍然是一样的,但是面积的表达式却不再相同,让这两个形式不同的表达式相等,就能得出一个新的关系式——勾股定理,所有勾股定理的证明方法都有这么个共同点。
数学勾股定理

勾股定理在我国,把直角三角形的两直角边的平方和等于斜边的平方这一特性叫做勾股定理或勾股弦定理,又称毕达哥拉斯定理或毕氏定理(Pythagoras Theorem)。
数学公式中常写作a²+b²=c²内容勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方。
这个定理在中国又称为“商高定理”,在外国称为“毕达哥拉斯定理”。
目前初二学生学,教材的证明方法采用赵爽弦图。
勾股定理(又称商高定理,毕达哥拉斯定理)是一个基本的几何定理,早在中国周朝由商高发现。
据说毕达哥拉斯发现了这个定理后,即斩了百头牛作庆祝,因此又称“百牛定理”。
勾股定理指出:直角三角形两直角边(即“勾”“股”短的为勾,长的为股)边长平方和等于斜边(即“弦”)边长的平方。
也就是说,设直角三角形两直角边为a和b,斜边为c,那么a的平方+b的平方=c的平方a^2+b^2=c^2勾股定理现发现约有500种证明方法,是数学定理中证明方法最多的定理之一。
勾股定理其实是余弦定理的一种特殊形式。
我国古代著名数学家商高说:“若勾三,股四,则弦五。
”它被记录在了《九章算术》中。
勾股数组满足勾股定理方程 a^2+b^2=c^2;的正整勾股定理数组(a,b,c)。
例如(3,4,5)就是一组勾股数组。
由于方程中含有3个未知数,故勾股数组有无数多组。
勾股数组的通式:a=√M^2-N^2b=√M²+N²c=√M^2+N^2(M>N,M,N为正整数)推广1、如果将直角三角形的斜边看作二维平面上的向量,将两直角边看作在平面直角坐标系坐标轴上的投影,则可以从另一个角度考察勾股定理的意义。
即,向量长度的平方等于它在其所在空间一组正交基上投影长度的平方之和。
2、勾股定理是余弦定理的特殊情况。
编辑本段勾股定理定理如果直角三角形两直角边分别为A,B,斜边为C,那么 A^2+B^2=C^2;;即直角三角形两直角边长的平方和等于斜边长的平方。
“毕达哥拉斯树”教学研究报告

“毕达哥拉斯树”教学研究报告文︳湘潭市小学数学名师工作室潇湘数学教育工作室思想·教学沙龙主持人:徐旺E-mail:zyb0522@一、问题“毕达哥拉斯树”这一教学内容源自人教版数学教材五年级上册总复习单元中的一道思考题:一个直角三角形的三条边长分别是3cm、4cm、5cm。
以这三条边分别为边长画三个正方形,这三个正方形的面积各是多少?通过研读教材,我们认为,教材的编写意图是让学生借助“以一个直角三角形的三条边为边长,分别向外作三个正方形”,发现这三个正方形面积之间的关系,进而研究直角三角形三边之间的关系,为今后中学学习勾股定理作铺垫。
而勾股定理的证明,人教版教材安排在八年级下册。
五年级的孩子研究这一高难度的内容,我们该如何把握好度?为此,我们进行了以下的思考与分析。
1.如果教学仅仅停留在解决“你能发现这三个正方形面积之间有什么关系吗”这一问题的层面,只需引导学生通过计算找出每组中三个正方形面积之间的关系即可,思维含量显然不够。
如果拔高为勾股定理的证明,学生又难以理解。
这节课的教学目标究竟该如何定位?2.根据教材要求,以直角三角形的三条边为边长,分别向外作三个正方形,再计算它们的面积,对大部分学生来说非常简单。
如何才能引导孩子们发现三个正方形面积之间的关系?并且发现在三角形中,唯有直角三角形才有此种关系?3.对五年级学生来说,勾股定理非常抽象,难以理解。
如何才能化抽象为具体,让学生经历完整的数学探究过程,形成解决实际问题的策略,培养研究事物的能力?根据五年级学生现有的知识基础和思维水平,经过讨论,我们将本节课的教学目标定位为:通过面积证法,经历直角三角形三边关系的探索过程,发展学生的合情推理能力,体会数形结合的思想;通过介绍有关勾股定理的知识,拓展学生的视野,丰富学生的数学知识。
为了达成教学目标,我们通过查找资料,发现“毕达哥拉斯树”可以作为这一内容的探究素材,它是根据勾股定理画出来的一个可以无限重复的图形。
毕达哥拉斯树原理

毕达哥拉斯树原理
嘿,朋友们!今天让我来给你们讲讲超级神奇的毕达哥拉斯树原理!你们知道吗,这就像是一个数学魔法!
想象一下,有一片神奇的数学森林,而毕达哥拉斯树就是这片森林中最独特的存在。
比如,我们建房子的时候,一砖一瓦都要按照一定的规则来,毕达哥拉斯树也是这样,每个部分都有着精确的安排。
你看啊,毕达哥拉斯树是从一个正方形开始的。
这就像一个小基地,然后呢,从这个正方形的每条边上长出一个新的正方形!就好像小基地开始繁衍啦,多有意思呀!而且这些新长出的正方形又会继续这个过程,不断扩展,就如同树木不断生长分支一样。
“哇塞,这也太奇妙了吧!”你可能会这么惊叹。
可不是嘛!这其中蕴含着深刻的数学道理呢。
就好像我们的生活,看似杂乱无章,但其实有着内在的规律和秩序。
有人会问了,研究这个毕达哥拉斯树原理有啥用呀?嘿嘿,用处可大了去啦!它能让我们更好地理解数学中的几何关系,就像给我们打开了一扇通往神秘数学世界的大门。
而且,在一些设计和艺术领域也能看到它的影子呢!
毕达哥拉斯树原理,真的是数学世界里的一颗璀璨明珠呀!它展现了数学的美妙和神奇,让我们对这个世界有了更深的认识。
所以呀,别小看这些看似枯燥的数学原理,其实它们背后藏着无数的惊喜等待我们去发现呢!咱们都要好好去探索一番呀,说不定会有更多意想不到的收获呢!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《走近毕达哥拉斯树》教学设计
教学内容:人教版小学数学五年级上册总复习114页“你知道吗?”
教学目标:
1、通过面积证法,经历探索直角三角形三边关系的过程,发展学生的合情推理能力,体会数形结合的思想。
2、通过介绍有关勾股定理的知识,拓展学生的视野,丰富学生的数学知识。
教学重点、难点:
经历探索直角三角形三边关系的过程。
教学准备:
课件、探究单、计算器。
教学过程:
一、谈话导入课题
师:同学们,这节课老师给大家带来了一棵树,它叫毕达哥拉斯树。
(贴课题)这棵树和我们数学有什么关系呢?这节课让我们一起走近神奇的毕达哥拉斯树(板书:走近)。
二、探索新知
1、观察毕达哥拉斯树,有什么发现?
2、研究毕达哥拉斯树中的第一组图形
(1)图中的直角三角形与三个正方形之间有什么关系?
(2)正方形甲、乙、丙之间有什么关系?猜一猜。
(3)已知a是3cm,b是4cm,c是5cm ,你能算出甲乙丙三个正方形的面积分别是多少吗?
(4)你能发现这三个正方形的面积之间有什么关系吗?(板书:S甲+S乙=S丙)(5)小结:我们通过计算、观察,发现以这个直角三角形的三条边为边长分别向外作三个正方形甲、乙、丙,可得到S甲+S乙=S丙这种关系。
3、那是不是以任意直角三角形的三条边为边长分别向外作三个正方形,都能得到这种关系呢?为了研究这个问题,从毕达哥拉斯树上又任意选取了10组图形进行研究。
(1)四人小组合作探究。
(2)汇报研究结果。
(3)小结:通过所有的同学参与验证,虽然大家研究的数据不一样,但结论都一样,都是S甲+S乙=S丙。
所以,我们能够得出结论:(边讲边用课件出示)以任意直角三角形的三条边为边长,向外作三个正方形,得到的三个正方形的面积之间都存在S甲+S乙=S丙这种关系。
4、借助这三个正方形的面积之间的关系,想一想:a、b、c之间有什么关系呢?(a2 +b2 =c2)
5、脱离三个正方形,只留下直角三角形,我们发现a2 +b2 =c2不仅是三个正方形的边长之间的关系,还是直角三角形三条边之间的关系。
小结:在直角三角形中,两直角边的平方和等于斜边的平方(贴板书)。
齐读,找关键词、前提条件(标记直角三角形)。
6、提问:学到这里,你还有什么疑问吗?
7、验证:a2 +b2 =c2在钝角三角形和锐角三角形中是否适用呢?
8、思考:如果a还是6cm,b还是8cm,要使a和b的夹角是90度,那么c应该是多少才能使组成的三角形是直角三角形呢?(10cm)
三、了解数学文化、总结下课。
1、课堂总结:同学们,今天我们通过对毕达哥拉斯树进行观察、研究,借助正方形的面积,探究出了直角三角形的三边关系,是(在直角三角形中,两直角边的平方和等于斜边的平方),用字母表示为:a2 +b2 =c2。
2、介绍毕达哥拉斯定理的来历(听故事)
3、欣赏毕达哥拉斯树的图片。
这些树虽然大小不同,形状各异,但是它们有一个共同的特点,都是运用毕达哥拉斯定理的原理画出来的,树上都藏着直角三角形的三边关系。
4、介绍勾股定理来历,早在三千多年前,我国数学家商高就提出“勾三、股四、弦五”,所以称勾股定理,或者商高定理。
5、课堂延伸:勾股定理在今后的中学、大学数学学习当中,都要进一步学习和研究。
板书设计:
走近毕达哥拉斯树
S甲+S乙=S丙
a2 +b2 =c2
在直角三角形中,两直角边的平方和等于斜边的平方。
