六年级数学-- 立体几何
小学六年级总复习之立体几何

数学问题中的立体几何应用
计算几何图形面积和体积 判断几何图形的形状和大小 解决几何图形的最值问题 确定几何图形的位置关系
科学问题中的立体几何应用
天文学:行星、 恒星和星系的形 状和运动规律可 以用立体几何来
描述。
物理学:电磁场、 引力场等物理现 象可以用立体几
何来描述。
化学:分子结构 可以通过立体几 何来描述,如分 子的键角、键长
立体几何中的基本概念
点、线、面的定义
平面几何的性质
空间几何体的构造
空间几何体的表面积和体积
03
立体图形的性质和 分类
立体图形的性质
定义:立体图 形是三维空间 中占据一定空 间的图形,具 有长度、宽度
和高度。
分类:根据几 何形状,立体 图形可以分为 多面体、旋转 体和组合体等。
性质:立体图 形具有三维性、 封闭性、占有 空间等性质。
特征:立体图 形具有空间感、 立体感和三维
性等特征。
立体图形的分类
柱体:包括圆柱、棱柱等 锥体:包括圆锥、棱锥等 球体:包括实心球、空心球等 其他多面体:包括长方体、正方体、三棱锥等
常见立体图形介绍
立方体:具有六个面,每个面都是正方形 球体:只有一个曲面,没有平面 圆柱体:由两个平行圆形面和一个曲面组成 圆锥体:由一个圆形底面和一个曲面组成
定义:立体几何是研究三维空间中图形和物体性质的一门学科。 基础概念:点、线、面、体等基本元素,以及它们的性质和关系。 目的:培养空间想象能力和逻辑思维能力。 应用:在建筑、工程、科学等领域有广泛应用。
立体几何中的基本元素
点:表示空间中的一个位置 直线:表示空间中一条无限延伸的线 平面:表示空间中一个无限延展的面 空间:表示三维的立体空间
六年级奥数-第五讲.几何-立体部分.教师版

第五讲 几何——立体部分教学目标:对于小学几何而言,立体图形的表面积和体积计算,既可以很好地考查学生的空间想象能力,又可以具体考查学生在公式应用中处理相关数据的能力,所以,很多重要考试都很重视对立体图形的考查.知识点拨:一、长方体和正方体如右图,长方体共有六个面(每个面都是长方形),八个顶点,十二条棱.c b aHGFED CBA①在六个面中,两个对面是全等的,即三组对面两两全等. (叠放在一起能够完全重合的两个图形称为全等图形.) ②长方体的表面积和体积的计算公式是: 长方体的表面积:2()S ab bc ca =++长方体; 长方体的体积:V abc =长方体.③正方体是各棱相等的长方体,它是长方体的特例,它的六个面都是正方形. 如果它的棱长为a ,那么:26S a =正方体,3V a =正方体.二、圆柱与圆锥例题精讲:【例 1】如右图,在一个棱长为10的立方体上截取一个长为8,宽为3,高为2的小长方体,那么新的几何体的表面积是多少?【解析】我们从三个方向(前后、左右、上下)考虑,新几何体的表面积仍为原立方体的表面积:10⨯10⨯6=600.【例 2】右图是一个边长为4厘米的正方体,分别在前后、左右、上下各面的中心位置挖去一个边长l厘米的正方体,做成一种玩具.它的表面积是多少平方厘米?(图中只画出了前面、右面、上面挖去的正方体)【解析】原正方体的表面积是4⨯4⨯6=96(平方厘米).每一个面被挖去一个边长是1厘米的正方形,同时又增加了5个边长是1厘米的正方体作为玩具的表面积的组成部分.总的来看,每一个面都增加了4个边长是1厘米的正方形.从而,它的表面积是:96+4⨯6=120平方厘米.【巩固】在一个棱长为50厘米的正方体木块,在它的八个角上各挖去一个棱长为5厘米的小正方体,问剩下的立体图形的表面积是多少?【解析】对于和长方体相关的立体图形表面积,一般从上下、左右、前后3个方向考虑.变化前后的表面积不变:50⨯50⨯6=15000(平方厘米).【例 3】下图是一个棱长为2厘米的正方体,在正方体上表面的正中,向下挖一个棱长为1厘米的正方体小洞,接着在小洞的底面正中向下挖一个棱长为12厘米的正方形小洞,第三个正方形小洞的挖法和前两个相同为14厘米,那么最后得到的立体图形的表面积是多少平方厘米?【解析】我们仍然从3个方向考虑.平行于上下表面的各面面积之和:2⨯2⨯2=8(平方厘米);左右方向、前后方向:2⨯2⨯4=16(平方厘米),1⨯1⨯4=4(平方厘米),12⨯12⨯4=1(平方厘米),1 4⨯14⨯4=14(平方厘米),这个立体图形的表面积为:816++4+1+14=1294(平方厘米).【例 4】一个正方体木块,棱长是1米,沿着水平方向将它锯成2片,每片又锯成3长条,每条又锯成4小块,共得到大大小小的长方体24块,那么这24块长方体的表面积之和是多少?【解析】锯一次增加两个面,锯的总次数转化为增加的面数的公式为:锯的总次数⨯2=增加的面数.原正方体表面积:1⨯1⨯6=6(平方米),一共锯了(2-1)+(3-1)+(4-1)=6次,6+1⨯1⨯2⨯6=18(平方米).【巩固】(2008年走美六年级初赛)一个表面积为256cm的长方体如图切成27个小长方体,这27个小长方体表面积的和是2cm.【解析】每一刀增加两个切面,增加的表面积等于与切面平行的两个表面积,所以每个方向切两刀后,表面积增加到原来的3倍,即表面积的和为2563168(cm)⨯=.【例 5】如图,25块边长为1的正方体积木拼成一个几何体,表面积最小是多少?25块积木【解析】当小积木互相重合的面最多时表面积最小.设想27块边长为1的正方形积木,当拼成一个333⨯⨯的正方体时,表面积最小,现在要去掉2块小积木,只有在两个角上各去掉一块小积木,或在同一个角去掉两块相邻的积木时,表面积不会增加,该几何体表面积为54.【例 6】要把12件同样的长a、宽b、高h的长方体物品拼装成一件大的长方体,使打包后表面积最小,该如何打包?⑴当b=2h时,如何打包?⑵当b<2h时,如何打包?⑶当b>2h时,如何打包?【解析】图2和图3正面的面积相同,侧面面积=正面周长⨯长方体长,所以正面的周长愈大表面积越大,图2的正面周长是8h+6b,图3的周长是12h+4b.两者的周长之差为2(b-2h).当b=2h时,图2和图3周长相等,可随意打包;当b<2h时,按图2打包;当b>2h时,按图3打包.图3图2图1hba【巩固】要把6件同样的长17、宽7、高3的长方体物品拼装成一件大的长方体,表面积最小是多少?【解析】考虑所有的包装方法,因为6=1⨯2⨯3,所以一共有两种拼接方式:第一种按长宽高1⨯1⨯6拼接,重叠面有三种选择,共3种包装方法.第二种按长宽高1⨯2⨯3拼接,有3个长方体并列方向的重叠面有三种选择,有2个长方体并列方向的重叠面剩下2种选择,一共有6种包装方法. 其中表面积最小的包装方法如图所示,表面积为1034.【例 7】 如图,在一个棱长为5分米的正方体上放一个棱长为4分米的小正方体,求这个立体图形的表面积.【解析】 我们把上面的小正方体想象成是可以向下“压缩”的,“压缩”后我们发现:小正方体的上面与大正方体上面中的阴影部分合在一起,正好是大正方体的上面.这样这个立体图形的表面积就可以分成这样两部分:上下方向:大正方体的两个底面;四周方向(左右、前后方向):小正方体的四个侧面,大正方体的四个侧面.上下方向:55250⨯⨯=(平方分米);侧面:554100⨯⨯=(平方分米),44464⨯⨯=(平方分米).这个立体图形的表面积为:5010064214++=(平方分米).【例 8】 (2008年“希望杯”五年级第2试)如图,棱长分别为1厘米、2厘米、3厘米、5厘米的四个正方体紧贴在一起,则所得到的多面体的表面积是_______平方厘米.【解析】 (法1)四个正方体的表面积之和为:2222(1235)6396234+++⨯=⨯=(平方厘米),重叠部分的面积为:22222222213(221)(321)(321)39141440⨯+⨯+++++++=+++=(平方厘米), 所以,所得到的多面体的表面积为:23440194-=(平方厘米).(法2)三视图法.从前后面观察到的面积为22253238++=平方厘米,从左右两个面观察到的面积为225334+=平方厘米,从上下能观察到的面积为2525=平方厘米.表面积为()3834252194++⨯=(平方厘米).【例 9】 把19个棱长为1厘米的正方体重叠在一起,按右图中的方式拼成一个立体图形.,求这个立体图形的表面积.【解析】从上下、左右、前后观察到的的平面图形如下面三图表示.因此,这个立体图形的表面积为:2个上面2+个左面2+个前面.上表面的面积为:9平方厘米,左表面的面积为:8平方厘米,前表面的面积为:10平方厘米.因此,这个立体图形的总表面积为:(9810)254++⨯=(平方厘米).上下面左右面前后面【巩固】用棱长是1厘米的立方块拼成如右图所示的立体图形,问该图形的表面积是多少平方厘米?【解析】该图形的上、左、前三个方向的表面分别由9、7、7块正方形组成.该图形的表面积等于(977)246++⨯=个小正方形的面积,所以该图形表面积为46平方厘米.【例 10】有30个边长为1米的正方体,在地面上摆成右上图的形式,然后把露出的表面涂成红色.求被涂成红色的表面积.【解析】44(1234)456⨯++++⨯=(平方米).【例 11】棱长是m厘米(m为整数)的正方体的若干面涂上红色,然后将其切割成棱长是1厘米的小正方体.至少有一面红色的小正方体个数和表面没有红色的小正方体个数的比为13:12,此时m的最小值是多少?【解析】切割成棱长是1厘米的小正方体共有3m个,由于其中至少有一面是红色的小正方体与没有红色面的个数之比为13:12,而131225+=,所以小正方体的总数是25的倍数,即3m是25的倍数,那么m是5的倍数.当5m =时,要使得至少有一面的小正方体有65个,可以将原正方体的正面、上面和下面涂色,此时至少一面涂红色的小正方体有5554265⨯+⨯⨯=个,表面没有红色的小正方体有1256560-=个,个数比恰好是13:12,符合题意.因此,m 的最小值是5.【例 12】 有64个边长为1厘米的同样大小的小正方体,其中34个为白色的,30个为黑色的.现将它们拼成一个444⨯⨯的大正方体,在大正方体的表面上白色部分最多可以是多少平方厘米? 【解析】 要使大正方体的表面上白色部分最多,相当于要使大正方体表面上黑色部分最少,那么就要使得黑色小正方体尽量不露出来.在整个大正方体中,没有露在表面的小正方体有3(42)8-=(个),用黑色的;在面上但不在边上的小正方体有2(42)624-⨯=(个),其中30822-=个用黑色.这样,在表面的44696⨯⨯=个11⨯的正方形中,有22个是黑色,962274-=(个)是白色,所以在大正方体的表面上白色部分最多可以是74平方厘米.【例 13】 三个完全一样的长方体,棱长总和是288厘米,每个长方体相交于一个顶点的三条棱长恰是三个连续的自然数,给这三个长方体涂色,一个涂一面,一个涂两面,一个涂三面.涂色后把三个长方体都切成棱长为1厘米的小正方体,只有一个面涂色的小正方体最少有多少个? 【解析】 每个长方体的棱长和是288396÷=厘米,所以,每个长方体长、宽、高的和是96424÷=厘米.因为,每个长方体相交于一个顶点的三条棱长恰是三个连续的自然数,所以,每个长方体的长、宽、高分别是9厘米、8厘米、7厘米.要求切割后只有一个面涂色的小正方体最少有多少个,则需每一个长方体按题意涂色时,应让切割后只有一个面涂色的小正方体最少.所以,涂一面的长方体应涂一个87⨯面,有8756⨯=个; 涂两面的长方体,若两面不相邻,应涂两个87⨯面,有872112⨯⨯=个;若两面相邻,应涂一个87⨯面和一个97⨯面,此时有()7892105⨯+-=个,所以涂两面的最少有105个;涂三面的长方体,若三面不两两相邻,应涂两个87⨯面、一个97⨯面,有()78894147⨯++-=个;若三面两两相邻,有()()()()()()718171918191146-⨯-+-⨯-+-⨯-=个,所以涂三面的最少有146个.那么切割后只有一个面涂色的小正方体最少有56105146307++=个.【例 14】 把一个大长方体木块表面上涂满红色后,分割成若干个同样大小的小正方体,其中恰好有两个面涂上红色的小正方体恰好是100块,那么至少要把这个大长方体分割成多少个小正方体? 【解析】 设小正方体的棱长为1,考虑两种不同的情况,一种是长方体的长、宽、高中有一个是1的情况,另一种是长方体的长、宽、高都大于1的情况.当长方体的长、宽、高中有一个是1时,分割后只有一层小正方体,其中有两个面涂上红色的小正方体是去掉最外层一圈的小正方体后剩下的那些.因为有两个面涂上红色的小正方体恰好是100块,设100a b =⨯,那么分成的小正方体个数为()()()()221242104a b ab a b a b +⨯+⨯=+++=++,为了使小正方体的个数尽量少,应使()a b +最小,而两数之积一定,差越小积越小,所以当10a b ==时它们的和最小,此时共有()()102102144+⨯+=个小正方体.当长方体的长、宽、高都大于1时,有两个面涂上红色的小正方体是去掉8个顶点所在的小正方体后12条棱上剩余的小正方体,因为有两个面涂上红色的小正方体恰好是100块,所以长方体的长、宽、高之和是10042331÷+⨯=.由于三个数的和一定,差越大积越小,为了使小正方体的个数尽量少,应该令312227=++,此时共有2227108⨯⨯=个小正方体.因为108144<,所以至少要把这个大长方体分割成108个小正方体.【例 15】 把正方体的六个表面都划分成9个相等的正方形.用红、黄、蓝三种颜色去染这些小正方形,要求有公共边的正方形染不同的颜色,那么,用红色染的正方形最多有多少个?【解析】 一个面最多有5个方格可染成红色(见左下图).因为染有5个红色方格的面不能相邻,可以相对,所以至多有两个面可以染成5个红色方格.红红红红红红红红红红红其余四个面中,每个面的四个角上的方格不能再染成红色,至多能染4个红色方格(见上中图).因为染有4个红色方格的面也不能相邻,可以相对,所以至多有两个面可以染成4个红色方格.最后剩下两个相对的面,每个面最多可以染2个红色方格(见右上图).所以,红色方格最多有52422222⨯+⨯+⨯=(个). (另解)事实上上述的解法并不严密,“如果最初的假设并没有两个相对的有5个红色方格的面,是否其他的四个面上可以出现更多的红色方格呢?”这种解法回避了这个问题,如果我们从约束染色方格数的本质原因入手,可严格说明22是红色方格数的最大值.对于同一个平面上的格网,如果按照国际象棋棋盘的方式染色,那么至少有一半的格子可以染成红色.但是现在需要染色的是一个正方体的表面,因此在分析问题时应该兼顾棱、角等面与面相交的地方:⑴ ⑵ ⑶ ⑴如图,每个角上三个方向的3个方格必须染成不同的三种颜色,所以8个角上最多只能有8个方格染成红色.⑵如图,阴影部分是首尾相接由9个方格组成的环,这9个方格中只能有4个方格能染成同一种颜色(如果有5个方格染同一种颜色,必然出现相邻,可以用抽屉原理反证之:先去掉一个白格,剩下的然后两两相邻的分成四个抽屉,必然有一个抽屉中有两个红色方格),像这样的环,在正方体表面最多能找到不重叠的两道(关于正方体中心对称的两道),涉及的18个方格中最多能有8个可染成红色. ⑶剩下633839212⨯⨯-⨯-⨯=个方格,分布在6条棱上,这12个格子中只能有6个能染成红色. 综上所述,能被染成红色的方格最多能有88622++=个格子能染成红色,第一种解法中已经给出22个红方格的染色方法,所以22个格子染成红色是最多的情况.【例 16】 一个长、宽、高分别为21厘米、15厘米、12厘米的长方形.现从它的上面尽可能大的切下一个正方体,然后从剩余的部分再尽可能大的切下一个正方体,最后再从第二次剩余的部分尽可能大的切下一个正方体,剩下的体积是多少立方厘米?【解析】 本题的关键是确定三次切下的正方体的棱长.由于21:15:127:5:4=,为了方便起见.我们先考虑长、宽、高分别为7厘米、5厘米、4厘米的长方体.因为754>>,容易知道第一次切下的正方体棱长应该是4厘米,第二次切时,切下棱长为3厘米的正方体符合要求.第三次切时,切下棱长为2厘米的正方体符合要求.那么对于原长方体来说,三次切下的正方体的棱长分别是12厘米、9厘米和6厘米,所以剩下的体积应是:()33321151212961107⨯⨯-++=(立方厘米).12129996663121263912【例 17】 有黑白两种颜色的正方体积木,把它摆成右图所示的形状,已知相邻(有公共面)的积木颜色不同,标A 的为黑色,图中共有黑色积木多少块?A【解析】 分层来看,如下图(切面平行于纸面)共有黑色积木17块.【巩固】这个图形,是否能够由112⨯⨯的长方体搭构而成?【解析】 每一个112⨯⨯的长方体无论怎么放,都包含了一个黑色正方体和一个白色正方体,而黑色积木有17块,白色积木有15块,所以该图形不能够由112⨯⨯的长方体搭构而成.【巩固】有许多相同的立方体,每个立方体的六个面上都写着同一个数字(不同的立方体可以写相同的数字)先将写着2的立方体与写着1的立方体的三个面相邻,再将写着3的立方体写着2的立方体相邻(见左下图).依这样构成右下图所示的立方体,它的六个面上的所有数字之和是多少?33223323322323111111【解析】 第一层如下图,第二层、第三层依次比上面一层每格都多1(见下图).765434565第三层654323454第二层第一层343212345上面的9个数之和是27,由对称性知,上面、前面、右面的所有数之和都是27.同理,下面的9个数之和是45,下面、左面、后面的所有数之和都是45.所以六个面上所有数之和是(2745)3216+⨯=.【例 18】 (05年武汉明心杯数学挑战赛)如图所示,一个555⨯⨯的立方体,在一个方向上开有115⨯⨯的孔,在另一个方向上开有215⨯⨯的孔,在第三个方向上开有315⨯⨯的孔,剩余部分的体积是多少?表面积为多少?【解析】 求体积:开了315⨯⨯的孔,挖去31515⨯⨯=,开了115⨯⨯的孔, 挖去11514⨯⨯-=;开了215⨯⨯的孔, 挖去215(22)6⨯⨯-+=,剩余部分的体积是:555(1546)100⨯⨯-++=.(另解)将整个图形切片,如果切面平行于纸面,那么五个切片分别如图:得到总体积为:22412100⨯+=. 求表面积:表面积可以看成外部和内部两部分.外部的表面积为55612138⨯⨯-=,内部的面积可以分为前 后、左右、上下三个方向,面积分别为()22515121320⨯⨯+⨯-⨯-⨯=、 ()2153513132⨯⨯+⨯-⨯-=、()2151511214⨯⨯+⨯-⨯-=,所以总的表面积为 138203214204+++=.(另解)运用类似于三视图的方法,记录每一方向上的不同位置上的裸露正方形个数: 前后方向:32上下方向:30 左右方向:40总表面积为()2323040204⨯++=.【总结】“切片法”:全面打洞(例如本题,五层一样),挖块成线(例如本题,在前一层的基础上,一条线一条线地挖),这里体现的思想方法是:化整为零,有序思考!【巩固】(2008年香港保良局第12届小学数学世界邀请赛)如图,原来的大正方体是由125个小正方体所构成的.其中有些小正方体已经被挖除,图中涂黑色的部分就是贯穿整个大正方体的挖除部分.请问剩下的部分共有多少个小正方体?第8题【解析】对于这一类从立体图形中间挖掉一部分后再求体积(或小正方体数目)的题目一般可以采用“切片法”来做,所谓“切片法”,就是把整个立体图形切成一片一片的(或一层一层的),然后分别计算每一片或每一层的体积或小正方体数目,最后再把它们相加.采用切片法,俯视第一层到第五层的图形依次如下,其中黑色部分表示挖除掉的部分.第1层第2层第3层第4层第5层从图中可以看出,第1、2、3、4、5层剩下的小正方体分别有22个、11个、11个、6个、22个,所以总共还剩下22111162272++++=(个)小正方体.【巩固】一个由125个同样的小正方体组成的大正方体,从这个大正方体中抽出若干个小正方体,把大正方体中相对的两面打通,右图就是抽空的状态.右图中剩下的小正方体有多少个?【解析】解法一:(用“容斥原理”来解)由正面图形抽出的小正方体有5525⨯=个,由侧面图形抽出的小正方体有5525⨯=个,由底面图形抽出的小正方体有4520⨯=个,正面图形和侧面图形重合抽出的小正方体有1221228⨯+⨯+⨯=个,正面图形和底面图形重合抽出的小正方体有13227⨯+⨯=个,底面图形和侧面图形重合抽出的小正方体有1211227⨯+⨯+⨯=个,三个面的图形共同重合抽出的小正方体有4个.根据容斥原理,252520877452++---+=,所以共抽出了52个小正方体.1255273-=,所以右图中剩下的小正方体有73个.注意这里的三者共同抽出的小正方体是4个,必须知道是哪4块,这是最让人头疼的事.但你可以先构造空的两个方向上共同部分的模型,再由第三个方向来穿过“花墙”. 这里,化虚为实的思想方法很重要. 解法二:(用“切片法”来解) 可以从上到下切五层,得: ⑴从上到下五层,如图:⑵或者,从右到左五片,如图:请注意这里的挖空的技巧是:先认一种方向.比如:从上到下的每一层,首先都应该有第一层的空四块的情况,即——如果挖第二层:第(1)步,把中间这些位置的四块挖走如图:第(2)步,把从右向左的两块成线地挖走.(请注意挖通的效果就是成线挖去),如图:第(3)步,把从前向后的一块(请注意跟第二层有关的只是一块!)挖成线!如图:【例 19】 (2009年迎春杯高年级组复赛)右图中的⑴⑵⑶⑷是同样的小等边三角形,⑸⑹也是等边三角形且边长为⑴的2倍,⑺⑻⑼⑽是同样的等腰直角三角形,⑾是正方形.那么,以⑸⑹⑺⑻⑼⑽⑾为平面展开图的立体图形的体积是以⑴⑵⑶⑷为平面展开图的立体图形体积的 倍.⑷⑶⑵⑴ ⑾⑽⑼⑻⑺⑹⑸【解析】 本题中的两个图都是立体图形的平面展开图,将它们还原成立体图形,可得到如下两图:其中左图是以⑴⑵⑶⑷为平面展开图的立体图形,是一个四个面都是正三角形的正四面体,右图以⑸⑹⑺⑻⑼⑽⑾为平面展开图的立体图形,是一个不规则图形,底面是⑾,四个侧面是⑺⑻⑼⑽,两个斜面是⑸⑹.对于这两个立体图形的体积,可以采用套模法来求,也就是对于这种我们不熟悉的立体图形,用一些我们熟悉的基本立体图形来套,看看它们与基本立体图形相比,缺少了哪些部分.由于左图四个面都是正三角形,右图底面是正方形,侧面是等腰直角三角形,想到都用正方体来套. 对于左图来说,相当于由一个正方体切去4个角后得到(如下左图,切去1ABDA 、1CBDC 、111D AC D 、111B AC B );而对于右图来说,相当于由一个正方体切去2个角后得到(如下右图,切去1BACB 、1DACD ).D 1C 1B 1A 1D CBAABCDA 1B 1C 1D 1假设左图中的立方体的棱长为a ,右图中的立方体的棱长为b ,则以⑴⑵⑶⑷为平面展开图的立体图形的体积为:3231114233a a a a -⨯⨯⨯=,以⑸⑹⑺⑻⑼⑽⑾为平面展开图的立体图形的体积为3231122233b b b b -⨯⨯⨯=.由于右图中的立方体的棱长即是题中正方形⑾的边长,而左图中的立方体的每一个面的对角线恰好是正三角形⑴的边长,通过将等腰直角三角形⑺分成4个相同的小等腰直角三角形可以得到右图中的立方体的棱长是左图中的立方体的棱长的2倍,即2b a =.那么以⑴⑵⑶⑷为平面展开图的立体图形的体积与以⑸⑹⑺⑻⑼⑽⑾为平面展开图的立体图形的体积的比为:()33331212::21:163333a b a a =⨯=,也就是说以⑸⑹⑺⑻⑼⑽⑾为平面展开图的立体图形的体积是以⑴⑵⑶⑷为平面展开图的立体图形体积的16倍.【例 20】 图⑴和图⑵是以正方形和等边三角形为面的立体图形的展开图,图中所有的边长都相同.请问:图⑴能围起来的立体图形的体积是图⑵能围起来的立体图形的体积的几倍?图⑴ 图⑵ 【解析】 首先,我们把展开图折成立体图形,见下列示意图:图⑴ 图⑵对于这类题目,一般采用“套模法”,即用一个我们熟悉的基本立体图形来套,这样做基于两点考虑,一是如果有类似的模型,可以直接应用其计算公式;二是如果可以补上一块或者放到某个模型里面,那么可以从这个模型入手.我们把图⑴中的立体图形切成两半,再转一转,正好放进去!我们看到图⑴与图⑶的图形位置的微妙关系:1和图3一致!60°图⑶ 图⑷由图⑷可见,图⑴这个立体的体积与图⑶这个被切去了8个角后的立体图形的体积相等.假设立方体的1条边的长度是1,那么一个角的体积是1111112222348⨯⨯⨯⨯=,所以切掉8个角后的体积是1518486-⨯=.再看图⑵中的正四面体,这个正四面体的棱长与图⑶中的每一条实线线段相等,所以应该用边长为12的立方体来套.如果把图⑵的立体图形放入边长为12的立方体里的话是可以放进去的.12这是切去了四个角后的图形,从上面的分析可知一个角的体积为148,所以图⑵的体积是:1111142224824⨯⨯-⨯=,那么前者的体积是后者的5120624÷=倍.【例 21】 如图,用高都是1米,底面半径分别为1.5米、1米和0.5米的3个圆柱组成一个物体.问这个物体的表面积是多少平方米?(π取3.14)1110.511.5【解析】 从上面看到图形是右上图,所以上下底面积和为22 3.14 1.514.13⨯⨯=(立方米),侧面积为2 3.14(0.51 1.5)118.84⨯⨯++⨯=(立方米),所以该物体的表面积是14.1318.8432.97+=(立方米).【例 22】 有一个圆柱体的零件,高10厘米,底面直径是6厘米,零件的一端有一个圆柱形的圆孔,圆孔的直径是4厘米,孔深5厘米(见右图).如果将这个零件接触空气的部分涂上防锈漆,那么一共要涂多少平方厘米?【解析】 涂漆的面积等于大圆柱表面积与小圆柱侧面积之和,为266π10π()24π560π18π20π98π307.722⨯+⨯⨯+⨯=++==(平方厘米).【例 23】 (第四届希望杯2试试题)圆柱体的侧面展开,放平,是边长分别为10厘米和12厘米的长方形,那么这个圆柱体的体积是________立方厘米.(结果用π表示)【解析】 当圆柱的高是12厘米时体积为210300π()122ππ⨯⨯=(立方厘米)当圆柱的高是12厘米时体积为212360π()102ππ⨯⨯=(立方厘米).所以圆柱体的体积为300π立方厘米或360π立方厘米.。
立体几何知识点归纳

一、立体几何知识点归纳 第一章 空间几何体(一)空间几何体的结构特征(1)多面体——由若干个平面多边形围成的几何体.围成多面体的各个多边形叫叫做多面体的面,相邻两个面的公共边叫做多面体的棱,棱与棱的公共点叫做顶点。
旋转体——把一个平面图形绕它所在平面内的一条定直线旋转形成的封闭几何体。
其中,这条定直线称为旋转体的轴。
(2)柱,锥,球的结构特征 1.棱柱1.1棱柱——有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱。
1.2相关棱柱几何体系列(棱柱、斜棱柱、直棱柱、正棱柱)的关系:①⎧⎪⎧−−−−−→⎨⎪−−−−−→⎨⎪⎪⎩底面是正多形棱垂直于底面斜棱柱棱柱正棱柱直棱柱其他棱柱 底面为矩形侧棱与底面边长相等1.3①侧棱都相等,侧面是平行四边形;②两个底面与平行于底面的截面是全等的多边形; ③过不相邻的两条侧棱的截面是平行四边形;④直棱柱的侧棱长与高相等,侧面与对角面是矩形。
1.4长方体的性质:①长方体一条对角线长的平方等于一个顶点上三条棱的平方和;【如图】222211AC AB AD AA =++②(了解)长方体的一条对角线1AC 与过顶点A 的三条棱所成的角分别是αβγ,,,那么222cos cos cos 1αβγ++=,222sin sin sin 2αβγ++=;③(了解)长方体的一条对角线1AC 与过顶点A 的相邻三个面所成的角分别是αβγ,,,则222coscos cos 2αβγ++=,222sin sin sin 1αβγ++=.1.5侧面展开图:正n 棱柱的侧面展开图是由n 个全等矩形组成的以底面周长和侧棱长为邻边的矩形.1.6面积、体积公式:2S c hS c h S S h=⋅=⋅+=⋅直棱柱侧直棱柱全底棱柱底,V (其中c 为底面周长,h为棱柱的高) 2.圆柱2.1圆柱——以矩形的一边所在的直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体叫圆柱. 2.2圆柱的性质:上、下底及平行于底面的截面都是等圆;过轴的截面(轴截面)是全等的矩形. 2.3侧面展开图:圆柱的侧面展开图是以底面周长和母线长为邻边的矩形. 2.4面积、体积公式:S 圆柱侧=2rh π;S 圆柱全=222rh r ππ+,V 圆柱=S 底h=2r h π(其中r 为底面半径,h 为圆柱高) 3.棱锥3.1棱锥——有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥。
数学思维导引-六年级-立体几何 (5)

(2)如果沿经过中轴线 AB 的平面切一刀,将该蛋糕分成完全相同的两部分,那表面积 之和又是多少?
【分析】 (1) 蛋糕的表面积为:
2 π1 2
1
2 π1 1
2π3 2
1
2
π23
2
10.5
π32.97
(平方分米)
(2)
新切一刀,表面积增加了
2
2
1 2
2
1
2
3 2
12
,则现在的表面积变为
44.97
【分析】 (1)每一次拼合会少两个面,拼了 3 次,表面积之和少了 32 1 6 平方厘米; (2)原正方体的表面积为 6 1 6 ,且一刀会增加两个面,增加的面积为 2,则两部分的表
面积之和为 8;根据图 2,总共切了 5 刀,表面积增加了 10,则这 18 块长方体的表面积 总和为 16。 (第四届华杯赛初赛第 3 题) 7、如图所示,有一个圆柱和一个圆锥,它们的高和底面直径标在图上,单位是厘米。请问:
超越篇
1、有一个棱长为 20 的大立方体,在它的每个角上按如图所示的方式各做一个小立方体, 于是得到 8 个小立方体。在这些立方体中,上面 4 个的棱长为 12,下面 4 个的棱长为 13。请问:所有这 8 个小立方体公共部分的体积是多少?
【分析】上面四个立方体的公共部分是一个长方体,其底面积为一个正方形,底面边长为
7、一个无盖木盒从外面量时,其长、宽、高分别为 10 厘米、8 厘米、5 厘米。已知木板厚 1 厘米,那么做一个木盒,需要这样的木板多少平方厘米?这个木盒的容积又是多少?
【分析】由于此无盖木盒的外部体积为 810 5 400 立方厘米,而木盒的容积为192 立方
厘米。则根据题意,可知需要这样的木板 400 1921208 立方厘米。
2023-2024学年六年级下学期数学图形与几何《立体图形》(教案)

2023-2024学年六年级下学期数学图形与几何《立体图形》(教案)教学内容本节课是六年级下学期数学图形与几何的教学内容,主题是《立体图形》。
通过本节课的学习,学生将了解立体图形的基本概念,掌握立体图形的分类、性质和计算方法,并能运用所学知识解决实际问题。
教学目标1. 让学生掌握立体图形的基本概念,包括点、线、面、体等。
2. 让学生了解立体图形的分类,包括柱体、球体、锥体等。
3. 让学生掌握立体图形的性质,包括表面积、体积等。
4. 让学生掌握立体图形的计算方法,包括表面积、体积的计算等。
5. 培养学生的空间想象能力和逻辑思维能力。
教学难点1. 立体图形的概念和分类。
2. 立体图形的性质和计算方法。
3. 空间想象能力和逻辑思维能力的培养。
教具学具准备1. 立体图形模型或图片。
2. 教学PPT或黑板。
3. 计算器。
4. 练习题或试卷。
教学过程1. 引入:通过展示一些生活中的立体图形,引起学生的兴趣,让学生初步感知立体图形的概念。
2. 讲解:讲解立体图形的基本概念、分类、性质和计算方法,通过示例和练习,让学生掌握所学知识。
3. 练习:让学生做一些练习题,巩固所学知识,提高学生的应用能力。
4. 应用:让学生解决一些实际问题,培养学生的解决问题的能力。
5. 总结:总结本节课所学知识,让学生明确自己的学习目标。
板书设计1. 立体图形2. 内容:- 立体图形的概念- 立体图形的分类- 立体图形的性质- 立体图形的计算方法作业设计1. 基础练习:让学生做一些基础题,巩固所学知识。
2. 提高练习:让学生做一些提高题,培养学生的空间想象能力和逻辑思维能力。
3. 应用练习:让学生解决一些实际问题,培养学生的解决问题的能力。
课后反思本节课通过讲解、练习和应用,让学生掌握了立体图形的基本概念、分类、性质和计算方法,提高了学生的空间想象能力和逻辑思维能力。
但在教学过程中,也发现了一些问题,如学生对立体图形的概念理解不够深入,计算方法掌握不够熟练等。
立体几何初步知识点全总结

立体几何初步知识点全总结一、空间几何体的结构。
1. 棱柱。
- 定义:有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱。
- 分类:- 按底面多边形的边数分为三棱柱、四棱柱、五棱柱等。
- 直棱柱:侧棱垂直于底面的棱柱。
正棱柱:底面是正多边形的直棱柱。
- 性质:- 侧棱都相等,侧面是平行四边形。
- 两个底面与平行于底面的截面是全等的多边形。
- 过不相邻的两条侧棱的截面(对角面)是平行四边形。
2. 棱锥。
- 定义:有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的多面体叫做棱锥。
- 分类:- 按底面多边形的边数分为三棱锥、四棱锥、五棱锥等。
- 正棱锥:底面是正多边形,且顶点在底面的射影是底面正多边形的中心的棱锥。
- 性质:- 正棱锥各侧棱相等,各侧面都是全等的等腰三角形,各等腰三角形底边上的高相等(它叫做正棱锥的斜高)。
- 棱锥的高、斜高和斜高在底面上的射影组成一个直角三角形;棱锥的高、侧棱和侧棱在底面上的射影也组成一个直角三角形。
3. 棱台。
- 定义:用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分叫做棱台。
- 分类:由三棱锥、四棱锥、五棱锥等截得的棱台分别叫做三棱台、四棱台、五棱台等。
- 性质:- 棱台的各侧棱延长后交于一点。
- 棱台的上下底面是相似多边形,侧面是梯形。
4. 圆柱。
- 定义:以矩形的一边所在直线为轴旋转,其余三边旋转所成的曲面所围成的几何体叫做圆柱。
- 性质:- 圆柱的轴截面是矩形。
- 平行于底面的截面是与底面全等的圆。
5. 圆锥。
- 定义:以直角三角形的一条直角边所在直线为轴旋转,其余两边旋转所成的曲面所围成的几何体叫做圆锥。
- 性质:- 圆锥的轴截面是等腰三角形。
- 平行于底面的截面是圆,截面半径与底面半径之比等于顶点到截面距离与圆锥高之比。
6. 圆台。
- 定义:用一个平行于圆锥底面的平面去截圆锥,底面与截面之间的部分叫做圆台。
立体几何知识点和例题(含有答案)

【考点梳理】一、考试内容1.平面。
平面的基本性质。
平面图形直观图的画法。
2.两条直线的位置关系。
平行于同一条直线的两条直线互相平行。
对应边分别平行的角。
异面直线所成的角。
两条异面直线互相垂直的概念。
异面直线的公垂线及距离。
3.直线和平面的位置关系。
直线和平面平行的判定与性质。
直线和平面垂直的判定与性质。
点到平面的距离。
斜线在平面上的射影。
直线和平面所成的角。
三垂线定理及其逆定理。
4.两个平面的位置关系。
平面平行的判定与性质。
平行平面间的距离。
二面角及其平面角。
两个平面垂直的判定与性质。
二、考试要求1.掌握平面的基本性质,空间两条直线、直线与平面、平面与平面的位置关系(特别是平行和垂直关系)以及它们所成的角与距离的概念。
对于异面直线的距离,只要求会计算已给出公垂线时的距离。
2.能运用上述概念以及有关两条直线、直线和平面、两个平面的平行和垂直关系的性质与判定,进行论证和解决有关问题。
对于异面直线上两点的距离公式不要求记忆。
3.会用斜二测画法画水平放置的平面图形(特别是正三角形、正四边形、正五边形、正六边形)的直观图。
能够画出空间两条直线、两个平面、直线和平面的各种位置关系的图形,能够根据图形想象它们的位置关系。
4.理解用反证法证明命题的思路,会用反证法证明一些简单的问题。
三、考点简析1.空间元素的位置关系2.平行、垂直位置关系的转化3.空间元素间的数量关系(1)角①相交直线所成的角;②异面直线所成的角——转化为相交直线所成的角;③直线与平面所成的角——斜线与斜线在平面内射影所成的角;④二面角——用二面角的平面角来度量。
(2)距离①两点之间的距离——连接两点的线段长;②点线距离——点到垂足的距离;③点面距离——点到垂足的距离;④平行线间的距离——平行线上一点到另一直线的距离;⑤异面直线间的距离——公垂线在两条异面直线间的线段长;⑥线面距离——平行线上一点到平面的距离;⑦面面距离——平面上一点到另一平面的距离;⑧球面上两点距离——球面上经过两点的大圆中的劣弧的长度。
六年级数学第5讲: 立体几何

目录第5讲立体几何 (1)兴趣篇 (1)拓展篇 (6)超越篇 (10)第5讲立体几何兴趣篇1.一个长方体的长、宽、高分别为3厘米、2厘米、1厘米。
若它的棱长总和等于另一个正方体的棱长总和,则长方体与正方体的表面积之比是多少?长方体体积比正方体体积少多少立方厘米?÷=;【分析】该长方体的棱长总和为:()++⨯=;则正方体的边长为24122321424长方体的表面积为:()⨯+⨯+⨯⨯=,体积为:3216323121222⨯⨯=;正方体的表面积为:62224⨯⨯=⨯⨯=;体积为:2228所以长方体与正方体的表面积之比为:11:12,长方体的体积比正方体的体积少2立方厘米。
2.如图所示,将长为13厘米,宽为9厘米的长方形硬纸板的四角去掉边长为2厘米的正方形,然后沿虚线折叠成长方体容器。
这个容器的体积是多少立方厘米?如果四角去掉边长为3厘米的正方形呢?【分析】四个角都截去边长为2的正方形之后,长方体容器的长为1349-=,-=;宽为945其体积为95290⨯⨯=(立方厘米)。
如果四个角去的都是边长为3的正方形,则新形成的长方体的长为1367-=,-=,宽为963高为3,则新长方体的体积为73363⨯⨯=(立方厘米)。
3.用棱长是1厘米的小立方体拼成如图所示的立体图形。
这个图形的表面积是多少平方厘米?【分析】三视图法:从前往后看:7214⨯=;从左往右看:7214⨯=;从上往下看:9218⨯=;则这个图形的表面积为:14141846++=(平方厘米)。
4.(1)如图所示,将一个棱长为6的正方体从某个角切掉一个长、宽、高分别为4、3、5的长方体,剩余部分的表面积是多少?(2)如图所示,将一个棱长为5的正方体,从左上方切去一个长、宽、高分别为5、4、3的长方体,它的表面积减少了百分之几?【分析】(1)切去该长方体之后,整个表面积没有发生变化,则其表面积总和还为原表面积,为666216⨯⨯=平方厘米。
人教版六年级数学下册第六单元图形的认识—立体图形

长方体
正方体
圆柱体
圆锥体
2厘米(高) 10厘米(长)
长方体的表面积=长×宽×2﹢长×高×2﹢宽×高×2 上 和下 前 和后 右 和左
0.7×0.5×2+0.7×0.4×2+0.5×0.4×2
长方体的表面积=(长×宽+长×高+高×宽)× 2
上(或下) 前(或后) 右(或左)
(0.7×0.5+0.7×0.4+0.5×0.4)×2
基本练习:
8、用铁丝做一个长10厘米,宽5厘米,高4厘米的长 方体框架,至少需要多长的铁丝?在这个长方体框 架外面糊一层纸,至少需要多少平方厘米的纸?
4 5
(1)求至少需要多长的铁丝? (10+5+4)×4=76 (厘米)
10
(2)求至少需要多少立方厘米的纸? (10×5+10×4+5×4)×2=220(平方厘米)
选择:
3、等高等体积的圆柱和圆锥,圆柱的底面积是6平
方厘米,那么圆锥的底面积是(
B )平方厘米。
A、6 C、2
B、18 D、36
选择:
4、把一个底面半径是2分米、高是3分米的圆柱形
容器中注满水,现垂直轻轻插入一根底面积是5平方分
米,高是4分米的方钢,溢出水的体积是(
A、20 B、15 C、20000
拓展练习:
1、把一根长30厘米的长方体木料锯成3段(如图),表面 积比原来增加了20平方厘米,这根木料原来的体积是多 少立方厘米?
20÷4=5(平方厘米) 30×5=150(平方厘米)
答:这根木材原来的体积是150平方厘米。
拓展练习:
2、一个底面是正方形的长方体,把它的侧面展开后 得到一个边长是12厘米的正方形。求这个长方体的体 积是多少?
小学六年级总复习之立体几何

一、习题精选。
1、一堆小麦堆成圆锥形,底面周长是18. 84米,高1.8米,这堆小麦的体积是()。
2、用边长为1分米的小正方体,拼成一个较大的正方体,至少需要()个这样的小正方体,把这些小正方体排成一行,它的长度是()分米。
3、一个圆柱体比和它等底等高的圆锥体体积大18立方厘米,那么圆柱体和圆锥体体积的和是()。
4、一根长3米,底面半径5厘米的圆柱形木料锯成两段,表面积增加()平方厘米或()平方厘米。
5、一个长方形长15厘米,宽10厘米,以长边为轴旋转一周,会得到一个圆柱形,它的表面积是()平方厘米,体积是()立方厘米。
6、一个用立方块搭成的立体图形,淘气从前面看到的图形是,从上面看是,那么搭成这样一个立体图形最少要()个小立方块。
7、一个半圆的周长是12.56厘米,将这个半圆扩大2倍,它的面积是()平方厘米。
8、把一个棱长是0.5米的正方体钢坯,锻成横截面面积是10平方分米的长方体钢材。
锻成的钢材长度为()。
9、把一个高为18厘米的圆锥形容器盛满水,将这些水全部倒入和这个圆锥形容器等底的圆柱形容器里,水的高度是()厘米。
二、判断题1、圆柱的体积相当于圆锥体积的3倍。
()2、一个圆柱体木料,把它加工成最大的圆锥体,削去的部分的体积和圆锥的体积比2:1. ()3、一个圆柱和圆锥等底等高,体积相差21立方厘米,圆锥的体积是7立方厘米()4、正方体的棱长缩小一半后,体积比原来少一半。
()5、一个长方体和一个圆柱,它们的体积和高都相等,那么,它们的底面积也相等。
()三、选择题。
1、甲圆柱形容器底面半径是乙圆柱形容器底面半径的2倍(容器直立放置)。
现以相同的流量同时向这两个容器内注入水,经过一定的时间,甲、乙两个容器内水面的高度的比是?(容器内的水都未加满) ()A.1∶2B.2∶1C.4∶1D.1∶42、.如果一个长方体的长、宽、高都扩大3倍,则它的体积扩大( )倍。
A.3B.9C.273、一个长方体油箱,里面长60厘米,宽50厘米,高40厘米,这个油箱可以装油()A.120升B. 12升C. 1.2升4、.把棱长2厘米的正方体木块装入长8厘米,宽6厘米,高3厘米的长方体盒子里,一共可以装( )块。
六年级数学专题思维训练—立体几何(含答案及解析)
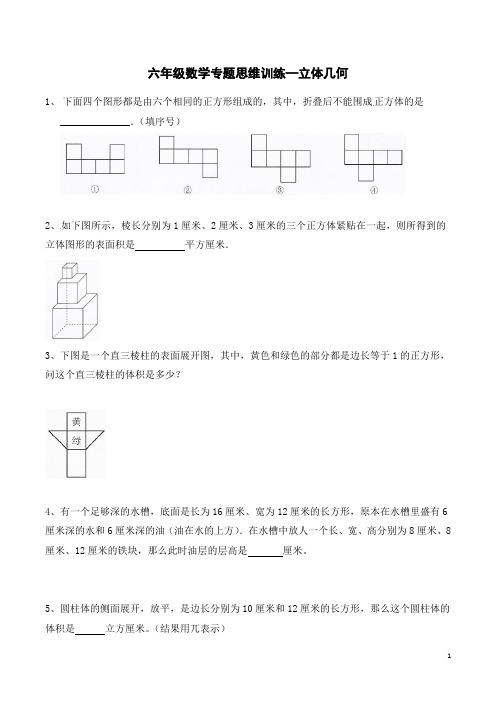
六年级数学专题思维训练—立体几何1、下面四个图形都是由六个相同的正方形组成的,其中,折叠后不能围成正方体的是______________.(填序号)2、如下图所示,棱长分别为1厘米、2厘米、3厘米的三个正方体紧贴在一起,则所得到的立体图形的表面积是平方厘米.3、下图是一个直三棱柱的表面展开图,其中,黄色和绿色的部分都是边长等于1的正方形,问这个直三棱柱的体积是多少?4、有一个足够深的水槽,底面是长为16厘米、宽为12厘米的长方形,原本在水槽里盛有6厘米深的水和6厘米深的油(油在水的上方).在水槽中放人一个长、宽、高分别为8厘米、8厘米、12厘米的铁块,那么此时油层的层高是厘米。
5、圆柱体的侧面展开,放平,是边长分别为10厘米和12厘米的长方形,那么这个圆柱体的体积是立方厘米。
(结果用兀表示)6、如下图所示,从正方形ABCD 上截去长方形DEFG ,其中AB=1厘米,DE=21厘米, DG=31厘米,将ABCGFE 以GC 边为轴旋转一周,所得几何体的表面积是 平方厘米,体积是 _____________ 立方厘米。
(结果用兀表示)7、若长方体的三个侧面的面积分别是6,8,12,则长方体的体积是 。
8、一个圆柱和一个圆锥(如下图所示),它们的高和底面直径都标在图上,单位是厘米。
请回答:圆锥体积与圆柱体积的比是多少?9、如下图所示,一个圆柱体形状的木棒,沿着底面直径竖直切成两部分,已知这两部分的表面积之和比圆柱体的表面积大2008平方厘米,则这个圆柱体木棒的侧面积是 平方厘米。
(兀取3. 14)10、两个同样材料做成的球A 和B ,一个实心,一个空心。
A 的直径为7、重量为22,B 的直径为10.6、重量为33.3。
问:哪个球是实心球?(球的体积公式V=34πr ³)11、铁路油罐车由两个半球面和一个圆柱面钢板焊接而成,尺寸如下图所示.问:该油罐车的容积是多少立方米?(兀=3. 1416)(球的体积公式V=34πr ³)12、某工厂原用长4米,宽1米的铁皮围成无底无顶的的正方体形状的围栏,现要将围栏容量增加27%,问:能否还用原来的铁皮围成?13、一个正方体的纸盒中,恰好能放人一个体积为6. 28立方厘米的圆柱体,纸盒的容积有多大?(兀=3. 14).14、用若干个小正方体拼成下图所示的造型.其中有一个小孔分别由左至右、由上至下以及由前至后穿透整个造型.拼成此造型共需使用多少个小正方体?15、一个圆锥形容器甲与一个半球形容器乙,它们圆形口的直径与容器的高的尺寸如下图所示,若用甲容器取水来注满乙容器,问:至少要注水多少次?(球的体积公式:V=34πr ³)16、下图是一个直圆柱形状的玻璃杯,一个长为12厘米的直棒状细吸管(不考虑吸管粗细)放在玻璃杯内,当吸管一端接触圆柱下底面时,另一端沿吸管最少可露出上底面边缘2厘米,最多能露出4厘米.则这个玻璃杯的容积为立方厘米.(取兀=3. 14)17、威力集团生产的某种洗衣机的外形是长方体,装衣物部分是圆柱形的桶,直径40厘米,深36厘米,已知该洗衣机装衣物的空间占洗衣机体积的25% ,长方体外形的长为52厘米,宽50厘米.问:高是多少厘米?(兀取3. 14,结果保留整数)18、有两个高度一样的水瓶,瓶子的底部被钉子分别戳了一个同样大的小洞.粗瓶子的水12分钟可以漏完,细瓶子的水8分钟可以漏完.若两个瓶子同时漏水,过了一段时间后,粗瓶子中水的高度是细瓶子中的2倍.这两个瓶子同时漏了分钟.19、世界上最早的灯塔建于公元270年,塔分三层,如下图所示,每层都高27米,底座呈正四棱柱,中间呈正八棱柱,上部呈正圆锥.上部的体积是底座的体积的 。
六年级火箭班第八讲------立体几何
六年级火箭班第八讲------立体几何复习:一个长方体的长是25厘米,宽是20厘米,高是18厘米,最大的面的长是()厘米,宽是()厘米,它的面积是()平方厘米;最小的面长是()厘米,宽是()厘米,它的面积是()平方厘米。
精选例题:表面积之一---图形的切割与拼接(图形的组合)【例1】把一个长宽高分别是7cm,6cm,5cm的长方体截成两个长方体,使这两个长方体的表面积之和最大,这时表面积之和是多少?【例2】一个长为5分米,宽3分米,高4分米的长方体,沿垂直长的方向切三刀,沿垂直宽的方向切两刀,沿垂直高的方向切一刀,共得到24块小长方体,则这24块小长方体的表面积的和为多少平方分米?表面积之二---对图形进行挖洞拿掉一个以后,表面积如何变化:【例3】在边长为4厘米的正方体木块的每个面中心打一个边与正方体的边平行的洞.洞口是边长为1厘米的正方形,洞深1厘米(如下图).求挖洞后木块的表面积.练习:在一棱长为5厘米的正方体右上方截去一个棱长分别是3厘米,2厘米和2厘米的长方体,剩下部分的表面积是多少平方厘米?【例4】有一个长方体形状的零件。
中间挖去一个正方体的孔(如下图)。
你能算出它的表面积吗?(单位:厘米)表面积之三---对图形进行染色【例5】一个正方体的棱长是3厘米,表面涂满了红漆,把它切成棱长为1厘米的小正方体若干块,问:在这些小正方体中,三面涂有红色的有多少块?两面涂有红色的有多少块?一面涂有红色的有多少块?六个面都没有涂上红色的有多少块?练习1:若是将正方体的棱长改为4呢,答案又是多少呢?练习2:一个大长方体由若干个小正方体组成,在达正方体表面涂色,其中一面涂色的小正方体有1014个,这个大正方体有多少个小正方体组成?【例6】将一个长6厘米,宽4厘米,高3厘米的长方体的六个面都涂上红色,然后把这个长方体切割成一个个边长为1厘米的小正方体,这些小正方体中恰好有两个面涂上红色的有多少个?表面积之四---求组合立体图形的表面积【例7】一个零件形状大小如下图:算一算,它的表面积是多少平方厘米。
小学六年级奥数--立体几何综合

学科培优 数学立体几何综合学生姓名 授课日期 教师姓名授课时长知识定位本讲复习已经学过的立体图形的相关知识和解题技巧,主要有:长方体、立方体、圆柱、圆锥的体积及表面积求解,立体几何计数及多面体顶点与棱以及表面的关系。
重难点在于:1.不规则立体图形的表面积或体积求解2.多面体的顶点与棱数计数 3.体积的等量代换主要的考点:1.规则立体图形的表面积(侧面积)与体积计算2.不规则立体图形的表面积与体积计算 3.染色问题4.立体图形的三视图与展开图知识梳理主要知识点 立体几何⑴规则立体图形的表面积和体积公式长方体:体积:长宽高 表面积:(长宽+宽高+长高) 立方体:体积:棱长的立方 表面积:棱长的平方6 圆柱: 体积:2r h π 侧面积:2rh π 圆锥: 体积:213r h π⑵不规则立体图形的表面积整体观照法⑶体积的等积变形①水中浸放物体:V 升水=V 物 ②测啤酒瓶容积:V=V 空气+V 水⑷三视图与展开图最短线路与展开图形状问题⑸染色问题几面染色的块数与“芯”、棱长、顶点、面数的关系。
例题精讲【试题来源】【题目】一个长方体的表面积是33.66平方分米,其中一个面的长是2.3分米,宽是2.1分米,它的体积是_____立方分米.【试题来源】 【题目】右图是一个棱长为2厘米的正方体,在正方体上面的正中向下挖一个棱长为1厘米的正方形小洞;接着在小洞的底面正中再挖一个棱长为21厘米的小洞;第三个小洞的挖法与前两个相同,棱长为41厘米.那么最后得到的立体图形的表面积是 平方厘米【试题来源】【题目】把一个长25厘米,宽10厘米,高4厘米的长方体木块锯成若干个大小相等的正方体,然后拼成一个大的正方体.这个大正方体的表面积是_____平方厘米。
【试题来源】【题目】右图是3层没有缝隙的小立方块组成的.如果它的外表面(包括底面)全都被涂成红色,那么把它们再分开成一个个小立方块时,有多少个小立方块恰有三面是红色的?【试题来源】【题目】一个正方体木块,棱长是15.从它的八个顶点处各截去棱长分别是1、2、3、4、5、6、7、8的小正方体.这个木块剩下部分的表面积最少是( ).【试题来源】【题目】把一根长2.4米的长方体木料锯成5段(如图),表面积比原来增加了96平方厘米.这根木料原来的体积是_____立方厘米.【试题来源】【题目】用棱长是1厘米的立方体拼成右图所示的立体图形.求这个立体图形的表面积.【试题来源】【题目】把1个棱长是3厘米的正方体分割成若干个小的正方体,这些小正方体的棱长必须是整厘米数.如果这些小正方体的体积不要求都相等,那么最少可分割成个小正方体.【试题来源】【题目】用10块长7厘米,宽5厘米,高3厘米的长方体积木堆成一个长方体,这个长方体的表面积最小是多少?【试题来源】【题目】一个盛有水的圆柱形容器,底面内半径为5厘米,深20厘米,水深15厘米.今将一个底面半径为2厘米,高为17厘米的铁圆柱垂直放人容器中.求这时容器的水深是多少厘米?【试题来源】【题目】有甲、乙两只圆柱形玻璃杯,其内直径依次是10厘米、20厘米,杯中盛有适量的水.甲杯中沉没着一铁块,当取出此铁块后,甲杯中的水位下降了2厘米;然后将铁块沉没于乙杯,且乙杯中的水未外溢.问:这时乙杯中的水位上升了多少厘米?【试题来源】【题目】将高都是1米,底面半径分别为1.5米、1米和0.5米的三个圆柱组成一个物体.求这个物体的表面积.【试题来源】【题目】这里有一个圆柱和一个圆锥(下图),它们的高和底面直径都标在图上,单位是厘米.请回答:圆锥体积与圆柱体积的比是多少?【试题来源】【题目】一个长、宽、高分别为21厘米、15厘米、12厘米的长方体.现从它的上面尽可能大的切下一个正方体.然后从剩余的部分再尽可能大的切下一个正方体.最后再从第二次剩余的部分尽可能大的切下一个正方体.剩下的体积是平方厘米.【试题来源】【题目】一个圆柱形玻璃杯内盛有水,水面高2.5厘米,玻璃杯内侧的底面积是72平方厘米.在这个杯中放进棱长6厘米的正方体铁块后,水面没有淹没铁块.这时水面高多少厘米?【试题来源】【题目】图1是下面的表面展开图①甲正方体;②乙正方体;③丙正方体;④甲正方体或丙正方体.【试题来源】【题目】如图,剪一块硬纸片可以做成一个多面体的纸模型(沿虚线折,沿实线粘).这个多面体的面数、顶点数和棱数的总和是多少?【试题来源】【题目】下面是一辆汽车模型纸工平面展开图,中轴线上面的一半标出了尺寸.将该图剪下折叠粘合(相同字母标记处粘合在一起)做成汽车模型的体积为V .请回答:①403<v<445②473<V<500,哪一个正确,为什么?【试题来源】【题目】现有一张长40厘米、宽20厘米的长方形铁皮,请你用它做一只深是5厘米的长方体无盖铁皮盒(焊接处及铁皮厚度不计,容积越大越好),你做出的铁皮盒容积是多少立方厘米?【试题来源】【题目】如图,在一个立方体的两对侧面的中心各打通一个长方体的洞在上下侧面的中心打通一个圆柱形的洞,已知立方体边长为10厘米,侧面上的洞口是边长为4厘米的正方形,上下侧面的洞口是直径为4厘米的圆,求该立方体的表面积和体积(取 =3.14).【试题来源】【题目】用大小相等的无色透明玻璃小正方体和红色玻璃小正方体拼成一个大正方体ABCD —1A 1B 1C 1D (如图),大正方体内的对角线A 1C ,B 1D ,C 1A ,D 1B 所穿的小正方体都是红色玻璃小正方体,其它部分都是无色透明玻璃小正方体,小红正方体共用了401个,问:无色透明小正方体用了多少个?习题演练【试题来源】【题目】一个长方体的各条棱长的和是48厘米,并且它的长是宽的2倍,高与宽相等,那么这个长方体的体积是______ 立方厘米【试题来源】【题目】右图是一个表面被涂上红色的棱长为lO厘米的正方体木块,如果把它沿虚线切成8个正方体,这些小正方体中没有被涂上红色的所有表面的面积和是_____平方厘米【试题来源】【题目】张大爷去年用长2米、宽1米的长方形苇席围成容积最大的圆柱形粮囤.今年改用了长3米、宽2米的长方形苇席围成容积最大的圆柱形粮囤.问:今年粮囤的容积是去年粮囤容积的多少倍?【试题来源】【题目】把一个大长方体木块表面上涂满红色后,分割成若干个同样大小的小长方体,其中只有两个面涂上红色的小长方体恰好是12块.那么至少要把这个大长方体分割成个小长方体.【试题来源】【题目】六个立方体A、B、C、D、E、F的可见部分如下图,下边是其中一个立体的侧面展开图,那么它是立方体____的侧面展开图.2。
六年级奥数-第五讲[1].几何-立体部分.教师版
![六年级奥数-第五讲[1].几何-立体部分.教师版](https://img.taocdn.com/s3/m/5cb2b3cf7c1cfad6195fa796.png)
第五讲 几何——立体部分教学目标:对于小学几何而言,立体图形的表面积和体积计算,既可以很好地考查学生的空间想象能力,又可以具体考查学生在公式应用中处理相关数据的能力,所以,很多重要考试都很重视对立体图形的考查.知识点拨:一、长方体和正方体如右图,长方体共有六个面(每个面都是长方形),八个顶点,十二条棱.c b aHGFED CBA①在六个面中,两个对面是全等的,即三组对面两两全等. (叠放在一起能够完全重合的两个图形称为全等图形.) ②长方体的表面积和体积的计算公式是: 长方体的表面积:2()S ab bc ca =++长方体; 长方体的体积:V abc =长方体.③正方体是各棱相等的长方体,它是长方体的特例,它的六个面都是正方形. 如果它的棱长为a ,那么:26S a =正方体,3V a =正方体.二、圆柱与圆锥【解析】我们从三个方向(前后、左右、上下)考虑,新几何体的表面积仍为原立方体的表面积:10⨯10⨯6=600.【例2】右图是一个边长为4厘米的正方体,分别在前后、左右、上下各面的中心位置挖去一个边长l厘米的正方体,做成一种玩具.它的表面积是多少平方厘米?(图中只画出了前面、右面、上面挖去的正方体)【解析】原正方体的表面积是4⨯4⨯6=96(平方厘米).每一个面被挖去一个边长是1厘米的正方形,同时又增加了5个边长是1厘米的正方体作为玩具的表面积的组成部分.总的来看,每一个面都增加了4个边长是1厘米的正方形.从而,它的表面积是:96+4⨯6=120平方厘米.【巩固】在一个棱长为50厘米的正方体木块,在它的八个角上各挖去一个棱长为5厘米的小正方体,问剩下的立体图形的表面积是多少?【解析】对于和长方体相关的立体图形表面积,一般从上下、左右、前后3个方向考虑.变化前后的表面积不变:50⨯50⨯6=15000(平方厘米).【例3】下图是一个棱长为2厘米的正方体,在正方体上表面的正中,向下挖一个棱长为1厘米的正方体小洞,接着在小洞的底面正中向下挖一个棱长为12厘米的正方形小洞,第三个正方形小洞的挖法和前两个相同为14厘米,那么最后得到的立体图形的表面积是多少平方厘米?【解析】我们仍然从3个方向考虑.平行于上下表面的各面面积之和:2⨯2⨯2=8(平方厘米);左右方向、前后方向:2⨯2⨯4=16(平方厘米),1⨯1⨯4=4(平方厘米),12⨯12⨯4=1(平方厘米),1 4⨯14⨯4=14(平方厘米),这个立体图形的表面积为:816++4+1+14=1294(平方厘米).【例4】一个正方体木块,棱长是1米,沿着水平方向将它锯成2片,每片又锯成3长条,每条又锯成4小块,共得到大大小小的长方体24块,那么这24块长方体的表面积之和是多少?【解析】锯一次增加两个面,锯的总次数转化为增加的面数的公式为:锯的总次数⨯2=增加的面数.原正方体表面积:1⨯1⨯6=6(平方米),一共锯了(2-1)+(3-1)+(4-1)=6次,6+1⨯1⨯2⨯6=18(平方米).【巩固】(2008年走美六年级初赛)一个表面积为256cm的长方体如图切成27个小长方体,这27个小长方体表面积的和是2cm.【解析】每一刀增加两个切面,增加的表面积等于与切面平行的两个表面积,所以每个方向切两刀后,表面积增加到原来的3倍,即表面积的和为2563168(cm)⨯=.【例5】如图,25块边长为1的正方体积木拼成一个几何体,表面积最小是多少?25块积木【解析】当小积木互相重合的面最多时表面积最小.设想27块边长为1的正方形积木,当拼成一个333⨯⨯的正方体时,表面积最小,现在要去掉2块小积木,只有在两个角上各去掉一块小积木,或在同一个角去掉两块相邻的积木时,表面积不会增加,该几何体表面积为54.【例6】要把12件同样的长a、宽b、高h的长方体物品拼装成一件大的长方体,使打包后表面积最小,该如何打包?⑴当b=2h时,如何打包?⑵当b<2h时,如何打包?⑶当b>2h时,如何打包?【解析】图2和图3正面的面积相同,侧面面积=正面周长⨯长方体长,所以正面的周长愈大表面积越大,图2的正面周长是8h+6b,图3的周长是12h+4b.两者的周长之差为2(b-2h).当b=2h时,图2和图3周长相等,可随意打包;当b<2h时,按图2打包;当b>2h时,按图3打包.图3图2图1hba【巩固】要把6件同样的长17、宽7、高3的长方体物品拼装成一件大的长方体,表面积最小是多少?【解析】考虑所有的包装方法,因为6=1⨯2⨯3,所以一共有两种拼接方式:第一种按长宽高1⨯1⨯6拼接,重叠面有三种选择,共3种包装方法.第二种按长宽高1⨯2⨯3拼接,有3个长方体并列方向的重叠面有三种选择,有2个长方体并列方向的重叠面剩下2种选择,一共有6种包装方法.其中表面积最小的包装方法如图所示,表面积为1034.【例 7】 如图,在一个棱长为5分米的正方体上放一个棱长为4分米的小正方体,求这个立体图形的表面积.【解析】 我们把上面的小正方体想象成是可以向下“压缩”的,“压缩”后我们发现:小正方体的上面与大正方体上面中的阴影部分合在一起,正好是大正方体的上面.这样这个立体图形的表面积就可以分成这样两部分:上下方向:大正方体的两个底面;四周方向(左右、前后方向):小正方体的四个侧面,大正方体的四个侧面.上下方向:55250⨯⨯=(平方分米);侧面:554100⨯⨯=(平方分米),44464⨯⨯=(平方分米).这个立体图形的表面积为:5010064214++=(平方分米).【例 8】 (2008年“希望杯”五年级第2试)如图,棱长分别为1厘米、2厘米、3厘米、5厘米的四个正方体紧贴在一起,则所得到的多面体的表面积是_______平方厘米.【解析】 (法1)四个正方体的表面积之和为:2222(1235)6396234+++⨯=⨯=(平方厘米),重叠部分的面积为:22222222213(221)(321)(321)39141440⨯+⨯+++++++=+++=(平方厘米),所以,所得到的多面体的表面积为:23440194-=(平方厘米).(法2)三视图法.从前后面观察到的面积为22253238++=平方厘米,从左右两个面观察到的面积为225334+=平方厘米,从上下能观察到的面积为2525=平方厘米. 表面积为()3834252194++⨯=(平方厘米).【例 9】 把19个棱长为1厘米的正方体重叠在一起,按右图中的方式拼成一个立体图形.,求这个立体图形的表面积.【解析】 从上下、左右、前后观察到的的平面图形如下面三图表示.因此,这个立体图形的表面积为:2个上面2+个左面2+个前面.上表面的面积为:9平方厘米,左表面的面积为:8平方厘米,前表面的面积为:10平方厘米.因此,这个立体图形的总表面积为:(9810)254++⨯=(平方厘米).上下面左右面 前后面【巩固】用棱长是1厘米的立方块拼成如右图所示的立体图形,问该图形的表面积是多少平方厘米?【解析】 该图形的上、左、前三个方向的表面分别由9、7、7块正方形组成.该图形的表面积等于(977)246++⨯=个小正方形的面积,所以该图形表面积为46平方厘米.【例 10】 有30个边长为1米的正方体,在地面上摆成右上图的形式,然后把露出的表面涂成红色.求被涂成红色的表面积.【解析】 44(1234)456⨯++++⨯=(平方米).【例 11】 棱长是m 厘米(m 为整数)的正方体的若干面涂上红色,然后将其切割成棱长是1厘米的小正方体.至少有一面红色的小正方体个数和表面没有红色的小正方体个数的比为13:12,此时m 的最小值是多少?【解析】 切割成棱长是1厘米的小正方体共有3m 个,由于其中至少有一面是红色的小正方体与没有红色面的个数之比为13:12,而131225+=,所以小正方体的总数是25的倍数,即3m 是25的倍数,那么m 是5的倍数.当5m =时,要使得至少有一面的小正方体有65个,可以将原正方体的正面、上面和下面涂色,此时至少一面涂红色的小正方体有5554265⨯+⨯⨯=个,表面没有红色的小正方体有 1256560-=个,个数比恰好是13:12,符合题意.因此,m 的最小值是5.【例 12】 有64个边长为1厘米的同样大小的小正方体,其中34个为白色的,30个为黑色的.现将它们拼成一个444⨯⨯的大正方体,在大正方体的表面上白色部分最多可以是多少平方厘米?【解析】 要使大正方体的表面上白色部分最多,相当于要使大正方体表面上黑色部分最少,那么就要使得黑色小正方体尽量不露出来.在整个大正方体中,没有露在表面的小正方体有3(42)8-=(个),用黑色的;在面上但不在边上的小正方体有2(42)624-⨯=(个),其中30822-=个用黑色.这样,在表面的44696⨯⨯=个11⨯的正方形中,有22个是黑色,962274-=(个)是白色,所以在大正方体的表面上白色部分最多可以是74平方厘米.【例 13】 三个完全一样的长方体,棱长总和是288厘米,每个长方体相交于一个顶点的三条棱长恰是三个连续的自然数,给这三个长方体涂色,一个涂一面,一个涂两面,一个涂三面.涂色后把三个长方体都切成棱长为1厘米的小正方体,只有一个面涂色的小正方体最少有多少个?【解析】 每个长方体的棱长和是288396÷=厘米,所以,每个长方体长、宽、高的和是96424÷=厘米.因为,每个长方体相交于一个顶点的三条棱长恰是三个连续的自然数,所以,每个长方体的长、宽、高分别是9厘米、8厘米、7厘米.要求切割后只有一个面涂色的小正方体最少有多少个,则需每一个长方体按题意涂色时,应让切割后只有一个面涂色的小正方体最少.所以,涂一面的长方体应涂一个87⨯面,有8756⨯=个; 涂两面的长方体,若两面不相邻,应涂两个87⨯面,有872112⨯⨯=个;若两面相邻,应涂一个87⨯面和一个97⨯面,此时有()7892105⨯+-=个,所以涂两面的最少有105个;涂三面的长方体,若三面不两两相邻,应涂两个87⨯面、一个97⨯面,有()78894147⨯++-=个;若三面两两相邻,有()()()()()()718171918191146-⨯-+-⨯-+-⨯-=个,所以涂三面的最少有146个.那么切割后只有一个面涂色的小正方体最少有56105146307++=个.【例 14】 把一个大长方体木块表面上涂满红色后,分割成若干个同样大小的小正方体,其中恰好有两个面涂上红色的小正方体恰好是100块,那么至少要把这个大长方体分割成多少个小正方体?【解析】 设小正方体的棱长为1,考虑两种不同的情况,一种是长方体的长、宽、高中有一个是1的情况,另一种是长方体的长、宽、高都大于1的情况.当长方体的长、宽、高中有一个是1时,分割后只有一层小正方体,其中有两个面涂上红色的小正方体是去掉最外层一圈的小正方体后剩下的那些.因为有两个面涂上红色的小正方体恰好是100块,设100a b =⨯,那么分成的小正方体个数为()()()()221242104a b ab a b a b +⨯+⨯=+++=++,为了使小正方体的个数尽量少,应使()a b +最小,而两数之积一定,差越小积越小,所以当10a b ==时它们的和最小,此时共有 ()()102102144+⨯+=个小正方体.当长方体的长、宽、高都大于1时,有两个面涂上红色的小正方体是去掉8个顶点所在的小正方体后12条棱上剩余的小正方体,因为有两个面涂上红色的小正方体恰好是100块,所以长方体的长、宽、高之和是10042331÷+⨯=.由于三个数的和一定,差越大积越小,为了使小正方体的个数尽量少,应该令312227=++,此时共有2227108⨯⨯=个小正方体. 因为108144<,所以至少要把这个大长方体分割成108个小正方体.【例 15】 把正方体的六个表面都划分成9个相等的正方形.用红、黄、蓝三种颜色去染这些小正方形,要求有公共边的正方形染不同的颜色,那么,用红色染的正方形最多有多少个?【解析】 一个面最多有5个方格可染成红色(见左下图).因为染有5个红色方格的面不能相邻,可以相对,所以至多有两个面可以染成5个红色方格.红红红红红红红红红红红其余四个面中,每个面的四个角上的方格不能再染成红色,至多能染4个红色方格(见上中图).因为染有4个红色方格的面也不能相邻,可以相对,所以至多有两个面可以染成4个红色方格.最后剩下两个相对的面,每个面最多可以染2个红色方格(见右上图).所以,红色方格最多有52422222⨯+⨯+⨯=(个). (另解)事实上上述的解法并不严密,“如果最初的假设并没有两个相对的有5个红色方格的面,是否其他的四个面上可以出现更多的红色方格呢?”这种解法回避了这个问题,如果我们从约束染色方格数的本质原因入手,可严格说明22是红色方格数的最大值.对于同一个平面上的格网,如果按照国际象棋棋盘的方式染色,那么至少有一半的格子可以染成红色.但是现在需要染色的是一个正方体的表面,因此在分析问题时应该兼顾棱、角等面与面相交的地方:⑴ ⑵ ⑶⑴如图,每个角上三个方向的3个方格必须染成不同的三种颜色,所以8个角上最多只能有8个方格染成红色. ⑵如图,阴影部分是首尾相接由9个方格组成的环,这9个方格中只能有4个方格能染成同一种颜色(如果有5个方格染同一种颜色,必然出现相邻,可以用抽屉原理反证之:先去掉一个白格,剩下的然后两两相邻的分成四个抽屉,必然有一个抽屉中有两个红色方格),像这样的环,在正方体表面最多能找到不重叠的两道(关于正方体中心对称的两道),涉及的18个方格中最多能有8个可染成红色. ⑶剩下633839212⨯⨯-⨯-⨯=个方格,分布在6条棱上,这12个格子中只能有6个能染成红色. 综上所述,能被染成红色的方格最多能有88622++=个格子能染成红色,第一种解法中已经给出22个红方格的染色方法,所以22个格子染成红色是最多的情况.【例 16】 一个长、宽、高分别为21厘米、15厘米、12厘米的长方形.现从它的上面尽可能大的切下一个正方体,然后从剩余的部分再尽可能大的切下一个正方体,最后再从第二次剩余的部分尽可能大的切下一个正方体,剩下的体积是多少立方厘米?【解析】 本题的关键是确定三次切下的正方体的棱长.由于21:15:127:5:4=,为了方便起见.我们先考虑长、宽、高分别为7厘米、5厘米、4厘米的长方体.因为754>>,容易知道第一次切下的正方体棱长应该是4厘米,第二次切时,切下棱长为3厘米的正方体符合要求.第三次切时,切下棱长为2厘米的正方体符合要求.那么对于原长方体来说,三次切下的正方体的棱长分别是12厘米、9厘米和6厘米,所以剩下的体积应是:()33321151212961107⨯⨯-++=(立方厘米).12129996663121263912【例 17】 有黑白两种颜色的正方体积木,把它摆成右图所示的形状,已知相邻(有公共面)的积木颜色不同,标A 的为黑色,图中共有黑色积木多少块?A【解析】 分层来看,如下图(切面平行于纸面)共有黑色积木17块.【巩固】这个图形,是否能够由112⨯⨯的长方体搭构而成? 【解析】 每一个112⨯⨯的长方体无论怎么放,都包含了一个黑色正方体和一个白色正方体,而黑色积木有17块,白色积木有15块,所以该图形不能够由112⨯⨯的长方体搭构而成.【巩固】有许多相同的立方体,每个立方体的六个面上都写着同一个数字(不同的立方体可以写相同的数字)先将写着2的立方体与写着1的立方体的三个面相邻,再将写着3的立方体写着2的立方体相邻(见左下图).依这样构成右下图所示的立方体,它的六个面上的所有数字之和是多少?33223323322323111111【解析】 第一层如下图,第二层、第三层依次比上面一层每格都多1(见下图).765434565第三层654323454第二层第一层343212345上面的9个数之和是27,由对称性知,上面、前面、右面的所有数之和都是27.同理,下面的9个数之和是45,下面、左面、后面的所有数之和都是45.所以六个面上所有数之和是(2745)3216+⨯=.【例 18】 (05年武汉明心杯数学挑战赛)如图所示,一个555⨯⨯的立方体,在一个方向上开有115⨯⨯的孔,在另一个方向上开有215⨯⨯的孔,在第三个方向上开有315⨯⨯的孔,剩余部分的体积是多少?表面积为多少?【解析】 求体积:开了315⨯⨯的孔,挖去31515⨯⨯=,开了115⨯⨯的孔,挖去11514⨯⨯-=;开了215⨯⨯的孔,挖去215(22)6⨯⨯-+=,剩余部分的体积是:555(1546)100⨯⨯-++=.(另解)将整个图形切片,如果切面平行于纸面,那么五个切片分别如图:得到总体积为:22412100⨯+=.求表面积:表面积可以看成外部和内部两部分.外部的表面积为55612138⨯⨯-=,内部的面积可以分为前后、左右、上下三个方向,面积分别为()22515121320⨯⨯+⨯-⨯-⨯=、()2153513132⨯⨯+⨯-⨯-=、()2151511214⨯⨯+⨯-⨯-=,所以总的表面积为138203214204+++=.(另解)运用类似于三视图的方法,记录每一方向上的不同位置上的裸露正方形个数:前后方向:32上下方向:30左右方向:40总表面积为()2323040204⨯++=.【总结】“切片法”:全面打洞(例如本题,五层一样),挖块成线(例如本题,在前一层的基础上,一条线一条线地挖),这里体现的思想方法是:化整为零,有序思考!【巩固】(2008年香港保良局第12届小学数学世界邀请赛)如图,原来的大正方体是由125个小正方体所构成的.其中有些小正方体已经被挖除,图中涂黑色的部分就是贯穿整个大正方体的挖除部分.请问剩下的部分共有多少个小正方体?第8题【解析】对于这一类从立体图形中间挖掉一部分后再求体积(或小正方体数目)的题目一般可以采用“切片法”来做,所谓“切片法”,就是把整个立体图形切成一片一片的(或一层一层的),然后分别计算每一片或每一层的体积或小正方体数目,最后再把它们相加.采用切片法,俯视第一层到第五层的图形依次如下,其中黑色部分表示挖除掉的部分.第1层第2层第3层第4层第5层从图中可以看出,第1、2、3、4、5层剩下的小正方体分别有22个、11个、11个、6个、22个,所以总共还剩下22111162272++++=(个)小正方体.【巩固】一个由125个同样的小正方体组成的大正方体,从这个大正方体中抽出若干个小正方体,把大正方【解析】解法一:(用“容斥原理”来解)5525⨯=个,由侧面图形抽出的小正方体有5525⨯=个,由底面图形抽出的小正方体有4520⨯=个,正面图形和侧面图形重合抽出的小正方体有1221228⨯+⨯+⨯=个,正面图形和底面图形重合抽出的小正方体有13227⨯+⨯=个,底面图形和侧面图形重合抽出的小正方体有1211227⨯+⨯+⨯=个,三个面的图形共同重合抽出的小正方体有4个.根据容斥原理,252520877452++---+=,所以共抽出了52个小正方体.1255273-=,所以右图中剩下的小正方体有73个.注意这里的三者共同抽出的小正方体是4个,必须知道是哪4块,这是最让人头疼的事.但你可以先构造空的两个方向上共同部分的模型,再由第三个方向来穿过“花墙”.这里,化虚为实的思想方法很重要.解法二:(用“切片法”来解)可以从上到下切五层,得:⑴从上到下五层,如图:⑵或者,从右到左五片,如图:请注意这里的挖空的技巧是:先认一种方向.比如:从上到下的每一层,首先都应该有第一层的空四块的情况,即——如果挖第二层:第(1)步,把中间这些位置的四块挖走如图:第(2)步,把从右向左的两块成线地挖走.(请注意挖通的效果就是成线挖去),如图:第(3)步,把从前向后的一块(请注意跟第二层有关的只是一块!)挖成线!如图:【例 19】 (2009年迎春杯高年级组复赛)右图中的⑴⑵⑶⑷是同样的小等边三角形,⑸⑹也是等边三角形且边长为⑴的2倍,⑺⑻⑼⑽是同样的等腰直角三角形,⑾是正方形.那么,以⑸⑹⑺⑻⑼⑽⑾为平面展开图的立体图形的体积是以⑴⑵⑶⑷为平面展开图的立体图形体积的 倍.⑷⑶⑵⑴ ⑾⑽⑼⑻⑺⑹⑸【解析】 本题中的两个图都是立体图形的平面展开图,将它们还原成立体图形,可得到如下两图:其中左图是以⑴⑵⑶⑷为平面展开图的立体图形,是一个四个面都是正三角形的正四面体,右图以⑸⑹⑺⑻⑼⑽⑾为平面展开图的立体图形,是一个不规则图形,底面是⑾,四个侧面是⑺⑻⑼⑽,两个斜面是⑸⑹.对于这两个立体图形的体积,可以采用套模法来求,也就是对于这种我们不熟悉的立体图形,用一些我们熟悉的基本立体图形来套,看看它们与基本立体图形相比,缺少了哪些部分.由于左图四个面都是正三角形,右图底面是正方形,侧面是等腰直角三角形,想到都用正方体来套. 对于左图来说,相当于由一个正方体切去4个角后得到(如下左图,切去1ABDA 、1CBDC 、111D AC D 、111B AC B );而对于右图来说,相当于由一个正方体切去2个角后得到(如下右图,切去1BACB 、1DACD ).D 1C 1B 1A 1D CBAABCDA 1B 1C 1D 1假设左图中的立方体的棱长为a ,右图中的立方体的棱长为b ,则以⑴⑵⑶⑷为平面展开图的立体图形的体积为:3231114233a a a a -⨯⨯⨯=,以⑸⑹⑺⑻⑼⑽⑾为平面展开图的立体图形的体积为3231122233b b b b -⨯⨯⨯=.由于右图中的立方体的棱长即是题中正方形⑾的边长,而左图中的立方体的每一个面的对角线恰好是正三角形⑴的边长,通过将等腰直角三角形⑺分成4个相同的小等腰直角三角形可以得到右图中的立方体的棱长是左图中的立方体的棱长的2倍,即2b a =.那么以⑴⑵⑶⑷为平面展开图的立体图形的体积与以⑸⑹⑺⑻⑼⑽⑾为平面展开图的立体图形的体积的比为:()33331212::21:163333a b a a =⨯=,也就是说以⑸⑹⑺⑻⑼⑽⑾为平面展开图的立体图形的体积是以⑴⑵⑶⑷为平面展开图的立体图形体积的16倍.【例 20】 图⑴和图⑵是以正方形和等边三角形为面的立体图形的展开图,图中所有的边长都相同.请问:图⑴能围起来的立体图形的体积是图⑵能围起来的立体图形的体积的几倍?图⑴ 图⑵ 【解析】 首先,我们把展开图折成立体图形,见下列示意图:图⑴ 图⑵对于这类题目,一般采用“套模法”,即用一个我们熟悉的基本立体图形来套,这样做基于两点考虑,一是如果有类似的模型,可以直接应用其计算公式;二是如果可以补上一块或者放到某个模型里面,那么可以从这个模型入手.我们把图⑴中的立体图形切成两半,再转一转,正好放进去!我们看到图⑴与图⑶的图形位置的微妙关系:1和图3一致!60°图⑶ 图⑷由图⑷可见,图⑴这个立体的体积与图⑶这个被切去了8个角后的立体图形的体积相等.假设立方体的1条边的长度是1,那么一个角的体积是1111112222348⨯⨯⨯⨯=,所以切掉8个角后的体积是1518486-⨯=.再看图⑵中的正四面体,这个正四面体的棱长与图⑶中的每一条实线线段相等,所以应该用边长为12的立方体来套.如果把图⑵的立体图形放入边长为12的立方体里的话是可以放进去的.12这是切去了四个角后的图形,从上面的分析可知一个角的体积为148,所以图⑵的体积是:1111142224824⨯⨯-⨯=,那么前者的体积是后者的5120624÷=倍.【例 21】 如图,用高都是1米,底面半径分别为1.5米、1米和0.5米的3个圆柱组成一个物体.问这个物体的表面积是多少平方米?(π取3.14)1110.511.5【解析】 从上面看到图形是右上图,所以上下底面积和为22 3.14 1.514.13⨯⨯=(立方米),侧面积为2 3.14(0.51 1.5)118.84⨯⨯++⨯=(立方米),所以该物体的表面积是14.1318.8432.97+=(立方米).【例 22】 有一个圆柱体的零件,高10厘米,底面直径是6厘米,零件的一端有一个圆柱形的圆孔,圆孔的直径是4厘米,孔深5厘米(见右图).如果将这个零件接触空气的部分涂上防锈漆,那么一共要涂多少平方厘米?【解析】 涂漆的面积等于大圆柱表面积与小圆柱侧面积之和,为266π10π()24π560π18π20π98π307.722⨯+⨯⨯+⨯=++==(平方厘米).【例 23】 (第四届希望杯2试试题)圆柱体的侧面展开,放平,是边长分别为10厘米和12厘米的长方形,那么这个圆柱体的体积是________立方厘米.(结果用π表示)【解析】 当圆柱的高是12厘米时体积为210300π()122ππ⨯⨯=(立方厘米)当圆柱的高是12厘米时体积为212360π()102ππ⨯⨯=(立方厘米).所以圆柱体的体积为300π立方厘米或360π立方厘米.【例 24】 如右图,是一个长方形铁皮,利用图中的阴影部分,刚好能做成一个油桶(接头处忽略不计),求这个油桶的容积.(π 3.14=)【解析】 圆的直径为:()16.561 3.144÷+=(米),而油桶的高为2个直径长,即为:428(m)⨯=,故体积为100.48立方米.【巩固】如图,有一张长方形铁皮,剪下图中两个圆及一块长方形,正好可以做成1个圆柱体,这个圆柱体的底面半径为10厘米,那么原来长方形铁皮的面积是多少平方厘米?(π 3.14=)【解析】 做成的圆柱体的侧面是由中间的长方形卷成的,可见这个长方形的长与旁边的圆的周长相等,则剪下的长方形的长,即圆柱体底面圆的周长为:2π1062.8⨯⨯=(厘米), 原来的长方形的面积为:10462.81022056⨯+⨯⨯=()()(平方厘米).【例 25】 把一个高是8厘米的圆柱体,沿水平方向锯去2厘米后,剩下的圆柱体的表面积比原来的圆柱体表面积减少12.56平方厘米.原来的圆柱体的体积是多少立方厘米?【解析】 沿水平方向锯去2厘米后,剩下的圆柱体的表面积比原来的圆柱体表面积减少的部分为减掉的2厘米圆柱体的侧面积,所以原来圆柱体的底面周长为12.562 6.28÷=厘米,底面半径为6.28 3.1421÷÷=厘米,所以原来的圆柱体的体积是2π188π25.12⨯⨯==(立方厘米).【例 26】 一个圆柱体的体积是50.24立方厘米,底面半径是2厘米.将它的底面平均分成若干个扇形后,再截开拼成一个和它等底等高的长方体,表面积增加了多少平方厘米? (π 3.14=)【解析】 从图中可以看出,拼成的长方体的底面积与原来圆柱体的底面积相同,长方体的前后两个侧面面积与原来圆柱体的侧面面积相等,所以增加的表面积就是长方体左右两个侧面的面积. (法1)这两个侧面都是长方形,且长等于原来圆柱体的高,宽等于圆柱体底面半径.可知,圆柱体的高为()250.24 3.1424÷⨯=(厘米),所以增加的表面积为24216⨯⨯=(平方厘米); (法2)根据长方体的体积公式推导.增加的两个面是长方体的侧面,侧面面积与长方体的长的乘积就是长方体的体积.由于长方体的体积与圆柱体的体积相等,为50.24立方厘米,而拼成的长方体的长等于圆柱体底面周长的一半,为3.142 6.28⨯=厘米,所以侧面长方形的面积为50.24 6.288÷=平方厘米,所以增加的表面积为8216⨯=平方厘米.【例 27】 (2008年”希望杯”五年级第2试)一个拧紧瓶盖的瓶子里面装着一些水(如图),由图中的数据可推知瓶子的容积是_______ 立方厘米.(π取3.14)。
六年级数学课件探索空间立体几何的魅力

感谢观看
地理学:地球的形状、地貌特征、气候变化等地理现象可以用空间立体几何的知识进行描述和建模。
数学:空间立体几何是数学的一个重要分支,对拓扑学、微分几何等领域的发展有重要影响。
05
六年级数学课件中空间立体几何的魅力展现
空间立体几何的美学价值
空间立体几何的动态美:通过旋转、平移等操作,可以创造出动态的立体几何图形,展现出动态的美感。
点:表示空间中的位置
直线:表示空间中的方向和长度
平面:表示空间中的面积和形状
立体:表示空间中的体积和表面积
空间立体几何的基本性质
空间立体几何是研究三维空间中物体的形状、大小、位置关系的数学分支。
空间立体几何的基本性质包括:点、线、面的基本性质,如两点确定一条直线,三点确定一个平面等。
空间立体几何中,平行、垂直、相交等关系也是其基本性质之一。
科学研究:在物理学、化学、生物学等科学领域中,空间立体几何知识也具有重要的作用。
06
六年级数学课件中空间立体几何的教学评价与反馈
空间立体几何的教学评价标准与方法
教学目标:是否明确、具体、可衡量,是否符合学生实际需求。
教学方法:是否合理、有效、多样化,是否能够引导学生主动思考。
教学过程:是否流畅、有序、有节奏感,是否能够调动学生积极性。
空间立体几何在数学竞赛中的应用
空间立体几何在数学建模竞赛中的应用
空间立体几何在数学奥林匹克竞赛中的应用
空间立体几何在几何证明中的应用
空间立体几何在解决实际问题中的应用
空间立体几何在科学领域中的应用
工程学:建筑设计、机械制造、航空航天等领域中,空间立体几何是必不可少的工具。
物理学:空间立体几何在描述物体运动轨迹、引力场、电磁场等方面有重要应用。
数学人教版六年级下册立体几何复习课

圆柱的组成有什么特征?
两个底面为圆,侧面为曲面 02
圆柱可由什么平面图形旋转而成? 圆柱的展开面是什么形状?
03 长方形,长方形
展开后的长方形的长、宽与原来的圆柱有什么关系?
长方形的长为圆柱的底面周长, 04 宽为圆柱的高.
圆柱
表面积
①圆柱的展开图为:
立体图形的表面积、体积
③由长方体的体积 公式,可得圆柱的 体积:圆柱的体积= 底面积×高
对立体几何的认识
圆锥
圆锥的组成
底面、侧面
圆锥的组成有什么特征?
底面为圆,侧面为曲面
圆锥可由什么平面图形旋转而成?
三角形
立体几何的表面积、体积
圆锥
体积
①实验
等底等高的圆柱、圆锥形容器, 将圆锥形容器装满水(或沙), 再倒入圆柱形容器中,会发现倒 3次,圆柱形容器刚好装满水 (或沙).
锥的底面积是15㎡,那么圆柱的底面积是(
),
如果圆柱的底面积是6㎡,那么圆锥的底面积是(
)。
(5),一个圆柱与一个圆锥体积相等底面积也相等,如
果圆锥的高是21cm,那么圆柱的高是 (
),如果圆
柱的高是6cm,那么圆锥的高是(
)。
(6),一个棱长为6cm的正方体里面挖出一个最大的圆锥, 求圆锥的体积( )cm³
对立体几何的认识
问题(1)
问题(1)
长方体与正 方体有什么 相同点和不 同点?
问题(2)
圆柱和圆锥 可以各由什 么平面图形 旋转而成?
问题(3)
圆柱与圆锥 之间有什么 联系和区别?
小试牛刀
(1),下图是等底等高的圆锥和圆柱,从不同方向看 会 看到不同的形状。从上面看到的形状分别是( ), ( ), 从左面看到的形状分别是( ),( ) 。
六年级立体几何
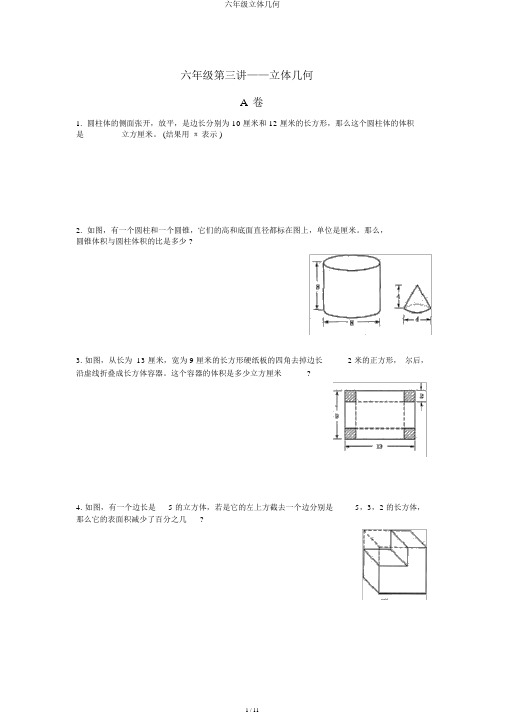
六年级第三讲——立体几何A卷1.圆柱体的侧面张开,放平,是边长分别为 10 厘米和 12 厘米的长方形,那么这个圆柱体的体积是 ________立方厘米。
(结果用π表示 )2.如图,有一个圆柱和一个圆锥,它们的高和底面直径都标在图上,单位是厘米。
那么,圆锥体积与圆柱体积的比是多少 ?3. 如图,从长为 13 厘米,宽为 9 厘米的长方形硬纸板的四角去掉边长 2 米的正方形,尔后,沿虚线折叠成长方体容器。
这个容器的体积是多少立方厘米?4. 如图,有一个边长是 5 的立方体,若是它的左上方截去一个边分别是5,3,2 的长方体,那么它的表面积减少了百分之几?5. 有大、中、小 3 个正方形水池,它们的内边长分别是吞没在中、小水池的水里,两个水池的水面分别高升了都吞没在大水池的水里,大水池的水面高升了多少厘米?6 米、 3 米、 2 米.把两堆碎石分别6 厘米和 4 厘米.若是将这两堆碎石6. 有一个棱长是 4 厘米的正方体,从它的一个极点处挖去一个棱长是 1 厘米的正方体后,剩下物体的体积和表面积各是多少?7.把两个完好同样的长方体木块粘成一个大长方体,这个大长方体的表面积比原来两个长方体的表面积的和减少了 46 平方厘米,而长是原来长方体的 2 倍。
若是拼成的长方体的长是 24 厘米,那么它的体积是多少立方厘米?8.把 4 块棱长都是 2 分米的正方体粘成一个长方体,它们的表面积最多会减少多少平方厘米?9.有 24 个正方体,每个正方体的体积都是 1 立方厘米,用这些正方体可以拼成几种不同样的长方体?10.一个长方体,前面和上面的面积之和是 209 平方厘米,这个长方体的长、宽、高是以厘米为单位的数且都是质数。
这个长方体的体积和表面积各是多少?B卷1.用棱长是 1 厘米的立方块拼成如图 11-1 所示的立体图形,问该图形的表面积是多少平方厘米 ?2.图中是一个边长为 4 厘米的正方体,分别在前后、左右、上下各面的中心地址挖去一个边长 l 厘米的正方体,做成一种玩具.它的表面积是多少平方厘米?3. 有一个正方体容器,边长是 24 厘米,里面注满了水。
