高中数学概率复习课件.ppt
合集下载
新人教版高中数学必修第二册概率全套PPT课件

[变式训练]
1.[变设问]若本例条件不变,问题改为用集合表示事件:P=“x +y 是偶数”. 解:“x+y 是偶数”包括两种情况,①x,y 都是奇数;②x, y 都是偶数,故“x+y 是偶数”这一事件包含以下 8 个样本点: (1,1),(1,3),(3,1),(3,3),(2,2),(2,4),(4,2),(4,4). 所以 P={(1,1),(1,3),(3,1),(3,3),(2,2),(2,4),(4,2),(4,4)}.
大于事件 A.其中正确命题的个数为
()
A.0
B.1
C.2
D.3
解析:对立必互斥,互斥不一定对立,∴②③对,①错;对
于④A⊆A∪B,即 A 与 B 的和事件包含事件 A,但两个事件
不能比较大小,故④错. 答案:C
5.从装有 2 个红球和 2 个白球的口袋内任取 2 个球观察颜色.设 事件 A 为“所取两个球至少有一个白球”,事件 B 为“所取 两个恰有一个红球”,则 A∩B 表示的事件为________. 解析:因为从装有 2 个红球和 2 个白球的口袋内任取 2 个球, 这一随机试验的样本空间 Ω={(白、白),(白、红),(红、红)}, 且 A={(白、红),(白、白)},B={(白,红)}.所以 A∩B= {(白、红)}.故 A∩B 表示的事件为恰有一个红球.
D.13 人中至少有 2 人生日在同一个月 解析:一年有 12 个月,因此无论 10、11、12 个人都有不
在同一月生日的可能,只有 13 个人肯定至少有 2 人在同
一月生日.本题属“三种事件”的概念理解与应用,解决
这类题型要很好地吃透必然事件的概念,明确它必定要发
生的特征,不可因偶尔巧合就下结论,故选 D. 答案:D
高中数学概率知识点全面解析PPT

乘法公式和全概率公式
乘法公式的应用 乘法公式在概率论中的应用广泛,例如计算两个事件同时发生的概 率,其计算公式为P(A并B)=P(A)*P(B)。根据统计数据,这种方法 的准确率高达90%以上。 全概率公式的价值 全概率公式可以解决复杂问题中的概率计算问题,如在多个互斥事 件中寻找某个事件发生的原因。根据一项研究,使用全概率公式解 决问题的效率比传统方法提高了约30%。
连续型随机变量
连续型随机变量定义 连续型随机变量是一个可能取无限多个值的随机变量。 概率密度函数 连续型随机变量的概率密度函数用于描述该随机变量在某一区 间内取值的概率。 期望与方差 连续型随机变量的期望和方差是其重要特性,它们描述了该随 机变量的平均水平和离散程度。 实际应用 连续型随机变量广泛应用于金融、工程等实际问题中,如期权 定价模型。
Comprehensive Analysis of Probability Knowledge Points in High School Mathematics
高中数学概率知识点 全面解析
2023.11.03
目录
Content
01 概率的基本概念 02 条件概率与独立性 03 随机变量及其分布 04 多维随机变量及其联合分布 05 大数定律与中心极限定理
THANK YOU
2023.11.03
中心极限定理的内容和应用
中心极限定理概念 中心极限定理是概率论中的一个重要定理,描述了大量随机变量和的分布趋近于正态分布的现象 大数定律与中心极限定理 大数定律揭示了样本数量增加时,样本平均值趋近于期望值,而中心极限定理则描述了这一过程的概率分布 正态分布在实际应用中的重要性 由于中心极限定理的作用,许多实际问题中的随机变量都可以近似为正态分布,方便进行统计分析 中心极限定理在高中数学教学中的地位 作为概率论的核心内容之一,中心极限定理对于培养学生的数学思维、解决实际问题具有重要意义
高中数学 第3章 概率 教师配套用书课件(共25张ppt)

第三章 概 率
章末复习课
本节知识目录
理网络、明结构
章 末 复 习 课
填要点、记疑点
题型一 随机事件的概率
题型二
互斥事件与对立事件
古典概型与几何概型
探题型、提能力
题型三
题型四 数形结合的思想在求概 率中的运用
理网络、明结构
填要点、记疑点
1.频率与概率 频率是概率的 近似值 ,是随机的,随着试验的不同而 变化 ;概率是多数次的 试验中 频率 的稳定值,是一个 常数 ,不要用一次或少数次试验中的频率来估 计概率. 2.求较复杂概率的常用方法 (1)将所求事件转化为彼此 互斥 的事件的和; (2)先求其 对立 事件的概率,然后再应用公式P(A)=1-P( A )求解.
解 (1)把四张债券分别编号1,2,3,4,其中3,4是中奖债券,用(2,3)表示“第一次取出 2号债券,第二次取出3号债券”,所有可能的结果组成的基本事件空间为Ω= {(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4), (4,1),(4,2),(4,3),(4,4)}.
探题型、提能力
题型二:互斥事件与对立事件
反思与感悟 在求有关事件的概率时,若从正面分析,包含的事件较多或较繁琐, 而其反面却较容易入手,这时,可以利用对立事件求解.
探题型、提能力
题型二:互斥事件与对立事件
跟踪训练2 有4张面值相同的债券,其中有2张中奖债券. (1)有放回地从债券中任取2张,每次取出1张,计算取出的2张中至少有1张是中奖 债券的概率. (2)无放回地从债券中任取2张,每次取出1张,计算取出的2张中至少有1张是中奖 债券的概率.
解 (1)从8人中选出数学、物理、化学成绩优秀者各1名,其一切可能的结果组成 的基本事件空间Ω={(A1,B1,C1),(A1,B1,C2),(A1,B2,C1),(A1,B2, C2),(A1,B3,C1),(A1,B3,C2),(A2,B1,C1),(A2,B1,C2),(A2,B2,C1), (A2,B2,C2),(A2,B3,C1),(A2,B3,C2),(A3,B1,C1),(A3,B1,C2),(A3, B2,C1),(A3,B2,C2),(A3,B3,C1),(A3,B3,C2)}.
章末复习课
本节知识目录
理网络、明结构
章 末 复 习 课
填要点、记疑点
题型一 随机事件的概率
题型二
互斥事件与对立事件
古典概型与几何概型
探题型、提能力
题型三
题型四 数形结合的思想在求概 率中的运用
理网络、明结构
填要点、记疑点
1.频率与概率 频率是概率的 近似值 ,是随机的,随着试验的不同而 变化 ;概率是多数次的 试验中 频率 的稳定值,是一个 常数 ,不要用一次或少数次试验中的频率来估 计概率. 2.求较复杂概率的常用方法 (1)将所求事件转化为彼此 互斥 的事件的和; (2)先求其 对立 事件的概率,然后再应用公式P(A)=1-P( A )求解.
解 (1)把四张债券分别编号1,2,3,4,其中3,4是中奖债券,用(2,3)表示“第一次取出 2号债券,第二次取出3号债券”,所有可能的结果组成的基本事件空间为Ω= {(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4), (4,1),(4,2),(4,3),(4,4)}.
探题型、提能力
题型二:互斥事件与对立事件
反思与感悟 在求有关事件的概率时,若从正面分析,包含的事件较多或较繁琐, 而其反面却较容易入手,这时,可以利用对立事件求解.
探题型、提能力
题型二:互斥事件与对立事件
跟踪训练2 有4张面值相同的债券,其中有2张中奖债券. (1)有放回地从债券中任取2张,每次取出1张,计算取出的2张中至少有1张是中奖 债券的概率. (2)无放回地从债券中任取2张,每次取出1张,计算取出的2张中至少有1张是中奖 债券的概率.
解 (1)从8人中选出数学、物理、化学成绩优秀者各1名,其一切可能的结果组成 的基本事件空间Ω={(A1,B1,C1),(A1,B1,C2),(A1,B2,C1),(A1,B2, C2),(A1,B3,C1),(A1,B3,C2),(A2,B1,C1),(A2,B1,C2),(A2,B2,C1), (A2,B2,C2),(A2,B3,C1),(A2,B3,C2),(A3,B1,C1),(A3,B1,C2),(A3, B2,C1),(A3,B2,C2),(A3,B3,C1),(A3,B3,C2)}.
概率基础知识ppt课件

n
② pi=1. i=1
③一般地,离散型随机变量在某一范围内取值的概率等于这 个范围内每个随机变量值的概率__之__和____. 思考探究 如何求离散型随机变量的分布列? 提示:首先确定随机变量的取值,求出离散型随机变量的每一 个值对应的概率,最后列成表格.
可编辑课件PPT
15
2.常见离散型随机变量的分布列
概率基础知识
可编辑课件PPT
1
基
基本事件
互斥事件
加
本
法
事
事
并(和)事件的概率
公
件
目ห้องสมุดไป่ตู้事件
件
对立事件
式
空
的
间
性
质
不可能事件
乘
概
独立事件
法
率 必然事件
交(积)事件的概率
公
式
条件概率
简
全
单
古典概型
概
概
率
随
率
比例算法
公
机
模
式
事
型
几何概型
件
频
率
随机试验
可编辑课件PPT
2
集合知识回顾: 1、集合之间的包含关系:
称为离散型随机变量X的概率分布列,简称X的分布列.有时 为了表达简单,也用等式__P_(_X_=__x_i_)=___p_i,__i=__1_,_2_,__…__,__n__表示
X的分布列.
可编辑课件PPT
14
(2)离散型随机变量分布列的性质 ①____p_i≥__0_,__i_=__1_,2_,__…__,__n_;
PA∩B
P(B|A)=___P__A_____,P(A)>0.
高中数学概率论复习(全)PPT
(2)有界性:对任意实数 x ,有 0 F(x) 1,且
F() lim F(x) 0 x
F() lim F(x) 1 x
(3)右连续性:F(x) 是右连续的函数,即对任
意实数 x ,有 F(x 0) F(x) . (4)对任意实数 x1, x2 (x1 x2 ) ,有 P{x1 X x2} P{X x2} P{X x1}
F (x2 ) F (x1)
【注】满足单调性、有界性和右连续性这三个性质的 函数,一定可以作为某个随机变量的分布函数.
离散型随机变量
离散型随机变量 X 的概率分布满足以下两个基本性质:
(1)非负性: pi 0 , i 1, 2, ;
(2)规范性: pi 1 . i 1
【注】满足非负性和规范性的数组 pi (i 1, 2, ) ,一 定是某个离散型随机变量的概率分布.
pij
( xi , y j )G
(4)
P{X xi} pij , i 1, 2, j 1
P{Y y j} pij , j 1, 2, i 1
二维连续型随机变量
(1)非负性 p(x, y) 0 ;
(2)规范性 p(x, y)dxdy F (, ) 1.
【注】若二元函数 p(x, y) 具有非负性和规范性,则 p(x, y) 一定是某个二维连续型随机变量的联合概率 密度函数.
定理 设随机变量 X 具有数学期望
E( X ) μ,方差 D( X ) σ 2,则对于任
(3)右连续性 F( x, y ) 分别对 x , y 右连续,即
F(x 0, y) lim F(x , y) F(x, y) 0
F(x, y 0) lim F(x, y ) F(x, y) 0
(4)非负性 对于任意的实数 x1 x2 , y1 y2 ,有
F() lim F(x) 0 x
F() lim F(x) 1 x
(3)右连续性:F(x) 是右连续的函数,即对任
意实数 x ,有 F(x 0) F(x) . (4)对任意实数 x1, x2 (x1 x2 ) ,有 P{x1 X x2} P{X x2} P{X x1}
F (x2 ) F (x1)
【注】满足单调性、有界性和右连续性这三个性质的 函数,一定可以作为某个随机变量的分布函数.
离散型随机变量
离散型随机变量 X 的概率分布满足以下两个基本性质:
(1)非负性: pi 0 , i 1, 2, ;
(2)规范性: pi 1 . i 1
【注】满足非负性和规范性的数组 pi (i 1, 2, ) ,一 定是某个离散型随机变量的概率分布.
pij
( xi , y j )G
(4)
P{X xi} pij , i 1, 2, j 1
P{Y y j} pij , j 1, 2, i 1
二维连续型随机变量
(1)非负性 p(x, y) 0 ;
(2)规范性 p(x, y)dxdy F (, ) 1.
【注】若二元函数 p(x, y) 具有非负性和规范性,则 p(x, y) 一定是某个二维连续型随机变量的联合概率 密度函数.
定理 设随机变量 X 具有数学期望
E( X ) μ,方差 D( X ) σ 2,则对于任
(3)右连续性 F( x, y ) 分别对 x , y 右连续,即
F(x 0, y) lim F(x , y) F(x, y) 0
F(x, y 0) lim F(x, y ) F(x, y) 0
(4)非负性 对于任意的实数 x1 x2 , y1 y2 ,有
《高二数学概率复习》课件

条件概率的公式
P(A|B) = P(A∩B) / P(B)。其中,P(A∩B)表示事件A和事件B同时发生的概率, P(B)表示事件B发生的概率。
条件概率的性质
非负性
P(A|B) ≥ 0。
规范性
当事件B是必然事件时,P(A|B) = P(A)。
条件概率的加法规则
如果两个事件B1和B2是互斥的,那么对于任一事件A,有 P(A|B1∪B2) = P(A|B1) + P(A|B2)。
04
概率的应用
概率在日常生活中的应用
天气预报
通过概率分析,预测未来天气变 化,为日常生活和出行提供参考
。
彩票
彩票中奖概率的计算,让人们理性 对待,避免盲目投入。
医学诊断
通过概率统计方法,提高疾病诊断 的准确率。
概率在科学实验中的应用
物理实验
在物理学中,概率被广泛应用于 粒子实验、量子力学等领域。
解析5
进阶题目5的答案是$frac{4}{8} times frac{3}{7} = frac{12}{56} = frac{3}{14}$,因为第一次摸出白球的概 率为$frac{4}{8}$,第二次摸出白球的概率为$frac{3}{7}$ 。
解析6
进阶题目6的答案是$frac{7}{10} times frac{3}{9} = frac{21}{90} = frac{7}{30}$,因为第一次摸出红球的概 率为$frac{7}{10}$,第二次摸出白球的概率为 $frac{3}{9}$。
《高二数学概率复习》ห้องสมุดไป่ตู้ppt课件
目 录
• 概率的基本概念 • 古典概型与几何概型 • 条件概率与独立性 • 概率的应用 • 复习题与答案解析
P(A|B) = P(A∩B) / P(B)。其中,P(A∩B)表示事件A和事件B同时发生的概率, P(B)表示事件B发生的概率。
条件概率的性质
非负性
P(A|B) ≥ 0。
规范性
当事件B是必然事件时,P(A|B) = P(A)。
条件概率的加法规则
如果两个事件B1和B2是互斥的,那么对于任一事件A,有 P(A|B1∪B2) = P(A|B1) + P(A|B2)。
04
概率的应用
概率在日常生活中的应用
天气预报
通过概率分析,预测未来天气变 化,为日常生活和出行提供参考
。
彩票
彩票中奖概率的计算,让人们理性 对待,避免盲目投入。
医学诊断
通过概率统计方法,提高疾病诊断 的准确率。
概率在科学实验中的应用
物理实验
在物理学中,概率被广泛应用于 粒子实验、量子力学等领域。
解析5
进阶题目5的答案是$frac{4}{8} times frac{3}{7} = frac{12}{56} = frac{3}{14}$,因为第一次摸出白球的概 率为$frac{4}{8}$,第二次摸出白球的概率为$frac{3}{7}$ 。
解析6
进阶题目6的答案是$frac{7}{10} times frac{3}{9} = frac{21}{90} = frac{7}{30}$,因为第一次摸出红球的概 率为$frac{7}{10}$,第二次摸出白球的概率为 $frac{3}{9}$。
《高二数学概率复习》ห้องสมุดไป่ตู้ppt课件
目 录
• 概率的基本概念 • 古典概型与几何概型 • 条件概率与独立性 • 概率的应用 • 复习题与答案解析
高中数学概率复习ppt课件

4 6
2 3
(2) (1,1),(1,2),(1,a),(2,1),(2,2),(2,a),(a,1),(a,2),(a,a)
P(B) .
4 9
例7 如图,在三角形AOB中,已知AOB=60°, OA=2,OB=5,在线段OB上任意选取一点C,求 △AOC为钝角三角形的概率.
A
OD
EC B
解P
OD EB OB .
2 5
0.4
例8 以半径为1的圆内任一点为中点作弦,求弦 长超过圆内接等边三角形边长的概率.
解 记事件 A 为“弦长超过圆内接等边三角形的 边长”,如图所示,作等边三角形 BCD 的内切圆,当 以小圆上任意一点作弦时,弦长都等于等边三角形的边 长,所以当弦的中点在小圆内时,弦长超过圆内接等边
三角形的边长,小圆的半径为12,所以由几何概型公式,
5
.
6.有一人在打靶中,连续射击2次,事
件“至少有1次中靶”的对立事件是( C
) A.至多有1次中靶 B.2次都中靶 C.2次都不中靶 D.只有1次中靶
.
7.某公务员去开会,他乘火车 轮船 汽车 飞机去 的概率分别为0.3 0.2 0.1 0.4
0.7 (1)求他乘火车或乘飞机去的概率; 0.8 (2)求他不乘轮船去的概率;
必修3第三章 概率复习课
.
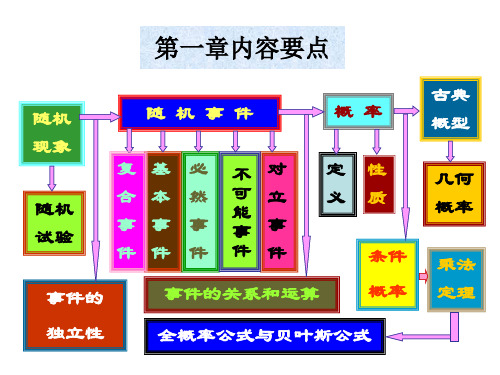
知识结构
随机事件
频率
概率的意义与性质
古典概型
概
率
的
几何概型
实 际
应
用
随机数与随机模. 拟
知识梳理
1.事件的有关概念
(1)必然事件: 在条件S下,一定会发生的事件. (2)不可能事件: 在条件S下,一定不会发生的事件.
人教版高中数学第三章第1节 3 概率的基本性质 (共21张PPT)教育课件

A,B是互斥事件
A,B是对立事件
判断下列每对事件是否为互斥事件。
(1)将一枚硬币抛两次,事件A:两次出现正面, 事件B:只有一次出现正面.
(2)将一枚硬币抛两次,事件A:至少一次出现正 面,事件B:只有一次出现正面.
(3)将一枚硬币抛两次,事件A:至少一次出现正 面,事件B:两次出现反面.
(4)某人射击一次,事件A:中靶,事件B:射中 9环.
电
:
那
你
的
第
一
口
罗
没
有
我
和
他
不
同
。
我
是
从
底
层
但
是
当
我
拍
完
但
是
我
年
轻
时
有
一
个
想
法
就
是
如
果
我
告
诉
你
怎
么
弄
–■
电
:
“
口
罗
部
爬
一
,
1
戏
有
上
来
的
我
个
5
分
钟
后
你
还
色
其
没
清
镜
没
有
楚 弄
有 怎
完 情
么
头
我
就
胆 运不怯作这,耐
烦
像
男
个
如
果
, 东 下
我
实
像
西
(
自
己
弄
费
电
影
一
五
分
钟
女
里
高二数学概率PPT课件

例2 某气象站天气预报的准确率为80%,计算(结果保留 两个有效数字):
(1) 5次预报中恰有4次准确的概率; (2) 5次预报中至少有4次准确的概率。 解:(1) 记‘‘预报1次,结果准确”为事件A.预报5次相当 于作5次独立重复试验,根据n次独立重复试验中事件发生 k次的概率公式, 5次预报中恰有4次准确的概率是:
第2页/共18页
例6.某工厂的产品要同时经过两名检验员检验合格方能出厂, 但在检验时也可能出现差错,将合格产品不能通过检验或将不合格 产品通过检验,对于两名检验员,合格品不能通过检验的概率分别 为1、2,不合格产品通过检验的概率分别为1、2,两名检验员 的工作独立.
求:(1)一件合格品不能出厂的概率, (2)一件不合格产品能出厂的概率
3:2获胜的概率是:
P2 P(A3 • A4 ) P(A3) • P(A4 )
C42 0.62 (1 0.6)2 0.6
0.20736
答:甲3:2获胜的概率是0.20736
第16页/共18页
小结:
1.独立重复试验是在同样条件下重复地,各次之 间独立地进行的一种试验,在这种试验中,每一 次试验的结果只有两种,即事件要么发生要么不 发生,并且任何一次试验中事件发生的概率都是 相等的。 2.n次独立重复试验中某事件恰好发生k次的概
(2)恰好有1颗骰子出现1点或6点,即A发生B不发生C不发生或 A不发生B发生C不发生或A不发生B不发生C发生,用符号表示
为事件 A B C, A B C, A B C
所求概率为:
P(A B C A B C A B C)
P(A B C) P(A B C) P(A B C)
P( A) P(B) P(C) P( A) P(B) P(C) P( A) P(B) P(C) 4
人教A版高中数学必修三课件概率复习课.pptx

解:完成由甲地到乙地这件事有三类办法:
第一类办法坐火车,一天中有4种不同走法。 第二类办法坐汽车,一天中有2种不同走法。 第三类办法坐轮船,一天中有3种不同走法。 由加法原理得:4+2+3=9 答:有9种不同的走法。
作为练习:由数字1、2、3、4、5可以组成多
少个允许有重复数字的三位数?无重复数字的三位 数?
必然事件:在一定条件下,必然发生的事件
不可能事件:在一定条件下,不可能发生的事件 随机事件:在一定条件下,可能发生也可能不发生
的事件
做一件事,完成它有n类办法,其中第一类办法中 有m1种方法,第二类中有m2种方法……,第n类办 法中有mn种方法,那么完成这件事共有 N=m1+m2+…+mn种不同的方法。
:30内的任意时刻到达预定地点的机会是等可能的
。解 设甲乙二人到达预定地点
y
的时刻分别为 x 及 y(分钟), 30
则
二人会面
10 10
x 30
Bertrant问题 已知半径为1的圆内接三角形的
边长为
在圆内随机取一条弦求弦长超过
的概率
ቤተ መጻሕፍቲ ባይዱ
B
A
D
B
O
A ① p = 1/3
A
B
D
② p = 1/2
③ p = 1/4
如果从A村经过B村到达C村可分为两个步骤完成: 第一步A村→B村,有3种不同的走法。 第二步B村→C村,有2种不同的走法。
由乘法原理,共有3×2=6种不同的走法。
分步计数原理也称为乘法原理。
问题:口袋里装有2个白球和2个黑球,这4个球除 颜色外完全相同,4个人按顺序依次从中摸 出一个球,试计算第二个人摸到白球的概率.
第一类办法坐火车,一天中有4种不同走法。 第二类办法坐汽车,一天中有2种不同走法。 第三类办法坐轮船,一天中有3种不同走法。 由加法原理得:4+2+3=9 答:有9种不同的走法。
作为练习:由数字1、2、3、4、5可以组成多
少个允许有重复数字的三位数?无重复数字的三位 数?
必然事件:在一定条件下,必然发生的事件
不可能事件:在一定条件下,不可能发生的事件 随机事件:在一定条件下,可能发生也可能不发生
的事件
做一件事,完成它有n类办法,其中第一类办法中 有m1种方法,第二类中有m2种方法……,第n类办 法中有mn种方法,那么完成这件事共有 N=m1+m2+…+mn种不同的方法。
:30内的任意时刻到达预定地点的机会是等可能的
。解 设甲乙二人到达预定地点
y
的时刻分别为 x 及 y(分钟), 30
则
二人会面
10 10
x 30
Bertrant问题 已知半径为1的圆内接三角形的
边长为
在圆内随机取一条弦求弦长超过
的概率
ቤተ መጻሕፍቲ ባይዱ
B
A
D
B
O
A ① p = 1/3
A
B
D
② p = 1/2
③ p = 1/4
如果从A村经过B村到达C村可分为两个步骤完成: 第一步A村→B村,有3种不同的走法。 第二步B村→C村,有2种不同的走法。
由乘法原理,共有3×2=6种不同的走法。
分步计数原理也称为乘法原理。
问题:口袋里装有2个白球和2个黑球,这4个球除 颜色外完全相同,4个人按顺序依次从中摸 出一个球,试计算第二个人摸到白球的概率.
高中数学必修三3.1.3概率的基本性质 课件 (共16张PPT)

概率的基本性质
(1)对于任何事件的概率的范围是:0≤P(A)≤1 其中不可能事件的概率是P(A)=0 必然事件的概率是P(A)=1 (2)当事件A与事件B互斥时,A∪B的频率 fn(A∪B)= fn(A)+ fn(B) 由此得到概率的加法公式: 如果事件A与事件B互斥,则 P(A∪B)=P(A)+P(B) (3)特别地,当事件A与事件B互为对立事件时, 有 P(A)=1- P(B)
在掷骰子的试验中,我们可以定义许多事件,如: C1 ={ 出现 1 点 }; C2 ={出现 2 点}; C3 ={ 出现 3 点 }; C4 ={ 出现 4 点 }; C5 ={出现 5 点}; C6 ={ 出现 6 点 };
D1 ={ 出现的点数不大于 1 }; D2 ={ 出现的点数大于 3 }; D3 ={ 出现的点数小于 5 }; E ={ 出现的点数小于 7 }; F ={ 出现的点数大于 6 }; G ={ 出现的点数为偶数 }; H ={ 出现的点数为奇数 };…… 思考: 1. 上述事件中有必然事件或不可能事件吗?有的话,哪些是? 2. 若事件C1发生,则事件 H 是否一定会发生? 反过来可以么? 3.上述事件中,哪些事件发生会使得 J={出现1点或5点}也发生? 4.上述事件中,哪些事件等价于:事件D2与事件D3同时发生? 5. 若只掷一次骰子,则事件C1 和事件C2 有可能同时发生么? 6. 在掷骰子实验中事件G 和事件H 是否一定有一个会发生?
例2、抛掷色子,事件A= “朝上一面的数是奇数”, 事件B = “朝上一面的数不超过3”, 求P(A∪B)
解法一: 因为P(A)=3/6=1/2,P(B)=3/6=1/2 所以P(A∪B)= P(A)+ P(B)=1 解法二: A∪B这一事件包括4种结果,即出现1,2,3和5 所以P(A∪B)= 4/6=2/3
相关主题
