有关液体对容器底部压力压强计算
压强公式p=F、S和p=ρgh的应用

3.用 p=FS=ρgh 求液体压强对于柱形容器内的液体对容器底部产生的压 F
强,也可以用 p=S来求解,可能会更简便一些。对于其他不规则的容器,计 算液体压强一定要用 p=ρ液 gh,液体对容器底部的压力不等于液体重力,计 算方法是“先压强再压力”,即先用 p=ρhg 求压强,再用 F=pS 求压力。
第九章 压强
压强公式p=F/S和p=ρgh的应用
1.用公式 p=FS求固体压强 若物体放在水平地面上,压力在数值上等于物体所受的重力 G, 则压强 p=FS=GS ;若是求盛液容器对水平面的压强,则 p=FS=G容+S G液。
2.用 p=ρgh 求柱体对水平面的压强 将一密度均匀、高为 h 的柱体(包括圆柱体、长方体、正方体等)
1.如图所示,甲、乙两个实心的圆柱体放在水平地面上,它们对地面的 压强相等,下列判断正确的是( A )
A.甲的密度大,甲受到的重力小 B.甲的密度小,甲受到的重力小 C.甲的密度大,甲受到的重力大 D.甲的密度小,甲受到的重力大
ห้องสมุดไป่ตู้
2.如图所示,由同种材料制成的实心圆柱体A和B放在水平地面上,它们的
(2)由图可知,矿泉水瓶内水的体积:
V=S 瓶底 h 立正=28 cm2×10 cm=280 cm3,由ρ=mV可得, 水的质量:m 水=ρV=1.0 g/cm3×280 cm3=280 g,
瓶重和厚度忽略不计,则倒立放置时矿泉水瓶对桌面的压力: F'=G 水=m 水 g=0.28 kg×10 N/kg=2.8 N, 倒立放置时矿泉水瓶对桌面的压强:p'=FS瓶'盖=8×21.80-N4 m2=3 500 Pa。
6.如图所示中的两个容器中盛有同种相同质量的液体,容器底部受到的液
探究液体对容器底部的压力
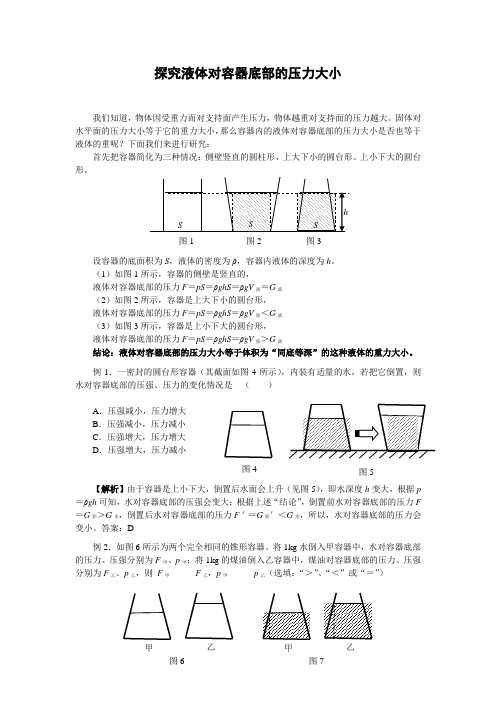
探究液体对容器底部的压力大小我们知道,物体因受重力而对支持面产生压力,物体越重对支持面的压力越大。
固体对水平面的压力大小等于它的重力大小,那么容器内的液体对容器底部的压力大小是否也等于液体的重呢?下面我们来进行研究:首先把容器简化为三种情况:侧壁竖直的圆柱形、上大下小的圆台形、上小下大的圆台形。
设容器的底面积为S,液体的密度为ρ,容器内液体的深度为h。
(1)如图1所示,容器的侧壁是竖直的,液体对容器底部的压力F=pS=ρghS=ρgV液=G液(2)如图2所示,容器是上大下小的圆台形,液体对容器底部的压力F=pS=ρghS=ρgV影<G液(3)如图3所示,容器是上小下大的圆台形,液体对容器底部的压力F=pS=ρghS=ρgV影>G液结论:液体对容器底部的压力大小等于体积为“同底等深”的这种液体的重力大小。
例1.一密封的圆台形容器(其截面如图4所示),内装有适量的水,若把它倒置,则水对容器底部的压强、压力的变化情况是()A.压强减小,压力增大B.压强减小,压力减小C.压强增大,压力增大D.压强增大,压力减小【解析】由于容器是上小下大,倒置后水面会上升(见图5),即水深度h变大,根据p =ρgh可知,水对容器底部的压强会变大;根据上述“结论”,倒置前水对容器底部的压力F=G影>G水,倒置后水对容器底部的压力F'=G影'<G水,所以,水对容器底部的压力会变小。
答案:D例2.如图6所示为两个完全相同的锥形容器。
将1kg水倒入甲容器中,水对容器底部的压力、压强分别为F甲、p甲;将1kg的煤油倒入乙容器中,煤油对容器底部的压力、压强分别为F乙、p乙,则F甲______F乙,p甲______p乙(选填:“>”、“<”或“=”)图1 图2 图3图4 图5甲图7乙甲图6乙【解析】根据上述结论,液体对容器底部的压力均等于阴影部分的液体重(如图7所示), 依据图形的对称性可知,阴影中虚线右侧的液体质量均为1kg ,说明液体深度确定,酒精底面积小时,酒精与水的质量可相等,而虚线左侧酒精的质量比水大(液体深度未变,虚线左侧酒精的底面积较大),所以,F 甲 <F 乙,又甲、乙容器的受力面积相同,根据S F p =可知,p 甲<p 乙。
压强计算

1、液体----计算水平桌面上放一质量为100g、底面积为的圆柱形茶杯(杯的厚度不计),杯中有10cm深的水,则水对杯底的压强为___Pa,桌面对杯子的支持力为__N,杯子对桌面的压强为___Pa(g取10N/kg)。
2、煤油对塞子的压力.油罐里装着4.8米深的煤油,在罐壁上有2厘米2的小孔,用塞于塞着,塞子中心距罐底0.3米,(煤油的密度是0.8×103千克/米3)3、水坝某水坝高50 m,上游水位40 m,则坝底受到的水的压强是多大?4、液体----计算在水平桌面上放着一个玻璃杯,水面距杯底10cm,水的质量是0.13kg,玻璃杯重0.5N,玻璃杯的底面积是,则水对杯底部的压强是___Pa,杯子对桌面的压强是___Pa.(取g=10N/kg)5、两端开口的玻璃管两端开口的玻璃管,下端管口用塑料挡住后插入水中,塑料片并不下沉,求:(1)若h=20厘米,塑料片受到液体的压强多大?(2)不计塑料片本身重,向管中慢慢注入酒精,求使塑料片恰好脱落时酒精柱的高度?6、塑料片并不下沉两端开口的玻璃管,下端管口用塑料挡住后插入水中,塑料片并不下沉,求:(1)若h=20厘米,塑料片受到液体的压强多大?(2)不计塑料片本身重,向管中慢慢注入酒精,求使塑料片恰好脱落时酒精柱的高度?7、封闭的L形容器是A端开口B端封闭的L形容器,内盛有水,已知B端顶面离容器底6厘米,A 端内液面离容器底26厘米。
8、求该液体的密度.底面积为40厘米2的圆筒形容器,内装某种液体,测得距液面30厘米处的器壁上的A点处所受到的液体的压强为2352帕斯卡.9、玻璃杯的质量.?一平底玻璃杯放在水平桌面上,内装150g的水,杯子与桌面的接触面积是10cm2.求:(1)水对杯底的压强;(2)若桌面所受玻璃杯的压强是2.7×103Pa,求玻璃杯的质量.(取g=10N/kg)10、箱内顶部受到水的压强和压力水平地面上放有一个边长为30cm的正方体箱子,箱子重50 N,其顶部有一根长20 cm、横截面积为4 cm2竖直的管子与箱子相通,管子重10 N,管子和箱子都灌满水,求:(1)箱内顶部受到水的压强和压力;(2)箱内底部受到水的压强和压力;(3)水的重力;(4)箱子对水平面的压力和压强.11、茶壶底部的压力?平底茶壶的质量是400g,底面积是40cm2,内盛0.6kg的开水,放置在面积为1m2的水平桌面中央。
有关液体对容器底部压力压强计算

有关液体对容器底部压力压强计算The Standardization Office was revised on the afternoon of December 13, 20201.如图11所示,水平地面上放置一个装有质量为5千克水的薄壁圆柱形容器,该容器的质量为1千克、高为0.7米、底面积为0.01米2。
①求容器中水的体积V水。
②求容器对水平地面的压力F容。
③求水对容器底部的压强p水。
2.质量为1千克的柱形薄壁容器放在水平面上,底面积为0.01米2,高为0.6米,装有0.5米深的酒精(ρ酒精=0.8×103千克/米3),如图11所示。
求:①酒精对容器底部的压强。
②容器对水平面的压强。
③在酒精中放入一个固体,保持酒精不溢出,使酒精对容器底部压强的增加量最大的情况下,同时使容器对水平面压强的增加量最小,请计算固体的质量,并判断固体密度ρ固与酒精密度ρ酒精之间的大小关系,即ρ固ρ酒精。
3.如图10所示,装有水的薄壁轻质圆柱形容器底面积为1×10-2米2,静止在水平面上。
①若容器内水的体积为2×10-3米3,求水的质量m水和水对容器底部的压强p水。
②若容器内水的质量为m,现有物体A、B(其密度、体积的关系如右表所示),请选择一个,当把物体浸没在水中时(水不会溢出),可使水对容器底部压强p′水与水平地面受到的压强p′地的比值最小。
选择______物体(选填“A”或“B”)。
求p′水与p′地的最小比值。
(用m、ρ水、ρ、V表示)图44.某实心均匀圆柱体放置在水平地面上,其质量为20千克、体积为8×10-3米3、底面积为4×10-2米2。
①求圆柱体的密度ρ;②求圆柱体对水平地面的压强p ;③水平面上还有A 、B 两个圆柱体(相关数据如表所示),请将其中_____(选填“A”或“B”)圆柱体竖直叠放在另一个圆柱体的上部中央,使上圆柱体对下圆柱体的压强最大。
压力与压强计算

一、公式 1、P F F P S(适合于固体、液体、气体)
S
2、P gh(只适合于液体) 二、例题分析:
例1. 冰面上能够承受的压强是4.2x104Pa.一辆坦克 的质量为2.8x104Kg,它的一条履带跟冰面的接触面 积为3.5m2,这辆坦克能否从冰面上驶过?一个人的 质量是70kg,一只鞋底的面积是150cm2,这个人能否 在该冰面上行走?
例5.盛水容器中投入一个质量为0.2N的木块后,水 面上升了1cm,容器的底面积为25cm2,则投入木块 后容器底受到的压力增加了多少?
解:压强增加:p=ρgh=1000kgx9.8N/kgx0.01m=98Pa
压力增加: p=F/S 所以 F=Ps=98Pax0.0025m2 =0.245N
例6.如图所示,将一个两端开口的玻璃管下端用橡皮膜封 住后,倒入12cm深的水,橡皮膜向下凸出,现将它竖直 放入装有密度为1.2x103Kg/m3的液体容器中,则( )
A、当玻璃管浸入深度为8cm时,橡皮膜变平; B、当玻璃管浸入深度为10cm时,橡皮膜向上凹; C、当玻璃管浸入深度为12cm时,橡皮膜向下凸; D、当玻璃管浸入深度为12cm时,橡皮膜向上凹
P1=2
Ρ1gh1= ρ2gh2 1000Kg/m3x0.12m=1200Kg/m3xh2
(3)G=ρvg=1000kgx9.8N/kgx0.004m3 =39.2N
拓展练习3:
如图所示的三个底面积相等的容器,质量相同,分别装 有___高=__度__相P等丙;的液同体种对液底体, 的. 则压液力体F甲对_底__=的__压F乙强__P_甲_==_____F_丙P;乙容 器对桌面的压强P甲’<____P乙<’____P丙’.
比较压强与压力大小的方法

比较液体内部压强大小与压力大小的方法(甘肃省兰州市三十一中学撖爱嵘)关键词:液体内部压强压力重力浸没深度密度底面积文章摘要:根据公式P=ρ液g h知液体内部压强与液体的密度ρ和深度h有关,再根据公式F=PS知液体对容器底部的压力与液体对容器底部的压强和容器底面积大小有关。
比较液体内部压强与压力时,应先根据公式P=ρ液g h比较P,再根据公式F=PS比较F。
学习液体内部压强以后,从公式p=ρ液g h来看这部分知识似乎很容易掌握,但是实际遇到的问题却很难处理,这部分内容是初中物理的重点也是难点,下面就怎样比较液体内部压强和压力大小给予讲解。
一、同种液体例1:如图所示:甲、乙、丙三个容器,底面积相同,高度相同,但形状不同,装满同一种液体:(不考虑容器本身的重力)(1)则容器底部所受到的压强: P甲 P乙P丙,(2)容器底部所受到的压力: F甲 F乙F丙,解析:(1)根据公式p=ρ液g h可知液体内部压强大小只与液体的密度ρ和深度h有关,所以容器底部受到的压强大小关系:P甲=P乙= P丙。
(2)再根据公式F=PS知液体对容器底部的压力与液体对容器底部压强和容器底面积大小有关,所以液体对容器底部的压力大小关系:F甲=F乙=F丙。
比较同种液体对容器底部的压强和压力时,应先根据P=ρ液g h比较P,再根据F=PS比较F。
二、不同种液体例2:如图所示:水平桌面并排放着两个完全相同的圆柱体容器,两容器中分别盛有质量相同的水和酒精,则容器底部受到液体的压强:(1) P甲 P乙;(2)容器底部受到液体的压力:F甲F乙;(3)容器底部所受到的压力与容器中液体的重力比较:F甲 G水, F乙G酒;解析:(1)根据公式P=ρ液g h与m液=ρ液v液=ρ液sh得:p=m液g/s,甲、乙是同一容器:S甲=S乙,且m水=m酒,因此液体对容器底部的压强:P甲=P乙。
(2)根据公式F=PS知液体对容器底部的压力:F甲=F乙。
(3)容器底部受到的压力与容器中液体的重力大小关系:F甲=G水,F乙=G酒。
压力压强(三)------对容器底部的压强压力与对桌面的压强压力计算

压力压强--两种压强压力的计算专题一:容器中液体对容器底部的压强压力计算。
解题思路:因为容器底部是被液体压着的,所以去求液体对容器底部的压强与压力时,应该用液体压强公式P=ρ液gh先算压强,再利用固体压强的变形公式F=PS去计算液体对容器底的压力。
步骤一:先求压强,利用公式P=ρ液gh步骤二:再求压力,利用公式F=PS专题二:容器对水平桌面的压强压力计算。
解题思路:容器放在水平桌面上,容器中的液体压在容器上,所以容器对水平桌面的压力求解对桌面的压强。
大小应该等于容器的重力加上液体的重力:F=G总=G液+G容。
再利用P=FS步骤一:先算压力,利用公式F=G液+G容步骤二:再算压强,利用公式P=FS练习题一.选择题1.(多选)小强将一只质量为1kg的平底水桶放在水平地面上,如图所示。
已知该水桶的底面积为5×10-2m2,桶内装有50cm深的水,水对桶底的压力比桶对地面的压力小40N,g取10N/kg。
下列判断中正确的是()A. 水对桶底的压强为5×105PaB. 水对桶底的压力为250NC. 桶对地面的压力为290ND. 桶内水的质量为28kg2.如图所示,玻璃杯里有3N的4℃的水(密度ρ水=1g/cm3),水的深度为10cm,玻璃杯重0.6N,玻璃杯底面积为20cm2(杯的厚度可以不计),g取10N/kg。
已知水在4℃时密度最大,不考虑玻璃杯的热胀冷缩,以及水的物态变化,则当水温从0℃逐渐升高到10℃的过程中()A. 水对杯底的压强可能是1001PaB. 杯子对桌面的压强始终是1500PaC. 杯子对水面的高度可能是9.9cmD. 水对杯底的压力一定先增大后减小3.如图所示,盛有水的平底紫砂壶静止在水平桌面上。
壶重1N ,高9cm ,底面积为30cm 2;壶内水重2N ,水深6cm ,水的密度为331.010kg/m ⨯ ,g 取10N/kg 。
下列选项中正确的是( )A. 水对壶底的压力为2NB. 水对壶底的压强为900PaC. 紫砂壶对桌面的压力为2.8ND. 紫砂壶对桌面的压强为1000Pa4.如图11所示,盛有水的杯子静止在水平桌面上。
液体的压强公式和计算

液体压强的特点
• 1、液体内部向各个方向都有压强; • 2、同一深度,液体向各个方向的压强相等。
3、 同种液体的压强随深度的增加而增大
探究实验2
研究液体内部压强大小与液体密度的关系。
实验步骤:保持金属盒在液体中的深度不 变,把金属盒分别放入三种液体(盐水、 水和煤油)中,记录U形管高度差,改变 深度在做两次。
液体对容器底和容器壁有压强液体内部向各个方向都有压强液体的压强随深度的增加而增大同一深度液体向各个方向的压强相等不同液体的压强还与密度有关深度一定时液体密度越大压强越大h1h2h3ah1h2二液体压强的特点液体在某一深度的压强有多大要知道液面下某处竖直向下的压强可以设想在此处有个水平放置的平面计算这个平面上方液柱对这个平面的压强即可设平面在液面下的深度为h平面的面积为s液体压强公式的推导水柱的体积为vsh水的密度为水柱的质量为mv水柱对底面积的压力为fgmgvgshg水柱对其底面积的压强为pfsshgsgh即深度为h处的液体压强p液体在任一深度的压强液体的密度g常数nkgh深度指从自由液面到液体内部某一位置的竖直距离三液体压强的公式区分深度和高度深度
p gh
三、液体压强的公式
p gh
p——液体在任一深度的压强
——液体的密度
g——常数 g 9.8 N/kg
h——深度 指从自由液面到液体内部 某一位置的竖直距离
区分深度和高度
深度:液体内一点到上面 自由液面的竖直距离。
高度:液体内一点到下面 容器底的竖直距离。
A点的深度和高度分别是 多少?
图中是探究液体内部压强的实验 (三个容器中都装有水),能得出的 结论是_液体内部朝各个方向都有压强
实验表格:
深度(cm) 3 3 3 6 6 6 9 9 9
有关固体、液体压力、压强的计算思路

有关固体、液体压力、压强的计算思路全文共四篇示例,供读者参考第一篇示例:关于固体、液体的压力和压强计算是物理学领域中的一个重要概念。
在日常生活中,我们经常会遇到需要计算压力和压强的情况,比如在工程项目中评估建筑物或桥梁的承载能力,或者在科学研究中分析液体在容器内的压力分布等等。
本文将简要介绍固体、液体的压力和压强的概念,并提供一些计算思路和方法,以帮助读者更好地理解和应用这些概念。
我们来了解一下固体、液体的压力和压强是什么意思。
在物理学中,压力是一个力对某个面积的作用程度的量度,通常用P来表示,其单位为帕斯卡(Pa),即牛顿每平方米(N/m2)。
而压强是指单位面积上的压力,通常用p表示,其单位也是帕斯卡。
比如说,一个物体受到100牛顿的力作用在一个面积为1平方米的表面上,那么该表面上的压力就是100帕斯卡。
固体和液体在受到外力作用时会产生压力,而这种压力会传递到物体的各个部分。
在固体中,分子之间的相互作用力较大,所以在外力的作用下,固体的形状和体积都会保持不变,这种状态称为固体的静水压力。
而在液体中,分子之间的相互作用力较小,所以在外力的作用下,液体会产生形变,但体积大小不会发生改变,这种状态称为液体的静水压力。
在计算固体、液体的压力和压强时,可以采用下面的方法:1. 计算固体的压力:在计算固体的压力时,可以使用公式P =F/A,其中P表示压力,F表示作用在物体上的力,A表示受力面积。
通过这个公式,我们可以很方便地计算出固体受到的压力大小。
在实际应用中,我们可以根据需要来选择不同的计算方法和公式,以求得准确的结果。
在进行计算时,还需要考虑一些可能影响计算结果的因素,比如液体的温度、密度和表面张力等。
只有充分考虑这些因素,我们才能得到更加准确和可靠的计算结果。
了解固体、液体的压力和压强计算方法是非常重要的。
通过本文的介绍,希望读者能够更深入地理解这些概念,并能够灵活运用到实际的问题中去。
希望读者能够在学习和工作中充分运用这些知识,以提高自己的理论水平和实践能力。
有关液体压强变化范围的计算

有关液体压强变化范围的计算考点小结1.将固体放入装有液体的容器,液体对容器底部或容器对水平面的压强的变化量的问题,需要思考的是液体是否装满,是否有液体溢出。
2.液体对容器底部压强的变化量:若容器中液体装满,压强增加量为0; 若液体溢出,压强增加量最大为:max max F F p g h p S S∆∆ρ∆∆===浮液或 (仅限于柱体)。
3.容器对水平桌面压强的变化量: 若液体未溢出,G F p S S∆∆==物; 若液体装满,()()=G G G F F p S S S∆∆--==溢浮物物(水未溢出)。
4.液体对容器底部的压力的增加量不一定等于放入物体的重力。
当物体漂浮或悬浮时,=F F pS g hS gV ρρ∆=∆=∆=浮液液排,F 浮=G 物,故增加的压力等于物体所受到的重力。
当物体沉底时,=F F pS g hS gV ρρ∆=∆=∆=浮液液排,F 浮<G 物故增加的压力小于物体所受到的重力。
5.如图1所示,以下仅限于柱体研究:V 浸=V 排。
图1典型例题例1 金属实心圆柱体甲的密度为2.0×103kg/m 3,体积为10-3m 3;底面积为2×10-2m 2的薄壁圆柱形容器乙放在水平地面上,容器内盛有水,水深0.2m 。
若将甲浸没在乙容器的水中,求水对容器底部的压强的变化量的范围。
【分析】将甲球放入水中,水面升高,水对容器底部的压强增加,由于容器中水是否盛满不确定,所以如果水满了,水对容器底部的压强不变,如果未满,将甲放入后,水不溢出,水对容器底部的压强增加最多。
水对容器底部的压力的最大增加量可以通过两个途径解决:①计算增加的深度的变化量//h V S V S ∆=∆=物,然后利用p g h ρ∆=∆液。
②柱形容器中液体对容器底部增加的压力等于物体在液体中所受到的浮力,F F ∆=浮,然后利用/p F S ∆=∆计算增加的压强。
【解答】方法一:若水是满的,p ∆=0;若水未满,未溢出,//h V S V S ∆=∆=物=10-3m 3/2×10-2m 2=5×10-2mp g h ρ∆=∆液=1×103kg/m 3×9.8N/kg×5×10-2m=490Pa方法二:若水是满的,p ∆=0若水未满,未溢出://=/p F S F S g V S ρ∆=∆=∆浮液=1×103kg/m 3×9.8N/kg×10-3m 3/2×10-2m 2=490Pa水对容器底部的压强的变化量的范围:0~490Pa 。
液体压强的计算

液体压强的计算
液体压强是指液体所产生的压力在单位面积上的大小,它是物理
学中的一个重要概念。
在现实生活中,我们常常能够观察到一些与液
体压强相关的现象,如水柱喷泉、水龙头流水等。
液体的压强可以通过以下公式计算得出:压强 = 压力 / 面积。
其中,压力是指液体对容器壁面产生的力,面积则是压力作用的范围。
这个公式的意义在于告诉我们,液体产生的压强与压力的大小和面积
的关系密切。
在液体压强的计算中,我们要注意使用正确的单位。
国际单位制中,压强的单位是帕斯卡(Pa),压力的单位是牛顿(N),面积的单
位是平方米(m²)。
如果液体压强的计算结果过大,常常会转换成较
大的单位,如千帕(kPa)或兆帕(MPa)。
液体压强的计算有很多实际应用。
在工程领域中,液体压强的计
算对于设计水坝、管道系统等起着重要的作用。
在建筑领域中,液体
压强的计算有助于确定水池或泳池的结构强度。
在医学领域中,液体
压强的计算被用于研究血液循环和呼吸系统。
液体压强的计算还可以帮助我们更好地理解一些自然现象。
例如,液体压强的计算可以解释为什么一个完全密闭的容器中的液体不会漏出,因为液体在容器壁面上产生的压强会阻止液体流出。
另外,液体
压强的计算也可以解释为什么潜水时,水压越来越大,因为随着深度
的增加,液体压强也随之增加。
总之,液体压强的计算对于理解液体力学和解决实际问题具有重要的指导意义。
通过正确运用液体压强的计算公式,我们能够更好地应用物理知识于生活和工作中,为工程设计、建筑结构、医学研究等领域的发展做出贡献。
底部压强公式

底部压强公式全文共四篇示例,供读者参考第一篇示例:底部压强公式是描述液体或气体在容器底部所受到的压力的数学公式。
在物理学和工程学中,底部压强公式是一个重要的概念,可以帮助我们理解和计算液体或气体在容器底部受到的压力大小。
在本文中,我们将介绍底部压强公式的推导过程和应用领域,并且讨论一些相关的实际问题。
让我们来看看底部压强公式的推导过程。
假设在一个封闭容器中有一种液体或气体,容器的底部面积为A,液体或气体的密度为ρ,液体或气体的高度为h。
根据流体静力学原理,液体或气体底部所受到的压力P可以用以下公式表示:P = ρghP表示压强,ρ表示液体或气体的密度,g表示重力加速度,h表示液体或气体的高度。
这就是底部压强公式的基本形式。
这个公式的推导过程其实很简单,我们可以通过流体静力学的基本原理来推导得到。
在一个封闭容器中,液体或气体的底部所受到的压力是由于整个液体或气体的重力所产生的。
而根据牛顿第二定律,压力等于力除以面积,所以底部压力可以表示为重力除以底部面积,即P = F/A。
重力F可以表示为液体或气体的密度乘以重力加速度乘以液体或气体的高度,即F = ρgh。
将这个表达式代入P = F/A中,就得到了底部压强公式P = ρgh。
底部压强公式在物理学和工程学中有着广泛的应用。
在液体力学中,底部压强公式可以帮助我们计算液体底部所受到的压力,进而计算液体的压力分布和流体力学性质。
在气体力学中,底部压强公式同样可以用来计算气体底部的压力情况,帮助设计气体系统和设备。
在工程实践中,底部压强公式也被广泛应用于水利工程、气体储存设备等领域。
除了以上的应用领域,底部压强公式还可以用来解决一些实际的问题。
在设计一个水池时,我们需要计算水底部所受到的压力,以确保水池的承载能力符合设计要求。
又如,在气体储存罐设计中,我们也需要考虑气体底部受到的压力,以确保罐体的安全性。
底部压强公式提供了一个简单而有效的计算方法,帮助我们解决这些问题。
压强的三个计算公式

压强的三个计算公式压强是物理学中的一个重要概念,它是指单位面积上所受到的力的大小。
在物理学中,压强是一个很常见的概念,它在力学、流体力学、热力学等领域都有着广泛的应用。
本文将介绍压强的三个计算公式,帮助读者更好地理解和应用压强概念。
一、压强的定义在介绍压强的计算公式之前,我们先来了解一下压强的定义。
压强是指单位面积上所受到的力的大小,通常用P表示,其计算公式为: P=F/A其中,F表示作用在面积A上的力的大小,A表示面积的大小。
压强的单位是帕斯卡(Pa),1Pa等于1牛顿/平方米。
二、压强的计算公式1.液体静压力的计算公式液体静压力是指液体静止时,作用在液体内部的压力。
液体静压力的计算公式为:P=ρgh其中,ρ表示液体的密度,g表示重力加速度,h表示液体的深度。
液体静压力的大小与液体的密度、深度和重力加速度有关。
2.气体压强的计算公式气体压强是指气体分子对容器壁的碰撞力,它由气体分子的热运动引起。
气体压强的计算公式为:P=nRT/V其中,n表示气体分子的数量,R表示气体常数,T表示气体的温度,V表示气体的体积。
气体压强的大小与气体分子的数量、温度、体积有关。
3.流体动压力的计算公式流体动压力是指流体在运动时,由于惯性作用所产生的压力。
流体动压力的计算公式为:P=ρv/2其中,ρ表示流体的密度,v表示流体的速度。
流体动压力的大小与流体的密度和速度有关。
三、压强的应用压强在生活中有着广泛的应用,如:1.水压力的应用水压力是指水流对容器壁的压力,它决定了水流的流速和流量。
在水压力的作用下,我们可以利用水泵将水从低处抽到高处,实现水的输送和供应。
2.气压力的应用气压力是指气体分子对容器壁的碰撞力,它决定了气体的压力和体积。
在气压力的作用下,我们可以利用气压力驱动气动工具、气动设备等,实现生产和制造。
3.流体动压力的应用流体动压力是指流体在运动时,由于惯性作用所产生的压力。
在流体动压力的作用下,我们可以利用水轮机、风力机等,将流体的动能转化为机械能,实现能源的转换和利用。
液体压强计算

液体压强计算液体压强计算是物理学中的一个重要概念,涉及到力、面积和液体的高度等因素。
通过正确计算液体压强,我们可以深入理解液体行为、设计和优化液体力学装置等领域。
首先,让我们来了解液体压强的含义。
液体压强指的是液体对一个单位面积的垂直力。
液体压强的大小与液体的高度和密度有关,以及液体所受到的外界压力。
液体压强的计算公式是P = ρgh,其中P表示压强,ρ表示液体的密度,g表示重力加速度,h表示液体的高度。
在这个公式中,液体的密度ρ是衡量液体质量的物理量。
密度是由液体的质量和体积决定的,计算公式为ρ = m/V,其中ρ代表密度,m代表液体的质量,V代表液体的体积。
液体的质量可以通过称量得到,而体积可以通过测量容器的尺寸得到(比如长度、宽度和高度),也可以通过其他方式测量(比如位移法或容量瓶等)。
液体压强还受到液体所受外界压力的影响。
这种外界压力可能来自液体上方存在的气体、其他液体的作用,或者来自容器结构自身的压力。
在计算液体压强时,我们需要将这些外界压力考虑在内。
计算液体压强的常见单位是帕斯卡(Pascal),它的定义是1帕斯卡等于1牛顿/平方米。
除了帕斯卡之外,液体压强也可以用其他单位表示,比如毫米汞柱(mmHg)、巴(bar)或标准大气压等。
接下来,让我们通过一个具体的例子来应用液体压强的计算方法。
假设我们有一个高度为10米的柱状容器,内部装满了水。
现在我们想要计算水底的压强。
首先,我们需要得到水的密度。
水的密度在20摄氏度下约为1000千克/立方米。
然后,我们需要考虑外界压力。
通常情况下,如果液体上方没有其他气体,我们可以忽略外界压力对压强的影响。
但是如果柱状容器有一个开口,上面有空气进入,我们需要考虑大气压力的影响。
标准大气压定义为101.325千帕,等于101325帕斯卡。
因此,我们可以使用液体压强的公式P = ρgh来计算水底的压强。
P = 1000 kg/m^3 * 9.8 m/s^2 * 10 m = 98000帕斯卡如果我们想要将压强换算成大气压,可以使用P = P/101325来计算。
物理专题6——液压不规则容器问题
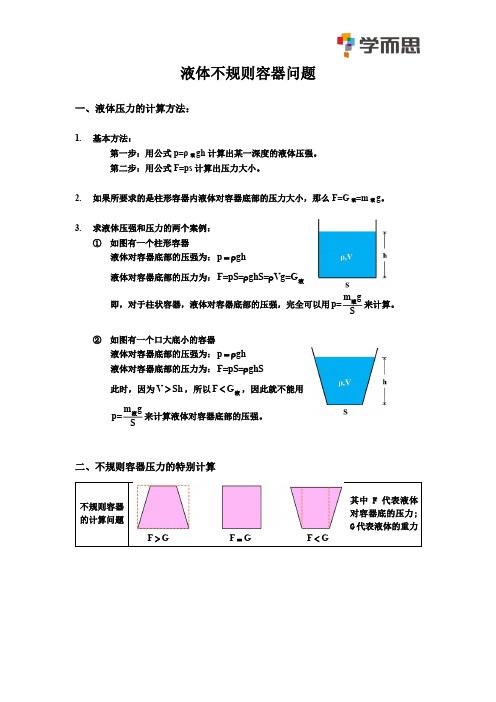
液体不规则容器问题一、液体压力的计算方法:1. 基本方法: 第一步:用公式p=ρ液gh 计算出某一深度的液体压强。
第二步:用公式F=ps 计算出压力大小。
2. 如果所要求的是柱形容器内液体对容器底部的压力大小,那么F=G 液=m 液g 。
3.求液体压强和压力的两个案例: ① 如图有一个柱形容器液体对容器底部的压强为:p gh =ρ液体对容器底部的压力为:F=pS=ghS=Vg=G ρρ液 即,对于柱状容器,液体对容器底部的压强,完全可以用m g p=S液来计算。
② 如图有一个口大底小的容器液体对容器底部的压强为:p gh =ρ 液体对容器底部的压力为:F=pS=ghS ρ此时,因为V Sh >,所以F G <液,因此就不能用m g p=S液来计算液体对容器底部的压强。
二、不规则容器压力的特别计算不规则容器的计算问题F G >F G = F G <其中F 代表液体对容器底的压力; G 代表液体的重力例题精选【例1】 如图所示,在一个上大下小的容器中放入重15N 的水,水对容器底部的压力( ) A. 大于15N B. 等于15N C. 小于15ND. 不能判断【例2】 如图所示的三个容器中分别装有酒精、清水与盐水。
它们对容器底部的压力相等,则所装三种液体中,质量最大的是 ,质量最小的是 。
【例3】 如图所示,两个完全相同的圆台形容器,放置在水平桌面上,容器内盛有深度相同的水,则水对容器底部的压强p a ______ p b ,水对容器底部的压力F a ______ F b ,容器对桌面的压力F ’a ______ F ’b 。
(选填“大于”、“等于”或“小于”)【例4】 如图所示,两个底面积相等而形状不同的容器,将1kg 水倒入甲容器中,水对容器底部的压强是p 甲;将1kg 水倒入乙容器中,水对容器底部的压强是p 乙,那么p 甲 p 乙,水对容器底部的压力F 甲 F 乙(填“>”、“ ”或“=”)【例5】 如图所示,容器重为G 1,放在水平桌面上,容器内盛有重为G 2的液体。
物体放入液体中压力压强变化的计算

物体放入液体中压力压强变化的计算初中物理压强习题中,将物体放入装有液体的规则容器,液体对容器底部或容器对水平面的压强的变化量的问题,一需要思考的是液体是否装满,是否有液体溢出。
二还要考虑物体在液体中是处于漂浮、悬浮还是沉底哪一种状态。
1、物体放入规则容器液体中,对容器底部压强的变化量:(1)、若容器中液体装满,物体放入后,液体溢出。
液体密度和高度都不变,所以液体对容器底部的压力和压强增加量为0;(不考虑物体在液体中的状态)(2)、若容器中液体未装满,液体未溢出,压力和压强增加量最大为:==F pS g hS g V F V F p g h gSS∆∆ρ∆ρ∆∆ρ∆ρ=====浮液液排排浮液液2、物体放入规则容器液体中,容器对水平桌面压力压强的变化量: (1)、若液体未溢出,G Fp SS∆∆==物;(2)、若液体装满,()()=G G G F Fp S S S∆∆--==浮物排物。
容器对桌面的压力和压强就要看物体在液体中的状态。
①、若物体在液体中处于漂浮、悬浮时,=G F 浮物,容器对桌面的压力和压强不变,若物体有外力悬挂在液体中处于浸没状态===0F F G F F --压浮支物拉对桌面的压力和压强也不变,②、若有物体在液体中处于沉底状态是,容器对水平桌面压力和压强才变大,===F G G G F F ∆∆--压浮物排物支()()==G G G F F Fp S S S S∆∆--==浮物排物支,1、装有液体的甲乙两烧杯,分别放人两个完全相同的物体,当物体静止后两烧杯中液面恰好相平,如图所示,液体对甲乙烧杯底部压强分别是P甲、P乙,液体对两物体的浮力分别是F甲、F乙,则对它们的判断正确的是()A.P甲=P乙,F甲>F乙B.P甲>P乙,F甲=F乙C.P甲=P ,F甲<F乙D.P甲<P乙,F甲=F乙【知识拓展】如果甲中木块沉底,那么这道题目的结果又会如何?2、在两个完全相同的容器A和B中分别装有等质量的水和酒精(p水>p酒精),现将两个完全相同的长方体木块甲和乙分别放到两种液体中,如图2所示,则此时甲和乙长方体木块下表面所受的压强P甲、P乙,以及A和B两容器底部所受的压力FA、FB的关系是()A.P甲<P乙FA<FB。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.如图11所示,水平地面上放置一个装有质量为5千克水的薄壁圆柱形容器,该容器的质量为1千克、高为0.7米、底面积为0.01米2。
①求容器中水的体积V水。
②求容器对水平地面的压力F容。
③求水对容器底部的压强p水。
2.质量为1千克的柱形薄壁容器放在水平面上,底面积为0.01米2,高为0.6米,装有0.5米深的酒精(ρ酒精=0.8×103千克/米3),如图11所示。
求:
①酒精对容器底部的压强。
②容器对水平面的压强。
③在酒精中放入一个固体,保持酒精不溢出,使酒精对容器底部压强的增加量最大的情况下,同时使容器对水平面压强的增加量最小,请计算固体的质量,并判断固体密度ρ固与酒精密度ρ酒精之间的大小关系,即ρ固ρ酒精。
3.如图10所示,装有水的薄壁轻质圆柱形容器底面积为1×10-2米2,静止在水平面上。
①若容器内水的体积为2×10-3米3,求水的质量m水和水对容器底部的压强p水。
②若容器内水的质量为m,现有物体A、B(其密度、体积的关系如右表所示),请选择一个,当把物体浸没在水中时(水不会溢出),可使水对容器底部压强p′水与水平地面受到的压强p′地的比值最小。
选择______物体(选填“A”或“B”)。
求p′水与p′地的最小比值。
(用m、ρ水、ρ、V表示)
图4
图5物体密度体积Aρ2V B3ρV
..
..
图14
4.某实心均匀圆柱体放置在水平地面上,其质量为20千克、体积为8×10-3米3、底面积为4×10-2米2。
①求圆柱体的密度ρ;
②求圆柱体对水平地面的压强p ;
③水平面上还有A 、B 两个圆柱体(相关数据如表所示),请将其中_____(选填“A”或“B”)圆柱体竖直叠放在另一个圆柱体的上部中央,使上圆柱体对下圆柱体的压强最大。
求出此最大压强p 最大。
5.某实心均匀圆柱体放置在水平地面上,其质量为20千克、体积为8×10-3米3、底面积为4×10-2米2。
①求圆柱体的密度ρ;
②求圆柱体对水平地面的压强p ;
③水平面上还有A 、B 两个圆柱体(相关数据如表所示),请将其中_____(选填“A”或“B”)圆柱体竖直叠放在另一个圆柱体的上部中央,使上圆柱体对下圆柱体的压强最大。
求出此最大压强p 最大。
6.如图所示,水平地面上足够深的轻质圆柱形容器中放有质量为2.1千克,密度为0.75×103千克/米3的圆柱形木块,木块、容器的底面积分别为3S 、8S 。
① 求圆柱形木块的体积V 木。
② 在容器中加入水,当水深为0.01米,求水对容器底部的压强p 。
③ 继续往容器中加水,当木块对容器底部的压力恰好为0时,求容器对桌面的压力F 。
圆柱体 底面积 质量 A S 5m B
5S
m
圆柱体 底面积 质量 A S 5m B
5S
m
7.如图12所示,底面积为2×10-2米2的圆柱形平底薄壁水槽放在水平地面上,一装有金属球的小盆漂浮在水槽的水面上,小盆的质量为1千克,金属球的质量为1.6千克,金属球的体积为0.2×10-3米3。
①若把金属球从盆中拿出并放入水槽中后,小球沉入水底,求容器对水平地面压强的变化量。
②求水对水槽底部的压强变化量。
图12
..。
