SVM-及SMO算法实现

合集下载

SVM-及SMO算法实现报告

直线f(x)呢？
最大距离Maximum Marginal
选择使得间隙最大的函数作为分割平面是由很多道理的，比如说从概
率的角度上来说，就是使得置信度最小的点置信度最大（听起来很拗口），从实践的角度来说，这样的效果非常好，等等。
最大距离
(x,y) M
M
wx+b=1 f(x)=wx+b=0 wx+b=-1
例如，当训练点数目超过4000时，存储核函数矩阵需要多达128兆。
求解方法：坐标上升法
min
a l 1 l l y i y j i j K ( x i , x j ) i 2 i 1 j 1 i 1
固定除 i 之外的所有参数，这时W可看作只是关于 i 的函数，那么直接对 i
问题提出
线性可分的分类问题：（令黑色的点 = -1，白色的点 =
+1）
f ( x) wr x b
+1 -1
所以当有一个新的点x需要预测属于哪个分类的时候，我们用sgn(f(x))，
就可以预测了，sgn表示符号函数，当f(x) > 0的时候，sgn(f(x)) = +1, 当f(x) < 0的时候sgn(f(x)) = –1。
w ,b a
f ( x) max min
a w ,b
f ( x)
求解
将两式带回L(w,b,a)得到对偶问题的表达式
1 2 L(w, b, a) w ai ( yi (w xi b) 1) 2 1 L(w, b, a) ai yi xi a j y j x j ai yi w xi ai yi b ai 2 i, j
l

支持向量机SMO算法实现（注释详细）

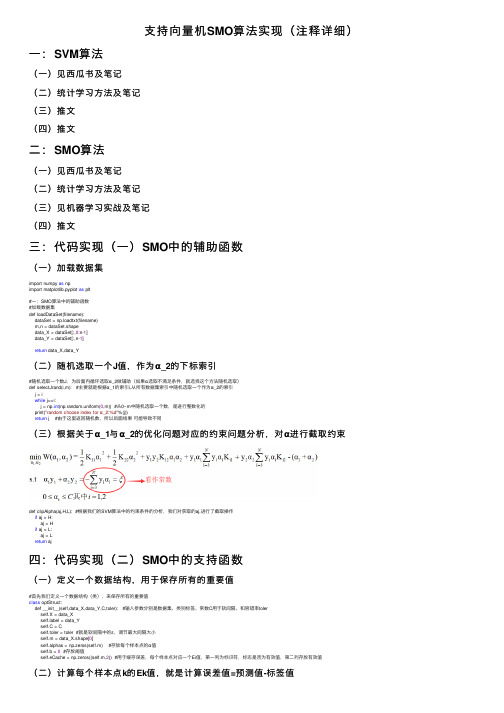
⽀持向量机SMO算法实现（注释详细）⼀：SVM算法（⼀）见西⽠书及笔记（⼆）统计学习⽅法及笔记（三）推⽂（四）推⽂⼆：SMO算法（⼀）见西⽠书及笔记（⼆）统计学习⽅法及笔记（三）见机器学习实战及笔记（四）推⽂三：代码实现（⼀）SMO中的辅助函数（⼀）加载数据集import numpy as npimport matplotlib.pyplot as plt#⼀：SMO算法中的辅助函数#加载数据集def loadDataSet(filename):dataSet = np.loadtxt(filename)m,n = dataSet.shapedata_X = dataSet[:,0:n-1]data_Y = dataSet[:,n-1]return data_X,data_Y（⼆）随机选取⼀个J值，作为α_2的下标索引#随机选取⼀个数J，为后⾯内循环选取α_2做辅助（如果α选取不满⾜条件，就选择这个⽅法随机选取）def selectJrand(i,m): #主要就是根据α_1的索引i,从所有数据集索引中随机选取⼀个作为α_2的索引j = iwhile j==i:j = np.int(np.random.uniform(0,m)) #从0~m中随机选取⼀个数，是进⾏整数化的print("random choose index for α_2:%d"%(j))return j #由于这⾥返回随机数，所以后⾯结果可能导致不同（三）根据关于α_1与α_2的优化问题对应的约束问题分析，对α进⾏截取约束def clipAlpha(aj,H,L): #根据我们的SVM算法中的约束条件的分析，我们对获取的aj,进⾏了截取操作if aj > H:aj = Hif aj < L:aj = Lreturn aj四：代码实现（⼆）SMO中的⽀持函数（⼀）定义⼀个数据结构，⽤于保存所有的重要值#⾸先我们定义⼀个数据结构（类），来保存所有的重要值class optStruct:def __init__(self,data_X,data_Y,C,toler): #输⼊参数分别是数据集、类别标签、常数C⽤于软间隔、和容错率tolerself.X = data_Xbel = data_Yself.C = Cself.toler = toler #就是软间隔中的ε，调节最⼤间隔⼤⼩self.m = data_X.shape[0]self.alphas = np.zeros(self.m) #存放每个样本点的α值self.b = 0 #存放阈值self.eCache = np.zeros((self.m,2)) #⽤于缓存误差，每个样本点对应⼀个Ei值，第⼀列为标识符，标志是否为有效值，第⼆列存放有效值（⼆）计算每个样本点k的Ek值，就是计算误差值=预测值-标签值#计算每个样本点k的Ek值，就是计算误差值=预测值-标签值def calcEk(oS,k):# 根据西⽠书6.24，我们可以知道预测值如何使⽤α值进⾏求解fxk = np.multiply(oS.alphas,bel).T@(oS.X@oS.X[k,:])+oS.b #np.multiply之后还是(m,1),(oS.X@oS.X[k,:])之后是(m,1),通过转置(1,m)@(m,1)-->实数后+b即可得到预测值fx#获取误差值EkEk = fxk - bel[k]return Ek（三）重点：内循环的启发式⽅法，获取最⼤差值|Ei-Ej|对应的Ej的索引J#内循环的启发式⽅法，获取最⼤差值|Ei-Ej|对应的Ej的索引Jdef selectJ(i,oS,Ei): #注意我们要传⼊第⼀个α对应的索引i和误差值Ei,后⾯会⽤到maxK = -1 #⽤于保存临时最⼤索引maxDeltaE = 0 #⽤于保存临时最⼤差值--->|Ei-Ej|Ej = 0 #保存我们需要的Ej误差值#重点：这⾥我们是把SMO最后⼀步（根据最新阈值b，来更新Ei)提到第⼀步来进⾏了，所以这⼀步是⾮常重要的oS.eCache[i] = [1,Ei]#开始获取各个Ek值，⽐较|Ei-Ej|获取Ej的所有#获取所有有效的Ek值对应的索引validECacheList = np.where(oS.eCache[:,0]!=0)[0] #根据误差缓存中第⼀列⾮0，获取对应的有效误差值if len(validECacheList) > 1: #如果有效误差缓存长度⼤于1(因为包括Ei),则正常进⾏获取j值，否则使⽤selectJradn⽅法选取⼀个随机J值for k in validECacheList:if k == i: #相同则不处理continue#开始计算Ek值，进⾏对⽐，获取最⼤差值Ek = calcEk(oS,k)deltaE = abs(Ei - Ek)if deltaE > maxDeltaE: #更新Ej及其索引位置maxK = kmaxDeltaE = deltaEEj = Ekreturn maxK,Ej #返回我们找到的第⼆个变量α_2的位置else: #没有有效误差缓存，则随机选取⼀个索引，进⾏返回j = selectJrand(i,oS.m)Ej = calcEk(oS,j)return j,Ej（四）实现更新Ek操作#实现更新Ek操作,因为除了最后我们需要更新Ei之外，我们在内循环中计算α_1与α_2时还是需要⽤到E1与E2，#因为每次的E1与E2由于上⼀次循环中更新了α值，所以这⼀次也是需要更新E1与E2值，所以单独实现⼀个更新Ek值的⽅法还是有必要的def updateEk(oS,k):Ek = calcEk(oS,k)oS.eCache[k] = [1,Ek] #第⼀列1，表⽰为有效标识五：代码实现（三）SMO中的内循环函数外循环是要找违背KKT条件最严重的样本点(每个样本点对应⼀个α),这⾥我们将外循环的该判别条件放⼊内循环中考虑。

SMO方法的实现及证明

SMO 方法的实现及证明1．问题的阐述SVM 是从线性可分情形下的最优分类面发展而来。

基本思想可以用图(2-16)的二维情况说明。

图2-16 线性可分情况下的最优分类线图中实心点和空心点代表两类样本，H 为分类线H1,H2分别为过各类中离分界线最近的样本且平行于分类线的直线，它们之间的距离叫做分类间隔(margin)。

所谓最优分类线就是要求分类线不仅能将两类正确分开(训练错误率为0)，而且使分类间隔最大。

推广到一般线性可分情形，假设分类方程为0,=+><b ωx 1,1{,−+∈∈y R d x ，对其进行归一化，样本集，满足},,,2,1),,(=n i y i i x K 01),(≥−+><b y i ωx i(1)构造损失函数作为目标函数及约束条件，即：()∑+=ii C w W ξ2:minimize 2α(2-a) ()i b x w y i i T i ∀−≥+,1 subject to ξ(2-b)i i ∀≥,0ξ(2-c)经过拉格朗日变换以及KKT 定理推导，式子变为：0 subject to 21)(:minimize ,=≤≤−=∑∑∑iii i ij i ji j i j i i yCx x y y W αααααα(3)引入核函数，最后的目标函数变为：()iC y K y y W i ni i i n i nj j i j i ni i ∀≤≤=−=∑∑∑∑====,00 subject to 21)(: maximize 1111ααααααj i x ,x (4)改写为矩阵相乘的格式，得到：l i C f i T ,....,1,00 subject to 21)(minT =≤≤=−=ααy αe Q αααT(5)其中e 为全1向量，为所有变量的上界，为C Q l l ×的半正定矩阵。

训练向量通过i x φ函数被映射到更高维的空间(可能为无穷维)，，其中为核函数。

svm求解序列最小优化算法

svm求解序列最小优化算法摘要：1.SMO 算法概述2.SMO 算法的关键步骤3.SMO 算法的代码实践4.SMO 算法在支持向量机中的应用5.总结正文：一、SMO 算法概述序列最小优化算法（Sequential Minimal Optimization，简称SMO）是一种求解支持向量机（Support Vector Machine，简称SVM）模型参数的迭代算法。

它通过每次优化一个变量，直至找到最优解，从而提高模型的预测性能。

二、SMO 算法的关键步骤1.初始化参数：初始化拉格朗日乘子α和阈值b。

2.预测误差：计算当前参数下的预测误差。

3.确定最小化目标：根据预测误差，确定需要最小化的目标函数。

4.优化拉格朗日乘子：通过最小化目标函数，更新拉格朗日乘子。

5.检查停止条件：当满足停止条件（如达到迭代次数限制或预测误差足够小）时，结束迭代。

6.输出结果：输出当前最优参数。

三、SMO 算法的代码实践以下是使用Python 实现SMO 算法的简单示例：```pythonimport numpy as npdef predict_error(X, y, alpha, b, X_test):# 计算预测误差passdef minimize_alpha(alpha, X, y, b, X_test):# 优化拉格朗日乘子passdef smo(X, y, max_iter, tol):# 初始化参数alpha = np.zeros(len(X[0]))b = 0# 迭代for _ in range(max_iter):# 计算预测误差error = predict_error(X, y, alpha, b, X_test)# 确定最小化目标if error > tol:# 优化拉格朗日乘子alpha = minimize_alpha(alpha, X, y, b, X_test)else:# 检查停止条件breakreturn alpha, b# 示例：使用SMO 算法构建半监督式支持向量机模型#...# 示例：使用SMO 算法求解序列最小优化问题#...```四、SMO 算法在支持向量机中的应用SMO 算法在支持向量机中应用广泛，可以用于求解分类问题和回归问题。

机器学习——支持向量机（SVM）之拉格朗日乘子法，KKT条件以及简化版SMO算法分析

机器学习——⽀持向量机（SVM）之拉格朗⽇乘⼦法，KKT条件以及简化版SMO算法分析SVM有很多实现，现在只关注其中最流⾏的⼀种实现，即序列最⼩优化（Sequential Minimal Optimization，SMO）算法，然后介绍如何使⽤⼀种核函数（kernel）的⽅式将SVM扩展到更多的数据集上。

1.基于最⼤间隔分隔数据⼏个概念：1.线性可分（linearly separable）：对于图6-1中的圆形点和⽅形点，如果很容易就可以在图中画出⼀条直线将两组数据点分开，就称这组数据为线性可分数据2.分隔超平⾯（separating hyperplane）：将数据集分隔开来的直线称为分隔超平⾯3.如果数据集是1024维的，那么就需要⼀个1023维的超平⾯来对数据进⾏分隔4.间隔（margin）：数据点到分隔⾯的距离称为间隔5.⽀持向量（support vector）:离分隔超平⾯最近的那些点⽀持向量机的优点：泛化错误率低，计算开销不⼤，结果易解释⽀持向量机的缺点：对参数调节和核函数的选择敏感，原始分类器不加修改仅适⽤于处理⼆类问题适⽤数据类型：数值型和标称型数据2.寻找最⼤间隔如何求解数据集的最佳分隔直线？分隔超平⾯的形式可以写成其中 w = (w1,w2,w3...wd)为法向量，决定了超平⾯的⽅向，其中d等于数据的维度，这很好理解，假设⼆维的(x1,x2)点可以被 ax+b=0 分隔，这⾥⾯直线 ax+b=0 是⼀维的，但是这⾥⾯a和x都是⼆维的b为位移项，决定了超平⾯与原点之间的距离对于图6-3中A点到分隔直线的距离为表⽰向量的模，，w与w共轭的内积再开⽅假设超平⾯（w,b）能将训练样本正确分类，即对于 ,有则两个异类⽀持向量到超平⾯的距离之和为欲找到具有“最⼤间隔（maximum margin）”的划分超平⾯，也就是要找到能满⾜中约束的参数w和b，使得最⼤，即，其中约束条件为　s.t. ，其实这个约束条件就是把两个不等式合并成了⼀个显然，为了最⼤化间隔，仅需最⼤化，这等价于最⼩化，于是上式可重写为，其中约束条件为　s.t.这就是⽀持向量机（Support Vector Machine，简称SVM）的基本型对于这类带有不等式约束的最优化问题，可以使⽤拉格朗⽇乘⼦法（Lagrange Multiplier）对其进⾏求解。

SVM算法说明和优化算法介绍

SVM算法说明和优化算法介绍SVM（Support Vector Machine，支持向量机）是一种常用的机器学习算法，用于分类和回归分析。

SVM的基本思想是通过在特征空间中构造一个最优超平面，将不同类别的样本分开。

本文将为您介绍SVM的基本原理、分类和回归问题的实现方法以及一些常见的优化算法。

SVM的基本原理是寻找一个能够最大化类别间间隔（margin）的超平面，从而达到更好的分类效果。

在特征空间中，样本点可以用向量表示，所以SVM也可以看作是在特征空间中寻找一个能够最优分割两类样本的超平面。

为了找到这个最优超平面，SVM使用了支持向量（Support Vector），即离超平面最近的样本点。

支持向量到超平面的距离被称为间隔，而最优超平面使得间隔最大化。

对于线性可分的情况，SVM的目标是最小化一个损失函数，同时满足约束条件。

损失函数由间隔和误分类样本数量组成，约束条件则包括对超平面的限制条件。

通过求解优化问题，可以得到最优超平面的参数值。

对于非线性可分的情况，SVM使用核函数进行转换，将低维特征空间中的样本映射到高维特征空间中，从而使得样本在高维空间中线性可分。

SVM在分类问题中的应用广泛，但也可以用于回归问题。

在回归问题中，SVM的目标是找到一个超平面，使得点到该平面的距离尽可能小，并且小于一个给定的阈值。

SVM回归的思想是通过引入一些松弛变量，允许样本点在一定程度上偏离超平面来处理异常数据，从而得到更好的回归结果。

在实际应用中，SVM的性能和效果受到许多因素的影响，如数据集的分布、样本的数量和特征的选择等。

为了进一步优化SVM的性能，许多改进算法被提出。

下面我们介绍几种常见的SVM优化算法。

1.序列最小优化算法（SMO）：SMO是一种简单、高效的SVM优化算法。

它通过将大优化问题分解为多个小优化子问题，并使用启发式方法进行求解。

每次选择两个变量进行更新，并通过迭代优化这些变量来寻找最优解。

SVM的SMO算法实现

SVM的SMO算法实现SVM（Support Vector Machine）是一种常用的分类算法，其原理是将数据集映射到一个高维空间中，使得不同类别的样本能够被一个超平面正确分割。

SMO（Sequential Minimal Optimization）算法是一种用于求解SVM问题的优化算法，其核心思想是将大问题分解为一系列的小问题，通过迭代求解这些小问题来得到最优解。

SMO算法允许一次只优化两个变量，即选择两个变量α_i和α_j进行优化。

具体的优化步骤如下：1. 选择一对需要优化的变量α_i和α_j，使用启发式方法选取这两个变量。

一般选择两个变量时，先遍历整个α向量，找到违反KKT条件最严重的点，KKT（Karush-Kuhn-Tucker）条件是SVM问题的最优性条件，通过判断α向量是否满足该条件来选择需要优化的变量。

2.固定其他变量，通过求解子问题的方式更新选择的两个变量。

通过求解两个变量的二次规划问题，得到更新后的α_i和α_j。

3.更新阈值b。

每次更新α_i和α_j之后，都需要计算新的阈值b。

根据KKT条件，选择满足条件的α_i或α_j来更新阈值b。

4.判断终止条件。

迭代过程中，根据一定的终止条件来决定是否终止算法，一般可以设置最大迭代次数或目标误差。

SMO算法的具体实现如下：1.初始化α向量、阈值b和错误率向量E。

2.选择需要优化的两个变量α_i和α_j。

3.计算变量α_i和α_j的边界。

4.根据变量α_i和α_j是否满足边界来选择优化方法。

5.在选择的两个变量上进行优化。

求解两个变量的二次规划子问题，得到更新后的α_i和α_j。

6.更新阈值b。

7.更新错误率向量E。

8.判断终止条件。

如果满足终止条件则停止迭代，否则返回第2步继续迭代。

完整的SMO算法实现如下：```pythondef smo(X, y, C, tol, max_iter):m, n = X.shapealpha = np.zeros(m)b=0iters = 0while iters < max_iter:alpha_changed = 0for i in range(m):E_i = np.sum(alpha * y * kernel(X, X[i, :])) + b - y[i]if (y[i] * E_i < -tol and alpha[i] < C) or (y[i] * E_i > tol and alpha[i] > 0):j = select_second_alpha(i, m)E_j = np.sum(alpha * y * kernel(X, X[j, :])) + b - y[j]alpha_i_old = alpha[i]alpha_j_old = alpha[j]if y[i] != y[j]:L = max(0, alpha[j] - alpha[i])H = min(C, C + alpha[j] - alpha[i])else:L = max(0, alpha[i] + alpha[j] - C)H = min(C, alpha[i] + alpha[j])if L == H:continueeta = 2 * kernel(X[i, :], X[j, :]) - kernel(X[i, :], X[i, :]) - kernel(X[j, :], X[j, :])if eta >= 0:continuealpha[j] = alpha[j] - y[j] * (E_i - E_j) / etaalpha[j] = clip_alpha(alpha[j], H, L)continuealpha[i] = alpha[i] + y[i] * y[j] * (alpha_j_old - alpha[j]) b1 = b - E_i - y[i] * (alpha[i] - alpha_i_old) *kernel(X[i, :], X[i, :]) - y[j] * (alpha[j] - alpha_j_old) * kernel(X[i, :], X[j, :])b2 = b - E_j - y[i] * (alpha[i] - alpha_i_old) *kernel(X[i, :], X[j, :]) - y[j] * (alpha[j] - alpha_j_old) * kernel(X[j, :], X[j, :])if 0 < alpha[i] < C:b=b1elif 0 < alpha[j] < C:b=b2else:b=(b1+b2)/2alpha_changed += 1if alpha_changed == 0:iters += 1else:iters = 0return alpha, b```以上是SMO算法的简单实现，其中使用了一些辅助函数（如选择第二个变量、计算核函数等），这些函数需要根据具体的问题进行实现。

SVM——详细讲解SMO算法优化两个变量以及变量的选择

SVM——详细讲解SMO算法优化两个变量以及变量的选择支持向量机（SVM）是一种二分类模型，它在分类超平面的构建过程中，通过优化二次规划问题求解得到最优的超平面。

而序列最小最优化（Sequential Minimal Optimization，SMO）算法则是一种用于求解SVM 二次规划问题的简化算法。

在SVM中，分类超平面可以表示为w*x+b=0，其中w为法向量，b为截距，x为输入样本。

SVM的目标是找到具有最大边界的超平面，使得训练样本与超平面的距离最大化。

优化SVM的问题可以转化为求解以下二次规划问题：\begin{align*}\min\limits_{\alpha} & \quad \frac{1}{2}\sum_{i=1}^{N}{\sum_{j=1}^{N}{\alpha_i \alpha_j y_i y_j K(x_i, x_j)}} - \sum_{i=1}^{N}{\alpha_i}\\s.t. & \quad \sum_{i=1}^{N}{\alpha_i y_i} = 0 \\& \quad 0 \leq \alpha_i \leq C, \quad i = 1, 2, ..., N\end{align*}\]其中，N是训练样本数量，C是惩罚参数，K(x_i,x_j)是核函数。

SMO算法通过迭代优化变量alpha_i和alpha_j，来逐渐优化整个二次规划问题。

SMO算法的核心步骤有两个：选择变量和优化变量。

1.变量的选择：在每次迭代中，SMO算法通过两个嵌套循环选择优化变量alpha_i和alpha_j。

首先，外层循环选择第一个变量alpha_i，通过遍历所有训练样本点，选择违反KKT条件的样本点。

KKT条件是SVM最优解必须满足的条件，对于正样本来说，条件是alpha_i=0，对于负样本来说，条件是alpha_i=C。

如果选择到了违反KKT条件的alpha_i，就进入内层循环。

SVM和SMO算法概述

SVM的简化版—SMO算法
• 通过另一个方法，即同时更新ai和aj，满足以下等式
就能保证和为0的约束。
SVM的简化版—SMO算法
• 利用上面的式子消去ai • 得到一个关于单变量aj的一个凸二次规划问题，不考虑其约束0<=aj<=C,可以得其解为：
• 其中：
SVM的简化版—SMO算法
• aj表示旧值，然后考虑约束0<=aj<=C可得到a 的解析解为：
• 其中：W=｛w1，w2，…wn｝是权重向量 H : WX+b=0 H1:WX+b=1 H2:WX+b=-1 • 几何间隔： • 目标函数等价于 • 约束条件 δ=y(wx+b)=|g(x)|
求解：凸二次规划
• 数据集合：
T {( x1, y1 ),...,( xl , yl )} (Rn y)l
• SVM算法优点：
• (1) SVM算法对大规模训练样本难以实施
– 由于SVM是借助二次规划来求解支持向量，而求解二次规划将涉及m阶矩阵的计算（m为样本的个数），当m数目很大时该矩阵的存储和计算将耗费大量的机器内存和运算时间。
• (2) 用SVM解决多分类问题存在困难
– 经典的支持向量机算法只给出了二类分类的算法，而在数据挖掘的实际应用中，一般要解决多类的分类问题。
SVM算法学习
SVM原理
SMO分析 SMO实现
SVM基本原理
• 原理： SVM使用一种非线性映射，把原训练数据映射到较高的维。在新的维上，搜索最佳分离超平面，两个类的数据总可以被超平面分开
问题提出：
• 线性可分的分类问题：（令黑色的点 = -1，白色的点 = +1） f(x ) w r x b

SVM算法原理及SMO算法概述

SVM算法原理及SMO算法概述SVM (Support Vector Machine) 是一种广泛应用于分类和回归问题的机器学习算法。

它基于统计学习理论中的VC理论，使用间隔最大化的方法进行分类。

在SVM中，我们将训练数据集视为一个在高维空间中的点集。

SVM的目标是找到一个超平面，能够将不同类别的点分开，并且使其离超平面的距离最大化。

这个超平面被称为最优分隔超平面。

具体来说，SVM算法的原理如下：1.数据预处理：将训练样本映射到高维特征空间，使得样本点能够被线性分隔。

2.寻找最优超平面：在高维特征空间中，寻找能够将不同类别的点分开的超平面。

通常情况下，有多个超平面可以进行分类，而SVM的目标是找到使得间隔最大化的那个超平面。

3.使用支持向量进行分类：SVM找到了最优超平面后，它会选择离该超平面最近的一些点，这些点被称为支持向量。

分类时，SVM根据测试点和支持向量的关系进行判断。

SMO (Sequential Minimal Optimization) 是一种用来训练SVM的优化算法。

传统的SVM算法需要同时优化所有的模型参数，计算量较大。

而SMO算法则是一种序列化的简化方法，每次只优化两个模型参数。

SMO算法的主要思想如下：1.初始化模型参数：选择两个待优化的参数α1和α22.选择两个参数：基于一定的策略，选择两个不同的参数α进行优化。

3.通过求解两个参数的约束最优化问题，更新模型参数。

4.更新阈值和偏置：根据更新后的模型参数，计算出新的阈值和偏置。

5.判断终止条件：检查是否满足终止条件，如果满足则停止优化，否则返回第2步。

SMO算法的核心在于选择两个参数进行优化，并通过解决约束最优化问题来更新参数。

通过反复迭代这个过程，最终得到训练好的SVM模型。

SMO算法的优点是可以有效地处理大规模数据集，并且能够避免陷入局部最优解。

同时，SMO算法还可以引入核函数，使得SVM具有非线性分类和回归能力。

总结来说，SVM是一种基于统计学习理论的分类和回归算法，通过间隔最大化的方法寻找最优分隔超平面。

Svm算法原理及实现

Svm算法原理及实现Svm（support Vector Mac）⼜称为⽀持向量机，是⼀种⼆分类的模型。

当然如果进⾏修改之后也是可以⽤于多类别问题的分类。

⽀持向量机可以分为线性核⾮线性两⼤类。

其主要思想为找到空间中的⼀个更够将所有数据样本划开的超平⾯，并且使得本本集中所有数据到这个超平⾯的距离最短。

⼀、基于最⼤间隔分隔数据1.1⽀持向量与超平⾯在了解svm算法之前，我们⾸先需要了解⼀下线性分类器这个概念。

⽐如给定⼀系列的数据样本，每个样本都有对应的⼀个标签。

为了使得描述更加直观，我们采⽤⼆维平⾯进⾏解释，⾼维空间原理也是⼀样。

举个简单⼦：如下图所⽰是⼀个⼆维平⾯，平⾯上有两类不同的数据，分别⽤圆圈和⽅块表⽰。

我们可以很简单地找到⼀条直线使得两类数据正好能够完全分开。

但是能将据点完全划开直线不⽌⼀条，那么在如此众多的直线中我们应该选择哪⼀条呢？从直观感觉上看图中的⼏条直线，是不是要更好⼀些呢？是的我们就是希望寻找到这样的直线，使得距离这条直线最近的点到这条直线的距离最短。

这读起来有些拗⼝，我们从图三中直观来解释这⼀句话就是要求的两条外⾯的线之间的间隔最⼤。

这是可以理解的，因为假如数据样本是随机出现的，那么这样分割之后数据点落⼊到其类别⼀侧的概率越⾼那么最终预测的准确率也会越⾼。

在⾼维空间中这样的直线称之为超平⾯，因为当维数⼤于三的时候我们已经⽆法想象出这个平⾯的具体样⼦。

那些距离这个超平⾯最近的点就是所谓⽀持向量，实际上如果确定了⽀持向量也就确定了这个超平⾯，找到这些⽀持向量之后其他样本就不会起作⽤了。

图 1 图21.2寻找最⼤间隔1.2.1点到超平⾯的距离公式既然这样的直线是存在的，那么我们怎样寻找出这样的直线呢？与⼆维空间类似，超平⾯的⽅程也可以写成⼀下形式：（1.1）有了超平⾯的表达式之后之后，我们就可以计算样本点到平⾯的距离了。

假设为样本的中的⼀个点，其中表⽰为第个特征变量。

那么该点到超平⾯的距离就可以⽤如下公式进⾏计算：（1.2）其中||W||为超平⾯的范数，常数b类似于直线⽅程中的截距。

基于SVM模式识别系统的设计与实现代码大全

基于SVM模式识别系统的设计与实现1．1 主要研究内容（1）现有的手写识别系统普遍采用k近邻分类器，在2000个数字中，每个数字大约有200个样本，但实际使用这个算法时，算法的执行效率并不高，因为算法需要为每个测试向量做2000次距离计算，每个距离计算包括了1024个维度浮点运算，总计要执行900次，此外需要保留所有的训练样本，还需要为测试向量准备2MB的存储空间。

因此我们要做的是在其性能不变的同时，使用更少的内存。

所以考虑使用支持向量机来代替kNN方法，对于支持向量机而言，其需要保留的样本少了很多，因为结果只是保留了支持向量的那些点，但是能获得更快更满意的效果。

（2）系统流程图step1. 收集数据（提供数字图片）step2. 处理数据（将带有数字的图片二值化）step3. 基于二值图像构造向量step4. 训练算法采用径向基核函数运行SMO算法step5. 测试算法（编写函数测试不同参数）1．2 题目研究的工作基础或实验条件（1）荣耀MagicBook笔记本（2）Linux ubuntu 18.6操作系统pycharm 2021 python31．3 数据集描述数据集为trainingDigits和testDigits，trainingDigits包含了大约2000个数字图片，每个数字图片有200个样本；testDigits包含了大约900个测试数据。

1．4 特征提取过程描述将数字图片进行二值化特征提取，为了使用SVM分类器，必须将图像格式化处理为一个向量，将把32×32的二进制图像转换为1×1024的向量，使得SVM可以处理图像信息。

得到处理后的图片如图所示：图1 二值化后的图片编写函数img2vector ，将图像转换为向量：该函数创建1x1024的NumPy 数组，然后打开给定的文件，循环读出文件的前32行，并将每行的头32个字符值存储在 NumPy 数组中，最后返回数组，代码如图2所示：图2 处理数组1．5 分类过程描述 1.5.1 寻找最大间隔寻找最大间隔，就要找到一个点到分割超平面的距离，就必须要算出点到分隔面的法线或垂线的长度。

手推SVM算法(含SMO证明)

手推SVM算法（含SMO证明）SVM（支持向量机）是一种二元分类模型，它通过在特征空间中找到一个最优的超平面来进行分类。

SVM算法的核心是构造最优的分类超平面，使得它能够有力地将两类样本分开，并且使得与超平面相距最近的样本点的距离最大化。

SMO（序列最小优化）算法是一种高效求解SVM问题的方法。

为了简化讲解，我们假设SVM的两类样本是线性可分的，即存在一个超平面可以将两类样本完全分开。

在此基础上，我们来推导最优化问题和SMO算法的推导。

1.SVM的最优化问题：我们可以将超平面w·x+b=0中的w归一化，并将超平面转化为w·x+b=0，其中，w，=1、其中，w表示超平面的法向量，b表示超平面的截距。

考虑到SVM的目标是使得距离超平面最近的点离超平面最远，我们可以引入几何间隔的概念。

对于一个样本点(xi, yi)，它距离超平面的几何间隔定义为γi=yi(w·xi+b)/，w。

SVM的最优化问题可以转化为如下的凸优化问题：min ，w，^2/2s.t. yi(w·xi+b)≥ 1, i=1,2,...,n这个优化问题的目标是最小化w的范数的平方，即使得超平面的间隔最大化。

约束条件确保了分类准确性。

2.SMO算法的推导：要解决SVM的最优化问题，可以使用Lagrange乘子法转化为对偶问题。

使用对偶问题可以通过求解其对偶变量来求解原始问题。

通过引入拉格朗日乘子αi≥0，对每个约束条件（yi(w·xi+b)≥1）引入拉格朗日乘子αi，可以得到拉格朗日函数：L(w, b, α) = 1/2，w，^2 - Σαi(yi(w·xi+b) - 1)其中，α=(α1,α2,...,αn)T是拉格朗日乘子向量。

然后，可以通过对L(w,b,α)分别对w和b求偏导并令其等于0，得到w和b的解：w = ΣαiyixiΣαiyi = 0将w代入拉格朗日函数中，可得到关于α的对偶问题：max Σα - 1/2ΣΣαiαjyiyj(xi·xj)s.t. Σαiyi = 0αi≥0,i=1,2,...,n这是一个凸优化问题，通过求解对偶问题得到的α可以进一步求解最优的超平面。

机器学习算法系列(12)：SVM(4)—SMO

SMO 算法是⼀一种启发式算法，其基本思想是：如果所有变量量的解都满⾜足最优化问题的KKT 条件，那么这个优化问题的解就得到了了，因为KKT 条件是该优化问题的充分必要条件。

否则，选择两个变量量，固定其他变量量，针对这两个变量量构建⼀一个⼆二次规划问题。

这个⼆二次规划问题关于这两个变量量的解应该是更更接近原始⼆二次规划问题的解，因为这会使得原始⼆二次规划问题的⽬目标函数值变得更更⼩小。

重要的是，这时⼦子问题可以通过解析⽅方法求解，这样就可以⼤大⼤大提升整个算法的计算速度。

⼦子问题有两个变量量，⼀一个是违反KKT 条件最严重的那个，另⼀一个由约束条件⾃自动确定。

如果SMO 算法将原问题不不断分解为⼦子问题并对⼦子问题求解，进⽽而达到求解原问题的⽬目的。

通常对于优化问题，我们没有办法的时候就会想到最笨的办法，也就是梯度下降。

注意我们这⾥里里的问题是要求最⼤大值，只要在前⾯面加上⼀一个负号就可以转化为求最⼩小值，所以和并没有什什么本质的区别，其基本思想直观上来说就是：梯度是函数值增幅最⼤大的⽅方向，因此只要沿着梯度的反⽅方向⾛走，就能使得函数值减⼩小得越⼤大，从⽽而期望迅速达到最⼩小值。

当然普通的并不不能保证达到最⼩小值，因为很有可能陷⼊入⼀一个局部极⼩小值。

不不过对于⼆二次规划问题，极值只有⼀一个，所以是没有局部极值的问题。

另外还有⼀一种叫做的变种，它每次只选择⼀一个维度，例例如，它每次选取为变量量，⽽而将其他都看成是常数，从⽽而原始的问题在这⼀一步编程⼀一个⼀一元函数，然后针对这个⼀一元函数求最⼩小值，如此反复轮换不不同的维度进⾏行行迭代。

的主要⽤用处在于那些原本很复杂，但是如果只限制在⼀一维的情况下则变得很简单甚⾄至可以直接求极值的情况，例例如我们这⾥里里的问题，暂且不不管约束条件，如果只看⽬目标函数的话，当只有⼀一个分量量是变量量的时候，这就是⼀一个普通的⼀一元⼆二次函数的极值问题，初中⽣生也会做，带⼊入公式即可。

SVM算法原理及SMO算法概述

SVM算法原理及SMO算法概述支持向量机（Support Vector Machine，SVM）是一种非常常用的机器学习算法，被广泛应用于分类和回归问题中。

SVM算法的原理基于统计学习理论，具有较强的理论基础和实际应用。

具体来说，SVM算法的原理可以分为以下几个步骤：1.数据预处理：对原始数据进行标准化处理，使得不同特征之间具有相同的尺度。

2.特征转换：将数据从低维特征空间转换到高维特征空间。

这个转换的方法可以通过核函数来实现，常用的核函数有线性核函数、多项式核函数和高斯核函数等。

3.寻找最优超平面：在高维特征空间中，通过优化问题求解，找到一个最优的超平面，使得样本点距离该超平面的间隔最大。

4.生成分类模型：根据最优超平面，将数据点分为不同的类别。

简单来说，SVM算法的目标是在保证分类精度的前提下，找到使得间隔最大化的超平面，从而提高模型的鲁棒性和泛化能力。

SMO算法（Sequential Minimal Optimization）是一种用于求解SVM 二次规划问题的优化算法。

SMO算法的基本思想是将大规模的二次规划问题分解为一系列求解两个变量的二次规划子问题。

SMO算法的基本流程如下：1.初始化：选择两个变量作为优化变量，然后初始化所有变量的值。

2.选择变量：选择两个变量作为待优化变量。

选择的原则一般是按照最大步长原则，即第一个变量选择违反KKT条件最严重的变量，第二个变量选择使得优化问题目标函数增大最快的变量。

3.优化变量：固定其他变量的值，针对选定的两个变量，求解二次规划问题，更新这两个变量的值。

4.更新阈值：根据更新后的变量值，更新阈值。

5.检验终止条件：检验是否满足终止条件，如果满足则输出最优解，否则返回第二步。

SMO算法的关键在于选择变量和优化变量这两个步骤。

通过选择合适的变量和高效的求解二次规划子问题的方法，可以有效地提高算法的运算效率。

总结来说，SVM算法是一种基于统计学习理论的强大分类算法，通过优化目标函数找到最优的超平面。

支持向量机原理（四）SMO算法原理

⽀持向量机原理（四）SMO算法原理在SVM的前三篇⾥，我们优化的⽬标函数最终都是⼀个关于\alpha向量的函数。

⽽怎么极⼩化这个函数，求出对应的\alpha向量，进⽽求出分离超平⾯我们没有讲。

本篇就对优化这个关于\alpha向量的函数的SMO算法做⼀个总结。

1. 回顾SVM优化⽬标函数我们⾸先回顾下我们的优化⽬标函数： \underbrace{ min }_{\alpha} \frac{1}{2}\sum\limits_{i=1,j=1}^{m}\alpha_i\alpha_jy_iy_jK(x_i,x_j) - \sum\limits_{i=1}^{m}\alpha_i s.t. \; \sum\limits_{i=1}^{m}\alpha_iy_i = 0 0 \leq \alpha_i \leq C 我们的解要满⾜的KKT条件的对偶互补条件为：\alpha_{i}^{*}(y_i(w^Tx_i + b) - 1 + \xi_i^{*}) = 0 根据这个KKT条件的对偶互补条件，我们有：\alpha_{i}^{*} = 0 \Rightarrow y_i(w^{*} \bullet \phi(x_i) + b) \geq 1 0 <\alpha_{i}^{*} < C \Rightarrow y_i(w^{*} \bullet \phi(x_i) + b) = 1 \alpha_{i}^{*}= C \Rightarrow y_i(w^{*} \bullet \phi(x_i) + b) \leq 1 由于w^{*} = \sum\limits_{j=1}^{m}\alpha_j^{*}y_j\phi(x_j),我们令g(x) = w^{*} \bullet \phi(x) + b=\sum\limits_{j=1}^{m}\alpha_j^{*}y_jK(x, x_j)+ b^{*}，则有：\alpha_{i}^{*} = 0 \Rightarrow y_ig(x_i) \geq 1 0 < \alpha_{i}^{*} < C\Rightarrow y_ig(x_i) = 1 \alpha_{i}^{*}= C \Rightarrow y_ig(x_i) \leq 12. SMO算法的基本思想上⾯这个优化式⼦⽐较复杂，⾥⾯有m个变量组成的向量\alpha需要在⽬标函数极⼩化的时候求出。

支持向量机（SVM）中的SMO算法

⽀持向量机（SVM）中的SMO算法1. 前⾔最近⼜重新复习了⼀遍⽀持向量机（SVM）。

其实个⼈感觉SVM整体可以分成三个部分：1. SVM理论本⾝：包括最⼤间隔超平⾯（Maximum Margin Classifier），拉格朗⽇对偶（Lagrange Duality），⽀持向量（Support Vector），核函数（Kernel）的引⼊，松弛变量的软间隔优化（Outliers），最⼩序列优化（Sequential Minimal Optimization）等。

2. 核⽅法（Kernel）：其实核⽅法的发展是可以独⽴于SVM来看待的，核⽅法在很多其它算法中也会应⽤到。

3. 优化理论：这⾥主要介绍的是最⼩序列优化（Sequential Minimal Optimization），优化理论的发展也是独⽴于SVM的。

2. SVM理论基础SVM的理论基础在上⼀篇博客的总结中可以参考：。

对于⽀持向量机（SVM）的简单总结：1. Maximum Margin Classifier2. Lagrange Duality3. Support Vector4. Kernel5. Outliers6. Sequential Minimal Optimization个⼈觉得SMO⼜可以分为两部分：（1）如何选择每次迭代时候的⽬标⼯作集，即选择哪两个拉格朗⽇乘⼦来迭代。

（2）如何对选择好的⼯作集（拉格朗⽇乘⼦）进⾏更新迭代。

3. SMO最初的版本（Platt，1998）SMO就是要解这个凸⼆次规划问题，这⾥的C是个很重要的参数，它从本质上说是⽤来折中经验风险和置信风险的，C越⼤，置信风险越⼤，经验风险越⼩；并且所有的拉格朗⽇乘⼦都被限制在了以C为边长的⼤盒⼦⾥。

SMO的出现使得我们不必去求助于昂贵的第三⽅⼯具去解决这个凸⼆次规划问题，⽬前对它的改进版本很多，这⼀节先介绍它的最初形式和思想。

SMO是Microsoft Research的John C. Platt在《Sequential Minimal Optimization:A Fast Algorithm for Training Support Vector Machines》⼀⽂中提出的，其基本思想是将Vapnik在1982年提出的Chunking⽅法推到极致，即：通过将原问题分解为⼀系列⼩规模凸⼆次规划问题⽽获得原问题解的⽅法，每次迭代只优化由2个点组成的⼯作集，SMO算法每次启发式地选择两个拉格朗⽇乘⼦同时固定其它拉格朗⽇乘⼦来找到这两个拉格朗⽇乘⼦的最优值，直到达到停⽌条件。

SVM的SMO算法实现

SVM 的SMO 算法实现自研0 谭李（006334）吴翔（006333）摘要支持向量机（Support Vector Machine ）是一种新近出现的解决模式识别问题的有效工具。

它的数学模型可以归结为一个有约束的二次规划问题。

如何快速准确地解这个二次规划，是SVM 推广应用中的一个重要环节。

我们尝试了数种可能的方法，用程序实现了其中最有效的一种——SMO 算法（Sequential MinimalOptimization algorithm ），并用块算法的思想（Chunking ）对其作出了改进。

本文将先给出待解决的数学模型，介绍我们所做的一些尝试，然后着重讨论SMO 算法的原理、程序实现及其独特优势，最后阐述我们自己的一些新思想，主要是经过改进的Chunking SMO 算法，并在附录中介绍SVM 的基本原理。

SVM 的数学模型这里简要介绍支持向量机（SVM ）数学模型的引出过程，关于SVM 的详细介绍将在附录中给出。

支持向量机的原理是用分类超平面将空间中两类样本点正确分离，并取得最大边缘（正样本与负样本到超平面的最小距离）这样，原问题为一个有约束非线性规划问题：l,...,2,1i 01)b (y 21)b ,(Minimize i 2=≥-+⋅=Φw x w w i 范数最小的满足约束的w 就是最优分类超平面的法向量。

目标函数是严格上凹的二次型，约束函数是下凹的，这是一个严格凸规划。

按照最优化理论中凸二次规划的解法，我们把它转化为Wolfe 对偶问题来求解：l,...,1i 00y .t .s y y 21)(W Maxmizei l 1i i i l j ,i j i i l 1i i j =≥α=α⋅αα-α=∑∑∑==j i x x α其中αi 正是样本点x i 的Lagrange 乘子。

Kuhn-Tunker 条件定理指出，无效约束所对应的Lagrange 乘子一定为0，在这里的物理意义也就是说非支持向量x i （对应着原问题中的约束 y i (w ’x i ＋b)－1>0 ）的Lagrange 乘子一定为0。

机器学习：支持向量机识别手写英文字母SMO算法实现二元分类器

机器学习：⽀持向量机识别⼿写英⽂字母SMO算法实现⼆元分类器本⽂只构建⼀个能够识别⼀种英⽂符号的SVM，在此选择了C字符。

⼀、SVM构建import numpy as npclass SMO:def__init__(self, C, tol, kernel='rbf', gamma=None):# 惩罚系数self.C = C# 优化过程中alpha步进阈值self.tol = tol# 核函数if kernel == 'rbf':self.K = self._gaussian_kernelself.gamma = gammaelse:self.K = self._linear_kerneldef _gaussian_kernel(self, U, v):'''⾼斯核函数'''if U.ndim == 1:p = np.dot(U - v, U - v)else:p = np.sum((U - v) * (U - v), axis=1)return np.exp(-self.gamma * p)def _linear_kernel(self, U, v):'''线性核函数'''return np.dot(U, v)def _g(self, x):'''函数g(x)'''alpha, b, X, y, E = self.argsidx = np.nonzero(alpha > 0)[0]if idx.size > 0:return np.sum(y[idx] * alpha[idx] * self.K(X[idx], x)) + b[0]return b[0]def _optimize_alpha_i_j(self, i, j):'''优化alpha_i, alpha_j'''alpha, b, X, y, E = self.argsC, tol, K = self.C, self.tol, self.K# 优化需有两个不同alphaif i == j:return 0# 计算alpha[j]的边界if y[i] != y[j]:L = max(0, alpha[j] - alpha[i])H = min(C, C + alpha[j] - alpha[i])else:L = max(0, alpha[j] + alpha[i] - C)H = min(C, alpha[j] + alpha[i])# L == H 时已⽆优化空间(⼀个点).if L == H:return 0# 计算etaeta = K(X[i], X[i]) + K(X[j], X[j]) - 2 * K(X[i], X[j])if eta <= 0:return 0# 对于alpha⾮边界, 使⽤E缓存. 边界alpha, 动态计算E.if 0 < alpha[i] < C:E_i = E[i]else:E_i = self._g(X[i]) - y[i]if 0 < alpha[j] < C:E_j = E[j]else:E_j = self._g(X[j]) - y[j]# 计算alpha_j_newalpha_j_new = alpha[j] + y[j] * (E_i - E_j) / eta# 对alpha_j_new进⾏剪辑if alpha_j_new > H:alpha_j_new = Helif alpha_j_new < L:alpha_j_new = Lalpha_j_new = np.round(alpha_j_new, 7)# 判断步进是否⾜够⼤if np.abs(alpha_j_new - alpha[j]) < tol * (alpha_j_new + alpha[j] + tol):return 0# 计算alpha_i_newalpha_i_new = alpha[i] + y[i] * y[j] * (alpha[j] - alpha_j_new)alpha_i_new = np.round(alpha_i_new, 7)# 计算b_newb1 = b[0] - E_i \-y[i] * (alpha_i_new - alpha[i]) * K(X[i], X[i]) \-y[j] * (alpha_j_new - alpha[j]) * K(X[i], X[j])b2 = b[0] - E_j \-y[i] * (alpha_i_new - alpha[i]) * K(X[i], X[j]) \-y[j] * (alpha_j_new - alpha[j]) * K(X[j], X[j])if 0 < alpha_i_new < C:b_new = b1elif 0 < alpha_j_new < C:b_new = b2else:b_new = (b1 + b2) / 2# 更新E缓存# 更新E[i],E[j]. 若优化后alpha若不在边界, 缓存有效且值为0.E[i] = E[j] = 0# 更新其他⾮边界alpha对应的E[k]mask = (alpha != 0) & (alpha != C)mask[i] = mask[j] = Falsenon_bound_idx = np.nonzero(mask)[0]for k in non_bound_idx:E[k] += b_new - b[0] + y[i] * K(X[i], X[k]) * (alpha_i_new - alpha[i]) \ + y[j] * K(X[j], X[k]) * (alpha_j_new - alpha[j])# 更新alpha_i, alpha_ialpha[i] = alpha_i_newalpha[j] = alpha_j_new# 更新bb[0] = b_newreturn 1def _optimize_alpha_i(self, i):'''优化alpha_i, 内部寻找alpha_j.'''alpha, b, X, y, E = self.args# 对于alpha⾮边界, 使⽤E缓存. 边界alpha, 动态计算E.if 0 < alpha[i] < self.C:E_i = E[i]else:E_i = self._g(X[i]) - y[i]# alpha_i仅在违反KKT条件时进⾏优化.if (E_i * y[i] < -self.tol and alpha[i] < self.C) or \(E_i * y[i] > self.tol and alpha[i] > 0):# 按优先级次序选择alpha_j.# 分别获取⾮边界alpha和边界alpha的索引mask = (alpha != 0) & (alpha != self.C)non_bound_idx = np.nonzero(mask)[0]bound_idx = np.nonzero(~mask)[0]# 优先级(-1)# 若⾮边界alpha个数⼤于１, 寻找使得|E_i - E_j|最⼤化的alpha_j.if len(non_bound_idx) > 1:if E[i] > 0:j = np.argmin(E[non_bound_idx])else:j = np.argmax(E[non_bound_idx])if self._optimize_alpha_i_j(i, j):return 1# 优先级(-2)# 随机迭代⾮边界alphanp.random.shuffle(non_bound_idx)for j in non_bound_idx:if self._optimize_alpha_i_j(i, j):return 1# 优先级(-3)# 随机迭代边界alphanp.random.shuffle(bound_idx)for j in bound_idx:if self._optimize_alpha_i_j(i, j):return 1return 0def train(self, X_train, y_train):'''训练'''m, _ = X_train.shape# 初始化向量alpha和标量balpha = np.zeros(m)b = np.zeros(1)# 创建E缓存E = np.zeros(m)# 将各⽅法频繁使⽤的参数收集到列表, 供调⽤时传递.self.args = [alpha, b, X_train, y_train, E]n_changed = 0examine_all = Truewhile n_changed > 0 or examine_all:n_changed = 0# 迭代alpha_ifor i in range(m):if examine_all or 0 < alpha[i] < self.C:n_changed += self._optimize_alpha_i(i)print('n_changed: %s' % n_changed)print('sv num: %s' % np.count_nonzero((alpha > 0) & (alpha < self.C)))# 若当前迭代⾮边界alpha, 且没有alpha改变, 下次迭代所有alpha.# 否则, 下次迭代⾮边界间alpha.examine_all = (not examine_all) and (n_changed == 0)# 训练完成后保存模型参数:idx = np.nonzero(alpha > 0)[0]# 1.⾮零alphaself.sv_alpha = alpha[idx]# 2.⽀持向量,self.sv_X = X_train[idx]self.sv_y = y_train[idx]# 3.b.self.sv_b = b[0]def _predict_one(self, x):'''对单个输⼊进⾏预测'''k = self.K(self.sv_X, x)return np.sum(self.sv_y * self.sv_alpha * k) + self.sv_bdef predict(self, X_test):'''预测'''y_pred = np.apply_along_axis(self._predict_one, 1, X_test)return np.squeeze(np.where(y_pred > 0, 1., -1.))⼆、数据集加载与变换/ml/machine-learning-databases/letter-recognition/import numpy as npX=np.genfromtxt('F:/python_test/data/letter-recognition.data',delimiter=',',usecols=range(1,17)) print(X)print(X.shape)y=np.genfromtxt('F:/python_test/data/letter-recognition.data',delimiter=',',usecols=0,dtype=np.str)print(y)y=np.where(y == 'C',1,-1)print(y)三、训练模型#选择惩罚系数，步长阈值，核函数，⾼斯核函数的gamma（绝对带宽⼤⼩）clf=SMO(C=1,tol=0.01,kernel='rbf',gamma=0.01)from sklearn.model_selection import train_test_splitX_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3)clf.train(X_train,y_train)from sklearn.metrics import accuracy_scorey_pred=clf.predict(X_test)accuracy=accuracy_score(y_test,y_pred)print(accuracy)虽然准确度达到了0.99，但是要明确数据集中的C⼤约是由5%，全部预测成-1都会有95%的准确度，所以可以观察⼀下把C 分类混淆矩阵可以发现没有将⼀个不是C的字符认为是C，将37个C认为是其他字符。

SVM-SMO算法分析及在运维中的应用

SVM-SMO算法分析及在运维中的应用李岩;吴国文【摘要】支持向量机(SVM)是一种基于统计学习理论的新型机器学习方法,由于其出色的性能,已成为当前机器学习界的研究热点之一.本文实现了基于SVM的SMO 算法的分析,并使用径向基高斯核函数对数据进行维度映射处理,最后结合系统运维中产生的仿真数据进行试验,实现了对该领域的应用研究.【期刊名称】《智能计算机与应用》【年(卷),期】2018(008)002【总页数】4页(P78-80,84)【关键词】SVM;SMO;高斯核函数;系统运维应用【作者】李岩;吴国文【作者单位】东华大学计算机科学与技术学院,上海201620;东华大学计算机科学与技术学院,上海201620【正文语种】中文【中图分类】TP391.41引言随着科技信息化的高速发展，特别是互联网的普及，信息服务已经深入到社会的各个领域，如今人们的衣、食、住、行都已离不开信息系统的服务；而各种各样的信息服务都离不开其底层系统的支持，因此，保障信息系统的稳定性已成为系统运维的重要事件。

对于系统的稳定性而言，除了自身硬件和软件的协同配合外，日常运行的数据指标分析，也是保障系统持续稳定长期运行的关键因素。

传统的系统运维，主要依靠人工的定期巡检及突发事件的应急响应机制，在绝大部分情况下可以满足设计指定的运维功能需求，但成本开销较大，而且对于系统历史运行产生的历史数据，也并未形成良好的回溯机制。

一种观念认为，人工智能在运维领域的应用发展已成为必然趋势[1]。

而一些已有的机器学习方法在该领域的研究进展，也多为采用K-近邻算法(KNN)对运维数据处理后的时间结果进行分类，不仅计算和空间复杂度高，其普适性也欠佳、又不好。

本文采用了另一种机器学习的方法，探讨和分析了支持向量机和已经获得广泛使用的序列最小优化算法的原理,并结合使用径向基核函数实现了对于非线性分类的优化[2-3]；同时,通过仿真样本数据进行了模拟实验[4]，结果证实了这一算法在系统运维领域中应用的可行性。

SVM-及SMO算法实现