正弦、余弦、正切

合集下载

正弦、余弦、正切函数图象及其性质

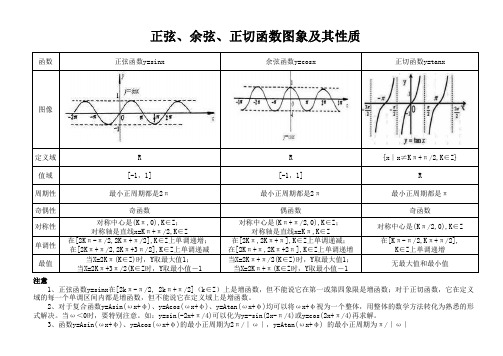
函数正弦函数y=sinx 余弦函数y=cosx 正切函数y=tanx图像定义域R R{x∣x≠Kπ+π/2,K∈Z}值域[-1，1][-1，1]R周期性最小正周期都是2π最小正周期都是2π最小正周期都是π奇偶性奇函数偶函数奇函数对称性对称中心是(Kπ,0),K∈Z；对称轴是直线x=Kπ+π/2,K∈Z对称中心是(Kπ+π/2,0),K∈Z；对称轴是直线x=Kπ,K∈Z对称中心是(Kπ/2,0),K∈Z单调性在[2Kπ-π/2,2Kπ+π/2],K∈Z上单调递增；在[2Kπ+π/2,2Kπ+3π/2],K∈Z上单调递减在[2Kπ,2Kπ+π],K∈Z上单调递减；在[2Kπ+π,2Kπ+2π],K∈Z上单调递增在[Kπ-π/2,Kπ+π/2],K∈Z上单调递增最值当X=2Kπ(K∈Z)时，Y取最大值1；当X=2Kπ+3π/2(K∈Z时，Y取最小值－1当X=2Kπ+π/2(K∈Z)时，Y取最大值1；当X=2Kπ+π(K∈Z时，Y取最小值－1无最大值和最小值正弦、余弦、正切函数图象及其性质注意1、正弦函数y=sinx在[2kπ-π/2, 2kπ+π/2]（k∈Z）上是增函数，但不能说它在第一或第四象限是增函数；对于正切函数，它在定义域的每一个单调区间内都是增函数，但不能说它在定义域上是增函数。

2、对于复合函数y=Asin(ωx+φ)、y=Acos(ωx+φ)、y=Atan(ωx+φ)均可以将ωx+φ视为一个整体，用整体的数学方法转化为熟悉的形式解决。

当ω＜0时，要特别注意。

如：y=sin(-2x+π/4)可以化为y=-sin(2x-π/4)或y=cos(2x+π/4)再求解。

3、函数y=Asin(ωx+φ)、y=Acos(ωx+φ)的最小正周期为2π/∣ω∣，y=Atan(ωx+φ) 的最小正周期为π/∣ω∣。

正弦、余弦、正切

精心整理直角三角形的边角关系—正弦、余弦、正切知识要点1.正弦:在直角三角形中,一个锐角所对的直角边与斜边的比,叫做这个角的正弦. 即:c a A A =∠=斜边的对边sin ；cbB B =∠=斜边的对边sin .2．余弦：在直角三角形中，一个锐角的邻边与斜边的比，叫做这个角的余弦．即:3.4︒0sin ︒0cos ︒0tan 56(90sin 7（1）平方和的关系：1cos sin 22=+A A ．（2）大小比较：当︒<<︒450A 时，A A sin cos >．当︒<<︒9045A 时，A A sin cos <.（3）正切、余切与正弦、余弦间的关系：αααcos sin tan =例题讲解例1根据下列图中给出的ABC Rt ∆的数据，求A sin ，A cos ，B sin ，B cos ，tanA,tanB 的值．例2已知等腰梯形AABCD 中，上底CD=2cm,下底AB=5cm,腰AD=3cm ，试求A sin ，A cos ,tanA 的值．例3求下列各式的值．(1)︒+︒-︒60cos 45cos 30sin (2)︒⋅︒-︒30cos 30sin 260sin (3)︒+︒+︒50cos 50sin 45cos 222(4)︒+︒60sin 30cos 22(5)︒-︒60cos 445cos 2(6)︒-︒︒60cos 245cos 45sin(7)︒-︒︒+︒30sin 30cos 60sin 60cos (8)()260cos 60sin ︒-︒(9)︒⋅︒+︒-︒30tan 45tan 130tan 45tan随堂练习：一、选择题1A ．2A ．3A ．C ．4.A.5.A.0﹡6A ．43 B.47 C.73 D.37 二、填空1．用“<”号连接︒︒︒44cos ,43cos ,41sin 是.2.在ABC Rt ∆中,B A C ∠∠︒=∠,,90和C ∠的对边分别是b a ,和c ,已知25=a ,215=b ,则c =,A ∠=,B ∠=．3．在ABC Rt ∆中，33,30,90=︒=∠︒=∠AC A C ，则AB=．4．在ABC Rt ∆中，CD 是斜边AB 上的高，AB=8cm ，AC=cm 34，则AD=.5.一梯形，它的两个下底角分别为︒30和︒45，较大的腰长为10cm ，则另一腰长为cm ，两底之差为.6.︒︒︒30cos ,45cos ,30sin 的大小关系是.7．在△ABC 中，若2sin cos 02A B ⎛⎫-+-= ⎪ ⎪⎝⎭，∠A 、∠B 都是锐角，则∠C=．8﹡9.123．在45．在61A 2A ．4B 5223．△ABC 中，若cos 2A =，cos 2B =，则此三角形是（）三角形。

余弦正弦正切大小关系

余弦正弦正切大小关系正弦余弦正切的关系：sinA/cosA=tanA，三角函数是基本初等函数之一，是以角度为自变量，角度对应任意角终边与单位圆交点坐标或其比值为因变量的函数。

也可以等价地用与单位圆有关的各种线段的长度来定义。

三角函数在研究三角形和圆等几何形状的性质时有重要作用，也是研究周期性现象的基础数学工具。

在数学分析中，三角函数也被定义为无穷级数或特定微分方程的解，允许它们的取值扩展到任意实数值，甚至是复数值。

正弦；在直角三角形中，任意一锐角∠a的对边与斜边的比叫做角a的正弦；余弦：在直角三角形中，任意一锐角∠a的邻边与斜边的比叫做角a的余弦；正切：在直角三角形中，任意一锐角∠a的对边与邻边的比叫做角a的正切；余切：在直角三角形中，任意一锐角∠a的邻边与对边的比叫做角a的余切。

关系：在直角三角形中，任意一个锐角的正弦值等于另一个锐角的余弦值；任意一个角的正弦值与余弦值的积为一。

正弦余弦正切余切九大关系公式：三角函数公式：正弦（sin）：角α的对边比上斜边。

余弦（cos）：角α的邻边比上斜边。

正切（tan）：角α的对边比上邻边。

余切（cot）：角α的邻边比上对边。

正割（sec）：角α的斜边比上邻边。

余割（csc）：角α的斜边比上对边。

同角三角函数：平方关系：sin^2(α）＋cos^2(α）＝1。

tan^2(α）＋1=sec^2(α）。

cot^2(α）＋1=csc^2(α）。

积的关系：sinα＝tanαcosαcosα＝cotαsinα。

tanα＝sinαsecαcotα＝cosαcscα。

secα＝tanαcscαcscα＝secαcotα。

初中正弦余弦正切公式

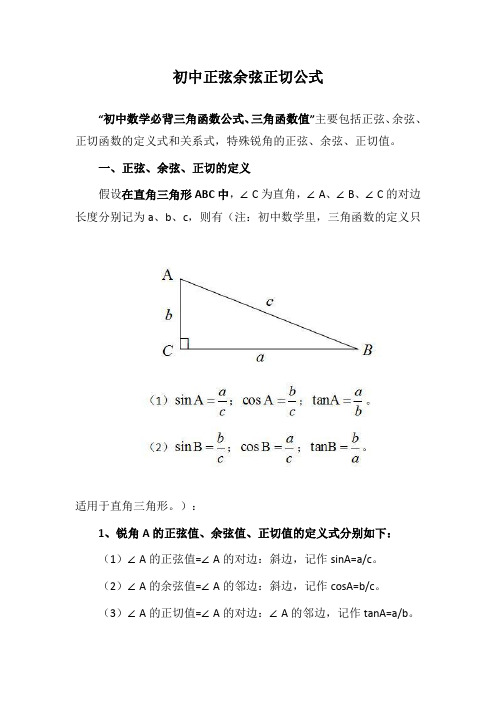
初中正弦余弦正切公式“初中数学必背三角函数公式、三角函数值”主要包括正弦、余弦、正切函数的定义式和关系式，特殊锐角的正弦、余弦、正切值。

一、正弦、余弦、正切的定义假设在直角三角形ABC中，∠C为直角，∠A、∠B、∠C的对边长度分别记为a、b、c，则有（注：初中数学里，三角函数的定义只适用于直角三角形。

）：1、锐角A的正弦值、余弦值、正切值的定义式分别如下：（1）∠A的正弦值=∠A的对边：斜边，记作sinA=a/c。

（2）∠A的余弦值=∠A的邻边：斜边，记作cosA=b/c。

（3）∠A的正切值=∠A的对边：∠A的邻边，记作tanA=a/b。

2、锐角B的正弦值、余弦值、正切值的定义式分别如下：（1）∠B的正弦值=∠B的对边：斜边，记作sinB=b/c。

（2）∠B的余弦值=∠B的邻边：斜边，记作cosB=a/c。

（3）∠B的正切值=∠B的对边：∠B的邻边，记作tanB=b/a。

【注】正弦=“对比斜”、余弦=“邻比斜”、正切=“对比邻”。

3、互余的两个角间的正弦、余弦、正切值关系假设在直角三角形ABC中，∠C为直角，则∠A与∠B互余。

通过∠A和∠B的正弦、余弦、正切值的定义式的对比，我们不难发现：∠A的正弦值与∠B的余弦值相等，∠A的余弦值与∠B的正弦值相等，∠A的正切值与∠B的正切值互为倒数。

所以，当∠A与∠B互余时我们有以下3个同时成立的等式关系：（1）sinA=cosB；（2）sinB=cosA；（3）tanA·tanB=1。

二、同角的正弦值、余弦值、正切值间的关系式1、商数关系：tanA=sinA/cosA；tanB=sinB/cosB.2、平方关系：同一个锐角的‘正弦的平方’与‘余弦的平方’的和为1，即(sinA)^2+(cosA)^2=1；(sinB)^2+(cosB)^2=1.3、倒数关系：tanA·cotA=1；tanB·cotB=1.【注】“cotA”称为为∠A的余切，它等于∠A的邻边比上∠A的对边。

余弦正弦正切转化公式

余弦正弦正切转化公式余弦、正弦和正切是三角函数中的基本函数，它们在数学和物理等领域中都有广泛的应用。

尽管它们之间存在着一定的关联，但是它们之间并没有简单的转化公式，即不能通过简单的代数方式将其中一个函数表示为另外两个函数的组合形式。

首先，我们来看一下余弦函数和正弦函数之间的关系。

根据三角函数的定义，余弦函数（cos）和正弦函数（sin）之间满足以下关系：cos^2(x) + sin^2(x) = 1这个关系被称为余弦函数和正弦函数的和角恒等式。

根据这个恒等式可以发现，正弦函数的平方与余弦函数的平方之和等于1，它们的取值是互相约束的。

如果我们已知一个角度的正弦值，那么可以通过平方根运算来计算出相应的余弦值，反之亦然。

接下来，我们来看一下正切函数和正弦函数或余弦函数之间的关系。

正切函数（tan）和正弦函数或余弦函数之间的关系可以通过以下恒等式来表示：tan(x) = sin(x) / cos(x)从这个恒等式可以发现，正切函数等于正弦函数与余弦函数的比值，也就是说，如果我们已知一个角度的正弦值和余弦值，那么可以通过除法运算来计算出相应的正切值，反之亦然。

综上所述，余弦、正弦和正切函数之间没有直接的转化公式，它们的关系是通过三角函数的定义和恒等式来确定的。

在实际的应用中，我们通常会利用这些关系来计算和推导各种三角函数的性质和数值。

除了以上的基本关系外，三角函数还有一些常见的性质和公式。

例如，三角函数具有周期性，即在特定的区间内重复出现相同的函数值。

以正弦函数为例，它在区间[0, 2π]内的函数值是周期性的，即sin(x) =sin(x + 2π)。

这一性质可用于简化计算和求解问题。

此外，三角函数还具有一系列的三角恒等式，包括和差恒等式、倍角恒等式、半角恒等式等。

这些恒等式可以用于证明和推导各种与三角函数相关的性质和公式。

综上所述，余弦、正弦和正切函数之间没有简单的转化公式，但它们之间有一定的关系，可以通过三角函数的定义和恒等式来确定。

正弦、余弦、正切

直角三角形的边角关系—正弦.余弦.正切常识要点1.正弦:在直角三角形中,一个锐角所对的直角边与斜边的比,叫做这个角的正弦. 即:c a A A =∠=斜边的对边sin ; cbB B =∠=斜边的对边sin .2．余弦：在直角三角形中,一个锐角的邻边与斜边的比,叫做这个角的余弦．即:cb A A =∠=斜边的邻边cos ; ca B B =∠=斜边的邻边cos3.正切:在直角三角形中,一个锐角所对的直角边与邻边的比,叫做这个角的正切.即:b a A A A =∠∠=的邻边的对边tan ; abB B B =∠∠=的邻边的对边tan .4．特别角的正弦,余弦值：=︒0sin 0;=︒30sin 21;=︒45sin 22;=︒60sin 23;=︒90sin 1;=︒0cos 1;=︒30cos 23;=︒45cos 22;=︒60cos 21;=︒90cos 0．=︒0tan 0 ;=︒30tan 33;=︒45tan 1 ;=︒60tan 3;︒90tan 不消失 ; 5．正.余弦.正切值随锐角大小的变更（即增减性）：正弦值随锐角的增大而增大,余弦值随锐角的增大而减小,正切值随锐角的增大而增大.6．互余两角的正弦,余弦间的关系：随意率性锐角的正弦值等于它的余角的余弦值,随意率性锐角的余弦值等于它的余角的正弦值．()ααcos 90sin =-︒; ()ααsin 90cos =-︒．7．同角的正弦,余弦间的关系：（1）平方和的关系：1cos sin 22=+A A ．（2）大小比较：当︒<<︒450A 时,A A sin cos >．当︒<<︒9045A 时,A A sin cos <.（3）正切.余切与正弦.余弦间的关系：αααcos sin tan = 例题讲授例1依据下列图中给出的ABC Rt ∆的数据,求A sin ,A cos ,B sin ,B cos ,tanA,tanB 的值．例2已知等腰梯形ABCD 中,上底CD=2cm,下底AB=5cm,腰AD=3cm,试求A sin ,A cos ,tanA 的值．例3求下列各式的值．(1)︒+︒-︒60cos 45cos 30sin (2)︒⋅︒-︒30cos 30sin 260sin (3)︒+︒+︒50cos 50sin 45cos 222(4)︒+︒60sin 30cos 22(5)︒-︒60cos 445cos 2(6)︒-︒︒60cos 245cos 45sin(7)︒-︒︒+︒30sin 30cos 60sin 60cos (8)()260cos 60sin ︒-︒ (9)︒⋅︒+︒-︒30tan 45tan 130tan 45tan随堂演习：一.选择题1．在ABC Rt ∆中,︒=∠︒=∠60,90A C ,BC=1,则AB=（） A ．2 B ．2 C ．23 D ．3322．在ABC Rt ∆中,52sin ,10,90==︒=∠B AB C ,BC 的长是（） A ．212 B ．4 C ．21D ．50213．下列表达式准确的是（）A ．︒=︒+︒90cos 60cos 30cosB ．145cos 45sin =︒⋅︒C ．163cos 27cos 22=︒+︒D ．3360cos 30sin =︒+︒ ︒>∠60A 时,A ∠的余弦值( )α是锐角,6.0sin =α,则( )A.︒<<300αB.︒<<︒4530αC.︒<<︒6045αD.︒<<︒9060αBA2 CB3AB﹡6．在ABC ∆中,︒=∠90C ,假如43sin =A ,那么=B tan （）A ．43 B.47 C.73 D.37 二.填空1．用“<”号衔接︒︒︒44cos ,43cos ,41sin 是.ABCRt ∆中,B A C ∠∠︒=∠,,90和C ∠的对边分离是b a ,和c ,已知25=a ,215=b ,则c =,A ∠=,B ∠=．3．在ABC Rt ∆中,33,30,90=︒=∠︒=∠AC A C ,则AB=．4．在ABC Rt ∆中,CD 是斜边AB 上的高,AB=8cm,AC=cm 34,则AD=.5.一梯形,它的两个下底角分离为︒30和︒45,较大的腰长为10cm,则另一腰长为cm,两底之差为.6.︒︒︒30cos ,45cos ,30sin 的大小关系是.7．在△ABC中,若2sin cos 02A B ⎛⎫-+-= ⎪ ⎪⎝⎭,∠A.∠B 都是锐角,则∠C=．8．在△ABC 中,∠C=90o ,若3AC =,则∠A=,cos B =．ABC Rt ∆中,︒=∠90C ,若135cos =A ,则=A tan . 功课一.填空1．式子12sin30cos30-︒︒=.2．已知Rt ABC ∆中,90C ∠=︒,5sin 13A =,则sin B =. 3．在Rt△ABC 中,∠C=90o ,4AB =,ABC S ∆=则tan tan A B +=4．等腰Rt△ABC 中,∠A=90o ,AB=AC,D 为AC 上一点,AC AD 31=,则DBC ∠tan =. 5．在Rt△ABC 中,∠C=90o ,AB=2,BC =,则tan 2A =. 6．在△ABC 中,∠B=30o ,tan 2,C =边AB=2,则BC=. 二.选择1．在△ABC 中,∠C=90°,则下列各式中不准确的是（）A ．sin a c A =B ．cos b c A =C ．cos b c B =D ．sin bc B= 2．在△ABC中,∠C=90°,3sin ,4B c ==则b 等于（）A ．4B D ．723．△ABC 中,若cos 2A =,cos 2B =,则此三角形是（）三角形.A ．锐角B ．直角C ．钝角D ．直角或钝角 4．等腰三角形的腰是底的2.5倍,则底角的余弦值等于（）A B ．15 D ．25三.盘算1．()032sin 451π-︒+2．()sin 45cos30sin 601sin 3032cos60︒+︒-︒-︒-︒3.︒-︒⋅︒45tan 330cos 60tan4.()230cos 30sin 260sin 145cos 60sin 145sin ︒-︒+︒-︒-︒+︒5.()222160sin 30tan 412160cos 2--︒⋅︒+++︒-6．︒-︒︒+︒+︒⋅︒30tan 60tan 60sin 60tan 145cos 30cos 四．在△ABC 中,已知021cos 21sin =-+-B A ,BC=1．（1）试断定△ABC 的外形;（2）求AB.AC 的长．。

直角三角形的正弦定理余弦定理与正切定理

直角三角形的正弦定理余弦定理与正切定理直角三角形的正弦定理、余弦定理与正切定理直角三角形是指其中一个角度为90度的三角形。

在解决与直角三角形相关的问题时，我们通常会用到三个重要的定理：正弦定理、余弦定理和正切定理。

这些定理能够帮助我们计算直角三角形中的各种不确定数值，从而解决实际问题。

1. 正弦定理正弦定理表明，在任意三角形ABC中，边长a、b、c与它们所对的角度A、B、C之间有如下关系：a/sinA = b/sinB = c/sinC在直角三角形中，我们可以根据正弦定理计算一侧边的长度。

例如，已知直角三角形中一条直角边的长度为a，另外一条直角边与直角边的夹角为θ，我们可以使用正弦定理计算斜边的长度c：c/sin90° = a/sinθc = a/sinθ2. 余弦定理余弦定理表示，在任意三角形ABC中，边长a、b、c与它们所对的角度A、B、C之间有如下关系：c² = a² + b² - 2abcosC对于直角三角形，余弦定理可以简化为毕达哥拉斯定理：c² = a² + b²3. 正切定理正切定理说明，在任意三角形ABC中，边长a、b、c与它们所对的角度A、B、C之间有如下关系：tanA = a/btanB = b/a在直角三角形中，以直角作为顶点，边长a和b所对的角分别为A和B，我们可以使用正切定理来计算两个角的正切值。

这些定理为解决直角三角形的相关问题提供了基础计算方法。

例如，我们可以使用余弦定理来计算一个直角三角形的斜边长度，或者使用正弦定理计算角的大小。

同时，正切定理也可以用于计算两个角的正切值。

在实际问题中，我们可以通过已知的信息和直角三角形的相关定理来解决各种几何问题。

例如，已知一个直角三角形的一条直角边和斜边长度，我们可以使用正弦定理或余弦定理来计算未知边的长度或角的大小。

同样地，已知两个角的正切值，我们也可以使用正切定理来计算这两个角的具体数值。

正弦余弦和正切之间的关系

正弦余弦和正切之间的关系正弦、余弦和正切是三角函数中最基本的三种函数，它们之间存在着密切的关系。

首先，我们来看它们的定义和计算方法。

正弦函数（sin）表示一个角的对边与斜边的比值，通常用a/h表示，其中a为对边，h为斜边。

余弦函数（cos）表示一个角的邻边与斜边的比值，通常用b/h表示，其中b为邻边。

正切函数（tan）表示一个角的对边与邻边的比值，通常用a/b表示。

这三个函数之间的关系可以通过三角恒等式来描述。

例如，tanθ = sinθ / cosθ，这意味着正切函数可以表示为正弦函数与余弦函数的比值。

另外，我们还可以通过sin²θ + cos²θ = 1这一三角恒等式得到sinθ与cosθ之间的关系，进而推导出tanθ与sinθ、cosθ之间的关系。

在三角函数的图像中，我们也可以清晰地看到它们之间的关系。

正弦函数的图像是一个周期性的波浪曲线，而余弦函数的图像则是正弦函数图像的相位延迟π/2。

正切函数的图像则是在余弦函数的零点处具有无穷大的间断点，这也反映了正切函数与正弦、余弦之间的关系。

除了上述数学关系和图像特点外，正弦、余弦和正切在实际问题中也有着丰富的应用。

在三角测量、物理学、工程学等领域，这三种函数经常被用来描述角度、振动、周期性变化等现象，它们之间的关系也为解决实际问题提供了重要的数学工具。

综上所述，正弦、余弦和正切之间存在着密切的数学关系，可以通过三角恒等式、图像特点和实际应用来全面理解它们之间的联系。

这些函数的相互关系不仅在数学领域具有重要意义，也在实际问题的求解中发挥着重要作用。

数学中的三角函数正弦余弦与正切的应用

数学中的三角函数正弦余弦与正切的应用在数学中，三角函数是一种基础的数学工具，常用于解决与角度和三角形相关的问题。

其中，正弦、余弦和正切是三角函数中最常见且广泛应用的三种。

它们在几何、物理、工程等领域中起到了重要的作用。

本文将介绍三角函数正弦、余弦和正切的定义、性质以及其在各个领域中的具体应用。

一、正弦函数的定义与性质在三角函数中，正弦函数(sin)是最基本且常见的函数之一。

它的定义如下：定义1：对于任意实数x，正弦函数sin(x)的值等于以x为角度的弧所对应的直角三角形中，斜边的长度与斜边所在直角的邻边的比值。

正弦函数的性质如下：性质1：正弦函数的周期为2π（或360°）。

即sin(x+2π) = sin(x)，对于任意实数x。

性质2：正弦函数的取值范围为[-1,1]。

即-1≤ sin(x) ≤1，对于任意实数x。

正弦函数在几何、物理等领域中有许多应用。

1. 几何中的应用正弦函数在解决几何问题中起到了重要的作用，尤其是在三角形中。

其中，正弦定理是一项基于正弦函数的重要几何定理。

它可以用于计算三角形的边长或角度。

利用正弦函数，可以得到正弦定理的数学表达式如下：对于任意三角形ABC，边长分别为a, b, c，对应的角度分别为A, B, C，那么有：sin(A)/a = sin(B)/b = sin(C)/c根据这个定理，我们可以根据已知的两个边与它们夹角的关系，求解未知边长或角度。

2. 物理中的应用正弦函数在物理学中的应用非常广泛。

例如，振动和波动等现象均可以通过正弦函数进行描述和分析。

在简谐振动中，物体以正弦函数的形式来回振动。

振动的幅度、频率以及相位差等都可以通过正弦函数来表示。

在波动中，正弦函数也被广泛应用。

例如，声波、光波等均可以表示为正弦函数的形式。

通过正弦函数可以描述波的振幅、频率、波长等特征。

3. 工程中的应用正弦函数在工程领域中也有很多应用。

例如，在电工学中，交流电信号可以表示为正弦函数。

三角函数的引入认识正弦余弦和正切

三角函数的引入认识正弦余弦和正切三角函数的引入认识正弦、余弦和正切三角函数是数学中的重要概念，它们由三角形的边长比例引出，可以帮助我们研究角度和距离之间的关系。

其中，最为常见的三角函数为正弦、余弦和正切。

在本文中，我们将探讨三角函数的引入以及它们的性质和用途。

一、正弦函数的引入正弦函数是最早被引入的三角函数之一，它定义了角度和其对边与斜边的比值之间的关系。

设一个锐角三角形ABC，其中∠ABC的对边为a，斜边为c，则正弦函数sinA的定义为sinA = a/c。

正弦函数可以描述角度大小与其对边长度的关系，它的值域为[-1, 1]。

正弦函数的引入可以追溯到古希腊数学家Hipparchus，他发现了角度与弧长之间的关系，并借此引入了正弦函数。

正弦函数在几何学、物理学和工程学中有广泛的应用，例如计算航空航天器的轨道、研究音波的传播等。

二、余弦函数的引入除了正弦函数，余弦函数也是三角函数中常见的一种。

余弦函数定义了角度和其邻边与斜边的比值之间的关系。

仍然考虑锐角三角形ABC，其中∠ABC的邻边为b，斜边为c，则余弦函数cosA的定义为cosA = b/c。

余弦函数描述了角度大小与其邻边长度的关系，它的值域也是[-1, 1]。

正弦函数和余弦函数之间存在着互补关系，即sinA = cos(π/2 - A)。

这个关系可以通过锐角三角形的基本性质推导得出。

余弦函数的引入可以追溯到Hipparchus的工作，并且在三角函数的研究中起到了重要的作用。

余弦函数在物理学、工程学和计算机图形学中广泛应用，例如计算机视觉中的图像处理、机器人学中的运动规划等。

三、正切函数的引入正切函数是三角函数中的另一种常见形式，它定义了角度的对边与邻边的比值。

在锐角三角形ABC中，∠ABC的对边为a，邻边为b，则正切函数tanA的定义为tanA = a/b。

正切函数描述了角度大小与其对边和邻边之间的关系，它的值域是整个实数集。

正切函数与正弦函数和余弦函数之间也存在一定的关系。

正弦、余弦和正切

正弦、余弦和正切直⾓三⾓形正弦、余弦和正切是⾥的主要函数，它们是基于⼀个⽽建⽴的。

在探索这些函数之前，我们先给三⾓形的每条边⼀个名字："对边" 是在⾓θ的对⾯"邻边" 是在⾓θ的旁边"斜边" 是长的⼀边邻边是在⾓的旁边对边是在⾓的对⾯正弦、余弦和正切正弦（sine）, 余弦（cosine）和正切（tangent）（英语符号简写为 sin, cos 和 tan) 是直⾓三⾓形边长的⽐：对⼀个特定的⾓θ来说，不论三⾓形的⼤⼩，这三个⽐是不变的计算⽅法：⽤⼀条边的长度除以另⼀条边的长度例⼦： 35°的正弦是多少？⽤这三⾓形来算（长度精确到⼀位⼩数）：sin(35°)= 对边 / 斜边= 2.8 / 4.9= 0.57...cos(35°)= 邻边 / 斜边= 4.0 / 4.9= 0.82……tan(35°)= 对边 / 邻边= 2.8 / 4.0= 0.70……好的计算器都会有 sin, cos 和 tan 的键，⽅便计算。

你只需输⼊⾓度然后按键。

可是你还是要记得它们的意思！⽤图来显⽰：在这⾥练习Sohcahtoa怎样去记住？想想，⽤这个怪怪的英⽂单词 "Sohcahtoa"！像这样：Soh...Sine = Opposite （对边） / Hypotenuse（斜边）...cah...Cosine = Adjacent （邻边）/ Hypotenuse （斜边）...toa Tangent = Opposite （对边）/ Adjacent （邻边）去这页了解更多。

记住它，考试时会有⽤！试试看！试试看！移动⿏标，不同的⾓（以或为单位）对正弦、余弦和正切的影响。

在这个动画⾥，斜边是 1，圆形是。

请注意邻边和对边可以是负值，导致正弦、余弦和正切的值也可正可负。

例⼦例⼦： 30° 的正弦、余弦和正切是什么？传统的 30° 三⾓形的斜边为 2、对边为 1 和邻边为 √3:30 degree triangle知道边长，便可以计算函数的值：正弦sin(30°) = 1 / 2 = 0.5余弦cos(30°) = 1.732 / 2 = 0.866...正切tan(30°) = 1 / 1.732 = 0.577...（⽤计算器来检查答案！）例⼦： 45° 的正弦、余弦和正切是什么？传统的 45° 三⾓形有两条边长为 1，斜边为 √2:45 度三⾓形正弦sin(45°) = 1 / 1.414 = 0.707...余弦cos(45°) = 1 / 1.414 = 0.707...正切tan(45°) = 1 / 1 = 1为什么？为什么这些函数重要？因为当我们知道边长时，我们可以⽤它们来计算⾓度同时，当我们知道⾓度时，我们也可以⽤它们来计算边长三⾓例⼦例⼦：⽤正弦函数来计算 "d"我们知道：电缆与海底成 39° 的⾓电缆长度为 30 ⽶。

正弦余弦与正切的关系

正弦余弦与正切的关系“哎呀，这正弦余弦与正切到底有啥关系呀？”好，那咱就来说说正弦余弦与正切的关系。

咱先从定义上来说哈，正弦是一个角的对边与斜边的比值，余弦呢是这个角的邻边与斜边的比值，而正切则是正弦除以余弦。

比如说，在一个直角三角形里，有个角 A。

那这个角 A 的正弦就是它对边 a 的长度除以斜边 c 的长度，记作 sinA=a/c。

角 A 的余弦就是邻边 b 的长度除以斜边 c 的长度，记作 cosA=b/c。

那正切呢，就是 sinA 除以cosA，也就是 a/b，记作 tanA=a/b。

举个实际例子吧，就说咱盖房子的时候，要搭个架子。

那架子和地面形成的角度，咱就可以用这些来分析。

比如知道了某个角度的正弦值和余弦值，咱就能算出正切值，然后就能知道这个架子倾斜的程度有多大，这对施工安全可是很重要的。

再比如说，在学习物理的时候，研究物体的摆动。

通过测量角度和相关边长，利用正弦余弦和正切的关系，能帮助我们更好地理解物体摆动的规律。

而且啊，它们之间还有一些特殊的关系呢。

比如 tanA=sinA/cosA，这是个很重要的式子哦。

还有，在一些特定的角度下，它们的值是固定的。

像30 度、45 度、60 度这些常见角度，它们的正弦、余弦、正切值都要记住，这在很多计算中都非常有用。

比如说，一个 30 度的直角三角形，那它的正弦值就是 1/2，余弦值是根号 3/2，正切值就是根号 3/3。

记住这些，以后遇到相关的问题就能很快算出来啦。

在数学和其他学科中，正弦余弦与正切的关系那可是无处不在的。

不管是计算几何图形的边长角度，还是分析物理现象，都离不开它们。

大家一定要好好理解和掌握它们之间的关系哦，这样才能在学习和生活中更好地运用它们来解决问题呀。