3-4简支梁受均布载荷
简支梁受均布载荷作用,试写出剪力和弯矩方程

一、简支梁的基本概念简支梁是一种常见的结构形式,其特点是两端固定支撑,中间无任何支撑,形成一个简单的横跨结构。
在工程建设中,简支梁常被用于桥梁、楼板等结构的设计与施工中。
当梁承受均布载荷时,其上产生的剪力和弯矩是设计和分析的重要参数。
二、受力分析的基本原理1. 剪力的定义和计算公式在简支梁上,当均布载荷作用时,梁体上的任意一截面上都受到来自上部和下部梁体的相互作用力。
剪力的大小可以通过以下公式计算:V = wL/2 - 信信其中,V代表该截面上的剪力,w代表均布载荷的大小,L代表梁的长度,x代表距离截面起点的距离。
2. 弯矩的定义和计算公式同样,在简支梁上,距离梁的任意一截面上也存在着弯矩。
弯矩的计算公式如下:M = wLx/2 - w*x^2/2其中,M代表该截面上的弯矩,w代表均布载荷的大小,L代表梁的长度,x代表距离截面起点的距离。
三、剪力和弯矩方程的推导1. 剪力方程的推导根据前文所述的剪力的计算公式,可以推导出简支梁受均布载荷作用时的剪力方程。
假设梁的起点为原点,横向为x轴方向,竖向为y轴方向,由上述公式可知,剪力V与距离x的关系为线性关系,斜率为wL/2,截距为0。
简支梁受均布载荷作用时的剪力方程为:V = wL/2 - 信信2. 弯矩方程的推导同样地,根据前文所述的弯矩的计算公式,可以推导出简支梁受均布载荷作用时的弯矩方程。
假设梁的起点为原点,横向为x轴方向,竖向为y轴方向,通过弯矩的计算公式可得知,弯矩M与距离x的关系为二次函数关系,并且开口向下。
简支梁受均布载荷作用时的弯矩方程为:M = wLx/2 - w*x^2/2四、结论与应用在工程设计中,通过以上剪力和弯矩方程的推导,可以为简支梁的设计、分析提供依据。
在实际工程中,根据预设的载荷情况和结构参数,可以通过计算得到不同截面处的剪力和弯矩,从而根据这些受力情况,进行梁的截面选取、钢筋布置、构造设计等工作。
剪力和弯矩方程的推导及其应用具有重要的实际意义和价值。
化工设备机械基础例题、习题解答

1.画受力图时,一定要先取分离体,再画受力图。
取分离体实质上是暴露或显示物体间相互作用的一种方式,只有把施力体和受力体分离开来,才能将它们之间的机械作用以力代替。
另外,工程上所要的分析结构或机构一般很复杂,如果不取分离体来画受力图,往往分不清施力体和受力体,分不清内力和外力,容易出错。
因此,根据题目的要求,选定某个或某些刚体作为研究对象后,一定要画出分离体,在分离体上画出受力图,对此不应怕麻烦。
2.如何判别二力刚体。
在工程实际中遇到的二力刚体,有以下特点:(1)刚体不受任何主动力的作用(包括不计自重);(2)刚体只受两个约束,而且每个约束都可用一个约束反力代替。
凡是满足以上两点的刚体,不论形状如何都为二力刚体。
3.光滑圆柱铰链连接是工程中各构件相互连接的主要形式,因此,认清光滑圆柱铰链的结构及其约束反力的方向特点是顺利进行受力分析的关键一环。
当一个光滑圆柱销钉与两个或两个以上带有相同孔径(其值略比销钉直径大)的构件呈光滑接触时,这种约束即为光滑圆柱铰链约束。
其约束的特点是能完全限制各被连接物体之间沿销钉径向的任何相对位移,而不能限制它们绕销钉轴向的任何相对转动,因此,各连接构件与销钉鞋之间的接触是销钉某条母线的光滑接触,其约束反力经过接触点并沿销钉的径向,被销钉连接的各构件间没有直接的相互作用,它们都分别只与销钉产生相互作用,根据同向平行力系必存在合力,任一被连构件与销钉之间可等效为一对作用与反作用力,且这对相互作用力的作用线必通过销钉中心。
由于接触的销钉母线的位置及其等效的约束反力的大小,都与被连构件的受力相关,故被连构件所受到的销钉约束反力的大小和方向都不能直接确定,通常用过销钉中心,且在销钉横截面内两已知方位的正交分量来表示,即把大小和方向这两个未知因素转化为两个方位已知而其代数值未知的两未知因素。
只有在某些特殊情况,如被连构件为二力刚体或三力平衡或力偶平衡或平行力系平衡时,销钉的约束反力的方向才可直接确定,此时只剩下约束反力的大小未知。
弹性力学与有限元程序设计--第三章

—— 对应于矩形梁的纯弯曲问题。
第三章 平面问题的直角坐标解答
§3-2 矩形梁的纯弯曲
应力函数取三次多项式
ay
3
M
h
M
2 2
对应的应力分量:
x 6ay y 0 xy yx 0
(a)
x
x
图
y
y
l
h
x
1
h
结论:应力函数(a)能解决 矩形梁受纯弯曲的问题。 如图,取单位宽度的梁来考察,并命每单位宽度上力偶的矩为 M 。这 里 M 的因次是[力][长度]/[长度],即[力]。 边界条件: 上下(主要)边界:
h 2 h 2
h 2 h 2
前一式总能满足,而后一式要求:
a 2M h3
代入式(a),得:
x
12 M y y 0 xy yx 0 3 h
第三章 平面问题的直角坐标解答
§3-3 位移分量的求出
1. 形变分量与位移分量
(1)形变分量 由前节可知,其应力分量为:
x M y
u x l 0, v x l 0
y 0 y 0
v x
x l y 0
0
o
l
x
y
(中点不动)
u0 0
M 2 l l v0 0 2 EI
(轴线在端部不转动)
u0 0
v0 Ml 2 EI
2
代入式(f),有
代回式(f),有
u M (l x) y EI
2 x 2 fx x y
(2-25)
2 y 2 fy y x
(2-24)
(b)边界条件
工程力学--材料力学(第五、六章)经典例题及讲解
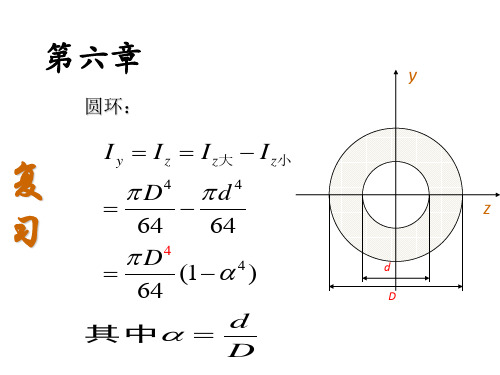
P
A
0.5 m
C D
0.4 m 1m
B
20
40
解:C点的应力 σ C = E ε = 200 × 10 3 × 6 × 10 − 4
= 120M Pa
C截面的弯矩
M C = σ C W z = 640 N ⋅ m
由 M C = 0.5 R A = 0.5 × 0.4 P = 0.2 P = 640 N ⋅ m 得 P = 3.2kN
度减小一半时,从正应力强度条件考虑, 该梁的承载能力将是原来的多少倍? 解: 由公式
σ max
M max M max = = 2 Wz bh 6
可以看出:该梁的承载能力将是原来的2 可以看出:该梁的承载能力将是原来的2倍。
例4:主梁AB,跨度为l,采用加副梁CD AB,跨度为l 采用加副梁CD
的方法提高承载能力, 的方法提高承载能力,若主梁和副梁材料 相同,截面尺寸相同, 相同,截面尺寸相同,则副梁的最佳长度 a为多少? 为多少?
2 2
2
bh b( d − b ) Wz = = 6 6
2 2 2
∂ Wz d 2 b 2 = − =0 ∂b 6 2
d 由此得 b = 3
d
2 2
h
h = d −b =
h = 2 ≈3:2 b
2 d 3
b
例12:跨长l =2m的铸铁梁受力如图示,已知材料许用拉、 12:跨长l =2m的铸铁梁受力如图示 已知材料许用拉、 的铸铁梁受力如图示,
10 kN / m
200 2m 4m 100
10 kN / m
200
2m
Fs( kN ) 25 Fs(
45 kN
4m
100
材料力学第4讲-利用微分关系绘制梁内力图

在CD和DB段,剪力为负值,弯矩图
1.7 为向下倾斜的直线.
最大弯矩发生在剪力改变正、负号的 C
截面处.说明剪力图和弯矩图是正确的.
27 +
例题3-4-2 一简支梁受均布荷载作用,其集度 q=100kN/m ,如图 所示.试用简
易法作此梁的剪力图和弯矩图. 解:(1) 计算梁的支反力
FRA FRB 0.5 100 1.6 80kN
(1)梁的载荷集度函数、剪力函数和弯矩函数之间的 微分关系
(2)利用微分关系的绘制简单梁的内力图 (3)利用微分关系绘制多跨静定的内力图 (4)根据梁的内力图反推梁的荷载图 2.5 应用叠加原理绘制梁的内力图(待学习) 2.6 刚架和组合变形杆件的内力分析(待学习)
2.4 利用微分关系绘制梁的内力图
dFS ( x) q( x) dx
dM ( x) dx
FS
(
x)
(3)内力的极值点位置的判断 1)最大剪力可能发生在集中力所在截面的一侧;或
发生在剪力图有转折的截面处或杆件的端部.
2)梁上最大弯矩 Mmax可能发生在均布荷载作用区段 内FS(x) = 0 的截面上; 或发生在杆件中部弯矩发生
转折或突变处,或发生在杆件的端部。
将梁分为 AC、CD、DB 三段.
AC和DB上无荷载,CD 段有向下的
均布荷载.
(2)剪力图 AC段 水平直线
FSA右 FRA 80kN
CD段 向右下方的斜直线
FRA
A C
0.2 1
FS
(kN)
80
q
FRB
B
D
1.6
2
+
FSC FRA 80kN
FSD FRB 80kN
弹性力学(徐芝纶四版)-第3章

—— 与材力中结果相同
(2)悬臂梁
边界条件
u x l 0 v x l 0
h y 2
h 2
由式(f)可知,此边界条件无法满足。 边界条件改写为:
M u xy y u0 EI (f) M 2 M 2 v y x x v0 2 EI 2 EI
第三章
平面问题的直角坐标解答
力学问题。
要点 —— 用逆解法、半逆解法求解平面弹性
主要内容
§3-1 多项式解答
§3-2 位移分量的求出
§3-3 简支梁受均布载荷
§3-4 楔形体受重力和液体压力
§3-5 级数式解答
§3-6 简支梁受任意横向载荷
§3-1 多项式解答
适用性:由一些直线边界构成的弹性体。 目的: 考察一些简单多项式函数作为应力函数φ(x,y) ,能解决什么样的 力学问题。 ——逆解法
说明: (1) 求位移的过程:
(a)将应力分量代入物理方程
xy 1 1 x ( x y) y ( y x) xy E G E
(b)再将应变分量代入几何方程
u x x
v y y
xy
u v y x
(c)再利用位移边界条件,确定常数。
M
l
M y
x
1
h
y 0 xy 0
M y My x I h3 / 12
(a)
1 My My xy 0 x y E I E I
(b)
(2)位移分量
将式(b)代入几何方程得:
平面应力情况下的物理方程:
x 1 ( x y)
E y 1 ( y x) E xy xy
材料力学讲解作业

材料力学讲解作业Document serial number【UU89WT-UU98YT-UU8CB-UUUT-UUT108】作下图所示梁的剪力图和弯矩图。
2m1m1mm1kN 2kN2kN 2kNA BCD梁分三段,AB 、BC 为空荷载段,CD 段为均布荷载段,均布荷载q=2kN/2m=1kN/m 。
A ,B ,D 三处剪力有突变,说明有集中力作用,在A 截面有向上集中力2kN ,在B 截面有向下集中力2kN ,在D 截面有向上集中力2kN 。
荷载图如图 (b)。
根据荷载图作弯矩图,如图 (c)所示。
如下图所示机构中,1,2两杆的横截面直径分别为cm d 101= ,cm d 202= ,P=10kN 。
横梁ABC ,CD 视为刚体。
求两杆内的应力。
p DCBA122m2m1.5m1m1mCD 杆的D 支座不受力,CD 杆内也不受力,所以p 可视为作用于ABC 杆的C 端。
取ABC 为受力体,受力图如图(b)所示。
MPaMPa A N MPaMPa A N kN N kN N 7.6310204103203.12710104101020210162222623111=⨯⨯⨯⨯===⨯⨯⨯⨯====--πσπσ,如图所示的阶梯形圆轴,直径分别为cm d 41=,cm d 72=。
轮上三个皮带轮,输入功率为kW N 171=,kW N 132=,kW N 303=。
轴的转速为n=200r/min ,材料的许用剪应力[τ]=60MPa 。
试校核其强度。
1计算各轮处的扭转外力偶矩。
mkN m kN m m kN m kN n N m m kN m kN n N m ⋅=⋅⨯=⋅=⋅⨯=⋅=⋅⨯==433.12003055.9621.02001355.9255.9812.02001755.9155.9321(c)(b)kN m 31图3 传动轴可简化为图3(b),⑦扭矩图如图3(c)。
AD 段的最大剪应力为[]τπτ>=⨯⨯⨯==-MPa Pa W M T TAD 6.64104168126311max BC 段的最大剪应力为[]τπτ>=⨯⨯⨯==-MPa Pa W M T TBC 3.211071614326322max AD 段的单位长度扭转角为[]θπθ>=⨯⨯⨯⨯⨯⨯==-m mGI M p TAD /1.23/104108018032812842911BC 段的单位长度扭转角为[]θπθ<=⨯⨯⨯⨯⨯⨯==-m m GIp MINC/44.0/1074108018032143222829由此可知轴的强度与刚度都不够。
材料力学第6章 弯曲内力

精品文档
6.1 梁的内力—剪力和弯矩
例题 6-2
(2)计算(jìsuàn)指定截面上的剪力和 弯矩
C截截面面C左(以侧梁的左力半:边为研究对象):
FAy 2 kN () (+)
FSC Fy FAy 2kN
C截面左侧的力矩:
FAy * 2m (+)
M e 8kN m (-)
M C
M F 2m - M -4kN m O
19
精品文档
6.2 剪力图和弯矩图
例题 6-3
(2) 作剪力图(lìtú)和弯矩图
由剪力、弯矩方程画剪力、弯矩图。
注意: 画图时应将剪力图、弯矩图与计算简图 对齐,并注明图名(FS图、M图)、 峰值点的值及正负号。
秦飞 编著《材料力学》 第6章 弯曲(wānqū)内
20
力
精品文档
6.2 剪力图和弯矩图
(plane bending)。当所有外力均作用在纵向对称面内时,梁只发生平面弯曲。
秦飞 编著《材料力学》 第6章 弯曲(wānqū)内力
6
精品文档
6.1 梁的内力(nèilì)—剪力和弯 矩
梁在外力作用下,其任一横截面上的内力可用截面法确定。
(1)截:在横截面m-m处假想地将梁分为两段
原来处于平衡状态的梁,被截出的任意段也处于平衡状态。
秦飞A编y 著《材料力学(cái lieào lìxué)》 第6章 弯
16
曲内力
精品文档
6.1 梁的内力(nèilì)—剪力和弯矩 例题 6-2
截面B(以梁右半边为研究对象):
B左截面
F 2kN (+)
FBy 4kN (-)
FSB左 F FBy -2kN
