02圆周运动的描述,角量与线量的关系,曲线运动
第3讲 圆周运动的角量描述

第四节圆周运动及其描述上一节学习了一般的平面曲线运动,本节学习一种特殊且常见的曲线运动――圆周运动。
1 圆周运动的线量描述回顾上一节,我们在自然坐标系下使用了位置、速度、加速度等量来描述曲线运动。
这些量称为线量,所以上一节对于曲线运动的描述称为线量描述。
由于圆周运动是一种特殊的曲线运动,因而上一节关于曲线运动的描述完全适用于圆周运动的描述。
所以可以把上一节的结论直接用于圆周运动的线量描述。
位置:s=s(t)速度:dsdt v=τ加速度:22d sdtτ=aτ(1a)2nvR=a n(1b)(1b)式中的R就是圆的半径,而v则是质点做圆周运动的速率。
质点作圆周运动时,如果切向加速度为0,就是所谓的匀速圆周运动......。
2 圆周运动的角量描述极坐标系2.1 角位移除了线量描述形式外,对于圆周运动还有一种常用的描述形式――角量描述。
如图1所示,以圆心为极点,沿着任意方向引出一条线作为极轴,就建立了一个坐标系,称为极坐标系。
在极坐标系中,质点的位置所对应的矢径r与极轴的夹角θ称为质点的角位置,而dθ称为dt时间内的角位移。
注意:1,角位移...d.θ.既有大小,又有方向.........(.但未必是矢量......1)。
其方向由右手定则确定,即:伸出右手,使四指沿着质点旋转的方向弯曲,与四指垂直的拇指所指的方向1矢量的严格定义是:矢量是在空间中有一定的方向和数值,并遵从平行四边形加法法则的量。
即为d θ的正方向。
2,有限大小的角位移不是矢量(因为角位移的合成不符合交换律,比如翻一本书:先x->90,再y ->90,最后z ->90得到的结果,与先x->90,再z ->90,最后y ->90得到的结果不一样),只有..当△..t . .0.时,角位移.....d .θ.才是矢量....。
3,质点作圆周运动时,其角位移只有两种可能的方向,因此可以在标量前...............................加正号或者是负号来指明角位移的方向.................。
高中物理新人教版必修2第五章曲线运动第5节《圆周运动》

[第5节圆周运动[精讲精析]知识精讲]知识点1. 描述匀速圆周运动的物理量(1)轨道半径(R):对于一般曲线运动,可以理解为曲率半径.(2)线速度(v):是描述质点沿圆周运动快慢的物理量。
大小等于物体在一段时间内运动的弧长(s)与时间(t)的比值,方向为圆周的切线方向.公式: v=s/t=2πr/T=2πrf (3)角速度(ω,又称为圆频率):是描述质点绕圆心转动快慢的物理量。
大小等于一段时间内转过的角度(θ)与时间t的比值.公式: ω=θ/t=2π/T=2πf(4)周期(T):质点做圆周运动一周所需要的时间.(5)频率(f,或转速n):质点在单位时间内完成的圆周运动的次数.[例1]静止在地球上的物体都要随地球一起转动,下列说法正确的是( )A.它们的运动周期都是相同的B.它们的线速度都是相同的C.它们的线速度大小都是相同的D.它们的角速度是不同的[思路分析]地球绕自转轴转动时,所有地球上各点的周期及角速度都是相同的。
地球表面物体做圆周运动的平面是物体所在纬度线平面,其圆心分布在整条自转轴上,不同纬度处物体做圆周运动的半径是不同的,只有同一纬度处的物体转动半径相等,线速度的大小才相等,但即使物体的线速度大小相同,方向也个不相同.[答案] A[总结]线速度是描述物体运动快慢的物理量,若比较两物体做匀速圆周运动的快慢,则只看其线速度的大小即可.角速度、周期和转速都是描述物体转动快慢的物理量。
物体做匀速圆周运动时,角速度越大、周期越小、转速越大,则物体转动的越快,反之则越慢,由于线速度和角速度的关系为v=ωr,所以在半径不确定的情况下,不能由角速度大小判断线速度的大小,也不能由线速度大小判断角速度大小.[误区警示]有的同学往往误认为物体转动半径为地球半径,进而导致失误.在解决圆周运动问题时,转动中心的确定至关重要.地球本身匀速转动,地表各点角速度相等(但两极ω=0),角速度又称整体量;线速度随着半径不同而不同,线速度又称局部量. [变式训练1] 由于地球自转,乌鲁木齐和广州两地所在处物体具有的角速度和线速度相比较( )A.乌鲁木齐处物体的角速度大,广州处物体的线速度大B.乌鲁木齐处物体的线速度大,广州处物体的角速度大C.两处地方物体的角速度、线速度都一样大D.两处地方物体的角速度一样大,但广州的线速度比乌鲁木齐处物体线速度要大[答案] D知识点2。
2第二讲自然坐标系圆周运动的角量描述

vx
u
dt
dy
gt
vy
dt
v u2 g 2 t 2
2
g
t
dv d
2
2 2
u g t
a
dt dt
u2 g 2 t 2
an a a
2
ug
2
u g t
2
2 2
相对运动
球
垂
直
往
返
运动具有相对性
球作曲线运动
如何变换?
描述运动三参量合成的约定
绝对量
建立自然坐标系:(P的切向)(P的法向)
p
o
ˆ
n̂
规定:切向单位矢量 ˆ , 指向运动方向
法向单位矢量 n̂
指向轨道的凹侧
用这样一对正交的切向、法向单位矢量构成坐
标系统称为自然坐标系。
在自然坐标系中,切向、法向单位矢量并不固
定,它们随质点的位置而变。
p
ˆ
o
ˆ
n̂
n̂
直角坐标系是静坐标系
教学基本要求:
能计算质点在平面内运动时的速度和加速度;
能计算质点作圆周运动时的角速度、角加速度
、切向加速度和法向加速度。
本节内容提纲
一,自然坐标系
1,运动方程
2,速度
3,加速度
二,圆周运动的角量描述
1,角位置
2,角速度
3,角加速度
三,角量与线量的关系
四,一般曲线运动
一、自然坐标系中的运动方程,速度及加速度表示:
=
tgα
=
−
tgα
《大学物理》课程教学大纲
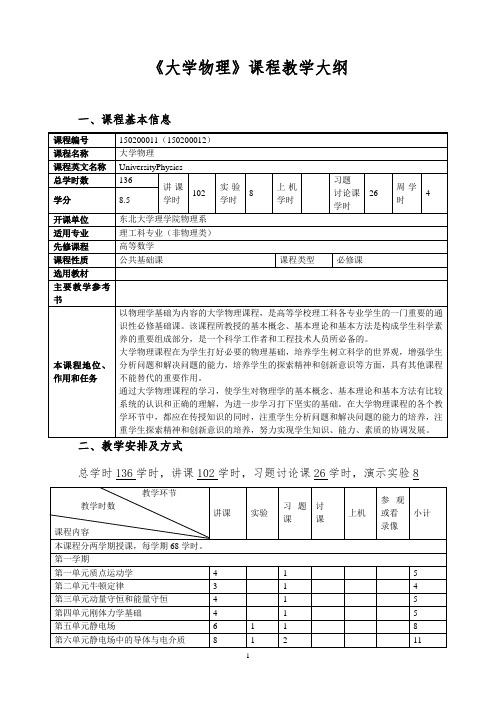
《大学物理》课程教学大纲一、课程基本信息总学时136学时,讲课102学时,习题讨论课26学时,演示实验8三、课程教学的有关说明1、本课程课内外学时比例:1:2;平均周学时:4。
2、本课程是公共基础课,分连续两个学期完成。
3、在教学中注意把传统教学手段和现代化教学手段相结合,充分利用现代化教学手段进行教学。
四、对于能力培养的基本要求通过大学物理课程教学,应注意培养学生以下能力:1.独立获取知识的能力——逐步掌握科学的学习方法,阅读并理解相当于大学物理水平的物理类教材、参考书和科技文献,不断地扩展知识面,增强独立思考的能力,更新知识结构;能够写出条理清晰的读书笔记、小结或小论文。
2.科学观察和思维的能力——运用物理学的基本理论和基本观点,通过观察、分析、综合、演绎、归纳、科学抽象、类比联想、实验等方法培养学生发现问题和提出问题的能力,并对所涉问题有一定深度的理解,判断研究结果的合理性。
3.分析问题和解决问题的能力——根据物理问题的特征、性质以及实际情况,抓住主要矛盾,进行合理的简化,建立相应的物理模型,并用物理语言和基本数学方法进行描述,运用所学的物理理论和研究方法进行分析、研究。
五、对于素质培养的基本要求通过大学物理课程教学,应注重培养学生以下素质:1.求实精神——通过大学物理课程教学,培养学生追求真理的勇气、严谨求实的科学态度和刻苦钻研的作风。
2.创新意识——通过学习物理学的研究方法、物理学的发展历史以及物理学家的成长经历等,引导学生树立科学的世界观,激发学生的求知热情、探索精神、创新欲望,以及敢于向旧观念挑战的精神。
3.科学美感——引导学生认识物理学所具有的明快简洁、均衡对称、奇异相对、和谐统一等美学特征,培养学生的科学审美观,使学生学会用美学的观点欣赏和发掘科学的内在规律,逐步增强认识和掌握自然科学规律的自主能力。
六、教学内容及基本要求模块1力学:第一单元质点运动学第一讲质点运动的描述,第二讲圆周运动与一般平面曲线运动,第三讲相对运动基本要求:1、质点运动的描述(1)掌握:位矢、位移、速度、加速度等物理量的定义及表达式,能够从已知的运动方程求导得到速度、加速度;同时能够从已知的速度或加速度积分得出运动方程。
自然坐标圆周运动相对运动

伽利略所取得的巨大成就,开创了近代物理学 的新纪元。
自然坐标、圆周运动、角量描述、相对运动
3、绝对运动、牵连运动、相对运动
(1)位矢的关系
r
r'
质点P在相对作匀速直线运动
的两个坐标系中的移动 y y' u
自然坐标、圆周运动、角量描述、相对运动
2、相对运动
物体运动的轨迹依赖于观察者所处的参考系
自然坐标、圆周运动、角量描述、相对运动
伽利略(Galileo Galilei,1564—1642)
伽利略杰出的意大利物理学家和 天文学家,实验物理学的先驱者。
他提出著名的相对性原理、惯性 原理、抛体的运动定律、摆振动的等 时性等。
2
1 x2g
y 2
v02
y
an
a
g
自然坐标、圆周运动、角量描述、相对运动
(2)
o v0
x
vx v0, vy gt
an
a
y
v
vx2 vy2
v02 g 2t 2
tan 1
gt v0
a
dv dt
g2t v02 g2t2
an g2 a 2
g
v0 g v02 g2t 2
与速度同向
与切向加速度垂直
总结:自然坐标
v v
a a an a ann
a
a
an
切向加速度
法向加速度
反映速度大小变 化的快慢
反映速度方向变 化的快慢程度
dv a dt
an
v2
aa
a 2 an 2
力学1-4复习和习题讲解

坐标原点,则该质点任意时刻的位矢是____.
解: 依题意,有 a F t i 4ti dv
m 0.25
dt
分离积
分变量
v
dv
2j
t
4t i
dt
v 2t 2 i 2 j
0
再由 v dr dr vdt dt
量大小为_m__v_d____。
分析: L r mv L rmv sin(r ,v )
mvr sin
mθ v
d θ•
r
o
mvd
11. (学习指导p27. 35 ) 质点P的质量为2kg,位移矢量为r ,
速度为v ,它受到力 F 的作用,这三个矢量均在Oxy面内,
且r =3.0m , v=4.0m/s , F=2N , 则该质点对原点O的角动
1
v5 m
5
5m(5
2t )dt
(25 5t 2)5
0
0
0
5.(学习指导p24. 16) 如图所示,光滑平面上有一个运动物体P,在P的 正前方有一个连有弹簧和挡板M的静止物体Q, 弹簧和挡板的质量不计, P与Q质量相同。物体P 与Q碰撞后P停止, Q以碰前P的速度运动。在此 碰撞过程中,弹簧压缩量最大的时刻是( )
(1)串联后总的劲度系数k满足: (2)并联后总的劲度系数k满足:
11 1
k k1 k2 k k1 k2
k1
k2
F
(1)
k1
k2
F
(2)
解(1) 串联时,两弹簧受力相等,均为F;伸长分 别为x1、x2.则总伸长x=x1+x2.
∴有 F=k1x1=k2x2
圆周运动角速度与线速度

圆周运动和向心加速度目标1、理解匀速圆周运动的特点,掌握描述匀速圆周运动快慢的几个物理量:线速度、角速度、周期、转速的定义,理解它们的物理意义并能灵活的运用它们解决问题。
2、理解并掌握描写圆周运动的各个物理量之间的关系。
3、理解匀速圆周运动的周期性的确切含义。
4、理解向心加速度产生的原因和计算方法。
重点描述匀速圆周运动快慢的几个物理量:线速度、角速度、周期、转速、向心加速度的定义以及它们的相互关系,是学习的重点。
学习难点弄清描写匀速圆周运动的各个物理量之间的关系,理解匀速圆周运动是变速运动且是变加速运动是学习的难点。
知识点一:圆周运动的线速度要点诠释:1、线速度的定义:圆周运动中,物体通过的弧长与所用时间的比值,称为圆周运动的线速度。
公式:(比值越大,说明线速度越大)方向:沿着圆周上各点的切线方向单位:m/s2、说明1)线速度是指物体做圆周运动时的瞬时速度。
2)线速度的方向就是圆周上某点的切线方向。
线速度的大小是的比值。
所以是矢量。
3)匀速圆周运动是一个线速度大小不变的圆周运动。
4)线速度的定义式,无论是对于变速圆周运动还是匀速圆周运动都成立,在变速圆周运动中,只要取得足够小,公式计算的结果就是瞬时线速度。
注:匀速圆周运动中的“匀速”二字的含义:仅指速率不变,但速度的方向(曲线上某点的切线方向)时刻在变化。
知识点二:描写圆周运动的角速度要点诠释:1、角速度的定义:圆周运动物体与圆心的连线扫过的角度与所用时间的比值叫做角速度。
公式:单位:(弧度每秒)2、说明:1)这里的必须是弧度制的角。
2)对于匀速圆周运动来说,这个比值是恒定的,即匀速圆周运动是角速度保持不变的圆周运动。
3)角速度的定义式,无论是对于变速圆周运动还是匀速圆周运动都成立,在变速圆周运动中,只要取得足够小,公式计算的结果就是瞬时角速度。
4)关于的方向:中学阶段不研究。
5)同一个转动的物体上,各点的角速度相等。
例如. 木棒OA以它上面的一点O为轴匀速转动时,它上面的各点与圆心O的连线在相等时间内扫过的角度相等。
2018版高中物理必修2《优化设计》第五章曲线运动第4节

第4节圆周运动一、线速度阅读教材第16~17页“线速度”部分,知道线速度的概念,了解线速度的方向,知道匀速圆周运动线速度大小特征。
1.定义:物体做圆周运动通过的弧长与通过这段弧长所用时间的比值。
2.公式:v=Δs Δt。
3.意义:描述做圆周运动的物体运动的快慢。
4.方向:线速度是矢量,方向与圆弧相切,与半径垂直。
5.匀速圆周运动:(1)定义:物体沿着圆周运动,并且线速度大小处处相等的运动。
(2)性质:线速度的方向是时刻变化的,所以圆周运动是一种变速运动。
思维拓展匀速圆周运动和匀速直线运动中的两个“匀速”的含义相同吗?有什么区别?答案不同。
前者指线速度的大小不变,后者指速度的大小和方向都不变。
二、角速度阅读教材第17~18页“角速度”和“角速度的单位”部分,了解角速度的概念,知道角速度的单位,知道转速、周期的概念。
1.定义:连接物体与圆心的半径转过的角度与转过这一角度所用时间的比值。
2.公式:ω=ΔθΔt。
3.意义:描述物体绕圆心转动的快慢。
4.单位:(1)角的单位:国际单位制中,弧长与半径的比值表示角的大小,称为弧度,符号:rad。
(2)角速度的单位:弧度每秒,符号是rad/s或rad·s-1。
思维拓展如图1所示,钟表上的秒针、分针、时针以不同的角速度做圆周运动。
图1(1)秒针、分针、时针它们转动的快慢相同吗?相同时间内,谁转动的角度大?谁转动得最快?(2)请指出秒针、分针和时针的周期。
答案(1)不相同。
根据角速度公式ω=ΔθΔt知,在相同的时间内,秒针转过的角度最大,时针转过的角度最小,所以秒针转得最快。
(2)秒针的周期为60 s,分针的周期为60 min,时针的周期为12 h。
三、线速度与角速度的关系阅读教材第18页“线速度与角速度的关系”部分,知道线速度与角速度的关系表达式。
1.在圆周运动中,线速度的大小等于角速度大小与半径的乘积。
2.关系式:v=ωr。
思维拓展月亮绕地球做圆周运动。
人教版(2019)物理高中必修第二册 6 圆周运动各物理量之间的关系考点

圆周运动各物理量之间的关系一、把握基础知识 1.线速度与角速度的关系在圆周运动中,v = ,即线速度的大小等于 与的乘积。
2.圆周运动中其他各量之间的关系(1)v 、T 、r 的关系:物体在转动一周的过程中,转过的弧长Δs =2πr ,时间为T ,则v =ΔsΔt= 。
答案:ωr ,半径,角速度大小,2πrT(2)ω、T 的关系:物体在转动一周的过程中,转过的角度Δθ=2π,时间为T ,则ω=ΔθΔt= 。
(3)ω与n 的关系:物体在1 s 内转过n 转,1转转过的角度为2π,则1 s 内转过的角度Δθ=2πn ,即ω=2πn 。
答案:2πT二、重难点突破 常见的传动装置及其特点(1)同轴转动:A 点和B 点在同轴的一个圆盘上,如图5-4-2所示,圆盘转动时,它们的角速度、周期相同:ωA =ωB ,T A =T B 。
线速度与圆周半径成正比,v A v B =r R。
(2)皮带传动:A 点和B 点分别是两个轮子边缘的点,两个轮子用皮带连起来,并且皮带不打滑。
如图5-4-3所示,轮子转动时,它们的线速度大小相同:v A =v B ,周期与半径成正比,角速度与半径成反比:ωA ωB =r R ,T A T B =Rr。
并且转动方向相同。
(3)齿轮传动:A 点和B 点分别是两个齿轮边缘上的点,两个齿轮轮齿啮合。
如图所示,齿轮转动时,它们的线速度、角速度、周期存在以下定量关系:v A =v B ,T A T B =r 1r 2,ωA ωB =r 2r 1。
A 、B 两点转动方向相反。
101小贴士:在处理传动装置中各物理量间的关系时,关键是确定其相同的量(线速度或角速度),再由描述圆周运动的各物理量间的关系,确定其他各量间的关系。
趁热打铁:如图所示的装置中,已知大齿轮的半径是小齿轮半径的3倍,A 点和B 点分别在两轮边缘C 点离大轮轴距离等于小轮半径。
如果不打滑,则它们的线速度之比v A ∶v B ∶v C 为A .1∶3∶3B .1∶3∶1C .3∶3∶1D .3∶1∶3解析:A 、C 两点转动的角速度相等,由v =ωr 可知,vA ∶vC =3∶1;A 、B 两点的线速度大小相等,即vA ∶vB =1∶1,则vA ∶vB ∶vC =3∶3∶1。
大学物理12圆周运动

基本参考系
S'系(O' x' y' z')
运动参考系
u是S’系相对S系
运动的速度
1-3 相对运动
yy'
P P'
*
oo'
xx'
t0
y
o
P
y'
D
r
P'
uQ
r'
xx'
ut o' t t
第一章 质点运动学
22
物理学
第五版
位移关系
r r'D 或 r r'ut
速度变换
r r' u t t v v'u
理解伽利略速度变换式, 并会用它求简 单的质点相对运动问题.
第一章 质点运动学
2
物理学
第五版
质点运动的自然坐标描述
自然坐标系 —— 坐标原点固接 于质点, 坐标轴沿质点运动轨道
1-2 圆周ev运t 动 evt B
的切向和法向的坐标系,叫做自
然坐标系。切向以质点前进方向 A
为 侧正方,向记 为做 正,ev记t ,做法ev向n以。曲线凹
y
A
r
二 圆周运动的角速度
❖ 角坐标 (t)
o
❖角位移
y
xx
B
❖ 角速度
lim
d
t0 t dt
r A
o
x
单位:rad·s-1
第一章 质点运动学
4
物理学
第五版
1-2 圆周运动
❖ 速率 v lim Δs r lim Δθ
Δt0 Δt
Δt0 Δt
圆周运动例题及相对运动n2讲解
bt v
at
dv dt
d(v0 bt ) dt
b
20得 a24n/10到 /13 avR的2 大(v小0 及 Rb方 t )2向。
an at Ra O
7
2.
由at
a
,
n
即b (v0 bt )2 求出t。 R
2024/10/13
8
例6,(例题1-4)一曲柄连杆结构,曲柄OA长为r, 连杆AB长为L,AB一端在A处与曲柄相连,另一端以销子 在B处与活塞相连,当曲柄以匀角速绕o旋转时,通过 连杆将带动B处活塞在汽缸内往返运动,求活塞运动方程。
A
L
r
Q
B
x’ o’ P R o
x
活塞t时刻运动分析图10
A
l B
r
= t
x
x
x OR RB
PR
O
起始点
x r cost l2 r2 sin 2 t
2024/10/13
11
写为:
l2
r2
sin 2
t
l 1
r2
sin 2 2l 2
t
;而
sin2 t 1 cos2t ,移项整理得:
26
例2,货车遇到5m/s垂直下落的大雨,木 板及挡板都是1m,问货车以多大的速度 行驶才使木板不被雨淋。
v牵连 5
2024/10/13
v相对
45o l=1 v牵连 = 5
v绝对= 5 h=1
27
例题3,一升降机以加速度1.22m/s2 上升,当上升 速度为2.44m/s时,有一螺帽自升降机的天花板上 松落,天花板与升降机的底面相距2.74m,计算螺 帽从天花板落到底面所需要的时间和螺帽相对于 升降机外固定柱的下降距离。
圆周运动的角量描述 角量与线量的关系

A
反映 反映 的方向变化 因素
的大小变化 因素
无限趋近法向
无限趋近切向
法向加速度
切向加速度
要点归纳法向加速度Fra bibliotek切向加速度
线量描述
切向加速度
0, , v 增大 at dv 0, , v 常量 dt 0, , v 减小
一般曲线运动(自然坐标)
y
a
o a x a
et
en
第三节
圆周运动
线量描述
1、自然坐标系:
切向:质点前进的方向 法向:与切向垂直,指向曲线 凹的一面。
et
en
2、圆周运动的切向加速度和法向加速度(自然
坐标系分析) S =S (t )
v v(t ),a a (t ) ds v et vet dt
线量描述
加速度问题
C
D B
截取 AD = AB 作矢量 和
v et
v ds et vet dt 2 d v d v v a et en dt dt
ds 其中 d 为曲率半径 .
en
例
角位置
角位移
角速度
角加速度
匀变速圆周运动
角线量关系
物理量小结
物理量小结2
角线简例
《大学物理》圆周运动

得切向加速度与角加速度的关系为a r
dt
而法向加速度an
v2 r
dt r 2
质点作匀变速圆周运动时的角速度、角位移与角加速度的关系式
为:
ω ω0 t
θ θ0 ω0t t 2 / 2
ω2 ω02 2 (θ θ0 )
v v0 at
x
x0
v0t
at2 / 2
v2
v02
2a( x
(R
sin
ti
R
c
ostj )
a(t)
dv(dtt)
2 (R
costi
R 2
sin tj)
dt
速度、加速度也可以用其在x、y方向上的分量来表示
二、自然坐标系下的描述
自然坐标系:以动点为坐标原点,以动点所在轨道处的切线和 法线为坐标轴(切向指向前进方向,法向指向曲率中心),、n 为切、法向的单位矢量。
1-16.飞轮作匀减速转动 , 在 5 秒内角速度由 40πrad/s 减到 10πrad/s , 则飞轮在这 5秒内总共转过了多少圈?飞轮再经过多 少时间才能停止转动?
课后习题 1-8 1-9 1-10
(2)如
匀变速直线运动
(3)如 a 0,a;则0 质点作
n
t
匀速直线运动
(4)如
a n
0,
a t
0;, 质 点 c作
一般曲线运动
(5)如 a 0, a 0;, 质点c作
n
t
变速圆周运动
(6)如
a n
0,
a t
c;, 质点c作
匀变速圆周运动
(7)如 a 0, a 0;, 质点c作
dt dt
dt dt
第六章-圆周运动章末复习-知识点和题型总结-2023年高一物理期末高效复习专题

第六章:圆周运动章末复习知识点一:匀速圆周运动及其描述一、匀速圆周运动1.圆周运动:物体的运动轨迹是圆的运动.2.匀速圆周运动:质点沿圆周运动,如果在相等的时间内通过的圆弧长度相等,这种运动就叫匀速圆周运动.二、匀速圆周运动的线速度、角速度和周期1.线速度(1)定义式:v=Δs Δt.如果Δt取的足够小,v就为瞬时线速度.此时Δs的方向就与半径垂直,即沿该点的切线方向.(2)线速度的方向:质点在圆周某点的线速度方向沿圆周上该点的切线方向.(3)物理意义:描述质点沿圆周运动的快慢.2.角速度:半径转过的角度Δφ与所用时间Δt的比值,即ω=ΔφΔt(如图所示).国际单位是弧度每秒,符号是rad/s.3.转速与周期(1)转速n:做圆周运动的物体单位时间内转过的圈数,常用符号n表示.(2)周期T:做匀速圆周运动的物体运动一周所用的时间叫做周期,用符号T 表示.(3)转速与周期的关系:若转速的单位是转每秒(r/s),则转速与周期的关系为T=1n .4.匀速圆周运动的特点(1)线速度的大小处处相等.(2)由于匀速圆周运动的线速度方向时刻在改变,所以它是一种变速运动.这里的“匀速”实质上指的是“匀速率”而不是“匀速度三、描述圆周运动的各物理量之间的关系1.线速度与周期的关系:v=2πr T.2.角速度与周期的关系:ω=2πT.3.线速度与角速度的关系:v=ωr.知识点二、同轴转动和皮带传动1.同轴转动(1)角速度(周期)的关系:ωA=ωB,T A=T B.(2)线速度的关系:vAvB=rR.2.皮带(齿轮)传动(1)线速度的关系:v A=v B(2)角速度(周期)的关系:ωAωB=rR、TATB=Rr.知识点三、向心力1.定义:物体做匀速圆周运动时所受合力方向始终指向圆心,这个指向圆心的合力就叫做向心力.2.大小:F=mω2r=m v2 r.3.方向:总是沿半径指向圆心,方向时刻改变.4.效果力向心力是根据力的作用效果来命名的,凡是产生向心加速度的力,不管属于哪种性质,都是向心力.二:向心力的来源物体做圆周运动时,向心力由物体所受力中沿半径方向的力提供.几种常见的实例如下:实例向心力示意图用细线拴住的小球在竖直面内转动至最高点时绳子的拉力和重力的合力提供向心力,F向=F+G用细线拴住小球在光滑水平面内做匀速圆周运动线的拉力提供向心力,F向=F T物体随转盘做匀速圆周运动,且相对转盘静止转盘对物体的静摩擦力提供向心力,F向=F f小球在细线作用下,在水平面内做圆周运动重力和细线的拉力的合力提供向心力,F向=F合知识点四:向心加速度的方向及意义1.物理意义描述线速度改变的快慢,只表示线速度的方向变化的快慢,不表示其大小变化的快慢.2.方向总是沿着圆周运动的半径指向圆心,即方向始终与运动方向垂直,方向时刻改变.3.圆周运动的性质不论向心加速度a n的大小是否变化,a n的方向是时刻改变的,所以圆周运动的向心加速度时刻发生改变,圆周运动一定是非匀变速曲线运动.“匀速圆周运动中”的“匀速”应理解为“匀速率”.4.变速圆周运动的向心加速度做变速圆周运动的物体,加速度一般情况下不指向圆心,该加速度有两个分量:一是向心加速度,二是切向加速度.向心加速度表示速度方向变化的快慢,切向加速度表示速度大小变化的快慢.所以变速圆周运动中,向心加速度的方向也总是指向圆心.二:向心加速度的公式和应用1.公式a n =v2r=ω2r=4π2T2r=4π2n2r=4π2f2r=ωv.2.向心加速度的大小与半径的关系(1)当半径一定时,向心加速度的大小与角速度的平方成正比,也与线速度的平方成正比.随频率的增大或周期的减小而增大.(2)当角速度一定时,向心加速度与运动半径成正比.(3)当线速度一定时,向心加速度与运动半径成反比.(4)a n与r的关系图象:如图552所示.由a nr图象可以看出:a n与r成正比还是反比,要看ω恒定还是v恒定.图552知识点五:生活在的圆周运动一:火车转弯问题1.轨道分析火车在转弯过程中,运动轨迹是一圆弧,由于火车转弯过程中重心高度不变,故火车轨迹所在的平面是水平面,而不是斜面.火车的向心加速度和向心力均沿水平面指向圆心.图5732.向心力分析如图573所示,火车速度合适时,火车受重力和支持力作用,火车转弯所需的向心力完全由重力和支持力的合力提供,合力沿水平方向,大小F=mg tan θ.3.规定速度分析若火车转弯时只受重力和支持力作用,不受轨道压力,则mg tan θ=m v 2 0R,可得v0=gR tan θ(R为弯道半径,θ为轨道所在平面与水平面的夹角,v0为转弯处的规定速度).4.轨道压力分析(1)当火车行驶速度v等于规定速度v0时,所需向心力仅由重力和弹力的合力提供,此时火车对内外轨道无挤压作用.(2)当火车行驶速度v与规定速度v0不相等时,火车所需向心力不再仅由重力和弹力的合力提供,此时内外轨道对火车轮缘有挤压作用,具体情况如下:①当火车行驶速度v>v0时,外轨道对轮缘有侧压力.②当火车行驶速度v<v0时,内轨道对轮缘有侧压力.二:拱形桥汽车过凸形桥(最高点)汽车过凹形桥(最低点) 受力分析牛顿第二定律求向心力 F n =mg -F N =m v 2rF n =F N -mg =m v 2r牛顿第三定律求压力F 压=F N =mg -m v 2rF 压=F N =mg +m v 2r讨论v 增大,F 压减小;当v 增大到rg 时,F 压=0v 增大,F 压增大 超、失重汽车对桥面压力小于自身重力,汽车处于失重状态汽车对桥面压力大于自身重力,汽车处于超重状态知识点六:离心运动1.离心运动的实质离心现象的本质是物体惯性的表现.做圆周运动的物体,由于惯性,总是有沿着圆周切线飞出去的趋向,之所以没有飞出去,是因为受到向心力的作用.从某种意义上说,向心力的作用是不断地把物体从圆周运动的切向方向拉回到圆周上来.2.离心运动的条件做圆周运动的物体,提供向心力的外力突然消失或者合外力不能提供足够大的向心力.3.离心运动、近心运动的判断如图578所示,物体做圆周运动是离心运动还是近心运动,由实际提供的向心力F n 与所需向心力⎝ ⎛⎭⎪⎫m v 2r 或mr ω2的大小关系决定.图578(1)若F n =mr ω2(或m v 2r)即“提供”满足“需要”,物体做圆周运动.(2)若F n>mrω2(或m v2r)即“提供”大于“需要”,物体做半径变小的近心运动.(3)若F n<mrω2(或m v2r)即“提供”不足,物体做离心运动.由以上关系进一步分析可知:原来做圆周运动的物体,若速率不变,所受向心力减少(或向心力不变,速率变大)物体将做离心运动;若速度大小不变,所受向心力增大(或向心力不变,速率减小)物体将做近心运动.知识点七.竖直平面的圆周运动1.“绳模型”如上图所示,小球在竖直平面内做圆周运动过最高点情况。
高中物理必修2第五章曲线运动知识点总结

精品文档第五章曲线运动知识点总结§ 5-1 曲线运动 & 运动的合成与分解一、曲线运动1. 定义:物体运动轨迹是曲线的运动。
2. 条件:运动物体所受合力的方向跟它的速度方向不在同一直线上。
3. 特点: ①方向:某点瞬时速度方向就是通过这一点的曲线的切线方向。
②运动类型:变速运动(速度方向不断变化) 。
③F 合 ≠0,一定有加速度 a 。
④F 合 方向一定指向曲线凹侧。
⑤F 合 可以分解成水平和竖直的两个力。
4. 运动描述——蜡块运动涉及的公式:vvyv v x 2v y 2v xv yPtan蜡块的位置v xθ二、运动的合成与分解1. 合运动与分运动的关系: 等时性、独立性、等效性、矢量性。
2. 互成角度的两个分运动的合运动的判断:①两个匀速直线运动的合运动仍然是匀速直线运动。
②速度方向不在同一直线上的两个分运动, 一个是匀速直线运动, 一个是匀变速直线运动,其合运动是匀变速 曲线运动, a 合为分运动的加速度。
③两初速度为 0 的匀加速直线运动的合运动仍然是匀加速直线运动。
④两个初速度不为 0 的匀加速直线运动的合运动可能是直线运动也可能是曲线运动。
当两个分运动的初速度的和速度方向与这两个分运动的和加速度在同一直线上时,合运动是匀变速直线运动,否则即为曲线运动。
三、有关“曲线运动”的两大题型(一)小船过河问题模型一: 过河时间 t 最短:模型二: 直接位移 x 最短:v 船vvv船ddθv 水θ v 水当 v 水<v 船 时, x min =d ,tm ind d td,v 船, xv 船 sinsintanv 船cosv 水v 水v 船.精品文档模型三:间接位移x 最短:v 船v船dθAθv 水当 v 水>v 船时,x min dcostd,cos v 船 sinsmin(v水 - v船cos )Lv船sin v水L,v船v 船v 水(二)绳杆问题 ( 连带运动问题 )1、实质:合运动的识别与合运动的分解。
圆周运动

圆周运动一、圆周运动的描述1、圆周运动:指物体沿着圆周的运动,即物体运动的轨迹是圆;(1)圆周运动是个变速运动,位移、速度方向时刻在改变;(2)圆周运动的原因:受到合力与速度方向不再一条直线上,沿垂直速度方向的力改变其方向,沿速度方向改变大小;圆周运动方向改变的程度一样,所以垂直于速度方向上的力,大小不变,方向沿半径指向圆心,改变速度方向程度一样,而言速度方向里随意变化;(3)圆周运动是个非匀变速曲线运动;因为其受到的力时刻在改变着;2、线速度:物体沿圆周运动时在△t时间内通过的弧长为△s,那么它们的比值就是物体做圆周运动的线速度,用v表示,则v=△s/△t;(1)物理意义:它是表述物体做圆周运动的运动快慢的物理量,只是以弧长变化角度来描述的;(2)线速度有平均线速度和瞬时线速度之分:当△t较大则表示平均线速度,当△t足够小时得到的就是瞬时线速度;(3)线速度是个矢量:大小为v=△s/△t,单位为m/s;方向是物体在圆周运动某点的线速度方向为该点的切线方向,即线速度方向一定是垂直于圆周的半径,和圆弧相切;3、匀速圆周运动:线速度的大小处处相等的圆周运动就是匀速圆周运动;(1)匀速圆周运动是一种变速运动,速度大小不变,方向时刻在改变,这里的“匀速”指的是其速率不变;(2)有曲线运动的原理可得,匀速圆周运动物体受到的合外力,时刻都是沿圆周的半径方向,指向圆心,方向不变,去改变物体运动的方向,速度反方向上没有分力所以速率不变;(3)匀速圆周运动是非匀变速曲线运动,合外力时刻改变,速度的变化量时刻在改变,有匀速圆周运动受力特点可得,速度变化量的大小不变,方向沿半径方向指向圆心时刻在改变。
4、角速度:物体在△t时间内有A点运动到B,半径OA在这段时间内转到半径OB,其角度变化△Q,他与时间△t之间的比值叫做物体圆周运动的角速度,用w来表示,即w= (1)物理意义:描述物体圆周运动的转动快慢的物理量,只是在转动角度方面描述;(2)角速度是个矢量:大小为△Q/△t,单位为弧度每秒,符号rad/s,弧度表示的是角度的大小,其大小为弧长△s比上半径R;方向是垂直于圆面(右手定则判断);(3)匀速圆周运动:是角速度不变的圆周运动,注意匀速圆周运动线速度时刻在改变;5、周期T、频率f和转速n(1)周期T:做圆周运动的物体,转过一周所用的时间就是匀速圆周运动的周期;单位s, (2)频率f:做圆周运动的物体,在1s内转过的圈数叫做频率,用f表示,单位1Hz=1/s;(3)转速n:做圆周运动的物体,在单位时间内沿圆周绕圆心转过的圈数叫做转数,用n表述,单位为r/s或r/min;①他们都是表述物体圆周运动快慢的物理量,只是在转过的圈数上来不同定义;②匀速圆周运动的周期、频率和转速都是固定不变的;二、描述圆周运动各种物理量间的关系(匀速圆周运动)1、线速度和角速度间关系:v =rw 或w=v/r(推到以整个圆来推导);由此可得:(1)半径相同时:线速度大的角速度也大,角速度大的线速度也大,且成正比;如图(一条直线,x轴为w,y周围v);(2)当角速度相同时,半径大的线速度大且成正比(如图x轴r,y轴v);(3)当线速度相同时,半径大角速度小,半径小角速度大,且成反比(如图:当x周围1/r 时,y轴为w,是一条直线;当x轴为r时,y轴为w时,是反比函数);2、线速度与周期的关系:v=2﹠r/T(推导过程一个周期来推到);由此可得只有当半径相同时,周期小的线速度大,当半径不同,周期小的线速度不一定大,所以线速度和周期表述圆周运动快慢是不一样的;3、角速度和周期关系:w=2﹠/T,(推导与前面一样);角速度和周期一定成反比,周期大的角速度一定小;所以周期和角速度描述匀速圆周运动快慢是一样的;4、w=2﹠fv=2﹠frf=nv=wr=2﹠/Tr=2﹠fr=2﹠nr三、常见的转动装置1、共轴转动:如图,物体在以同心的半径不同的圆盘上的运动;两盘转动方向相同;(1)当圆盘转动时由于是同一个圆盘,其不同半径上任意一点出的角速度相同,转动周期相同,都等于圆盘的转动周期和角速度;(2)线速度与半径成正比;2、皮带转动:如图,皮带套着两个圆盘转动过程;注意过程皮带不打滑,(1)在两轮的边缘上任意一定的线速度大小都相同,都等于皮带本身的线速度,原因是由于他们都是由皮带的转动所带动的;(2)两圆盘边缘角速度、周期根据其各自半径,和线速度计算即可;(3)同一个盘上,由于已知边缘线速度,再根据前面共轴转动过程求解即可;3、齿轮转动:如有图,两盘由于边缘齿轮相互作用而转动;两盘转动方向相反;具体原理同皮带转动情况一样处理;四、题型和练习:本节题型(1)匀速圆周运动概念的理解(2)描述匀速圆周运动物理量见关系的计算主要是三种转动装置应用,(3)有关匀速圆周运动的计算1、关于匀速圆周运动线速度、角速度、周期说法正确的是:A线速度大角速度一定大B线速度大周一一定小C角速度大的半径一定小D角速度大的周期一定小(D)2、质点匀速圆周运动则A在任何相等时间内,质点位移相等B任何相等时间内,质点通过路程都相等C任何相等时间内质点运动的平均速度都相等D任何相等时间内,链接质点和圆心的半径转过的角速度相等(BD)3、质点做匀速圆周运动,不变的物理量是A速度B速率C角速度D加速度(BC)4、如图皮带带动两个轮,a、b分别是两轮边缘的两点,c点在O1轮上,且有ra=2rb=2rc,则有A va=vb B wz=wb C va=vc D wa=wc (AD)5、如图BC两轮固定与同一转轴上,C轮半径为B轮半径的两倍,A、B两轮有一个皮带带着转动,且A轮半径是B轮的两倍,皮带不打滑,球A、B、C轮边缘上的a、b、c三点的角速度之比和线速度之比?6、设一个半径为R的圆盘水平放置,并绕其中心竖直方向的轴做匀速圆周运动;现有一小球在圆盘中央中心正上方高h处沿OB方向水平抛出,要使小球下落到B点,问盘转动的角速度和小球的水平速度各是多少?。
高中物理《必修2》5.4《圆周运动》人教版

一、线速度
如果物体在一段时间Δt内通过的 弧长ΔS越长,那么就表示运动得 越快.
Δt ΔS
一、线速度
1、物理意义:描述质点沿 圆周运动的快慢。
A ∆s B
2、定义:质点做圆周运动通过的
弧长Δs和所用时间Δt 的比值
叫做线速度。 Δs是弧长并非位移
3、定义式: v
=
Δs Δt
当Δt 趋近零时,弧长Δs就等
4、方向:沿圆周在该 点的切线方向
于物体的位移,v 就是直线运 动中学过的瞬时速度.
【讨论与交流】匀速圆周运动的"匀速"同" 匀速直线运动"的"匀速"一样吗?
v
o
v v
“匀速”是指速率不变,匀速圆周运动是 一种变速运动.
(1)物理意义:描述质点沿圆周运动的快慢。 (2)定义:质点做圆周运动通过的弧长△s和所用时 间△t的比值叫做线速度。(比值定义法,这里是弧 长,而直线运动中是位移)
(2)角速度 1.定义:做圆周运动的物体的半径扫过的角度与所用 时间的比值 2.公式:ω =△θ /△t. 3.单位:rad/s 4.物理意义:
(3)转速和周期 2、线速度,角速度、周期间的关系
v=rω =2π r/T ω =2π /T
①
由v=ω r得 ω a∶ω b=rB∶rA=1∶2
②
B、C两轮固定在一起绕同一轴转动,则B、C两轮的角速度相同,即
ω b=ω c或 ω b∶ω c=1∶1 由v=ω r得 vb∶vc=rB∶rC=1∶2 由②③得 ω a∶ω b∶ω c=1∶2∶2 由①④得 va∶vb∶vc=1∶1∶2
③ ④
【分析】 解这类题时要注意抓住传动装置的特点:同轴传动的是
圆周运动的角量描述角量与线量的关系

圆周运动的角量表示
角量与动
变速(率)圆周运动
怎样定量描述其运动规律?
切向:质点前进的方向法向:与切向垂直,指向曲线凹的一面。
2、圆周运动的切向加速度和法向加速度(自然坐标系分析)
1、自然坐标系:
一、圆周运动的线量表示
1、圆周运动的速度
路程、速度、加速度、法向加速度、切向加速度
切向加速度
一般曲线运动(自然坐标)
t
二、圆周运动的角量表示
角位移
二、圆周运动的角量表示
角速度
二、圆周运动的角量表示
( )
角加速度
二、圆周运动的角量表示
匀变速圆周运动
角量与线量的关系
运动状态
运动状态的变化
当质点作圆周运动时
速度
加速度
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
v = Rω aτ = Rβ 2 an = Rω = vω
Fan
很小并趋于零时, 在∆t很小并趋于零时,有: 很小并趋于零时
ˆ τ t时刻,速度单位矢量为: 时刻,速度单位矢量为:
ˆ n dθ
o ρ
P
p′ dθ
ˆ τ ˆ τ
,
ˆ ˆ | ∆τ |=| τ | ∆θ ˆ ˆ ˆ | dτ |= lim | ∆τ | = lim | τ | ∆θ = dθ
ds
ˆ 在∆t趋于零时, τ 的方向τ 跟垂直并指向 趋于零时, ˆ 趋于零时 d 圆心, 圆心,即指向圆周轨道的法向 n 的方向。 ˆ 的方向。
ˆ ˆ = aτ τ + an n
dv a 切向加速度: 表示速度大小变化的快慢。 切向加速度: τ = 表示速度大小变化的快慢。 dt v2 法向加速度: 速度方向的变化快慢。 法向加速度:an = 速度方向的变化快慢。
ρ
a
an
s
Fan
θ
aτ
讨论:在圆周运动中 讨论:在圆周运动中ρ=R
r a
r a
质点运动时的速度方向是沿 着运动轨道的切线并指向前进 的方向。 的方向。 r 速度可表示为: 速度可表示为: v = vτ ˆ
A
r vA
B
为沿速度方向的单位矢量。 τˆ 为沿速度方向的单位矢量。是一个大小不
r vB
变(恒为1)但方向不断变化的矢量。 恒为 )但方向不断变化的矢量。 根据加速度的定义, 根据加速度的定义,有:
自然坐标系 的表示: 的表示
r an φ •
r ˆ n
r aτ
r ˆ t
矢量: 矢量
r r r a = an + aτ
2 n
v v dv v = n+ τ R dt
2
2
大小: 大小
a = a + aτ
aτ tgφ = , an
方向: 方向
必须指明角度. 必须指明角度
Fan
§1.5 圆周运动的角量表示角量与线量的关系
可以将加速度分解为切向和法向两个分量。 可以将加速度分解为切向和法向两个分量。
dv aτ = 切向加速度 dt
an =
v2
ρ
法向加速度
Fan
v2 ˆ dv r dv dτ ˆ τˆ + = n ˆ ∴a = τ + v ρ dt dt dt
切向加速度与法向加速度的意义: 切向加速度与法向加速度的意义:
Fan
三、角量和线量的关系
ds v= dt
s = Rθ
d ( Rθ ) Rdθ v= = dt dt = Rω
圆周运动加速度: 圆周运动加速度:
dv d (ωR) dω aτ = = =R = Rβ dt dt dt
v (ωR) an = = = ω 2R R R
2 2
Fan
线量与角量的关系: 线量与角量的关系:
d τˆ ˆ ˆ dθ dτ (dθn) v 可改写为: 可改写为: v ˆ =v =v n dt dt dt dt
∆t →0
∆t →0
ˆ τ′
ˆ ∆τ
ˆ dθτ
ˆ ˆ dτ = dθn
Fan
ˆ dθ dτ (dθn) ˆ v =v =v n dt dt dt
设轨道在P点的曲率半径为ρ 设轨道在 点的曲率半径为ρ, 点的曲率半径为
v1 P x
θ
Fan
y
B:t+∆t : ∆ ∆θ O A:t :
质点在oxy平面内绕 质点在 平面内绕O点沿 半径为R的圆周运动 的圆周运动, 半径为 的圆周运动,以Ox 轴为参考方向. 轴为参考方向 设 t 时刻质点在 A 处, 质点 的角位置为θ ; t + ∆t 时刻质 点在B处 点在 处. 在 ∆t 时间内质点的角位 规定逆时针为正. 移为 ∆θ , 规定逆时针为正
一、圆周运动中的角量
用位置矢量、速度、加速度描写圆周运动的方法, 用位置矢量、速度、加速度描写圆周运动的方法, 称线量描述法;也可用角度来确定其位置, 称线量描述法;也可用角度来确定其位置,称角量描 述法。 述法。
r 线量: 线量: r
r v
r a
y
v2 R
∆θ
P’
角量: 角量:θ ω β 角位置: 角位移: 角位置: θ 角位移:∆θ 角速度: 角加速度: 角速度: ω 角加速度: β
θ
x
平均角速度为
ω = ∆θ ∆t
Fan
角速度
ω = lim
∆t →0
∆θ ∆t
dθ ω= dt
平均角加速度
∆ω β= ∆t
角加速度
dω d θ = 2 β= dt dt
2
Fan
线量: 线位移(弧长 线量: S ——线位移 弧长 线位移 弧长)
v = ds / dt aτ = dv / dt 2 an = v / R
1 匀速率圆周运动
ω = 常量, 故 常量,
如 t = 0 时,
θ =θ 可得: 可得: θ =周运动
dω β= =常量, 常量, dt ω 如 t = 0 时, θ =θ , =ω
0
0
ω =ω0 + β t 1 2 可得: 可得: θ = θ 0 + ω 0 t + β t 2 2 2 ω =ω0 + 2β (θ −θ0 )
——线速度 线速度 ——切向加速度 切向加速度 ——法向加速度 法向加速度
角量: 角位移(rad) 角量:θ ——角位移 角位移 角速度(rad/s) 角速度 ω = dθ / dt ——角速度 2 2 ——角加速度 角加速度(rad/s2) 角加速度 β = d θ / dt
Fan
二、圆周运动中的角量描述
τ
A s o
r
B
τ
∆s
∆s
r n
r n
3. 速度: 沿切线方向。 速度:
Fan
r ˆ ˆ 为沿速度方向的单位矢量。 v = vτ τ 为沿速度方向的单位矢量。是一个大小
不变(恒为 )但方向不断变化的矢量。 不变(恒为1)但方向不断变化的矢量。 在自然坐标系中, 在自然坐标系中, 运动方程为
s = s(t )
r ˆ r dv d (vτ ) dv ˆ dτ ˆ = τ +v a= = dt dt dt dt
dv 代表着质点运动速度大小的变化。 代表着质点运动速度大小的变化。 dt
ˆ dτ v ? dt
Fan
增量为: ˆ ˆ ˆ τˆ 增量为: ∆τ = τ ′ − τ
ˆ t+Δt时刻, t+Δt时刻,速度单位矢量为τ ′ 时刻
根据速度的定义, 根据速度的定义,
r r dr v= dt
s
O’
ˆ τ
c
s+
r 因为 | dr |= ds •切向坐标 τ 沿运动轨迹的切线并指向质点运动的 切向坐标 ˆ
方向; 方向;
r 所以: dr = dsτ , 所以: ˆ
r ds ˆ ˆ v = τ = vτ dt
ds ∴v = dt
Fan
二、切向加速度与法向加速度
r
dθ p′ o dθ ρ
P
ˆ τ ˆ τ
,
ds ds ds Qρ = , v= dt dθ 2 r dτ dθ dθ ds dθ ds = v n ˆ ˆ ˆ ˆ ∴v =v n =v n =v n ρ dt dt ds dt ds dt 2 v ˆ r dv dτ dv ˆ τˆ + = n = aτ τ + an n ˆ ˆ ˆ ∴a = τ + v dt ρ dt dt
第1章
质点运动学
Fan
§1.4 用自然坐标表示平面曲线 运动中的速度和加速度
一、自然坐标系中的速度
坐标原点固接于质点, 自然坐标系 —— 坐标原点固接于质点 坐标轴沿质点运 动轨道的切向和法向的坐标系,叫做自然坐标系。 动轨道的切向和法向的坐标系,叫做自然坐标系。切向 r 以质点前进方向为正, 以质点前进方向为正,记做 τ ,法向以曲线凹侧方向 r 为正, 为正,记做 n 。 r 1. 位置:在轨道上取一固定点O, 位置:在轨道上取一固定点 , 用质点距离O的路程长度 , 用质点距离 的路程长度 s,可 惟一确定质点的位置。 惟一确定质点的位置。 位置 s有 有 正负之分。 正负之分。 2. 位置变化: 位置变化:
