(完整)沪科版初三数学二次函数经典习题

合集下载

沪科版九年级上册数学第21章二次函数与反比例函数含答案(含解析)

沪科版九年级上册数学第21章二次函数与反比例函数含答案一、单选题(共15题，共计45分)1、如图，抛物线y=ax2+bx+c与x轴相交于A、B两点，与y轴相交于C点，图中虚线为抛物线的对称轴，则下列正确的是( )A.a＜0B.b＜0C.c＞0D.b 2-4ac＜02、若A（1，y1），B（2，y2）两点都在反比例函数y= 的图象上，则y1与y2的大小关系是（）A.y1＜y2B.y1=y2C.y1＞y2D.无法确定3、直角三角形两直角边的长分别为x，y，它的面积为3，则y与x之间的函数关系用图象表示大致是（）A. B. C. D.4、如图，将直线y=x向下平移b个单位长度后得到直线l，l与反比例函数y= （k＞0，x＞0）的图象相交于点A，与x轴相交于点B，则OA2﹣OB2=10，则k 的值是（）A.5B.10C.15D.205、若是反比例函数，则必须满足（）A. B. C. 或 D. 且6、小明从图所示的二次函数y=ax2+bx+c的图象中，观察得出了下面五条信息：①c＜0；②abc＞0；③a-b+c＞0；④2a-3b=0；⑤c-4b＞0，你认为其中正确信息的个数有（）A.2个B.3个C.4个D.5个7、若点A（a，b）在反比例函数y=的图象上，则代数式ab﹣4的值为（）A.0B.-2C.2D.-68、二次函数y=ax2+bx+c（a≠0）的图象如图，则反比例函数与一次函数y=bx﹣c在同一坐标系内的图象大致是（）A. B. C.D.9、一次函数与二次函数在同一平面直角坐标系中的图象可能是（）A. B. C.D.10、将抛物线y＝2x2平移，得到抛物线y＝2（x+4）2+1，下列平移正确的是（）A.先向左平移4个单位，再向上平移1个单位B.先向左平移4个单位，再向下平移1个单位C.先向右平移4个单位，再向上平移1个单位 D.先向右平移4个单位，再向下平移1个单位11、将抛物线y＝（x﹣2）2+2向左平移2个单位，得到的新抛物线为（）A.y＝（x﹣2）B.y＝（x﹣2）+4C.y＝x +2D.y＝（x﹣4）+212、已知二次函数y=ax2+bx+c的图象如图所示，则（）A.b＞0，c＞0B.b＞0，c＜0C.b＜0，c＜0D.b＜0，c＞013、如图，△ABC．的三个顶点分别为A（1，2），B（5，2），C（5，5）．若反比例函数在第一象限内的图象与△ABC有交点，则k的取值范围是（）A.2≤k≤25B.2≤k≤10C.1≤k≤5D.10≤k≤2514、将二次函数y=x2的图象向右平移1个单位，再向上平移2个单位后，所得图象的函数表达式是（）A.y=（x-1）2+2B.y=（x+1）2+2C.y=（x-1）2-2D.y=（x+1）2-215、如图，在平面直角坐标系中，点A、B的坐标分别为（-2，3）、（0，1），将线段AB沿x轴的正方向平移m（m>0）个单位，得到线段A' B'。

沪科版数学九年级上册二次函数精品习题讲义

沪科版数学九年级上册二次函数[讲义]【考点一：二次函数定义】例1、下列函数中是二次函数的是（）、A. y=1x2B. y=2x+1 C. y=12x2+2x3 D. y=−4x2+5变式1-1、已知y=mx|m−2|+2mx+1是y关于x的二次函数，则m的值为（）A.0B.1C.4 D．0或4变式1-2、二次函数y=x2−6x−1的二次项系数、一次项系数和常数项分别是（）A. 1,-6,-1 B. 1,6,1 C. 0,-6,1 D. 0,6,-1变式1-3、有下列函数：①y=5x−4②y=2x3−8x+3③y=3x2−1x−2④y=38x2−1x2−6x其中属于二次函数的是_____________（填序号）.⑤y=23变式1-4、函数y=2(m+2)x m2−2+2x−1（x≠0）当m＝________时，它是二次函数，当m＝___________时，它为一次函数.2．如图，正方形ABCD和圆O的周长之和为20cm，设圆的半径为xcm，正方形的边长为ycm，阴影部分的面积为Scm²．当x在一定范围内变化时，y和S都随x的变化而变化，则y与x，S与x满足的函数关系分别是（）A.一次函数关系，一次函数关系B.一次函数关系，二次函数关系C.二次函数关系，二次函数关系D.二次函数关系，一次函数关系【考点二：列二次函数表达式】例2、若二次函数y=mx2+(2m+n)x+3n的二次项系数比一次项系数小12，一次项系数比常数项大8，则这个二次函数的解析式为___________.变式2-1．（2022秋·承德县期末）“抖音直播带货”已经成为一种热门的销售方式，某抖音主播代销某一品牌的电子产品（这里代销指厂家先免费提供货源，待货物销售后再进行结算，未售出的由厂家负责处理）．销售中发现每件售价99元时，日销售量为200件，当每件电子产品每下降5元时，日销售量会增加10件，已知每售出1件电子产品，该主播需支付厂家和其他费用共50元，设每件电子产品售价为x（元），主播每天的利润为w（元），则w与x之间的函数解析式为（)A. w=(99−x)[200+10(x−50)]B.w=(x−50)[200+10(99−x)]×10]C. w=(x−50)[200+x−995D. w=(x−50)[200+x−995×10]变式2-1．（2023·金水区校级模拟）将一根长为50cm的铁丝弯成一个长方形（铁丝全部用完且无损耗）如图所示，设这个长方形的一边长为x（cm），它的面积为y（c㎡），则y与x之间的函数关系式为（）A. y=−x2+50xB. y=x2−50xC. y=−x2+25xD. y=−2x2+25变式2-2（2023春·沈北新区期末）如图，李大爷用24米长的篱笆靠墙围成一个长方形（ABCD）菜园，若菜园靠墙的一边（AD）长为x（米），那么菜园的面积y（平方米）与x的关系式为（)A. y=x(12−x)2B. y=x(12−x) C. y=x(24−x)2D. y=x(24−x)变式2-3．（2022秋·亭湖区校级期末）如图，某农场要盖一排三间长方形的羊圈，打算一面利用旧墙，其余各面用木材围成栅栏，该农场计划用木材围成总长24m的栅栏，设面积为s(m²)，垂直于墙的一边长为x（m）．则s关于x的函数关系式：_____________（并写出自变量的取值范围）变式2-4（2023春·石景山区期末）如图，在矩形ABCD中，AB＝10，BC＝5，点P从点A出发，沿线段AD以每秒1个单位长度的速度向终点D运动；点Q从点B出发，沿线段BA以每秒2个单位长度的速度向终点A运动.P，Q两点同时出发，设点P运动的时间为t（单位：秒），ΔAPQ的面积为y.则y关于t的函数表达式为________1．（2022秋·蜀山区校级月考）若y=(a+1)x|a+3|−x+3是关于x的二次函数，则a的值是（)A. 1B. -5C. -1 D．-5或-12．（2022秋·石景山区期末）如图，线段AB＝10cm，点P在线段AB上（不与点A，B重合），以AP为边作正方形APCD.设AP＝x cm，BP＝y cm，正方形APCD的面积为S cm²，则y与x，S与x满足的函数关系分别为（)A.一次函数关系，二次函数关系B.反比例函数关系，二次函数关系C.一次函数关系，反比例函数关系D.反比例函数关系，一次函数关系3．（2020秋·龙凤区校级月考）已知函数y=(m2−m)x2+(m−1)x+m+1（1）当m为何值时，这个函数是关于x的一次函数；（2）当m为何值时，这个函数是关于x的二次函数．4．（2020秋·滨州月考）某商品的进价为每件40元，如果售价为每件50元，每个月可卖出210件；如果售价超过50元但不超过80元，每件商品的售价每上涨1元，则每个月少卖1件，如果售价超过80元后，若再涨价，则每涨1元每月少卖3件．设每件商品的售价x元（x为整数），每个月的销售量为y件.（1）求y与x的函数关系式并直接写出自变量x的取值范围；（2）设每月的销售利润为W，请直接写出W与x的函数关系式．。

初中数学沪科版九年级上册第二十一章《二次函数的应用》练习题(解析版)

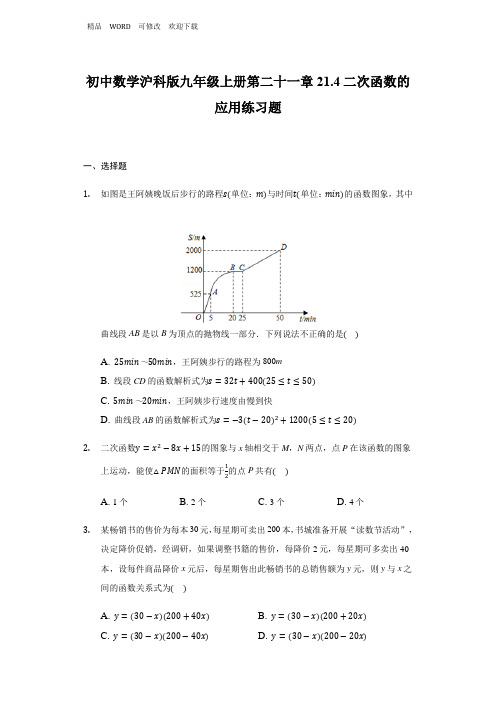
初中数学沪科版九年级上册第二十一章21.4二次函数的应用练习题一、选择题1.如图是王阿姨晚饭后步行的路程s(单位：m)与时间t(单位：min)的函数图象，其中曲线段AB是以B为顶点的抛物线一部分．下列说法不正确的是()A. 25min～50min，王阿姨步行的路程为800mB. 线段CD的函数解析式为s=32t+400(25≤t≤50)C. 5min～20min，王阿姨步行速度由慢到快D. 曲线段AB的函数解析式为s=−3(t−20)2+1200(5≤t≤20)2.二次函数y=x2−8x+15的图象与x轴相交于M，N两点，点P在该函数的图象上运动，能使△PMN的面积等于1的点P共有()2A. 1个B. 2个C. 3个D. 4个3.某畅销书的售价为每本30元，每星期可卖出200本，书城准备开展“读数节活动”，决定降价促销，经调研，如果调整书籍的售价，每降价2元，每星期可多卖出40本，设每件商品降价x元后，每星期售出此畅销书的总销售额为y元，则y与x之间的函数关系式为()A. y=(30−x)(200+40x)B. y=(30−x)(200+20x)C. y=(30−x)(200−40x)D. y=(30−x)(200−20x)4.某农产品市场经销一种销售成本为40元的水产品．据市场分析，若按每千克50元销售，一个月能售出500千克；销售单价每涨一元，月销售量就减少10千克．设销售单价为每千克x元，月销售利润为y元，则y与x的函数关系式为()A. y=(x−40)(500−10x)B. y=(x−40)(10x−500)C. y=(x−40)[500−10(x−50)]D. y=(x−40)[500−10(50−x)]5.进入夏季后，某电器商场为减少库存，对电热取暖器连续进行两次降价．若设平均每次降价的百分率是x，降价后的价格为y元，原价为a元，则y与x之间的函数关系式为()A. y=2a(x−1)B. y=2a(1−x)C. y=a(1−x2)D. y=a(1−x)26.为解决药价虚高给老百姓带来的求医难问题，国家决定对药品价格分两次降价，若设平均每次降价的百分率为x，该药品的原价是18元/盒，降价后的价格为y元/盒，则y与x之间的函数关系式是()A. y=36(1−x)B. y=36(1+x)C. y=18(1−x)2D. y=18(1+x2)7.在一个边长为2的正方形中挖去一个边长为x(0<x<2)的小正方形，如果设剩余部分的面积为y，那么y关于x的函数解析式是()A. y=x2B. y=4−x2C. y=x2−4D. y=4−2x8.矩形的周长为12cm，设其一边长为xcm，面积为ycm2，则y与x的函数关系式及其自变量x的取值范围均正确的是()A. y=−x2+6x(3<x<6)B. y=−x2+6x(0<x<6)C. y=−x2+12x(6<x<12)D. y=−x2+12x(0<x<12)9.长方形的周长为24cm，其中一边为xcm(其中x>0)，面积为ycm2，则这样的长方形中y与x的关系可以写为()A. y=x2B. y=(12−x)2C. y=(12−x)xD. y=2(12−x)10.广场上喷水池中的喷头微露水面，喷出的水线呈一条抛物线，水线上水珠的高度y(x2+6x(0≤x≤4)，米)关于水珠和喷头的水平距离x(米)的函数解析式是y=−32那么水珠的高度达到最大时，水珠与喷头的水平距离是()A. 1米B. 2米C. 5米D. 6米二、填空题11.某厂今年一月份新产品的研发资金为a元，以后每月新产品的研发资金与上月相比增长率都是x，则该厂今年三月份新产品的研发资金y(元)关于x的函数关系式为y=________．12.据权威部门发布的消息，2021年第一季度安徽省城镇居民人均可支配收入约为0.75万元，若第三季度安徽省城镇居民人均可支配收人为y万元，平均每个季度城镇居民人均可支配收入增长的百分率为x，则y与x之间的函数表达式是____．13.如图，用一段长为40m的篱笆围成一个一边靠墙的矩形菜园ABCD，墙长为18m，设AD的长为x m，菜园ABCD的面积为y m2，则y关于自变量x的函数关系式是___________________________．14.某商品现在的售价为每件60元，每星期可卖出300件，市场调查反映：如调整价格，每涨价1元，每星期要少卖出10件，商品进价为每件40元，若设涨价x(x>0)元，总利润为y元，则y与x的函数关系式为______．15.某工厂今年一月份生产防疫护目镜的产量是20万件，计划之后两个月增加产量，如果月平均增长率为x，那么第一季度防疫护目镜的产量万件与x之间的关系应表示为______．三、解答题16.已知抛物线y=−x2+bx+c的对称轴为直线x=1，其图象与x轴相交于A，B两点，与y轴相交于点C(0,3)．(1)求b，c的值；(2)直线1与x轴相交于点P．①如图1，若l//y轴，且与线段AC及抛物线分别相交于点E，F，点C关于直线x=1的对称点为点D，求四边形CEDF面积的最大值；②如图2，若直线1与线段BC相交于点Q，当△PCQ∽△CAP时，求直线1的表达式．17.如图1，在平面直角坐标系中，已知抛物线y=ax2+bx−5与x轴交于A(−1,0)，B(5,0)两点，与y轴交于点C．(1)求抛物线的函数表达式；(2)如图2，CE//x轴与抛物线相交于点E，点H是直线CE下方抛物线上的动点，过点H且与y轴平行的直线与BC，CE分别相交于点F，G，试探究当点H运动到何处时，四边形CHEF的面积最大，求点H的坐标；(3)若点K为抛物线的顶点，点M(4,m)是该抛物线上的一点，在x轴，y轴上分别找点P，Q，使四边形PQKM的周长最小，求出点P，Q的坐标．18.在平面直角坐标系中，函数y=x2−2ax−1(a为常数)的图象与y轴交于点A．(1)求点A的坐标．(2)当此函数图象经过点(1,2)时，求此函数的表达式，并写出函数值y随x的增大而增大时x的取值范围．(3)当x≤0时，若函数y=x2−2ax−1(a为常数)的图象的最低点到直线y=2a的距离为2，求a的值．(4)设a<0，Rt△EFG三个顶点的坐标分别为E(−1,−1)、F(−1,a−1)、G(0,a−1).当函数y=x2−2ax−1(a为常数)的图象与△EFG的直角边有交点时，交点记为点P.过点P作y轴的垂线，与此函数图象的另一个交点为P′(P′与P不重合)，过点A 作y轴的垂线，与此函数图象的另一个交点为A′.若AA′=2PP′，直接写出a的值．答案和解析1.【答案】C【解析】【分析】本题考查了二次函数的应用，一次函数的应用，正确的识别图象、数形结合是解题的关键.根据函数图象中的信息，利用数形结合求相关线段的解析式解答即可．【解答】解：A.25min ～50min ，王阿姨步行的路程为2000−1200=800m ，故A 正确；B .设线段CD 的函数解析式为s =kt +b ，把(25,1200)，(50,2000)代入得，{1200=25k +b 2000=50k +b，解得：{k =32b =400， ∴线段CD 的函数解析式为s =32t +400(25≤t ≤50)，故B 正确；C .在A 点的速度为5255=105m/min ，在B 点的速度为1200−52520−5=67515=45m/min ，速度从快变慢，故C 错误；D .当t =5，20时，由图象可得s =525，1200m ，将t =5，20分别代入s =−3(t −20)2+1200(5≤t ≤20)得s =525，s =1200，故D 正确．故选C ．2.【答案】D【解析】【分析】本题结合图象的性质考查二次函数的综合应用，难度中等．要注意函数求出的各个解是否符合实际．由题可求出MN 的长，即△MNP 的底边已知，要求面积为12，那么根据面积即可求出高，只要把相应的y 值代入即可解答．【解答】解：y =x 2−8x +15的图象与x 轴交点(3,0)和(5,0)，|MN|=2，设p 点(x,y)，y =x 2−8x +15，面积=12=12|MN|⋅|y|，可得y 1=12，或者y 2=−12，当y =12时，x =8±√62；当y =−12时，x =8±√22，所以共有四个点．故选：D ．3.【答案】B【解析】【分析】本题考查由实际问题列二次函数关系式，解答本题的关键是明确题意，列出相应的函数关系式．根据降价x 元，则售价为(30−x)元，销售量为(200+20x)本，由题意可得等量关系：总销售额为y =销量×售价，根据等量关系列出函数解析式即可．【解答】解：设每本降价x 元，则售价为(30−x)元，销售量为(200+20x)本，根据题意得，y =(30−x)(200+20x)，故选B ．4.【答案】C【解析】【分析】此题主要考查了根据实际问题抽象出二次函数关系式，正确表示出销量是解题关键．直接利用每千克利润×销量=总利润，进而得出关系式．【解答】解：设销售单价为每千克x 元，月销售利润为y 元，则y 与x 的函数关系式为：y =(x −40)[500−10(x −50)]．故选：C ．5.【答案】D【解析】解：由题意得第二次降价后的价格是a(1−x)2．则函数解析式是y=a(1−x)2．故选D．原价为a，第一次降价后的价格是a×(1−x)，第二次降价是在第一次降价后的价格的基础上降价的，为a×(1−x)×(1−x)=a(1−x)2．本题需注意第二次降价是在第一次降价后的价格的基础上降价的．6.【答案】C【解析】【分析】此题主要考查了根据实际问题抽象出二次函数关系式，本题需注意第二次降价是在第一次降价后的价格的基础上降价的．原价为18，第一次降价后的价格是18(1−x)，第二次降价是在第一次降价后的价格的基础上降价的为：18(1−x)×(1−x)=18(1−x)2，则函数关系式即可求得．【解答】解：原价为18，第一次降价后的价格是18(1−x)；第二次降价是在第一次降价后的价格的基础上降价的为：18(1−x)×(1−x)=18(1−x)2．则函数解析式是：y=18(1−x)2．故选C．7.【答案】B【解析】解：设剩下部分的面积为y，则：y=−x2+4(0<x<2)，故选：B．根据剩下部分的面积=大正方形的面积−小正方形的面积得出y与x的函数关系式即可．此题主要考查了根据实际问题列二次函数关系式，利用剩下部分的面积=大正方形的面积−小正方形的面积得出是解题关键．8.【答案】B【解析】【分析】此题主要考查了根据实际问题列二次函数关系式的知识，解题的关键是用x表示出矩形的另一边，此题难度一般．已知一边长为xcm，则另一边长为(6−x)cm，根据矩形的面积公式即可解答．【解答】解：已知一边长为xcm，则另一边长为(6−x)．则y=x(6−x)化简可得y=−x2+6x，(0<x<6)，故选：B．9.【答案】C【解析】【分析】本题考查列二次函数关系式，得到长方形的另一边长是解决本题的关键点．先得到长方形的另一边长，那么面积=一边长×另一边长．【解答】解：∵长方形的周长为24cm，其中一边为x(其中x>0)，∴长方形的另一边长为12−x，∴y=(12−x)⋅x．故选C．10.【答案】B【解析】【分析】本题考查了二次函数的应用，解决本题的关键是掌握二次函数的顶点式．根据二次函数的顶点式即可求解．【解答】解：方法一：根据题意，得y=−32x2+6x(0≤x≤4)，=−32(x−2)2+6所以水珠的高度达到最大时，水珠与喷头的水平距离是2米．方法二：因为对称轴x=−62×(−32)=2，所以水珠的高度达到最大时，水珠与喷头的水平距离是2米．故选：B．11.【答案】a(1+x)2【解析】【分析】本题考查根据实际问题列二次函数关系式，关键是由一月份新产品的研发资金为a元，根据题意可以得到2月份研发资金为a×(1+x)，而三月份在2月份的基础上又增长了x，那么三月份的研发资金也可以用x表示出来，由此即可确定函数关系式．【解答】解：∵一月份新产品的研发资金为a元，二月份起，每月新产品的研发资金与上月相比增长率都是x，∴二月份新产品的研发资金为a(1+x)元，∴三月份新产品的研发资金为a(1+x)(1+x)=a(1+x)2元，即y=a(1+x)2．12.【答案】y=0.75(1+x)2【解析】【分析】此题主要考查了根据实际问题列二次函数关系式，属于中考常考题型．第一季度安徽省城镇居民人均可支配收入约为0.75万元，第二季度安徽省城镇居民人均可支配收入是0.75(1+x)元，第三季度安徽省城镇居民人均可支配收人为0.75(1+x)2元，则函数解析式即可求得．【解答】解：平均每个季度城镇居民人均可支配收入增长的百分率为x，根据题意可得：y与x之间的函数关系为：y=0.75(1+x)2．故答案为y=0.75(1+x)2．13.【答案】y=−2x2+40x(11≤x<20)【解析】【分析】本题考查了根据实际问题列二次函数关系式、矩形的面积公式的运用，利用篱笆的总长用含x的代数式表示出平行于墙的边长是解题的关键．先用含x的代数式表示出平行于墙的边长，再由矩形的面积公式就可以得出结论；【解答】解：根据题意，AD边的长为x米，则AB边的长为(40−2x)米，∴y=x(40−2x)，即y与x之间的函数关系式为y=−2x2+40x；0<40−2x≤18，11≤x<20，故答案为y=−2x2+40x(11≤x<20)．14.【答案】y=10x2−500x+6000【解析】解：设涨价x(x>0)元，总利润为y元，则y与x的函数关系式为：y=(60−40−x)(300−10x)=10x2−500x+6000．故答案为：y=10x2−500x+6000．直接利用销量×每件利润=总利润，进而得出函数关系式．此题主要考查了根据实际问题列二次函数关系式，正确表示出销量和每件利润是解题关键．15.【答案】y=20+20(x+1)+20(x+1)2【解析】解：y与x之间的关系应表示为：y=20+20(x+1)+20(x+1)2．故答案为：y=20+20(x+1)+20(x+1)2．根据平均增长问题，可得答案．本题考查了根据实际问题列二次函数关系式，利用增长问题获得函数解析式是解题关键． 16.【答案】解：(1)由题意得：{b2=1c =3， ∴b =2，c =3，(2)①如图1，∵点C 关于直线x =1的对称点为点D ，∴CD//OA ，∴3=−x 2+2x +3，解得：x 1=0，x 2=2，∴D(2,3)，∵抛物线的解析式为y =−x 2+2x +3，∴令y =0，解得x 1=−1，x 2=3，∴B(−1,0)，A(3,0)，设直线AC 的解析式为y =kx +b ，∴{3k +b =0b =3，解得：{k =−1b =3， ∴直线AC 的解析式为y =−x +3，设F(a,−a 2+2a +3)，E(a,−a +3)，∴EF =−a 2+2a +3+a −3=−a 2+3a ，四边形CEDF 的面积=S △EFC +S △EFD =12EF ⋅CD =12×(−a 2+3a)×2=−a 2+3a =−(a −32)2+94， ∴当a =32时，四边形CEDF 的面积有最大值，最大值为94．②当△PCQ∽△CAP 时，∴∠PCA =∠CPQ ，∠PAC =∠PCQ ，∴PQ//AC ，∵C(0,3)，A(3,0)，∴OA =OC ，∴∠OCA=∠OAC=∠PCQ=45°，∴∠BCO=∠PCA，如图2，过点P作PM⊥AC交AC于点M，∴tan∠PCA=tan∠BCO=OBOC =13，设PM=b，则CM=3b，AM=b，∵AC=√OC2+OA2=3√2，∴b+3b=3√2，∴b=34√2，∴PA=34√2×√2=32，∴OP=OA−PA=3−32=32，∴P(32,0)，设直线l的解析式为y=−x+n，∴−32+n=0，∴n=32．∴直线l的解析式为y=−x+32．【解析】(1)根据抛物线的对称轴及抛物线与y轴的交点坐标可求出b、c的值；(2)由题意先求出D点坐标为(2,3)，求出直线AC的解析式，设F(a,−a2+2a+3)，E(a,−a+3)，则EF=−a2+3a，四边形CEDF的面积可表示为12EF⋅CD，利用二次函数的性质可求出面积的最大值；(3)当△PCQ∽△CAP时，可得∠PCA=∠CPQ，∠PAC=∠PCQ=∠OCA=45°，则PQ//AC，∠BCO=∠PCA，过点P作PM⊥AC交AC于点M，可求出PM、PA、OP的长，用待定系数法可求出函数解析式．本题考查了二次函数的综合题：熟练掌握二次函数的性质和轴对称的性质；会利用待定系数法求函数解析式；理解坐标与图形性质，会利用相似三角形的性质解题；要会利用数形结合的思想把代数和几何图形结合起来，利用点的坐标的意义表示线段的长度是解题的关键．17.【答案】解：(1)∵点A(−1,0)，B(5,0)在抛物线y =ax 2+bx −5上，∴{a −b −5=025a +5b −5=0，解得{a =1b =−4，∴抛物线的表达式为y =x 2−4x −5，(2)设H(t,t 2−4t −5)，∵CE//x 轴，∴点E 的纵坐标为−5，∵E 在抛物线上，∴x 2−4x −5=−5，∴x =0(舍)或x =4，∴E(4,−5)，∴CE =4，∵B(5,0)，C(0,−5)，∴直线BC 的解析式为y =x −5，∴F(t,t −5)，∴HF =t −5−(t 2−4t −5)=−(t −52)2+254，∵CE//x 轴，HF//y 轴，∴CE ⊥HF ，∴S 四边形CHEF =12CE ⋅HF =−2(t −52)2+252，∴H(52,−354)；(3)如图2，∵K 为抛物线的顶点，∴K(2,−9)，∴K 关于y 轴的对称点K′(−2,−9)，∵M(4,m)在抛物线上，∴M(4,−5)，∴点M关于x轴的对称点M′(4,5)，∴直线K′M′的解析式为y=73x−133，∴P(137,0)，Q(0,−133).【解析】(1)根据待定系数法直接确定出抛物线解析式；(2)先求出直线BC的解析式，进而求出四边形CHEF的面积的函数关系式，即可求出；(3)利用对称性找出点P，Q的位置，进而求出P，Q的坐标．此题是二次函数综合题，主要考查了待定系数法，四边形的面积的计算方法，对称性，解的关键是利用对称性找出点P，Q的位置，是一道中等难度的题目．18.【答案】解：(1)当x=0时，y=x2−2ax−1=−1，∴点A的坐标为：(0,−1)；(2)将点(1,2)代入y=x2−2ax−1，得：2=1−2a−1，解得：a=−1，∴函数的表达式为：y=x2+2x−1，∵y=x2+2x−1=(x+1)2−2，∴抛物线的开口向上，对称轴为x=−1，如图1所示：∴当x>−1时，y随x的增大而增大；(3)抛物线y=x2−2ax−1=(x−a)2−a2−1的对称轴为：x=a，顶点坐标为：(a,−a2−1)，当a>0时，对称轴在y轴右侧，如图2所示：∵x≤0，∴最低点就是A(0,−1)，∵图象的最低点到直线y=2a的距离为2，∴2a−(−1)=2，解得：a=12；当a<0，对称轴在y轴左侧，顶点(a,−a2−1)就是最低点，如图3所示：∴2a −(−a 2−1)=2，整理得：(a +1)2=2，解得：a 1=−1−√2，a 2=−1+√2(不合题意舍去)；综上所述，a 的值为12或−1−√2；(4)∵a <0，Rt △EFG 三个顶点的坐标分别为E(−1,−1)、F(−1,a −1)、G(0,a −1)， ∴直角边为EF 与FG ，∵抛物线y =x 2−2ax −1=(x −a)2−a 2−1的对称轴为：x =a ，A(0,−1)， ∴AA′=−2a ，当点P 在EF 边上时，如图4所示：则x p =−1，∵EA =OA =1，∴点P 在对称轴x =a 的左侧，∴PP′=2(a +1)，∵AA′=2PP′，∴−2a =2×2(a +1)，解得：a =−23；当点P 在FG 边上时，如图5所示：则y p =a −1，∴x 2−2ax −1=a −1，解得：x 1=a +√a 2+a ，x 2=a −√a 2+a ，∴PP′=a +√a 2+a −(a −√a 2+a)=2√a 2+a ，∵AA′=2PP′，∴−2a =4√a 2+a ，解得：a 1=−43，a 2=0(不合题意舍去)；综上所述，a 的值为−23或−43．【解析】(1)当x =0时，代入y =x 2−2ax −1，即可得出结果；(2)将点(1,2)代入y =x 2−2ax −1，得a =−1，则函数的表达式为y =x 2+2x −1，由y =x 2+2x −1=(x +1)2−2，得出抛物线的开口向上，对称轴为x =−1，则当x >−1时，y 随x 的增大而增大；(3)抛物线y =x 2−2ax −1=(x −a)2−a 2−1的对称轴为x =a ，顶点坐标为(a,−a 2−1)，当a >0时，对称轴在y 轴右侧，最低点就是A(0,−1)，则2a −(−1)=2，即可得出结果；当a <0，对称轴在y 轴左侧，顶点(a,−a 2−1)就是最低点，则2a −(−a 2−1)=2，即可得出结果；(4)易证直角边为EF 与FG ，由抛物线的对称轴为x =a ，A(0,−1)，则AA′=−2a ，当点P 在EF 边上时，PP′=2(a +1)，则−2a =2×2(a +1)，即可得出结果；当点P 在FG 边上时，求出PP′=2√a 2+a ，则−2a =4√a 2+a ，即可得出结果．本题是二次函数综合题，主要考查了二次函数图象与性质、待定系数法求解析式、直角三角形的性质、解一元二次方程、分类讨论等知识；熟练掌握二次函数图象与性质是解题的关键．1、最困难的事就是认识自己。

沪科版数学九年级上册 21.1 二次函数基础课时练习题(含答案)

二次函数基础分类练习题练习一二次函数1、一个小球由静止开始在一个斜坡上向下滚动，通过仪器观察得到小球滚动的距离s （米）与时间t （秒）的数据如下表：时间t （秒） 1 2 3 4 … 距离s （米）281832…写出用t 表示s 的函数关系式. 2、下列函数：① 23y x ；② 21y x x x ；③ 224y x x x ；④ 21yx x ；⑤ 1yx x ，其中是二次函数的是，其中a，b，c3、当m 时，函数2235y mx x（m 为常数）是关于x 的二次函数4、当____m 时，函数2221mm y m m x 是关于x 的二次函数5、当____m时，函数2564mm ymx +3x 是关于x 的二次函数6、若点 A ( 2, m ) 在函数 12-=x y 的图像上，则 A 点的坐标是＿＿＿＿.7、在圆的面积公式 S ＝πr 2 中，s 与 r 的关系是（）A 、一次函数关系B 、正比例函数关系C 、反比例函数关系D 、二次函数关系8、正方形铁片边长为15cm ，在四个角上各剪去一个边长为x （cm ）的小正方形，用余下的部分做成一个无盖的盒子． (1)求盒子的表面积S （cm 2）与小正方形边长x （cm ）之间的函数关系式； (2)当小正方形边长为3cm 时，求盒子的表面积．9、如图，矩形的长是 4cm ，宽是 3cm ，如果将长和宽都增加 x cm ，那么面积增加 ycm 2， ① 求 y 与 x 之间的函数关系式. ② 求当边长增加多少时，面积增加 8cm 2.10、已知二次函数),0(2≠+=a c ax y 当x=1时，y= -1；当x=2时，y=2，求该函数解析式.11、富根老伯想利用一边长为a 米的旧墙及可以围成24米长的旧木料，建造猪舍三间，如图，它们的平面图是一排大小相等的长方形.（1）如果设猪舍的宽AB 为x 米，则猪舍的总面积S （米2）与x 有怎样的函数关系？（2）请你帮富根老伯计算一下，如果猪舍的总面积为32米2，应该如何安排猪舍的长BC 和宽AB 的长度？旧墙的长度是否会对猪舍的长度有影响？怎样影响？练习二函数2ax y =的图象与性质1、填空：（1）抛物线221x y =的对称轴是（或），顶点坐标是，当x 时，y 随x 的增大而增大，当x 时，y 随x 的增大而减小，当x= 时，该函数有最值是；（2）抛物线221x y -=的对称轴是（或），顶点坐标是，当x 时，y 随x 的增大而增大，当x 时，y 随x 的增大而减小，当x= 时，该函数有最值是； 2、对于函数22x y =下列说法：①当x 取任何实数时，y 的值总是正的；②x 的值增大，y 的值也增大；③y 随x 的增大而减小；④图象关于y 轴对称.其中正确的是 . 3、抛物线 y ＝－x 2 不具有的性质是（）A 、开口向下B 、对称轴是 y 轴C 、与 y 轴不相交D 、最高点是原点4、苹果熟了，从树上落下所经过的路程 s 与下落时间 t 满足 S ＝12gt 2（g ＝9.8），则 s 与 t 的函数图像大致是（）st Os tOs tOs tOA B C D5、函数2ax y =与b ax y +-=的图象可能是（）A ．B ．C ．D ．6、已知函数24mm y mx 的图象是开口向下的抛物线，求m 的值.7、二次函数12-=m mx y 在其图象对称轴的左侧，y 随x 的增大而增大，求m 的值.8、二次函数223x y -=，当x 1＞x 2＞0时，求y 1与y 2的大小关系.9、已知函数()422-++=m mx m y 是关于x 的二次函数，求：（1）满足条件的m 的值；（2） m 为何值时，抛物线有最低点？求出这个最低点，这时x 为何值时，y 随x 的增大而增大；（3） m 为何值时，抛物线有最大值？最大值是多少？当x 为何值时，y 随x 的增大而减小？练习三函数c ax y +=2的图象与性质1、抛物线322--=x y 的开口 ,对称轴是 ,顶点坐标是 ,当x 时, y 随x 的增大而增大, 当x 时, y 随x 的增大而减小. 2、将抛物线231x y =向下平移2个单位得到的抛物线的解析式为 ,再向上平移3个单位得到的抛物线的解析式为 ,并分别写出这两个函数的顶点坐标、 .3、任给一些不同的实数k ，得到不同的抛物线k x y +=2，当k 取0，1±时，关于这些抛物线有以下判断：①开口方向都相同；②对称轴都相同；③形状相同；④都有最底点.其中判断正确的是 .4、将抛物线122-=x y 向上平移4个单位后，所得的抛物线是，当x= 时，该抛物线有最（填大或小）值，是 .5、已知函数2)(22+-+=x m m mx y 的图象关于y 轴对称，则m ＝________；6、二次函数c ax y +=2()0≠a 中，若当x 取x 1、x 2（x 1≠x 2）时，函数值相等，则当x 取x 1+x 2时，函数值等于 .练习四函数()2h x a y -=的图象与性质1、抛物线()2321--=x y ，顶点坐标是 ,当x 时,y 随x 的增大而减小，函数有最值 2、试写出抛物线23x y =经过下列平移后得到的抛物线的解析式并写出对称轴和顶点坐标. （1）右移2个单位；（2）左移32个单位；（3）先左移1个单位，再右移4个单位.3、请你写出函数()21+=x y 和12+=x y 具有的共同性质（至少2个）.4、二次函数()2h x a y -=的图象如图：已知21=a ，OA=OC ，试求该抛物线的解析式.5、抛物线2)3(3-=x y 与x 轴交点为A ，与y 轴交点为B ，求A 、B 两点坐标及⊿AOB 的面积.6、二次函数2)4(-=x a y ，当自变量x 由0增加到2时，函数值增加6. （1）求出此函数关系式.（2）说明函数值y 随x 值的变化情况.7、已知抛物线9)2(2++-=x k x y 的顶点在坐标轴上，求k 的值.练习五 ()k h x a y +-=2的图象与性质1、请写出一个二次函数以（2, 3）为顶点，且开口向上.＿＿＿＿＿＿＿＿＿＿＿＿.2、二次函数 y ＝(x －1)2＋2，当 x ＝＿＿＿＿时，y 有最小值.3、函数 y ＝12(x －1)2＋3，当 x ＿＿＿＿时，函数值 y 随 x 的增大而增大.4、函数y=21(x+3)2-2的图象可由函数y=21x 2的图象向平移3个单位，再向平移2个单位得到. 5、已知抛物线的顶点坐标为2,1，且抛物线过点3,0，则抛物线的关系式是6、如图所示，抛物线顶点坐标是P （1，3），则函数y 随自变量x 的增大而减小的x 的取值范围是（） A 、x>3 B 、x<3 C 、x>1 D 、x<17、已知函数()9232+--=x y .（1）确定下列抛物线的开口方向、对称轴和顶点坐标；（2）当x= 时，抛物线有最值，是 .（3）当x 时，y 随x 的增大而增大；当x 时，y 随x 的增大而减小. （4）求出该抛物线与x 轴的交点坐标及两交点间距离；（5）求出该抛物线与y 轴的交点坐标；（6）该函数图象可由23x y -=的图象经过怎样的平移得到的？8、已知函数()412-+=x y .（1）指出函数图象的开口方向、对称轴和顶点坐标；（2）若图象与x 轴的交点为A 、B 和与y 轴的交点C ，求△ABC 的面积；（3）指出该函数的最值和增减性；（4）若将该抛物线先向右平移2个单位，在向上平移4个单位，求得到的抛物线的解析式；（5）该抛物线经过怎样的平移能经过原点.（6）画出该函数图象，并根据图象回答：当x 取何值时，函数值大于0；当x 取何值时，函数值小于0.练习六 c bx ax y ++=2的图象和性质1、抛物线942++=x x y 的对称轴是 .2、抛物线251222+-=x x y 的开口方向是，顶点坐标是 .3、试写出一个开口方向向上，对称轴为直线x=-2，且与y 轴的交点坐标为（0，3）的抛物线的解析式 .4、将 y ＝x 2－2x ＋3 化成 y ＝a (x －h)2＋k 的形式，则 y ＝＿＿＿＿.5、把二次函数215322yx x的图象向上平移3个单位，再向右平移4个单位，则两次平移后的函数图象的关系式是6、抛物线1662--=x x y 与x 轴交点的坐标为_________； 7、函数x x y +-=22有最____值，最值为_______；8、二次函数c bx x y ++=2的图象沿x 轴向左平移2个单位，再沿y 轴向上平移3个单位，得到的图象的函数解析式为122+-=x x y ，则b 与c 分别等于（） A 、6，4 B 、－8，14 C 、－6，6 D 、－8，－149、二次函数122--=x x y 的图象在x 轴上截得的线段长为（） A 、22 B 、23 C 、32 D 、3310、通过配方，写出下列函数的开口方向、对称轴和顶点坐标：（1）12212+-=x x y ；（2）2832-+-=x x y ；（3）4412-+-=x x y11、把抛物线1422++-=x x y 沿坐标轴先向左平移2个单位，再向上平移3个单位，问所得的抛物线有没有最大值，若有，求出该最大值；若没有，说明理由.12、求二次函数62+--=x x y 的图象与x 轴和y 轴的交点坐标13、已知一次函数的图象过抛物线223y x x 的顶点和坐标原点1）求一次函数的关系式； 2）判断点2,5是否在这个一次函数的图象上14、某商场以每台2500元进口一批彩电.如每台售价定为2700元，可卖出400台，以每100元为一个价格单位，若将每台提高一个单位价格，则会少卖出50台，那么每台定价为多少元即可获得最大利润？最大利润是多少元？练习七 c bx ax y ++=2的性质1、函数2yx px q 的图象是以3,2为顶点的一条抛物线，这个二次函数的表达式为 2、二次函数2224y mx x mm 的图象经过原点，则此抛物线的顶点坐标是3、如果抛物线2yax bxc 与y 轴交于点A (0,2)，它的对称轴是1x ，那么ac b4、抛物线c bx x y ++=2与x 轴的正半轴交于点A 、B 两点，与y 轴交于点C ，且线段AB 的长为1，△ABC 的面积为1，则b 的值为______.5、已知二次函数c bx ax y ++=2的图象如图所示，则a___0，b___0，c___0，ac b 42-____0；6、二次函数c bx ax y ++=2的图象如图，则直线bc ax y +=的图象不经过第象限.7、已知二次函数2yax bx c （0≠a ）的图象如图所示，则下列结论：1）,a b 同号；2）当1x 和3x 时，函数值相同；3）40a b ；4）当2y 时，x 的值只能为0；其中正确的是 8、已知二次函数2224m mx x y +--=与反比例函数xm y 42+=的图象在第二象限内的一个交点的横坐标是-2，则m= 9、二次函数2yx ax b 中，若0a b ，则它的图象必经过点（）A 1,1B 1,1C 1,1 D1,110、函数b ax y +=与c bx ax y ++=2的图象如图所示，则下列选项中正确的是（）A 、0,0>>c abB 、0,0><c abC 、0,0<>c abD 、0,0<<c ab11、已知函数c bx ax y ++=2的图象如图所示，则函数b ax y +=的图象是（）12、二次函数c bx ax y ++=2的图象如图，那么abc 、2a+b 、a+b+c 、a-b+c 这四个代数式中，值为正数的有（） A ．4个 B ．3个 C ．2个 D ．1个 13、抛物线的图角如图，则下列结论：①＞0；②；③＞；④＜1.其中正确的结论是（）.（A ）①② （B ）②③ （C ）②④ （D ）③④ 14、二次函数2y ax bx c 的最大值是3a ，且它的图象经过1,2，1,6两点，求a 、b 、c15、试求抛物线2yax bx c 与x 轴两个交点间的距离（240b ac练习八二次函数解析式1、抛物线y=ax 2+bx+c 经过A(-1,0), B(3,0), C(0,1)三点，则a= , b= , c=2、把抛物线y=x 2+2x-3向左平移3个单位，然后向下平移2个单位，则所得的抛物线的解析式为 .3、二次函数有最小值为1，当0x 时，1y ，它的图象的对称轴为1x ，则函数的关系式为 4、根据条件求二次函数的解析式（1）抛物线过（-1，-6）、（1，-2）和（2，3）三点（2）抛物线的顶点坐标为（-1，-1），且与y轴交点的纵坐标为-3（3）抛物线过（－1，0），（3，0），（1，－5）三点；（4）抛物线在x轴上截得的线段长为4，且顶点坐标是（3，－2）；5、已知二次函数的图象经过1,1、2,1两点，且与x轴仅有一个交点，求二次函数的解析式6、抛物线y=ax2+bx+c过点(0,-1)与点(3,2)，顶点在直线y=3x-3上，a<0,求此二次函数的解析式.7、已知二次函数的图象与x轴交于A（-2，0）、B（3，0）两点，且函数有最大值是2.（1）求二次函数的图象的解析式；（2）设次二次函数的顶点为P ，求△ABP 的面积.8、以x 为自变量的函数)34()12(22-+-++-=m m x m x y 中，m 为不小于零的整数，它的图象与x 轴交于点A 和B ，点A 在原点左边，点B 在原点右边.(1)求这个二次函数的解析式；(2)一次函数y=kx+b 的图象经过点A ，与这个二次函数的图象交于点C ，且ABC S ∆=10,求这个一次函数的解析式.练习九二次函数与方程和不等式1、已知二次函数772--=x kx y 与x 轴有交点，则k 的取值范围是 .2、关于x 的一元二次方程02=--n x x 没有实数根，则抛物线n x x y --=2的顶点在第_____象限；3、抛物线222++-=kx x y 与x 轴交点的个数为（） A 、0 B 、1 C 、2 D 、以上都不对4、二次函数c bx ax y ++=2对于x 的任何值都恒为负值的条件是（） A 、0,0>∆>a B 、0,0<∆>a C 、0,0>∆<a D 、0,0<∆<a5、12++=kx x y 与k x x y --=2的图象相交，若有一个交点在x 轴上，则k 为（） A 、0 B 、-1 C 、2 D 、41 6、若方程02=++c bx ax 的两个根是－3和1，那么二次函数c bx ax y ++=2的图象的对称轴是直线（）A 、x ＝－3B 、x ＝－2C 、x ＝－1D 、x ＝1 7、已知二次函数2yx px q 的图象与x 轴只有一个公共点，坐标为1,0，求,p q 的值8、画出二次函数322--=x x y 的图象，并利用图象求方程0322=--x x 的解，说明x 在什么范围时0322≤--x x .9、如图：（1）求该抛物线的解析式；（2）根据图象回答：当x 为何范围时，该函数值大于0.10、二次函数c bx ax y ++=2的图象过A(-3,0),B(1,0),C(0,3),点D 在函数图象上，点C 、D 是二次函数图象上的一对对称点，一次函数图象过点B、D，求（1）一次函数和二次函数的解析式，（2）写出使一次函数值大于二次函数值的x的取值范围.y x mx m.11、已知抛物线22（1）求证此抛物线与x轴有两个不同的交点；y x mx m与x轴交于整数点，求m的值；（2）若m是整数，抛物线22（3）在（2）的条件下，设抛物线顶点为A，抛物线与x轴的两个交点中右侧交点为B.若M为坐标轴上一点，且MA=MB，求点M的坐标.练习十二次函数解决实际问题1、某农场种植一种蔬菜，销售员张平根据往年的销售情况，对今年种蔬菜的销售价格进行了预测，预测情况如图，图中的抛物线表示这种蔬菜销售价与月份之间的关系.观察图像，你能得到关于这种蔬菜销售情况的哪些信息？（至少写出四条）2、某企业投资100万元引进一条农产品生产线，预计投产后每年可创收33万元，设生产线投产后，从第一年到第x 年维修、保养费累计．．为y（万元），且y＝ax2＋bx，若第一年的维修、保养费为 2 万元，第二年的为 4 万元.求：y 的解析式.3、校运会上，小明参加铅球比赛，若某次试掷，铅球飞行的高度y (m) 与水平距离x (m) 之间的函数关系式为y＝－112x2＋23x＋53，求小明这次试掷的成绩及铅球的出手时的高度.4、用6m 长的铝合金型材做一个形状如图所示的矩形窗框，应做成长、宽各为多少时，才能使做成的窗框的透光面积最大？最大透光面积是多少？3.50.50 2 7月份千克销售价(元)5、商场销售一批衬衫，每天可售出20 件，每件盈利40 元，为了扩大销售，减少库存，决定采取适当的降价措施，经调查发现，如果一件衬衫每降价 1 元，每天可多售出 2 件.①设每件降价x 元，每天盈利y 元，列出y 与x 之间的函数关系式；②若商场每天要盈利1200 元，每件应降价多少元？③每件降价多少元时，商场每天的盈利达到最大？盈利最大是多少元？6、有一个抛物线形的拱形桥洞，桥洞离水面的最大高度为4m，跨度为10m，如图所示，把它的图形放在直角坐标系中.①求这条抛物线所对应的函数关系式.②如图，在对称轴右边1m 处，桥洞离水面的高是多少？7、有一座抛物线形拱桥，正常水位时桥下水面宽度为20m，拱顶距离水面4m.（1）在如图所示的直角坐标系中，求出该抛物线的解析式.（2）在正常水位的基础上，当水位上升h(m)时，桥下水面的宽度为d(m)，试求出用d表示h的函数关系式；（3）设正常水位时桥下的水深为2m，为保证过往船只顺利航行，桥下水面的宽度不得小于18m，求水深超过多少米时就会影响过往船只在桥下顺利航行？8、某一隧道内设双行线公路，其截面由一长方形和一抛物线构成，如图所示，为保证安全，要求行驶车辆顶部（设为平顶）与隧道顶部在竖直方向上高度之差至少要有0.5m，若行车道总宽度AB为6m，请计算车辆经过隧道时的限制高度是多少米？（精确到0.1m）.练习一二次函数参考答案1：1、22t s =；2、⑤，-1，1，0；3、≠2，3，1；6、（2，3）；7、D ；8、),2150(2254S 2<<+-=x x 189；9、x x y 72+=，1；10、22-=x y ；11、,244S 2x x +-=当a<8时，无解，168<≤a 时，AB=4,BC=8，当16≥a 时，AB=4,BC=8或AB=2,BC=16.练习二函数2ax y =的图象与性质参考答案2：1、(1)x=0,y 轴，（0，0），>0，，<0，0，小，0; (2)x=0,y 轴，（0，0），<，>， 0，大，0;2、④；3、C ；4、A ；5、B ；6、-2；7、3-；8、021<<y y ；9、（1）2或-3，（2）m=2、y=0、x>0，（3）m=-3，y=0，x>0；10、292x y =练习三函数c ax y +=2的图象与性质参考答案3：1、下，x=0，（0，-3），<0，>0；2、2312-=x y ，1312+=x y ，（0，-2），（0，1）；3、①②③；4、322+=x y ，0，小，3；5、1；6、c.练习四函数()2h x a y -=的图象与性质参考答案4：1、（3，0），>3，大，y=0;2、2)2(3-=x y ，2)32(3-=x y ，2)3(3-=x y ;3、略；4、2)2(21-=x y ；5、（3，0），（0，27），40.5；6、2)4(21--=x y ，当x<4时，y 随x 的增大而增大，当x>4时，y 随x 的增大而减小；7、-8，-2，4.练习五 ()k h x a y +-=2的图象与性质参考答案5：1、略；2、1；3、>1；4、左、下；5、342-+-=x x y ；6、C ；7、（1）下，x=2，（2，9），（2）2、大、9，（3）<2、>2,(4)( 32-,0)、( 32+,0)、 32，（5）（0，-3）；（6）向右平移2个单位，再向上平移9个单位；8、（1）上、x=-1、（-1，-4）；（2）（-3，0）、（1，0）、（0，-3）、6，（3）-4，当x>-1 时，y 随x 的增大而增大；当x<-1 时，y 随x 的增大而减小,(4) 2)1(-=x y ；（5）向右平移1个单位，再向上平移4个单位或向上平移3个单位或向左平移1个单位；（6）x>1或x<-3、-3<x<1练习六 c bx ax y ++=2的图象和性质参考答案6：1、x=-2；2、上、（3，7）；3、略；4、2)1(2+-x ；5、5)1(212+--=x y ；6、（-2，0）（8，0）；7、大、81；8、C ；9、A ；10、（1）1)2(212--=x y 、上、x=2、（2，-1），（2）310)34(32+--=x y、下、34=x 、（310,34），（3）3)2(412---=x y 、下、x=2、（2，-3）；11、有、y=6；12、（2，0）（-3，0）（0，6）；13、y=-2x 、否；14、定价为3000元时，可获最大利润125000元练习七 c bx ax y ++=2的性质参考答案7：1、1162+-=x x y ；2、（-4，-4）；3、1；4、-3；5、>、<、>、>；6、二；7、②③；8、-7；9、C ；10、D ；11、B ；12、C ；13、B ；14、4422++-=x x y ；15、aacb 42-练习八二次函数解析式参考答案8：1、31-、32、1；2、1082++=x x y ；3、1422+-=x x y ；4、（1）522-+=x x y 、（2）3422---=x x y 、（3）41525452--=x x y 、（4）253212+-=x x y ；5、9194942+-=x x y ；6、142-+-=x x y ；7、（1）25482582582++-=x x y 、5；8、322++-=x x y 、y=-x-1或y=5x+5练习九二次函数与方程和不等式参考答案9：1、47-≥k 且0≠k ；2、一；3、C ；4、D ；5、C ；6、C ；7、2，1；8、31,3,121≤≤-=-=x x x ；9、（1）x x y 22-=、x<0或x>2；10、y=-x+1，322+--=x x y ,x<-2或x>1;11、（1）略,(2)m=2,(3)(1，0)或（0，1）练习十二次函数解决实际问题参考答案10：1、①2月份每千克3.5元 ②7月份每千克0.5克 ③7月份的售价最低④2～7月份售价下跌；2、y ＝x 2＋x ；3、成绩10米，出手高度35米；4、23)1(232+--=x S ，当x ＝1时，透光面积最大为23m 2；5、（1）y ＝(40－x) (20＋2x)＝－2x 2＋60x ＋800，（2）1200＝－2x 2＋60x ＋800，x 1＝20，x 2＝10 ∵要扩大销售 ∴x 取20元，（3）y ＝－2 (x 2－30x)＋800＝－2 (x －15)2＋1250 ∴当每件降价15元时，盈利最大为1250元；6、（1）设y ＝a (x －5)2＋4，0＝a (－5)2＋4，a ＝－254，∴y ＝－254(x －5)2＋4，（2）当x ＝6时，y ＝－254＋4＝3.4(m)；7、（1）2251x y -=，（2）h d -=410，（3）当水深超过2.76m 时；8、)64(6412≤≤-+-=x x y ，x =3，m y 75.3496=-=，m 2.325.35.075.3≈=-，货车限高为3.2m.。

沪科版九年级数学上册《21.2二次函数的图像和性质》同步练习题(带答案)

沪科版九年级数学上册《21.2二次函数的图像和性质》同步练习题(带答案)一、选择题（在每小题列出的选项中，选出符合题目的一项）1.已知y=(m+2)x|m|+2是关于x的二次函数，那么m的值为( )A. −2B. 2C. ±2D. 02.对于二次函数y=−(x−1)2的图象的特征，下列描述正确的是( )A. 开口向上B. 经过原点C. 对称轴是y轴D. 顶点在x轴上3.当1≤x≤3时，二次函数y=x2−2ax+3的最小值为−1，则a的值为( )A. 2B. ±2C. 2或52D. 2或1364.已知点A(−2,y1)。

B(−1,y2)，C(5,y3)都在二次函数y=−x2+2x+k的图象上，则( )A. y1<y2<y3B. y3<y2<y1C. y3<y1<y2D. y2<y1<y35.若对于任意非零实数a，抛物线y=ax2+ax−2a总不经过点P(m−3,m2−16)，则符合条件的点P( )A. 有且只有1个B. 有且只有2个C. 至少有3个D. 有无穷多个6.用配方法将二次函数y=x2−8x−9化为y=a(x−ℎ)2+k的形式为( )A. y=(x−4)2+7B. y=(x+4)2+7C. y=(x−4)2−25D. y=(x+4)2−257.将抛物线y=x2−6x+5绕坐标原点旋转180°后，得到的抛物线的解析式为( )A. y=−x2−6x−5B. y=−x2+6x+5C. y=x2+6x+5D. y=x2+6x−58.二次函数y=ax2+bx+c(a≠0)与一次函数y=ax+c在同一坐标系中的图象大致为( )A. B.C. D.9.二次函数y=3(x−2)2−5与y轴交点坐标为( )A. (0,2)B. (0,−5)C. (0,7)D. (0,3)10.要得到函数y=−(x−2)2+3的图象，可以将函数y=−(x−3)2的图象( )A. 向右平移1个单位，再向上平移3个单位B. 向右平移1个单位，再向下平移3个单位C. 向左平移1个单位，再向上平移3个单位D. 向左平移1个单位，再向下平移3个单位11.已知抛物线y1:y=−2(x−4)2+2和抛物线y2:y=2x2+8x+18，若无论k取何值，直线y=kx−kp+ q被两条抛物线所截的两条线段都保持相等，则( )A. pq=3B. pq=4C. pq=5D. pq=612.如图，已知二次函数y=ax2+bx+c(a≠0)的图象如图所示，有下列5个结论：①abc>0②b−a>c③4a+2b+c>0 ④3a>−c⑤a+b>m(am+b)(m≠1的实数).其中正确结论有( )A. ①②③B. ②③⑤C. ②③④D. ③④⑤二、填空题13.将抛物线y=5x2向上平移2个单位，再向右平移3个单位，所得的抛物线的表达式为______．14.已知点A(−2,3)，B(0,3)是抛物线y=−x2+bx+c上两点，该抛物线的顶点坐标是．15.函数y=−(x−3)2+1中，当x时，y随x的增大而减小．16.若直线y=ax+b(ab≠0)经过第一、二、三象限，那么抛物线y=ax2+bx顶点在第______象限．17.二次函数y=2x2+bx+3的图象的对称轴是直线x=1，则常数b的值为．18.如图所示为函数y=x2+bx−1的图象，根据图象提供的信息，当−1≤x≤4时，y的取值范围是______ ．19.将抛物线y=ax2+b向左平移3个单位长度，再向上平移2个单位长度，得到抛物线的解析式是y=2(x+ 3)2+4，则原抛物线的解析式为______ ．20.小聪在画一个二次函数的图象时，列出了下面几组y与x的对应值：x˙˙˙012345˙˙˙y˙˙˙50−3−4−30˙˙˙该二次函数的表达式为．三、解答题（解答应写出文字说明，证明过程或演算步骤）x2−x−321. (1)已知二次函数y=14①求出函数图象顶点坐标、对称轴，并写出图象的开口方向②列表，并在所给网格中建立平面直角坐标系井直接画出此函数的图象(2)抛物线y=ax2+bx+c过(−3,0)，(1,0)两点，与y轴的交点为(0,4)，求抛物线的解析式．22.把抛物线C1：y=x2+2x+3先向右平移4个单位长度，再向下平移5个单位长度得到抛物线C2．(1)直接写出抛物线C2的函数关系式；(2)动点P(a,−6)能否在抛物线C2上？请说明理由；(3)若点A(m,y1)，B(n,y2)都在抛物线C2上，且m<n<0，比较y1，y2的大小，并说明理由．23.二次函数y=ax2+bx+c的部分图象如图所示，其中图象与x轴交于点A(−1,0)，与y轴交于点C(0,−5)，且经过点D(3,−8)．(1)求此二次函数的解析式；(2)将此二次函数的解析式写成y=a(x−ℎ)2+k的形式，并直接写出此二次函数图象的顶点坐标以及它与x 轴的另一个交点B的坐标．答案1.【答案】B2.【答案】D3. 【答案】A4.【答案】C5. 【答案】B6. 【答案】C7. 【答案】A8.【答案】D9.【答案】C10.【答案】C11. 【答案】D12.【答案】B13.【答案】y=5(x−3)2+214. 【答案】(−1,4)15. 【答案】>316. 【答案】三17. 【答案】−418. 【答案】−2≤y≤719. 【答案】y=2x2+220.【答案】y=(x−3)2−4(或y=x2−6x+5)21. 【答案】解：(1)y=14x2−x−3=14(x−2)2−4①∴函数图象顶点坐标(2,−4)、对称轴直线x=2，开口向上②x……01214……y……−3−154−4−154−3……(2)y=ax2+bx+c过(−3,0)，(1,0)两点，与y轴的交点为(0,4)用交点式，则表达式为：y=a(x−1)(x+3)，把(0,4)代入得：4=−a·3，解得a=−43函数解析式为：y=−43(x−1)(x+3)=−43x2−83x+4．22.【答案】解：(1)y=(x−3)2−3；(2)动点P(a,−6)不在抛物线C2上，理由如下：∵抛物线C2的函数关系式为：y=(x−3)2−3∴函数的最小值为−3∵−6<−3∵动点P(a,−6)不在抛物线C2上；(3)∵抛物线C2的函数关系式为：y=(x−3)2−3∴抛物线的开口向上，对称轴为x=3∴当x<3时，y随x的增大而减小∵点A(m,y1)，B(n,y2)都在抛物线C2上，且m<n<0<3∴y1>y2．23. 【答案】解：(1)根据题意得，{a−b+c=0①c=−5②9a+3b+c=−8③②分别代入①、③得a−b=5④3a+b=−1⑤④+⑤得，4a=4解得a=1把a=1代入④得1−b=5解得b=−4∴方程组的解是{a=1 b=−4 c=−5∴此二次函数的解析式为y=x2−4x−5；(2)y=x2−4x−5=x2−4x+4−4−5=(x−2)2−9二次函数的解析式为y=(x−2)2−9顶点坐标为(2,−9)对称轴为x=2设另一点坐标为B(a,0)则−1+a=2×2解得a=5∴点B的坐标是B(5,0)．。

沪科版九年级数学习题-二次函数

21.1 二次函數1．函數y＝mx2＋2x＋3－m表示二次函數，則m的取值範圍是()A．m＞0 B．m＜0 C．m≠0 D．m為全體實數x2(x＞0)，2．某車的刹車距離y(m)與開始刹車時的速度x(m/s)之間滿足二次函數y＝120若該車某次的刹車距離為5 m，則開始刹車時的速度為()A．40 m/s B．20 m/s C．10 m/s D．5 m/s3．在邊長為6 cm的正方形中間剪去一個邊長為x cm(0＜x＜6)的小正方形，剩下的面積為y cm2，則y與x之間的函數關係式是________．4．函數y＝ax2＋bx＋c，當________時，表示一次函數．5．y＋2與x2成正比例，當x＝－3時，y＝1，則y與x之間的函數關係式為________．6．正方形的邊長為1 cm，假設邊長增加x cm時，正方形的面積增加y cm2.(1)請寫出y與x之間的函數關係式；(2)當正方形邊長分別增加1 cm cm,2 cm時，正方形的面積增加多少？7．某化工材料經銷公司購進了一種化工原料，購進價格為每千克30元，物價部門規定其銷售單價不得高於每千克70元，也不得低於30元，市場調查發現：單價定為70元時，日均銷售60千克；單價每降低1元時，日均多售出2千克，在銷售過程中，每天還要支出其他費用500元(天數不足一天時，按整天計算)．設單價為x元時，日均獲利為y元．求y 關於x的函數關係式，並注明x的取值範圍．8．某批發市場批發甲、乙兩種水果，根據以往經驗和市場行情，預計夏季某一段時間內，甲種水果的銷售利潤y甲(萬元)與進貨量x(噸)近似滿足函數關係y甲＝0.3x；乙種水果的銷售利潤y乙(萬元)與進貨量x(噸)近似滿足函數關係y乙＝ax2＋bx(其中a≠0，a，b為常數)，且進貨量x為1噸時，銷售利潤y乙為1.4萬元；進貨量x為2噸時，銷售利潤y乙為2.6萬元．(1)求y乙(萬元)與x(噸)之間的函數關係式；(2)如果市場準備進甲、乙兩種水果共10噸，設乙種水果的進貨量為t噸，請你寫出這兩種水果所獲得的銷售利潤之和W(萬元)與t(噸)之間的函數關係式．9．(創新應用)觀察下圖中小黑點的擺放規律，並按照這樣的規律繼續擺放．記第n個圖中小黑點的個數為y.解答下列問題：(1)填表：(2)當n＝8時，y＝(3)根據上表中的數據，試求y與n之間的函數關係式．參考答案1. 答案：C2. 解析：由題意，得5＝120x 2，∴x ＝10.故選C ．答案：C3. 解析：剩餘面積等於原正方形的面積減去剪掉的小正方形的面積．答案：y ＝36－x 2(0＜x ＜6)4. 答案：a ＝0且b ≠05. 解析：由題意，設y ＋2＝k x 2,3＝9k ，k ＝13，∴y ＝13x 2－2.答案：y ＝13x 2－26. 解：(1)y ＝(x ＋1)2－1，∴y ＝x 2＋2x .(2)當x ＝1時，y ＝3；當xy ＝(3＋)；當x ＝2時，y ＝8.即正方形的面積分別增加3 cm 2，(3＋2，8 cm 2.7. 解：由銷售單價為x 元，則每千克降低(70－x )元，日均銷售量為[60＋2(70－x )]千克，每千克獲利為(x －30)元，所以y ＝(x －30)·[60＋2(70－x )]－500＝－2x 2＋260x －6 500(30≤x ≤70)．8. 解：(1)由題意，得a b 1.44a 2b 2.6⎧⎨⎩＋＝，＋＝，解得a 0.1b 1.5.⎧⎨⎩＝－，＝∴y 乙＝－0.1x 2＋1.5x .(2)W ＝y 甲＋y 乙＝0.3(10－t)＋(－0.1t 2＋1.5t)，整理，得W ＝－0.1t 2＋1.2t ＋3. 9. 解：(1)21 (2)57(3)把最中間的點先去掉，在第n 個圖中，在每條“線段”上有n －1個點．所以總點數為n (n －1)＋1.所以y 與n 之間的函數關係式為y ＝n 2－n ＋1.。

沪科版九年级数学上21.2二次函数的图象和性质基础知识和同步测试题含答案初三

九年级上册第21章二次函数和反比例函数21.2二次函数的图象和性质21.2.1二次函数y＝ax2的图象和性质基础知识和同步测试题基础知识1．函数y＝ax2(a≠0)的图象是一条关于____对称的抛物线，它具有如下性质：当a＞0时，抛物线的开口向____，顶点是抛物线的最____点，当x＞0时，y随x的增大而________；当x ＜0时，y随x的增大而____；当x＝____时，y最小值＝____．2．对于函数y＝ax2(a≠0)当a＜0时，抛物线的开口向____，顶点是抛物线的最____点．当x ＞0时，y随x的增大而________；当x＜0时，y随x的增大而__________；当x＝____时，y最大值＝____．答案1. y轴上低增大减小0 02. 下高减小增大0 0同步测试题二次函数y＝ax2与一次函数y＝－ax(a＞0)在同一坐标系里，大致图象是( )2．抛物线y＝－3x2的开口向____，顶点坐标是_________，顶点是抛物线的最____点，当x ＝____时，函数有最____值，为____．3．若y＝(m＋3)xm2－9是开口向上的抛物线，则m＝____．4．如图，是函数y1＝3x2，y2＝(1－k)x2，y3＝(k－2)x2的图象，则k的取值范围是________．5. 如图，边长为2的正方形ABCD的中心在原点O，AD∥x轴，以O为顶点，且过A，D两点的抛物线与以O为顶点且过B，C两点的抛物线将正方形分割成几部分，则图中的阴影部分的面积是____．6．已知点A (－1，y 1)、点B (－2，y 2)、点C (－2，y 3)都在函数y ＝－12x 2的图象上，则( ) A ．y 1>y 2>y 3 B ．y 1>y 3>y 2C ．y 3>y 2>y 1D ．y 2>y 1>y 37．下列说法错误的是( )A ．二次函数y ＝3x 2中，当x ＞0时，y 随x 的增大而增大B ．二次函数y ＝－6x 2中，当x ＝0时，y 有最大值0C ．二次函数y ＝ax 2图象中，开口方向与a 无关D ．不论a 是正数还是负数，抛物线y ＝ax 2(a ≠0)的顶点一定是坐标原点8. 在函数y ＝－x 2中，当－3<x <1时，则y 的取值范围是___________9．函数y ＝(m －3)xm 2－3m －2为二次函数．(1)若其图象开口向上，求函数的关系式；(2)若当x ＞0时，y 随x 的增大而减小，求函数的关系式．10．给出下列函数：①y ＝3x ；②y ＝－3x －1；③y ＝－5x 2(x <0)；④y ＝23x 2(x <0)，其中y 随x 的增大而增大的函数有( )A ．4个B ．3个C ．2个D ．1个11．函数y ＝2x 2，y ＝－3x 2，y ＝13x 2的图象的共同点是( ) A ．都关于y 轴对称，开口向上B ．都关于y 轴对称，开口向下C ．都关于原点对称，顶点在原点D ．都关于y 轴对称，顶点在原点12．如图所示，正方形ABCD 的边长为10，四个全等的小正方形的对称中心分别在正方形ABCD 的顶点上，且它们的各边与正方形ABCD 的各边平行或垂直，若小正方形的边长为x ，且0<x ≤10，阴影部分的面积为y ，则能反映y 与x 之间的函数关系的大致图象是( )13．抛物线y ＝(m ＋1)x 2上有点A (－5，2)，则它的对称点B 的坐标是___________．14．二次函数y ＝mxm 2一2有最大值，则m ＝____，当x ____时，y 随x 的增大而减小．15．如图，⊙O 的半径为3，C 1是函数y ＝12x 2的图象，C 2是函数y ＝－12x 2的图象，则阴影部分的面积是____．16．如图，请把图中图象的序号填在它的解析式后面．y ＝2x 2的图象为____．y ＝12x 2的图象为____． y ＝－x 2的图象为____．y ＝－23x 2的图象为____．17．已知抛物线y ＝ax 2经过点A (－2，－8)．(1)求抛物线的解析式；(2)当x 为何值时，y 随x 的增大而减小？(3)当x 为何值时，它有最大(小)值，是多少？18．有一条抛物线形状的隧道，隧道的最大高度为6 m ，跨度为8 m ，把它放在如图所示的平面直角坐标系中．(1)求这条抛物线所对应的函数关系式；(2)若要在离地面4.5 m 的隧道壁上，安装两盏照明灯，求两灯之间的距离．19. 如图，直线AB 过x 轴上的一点A (2，0)，且与抛物线y ＝ax 2相交于B ，C 两点，点B 的坐标为(1，1)．(1)求直线AB 和抛物线y ＝ax 2的解析式；(2)若抛物线在第一象限内有一点D ，使得S △AOD ＝S △BOC ，求点D 的坐标．答案1. B2. 下 (0，0) 高 0 大 03. 114. 1<k<325. 26. A7. C8. －9<y ≤09. 解：∵函数y ＝(m －3)xm 2－3m －2为二次函数，∴m 2－3m －2＝2，解得m ＝－1或m ＝4 (1)∵函数图象开口向上，∴m －3＞0，∴m ＝4，此时函数关系式为y ＝x 2 (2)∵当x ＞0时，y 随x 的增大而减小，∴m －3＜0，∴m ＝－1，此时函数关系式为y ＝－4x 210. C11. D12. D13. (5，2)14. －2 >015. 92π16 ④③②②17. 解：(1)y ＝－2x 2(2)x>0 (3)x ＝0，y 最大值＝018. 解：(1)y ＝－38x 2 (2)设两灯为点P 、点Q ，则它们的纵坐标为－1.5，令－38x 2＝－32，解得x 1＝－2，x 2＝2，∴两灯间的距离PQ ＝4 m。

【完整版】沪科版九年级上册数学第21章二次函数与反比例函数含答案

沪科版九年级上册数学第21章二次函数与反比例函数含答案一、单选题(共15题，共计45分)1、已知二次函数y=ax2+bx+c（a≠0）的图象如图，给出以下结论，其中正确的结论的个数是（）①abc＜2；②当x=1时，函数有最大值；③当x=-1或x=3时，函数y的值都等于0；④4a+2b+c＜0．A.1个B.2个C.3个D.4个2、下列四个命题中，其正确命题的个数是（）①若a＞b，则＞；②垂直于弦的直径平分弦；③平行四边形的对角线互相平分；④反比例函数y= ，当k＜0时，y随x的增大而增大．A.1B.2C.3D.43、已知点是一次函数的图像和反比例函数的图象的交点，当一次函数的值大于反比例函数的值时，的取值范围是（）A. 或 B. C. 或 D.4、根据二次函数y=ax2+bx+c（a≠0，a、b、c为常数）得到一些对应值，列表如下：判断一元二次方程ax2+bx+c=0的一个解x的范围是（）1x 2.2 2.3 2.4 2.5y ﹣0.76 ﹣0.11 0.56 1.25A.2.1＜x1＜2.2 B.2.2＜x1＜2.3 C.2.3＜x1＜2.4 D.2.4＜x1＜2.55、某反比例函数的图象经过点（-2,3），则此函数图象也经过（）A.（2，-3）B.（-3,3）C.（2,3）D.（-4,6）6、下列函数中，开口方向向上的是（）A.y=ax 2B.y=﹣2x 2C.D.7、已知函数y=(k-3)x2+2x+1的图象与x轴有交点，则k的取值范围是（）．A.k＜4B.k≤4C.k＜4且k≠3D.k≤4且k≠38、将抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线解析式是( ）A. B. C. D.9、二次函数y=ax2+bx+c（a≠0）的部分图象如图所示，图象过点（﹣1，0），对称轴为直线x=2，下列结论：（1）4a+b=0；（2）9a+c＞﹣3b；（3）7a﹣3b+2c＞0；（4）若点A（﹣3，y1）、点B（﹣，y2）、点C（7，y3）在该函数图象上，则y1＜y3＜y2；（5）若方程a（x+1）（x﹣5）=﹣3的两根为x1和x 2，且x1＜x2，则x1＜﹣1＜5＜x2．其中正确的结论有（）A.2个B.3个C.4个D.5个10、已知抛物线与x轴没有交点，则函数的大致图象是（）A. B. C. D.11、已知函数y1＝mx2+n，y2＝nx+m（mn≠0），则两个函数在同一坐标系中的图象可能为（）A. B. C.D.12、抛物线y=x2-4x的对称轴是 ( )A.x＝-2B.x＝4C.x＝2D.x＝-413、已知二次函数的图象如图所示，有下列4个结论，其中正确的结论是（）A. B. C. D.14、抛物线y=2（x﹣3）2+1的顶点坐标是（）A.（3，1）B.（3，﹣1）C.（﹣3，1）D.（﹣3，﹣1）15、不论x为何值时，y=ax2+bx+c恒为正值的条件是( )A.a＞0，△＞0B.a<0，△＞0C.a＞0，△＜0D.a＜0，△＜0二、填空题(共10题，共计30分)16、下列函数（其中n为常数，且n＞1）① y=（x＞0）；② y=（n﹣1）x；③ y=（x＞0）；④ y=（1﹣n）x+1；⑤ y=﹣x2+2nx（x＜0）中，y 的值随 x 的值增大而增大的函数有________个．17、若点，在反比例函数的图象上，则________ .（填“>”“<”或“=”）18、如图，在平面直角坐标系中，抛物线经过坐标原点，与轴的另一个交点为，且，过抛物线的顶点分别作轴于、轴于，则图中阴影部分图形的面积的和为________.19、一汽车在京福高速公路上由南平驶往相距170km的福州，已知它的平均速度为80km/h，则汽车距福州的路程S（km）与行驶时间t（h）的函数关系式是________20、如图，点A是反比例函数的图象上任意一点，AB∥x轴交反比例函数的图象于点B，以AB为边作，其中C，D在x轴上，若的面积为5，则k的值为________．21、将二次函数y＝x2+1的图象向左平移2个单位，再向下平移3个单位，所得二次函数解析式为________．22、如图，在直角坐标系中，，边、都在轴的正半轴上，点的坐标为，，．反比例函数的图象经过点，交边于点．则的值为________．23、定义：给定关于x的函数y，对于该函数图象上任意两点(x1， y1)，(x2， y2)，当x1＜x2时，都有y1＜y2，称该函数为增函数，根据以上定义，可以判断下面所给的函数中：①y＝2x；②y＝﹣x+1；③y＝x2(x＞0)；④y＝﹣.是增函数的有________(填上所有正确答案的序号)24、如图，矩形OABC的顶点A、C的坐标分别为（4，0）、（0，2），对角线的交点为P，反比例函数y= （k＞0）的图象经过点P，与边BA、BC分别交于点D、E，连接OD、OE、DE，则△ODE的面积为________．25、抛物线y=2x2﹣4x+m的图象的部分如图所示，则关于x的一元二次方程2x2﹣4x+m=0的解是________．三、解答题(共5题，共计25分)26、已知抛物线y＝（m﹣1）x2+（m﹣2）x﹣1与x轴相交于A、B两点，且AB ＝2，求m的值．27、在平面直角坐标系中，反比例函数y=（x＞0，k＞0）的图象经过点A（m，n），B（2，1），且n＞1，过点B作y轴的垂线，垂足为C，若△ABC的面积为2，求点A的坐标．28、已知二次函数的图象过点（0，3），顶点坐标为（﹣4，11）．（1）求这个二次函数的表达式；（2）求这个二次函数图象与x轴交点坐标．29、反比例函数与在第一象限内的图象如图所示，过x轴上点A 作y轴的平行线，与函数，的图象交点依次为P、Q两点.若PQ ＝2，求PA的长.30、己知抛物线经过点，，．求此抛物线的解析式．参考答案一、单选题(共15题，共计45分)1、C2、B3、C4、C5、A6、C7、B8、C9、B10、C11、A12、C13、C14、A15、C二、填空题(共10题，共计30分)17、18、19、20、21、22、23、24、25、三、解答题(共5题，共计25分)26、28、29、。

沪科版九年级上册数学第21章二次函数与反比例函数含答案

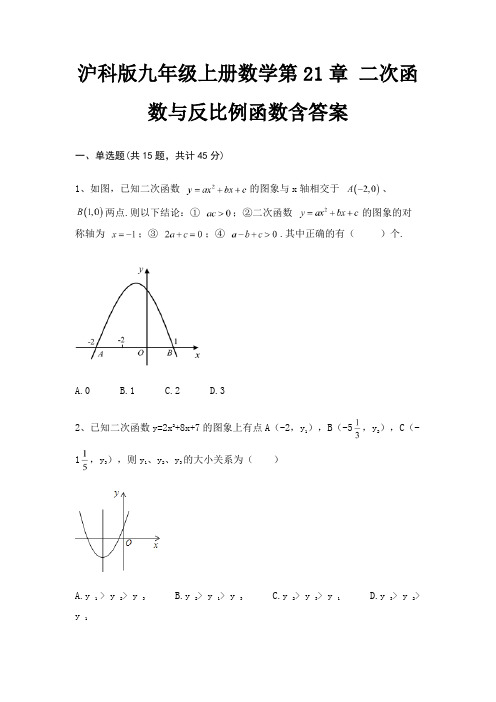
沪科版九年级上册数学第21章二次函数与反比例函数含答案一、单选题(共15题，共计45分)1、如图，已知二次函数的图象与x轴相交于、两点.则以下结论：①；②二次函数的图象的对称轴为；③；④.其中正确的有（）个.A.0B.1C.2D.32、已知二次函数y=2x2+8x+7的图象上有点A（-2，y1），B（-5，y2），C（-1，y3），则y1、y2、y3的大小关系为（）A.y1 > y2> y3B.y2> y1> y3C.y2> y3> y1D.y3> y2>y13、如图，是抛物线y＝ax2＋bx＋c(a≠0)图象的一部分，已知抛物线的对称轴为x＝2，与x轴的一个交点是(－1，0).有下列结论：①abc>0；②4a－2b＋c<0；③4a＋b＝0；④抛物线与x轴的另一个交点是(5，0)；⑤点(－3，y1)、(6，y2)都在抛物线上，则有y1<y2，其中正确的是( )A.①②③B.②④⑤C.①③④D.③④⑤4、下面四个关系中，y是x的反比例函数的是（）A. B.yx=- C.y=5x+6 D.5、如图，二次函数y＝ax2+bx+c（a≠0）的图象与x轴正半轴相交于A、B两点，与y轴相交于点C，对称轴为直线x＝2，且OA＝OC，则下列结论：①abc ＞0；②9a+3b+c＜0；③c＞﹣1；④关于x的方程ax2+bx+c＝0（a≠0）有一个根为4+c，其中正确的结论个数有（）A.1个B.2个C.3个D.4个6、若反比例函数y＝的图象经过点（1，-2），则k的值为（）A.2B.-2C.-1D.17、公元前世纪，古希腊数学家阿基米德发现了杠杆平衡，后来人们把它归纳为“杠杆原理”，即“阻力阻力臂动力动力臂”.若现在已知某一杠杆的阻力和阻力臂分别为和，则动力(单位: )关于动力臂(单位: )的函数图象大致是（）A. B. C.D.8、若A，B，C为二次函数y＝x²＋4x－5 的图象上的三点，则的大小关系是( )A. B. C. D.9、如图，二次函数y=ax2+bx+c（a≠0）的图象与x轴交于点A、B两点，与y 轴交于点C，对称轴为直线x=﹣1，点B的坐标为（1，0），则下列结论：①AB=4；②b2﹣4ac＞0；③ab＜0；④a2﹣ab+ac＜0，其中正确的结论有（）个．A.1个B.2个C.3个D.4个10、如图所示，抛物线y=ax2+bx+c（a≠0）与x轴交于点A（﹣2，0）、B （1，0），直线x=﹣0.5与此抛物线交于点C，与x轴交于点M，在直线上取点D，使MD=MC，连接AC、BC、AD、BD，某同学根据图象写出下列结论：①a﹣b=0；②当﹣2＜x＜1时，y＞0；③四边形ACBD是菱形；④9a﹣3b+c＞0 你认为其中正确的是（）A.②③④B.①②④C.①③④D.①②③11、当x取一切实数时，函数y=x2+2x+3的最小值为（）A.-2B.2C.-1D.112、一次函数y=ax+b和反比例函数y= 在同一平面直角坐标系中的图象如图所示，则二次函数y=ax2+bx+c的图象大致为（）A. B. C. D.13、一次函数y=ax+b与二次函数y=ax2+bx+c在同一坐标系中的图象可能是（）A. B. C. D.14、如图，于点A，AB交反比例函数（x＜0）的图象于点C，且，若，则k＝（）A.4B.﹣4C.2D.﹣215、下列各点在反比例函数y= 的图象上的是（）A.（1，0.5）B.（2，－1）C.（－1，－2）D.（－2，1）二、填空题(共10题，共计30分)16、在函数（为常数）的图象上有三个点，，，将，，用“”号连接为________.17、如图，在平面直角坐标系中，菱形ABCD在第一象限内，边BC与x轴平行，A，B两点的纵坐标分别为3，1，反比例函数y= 的图象经过A，B两点，则菱形ABCD的面积为________．18、反比例函数，当时，随的增大而减小，写出一个的可能值________.19、若二次函数的图象与x轴只有一个公共点，则实数n=________.20、实验表明，当导线的长度一定时，导线的电阻与它的横截面积成反比例．一条长为100 cm的导线的电阻R(Ω)与它的横截面积S(cm2)的函数图象如图所示，那么，其函数关系式为________，当S＝2 cm2时， R=________(Ω)21、如图，在平面直角坐标系中，抛物线y＝x2﹣2x﹣1交y轴于点A，过点A 作AB∥x轴交抛物线于点B，点P在抛物线上，连结PA、PB，若点P关于x轴的对称点恰好落在直线AB上，则△ABP的面积是________.22、如图，P是抛物线y=﹣x2+x+2在第一象限上的点，过点P分别向x轴和y 轴引垂线，垂足分别为A，B，则四边形OAPB周长的最大值为________．23、如图，正方形ABOC的边长为1，反比例函数过点A，则k的值是________．24、边长为1的8个正方形如图摆放在直角坐标系中，直线平分这8个正方形所组成的图形的面积，交其中两个正方形的边于，两点，过点的双曲线的一支交其中两个正方形的边于，两点，连接，，，则________.25、如图，点A在双曲线y＝上，AB⊥x轴于点B，若△ABO的面积是3，则k＝________.三、解答题(共5题，共计25分)26、已知抛物线的顶点坐标是（3，-1），与y轴的交点是（0，-4），求这个二次函数的解析式．27、已知抛物线y=（m﹣1）x2+（m﹣2）x﹣1与x轴相交于A、B两点，且AB=2，求m的值．28、如图，点A（1，a）在反比例函数y=（x＞0）的图象上，AB垂直于x 轴，垂足为点B，将△ABO沿x轴向右平移2个单位长度，得到Rt△DEF，点D 落在反比例函数y=（x＞0）的图象上．（1）求点A的坐标；（2）求k值．29、已知反比例函数y=（m为常数）的图象在一，三象限．（1）求m的取值范围；（2）如图，若该反比例函数的图象经过▱ABOD的顶点D，点A、B的坐标分别为（0，4），（﹣3，0）．①求出函数解析式；②设点P是该反比例函数图象上的一点，若OD=OP，则P点的坐标为多少？30、已知抛物线的顶点坐标为（3，-4），且过点（0，5），求抛物线的表达式 .参考答案一、单选题(共15题，共计45分)1、C2、C3、C4、B5、C6、D7、A8、B9、C11、B12、C13、B14、D15、C二、填空题(共10题，共计30分)16、17、18、19、20、21、22、23、25、三、解答题(共5题，共计25分)26、27、28、。

沪科版九年级上21.1二次函数同步测试题含答案

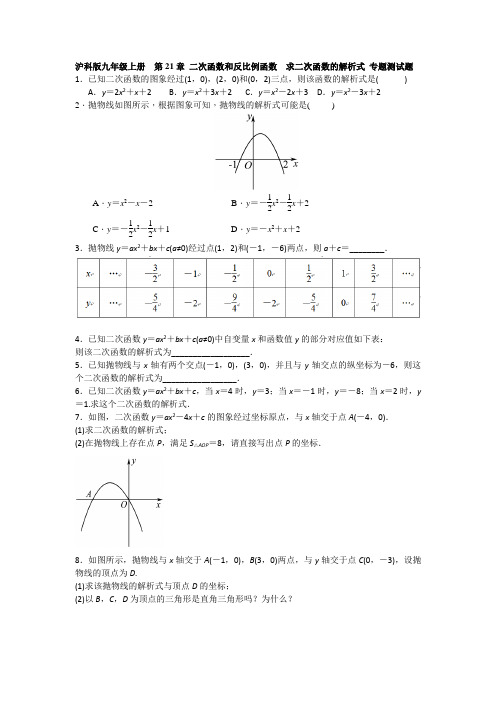
沪科版九年级上册第21章二次函数和反比例函数求二次函数的解析式专题测试题1．已知二次函数的图象经过(1，0)，(2，0)和(0，2)三点，则该函数的解析式是( )A ．y ＝2x 2＋x ＋2B ．y ＝x 2＋3x ＋2C ．y ＝x 2－2x ＋3D ．y ＝x 2－3x ＋22．抛物线如图所示，根据图象可知，抛物线的解析式可能是( )A ．y ＝x 2－x －2B ．y ＝－12x 2－12x ＋2 C ．y ＝－12x 2－12x ＋1 D ．y ＝－x 2＋x ＋2 3．抛物线y ＝ax 2＋bx ＋c (a ≠0)经过点(1，2)和(－1，－6)两点，则a ＋c ＝________．4．已知二次函数y ＝ax 2＋bx ＋c (a ≠0)中自变量x 和函数值y 的部分对应值如下表：则该二次函数的解析式为__________________．5．已知抛物线与x 轴有两个交点(－1，0)，(3，0)，并且与y 轴交点的纵坐标为－6，则这个二次函数的解析式为_________________．6．已知二次函数y ＝ax 2＋bx ＋c ，当x ＝4时，y ＝3；当x ＝－1时，y ＝－8；当x ＝2时，y ＝1.求这个二次函数的解析式．7．如图，二次函数y ＝ax 2－4x ＋c 的图象经过坐标原点，与x 轴交于点A (－4，0)．(1)求二次函数的解析式；(2)在抛物线上存在点P ，满足S △AOP ＝8，请直接写出点P 的坐标．8．如图所示，抛物线与x 轴交于A (－1，0)，B (3，0)两点，与y 轴交于点C (0，－3)，设抛物线的顶点为D .(1)求该抛物线的解析式与顶点D 的坐标；(2)以B ，C ，D 为顶点的三角形是直角三角形吗？为什么？9．已知某二次函数的图象如图所示，则这个二次函数的解析式为( )A ．y ＝2(x ＋1)2＋8B ．y ＝18(x ＋1)2－8C ．y ＝29(x －1)2＋8D ．y ＝2(x －1)2－810．一抛物线的形状、开口方向与y ＝12x 2－4x ＋3相同，顶点在(－2，1)，则此抛物线的解析式为( )A ．y ＝12(x －2)2＋1B ．y ＝12(x ＋2)2－1 C ．y ＝12(x ＋2)2＋1 D ．y ＝－12(x ＋2)2＋111．已知抛物线经过两点A (1，0)，B (0，3)，且对称轴是直线x ＝2，求其解析式．12．在平面直角坐标系内，二次函数图象的顶点为A (1，－4)，且过点B (3，0)．(1)求该二次函数的解析式；(2)将该二次函数图象向右平移几个单位，可使平移后所得图象经过坐标原点？并直接写出平移后所得图象与x 轴的另一个交点的坐标．13．把抛物线y ＝12x 2－1先向右平移1个单位，再向下平移2个单位，得到的抛物线的解析式为( )A ．y ＝12(x ＋1)2－3B ．y ＝12(x －1)2－3C ．y ＝12(x ＋1)2＋1D ．y ＝12(x －1)2＋1 14．如图所示，已知抛物线y ＝－2x 2－4x 的图象E ，将其向右平移两个单位后得到图象F .求图象F 所表示的抛物线的解析式．15．已知二次函数y ＝ax 2＋bx －3的图象经过点A (2，3)，B (－1，0)．(1)求二次函数的解析式；(2)填空：要使二次函数的图象与x 轴只有一个交点，应把图象沿y 轴向上平移______个单位．答案1. D2. D3. －24. y ＝x 2＋x －25. y ＝2x 2－4x －66. 根据题意，得⎩⎨⎧16a ＋4b ＋c ＝3，a －b ＋c ＝－8，4a ＋3b ＋c ＝1，解得a ＝－25，b ＝175，c ＝－215.∴y ＝－25x 2＋175x －215 7. (1)由已知条件得⎩⎨⎧c ＝0，a ×（－4）2－4×（－4）＋c ＝0，解得⎩⎨⎧a ＝－1，c ＝0所以，此二次函数的解析式为y ＝－x 2－4x (2)∵点A 的坐标为(－4，0)，∴AO ＝4，设点P 到x 轴的距离为h ，则S △AOP ＝12×4h ＝8，解得h ＝4，①当点P 在x 轴上方时，－x 2－4x ＝4，解得x ＝－2，所以，点P 的坐标为(－2，4)；②当点P 在x 轴下方时，－x 2－4x ＝－4，解得x 1＝－2＋22，x 2＝－2－22，所以点P 的坐标为(－2＋22，－4)或(－2－22，－4)，综上所述，点P 的坐标是(－2，4)或(－2＋22，－4)或(－2－22，－4)8. (1)设该抛物线的解析式为y ＝ax 2＋bx ＋c.由抛物线与y 轴交于点C (0，－3)，可知c ＝－3，即抛物线的解析式为y ＝ax 2＋bx －3.把点A (－1，0)，B (3，0)代入，得⎩⎨⎧a －b －3＝0，9a ＋3b －3＝0.解得a ＝1，b ＝－2，∴抛物线的解析式为y ＝x 2－2x －3.∴顶点D 的坐标为(1，－4) (2)以B ，C ，D 为顶点的三角形是直角三角形．理由如下：过点D 分别作x 轴，y 轴的垂线，垂足分别为E ，F.在Rt △BOC 中，OB ＝3，OC ＝3，∴BC 2＝18.在Rt △CDF 中，DF ＝1，CF ＝OF －OC ＝4－3＝1，∴CD 2＝2.在Rt △BDE 中，DE ＝4，BE ＝OB －OE ＝3－1＝2，∴BD 2＝20.∴BC 2＋CD 2＝BD 2.故△BCD 为直角三角形9. D10. C11. 依题意设抛物线的解析式为y ＝a (x －2)2＋k ，将A (1，0)，B (0，3)代入得⎩⎨⎧a ＋k ＝0，4a ＋k ＝3，解得⎩⎨⎧a ＝1，k ＝－1.即抛物线的解析式为y ＝(x －2)2－1＝x 2－4x ＋3 12. (1)设二次函数的解析式为y ＝a (x －1)2－4，∵二次函数图象过点B (3，0)．∴0＝4a －4，得a ＝1.∴二次函数的解析式为y ＝(x －1)2－4(2)令y ＝0，得(x －1)2－4＝0.解方程，得x 1＝3，x 2＝－1.∴二次函数图象与x 轴的两个交点坐标分别为(3，0)和(－1，0)．∴二次函数图象向右平移1个单位后所得图象经过坐标原点，平移后所得图象与x 轴的另一个交点坐标为(4，0)13. B14. 由平移知图象F 的二次项系数为－2，y ＝－2x 2－4x ＝－2(x ＋1)2＋2，顶点坐标为(－1，2)，平移后图象F 的顶点坐标为(1，2)，所以图象F 的解析式为y ＝－2(x －1)2＋215. (1) (1)∵二次函数y ＝ax 2＋bx －3的图象经过点A (2，3)，B (－1，0)，∴⎩⎨⎧4a ＋2b －3＝3，a －b －3＝0，解得⎩⎨⎧a ＝2，b ＝－1，∴二次函数的解析式为y ＝2x 2－x －3 (2)y ＝2x 2－x －3＝2(x －14)2－258，所以要使二次函数的图象与x 轴只有一个交点，应把图象沿y 轴向上平移258个单位 (2) 258。