二次函数应用(最大面积问题)
5.5二次函数应用(2)面积最大问题

当垂直于墙的边长为7.5米时,花圃
的面积最大为112.5平方米。
∴x=7.5时,S最大=112.5 ∵ 6≤x<15
(3) -2x2+30x=88
解得:x1=4
∵6≤X ≤15
,x2=11
15
∴当 6≤X ≤11时,
花圃园的面积不小于88平方米
变式:
学校要建一个生物花圃园,其中一边靠墙, 另三边用长为30米的篱笆围成,已知墙长为12 米,垂直于墙的一边的长为多少米时,这个花 圃的面积最大,并求这个最大值;
解:(1)s=x(24-4x) =-4x +24x
∵0<24-4x≤8 ∴4≤ x < 6
2
(2)y=-4x +24x =-4(x-3) 36
2
2
∵ 当 x ≥3时,y随x的增大而减小 又 4≤ x < 6
∴当X=4时,面积最大为32平方米
二次函数的应用(2)
——面积最大问题
尝试练习 如图,一边靠校园院墙(足够长),另外三边用50m长 的篱笆,围起一个长方形场地,设垂直院墙的边长为xm. (1)写出长方形场地面积y(m2)与x的函数关系式; (2)求边长为多少时,长方形面积最大,最大是多少?
(1)解:y x(50 2 x) 2 x 30 2 x 18
6 x 15
(1) y=30-2x (6 x<15) 解: (2)设花圃的面积为S:
则S=x(30-2x)=-2x2+30x
. 2 2 =-2(x -15x)=-2(x -2 . x 7.5+7.52-7.52)
=-2[(x-7.5)2-56.25]=-2(x-7.5)2+112.5
2
3.11二次函数的应用 最大面积1
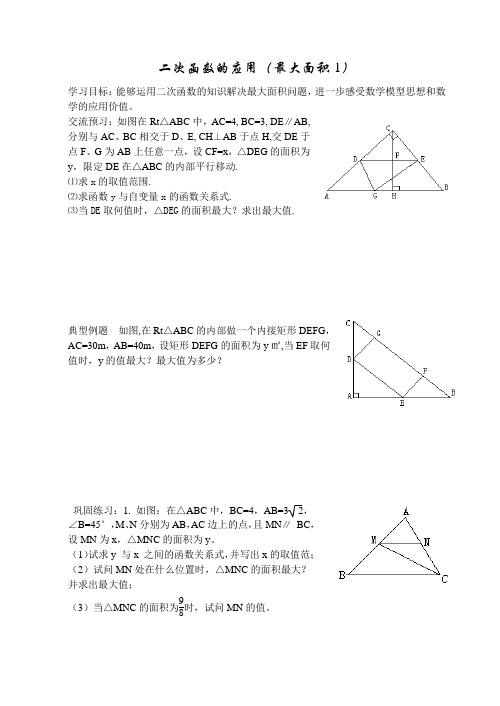
二次函数的应用(最大面积1)学习目标:能够运用二次函数的知识解决最大面积问题,进一步感受数学模型思想和数学的应用价值。
交流预习:如图在Rt △ABC 中,AC=4, BC=3, DE ∥AB,分别与AC 、BC 相交于D 、E, CH ⊥AB 于点H,交DE 于点F 、G 为AB 上任意一点,设CF=x ,△DEG 的面积为y ,限定DE 在△ABC 的内部平行移动.⑴求x 的取值范围.⑵求函数y 与自变量x 的函数关系式.⑶当DE 取何值时,△DEG 的面积最大?求出最大值.典型例题 如图,在Rt △ABC 的内部做一个内接矩形DEFG ,AC=30m ,AB=40m ,设矩形DEFG 的面积为y ㎡,当EF 取何值时,y 的值最大?最大值为多少?巩固练习:1. 如图:在△ABC 中,BC=4,AB=3 2,∠B=45°,M 、N 分别为AB ,AC 边上的点,且MN ∥ BC ,设MN 为x ,△MNC 的面积为y 。
(1)试求y 与x 之间的函数关系式,并写出x 的取值范;(2)试问MN 处在什么位置时,△MNC 的面积最大?并求出最大值;(3)当△MNC 的面积为98时,试问MN 的值。
2、要在底边BC=160, 高AD=120的△ABC铁皮余料上截取一个矩形EFGH, 使点H 在AB上,点G在AC上,点E、F在BC上,设矩形EFGH的长HG=x,宽HE=y,(1)试确定y与x之间的函数表达式.(2)当x为何值时,矩形EFGH的面积S最大?拓展延伸、如图在矩形ABCD中,AB=12cm,BC=6cm,点P沿BA从点B开始向点A以2cm/秒的速度移动;点Q沿CB边从点C开始向点B以1cm/秒的速度移动,如果P、Q同时出发,用t秒表示移动时间(0≤t≤6)那么(1)当t=2秒时,请你猜想下△QPB是个什么特殊三角形,并证明你的结论;(2)求:四边形PBQD的面积s与时间t的关系式。
利用二次函数解决面积最大问题

S x(30 x)
x
x2 30x (x 15)2 225
30-x
(0 x 30)
当x 15时,S有最大值,S 225
答:当长、宽各是15m时,羊圈的面积S最大
变式1 小孟有总长为60m的篱笆,想围成一个一边靠
墙的矩形羊圈,墙长32m,这个羊圈的长、宽各为多少
时,羊圈的面积最大,最大面积是多少?
180 135 90 45
x -1 0 3 6 9 12 15 18 21 24 27 30
小 孟
例1 小孟有总长为60m的篱笆,想围成一个矩形羊圈, 这个羊圈的长、宽各为多少时,羊圈的面积最大?
1、设 2、列式
3、范围 4、最值 5、答
解:设羊圈的面积为S,最大羊圈的 一边长为x米, 则另一边为(30 - x)米
最大面积为450m 2
变式2 小孟有总长为60m的篱笆,想围成一个一边靠 墙的矩形羊圈,墙长18m,这个羊圈的长、宽各为多少 时,羊圈的面积最大,最大面积是多少?
解:设羊圈面积为Sm2,与墙垂直的一边为x米, 则与墙垂直的一边为(60-2x)米
S x(60 2x)
x
2x 2 60x
2(x 15) 2 450
32
1、设
2、列式
3、范围
4、最值 5、答
解:设羊圈的面积为Sm 2 ,与墙垂直的一边
为x米, 则与墙平行的一边为(60 - 2x)米
S x(60 2x)
32
2x 2 60x
.
2( x
15)2
450
x
(14 x 30)
当x 15时S有最大值,S 450
x 60-2x
答:当长为30m,宽为15m时,羊圈的面积S最大,
二次函数的实际应用——面积最大(小)值问题

二次函数的实际应用——面积最大(小)值问题[例1]:在矩形ABCD 中,AB=6cm ,BC=12cm ,点P 从点A 出发,沿AB 边向点B 以1cm /s 的速度移动,同时点Q 从点B 出发沿BC 边向点C 以2cm /s 的速度移动,如果P 、Q 两点同时出发,分别到达B 、C 两点后就停止移动.(1)运动第t 秒时,△PBQ 的面积y(cm²)是多少?(2)此时五边形APQCD 的面积是S(cm²),写出S 与t 的函数关系式,并指出自变量的取值范围.(3)t 为何值时s 最小,最小值时多少?答案:6336333607266126262621)1(2222有最小值等于时;当)()()()()()(S t t S t t t t t S t t t t y =∴+-=<<+-=+--⨯=+-=⋅-=[例2]某居民小区要在一块一边靠墙(墙长15m)的空地上修建一个矩形花园ABCD ,花园的一边靠墙,另三边用总长为40m 的栅栏围成.若设花园的宽为x(m) ,花园的面积为y(m²).(1)求y 与x 之间的函数关系,并写出自变量的取值范围;(2)根据(1)中求得的函数关系式,描述其图象的变化趋势;并结合题意判断当x 取何值时,花园的面积最大,最大面积是多少?解:)240(x x y -=)20(22x x --=200)10(22+--=x∵152400≤-<x∴205.12<≤x∵二次函数的顶点不在自变量x 的范围内,而当205.12<≤x 内,y 随x 的增大而减小,∴当5.12=x 时,5.187200)105.12(22max =+--=y (平方米)答:当5.12=x 米时花园的面积最大,最大面积是187.5平方米.[例3]如图,要建一个长方形养鸡场,鸡场的一边靠墙,如果用50 m 长的篱笆围成中间有一道篱笆隔墙的养鸡场,设它的长度为x 米.(1)要使鸡场面积最大,鸡场的长度应为多少m ?(2)如果中间有n (n 是大于1的整数)道篱笆隔墙,要使鸡场面积最大,鸡场的长应为多少米?比较(1)(2)的结果,你能得到什么结论?解:(1)∵长为x 米,则宽为350x -米,设面积为S 平方米. )50(313502x x x x S --=-⋅= 3625)25(312+--=x ∴当25=x 时,3625max =S (平方米) 即:鸡场的长度为25米时,面积最大.(2) 中间有n 道篱笆,则宽为250+-n x 米,设面积为S 平方米. 则:)50(212502x x n n x x S -+-=+-⋅= 2625)25(212++-+-=n x n ∴当25=x 时,2625max +=n S (平方米) 由(1)(2)可知,无论中间有几道篱笆墙,要使面积最大,长都是25米.即:使面积最大的x 值与中间有多少道隔墙无关.。
二次函数的应用——最大面积问题教学设计

二次函数的应用——最大面积问题的教学设计一、学情分析:众所周知,二次函数与解析几何是初中数学的两个难点,而在中考中往往都是将二者融合形成综合性问题,当然也是学生一直感觉头疼的一个问题。
新课程标准指出,学生对有关的数学内容进行探索、实践和思考的过程就是数学学习的过程,也是学生获得数学活动经验的过程。
将时间还给学生、以学生为主体是每一节课的追求。
通过学生自主学习在反比例函数中求三角形时所用到的方法分享,对其中分割法中的竖直高乘以水平宽的一半进行着重分析,探究其基本原理,从而用此通法解决二次函数中三角形最大面积问题,当然重点分析此发的同时也鼓励一题多解、多解归一。
二、教学目标1、借助反比例函数中三角形面积的几种计算方法总结得出通法:“水平宽乘以竖直高的一半”。
2、通过自主学习小组合作讨论,从特殊的图形出发、层层深入让学生在探索过程中体会“水平宽乘以竖直高的一半”这一方法。
从而从本质理解“水平宽乘以竖直高的一半”。
3、运用“水平宽乘以竖直高的一半”表示出二次函数中基本三角形的面积结合二次函数的最值思想求出三角形面积的最值问题。
三、教学重难点:教学重点:运用“水平宽乘以竖直高的一半”表示出二次函数中基本三角形的面积结合二次函数的最值思想求出三角形面积的最值问题教学难点:从特殊的图形出发、层层深入让学生在探索过程中体会“水平宽乘以竖直高的一半”这一方法。
从而从本质理解“水平宽乘以竖直高的一半”。
四、教学设计【自主学习】学生课前自主完成、并在上课时小组讨论、交流并与大家分享。
的图象都引例:如图,在平面直角坐标xOy中,正比例函数y=kx的图象与反比例函数y=mx经过点A(2,﹣2).(1)分别求这两个函数的表达式;(2)将直线OA向上平移3个单位长度后与y轴交于点B,与反比例函数图象在第四象限内的交点为C,连接AB,AC,求点C的坐标及△ABC的面积.方法提炼:补:补成矩形减去三个直角三角形。
补:延长CA与y轴交于点D,用三角形BCD面积减去三角形BAD面积。
二次函数应用几何图形的最大面积问题教学课件

求解极值点
通过求导数并令其为0,找到函 数的极值点。
确定最大面积
根据极值点和单调性,确定几 何图形的最大面积对应的点。
05
练习题与答案解析
练习题
01
02
03
题目1
一个矩形ABCD的面积为 12,其中AB=2,求BC的 最大值。
题目2
一个直角三角形ABC的面 积为6,其中∠C=90°, AC=3,求BC的最大值。
详细描述
首先设定三角形的底和高为二次函数 的变量,然后根据二次函数的性质, 找到使面积最大的底和高的值。
利用二次函数求圆形面积的最大值
总结词
通过设定圆的半径为二次函数的变量 ,利用二次函数的性质求圆的最大面 积。
详细描述
首先设定圆的半径为二次函数的变量 ,然后根据二次函数的性质,找到使 面积最大的半径的值。
02
几何图形可以由二次函数图像与x 轴、y轴的交点确定,进而形成三 角形、矩形、平行四边形等。
二次函数的最值与几何图形面积的关系
二次函数的最值出现在顶点处,此时 对应的x值为函数的零点或对称轴。
几何图形面积的最大值或最小值出现 在二次函数最值处,可以通过求导数 或配方法找到最值点。Βιβλιοθήκη 02常见几何图形面积公式
题目3
一个等腰三角形ABC的面 积为10,其中AB=AC, ∠B=45°,求BC的最大值 。
答案解析
解析1
设BC=x,则矩形的面积可以表 示为2x=12,解得x=6。由于AB 已经给定为2,所以BC的最大值
为6。
解析2
设BC=x,则直角三角形的面积 可以表示为1/2×3x=6,解得 x=4。由于AC已经给定为3,所
二次函数求面积最大值

二次函数求面积最大值二次函数是高中数学中比较重要的一章内容,它在数学和物理中都有广泛的应用。
其中,求二次函数的最值是一个常见的问题,而二次函数求面积最大值也是其中一个重要的应用。
一、二次函数的基本概念二次函数是形如y=ax+bx+c的函数,其中a、b、c是实数且a≠0。
二次函数的图像是一条开口向上或向下的抛物线,其顶点坐标为(-b/2a, c-b/4a)。
二、二次函数求面积最大值的问题对于给定的二次函数y=ax+bx+c,我们要求其在区间[a, b]上的面积最大值。
这个问题可以转化为求y=ax+bx+c在区间[a, b]上的最大值和最小值,然后再利用定积分求解。
三、求二次函数的最值我们知道,二次函数的最值只可能出现在其顶点处,因此我们可以先求出二次函数的顶点坐标,然后再判断其是否在区间[a, b]内。
对于y=ax+bx+c,其顶点坐标为(-b/2a, c-b/4a)。
如果顶点坐标不在区间[a, b]内,则最值出现在区间端点处,即y(a)和y(b)中的较大值。
四、利用定积分求解面积最大值已知y=ax+bx+c在区间[a, b]上的最大值和最小值,我们可以利用定积分求解其面积最大值。
设y=ax+bx+c在区间[a, b]上的最大值和最小值分别为y1和y2,则其面积最大值为∫[a, b] (y1-y2)dx。
五、例题解析下面通过一个例题来说明如何利用二次函数求面积最大值。
例1:求函数y=-x+4x+5在区间[0, 4]上的面积最大值。
首先,求出该函数的顶点坐标:x0 = -b/2a = -4/(-2) = 2y0 = -x0+4x0+5 = -4+8+5 = 9因为顶点坐标(2, 9)在区间[0, 4]内,所以函数的最值为y(2)=9。
然后,利用定积分求解面积最大值:∫[0, 4] (y(2)-y)dx = ∫[0, 4] (9+x-4x)dx = 20/3因此,函数y=-x+4x+5在区间[0, 4]上的面积最大值为20/3。
二次函数的应用——面积最大问题》说课稿—获奖说课稿

二次函数的应用——面积最大问题》说课稿—获奖说课稿22.过程与方法:培养学生利用所学知识构建数学模型,解决实际问题的能力,掌握建模思想,熟练掌握最值问题的解法。
23.情感态度与价值观:通过实际问题的应用,让学生感受到数学在生活中的实际应用价值,培养学生对数学的兴趣和热爱。
本节课的重点是最值问题的解法和建模思想的培养,难点是对实际问题的分析和建模思想的掌握。
三、教学方法的选择本节课采用“引导发现、归纳总结、启发式教学”等多种教学方法,其中引导发现法是本节课的核心教学方法,通过引导学生发现实际问题中的规律和模式,培养学生独立思考和解决问题的能力;归纳总结法是巩固知识的有效方法,通过对学生已有的知识进行梳理和总结,加深对知识的理解和记忆;启发式教学法则是在教学中采用启发式问题,激发学生的思考和求知欲,提高学生的研究兴趣和积极性。
四、教学过程的设计本节课的教学过程分为四个环节:导入、讲授、练、归纳总结。
导入环节通过引入实际问题,激发学生的兴趣和求知欲,让学生认识到最值问题的实际应用价值;讲授环节通过具体例子和图像分析,讲解最值问题的解法和建模思想;练环节则通过多种形式的练,巩固学生的知识和技能;归纳总结环节则对本节课的知识点进行总结和梳理,加深对知识的理解和记忆。
五、教学效果预测通过本节课的教学,学生将能够掌握最值问题的解法和建模思想,能够熟练应用所学知识解决实际问题,同时也能够感受到数学在生活中的实际应用价值,培养学生对数学的兴趣和热爱,为学生今后的研究打下坚实的理论和思想方法基础。
2、___要在一块长为20米、宽为15米的空地上建一个长方形花园,他想让花园的面积最大,你能帮他算一下最大面积是多少吗?3、某公司生产一种产品,销售价格为每个10元,生产成本为每个5元,每天能生产1000个,你能帮助他们算一下每天的最大利润是多少吗?设计思路]通过这三个问题,引导学生发现实际问题中的最值问题,从而引出二次函数的最值问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、教学过程
AB 和AD 分别在两直角边上,1、如图。
在一个直角三角形的内部画一个矩形ABCD,其中
AN=40m, AM=30m
(1)设矩形的一边AB= xm,那么 AD 边的长度如何表示?
(2)设矩形的面积为ym2,当x 取何值时,y 的最大值是多少?
(二)变式探究
【探究一】在上一个问题中,如果把矩形改成如图所示的位置,其顶点 A 和顶点 D 分别在两直角边上, BC 在斜边上,其他条件不变,那么矩形的最大面积是什么?
【探究二】如图,已知△ABC是一等腰三角形铁板余料,AB=AC=20cm, BC=24cm,若在
△ABC 上,截出一零件 DEFG,使得 EF在 BC上,点 D、G 分别在边 AB、AC上,问矩形 DEFG 的最大面积是多少?
(三)课下作业
1、如图,在一面靠墙的空地上用长为24 米的篱笆,围成中间隔有两道篱笆的长方形花圃,
设花圃的宽AB 为 x 米,面积S 平方米
(1)求 S 与 x 的函数关系式及自变量的取值范围;
(2)当 x 取何值时所围成的花圃面积最大,最大值是多少?
(3)若墙的最大利用长度为8 米,求此时围成花圃的最大面积和最小面积分别是多少?
2、如图, AD 是△ ABC的高, BC=60cm,AD=40cm,点 P,Q 是 BC边上的点,点 S 在 AB 边上,点 R 在 AC 边上,四边形 SPQR是矩形,求矩形 SPQR面积最大值
BC、 CD 上的两个动点,当M 点在BC 上运动时,3、正方形ABCD边长为 4, M 、N 分别是
保持 AM和MN垂直
(1)证明: RT△ ABM∽ RT△ MCN
(2)设 BM=x,梯形 ABCN 的面积为y,求y与x之间的函数关系式:当 M 点运动到什么位
置时,
(3)四边形ABCN 面积最大,并求出最大面积
4、在矩形 ABCD中, AB=6cm, BC=12cm,点 P 从点 A 出发沿 AB 向点 B 以 1cm/s 的速度移动,同时同时点 Q 从点 B 出发沿 BC边向点 C 以 2cm/s 的速度移动 ,如果 P、Q 两点在分别到达 B、 C 两点后就停止运动 ,回答下列问题:
(1)运动开始后第多少秒时 ,三角形 PBQ的面积等于 8 平方厘米;
(2)设运动开始后第 t 秒时 ,五边形 APQCD的面积为 S 平方厘米 ,写出 S 与 t 的函数关系式 ,
并指出自变量t 的取值范围;
(3) t 为何值时S 最小 ?求出 S 的最小值 .。
