2.3 系统的传递函数方框图及其简化
2.3 传递函数的方块图表示及运算

闭环控制系统方块图
(1)前向通路传递函数--假设N(s)=0 打开反馈后,输出X0(s)与Xi(s)之比。等价于X0(s) 与误差E(s)之比 X 0 ( s) G1 ( s)G2 ( s) G( s) E ( s)
2.3.2 闭环控制系统的方块图
(2)反馈回路传递函数 假设N(s)=0
主反馈信号B(s) 与输出信号X0(s) 之比。 B( s) H ( s ) 当H(s)=1时,系统叫单位反馈系统。 X 0 (s)
图2-30
G5 G2 G3 G4
R(s)
G7
串联和并联
G5
G6
G1
C(s)
-
H1G2
H2
1 G5
G5 G6 1 G5 H 2
G7 G1G5 G1 (G2 G3 G4 ) C ( s) G( s) R( s ) 1 G7 1 G5 H 2 G1 H1G2 G1G5 1 (G2 G3 G4 )(G1 H 2 ) G1 H1G2
R(s) G(s) (b)
C(s)
图2-24 环节的并联连接
2.3.4 方块图的简化-等效变换 (2)并联连接
C (s) C1 (s) C2 (s) C3 (s) G1 (s) R(s) G2 (s) R(s) G3 (s) R(s) [G1 (s) G2 (s) G3 (s)]R(s)
2.3.4 方块图的简化-等效变换 为了由系统的方块图方便地写出它的闭环传递 函数,通常需要对方块图进行等效变换。方块图的 等效变换必须遵守一个原则,即变换前后输入输出 之间总的数学关系保持不变。 1、框图的连接方式及运算法则 在控制系统中,任何复杂系统主要由响应环节的方 块经串联、并联和反馈三种基本形式连接而成。三 种基本形式的等效法则一定要掌握。
自动控制原理第四次课—传递函数及结构图简化

Mm(s)=CmIa(s)
Eb(s)=Kbsm(s)
J s2 m (s)=M m fsm (s)
c(s) = 1i m(s)
r (s)
e (s) Ks Us(s)
K Ua(s) a
1 Las Ra
c (s)
Eb(s)
Ia(s)
Cm Mm(s)
精选2021版课件
26
系统各元部件的动态结构图(6)
式的连接称为并联连接。
精选2021版课件
17
3. 反馈连接
R(s)
-
C(s) G(s)
H(s)
一个方框的输出信号输入到另一个方框后,得 到的输出再返回到这个方框的输入端,构成输 入信号的一部分。这种连接形式称为反馈连接。
精选2021版课件
18
三、系统动态结构图的构成
• 构成原则:
按照动态结构图的基本连接形式,构 成系统的各个环节,连接成系统的动 态结构图。
31
1. 串联结构的等效变换(2)
• 等效变换证明推导
R(s)
U(s)
G1(s)
G2(s) C(s)
U (s)= G 1 (s)R C ( (s s ) )= G 2 (s)U (s)
精选2021版课件
32
1. 串联结构的等效变换(3)
• 等效变换证明推导
R(s)
U(s)
C(s)
G1(s)
G2(s)
Ua(s)=KaUs(s) Ua(s)=RaIa(s)LasIa(s)
Eb(s)
Eb(s)=Kbsm(s)
J s2 m (s)=M m fsm (s)
c(s) = 1i m(s)
r (s)
e (s) K s Us(s) c (s)
机械控制工程基础2.3系统的传递函数方框图及其简化

X(s) X(s) X(s)
2011年9月
第 5 页/53
机电汽车工程学院
Block diagram establishing
2、系统方框图的建立
建立系统方框图的步骤如下:
(1) 建立系统(或元件)的原始微分方程; (2) 对这些原始微分方程进行Laplace变换,并根据各变换 式中的因果关系,绘出相应的方框图; (3) 按照信号在系统中传递、变换的过程,依次将各传递函 数方框图连接起来(同一变量的信号通路连接在一起),系 统输入量置于左端。输出量置于右端,便得到系统的传递 函数方框图。
X(s)
+
Kq
_
Q(s)
P(s) A Y(s)
1/Kc
ms2 cs
(c)
As
2011年9月
第 12 页/53
机电汽车工程学院
例2:如图2.1.2所示电枢控制式直流时机,由第2.1节例2的
推导可知其运动微分方程可列写如下:
练习题: Ldia dt
ia R ed
ua
ed kd
输入:Ua(s), ML(s)
Q(s)
(c)
P(s)
1/Kc
P(s) A Y(s) ms2 cs
(a)
Q(s) As Y(s)
输入:X(s) 输出:Y(2s0) 11年9月 中间变量:P(s) Q(s)
(b)
第 11 页/53
机电汽车工程学院
最后,将上述各传递函数方框图按信号的传递关系连接起 来,便得到下图所示的系统的传递函数的方框图。
Ur(s) +
I(s)
Uc(s)
1/R
机械控制工程基础2.3系统的传递函数方框图及其简化

Xi(s)
E(s)
G(s)
+
—
+ H(s)
B(s)
Xo(s)
Xi(s)
G(s)
Xo(s)
1 G(s)H(s)
等效
反馈环节等效变换
2011年9月
第 24 页/53
机电汽车工程学院
Xi(s)
E(s)
G(s)
Xo(s)
+
—
+ H(s)
B(s)
图中G(s)称为前向通道传递函数,它是输出Xo(s)与偏差
E(s) 之比。即
第 13 页/53
机电汽车工程学院
按各变量的因果关系,分别绘出上述各式的传递函数方框 图,如图所示。
Ua(s) +
_
Ed(s)
M(s) +
_
ML(s)
1 Ia(s) (s)
Ls R
(a)
1 (s) Ia(s)
Js
(c)
2011年9月
第 14 页/53
Kd Ed(s)
(b)
Km M(s)
(d)
机电汽车工程学院
两个环节相并联等效框图
Xi(s)
G1(s) G2(s)
Xo(s)
2011年9月
第 23 页/53
机电汽车工程学院
Feedback 3.方框图的反馈联接及其等效规则
如图所示称为反馈联接,实际上它也是闭环系统传递 函数方框图的最基本形式。单输入作用的闭环系统,无论 组成系统的环节有多复杂,其传递函数方框图总可以简化 成右图所示的基本形式。
输出:(s)
J
d
dt
M
ML
机械工程控制基础知识总结
()o x ∞时所需的时间4nξω≈当增加系统的型别时,系统的准确性将提高。
当系统采用增加开环传递函数中积分环节的数0]或滞后0]的特性。
正负:正值:逆时针方向;负值:顺时针方向幅频特性()A ω和相频特性()ϕω的总称|()|G j e ω=是将()G s90对数幅频特性曲线:在整个频率范围内是一的直线。
当90的水平线。
ω=时,90对数幅频特性曲线:在整个频率范围内是一直线当90的水平线。
、将系统的传递函数准形式的环节的传递函数(即惯性、一阶微0,00a ;、三阶系统(3)n =稳定的充要条件:0,00a ,120a a 。
、在Routh 表中任意一行的第一个元为零,后各元均不为零或部分不为零:用一个很小的正ε来代替第一列等于零的元,然后计算表的其余各元;、当Routh 表的任意一行中的所有元均为零:用该行的上一行的元构成一个辅助多项式,并用180开始向上。
j-(1,0)180开始向下。
+∞时,在开环对数幅频特性曲线为正值的频率范围内,开环对数180线正穿越与负穿越次数之时,闭环系统稳定;否则不稳定。
g ω,则闭环系统稳定;g ω,则闭环系统不稳定;g ω=,则闭环系统临界稳定;为剪切频率0)时,相频特性180线的相位差值γ。
(ϕω+对于稳定系统,γ必在Bode 180线以上。
:对于稳定系统,自:第三象限。
180线以下。
:对于稳定系统,自:第二象限。
0)时,开环幅频的倒数。
()|H j K ω记0;:对于稳定系统,1。
右侧通过。
:对于稳定系统,K 必在0分贝线以0;:对于稳定系统,1。
左侧通过。
线以上;分贝线以下。
8086汇编指令速查手册一、数据传输指令它们在存贮器和寄存器、寄存器和输入输出端口之间传送数据.1. 通用数据传送指令.MOV 传送字或字节.MOVSX 先符号扩展,再传送.MOVZX 先零扩展,再传送.PUSH 把字压入堆栈.POP 把字弹出堆栈.PUSHA 把AX,CX,DX,BX,SP,BP,SI,DI依次压入堆栈.POPA 把DI,SI,BP,SP,BX,DX,CX,AX依次弹出堆栈.PUSHAD 把EAX,ECX,EDX,EBX,ESP,EBP,ESI,EDI依次压入堆栈.POPAD 把EDI,ESI,EBP,ESP,EBX,EDX,ECX,EAX依次弹出堆栈.BSWAP 交换32位寄存器里字节的顺序XCHG 交换字或字节.( 至少有一个操作数为寄存器,段寄存器不可作为操作数)CMPXCHG 比较并交换操作数.( 第二个操作数必须为累加器AL/AX/EAX )XADD 先交换再累加.( 结果在第一个操作数里 )XLAT 字节查表转换.── BX 指向一张 256 字节的表的起点, AL 为表的索引值(0-255,即0-FFH); 返回 AL 为查表结果. ( [BX+AL]->AL )2. 输入输出端口传送指令.IN I/O端口输入. ( 语法: IN 累加器, {端口号│DX} )OUT I/O端口输出. ( 语法: OUT {端口号│DX},累加器 ) 输入输出端口由立即方式指定时, 其范围是 0-255; 由寄存器 DX 指定时,其范围是 0-65535.3. 目的地址传送指令.LEA 装入有效地址.例: LEA DX,string ;把偏移地址存到DX.LDS 传送目标指针,把指针内容装入DS.例: LDS SI,string ;把段地址:偏移地址存到DS:SI.LES 传送目标指针,把指针内容装入ES.例: LES DI,string ;把段地址:偏移地址存到ES:DI.LFS 传送目标指针,把指针内容装入FS.例: LFS DI,string ;把段地址:偏移地址存到FS:DI.LGS 传送目标指针,把指针内容装入GS.例: LGS DI,string ;把段地址:偏移地址存到GS:DI.LSS 传送目标指针,把指针内容装入SS.例: LSS DI,string ;把段地址:偏移地址存到SS:DI.4. 标志传送指令.LAHF 标志寄存器传送,把标志装入AH.SAHF 标志寄存器传送,把AH内容装入标志寄存器.PUSHF 标志入栈.POPF 标志出栈.PUSHD 32位标志入栈.POPD 32位标志出栈.二、算术运算指令ADD 加法.ADC 带进位加法.INC 加 1.AAA 加法的ASCII码调整.DAA 加法的十进制调整.SUB 减法.SBB 带借位减法.DEC 减 1.NEC 求反(以 0 减之).CMP 比较.(两操作数作减法,仅修改标志位,不回送结果).AAS 减法的ASCII码调整.DAS 减法的十进制调整.MUL 无符号乘法.IMUL 整数乘法.以上两条,结果回送AH和AL(字节运算),或DX和AX(字运算), AAM 乘法的ASCII码调整.DIV 无符号除法.IDIV 整数除法.以上两条,结果回送:商回送AL,余数回送AH, (字节运算);或商回送AX,余数回送DX, (字运算).AAD 除法的ASCII码调整.CBW 字节转换为字. (把AL中字节的符号扩展到AH中去)CWD 字转换为双字. (把AX中的字的符号扩展到DX中去)CWDE 字转换为双字. (把AX中的字符号扩展到EAX中去)CDQ 双字扩展. (把EAX中的字的符号扩展到EDX中去) 三、逻辑运算指令AND 与运算.OR 或运算.XOR 异或运算.NOT 取反.TEST 测试.(两操作数作与运算,仅修改标志位,不回送结果). SHL 逻辑左移.SAL 算术左移.(=SHL)SHR 逻辑右移.SAR 算术右移.(=SHR)ROL 循环左移.ROR 循环右移.RCL 通过进位的循环左移.RCR 通过进位的循环右移.以上八种移位指令,其移位次数可达255次.移位一次时, 可直接用操作码. 如 SHL AX,1.移位>1次时, 则由寄存器CL给出移位次数.如 MOV CL,04SHL AX,CL四、串指令DS:SI 源串段寄存器 :源串变址.ES:DI 目标串段寄存器:目标串变址.CX 重复次数计数器.AL/AX 扫描值.D标志 0表示重复操作中SI和DI应自动增量; 1表示应自动减量.Z标志用来控制扫描或比较操作的结束.MOVS 串传送.( MOVSB 传送字符. MOVSW 传送字. MOVSD 传送双字. )CMPS 串比较.( CMPSB 比较字符. CMPSW 比较字. )SCAS 串扫描.把AL或AX的内容与目标串作比较,比较结果反映在标志位.LODS 装入串.把源串中的元素(字或字节)逐一装入AL或AX中.( LODSB 传送字符. LODSW 传送字. LODSD 传送双字. )STOS 保存串.是LODS的逆过程.REP 当CX/ECX<>0时重复.REPE/REPZ 当ZF=1或比较结果相等,且CX/ECX<>0时重复.REPNE/REPNZ 当ZF=0或比较结果不相等,且CX/ECX<>0时重复. REPC 当CF=1且CX/ECX<>0时重复.REPNC 当CF=0且CX/ECX<>0时重复.五、程序转移指令1>无条件转移指令 (长转移)JMP 无条件转移指令CALL 过程调用RET/RETF过程返回.2>条件转移指令 (短转移,-128到+127的距离内)( 当且仅当(SF XOR OF)=1时,OP1<OP2 )JA/JNBE 不小于或不等于时转移.JAE/JNB 大于或等于转移.JB/JNAE 小于转移.JBE/JNA 小于或等于转移.以上四条,测试无符号整数运算的结果(标志C和Z).JG/JNLE 大于转移.JGE/JNL 大于或等于转移.JL/JNGE 小于转移.JLE/JNG 小于或等于转移.以上四条,测试带符号整数运算的结果(标志S,O和Z).JE/JZ 等于转移.JNE/JNZ 不等于时转移.JC 有进位时转移.JNC 无进位时转移.JNO 不溢出时转移.JNP/JPO 奇偶性为奇数时转移.JNS 符号位为 "0" 时转移.JO 溢出转移.JP/JPE 奇偶性为偶数时转移.JS 符号位为 "1" 时转移.3>循环控制指令(短转移)LOOP CX不为零时循环.LOOPE/LOOPZ CX不为零且标志Z=1时循环.LOOPNE/LOOPNZ CX不为零且标志Z=0时循环.JCXZ CX为零时转移.JECXZ ECX为零时转移.4>中断指令INT 中断指令INTO 溢出中断IRET 中断返回5>处理器控制指令HLT 处理器暂停, 直到出现中断或复位信号才继续.WAIT 当芯片引线TEST为高电平时使CPU进入等待状态. ESC 转换到外处理器.LOCK 封锁总线.NOP 空操作.STC 置进位标志位.CLC 清进位标志位.CMC 进位标志取反.STD 置方向标志位.CLD 清方向标志位.STI 置中断允许位.CLI 清中断允许位.六、伪指令DW 定义字(2字节).PROC 定义过程.ENDP 过程结束.SEGMENT 定义段.ASSUME 建立段寄存器寻址. ENDS 段结束.END 程序结束.。
233控制系统方框图的化简及传递函数
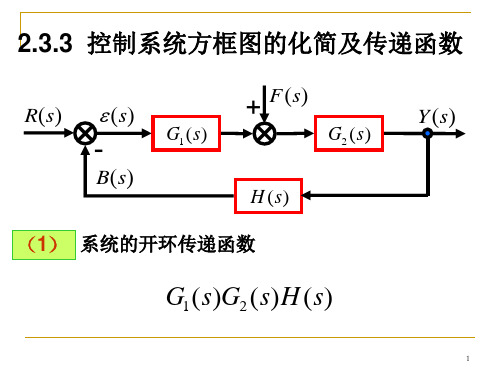
U 2 ( s)
22
两个相加点互相交换移动
U1 ( s )
A
-
-
1 R1
1 sC1
1 R2C2 s 1
R1C2 s
U 2 ( s)
U1 ( s )
A
-
-
1 R1
1 sC1
1 R2C2 s 1
R1C2 s
U 2 ( s)
23
小回路化简
U1 ( s ) A
-
-
1 R1
1 sC1
1 R2C2 s 1
12
结论
下列闭环传递函数
(s)
F ( s)
(s)
F ( s )
具有相同的特征多项式
13
闭环特征多项式:
1 G1 (s)G2 (s) H (s)
14
G1 (s)G2 (s) (s) 1 G1 (s)G2 (s) H (s)
输出对输入 对 比
G2 (s) F ( s) 1 G1 (s)G2 (s) H (s)
R( s )
+
E ( s )
G1 ( s )
G2 (s)
Y ( s)
35
G3 ( s) G1 ( s)
R( s )
+
E ( s )
G1 ( s )
G2 (s)
Y ( s)
小回路化简
R( s )
G1 ( s) G3 ( s) G1 ( s)
G1 ( s)G2 ( s) 1 G1 ( s)G2 ( s)
1 G2 ( s)G3 ( s) 1 G1 ( s)G2 ( s)
E (s)
E ( s) 1 G2 (s)G3 (s) R(s) 1 G1 (s)G2 (s)
# 23传递函数方块图(系统动态结构图)及其等效变换

– F4(s)
1 F3(s) 1 Xo(s) X o (s) F3 ( s) — K2 K2
sf F4 ( s) sX o ( s) f F3 ( s) k2
F3(s)
S2f/k2 Sf/k2
F4(s)
Xi(s)
–
Sf2 F4(s) —— K2 – F1(s) F2(s) F(s) Sf1 1 Xo(s) —— — K1 K1 F3(s) K2 +
例一、直流电动机动态结构图的绘制 解: U ( s ) R i La dia E a a a b
dt
M m Cmia d m dm J f Mm ML 2 dt dt
2
dm Eb K b dt
求拉氏变换并用元件方块图表示出信号间的 关系得:
U a ( s) Ra I a ( s) La SIa ( s) Eb ( s) U a ( s) Eb ( s) I a ( s) Ra La S
U a K AU S dia U a Ra ia La Eb dt M m Cm ia
d 2m dm J f Mm ML 2 dt dt 1 c m i dm Eb K b dt
求它们的拉氏变换并用方块图表示得:
e (s) r (s) c (s)
U2(s)
–
1 I2(s) — R E0(s)
3
1 E0 ( s ) I 2 ( s ) CS
I2(s)
E0(s) 1 — CS
# 2—5 传递函数方块图(系统动态结构图) 及其等效变换 最后的方块图为: I2(s) Ei(s)
– U2(s)
1 — R1
I(s)
系统传递函数方框图及其简化

X1 X2
X1 X 2 X 3
分支点 系统方框图的建立步骤
同一信号向不同方向传递
建立系统各元部件的微分方程,明确信号的因果关系(输入/ 输出)。 对上述微分方程进行拉氏变换,绘制各部件的方框图。 按照信号在系统中的传递、变换过程,依次将各部件的方框 图连接起来,得到系统的方框图。
2
示例 无源RC网络
4
传递函数的等效 变化
1.串联传递函数等于各相串传函之积。
Xi(s) X(s)
G1(S)
G2(S)
X o(s)
X i(s)
G1(S) G2(S)
n
X o(s)
X ( s ) X o ( s ) X ( s ) G (s)G (s) G (s) o 2 1 X i (s) X (s) X i (s)
X1 +
+ (-)
G ( s)
1 G (s)
X3
X2
前移:从G(s)的输出端移到输入端;
后移:从G(s)的输入端移到输出端。
注意:分支 点和相加点 之间不能相 互移动。
9
例:求下图所示系统的传递函数。
H2(s) Xi(s)
+
B
G1(s)
H1(s)
G2(s)
G3(s)
A Xo(s)
H3(s)
X o (s)[1 G(s)H (s)] H (s) X i (s)
X o ( s) G( s) G( s) GB ( s) X i (s) 1 G ( s ) H ( s ) 1 Gk ( s )
7
讨论: 单位反馈:H(s)=1
Xi(s) + -
控制工程-系统传递函数方块图及其简化

比较点: x 1 方框: x i (s)
x x2 G(s)
信号从某点分开,信号相加减(相减必须标注负号)
x o(s)
表示输入和输出信号的传递关系
§2-4 系统传递函数方块图及其简化
南华大学
二、环节的串联、并联的等效规则
1.环节的串联
Xi(s)
G1(s) X1(s) G2(s)
X0(s) G(s) = X0 (s) = X0 (s) X1(s)
s 1
) +
G1( s G1(Gs1()
) GG22((ss)) sG)2G( 2s ()Hs )(Hs
()
s
)
且 XG0N1((ss))=HN( s()s )>G> N1( s )
=
N≈
(Ns
() s1)+GG1(
G12( s ) s ) GH2((ss))H(
s
)
δ
N
(
s
)
系统抗干扰性较强
§2-4 系统传递函数方块图及其简化
Xi (s)
X i (s)
+ X0(s) +
若这里的+改为 -的话?
= G1 (s) + G2 (s)
n
G(s) = Gi (s)
i =1
§2-4 系统传递函数方块图及其简化
南华大学
三、开环与闭环传递函数
xi(t)
ε(t)
g x0(t)
-
xb(t)
h
Xi(s)
E(s)
G(s)
-
XB(s)
H(s)
1 G1
G1G2·G3 1-G1G2H1
E
F X0
第2章4传递函数方块图及其化简ppt课件

G1
+ (+-)
A G1
G2 AG2
AG1 AG1+ AG2
++
1 G1
G2 AG2
A G1
1 G1
AG1 AG2
G2 + +
分支点移动 A G2
1 G2
AG1 AG1+ AG2 G1 + +
AG2
(2)反馈化成单位反馈
A+ -
G1 A G1 1 + G1G2
A1+
G2
-
G1
G1 G2 1+ G1G2
(3)根据因果关系,确定各个原始微分方程分中的输入量与 输出量,并将拉斯变换的结果表示成传递函数方框图的形 式;
(4)按信号的传递过程,依次将上述各个方框图连接起来, 构成整个系统的传递函数方框图,一般输入在左边,输出 在右边。
jik 04
2
例2: 绘制电枢控制式直流电动机的传递函数
方框图 。
R
i1 (t)
G1 +
G2 +
1 G3
-A
G3
Xo(s)
C
H2
H1
H3
Xi 1(s)
+
-
G1 +
G2
-
1 G3
G3 1+H2 G3
Xo(s)
C
略
H1
jik 04
15
X (s) 0 求 Xo(s) 。令
Xi2(s)
i1
Xi 1(s)
H3
+
-
-
G1 B +
G2
,
Xi
机械工程控制基础(2)

2.2 系统的传递函数
(4)传递函数有无量纲和取何种量纲,取决于系统输出的量 纲与输入的量纲。 (5)不同用途、不同物理组成的不同类型系统、环节或元件, 可以具有相同形式的传递函数。 (6)传递函数非常适用于对单输入、单输出线性定常系统的 动态特性进行描述。但对于多输入、多输出系统,需要对 不同的输入量和输出量分别求传递函数。另外,系统传递 函数只表示系统输入量和输出量的数学关系(描述系统的 外部特性),而未表示系统中间变量之间的关系(描述系 统的内部特性)。针对这个局限性,在现代控制理论中, 往往采用状态空间描述法对系统的动态特性进行描述。
量的方程式; (4).将与输入有关的项写在微分方程的右边,与输出有关的项写在微
分方程的左边,并且各阶导数项按降幂排列。 在列写微分方程的各步中,关键在于掌握组成系统的各个元件
或环节所遵循的有关定律。对于机械类的学生,往往需要列写机 械系统和电网络系统的微分方程,因此,有必要掌握常见元件的 物理定律。
系统的零初始条件有两方面的含义,一是指在t=0-时输入Xi(t) 才开始作用于系统,因此, t=0-时, Xi(t)及其各阶导数均为零; 二是指在t=0-时系统处于相对静止的状态,即系统在工作点上运 行,因此t=0-时,输出X0(t)及其各阶导数也均为零。现实的工程 控制系统多属此类情况。
2.2 系统的传递函数
2.2 系统的传递函数
二、传递函数的零点、极点和放大系数 传递函数是一个复变函数,一般具有零点、极点。根据复变函数知
识,凡能使复变函数为0的点均称为零点;凡能使复变函数为趋于∞的 点均称为极点。
若将传递函数写成如下的形式:
则,s=zj (j=1,2,…,m)为传递函数的零点,s=pj (j=1,2,…,n)为传递函 数的极点,而将K称为系统的放大系数。传递函数的零点和极点的分布 影响系统的动态性能。一般极点影响系统的稳定性,零点影响系统的瞬 态响应曲线的形状。系统的放大系数决定了系统的稳态输出值。因此, 对系统的研究可变成对系统传递函数的零点、极点和放大系数的研究。
2.3 系统的传递函数方框图及其简化

X (s)
G (s)
b. 相加点后移
X 1 ( s)
X (s)
X 2 ( s)
G (s)
X 1 ( s)
X 2 ( s)
X 1 ( s)
X1 (s) X 2 (s) X (s)G(s)
X (s)
G (s)
X1 (s) [ X (s) X 2 (s)]G(s)
1 JLs2 JRs km ka
( s )
【例】
解 按图2-22所示的步骤,利用环 节串联、并联和反馈连接合并的规 则进行。多层回环的处理按由内向 外的顺序依次进行变换。得:
【例 】
4.分支点移动的规则
a.分支点前移
X (s)
G (s)
b.分支点后移
X (s)
G (s)
X1 (s) G(s) X (s) X 2 ( s)
X o ( s) GB ( s) X i ( s)
注意:我们所指的前向通道的传递函数、反馈回路的 传递函数和开环传递函数都是针对一个闭环系统而 言的。它们都是闭环系统的一部分。系统闭环传递 函数是闭环系统的传递函数。看一个传递函数是什 么具体类型,要从定义出发,而不能只看其符号。
系统闭环传递函数
2)相加点
相加点是信号之间代数求和运算的图解表示.在相 加点处,输出信号(离开相加点的箭头表示)等于各 输入信号(指向相加点的箭头表示)的代数和,每一 个指向相加点的箭头前方的+号或-号表示信号在 代数运算时的符号.必须是具有相同量纲的.
X 1 ( s)
X 1 ( s) X 2 ( s)
X 2 ( s)
E ( s)
d
2.3系统的传递函数方框图及其简化

2.3 系统的传递函数方框图及其简化
二、传递函数方框图的化简:等效化简,变换前后输入输出数学关系不变 例 教材图2.3.13化简(p53)
(1)相加点前移
(2)小环回路化为单一传递函数
2.3 系统的传递函数方框图及其简化
二、传递函数方框图的化简:等效化简,变换前后输入输出数学关系不变 例 教材图2.3.13化简(p53)
G (s )
H (s )
B(s)
由于B(s)与E(s)在相加点的量纲相同,因此开环传递函数无量纲。因此,G(s) 与H(s)的量纲互为倒数。
2.3 系统的传递函数方框图及其简化
二、传递函数方框图的化简:等效化简,变换前后输入输出数学关系不变 3. 反馈连接及其等效规则 闭环传递函数:
由图可知:
GB ( s ) X o (s) X i (s)
反馈环节
闭环传递函数为输出信号Xo(s)与输入信号Xi(s)之比 G(s) 1 G ( s) H ( s)
从而,可得闭环传递函数为
注:若相加点B(s) 处为负号时,闭环传递函数分母G(s)H(s)前为正号; 若相加点B(s) 处为正号时,闭环传递函数分母G(s)H(s)前为负号;
2.3 系统的传递函数方框图及其简化
一、传递函数方框图的建立
• 3、方框图的结构要素
(1)函数方框
X i (s)
G (s )
X o (s)
X o (s) G(s) X i (s)
函数方块具有运算功能,是传递函数的图解表示 输出信号的量纲等于输入信号的量纲与传递函数的量纲的 乘积。
2.3 系统的传递函数方框图及其简化
一、传递函数方框图的建立
2.3 系统的传递函数方框图及其简化
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
km
M ( s)
M L ( s)
1 Js
( s )
kd
E (s)
d
1
M L ( s)
-1
1 ( Ls R )
I a (s)
km
M ( s)
M L ( s)
1 Js
( s )
kd
Ed (s)
1 Js
M L ( s)
( s )
Ed (s)
kd km Ls R
M L ( s)
X ( s) X 1 ( s) X 2 ( s) X 3 ( s)
b.相加点之合并与拆分
X 1 ( s)
X (s)
X 2 ( s ) X 3 ( s)
X 1 ( s)
X (s)
X 3 ( s)
X 2 ( s)
7. 分支点变换的其他规则
a.分支点之间相互交换
X (s) X (s) X (s) X (s) X (s) X (s) X (s) X (s)
前向通道传递函数 G ( s ) 与反馈回路传递函数 H ( s )
的乘积定义为开环传递函数 GK (s) B( s) GK ( s ) G ( s ) H ( S ) E ( s)
前向通道传递函数 G ( s ) 与反馈回路传递函数 H ( s ) 的乘积定义为开环传递函数 GK (s) B( s) GK ( s ) G ( s ) H ( s ) E (s) 无量纲. 系统闭环传递函数
2.3 系统的传递函数方框图及其简化
一、传递函数方框图
一个系统可由若干个环节按一定的关系组成,将这些环 节用方框表示,其间用相应的变量及信号流向联系起来, 就构成系统的传递函数方框图. 可以形象地表示系统的内部情况及各环节、变量之间 的关系; 可以由局部环节的方框图联成整个系统的方框图,再 将其简化,以便写出系统的传递函数; 可以揭示和评价每个环节对系统的影响.
X o ( s)
X i ( s)
B( s )
G (s) 1 G (s)
X o ( s)
U a ( s)
例
1 ( Ls R )
I a (s)
km
M ( s)
M L ( s)
1 Js
( s )
Ed (s)
kd
( s ) 为输出时,令 M L (s) 0
I a (s) 1 ( Ls R )
M ( s)
U a ( s)
E ( s)
d
L
1 ( Ls R )
I a (s)
( s )
kd
km
Ed (s)
M ( s)
U a ( s)
M ( s)
Ed (s)
1 Js
( s )
I a (s)
M ( s)
I a (s) 1 ( Ls R )
km
M ( s)
M L ( s)
“实质上是一种数学模型.”
1.方框图的结构要素
1)函数方框
由方框及指向方框的箭头和离开方框的箭头三 个部分组成.其中,方框表示环节的传递函数,指 向方框的箭头表示输入的Laplace变换;离开方 框的箭头表示输出的Laplace变换.
X i ( s)
G (s)
X o ( s)
X o (s) G(s) X i (s)
X1 (s) G(s) X (s)
X 2 ( s) X ( s)
X (s)
G (s)
X1 (s) G(s) X (s)
X (s)
G (s)
X1 (s) G(s) X (s)
G (s)
X 2 (s) G(s) X (s)
1 / G ( s)
X 2 ( s) X ( s)
5. 相加点移动的规则
X o ( s) GB ( s) X i ( s)
注意:我们所指的前向通道的传递函数、反馈回路的 传递函数和开环传递函数都是针对一个闭环系统而 言的。它们都是闭环系统的一部分。系统闭环传递 函数是闭环系统的传递函数。看一个传递函数是什 么具体类型,要从定义出发,而不能只看其符号。
系统闭环传递函数
B( s) 前向通道传递函数
E(s) X i (s) B(s)
G ( s ) 前向通道传递函数 X o (s) G ( s) E (s)
X i ( s) E ( s ) G ( s )
X o ( s)
B( s )
H (s)
B( s) H ( s ) 反馈回路传递函数 H ( s ) X o ( s)
a.相加点前移
X (s)
G (s)
b. 相加点后移
X 1 ( s)
X (s)
X 2 ( s)
G (s)
X 1 ( s)
X 2 ( s)
X 1 ( s)
X1 (s) X 2 (s) X (s)G(s)
X (s)
G (s)
X1 (s) [ X (s) X 2 (s)]G(s)
X (s)
G (s) G (s)
X 1 ( s) X 2 ( s)
1 / G ( s)
X 2 ( s)
6. 相加点变换的其他规则
a.相加点之间相互交换
X 1 ( s)
X (s)
X 1 ( s)
X (s)
X 2 ( s ) X 3 ( s)
X ( s) X ( s ) 2 3
X i ( s)
G (s)
X o ( s)
例1
R( s )
G1
G2
G
H2
H4
3
G4
G5
G6
C (s)
H1
1 G2
H4
R( s )
G1
( Ls R) I a (s) Ed (s) U a (s)
Ed (s) kd (s)
J ( s) km I a ( s)
1 I a (s) [U a ( s) Ed ( s)] ( Ls R)
U a ( s)
1 Js
( s )
kd
二、传递函数方框图的等效变换
1.串联环节的等效变换规则 前一环节的输出为后一环节输入的联接方式成为 环节的串联.若各个环节之间不存在负载效应时,则 串联联接后的传递函数为各个环节传递函数之积.
X i ( s)
G1 ( s )
G( s)
X 1 ( s)
G2 (s)
X o ( s) GB ( s) X i ( s)
X i ( s) E ( s ) G ( s )
X o ( s)
B( s )
由图可知
H (s)
E ( s) X i ( s) B( s) X i ( s) X o ( s) H ( s) X o ( s ) G ( s ) E ( s ) G ( s )[ X i ( s ) X o ( s ) H ( s )] G (s) X i (s) G (s) X o (s) H (s) 由此可得: X o (s) G (s) G (s) GB ( s ) X i (s) 1 G (s) H (s) 1 G (s) H (s)
1 JLs2 JRs km ka
( s )
【例】
解 按图2-22所示的步骤,利用环 节串联、并联和反馈连接合并的规 则进行。多层回环的处理按由内向 外的顺序依次进行变换。得:
【例 】
4.分支点移动的规则
a.分支点前移
X (s)
G (s)
b.分支点后移
X (s)
G (s)
X1 (s) G(s) X (s) X 2 ( s)
3)分支点
分支点表示同一信号向不同方向的传递,在分支 点引出的信号不仅量纲相同,而且数值也相等.
X 1 ( s) X 1 ( s) X 1 ( s)
2.建立系统方框图的步骤
1)建立系统元件的原始微分方程; 2)分别对上述微分方程在初始条件为零的条 件下进行Laplace变换,并根据各Laplace变 换的因果关系,分别绘出各自的方框图; 3)按照信号在系统中传递、变换的过程,依 次将上述各个传递函数方框图连接起来 (同一变量的信号通路连在一起),系统 的输入量置于左端,输出量置于右端,便 得到系统的传递函数方框图。
X 1 ( s) X 2 ( s)
X 1 ( s)
X 2 ( s)
X 1 ( s) X 2 ( s)
X 2 ( s)
一般应避免分支点和相加点之间的相互移动
三、方框图简化的一般方法 (法1)
1.确定系统的输入量和输出量.若作用在系统上的输 入量或输出量有多个,则必须分别对每一输入量,逐个 进行方框图的简化,以求得各自的传递函数. 2.若方框图中有交叉连接,则利用分支点或相加点的 移动规则,将交叉消除,简化成无交叉的多回路方框图 的形式.(大回路套小回路) 3.对多回路方框图,按照先里后外的顺序依次对各个 回路进行简化. 4.写出系统的传递函数.
2)相加点
相加点是信号之间代数求和运算的图解表示.在相 加点处,输出信号(离开相加点的箭头表示)等于各 输入信号(指向相加点的箭头表示)的代数和,每一 个指向相加点的箭头前方的+号或-号表示信号在 代数运算时的符号.必须是具有相同量纲的.
X 1 ( s)
