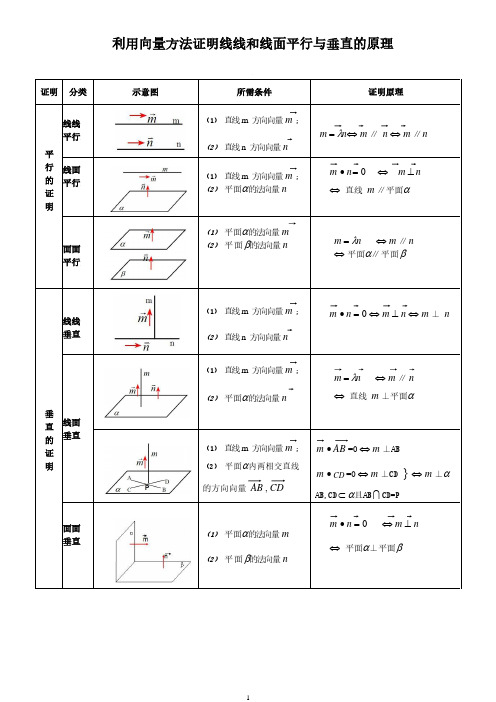
用空间向量证明线线垂直与线面垂直

第二节 用空间向量证明线线垂直与线面垂直

一、空间向量及其数量积

1、 在空间，既有大小又有方向的量称为空间向量。用AB 或a 表示，其中向量的大小称为向量的长度或

或a

。正如平面向量可用坐标(x,y.)表示，空间向量也可用坐标(x,y,z)表示。若已知点A 坐标为（x 1，y 1，z 1）,点B 坐标为（x 2，y 2，z 2） 则向量AB =（x 2 -x 1，y 2- y 1，z 2 -z 1

在空间，知道向量=（x

，y ，z

2、 空间向量数量积

① 已知两个非零向量a 、b a 与b 的

夹角，记作＜a ，b ＞规定，若0a ⊥。

② 已知空间两个向量、COS

例１ 1B 1、A 1C 1中点，若BC=CA=CC 1，

C 1

B 1 Ａ1

Ａ

Ｃ

Ｂ D 1 E 1

练习：已知正方体ABCD —1111D C B A 中，11E B =11F D =4

1

1B A ，求向量1BE 与1DF 所成角的余弦值。

二 、利用向量证线线垂直与线面垂直

例2 在正方体ABCD —1111D C B A 中，求证A 1C ⊥平面AB 1D 1

P 为DD 1的中点，

例3 如图，PA ⊥矩形ABCD 所在平面，M, N 分别是AB ,PC 中点 （1）求证：M N ⊥CD

E D A 1

F

D 1

A

B 1

C B

C 1 P

N

（2）若∠PDA=450，求证：MN ⊥平面PCD

练习：正方体ABCD —1111D C B A 中，M 是棱D 1D

P 为棱A 1B 1上任一点。求证：NP ⊥AM

作业：

1.如图，正方体ABCD —1111D C B A 中，E 是BB 1中点，O 求证：O E ⊥平面D 1AC.

2.如图，正方体ABCD —1111D C B A 中，O ,M 分别是BD 1, AA 1中点，求证：OM 是异面直线AA 1和BD 1的公垂线.

3、如图，直三棱柱ABC-—A 1B 1C 1中，∠ACB=900

，AC=1，CB=2，侧棱AA 1=1，，侧面AA 1B 1B 的两

条对角线交点为D ，B 1C 1的中点为M 。求证：CD ⊥平面BDM

A 1

A

C 1

O

M

B 1

A 1

D

C

B

A

C 1

D 1

4在棱长为a 的正方体ABCD —1111D C B A 中，E ， F 分别为棱AB 和BC 的中点，M 为棱B 1B

上任一点，当MB

M

B 1值为多少时能使D 1M ⊥平面EFB 1

5、如图， ABC 为正三角形，AE 和CD 都垂直于平面ABC ，且AE=AB=2a ， CD=a ，F 为BE 中点，求证：A F ⊥BD

6、如图，已知直三棱柱ABC-A 1B 1C 1中B 1C 1=A 1C 1，A 1B ⊥AC 1。 求证：A 1B ⊥B 1C

F

E D C B A

Ａ

Ｃ

Ｂ

第三节 利用空间向量求二面角及证明面面垂直

一、二面角

二面角 l ，若 的一个法向量为m ， 的一个法向量为n ，则|

|||,cos n m n m

，二面角的

大小为 n m ,或 n m ,

例1．如图，正三棱柱111C B A ABC 中，E 为

BB 的中点，B A AA ，求平面EC A 与平面111C B A 所成锐角的大小。

例2．（05年全国）如图，在四棱锥V-ABCD ,平面V AD ⊥底面

（1）证明（2）求面

ABCD 求二面角B

二．证面面垂直

若平面 的一个法向量为m ，平面 的一个法向量为n ，且n m ，则 。

例3．在四棱锥P-ABCD 中，侧面PCD 是正三角形，且与底面ABCD 垂直，已知底面是面积为32的菱形，

060 ADC ，M 是PB 的中点。

（1）求证：CD PA

（2）求二面角D AB P 的度数； （3）求证：平面 PAB 平面CDM 。

练习：（04年辽宁）已知四棱锥P-ABCD 中，底面ABCD 是菱形，平面ABCD ，PD=AD ，点E 为AB 的中点，点F 为 PD 的中点。

（1）证明平面PED ⊥平面PAB ；

（2）求二面角P-AB-F 的平面角的余弦值.

作业：

1．（04年广东）如图，在长方体1111D C B A ABCD 中，已知F E AA AD AB ,,2,3,41 分别是线段BC AB ,上的点，且1 FB EB 。 （Ⅰ）求二面角C-DE-C 1的正切值；

（Ⅱ）求直线EC 1与FD 1所成角的余弦值。

D

A

A

C

A

M

A

B

P

A

F E

P

D

C

B

A

2．（05年全国）已知四棱锥P-ABCD 的底面为直角梯形，AB ∥DC ， PA DAB ,90

底面ABCD ，且PA=AD=DC=

2

1

AB=1，M 是PB 的中点。 （1）证明：面PAD ⊥面PCD ； （2）求AC 与PB 所成的角；

（3）求面AMC 与面BMC 所成二面角的大小。

3．已知四棱锥P-ABCD 的底面是边长为2的正方形，侧棱 PA 底面ABCD ，PA ＝2，M 、N 分别是AD 、BC 的中点，PD MQ 于Q

（1）求证：平面PMN 平面PAD ；

（2）求PM 与平面PCD 所成角的正弦值； （3）求二面角Q MN P 的余弦值。

4．（06年全国）如图，在直三棱柱ABC －A 1B 1C 1中，AB ＝BC ， D 、E 分别为BB 1、AC 1的中点．

（1）证明：ED 为异面直线BB 1与AC 1的公垂线； （2）设AA 1＝AC ＝2AB ，求二面角A 1－AD －C 1的大小．

B

C

D

E

A 1

B 1

C 1

N N

M

Q

A

P

D

C

B